Experimental Study on the Influence of New Permeable Spur Dikes on Local Scour of Navigation Channel
Abstract
1. Introduction
2. Materials and Methods
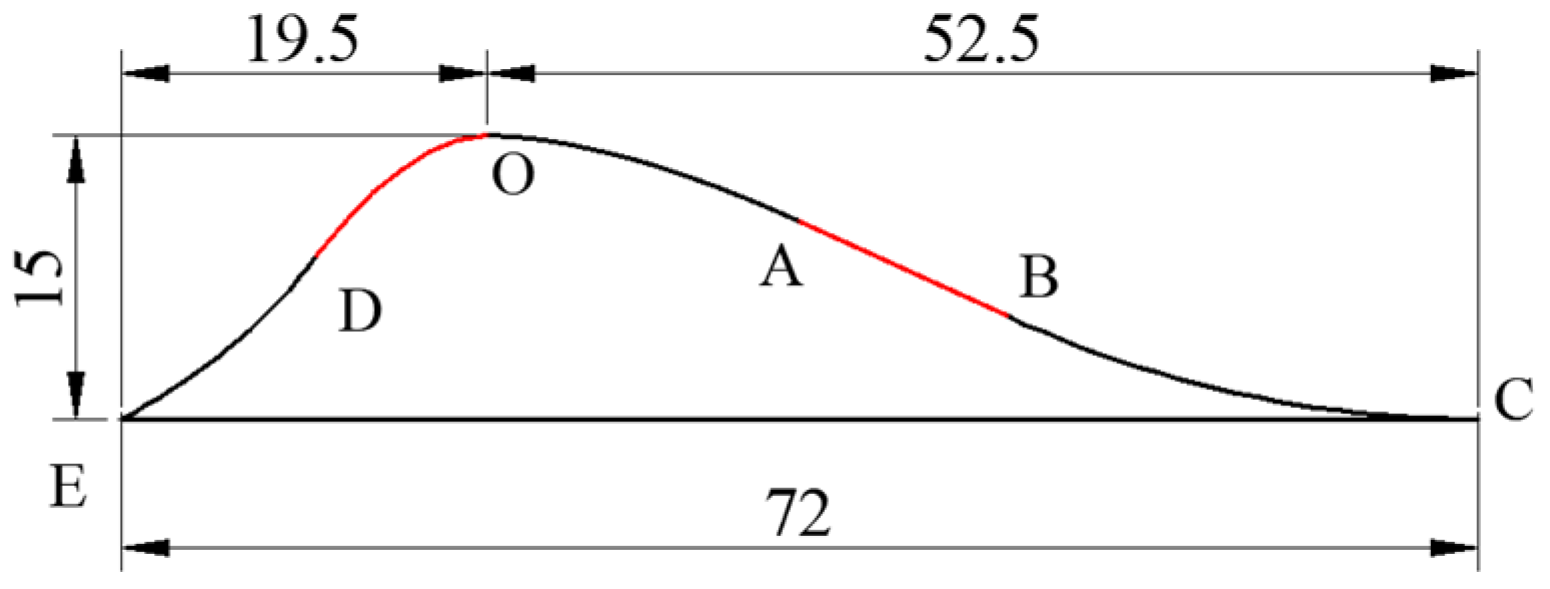
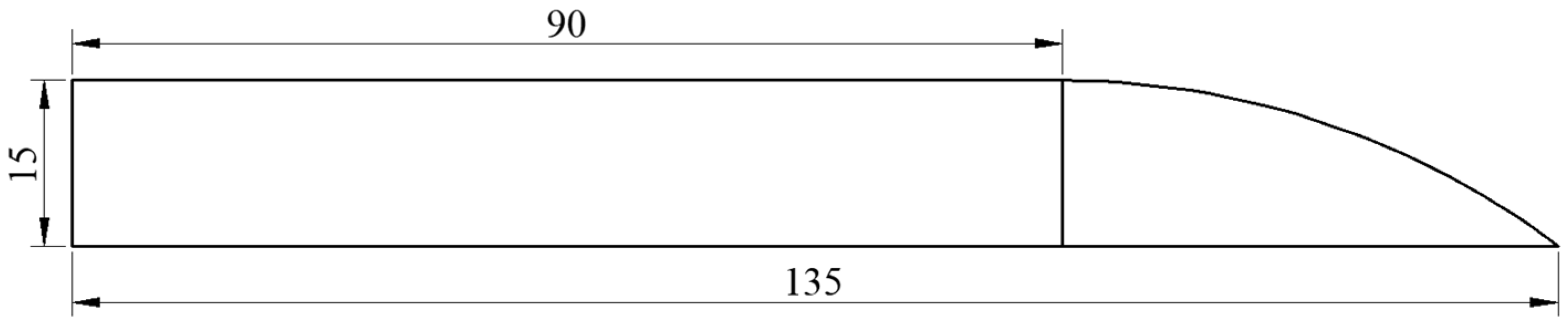
2.1. Rock-Fill Spur Dike Model Design
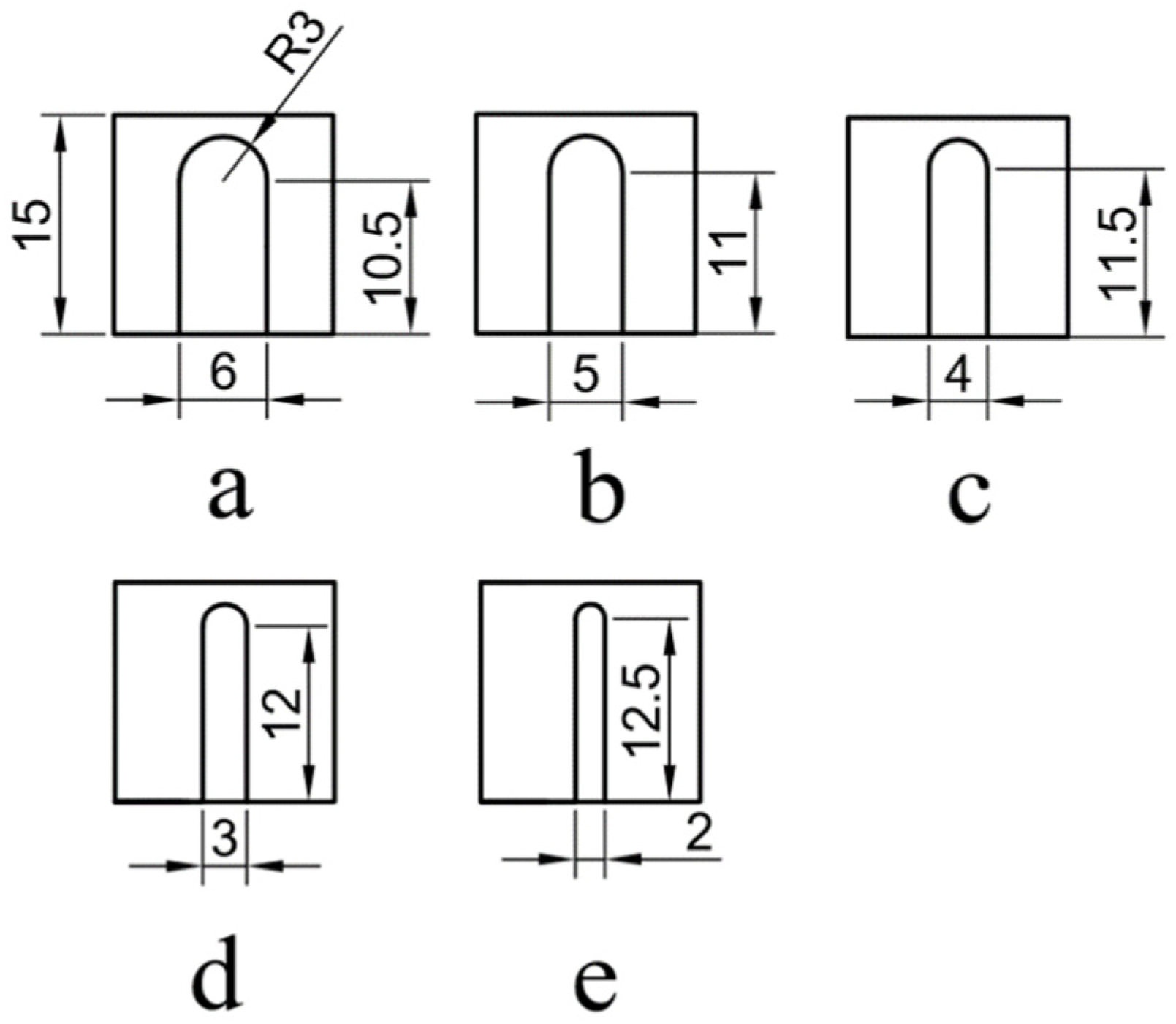
2.2. New Permeable Spur Dike Model Design
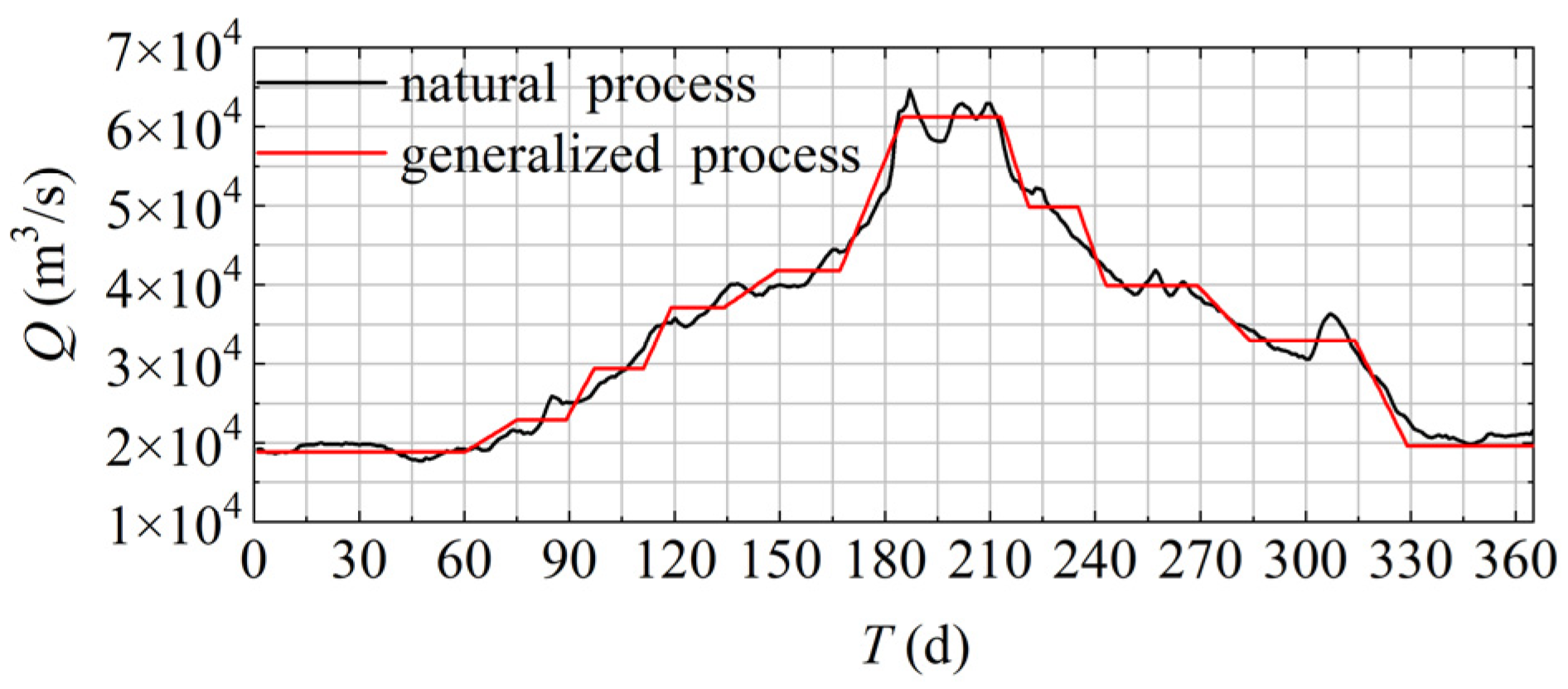
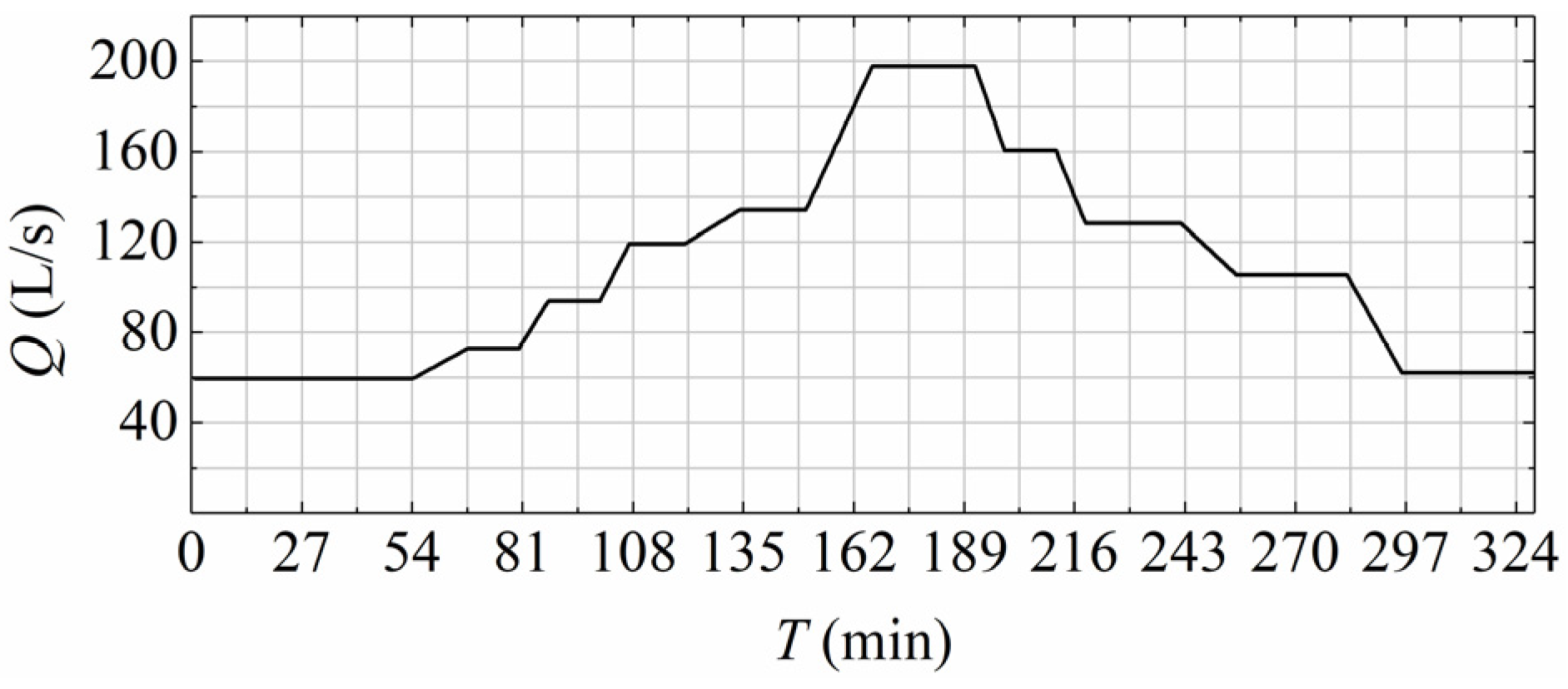
2.3. Flow Process Design
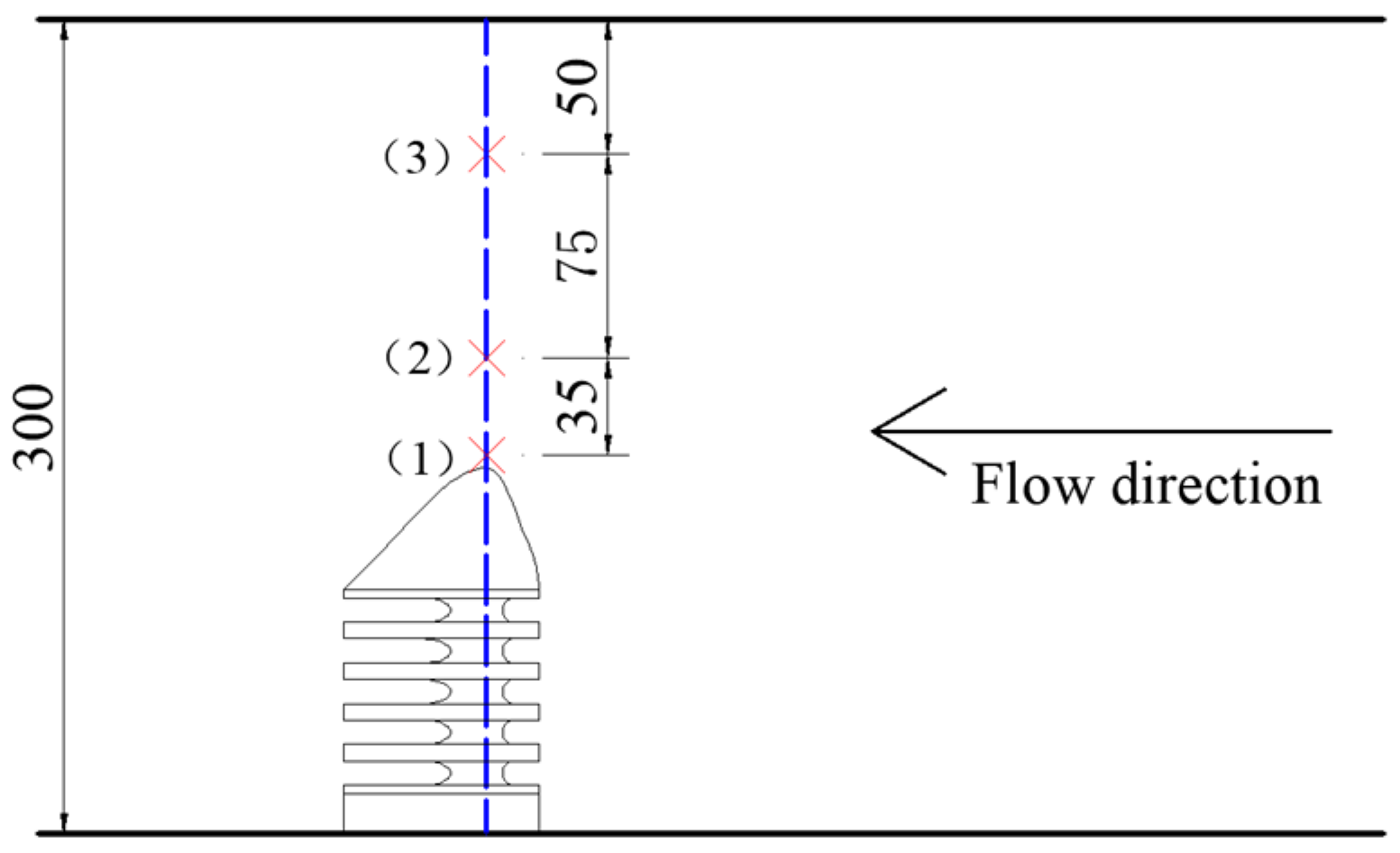
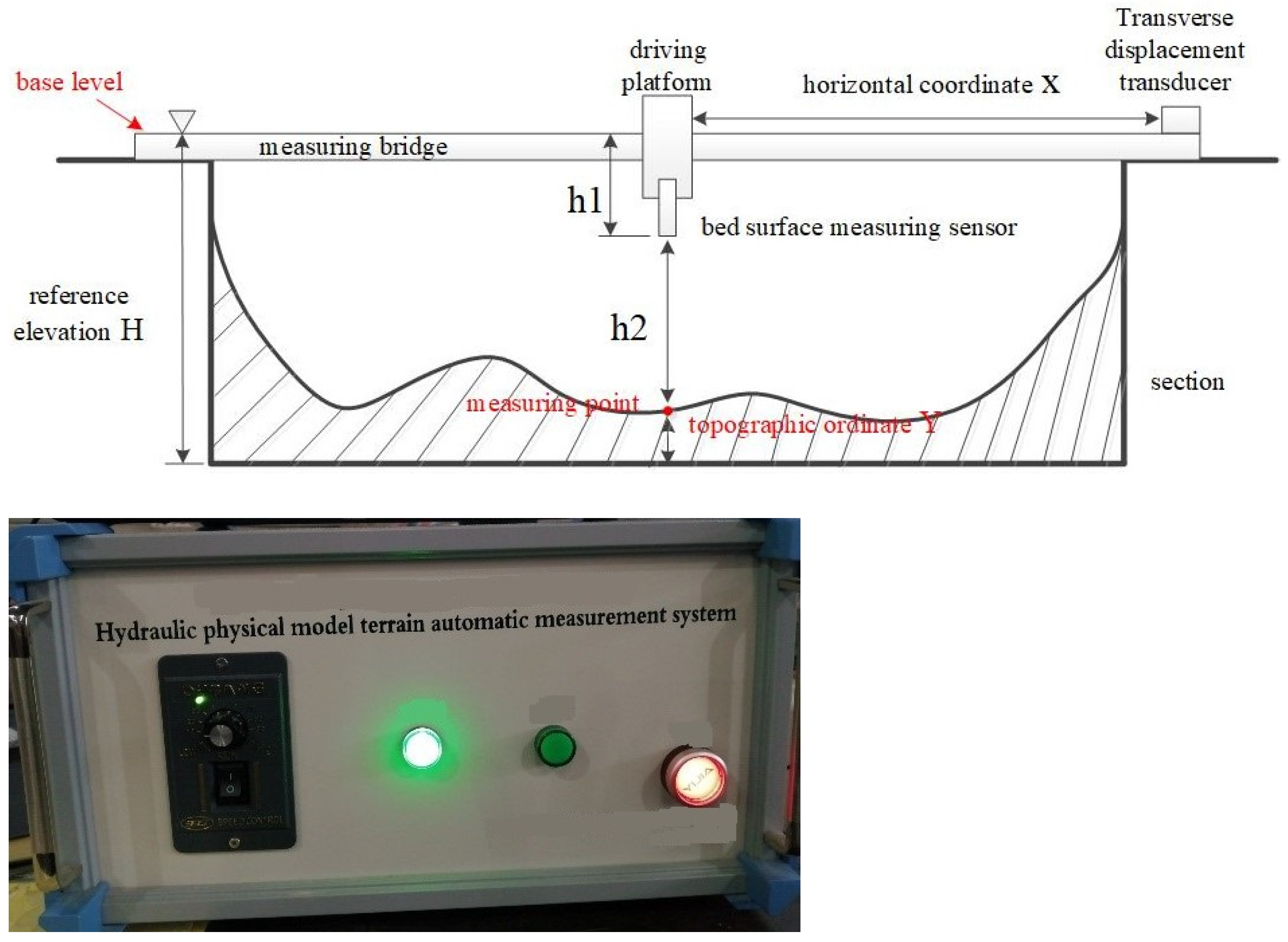
2.4. Flow Velocity and Topographic Measuring Equipment
3. Results
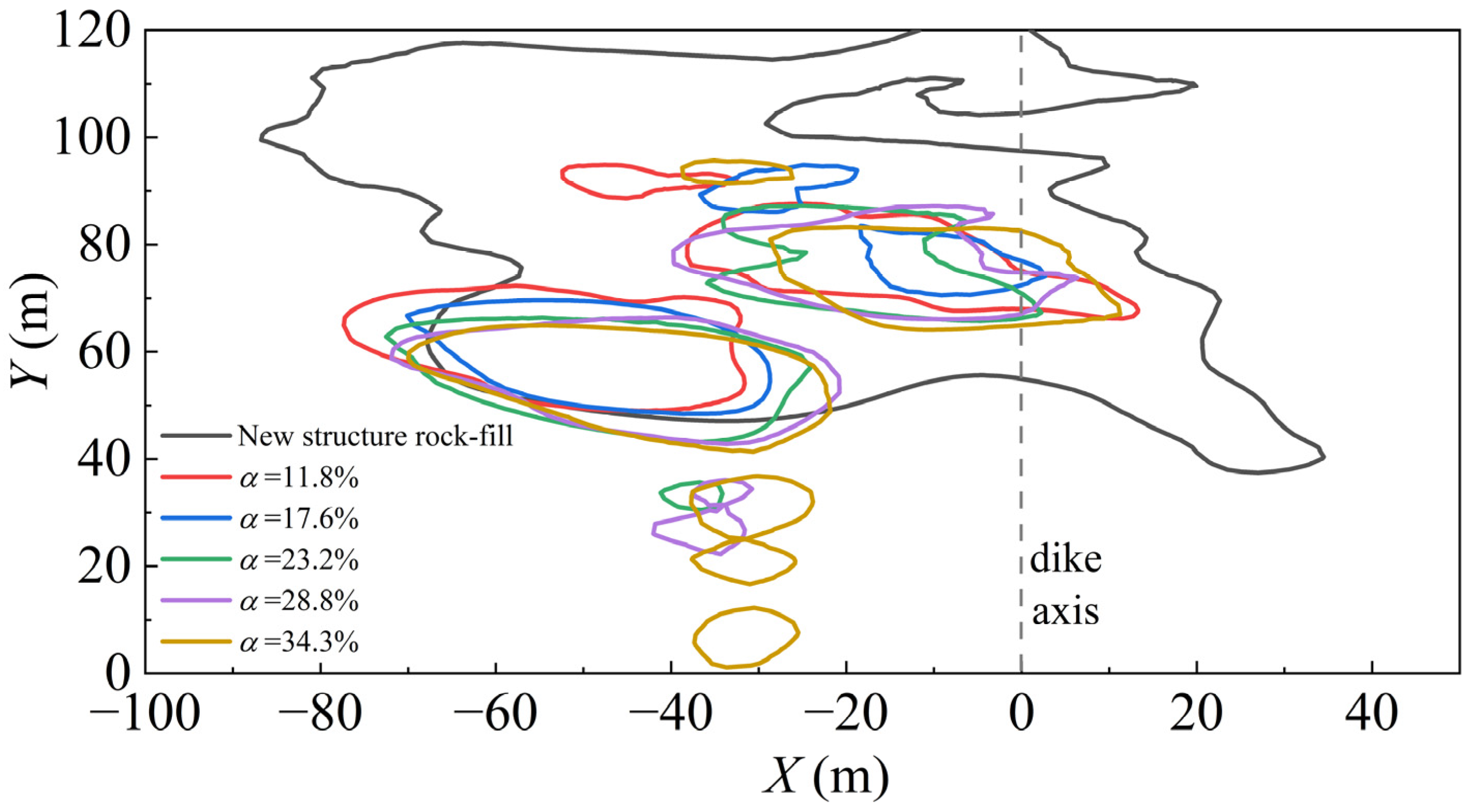
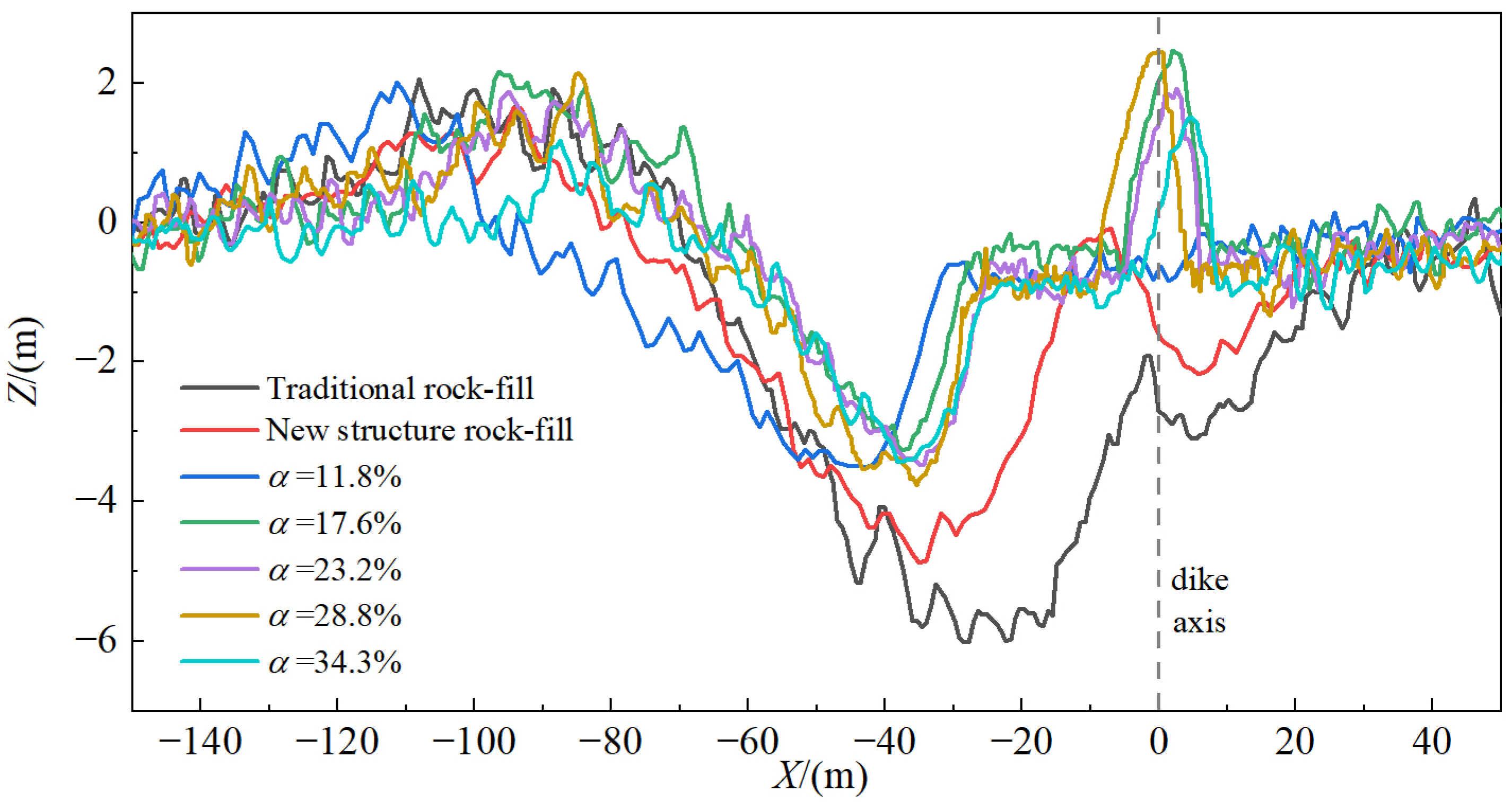
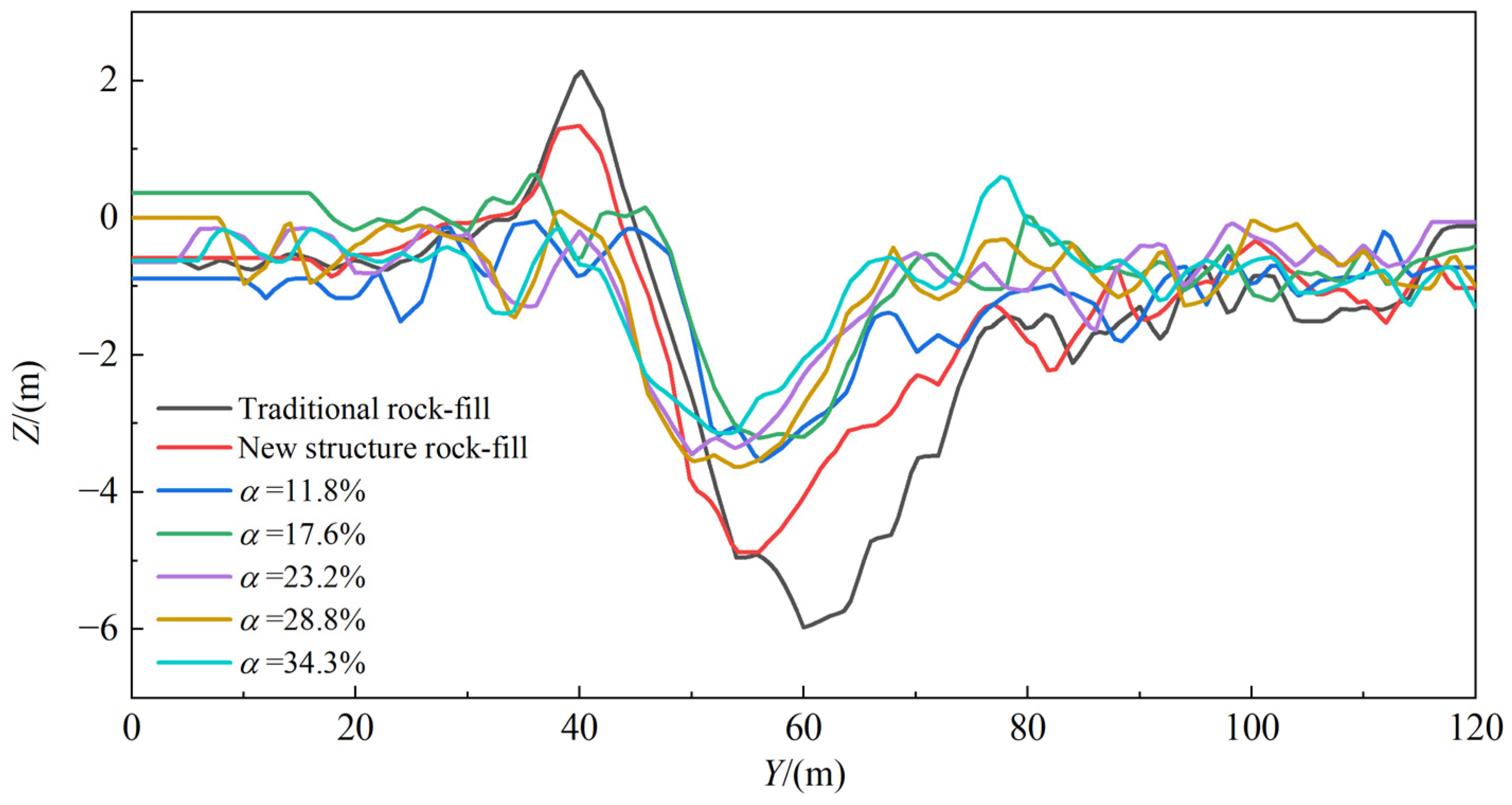
3.1. Analysis of Channel Scour Characteristics
- (1)
- The scouring area around the rock-fill spur dike was much larger than that around the permeable spur dike, because the rock-fill spur dike was composed of rubble, and the permeability coefficient was much smaller than that of the permeable spur dike, resulting in a greatly reduced cross-section of the channel. The flow was concentrated at the front and downstream of the dike head, greatly increasing the flow velocity here, and intensifying the scouring.
- (2)
- The two scour holes formed at the front and downstream of the permeable spur dike head are independent, and the two scour holes of spur dikes with different permeabilities had scouring in the same location. The area of the scour hole of the permeable spur dike was much smaller than that of the rock-fill spur dike.
- (3)
- The scour holes occurred downstream of the dike body when the permeability coefficients of spur dikes were 23.2%, 28.8%, and 34.3%. The reason for this was that with an increase in the permeability coefficient, the current through the permeable holes increases, which leads to an increase in the flow velocity downstream of the dike body, intensifying the scour downstream of the dike body and forming scour holes.
- (4)
- The scour areas around the new structure rock-fill spur dike, the spur dike with a permeability coefficient of α = 11.8%, the spur dike for which α = 17.6%, the spur dike for which α = 23.2%, the spur dike for which α = 28.8%, and the spur dike for which α = 34.3% were 5528 m2, 1457.75 m2, 895.7 m2, 1466.9 m2, 1309.5 m2, and 1618.1 m2, respectively. With an increase in the permeability coefficient, the scour area at the front and downstream of the dike head decreased gradually. However, when the permeability coefficient was greater than 17.6%, the scour area downstream of the dike body increased with an increase in the permeability coefficient. Therefore, the total scour area around the spur dike decreases first and then increases with an increase in the permeability coefficient. When the permeability coefficient was 17.6%, the total scour area was the smallest.
3.2. Analysis of Spatial Characteristics of Scour Holes
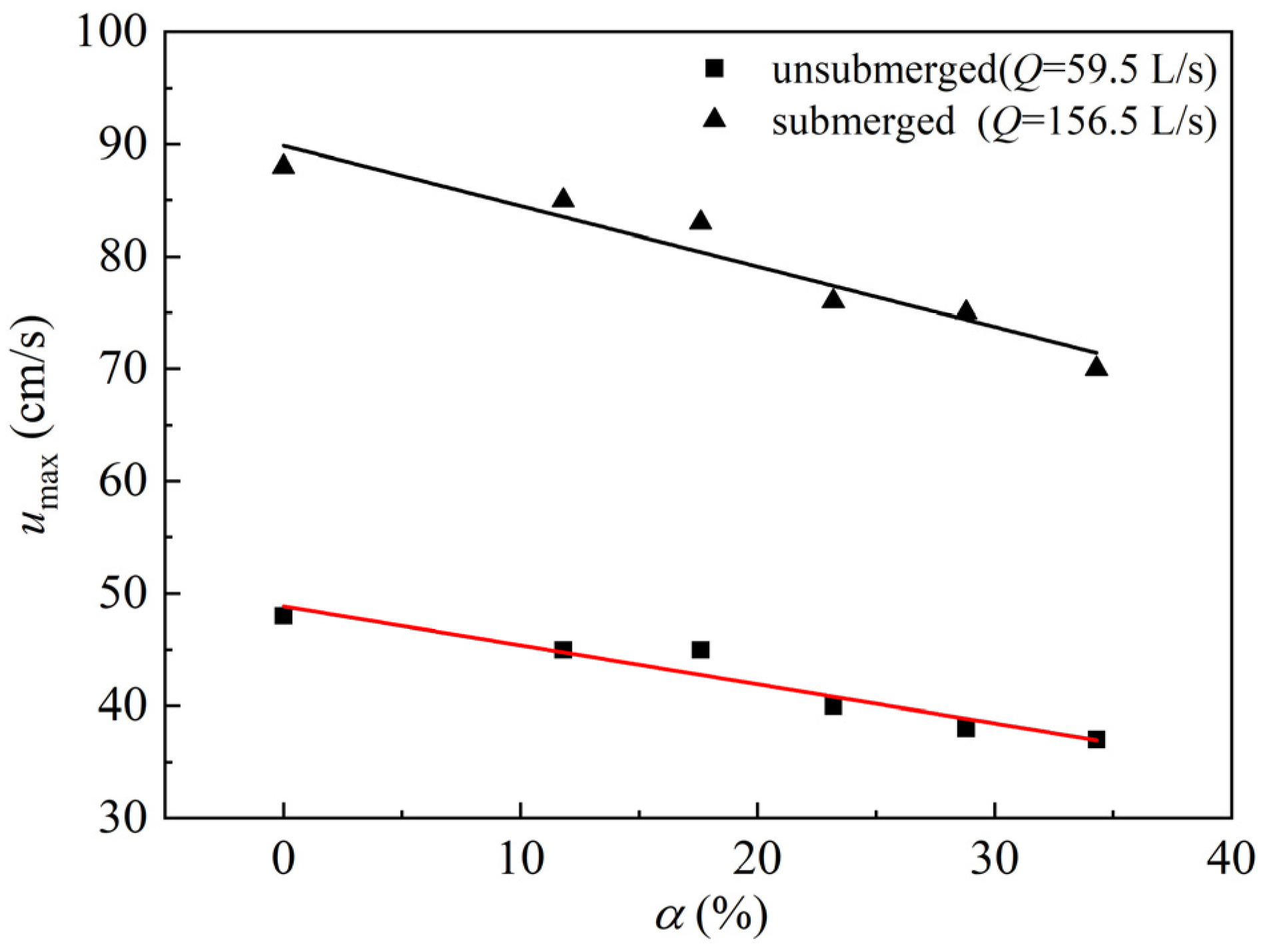
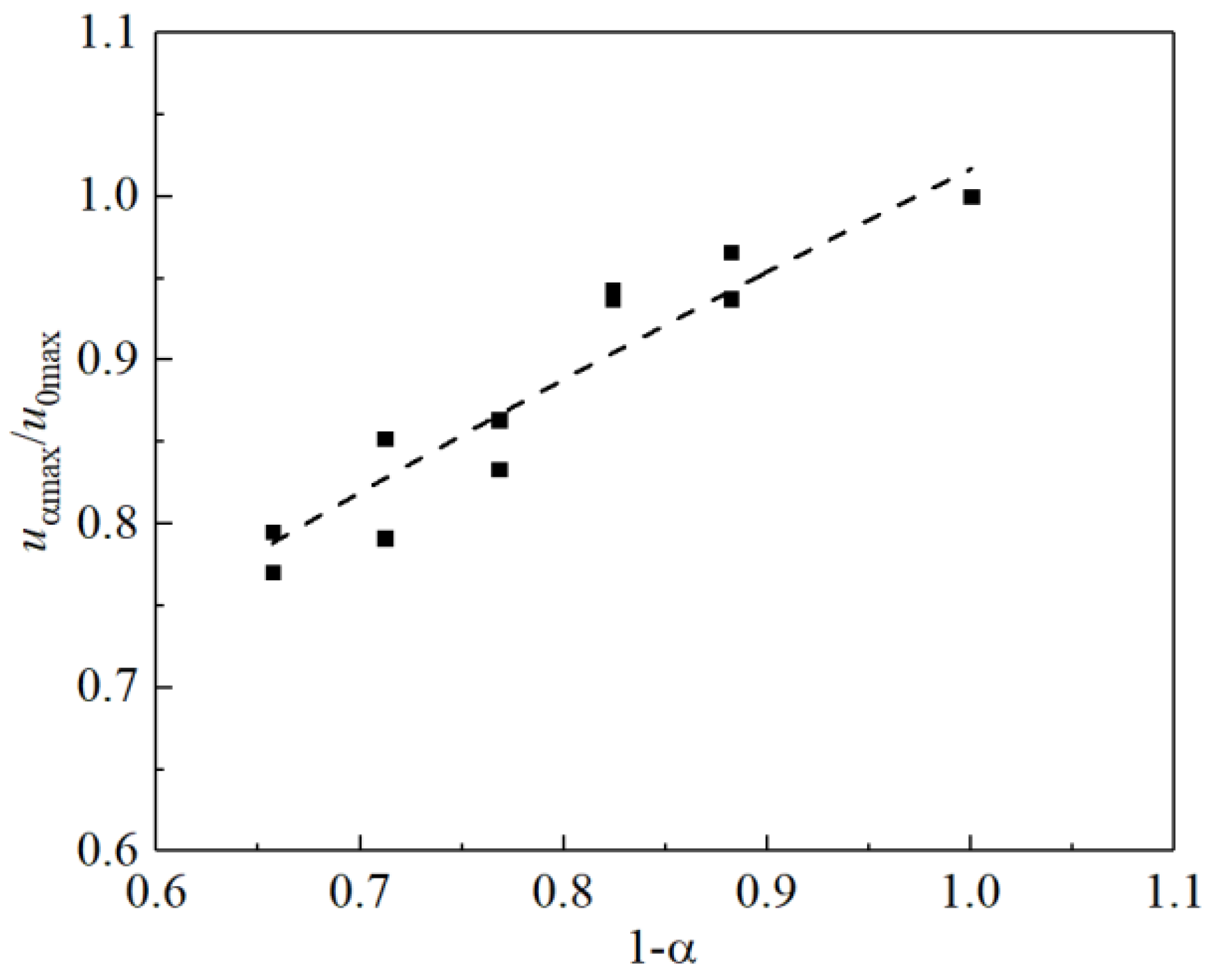
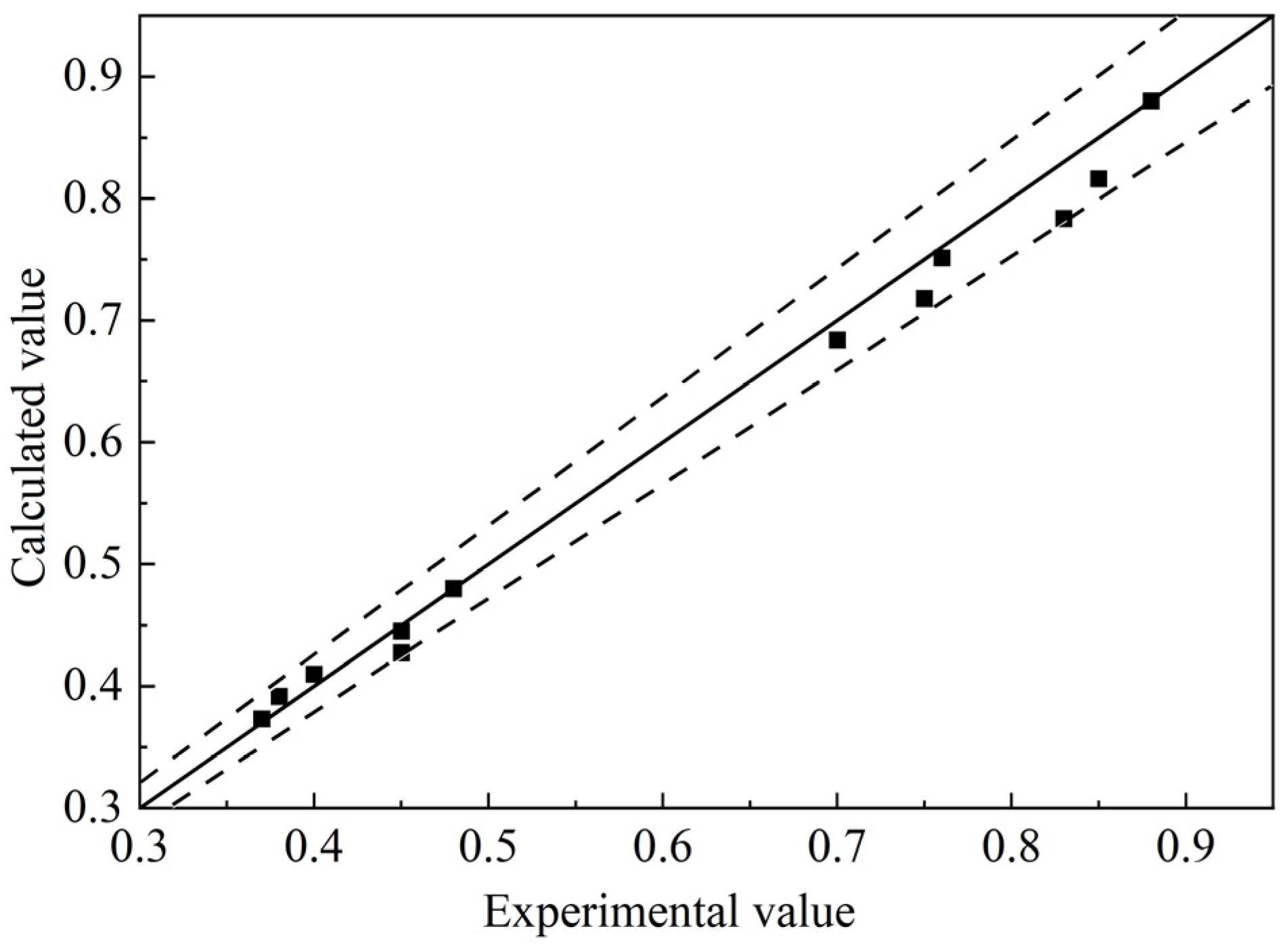
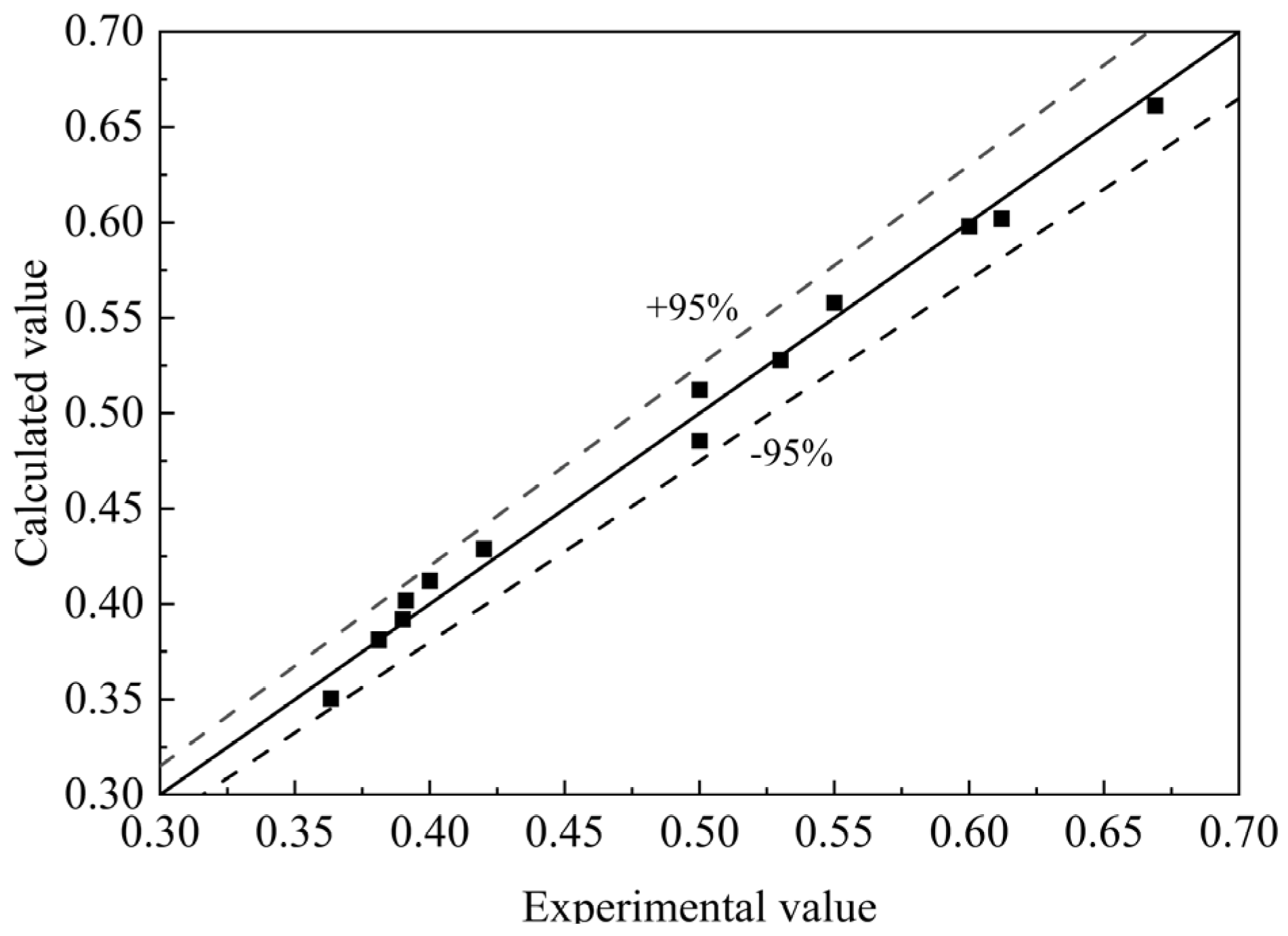
3.3. Analysis of Maximum Depth of Scour Holes
4. Discussion
5. Conclusions
- (1)
- The maximum depth and area of scour holes at the head of the spur dike decrease with an increase in the spur dike permeability coefficient. When the permeability is greater than 17.6%, the depth and area of scour holes downstream of the dike body will increase. Overall, the structure is the most stable when the permeability coefficient of the spur dike is 17.6%.
- (2)
- The maximum depth of the scour hole at the head of a permeable spur dike is mainly affected by the permeability coefficient of the spur dike, the width of the bottom protection structure, and the effective scouring time, among which the permeability coefficient of the spur dike is the most important factor.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pandey, M.; Ahmad, Z.; Sharma, P.K. Scour around impermeable spur dikes: A review. ISH J. Hydraul. Eng. 2018, 24, 25–44. [Google Scholar] [CrossRef]
- Singh, U.K.; Ahmad, Z.; Kumar, A.; Pandey, M. Incipient motion for gravel particles in cohesionless sediment mixtures. Iran. J. Sci. Technol. Trans. Civ. Eng. 2019, 43, 253–262. [Google Scholar] [CrossRef]
- Azamathulla, H.M.; Ghani, A.A.; Zakaria, N.A.; Guven, A. Genetic programming to predict bridge pier scour. J. Hydraul. Eng. 2010, 136, 165. [Google Scholar] [CrossRef]
- Azamathulla, H.M.; Yusoff, M.; Azlan, M. Soft computing for prediction of river pipeline scour depth. Neural Comput. Appl. 2013, 23, 2465–2469. [Google Scholar] [CrossRef]
- Pandey, M.; Lam, W.H.; Cui, Y.; Khan, M.A.; Singh, U.K.; Ahmad, Z. Scour around spur dike in sand–gravel mixture bed. Water 2019, 11, 1417. [Google Scholar] [CrossRef]
- Haghnazar, H.; Hashemzadeh Ansar, B.; Asadzadeh, F.; Salehi Neyshabouri, A.A. Experimental study on the effect of single spur-dike with slope sides on local scour pattern. J. Civ. Eng. Mater. Appl. 2018, 2, 111–120. [Google Scholar]
- Fazli, M.; Ghodsian, M.; Neyshabouri, S.A.A.S. Scour and flow field around a spur dike in a 90 bend. Int. J. Sediment Res. 2008, 23, 56–68. [Google Scholar] [CrossRef]
- Kuhnle, R.A.; Alonso, C.V.; Shields, F.D. Geometry of scour holes associated with 90 spur dikes. J. Hydraul. Eng. 1999, 125, 972–978. [Google Scholar] [CrossRef]
- Masjedi, A.; Bejestan, M.S.; Moradi, A. Experimental study on the time development of local scour at a spur dike in a 180 flume bend. J. Food Agric. Environ. 2010, 8, 904–907. [Google Scholar]
- Nasrollahi, A.; Ghodsian, M.; Neyshabouri, S. Local scour at permeable spur dikes. J. Appl. Sci. 2008, 8, 3398–3406. [Google Scholar] [CrossRef]
- Mioduszewski, T.; Maeno, S.; Uema, Y. Influence of the spur dike permeability on flow and scouring during a surge pass. In International Conference on Estuaries and Coasts; ICEC: Irvine, CA, USA, 2003; pp. 380–388. [Google Scholar]
- Zhou, Y.J.; Qian, S.; Sun, N.N. Application of permeable spur dike in mountain river training. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2014; pp. 236–240. [Google Scholar]
- Osman, M.A.; Saeed, H.N. Local scour depth at the nose of permeable and impermeable spur dykes. Univ. Khartoum Eng. J. 2012, 2. [Google Scholar] [CrossRef]
- Elawady, E.; Michiue, M.; Hinokidani, O. Movable bed scour around submerged spur-dikes. Proc. Hydraul. Eng. 2001, 45, 373–378. [Google Scholar] [CrossRef]
- Nath, D.; Misra, U.K. Experimental study of local scour around single spur dike in an open channel. Int. Res. J. Eng. Technol. IRJET 2017, 4, 2728–2734. [Google Scholar]
- Li, Y.; Altinakar, M. Effects of a Permeable Hydraulic Flashboard Spur Dike on Scour and Deposition. In World Environmental and Water Resources Congress; ASCE: New York, NY, USA, 2016; pp. 399–409. [Google Scholar]
- Ezzeldin, R.M. Numerical and experimental investigation for the effect of permeability of spur dikes on local scour. J. Hydroinformatics 2019, 21, 335–342. [Google Scholar] [CrossRef]
- Pandey, M.; Ahmad, Z.; Sharma, P.K. Estimation of maximum scour depth near a spur dike. Can. J. Civ. Eng. 2016, 43, 270–278. [Google Scholar] [CrossRef]
- Dey, S.; Barbhuiya, A.K. Time variation of scour at abutments. J. Hydraul. Eng. 2005, 131, 11–23. [Google Scholar] [CrossRef]
- Froehlich, D.C. Local scour at bridge abutments. In Hydraulic Engineering; ASCE: New York, NY, USA, 1989; pp. 13–18. [Google Scholar]
- Nagy, H.M. Maximum depth of local scour near emerged vertical wall spur dike. Alex. Eng. J. 2004, 43, 819–829. [Google Scholar]
- Patel, M. Scour Control at Skew Bridge Abutments by the Use of Spur Dikes, a Report for CE 406-Special Problems in Civil Engineering. By MS Patel, Submitted to JB Herbich. 1961. Available online: https://core.ac.uk/download/pdf/228624277.pdf (accessed on 23 November 2022).
- Gill, M.A. Erosion of sand beds around spur dikes. J. Hydraul. Div. 1972, 98, 1587–1602. [Google Scholar] [CrossRef]
- Lauchlan, C.S.; Melville, B.W. Riprap protection at bridge piers. J. Hydraul. Eng. 2001, 127, 412–418. [Google Scholar] [CrossRef]
- Ying, Q. Formula Type of Local Scour Depth on Spur Dike Nose. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2014; pp. 271–274. [Google Scholar]
- Pandey, M.; Valyrakis, M.; Qi, M.; Sharma, A.; Lodhi, A.S. Experimental assessment and prediction of temporal scour depth around a spur dike. Int. J. Sediment Res. 2021, 36, 17–28. [Google Scholar] [CrossRef]
- Kothyari, U.C.; Hager, W.H.; Oliveto, G. Generalized approach for clear-water scour at bridge foundation elements. J. Hydraul. Eng. 2007, 133, 1229–1240. [Google Scholar] [CrossRef]
- Singh, U.K.; Jamei, M.; Karbasi, M.; Malik, A.; Pandey, M. Application of a modern multi-level ensemble approach for the estimation of critical shear stress in cohesive sediment mixture. J. Hydrol. 2022, 607, 127549. [Google Scholar] [CrossRef]
- Pandey, M.; Jamei, M.; Ahmadianfar, I.; Karbasi, M.; Lodhi, A.; Chu, X. Assessment of scouring around spur dike in cohesive sediment mixtures: A comparative study on three rigorous machine learning models. J. Hydrol. 2022, 606, 127330. [Google Scholar] [CrossRef]
- Ambari, A.; Gauthier-Manuel, B.; Guyon, E. Backflow effect in model sedimentation experiments. Phys. Fluids Fluid Dyn. 1993, 5, 2061–2063. [Google Scholar] [CrossRef]
- Azinfar, H.; Kells, J. Backwater effect due to a single spur dike. Can. J. Civ. Eng. 2007, 34, 107–115. [Google Scholar] [CrossRef]
- Wang, H. Impact Distance of Spur Dike Head on Navigable Flow Conditions; Changsha University of Technology: Changsha, China, 2010; (In Chinese with English abstract). [Google Scholar]
- Zhou, Y.; Liu, H.; He, C. Rational Selection of Design Parameters for Pervious Spur Dikes. J. Water Resour. Water Eng. 2006, 17, 42–45, (In Chinese with English abstract). [Google Scholar]
- Kothyari, U.C.; Garde, R.C.J.; Ranga Raju, K.G. Temporal variation of scour around circular bridge piers. J. Hydraul. Eng. 1992, 118, 1091–1106. [Google Scholar] [CrossRef]
- Fael, C.M.S.; Simarro-Grande, G.; Martín-Vide, J.P.; Cardoso, A.H. Local scour at vertical-wall abutments under clear-water flow conditions. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, P.; Yang, W.; Zuo, W.; Gu, X.; Yang, X. Geometric characteristics of spur dike scour under clear-water scour conditions. Water 2018, 10, 680. [Google Scholar] [CrossRef]
- Rodrigue-Gervais, K.; Biron, P.M.; Lapointe, M.F. Temporal development of scour holes around submerged stream deflectors. J. Hydraul. Eng. 2011, 137, 781–785. [Google Scholar] [CrossRef]
- Kuhnle, R.A.; Alonso, C.V.; Shields, F.D., Jr. Local scour associated with angled spur dikes. J. Hydraul. Eng. 2002, 128, 1087–1093. [Google Scholar] [CrossRef]
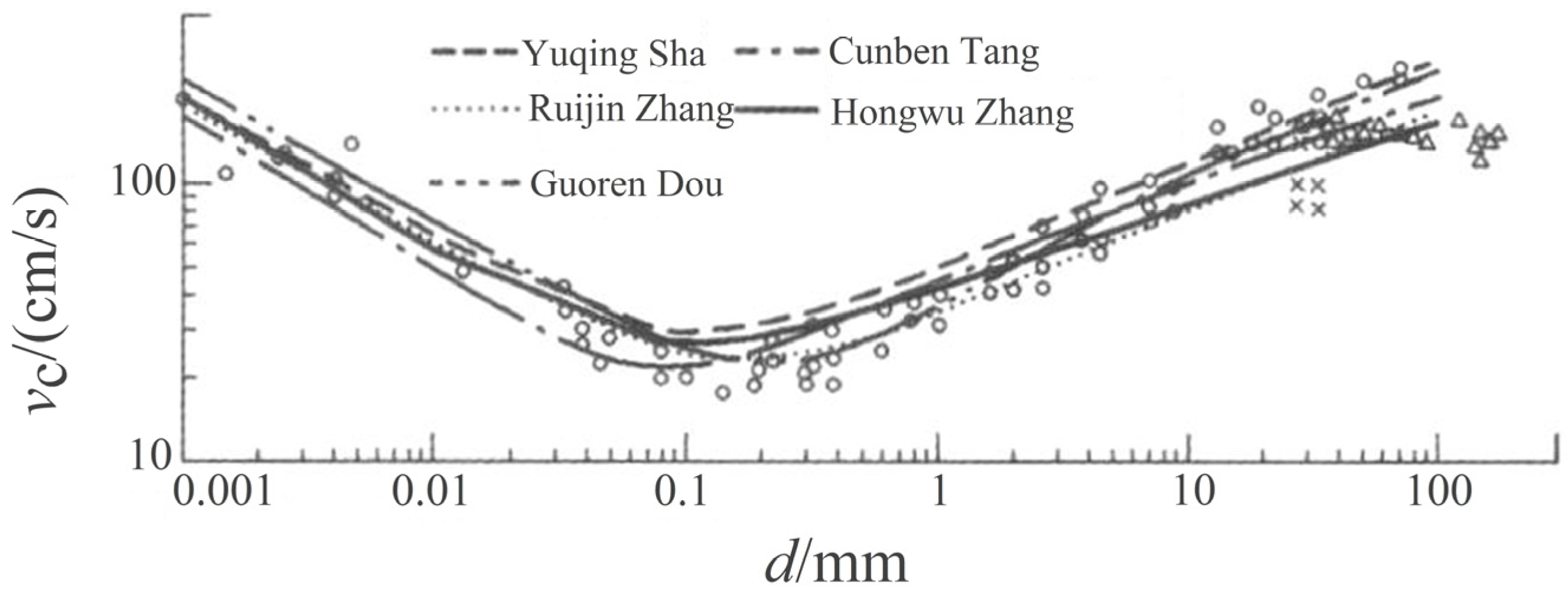
- Zhang, H. Unified formula for incipient velocity of sediment. J. Water Conserv. 2012, 43, 1387–1396, (In Chinese with English abstract). [Google Scholar]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, J.; Wang, G.; Wang, P.; Yu, T.; Chen, H. Experimental Study on the Influence of New Permeable Spur Dikes on Local Scour of Navigation Channel. Sustainability 2023, 15, 570. https://doi.org/10.3390/su15010570
Hu J, Wang G, Wang P, Yu T, Chen H. Experimental Study on the Influence of New Permeable Spur Dikes on Local Scour of Navigation Channel. Sustainability. 2023; 15(1):570. https://doi.org/10.3390/su15010570
Chicago/Turabian StyleHu, Jielong, Guangsheng Wang, Pingyi Wang, Tong Yu, and Hanbao Chen. 2023. "Experimental Study on the Influence of New Permeable Spur Dikes on Local Scour of Navigation Channel" Sustainability 15, no. 1: 570. https://doi.org/10.3390/su15010570
APA StyleHu, J., Wang, G., Wang, P., Yu, T., & Chen, H. (2023). Experimental Study on the Influence of New Permeable Spur Dikes on Local Scour of Navigation Channel. Sustainability, 15(1), 570. https://doi.org/10.3390/su15010570




