Numerical Analysis of Groundwater Effects on the Stability of an Abandoned Shallow Underground Coal Mine
Abstract
1. Introduction
2. Materials and Methods
2.1. Stratigraphy and Soil Properties
2.2. Numerical Methodology
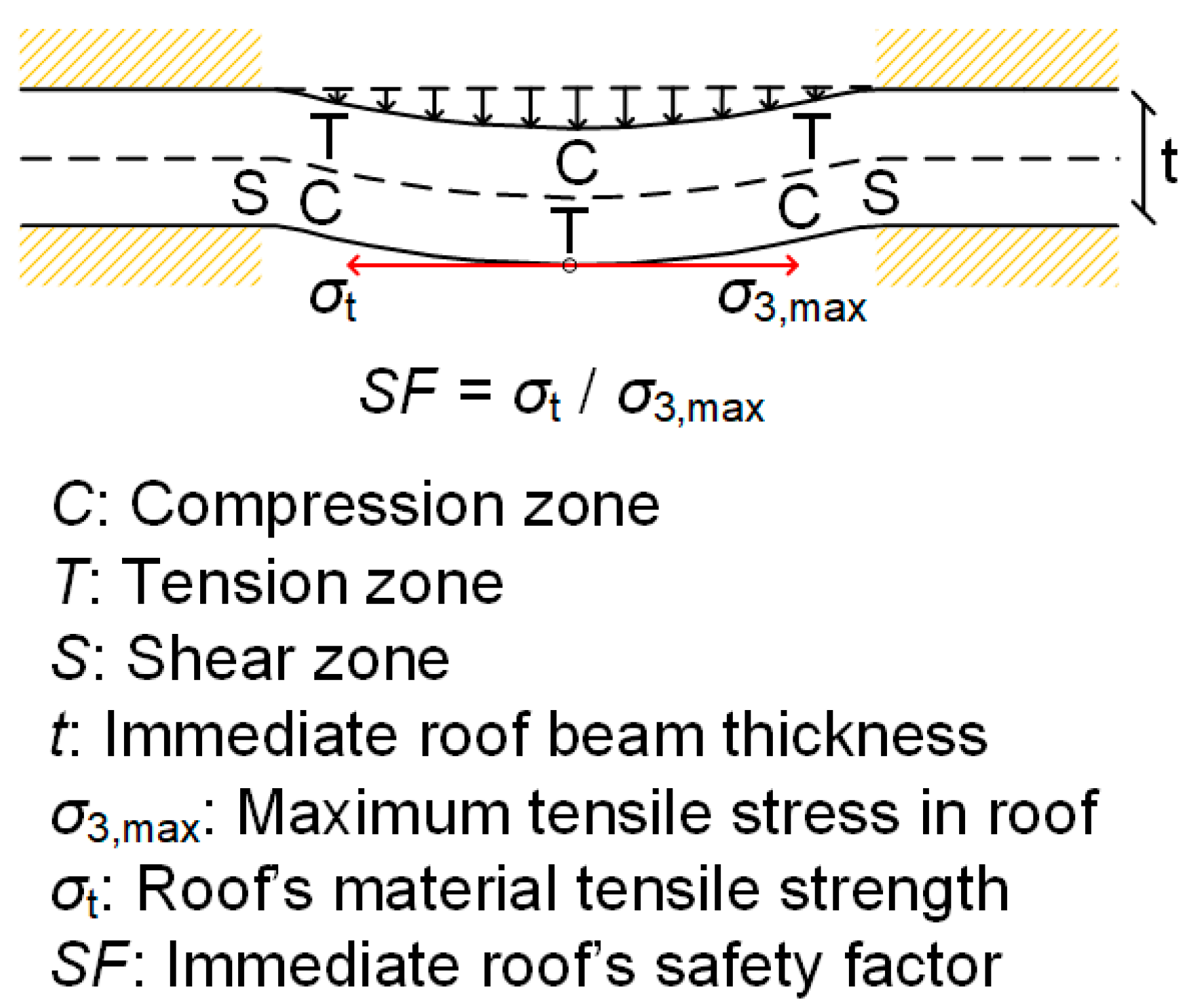
2.3. Safety Definition
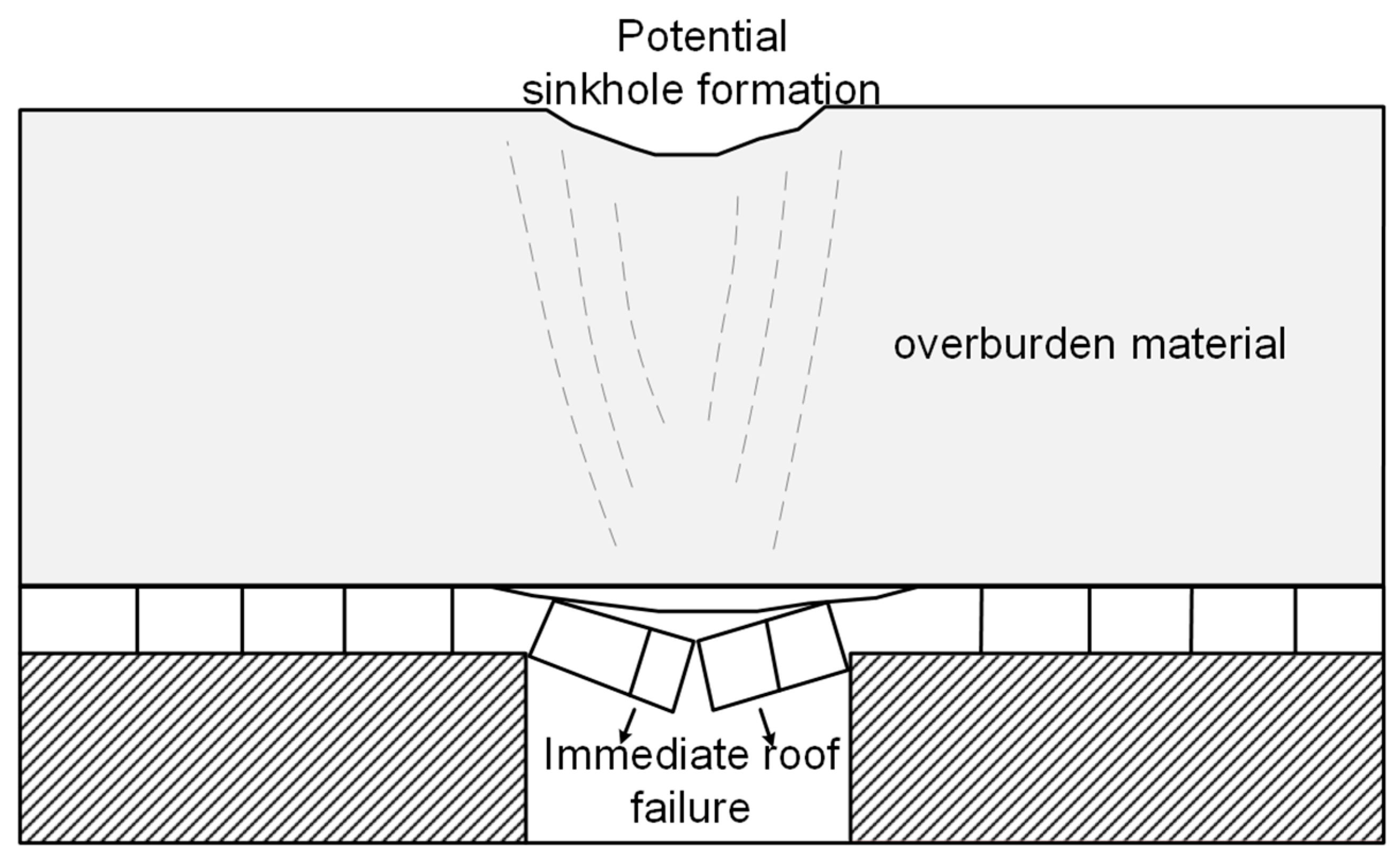
3. Results and Discussion
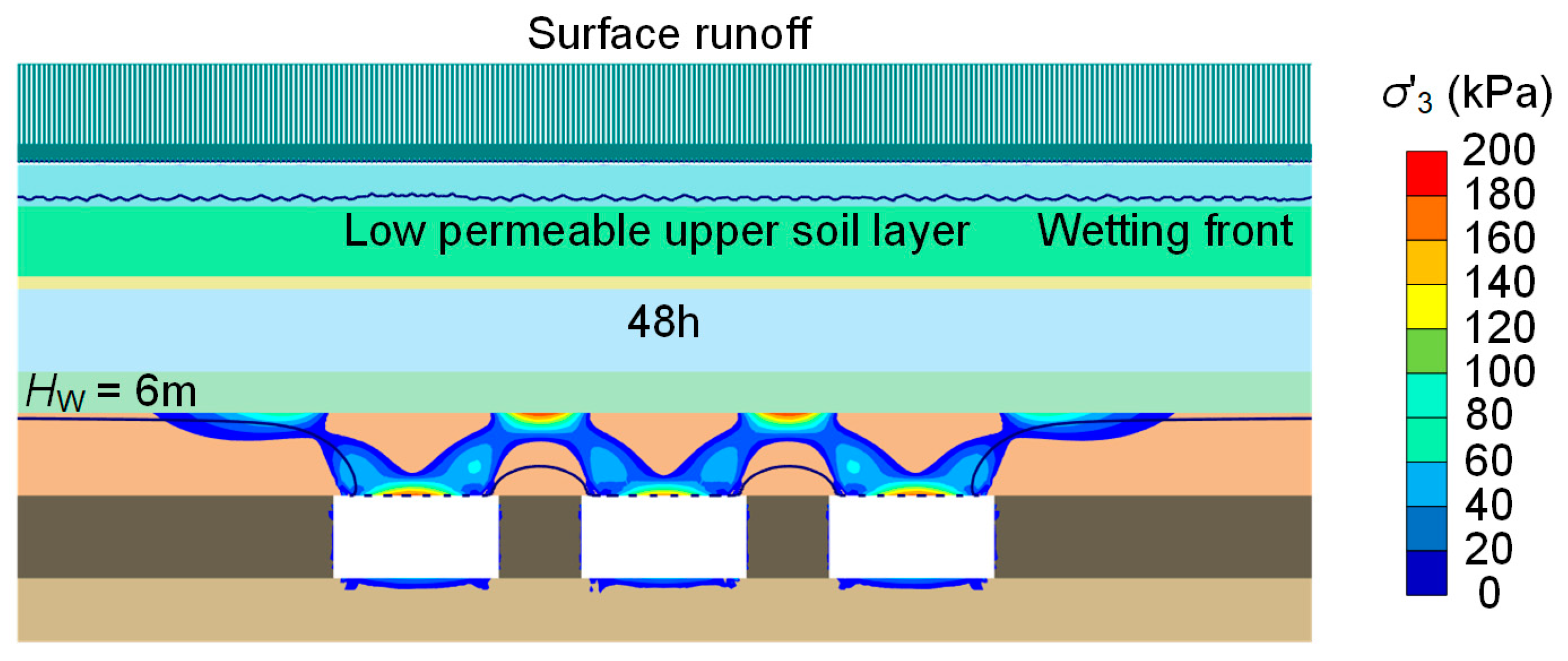
3.1. Individual Rainfall Event
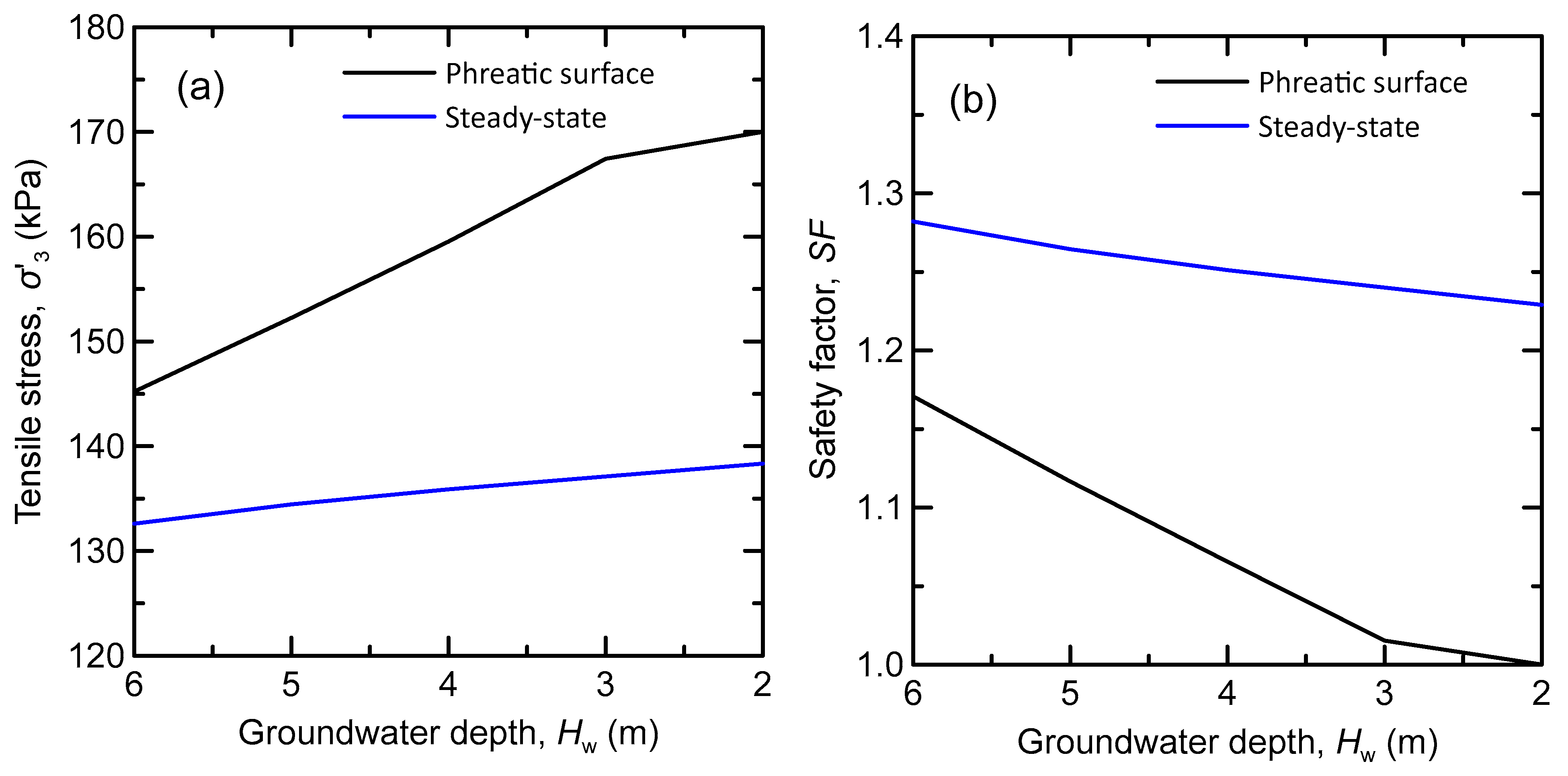
3.2. Groundwater Recharge
4. Conclusions
- (1)
- The short-term safety remained unaffected by an individual rainfall event as a lowpermeability upper soil layer (silty clay) limited rainfall’s infiltration into the materials surrounding the underground openings to form perched water above an aquitard.
- (2)
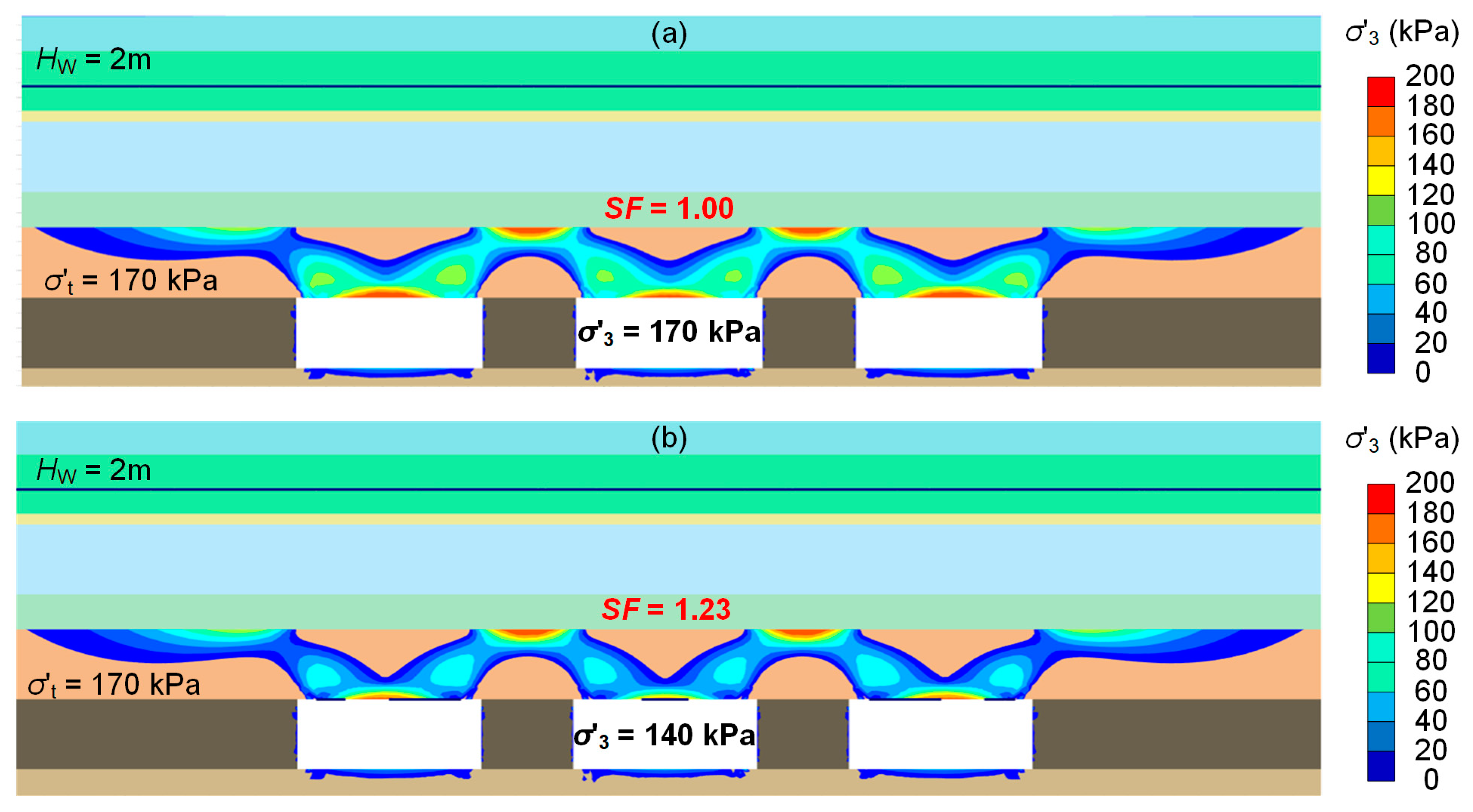
- The long-term safety deteriorated when considering the gradual recharge of groundwater, representing the accumulation of infiltrated stormwater from several rainfall events. This decrease in the safety factor was due to the increase of the tensile stresses in the roof of the underground openings with the rise of the groundwater table for both examined approaches for porewater pressure calculation limits (phreatic line versus steady-state flow).
- (3)
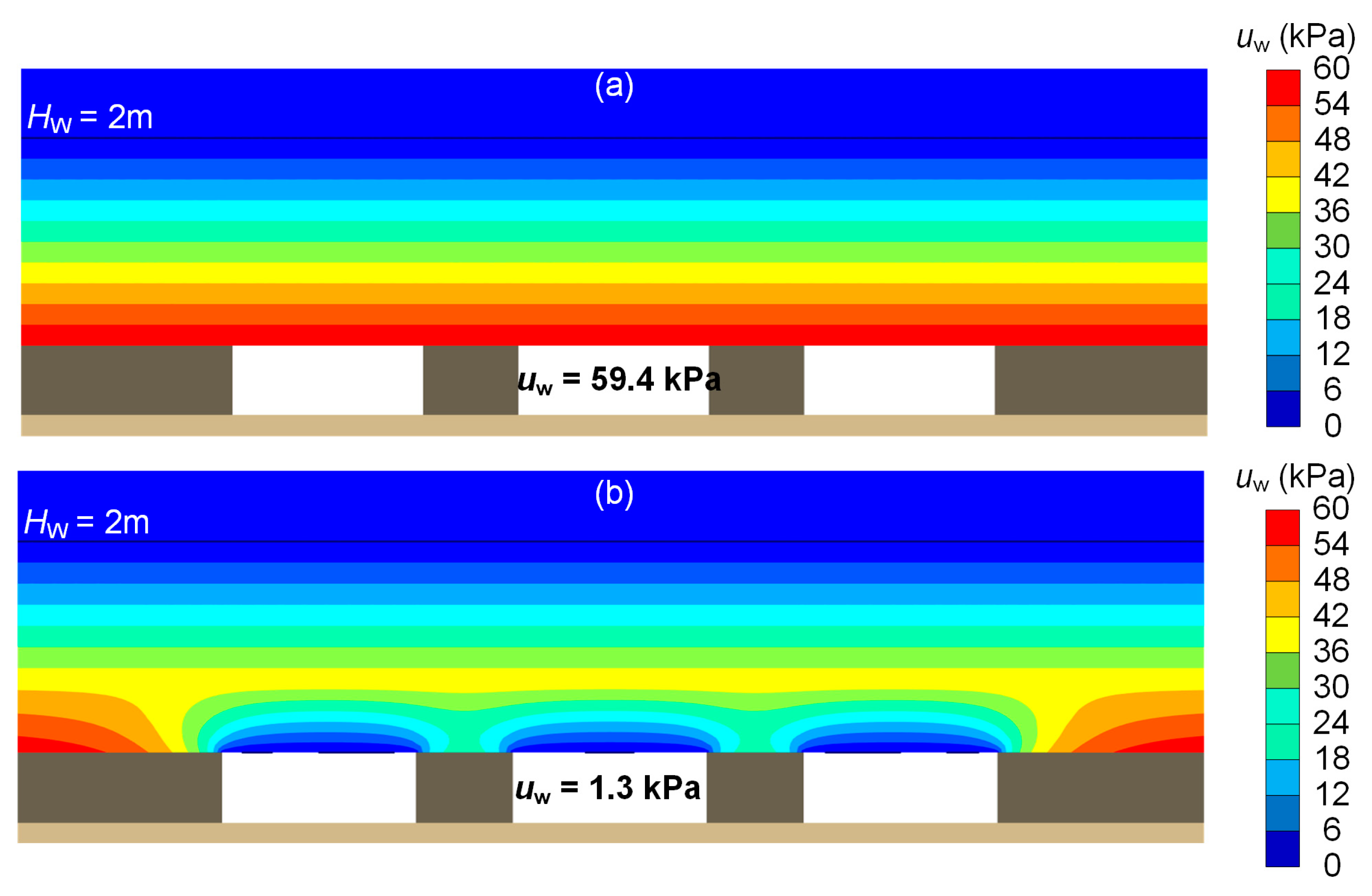
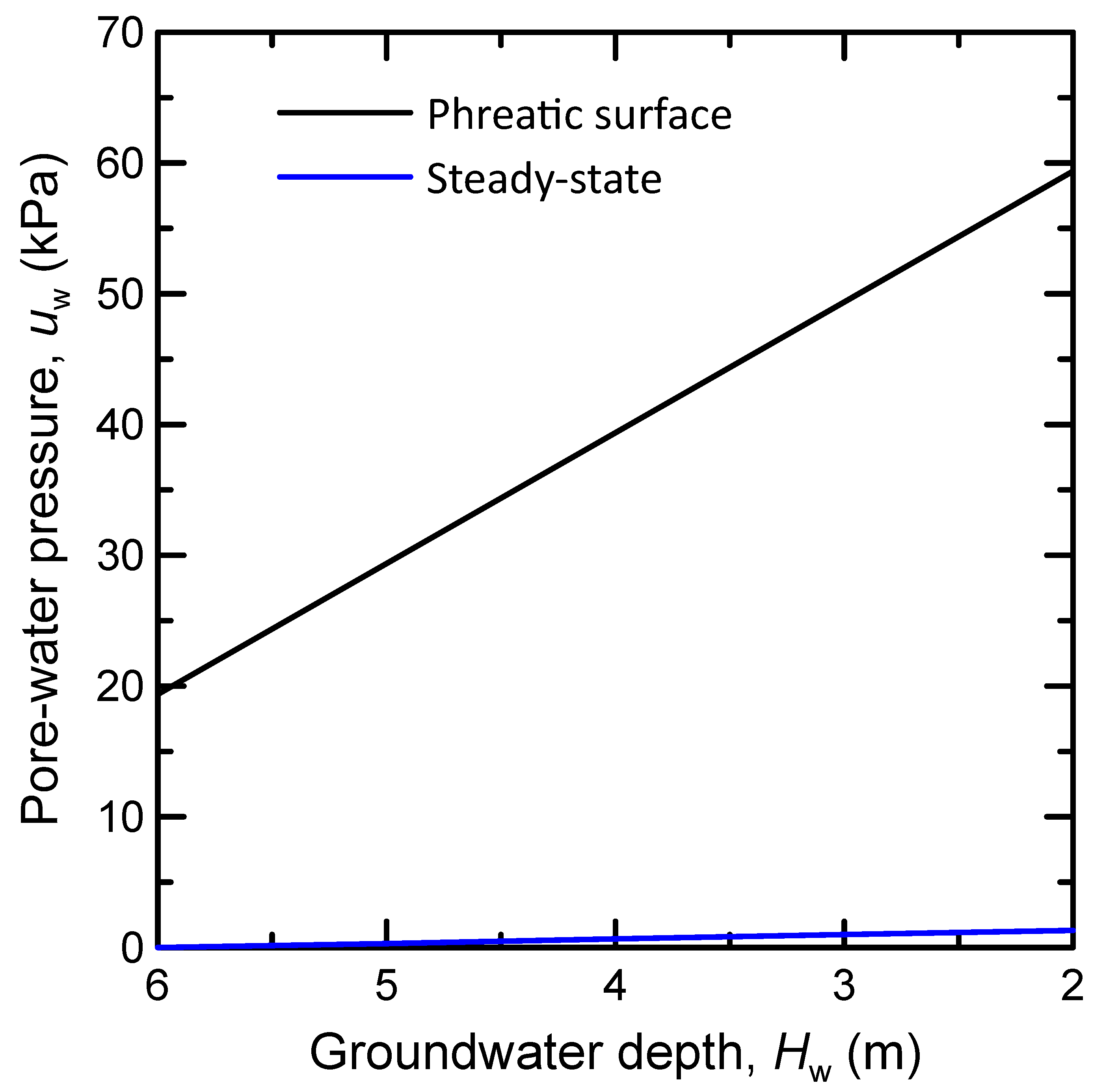
- The phreatic line approach is the most conservative, resulting in lower safety factors than the steady-state flow analysis due to the build-up of higher hydrostatic pressure on the roof of the opening.
- (4)
- The steady-state analysis provided smaller tensile stresses on the opening’s roof due to groundwater flow conditions. In this case, the porewater pressure inside the openings was, by definition, zero and very small at the openings’ edges and roofs.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| c’ | effective cohesion |
| E | Young’s modulus |
| ga | fitting parameter of the SWCC related to the air entry value |
| gl | fitting parameter of the SWCC equal to 0.5 |
| gn | fitting parameter of the SWCC governing its shape that is a function of the rate of water extraction from the soil once the air entry value has been exceeded |
| GWT | groundwater table |
| Hp | height of the coal layer |
| Hw | groundwater depth |
| ks | permeability coefficient |
| kw | unsaturated soil permeability coefficient |
| q | rainfall intensity |
| SF | Safety Factor |
| Se | effective soil saturation |
| Sr | residual soil saturation |
| Ss | soil saturation at the fully saturated state |
| Sw | saturation degree |
| uw | porewater pressure |
| γ | moist soil unit weight |
| γsat | saturated soil unit weight |
| γw | unit weight of water equal to 9.81 kN/m3 |
| ν | Poisson ratio |
| σ’yy | vertical effective stress |
| σt | tensile strength |
| σ’xx | horizontal effective stress |
| φ’ | effective friction angle |
| ψ | dilation angle |
References
- Whittaker, B.N.; Reddish, D.J. Subsidence: Occurrence, Prediction and Control; Elsevier Science Publishers B.V.: Amsterdam, The Netherlands, 1989. [Google Scholar]
- Galvin, J. Ground Engineering-Principles and Practices for Underground Coal Mining; Springer International Publishing: London, UK, 2016. [Google Scholar]
- Karfakis, M.G. Residual Subsidence Over Abandoned Coal Mines. In Surface and Underground Project Case Histories; Hoek, E., Ed.; Pergamon: Oxford, UK, 1993; pp. 451–476. [Google Scholar]
- Brady, B.H.; Brown, E.T. Rock Mechanics: For Underground Mining; Springer International Publishing: London, UK, 2006. [Google Scholar]
- Singh, K. Causes and remedial measures of pot-hole subsidence due to coal mining. J. Sci. Ind. Res. 2000, 59, 280–285. [Google Scholar]
- Karfakis, M.G. Chimney subsidence over abandoned coal mines. Int. J. Min. Geol. Eng. 1987, 5, 131–141. [Google Scholar] [CrossRef]
- Singh, K.B.; Dhar, B.B. Sinkhole subsidence due to mining. Geotech. Geol. Eng. 1997, 15, 327–341. [Google Scholar] [CrossRef]
- Canbulat, I.; Zhang, C.; Black, K.; Johnston, J.; McDonald, S. Assessment of sinkhole risk in shallow coal mining. In Proceedings of the 10th Triennial Conference on Mine Subsidence, Pokolbin, Australia, 5–7 November 2017; pp. 331–337. [Google Scholar]
- Hood, M.; Ewy, R.T.; Riddle, L.R. Empirical methods of subsidence prediction—A case study from Illinois. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1983, 20, 153–170. [Google Scholar] [CrossRef]
- O’Rourke, T.; Turner, S. Empirical methods for estimating subsidence in US coal fields. In Proceedings of the 22nd US Symposium on Rock Mechanics (USRMS), Cambridge, MA, USA, 22–24 June 1981. [Google Scholar]
- Goel, S.C.; Page, C.H. An empirical method for predicting the probability of chimney cave occurence over a mining area. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1982, 19, 325–337. [Google Scholar] [CrossRef]
- Drumm, E.C.; Kane, W.F.; Yoon, C.J. Application of limit plasticity to the stability of sinkholes. Eng. Geol. 1990, 29, 213–225. [Google Scholar] [CrossRef]
- Xu, D.; Peng, S.; Xiang, S.; Liang, M.; Liu, W. The Effects of Caving of a Coal Mine’s Immediate Roof on Floor Strata Failure and Water Inrush. Mine Water Environ. 2016, 35, 337–349. [Google Scholar] [CrossRef]
- Strzałkowski, P.; Litwa, P. Environmental protection problems in the areas of former mines with emphasis on sinkholes: Selected examples. Int. J. Environ. Sci. Technol. 2021, 18, 771–780. [Google Scholar] [CrossRef]
- Alejano, L.; Ramírez-Oyanguren, P.; Taboada, J. FDM predictive methodology for subsidence due to flat and inclined coal seam mining. Int. J. Rock Mech. Min. Sci. 1999, 36, 475–491. [Google Scholar] [CrossRef]
- Helm, P.R.; Davie, C.T.; Glendinning, S. Numerical modelling of shallow abandoned mine working subsidence affecting transport infrastructure. Eng. Geol. 2013, 154, 6–19. [Google Scholar] [CrossRef]
- Najjar, Y.; Zaman, M. Surface Subsidence Prediction by Nonlinear Finite Element Analysis. J. Geotech. Eng. 1993, 119, 1790–1804. [Google Scholar] [CrossRef]
- Salmi, E.F.; Karakus, M.; Nazem, M. Assessing the effects of rock mass gradual deterioration on the long-term stability of abandoned mine workings and the mechanisms of post-mining subsidence—A case study of Castle Fields mine. Tunn. Undergr. Space Technol. 2019, 88, 169–185. [Google Scholar] [CrossRef]
- Khadka, S.; Wang, Z.-M.; Hu, L.-B. Exploring a Coupled Approach to Model the Geomechanical Processes of Sinkholes. In Proceedings of the GeoShanghai 2018 International Conference: Geoenvironment and Geohazard, Shanghai, China, 27–30 May 2018; GSIC 2018. Springer: Singapore, 2018; pp. 99–107. [Google Scholar]
- Salmi, E.F.; Nazem, M.; Karakus, M. The effect of rock mass gradual deterioration on the mechanism of post-mining subsidence over shallow abandoned coal mines. Int. J. Rock Mech. Min. Sci. 2017, 91, 59–71. [Google Scholar] [CrossRef]
- Poulsen, B.A.; Shen, B. Subsidence risk assessment of decommissioned bord-and-pillar collieries. Int. J. Rock Mech. Min. Sci. 2013, 60, 312–320. [Google Scholar] [CrossRef]
- Prakash, A.; Lokhande, R.; Singh, K. Impact of rainfall on residual subsidence in old coal mine workings. J. Environ. Sci. Eng. 2010, 52, 75–80. [Google Scholar]
- Singh, K. Pot-hole subsidence in Son-Mahanadi master coal basin. Eng. Geol. 2007, 89, 88–97. [Google Scholar] [CrossRef]
- Lu, N.; Likos, W.J. Unsaturated Soil Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Fredlund, D.G.; Rahardjo, H. Soil Mechanics for Unsaturated Soils; John Wiley & Sons: Hoboken, NJ, USA, 1993. [Google Scholar]
- Bear, J. Dynamics of Fluids in Porous Media; American Elsevier Publishing Company, Inc.: New York, NY, USA, 1972. [Google Scholar]
- Diamantopoulos, E.; Durner, W. Dynamic Nonequilibrium of Water Flow in Porous Media: A Review. Vadose Zone J. 2012, 11, vzj2011-0197. [Google Scholar] [CrossRef]
- Hu, R.; Chen, Y.-F.; Liu, H.-H.; Zhou, C.-B. A water retention curve and unsaturated hydraulic conductivity model for deformable soils: Consideration of the change in pore-size distribution. Géotechnique 2013, 63, 1389–1405. [Google Scholar] [CrossRef]
- Yan, G.; Bore, T.; Schlaeger, S.; Scheuermann, A.; Li, L. Investigating scale effects in soil water retention curve via spatial time domain reflectometry. J. Hydrol. 2022, 612, 128238. [Google Scholar] [CrossRef]
- Yan, G.; Li, Z.; Bore, T.; Galindo Torres, S.A.; Scheuermann, A.; Li, L. A lattice Boltzmann exploration of two-phase displacement in 2D porous media under various pressure boundary conditions. J. Rock Mech. Geotech. Eng. 2022, 14, 1782–1798. [Google Scholar] [CrossRef]
- Hu, R.; Lan, T.; Wei, G.-J.; Chen, Y.-F. Phase diagram of quasi-static immiscible displacement in disordered porous media. J. Fluid Mech. 2019, 875, 448–475. [Google Scholar] [CrossRef]
- Carsel, R.F.; Parrish, R.S. Developing joint probability distributions of soil water retention characteristics. Water Resour. Res. 1988, 24, 755–769. [Google Scholar] [CrossRef]
- Zhang, L.; Fredlund, D.; Zhang, L.; Tang, W. Numerical study of soil conditions under which matric suction can be maintained. Can. Geotech. J. 2004, 41, 569–582. [Google Scholar] [CrossRef]
- Lin, H.; Zhong, W. Influence of Rainfall Intensity and Its Pattern on the Stability of Unsaturated Soil Slope. Geotech. Geol. Eng. 2019, 37, 615–623. [Google Scholar] [CrossRef]
- Kim, J.; Jeong, S.; Regueiro, R.A. Instability of partially saturated soil slopes due to alteration of rainfall pattern. Eng. Geol. 2012, 147, 28–36. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Plaxis 2D Finite Element Geotechnical Analysis Software, V20.3; Bentley: Dublin, Ireland, 2020.
- Jaky, J. Pressure in silos. In Proceedings of the 2nd International Conference on Soil Mechanics and Foundation Engineering, Rotterdam, The Netherlands, 21–30 June 1948; pp. 103–107. [Google Scholar]
- Plaxis. Material Models Manual; Bentley: Dublin, Ireland, 2020.
- Deliveris, A.V.; Benardos, A. Evaluating performance of lignite pillars with 2D approximation techniques and 3D numerical analyses. Int. J. Min. Sci. Technol. 2017, 27, 929–936. [Google Scholar] [CrossRef]
- Pariseau, W.; Sorensen, W. 3D mine pillar design information from 2D FEM analysis. Int. J. Numer. Anal. Methods Geomech. 1979, 3, 145–157. [Google Scholar] [CrossRef]
- Duncan Fama, M.E.; Trueman, R.; Craig, M.S. Two- and three-dimensional elasto-plastic analysis for coal pillar design and its application to highwall mining. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1995, 32, 215–225. [Google Scholar] [CrossRef]
- Rahimi, A.; Rahardjo, H.; Leong, E.-C. Effect of hydraulic properties of soil on rainfall-induced slope failure. Eng. Geol. 2010, 114, 135–143. [Google Scholar] [CrossRef]
- Myhre, G.; Alterskjær, K.; Stjern, C.W.; Hodnebrog, Ø.; Marelle, L.; Samset, B.H.; Sillmann, J.; Schaller, N.; Fischer, E.; Schulz, M.; et al. Frequency of extreme precipitation increases extensively with event rareness under global warming. Sci. Rep. 2019, 9, 16063. [Google Scholar] [CrossRef] [PubMed]
- Fredlund, D.G. The 1999 R.M. Hardy Lecture: The implementation of unsaturated soil mechanics into geotechnical engineering. Can. Geotech. J. 2000, 37, 963–986. [Google Scholar] [CrossRef]
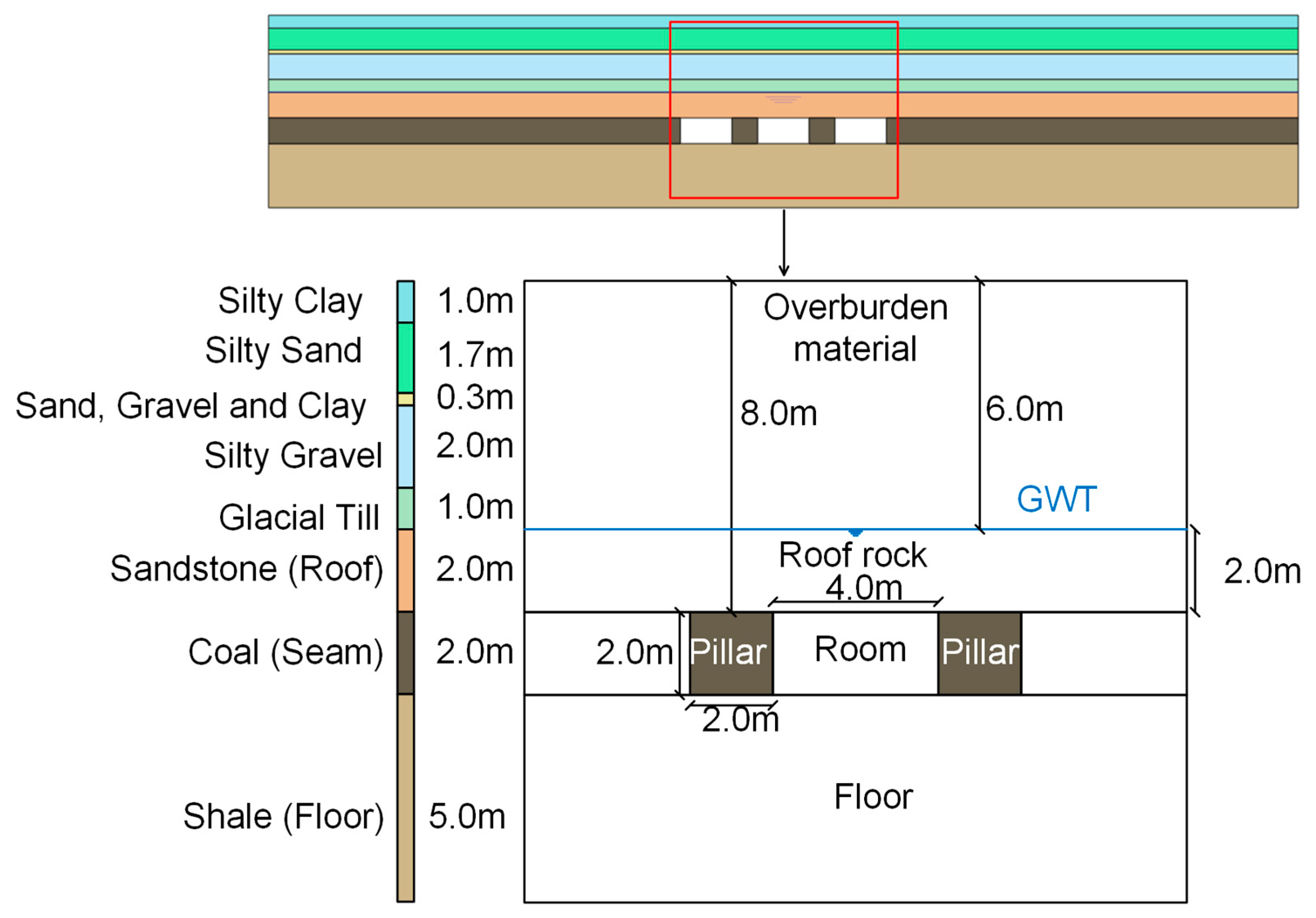


| Material Parameters | γ (kN/m3) | γsat (kN/m3) | Ε (MPa) | ν (-) | c’ (kPa) | φ’ (deg) | ψ (deg) | σt (kPa) | ks (cm/s) |
|---|---|---|---|---|---|---|---|---|---|
| Silty clay | 15.4 | 17.4 | 5.2 | 0.30 | 11 | 38.5 | 0 | 0 | 5 × 10−6 |
| Silty sand | 15.4 | 17.4 | 52 | 0.30 | 2 | 30.5 | 0 | 0 | 4 × 10−3 |
| Sand, gravel, and clay | 16.2 | 18.2 | 52 | 0.30 | 3 | 35.5 | 0 | 0 | 3 × 10−4 |
| Silty gravel | 16.2 | 18.2 | 21.84 | 0.30 | 3 | 29.5 | 0 | 0 | 8 × 10−3 |
| Glacial till | 16.2 | 18.2 | 52 | 0.30 | 10 | 29.5 | 0 | 0 | 3 × 10−4 |
| Sandstone (roof) | 25.0 | 26.0 | 4300 | 0.34 | 360 | 35.0 | 0 | 170 | 4 × 10−3 |
| Coal (pillar) | 15.0 | 15.0 | 4630 | 0.33 | 460 | 36.0 | 0 | 230 | non-porous |
| Shale (floor) | 27.0 | 27.0 | 11,550 | 0.30 | 1300 | 43.0 | 0 | 750 | non-porous |
| Material Parameters | Sr (-) | Ss (-) | ga (1/m) | gn (-) |
|---|---|---|---|---|
| Silty clay | 0.20 | 1.00 | 0.05 | 1.09 |
| Silty sand | 0.15 | 1.00 | 1.24 | 2.28 |
| Sand, gravel, and clay | 0.25 | 1.00 | 0.59 | 1.48 |
| Silty gravel | 0.10 | 1.00 | 1.45 | 2.68 |
| Glacial till | 0.25 | 1.00 | 0.27 | 1.23 |
| Sandstone (roof) | 0.15 | 1.00 | 3.30 | 3.56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zevgolis, I.E.; Theocharis, A.I.; Deliveris, A.V.; Koukouzas, N.C. Numerical Analysis of Groundwater Effects on the Stability of an Abandoned Shallow Underground Coal Mine. Sustainability 2023, 15, 529. https://doi.org/10.3390/su15010529
Zevgolis IE, Theocharis AI, Deliveris AV, Koukouzas NC. Numerical Analysis of Groundwater Effects on the Stability of an Abandoned Shallow Underground Coal Mine. Sustainability. 2023; 15(1):529. https://doi.org/10.3390/su15010529
Chicago/Turabian StyleZevgolis, Ioannis E., Alexandros I. Theocharis, Alexandros V. Deliveris, and Nikolaos C. Koukouzas. 2023. "Numerical Analysis of Groundwater Effects on the Stability of an Abandoned Shallow Underground Coal Mine" Sustainability 15, no. 1: 529. https://doi.org/10.3390/su15010529
APA StyleZevgolis, I. E., Theocharis, A. I., Deliveris, A. V., & Koukouzas, N. C. (2023). Numerical Analysis of Groundwater Effects on the Stability of an Abandoned Shallow Underground Coal Mine. Sustainability, 15(1), 529. https://doi.org/10.3390/su15010529








