Integration of Distributed Generations in Smart Distribution Networks Using Multi-Criteria Based Sustainable Planning Approach
Abstract
1. Introduction
- Type-I: DGs injecting only active power.
- Type-II: DGs injecting only reactive power.
- Type-III: DGs injecting both active and reactive power.
- Type-IV: DGs injecting active but consuming reactive power.
- (i)
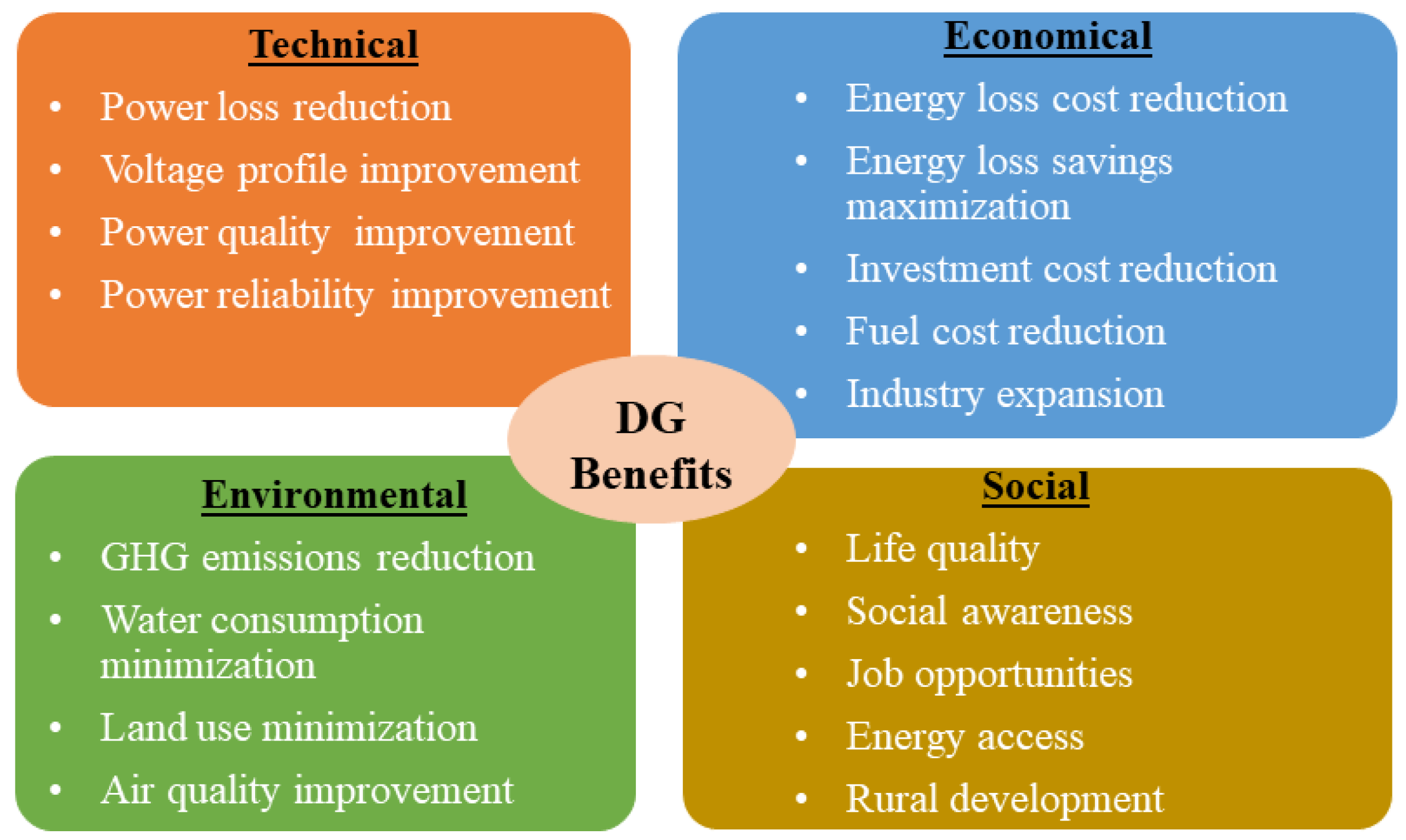
- Evaluation with techno-economic-environmental-social performance metrics.
- (ii)
- Power loss minimization and maximization of voltage profile are considered.
- (iii)
- Studying the penetration of DGs to enhance the techno-economic and environmental challenges of distribution networks.
- (iv)
- Cost-economic analysis of adopting DGs is considered.
- (v)
- Reduction in water consumption and GHG emissions, which is essential to mitigate climate change, as set forth in SDGs.
- (vi)
- Social impacts of the penetration of DGs.
- (vii)
- Evaluation of trade-off solutions across sets of alternatives.
- (viii)
- Numerical evaluations are conducted across IEEE 33-bus and 69-bus ADNs.
- (ix)
- Validation of results with those reported in the literature as a benchmark.
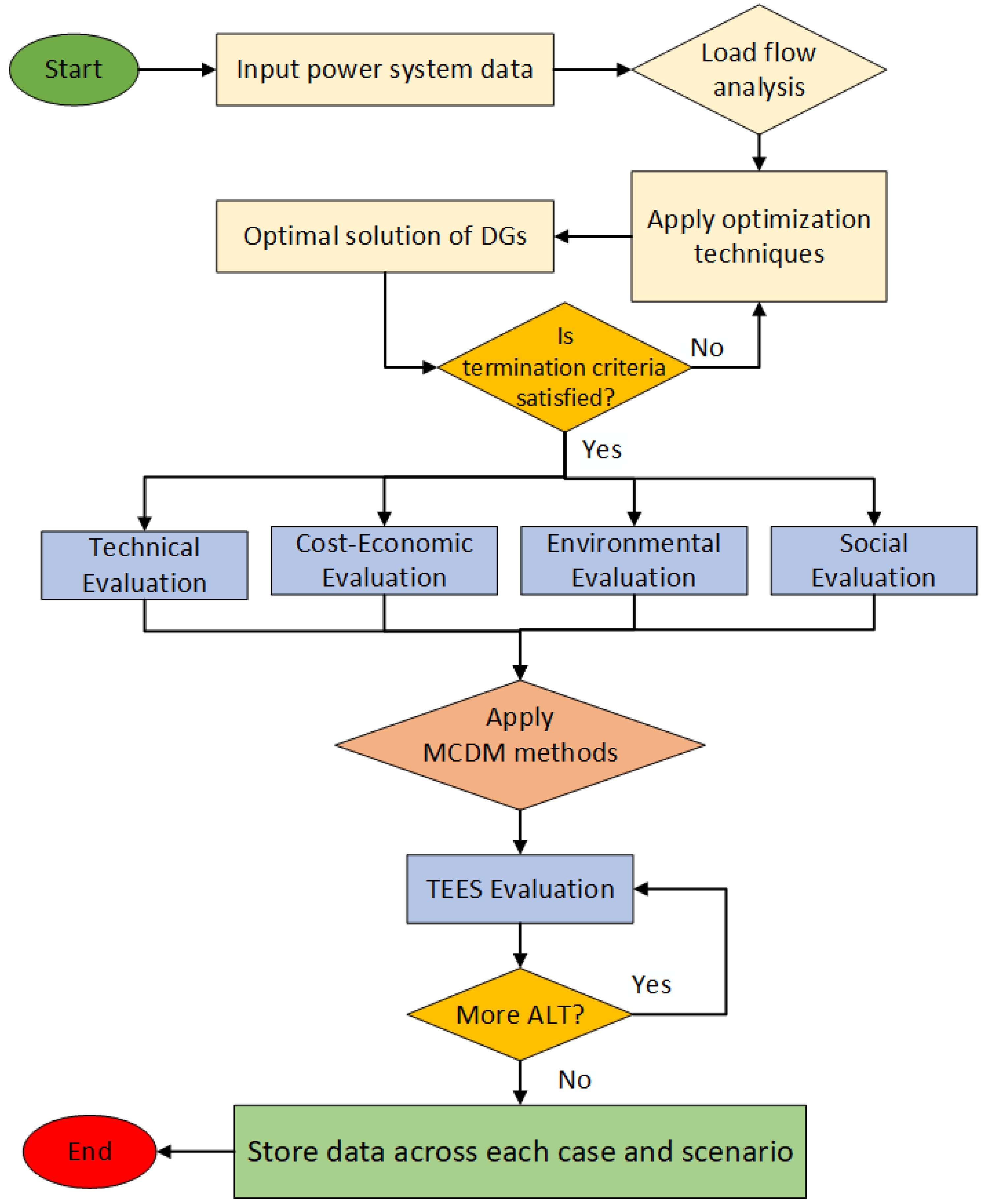
2. Problem Formulation
2.1. Power Flow Computation
2.2. Performance Evaluation Indices
2.2.1. Technical Performance Indices
Power Loss
DG Penetration Level
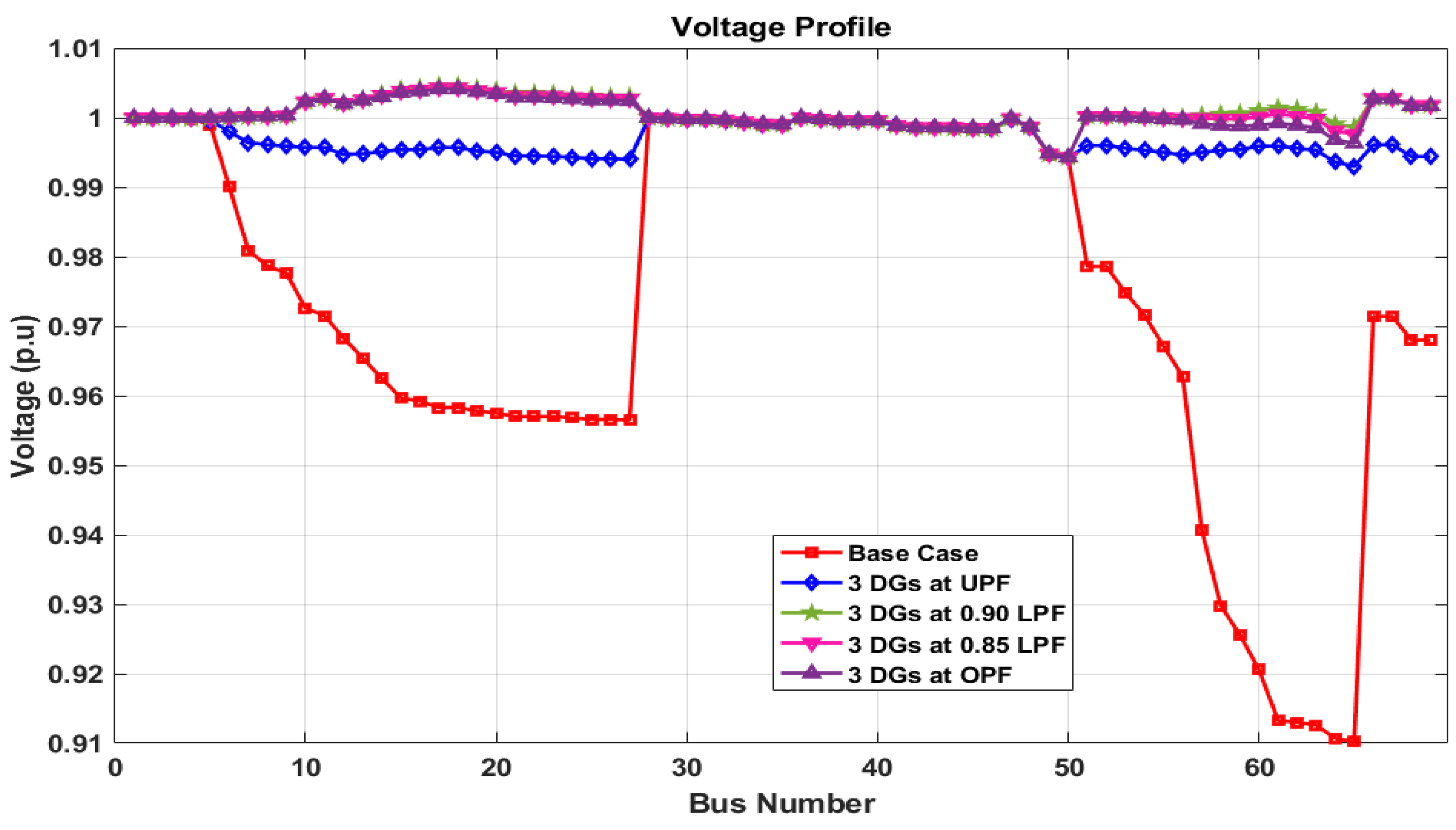
Voltage Profile
Voltage Stability Index
2.2.2. Cost-Econonmic Performance Indices
Cost of Energy Loss
Energy Loss Saving
Cost of DG
Cost of Annual Investment
2.2.3. Environmental Performance Indices
Pollution Emission
Water Consumption
Land Use
2.2.4. Social Performance Indices
Life Quality
Social Awareness
2.3. Operational Constraints
2.3.1. Equality Constraints
2.3.2. Inequality Constraints
Voltage Constraint
DG Sizing Constraint
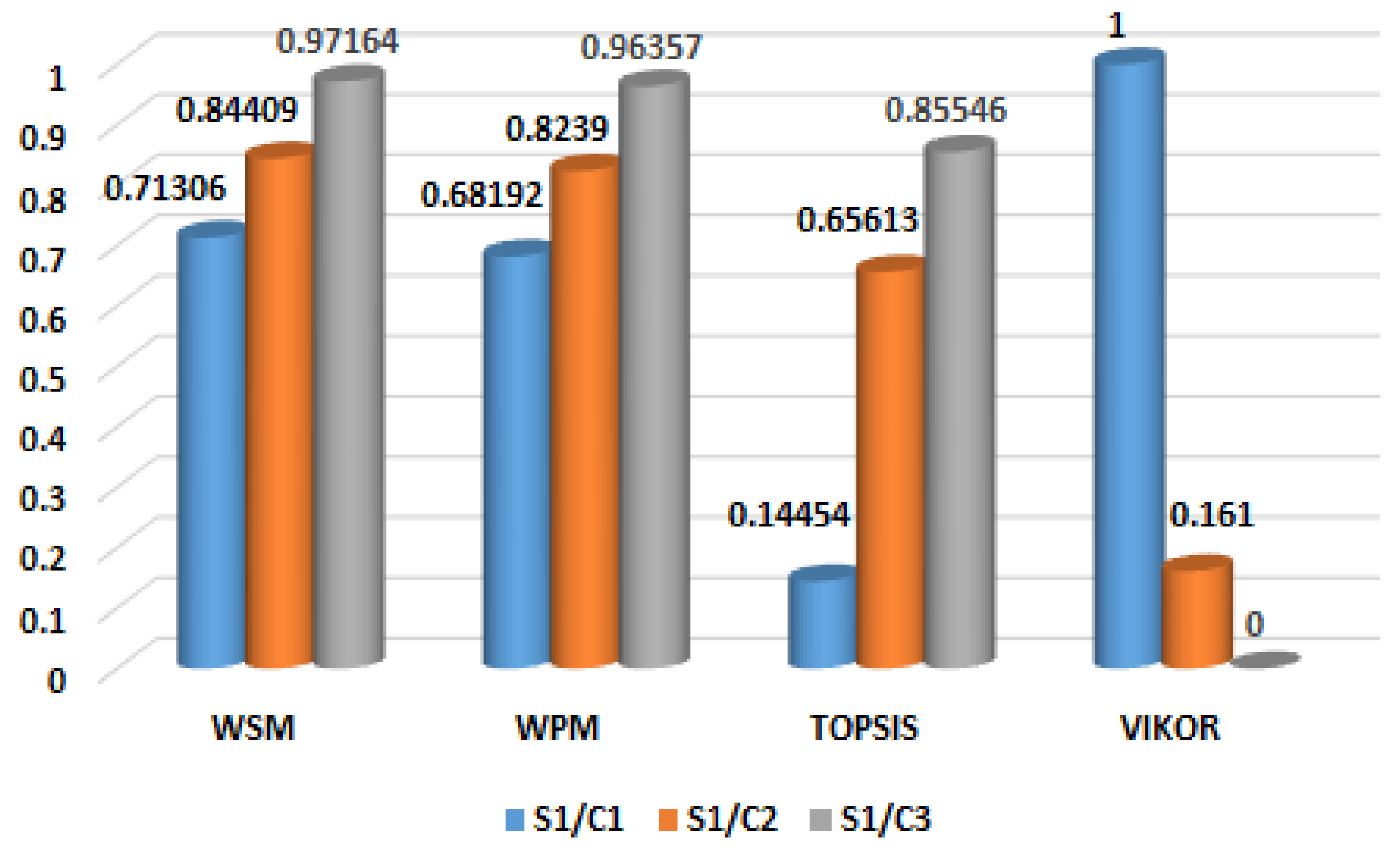
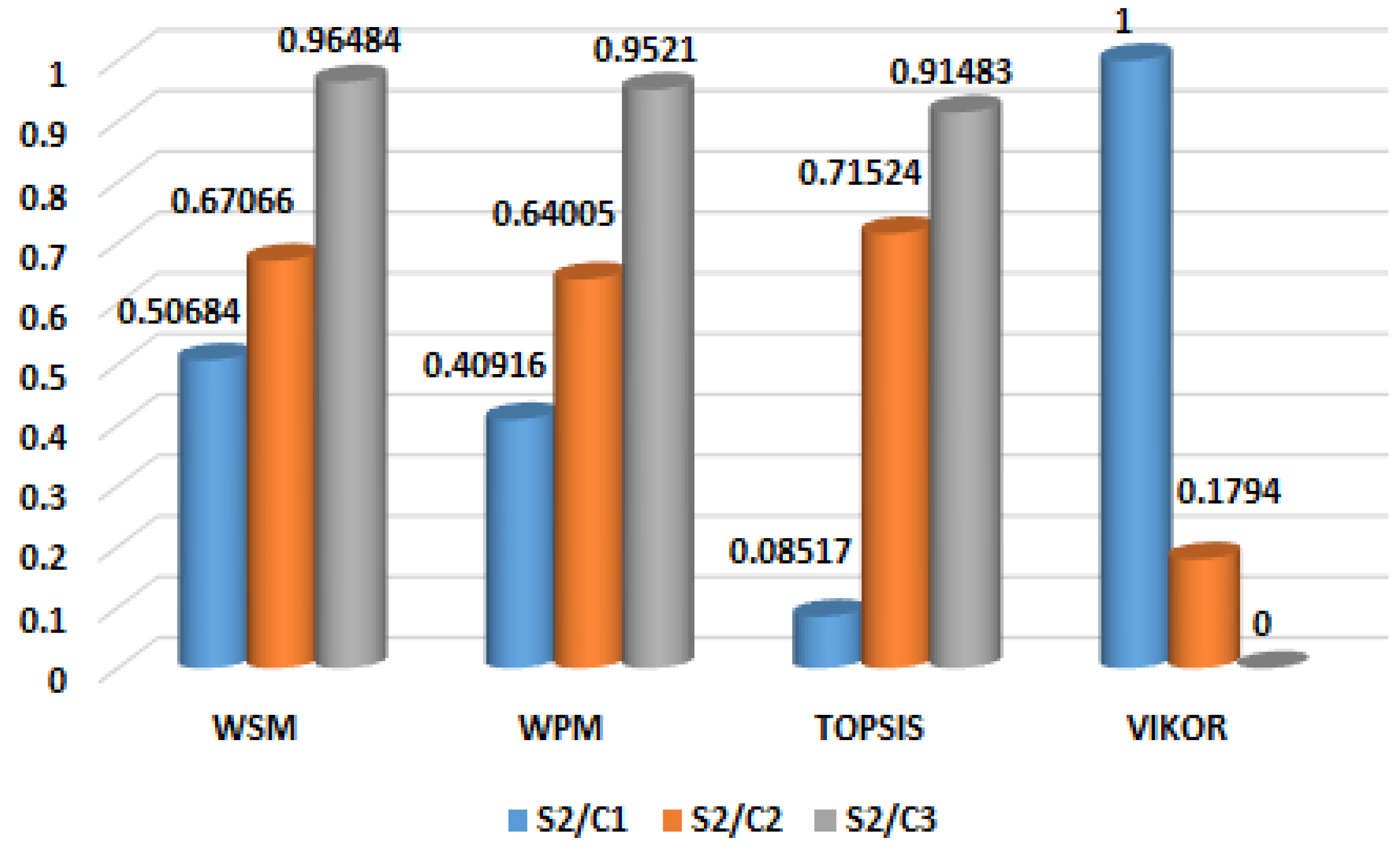
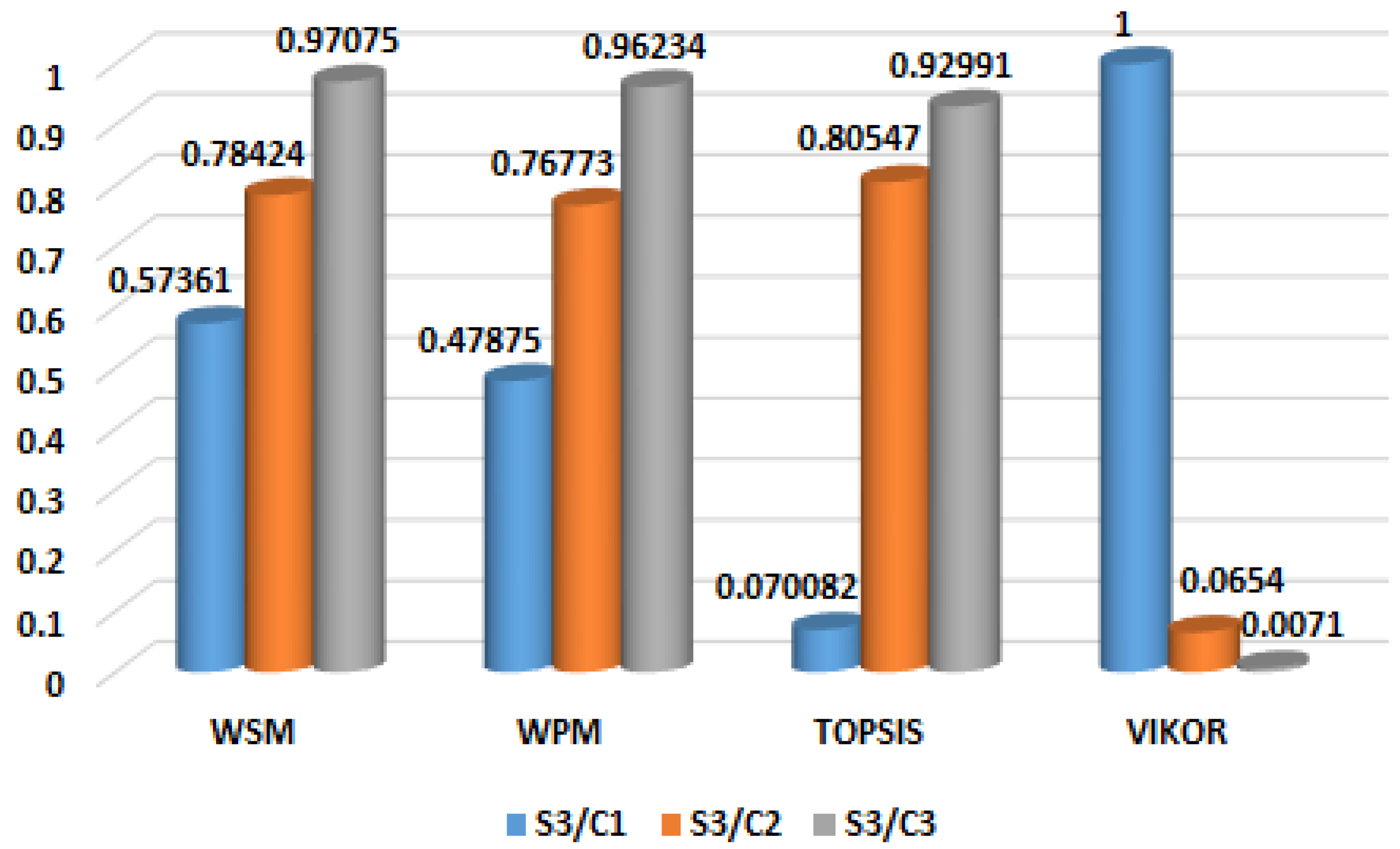
2.4. Multi-Criteria Decision Making Analysis
2.4.1. Weighted Sum Method
2.4.2. Weighted Product Method
2.4.3. Technique for Order of Preference by Similarity to Ideal Solution
2.4.4. VIseKriterijumska Optimizacija I Kompromisno Resenje
3. Overview of Optimization Techniques
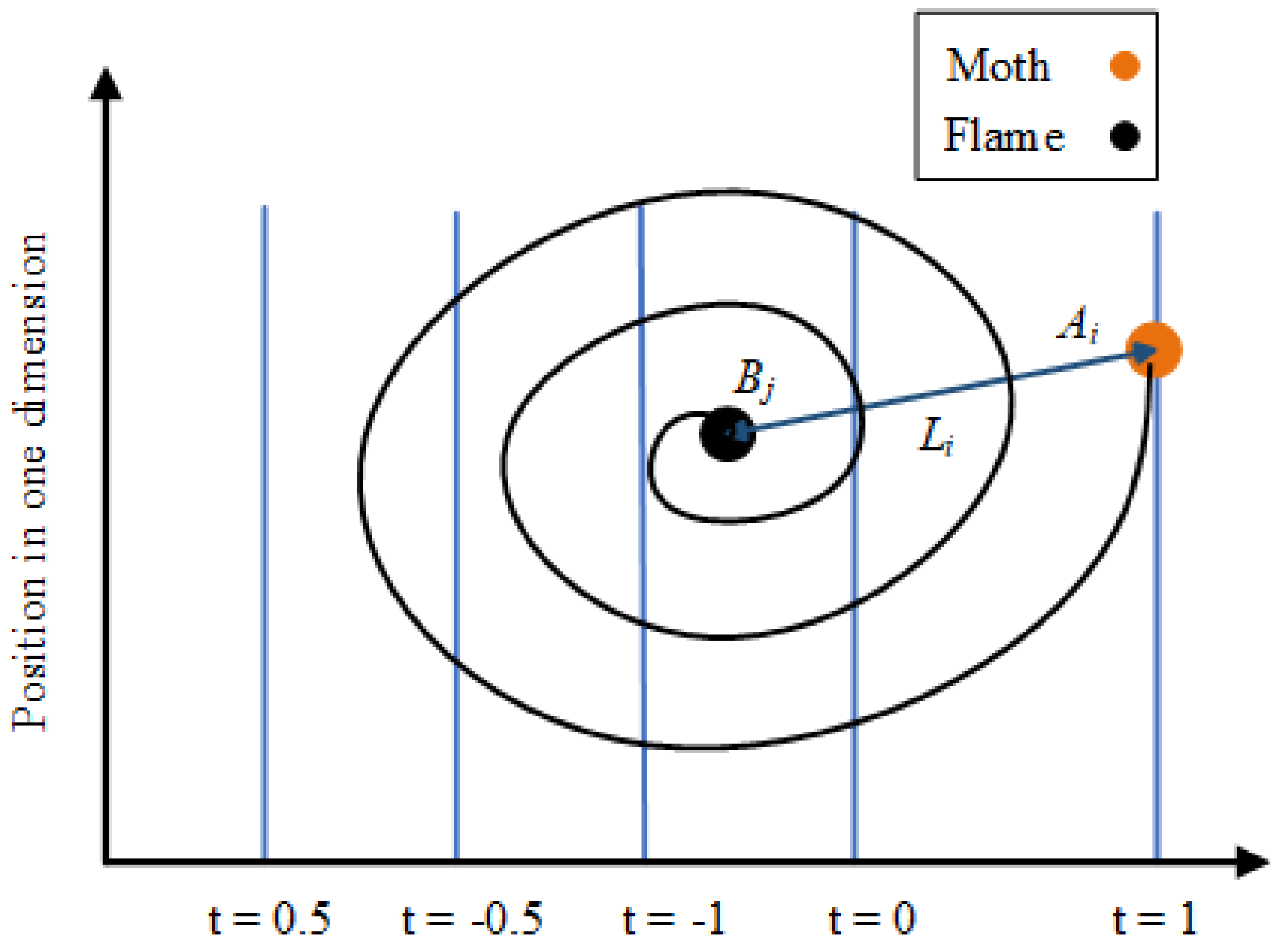
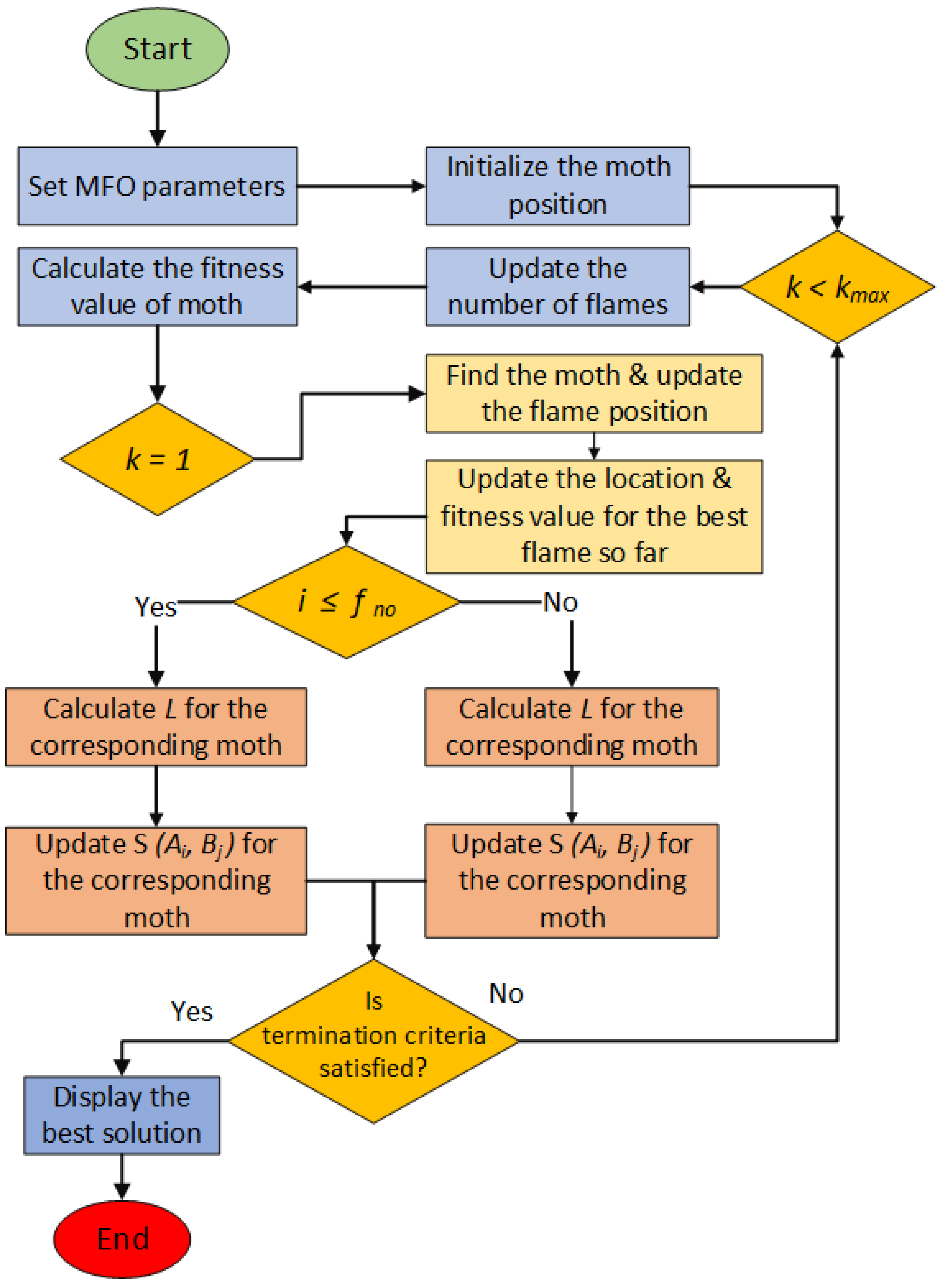
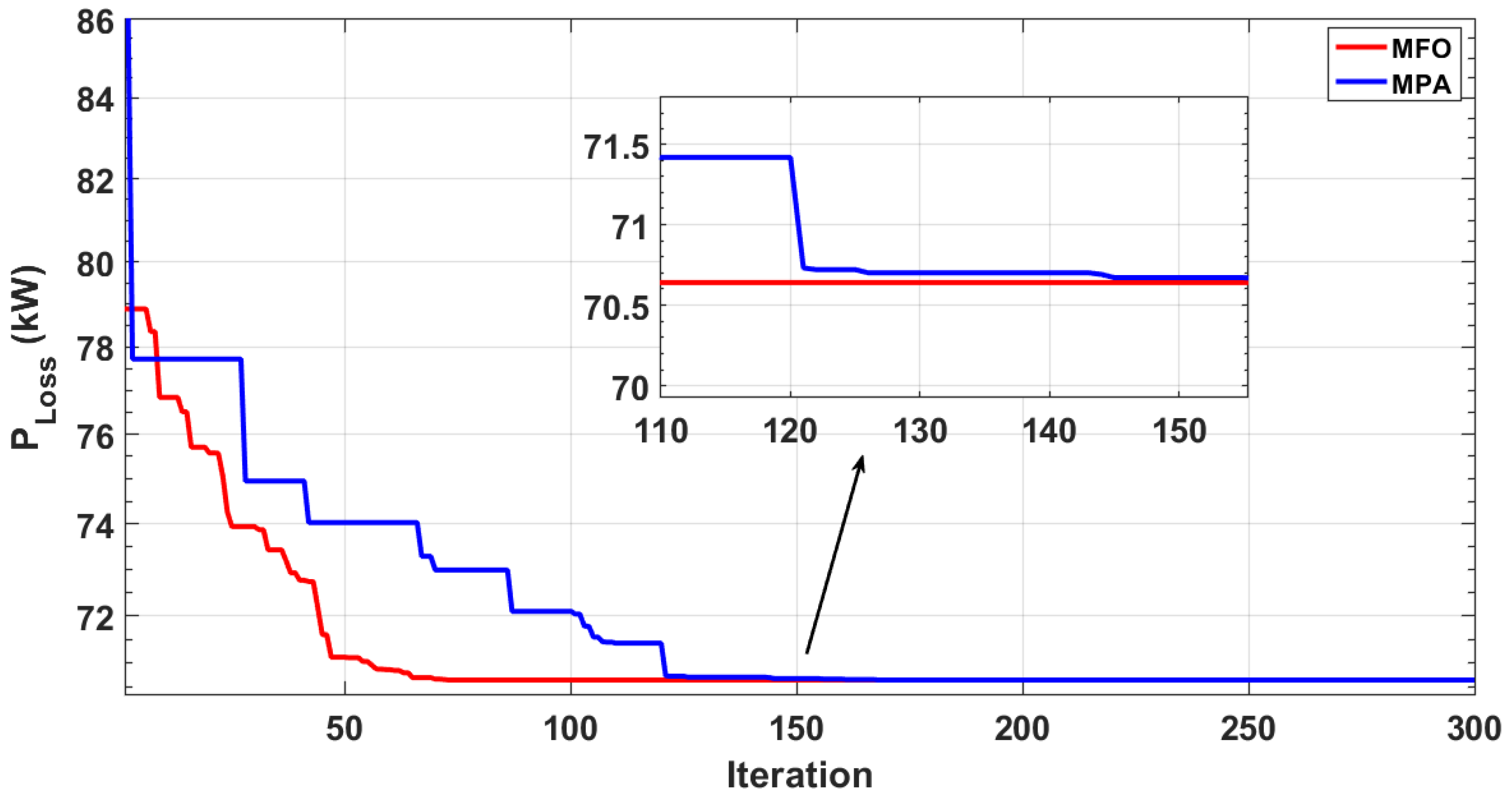
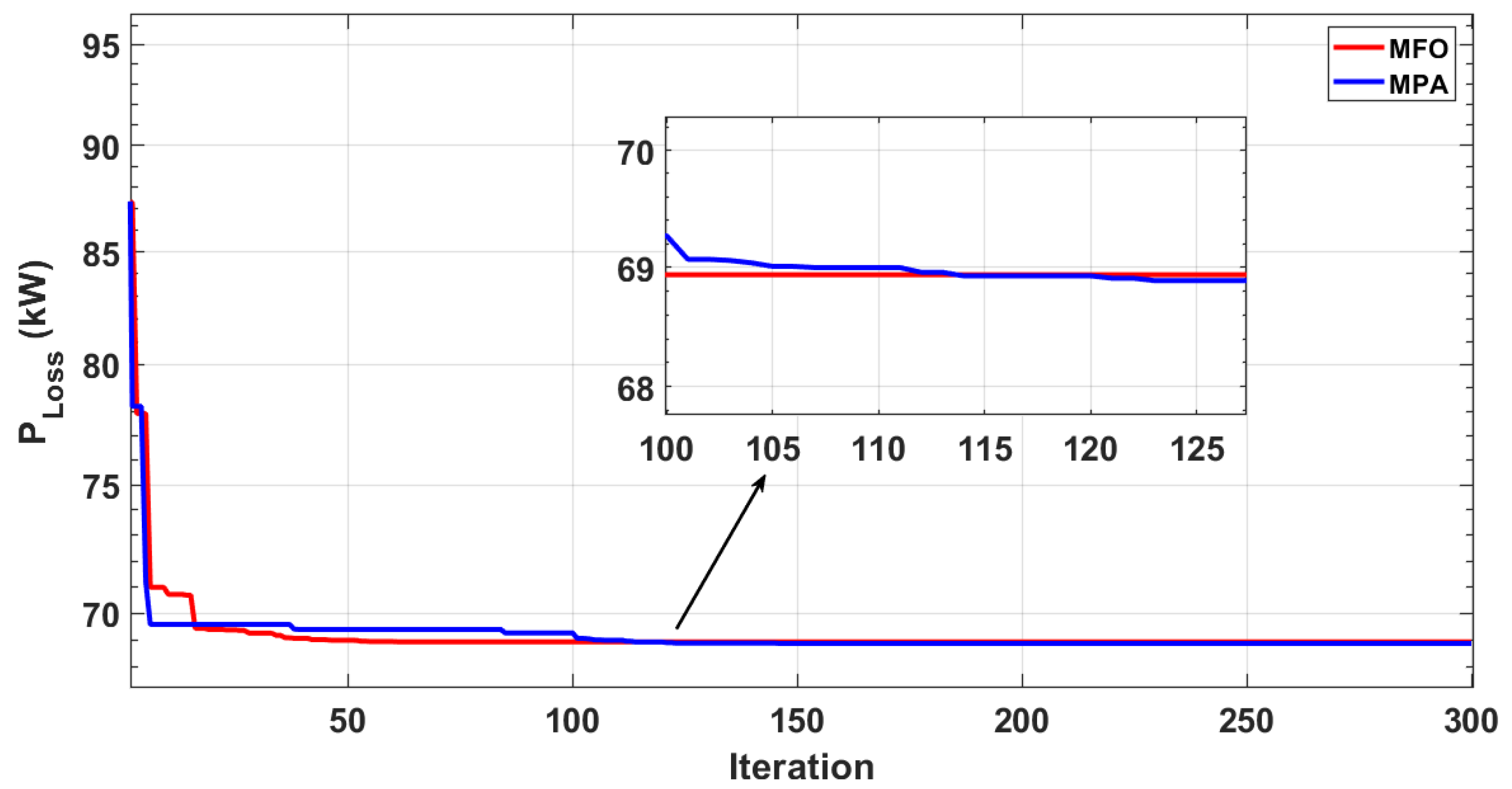
3.1. Moth Flame Optimization
| Algorithm 1 Pseudo Code of MFO |
|
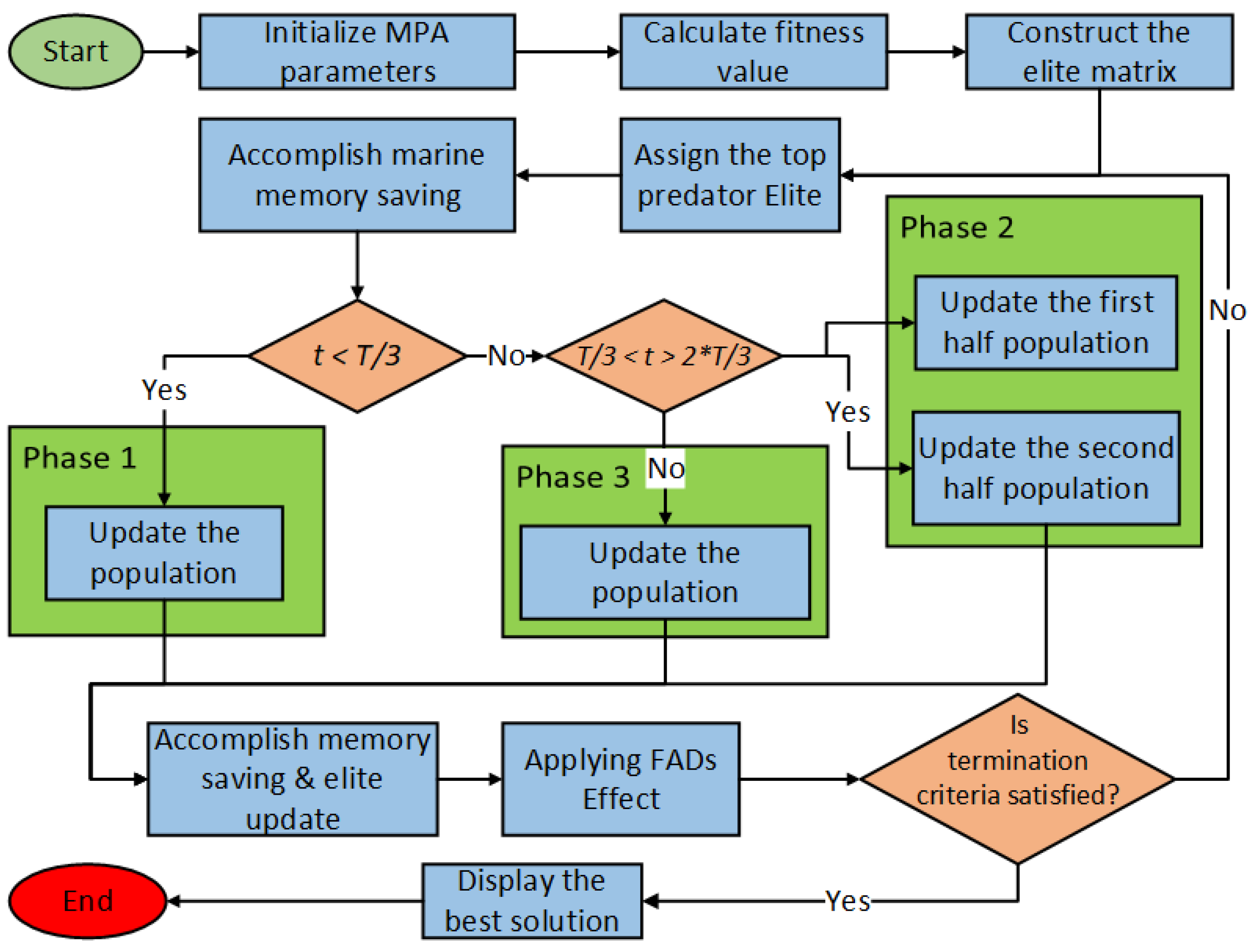
3.2. Marine Predators Algorithm
3.2.1. Phase 1
3.2.2. Phase 2
- First half of the population:where indicates Lévy movement and is a vector of random numbers based on the Lévy distribution.
- Second half of the population:where is an adaptive parameter that controls the predator’s step length during movement.
3.2.3. Phase 3
| Algorithm 2 Pseudo Code of MPA |
|
4. Results and Discussion
- (S0/C0): Base case (without DG).
- (S1/C1-3): Integrating DGs at UPF.
- (S2/C1-3): Integrating DGs at 0.90 LPF.
- (S3/C1-3): Integrating DGs at 0.85 LPF.
- (S4/C3): Integrating DGs at OPF.
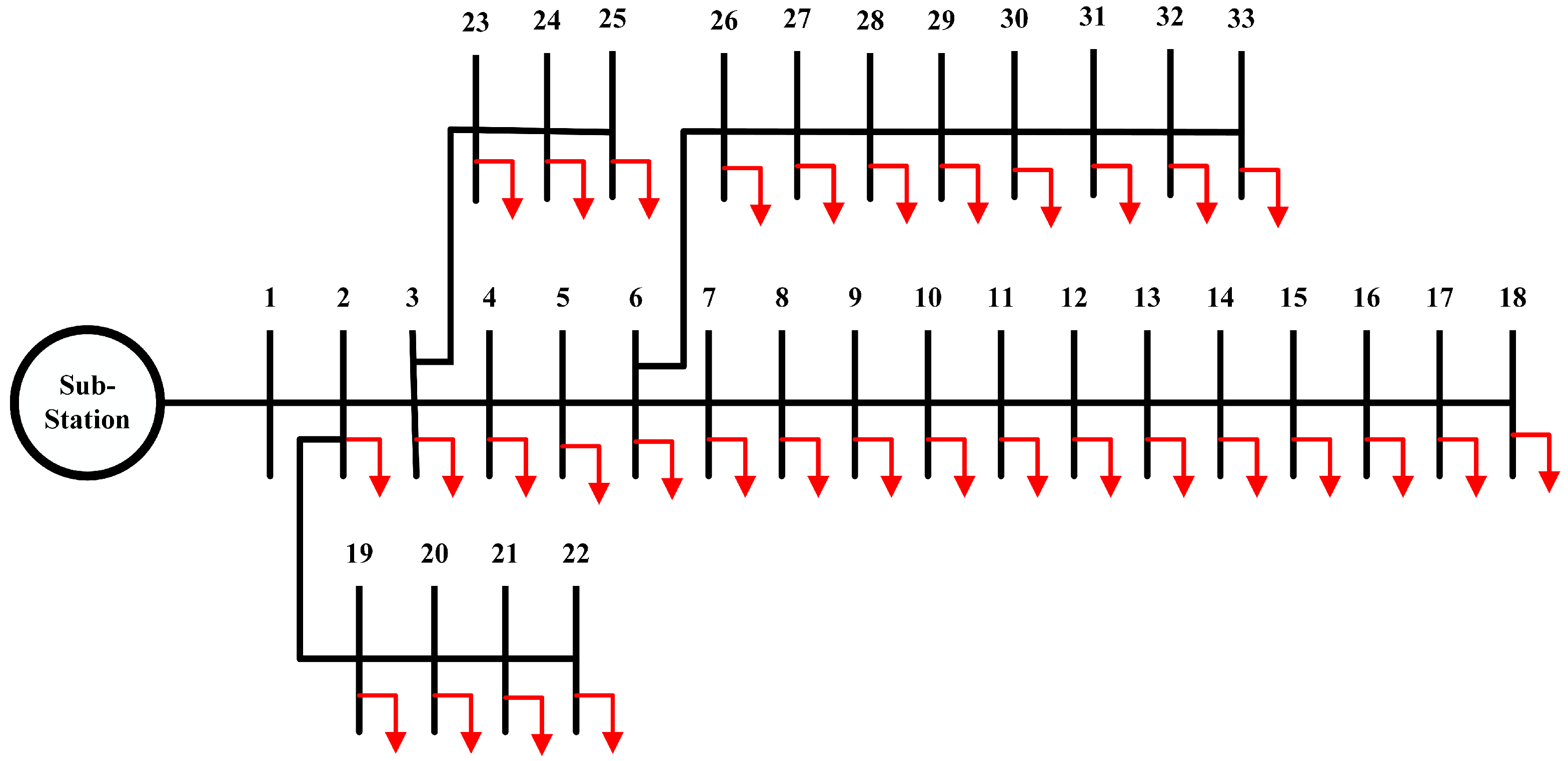
4.1. Test System 1
4.1.1. TEES Performance Evaluation
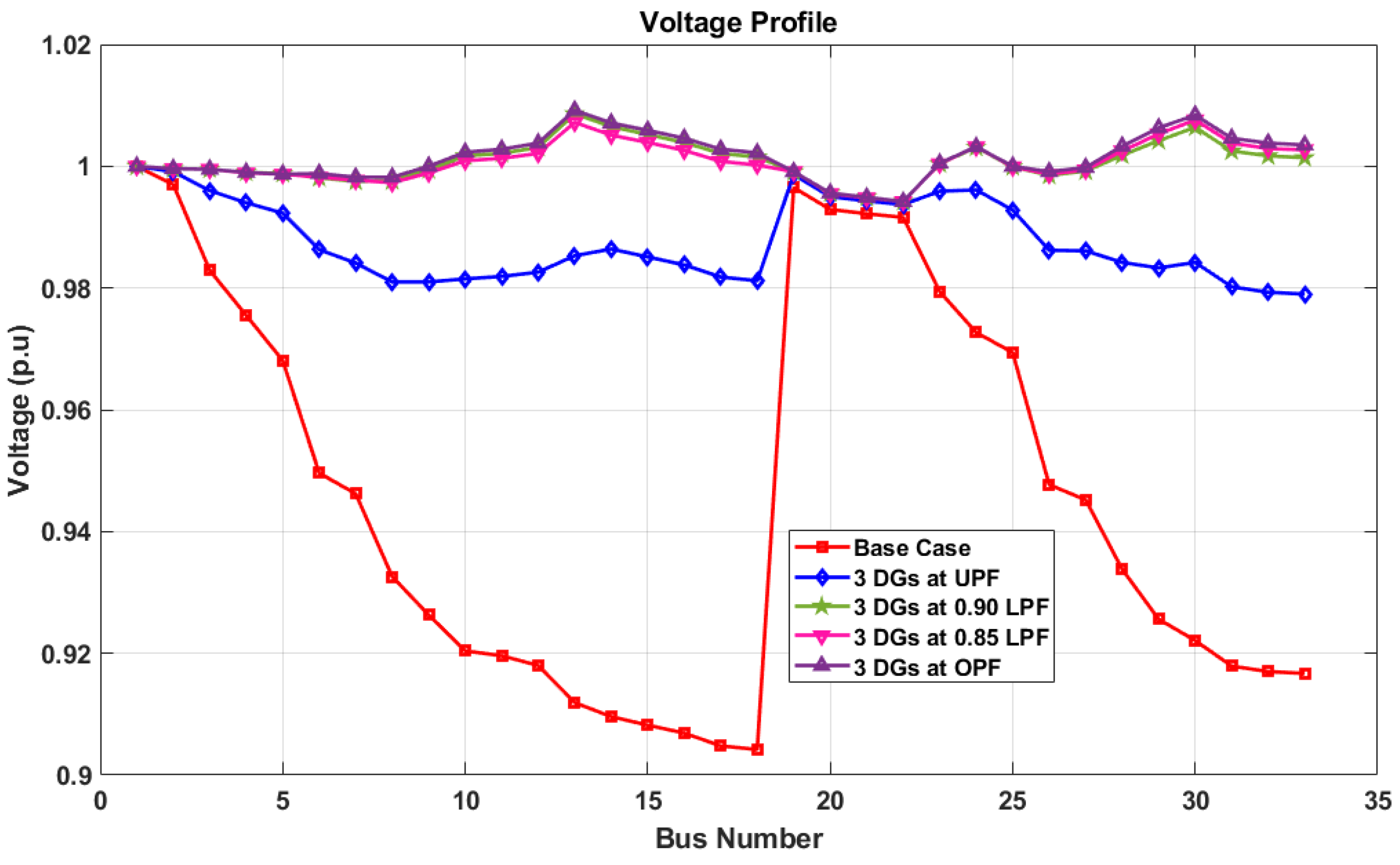
4.1.2. Scenario 1
4.1.3. Scenario 2
4.1.4. Scenario 3
4.1.5. Scenario 4
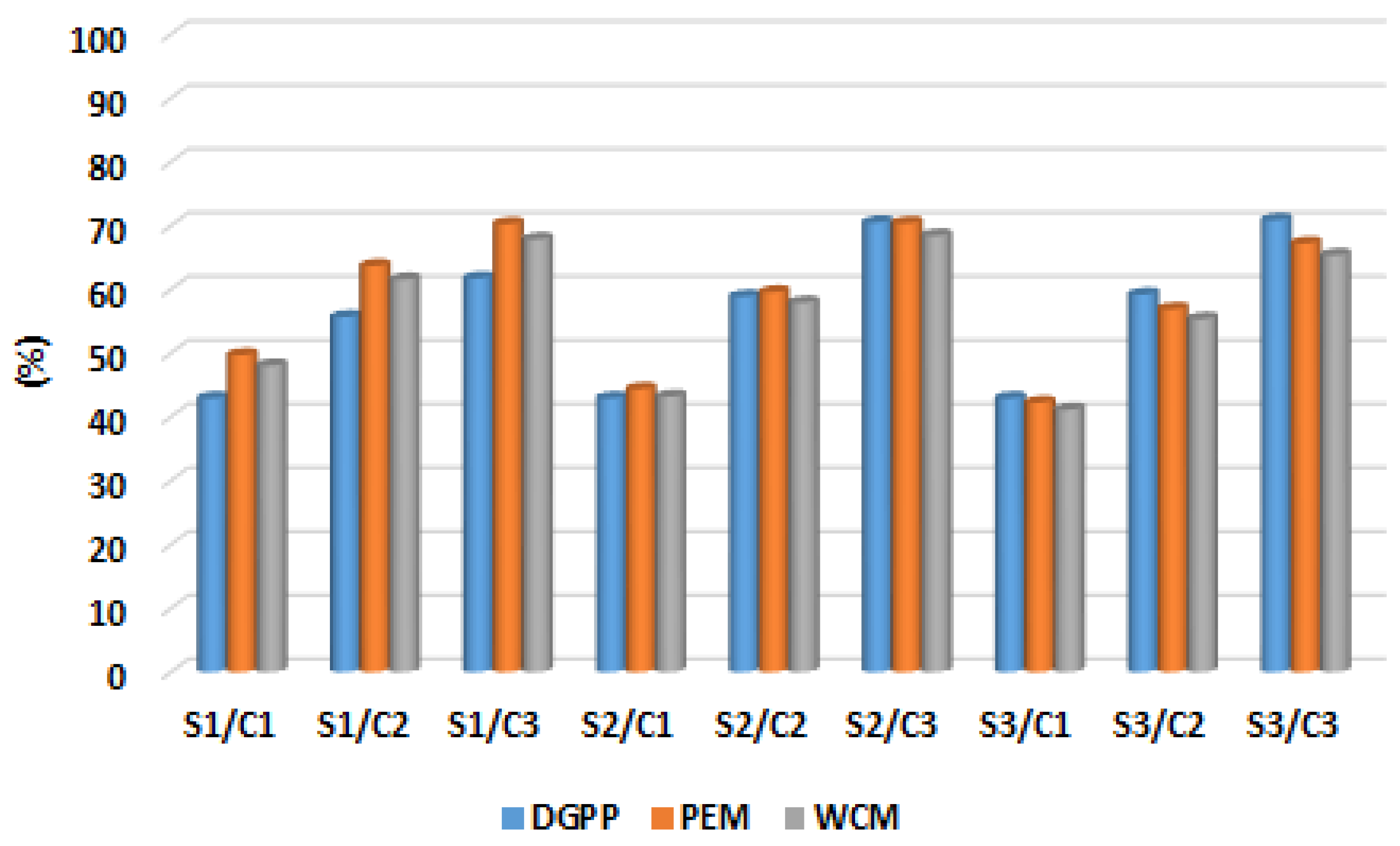
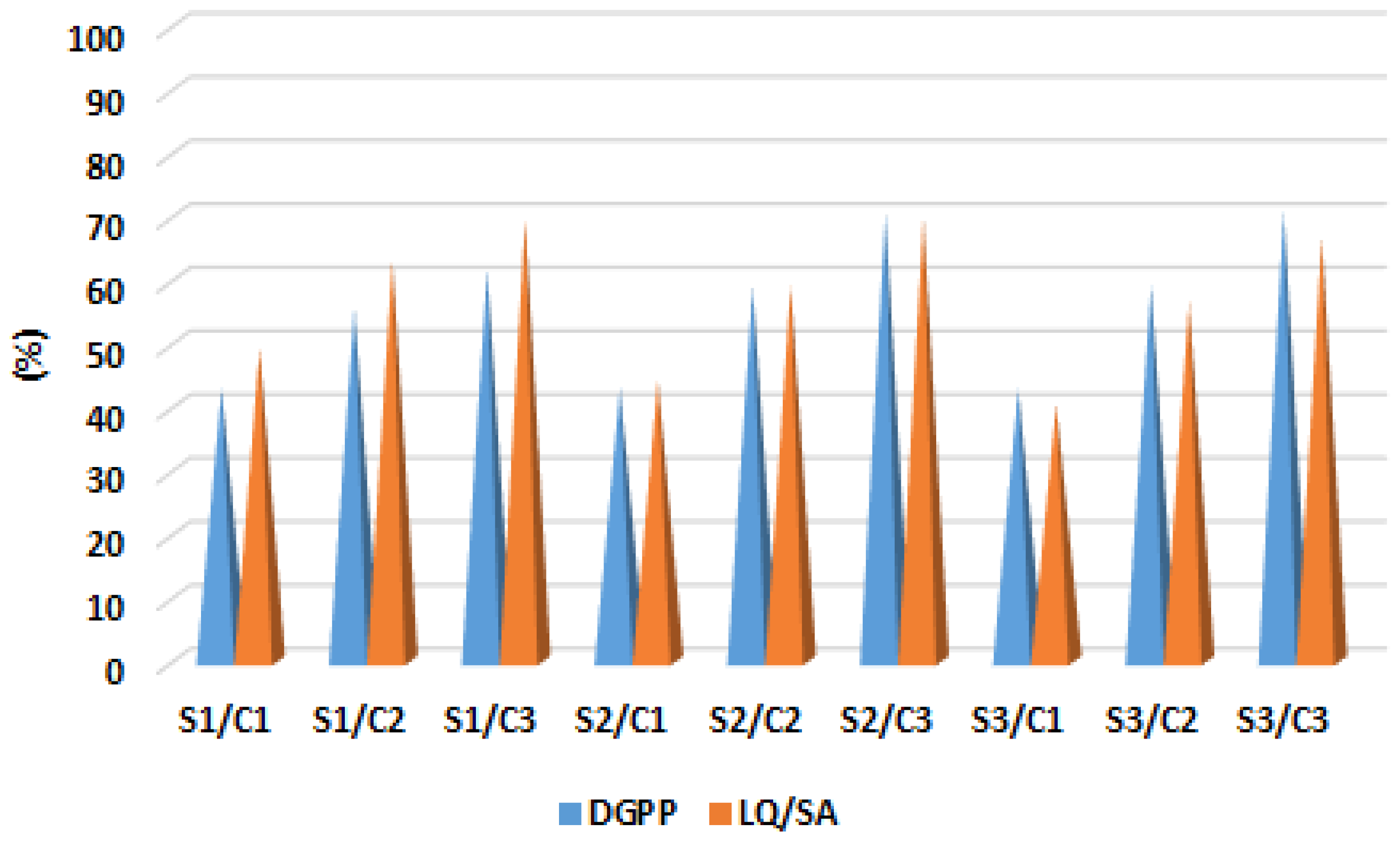
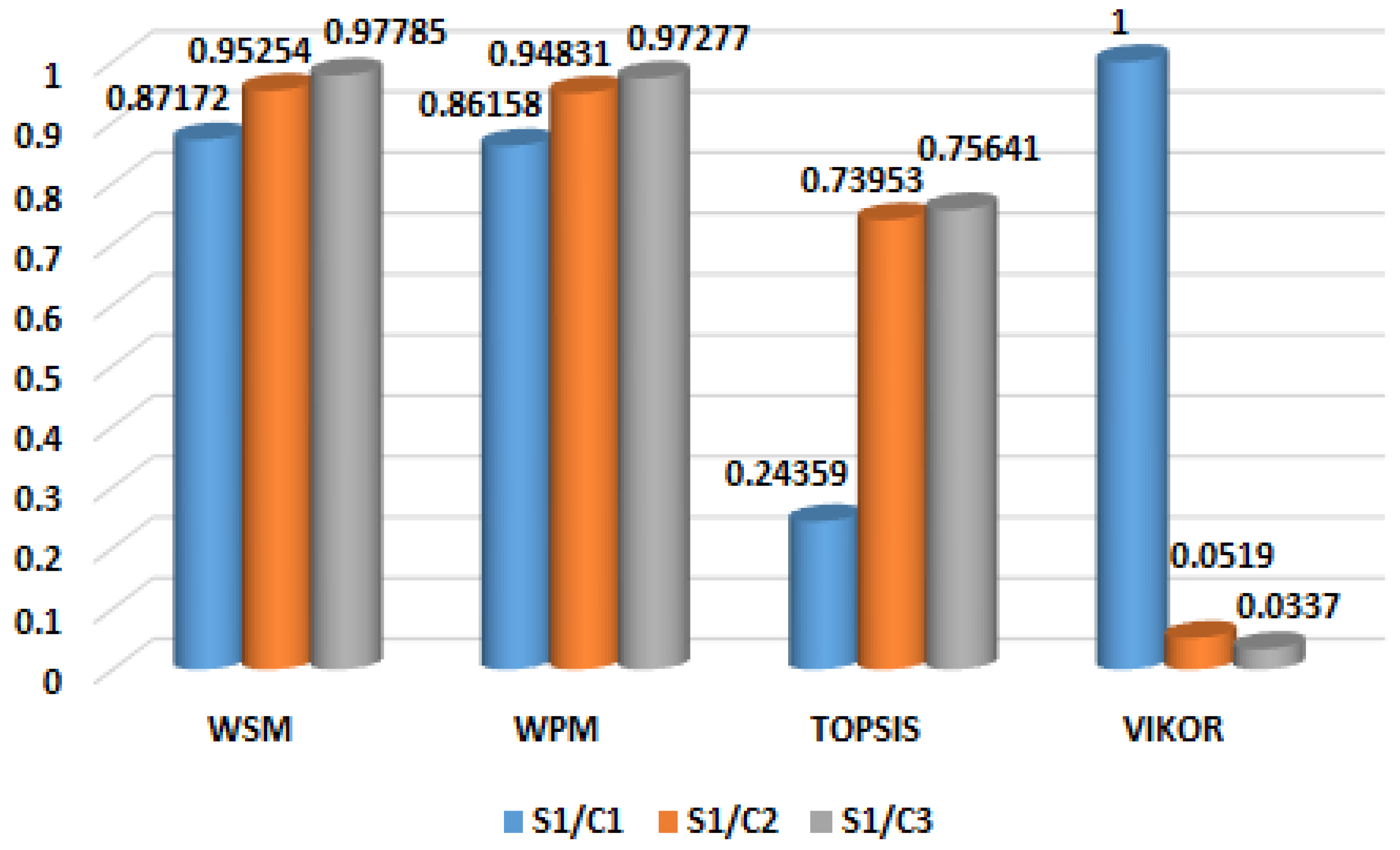
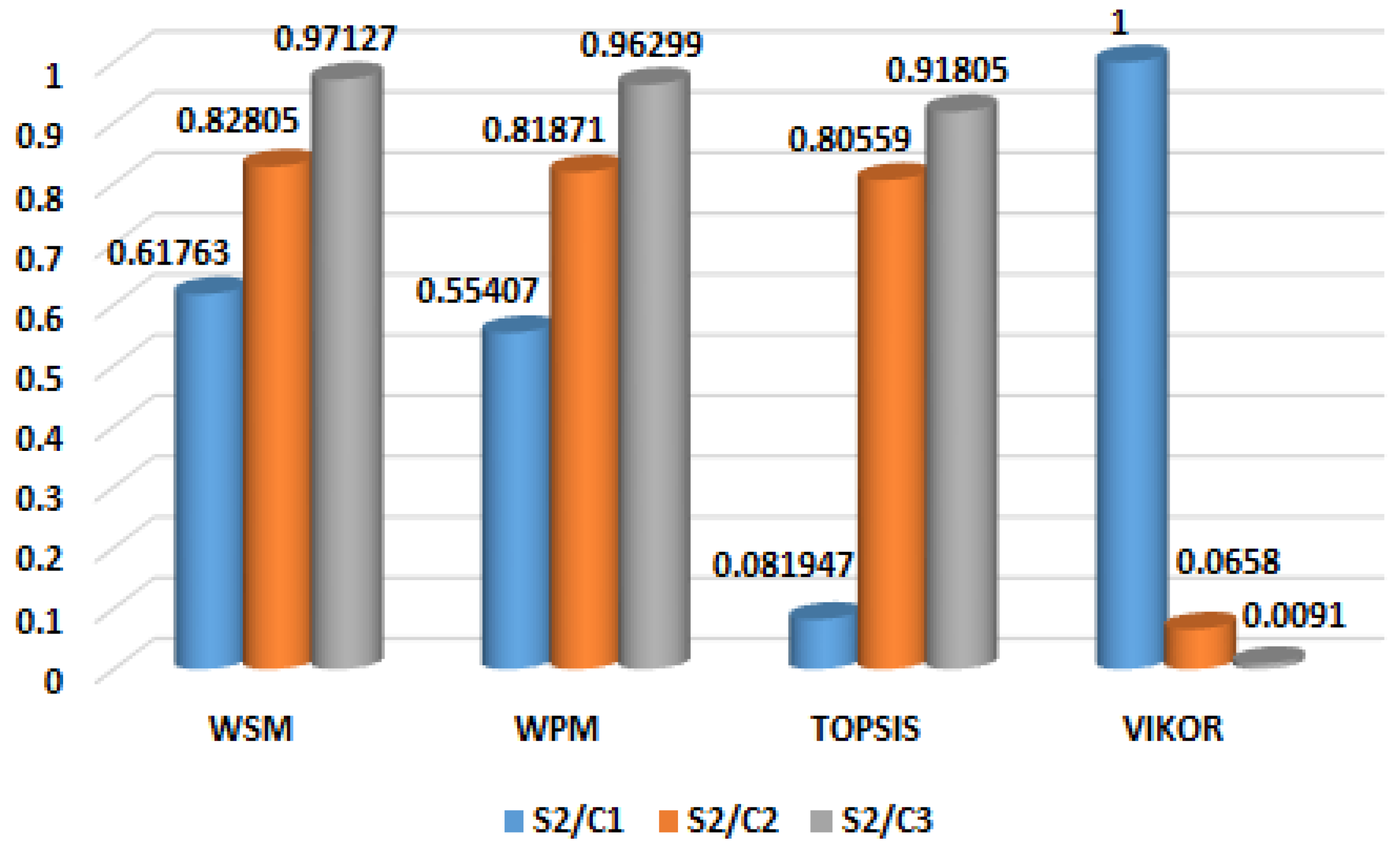
4.1.6. Performance Analysis for the Proposed Method
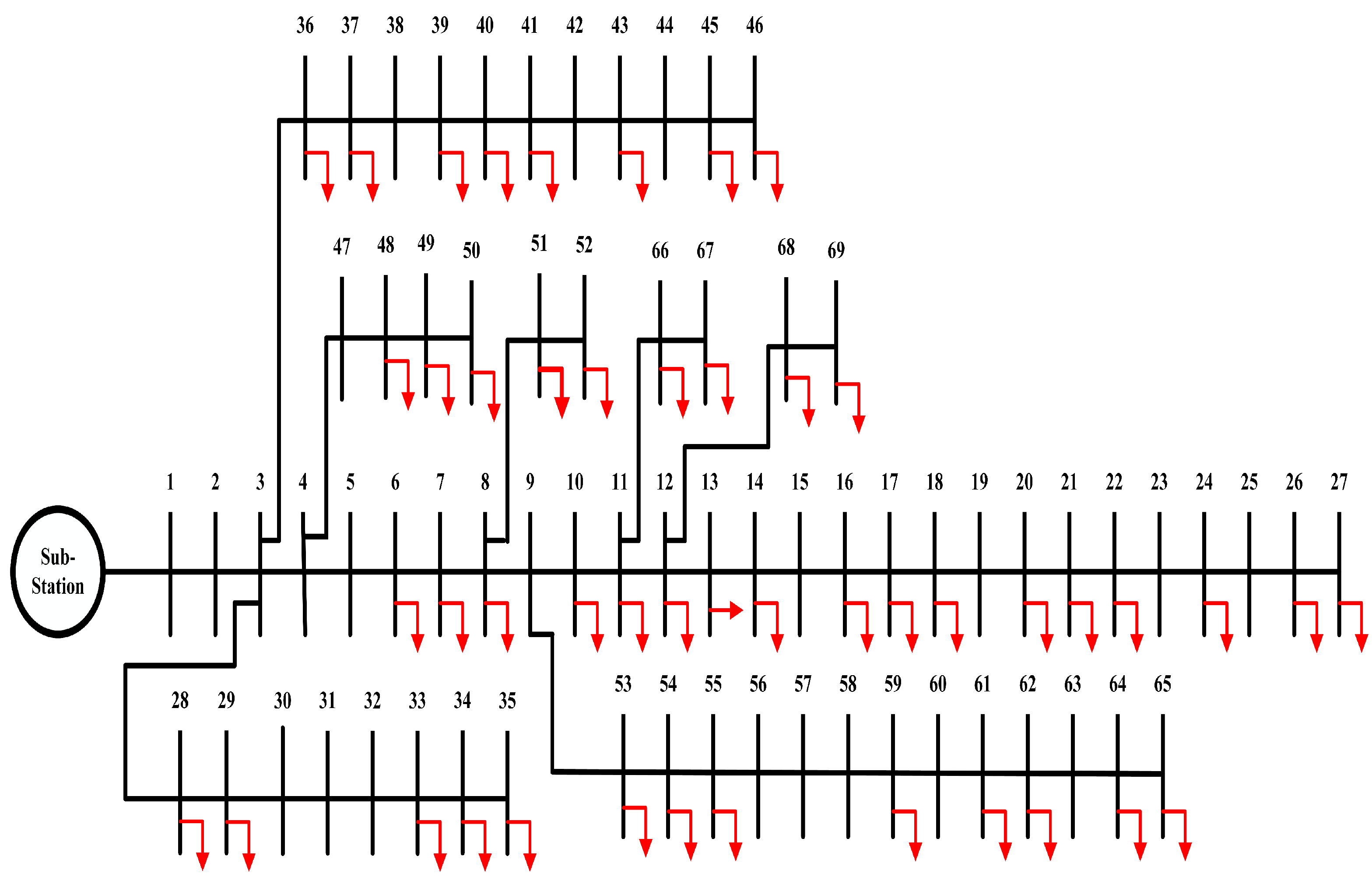
4.2. Test System 2
4.2.1. TEES Performance Evaluation
4.2.2. Scenario 1
4.2.3. Scenario 2
4.2.4. Scenario 3
4.2.5. Scenario 4
4.2.6. Performance Analysis for the Proposed Method
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ADN | Active distribution network |
| AF | Annualized factor |
| CE | Cost of electricity unit |
| CAI | Cost of annual investment |
| CPDG | Cost of active power DG |
| CQDG | Cost of reactive power DG |
| CUDG | Cost of a DG unit |
| CEPI | Cost-economic performance indices |
| Cost of energy loss/active power loss cost | |
| DG | Distributed generation |
| DN | Distribution network |
| EPI | Environmental performance indices |
| EgAj | Amount of energy produced by jth conventional power plant without employment of DG |
| Egj | Amount of energy produced by jth conventional power plant with employment of DG |
| Amount of energy produced by kth DG plant | |
| EFi | Emission factor of ith pollutant |
| IR | Interest rate based on annual cost |
| LUI | Land use intensity |
| LPF | Lagging power factor |
| M$ | Millions of USD |
| MCDM | Multiple-criteria decision making |
| ODGA | Optimal DG allocation |
| OPF | Optimal power factor |
| PF | Power factor |
| PEM | Pollution emission minimization |
| PLD | Active power load |
| PLoss | Active power loss |
| PLM | Active power loss minimization |
| PSS | Active power release from sub-station |
| QLD | Reactive power load |
| QLoss | Reactive power loss |
| QLM | Reactive power loss minimization |
| QSS | Reactive power release from sub-station |
| SPI | Social performance indices |
| Energy loss saving | |
| TEES | Techno-economic-environmental-social |
| TPI | Technical performance indices |
| UPF | Unity power factor |
| WCF | Water consumption factor |
| WCM | Water consumption minimization |
References
- Haseeb, M.; Kazmi, S.A.A.; Malik, M.M.; Ali, S.; Bukhari, S.B.A.; Shin, D.R. Multi objective based framework for energy management of smart micro-grid. IEEE Access 2020, 8, 220302–220319. [Google Scholar] [CrossRef]
- Wagh, M.; Kulkarni, V. Modeling and optimization of integration of Renewable Energy Resources (RER) for minimum energy cost, minimum CO2 Emissions and sustainable development, in recent years: A review. Mater. Today Proc. 2018, 5, 11–21. [Google Scholar] [CrossRef]
- Ackermann, T.; Andersson, G.; Söder, L. Distributed generation: A definition. Electr. Power Syst. Res. 2001, 57, 195–204. [Google Scholar] [CrossRef]
- Selim, A.; Kamel, S.; Jurado, F. Efficient optimization technique for multiple DG allocation in distribution networks. Appl. Soft Comput. 2020, 86, 105938. [Google Scholar] [CrossRef]
- Quadri, I.A.; Bhowmick, S.; Joshi, D. A hybrid teaching–learning-based optimization technique for optimal DG sizing and placement in radial distribution systems. Soft Comput. 2019, 23, 9899–9917. [Google Scholar] [CrossRef]
- Suresh, M.; Belwin, E.J. Optimal DG placement for benefit maximization in distribution networks by using Dragonfly algorithm. Renew. Wind. Water Sol. 2018, 5, 1–8. [Google Scholar] [CrossRef]
- Khodabakhshian, A.; Andishgar, M.H. Simultaneous placement and sizing of DGs and shunt capacitors in distribution systems by using IMDE algorithm. Int. J. Electr. Power Energy Syst. 2016, 82, 599–607. [Google Scholar] [CrossRef]
- Selim, A.; Kamel, S.; Mohamed, A.A.; Elattar, E.E. Optimal Allocation of Multiple Types of Distributed Generations in Radial Distribution Systems Using a Hybrid Technique. Sustainability 2021, 13, 6644. [Google Scholar] [CrossRef]
- Hung, D.Q.; Mithulananthan, N.; Bansal, R. Analytical expressions for DG allocation in primary distribution networks. IEEE Trans. Energy Convers. 2010, 25, 814–820. [Google Scholar] [CrossRef]
- Georgilakis, P.S.; Hatziargyriou, N.D. Optimal distributed generation placement in power distribution networks: Models, methods, and future research. IEEE Trans. Power Syst. 2013, 28, 3420–3428. [Google Scholar] [CrossRef]
- Jain, S.; Kalambe, S.; Agnihotri, G.; Mishra, A. Distributed generation deployment: State-of-the-art of distribution system planning in sustainable era. Renew. Sustain. Energy Rev. 2017, 77, 363–385. [Google Scholar] [CrossRef]
- Trivedi, I.N.; Jangir, P.; Bhoye, M.; Jangir, N. An economic load dispatch and multiple environmental dispatch problem solution with microgrids using interior search algorithm. Neural Comput. Appl. 2018, 30, 2173–2189. [Google Scholar] [CrossRef]
- Marwali, M.N.; Jung, J.W.; Keyhani, A. Stability analysis of load sharing control for distributed generation systems. IEEE Trans. Energy Convers. 2007, 22, 737–745. [Google Scholar] [CrossRef]
- Esmaili, M.; Firozjaee, E.C.; Shayanfar, H.A. Optimal placement of distributed generations considering voltage stability and power losses with observing voltage-related constraints. Appl. Energy 2014, 113, 1252–1260. [Google Scholar] [CrossRef]
- Parhizi, S.; Lotfi, H.; Khodaei, A.; Bahramirad, S. State of the art in research on microgrids: A review. IEEE Access 2015, 3, 890–925. [Google Scholar] [CrossRef]
- Naik, S.G.; Khatod, D.; Sharma, M. Optimal allocation of combined DG and capacitor for real power loss minimization in distribution networks. Int. J. Electr. Power Energy Syst. 2013, 53, 967–973. [Google Scholar] [CrossRef]
- Mahmoud, K.; Yorino, N.; Ahmed, A. Optimal distributed generation allocation in distribution systems for loss minimization. IEEE Trans. Power Syst. 2015, 31, 960–969. [Google Scholar] [CrossRef]
- Ehsan, A.; Yang, Q. Optimal integration and planning of renewable distributed generation in the power distribution networks: A review of analytical techniques. Appl. Energy 2018, 210, 44–59. [Google Scholar] [CrossRef]
- Niknam, T.; Taheri, S.I.; Aghaei, J.; Tabatabaei, S.; Nayeripour, M. A modified honey bee mating optimization algorithm for multiobjective placement of renewable energy resources. Appl. Energy 2011, 88, 4817–4830. [Google Scholar] [CrossRef]
- Moradi, M.H.; Abedini, M. A combination of genetic algorithm and particle swarm optimization for optimal DG location and sizing in distribution systems. Int. J. Electr. Power Energy Syst. 2012, 34, 66–74. [Google Scholar] [CrossRef]
- García, J.A.M.; Mena, A.J.G. Optimal distributed generation location and size using a modified teaching–learning based optimization algorithm. Int. J. Electr. Power Energy Syst. 2013, 50, 65–75. [Google Scholar] [CrossRef]
- Ameli, A.; Bahrami, S.; Khazaeli, F.; Haghifam, M.R. A multiobjective particle swarm optimization for sizing and placement of DGs from DG owner’s and distribution company’s viewpoints. IEEE Trans. Power Deliv. 2014, 29, 1831–1840. [Google Scholar] [CrossRef]
- Sheng, W.; Liu, K.y.; Liu, Y.; Ye, X.; He, K. Reactive power coordinated optimisation method with renewable distributed generation based on improved harmony search. IET Gener. Transm. Distrib. 2016, 10, 3152–3162. [Google Scholar] [CrossRef]
- Ali, E.; Abd Elazim, S.; Abdelaziz, A. Ant Lion Optimization Algorithm for optimal location and sizing of renewable distributed generations. Renew. Energy 2017, 101, 1311–1324. [Google Scholar] [CrossRef]
- Abou El-Ela, A.A.; El-Sehiemy, R.A.; Abbas, A.S. Optimal placement and sizing of distributed generation and capacitor banks in distribution systems using water cycle algorithm. IEEE Syst. J. 2018, 12, 3629–3636. [Google Scholar] [CrossRef]
- Ramadan, A.; Ebeed, M.; Kamel, S.; Nasrat, L. Optimal allocation of renewable energy resources considering uncertainty in load demand and generation. In Proceedings of the 2019 IEEE Conference on Power Electronics and Renewable Energy (CPERE); 2019; pp. 124–128. [Google Scholar]
- Mohamed, M.A.E.S.; Mohammed, A.A.E.; Abd Elhamed, A.M.; Hessean, M.E. Optimal allocation of photovoltaic based and DSTATCOM in a distribution network under multi load levels. Eur. J. Eng. Technol. Res. 2019, 4, 114–119. [Google Scholar]
- Sambaiah, K.S.; Jayabarathi, T. Optimal allocation of renewable distributed generation and capacitor banks in distribution systems using salp swarm algorithm. Int. J. Renew. Energy Res. 2019, 9, 96–107. [Google Scholar]
- Remha, S.; Chettih, S.; Arif, S. A novel multi-objective bat algorithm for optimal placement and sizing of distributed generation in radial distributed systems. Adv. Electr. Electron. Eng. 2018, 15, 736–746. [Google Scholar] [CrossRef]
- Ganguly, S.; Samajpati, D. Distributed generation allocation with on-load tap changer on radial distribution networks using adaptive genetic algorithm. Appl. Soft Comput. 2017, 59, 45–67. [Google Scholar] [CrossRef]
- Prasad, C.H.; Subbaramaiah, K.; Sujatha, P. Cost–benefit analysis for optimal DG placement in distribution systems by using elephant herding optimization algorithm. Renew. Wind Water Solar 2019, 6, 1–12. [Google Scholar] [CrossRef]
- Almabsout, E.A.; El-Sehiemy, R.A.; An, O.N.U.; Bayat, O. A hybrid local search-genetic algorithm for simultaneous placement of DG units and shunt capacitors in radial distribution systems. IEEE Access 2020, 8, 54465–54481. [Google Scholar] [CrossRef]
- Nagaballi, S.; Kale, V.S. Pareto optimality and game theory approach for optimal deployment of DG in radial distribution system to improve techno-economic benefits. Appl. Soft Comput. 2020, 92, 106234. [Google Scholar] [CrossRef]
- Hemeida, M.G.; Ibrahim, A.A.; Mohamed, A.A.A.; Alkhalaf, S.; El-Dine, A.M.B. Optimal allocation of distributed generators DG based Manta Ray Foraging Optimization algorithm (MRFO). Ain Shams Eng. J. 2021, 12, 609–619. [Google Scholar] [CrossRef]
- Rupa, J.M.; Ganesh, S. Power flow analysis for radial distribution system using backward/forward sweep method. Int. J. Electr. Comput. Electron. Commun. Eng. 2014, 8, 1540–1544. [Google Scholar]
- Buayai, K.; Ongsakul, W.; Mithulananthan, N. Multi-objective micro-grid planning by NSGA-II in primary distribution system. Eur. Trans. Electr. Power 2012, 22, 170–187. [Google Scholar] [CrossRef]
- Selim, A.; Kamel, S.; Alghamdi, A.S.; Jurado, F. Optimal placement of DGs in distribution system using an improved harris hawks optimizer based on single-and multi-objective approaches. IEEE Access 2020, 8, 52815–52829. [Google Scholar] [CrossRef]
- Murty, V.V.; Kumar, A. Optimal placement of DG in radial distribution systems based on new voltage stability index under load growth. Int. J. Electr. Power Energy Syst. 2015, 69, 246–256. [Google Scholar] [CrossRef]
- Kazmi, S.A.A.; Ameer Khan, U.; Ahmad, W.; Hassan, M.; Ibupoto, F.A.; Bukhari, S.B.A.; Ali, S.; Malik, M.M.; Shin, D.R. Multiple (TEES)-Criteria-Based Sustainable Planning Approach for Mesh-Configured Distribution Mechanisms across Multiple Load Growth Horizons. Energies 2021, 14, 3128. [Google Scholar] [CrossRef]
- Oda, E.S.; Abd El Hamed, A.M.; Ali, A.; Elbaset, A.A.; Abd El Sattar, M.; Ebeed, M. Stochastic Optimal Planning of Distribution System Considering Integrated Photovoltaic-Based DG and DSTATCOM Under Uncertainties of Loads and Solar Irradiance. IEEE Access 2021, 9, 26541–26555. [Google Scholar] [CrossRef]
- Chiradeja, P.; Ramakumar, R. An approach to quantify the technical benefits of distributed generation. IEEE Trans. Energy Convers. 2004, 19, 764–773. [Google Scholar] [CrossRef]
- Baldwin, S. Carbon footprint of electricity generation. Lond. Parliam. Off. Sci. Technol. 2006, 268. [Google Scholar]
- Macknick, J.; Newmark, R.; Heath, G.; Hallett, K. Review of Operational Water Consumption and Withdrawal Factors for Electricity Generating Technologies; Technical Report; National Renewable Energy Lab.(NREL): Golden, CO, USA, 2011. [Google Scholar]
- Fritsche, U.; Berndes, G.; Cowie, A.; Johnson, F.; Dale, V.; Langeveld, H.; Sharma, N.; Watson, H.; Woods, J. Energy and Land Use: Global Land Outlook Working Paper; United Nations Convention to Combat Desertification (UNCCD): Bonn, Germany, 2017. [Google Scholar]
- Kumar, A.; Sah, B.; Singh, A.R.; Deng, Y.; He, X.; Kumar, P.; Bansal, R. A review of multi criteria decision making (MCDM) towards sustainable renewable energy development. Renew. Sustain. Energy Rev. 2017, 69, 596–609. [Google Scholar] [CrossRef]
- Jin, J.; Rothrock, L.; McDermott, P.L.; Barnes, M. Using the analytic hierarchy process to examine judgment consistency in a complex multiattribute task. IEEE Trans. Syst. Man, Cybern. Part A Syst. Hum. 2010, 40, 1105–1115. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl.-Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine Predators Algorithm: A nature-inspired metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar] [CrossRef]
- Sultana, S.; Roy, P.K. Multi-objective quasi-oppositional teaching learning based optimization for optimal location of distributed generator in radial distribution systems. Int. J. Electr. Power Energy Syst. 2014, 63, 534–545. [Google Scholar] [CrossRef]
- Sultana, S.; Roy, P.K. Krill herd algorithm for optimal location of distributed generator in radial distribution system. Appl. Soft Comput. 2016, 40, 391–404. [Google Scholar] [CrossRef]
- Sharma, S.; Bhattacharjee, S.; Bhattacharya, A. Quasi-Oppositional Swine Influenza Model Based Optimization with Quarantine for optimal allocation of DG in radial distribution network. Int. J. Electr. Power Energy Syst. 2016, 74, 348–373. [Google Scholar] [CrossRef]
- Truong, K.H.; Nallagownden, P.; Elamvazuthi, I.; Vo, D.N. A quasi-oppositional-chaotic symbiotic organisms search algorithm for optimal allocation of DG in radial distribution networks. Appl. Soft Comput. 2020, 88, 106067. [Google Scholar] [CrossRef]
- Meena, N.K.; Swarnkar, A.; Gupta, N.; Niazi, K.R. Multi-objective Taguchi approach for optimal DG integration in distribution systems. IET Gener. Transm. Distrib. 2017, 11, 2418–2428. [Google Scholar] [CrossRef]
- Meena, N.K.; Parashar, S.; Swarnkar, A.; Gupta, N.; Niazi, K.R. Improved elephant herding optimization for multiobjective DER accommodation in distribution systems. IEEE Trans. Ind. Inform. 2017, 14, 1029–1039. [Google Scholar] [CrossRef]
- Saha, S.; Mukherjee, V. A novel multiobjective chaotic symbiotic organisms search algorithm to solve optimal DG allocation problem in radial distribution system. Int. Trans. Electr. Energy Syst. 2019, 29, e2839. [Google Scholar] [CrossRef]
- Ali, A.; Keerio, M.; Laghari, J. Optimal Site and Size of Distributed Generation Allocation in Radial Distribution Network Using Multi-objective Optimization. J. Mod. Power Syst. Clean Energy 2020, 9, 404–415. [Google Scholar] [CrossRef]
- Nguyen, T.P.; Vo, D.N. A novel stochastic fractal search algorithm for optimal allocation of distributed generators in radial distribution systems. Appl. Soft Comput. 2018, 70, 773–796. [Google Scholar] [CrossRef]
- AlRashidi, M.; AlHajri, M. Optimal planning of multiple distributed generation sources in distribution networks: A new approach. Energy Convers. Manag. 2011, 52, 3301–3308. [Google Scholar] [CrossRef]
- Nekooei, K.; Farsangi, M.M.; Nezamabadi-Pour, H.; Lee, K.Y. An improved multi-objective harmony search for optimal placement of DGs in distribution systems. IEEE Trans. Smart Grid 2013, 4, 557–567. [Google Scholar] [CrossRef]









| Description | Simulation Parameters | |
|---|---|---|
| DG Technology | Photovoltaic | Gas-turbine |
| DG Type by PF | UPF/Type-I | LPF/Type-III |
| (MW/MVA) | 0.001 to 2 | 0.001 to 2 |
| ($/kVA) | 770 | 1800 |
| Service life (years) | 20 | 10 |
| Interest rate (%) | 7% | 7% |
| EF (kgCO2/kWh) | 0.058 | 0.093 |
| WCF (gal/MWh) | 26 | 35 |
| LUI (m2/MWh) | 10 | 500 |
| PI | Objective | PI | Objective | PI | Objective |
|---|---|---|---|---|---|
| Vmin | ↑ | CELoss | ↓ | PEM | ↑ |
| VSI | ↑ | CPDG | ↓ | WCM | ↑ |
| PLM | ↑ | CQDG | ↓ | LQ | ↑ |
| QLM | ↑ | CAI | ↓ | SA | ↑ |
| DGPP | ↑ | LU | ↓ | SELoss | ↑ |
| Alternatives/Solutions | Weighted Attributes | ||||
|---|---|---|---|---|---|
| C1× W1 | C2 × W2 | C3 × W3 | ⋯ | Ck × Wk | |
| A1 | S11 | S12 | S13 | ⋯ | S1m |
| A2 | S21 | S22 | S23 | ⋯ | S2m |
| A3 | S31 | S32 | S33 | ⋯ | S3m |
| ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
| An | Sn1 | Sn2 | Sn3 | ⋯ | Snm |
| Performance | IEEE 33-bus | IEEE 69-bus |
|---|---|---|
| Indices | (S0/C0_1) | (S0/C0_2) |
| DG Size @ Bus (kVA) | - | - |
| Vmin (p.u) | 0.9042 | 0.9102 |
| PLoss (kW) | 210.1 | 224.6 |
| QLoss (kVAR) | 142.4 | 101.9 |
| VSI (p.u) | 0.6672 | 0.6832 |
| Sr. No. | DG Size @ Bus | Vmin | PLoss | QLoss | PLM | QLM | DGPP | PSS | QSS |
|---|---|---|---|---|---|---|---|---|---|
| (kW) | (p.u) | (kW) | (kVAR) | (%) | (%) | (%) | (kW) | (kVAR) | |
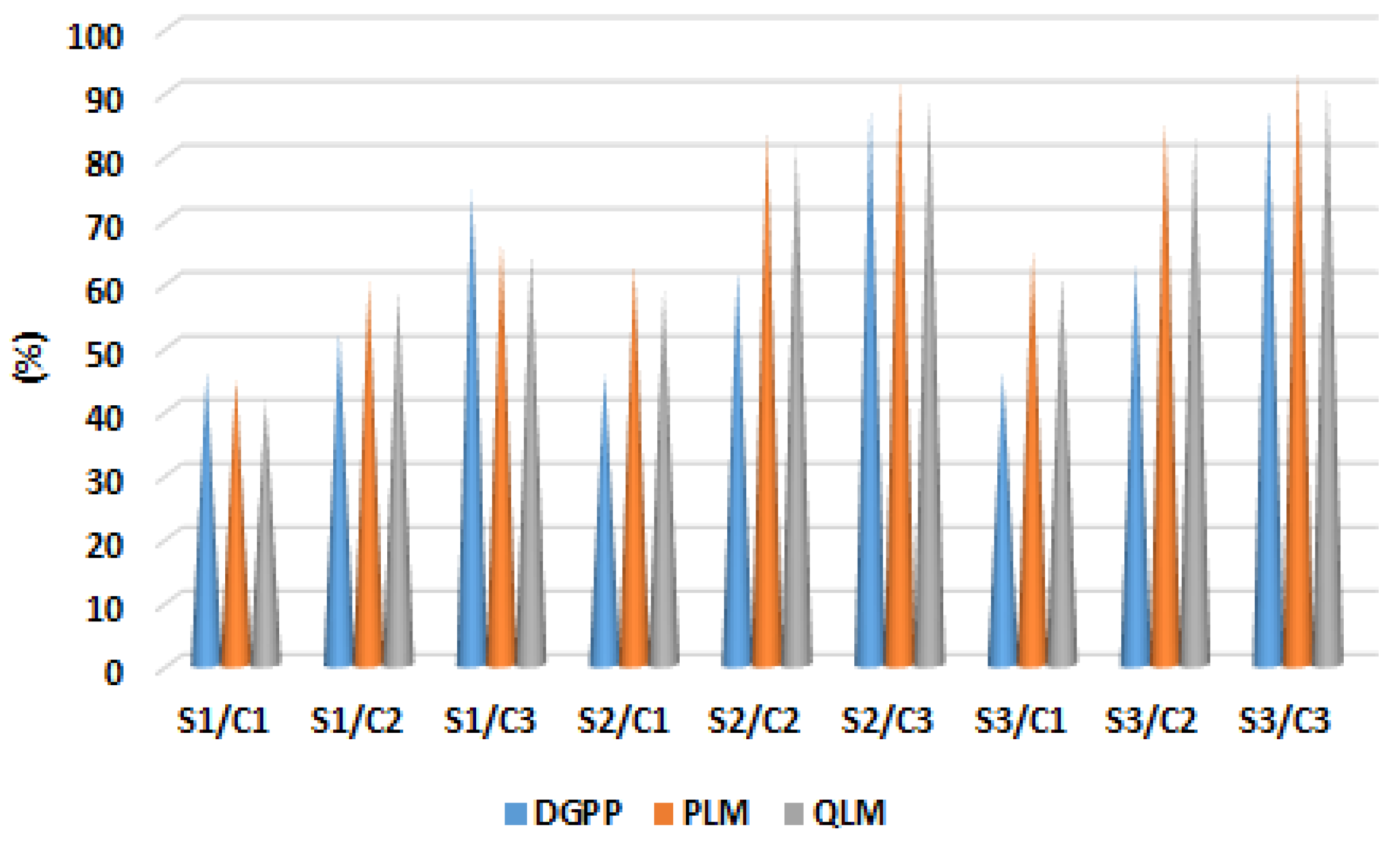
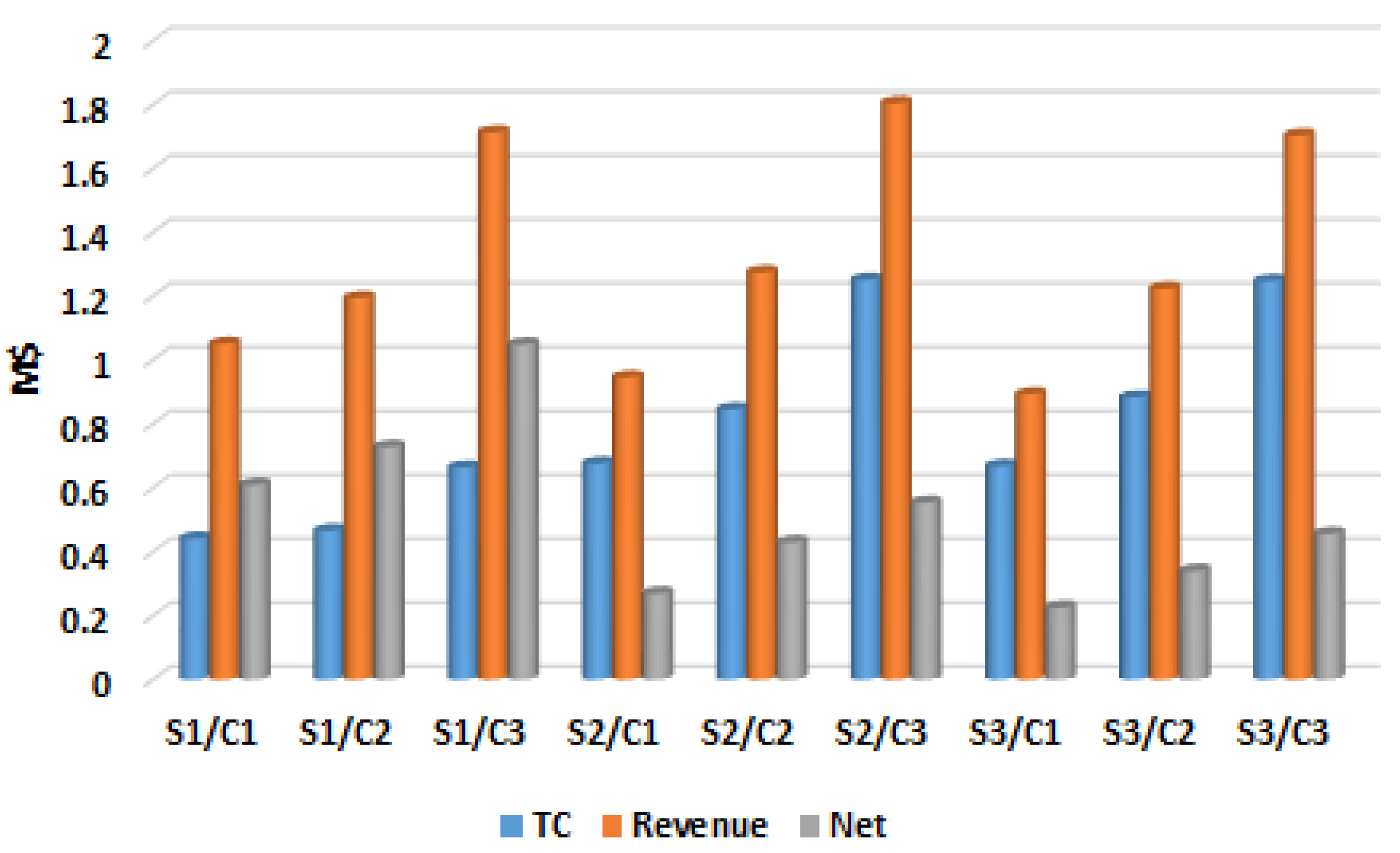
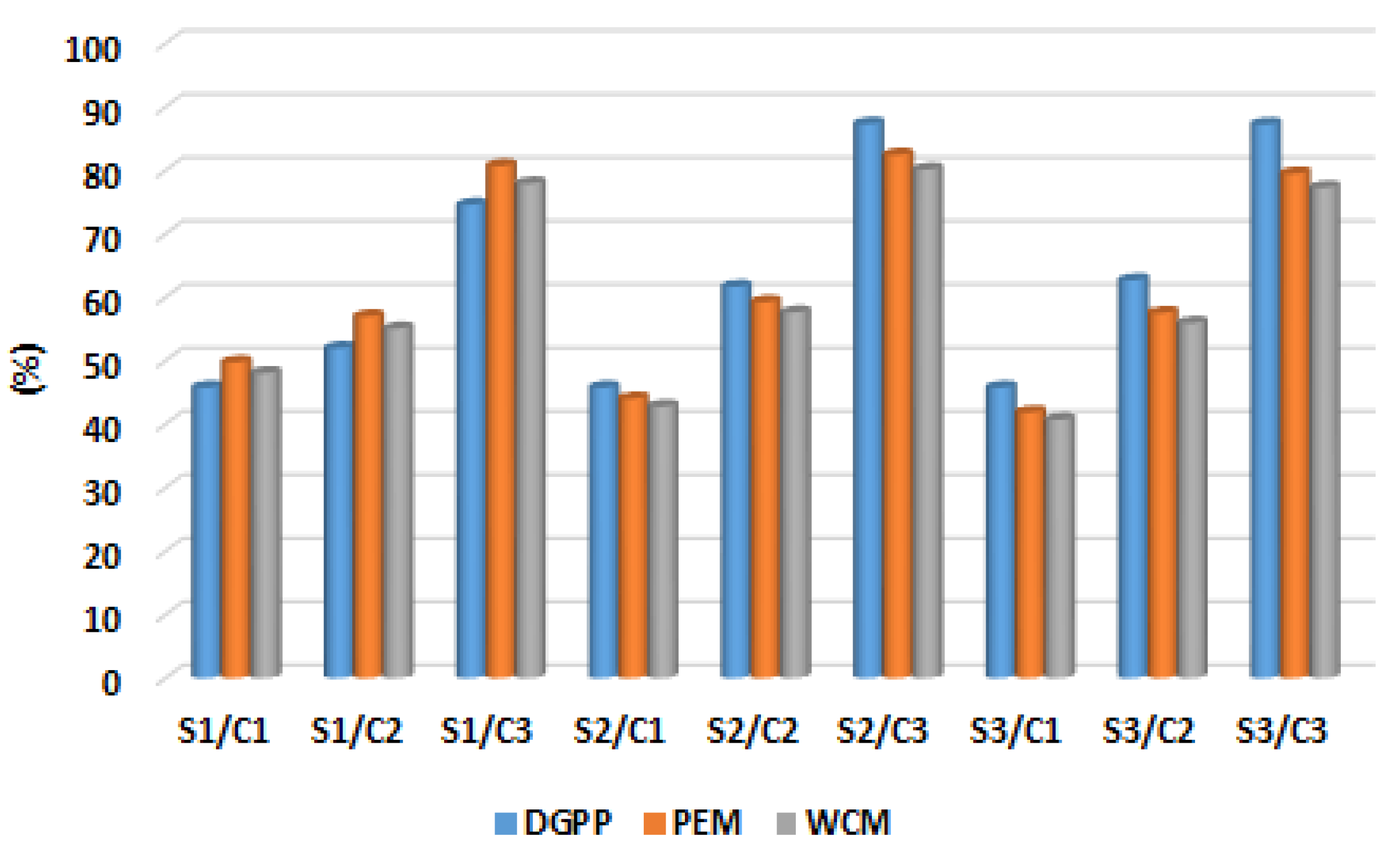
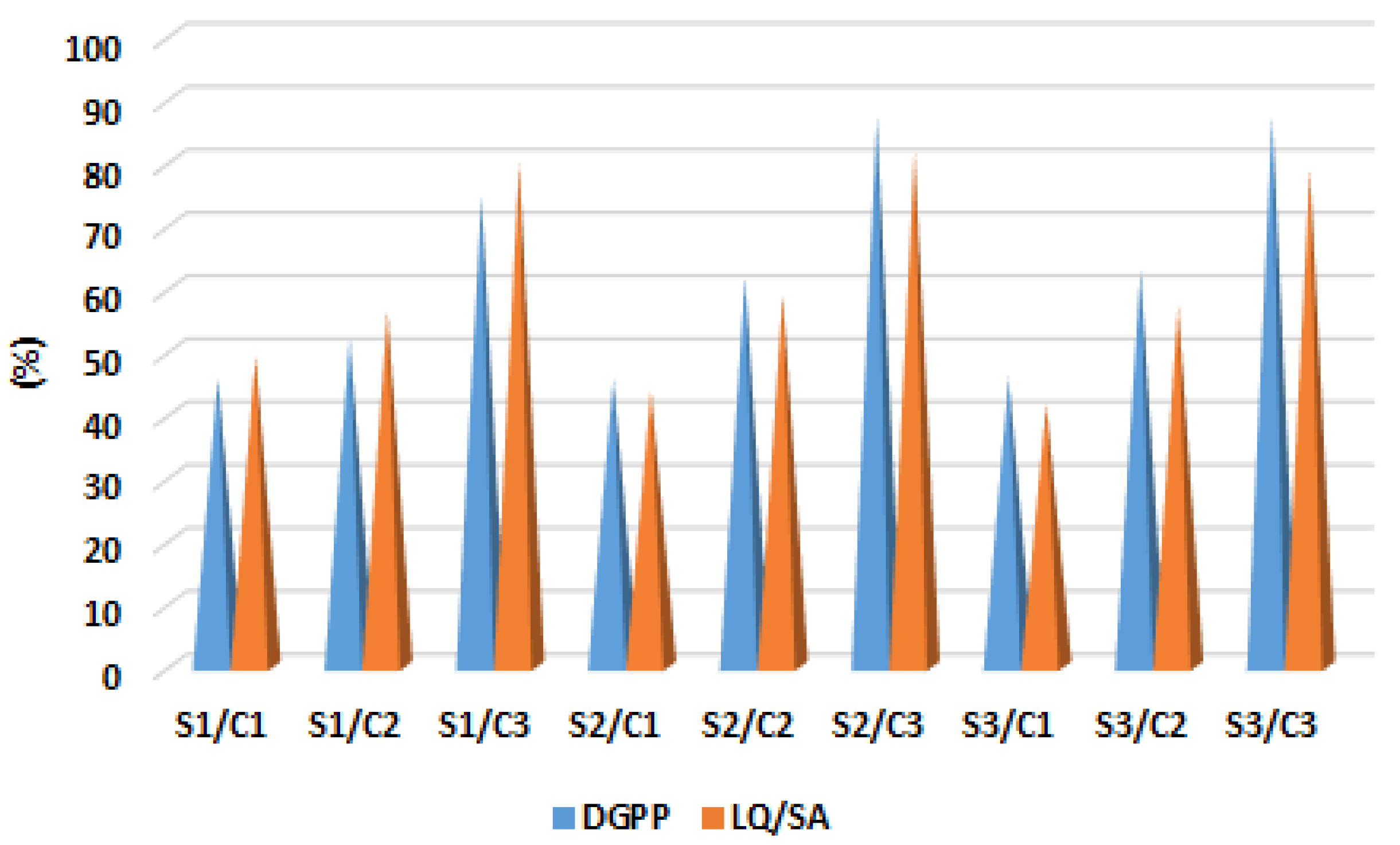
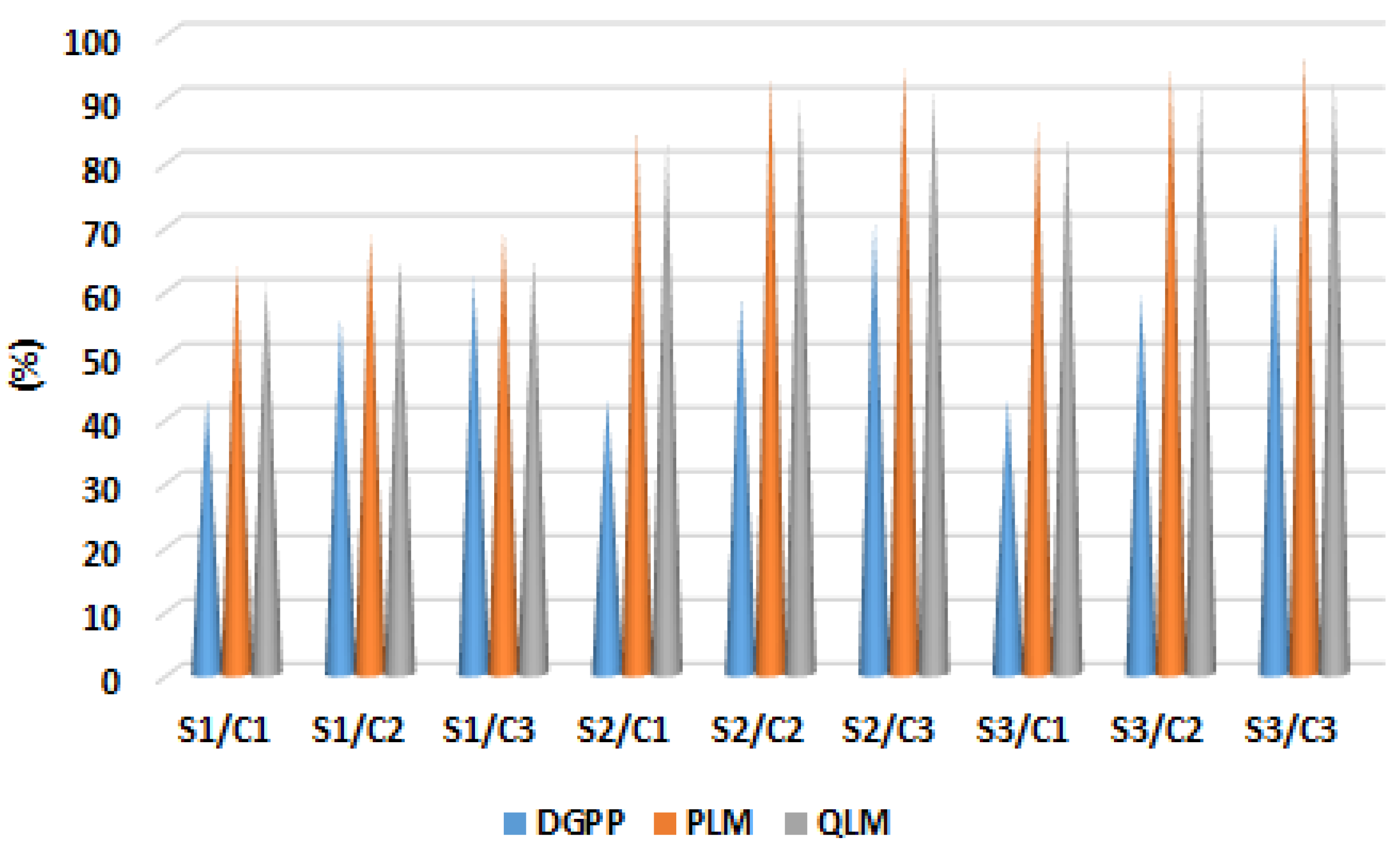
| S1/C1 | 2000 @ 8 | 0.9478 | 115.7 | 83.4 | 44.91 | 41.47 | 45.77 | 1830.7 | 2383.4 |
| S1/C2 | 1319 @ 30 | 0.9789 | 84.1 | 59.3 | 59.99 | 58.39 | 51.99 | 1527.1 | 2359.3 |
| 953 @ 13 | |||||||||
| 1217 @ 30 | |||||||||
| S1/C3 | 1175 @ 24 | 0.9790 | 70.6 | 50.6 | 66.37 | 64.46 | 74.58 | 526.6 | 2350.6 |
| 867 @ 14 | |||||||||
| CELoss | SELoss | CPDG | CQDG | CAI | PEM | WCM | LU | LQ | SA |
| (M$) | (%) | ($/MWh) | ($/MVARh) | (M$) | (%) | (%) | (km2) | (%) | (%) |
| 0.060822 | 44.90 | 40.25 | 0 | 0.077462 | 49.75 | 48.05 | 0.175200 | 49.35 | 49.35 |
| 0.044176 | 59.98 | 45.69 | 0 | 0.087996 | 57.00 | 55.07 | 0.199027 | 56.55 | 56.55 |
| 0.037128 | 66.37 | 65.43 | 0 | 0.126224 | 80.70 | 77.94 | 0.285488 | 80.06 | 80.06 |
| Sr. No. | DG Size @ Bus | Vmin | PLoss | QLoss | PLM | QLM | DGPP | PSS | QSS |
|---|---|---|---|---|---|---|---|---|---|
| (kW) | (p.u) | (kW) | (kVAR) | (%) | (%) | (%) | (kW) | (kVAR) | |
| S2/C1 | 2000 @ 30 | 0.9401 | 77.9 | 58.6 | 62.89 | 58.86 | 45.77 | 1992.9 | 1486.6 |
| S2/C2 | 1035 @ 13 | 0.9814 | 34.8 | 26.65 | 83.43 | 81.29 | 61.67 | 1323.8 | 1151.7 |
| 1660 @ 30 | |||||||||
| 1310 @ 24 | |||||||||
| S2/C3 | 975 @ 13 | 0.9942 | 18.1 | 15.9 | 91.38 | 88.78 | 87.31 | 299.1 | 652.9 |
| 1530 @ 30 | |||||||||
| CELoss | SELoss | CPDG | CQDG | CAI | PEM | WCM | LU | LQ | SA |
| (M$) | (%) | ($/MWh) | ($/MVARh) | (M$) | (%) | (%) | (km2) | (%) | (%) |
| 0.040970 | 62.89 | 36.25 | 3.0 | 0.361080 | 44.09 | 42.80 | 7.8840 | 43.74 | 43.74 |
| 0.018285 | 83.43 | 48.77 | 4.035 | 0.486555 | 59.26 | 57.62 | 10.6236 | 58.88 | 58.88 |
| 0.009513 | 91.38 | 68.93 | 5.715 | 0.688760 | 82.45 | 80.13 | 15.0387 | 81.92 | 81.92 |
| Sr. No. | DG Size @ Bus | Vmin | PLoss | QLoss | PLM | QLM | DGPP | PSS | QSS |
|---|---|---|---|---|---|---|---|---|---|
| (kW) | (p.u) | (kW) | (kVAR) | (%) | (%) | (%) | (kW) | (kVAR) | |
| S3/C1 | 2000 @ 30 | 0.9403 | 74.0 | 55.5 | 64.77 | 61.05 | 45.77 | 2089.0 | 1301.5 |
| S3/C2 | 1031 @ 13 | 0.9816 | 30.9 | 24.2 | 85.26 | 82.99 | 62.68 | 1402.9 | 905.2 |
| 1708 @ 30 | |||||||||
| 1570 @ 30 | |||||||||
| S3/C3 | 1310 @ 24 | 0.9942 | 14.4 | 13.4 | 93.14 | 90.60 | 87.24 | 437.4 | 392.4 |
| 932 @ 13 | |||||||||
| CELoss | SELoss | CPDG | CQDG | CAI | PEM | WCM | LU | LQ | SA |
| (M$) | (%) | ($/MWh) | ($/MVARh) | (M$) | (%) | (%) | (km2) | (%) | (%) |
| 0.038899 | 64.76 | 34.25 | 4.5 | 0.361080 | 41.86 | 40.17 | 7.4460 | 41.60 | 41.60 |
| 0.016277 | 85.25 | 47.11 | 6.1627 | 0.494499 | 57.52 | 55.95 | 10.1972 | 57.16 | 57.16 |
| 0.007568 | 93.14 | 66.09 | 8.577 | 0.688218 | 79.49 | 77.29 | 14.1920 | 78.98 | 78.98 |
| Technique | DG Size @ Bus | PLoss (kW) | QLoss | Vmin | VSI | CELoss | SELoss |
|---|---|---|---|---|---|---|---|
| (kW) | (PLM) | (kVAR) | (p.u) | (p.u) | (M$) | (M$) | |
| TLBO [49] | 824.6 @ 10 | 75.5 | - | - | 0.8365 | 0.039703 | 0.070701 |
| 1031.1 @ 24 | (64.20%) | ||||||
| 886.2 @ 31 | |||||||
| QOTLBO [49] | 880.8 @ 12 | 74.1 | - | - | 0.8656 | 0.038947 | 0.071457 |
| 1059.2 @ 24 | (64.88%) | ||||||
| 1071.4 @ 29 | |||||||
| KHA [50] | 810.7 @ 13 | 75.4 | - | - | 0.8528 | 0.039636 | 0.070768 |
| 836.8 @ 25 | (64.26%) | ||||||
| 841.0 @ 30 | |||||||
| SIMBO-Q [51] | 763.8 @ 14 | 73.4 | - | - | 0.8738 | 0.038579 | 0.071825 |
| 1041.5 @ 24 | (65.19%) | ||||||
| 1135.2 @ 29 | |||||||
| QOSIMBO-Q [51] | 770.8 @ 14 | 72.8 | - | - | 0.8804 | 0.038263 | 0.072141 |
| 1096.5 @ 24 | (65.48%) | ||||||
| 1065.5 @ 30 | |||||||
| QOCSOS [52] | 801.7 @ 13 | 72.8 | - | - | 0.8805 | 0.038256 | 0.072148 |
| 1091.3 @ 24 | (65.50%) | ||||||
| 1053.7 @ 30 | |||||||
| IRRO [33] | 801 @ 13 | 72.8 | 50.7 | - | - | 0.038253 | 0.072151 |
| 1090 @ 24 | (65.50%) | ||||||
| 1054 @ 30 | |||||||
| MRFO [34] | 1017.1 @ 24 | 72.9 | - | - | - | 0.038303 | 0.072101 |
| 788.28 @ 13 | (65.46%) | ||||||
| 1035.3 @ 30 | |||||||
| MPA | 1181 @ 24 | 70.6 | 50.7 | 0.9792 | 0.8943 | 0.037128 | 0.073276 |
| 868 @ 14 | (66.37%) | ||||||
| 1222 @ 30 | |||||||
| Proposed | 1217 @ 30 | 70.6 | 50.6 | 0.9790 | 0.8949 | 0.037128 | 0.073276 |
| 1175 @ 24 | (66.37%) | ||||||
| 867 @ 14 |
| Technique | DG Size @ Bus | PLoss (kW) | QLoss | Vmin | VSI | CELoss | SELoss |
|---|---|---|---|---|---|---|---|
| (kW) | (PLM) | (kVAR) | (p.u) | (p.u) | (M$) | (M$) | |
| MOTA [53] | 880 @ 14 | 15.7 | |||||
| 920 @ 25 | (92.25%) | 12.7 | - | 0.9760 | 0.008251 | 0.102153 | |
| 1560 @ 30 | |||||||
| IMOEHO [54] | 929 @ 13 | 14.9 | |||||
| 1181 @ 24 | (92.64%) | - | - | 0.9814 | 0.007831 | 0.102573 | |
| 1473 @ 30 | |||||||
| MOPSO [55] | 1124.6 @ 11 | 17.2 | |||||
| 989 @ 24 | (91.84%) | 13.5 | - | 0.9782 | 0.009040 | 0.101364 | |
| 1505.2 @ 30 | |||||||
| MOCSOS [55] | 926.1 @ 13 | 15.1 | |||||
| 1257 @ 24 | (92.83%) | 12.3 | - | 0.9777 | 0.007936 | 0.102468 | |
| 1481.2 @ 30 | |||||||
| I-DBEA [56] | 749.1 @ 13 | 14.6 | |||||
| 1042 @ 24 | (92.81%) | - | - | 0.9733 | 0.007657 | 0.102747 | |
| 1239.5 @ 30 | |||||||
| MPA | 1293.30 @ 24 | 14.4 | |||||
| 1583.43 @ 30 | (93.14%) | 13.4 | 0.9942 | 0.9794 | 0.007568 | 0.102836 | |
| 931.25 @ 14 | |||||||
| Proposed | 1570 @ 30 | 14.4 | |||||
| 1310 @ 24 | (93.14%) | 13.3 | 0.9942 | 0.9803 | 0.007568 | 0.102836 | |
| 932 @ 13 |
| Sr. No. | DG Size @ Bus | PF | Vmin | VSI | PLoss | QLoss | PLM | QLM | DGPP |
|---|---|---|---|---|---|---|---|---|---|
| (kVA) | (p.u) | (p.u) | (kW) | (kVAR) | (%) | (%) | (%) | ||
| S4/C3_1 | 1597.50 @ 30 | 0.70 | |||||||
| 1324.33 @ 24 | 0.90 | 0.9942 | 0.9801 | 11.7 | 11.3 | 94.41 | 92.03 | 89.20 | |
| 975.95 @ 13 | 0.82 | ||||||||
| S4/C3_2 | 2000 @ 61 | 0.80 | |||||||
| 815.96 @ 11 | 0.82 | 0.9943 | 0.9934 | 6.4 | 7.0 | 97.13 | 93.12 | 71.26 | |
| 504.89 @ 17 | 0.82 | ||||||||
| CELoss | SELoss | CPDG | CQDG | CAI | PEM | WCM | LU | LQ | SA |
| (M$) | (%) | ($/MWh) | ($/MVARh) | (M$) | (%) | (%) | (km2) | (%) | (%) |
| 0.006170 | 94.41 | 62.45 | 11.8167 | 0.703705 | 78.05 | 75.94 | 13.62 | 77.56 | 77.56 |
| 0.003379 | 97.13 | 53.91 | 9.56 | 0.599546 | 64.71 | 62.94 | 11.75 | 64.29 | 64.29 |
| Technique | DG Size @ Bus/PF | PLoss (kW) | QLoss | Vmin | VSI | CELoss | SELoss |
|---|---|---|---|---|---|---|---|
| (kW) | (PLM) | (kVAR) | (p.u) | (p.u) | (M$) | (M$) | |
| SFSA [57] | 876.8 @ 13/0.904 | 11.8 | |||||
| 1155.3 @ 24/0.892 | (94.43%) | - | - | 0.9691 | 0.006182 | 0.104222 | |
| 1454.9 @ 30/0.716 | |||||||
| SOS [52] | 877.3 @ 13/0.905 | 11.7 | |||||
| 1188.4 @ 24/0.90 | (94.44%) | - | - | 0.9688 | 0.006171 | 0.104233 | |
| 1443.4 @ 30/0.713 | |||||||
| QOCSOS [52] | 877.3 @ 13/0.905 | 11.7 | |||||
| 1188.4 @ 24/0.90 | (94.44%) | - | - | 0.9688 | 0.006171 | 0.104233 | |
| 1443.4 @ 30/0.713 | |||||||
| MPA | 1324.16 @ 24/0.91 | 11.7 | |||||
| 1596.78 @ 30/0.71 | (94.40%) | 11.3 | 0.9942 | 0.9797 | 0.006175 | 0.104229 | |
| 972.78 @ 13/0.82 | |||||||
| Proposed | 1597.50 @ 30/0.70 | 11.7 | |||||
| 1324.33 @ 24/0.90 | ( 94.41%) | 11.3 | 0.9942 | 0.9801 | 0.006170 | 0.104234 | |
| 975.95 @ 13/0.82 |
| Sr. No. | DG Size @ Bus | Vmin | PLoss | QLoss | PLM | QLM | DGPP | PSS | QSS |
|---|---|---|---|---|---|---|---|---|---|
| (kW) | (p.u) | (kW) | (kVAR) | (%) | (%) | (%) | (kW) | (kVAR) | |
| S1/C1 | 2000 @ 61 | 0.9700 | 81.8 | 39.7 | 63.57 | 61.10 | 42.91 | 1884 | 2734.3 |
| S1/C2 | 2000 @ 61 | 0.9913 | 70.5 | 35.9 | 68.63 | 64.85 | 55.66 | 1278.7 | 2730.5 |
| 594 @ 18 | |||||||||
| 2000 @ 61 | |||||||||
| S1/C3 | 451 @ 18 | 0.9930 | 68.9 | 35.5 | 69.30 | 65.10 | 61.71 | 995.1 | 2730.2 |
| 425 @ 66 | |||||||||
| CELoss | SELoss | CPDG | CQDG | CAI | PEM | WCM | LU | LQ | SA |
| (M$) | (%) | ($/MWh) | ($/MVARh) | (M$) | (%) | (%) | (km2) | (%) | (%) |
| 0.042999 | 63.57 | 40.25 | 0 | 0.077462 | 49.70 | 48.04 | 0.175200 | 49.31 | 49.31 |
| 0.037033 | 68.62 | 52.13 | 0 | 0.100468 | 63.68 | 61.54 | 0.227234 | 63.18 | 63.18 |
| 0.036234 | 69.30 | 57.77 | 0 | 0.111390 | 70.23 | 67.85 | 0.251937 | 69.68 | 69.68 |
| Sr. No. | DG Size @ Bus | Vmin | PLoss | QLoss | PLM | QLM | DGPP | PSS | QSS |
|---|---|---|---|---|---|---|---|---|---|
| (kW) | (p.u) | (kW) | (kVAR) | (%) | (%) | (%) | (kW) | (kVAR) | |
| S2/C1 | 2000 @ 61 | 0.9711 | 33.9 | 17.5 | 84.92 | 82.88 | 42.91 | 2036.1 | 1840.1 |
| S2/C2 | 2000 @ 61 | 0.9943 | 15.4 | 10.4 | 93.16 | 89.76 | 58.86 | 1348.6 | 1509.0 |
| 743 @ 17 | |||||||||
| 505 @ 18 | |||||||||
| S2/C3 | 2000 @ 61 | 0.9943 | 11.1 | 9.2 | 95.06 | 91.013 | 70.49 | 857.3 | 1271.8 |
| 780 @ 11 | |||||||||
| CELoss | SELoss | CPDG | CQDG | CAI | PEM | WCM | LU | LQ | SA |
| (M$) | (%) | ($/MWh) | ($/MVARh) | (M$) | (%) | (%) | (km2) | (%) | (%) |
| 0.017802 | 84.91 | 36.25 | 3.0 | 0.361080 | 44.36 | 43.17 | 7.8840 | 44.10 | 44.10 |
| 0.008073 | 93.16 | 49.63 | 4.1145 | 0.495221 | 59.55 | 57.92 | 10.8129 | 59.17 | 59.17 |
| 0.005834 | 95.05 | 59.37 | 4.9275 | 0.593073 | 70.38 | 68.43 | 12.9494 | 69.93 | 69.93 |
| Sr. No. | DG Size @ Bus | Vmin | PLoss | QLoss | PLM | QLM | DGPP | PSS | QSS |
|---|---|---|---|---|---|---|---|---|---|
| (kW) | (p.u) | (kW) | (kVAR) | (%) | (%) | (%) | (kW) | (kVAR) | |
| S3/C1 | 2000 @ 61 | 0.9711 | 30.5 | 15.9 | 86.40 | 84.39 | 42.91 | 2132.7 | 1656.5 |
| S3/C2 | 2000 @ 61 | 0.9940 | 11.5 | 8.7 | 94.87 | 91.45 | 59.18 | 1469.7 | 1250.3 |
| 758 @ 17 | |||||||||
| 2000 @ 61 | |||||||||
| S3/C3 | 798 @ 11 | 0.9943 | 7.0 | 7.2 | 96.87 | 92.87 | 70.85 | 1002.2 | 961.9 |
| 504 @ 18 | |||||||||
| CELoss | SELoss | CPDG | CQDG | CAI | PEM | WCM | LU | LQ | SA |
| (M$) | (%) | ($/MWh) | ($/MVARh) | (M$) | (%) | (%) | (km2) | (%) | (%) |
| 0.016051 | 86.40 | 34.25 | 4.5 | 0.361080 | 42.24 | 41.12 | 7.4460 | 40.40 | 40.40 |
| 0.006054 | 94.87 | 47.13 | 6.2055 | 0.497929 | 56.89 | 55.35 | 10.2680 | 56.54 | 56.54 |
| 0.003694 | 96.87 | 56.39 | 7.4295 | 0.596143 | 67.20 | 65.35 | 12.2933 | 66.77 | 66.77 |
| Technique | DG Size @ Bus | PLoss (kW) | QLoss | Vmin | VSI | CELoss | SELoss |
|---|---|---|---|---|---|---|---|
| (kW) | (PLM) | (kVAR) | (p.u) | (p.u) | (M$) | (M$) | |
| 591.9 @ 15 | 72.4 | ||||||
| TLBO [49] | 818.8 @ 61 | (67.77%) | - | - | 0.9167 | 0.038056 | 0.079991 |
| 900.3 @ 63 | |||||||
| 533.4 @ 18 | 71.6 | ||||||
| QOTLBO [49] | 1198.6 @ 61 | (68.12%) | - | - | 0.9196 | 0.037646 | 0.080401 |
| 567.2 @ 63 | |||||||
| 496.2 @ 12 | 69.6 | ||||||
| KHA [50] | 311.3 @ 22 | (69.04%) | - | - | 0.9185 | 0.036562 | 0.081485 |
| 1735.4 @ 61 | |||||||
| 1500 @ 61 | 71.3 | ||||||
| SIMBO-Q [51] | 618.9 @ 9 | (68.29%) | - | - | 0.8954 | 0.037475 | 0.080572 |
| 529.7 @ 17 | |||||||
| 833.6 @ 9 | 71.0 | ||||||
| QOSIMBO-Q [51] | 451.1 @ 18 | (68.43%) | - | - | 0.8984 | 0.037317 | 0.08073 |
| 1500 @ 61 | |||||||
| 526.9 @ 11 | 69.4 | ||||||
| QOCSOS [52] | 380.3 @ 18 | (69.14%) | - | - | 0.9185 | 0.036491 | 0.081556 |
| 1719 @ 61 | |||||||
| 1780 @ 61 | 71.1 | ||||||
| IRRO [33] | 863 @ 50 | (68.38%) | 32.5 | - | - | 0.037406 | 0.080641 |
| 784 @ 12 | |||||||
| 1713.4 @ 61 | 69.4 | ||||||
| MRFO [34] | 369.12 @ 18 | (69.14%) | - | - | - | 0.036492 | 0.081555 |
| 524.23 @ 11 | |||||||
| 465 @ 17 | 68.9 | ||||||
| MPA | 1942 @ 61 | (69.32%) | 35.3 | 0.9911 | 0.9694 | 0.036208 | 0.081839 |
| 425 @ 66 | |||||||
| 2000 @ 61 | 68.9 | ||||||
| Proposed | 451 @ 18 | (69.30%) | 35.5 | 0.9930 | 0.9697 | 0.036234 | 0.081813 |
| 425 @ 66 |
| Technique | DG Size @ Bus | PLoss (kW) | QLoss | Vmin | VSI | CELoss | SELoss |
|---|---|---|---|---|---|---|---|
| (kW) | (PLM) | (kVAR) | (p.u) | (p.u) | (M$) | (M$) | |
| 1278 @ 61 | 12.8 | ||||||
| PSO [58] | 301 @ 64 | (94.30%) | - | - | 0.9541 | 0.006727 | 0.111320 |
| 324 @ 21 | |||||||
| 1455.2 @ 61 | 10.5 | ||||||
| IMOHS [59] | 476.9 @ 11 | (95.33%) | - | - | 0.9468 | 0.005518 | 0.112556 |
| 312.4 @ 21 | |||||||
| 1500 @ 61 | 7.9 | ||||||
| I-DBEA [56] | 370 @ 59 | (96.45%) | - | - | 0.9774 | 0.004183 | 0.113864 |
| 575 @ 16 | |||||||
| 471.5 @ 21 | 7.1 | ||||||
| MPA | 854.15 @ 11 | (96.86%) | 7.3 | 0.9943 | 0.9943 | 0.003705 | 0.114342 |
| 2000 @ 61 | |||||||
| 2000 @ 61 | 7.0 | ||||||
| Proposed | 798 @ 11 | (96.87%) | 7.2 | 0.9943 | 0.9944 | 0.003694 | 0.114353 |
| 504 @ 18 |
| Technique | DG Size @ Bus/PF | PLoss (kW) | QLoss | Vmin | VSI | CELoss | SELoss |
|---|---|---|---|---|---|---|---|
| (kW) | (PLM) | (kVAR) | (p.u) | (p.u) | (M$) | (M$) | |
| 471.10 @ 17/0.570 | 6.6 | ||||||
| HHO [37] | 2016.92 @ 61/0.760 | (97.10%) | - | - | - | 0.003458 | 0.114589 |
| 719.10 @ 66/0.970 | |||||||
| 608.1 @ 11/0.813 | 4.3 | ||||||
| QOCSOS [52] | 2057.3 @ 61/0.814 | (98.10%) | - | - | 0.9772 | 0.002239 | 0.115808 |
| 454.9 @ 18/0.833 | |||||||
| 472.95 @ 21/0.80 | 6.4 | ||||||
| MPA | 2000 @ 61/0.82 | (97.15%) | 7.0 | 0.9943 | 0.9936 | 0.003358 | 0.114689 |
| 843.69 @ 11/0.82 | |||||||
| 2000 @ 61/0.80 | 6.4 | ||||||
| Proposed | 815.96 @ 11/0.82 | ( 97.14%) | 7.0 | 0.9943 | 0.9934 | 0.003379 | 0.114668 |
| 504.89 @ 17/0.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khalil, M.W.; Altamimi, A.; Kazmi, S.A.A.; Khan, Z.A.; Shin, D.R. Integration of Distributed Generations in Smart Distribution Networks Using Multi-Criteria Based Sustainable Planning Approach. Sustainability 2023, 15, 384. https://doi.org/10.3390/su15010384
Khalil MW, Altamimi A, Kazmi SAA, Khan ZA, Shin DR. Integration of Distributed Generations in Smart Distribution Networks Using Multi-Criteria Based Sustainable Planning Approach. Sustainability. 2023; 15(1):384. https://doi.org/10.3390/su15010384
Chicago/Turabian StyleKhalil, Muhammad Waqas, Abdullah Altamimi, Syed Ali Abbas Kazmi, Zafar A. Khan, and Dong Ryeol Shin. 2023. "Integration of Distributed Generations in Smart Distribution Networks Using Multi-Criteria Based Sustainable Planning Approach" Sustainability 15, no. 1: 384. https://doi.org/10.3390/su15010384
APA StyleKhalil, M. W., Altamimi, A., Kazmi, S. A. A., Khan, Z. A., & Shin, D. R. (2023). Integration of Distributed Generations in Smart Distribution Networks Using Multi-Criteria Based Sustainable Planning Approach. Sustainability, 15(1), 384. https://doi.org/10.3390/su15010384








