Long-Term Cross-Slope Variation in Highways Built on Soft Soil under Coupling Action of Traffic Load and Consolidation
Abstract
1. Introduction
2. Methodology
2.1. Cumulative Deformation Caused by Traffic Load
- Dynamic deviatoric stress . The real stress field induced by traffic loading includes a simultaneous cyclic variation in vertical normal stress, horizontal normal stress, and shear stress. The distribution of dynamic deviatoric stress along the cross-section of the road is influenced by the position of vehicle load [18]. Several points along the road cross-section direction as (shown in Figure 1) were selected to obtain the lateral distribution characteristics of dynamic deflection stress. The dynamic deviatoric stress can be calculated as follows:where , and = the normal stress amplitudes in x, y and z directions, respectively; = shear stress component amplitude.
- Initial deviatoric stress . It is included in the static distribution in subsoil using finite element simulations and manual calculations and is calculated in the paper as follows:where = vertical stress; = lateral stress; = effective stress due to the gravity force of subsoil; = lateral soil pressure coefficient; = vertical stress increment of i-th layer of soil.
- Undrained shear strength of soft subsoil . According to the existing consolidation theory, the undrained shear strength of soft subsoil can be calculated as the following:where = cohesion of soil; = Internal friction angle of soil; = normal stress in the soil along the vertical direction.
- Stress sensitivity . Stress sensitivity was proposed by Chandler [19] to respond to the influence of soil properties on accumulated deformation, which reflects the difference between remodeled soils and structural soils from the perspective of structural resistance during loading compression deformation. The stress sensitivity corresponding to the solidified yield state can be calculated as follows:where = structural yield stress, obtained from the in situ soil compression curve; = corresponding value of vertical effective stress on intrinsic compression line.
- Parameters and . The parameter controls the effect weight of dynamic and static deviatoric stresses on the accumulation of plastic strain. Xu [17] showed that the greater the sum of dynamic and static deviatoric stresses, the more cumulative the plastic deformation. The effect of dynamic stress is more pronounced when the total dynamic and static partial stresses are known. The recommended range of is 0.5~0.75647. The softening index is widely used to describe the strength weakening of soils under cyclic loading, while the parameter determines the magnitude of the softening index under dynamic and static deviatoric stresses. The recommended value of is 0.767.
- Constants , and . The constants and describe the impact of dynamic and static stress levels on the accumulated strain in the first axial cycle, where the accumulated strain grows exponentially with the first axial cycle strain. Constants and can be obtained from the fitting curve of indoor tests. The constant controls the impact of confining pressure on accumulated strain, with suggested value for 0.5 [20].
- Constants and . The parameters and control the increment rate of plastic strain with the number of repeated load applications. The parameter b taken ranges from 0.5 to 0.7, while the parameter k varied significantly according to the indoor test results [21]. The type of soil has an impact on the value of k, the value for soft soil is determined by indoor testing in most studies, while the value of k for compacted embankment is infrequently discussed. According to the Mechanistic-Empirical Pavement Design Guide (MEPDG) [22], the parameters and for embankment can be determined as follows:where = water content; = constant influenced by elastic modulus.
2.2. Cumulative Deformation Due to Soil Consolidation
2.3. Highway Long-Term Deformation Calculation Model
3. Results
3.1. Description of Rongwu Highway
3.2. Practical Application Analysis
- (1)
- Solidification settlement
- (2)
- Traffic load-induced settlement
- (3)
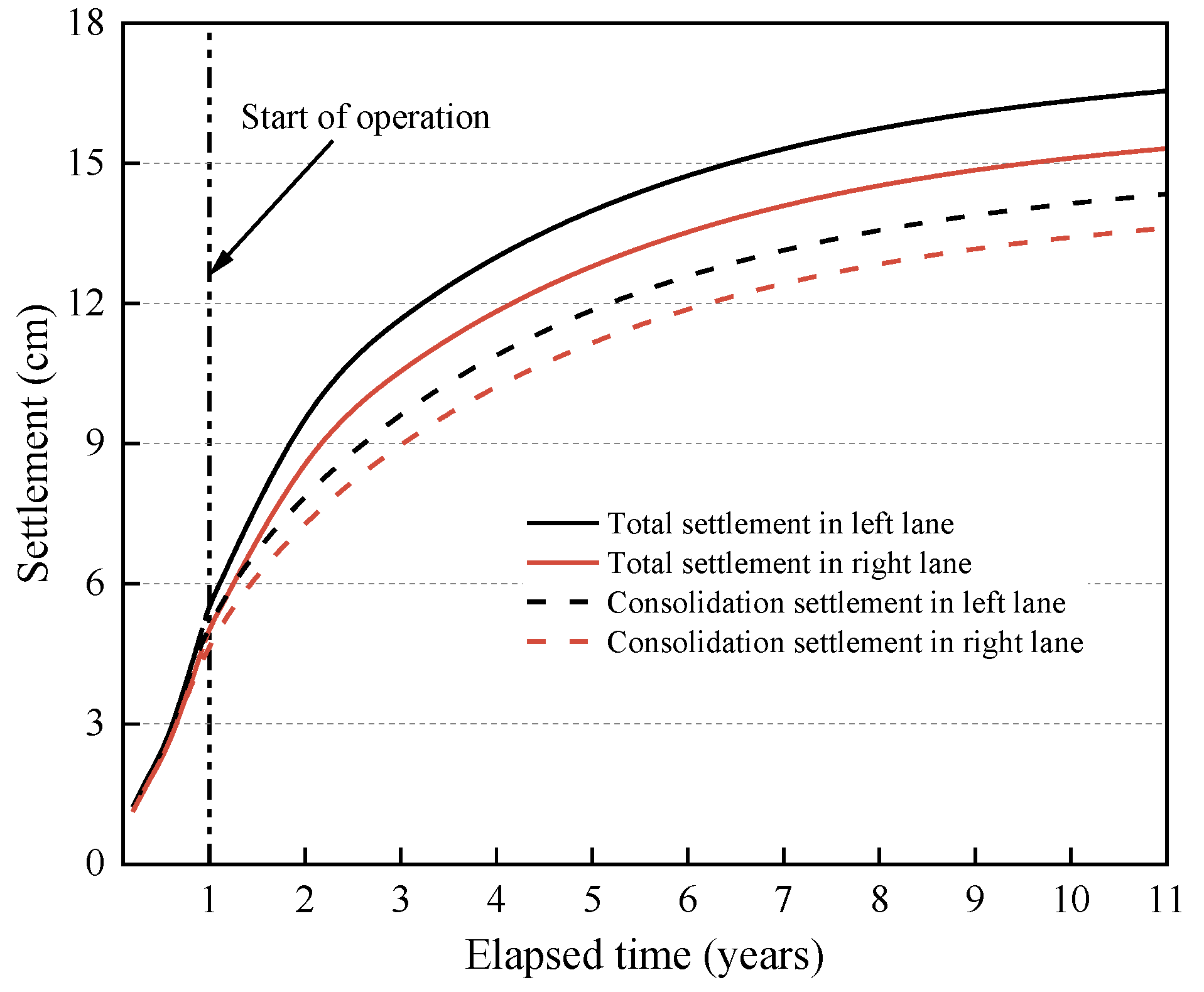
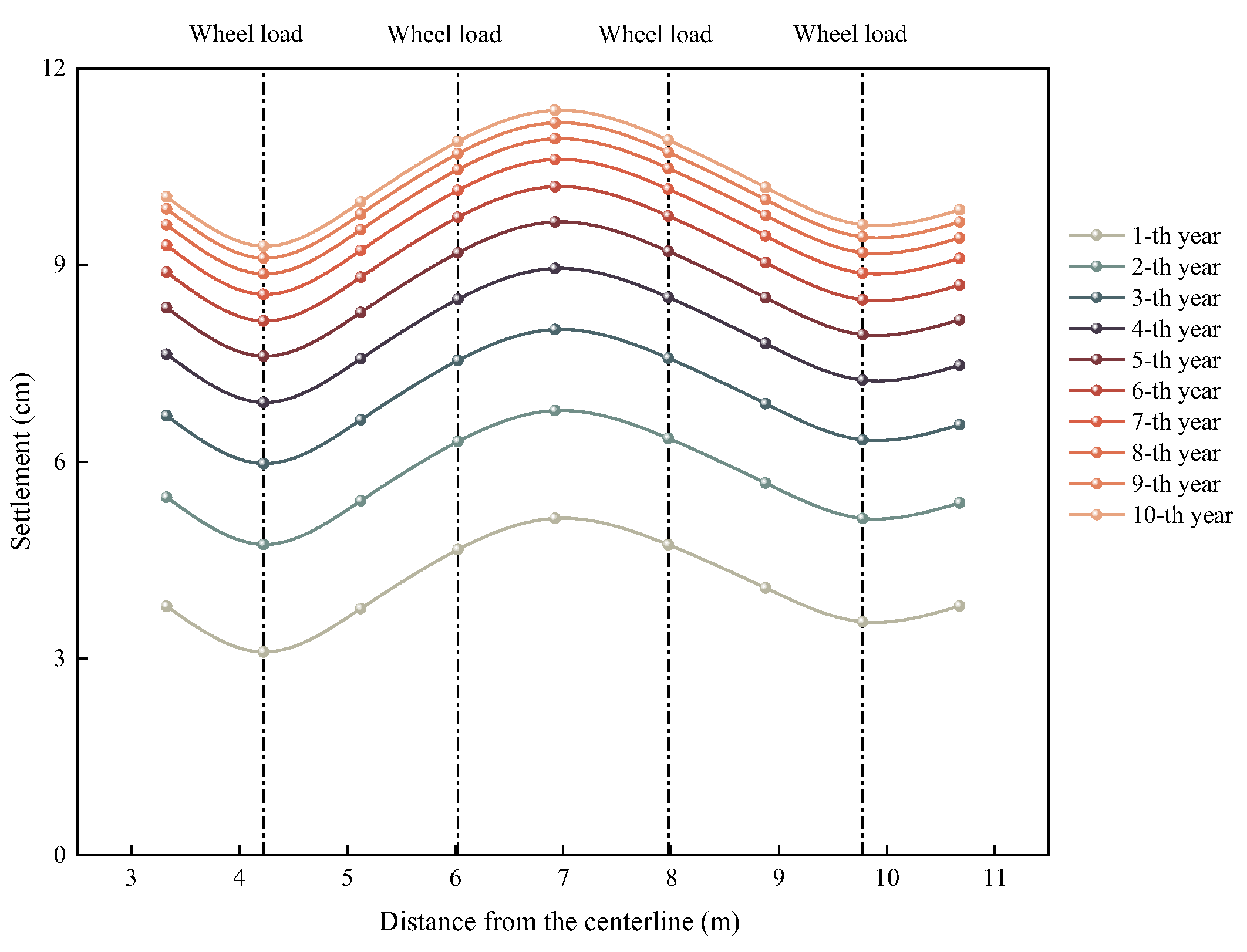
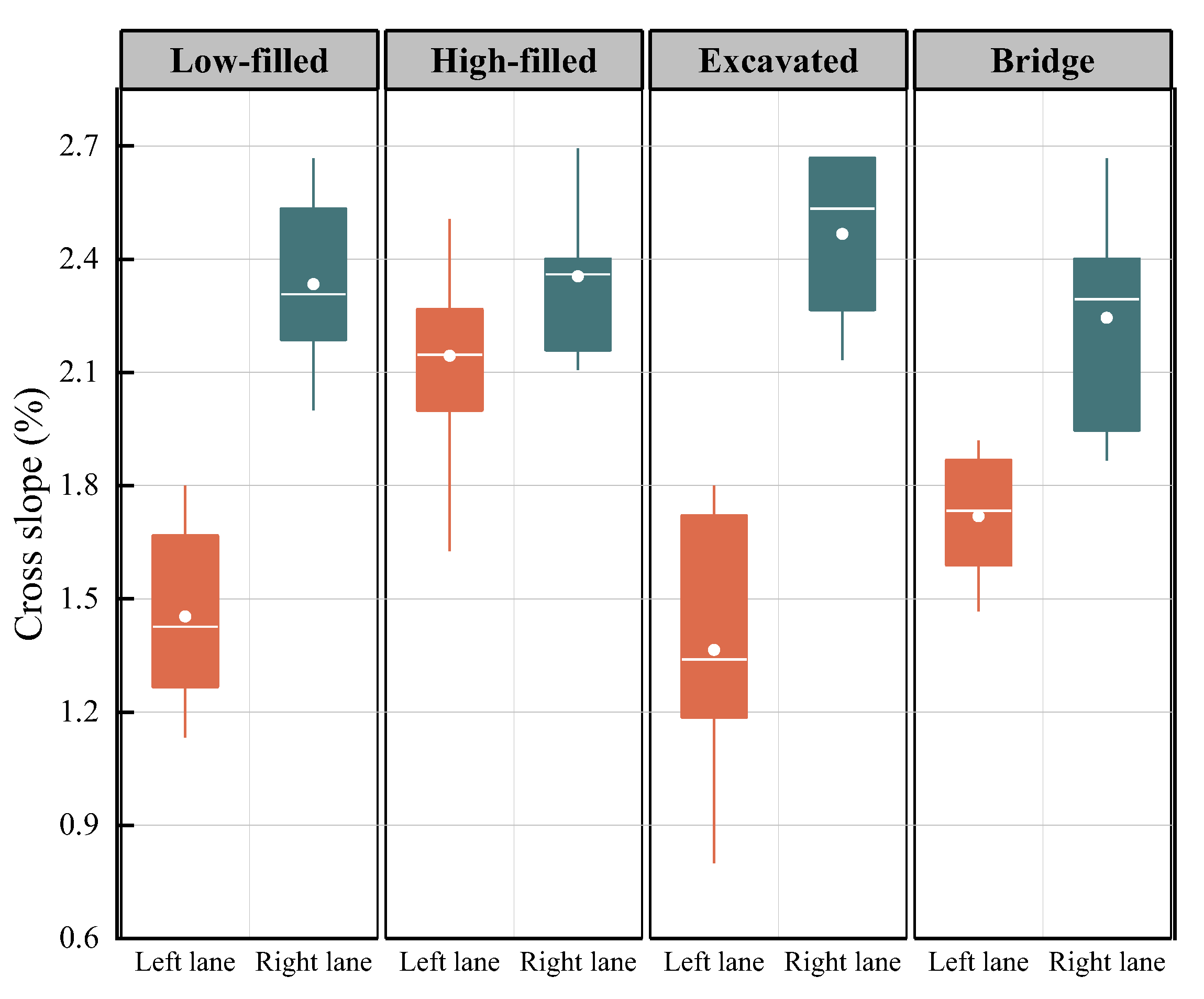
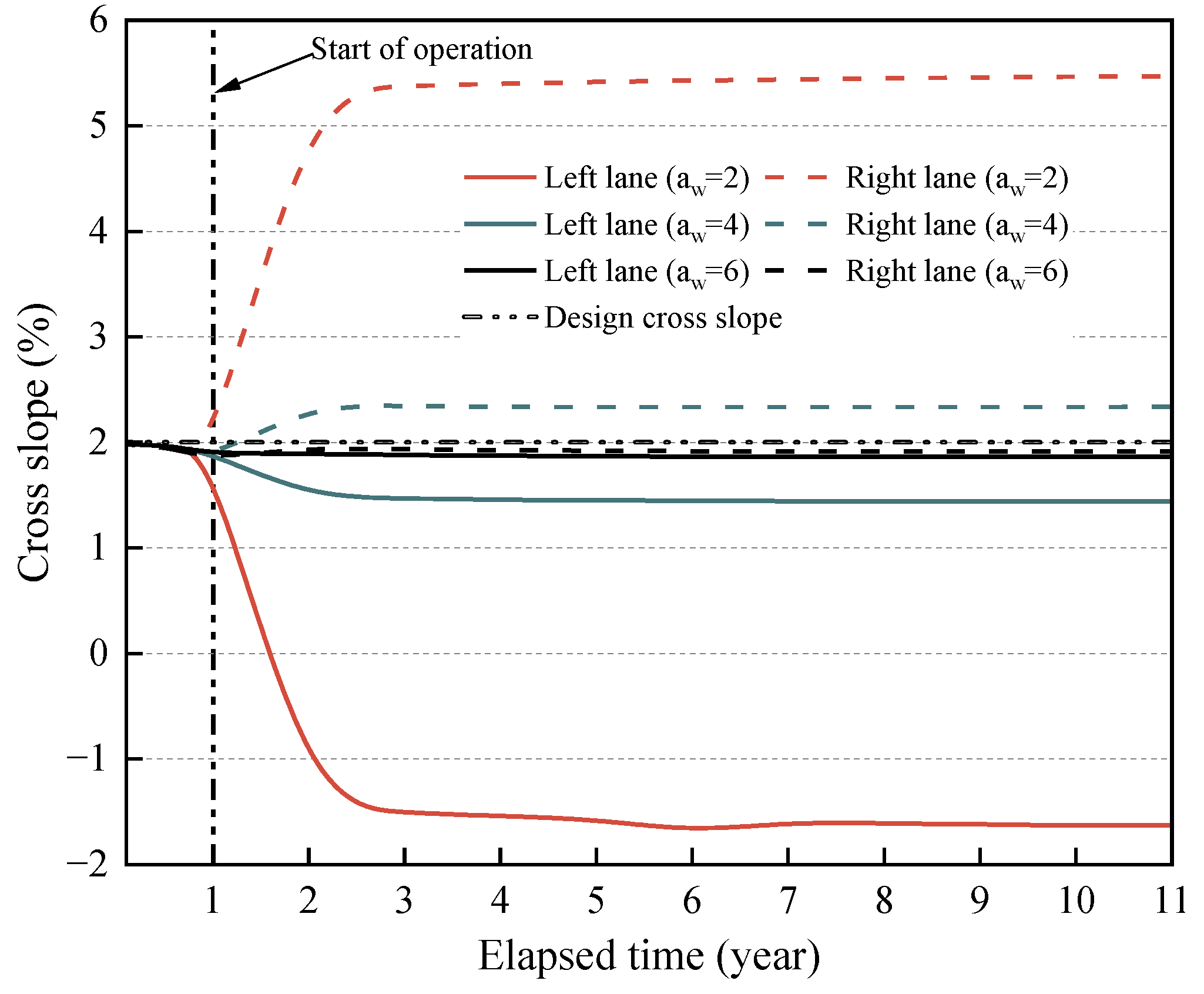
- Long-term deformation of highway cross-sections
- (4)
- Variation in highway cross slope
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gargoum, S.A.; El-Basyouny, K.; Froese, K.; Gadowski, A. A Fully Automated Approach to Extract and Assess Road Cross Sections from Mobile LiDAR Data. IEEE Trans. Intell. Transp. Syst. 2018, 19, 3507–3516. [Google Scholar] [CrossRef]
- Biot, M.A. General Theory of Three-Dimensional Consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Santos, J.E. General Theory of Three-Dimensional Consolidation. Esaim Math. Model. Numer. Anal. 1986, 20, 49–50. [Google Scholar]
- Sandhu, R.S. Finite-Element Analysis of Seepage in Elastic Media. Proc. ASCE 1969, 95, 641–652. [Google Scholar] [CrossRef]
- Loganathan, N.; Balasubramaniam, A.S.; Bergado, D.T. Deformation Analysis of Embankments. J. Geotech. Eng. 1993, 119, 1185–1206. [Google Scholar] [CrossRef]
- Zhu, Z.D.; Zhou, L.H. Application of Logistic model in settlement prediction during complete process of embankment construction. Chin. J. Geotech. Eng. 2009, 31, 965–969. [Google Scholar]
- Liu, W.; Li, X.; Hu, W. Highway subsidence prediction based on neural network and hyperbolic hybrid model. Dongnan Daxue Xuebao Ziran Kexue Ban/J. Southeast Univ. Nat. Sci. Ed. 2013, 43, 380–383. [Google Scholar]
- Huang, J.J. Numerical Simulation Study on Soft Roadbed Settlement of Highway. J. Shandong Univ. Sci. Technol. (Nat. Sci.) 2006, 1, 117–119. [Google Scholar]
- Zhang, Q.; Zhang, J.; Liu, G.; Li, Y. Highway Subsidence Analysis Based on the Advanced InSAR Time Series Analysis Method. In Proceedings of the Dragon 3 Final Results and Dragon 4 Kick-Off, Wuhan, China, 4–8 July 2018; pp. 20–26. [Google Scholar]
- Monismith, C.L.; Ogawa, N.; Freeme, C.R. Permanent Deformation Characteristics of Subgrade Soils Due to Repeated Loading. Transp. Res. Rec. J. Transp. Res. Board 1975, 537, 1–17. [Google Scholar]
- Li, D.; Selig, E.T. Cumulative Plastic Deformation for Fine-Grained Subgrade Soils. J. Geotech. Eng. 1996, 122, 1006–1013. [Google Scholar] [CrossRef]
- Chai, J.C.; Miura, N. Cement/Lime Mixing Ground Improvement for Road Construction on Soft Ground-ScienceDirect. Ground Improv. Case Hist. 2015, 3–29. [Google Scholar] [CrossRef]
- Sakai, A.; Samang, L.; Miura, N. Partially-drained cyclic behavior and its application to the settlement of a low embankment road on silty-clay. J. Jpn. Geotech. Soc. 2008, 43, 33–46. [Google Scholar] [CrossRef]
- Wei, X.; Huang, M.S. A simple method to predict traffic-load-induced permanent settlement of road on soft subsoil. Rock Soil Mech. 2009, 30, 3342–3346. [Google Scholar]
- Zhuang, Y.; Li, S. Three-dimensional finite element analysis of arching in a piled embankment under traffic loading. Arab. J. Geosci. 2015, 8, 7751–7762. [Google Scholar] [CrossRef]
- Lü, X.L.; Fang, H.; Zhang, J.F. A theoretical solution for long-term settlement of soft subgrade induced by traffic loading. Rock Soil Mech. 2016, 37, 435–440. [Google Scholar]
- Xu, L.; Chen, Y.; Shang, Y.; Feng, D.; Ding, K. Long-term settlement calculation of soft soil foundation under traffic load based on mechanical-empirical model. J. Chang. Univ. Nat. Sci. Ed. 2021, 41, 1–10. [Google Scholar]
- Sun, L.; Cai, Y.-q.; Gu, C.; Wang, J.; Guo, L. Cyclic deformation behaviour of natural K (0)-consolidated soft clay under different stress paths. J. Cent. South Univ. 2015, 22, 4828–4836. [Google Scholar] [CrossRef]
- Chandler, R.J. The Third Glossop Lecture: Clay Sediments in Depositional Basins: The Geotechnical Cycle. Q. J. Eng. Geol. 2000, 33, 7–39. [Google Scholar] [CrossRef]
- Huang, M.S.; Yao, Y.M. Explicit model for cumulative strain of saturated clay subjected to cyclic loading. Chin. J. Geotech. Eng. 2011, 33, 325–331. [Google Scholar]
- Qu, S.; Liu, W.Z.; Nie, Z.H. Change law and prediction model for accumulative deformation of artificial structured soft soil under long-term cyclic loading. J. Eng. Geol. 2017, 25, 975–984. [Google Scholar]
- AASHTO. Mechanistic-Empirical Pavement Design Guide; Interim Edition: A Manual of Practice; AASHTO: Washington, DC, USA, 2015. [Google Scholar]
- Shan, Y.; Lu, Y.; Zhou, S.H.; Wang, B.L. Centrifugal model test study on lateral differential settlement between the trampile-plank subgrade and the road subgrade. Chin. J. Rock Mech. Eng. 2020, 39, 1049–1060. [Google Scholar]
- Cai, Y.; Chen, Y.; Cao, Z.; Ren, C. A combined method to predict the long-term settlements of roads on soft soil under cyclic traffic loadings. Acta Geotech. 2018, 13, 1215–1226. [Google Scholar] [CrossRef]
- Chen, S.; Wang, D.; Zhang, R.; Feng, D. The theoretical solution and mechanical analysis for elastic half-space under asymmetrical loading. China Sci. 2017, 12, 806–811. [Google Scholar]
- JTG D50-2017; Specifications for Design of Highway Asphalt Pavement. China Standard Press: Beijing, China, 2017.
- Liu, W.Z.; Shi, Z.G.; Zhang, D.W.; Qu, S. Long-term settlement calculation of structured soft clay foundation under traffic loading. J. Southeast Univ. Nat. Sci. Ed. 2018, 48, 726–735. [Google Scholar]
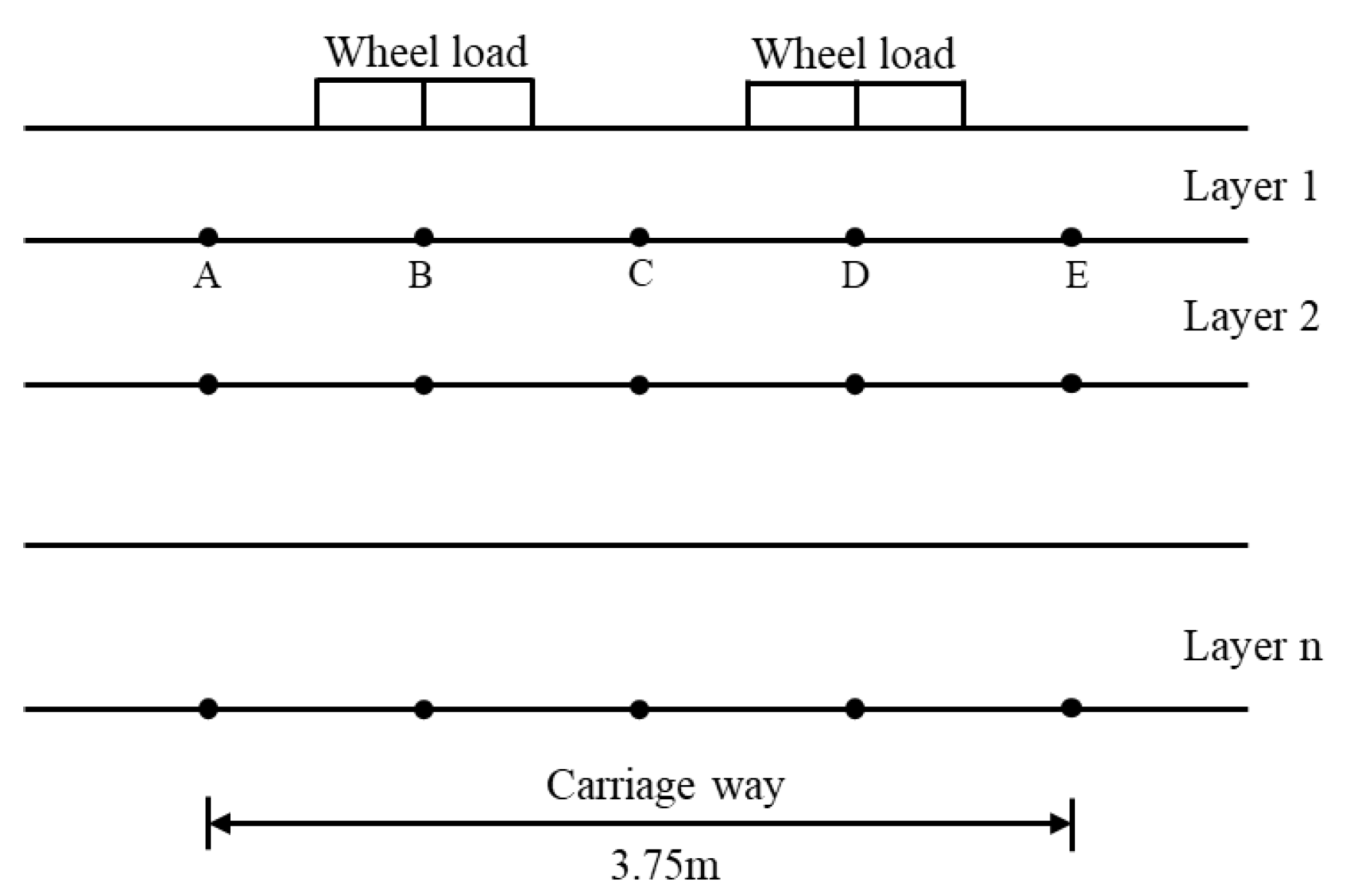

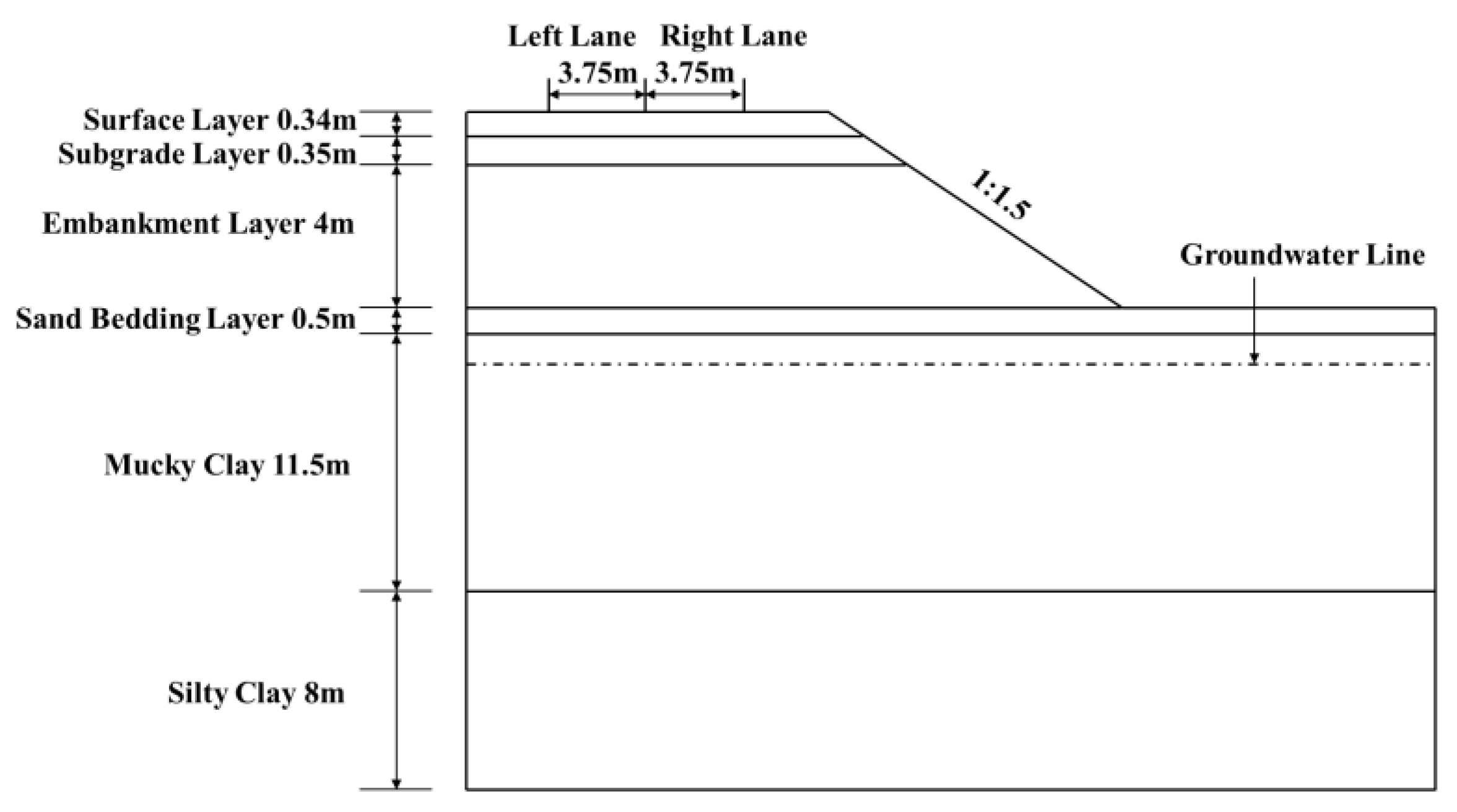




| Soil Layer | Thickness (m) | Unit Weight (kN/m3) | Young’s Modulus (MPa) | Poisson’s Ratio | Cohesion (kPa) | Angle of Friction (°) | Permeability Coefficient (m/d) |
|---|---|---|---|---|---|---|---|
| Surface | 0.35 | 24.2 | 1200 | 0.3 | - | - | - |
| Subgrade | 0.35 | 23.6 | 1000 | 0.3 | - | - | - |
| Embankment | 4 | 18.3 | 20 | 0.4 | 29.3 | 36.5 | - |
| Sand bedding | 0.5 | 20 | 50 | 0.3 | - | - | - |
| Mucky clay | 11.5 | 17.6 | 2.5 | 0.35 | 8 | 24 | 0.00012 |
| Silty clay | 8 | 17.8 | 6.0 | 0.31 | 22.4 | 31.6 | 0.00006 |
| Soil Layer | (°) | (°) | |
|---|---|---|---|
| Embankment | 28.7 | 1.00 | 28.7 |
| Mucky clay | 35.3 | 1.00 | 35.3 |
| Soil Layer | ||||||
|---|---|---|---|---|---|---|
| Silty clay | 0.02 | 0.07 | 1.27 | 1.00 | 1.00 | 1.02 |
| Soil Layer | ||||||||
|---|---|---|---|---|---|---|---|---|
| Embankment | 4.5 | 0.60 | 21.6 | 0.767 | 2.5 | 0.5 | 0.24 | 743 |
| Mucky clay | 3.1 | 0.60 | 21.6 | 0.767 | 3 | 0.5 | 0.32 | 3,100,000 |
| Silty clay | 5.4 | 0.60 | 21.6 | 0.767 | 2 | 0.5 | 0.73 | 82,000,000 |
| Soil Layer | Depth (m) | (kPa) | (kPa) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | H | I | ||||
| Embankment | 1 | 14.3 | 18.6 | 7.53 | 8.06 | 7.63 | 6.85 | 6.20 | 6.53 | 7.01 | 7.26 | 6.88 |
| 2 | 20.4 | 26.5 | 6.59 | 6.81 | 6.36 | 5.67 | 5.26 | 5.57 | 6.08 | 6.43 | 6.23 | |
| 3 | 26.5 | 33.6 | 6.12 | 6.14 | 5.31 | 4.27 | 3.75 | 4.22 | 5.24 | 6.05 | 6.23 | |
| 4 | 32.6 | 39.4 | 5.37 | 5.32 | 4.55 | 3.15 | 2.33 | 2.98 | 4.22 | 5.12 | 5.29 | |
| Mucky clay | 6 | 61.9 | 45.4 | 1.35 | 1.53 | 1.68 | 1.77 | 1.82 | 1.78 | 1.68 | 1.51 | 1.30 |
| 8 | 78.1 | 55.9 | 0.03 | 0.03 | 0.04 | 0.05 | 0.06 | 0.05 | 0.04 | 0.03 | 0.03 | |
| 10 | 94.4 | 66.6 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 12 | 110.6 | 77.6 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 14 | 126.9 | 88.8 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 16 | 143.1 | 101.9 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| Silty clay | 18 | 197.5 | 32.8 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 20 | 217.9 | 31.6 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 22 | 238.2 | 30.3 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 24 | 258.6 | 29.2 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| Operation Years | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Left lane | 1.90 | 1.49 | 1.47 | 1.46 | 1.45 | 1.45 | 1.44 | 1.44 | 1.44 | 1.44 | 1.44 |
| Right lane | 1.84 | 2.35 | 2.34 | 2.34 | 2.34 | 2.33 | 2.33 | 2.33 | 2.33 | 2.34 | 2.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, M.; Xu, J.; Gao, C.; Mu, M.; E, G. Long-Term Cross-Slope Variation in Highways Built on Soft Soil under Coupling Action of Traffic Load and Consolidation. Sustainability 2023, 15, 33. https://doi.org/10.3390/su15010033
Jia M, Xu J, Gao C, Mu M, E G. Long-Term Cross-Slope Variation in Highways Built on Soft Soil under Coupling Action of Traffic Load and Consolidation. Sustainability. 2023; 15(1):33. https://doi.org/10.3390/su15010033
Chicago/Turabian StyleJia, Miao, Jinliang Xu, Chao Gao, Minghao Mu, and Guangxun E. 2023. "Long-Term Cross-Slope Variation in Highways Built on Soft Soil under Coupling Action of Traffic Load and Consolidation" Sustainability 15, no. 1: 33. https://doi.org/10.3390/su15010033
APA StyleJia, M., Xu, J., Gao, C., Mu, M., & E, G. (2023). Long-Term Cross-Slope Variation in Highways Built on Soft Soil under Coupling Action of Traffic Load and Consolidation. Sustainability, 15(1), 33. https://doi.org/10.3390/su15010033






