A Novel Transfer Learning Method Based on Conditional Variational Generative Adversarial Networks for Fault Diagnosis of Wind Turbine Gearboxes under Variable Working Conditions
Abstract
:1. Introduction
2. Conditional Variational Generative Adversarial Networks and Domain Adaptive Technology
2.1. Conditional Variational Generative Adversarial Networks (CVAE-GAN)
2.2. Domain Adaptive Technology (DA)
- (1)
- Sample adaptation: resampling samples in the source domain so that their distribution converges with the target domain distribution.
- (2)
- Feature adaptation: projecting the source and target domains into a common feature subspace.
- (3)
- Model adaption: modification of the source domain error function.
3. Transfer Learning Based on Conditional Variational Generative Adversarial Networks (TL-CVAE-GAN)
| Algorithm 1. TL-CVAE-GAN |
| Input: Input training data, , testing data, , classified model, fC. In the CVAE-GAN1 model: encoder network, fE1, decoder network, fDE1, generator network, fG1, and discriminator network, fD1. In the CVAE-GAN2 model: encoder network, fE2, generator network, fG2, discriminator network, fD2.The learning rate, lr. ########################Cycle 5 times #################### 1: For f from 0 to 4: ########################train CVAE-GAN1 model #################### 2: For each training epoch, do: 3: For each batch, do: 4: zi = fE1(xs1i, Speed1), xs1i’ = fDE1(zi), the mean value, usi, and variance, σsi, are obtained from zi, sample e from the random noise S. zsi = usi +σsi *e, xs2i’= fG1(zsi, Speed2), ds2i’= fD1(xs2i’), ds2i= fD1(xs2i) 5: Backward propagation by Equation (9). 6: end 7: save CVAE-GAN1 model #################### train CVAE-GAN2 model use MMD ####################### 8: download CVAE-GAN1 model. Use the parameters of the CVAE-GAN1 model as the initial parameters of CVAE-GAN2. 9: For each training, do: 10: For each batch, do: 11: zi = fE2(xt1i), zti = uti +σti *e, xt2i’= fG2(zti), 12: Backward propagation by Equation (12). 13: end 14: save CVAE-GAN2 model 15: lr = lr/2 16: if f > 0: 17: download the CVAE-GAN2 model. Use the parameters of the CVAE-GAN2 model as the initial parameters of CVAE-GAN1. 18: end ########### train classifier net use Tr and the generate data XT2′ ################# ########the input data is X = {(XS1, YS1), (XS2, YS2), (XT1, YT1), (XT2′, YT2)}########### 19: For each training, do: 20: For each batch, do: 21: yi’ = fC(xi) 22: Backward propagation by Equation (13). 23: end ###################### testing results and t-SNE ######################### 24: For the test set, calculate cTi = fC (Tei), calculate the accuracy, and draw the t-SNE diagram. Output: testing results. |
4. Case Analysis
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Conflicts of Interest
References
- Li, W.; Chen, Z.; He, G. A novel weighted adversarial transfer network for partial domain fault diagnosis of machinery. IEEE Trans. Ind. Inform. 2020, 17, 1753–1762. [Google Scholar] [CrossRef]
- Huang, R.; Li, J.; Liao, Y.; Chen, J.; Wang, Z.; Liu, W. Deep adversarial capsule network for compound fault diagnosis of machinery toward multidomain generalization Task. IEEE Trans. Instrum. Meas. 2020, 70, 3506311. [Google Scholar] [CrossRef]
- Li, J.; Huang, R.; He, G.; Liao, Y.; Wang, Z.; Li, W. A two-stage transfer adversarial network for intelligent fault diagnosis of rotating machinery with multiple new faults. IEEE ASME Trans. Mechatron. 2020, 26, 1591–1601. [Google Scholar] [CrossRef]
- Chen, Z.; Gryllias, K.; Li, W. Intelligent fault diagnosis for rotary machinery using transferable convolutional neural network. IEEE Trans. Ind. Inform. 2020, 16, 339–349. [Google Scholar] [CrossRef]
- Li, J.; Huang, R.; He, G.; Wang, S.; Li, G.; Li, W. A deep adversarial transfer learning network for machinery emerging fault detection. IEEE Sens. J. 2020, 20, 8413–8422. [Google Scholar] [CrossRef]
- Li, S.; An, Z.; Lu, J. A novel data-driven fault feature separation method and its application on intelligent fault diagnosis under variable working conditions. IEEE Access 2020, 8, 113702–113712. [Google Scholar] [CrossRef]
- Qian, W.; Li, S.; Yi, P.; Zhang, K. A novel transfer learning method for robust fault diagnosis of rotating machines under variable working conditions. Measurement 2019, 138, 514–525. [Google Scholar] [CrossRef]
- Guo, L.; Lei, Y.; Xing, S.; Yan, T.; Li, N. Deep convolutional transfer learning network: A new method for intelligent fault diagnosis of machines with unlabeled data. IEEE Trans. Ind. Electron. 2019, 66, 7316–7325. [Google Scholar] [CrossRef]
- Yang, B.; Lei, Y.; Jia, F.; Xing, S. An intelligent fault diagnosis approach based on transfer learning from laboratory bearings to locomotive bearings. Mech. Syst. Signal Process. 2019, 122, 692–706. [Google Scholar] [CrossRef]
- Gretton, A.; Borgwardt, K.M.; Rasch, M.J.; Schölkopf, B.; Smola, A. A kernel two-sample test. Mach. Learn. Res. 2012, 13, 723–773. [Google Scholar]
- Venkateswara, H.; Chakraborty, S.; Panchanathan, S. Deep-learning systems for domain adaptation in computer vision learning transferable feature representations. IEEE Signal Process. 2017, 34, 117–129. [Google Scholar] [CrossRef]
- Sun, S.; Zhang, B.; Xie, L.; Zhang, Y. An unsupervised deep domain adaptation approach for robust speech recognition. Neurocomputing 2017, 257, 79–87. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, H.; Li, S.; An, Z. Unsupervised domain adaptation via enhanced transfer joint matching for bearing fault diagnosis. Measurement 2020, 165, 108071. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, H.; Li, S.; An, Z.; Wang, J. A novel geodesic flow kernel based domain adaptation approach for intelligent fault diagnosis under varying working conditions. Neurocomputing 2019, 376, 54–64. [Google Scholar] [CrossRef]
- An, Z.; Li, S.; Jiang, X.; Xin, Y.; Wang, J. Adaptive cross-domain feature extraction method and its application on machinery intelligent fault diagnosis under different working conditions. IEEE Access 2019, 8, 535–546. [Google Scholar] [CrossRef]
- Qian, W.; Li, S.; Jiang, X. Deep transfer network for rotating machine fault analysis. Pattern Recognit. 2019, 96, 106993. [Google Scholar] [CrossRef]
- Yang, B.; Lei, Y.; Jia, F.; Li, N.; Du, Z. A polynomial kernel induced distance metric to improve deep transfer learning for fault diagnosis of machines. IEEE Trans. Ind. Electron. 2019, 67, 9747–9757. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B. Generative adversarial nets. In Proceedings of the International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 1–9. [Google Scholar]
- Zheng, T.; Song, L.; Wang, J.; Teng, W.; Xu, X. Data synthesis using dual discriminator conditional generative adversarial networks for imbalanced fault diagnosis of rolling bearings. Measurement 2020, 158, 107741. [Google Scholar] [CrossRef]
- Wang, J.; Li, S.; Han, B.; An, Z.; Bao, H.; Ji, S. Generalization of deep neural networks for imbalanced fault classification of machinery using generative adversarial networks. IEEE Access 2019, 7, 111168–111180. [Google Scholar] [CrossRef]
- Schlegl, T.; Seebck, P.; Waldstein, S.M.; Schmidt-Erfurth, U.; Langs, G. Unsupervised anomaly detection with generative adversarial networks to guide marker discovery. Comput. Vis. Pattern Recognit. 2017, 10265, 146–157. [Google Scholar]
- Akcay, S.; Atapour-Abarghouei, A.; Breckon, T.P. GANomaly: Semi-supervised anomaly detection via adversarial training. Comput. Vis. Pattern Recognit. 2018, 11363, 622–637. [Google Scholar]
- Guo, Q.; Li, Y.; Song, Y.; Wang, D.; Chen, W. Intelligent fault diagnosis method based on full 1-D convolutional generative adversarial network. IEEE Trans. Ind. Inform. 2019, 16, 2044–2053. [Google Scholar] [CrossRef]
- Lyu, Y.; Han, Z.; Zhong, J.; Li, C.; Liu, Z. A generic anomaly detection of catenary support components based on generative adversarial networks. IEEE Trans. Instrum. Meas. 2020, 69, 2439–2448. [Google Scholar] [CrossRef]
- Yan, K.; Su, J.; Huang, J.; Mo, Y. Chiller fault diagnosis based on VAE-enabled generative adversarial networks. IEEE Trans. Autom. Sci. Eng. 2020, 19, 387–395. [Google Scholar] [CrossRef]
- Liu, S.; Jiang, H.; Wu, Z.; Li, X. Data synthesis using deep feature enhanced generative adversarial networks for rolling bearing imbalanced fault diagnosis. Mech. Syst. Signal Process. 2022, 163, 108139. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2014, arXiv:1312.6114. [Google Scholar]
- Makhzani, A.; Shlens, J.; Jaitly, N.; Goodfellow, I.; Frey, B. Adversarial autoencoders. arXiv 2015, arXiv:1511.05644. [Google Scholar]
- Qu, F.; Liu, J.; Ma, Y.; Zang, D.; Fu, M. A novel wind turbine data imputation method with multiple optimizations based on GANs. Mech. Syst. Signal Process. 2020, 139, 106610. [Google Scholar] [CrossRef]
- Guo, Z.; Pu, Z.; Du, W.; Wang, H.; Li, C. Improved adversarial learning for fault feature generation of wind turbine gearbox. Renew. Energy 2022, 185, 255–266. [Google Scholar] [CrossRef]
- Jiang, N.; Li, N. A wind turbine frequent principal fault detection and localization approach with imbalanced data using an improved synthetic oversampling technique. Int. J. Electr. Power Energy Syst. 2021, 126, 106595. [Google Scholar] [CrossRef]
- Jing, B.; Pei, Y.; Qian, Z.; Wang, A.; Zhu, S.; An, J. Missing wind speed data reconstruction with improved context encoder network. Energy Rep. 2022, 8, 3386–3394. [Google Scholar] [CrossRef]
- Wang, A.; Qian, Z.; Pei, Y.; Jing, B. A de-ambiguous condition monitoring scheme for wind turbines using least squares generative adversarial networks. Renew. Energy 2022, 185, 267–279. [Google Scholar] [CrossRef]
- Yu, X.; Zhang, X.; Cao, Y.; Xia, M. VAEGAN: A collaborative filtering framework based on adversarial variational autoencoders. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence (IJCAI-19), Macao, China, 10–16 August 2019; pp. 4206–4212. [Google Scholar]
- Bao, J.; Chen, D.; Wen, F.; Li, H.; Hua, G. CVAE-GAN: Fine-grained image generation through asymmetric training. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2745–2754. [Google Scholar]
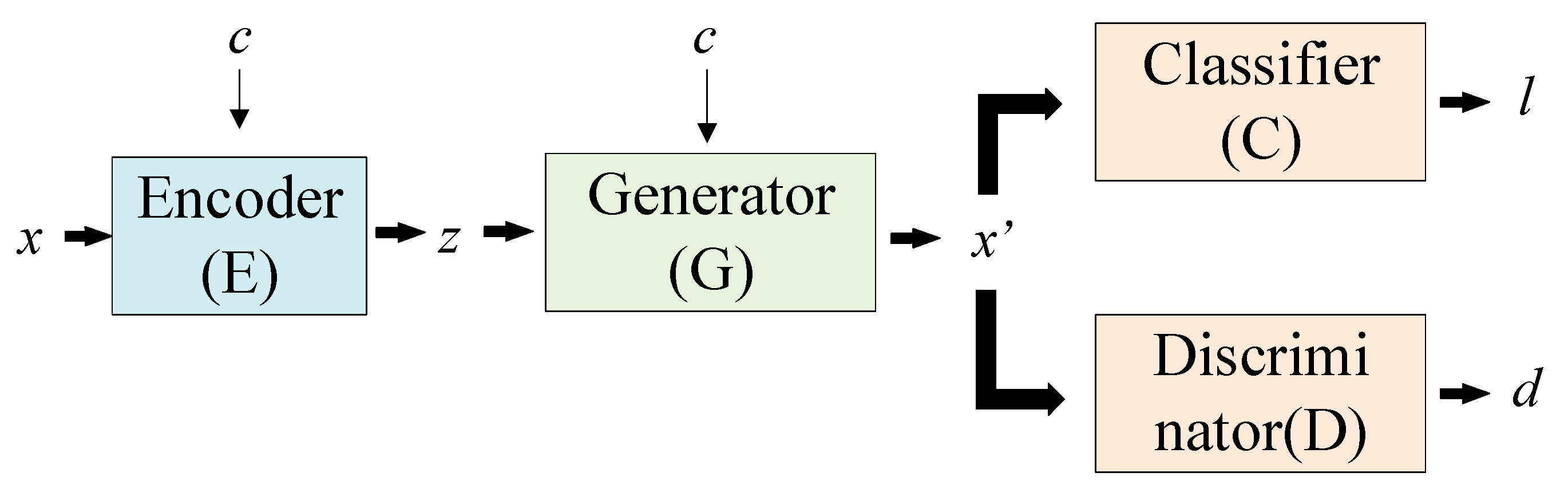
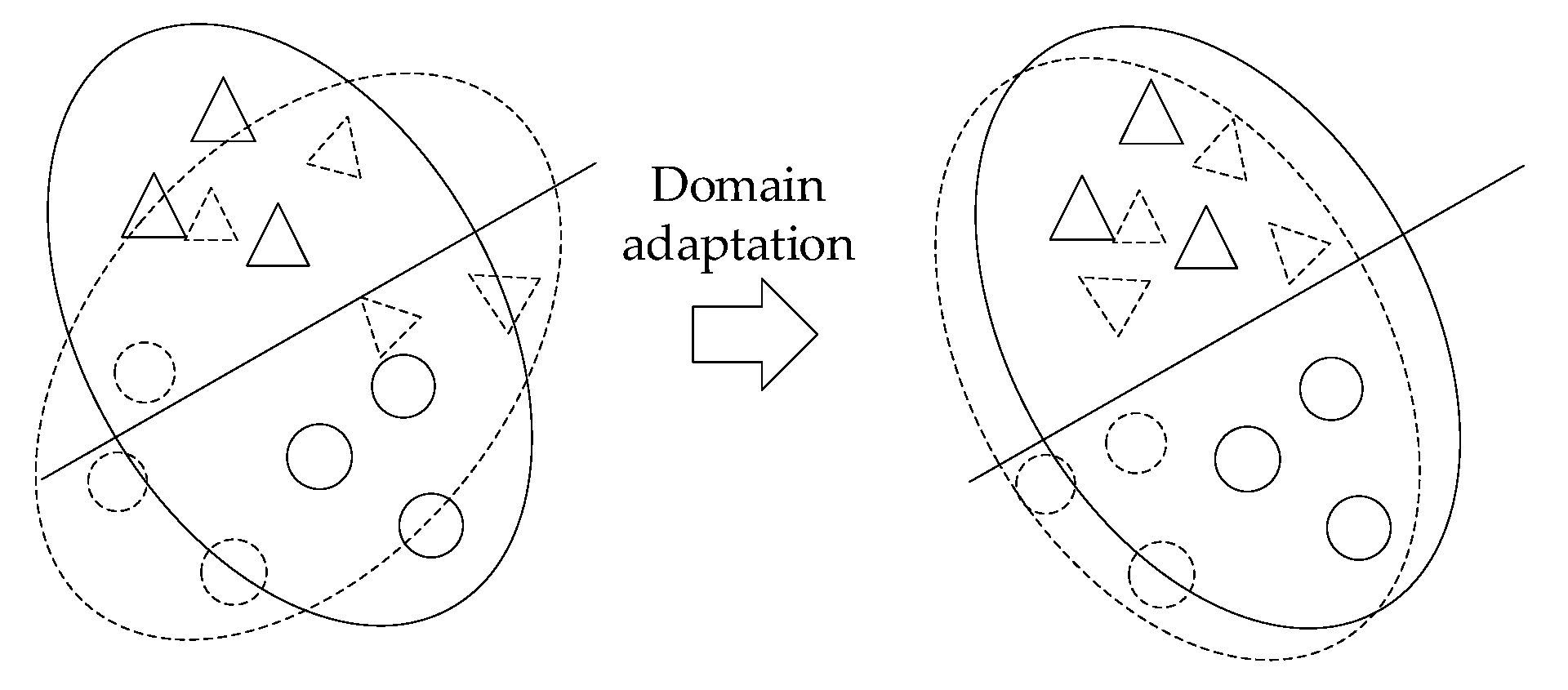

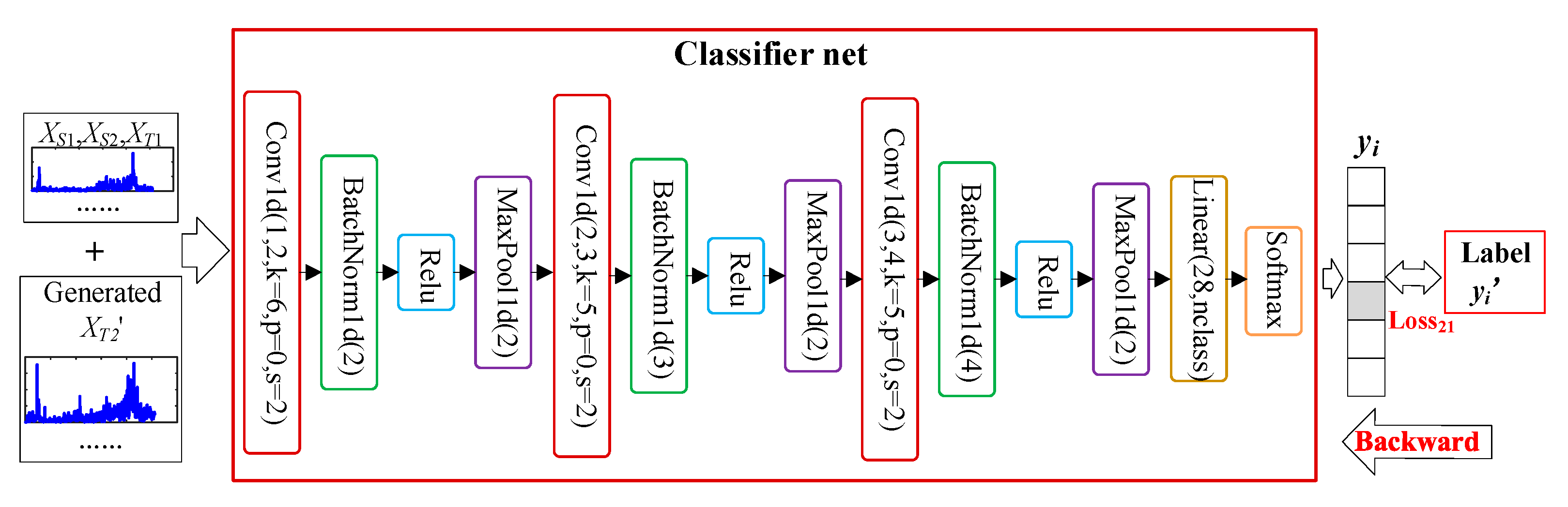

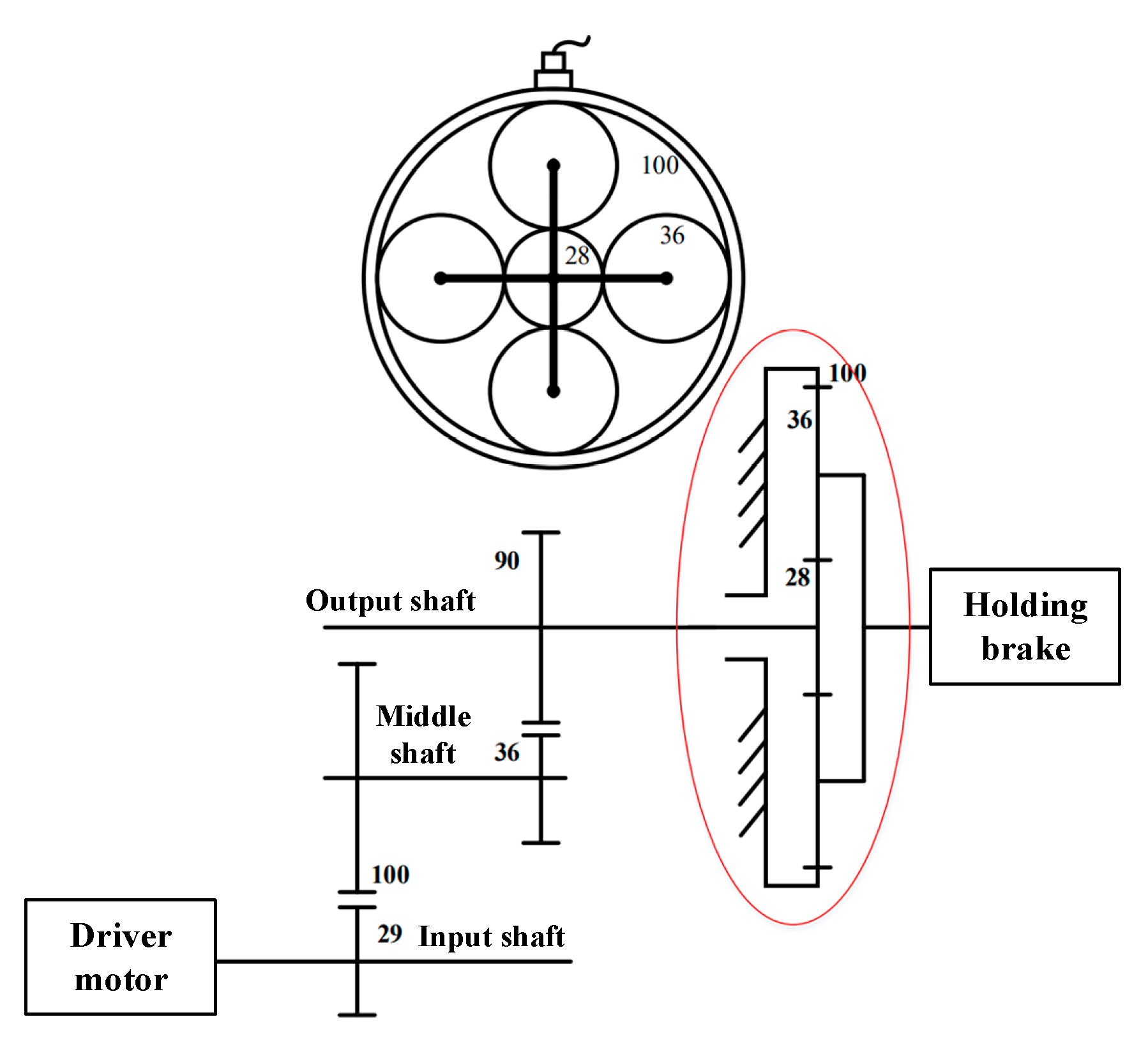
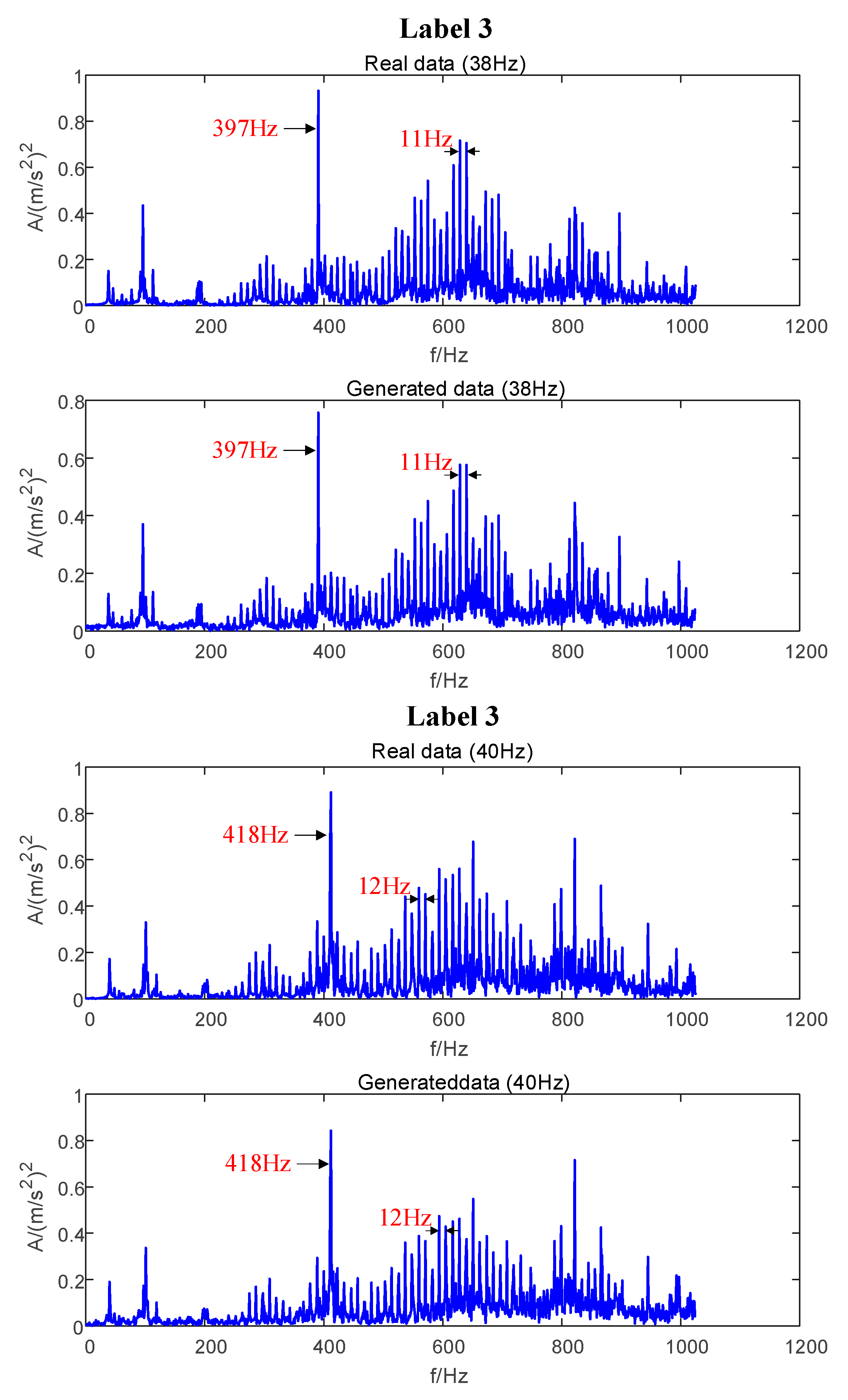

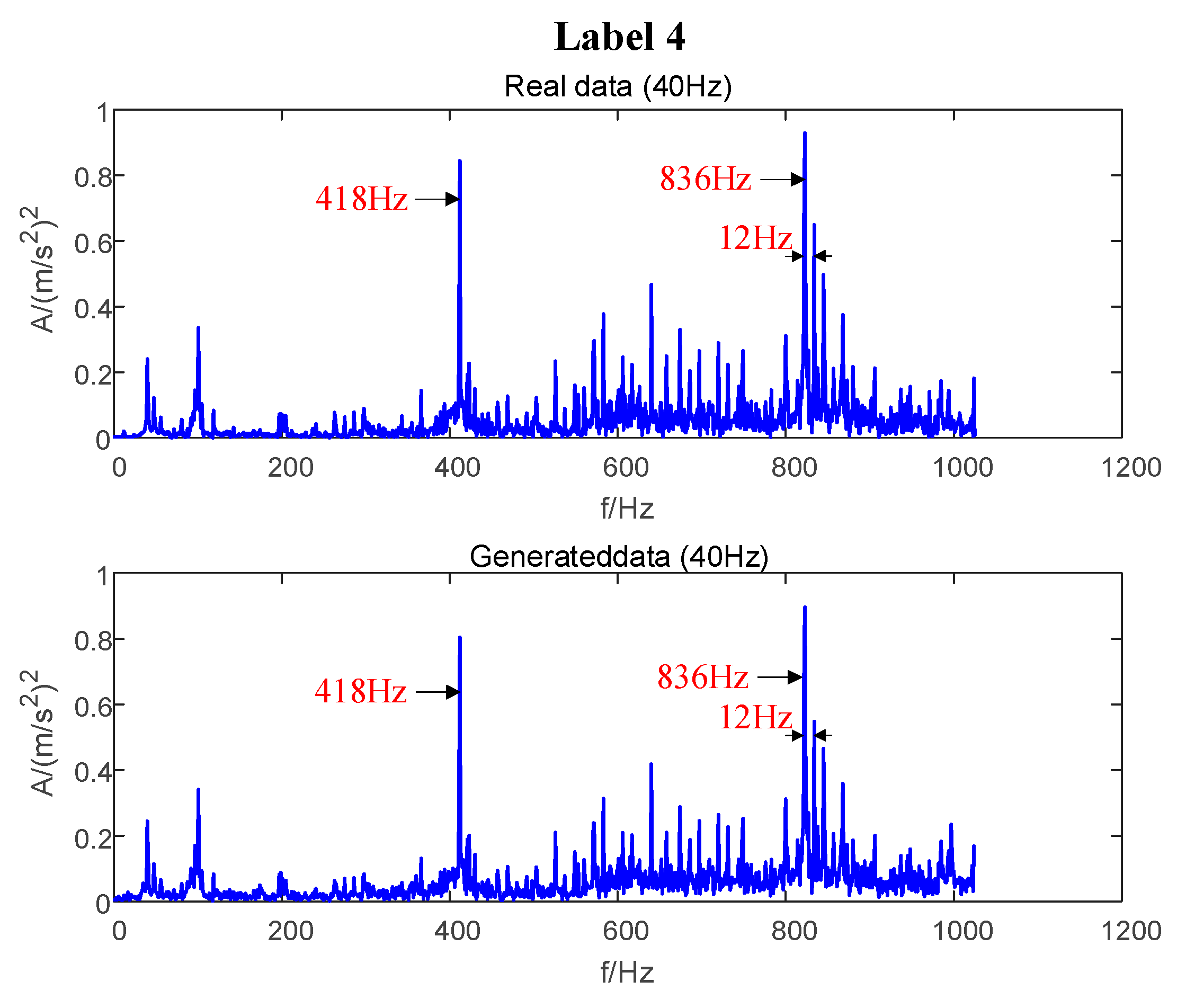
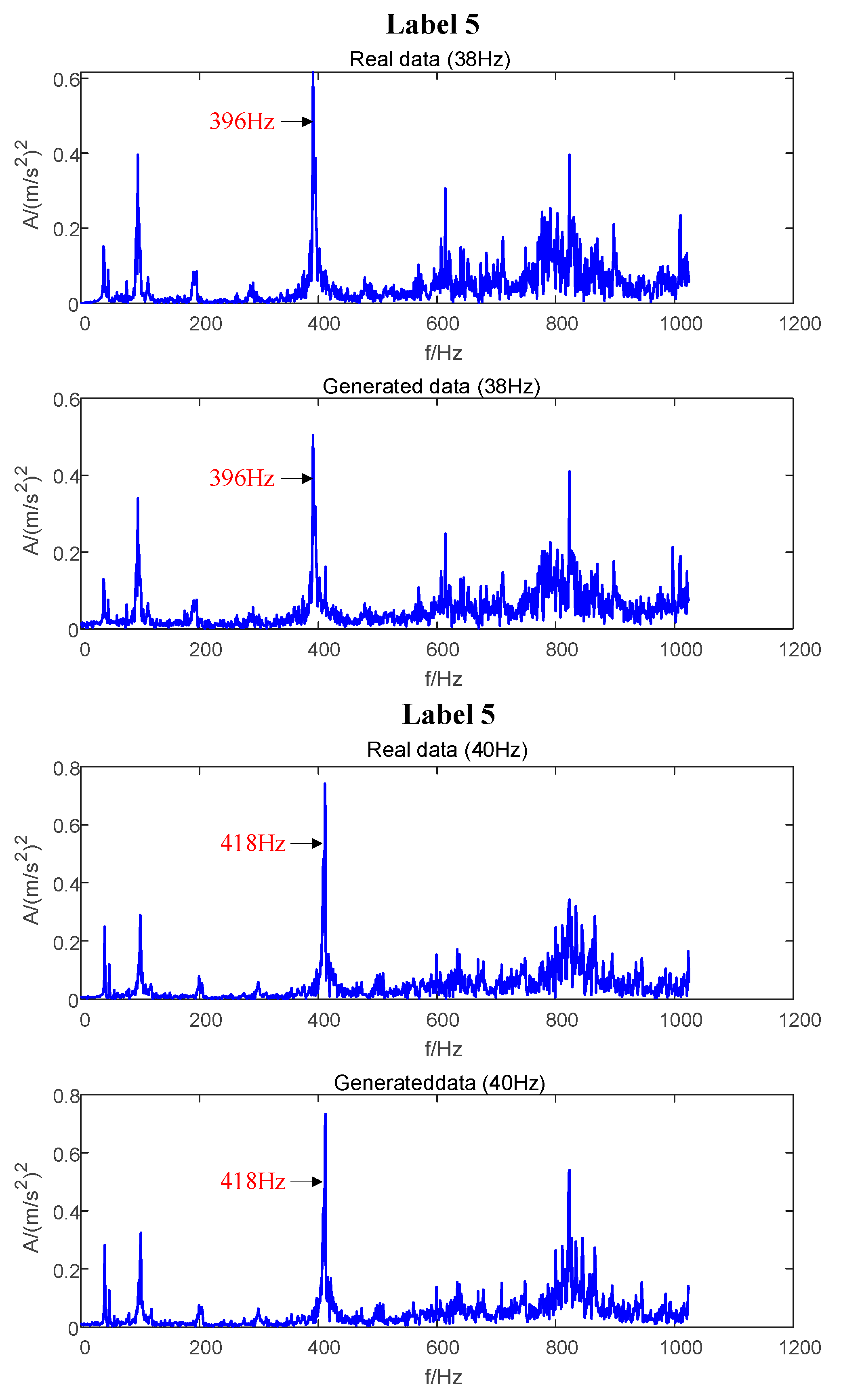
| Domain | Data | Work Condition | Known or Not |
|---|---|---|---|
| Source domain | XS1 | Speed1 | Data available |
| XS2 | Speed2 | Data available | |
| Target domain | XT1 | Speed1 | Data available |
| XT2 | Speed2 | Data not available |
| Fault Modes | Label | Speed (Hz) | Sampling Frequency | Number of Dataset |
|---|---|---|---|---|
| Normal | 0 | 38, 40, 43, 45 | 8192 Hz | 256 × 4 |
| Cracked | 1 | 38, 40, 43, 45 | 8192 Hz | 256 × 4 |
| Chipped | 2 | 38, 40, 43, 45 | 8192 Hz | 256 × 4 |
| Missing | 3 | 43, 45 | 8192 Hz | 256 × 2 |
| Wear | 4 | 43, 45 | 8192 Hz | 256 × 2 |
| Eccentricity | 5 | 43, 45 | 8192 Hz | 256 × 2 |
| Data | Label | Speed (Hz) | Number of Training Dataset | Number of Testing Dataset | |
|---|---|---|---|---|---|
| Source domain | XS1 | 0, 1, 2 | 43, 45 | 160 × 3 × 2 | 256 × 3 × 2 |
| XS2 | 0, 1, 2 | 38, 40 | 160 × 3 × 2 | 256 × 3 × 2 | |
| Target domain | XT1 | 3, 4, 5 | 43, 45 | 160 × 3 × 2 | 256 × 3 × 2 |
| XT2 | 3, 4, 5 | 38, 40 | 0 | 256 × 3 × 2 |
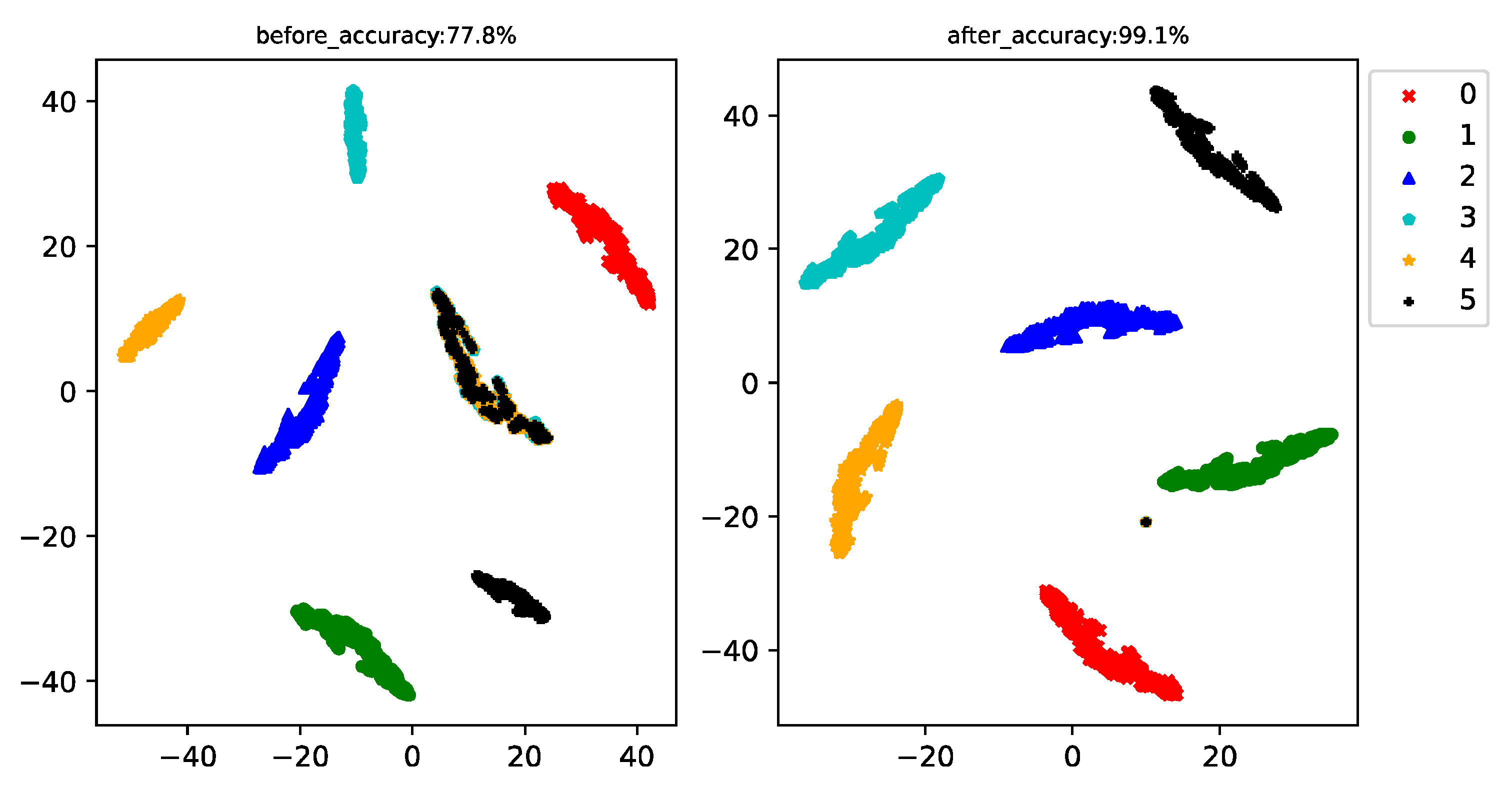
| Only the Training Set Trains the Classifier | Training Set and Generated Data together to Train the Classifier | Improved | |
|---|---|---|---|
| Classification accuracy | 77.8% | 99.1% | 21.3% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Ma, H.; Liu, Y. A Novel Transfer Learning Method Based on Conditional Variational Generative Adversarial Networks for Fault Diagnosis of Wind Turbine Gearboxes under Variable Working Conditions. Sustainability 2022, 14, 5441. https://doi.org/10.3390/su14095441
Liu X, Ma H, Liu Y. A Novel Transfer Learning Method Based on Conditional Variational Generative Adversarial Networks for Fault Diagnosis of Wind Turbine Gearboxes under Variable Working Conditions. Sustainability. 2022; 14(9):5441. https://doi.org/10.3390/su14095441
Chicago/Turabian StyleLiu, Xiaobo, Haifei Ma, and Yibing Liu. 2022. "A Novel Transfer Learning Method Based on Conditional Variational Generative Adversarial Networks for Fault Diagnosis of Wind Turbine Gearboxes under Variable Working Conditions" Sustainability 14, no. 9: 5441. https://doi.org/10.3390/su14095441
APA StyleLiu, X., Ma, H., & Liu, Y. (2022). A Novel Transfer Learning Method Based on Conditional Variational Generative Adversarial Networks for Fault Diagnosis of Wind Turbine Gearboxes under Variable Working Conditions. Sustainability, 14(9), 5441. https://doi.org/10.3390/su14095441






