Digital Twin-Driven Adaptive Scheduling for Flexible Job Shops
Abstract
:1. Introduction
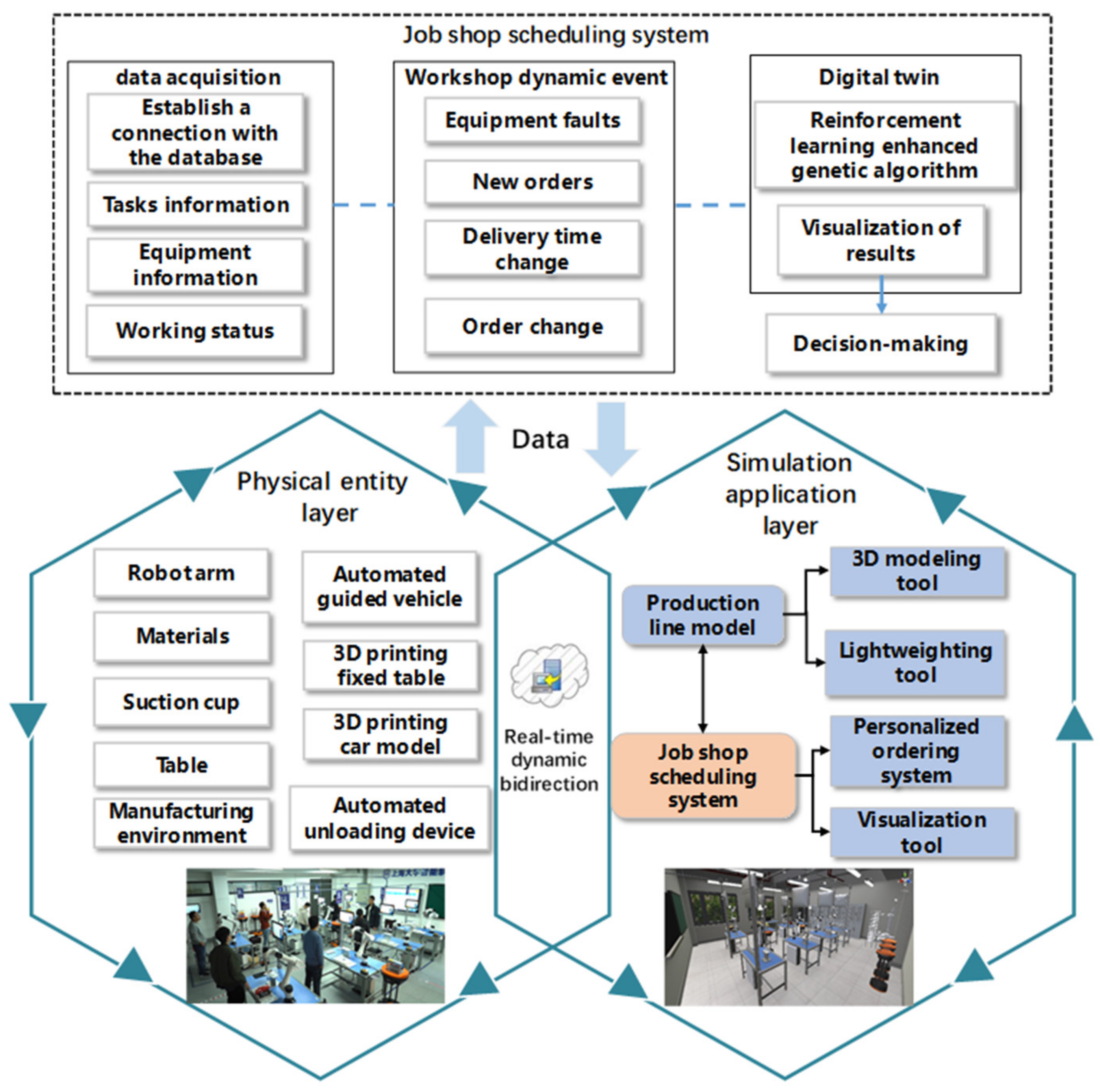
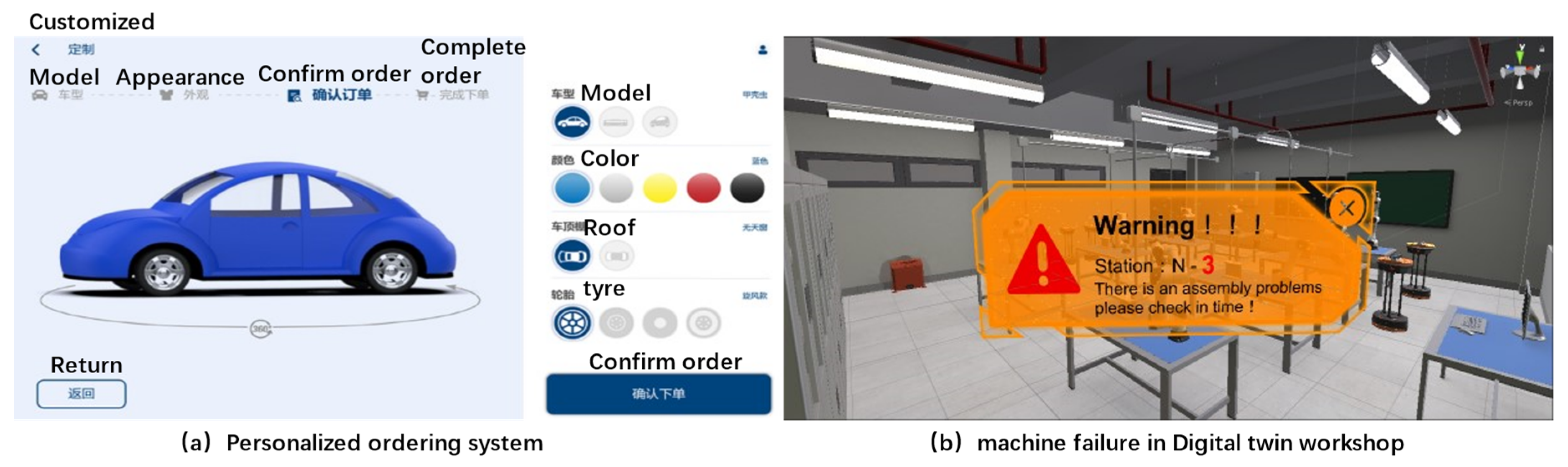
2. Digital Twin Workshop Modelling
2.1. Data Acquisition and Processing
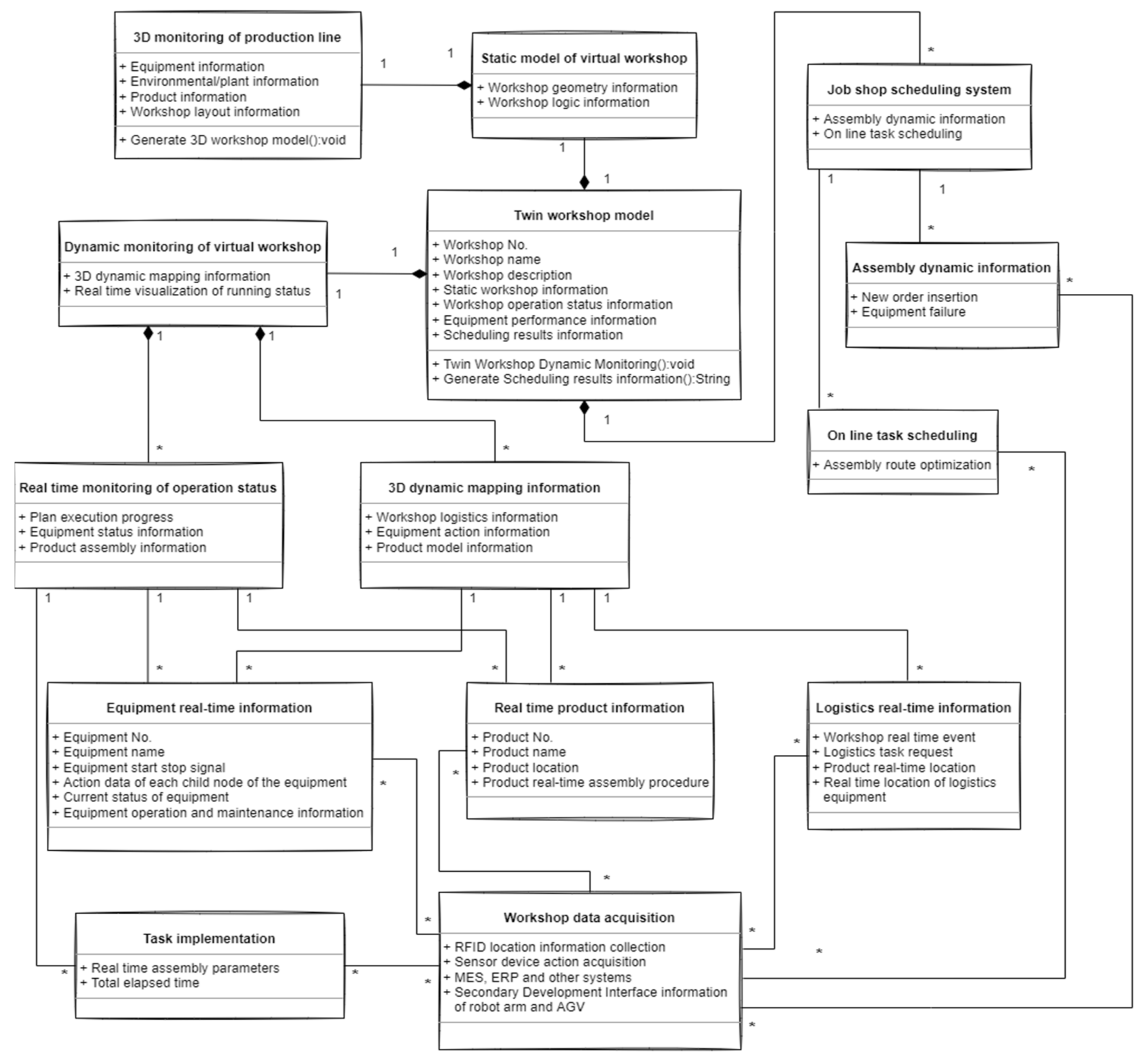
2.2. Data Modelling for Job-Shop Scheduling
2.3. Synchronous Mapping of Digital Twin Workshop
3. Problem Description and Modeling
4. Reinforcement Learning Enhanced Genetic Algorithm
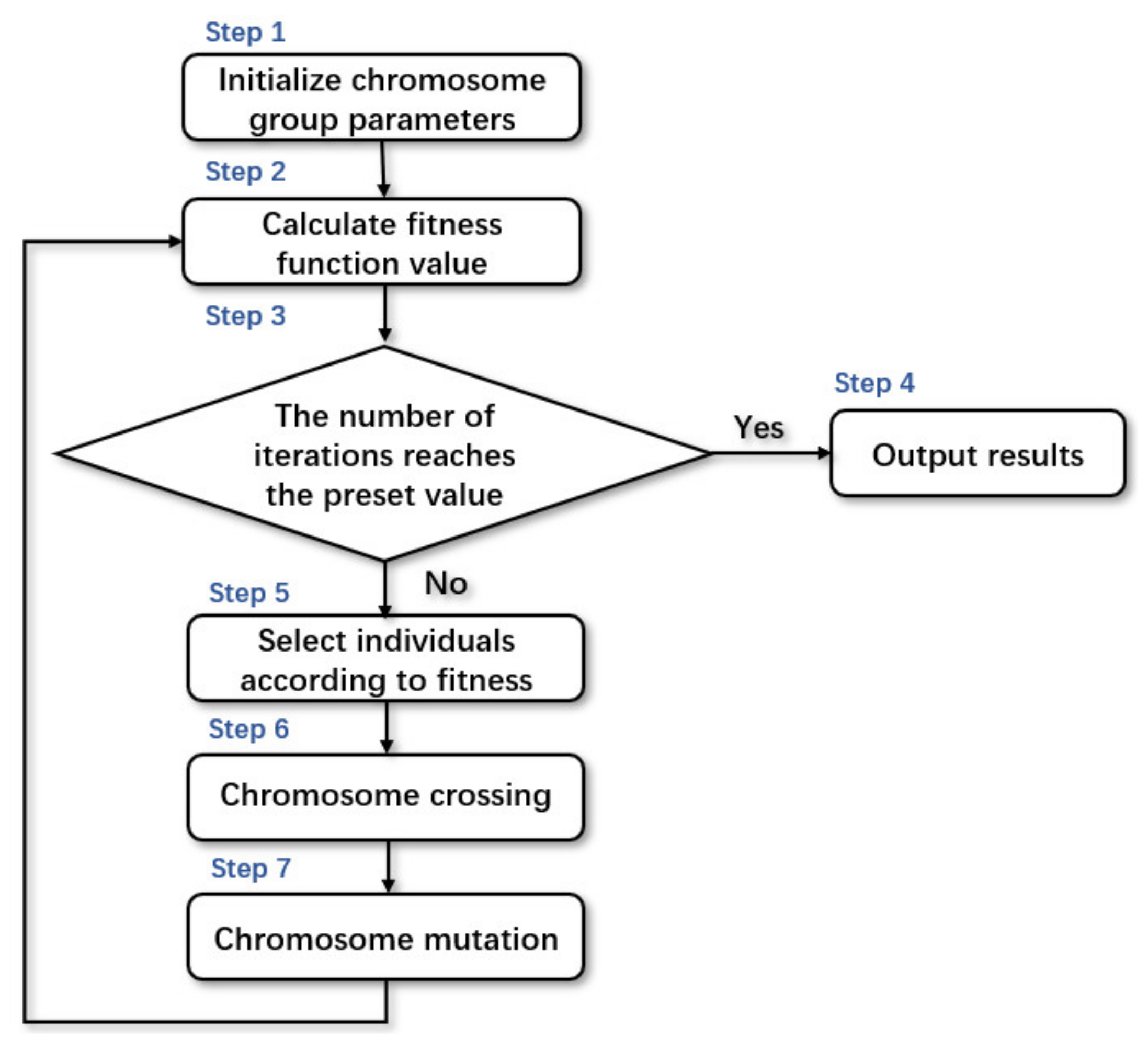
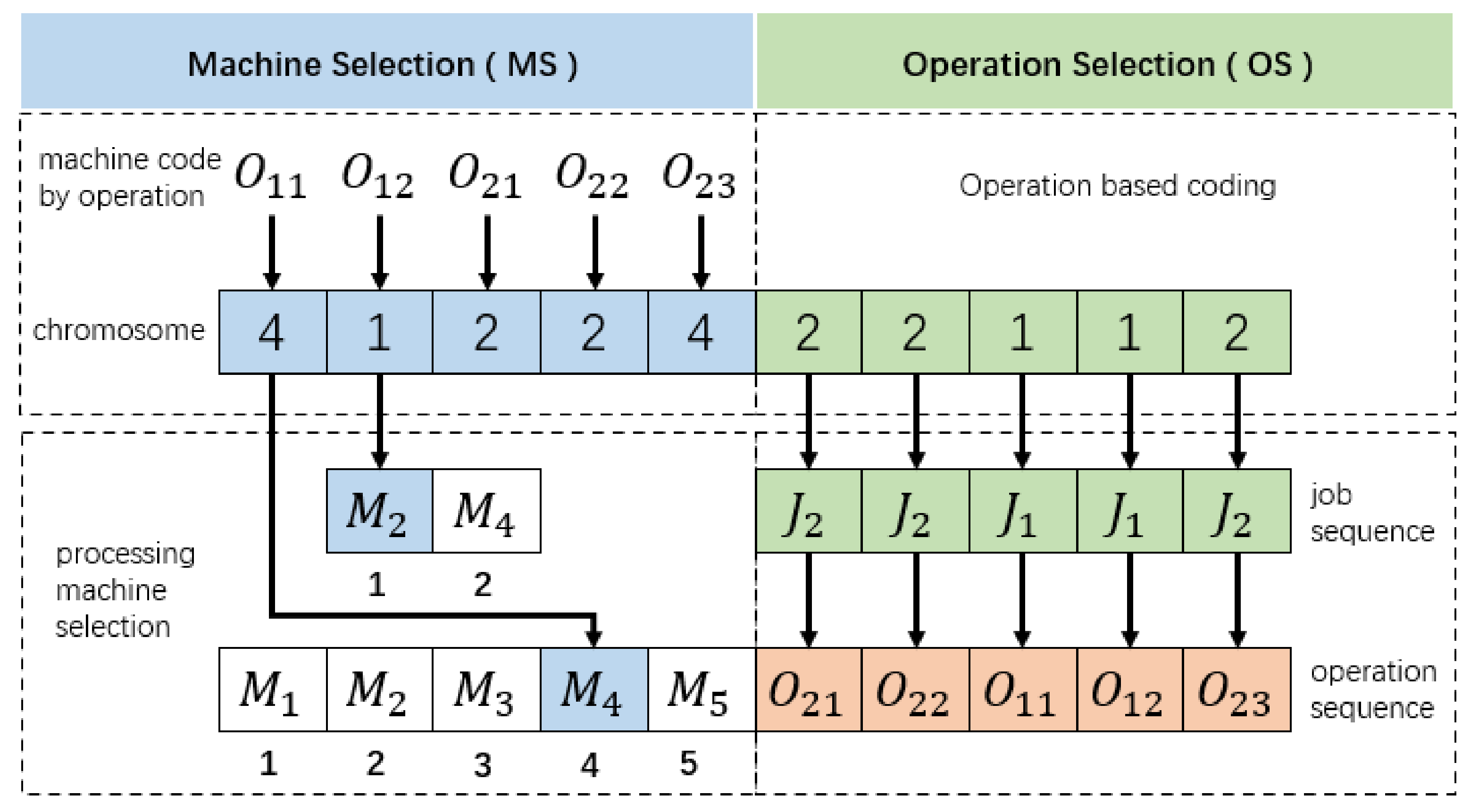
4.1. Genetic Algorithm
- Population size . Population size affects the final result of genetic optimization and the execution efficiency of genetic algorithm. When the population size is too small, the performance of genetic optimization is generally not very good. Larger population size can reduce the chance of genetic algorithm falling into local optimal solution, but larger population size means higher computational complexity.
- Crossover probability . The crossover probability controls the frequency with which the crossover operation is used. Larger crossover probability can enhance the ability of genetic algorithm to open up new search areas, but the possibility of the high-performance mode being destroyed increases. If the crossover probability is too low, the genetic algorithm search may fall into a slow state.
- Mutation probability . Mutation is an auxiliary search operation in genetic algorithms. Its main purpose is to maintain the diversity of the population. Generally, low-frequency mutation can prevent the possible loss of important genes in the population. High-frequency mutation makes the genetic algorithm tend to pure random search.
- Termination evolution algebra of genetic operation. The terminating evolution algebra is a parameter representing the end condition of the genetic algorithm.
4.2. State, Action, and Reward
4.3. Training Process
| Algorithm 1 Pseudocode of the RLEGA Algorithm |
| 1: Initialize the GA: population size N, maximum iterations T 2: Initialize the RL: replay memory D, initialize action-value function Q with random weights θ, and initialize target action-value function 3. for do 4. = ] 5. with probability 6. with probability 7. 8. 9. 10. 11. 12. using gradient descent 12. 13. end |
5. Experiment and Analysis
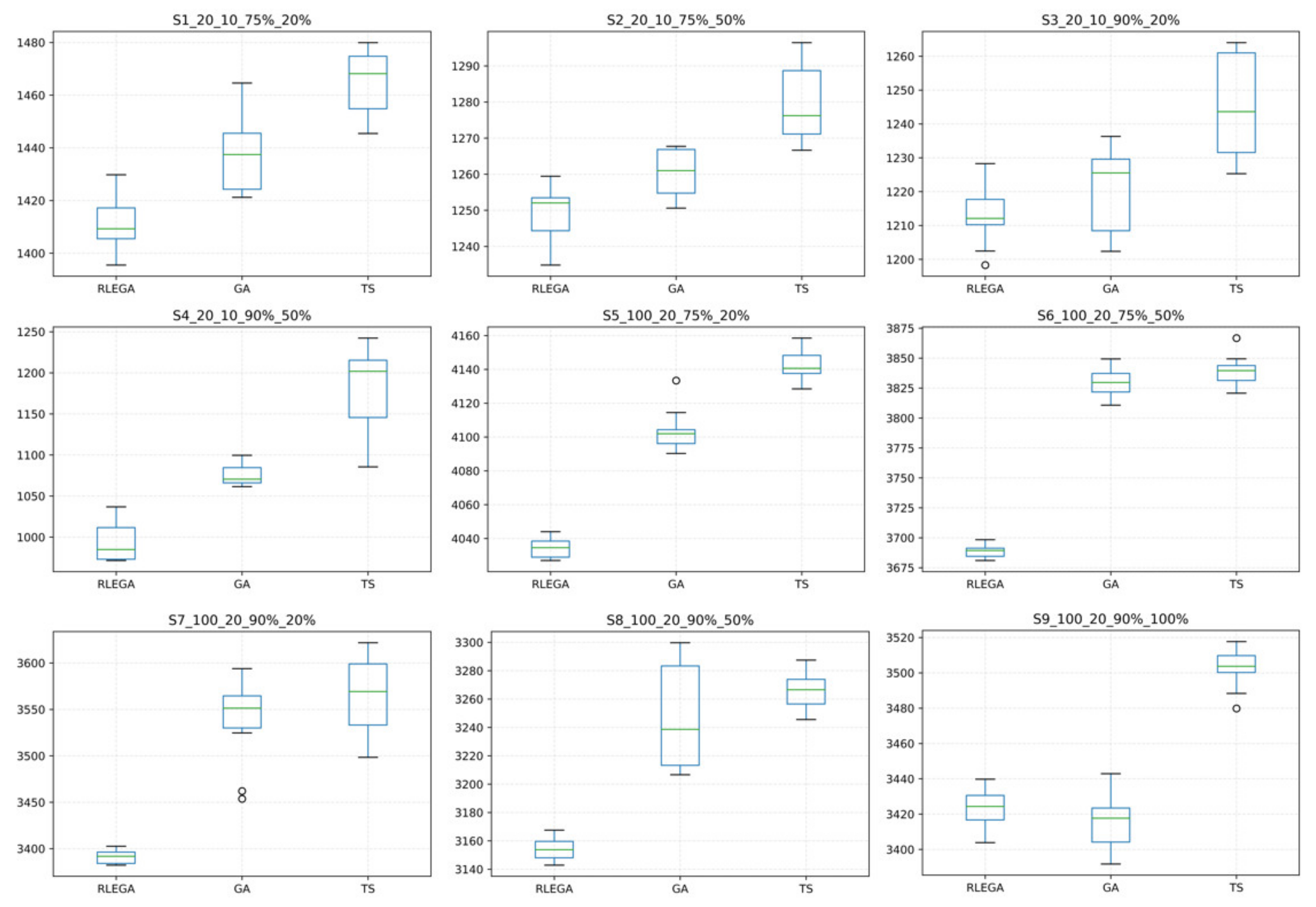
5.1. Simulation Results
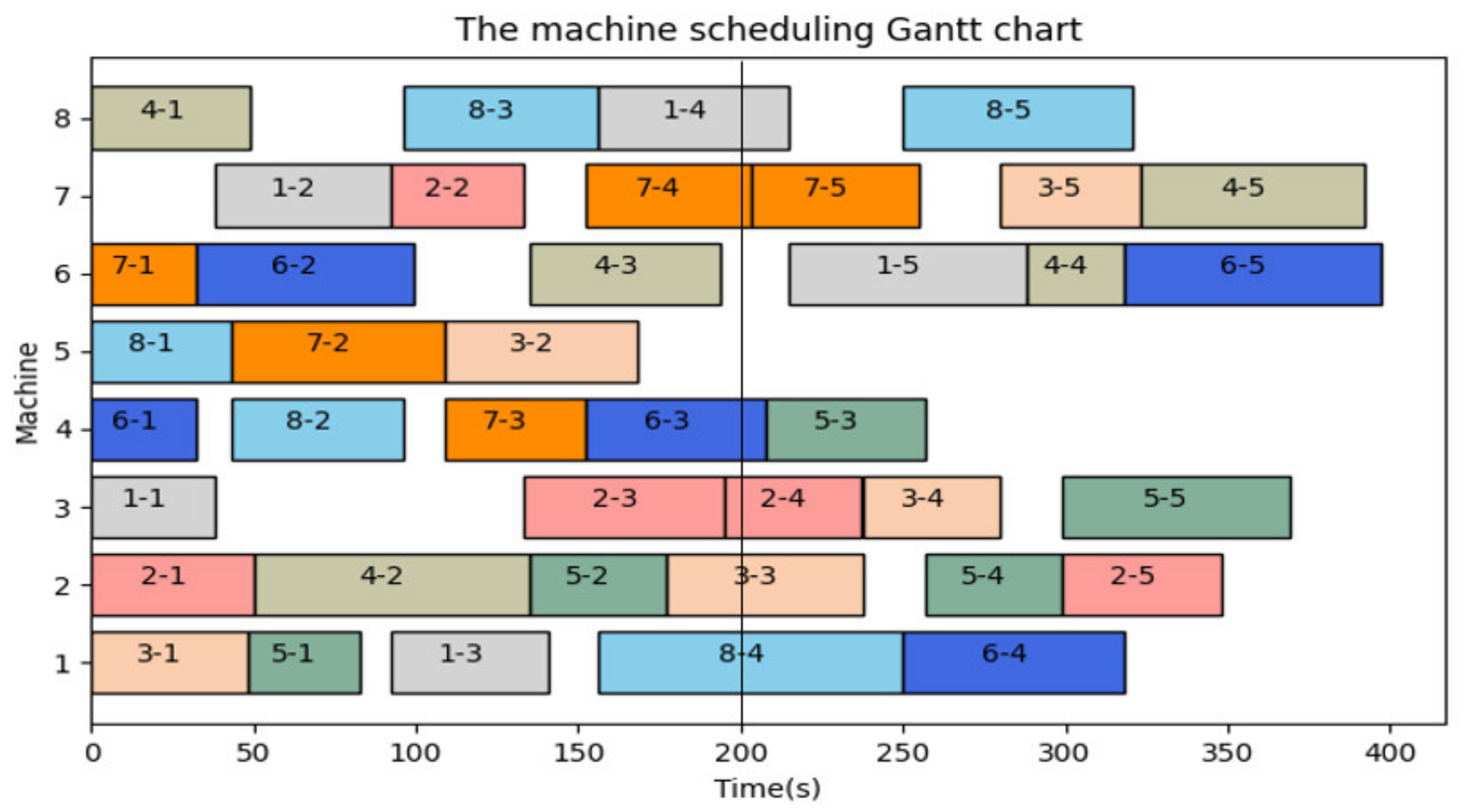
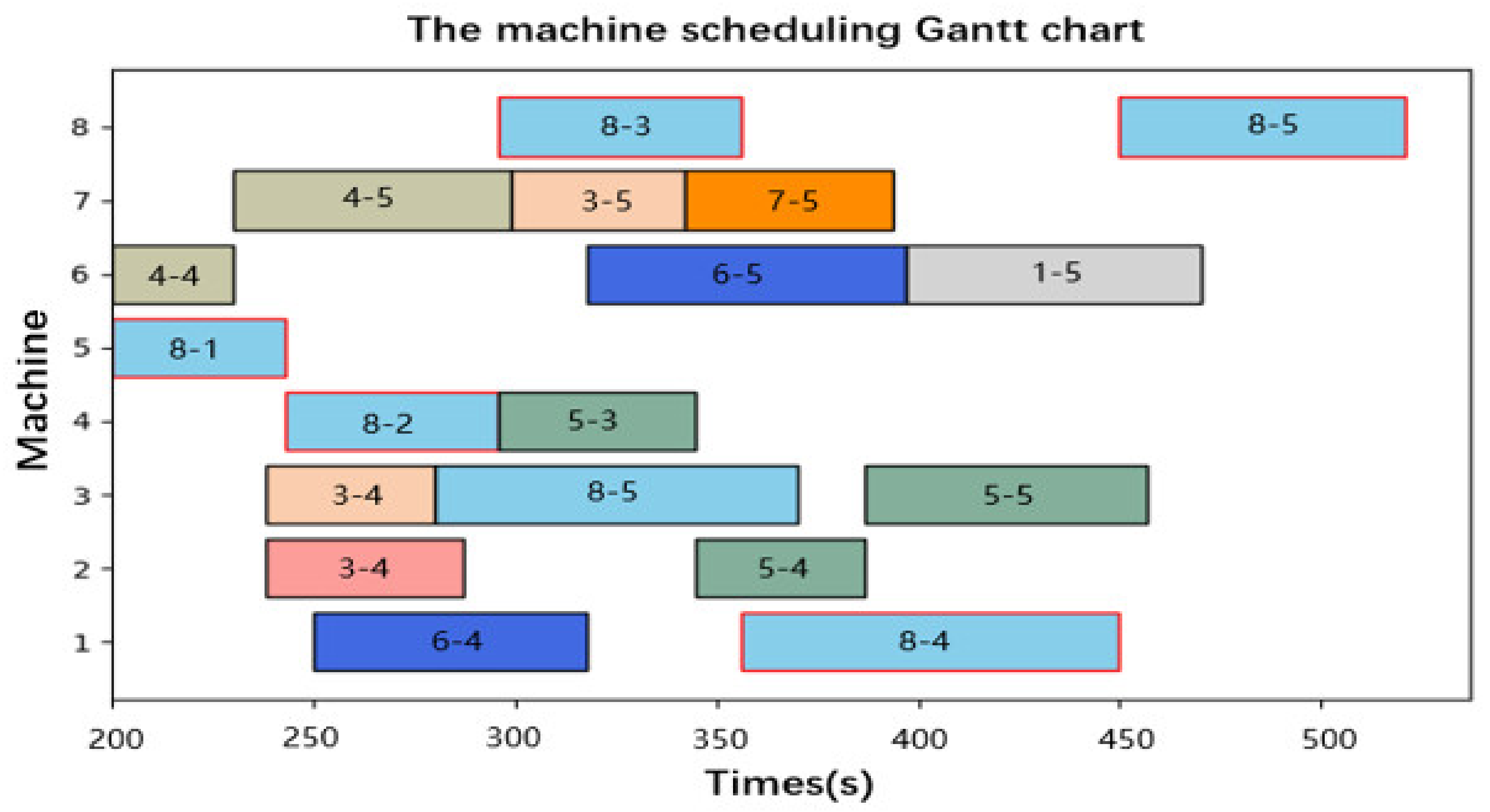
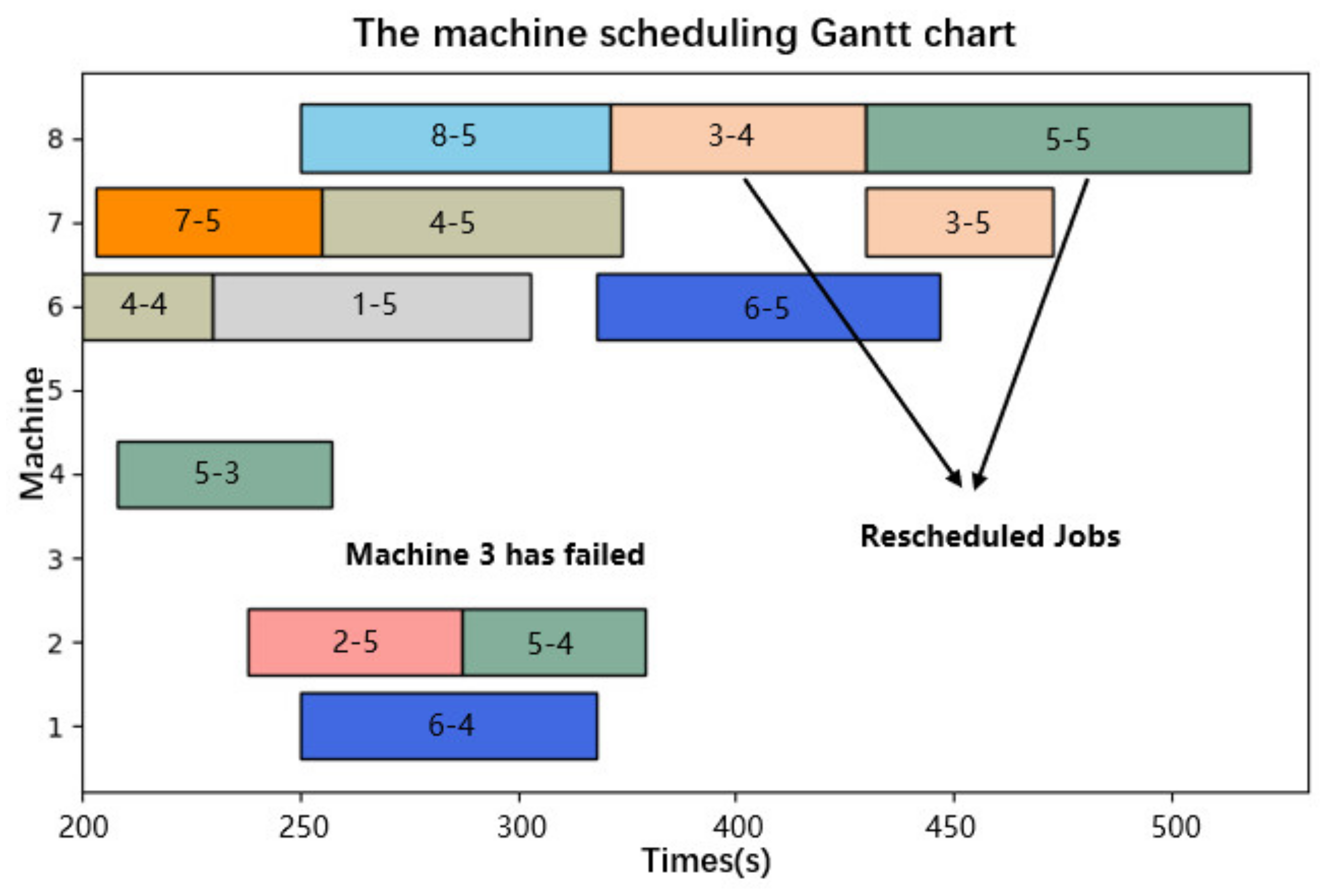
5.2. Case Study
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jazdi, N. Cyber physical systems in the context of Industry 4.0. In Proceedings of the 2014 IEEE International Conference on Automation, Quality and Testing, Robotics, Cluj-Napoca, Romania, 22–24 May 2014; pp. 14–16. [Google Scholar] [CrossRef]
- Mosterman, P.J.; Zander, J. Industry 4.0 as a Cyber-Physical System study. Softw. Syst. Model. 2016, 15, 17–29. [Google Scholar] [CrossRef]
- Liu, S.X. Innovation Design: Made in China 2025. Des. Manag. Rev. 2016, 27, 53–58. [Google Scholar]
- Saracco, R. Digital Twins: Bridging Physical Space and Cyberspace. Computer 2019, 52, 58–64. [Google Scholar] [CrossRef]
- Tao, F.; Zhang, M. Digital Twin Shop-Floor: A New Shop-Floor Paradigm towards Smart Manufacturing. IEEE Access 2017, 5, 20418–20427. [Google Scholar] [CrossRef]
- Milton, M.; De La, O.C.; Ginn, H.L.; Benigni, A. Controller-Embeddable Probabilistic Real-Time Digital Twins for Power Electronic Converter Diagnostics. IEEE Trans. Power Electron. 2020, 35, 9850–9864. [Google Scholar] [CrossRef]
- Mi, S.; Feng, Y.; Zheng, H.; Wang, Y.; Gao, Y.; Tan, J. Prediction maintenance integrated decision-making approach supported by digital twin-driven cooperative awareness and interconnection framework. J. Manuf. Syst. 2021, 58, 329–345. [Google Scholar] [CrossRef]
- Song, Y.; Shi, Y.Y.; Yu, J.S.; Tang, D.Y.; Tao, F. Application of digital twin model in performance prediction of electro-optical detection system. Comput. Integr. Manuf. Syst. 2019, 25, 1559–1567. [Google Scholar]
- Fedorko, G.; Molnár, V.; Vasiľ, M.; Salai, R. Proposal of digital twin for testing and measuring of transport belts for pipe conveyors within the concept Industry 4.0. Measurement 2021, 174, 108978. [Google Scholar] [CrossRef]
- Lu, C.; Wang, J.; Yin, P.; Wang, L. Error identification of measurement software based on digital twin of gear measuring center. Measurement 2021, 173, 108666. [Google Scholar] [CrossRef]
- Brucker, P.; Schlie, R. Job-shop scheduling with multi-purpose machines. Computing 1990, 45, 369–375. [Google Scholar] [CrossRef]
- Tian, S.; Wang, T.; Zhang, L.; Wu, X. Real-time shop floor scheduling method based on virtual queue adaptive control: Algorithm and experimental results. Measurement 2019, 147, 106689. [Google Scholar] [CrossRef]
- Reddy, M.B.S.S.; Ratnam, C.; Rajyalakshmi, G.; Manupati, V.K. An effective hybrid multi objective evolutionary algorithm for solving real time event in flexible job shop scheduling problem. Measurement 2018, 114, 78–90. [Google Scholar] [CrossRef]
- Yu, T.; Zhou, J.; Fang, J.; Gong, Y.; Wang, W. Dynamic scheduling of flexible job shop based on genetic algorithm. In Proceedings of the 2008 IEEE International Conference on Automation and Logistics, Qingdao, China, 1–3 September 2008; pp. 2014–2019. [Google Scholar] [CrossRef]
- Chang, H.-C.; Liu, T.-K. Optimisation of distributed manufacturing flexible job shop scheduling by using hybrid genetic algorithms. J. Intell. Manuf. 2017, 28, 1973–1986. [Google Scholar] [CrossRef]
- Dolgui, A.; Ivanov, D.; Sethi, S.P.; Sokolov, B. Scheduling in production, supply chain and Industry 4.0 systems by optimal control: Fundamentals, state-of-the-art and applications. Int. J. Prod. Res. 2019, 57, 411–432. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Y.; Liu, Y.; Wu, N. Multiagent and Bargaining-Game-Based Real-Time Scheduling for Internet of Things-Enabled Flexible Job Shop. IEEE Internet Things J. 2019, 6, 2518–2531. [Google Scholar] [CrossRef] [Green Version]
- Fang, Y.; Peng, C.; Lou, P.; Zhou, Z.; Hu, J.; Yan, J. Digital-Twin-Based Job Shop Scheduling Toward Smart Manufacturing. IEEE Trans. Ind. Inform. 2019, 15, 6425–6435. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, W.; Zhang, C.; Yang, C.; Cheng, Q. Intelligent scheduling of a feature- process-machine tool supernetwork based on digital twin workshop. J. Manuf. Syst. 2021, 58, 157–167. [Google Scholar] [CrossRef]
- Luo, S. Dynamic scheduling for flexible job shop with new job insertions by deep reinforcement learning. Appl. Soft Comput. 2020, 91, 106208. [Google Scholar] [CrossRef]
- Zhang, M.; Tao, F.; Nee, A.Y.C. Digital Twin Enhanced Dynamic Job-Shop Scheduling. J. Manuf. Syst. 2021, 58, 146–156. [Google Scholar] [CrossRef]
- Tao, F.; Zhang, H.; Qi, Q.; Xu, J.; Sun, Z.; Hu, T.; Liu, X.; Liu, T.; Guan, J.; Chen, C.; et al. Construction theory and application of digital twin model. Comput. Integr. Manuf. Syst. 2021, 27, 1–15. [Google Scholar] [CrossRef]
- Zhang, C.; Tao, F. Evaluation index system of digital twin model. Comput. Integr. Manuf. Syst. 2021, 27, 2171–2186. [Google Scholar] [CrossRef]
- Wu, Y.; Yao, L.Y.; Xiong, H.; Zhuang, C.B.; Zhao, H.R.; Liu, J.H. Quality control method of complex product assembly process based on digital twin technology. Comput. Integr. Manuf. Syst. 2019, 25, 1568–1575. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Van Hasselt, H. Double Q-learning. In Advances in Neural Information Processing Systems; MIT Press: Vancouver, BC, Canada, 2010; pp. 2613–2621. [Google Scholar]
- Van Hasselt, H.; Guez, A.; Silver, D. Deep reinforcement learning with double Q-learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Menlo Park, CA, USA, 12–17 February 2016; pp. 2094–2100. [Google Scholar]
- Wang, Z.; Schaul, T.; Hessel, M.; Hasselt, H.; Lanctot, M.; Freitas, N. Dueling network architectures for deep reinforcement learning. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 20–22 June 2016; Volume 48, pp. 1995–2003. [Google Scholar]

| Parameters | Descriptions |
|---|---|
| The total number of jobs | |
| The total number of machines | |
| The number of machines | |
| The number of jobs | |
| The total number of operations of job j | |
| The number of operations | |
| The number of optional processing machines for the h operation of the job j | |
| The hth operation of the jth job | |
| The time of operation h of job j on machine i | |
| The start time of the h operation of the job j | |
| The completion time of the h operation of the job j | |
| A positive number large enough | |
| When machine i is selected for operation Ojh, the value is 1, otherwise 0 | |
| , the value is 1, otherwise 0 |
| Jobs | Operation | Optional Processing Machine | ||||
|---|---|---|---|---|---|---|
| 2 | 6 | 5 | 3 | 4 | ||
| 8 | 4 | |||||
| 3 | 6 | 5 | ||||
| 4 | 6 | 5 | ||||
| 7 | 11 | 5 | 8 | |||
| Parameter | Value |
|---|---|
| RLEGA | |
| Number of iterations | 1000 |
| Learning rate | |
| Discount rate | 0.95 |
| Batch size | 128 |
| Buffer size | 100,000 |
| Greedy rate | 0.9 |
| TS | |
| Number of iterations | 500 |
| Preset probability | 0.5 |
| Taboo table length | 10 |
| RLEGA | GA | TS | LWT + SPT | LWT + LPT | LWT + SSO | LWT + LSO | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Test Case | Avg | Max | Min | Avg | Max | Min | Avg | Max | Min | ||||
| S1_20_10_75%_20% | 1411.50 | 1429.79 | 1395.49 | 1437.32 | 1464.59 | 1421.19 | 1464.63 | 1479.95 | 1445.47 | 1575.62 | 1602.94 | 1557.72 | 1620.02 |
| S2_20_10_75%_50% | 1249.41 | 1259.43 | 1234.84 | 1261.00 | 1267.74 | 1250.62 | 1280.08 | 1296.46 | 1266.64 | 1520.51 | 1480.45 | 1540.22 | 1534.42 |
| S3_20_10_90%_20% | 1213.56 | 1228.29 | 1198.31 | 1220.30 | 1236.31 | 1202.35 | 1245.30 | 1264.03 | 1225.31 | 1402.51 | 1450.21 | 1395.66 | 1380.61 |
| S4_20_10_90%_50% | 993.15 | 1036.82 | 971.48 | 1075.19 | 1099.60 | 1061.45 | 1178.12 | 1242.36 | 1085.55 | 1320.94 | 1360.73 | 1376.72 | 1342.61 |
| S5_100_20_75%_20% | 4036.58 | 4044.01 | 4026.97 | 4103.53 | 4133.43 | 4090.29 | 4142.77 | 4158.52 | 4128.5 | 4755.28 | 4757.21 | 4927.13 | 4838.95 |
| S6_100_20_75%_50% | 3688.92 | 3698.43 | 3681.02 | 3829.52 | 3849.34 | 3810.76 | 3839.14 | 3866.76 | 3820.79 | 4668.86 | 4681.28 | 4601.55 | 4797.52 |
| S7_100_20_90%_20% | 3391.53 | 3402.65 | 3382.3 | 3538.60 | 3593.95 | 3453.70 | 3565.44 | 3621.85 | 3498.41 | 4396.96 | 4273.13 | 4029.85 | 4341.45 |
| S8_100_20_90%_50% | 3154.40 | 3167.56 | 3142.88 | 3247.31 | 3299.77 | 3206.68 | 3266.01 | 3287.50 | 3245.60 | 4164.51 | 4033.08 | 4166.68 | 4013.11 |
| S9_100_20_90%_100% | 3423.31 | 3439.81 | 3403.85 | 3415.46 | 3442.91 | 3391.76 | 3502.81 | 3517.72 | 3479.84 | 4287.91 | 4213.23 | 4333.08 | 4233.95 |
| Job | O1 | O2 | O3 | O4 | O5 |
|---|---|---|---|---|---|
| J1 | [3,8] | [1,7] | [1,4] | [2,8] | [6,7] |
| J2 | [2,8] | [4,7] | [3,5] | [1,3] | [2,3] |
| J3 | [1,4,6] | [4,5] | [2,5] | [3,8] | [7] |
| J4 | [4,8] | [1,2] | [6,8] | [6] | [6,7] |
| J5 | [1,6] | [2,5] | [1,4] | [2,7] | [3,8] |
| J6 | [1,2,4,7] | [1,6] | [4,8] | [1,3] | [6] |
| J7 | [1,6] | [2,5] | [1,4] | [7,8] | [3,7] |
| J8 | [2,5,7] | [2,4] | [5,8] | [1,3] | [3,8] |
| Job | O1 | O2 | O3 | O4 | O5 |
|---|---|---|---|---|---|
| J1 | [38,49] | [72,54] | [49,65] | [76,59] | [73,43] |
| J2 | [50,49] | [53,41] | [62,66] | [51,42] | [49,70] |
| J3 | [48,60,68] | [53,59] | [61,66] | [42,59] | [43] |
| J4 | [60,49] | [72,85] | [59,66] | [30] | [73,69] |
| J5 | [35,68] | [42,69] | [67,49] | [42,30] | [70,88] |
| J6 | [43,35,32,57] | [68,67] | [56,93] | [68,105] | [79] |
| J7 | [48,32] | [85,66] | [49,43] | [51,73] | [102,52] |
| J8 | [50,43,57] | [85,53] | [66,60] | [94,100] | [90,71] |
| RLEGA | GA | TS | |
|---|---|---|---|
| Maximum | 404 | 433 | 466 |
| Average | 400 | 420 | 453.6 |
| Minimum | 397 | 411 | 435 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Guo, K.; Gao, Z.; Li, J.; Sun, J. Digital Twin-Driven Adaptive Scheduling for Flexible Job Shops. Sustainability 2022, 14, 5340. https://doi.org/10.3390/su14095340
Liu L, Guo K, Gao Z, Li J, Sun J. Digital Twin-Driven Adaptive Scheduling for Flexible Job Shops. Sustainability. 2022; 14(9):5340. https://doi.org/10.3390/su14095340
Chicago/Turabian StyleLiu, Lilan, Kai Guo, Zenggui Gao, Jiaying Li, and Jiachen Sun. 2022. "Digital Twin-Driven Adaptive Scheduling for Flexible Job Shops" Sustainability 14, no. 9: 5340. https://doi.org/10.3390/su14095340
APA StyleLiu, L., Guo, K., Gao, Z., Li, J., & Sun, J. (2022). Digital Twin-Driven Adaptive Scheduling for Flexible Job Shops. Sustainability, 14(9), 5340. https://doi.org/10.3390/su14095340






