A Unified Inner Current Control Strategy Based on the 2-DOF Theory for a Multifunctional Cascade Converter in an Integrated Microgrid System
Abstract
1. Introduction
- Differences and internal relations between the control structures of the microgrid converter in UC/CCS mode and SA/CVS mode are demonstrated for further research, especially for the cascaded multilevel topology.
- Unified inner loop based on the 2-DOF strategy of the multifunctional microgrid converter for the transfer modes is established to obtain a satisfactory power quality for both the steady and the transient processes.
- Detailed parameter tuning is deduced, as well as the influences on the tracking and stability performances from the variations in the main circuit and controlling parameters, which proves the practical feasibility of the proposed control strategy.
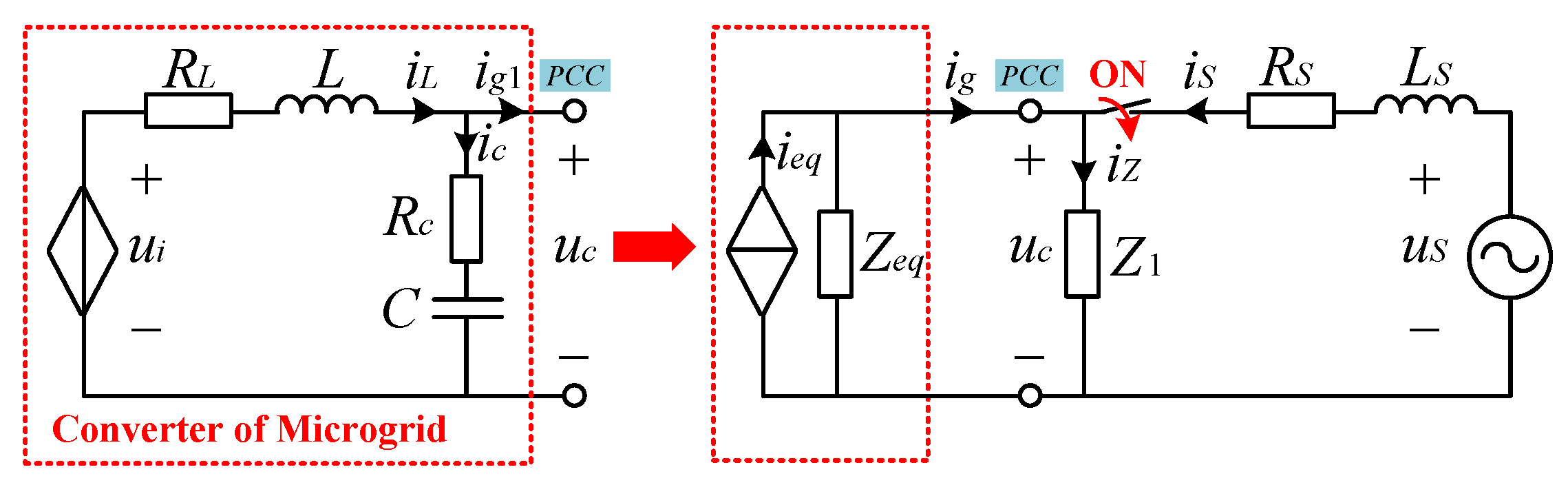
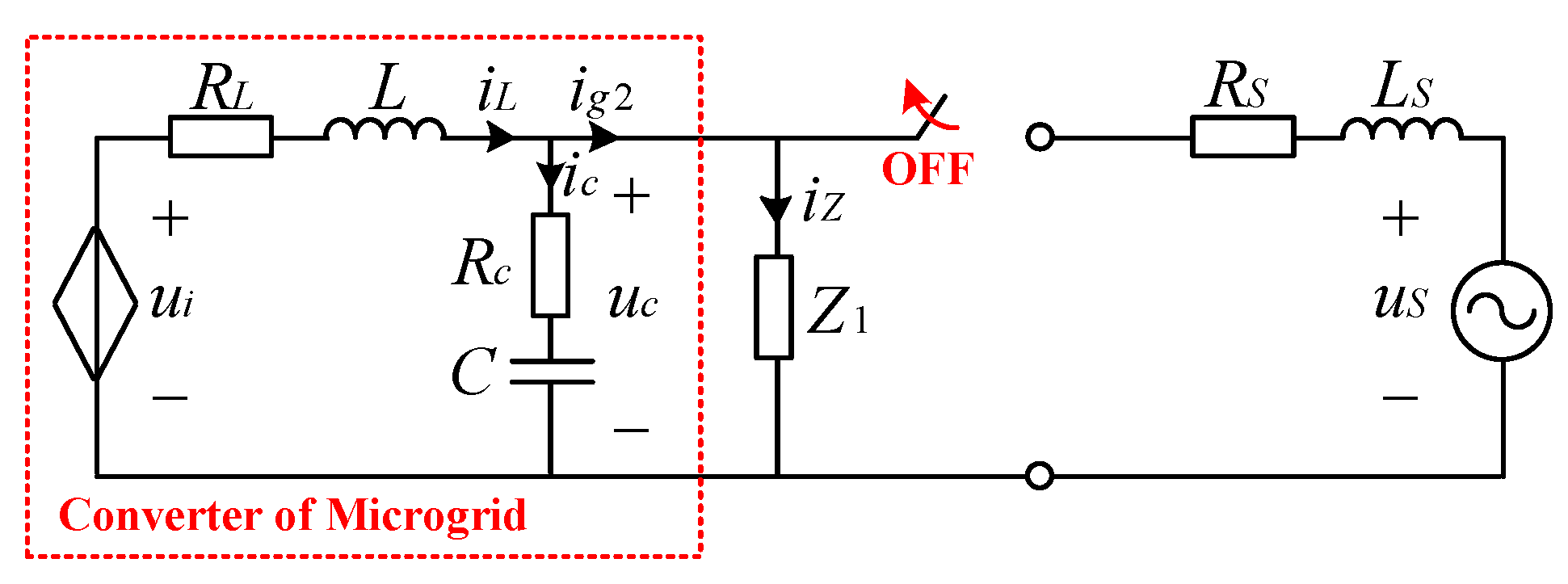
2. System Configuration
- The three-phase system and local load are symmetrical;
- The fault detection and HVSTS operation time is short and can be ignored;
- The capacity of energy storage is sufficient to meet the load’s demand.
2.1. Control Strategy for the UC Mode
2.2. Control Strategy for the SA Mode
2.3. Instability of the Transition Modes
2.3.1. From SA Mode to UC Mode
2.3.2. From the UC Mode to SA Mode
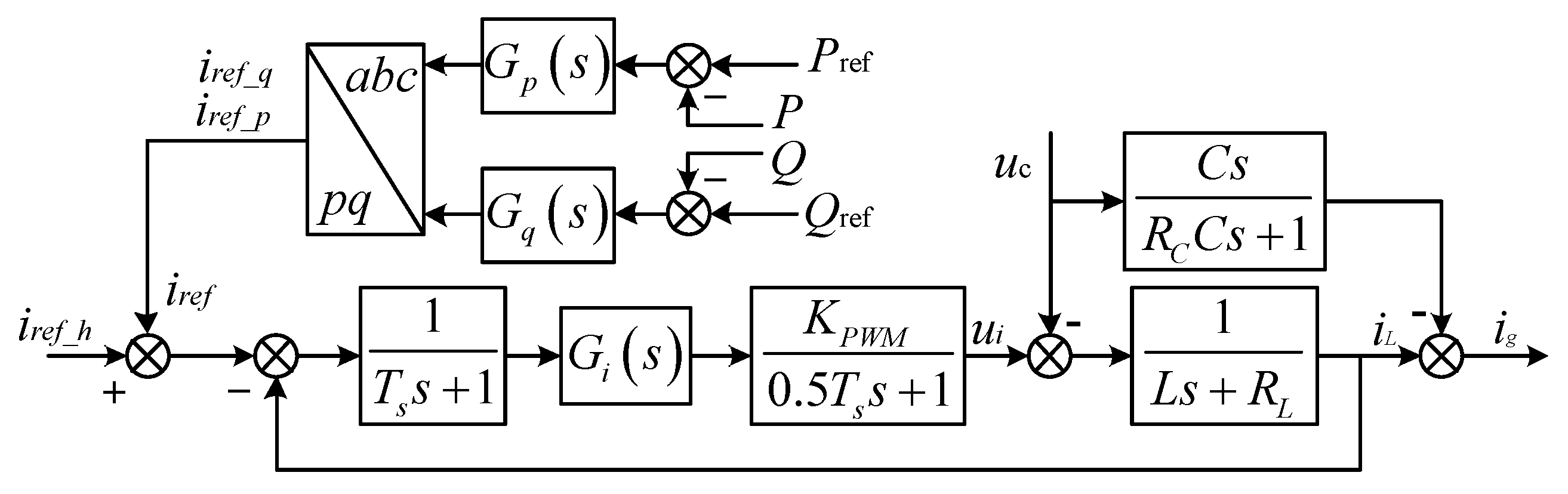
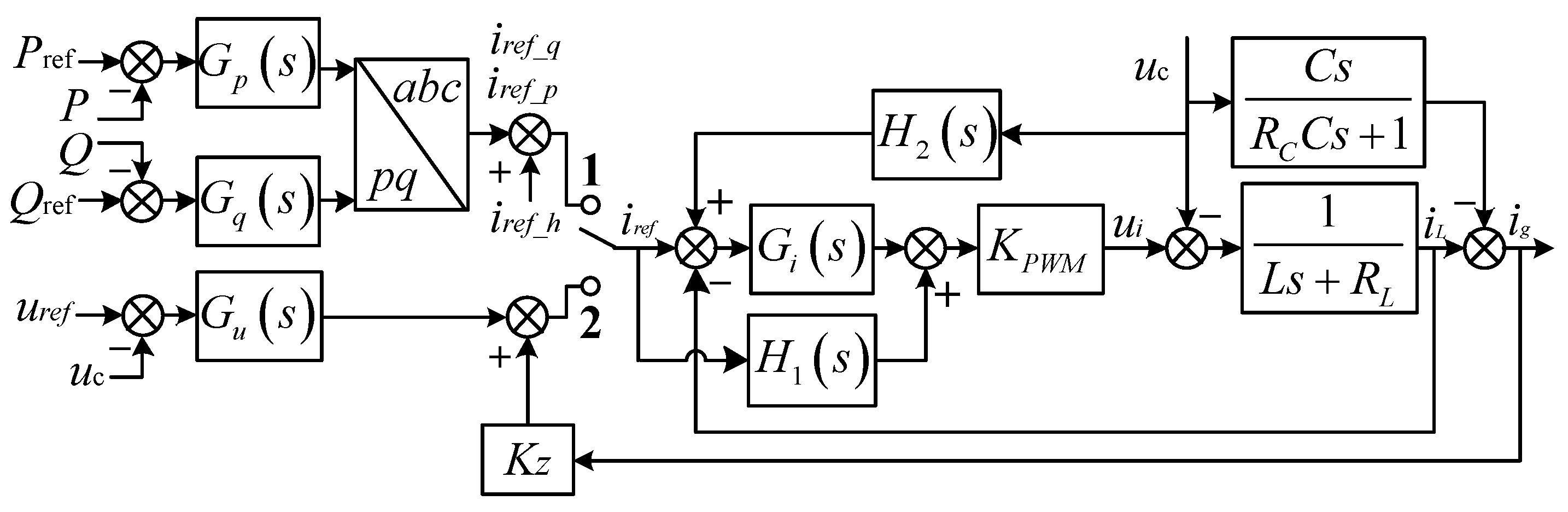
3. Unified Inner Loop Based on the 2-DOF Theory
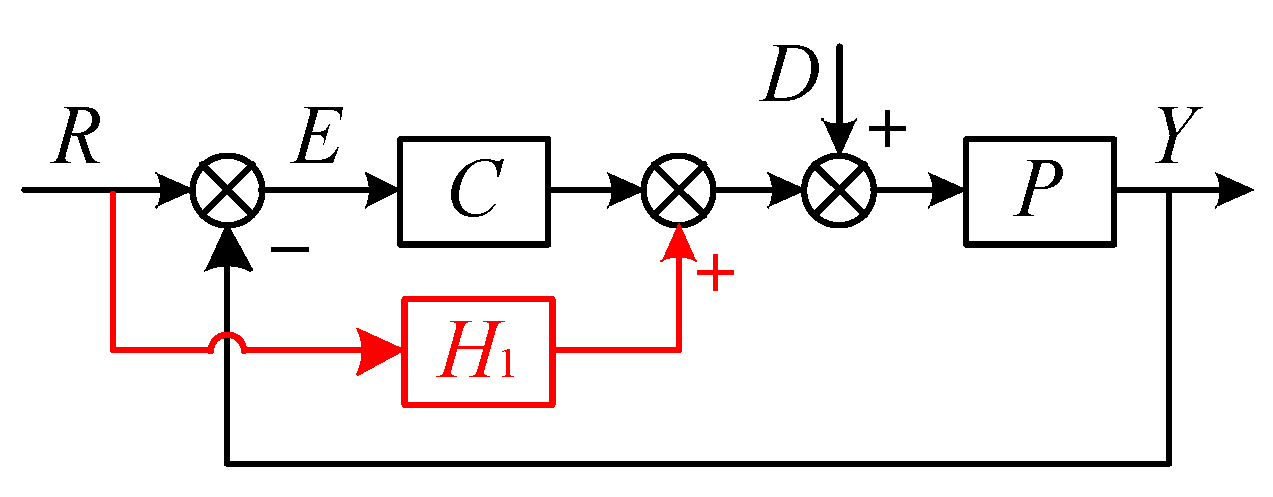
3.1. The 2-DOF Theory
3.2. Construction of the Proposed Strategy
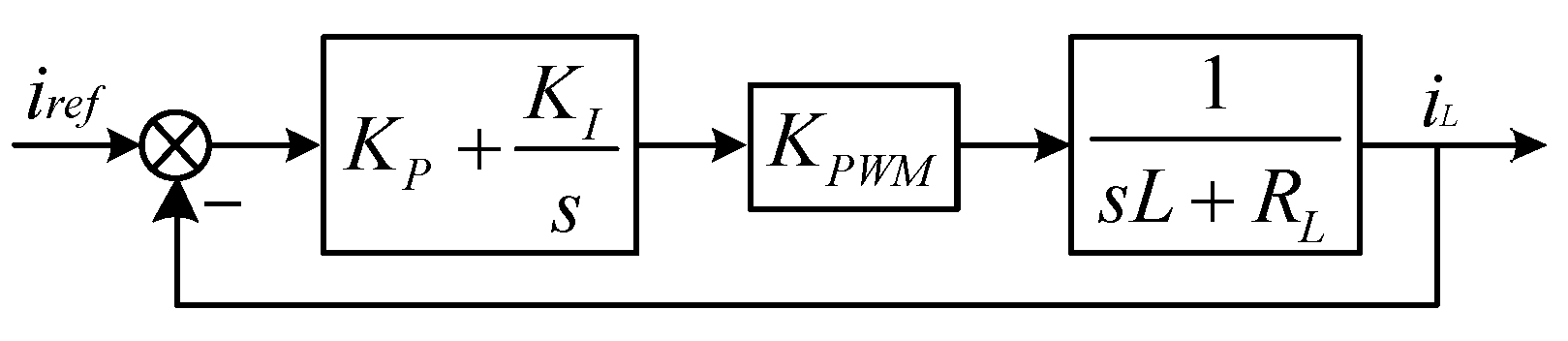
3.3. Design of the Proposed Control System
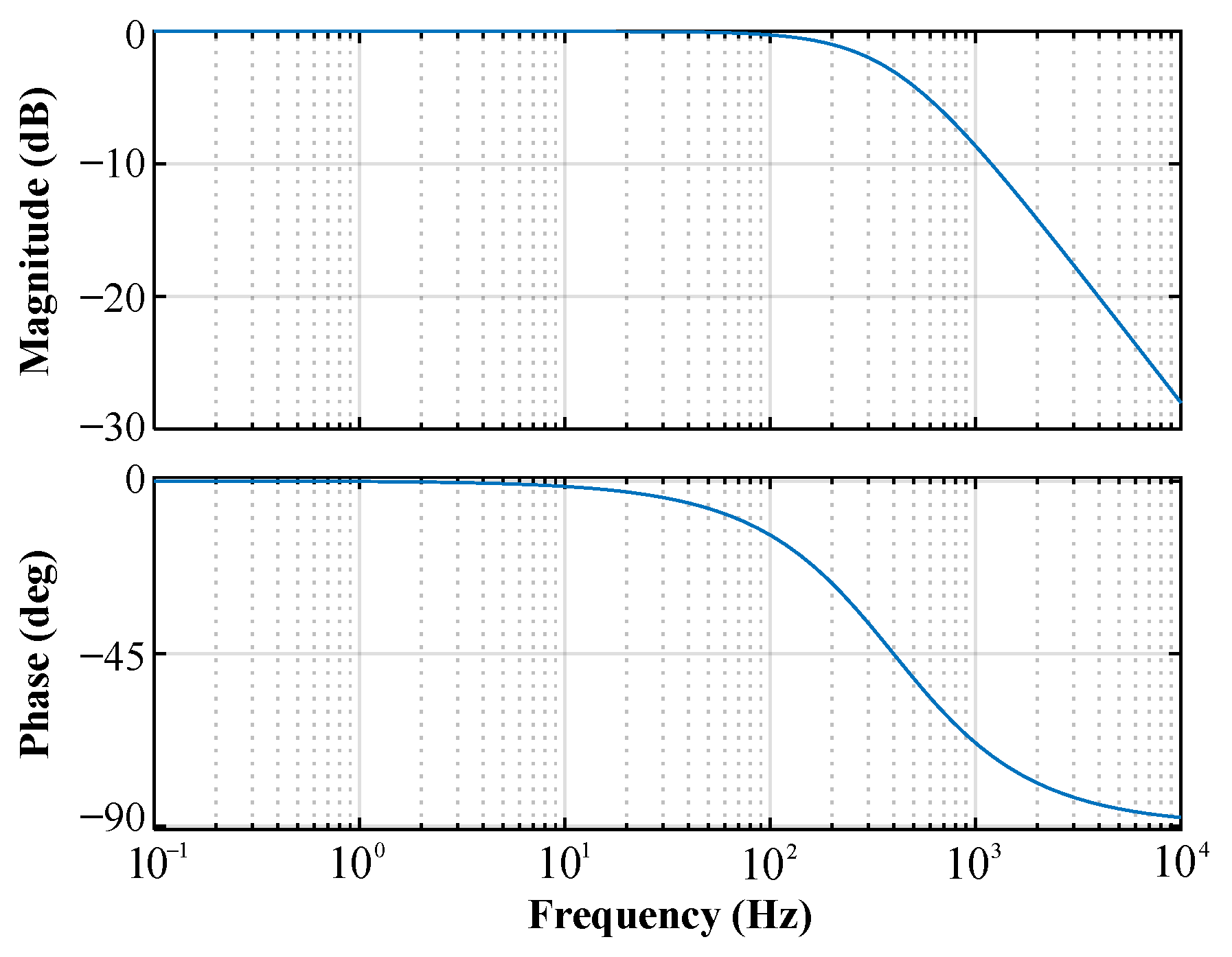
3.4. The Influence of the Changing Plant Parameters
4. Simulation Results and Experimental Verification
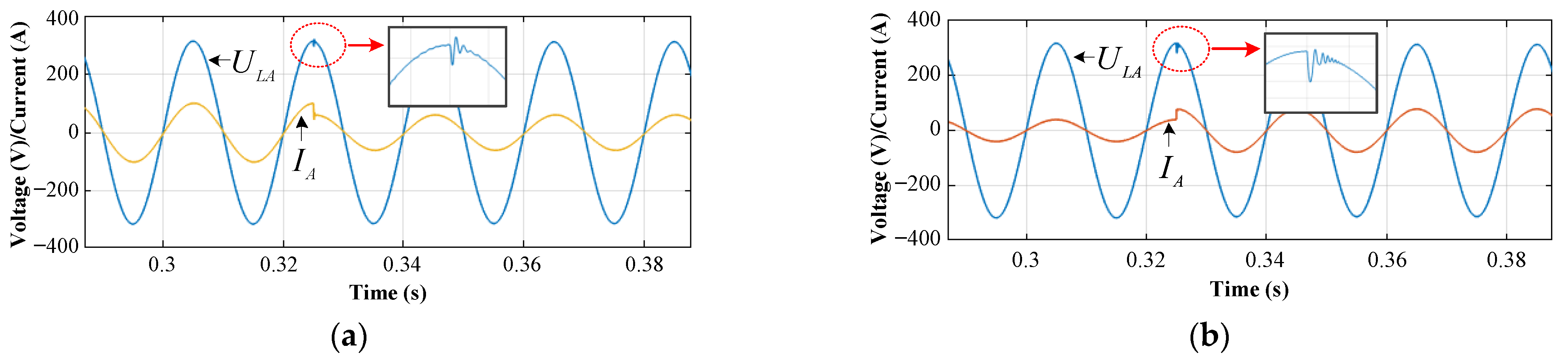
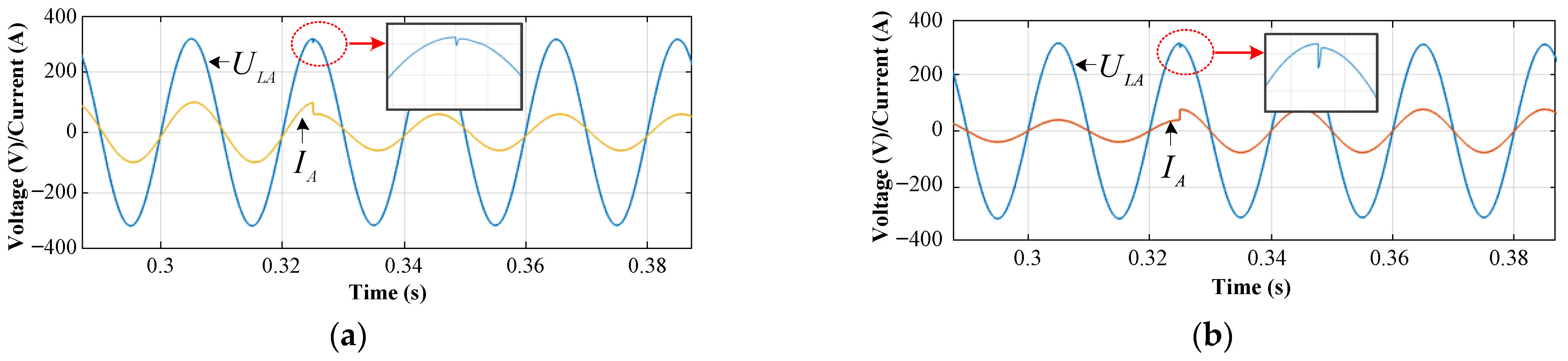
4.1. Simulation Results
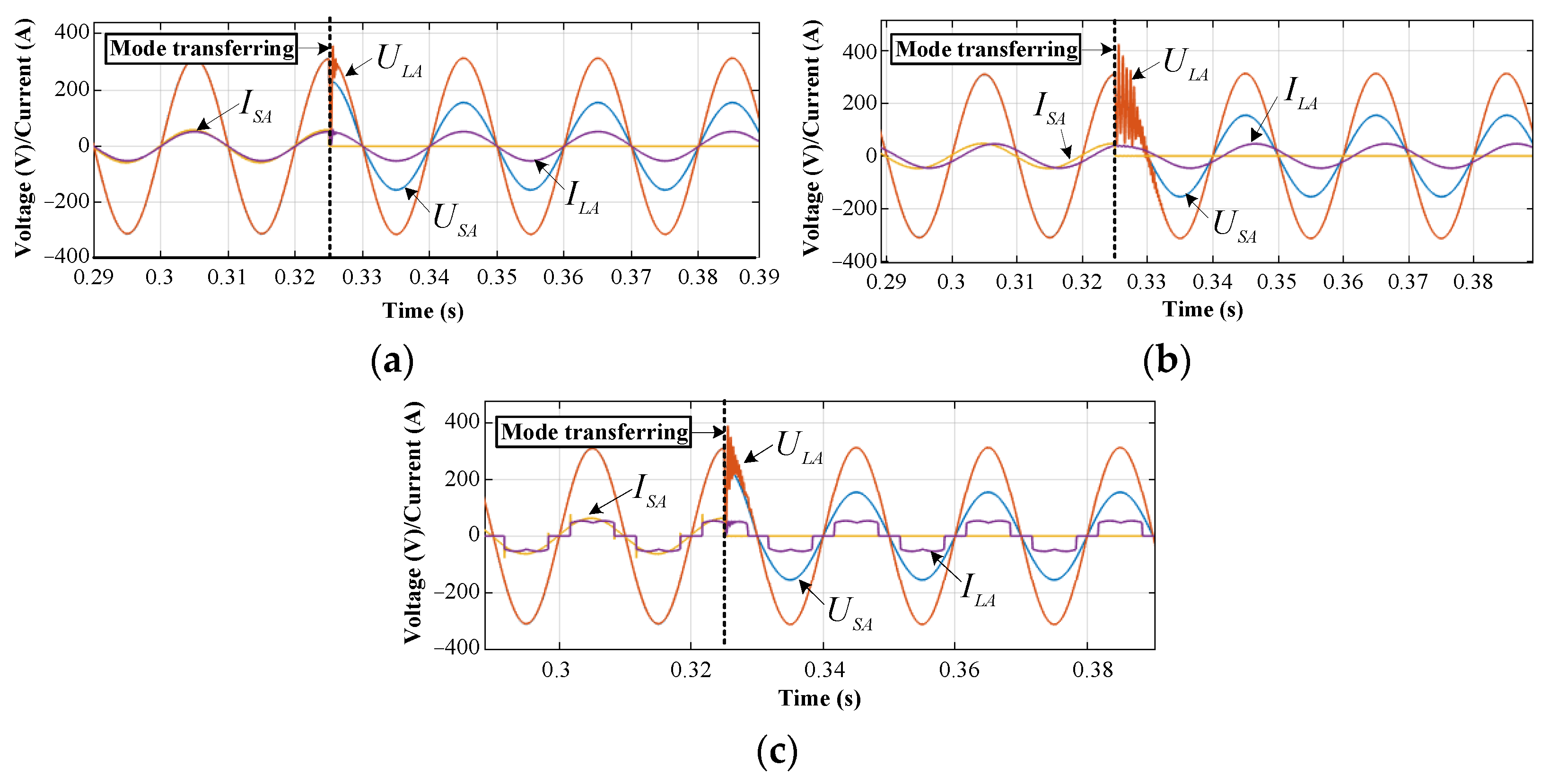
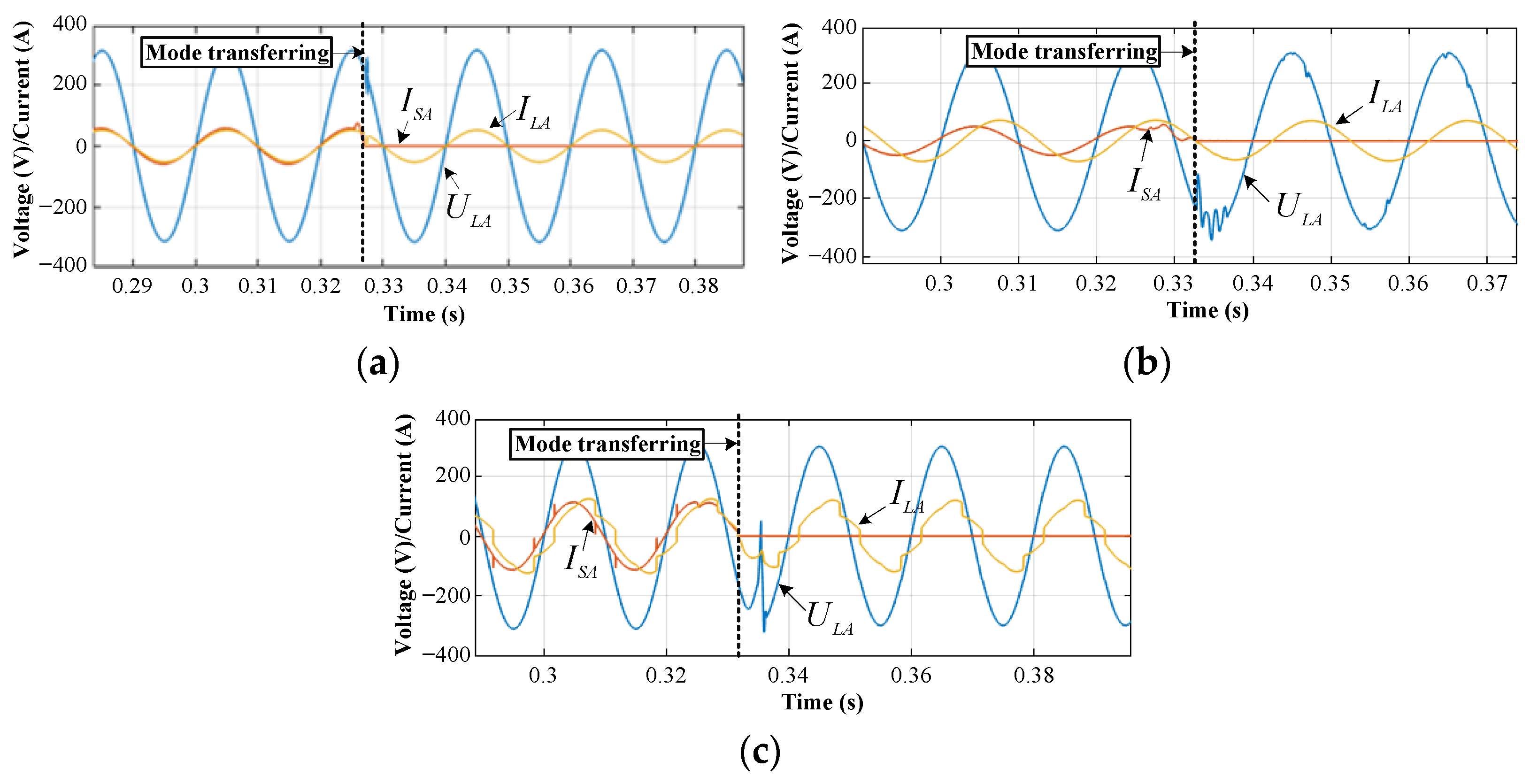
4.1.1. From the UC Mode to SA Mode
4.1.2. From the SA Mode to UC Mode
4.1.3. Saltation of the Input for the Inner Current Loop in the Steady Operation Mode
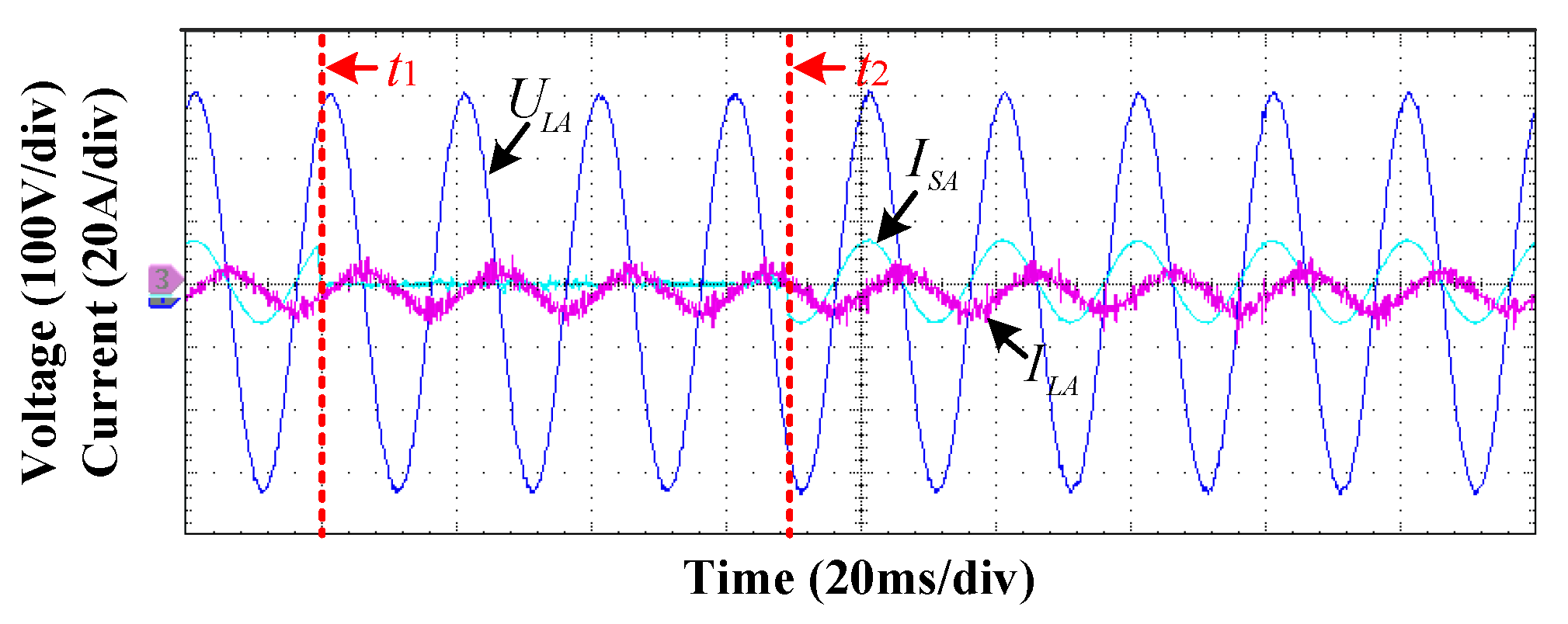
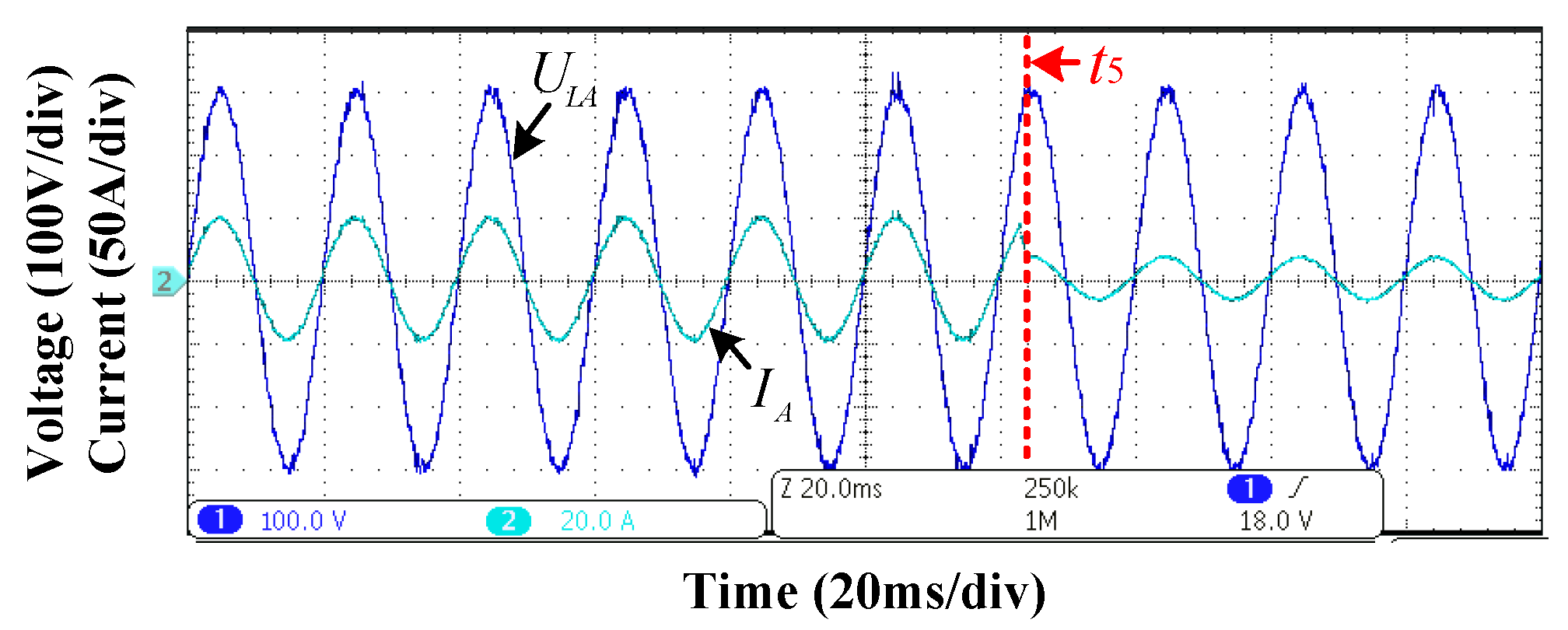
4.2. Experimental Verification
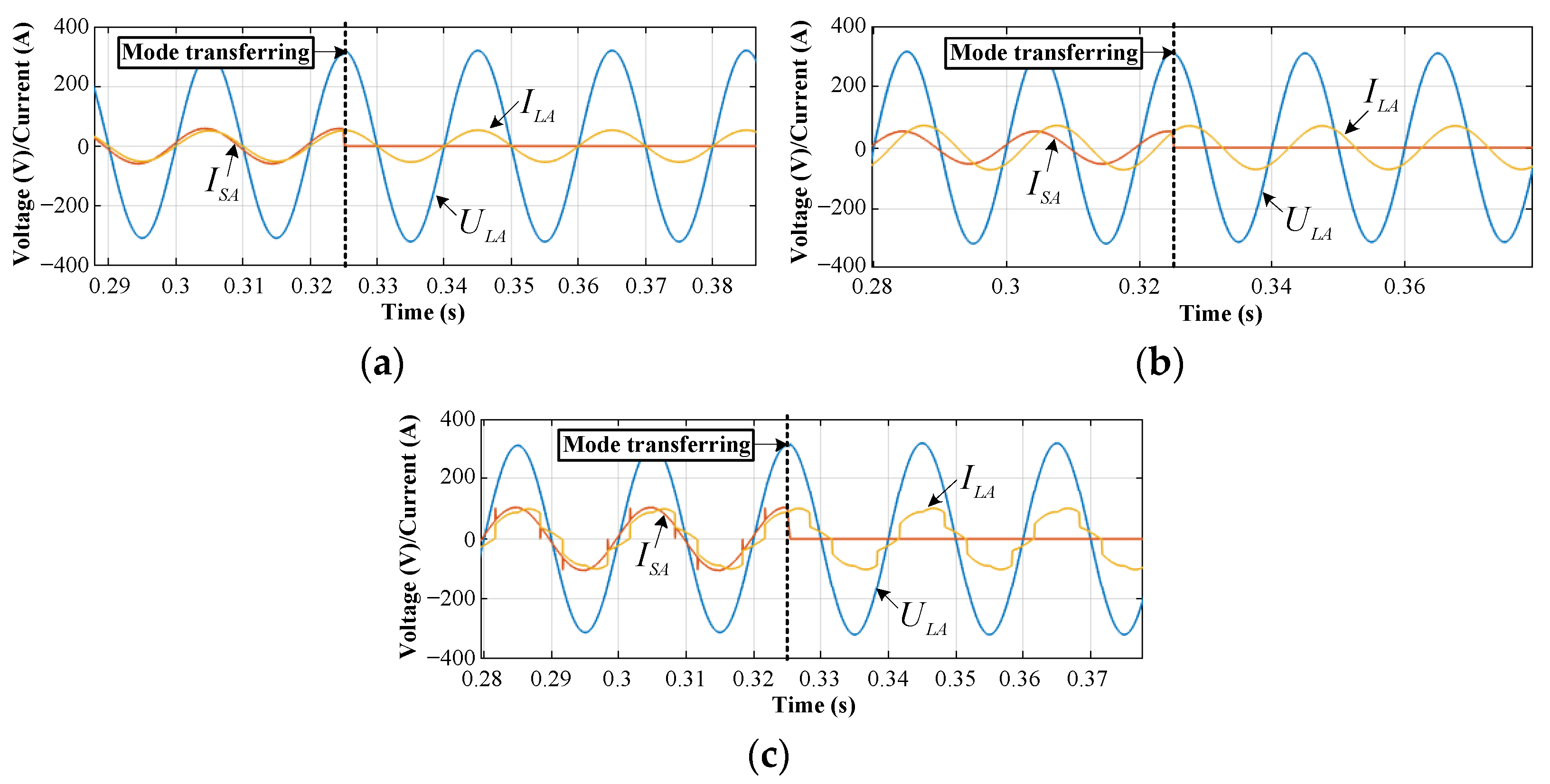
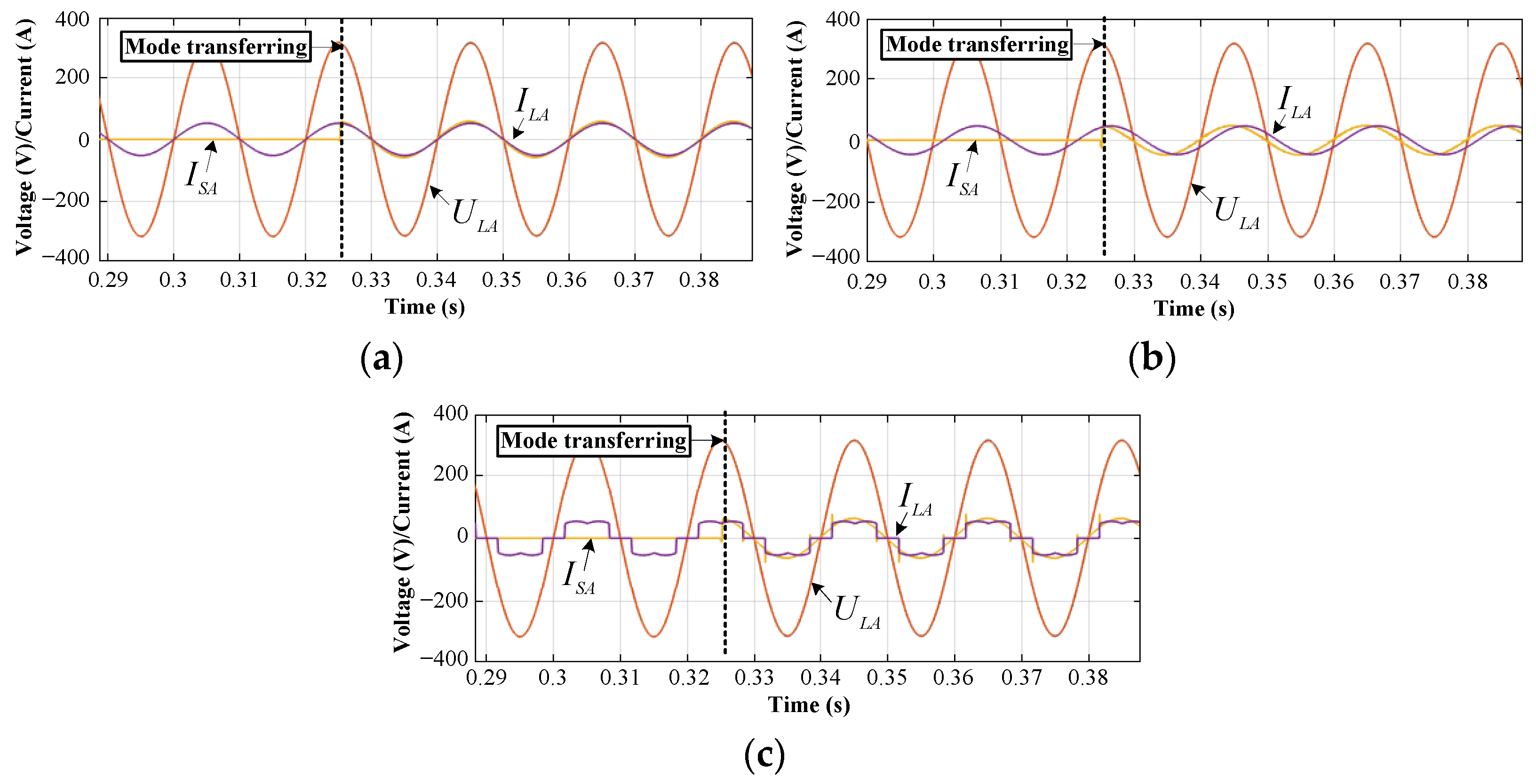
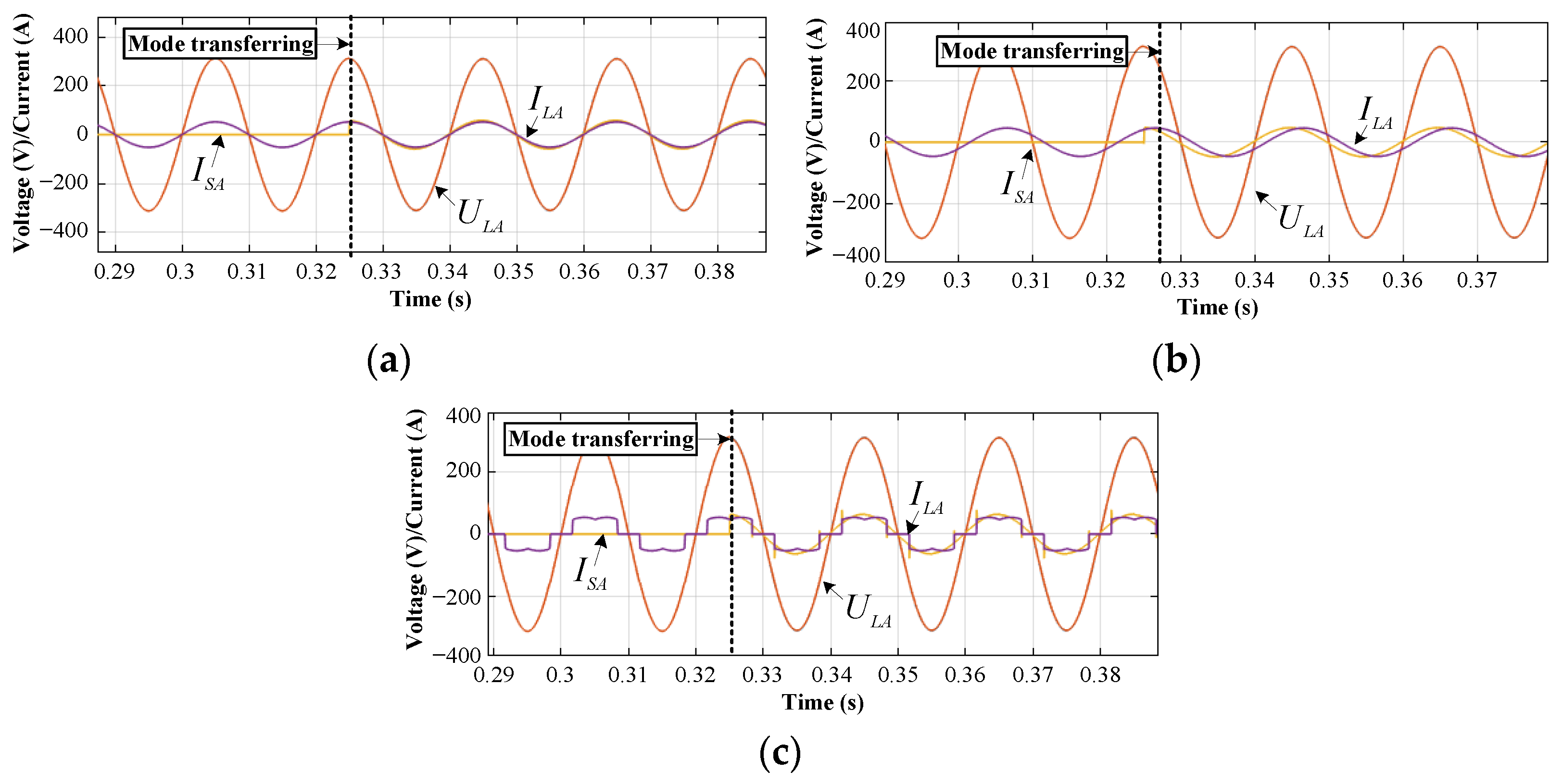
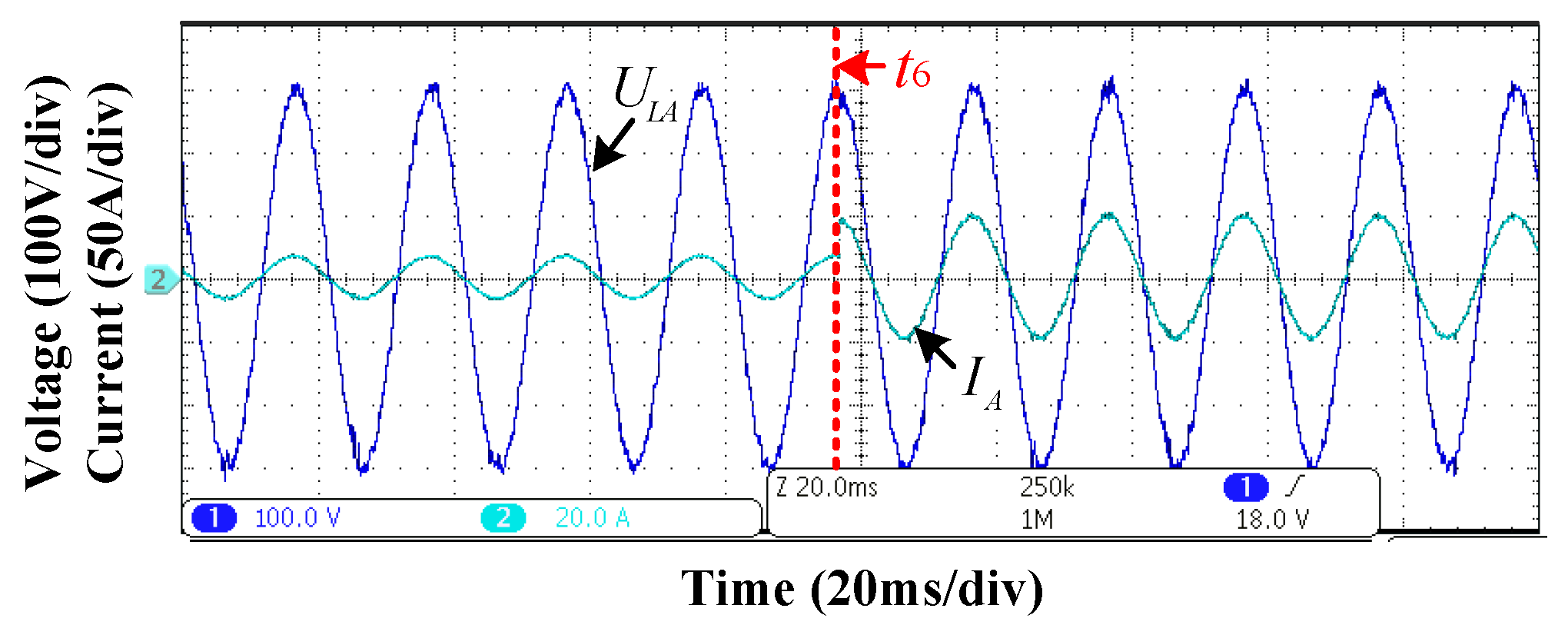
4.2.1. Operation Mode Transition
4.2.2. Saltation of the Inner Current Loop Input in a Steady Operation
4.3. Limitations
- (1)
- Mechanism for handling the faults of the load side during modes of transition and for restoring the voltage in the shortest time;
- (2)
- Redundancy configuration of H-bridges in a cascaded multilevel topology;
- (3)
- Measures to improve the inherent effects of sampling and control delay in digital control systems.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, Q.; Zhuang, X.; Liu, Y.; Wang, C.; Guo, H. A novel control strategy for mode seamless switching of PV converter in DC microgrid based on double integral sliding mode control. ISA Trans. 2020, 100, 469–480. [Google Scholar] [CrossRef] [PubMed]
- Sahoo, B.; Routray, S.K.; Rout, P.K. AC DC and hybrid control strategies for smart microgrid application: A review. Int. Trans. Electr. Energy Syst. 2021, 31, e12683. [Google Scholar] [CrossRef]
- Cagnano, A.; De Tuglie, E.; Mancarella, P. Microgrids: Overview and guidelines for practical implementations and operation. Appl. Energy 2020, 258, 114039. [Google Scholar] [CrossRef]
- Delghavi, M.B.; Yazdani, A. A Unified Control Strategy for Electronically Interfaced Distributed Energy Resources. IEEE Trans. Power Deliv. 2012, 27, 803–812. [Google Scholar] [CrossRef]
- D’Silva, S.; Shadmand, M.; Bayhan, S.; Abu-Rub, H. Towards Grid of Microgrids: Seamless Transition between Grid-Connected and Islanded Modes of Operation. IEEE Open J. Ind. Electron. Soc. 2020, 1, 66–81. [Google Scholar] [CrossRef]
- Lo, K.; Chen, Y. Design of a Seamless Grid-Connected Inverter for Microgrid Applications. IEEE Trans. Smart Grid 2020, 11, 194–202. [Google Scholar] [CrossRef]
- Tran, T.; Chun, T.; Lee, H.; Kim, H.; Nho, E. PLL-Based Seamless Transfer Control Between Grid-Connected and Islanding Modes in Grid-Connected Inverters. IEEE Trans. Power Electron. 2014, 29, 5218–5228. [Google Scholar] [CrossRef]
- Gao, F.; Iravani, M.R. A Control Strategy for a Distributed Generation Unit in Grid-Connected and Autonomous Modes of Operation. IEEE Trans. Power Electron. 2008, 23, 850–859. [Google Scholar]
- Zhang, L.; Hou, M.; Zhu, G.; Lu, Z.; Geng, Y.; Liu, Y. Seamless transfer strategy of operation mode for microgrid based on collaborative control of voltage and current. AEPS 2019, 43, 129–135. [Google Scholar]
- Yuan, Z.; Wei, Y.; Liu, W.; Ma, H.; Yu, X.; Guo, P. Connecting and islanding universal control strategy for VSC of AC distribution grids. EPAE 2020, 40, 1–7, 304–305. [Google Scholar]
- Abadi, M.; Sadeghzadeh, S.M. A control approach with seamless transition capability for a single-phase inverter operating in a microgrid. Int. J. Electr. Power Energy Syst. 2019, 111, 475–485. [Google Scholar] [CrossRef]
- Trinh, Q.N.; Wang, P.; Choo, F.H.; Jin, C.; Pan, X.; Lee, H.H. A novel control strategy for smooth transition between stand-alone and grid-connected operations of distributed generation. In Proceedings of the 9th International Conference on Power Electronics, Korean Institute of Power Electronics, Seoul, Korea, 1–5 June 2015; pp. 1276–1281. [Google Scholar]
- Jha, S.K.; Kumar, D.; Lehtonen, M. Modified V-I droop based adaptive vector control scheme for demand side management in a stand-alone microgrid. Int. J. Electr. Power Energy Syst. 2021, 130, 106950. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, W.; Sun, B.; Loh, P.C.; Wang, W.; Xu, D.; Blaabjerg, F. Seamless Transfer Scheme with Unified Control Core for Paralleled Systems. IEEE Trans. Power Electron. 2019, 34, 6286–6298. [Google Scholar] [CrossRef]
- Ganjian-Aboukheili, M.; Shahabi, M.; Shafiee, Q.; Guerrero, J.M. Seamless Transition of Microgrids Operation from Grid-Connected to Islanded Mode. IEEE Trans. Smart Grid 2020, 11, 2106–2114. [Google Scholar] [CrossRef]
- Hou, X.; Sun, Y.; Lu, J.; Zhang, X.; Koh, L.H.; Su, M.; Guerrero, J.M. Distributed Hierarchical Control of AC Microgrid Operating in Grid-Connected, Islanded and Their Transition Modes. IEEE Access 2018, 6, 77388–77401. [Google Scholar] [CrossRef]
- Lou, G.; Gu, W.; Zhu, J.; Li, P.; Zhang, X. A novel control strategy for the seamless transfer of microgrids based on disturbance observer. Int. J. Electr. Power Energy Syst. 2020, 118, 105804. [Google Scholar] [CrossRef]
- El-Sharawy, K.M.; Diab, H.Y.; Abdelsalam, M.O.; Marei, M.I. A Unified Control Strategy of Distributed Generation for Grid-Connected and Islanded Operation Conditions Using an Artificial Neural Network. Sustainability 2021, 13, 6388. [Google Scholar] [CrossRef]
- Hmad, J.; Houari, A.; Trabelsi, H.; Machmoum, M. Fuzzy logic approach for smooth transition between grid-connected and stand-alone modes of three-phase DG-inverter. Electr. Power Syst. Res. 2019, 175, 105892. [Google Scholar] [CrossRef]
- He, J.; Li, Y.W.; Munir, M.S. A Flexible Harmonic Control Approach Through Voltage-Controlled DG–Grid Interfacing Converters. IEEE Trans. Ind. Electron. 2012, 59, 444–455. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, J.; Zhao, Y. A Unified Control Strategy for Three-Phase Inverter in Distributed Generation. IEEE Trans. Power Electron. 2014, 29, 1176–1191. [Google Scholar] [CrossRef]
- Lee, W.C. Cost-effective APF/UPS system with seamless mode transfer. J. Electr. Eng. Technol. 2015, 10, 195–204. [Google Scholar] [CrossRef]
- Shan, S.; Umanand, L. A Unified Controller for Utility-Interactive Uninterruptible Power Converters for Grid Connected and Autonomous Operations. IEEE Trans. Power Electron. 2019, 34, 3871–3887. [Google Scholar]
- Araki, M.; Taguchi, H. Two-Degree-of-Freedom PID Controllers. Int. J. Control. Autom. Syst. 2003, 1, 18–25. [Google Scholar]
- Herong, G.; Deyu, W.; Xiaoqiang, G.; Guocheng, S.; Wei, Z.; Ying, Z.; Weiyang, W. Two-degree-of-freedom current regulation of grid-connected inverters in microgrid. In Proceedings of the 2nd IEEE International Symposium on Power Electronics for Distributed Generation Systems, Hefei, China, 16–18 June 2010; pp. 512–515. [Google Scholar]
- Lin, R.; Wang, D.; Xu, L.; Ding, L.; Yang, H. Using STATCOM based on two-degree-of-freedom internal model control to improve the voltage stability of islanded micro-grid. In Proceedings of the 2017 IEEE 2nd Information Technology, Networking, Electronic and Automation Control Conference, Chengdu, China, 15–17 December 2017; pp. 1192–1196. [Google Scholar]
- Kahrobaeian, A.; Mohamed, Y.A.I. Interactive Distributed Generation Interface for Flexible Micro-Grid Operation in Smart Distribution Systems. IEEE Trans. Sustain. Energy 2012, 3, 295–305. [Google Scholar] [CrossRef]
- Kim, J.; Lee, J.; Nam, K. Inverter-Based Local AC Bus Voltage Control Utilizing Two DOF Control. IEEE Trans. Power Electron. 2008, 23, 1288–1298. [Google Scholar]
- Babazadeh, M.; Karimi, H. A Robust Two-Degree-of-Freedom Control Strategy for an Islanded Microgrid. IEEE Trans. Power Deliv. 2013, 28, 1339–1347. [Google Scholar] [CrossRef]
- Zheng, F.; Lin, X.; Lin, Y.; Zhang, Y.; Zhang, Y. Design of a Novel Hybrid Control Strategy for ES Grid-Connected Inverter for Smooth Microgrid Transition Operation. IEEE Access 2019, 7, 171950–171965. [Google Scholar] [CrossRef]
- Shehu, G.S.; Kunya, A.B.; Shanono, I.H.; Yalcinoz, T. A Review of Multilevel Inverter Topology and Control Techniques. J. Autom. Control. Eng. 2016, 4, 233–241. [Google Scholar] [CrossRef][Green Version]
- Villanueva, E.; Correa, P.; Rodriguez, J.; Pacas, M. Control of a Single-Phase Cascaded H-Bridge Multilevel Inverter for Grid-Connected Photovoltaic Systems. IEEE Trans. Ind. Electron. 2009, 56, 4399–4406. [Google Scholar] [CrossRef]
- Samadhiya, A.; Namrata, K. Modeling and Control of a Cascaded H-bridge Multilevel Inverter for Hybrid Generation Sources based Islanded Microgrid. In Proceedings of the International Conference on Computing, Power and Communication Technologies, New Delhi, India, 27–28 September 2019; pp. 634–639. [Google Scholar]
- Wan, J.; Hua, W.; Wang, B. Compulsory Islanding Transition Strategy Based on Fuzzy Logic Control for a Renewable Microgrid System. Math. Probl. Eng. 2021, 2021, 9959222. [Google Scholar] [CrossRef]
- Mortezaei, A.; Simoes, M.G.; Bubshait, A.S.; Busarello, T.D.C.; Marafao, F.P.; Al-Durra, A. Multifunctional Control Strategy for Asymmetrical Cascaded H-Bridge Inverter in Microgrid Applications. IEEE Trans. Ind. Appl. 2017, 53, 1538–1551. [Google Scholar] [CrossRef]
- Delghavi, M.B.; Yazdani, A. Islanded-Mode Control of Electronically Coupled Distributed-Resource Units Under Unbalanced and Nonlinear Load Conditions. IEEE Trans. Power Deliv. 2011, 26, 661–673. [Google Scholar] [CrossRef]
- Wu, S.; Xu, G. Analysis and damping of transient oscillation in is-landing switching-over process for microgrid under master-slave control. PST 2017, 41, 1989–1997. [Google Scholar]









| Features | Implication | Values | Unit |
|---|---|---|---|
| L | Inductance of the LC filter | 0.8 | mH |
| RL | Resistance of L in the LC filter | 2 | mΩ |
| C | Capacitance of the LC filter | 20 | μF |
| Features | Implication | Values | Unit |
|---|---|---|---|
| US | Rated AC voltage of the utility | 220 | V |
| f0 | Rated frequency of the utility | 50 | Hz |
| NH | Number of H-bridges in each phase | 3 | — |
| UDC | DC voltage of each H-bridge | 200 | V |
| Csup | Value of series DC super-capacitors | 6.5 | F |
| fs | Switching frequency | 5 | kHz |
| td | Dead time of switching | 3 | μs |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, J.; Hua, W.; Wang, B. A Unified Inner Current Control Strategy Based on the 2-DOF Theory for a Multifunctional Cascade Converter in an Integrated Microgrid System. Sustainability 2022, 14, 5074. https://doi.org/10.3390/su14095074
Wan J, Hua W, Wang B. A Unified Inner Current Control Strategy Based on the 2-DOF Theory for a Multifunctional Cascade Converter in an Integrated Microgrid System. Sustainability. 2022; 14(9):5074. https://doi.org/10.3390/su14095074
Chicago/Turabian StyleWan, Jiexing, Wei Hua, and Baoan Wang. 2022. "A Unified Inner Current Control Strategy Based on the 2-DOF Theory for a Multifunctional Cascade Converter in an Integrated Microgrid System" Sustainability 14, no. 9: 5074. https://doi.org/10.3390/su14095074
APA StyleWan, J., Hua, W., & Wang, B. (2022). A Unified Inner Current Control Strategy Based on the 2-DOF Theory for a Multifunctional Cascade Converter in an Integrated Microgrid System. Sustainability, 14(9), 5074. https://doi.org/10.3390/su14095074







