Novel Evolutionary-Optimized Neural Network for Predicting Fresh Concrete Slump
Abstract
:1. Introduction
2. Data and Modeling Methodology
2.1. Data Provision
2.2. Methodology
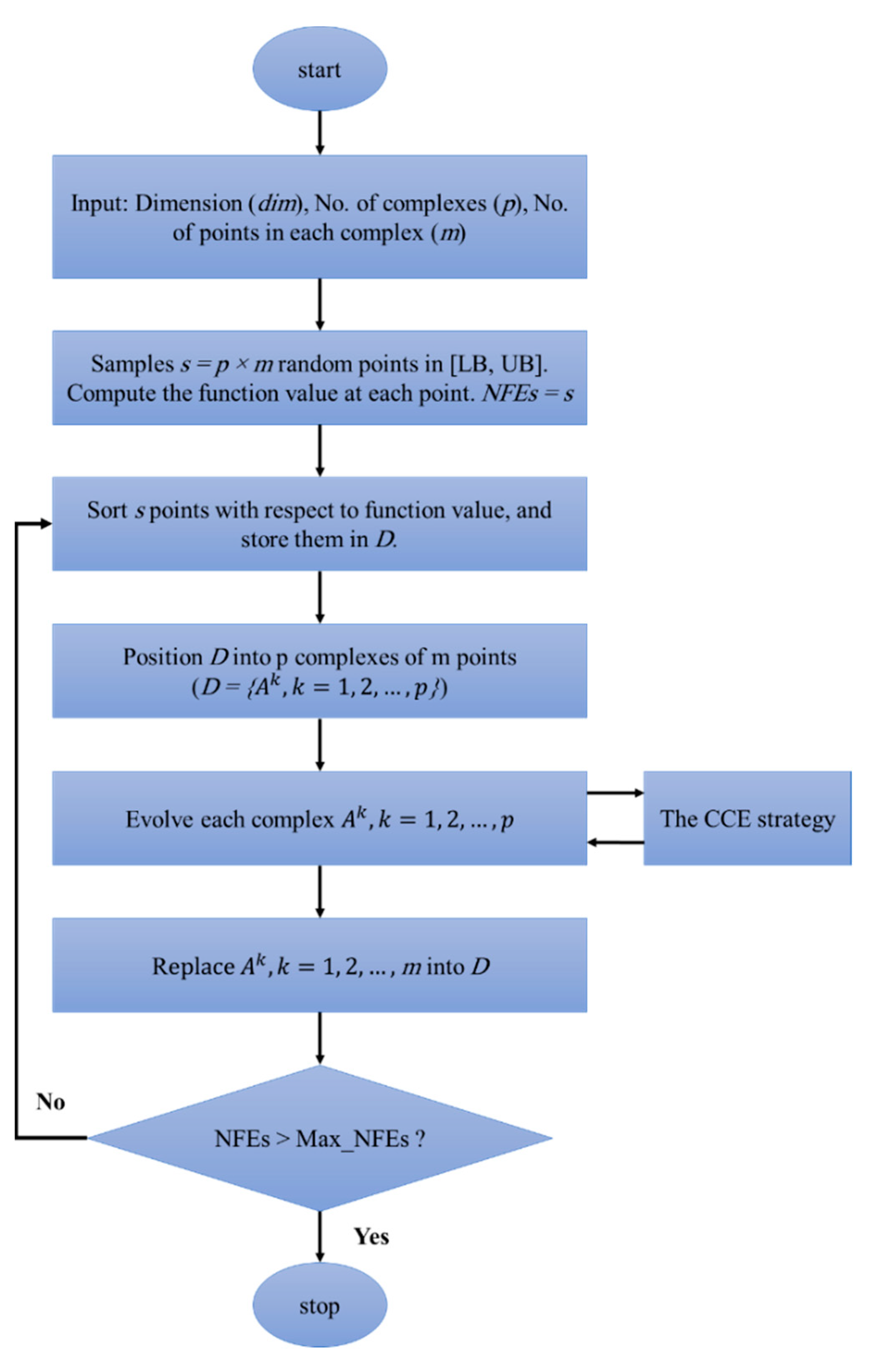
2.2.1. Shuffled Complex Evolution
- I.
- Initialize: three parameters of q, α, and β are selected where m ≥ q ≥ 2, β ≥ 1, and α ≥ 1.
- II.
- Weight assignment: a triangular probability distribution is assigned to the complex, as expressed in Equation (1):
- III.
- Selecting parents: based on the above equation, q different points (i.e., u1, u2, …, uq) are chosen from the proposed complex. They are then stored in an array, as expressed in Equation (2).in which, the function (FV) is the value of the corresponding point. The locations of the complex, which are used for constructing the simplex B, are also stored in L.B = {uj, Fj, i = 1, 2, …, q}
- IV.
- Generating the offspring: based on the function values, the points are sorted and the centroid c is calculated as follows:
- (a)
- If the new point is within the existing space, the FV is calculated and the number of evaluations (NFEs) is changed to NFEs + 1.
- (b)
- Otherwise, the smallest hypercube H (which contains the proposed complex) is computed. The point uz is randomly produced within H. The NFEs is changed to NFEs + 1, and in the mutation stage, ur and Fr will equate uz and Fz.
- V.
- In the last step, the parents are replaced by offspring and the complex is sorted regarding the obtained FVs.
- VI.
- Steps a to e are repeated β times [52].
2.2.2. Benchmark Optimization Models
3. Results and Discussion
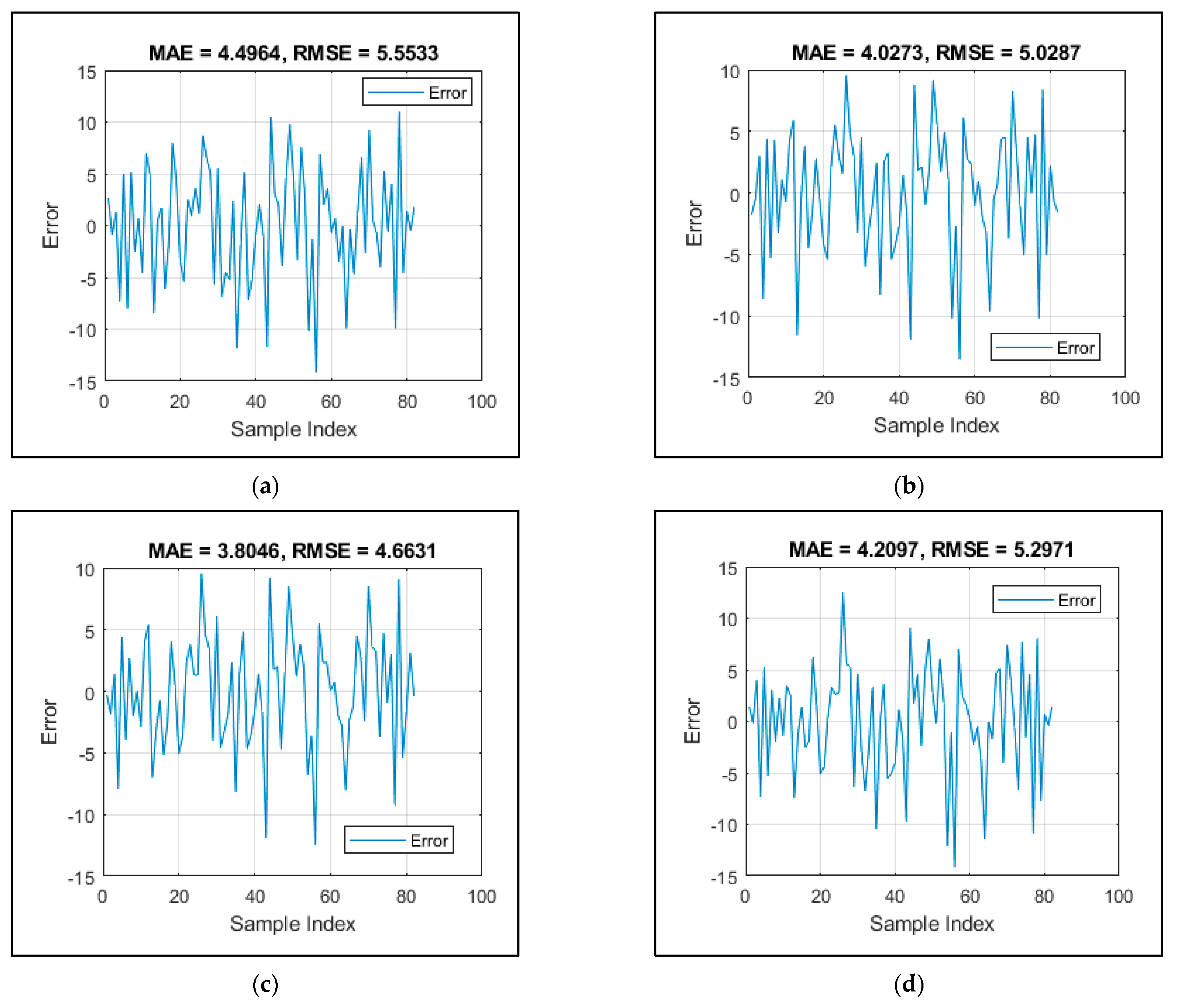
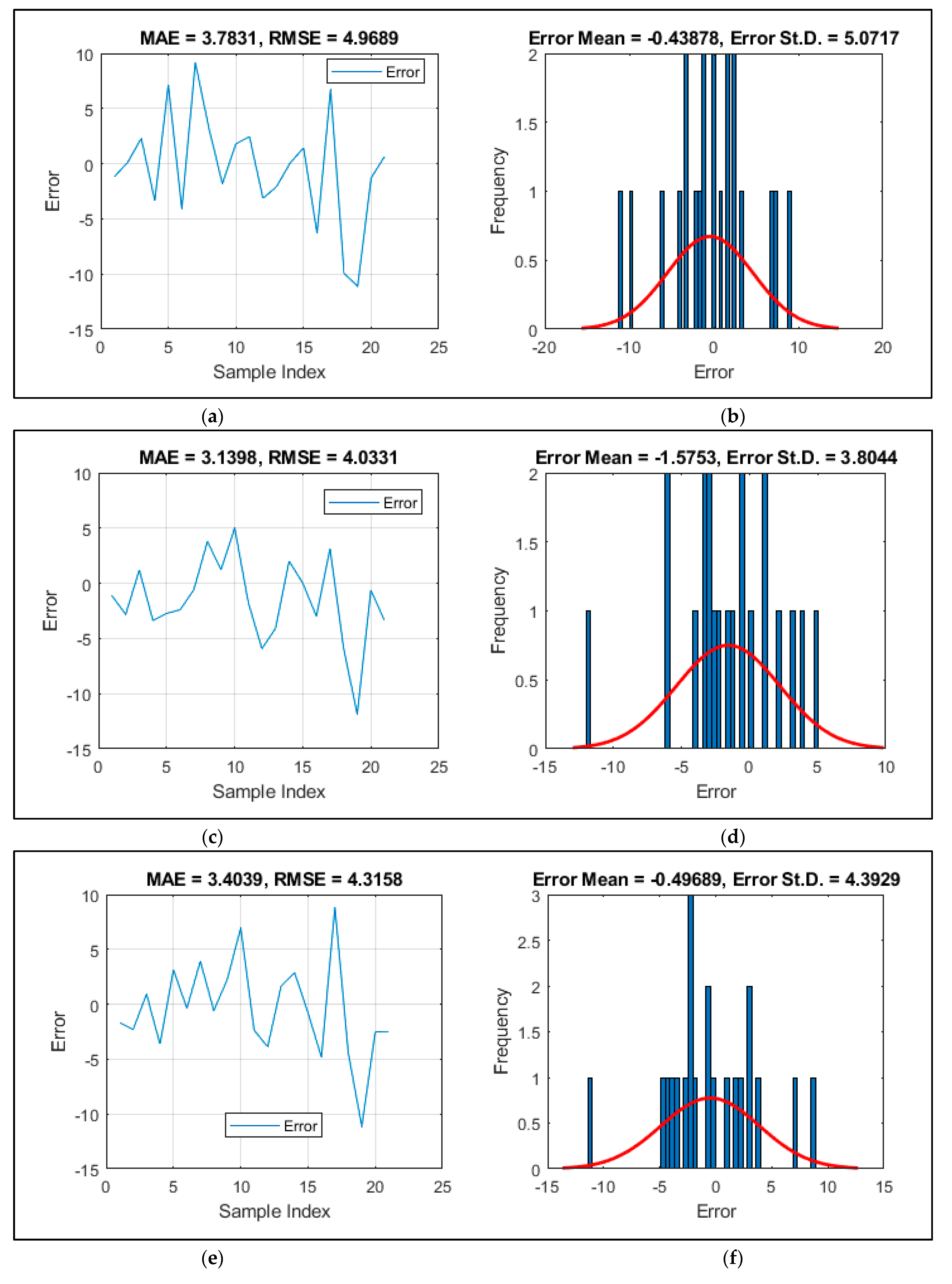
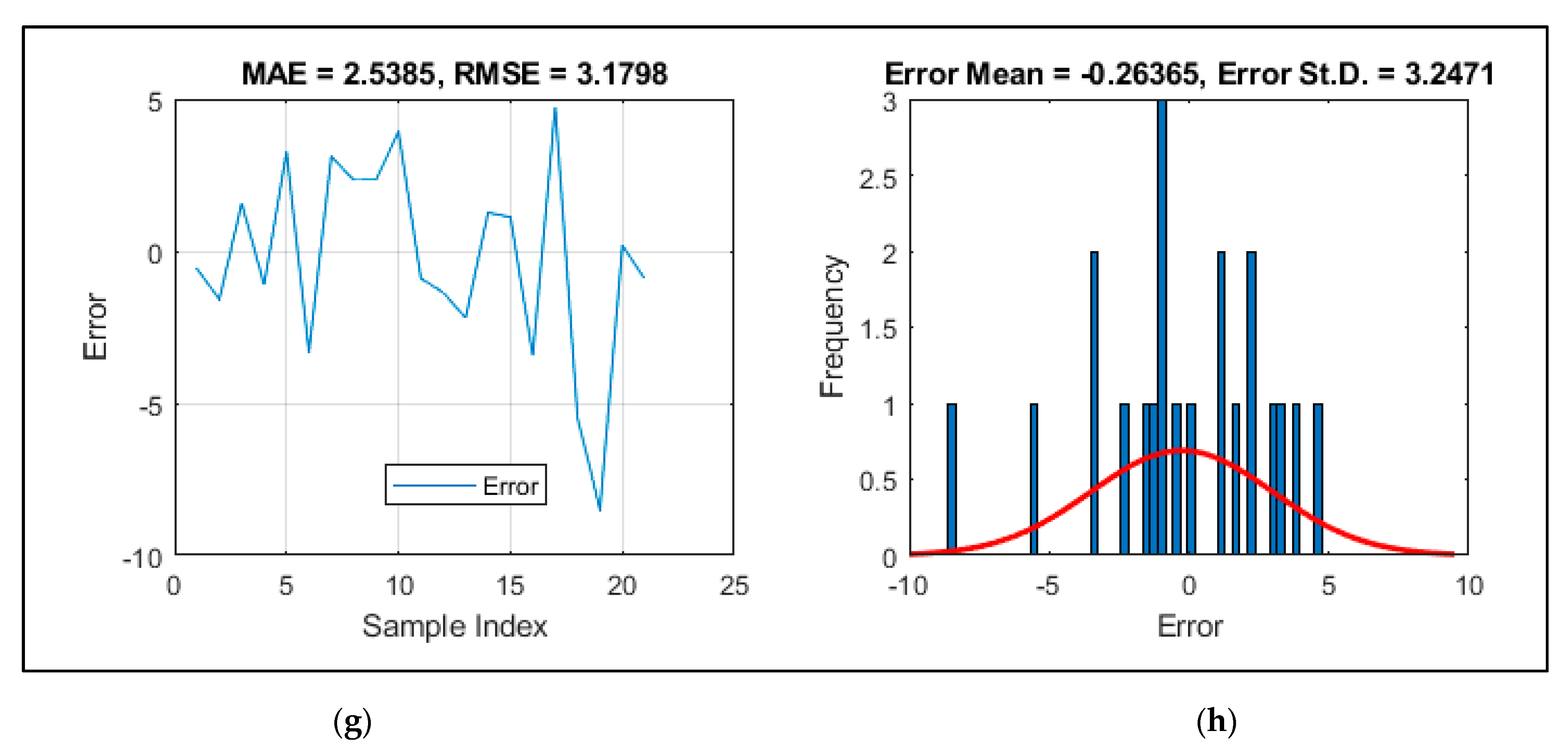
3.1. Accuracy Indices
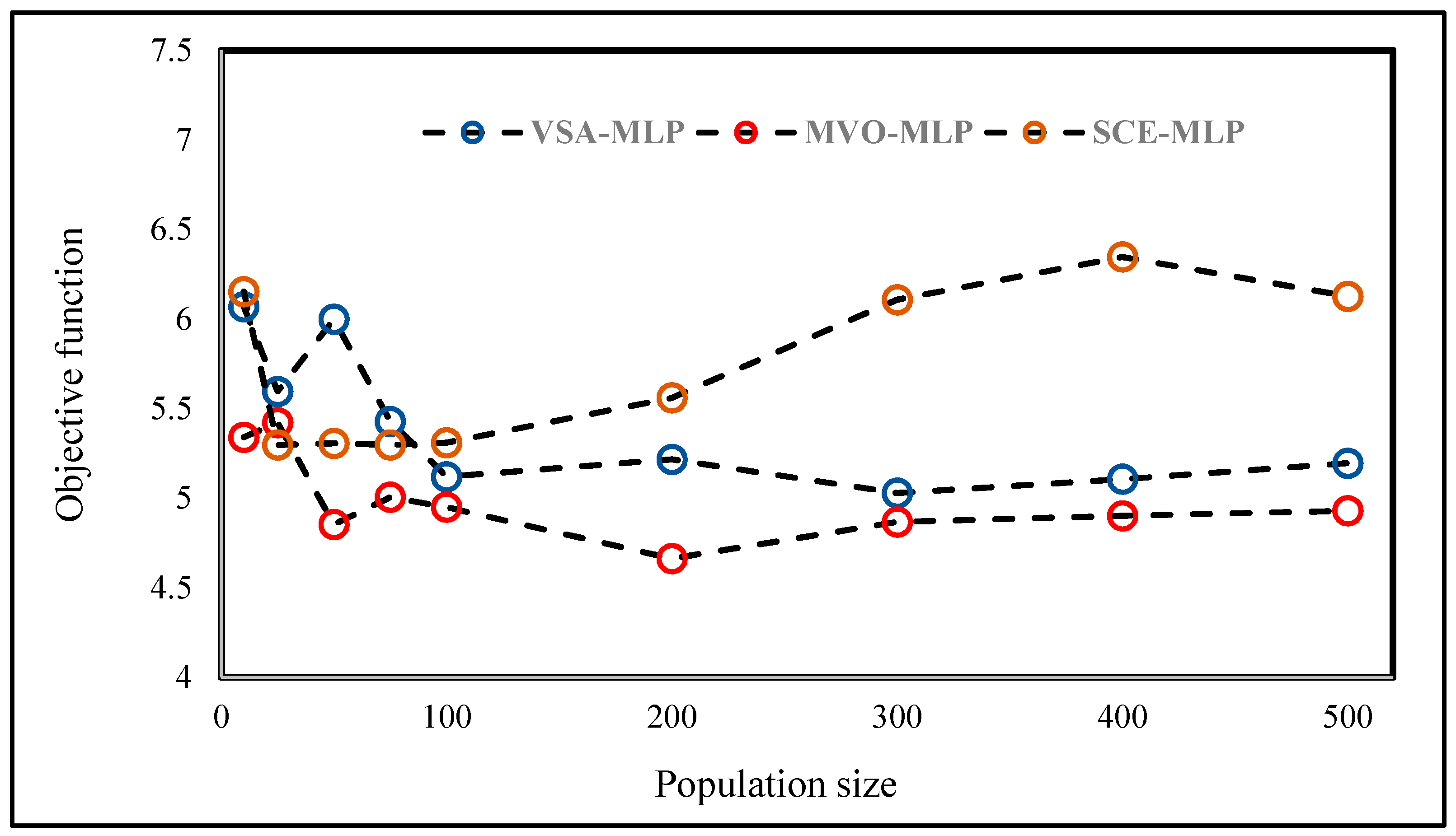
3.2. Improving ANN Using VSA, MVO, and SCE
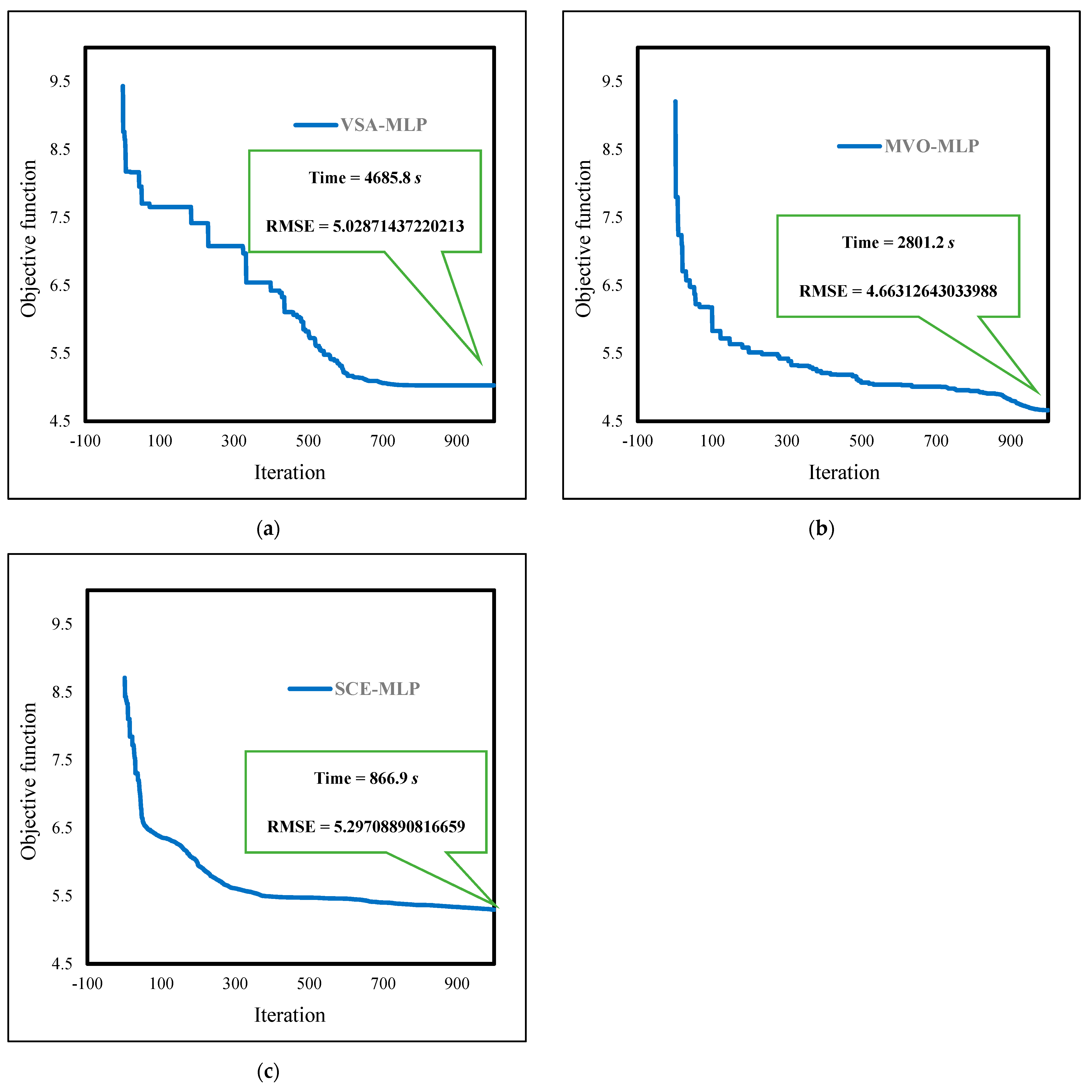
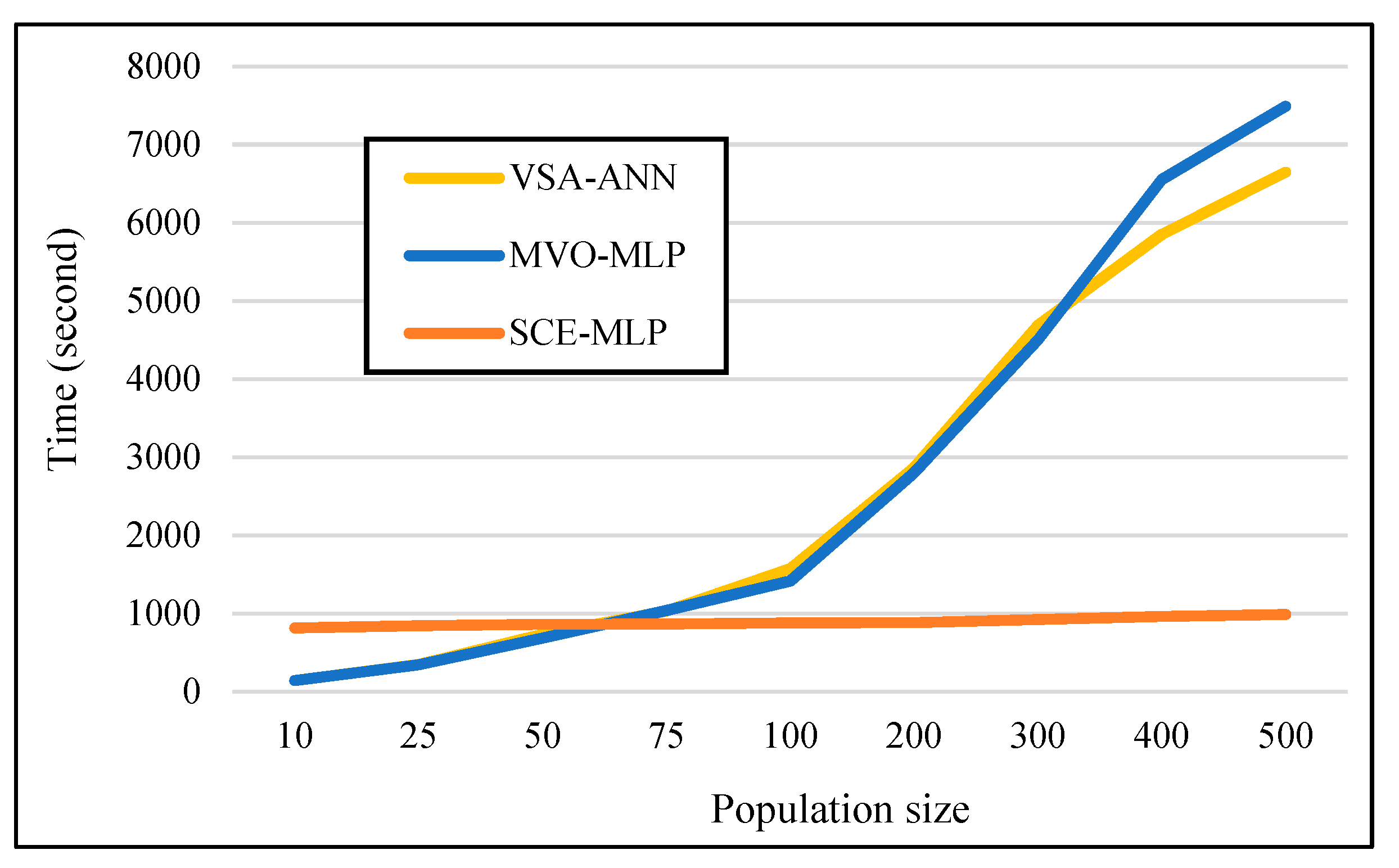
3.3. Efficiency Assessment
3.4. Slump Predictive Model
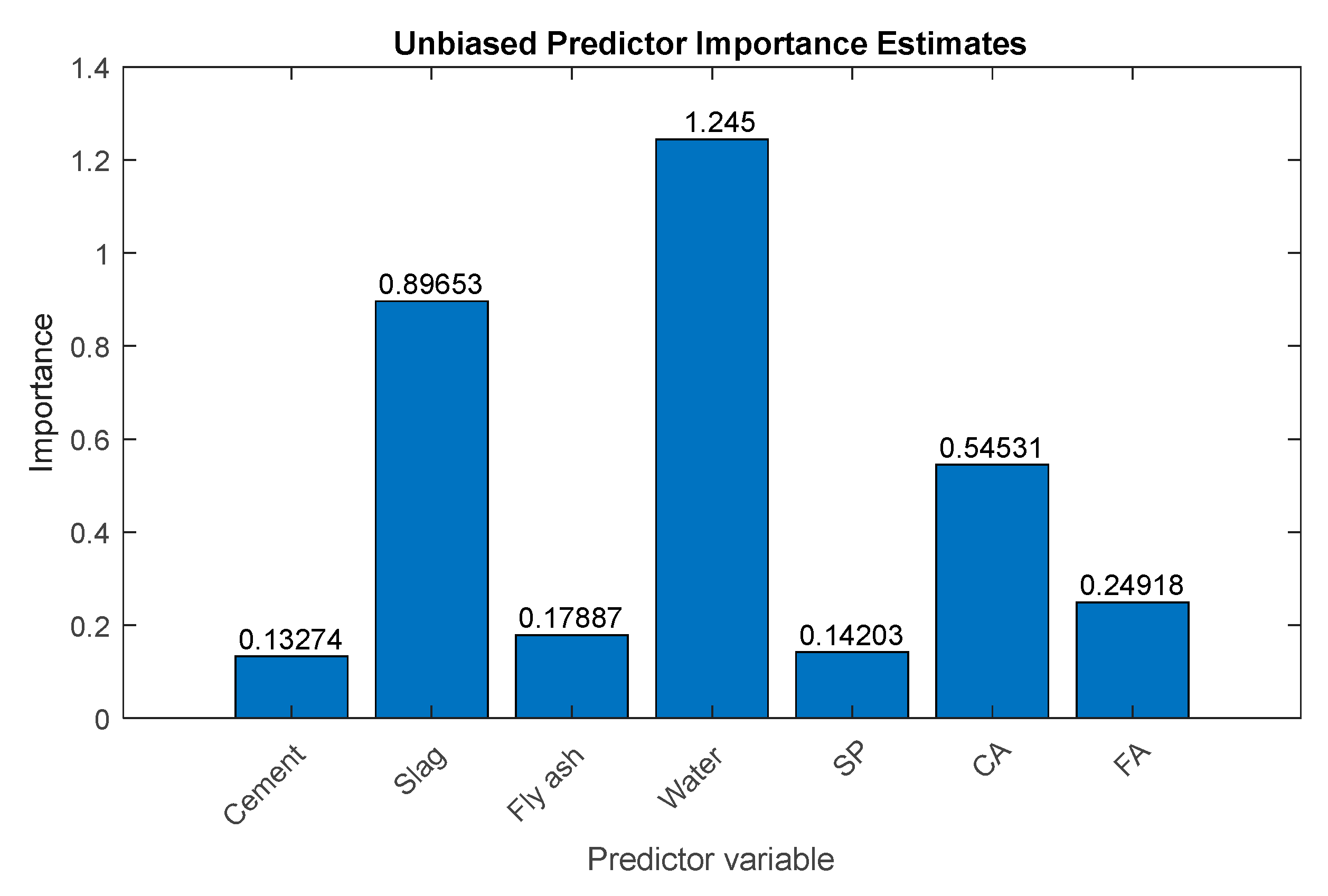
3.5. Importance Analysis
3.6. Further Comparison
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Begum, S.J.; Anjaneyulu, P.; Ratnam, M. A Study on Effect of Steel Fiber in Fly Ash Based Self-Compacting Concrete. IJIRST—Int. J. Innov. Res. Sci. Technol. 2018, 5, 95–99. [Google Scholar]
- Liu, W.; Guo, Z.; Wang, C.; Niu, S. Physico-mechanical and microstructure properties of cemented coal Gangue-Fly ash backfill: Effects of curing temperature. Constr. Build. Mater. 2021, 299, 124011. [Google Scholar] [CrossRef]
- Shi, T.; Liu, Y.; Zhang, Y.; Lan, Y.; Zhao, Q.; Zhao, Y.; Wang, H. Calcined Attapulgite Clay as Supplementary Cementing Material: Thermal Treatment, Hydration Activity and Mechanical Properties. Int. J. Concr. Struct. Mater. 2022, 16, 1–10. [Google Scholar] [CrossRef]
- Feng, J.; Chen, B.; Sun, W.; Wang, Y. Microbial induced calcium carbonate precipitation study using Bacillus subtilis with application to self-healing concrete preparation and characterization. Constr. Build. Mater. 2021, 280, 122460. [Google Scholar] [CrossRef]
- Chen, F.; Jin, Z.; Wang, E.; Wang, L.; Jiang, Y.; Guo, P.; Gao, X.; He, X. Relationship model between surface strain of concrete and expansion force of reinforcement rust. Sci. Rep. 2021, 11, 4208. [Google Scholar] [CrossRef]
- Shi, T.; Lan, Y.; Hu, Z.; Wang, H.; Xu, J.; Zheng, B. Tensile and Fracture Properties of Silicon Carbide Whisker-Modified Cement-Based Materials. Int. J. Concr. Struct. Mater. 2022, 16, 2. [Google Scholar] [CrossRef]
- Zhang, W.; Tang, Z.; Yang, Y.; Wei, J.; Stanislav, P. Mixed-mode debonding behavior between CFRP plates and concrete under fatigue loading. J. Struct. Eng. 2021, 147, 04021055. [Google Scholar] [CrossRef]
- Somala, S.N.; Karthikeyan, K.; Mangalathu, S. Time period estimation of masonry infilled RC frames using machine learning techniques. Structures 2021, 34, 1560–1566. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, M.; Zheng, B. Design of cold-formed stainless steel circular hollow section columns using machine learning methods. Structures 2021, 33, 2755–2770. [Google Scholar] [CrossRef]
- Wang, X.; Liu, Y.; Xin, H. Bond strength prediction of concrete-encased steel structures using hybrid machine learning method. Structures 2021, 32, 2279–2292. [Google Scholar] [CrossRef]
- Okere, C.; Onwuka, D.; Onwuka, S.; Arimanwa, J. Simplex-based Concrete mix design. IOSR J. Mech. Civ. Eng. 2013, 5, 46–55. [Google Scholar] [CrossRef]
- Ibearugbulem, O.; Ettu, L.; Ezeh, J.; Anya, U. A new regression model for optimizing concrete mixes. Int. J. Eng. Sci. Res. Technol. 2013, 2, 1735–1742. [Google Scholar]
- Chidiac, S.; Habibbeigi, F.; Chan, D. Slump and slump flow for characterizing yield stress of fresh concrete. ACI Mater. J. 2006, 103, 413. [Google Scholar]
- Zhang, W.; Tang, Z. Numerical modeling of response of CFRP–Concrete interfaces subjected to fatigue loading. J. Compos. Constr. 2021, 25, 04021043. [Google Scholar] [CrossRef]
- Chou, J.-S.; Tsai, C.-F.; Pham, A.-D.; Lu, Y.-H. Machine learning in concrete strength simulations: Multi-nation data analytics. Constr. Build. Mater. 2014, 73, 771–780. [Google Scholar] [CrossRef]
- Rafiei, M.H.; Khushefati, W.H.; Demirboga, R.; Adeli, H. Neural Network, Machine Learning, and Evolutionary Approaches for Concrete Material Characterization. ACI Mater. J. 2016, 113, 781–789. [Google Scholar] [CrossRef]
- Ali, A.; Zhang, C.; Bibi, T.; Zhu, L.; Cao, L.; Li, C.; Hsiao, P.-C. Investigation of five different low-cost locally available isolation layer materials used in sliding base isolation systems. Soil Dyn. Earthq. Eng. 2022, 154, 107127. [Google Scholar] [CrossRef]
- Xu, J.; Wu, Z.; Chen, H.; Shao, L.; Zhou, X.; Wang, S. Study on strength behavior of basalt fiber-reinforced loess by digital image technology (DIT) and scanning electron microscope (SEM). Arab. J. Sci. Eng. 2021, 46, 11319–11338. [Google Scholar] [CrossRef]
- Lu, N.; Wang, H.; Wang, K.; Liu, Y. Maximum probabilistic and dynamic traffic load effects on short-to-medium span bridges. Comput. Modeling Eng. Sci. 2021, 127, 345–360. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, H.; Cao, R.; Zhang, C. Slope stability analysis considering different contributions of shear strength parameters. Int. J. Geomech. 2021, 21, 04020265. [Google Scholar] [CrossRef]
- Moayedi, H.; Mehrabi, M.; Bui, D.T.; Pradhan, B.; Foong, L.K. Fuzzy-metaheuristic ensembles for spatial assessment of forest fire susceptibility. J. Environ. Manag. 2020, 260, 109867. [Google Scholar] [CrossRef] [PubMed]
- Xie, S.-J.; Lin, H.; Chen, Y.-F.; Wang, Y.-X. A new nonlinear empirical strength criterion for rocks under conventional triaxial compression. J. Cent. South. Univ. 2021, 28, 1448–1458. [Google Scholar] [CrossRef]
- Cao, B.; Zhao, J.; Liu, X.; Arabas, J.; Tanveer, M.; Singh, A.K.; Lv, Z. Multiobjective Evolution of the Explainable Fuzzy Rough Neural Network with Gene Expression Programming. In IEEE Transactions on Fuzzy Systems; IEEE: Piscataway, NJ, USA, 2022. [Google Scholar]
- Tian, J.; Liu, Y.; Zheng, W.; Yin, L. Smog prediction based on the deep belief-BP neural network model (DBN-BP). Urban Clim. 2022, 41, 101078. [Google Scholar] [CrossRef]
- Wang, Y.; Zou, R.; Liu, F.; Zhang, L.; Liu, Q. A review of wind speed and wind power forecasting with deep neural networks. Appl. Energy 2021, 304, 117766. [Google Scholar] [CrossRef]
- Liu, Z.; Fang, L.; Jiang, D.; Qu, R. A Machine-learning Based Fault Diagnosis Method with Adaptive Secondary Sampling for Multiphase Drive Systems. In IEEE Transactions on Power Electronics; IEEE: Piscataway, NJ, USA, 2022. [Google Scholar]
- Zhan, C.; Dai, Z.; Soltanian, M.R.; Zhang, X. Stage-Wise Stochastic Deep Learning Inversion Framework for Subsurface Sedimentary Structure Identification. Geophys. Res. Lett. 2022, 49, e2021GL095823. [Google Scholar] [CrossRef]
- Xu, H.; Wang, X.-Y.; Liu, C.-N.; Chen, J.-N.; Zhang, C. A 3D root system morphological and mechanical model based on L-Systems and its application to estimate the shear strength of root-soil composites. Soil Tillage Res. 2021, 212, 105074. [Google Scholar] [CrossRef]
- Hoang, N.-D.; Pham, A.-D. Estimating Concrete Workability Based on Slump Test with Least Squares Support Vector Regression. J. Constr. Eng. 2016, 2016, 5089683. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, C.H.; Tran, L.H.; Ho, K.N. Application of Neural Network to predict the workability Parameters of Self-Compacting Concrete. In CIGOS 2019, Innovation for Sustainable Infrastructure; Springer: Berlin/Heidelberg, Germany, 2020; pp. 1161–1166. [Google Scholar]
- Fan, Z.; Chiong, R.; Hu, Z.; Lin, Y. A fuzzy weighted relative error support vector machine for reverse prediction of concrete components. Comput. Struct. 2020, 230, 106171. [Google Scholar] [CrossRef]
- Amlashi, A.T.; Abdollahi, S.M.; Goodarzi, S.; Ghanizadeh, A.R. Soft computing based formulations for slump, compressive strength, and elastic modulus of bentonite plastic concrete. J. Clean. Prod. 2019, 230, 1197–1216. [Google Scholar] [CrossRef]
- Hammoudi, A.; Moussaceb, K.; Belebchouche, C.; Dahmoune, F. Comparison of artificial neural network (ANN) and response surface methodology (RSM) prediction in compressive strength of recycled concrete aggregates. Constr. Build. Mater. 2019, 209, 425–436. [Google Scholar] [CrossRef]
- Onikeku, O.; Shitote, S.M.; Mwero, J.; Adedeji, A.; Kanali, C. Compressive Strength and Slump Prediction of Two Blended Agro Waste Materials Concretes. Open Civil. Eng. J. 2019, 13, 118–128. [Google Scholar] [CrossRef]
- Mehrabi, M.; Moayedi, H. Landslide susceptibility mapping using artificial neural network tuned by metaheuristic algorithms. Environ. Earth Sci. 2021, 80, 1–20. [Google Scholar] [CrossRef]
- Mehrabi, M.; Pradhan, B.; Moayedi, H.; Alamri, A. Optimizing an adaptive neuro-fuzzy inference system for spatial prediction of landslide susceptibility using four state-of-the-art metaheuristic techniques. Sensors 2020, 20, 1723. [Google Scholar] [CrossRef] [Green Version]
- Sadowski, Ł.; Nikoo, M.; Shariq, M.; Joker, E.; Czarnecki, S. The nature-inspired metaheuristic method for predicting the creep strain of green concrete containing ground granulated blast furnace slag. Materials 2019, 12, 293. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baykasoğlu, A.; Öztaş, A.; Özbay, E. Prediction and multi-objective optimization of high-strength concrete parameters via soft computing approaches. Expert Syst. Appl. 2009, 36, 6145–6155. [Google Scholar] [CrossRef]
- Bui, D.T.; Ghareh, S.; Moayedi, H.; Nguyen, H. Fine-tuning of neural computing using whale optimization algorithm for predicting compressive strength of concrete. Eng. Comput. 2019, 37, 701–712. [Google Scholar]
- Carbas, S.; Artar, M. Optimum design of cold-formed steel frames via five novel nature-inspired metaheuristic algorithms under consideration of seismic loading. Structures 2021, 33, 4011–4030. [Google Scholar] [CrossRef]
- Luo, H.; Paal, S.G. Metaheuristic least squares support vector machine-based lateral strength modelling of reinforced concrete columns subjected to earthquake loads. Structures 2021, 33, 748–758. [Google Scholar] [CrossRef]
- Chandwani, V.; Agrawal, V.; Nagar, R. Modeling slump of ready mix concrete using genetic algorithms assisted training of Artificial Neural Networks. Expert Syst. Appl. 2015, 42, 885–893. [Google Scholar] [CrossRef]
- Nguyen, T.-D.; Tran, T.-H.; Hoang, N.-D. Prediction of interface yield stress and plastic viscosity of fresh concrete using a hybrid machine learning approach. Adv. Eng. Inform. 2020, 44, 101057. [Google Scholar] [CrossRef]
- Javid, A.A.S.; Naseri, H.; Ghasbeh, M.A.E. Estimating the Optimal Mixture Design of Concrete Pavements Using a Numerical Method and Meta-heuristic Algorithms. Iran. J. Sci. Technol. Trans. Civ. Eng. 2021, 45, 913–927. [Google Scholar] [CrossRef]
- Aydogmus, H.Y.; Erdal, H.; Karakurt, O.; Namli, E.; Turkan, Y.S.; Erdal, H. A comparative assessment of bagging ensemble models for modeling concrete slump flow. Comput. Concr. 2015, 16, 741–757. [Google Scholar] [CrossRef]
- Moayedi, H.; Kalantar, B.; Foong, L.K.; Tien Bui, D.; Motevalli, A. Application of three metaheuristic techniques in simulation of concrete slump. Appl. Sci. 2019, 9, 4340. [Google Scholar] [CrossRef] [Green Version]
- Yeh, I.-C. Modeling slump flow of concrete using second-order regressions and artificial neural networks. Cem. Concr. Compos. 2007, 29, 474–480. [Google Scholar] [CrossRef]
- American Society for Testing and Materials. Standard Test Method for Slump of Hydraulic Cement Concrete; ASTMC 143; ASTM International: West Conshohocken, PA, USA, 2005. [Google Scholar]
- Qiu, C.; Gong, S.; Gao, W. Three artificial intelligence-based solutions predicting concrete slump. UPB Sci. Bull. Ser. C 2019, 81, 2019. [Google Scholar]
- Duan, Q.; Gupta, V.K.; Sorooshian, S. Shuffled complex evolution approach for effective and efficient global minimization. J. Optim. Theory Appl. 1993, 76, 501–521. [Google Scholar] [CrossRef]
- Singer, S.; Nelder, J. Nelder-mead algorithm. Scholarpedia 2009, 4, 2928. [Google Scholar] [CrossRef]
- Gao, X.; Cui, Y.; Hu, J.; Xu, G.; Wang, Z.; Qu, J.; Wang, H. Parameter extraction of solar cell models using improved shuffled complex evolution algorithm. Energy Convers. Manag. 2018, 157, 460–479. [Google Scholar] [CrossRef]
- Doğan, B.; Ölmez, T. A new metaheuristic for numerical function optimization: Vortex Search algorithm. Inf. Sci. 2015, 293, 125–145. [Google Scholar] [CrossRef]
- Doğan, B.; Ölmez, T. Vortex search algorithm for the analog active filter component selection problem. AEU-Int. J. Electron. Commun. 2015, 69, 1243–1253. [Google Scholar] [CrossRef]
- Özkış, A.; Babalık, A. A novel metaheuristic for multi-objective optimization problems: The multi-objective vortex search algorithm. Inf. Sci. 2017, 402, 124–148. [Google Scholar] [CrossRef]
- Ali, W.; Qyyum, M.A.; Qadeer, K.; Lee, M. Energy optimization for single mixed refrigerant natural gas liquefaction process using the metaheuristic vortex search algorithm. Appl. Therm. Eng. 2018, 129, 782–791. [Google Scholar] [CrossRef]
- Dogan, B.; Ölmez, T. Modified off-lattice AB model for protein folding problem using the vortex search algorithm. Int. J. Mach. Learn. Comput. 2015, 5, 329. [Google Scholar] [CrossRef] [Green Version]
- Mirjalili, S.; Mirjalili, S.M.; Hatamlou, A. Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 2016, 27, 495–513. [Google Scholar] [CrossRef]
- Faris, H.; Hassonah, M.A.; Ala’M, A.-Z.; Mirjalili, S.; Aljarah, I. A multi-verse optimizer approach for feature selection and optimizing SVM parameters based on a robust system architecture. Neural Comput. Appl. 2018, 30, 2355–2369. [Google Scholar] [CrossRef]
- Ewees, A.A.; El Aziz, M.A.; Hassanien, A.E. Chaotic multi-verse optimizer-based feature selection. Neural Comput. Appl. 2019, 31, 991–1006. [Google Scholar] [CrossRef]
- Azizi, M.; Ghasemi, S.A.M.; Ejlali, R.G.; Talatahari, S. Optimal tuning of fuzzy parameters for structural motion control using multiverse optimizer. Struct. Des. Tall Spec. Build. 2019, 28, e1652. [Google Scholar] [CrossRef]
- Fathy, A.; Rezk, H. Multi-verse optimizer for identifying the optimal parameters of PEMFC model. Energy 2018, 143, 634–644. [Google Scholar] [CrossRef]
- Moré, J.J. The Levenberg-Marquardt algorithm: Implementation and theory. In Numerical Analysis; Springer: Berlin/Heidelberg, Germany, 1978; pp. 105–116. [Google Scholar]
- Seyedashraf, O.; Mehrabi, M.; Akhtari, A.A. Novel approach for dam break flow modeling using computational intelligence. J. Hydrol. 2018, 559, 1028–1038. [Google Scholar] [CrossRef]
- Mehrabi, M. Landslide susceptibility zonation using statistical and machine learning approaches in Northern Lecco, Italy. Nat. Hazards 2021, 111, 901–937. [Google Scholar] [CrossRef]
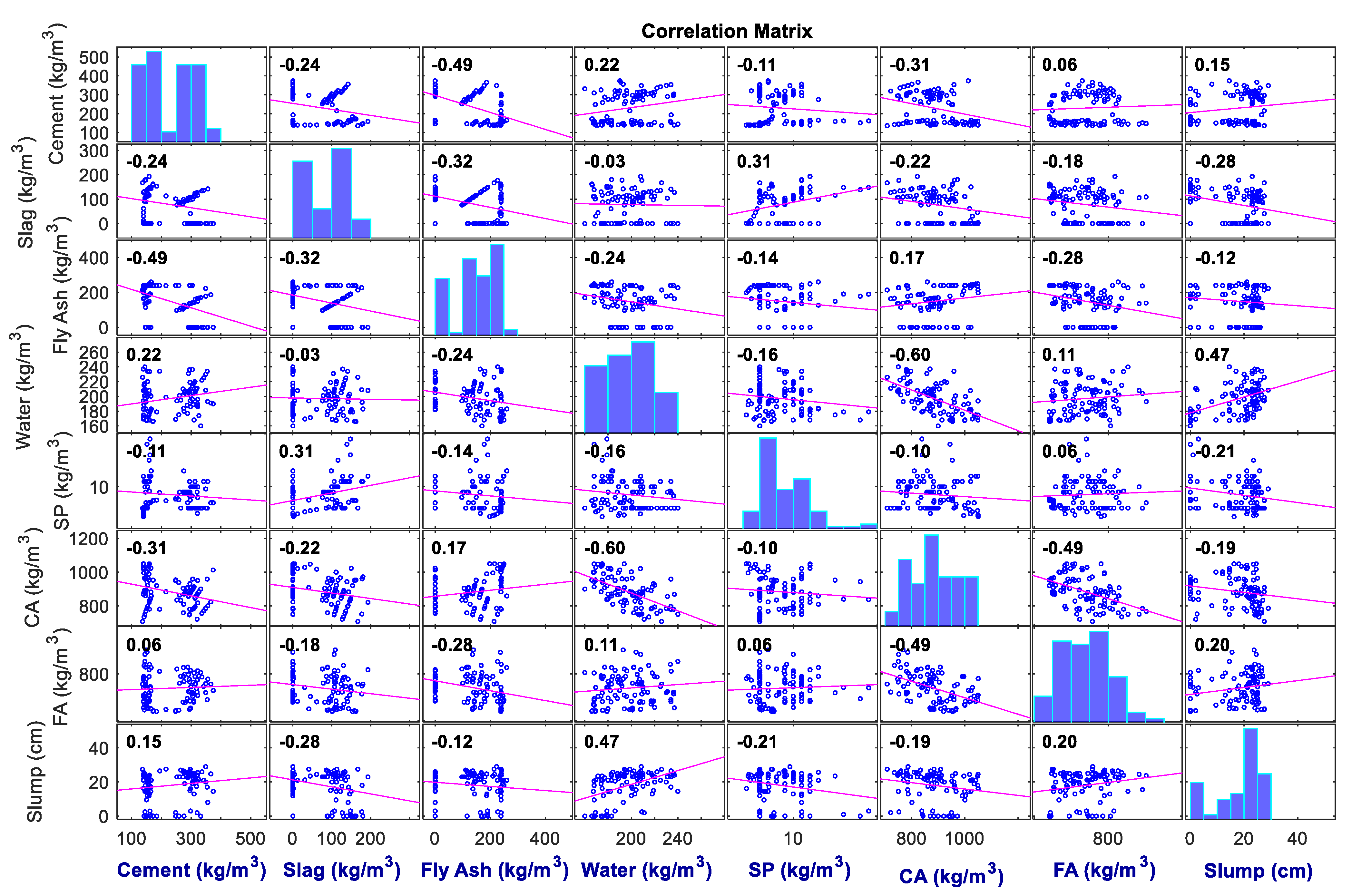
| Slump (cm) | Cement (kg/m3) | Slag (kg/m3) | Water (kg/m3) | Fly Ash (kg/m3) | SP (kg/m3) | FA (kg/m3) | CA (kg/m3) | |
|---|---|---|---|---|---|---|---|---|
| Minimum | 0.0 | 137.0 | 0.0 | 160.0 | 0.0 | 4.4 | 640.6 | 708.0 |
| Maximum | 29.0 | 374.0 | 260.0 | 240.0 | 193.0 | 19.0 | 902.0 | 1049.9 |
| Mean | 18.0 | 229.9 | 149.0 | 197.2 | 78.0 | 8.5 | 739.6 | 884.0 |
| Standard deviation | 8.7 | 78.9 | 85.4 | 20.2 | 60.5 | 2.8 | 63.3 | 88.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Safayenikoo, H.; Khajehzadeh, M.; Nehdi, M.L. Novel Evolutionary-Optimized Neural Network for Predicting Fresh Concrete Slump. Sustainability 2022, 14, 4934. https://doi.org/10.3390/su14094934
Safayenikoo H, Khajehzadeh M, Nehdi ML. Novel Evolutionary-Optimized Neural Network for Predicting Fresh Concrete Slump. Sustainability. 2022; 14(9):4934. https://doi.org/10.3390/su14094934
Chicago/Turabian StyleSafayenikoo, Hamed, Mohammad Khajehzadeh, and Moncef L. Nehdi. 2022. "Novel Evolutionary-Optimized Neural Network for Predicting Fresh Concrete Slump" Sustainability 14, no. 9: 4934. https://doi.org/10.3390/su14094934
APA StyleSafayenikoo, H., Khajehzadeh, M., & Nehdi, M. L. (2022). Novel Evolutionary-Optimized Neural Network for Predicting Fresh Concrete Slump. Sustainability, 14(9), 4934. https://doi.org/10.3390/su14094934







