Application of Neural Networks and Regression Modelling to Enable Environmental Regulatory Compliance and Energy Optimisation in a Sequencing Batch Reactor

Abstract

Real-time control of wastewater treatment plants (WWTPs) can have significant environmental and cost advantages. However, its application to small and decentralised WWTPs, which typically have highly varying influent characteristics, remains limited to date due to cost, reliability and technical restrictions. In this study, a methodology was developed using numerical models that can improve sustainability, in real time, by enhancing wastewater treatment whilst also optimising operational and energy efficiency. The methodology leverages neural network and regression modelling to determine a suitable soft sensor for the prediction of ammonium-nitrogen trends. This study is based on a case-study decentralised WWTP employing sequencing batch reactor (SBR) treatment and uses pH and oxidation-reduction potential sensors as proxies for ammonium-nitrogen sensors. In the proposed method, data were pre-processed into 15 input variables and analysed using multi-layer neural network (MLNN) and regression models, creating 176 soft sensors. Each soft sensor was then analysed and ranked to determine the most suitable soft sensor for the WWTP. It was determined that the most suitable soft sensor for this WWTP would achieve a 67% cycle-time saving and 51% electricity saving for each treatment cycle while meeting the criteria set for ammonium discharges. This proposed soft sensor selection methodology can be applied, in full or in part, to existing or new WWTPs, potentially increasing the adoption of real-time control technologies, thus enhancing their overall effluent quality and energy performance.

1. Introduction

Advances in instrumentation, control and automation are aiding the development of intelligent real-time control (RTC) systems that can be used to predict, analyse and judge the real-time state of a system and self-adapt/organise based on input signals from sensors [1,2,3,4,5]. RTC systems can improve decision making and optimise system performance and are well suited to the control of complex and dynamic processes. However, sensors and detectors can produce large quantities of data that can be challenging to store, process and analyse. Thus, advances in analytic, decision-making, and process optimisation tools are required to enable the development of RTC systems. 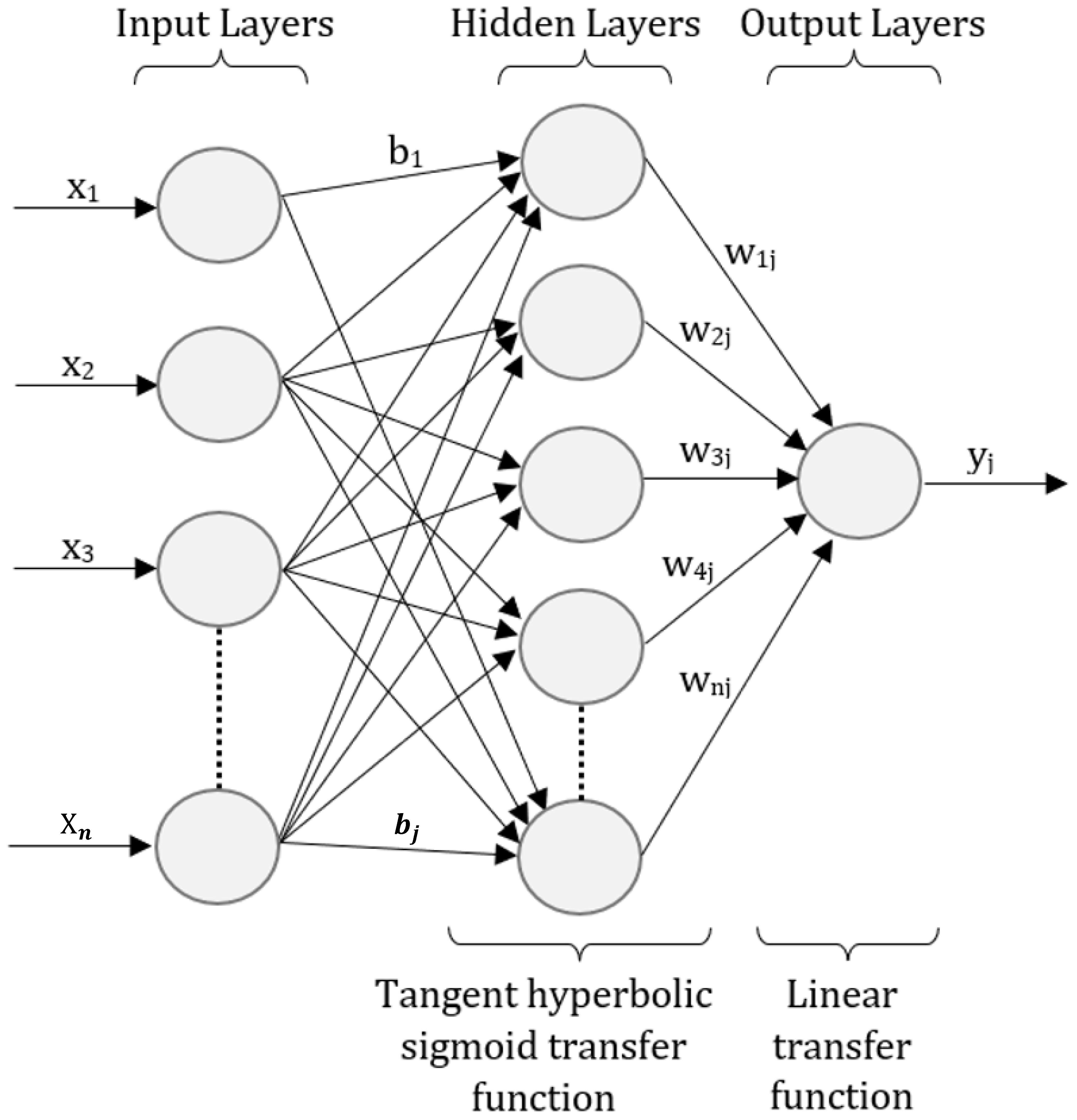This has driven research into the use of numerical modelling techniques in a variety of engineering applications such as water fault detection, aquaculture and vaccine development [1,3,6,7,8,9].

An area where RTC can disruptively innovate and increase process efficiencies is in wastewater treatment. Protection of water resources and water quality is a key sustainable development goal [10], and the effective and sustainable treatment of wastewater is essential to this. Untreated wastewater results in water pollution, which affects both environmental quality and public health [11,12]. Therefore, environmental regulatory compliance in the wastewater treatment sector is vital. However, in the process of meeting regulatory compliance, wastewater treatment plants (WWTPs) can often inefficiently consume energy and be operated inefficiently due to a lack of suitable control processes.

1.1. RTC in Wastewater Treatment Facilities

Wastewater hydraulic flow rates and organic concentrations fluctuate over time; however, wastewater treatment plants are typically rigidly designed and operated to process worst-case scenarios (e.g., maximum hydraulic and design mass loading rates) [13,14,15]. This, in addition to stringent regulatory requirements, can result in inefficiencies in treatment capacity and energy consumption [13]. It has been noted that providing effective and efficient operation requires advanced or RTC solutions that can increase process control and efficiencies [5,16]. This is particularly true for small-scale WWTPs commonly located in towns and villages which have the additional challenges of (i) a lack of permanent operators and local expertise, (ii) relatively high energy costs, (iii) sludge handling, (iv) variable influent hydraulic or organic loads, and (v) inflexible operating regimes [17,18]. Despite these challenges, small WWTP operators are required to comply with tight regulations, which are proving difficult to meet. In Europe, the Urban Wastewater Treatment Directive (UWWTD) (91/271/EEC) specifies the standards for effluent discharged from WWTPs with population equivalents (Pes) exceeding 2000. These regulated parameters include biochemical oxygen demand (BOD), chemical oxygen demand (COD), ammonium-nitrogen (NH₄-N) and total suspended solids (TSS). In sensitive locations, additional parameters can include the monitoring of total phosphorus (TP) and total nitrogen (TN). The implementation of the Water Framework Directive (2000/60/EC) means more stringent limits can be attached to smaller WWTPs depending on status of the receiving waters.

RTC presents a viable means of advanced and targeted control which has significant potential to improve energy efficiency and environmental performance [19], this can lead to improved sustainability [20] in both large- and small-scale WWTPs. Despite considerable developments in sensor technology, real-time analysis of key parameters such as NH₄-N remains a challenge in terms of robustness, accuracy and affordability [4,20,21,22]. Therefore, the use of cost-efficient and reliable soft sensors as surrogates to predict certain parameters holds significant potential for disruptive innovation [23,24]. Several studies have demonstrated that sensors measuring parameters such as oxidation-reduction potential (ORP) and pH can act as surrogates for NH₄-N sensors [15,25,26,27,28,29,30] (Table 1). However, the implementation of these results at small-scale WWTPs is limited. Much of this research is limited to raw and differentiated pH and ORP sensor data as input variables. To the knowledge of the authors, no research has been conducted using a suite of pH and ORP variables (i.e., variables identified from the pH and ORP profile characteristics).

Table 1. Summary of research on advanced RTC methodologies with surrogate sensors.

Objectives	Control Methodology	Influent Type	Study Type	References
Advanced RTC Methodologies
Strategy proposal for SBR optimisation using pH, ORP and DO profiles and fuzzy clustering algorithms for detecting critical process transitions	Fuzzy clustering with wavelet de-noising	Synthetic wastewater	Strategy examined using data collected from a pilot-scale SBR reactor	[16]
Investigation into the use of pH, ORP and DO sensors with an advanced control strategy to optimise nitrogen removal in a continuous system	Fuzzy logic	Urban wastewater with a small industrial input	Pilot-scale continuous flow plant	[31]
Development of an RTC strategy using artificial NNs with ORP and pH sensors for optimised nitrogen removal and phosphorus uptake	Artificial NNs	Synthetic wastewater	Laboratory-scale continuous flow SBR reactor	[28]
Examination of using NNs for predicting biological nitrogen and phosphorus removal using ORP and pH	NNs	Synthetic wastewater	Laboratory-scale SBR reactor	[32]
Examination of the establishment of an online controlling system for nitrogen and phosphorus removal.	A primary professional intelligent control filtered noise by filtration wave and used NNs, database and deducing machine to identify each breakpoint.	Municipal Wastewater	Laboratory-scale SBR reactor	[33]
Methodology development for process monitoring and process analysis for nitrogen and phosphorus removal	Use of multi-way principal component analysis (MPCA) and clustering using historical process data	Domestic strength Synthetic wastewater	Pilot-scale SBR reactor	[34]
Validation study to assess the ability of an algorithm using networks to detect breakpoints using pH, ORP and DO sensors	NNs, de-noising was achieved using a regularisation algorithm	Municipal wastewater	Pilot-scale SBR reactor	[13]
Examination of using a software sensor for real-time estimation of nutrient concentration using pH, ORP and DO sensors	Fuzzy NN analysis	Synthetic wastewater	Bench-scale SBR reactor	[23]
Examination of using a software sensor for real-time estimation of nutrient concentration using pH, ORP and DO sensors	Genetic algorithm-based neural fuzzy system, using self-adapting fuzzy c-means clustering and genetic algorithms	Synthetic wastewater	Laboratory-scale SBR reactor	[24]
Examination of an intelligent control system to achieve advanced nitrogen removal using DO, pH and ORP sensors.	Three-layer network technology with high-performance PLCs and fuzzy control for break point identification	Municipal wastewater	Pilot-scale SBR reactor	[35]
Review article on the general use of artificial NNSAT modelling biological water and wastewater treatment processes	Artificial NNs	Several types	Several types	[36]
Examination of the use of a Gaussian-process (GP) model for the online optimisation of batch phases using pH, ORP and DO sensors.	GP regression was used to smooth the signals and GP classification was used for pattern recognition	Not specified	Laboratory-scale SBR reactor	[37]
Examination of the optimisation of a fuzzy logic controlled DO SBR system using pH and OUR trends for carbon and NH4-N removal	Fuzzy control was used to switch on and off DO input, in order to smooth out pH and OUR profiles. The breaking point was identified using episode representation	Urban wastewater	Pilot-scale SBR reactor	[38]
Examination of a methodology to develop a soft sensor monitoring of an SBR for enhanced biological phosphorus removal.	Artificial NNs	Synthetic wastewater	Laboratory-scale SBR reactor	[21]
Examination of a soft sensor for the optimisation of an SBR for biological nutrient removal	NNs	Synthetic wastewater	Laboratory-scale SBR reactor	[39]
Development of a control strategy to enhance nitrogen and phosphorus removal in an SBR reactor using pH, ORP and OUR	Use of a data acquisition system with curve fitting and characteristic point detection	Municipal wastewater	Semi industrial pilot SBR reactor	[40]
Development of a reliable RTC and supervision tool for DO control	Fuzzy NNs	Industrial wastewater	Aerated submerged biofilm wastewater treatment process	[41]
Development of a soft computing method to predict sludge volume index (SVI) values in a real WWTP	Recurrent self-organising NN	Municipal WWTP	Model based on SBR WWTP	[42]
Examination applies a self-organising cascade neural network (SCNN) with random weights to a non-linear system	Cascade NNs	Municipal WWTP	Model based on municipal WWTP	[43]
Proposal using a model-free learning control (MFLC) system to control advanced oxidation in the treatment of industrial wastewaters	Reinforcement learning	Phenol wastewater	Laboratory pilot plant	[44]
Development of a model for predicting TSS and chemical oxygen demand removal	Fuzzy inference system with principal control analysis	Papermill process wastewater	Papermill WWTP with an anaerobic digester and submerged biofilm biological reactor	[45]
Identifying model to predict effluent nitrogen concentrations and assessment of controller efficiency in terms of economic and environmental performances	Recurrent NNs for model identification and dynamic matrix control as predictive control (PC) algorithm and Benchmark Simulation Model 1 to test these PC configurations	Biological wastewater	Activated sludge process of a municipal WWTP	[46]
Development of soft sensor to predict effluent concentrations such as COD, TSS and TN content	NN with principal component analysis	Biological wastewater	Activated sludge process of large-scale municipal WWTP	[30]

RTC using surrogate sensors requires developing relationships between the primary variable(s) of interest and the surrogate variables being measured. For example, an operator may wish to employ the following rule for controlling a wastewater treatment plant: “when y < t, stop processing”, where y is the concentration of the chemical of interest and t is a threshold for safe discharge. When using surrogate sensors, the task then reduces to a non-linear modelling problem since “y” is not measured directly. Instead, a number of variables (x_n) are analysed to develop functions, whereby y = f(x₁, x₂, … x_n). Several authors have taken this type of approach (Table 1), focusing particularly on fuzzy modelling and advanced neural network (NN) approaches, including recurrent networks [23], cascade networks [43], self-organising network structures [42,43] and fuzzy-neural network hybrids [24,41,45]. There has also been work in developing NN-based soft sensors, using principal component analysis (PCA) to select the optimal number of input vectors [30,47]. These PCA-based NNs were applied to a large-scale municipal wastewater plant, where they predicted concentrations of COD, TN and TSS (among others) using measurements of oxygen and nitrogen concentrations with influent flow rate and alkalinity. However, to the authors’ knowledge, no work has been reported on using a standard feed-forward NN for regression. Standard feed-forward NNs often perform well in non-linear system modelling, so this is an important research gap.

The current study proposes a range of soft sensors, which can be selected according to weights assigned to criteria that might vary with site-specific requirements. There is an abundance of labelled data collected in real-world conditions (which reflect the application of the methodology in practice); hence, there is no need for a self-organising structure. The appropriate network structure can be investigated by comparing the performance of alternative structures directly.

Finally, this study takes a different approach to dealing with non-linear time-varying system dynamics, by using a recurrent or other dynamic network for this aspect. The data are pre-processed to produce a large selection of input variables, which encode information about time-varying aspects of the data. This approach makes the choice of input variables crucial. To address this, this study compares several variable sets (combinations of input variables)—each of which is assessed using a set of criteria describing key, usable features for performance optimisation. In contrast to [45] this study employs regularisation for feature reduction where needed, and leverages manually investigated feature subsets, rather than using PCA. This study presents a methodology capable of identifying the most suitable soft sensor, utilising surrogate probes and inferential estimating models, for RTC of small and decentralised WWTPs. This methodology can cater for the dynamic nature of small and decentralised WWTPs as well as ensuring key onsite goals which can be prioritised in soft sensor selection.

1.2. Numerical Modelling Methods

Regression is the task of modelling a real dependent variable y as a function of independent variables f(x_n), minimising the errors between y and f(x_n). A training set, a dataset of known values for x_n and y, is required to develop the model with the goal of accurate out-of-sample prediction, which is typically measured using a hold-out or test set. A common regression technique is multiple linear regression (MLR), a linear least-squares approximation of the data. MLR provides equations linking a number of input variables (x_n) to a target variable (y) using Equation (1) [48].

$$y=w_0+w_1{x}_1+\cdots +w_n{x}_n$$

(1)

where w₀ is the intercept, w_n is a coefficient (or slope) for x_n and n is the number of input variables. Out-of-sample accuracy can be improved by using regularisation methods which add a penalty term to the model input variables, shrinking the freedom of the input variable during learning [48]. A popular regularisation method is the least absolute shrinkage and selection operator (LASSO) [22,49].

In contrast, NNs are non-linear models with many more degrees of freedom, hence they can be used to model more complex systems. They do not require a priori knowledge about the systems’ structure. They are trained using various gradient descent algorithms [32,50]. A typical NN structure can have one input layer, one or more hidden layers, and one output layer, as illustrated in Figure 1 [39]. Each layer has several nodes. Within a layer, the jth node computes a linear combination of its input variables (x₁, x₂, x₃, …,x_n), coming from the previous layer, with each signal having an associated weight (w_1j, w_2j, w_3j, …, w_nj) [51]. A second input to the node is the bias (b_j), a constant that governs the node’s net input. Weights are multiplied by corresponding inputs to create a weighted input using Equation (2).

$$y_j=b_j+{\displaystyle \sum }_{i=1}^n{w}_{ij}\times x_i$$

(2)

where i represents the inputs and j represents each node.

Figure 1. Typical NN structure with n inputs, j nodes in the hidden layer, a hyperbolic tangent sigmoid transfer function, and a single output layer with a linear transfer function.

The node then applies a transfer function to give its output. Several transfer functions are commonly used including logistic sigmoid, hyperbolic tangent sigmoid and linear functions.

Beginning with the independent variables, values are fed into each successive layer, with outputs from one layer becoming inputs to the next. At the output layer, a single value is output, which is the predicted value of y for the current inputs x_n. Training proceeds by adjusting weights and biases using gradient descent algorithms, such as Levenberg–Marquardt back-propagation [52,53,54,55,56] and Levenberg–Marquardt back-propagation with Bayesian regularisation [57,58,59,60], to minimise error at the output.

The specific goal, in this study, was to create a model to accurately predict current NH₄-N concentration (output) given current and previous ORP and pH values (inputs). This study investigated two types of regression methods, (i) multiple linear regression (MLR) (R_lin) and (ii) MLR with LASSO regularisation (R_reg), and two types of NN training algorithms, (i) Levenberg–Marquardt back-propagation (NN_lm) and (ii) Levenberg–Marquardt back-propagation with Bayesian regularisation (NN_br). Results were analysed in two ways, (i) prediction of the general NH₄-N trend and (ii) performance when predicting a specific NH₄-N concentration—for example a regulatory discharge limit (performance was assessed in terms of accuracy of prediction, and time and energy savings achieved in the treatment cycle). Furthermore, a weighting and ranking system was used to determine the overall best setup that can enable optimal operational, environmental and energy performance.

2. Materials and Methods

The case-study site comprised a sequencing batch reactor (SBR), receiving wastewater from a residential development. The influent wastewater to the SBR comprised domestic wastewater that had undergone primary clarification. The SBR comprised a two-chamber precast concrete tank (a primary settlement chamber and a reaction chamber), with working volumes of 2.42 m³ (hydraulic retention time (HRT) of 4 days) and 1.56 m³ (HRT of 2.6 days), respectively (Figure 2). Influent raw wastewater fed into the primary tank using a pump. This pump was operated using a programme that mimicked the typical diurnal domestic house flow pattern (Table 2) according to the European Standards for evaluation of domestic wastewater treatment systems (CEN 12566-3 2006) [61]. The system was aerated mechanically as required.

Figure 2. Schematic of pilot SBR unit.

Table 2. Diurnal flow pattern used to feed the primary chamber of the SBR pilot unit (CEN, 2006).

Time of Day	% of Total Volume	Volume (Litres)	Time of Day	% of Total Volume	Volume (Litres)
0:00–6:00	0	0	15:00–16:00	0	0
6:00–7:00	10	60	16:00–17:00	0	0
7:00–8:00	10	60	17:00–18:00	0	0
8:00–9:00	10	60	18:00–19:00	20	120
9:00–10:00	5	30	19:00–20:00	20	120
10:00–11:00	5	30	20:00–21:00	5	30
11:00–12:00	5	30	21:00–22:00	5	30
12:00–13:00	0	0	22:00–23:00	5	30
13:00–14:00	0	0	23:00–0:00	0	0
14:00–15:00	0	0

2.1. Cycle Control

A Siemens LOGO! PLC controlled a 464 min cycle comprising the following phases: 2 min fill phase, 400 min aeration phase, 60 min settlement phase and 2 min discharge phase (Figure 3). The aerated phase comprised 20 min blocks, each of which had a 5 min period during which the aeration system was turned on, followed by a 15 min quiescent period.

Figure 3. Illustration of cycle sequence (the on-off aeration pattern is demonstrated using the grey and white sequence in the aeration period).

A feed pump installed in the reactor chamber (switched on for 5 s, to create a siphon) moved liquid from the primary settlement chamber into the reaction chamber as required. Siphoning was terminated when the liquid level in the primary chamber went below (i) the inlet level of the feed pipe, (ii) the liquid level, or (iii) once the two chambers had equalised. As only the volume available over the feed pipe was transferred for treatment, this technique resulted in a dynamic feed volume. Table 3 details the operations in each phase.

Table 3. Overview of the SBR treatment cycle.

Phase (Step)	Operation	Description	Illustration
Fill (1)	Pump: A-On	The pump was switched on for 5 s, subsequently creating a siphon that moved liquid from the primary chamber into the reaction chamber. Siphoning terminated when the liquid level in the primary chamber went below the inlet level of the feed pipe or the liquid level or once the two chambers had equalised.
Aerobic—Repeated for 400 min (2)	(a) Aeration: B-On	The aeration period consisted of a”repetitive sequence of (a) aeration on for 5 min and (b) off for 15 min.
	(b) Rest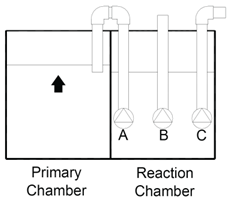
(3)	Settle	A settle time allowed an activated sludge settle prior to discharge creating an upper layer of clarified treated wastewater.
(4)	Discharge: C-On	The discharge pump I is used to remove the clarified treated wastewater from the upper portion of the reactor tank.
Symbol Definition		Pump On ; Pump Off
Legend		A—transfer pump, B—mechanical aerator, C—discharge pump

2.2. Monitoring

Influent and effluent wastewater samples were taken from the primary tank and from a collection vessel placed on the discharge line of the SBR, respectively. Filtered COD and TSS were tested in accordance with standard methods [62] whereby samples were passed through 1.2 μm Whatman GF/C microfiber filters. Total nitrogen (TN) was measured using a Biotector TOC TN TP Analyser (BioTector Analytical Limited, Cork, Ireland). Filtered NH₄-N and NO₃-N were measured using a Thermo Clinical Labsystem, Konelab 20 Nutrient Analyser (Fisher Scientific, Waltham, MA, USA). Hach sc1000 multi-meters monitored data collected from pH, ORP and NH₄-N sensors, in the reactor chamber. pH and ORP were measured at 1 min intervals while NH₄-N was measured at 5 min intervals on a 24 h basis (to match the pH and ORP data, NH₄-N data were linearly interpolated to create a data point every 1 min). All sensors were fitted approximately 500 mm below the lowest liquid level within the reaction chamber and above any potential sludge blanket that might be formed during settlement. All instruments were calibrated, maintained and operated in accordance with manufacturers’ instructions.

2.3. Overview of NH₄-N, pH and ORP Profiles

A typical profile for NH₄-N saw an increase in concentrations as influent was mixed with the treated wastewater remaining in the reactor from the previous cycle. NH₄-N concentrations peaked soon after the fill phase. The time and magnitude of this peak varied depending on influent hydraulic volumes, organic carbon and NH₄-N concentrations. Following this peak, NH₄-N concentrations decreased due to organic carbon oxidation and subsequent nitrification. At approximately 225 min, the rate of decrease in NH₄-N concentrations reduced/levelled off and continued thus for the remainder of the cycle.

A cyclical rise and fall in both pH’ (Figure 4a) and ORP (Figure 4c) profiles during the aeration phase occurred, as the aerator switched on and off, resulting in a peak (or apex) and trough (nadir) in each aeration period in both pH (Figure 4b) and ORP (Figure 4d) profiles. The increase in pH, corresponding to the aeration-on period, was likely, in this case, to be due to CO₂ stripping [28]. The decreases in pH and ORP profiles during the 15 min quiescent period were likely due to a reduction in microbial activity over the course of the aerobic phase [63]. pH reduction was greatest and tailed off following the apex before a subsequent nadir was reached. A similar pattern was observed in the ORP profile. In general, pH decreases as alkalinity is consumed during the nitrification progresses [25]. The trend in pH decreased in response to aeration-on periods as a result of CO₂ stripping (Figure 4b). ORP generally increased during aeration; on completion of nitrification, ORP change accelerated; this acceleration was caused by an abundance of DO [64].

Figure 4. (a) pH and NH₄-N plotted against time for a sample cycle. (b) Example of a pH profile within three aeration periods plotted against time for a sample cycle. The black lines indicate “aeration-on” periods. (c) ORP and NH₄-N plotted against time for a sample cycle. (d) Example of an ORP profile with three aeration periods plotted against time for a sample cycle. The black lines indicate “aeration-on” periods.

3. Application

The methodology consisted of four main steps, namely, (i) data collection and pre-processing, (ii) experimental setup, (iii) soft sensor analyses and (iv) weighting and ranking application (Figure 5).

Figure 5. Summary of overall procedure.

3.1. Assessed Input Variables

A number of unprocessed (pH and ORP) and processed input variables were constructed and added to the set of independent variables (Table 4). The selected processed input variables were constructed using the profile features identified in Section 2.3. For example, the change in pH_apex values (pH_∆apex) was observed to decrease with NH₄-N reduction and was considered useful in identifying the end of NH₄-N removal. The set of independent variables was then analysed in 22 variable sets encompassing a broad range of combinations. Each variable set included a unique collection of input variables (Table 5).

Table 4. pH and ORP processed input variables.

Input Variable	Description
pH	Raw pH data
pHma20	Moving average of pH over the previous 20 min of data (i.e., 1 aeration block; Section 2.1)
pHcum	Cumulative sum of pH data over the duration of the cycle
pHapex	pH apex values during each aeration period
pH∆apex	Change in sequential pH apex values over a treatment cycle
pHnadir	pH nadir values during each aeration period
pHnadir-apex	pH nadir value minus pH apex value for each aeration period
ORP	Raw ORP data
ORPma20	Moving average of ORP over the previous 20 min of data
ORPcum	Cumulative sum of ORP data over the duration of the cycle
ORPapex	ORP apex values during each aeration period
ORP∆apex	Change in sequential ORP apex values over a treatment cycle
ORPnadir	ORP nadir values during each aeration period
ORPnadir-apex	ORP nadir value minus ORP apex value for each aeration period
pHma20XORPma20	pHma20 input variable multiplied by the ORPma20 input variable

Table 5. Input variables to each variable set.

Variable Sets	Input Variables
	pH	pHma20	pHcum	pHapex	pH∆apex	pHnadir	pHnadir-apex	ORP	ORPma20	ORPcum	ORPapex	ORP∆apex	ORPnadir	ORPnadir-apex	pHma20.ORPma20
A	X	X	X	X	X	X	X	X	X	X	X	X	X	X	X
B	X	X		X	X	X	X	X	X		X	X	X	X	X
C		X		X	X	X	X		X		X	X	X	X	X
D		X		X	X	X	X		X		X	X	X	X
E		X		X	X		X		X		X	X		X
F		X	X	X	X		X		X		X	X		X
G		X	X	X	X		X
H			X		X		X
I		X	X		X		X					X		X
J									X	X	X	X		X
K			X				X
L			X		X
M										X				X
N										X		X
O										X		X		X
P		X		X	X		X
Q		X		X					X		X
R				X	X						X	X
S		X			X				X			X
T							X							X
U		X					X		X					X
V		X					X

Within each 464 min cycle, data collected between 0 and 45 min and 402 and 464 min were excluded to eliminate the effects of filling and settlement periods (as these phases were not part of the biological reaction phases of the treatment cycle). Between 0 and 45 min, the effects of the filling stage were still apparent in terms of raw influent mixing with existing wastewater in the system. The settlement and discharge phase was between 402 and 464 min. Data from 41 treatment cycles (each 464 min in duration) were collected, 12 of which (approximately 30%) were randomly separated for use as a test dataset, and the remainder were used as a training dataset.

3.2. Models

Two types of inferential estimation models were examined, namely regression and NNs. Two regression models were assessed, MLR without regularisation (R_lin) and MLR with LASSO regularisation (R_reg). Levenberg–Marquardt back-propagation (NN_lm) and Levenberg–Marquardt back-propagation with Bayesian regularisation (NN_br) were the two NN training models used. Within the NN training models, a hyperbolic tangent sigmoid hidden layer transfer function and a linear output layer transfer function were used. Each model contained one hidden layer of X neurons, notated as NN_lm[X] and NN_br[X] (X being the number of input variables in the variable set under investigation). Additional NN_lm and NN_br models were created by adjusting the number of neurons in the hidden layer to half the number of input variables, i.e., X/2 (NN_lm[0.5X] and NN_br[0.5X]) and twice the number of input variables, i.e., 2X (NN_lm[2X] and NN_br[2X]).

The feed-forward neural network architecture we have chosen is suitable for non-linear system modelling. As the input data are structured, not spatial, we do not need weight-sharing schemes such as convolution. Since we aim to produce an instantaneous soft sensor (i.e., its output reflects the current state of the system), we do not need a stateful network such as a recurrent network. Our choices for (i) transfer function and regularisation, (ii) the number of hidden nodes tested as a hyperparameter and (iii) values chosen, relative to the number of input variables (≤15), are long-standing best practice [58,65]. The main advantages of our design are that it is simple, robust, easy to train, and not demanding to run even on low-power devices in the field. More sophisticated designs are possible and could have potential performance advantages but were considered out of scope.

In total, 176 soft sensors (i.e., a model applied to a variable set) were analysed. These soft sensors consisted of eight models with 22 identified variable sets using 15 input variables (Table 5, Figure 6). MATLAB was used as the computing environment to apply each of the models.

Figure 6. Breakdown of methods, models, variable sets, soft sensors and input variables.

3.3. Analyses

The effectiveness of the models was assessed across six criteria, split between two categories. Category A assessed the accuracy of the general NH₄-N trend prediction; and Category B the accuracy of the predicted trend at a selected NH₄-N concentration, known as the “cut-off threshold value”. This value was set at 2 mg NH₄-N/l for the purposes of this study; site-specific values can vary due to local regulations. The assessment criteria are listed in Table 6.

Table 6. Analyses criteria.

Criterion	Description	Practical Application
Category A
Criterion 1A: R2	Referred to as the coefficient of determination, it is an indicator of the strength of the relationship between variables. 0 indicates a poor relationship, while 1 indicates a very close relationship.	Measures the strength of the relationship between predicted NH4-N trend and actual NH4-N trend
Criterion 2A: RMSE	Root mean square error (RMSE) is a standard statistical metric to measure model performance; it measures the difference between sample and predictor values and is a good measure of accuracy. The lower the RMSE value the more accurate the prediction.	Measures the average accuracy of the predicted NH4-N trend against the actual NH4-N trend
Category B
Criterion 1B: Percentage of NH4-N removal (NH4rem(%))	This criterion returns the percentage NH4-N removal from the peak NH4-N (NH4 peak) concentration (during any given cycle) from a model controlled cycleto the actual NH4-N concentration achieved on-site in a full (non-controlled) treatment cycle (NH4 final). The higher the NH4rem value the better the soft sensor. ${\mathrm{NH}}_{4 \mathrm{rem}}=\left(\frac{{\mathrm{NH}}_{4 \mathrm{thres}}-{\mathrm{NH}}_{4 \mathrm{final}}}{{\mathrm{NH}}_{4 \mathrm{peak}}-{ \mathrm{NH}}_{4 \mathrm{final}}}\right)\times 100\%$ where NH4rem is the percentage of potential NH4-N removal achieved, NH4 thres is the actual NH4-N concentration where the cycle was terminated by the selected cut-off threshold (mg NH4-N/l), NH4 final is the final NH4-N concentration at the end of a full cycle (mg NH4-N/l) and NH4 peak is the highest NH4-N concentration. NH4 thres could be related to an ammonium discharge limit at a given site.	Provides a comparison of the NH4-N concentration at which the cycle would have been ended by the model during a controlled cycle and the actual final NH4-N concentration at the end of a non-controlled cycle
Criterion 2B: Percentage of time saved (Tsave)	This criterion returns the time saved (as a percentage of a non-controlled cycle) by the soft sensor in question, at the selected cut-off threshold value, when compared to the full treatment cycle (and expressed as a percentage). The higher the Tsave value, the better the soft sensor. ${\mathrm{T}}_{\mathrm{save}}=(1-\frac{{\mathrm{T}}_{\mathrm{thres}}}{{\mathrm{T}}_{\mathrm{fixed}}})\times 100$ where Tsave is the time saving (%), Tthres is the time at which the cycle would be ended by the model in a controlled scenario and Tfixed is the fixed time cycle length (min) set in an uncontrolled scenario.	Indicates the time saved with the selected cut-off threshold value. For example, the model might be asked to terminate the treatment cycle when NH4-N concentrations are predicted to reach a certain concentration (e.g., a discharge limit concentration). In general, the greater the time saved, the better, as in practice it increases system capacity
Criterion 3B: Number of successful cycles (SC)	During the application of the soft sensors, it was noticed that some soft sensors may end a treatment cycle very early due to the addition and subsequent mixing of influent at the start of a treatment cycle. This can influence pH and ORP trends temporarily and cause cycles to be ended at an early stage (often prior to the new influent beign completely missed with existing wastewater in the system). Where a cycle was ended before NH4 peak occurred, a soft sensor was deemed unsuccessful for that cycle.	Allows for elimination of soft sensors that would end cycles too early
Criterion 4B: Absolute error (Aberror)	This criterion assessed the accuracy of the soft sensor in meeting a specific threshold concentration for effluent NH4-N discharges.	Indicates the accuracy of each soft sensor at the cut-off threshold value

3.4. Ranking System

A ranking and weighting system was developed to compare the overall impact of each soft sensor. This was necessary as soft sensors may differ in their impact on the overall performance and efficiency of the SBR. For example, a soft sensor may achieve good R² performance, but also return a poor RMSE result. This example scenario would produce results in line with the actual NH₄-N trend but not necessarily close to the actual concentration, thus the overall result would not be acceptable. In consultation with WWTP operators, weights were applied to each of the criteria (Table 7). In general, the overriding concern in WWTPs is to meet environmental regulation, thus Ab_error would be considered vital. For indicative purposes, the weights outlined in Table 7 were applied to this study. It should be noted that weightings may vary depending on site-specific requirements and demands. In addition, these weights can be adjusted to promote site-specific goals. For example, increasing T_save would promote the selection of a soft sensor with good energy saving characteristics, but this may result in poor effluent quality.

Table 7. Applied weights.

Criterion	Weight	Comments
Aberror	10	Aberror indicates the accuracy of the soft sensor at the selected cut-off threshold value. Important as facilities must achieve regulatory compliance
RMSE	5	RMSE indicates the accuracy of the soft sensor when estimating the concentration over a cycle
NH4rem	4	Provides an indication of the NH4-N removal performance of the soft sensor
R2	3	Indicates how well the predicted NH4-N trend matches the actual trend
Tsave	2	Indicates the time saving and energy savings of the soft sensor
SC	1	Least important as low SC values indicate more cycles will finish earlier than they should

Soft sensor results were ranked against each other for each criterion, with better results receiving a higher rank value (ranked values are 1 to n, where n is the number of soft sensors in question). The ranked value was then multiplied by the corresponding criterion weight to acquire the weighted value. Weighted values were then added together and compared to determine the most appropriate soft sensor as follows:

Step 1, determine the best soft sensor (highest weighted value) for each model using the system described above (Equation (3));

Step 2, determine the best soft sensor (highest weighted value) (and thus the overall best soft sensor) from Step 1 results using the system described above.

$$Weighted Valu{e}_{Softsensor}={\displaystyle \sum }_{n=1}^{n=i}\left(Ran{k}_n \times Weigh{t}_n\right)$$

(3)

where $n=\mathrm{each} \mathrm{criterion} \mathrm{detailed} \mathrm{in}$ Table 7.

3.5. Further Analyses

Although determining the best soft sensor was the main objective of this study, a number of other studies, using the same criteria and weights, were also executed including (i) whether MLR and NN regularisation improved results, (ii) a comparison between MLR and NN methods, (iii) how adjusting the number of neurons in the NN hidden layers affected results, and (iv) an examination of which variable sets, which variables and which models were best. It should be noted that the model, variable set, etc., identified for the best soft sensor may differ from that for the best identified model, variable set, etc. The aim of this study was not just to identify the best soft sensor (combination of model and variable set), but also the best overall model and variable set.

4. Results

The overall influent and effluent results for the SBR are summarised in Table 8.

Table 8. Average influent and effluent results (average daily hydraulic volume = 0.9 m³).

Parameter	Average Influent	Influent st.dev.	Average Effluent	Influent st.dev.	% Removal	n Inf/Eff
	mg/L	mg/L	mg/L	mg/L
CODf	405	126	120	85	70.3	9/14 14
TN	87.4	36	16.2	7.9	81.5	12/18
NH4-N	49.6	20	1.1	1.2	97.8	17/28
NO3-N	-	-	2.5	4.3	-	-/27

n is number of samples; Inf—influent; Eff—effluent.

4.1. Regression Results

Two regression models were assessed, R_lin and R_reg. Detailed results for each model are displayed in Table A1 and Table A2, respectively. For NH_4rem, results varied between 20% and 97% for R_lin (average value of 66%) and between 75% and 93% for R_reg (average value of 84%). Average T_save and ab_error results were 51% and 0.98 mg NH₄-N/l for R_lin and 51% and 0.73 mg NH₄-N/l R_reg. An overview of these results shows that R_reg was better than R_lin, as it, on average, achieved better NH_4rem and ab_error results while maintaining a similar T_save result, thus resulting in better and more reliable effluent concentration predictions.

4.2. Neural Network Results

NNs were assessed using two algorithms, namely NN_lm and NN_br. Overall results for NN_lm[X] are displayed in Table A3. The average NH_4rem result for NN_lm[X] was 65% with corresponding T_save and ab_error results of 60% and 1.52 mg NH₄-N/l, respectively. The application of NN_lm[0.5X] (Table A4) returned an average NH_4rem result of 72% and average T_save and ab_error results of 59% and 0.84 mg NH₄-N/l, respectively. Average results for NN_lm[2X] (Table A5) were 59%, 65% and 1.52 mg NH₄-N/l for NH_4rem, T_save and ab_error, respectively.

NN_br[X] returned average T_save, ab_error and NH_4rem results of 60%, 1.35 mg NH₄-N/l and 67%, respectively (Table A6). NN_br[X] was further assessed using NN_br[0.5X] and NN_br[2X]. NN_br[0.5X] returning average T_save, ab_error and NH_4rem results of 60%, 1.03 mg NH₄-N/l and 69%, respectively, while NN_br[2X] results for T_save, ab_error and NH_4rem were 64%, 1.33 mg NH₄-N/l and 61%, respectively. Overall results for NN_br[0.5X] and NN_br[2X] are displayed in Table A7 and Table A8, respectively.

NN_lm[0.5X] was the best soft sensor in terms of NH_4rem and ab_error results, while NN_lm[2X] had the best T_save result. It should be noted that these average results are only indicative of the overall performance of the soft sensor and do not represent the ability of individual soft sensors at predicting NH₄-N trends during the cycle itself.

4.3. Weighting and Ranking Results

To decide the best soft sensor a weighting and ranking system was applied. Table 9 summarises the overall results from this study (full details are available in Table A9). The first step determined the best variable set (i.e., combination of independent input variables) for each model and the second step determined the best soft sensor.

Table 9. Step 1 ranking results and Step 2 ranking.

Soft Sensor	Comparison of the Best Soft Sensor for Each Model against Each Criterion (Step 1)						Overall Ranking (Step 2)
	Average R2 in Last 200 Min of the Cycle	Average RMSE in Last 200 Min of the Cycle	Averages at 2 mg NH4-N/l Trigger				Ranking
			NH4rem (%)	Tsave (%)	aberror (mg/L)	SC
RlinH	0.553	0.5	86	53	0.58	12	6
RregL	0.646	0.479	85	55	0.58	12	4
NNlm[X]O	0.675	0.464	91	37	0.69	12	9
NNlm[0.5X]M	0.634	0.457	92	36	0.59	12	7
NNlm[X]R	0.465	0.457	77	63	0.48	11	3
NNlm[X]K	0.653	0.441	64	60	0.80	12	8
NNbr[X]T	0.584	0.346	73	56	0.60	11	4
NNbr[0.5X]V	0.723	0.402	75	59	0.58	11	2
NNbr[2X]U	0.769	0.196	88	67	0.57	11	1

Overall, NN_br[2X]U was determined to be the most efficient soft sensor based on the weighting system. Variable set U used a combination of moving averages with nadir-apex values for both pH and ORP. This soft sensor achieved an average NH_4rem result of 88% over the 12 test cycles with corresponding T_save and ab_error results of 67%, 0.57 mg NH₄-N/l, respectively (Figure 7). This equated to a 51% reduction in electricity costs for the SB system due to the time savings during the treatment cycle (which in commercial settings may reduce aeration costs).

Figure 7. Comparison of modelled and measured NH₄-N concentrations for 4 of the 12 test cycles with the application of NN_br[2X]U soft sensor.

4.4. Comparison between Methodologies Applied

Using the weighting and ranking method and comparing R_lin to R_reg for each variable set, it was observed that R_lin was marginally better than R_reg (in this comparison R_lin performed better for 54.5% of the model/variable set combinations). A similar comparison was carried out comparing individual variable sets for the three sets of hidden layer neuron models for NN_lm (NN_lm[X], NN_lm[0.5X] and NN_lm[2X]) and NN_br (NN_br[X], NN_br[0.5X] and NN_br[2X]). For both NN_lm (77.3% of total number of variable sets) and NN_br (45.5%), 0.5X was most efficient, while 2X was least efficient (performed best for only 4.5% and 18.2% model/variable set combinations), for NN_lm and NN_br, respectively. Bearing this in mind, and comparing NN_lm against NN_br for 0.5X, the non-regularised model, NN_lm (68.2%), was the better performing NN model. A further comparison was carried out to compare the leading NN (NN_lm[0.5X]) and regression (R_lin) models for individual input variables. This showed that R_lin performed better in 54.5% of variable sets. Alternatively, a study of the final ranked results (Table 9) shows that three of the top four ranked soft sensors use the NN_br model; therefore, for future applications, it may be possible to use this model only. This result suggests that regularisation has indeed helped to avoid some over-fitting suffered by the unregularised NN_lm models. Table 10 compares each variable set for each soft sensor. The aggregate of variable set rank gives an indication of overall variable set performance (when compared to other models).

Table 10. Ranking results for each variable set model for each soft sensor.

Soft Sensor	Rlin	Rreg	NNlin[X]	NNlin[0.5X]	NNlin[2X]	NNbr[X]	NNbr[0.5X]	NNbr[2X]
A	3	1	5	2	6	7	4	8
B	1	3	5	2	8	7	4	6
C	1	2	4	2	8	6	7	5
D	4	3	7	1	5	6	2	8
E	4	2	7	1	4	3	6	8
F	2	4	6	1	5	3	7	8
G	2	3	7	1	4	6	5	8
H	4	5	7	1	2	8	3	6
I	4	2	7	1	3	6	8	5
J	4	1	8	2	6	5	3	7
K	2	3	8	5	1	7	3	5
L	7	2	8	1	3	4	6	5
M	8	6	3	1	2	5	4	7
N	7	4	5	2	6	7	1	3
O	8	2	1	3	7	4	5	6
P	1	3	7	2	3	5	6	8
Q	1	4	5	2	6	3	7	8
R	6	3	5	1	7	2	4	8
S	3	1	6	5	7	4	2	8
T	8	3	6	4	6	1	2	5
U	3	6	2	4	8	5	7	1
V	4	6	5	3	6	8	2	1
Sum	87	692	124	47	113	112	98	64
Rank	3	2	7	1	6	5	4	8

A similar study comparing variable sets (Table A9) identified the top three variable sets as T (pH_nadir-apex and ORP_nadir-apex), V (pH_ma20 and pH_nadir-apex) and M (ORP_cum and ORP_nadir-apex)—each of these used only two input variables, suggesting that simpler variable sets can lead to better models. The nadir-apex input variable seems particularly useful, and more generally the processed input variables were clearly providing added value to the numerical modelling.

5. Discussion

As detailed in the results, soft sensors selected using NNs and regression models, in this case the NN_br[2X]U soft sensor, have the potential to generate large operational savings such as reduced treatment cycle duration and reduced electricity usage, whilst also meeting discharge requirements. This study was conducted in a small-scale WWTP, using a suite of pH and ORP variables (i.e., variables identified from both pH and ORP profile characteristics in the SBR). Several studies have demonstrated that ORP and pH sensors can act as surrogates for NH₄-N sensors [15,25,26,27,28,29,31]; however, the implementation of these results at small-scale WWTPs is limited, and many of these studies did not look at pH and ORP sensors in a combined manner.

For the task at hand, the use of the NN training (optimisation) method was quite standard. The main advantage of the linear regression model was interpretability. The effect of each variable on the output of the model was easy to understand. Neural network models are often able to fit data better at the cost of interpretability. However, neural network models can be interrogated and visualised to give a good understanding of their effect. The motivation for using Bayesian regularisation was to help avoid over-fitting. Over-fitting is the scenario where the model fits the training data well but fails to generalise to unseen data. Regularisation pushes the model towards a simpler form which may fit the training data slightly less but is more likely to generalise.

Wastewater pollutant concentration datasets are suitable for application in NNs as they have a large number of inputs, each of which can vary significantly. In addition, given the 24/7 nature of wastewater treatment, large datasets can be collected from wastewater sensors, which can improve NN suitability even further. However, as discussed in Section 3 of this paper, NNs must be carefully designed and trained to ensure that the outputs are suitable for use in real-time control applications. Given the black box nature of NNs, careful attention is required when assessing input variables, selecting models and assign rankings.

The methodology proposed in this paper creates an opportunity for WWTPs utilising SBRs (and indeed any WWTP utilising other batch treatment processes) to select their own custom soft sensor to optimise on-site treatment processes. In addition, the methodology can be repeated over time in WWTPs to adapt to any significant on-site changes such as, substantial changes in influent wastewater constitution due to the connection of new wastewater sources, etc. However, it can be labour intensive to apply the methodology in a new site, particularly if it is difficult to source the database of parameters required to train the model. To assist with this, further research on this topic would include the application of the best sensor across a larger number of site-based systems, and further adaptation to enable control of biological nitrogen and phosphorous removal where required. Recent work investigated the prediction of N and P removal in municipal wastewater using microalgae modelling response surface methodology, multilayer perceptron artificial neural network and support vector regression [66]. However, despite this and other recent work there is a need to focus on robust methods for system control.

RTC using soft sensors offers many benefits from a managerial perspective. Improved treatment efficacy (in terms of discharge compliance) can be achieved in a more consistent manner without the need for manual intervention by WWTP operatives, whilst electrical energy savings can ease the burden in terms of financial management and assist with meeting targets such as the EU Energy Efficiency Directive (EED). As the equipment required for this methodology is economical, readily available, and easy to use, highly skilled operators are not required to apply the technology, the capital and operating costs are low which enhances sustainability of the technology in smaller WWTPs.

RTC may also be particularly advantageous in WWTPs which are subject to changing loadings due to seasonal changes in tourism, which can lead to seasonal, weekly or daily fluctuations, both hydraulically and organically, which can be difficult to manage. The technology could also be used to extend the duration of treatment cycles to ensure discharge compliance in the instance where a WWTP may be over-loaded in terms of pollutant load (dependent on site-specific conditions such as upstream wastewater storage provisions and other operational considerations allowing for extended cycle times), or reduce the treatment cycle duration to the minimum time required to meet discharge regulations, which can allow a WWTP to treat additional hydraulic load, if required.

6. Conclusions and Outlook

This research presents a methodology for enabling real-time control of NH₄-N removal in wastewater treatment systems. The methodology was developed using a case-study SBR system treating residential wastewater. MLR and NN techniques were used and compared to develop suitable soft sensors that could enable RTC of wastewater treatment systems. This study also presented a method for selecting the optimal soft sensor based on the specific outcomes required at any site.

The estimating models’ studies included linear regression (R_lin) and regularised linear regression (R_reg) and NN models leveraging Levenberg–Marquardt back-propagation (NN_lm) and Levenberg–Marquardt back-propagation with Bayesian regularisation (NN_br). The impact of neuron numbers in each NN model was also analysed. It was determined that for a typical treatment cycle, the best preforming soft sensor, using the site-specific criteria at this site (which heavily weighted accuracy in effluent NH₄-N concentration prediction) used Bayesian regularisation and would achieve an average treatment time saving of 67%, resulting in an average energy saving of 51% of electricity costs. The controlled treatment cycle would achieve 88% NH₄-N removal when compared to the fixed time treatment cycle but, significantly, ensured discharges remained within the threshold discharge concentration set. These results highlight how the methodology can provide a level of targeted control, which can significantly improve the sustainability of wastewater treatment by balancing the needs of safe discharge and efficient energy usage.

The methodology proposed to determine the most efficient soft sensor for any given site can allow a more targeted approach to enable a site to adapt as on-site considerations change. The models studied can be implemented on basic programmable logic controllers typically used for small-scale SBR systems, making the methodology suitable even in small WWTPs with limited resources. The methodology also has the potential to be applied to existing SBRs, making it a cost-effective option for process upgrade works in existing WWTPs.

One limitation of this research is that the methodology is focused specifically on SBRs. There is additional potential for the procedure to be modified to suit other technologies; in particular, systems that treat wastewater in batches. Further research on this topic would include the application of the best sensor across a larger number of site-based systems and further adaptation to enable control of biological nitrogen and phosphorous removal where required.