Abstract
Changes in streamflow within catchments can have a significant impact on agricultural production, as soil moisture loss, as well as frequent drying and wetting, may have an effect on the nutrient availability of many soils. In order to predict future changes and explore the impact of different scenarios, machine learning techniques have been used recently in the hydrological sector for simulation streamflow. This paper compares the use of four different models, namely artificial neural networks (ANNs), support vector machine regression (SVR), wavelet-ANN, and wavelet-SVR as surrogate models for a geophysical hydrological model to simulate the long-term daily water level and water flow in the River Shannon hydrological system in Ireland. The performance of the models has been tested for multi-lag values and for forecasting both short- and long-term time scales. For simulating the water flow of the catchment hydrological system, the SVR-based surrogate model performs best overall. Regarding modeling the water level on the catchment scale, the hybrid model wavelet-ANN performs the best among all the constructed models. It is shown that the data-driven methods are useful for exploring hydrological changes in a large multi-station catchment, with low computational cost.
1. Introduction
In understanding the hydrological consequences of climate change for long-term water resource management, it is essential to be able to simulate and forecast hydrological parameters on a daily time step, particularly daily streamflow and water level, with high accuracy on a catchment scale [1]. In order to achieve better management of water resources, water authorities need reliable models and projections to aid them in allocating water supplies to meet the demands of users, such as agricultural, domestic, and power plant uses. A hydrometric station’s modeling and forecast results will vary depending on the catchment’s climate zone and other characteristics [2]. Geophysical models, such as GEO-CWB, are capable of accurate and reliable modelling of catchments on a coarse scale; however, they are unsuitable for localized point projections due to the enormous computational cost associated with a refined spatial grid [3]. For this reason, there is increasing interest in ‘surrogate’ models, which are data-driven models trained on results from hydrological models, such as GEO-CWB, and which can be run rapidly to explore both long and short-term forecasts on localized scales.
Researchers have concluded that methods that have been demonstrated to be beneficial for streamflow prediction in water-abundant areas are unsuccessful for modeling streamflow in drier catchments (due to the stochastic nature of streams) [4,5,6,7]. More study is needed to better understand the usefulness of various forecasting algorithms in different regions since the specific parameters of the catchment zone, such as water level and streamflow dynamics, are also significant contributory elements in the severity of effects predicted by different forecasting systems [8]. These dynamics are represented by a wide range of physical processes that act over wide temporal and spatial scales. Additionally, these processes and relationships may be simulated using physics-based, conceptual, or data-driven models [9]. While physics-based and conceptual models are employed to give physical insight for processes occurring at the catchment scale, they have drawn criticism for their inability to execute high-resolution forecasting and for their dependency on a variety of different types of datasets that are frequently difficult to collect [8,10,11].
In recent years, machine learning techniques or data-driven models have been increasingly used in simulating and forecasting hydrological processes [12,13,14,15,16]. This is due to technological advancements, which have resulted in the development of sophisticated machine learning algorithms, which can exploit large datasets to provide accurate and high-resolution predictions of streamflow and water level [7,17,18].
Usually, for hydrological processes, the data are nonstationary and not linearly correlated [19]. Multiple linear regression (MLR) and autoregressive integrated moving average (ARIMA) models perform well for long-term variation analysis and forecasts [20,21]; however, both have the assumption of linearity in the data. Because of this, nonlinear algorithms that use machine learning techniques, such as artificial neural networks (ANNs), support vector machines (SVMs), and support vector machine regression (SVR), have been applied in hydrological modeling and forecasting [22].
It has been shown that ANNs, SVMs, and SVR are useful tools for predictive modeling and exploratory data analysis systems for the hydrological forecasting processes (i.e., water quality assessment, streamflow, sediment load, and water level predictions) [23]. In the 1990s, there was a massive increase in the use of ANNs for rainfall–runoff simulation [24]. The benefit of employing ANNs in numerous domains of research, especially in forecasting modeling, is that they have been shown to be capable of accurately and reliably representing extremely nonlinear relationships between variables [25]. Several recently published examples of the use of ANNs in hydrology include [26,27,28,29,30].
The authors of [31] first proposed the concept of SVMs; since then, there has been a tremendous growth in interest in their application to data-driven modelling problems, not least in the field of hydrology. In 2006, [32] used SVM in the hydrology sector, demonstrating that an SVR model outperformed multi-layer perceptron (MLP) ANNs in predicting the water levels of a lake over a 3–12-month time period. Numerous research works have since promoted and recommended the use of SVM in hydrology, with examples in flood forecasting, river water quality prediction, river flow prediction, and potential groundwater mapping. The articles [33,34] are comprehensive review papers on the use of machine and deep learning methods in hydrological and water resources. Examples of recently published applications for the use of SVMs in hydrology include [35,36,37,38,39].
In order to deal with the issue of nonstationary data in hydrology, i.e., the distribution of data has changing mean and variance over time, machine learning techniques have been used with preprocessing methods to develop hybrid models. These models use various methods to identify nonstationary characteristics before applying the preprocessed data to machine learning. One promising data preprocessing method is the wavelet transformation, which decomposes the input time series into a comprehensible time–frequency representation on different scales. Both the discrete wavelet transform (DWT) and the continuous wavelet transform (CWT) have been used in a variety of ways in hydrology. Wavelet transforms can be used to analyze rainfall trends, streamflow, and river sediment (e.g., [40,41,42,43]). Moreover, wavelet transforms in conjunction with an artificial neural network (WANN) are the most commonly used hybrid model nowadays for short-term forecasts (i.e., daily) due to their high accuracy and reliability [39,43,44,45].
One of the earliest hydrological uses of the hybrid WANN model was for drought assessment and forecasting in the Conchos River Basin, Mexico [46]. WANN has since been used in a wide range of hydrological modeling and prediction applications, including streamflow forecasting. All studies comparing ANN and WANN performance have shown that the hybrid WANN models’ accuracy and efficiency are higher over a wider range of time scales (both short- and long-term) [47]. See [48,49,50,51] for examples of recently published applications of WANN in hydrology.
In contrast, the application of wavelet transforms with SVM/SVR has been less well investigated in hydrological applications. A comparative study of four distinct models, ANNs, SVR, hybrid WANN, and WSVR, was conducted in Mediterranean, Oceanic, and Hemiboreal watersheds [52]. Overall, SVR-based models outperformed all other models; however, no model exceeded the others in more than one watershed, indicating that certain models may be better suited to specific types of data. The authors of [53] used the WSVR models in conjunction with other approaches to stimulate monthly streamflow and found that the hybrid WSVR models have better efficiency and accuracy over the SVR.
While it is evident that data-driven modelling methods are useful for making hydrological predictions and that performance may be improved by using wavelet transforms for preprocessing the data, there has been little research carried out on how well such methods perform in simulating both water flow and water level in multi-station large hydrological systems. How such models can be exploited to analyze long-term impacts under different climatic scenarios also has not been explored. In this work, we compare ANN and SVR models with and without wavelet transform preprocessing for the Shannon River catchment in Ireland. We investigate the potential of these methods as surrogate models, trained on results from GEO-CWB, for short-term forecasts of water flow and level with validation against the past four years of observed catchment-scale data adapted from [54]. The validated models are then used to explore future projections for water flow and level at the Lower-Shannon hydrometric station for the period 2014–2080 using two representative concentration pathways: RCP 4.5 (medium–low radiative forcing) and RCP 8.5 (higher radiative forcing). It is shown that the approach provides useful information on expected future statistical variations in the catchment streamflow.
2. Materials and Methods
2.1. Catchment Description
As shown in Figure 1, this catchment covers much of middle and western Ireland. There are 17,963 km2 of land and 1487 km2 of coastal and transitional water in the Shannon River basin, making it Ireland’s largest river basin district. The Shannon catchment is categorized as an International River Basin District because it receives some of its groundwater flow from County Fermanagh (Northern Ireland). Between the Shannon’s headwaters in County Cavan and the Shannon estuary’s mouth, the catchment area of the Shannon River drains includes large parts of the counties of Cavan, Kerry, Westmeath, Limerick, Longford, Clare, Galway, and Offaly, as well as smaller portions of the counties of Mayo, Cork, Sligo, Laois, and Meath. The Shannon River catchment includes 7666 km of rivers; 1220 km of shoreline, including estuaries; and 113 lakes, 53 of which are more than 50 hectares in size [55]. To the southwest and southeast, the soils are mostly grey brown lithosols, podzolics, and gley, whereas the middle and northern parts of the Shannon basin catchment have more peaty, cutover peat, and acid brown podzolics soils. The subsoil is mainly composed of limestone till interspersed with sandstone/shales till, with cutover peat in the northern and central part and mostly limestone in the southwest and south regions. Agriculture is the largest land use type (71%) in the Shannon basin catchment. While grazing and livestock raising are the most prevalent agricultural activities, near the Shannon Callows, farming practices tend to be less intense. There are large tracts of peat/wetland (9%) and some woodland and semi-natural regions (approximately 12%), with water covering 2% of the land and constructed land accounting for 1%. Forest has greatly increased in recent years, particularly in northern Leitrim and Tipperary [56]. The four main catchments in the Shannon River basin are Inny, Nenagh, Suck, Brosna, and Lower Shannon, and these have been selected for investigation in this study. Moreover, these Shannon River catchments are mostly used for agricultural purposes [55]. The area is largely rural, with many protected sites that depend on water (54% of rivers have protected areas associated with them). Water is critical to the economy of the region, generating and sustaining wealth through activities such as agriculture, forestry, aquaculture, power generation, industry, services, transport, and tourism.
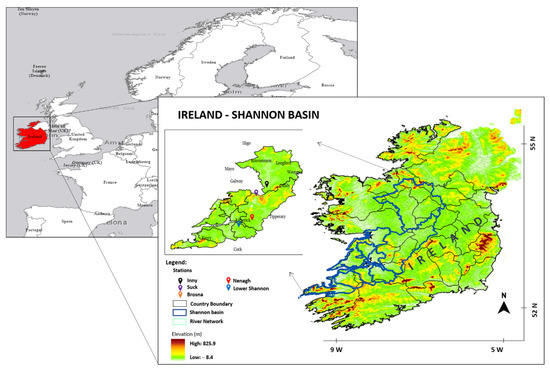
Figure 1.
Study area (Ireland, Shannon River Basin).
2.2. Data Setup and Hydrometric Stations
The models were trained and validated on three types of 30-year (climatic period) daily time series datasets (1983–2013) from the five selected stations shown in Figure 1: (1) observed data (maximum temperature (Tmax) (°C), minimum temperature (Tmin) (°C), water level (WL) (m), and water flow (Q)(m3/s)); (2) monthly simulated runoff values (mm) by GEO-CWB; and (3) daily runoff values (mm), which were downscaled from the GEO-CWB simulations using the observed daily precipitation data through the developed GIS-based downscaling algorithm [57,58]. All the datasets are related to each of the five main hydrometric stations in the Shannon River catchment. Table A1 (Appendix A) shows the descriptive statistics for the input data-sets related to each hydrometric station.
2.3. Workflow and Framework
Four different types of models were adapted in this study: ANNs, WANNs, SVRs, and WSVRs. For each of the four daily time series variables discussed in the previous section (maximum temperature, minimum temperature, water level, and water flow), two sets of inputs were created: the variables themselves delayed by 1 (t − 1), 2 (t − 2), 3 (t − 3), 4 (t − 4) days and so on up to 15 (t − 15) days. The same lagged variables were then decomposed by wavelet transformation into their respective high- and low-frequency components (details and approximations). In addition, monthly time step runoff data simulated for all the sub-catchments using the GEO-CWB were used as input datasets to train each of the models for each of the sub-catchments. The delayed variables became the inputs for the ANNs and SVRs, whereas the delayed wavelet sub-time series were the inputs for the WANNs and WSVRs. Figure 2 shows the data and simulation flowchart and structure. In this study, a combination of off-the-shelf software packages and self-coded algorithms were used to run the simulations. RapidMiner was used as a processor to run and optimize the ANN and the SVR models. A Python package (PyWavelets) was used to run the wavelet transforms, and self-developed algorithms were used to connect all the steps.
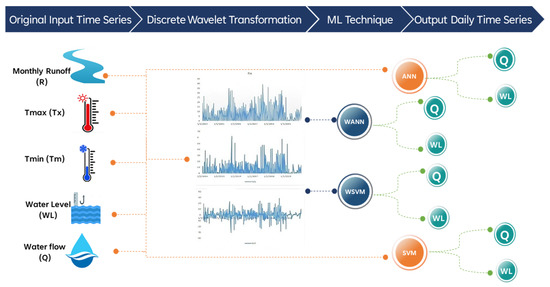
Figure 2.
The structure and framework of the proposed hybrid combination models.
2.4. Artificial Neural Network (ANN)
The author of [59] provides an extensive description of the ANN approach and equations. A backpropagation method for a three-layer feedforward neural network [60,61], which contains one input layer, one hidden layer, and one output layer, was applied here. The node activation function is a very important aspect in ANN models—these can be bounded, continuous, and discontinuous functions. The most frequently employed activation function is the sigmoid function. This function is differentiable, continuous, and monotonically increasing. The application of ANN for predicting water level and water flow consists of two steps. The first step is training the ANN models and the second one is testing the models. In ANN modeling, two important items should be considered: the ANN structure and the training iteration number (epoch). Appropriate selection of both helps to prevent over-trained models. In this research, it was concluded that, considering a learning rate of 0.1 and a momentum of 0.1, 500 epochs are sufficient for the training network. In ANN models, another critical point is determining the number of neurons in input and hidden layers to provide the best training results. Here, the number of neurons required in the hidden layer for function simulation was determined and optimized using an automated RapidMiner approach [62]. Once the training stage was completed, the testing stage began, using the optimum values found for the number of neurons in each input layer and hidden layer. The data were divided into 85% training and 15% validation. The first 85% (30 years of daily data) of the time series were used for training and the last 15% for validation (5 years of daily data).
2.5. Support Vector Machine Regression (SVR)
Support Vector Machine Regression is an extension of the Support Vector Machine algorithm [63]. The essential principle of SVR is the mapping of the data to a higher dimensional space, where a linear regression is applied to give predictions within a defined margin of error from the true value. SVR algorithms apply different mapping schemes to calculate dot products in terms of original space variables by defining the variables in terms of a kernel function (which characterizes a sample-to-sample relationship) to reduce the load of computations. For a theoretical review on SVM/SVR and applications, the following papers are recommended: [64,65,66,67,68]. RapidMiner is a visual workflow designer and processor for data science. The RapidMiner platform is used as the machine learning processor, so all the data are preprocessed in Python and then fed to the RapidMiner platform to run the ANN and SVR. Similar to the ANN models, there is a maximum of 16 inputs for each SVR model. The data are divided into 85% training and 15% validation.
A Radial Basis Function (RBF) kernel was used for this study. Unlike a linear kernel, it can handle nonlinear relationships in the data. The SVR model requires the tuning of two parameters, namely cost (C) (which determines the tradeoff between model complexity and the amount to which predictions outside the margin are tolerated) and epsilon (ε) (which defines the margin). The C value was set to 0.0001 and the ε value to 0.001. Through a trial-and-error procedure, the chosen combination of parameters was fine-tuned for more targeted optimization of the model parameters.
2.6. Wavelet Transformation
The original time series was decomposed using discrete wavelet transforms (DWTs) into a number of time series in different frequency bands (wavelet sub-time series). Over the past two decades, wavelet transforms have been used and developed for many wide-ranging applications in signal and image processing and time series analysis (see [68]). The redundant à trous technique [69] was used to decompose the signals into three levels, with the nonsymmetric db1 wavelet serving as the mother function, which then effectively tuned to the model to select a higher-order wavelet as it carried on the simulation. Three sets of wavelet sub-time series were constructed at different frequency scales, one of which contained the low frequency variations (Approximation) that revealed the signal’s trend and the other two capturing the mid- and high-frequency variations (Details). The use of the à trous algorithm with the db1 wavelet mother function was a result of the optimization scheme of the Python Wavelet tool [70]. Simply put, the original signal can always be reconstructed from the coefficients of the decomposed signal. The specified wavelet transform was applied to every input time series, and the resulting sub-time series were employed in the two-hybrid models WANN and WSVR.
2.6.1. Wavelet-ANN
In WANN models, the decomposed time series are supplied to the ANN for one-day-ahead forecasting of water level and flow (see Figure 2). As discussed in the Introduction section, the wavelet transform is a popular technique to deal with the nonstationary features of a time series prior to modelling with an ANN. In this study, not only was the sensitivity of the preprocessing to the wavelet type and decomposition level investigated, but the effect of a number of input features was examined as a multivariate simulation as well.
2.6.2. Wavelet-SVR
The WSVR models are built similarly to the WANN models. Wavelet sub-time series are fed as inputs for the SVR models, and the training and validation datasets proceed as shown in Figure 2.
2.7. Validation and Performance Evaluation
The authors of [71] confirmed that use of just the correlation coefficient (R) is unsuitable for the evaluation of machine learning models. Instead, it has been suggested that a perfect evaluation of model performance should include one ‘goodness-of-fit’ or relative error measure and one absolute error measure. In this study, the ANN, WANN, SVR, and WSVR model performances were evaluated using the coefficient of determination (R2), root mean square error (RMSE), and mean absolute error (MAE) on the 20% validation dataset. In brief, the model predictions were accurate if R2, MAE, and RMSE were close to 1, 0, and 0, respectively.
2.8. Lag Value
GIS spatial analysis for the travel time of the water between the sub-catchments in the Shannon River catchment revealed the shortest and the longest traveling times to be from the Suck sub-catchment and Lower Shannon sub-catchment, respectively. Both sub-catchments Suck and Lower Shannon were used in the analysis process to choose a single day lag value for the input parameters from all of the original 1- to 15-day lag values in the input data. The four models, ANN, SVR, WANN, and WSVR, were run for both sub-catchments using different lag values, as presented in Table A2 and Table A3. The model performance metrics were compared to choose the best lag value for both water flow and water level.
3. Results and Discussion
3.1. Simulated Models Using Different Lag Values
3.1.1. Water Flow Models Lag Value
It can be seen from Table A2 and Figure 3a,b that all the water flow models performed best with a lag value of 3 for the input parameters. Lag values 2 and 1 have were not used, as they each resulted in model overfitting to the training data.
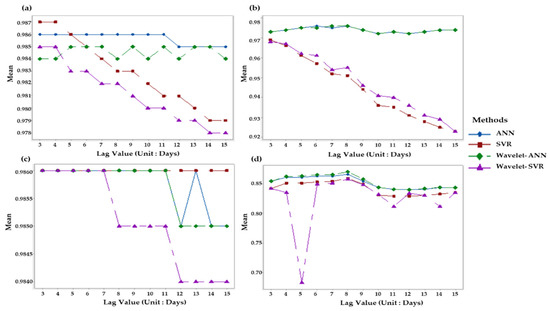
Figure 3.
Mean validation data R2 interaction diagram with the simulated lag values (Unit: Days) and the four different models: (a) Water flow for the Suck station; (b) Water flow for the Lower Shannon station; (c) Water level for the Suck station; (d) Water level for the Lower Shannon station.
3.1.2. Water Level Models Lag Value
It can be seen from Table A3 and Figure 3c,d that all the water level models also performed the best with a lag value of 3 days for the input parameters. As with the water flow models, lag values 2 and 1 were not used because they resulted in model overfitting. In Figure 3c, all the models performed similarly for the first seven lag values due to the fact that the actual absolute water level values of the Suck station do not change significantly over a short period of time. Therefore, the models’ sensitivity to changes can be very slow. In Figure 3d, some of the models performed better at lag value 8 than at lag value 3, but as the difference in the R2 value is negligible in addition to the risk of missing useful information with a long lag value, lag value 3 was selected.
3.2. Model Evaluation
3.2.1. Flow Evaluation
Although all the simulated flow models performed very well, as presented in Figure 4, SVR performed the best overall, as confirmed by Figure 5a, which shows the R2 distribution. The mean absolute error (MAE) depends on the absolute value of the water flow; therefore, MAE values for the Lower Shannon are high, as the water flow rate in the Lower Shannon is the highest. The average water flow rate in the Lower Shannon is around 150 m3/s; however, in the Suck station, which has the second fastest water flow rate after the Lower Shannon, the water flow rate is around 20 m3/s.
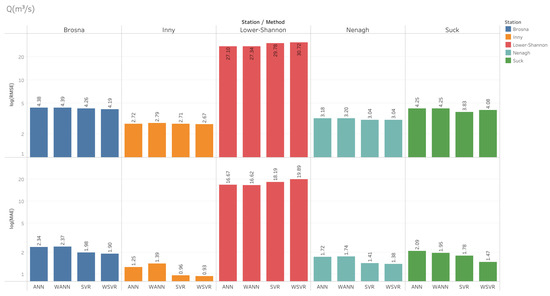
Figure 4.
Log10 of MAE and RMSE values for water flow (Q) (m3/s) by ANN, SVR, WANN, and WSVR models in the validation data.
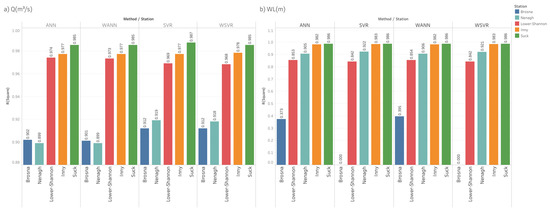
Figure 5.
Validation R2 for the models and stations: (a) Water flow (Q) and (b) Water level (WL).
3.2.2. Water Level Evaluation
All the simulated water level models performed very well for all stations except Brosna, as presented in Figure 6. However, the hybrid WANN model performed the best of all the models. One can notice that WANN and ANN performed significantly better than the SVR-based models for the Brosna hydrometric station. Figure 5b shows the visual R2 distribution, which confirms that WANN is the best model for water level prediction.
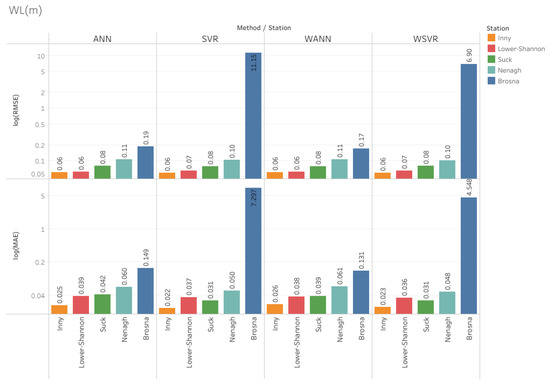
Figure 6.
Log10 of MAE and RMSE values for the water level (WL) (m) by ANN, SVR, WANN, and WSVR models in the validation period.
3.3. Flow Simulation
Equation (1) summarizes the trained and validated models for the water flow. The performances over time of the flow models for the Shannon River Catchment, evaluated in Section 3.2, are compared here. The SVR model has the highest R2 and overall performs better than the two hybrid models. Figure 7 and Figure 8 show the comparison of observed versus forecasted water flow values for the ANN, SVR, WANN, and WSVR models for the Suck and Lower-Shannon hydrometric stations in the structured system for the Shannon River Catchment. Figure 9a,b shows the residuals of the SVR water flow model for the Suck and Lower Shannon hydrometric stations. In general, the models are able to simulate and predict the water flow, capturing the regular and no-flow periods and, to some extent, some peaks. However, the models did not capture the very high flow peaks very accurately. Figure 10a,b shows the residuals of the best performing models for flow prediction for the Lower Shannon and Nenagh stations. The residuals for the Lower Shannon station are consistent over the full range of flowrates due to the fact that it is a large catchment with a high retention time, which results in high flow rates at the hydrometric station at all times. However, Nenagh is similar to the other stations, which usually have low flowrates, and it can be seen that the residuals are higher for the extreme peak levels.
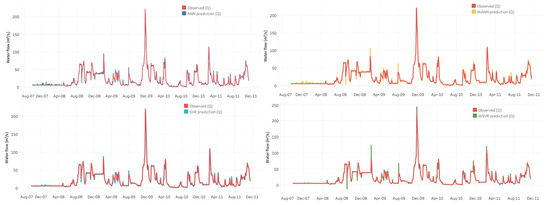
Figure 7.
Comparisons between the measured and predicted flow (m3/s) based on the testing data for the Suck hydrometric station.
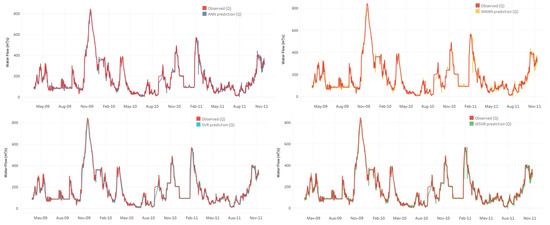
Figure 8.
Comparisons between the measured and predicted flow (m3/s) based on the testing data for the Lower Shannon hydrometric station.
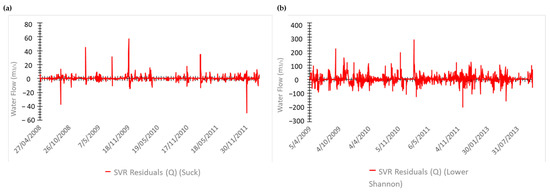
Figure 9.
Residuals of the best-performing flow SVR model: (a) Suck and (b) Lower Shannon.
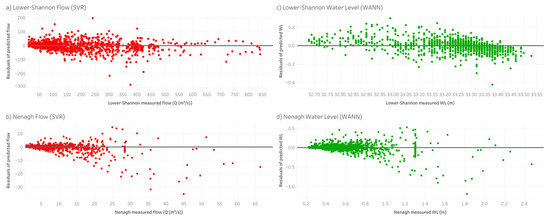
Figure 10.
Residuals vs absolute flow or water level values of the best performing models for Lower-Shannon and Nenagh stations ((a,b) for water flow and (c,d) for water level).
Here is the water flow (m3/s) for day n, is the simulated monthly runoff (mm), is the maximum temperature for day n, is the minimum temperature for day n, and is the error term.
3.4. Water Level Simulation
Equation (2) summarizes the trained and validated models for the water level. The water level models’ performance, evaluated in Section 3.2, for the Shannon River catchment over time are presented here. The hybrid WANN model had the highest testing R2, and, overall, WANN performed better than the WSVR hybrid model. Preprocessing the data with the discrete wavelet transform improved model performance for the ANN; however, it decreased the model performance of the SVR models. It should be noted that a similar conclusion was reached for streamflow forecasting, as reported by [52].
Figure 11a–c shows the residuals of the WANN water level model among the selected hydrometric stations. Figure 12, Figure 13 and Figure 14 show the comparison of observed versus forecasted water level values for the ANN, SVR, WANN, and WSVR models for selected hydrometric stations for the Shannon River catchment Again, in general, the models are able to simulate and predict the water level, and they do capture regular and no-flow periods and, to some extent, the peaks. However, the models did not capture the very high-level peaks very accurately. Figure 10c,d shows the residuals for water level prediction for the Lower Shannon and Nenagh stations. The extreme high levels at Nenagh had large residuals, which was typical of all the stations except Lower Shannon, which, as discussed above, has consistently high water levels.
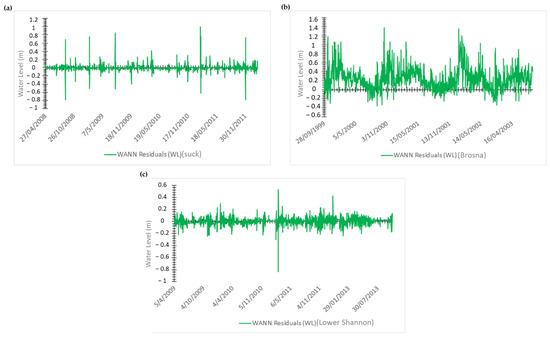
Figure 11.
Residuals of the best-performing water level WL (m) WANN model: (a) Suck, (b) Brosna, and (c) Lower Shannon.
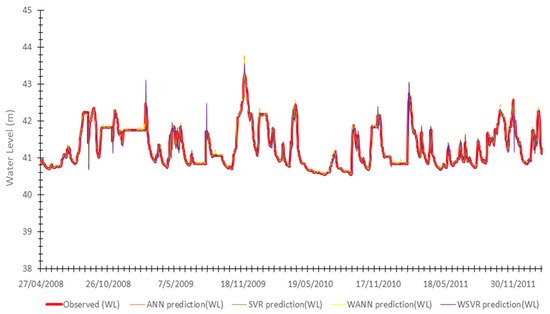
Figure 12.
Comparisons between the measured and predicted water levels (m) based on the testing data for the Suck hydrometric station.
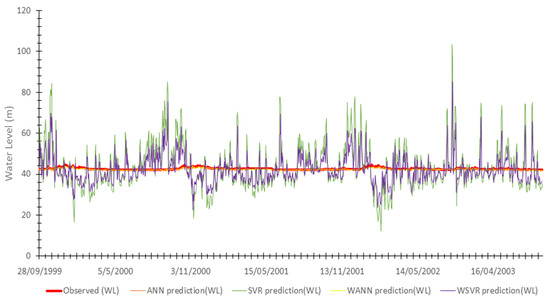
Figure 13.
Comparisons between the measured and predicted water levels (m) based on the validation data for the Brosna hydrometric station.
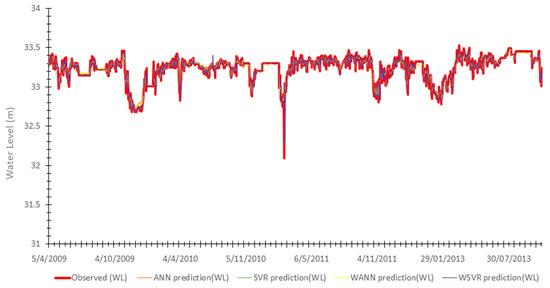
Figure 14.
Comparisons between the measured and predicted water levels (m) based on the testing data for the Lower Shannon hydrometric station.
Here, is the water level (m) for day n, is the simulated monthly runoff (mm), is the maximum temperature for day n, is the minimum temperature for day n, and is the error term.
For the Brosna hydrometric station, Figure 13, all the models produced noise except WANN and ANN. They were the only models that captured the signal. However, WANN performed best in capturing the signal, and that was due to the fact that Brosna is a very small, flashy sub-catchment with a nonstationary dataset, and, as described before this, hybrid WANN can be the solution to model such a case, as can be seen in Figure 11b.
3.5. Projections Based on Climate Change Scenarios
This study used long-term datasets (1983–2013) to train data-driven modelling algorithms, and, as presented in previous sections, the models were validated against 4 years of observed data on the catchment scale. The resultant SVR flow model and WANN level model were then used to predict the long-term future daily water levels and flows for the Lower Shannon hydrometric station for the period 2014–2080, based on data from GEO-CWB simulations of different climatic scenarios adapted from [58]. For the long-term projections, the GEO-CWB simulated data provided only monthly run-off data and daily temperature data. Note that future daily temperature projection data could also be used from other downscaled global climate models (GCMs) that may already be available. This study used the trained and validated data-driven models to provide long-term daily time-step projections for water flow and level in the catchment, which would be computationally very expensive to perform using fine-scale spatially distributed physics-based hydrological models.
The Representative Concentration Pathways (RCPs) represent four alternative greenhouse gas (GHG) emissions and atmospheric concentrations, air pollutant emissions, and land use scenarios for the 21st century. The RCPs were initially used as a basis for the report’s findings in the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (IPCC) in 2014 [72]. Previous assessments defined RCPs within distinct scenarios from the Special Report on Emissions Scenarios (SRES). However, in the most recent reports, the RCPs employed a considerably broader variable input due to the inclusion of a broader range of emissions analyzed [73].
Table 1 and Table 2 represent the descriptive statistics for the river’s predicted flow and levels, respectively. Figure 15 and Figure 16 show the predicted flow and level time series based on the different scenarios. The two climatic scenarios relating to RCP 8.5 provide the highest increase in water level trends; however, RCP4.5 (75%) and RCP 8.5 (75%) provide the highest increase in water flow trends. Both scenarios, RCP 4.5 75% and RCP 8.5 75%, have significant standard variations over the time scale. From Table 1 and Table 2, the flow sum for all scenarios from RCP 4.5 50% to RCP 8.5 75%, respectively, shows significant increases in the total amount of flow in the catchment due to climate change. The average increase in the water flow among all the simulated scenarios is around 2–4% from the baseline.

Table 1.
Lower Shannon water flows (m3/s) daily projections (2014–2080) statistics based on the four different climatic scenarios using the developed SVR model.

Table 2.
Lower Shannon water level (m) daily projections (2014–2080) statistics based on the four different climatic scenarios using the developed WANN model.
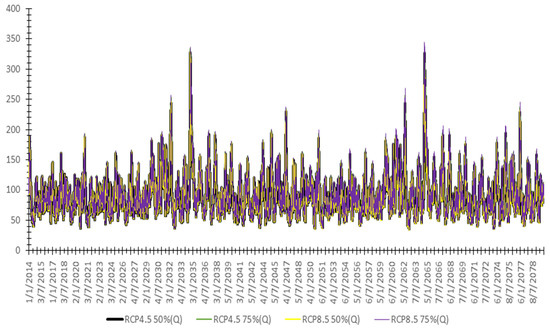
Figure 15.
Lower Shannon water flow (m3/s) daily projections (2014–2080) for the four different climatic scenarios using the developed SVR model.
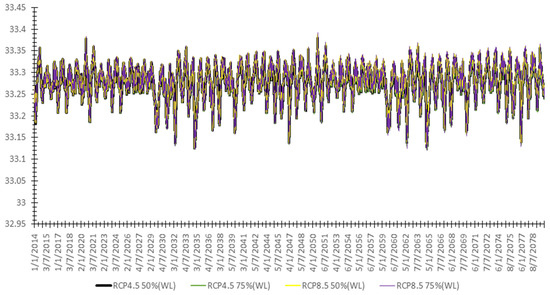
Figure 16.
Lower Shannon water level (m) daily projections (2014–2080) for the four different climatic scenarios using the developed WANN model.
Based on the two scenarios, RCP 4.5 75% and RCP 8.5 75%, it has been concluded that for both variables, water level and flow, there will be increases in the predicted data skewness with time. Skewness is a measure of the asymmetry of the probability distribution about the mean value, which means that water level and flow predictions gradually depart more from normality, which means that the more commonly used statistical time series models cannot be used for predicting water level and flow, and using modeling techniques such as this study to address the nonstationary problem is necessary.
4. Conclusions
The purpose of this study is to demonstrate and compare promising data-driven approaches for modeling and forecasting daily streamflow and water level for a large multi-station hydrological system in order to aid water resource management for the catchment area. The study compares four different models, namely artificial neural networks (ANNs), support vector machine regression (SVR), wavelet-ANN, and wavelet-SVR as surrogate models for GEO-CWB to simulate both short and long-term water level and flow in the Shannon River hydrological system, which is of high economic and social importance in Ireland.
The ANN and SVR models were trained and validated on 30-year daily time series datasets (1983–2013). The inputs for the WANN and WSVR models consisted of the same datasets decomposed by a discrete wavelet transformation into three frequency levels of wavelet sub-time series. The models’ performances were tested for the 15 different lag values, and the results show that a lag value of 3 days resulted in the best model performance.
For simulating the flow parameter on the catchment hydrological system, SVR-based models performed best overall. Regarding modeling the water level parameter on the catchment scale, the hybrid model wavelet-ANN performed the best among all the constructed models. The best-performing models were then used for long-term daily simulations in the Shannon River catchment system based on different climate change scenarios.
From this study, it has been concluded that the hybrid WANN models perform better than the hybrid WSVR models for both water level and flow modeling and forecasting. It has been proven that data-driven models can be used for long-term multi-station large hydrological systems modeling and projection on a catchment scale. The use of temperature as an input variable for the prediction aided in the capture of the climate effect signal into the model. We show that although the data-driven modelling approaches do not always accurately predict the extremely high water flow and level peaks, they otherwise give sufficiently accurate three-day-ahead predictions on a localized water station scale, at a much lower computational cost than using geophysical models. Furthermore, the models allow for daily resolution long-term projections using monthly projection data from physical-based hydrological models. This temporal downscaling provides useful information on expected future statistical variations in the catchment streamflow. Therefore, the surrogate model approach investigated here can provide useful information for effective management of the hydrological system to minimize the impact of streamflow changes on regional agriculture, power generation, aquaculture, forestry, and other industries.
Author Contributions
Conceptualization, S.G., L.G., F.P. and P.J.; methodology, S.G.; validation, S.G. and G.M.; formal analysis, S.G. and G.M.; investigation, S.G.; data curation, S.G.; writing—original draft preparation, S.G.; writing—review and editing, S.G., K.R., I.A., L.G., L.C., M.M. and F.P.; visualization, S.G., I.A. and K.R.; supervision, L.G. and F.P.; funding acquisition, S.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received funding from Trinity College, Dublin through the Postgraduate Ussher Fellowship Award and from the Smart Control of Climate Resilience in European Coastal Cities (SCORE) project, which is funded by the European Union’s Horizon 2020 research and innovation program under grant agreement no. 101003534.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data on the findings of this study are available from the corresponding author, Salem Gharbia, upon request.
Acknowledgments
We would like to acknowledge the funding received from Trinity College, Dublin through the Postgraduate Ussher Fellowship Award and from the Smart Control of Climate Resilience in European Coastal Cities (SCORE) project, which is funded by the European Union’s Horizon 2020 research and innovation program under grant agreement no. 101003534.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| ANN | Artificial Neural Networks |
| ARIMA | Autoregressive Integrated Moving Average |
| C | Cost |
| CWT | Continuous Wavelet Transform |
| DWT | Discrete Wavelet Transform |
| GEO-CWB | Geographical Spatially Distributed Water Balance Model |
| GHG | Greenhouse Gas |
| IPCC | Intergovernmental Panel on Climate Change |
| IQR | The Interquartile Range |
| MAE | Mean Absolute Error |
| MLR | Multiple Linear Regression |
| MSSD | Mean of the Squared Successive Difference |
| Q | Water Flow |
| Q1 | The First Quarter |
| Q3 | The Third Quarter |
| R | The Correlation Coefficient |
| R2 | The Coefficient of Determination |
| RBF | The Radial Basis Function |
| RCP | Representative Concentration Pathways |
| RMSE | Root Mean Square Error |
| SRE | Special Report on Emissions Scenarios |
| SSQ | The Uncorrected Sum of Squares |
| SVM | Support Vector Machine |
| SVR | Support Vector Machine Regression |
| TRMean | The Mean of the Data |
| Tmax | Maximum Temperature |
| Tmin | Minimum Temperature |
| WANN | Wavelet Artificial Neural Network |
| WL | Water Level |
| WSVR | Wavelet Support Vector Machine Regression |
Appendix A

Table A1.
Descriptive statistics for the variables’ training and testing datasets.
Table A1.
Descriptive statistics for the variables’ training and testing datasets.
| Station | Parameters | Datasets | Mean | SEMean | StDev | Variance | Q1 | Median | Q3 | IQR | TRMean | Min. | Max. | Range | Skewness | Kurtosis | MSSD | N |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Inny | Daily average Tmax (°C) | Training | 13.895 | 0.058 | 5.108 | 26.090 | 10.200 | 13.500 | 17.600 | 7.400 | 13.843 | −1.500 | 30.600 | 32.100 | 0.159 | −0.391 | 2.488 | 7697 |
| Testing | 14.212 | 0.120 | 5.246 | 27.523 | 10.700 | 14.500 | 18.500 | 7.800 | 14.366 | −6.500 | 28.000 | 34.500 | −0.420 | −0.041 | 2.432 | 1925 | ||
| Daily average T min (°C) | Training | 5.525 | 0.058 | 5.082 | 25.829 | 1.700 | 5.700 | 9.500 | 7.800 | 5.579 | −8.900 | 18.300 | 27.200 | −0.145 | −0.666 | 6.974 | 7697 | |
| Testing | 5.313 | 0.126 | 5.513 | 30.389 | 1.000 | 6.000 | 9.900 | 8.900 | 5.447 | −14.000 | 17.100 | 31.100 | −0.324 | −0.572 | 7.594 | 1925 | ||
| Daily average simulated runoff (mm) | Training | 2.547 | 0.051 | 4.490 | 20.163 | 0.000 | 0.600 | 3.200 | 3.200 | 1.874 | 0.000 | 65.000 | 65.000 | 3.538 | 20.781 | 16.360 | 7697 | |
| Testing | 2.765 | 0.113 | 4.939 | 24.396 | 0.000 | 0.600 | 3.600 | 3.600 | 1.993 | 0.000 | 40.500 | 40.500 | 3.257 | 14.115 | 19.530 | 1925 | ||
| Daily average water level (mm) | Training | 45.471 | 0.004 | 0.372 | 0.138 | 45.140 | 45.398 | 45.716 | 0.576 | 45.450 | 44.923 | 47.124 | 2.201 | 0.786 | −0.015 | 0.002 | 7697 | |
| Testing | 45.531 | 0.010 | 0.453 | 0.205 | 45.140 | 45.357 | 45.802 | 0.662 | 45.503 | 44.996 | 47.294 | 2.298 | 0.925 | −0.286 | 0.002 | 1925 | ||
| Daily average water flow (m3/s) | Training | 16.988 | 0.165 | 14.479 | 209.644 | 5.070 | 12.341 | 24.476 | 19.406 | 15.661 | 1.656 | 104.231 | 102.575 | 1.355 | 1.951 | 3.542 | 7697 | |
| Testing | 18.453 | 0.391 | 17.154 | 294.249 | 5.070 | 10.911 | 25.745 | 20.675 | 17.044 | 2.543 | 105.846 | 103.303 | 1.302 | 0.839 | 3.400 | 1925 | ||
| Suck | Daily average T max (°C) | Training | 14.173 | 0.058 | 4.983 | 24.827 | 10.500 | 14.000 | 18.000 | 7.500 | 14.139 | −3.000 | 30.300 | 33.300 | 0.102 | −0.430 | 2.467 | 7303 |
| Testing | 13.922 | 0.129 | 5.520 | 30.467 | 10.200 | 14.000 | 18.200 | 8.000 | 14.014 | −6.500 | 29.200 | 35.700 | −0.236 | −0.192 | 2.573 | 1826 | ||
| Daily average T min (°C) | Training | 5.723 | 0.059 | 5.014 | 25.136 | 2.000 | 6.000 | 9.700 | 7.700 | 5.789 | −8.600 | 18.300 | 26.900 | −0.179 | −0.668 | 7.118 | 7303 | |
| Testing | 5.252 | 0.133 | 5.673 | 32.178 | 0.900 | 5.850 | 9.900 | 9.000 | 5.369 | −14.000 | 17.500 | 31.500 | −0.285 | −0.621 | 7.152 | 1826 | ||
| Daily average simulated runoff (mm) | Training | 2.752 | 0.055 | 4.698 | 22.069 | 0.000 | 0.600 | 3.700 | 3.700 | 2.053 | 0.000 | 61.800 | 61.800 | 3.057 | 14.385 | 17.800 | 7303 | |
| Testing | 3.053 | 0.126 | 5.397 | 29.130 | 0.000 | 0.500 | 4.000 | 4.000 | 2.230 | 0.000 | 49.400 | 49.400 | 3.172 | 14.133 | 22.321 | 1826 | ||
| Daily average water level (mm) | Training | 41.201 | 0.006 | 0.513 | 0.263 | 40.855 | 40.946 | 41.519 | 0.664 | 41.163 | 40.540 | 42.782 | 2.242 | 1.092 | 0.010 | 0.004 | 7303 | |
| Testing | 41.409 | 0.016 | 0.673 | 0.453 | 40.855 | 41.095 | 41.841 | 0.986 | 41.385 | 40.544 | 43.279 | 2.735 | 0.683 | −0.944 | 0.004 | 1826 | ||
| Daily flow volume (m3/s) | Training | 20.867 | 0.253 | 21.613 | 467.104 | 5.589 | 10.763 | 30.382 | 24.793 | 18.522 | 1.140 | 123.518 | 122.378 | 1.542 | 1.762 | 7.313 | 7303 | |
| Testing | 32.055 | 0.773 | 33.032 | 1091.110 | 6.101 | 15.960 | 42.920 | 36.819 | 29.744 | 1.493 | 221.214 | 219.721 | 1.360 | 1.788 | 8.952 | 1826 | ||
| Brosna | Daily average T max (°C) | Training | 13.746 | 0.074 | 5.179 | 26.824 | 10.000 | 13.500 | 17.500 | 7.500 | 13.714 | −3.000 | 30.600 | 33.600 | 0.089 | −0.367 | 2.590 | 4844 |
| Testing | 13.872 | 0.142 | 4.927 | 24.275 | 10.300 | 13.600 | 17.600 | 7.300 | 13.875 | −1.500 | 29.200 | 30.700 | 0.028 | −0.470 | 2.422 | 1211 | ||
| Daily average T min (°C) | Training | 5.482 | 0.074 | 5.130 | 26.322 | 1.600 | 5.600 | 9.500 | 7.900 | 5.543 | −9.000 | 18.000 | 27.000 | −0.156 | −0.672 | 7.101 | 4844 | |
| Testing | 5.459 | 0.145 | 5.030 | 25.304 | 1.600 | 5.600 | 9.400 | 7.800 | 5.519 | −7.800 | 17.000 | 24.800 | −0.148 | −0.644 | 6.503 | 1211 | ||
| Daily average simulated runoff (mm) | Training | 2.499 | 0.067 | 4.664 | 21.754 | 0.000 | 0.300 | 3.000 | 3.000 | 1.777 | 0.000 | 57.000 | 57.000 | 3.488 | 18.270 | 18.106 | 4844 | |
| Testing | 2.369 | 0.121 | 4.216 | 17.771 | 0.000 | 0.400 | 3.200 | 3.200 | 1.731 | 0.000 | 38.100 | 38.100 | 3.248 | 15.421 | 15.976 | 1211 | ||
| Daily average water level (mm) | Training | 40.375 | 0.136 | 9.472 | 89.712 | 42.155 | 42.433 | 42.806 | 0.651 | 42.423 | 0.000 | 45.056 | 45.056 | −4.018 | 14.204 | 9.010 | 4844 | |
| Testing | 42.574 | 0.015 | 0.527 | 0.278 | 42.186 | 42.398 | 42.748 | 0.562 | 42.522 | 41.941 | 44.662 | 2.721 | 1.423 | 1.690 | 0.009 | 1211 | ||
| Daily flow volume (m3/s) | Training | 17.972 | 0.220 | 15.341 | 235.349 | 7.149 | 13.031 | 23.520 | 16.371 | 16.378 | 1.141 | 112.674 | 111.533 | 1.718 | 3.575 | 13.693 | 4844 | |
| Testing | 17.339 | 0.398 | 13.861 | 192.140 | 8.325 | 12.935 | 21.164 | 12.839 | 15.601 | 1.846 | 91.496 | 89.650 | 2.125 | 5.453 | 10.953 | 1211 | ||
| Nenagh | Daily average T max (°C) | Training | 14.198 | 0.060 | 5.083 | 25.837 | 10.500 | 14.000 | 18.000 | 7.500 | 14.173 | −1.500 | 30.600 | 32.100 | 0.086 | −0.397 | 2.508 | 7278 |
| Testing | 14.026 | 0.129 | 5.506 | 30.312 | 10.425 | 14.300 | 18.300 | 7.875 | 14.132 | −6.500 | 29.200 | 35.700 | −0.283 | −0.159 | 2.550 | 1820 | ||
| Daily average T min (°C) | Training | 5.668 | 0.060 | 5.085 | 25.859 | 1.800 | 6.000 | 9.700 | 7.900 | 5.732 | −9.000 | 18.300 | 27.300 | −0.174 | −0.684 | 7.134 | 7278 | |
| Testing | 5.363 | 0.133 | 5.676 | 32.217 | 1.000 | 6.000 | 10.000 | 9.000 | 5.491 | −14.000 | 17.500 | 31.500 | −0.311 | −0.598 | 7.221 | 1820 | ||
| Daily average simulated runoff (mm) | Training | 2.619 | 0.055 | 4.730 | 22.369 | 0.000 | 0.500 | 3.300 | 3.300 | 1.890 | 0.000 | 55.200 | 55.200 | 3.329 | 16.389 | 16.659 | 7278 | |
| Testing | 2.740 | 0.120 | 5.131 | 26.323 | 0.000 | 0.500 | 3.400 | 3.400 | 1.944 | 0.000 | 59.800 | 59.800 | 3.796 | 22.195 | 20.356 | 1820 | ||
| Daily average water level (mm) | Training | 0.484 | 0.003 | 0.226 | 0.051 | 0.384 | 0.405 | 0.524 | 0.140 | 0.458 | 0.139 | 2.597 | 2.458 | 2.710 | 11.208 | 0.005 | 7278 | |
| Testing | 0.669 | 0.008 | 0.343 | 0.118 | 0.430 | 0.534 | 0.767 | 0.337 | 0.649 | 0.230 | 2.475 | 2.245 | 1.259 | 1.051 | 0.005 | 1820 | ||
| Daily flow volume (m3/s) | Training | 5.701 | 0.074 | 6.279 | 39.422 | 2.821 | 2.964 | 6.161 | 3.340 | 4.822 | 0.221 | 70.948 | 70.727 | 3.131 | 13.730 | 4.273 | 7278 | |
| Testing | 10.508 | 0.231 | 9.846 | 96.952 | 3.444 | 5.848 | 14.037 | 10.593 | 9.821 | 0.748 | 66.395 | 65.648 | 1.342 | 1.330 | 4.007 | 1820 | ||
| Lower Shannon | Daily average T max (°C) | Training | 14.087 | 0.062 | 4.965 | 24.655 | 10.500 | 13.800 | 18.000 | 7.500 | 14.054 | −3.000 | 30.600 | 33.600 | 0.106 | −0.399 | 2.744 | 6494 |
| Testing | 14.338 | 0.138 | 5.563 | 30.943 | 10.500 | 14.850 | 18.500 | 8.000 | 14.473 | −6.500 | 29.200 | 35.700 | −0.360 | −0.074 | 2.548 | 1624 | ||
| Daily average T min (°C) | Training | 5.603 | 0.062 | 5.030 | 25.299 | 1.800 | 5.800 | 9.500 | 7.700 | 5.665 | −9.400 | 18.300 | 27.700 | −0.165 | −0.696 | 7.417 | 6494 | |
| Testing | 5.592 | 0.143 | 5.744 | 32.990 | 1.000 | 6.100 | 10.100 | 9.100 | 5.745 | −14.000 | 17.500 | 31.500 | −0.382 | −0.562 | 7.279 | 1624 | ||
| Daily average simulated runoff (mm) | Training | 3.077 | 0.062 | 5.007 | 25.074 | 0.000 | 0.700 | 4.200 | 4.200 | 2.344 | 0.000 | 44.100 | 44.100 | 2.692 | 9.640 | 19.984 | 6494 | |
| Testing | 3.017 | 0.123 | 4.945 | 24.448 | 0.000 | 0.700 | 4.200 | 4.200 | 2.321 | 0.000 | 52.500 | 52.500 | 3.033 | 14.490 | 19.669 | 1624 | ||
| Daily average water level (mm) | Training | 33.233 | 0.002 | 0.153 | 0.023 | 33.160 | 33.300 | 33.300 | 0.140 | 33.244 | 32.640 | 33.950 | 1.310 | −1.242 | 1.700 | 0.003 | 6494 | |
| Testing | 33.210 | 0.004 | 0.163 | 0.027 | 33.050 | 33.250 | 33.320 | 0.270 | 33.219 | 32.090 | 33.530 | 1.440 | −0.945 | 1.553 | 0.002 | 1624 | ||
| Daily flow volume (m3/s) | Training | 151.754 | 1.780 | 143.425 | 20570.800 | 37.890 | 91.050 | 239.053 | 201.163 | 138.929 | 10.000 | 741.700 | 731.700 | 1.177 | 0.577 | 758.298 | 6494 | |
| Testing | 218.997 | 4.133 | 166.565 | 27743.900 | 85.690 | 163.875 | 390.830 | 305.140 | 211.779 | 10.500 | 842.320 | 831.820 | 0.702 | −0.312 | 354.854 | 1624 |
Appendix B

Table A2.
Different lag values evaluation among the four different machine learning techniques for water flow models based on the training datasets.
Table A2.
Different lag values evaluation among the four different machine learning techniques for water flow models based on the training datasets.
| Water Flow (Q) m3 | |||||||
|---|---|---|---|---|---|---|---|
| Station | Lag Value (Days) | Suck | Lower Shannon | ||||
| Method | RMSE | MAE | R-Squared | RMSE | MAE | R-Squared | |
| ANN | 3 | 4.145 | 2.085 | 0.986 | 27.249 | 16.645 | 0.973 |
| 4 | 4.111 | 2.09 | 0.986 | 27.391 | 16.827 | 0.974 | |
| 5 | 4.101 | 2.124 | 0.986 | 27.114 | 16.842 | 0.975 | |
| 6 | 4.109 | 2.135 | 0.986 | 26.918 | 17.125 | 0.976 | |
| 7 | 4.13 | 2.217 | 0.986 | 27.38 | 17.645 | 0.975 | |
| 8 | 4.122 | 2.22 | 0.986 | 26.935 | 17.447 | 0.976 | |
| 9 | 4.038 | 2.153 | 0.986 | 26.809 | 17.1 | 0.974 | |
| 10 | 4.171 | 2.263 | 0.986 | 27.369 | 17.73 | 0.972 | |
| 11 | 4.192 | 2.247 | 0.986 | 26.9 | 17.264 | 0.973 | |
| 12 | 4.278 | 2.327 | 0.985 | 27.162 | 17.408 | 0.972 | |
| 13 | 4.362 | 2.432 | 0.985 | 26.784 | 17.091 | 0.973 | |
| 14 | 4.314 | 2.366 | 0.985 | 26.581 | 16.844 | 0.974 | |
| 15 | 4.299 | 2.341 | 0.985 | 26.697 | 16.99 | 0.974 | |
| SVR | 3 | 3.831 | 1.783 | 0.987 | 29.782 | 18.191 | 0.969 |
| 4 | 3.983 | 1.939 | 0.987 | 31.83 | 19.736 | 0.966 | |
| 5 | 4.136 | 2.059 | 0.986 | 34.751 | 22.274 | 0.961 | |
| 6 | 4.269 | 2.15 | 0.985 | 36.915 | 24.174 | 0.957 | |
| 7 | 4.429 | 2.271 | 0.984 | 39.569 | 26.244 | 0.952 | |
| 8 | 4.592 | 2.41 | 0.983 | 40.254 | 27.146 | 0.951 | |
| 9 | 4.709 | 2.464 | 0.983 | 40.727 | 27.775 | 0.944 | |
| 10 | 4.842 | 2.55 | 0.982 | 43.105 | 29.739 | 0.936 | |
| 11 | 4.986 | 2.631 | 0.981 | 44.354 | 30.758 | 0.935 | |
| 12 | 5.121 | 2.718 | 0.981 | 45.906 | 31.881 | 0.931 | |
| 13 | 5.226 | 2.773 | 0.98 | 47.71 | 33.456 | 0.928 | |
| 14 | 5.311 | 2.824 | 0.979 | 49.316 | 34.83 | 0.925 | |
| 15 | 5.412 | 2.896 | 0.979 | 50.925 | 36.143 | 0.923 | |
| Wavelet-ANN | 3 | 4.373 | 2.01 | 0.984 | 27.398 | 16.696 | 0.973 |
| 4 | 4.396 | 2.073 | 0.984 | 27.242 | 16.483 | 0.974 | |
| 5 | 4.222 | 1.971 | 0.985 | 27.173 | 16.882 | 0.975 | |
| 6 | 4.238 | 2.003 | 0.985 | 27.303 | 17.019 | 0.975 | |
| 7 | 4.21 | 2.063 | 0.985 | 27.184 | 17.24 | 0.976 | |
| 8 | 4.396 | 2.08 | 0.984 | 26.863 | 17.074 | 0.976 | |
| 9 | 4.299 | 2.08 | 0.985 | 26.908 | 17.031 | 0.974 | |
| 10 | 4.409 | 2.107 | 0.984 | 27.02 | 16.959 | 0.972 | |
| 11 | 4.257 | 2.052 | 0.985 | 26.844 | 17.034 | 0.973 | |
| 12 | 4.379 | 2.087 | 0.984 | 27.18 | 17.275 | 0.972 | |
| 13 | 4.309 | 2.018 | 0.985 | 26.646 | 16.672 | 0.973 | |
| 14 | 4.32 | 2.078 | 0.985 | 26.502 | 16.507 | 0.974 | |
| 15 | 4.363 | 2.08 | 0.984 | 26.623 | 16.71 | 0.974 | |
| Wavelet-SVR | 3 | 4.076 | 1.469 | 0.985 | 30.715 | 19.89 | 0.968 |
| 4 | 4.162 | 1.541 | 0.985 | 32.622 | 22.14 | 0.967 | |
| 5 | 4.348 | 1.606 | 0.983 | 35.886 | 24.724 | 0.962 | |
| 6 | 4.407 | 1.636 | 0.983 | 37.706 | 26.697 | 0.961 | |
| 7 | 4.507 | 1.682 | 0.982 | 40.553 | 28.669 | 0.954 | |
| 8 | 4.59 | 1.744 | 0.982 | 40.994 | 29.541 | 0.955 | |
| 9 | 4.688 | 1.805 | 0.981 | 42.131 | 30.602 | 0.946 | |
| 10 | 4.77 | 1.871 | 0.98 | 44.82 | 33.058 | 0.941 | |
| 11 | 4.86 | 1.921 | 0.98 | 46.581 | 34.25 | 0.94 | |
| 12 | 4.943 | 1.992 | 0.979 | 48.838 | 36.101 | 0.936 | |
| 13 | 5.019 | 2.04 | 0.979 | 50.707 | 37.381 | 0.931 | |
| 14 | 5.083 | 2.093 | 0.978 | 52.751 | 39.24 | 0.929 | |
| 15 | 5.141 | 2.142 | 0.978 | 55.401 | 41.331 | 0.923 | |
Appendix C

Table A3.
Different lag values evaluation among the four different machine learning techniques for water level models based on the training datasets.
Table A3.
Different lag values evaluation among the four different machine learning techniques for water level models based on the training datasets.
| Water Level (WL) m | |||||||
|---|---|---|---|---|---|---|---|
| Station | Lag Value (Days) | Suck | Lower Shannon | ||||
| Method | RMSE | MAE | R-Squared | RMSE | MAE | R-Squared | |
| ANN | 3 | 0.08 | 0.042 | 0.986 | 0.063 | 0.039 | 0.854 |
| 4 | 0.079 | 0.041 | 0.986 | 0.062 | 0.038 | 0.861 | |
| 5 | 0.079 | 0.042 | 0.986 | 0.064 | 0.039 | 0.861 | |
| 6 | 0.08 | 0.043 | 0.986 | 0.064 | 0.038 | 0.863 | |
| 7 | 0.08 | 0.042 | 0.986 | 0.064 | 0.039 | 0.863 | |
| 8 | 0.081 | 0.044 | 0.986 | 0.063 | 0.038 | 0.866 | |
| 9 | 0.081 | 0.044 | 0.986 | 0.064 | 0.038 | 0.854 | |
| 10 | 0.081 | 0.044 | 0.986 | 0.062 | 0.037 | 0.844 | |
| 11 | 0.082 | 0.045 | 0.986 | 0.062 | 0.037 | 0.841 | |
| 12 | 0.084 | 0.047 | 0.985 | 0.062 | 0.037 | 0.84 | |
| 13 | 0.082 | 0.045 | 0.986 | 0.062 | 0.037 | 0.841 | |
| 14 | 0.085 | 0.048 | 0.985 | 0.062 | 0.036 | 0.844 | |
| 15 | 0.085 | 0.048 | 0.985 | 0.062 | 0.037 | 0.844 | |
| SVR | 3 | 0.079 | 0.031 | 0.986 | 0.066 | 0.037 | 0.842 |
| 4 | 0.08 | 0.031 | 0.986 | 0.065 | 0.035 | 0.851 | |
| 5 | 0.081 | 0.033 | 0.986 | 0.066 | 0.036 | 0.851 | |
| 6 | 0.081 | 0.033 | 0.986 | 0.066 | 0.035 | 0.853 | |
| 7 | 0.08 | 0.03 | 0.986 | 0.066 | 0.035 | 0.854 | |
| 8 | 0.081 | 0.03 | 0.986 | 0.065 | 0.034 | 0.859 | |
| 9 | 0.082 | 0.033 | 0.986 | 0.065 | 0.034 | 0.849 | |
| 10 | 0.082 | 0.032 | 0.986 | 0.065 | 0.034 | 0.831 | |
| 11 | 0.082 | 0.033 | 0.986 | 0.065 | 0.034 | 0.829 | |
| 12 | 0.083 | 0.033 | 0.986 | 0.065 | 0.034 | 0.829 | |
| 13 | 0.082 | 0.031 | 0.986 | 0.065 | 0.033 | 0.83 | |
| 14 | 0.083 | 0.034 | 0.986 | 0.064 | 0.033 | 0.833 | |
| 15 | 0.082 | 0.033 | 0.986 | 0.064 | 0.033 | 0.835 | |
| Wavelet-ANN | 3 | 0.079 | 0.039 | 0.986 | 0.063 | 0.039 | 0.854 |
| 4 | 0.08 | 0.04 | 0.986 | 0.062 | 0.038 | 0.862 | |
| 5 | 0.079 | 0.039 | 0.986 | 0.063 | 0.038 | 0.863 | |
| 6 | 0.08 | 0.039 | 0.986 | 0.063 | 0.038 | 0.865 | |
| 7 | 0.08 | 0.038 | 0.986 | 0.064 | 0.038 | 0.865 | |
| 8 | 0.081 | 0.04 | 0.986 | 0.062 | 0.037 | 0.87 | |
| 9 | 0.081 | 0.038 | 0.986 | 0.063 | 0.037 | 0.858 | |
| 10 | 0.081 | 0.039 | 0.986 | 0.062 | 0.037 | 0.844 | |
| 11 | 0.082 | 0.039 | 0.986 | 0.062 | 0.036 | 0.841 | |
| 12 | 0.084 | 0.041 | 0.985 | 0.062 | 0.037 | 0.84 | |
| 13 | 0.083 | 0.041 | 0.985 | 0.062 | 0.037 | 0.842 | |
| 14 | 0.083 | 0.04 | 0.985 | 0.062 | 0.036 | 0.844 | |
| 15 | 0.084 | 0.041 | 0.985 | 0.062 | 0.037 | 0.843 | |
| Wavelet-SVR | 3 | 0.08 | 0.031 | 0.986 | 0.066 | 0.036 | 0.842 |
| 4 | 0.08 | 0.03 | 0.986 | 0.069 | 0.044 | 0.835 | |
| 5 | 0.081 | 0.03 | 0.986 | 0.102 | 0.082 | 0.684 | |
| 6 | 0.082 | 0.03 | 0.986 | 0.067 | 0.038 | 0.849 | |
| 7 | 0.082 | 0.03 | 0.986 | 0.067 | 0.038 | 0.851 | |
| 8 | 0.083 | 0.031 | 0.985 | 0.065 | 0.036 | 0.858 | |
| 9 | 0.084 | 0.03 | 0.985 | 0.065 | 0.035 | 0.848 | |
| 10 | 0.085 | 0.031 | 0.985 | 0.065 | 0.034 | 0.832 | |
| 11 | 0.085 | 0.031 | 0.985 | 0.069 | 0.045 | 0.812 | |
| 12 | 0.086 | 0.031 | 0.984 | 0.067 | 0.041 | 0.834 | |
| 13 | 0.086 | 0.032 | 0.984 | 0.065 | 0.033 | 0.83 | |
| 14 | 0.086 | 0.031 | 0.984 | 0.068 | 0.045 | 0.812 | |
| 15 | 0.087 | 0.032 | 0.984 | 0.064 | 0.033 | 0.835 | |
References
- Alnahit, A.O.; Mishra, A.K.; Khan, A.A. Evaluation of High-Resolution Satellite Products for Streamflow and Water Quality Assessment in a Southeastern US Watershed. J. Hydrol. Reg. Stud. 2020, 27, 100660. [Google Scholar] [CrossRef]
- Arsenault, R.; Brissette, F.; Martel, J.-L.; Troin, M.; Lévesque, G.; Davidson-Chaput, J.; Gonzalez, M.C.; Ameli, A.; Poulin, A. A Comprehensive, Multisource Database for Hydrometeorological Modeling of 14,425 North American Watersheds. Sci. Data 2020, 7, 243. [Google Scholar] [CrossRef] [PubMed]
- Gharbia, S.S.; Gill, L.; Johnston, P.; Pilla, F. GEO-CWB: GIS-Based Algorithms for Parametrising the Responses of Catchment Dynamic Water Balance Regarding Climate and Land Use Changes. Hydrology 2020, 7, 39. [Google Scholar] [CrossRef]
- Molden, D. Water for Food Water for Life: A Comprehensive Assessment of Water Management in Agriculture; Routledge: London, UK, 2013; ISBN 1-84977-379-3. [Google Scholar]
- Jiang, Y. China’s Water Security: Current Status, Emerging Challenges and Future Prospects. Environ. Sci. Policy 2015, 54, 106–125. [Google Scholar] [CrossRef]
- Patterson, E.A.; Whelan, M.P. A Framework to Establish Credibility of Computational Models in Biology. Prog. Biophys. Mol. Biol. 2017, 129, 13–19. [Google Scholar] [CrossRef] [Green Version]
- Koch, J.; Gotfredsen, J.; Schneider, R.; Troldborg, L.; Stisen, S.; Henriksen, H.J. High Resolution Water Table Modeling of the Shallow Groundwater Using a Knowledge-Guided Gradient Boosting Decision Tree Model. Front. Water 2021, 3, 81. [Google Scholar] [CrossRef]
- Ayzel, G.; Izhitskiy, A. Coupling Physically Based and Data-Driven Models for Assessing Freshwater Inflow into the Small Aral Sea. Proc. Int. Assoc. Hydrol. Sci. 2018, 379, 151–158. [Google Scholar] [CrossRef] [Green Version]
- Lees, T.; Buechel, M.; Anderson, B.; Slater, L.; Reece, S.; Coxon, G.; Dadson, S.J. Benchmarking Data-Driven Rainfall–Runoff Models in Great Britain: A Comparison of Long Short-Term Memory (LSTM)-Based Models with Four Lumped Conceptual Models. Hydrol. Earth Syst. Sci. 2021, 25, 5517–5534. [Google Scholar] [CrossRef]
- Ghaith, M.; Siam, A.; Li, Z.; El-Dakhakhni, W. Hybrid Hydrological Data-Driven Approach for Daily Streamflow Forecasting. J. Hydrol. Eng. 2020, 25, 04019063. [Google Scholar] [CrossRef]
- Sikorska-Senoner, A.E.; Quilty, J.M. A Novel Ensemble-Based Conceptual-Data-Driven Approach for Improved Streamflow Simulations. Environ. Model. Softw. 2021, 143, 105094. [Google Scholar] [CrossRef]
- Costache, R.; Hong, H.; Pham, Q.B. Comparative Assessment of the Flash-Flood Potential within Small Mountain Catchments Using Bivariate Statistics and Their Novel Hybrid Integration with Machine Learning Models. Sci. Total Environ. 2020, 711, 134514. [Google Scholar] [CrossRef] [PubMed]
- Kabir, S.; Patidar, S.; Pender, G. Investigating Capabilities of Machine Learning Techniques in Forecasting Stream Flow; Thomas Telford Ltd.: London, UK, 2020; Volume 173, pp. 69–86. [Google Scholar]
- Mohammadi, B. A Review on the Applications of Machine Learning for Runoff Modeling. Sustain. Water Resour. Manag. 2021, 7, 98. [Google Scholar] [CrossRef]
- Mohammadi, B.; Guan, Y.; Moazenzadeh, R.; Safari, M.J.S. Implementation of Hybrid Particle Swarm Optimization-Differential Evolution Algorithms Coupled with Multi-Layer Perceptron for Suspended Sediment Load Estimation. Catena 2021, 198, 105024. [Google Scholar] [CrossRef]
- Mohammadi, B.; Moazenzadeh, R.; Christian, K.; Duan, Z. Improving Streamflow Simulation by Combining Hydrological Process-Driven and Artificial Intelligence-Based Models. Environ. Sci. Pollut. Res. 2021, 28, 65752–65768. [Google Scholar] [CrossRef] [PubMed]
- Seyoum, W.M.; Kwon, D.; Milewski, A.M. Downscaling GRACE TWSA Data into High-Resolution Groundwater Level Anomaly Using Machine Learning-Based Models in a Glacial Aquifer System. Remote Sens. 2019, 11, 824. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, A.M.; Deo, R.C.; Feng, Q.; Ghahramani, A.; Raj, N.; Yin, Z.; Yang, L. Deep Learning Hybrid Model with Boruta-Random Forest Optimiser Algorithm for Streamflow Forecasting with Climate Mode Indices, Rainfall, and Periodicity. J. Hydrol. 2021, 599, 126350. [Google Scholar] [CrossRef]
- Quilty, J.M.; Sikorska-Senoner, A.E.; Hah, D. A Stochastic Conceptual-Data-Driven Approach for Improved Hydrological Simulations. Environ. Model. Softw. 2022, 149, 105326. [Google Scholar] [CrossRef]
- Dwivedi, D.; Kelaiya, J.; Sharma, G. Forecasting Monthly Rainfall Using Autoregressive Integrated Moving Average Model (ARIMA) and Artificial Neural Network (ANN) Model: A Case Study of Junagadh, Gujarat, India. J. Appl. Nat. Sci. 2019, 11, 35–41. [Google Scholar] [CrossRef]
- Rodrigues, J.; Deshpande, A. Prediction of Rainfall for All the States of India Using Auto-Regressive Integrated Moving Average Model and Multiple Linear Regression. In Proceedings of the 2017 International Conference on Computing, Communication, Control and Automation (ICCUBEA), Pune, India, 17–18 August 2017; pp. 1–4. [Google Scholar]
- Wu, J.; Liu, H.; Wei, G.; Song, T.; Zhang, C.; Zhou, H. Flash Flood Forecasting Using Support Vector Regression Model in a Small Mountainous Catchment. Water 2019, 11, 1327. [Google Scholar] [CrossRef] [Green Version]
- Shortridge, J.E.; Guikema, S.D.; Zaitchik, B.F. Machine Learning Methods for Empirical Streamflow Simulation: A Comparison of Model Accuracy, Interpretability, and Uncertainty in Seasonal Watersheds. Hydrol. Earth Syst. Sci. 2016, 20, 2611–2628. [Google Scholar] [CrossRef] [Green Version]
- Solaimani, K. Rainfall-Runoff Prediction Based on Artificial Neural Network (A Case Study: Jarahi Watershed). Am.-Eurasian J. Agric. Environ. Sci. 2009, 5, 856–865. [Google Scholar]
- Freire, P.K.; Santos, C.A.G.; da Silva, G.B.L. Analysis of the Use of Discrete Wavelet Transforms Coupled with ANN for Short-Term Streamflow Forecasting. Appl. Soft Comput. 2019, 80, 494–505. [Google Scholar] [CrossRef]
- Jahan, K.; Pradhanang, S.M. Predicting Runoff Chloride Concentrations in Suburban Watersheds Using an Artificial Neural Network (ANN). Hydrology 2020, 7, 80. [Google Scholar] [CrossRef]
- Khan, M.M.; Muhammad, N.S.; El-Shafie, A. Wavelet Based Hybrid ANN-ARIMA Models for Meteorological Drought Forecasting. J. Hydrol. 2020, 590, 125380. [Google Scholar] [CrossRef]
- Ntokas, K.F.F.; Odry, J.; Boucher, M.-A.; Garnaud, C. Investigating ANN Architectures and Training to Estimate Snow Water Equivalent from Snow Depth. Hydrol. Earth Syst. Sci. 2021, 25, 3017–3040. [Google Scholar] [CrossRef]
- Seo, Y.; Kwon, S.; Choi, Y. Short-Term Water Demand Forecasting Model Combining Variational Mode Decomposition and Extreme Learning Machine. Hydrology 2018, 5, 54. [Google Scholar] [CrossRef] [Green Version]
- Mei, X.; Smith, P.K. A Comparison of In-Sample and Out-of-Sample Model Selection Approaches for Artificial Neural Network (ANN) Daily Streamflow Simulation. Water 2021, 13, 2525. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Lu, W.; Wang, W.; Leung, A.Y.; Lo, S.M.; Yuen, R.K.; Xu, Z.; Fan, H. Air Pollutant Parameter Forecasting Using Support Vector Machines. In Proceedings of the 2002 International Joint Conference on Neural Networks IJCNN’02 (Cat. No.02CH37290), Honolulu, NI, USA, 12–17 May 2002; Volume 1, pp. 630–635. [Google Scholar]
- Bafitlhile, T.M.; Li, Z. Applicability of ε-Support Vector Machine and Artificial Neural Network for Flood Forecasting in Humid, Semi-Humid and Semi-Arid Basins in China. Water 2019, 11, 85. [Google Scholar] [CrossRef] [Green Version]
- Sit, M.; Demiray, B.Z.; Xiang, Z.; Ewing, G.J.; Sermet, Y.; Demir, I. A Comprehensive Review of Deep Learning Applications in Hydrology and Water Resources. Water Sci. Technol. 2020, 82, 2635–2670. [Google Scholar] [CrossRef]
- Ardabili, S.; Mosavi, A.; Dehghani, M.; Várkonyi-Kóczy, A.R. Deep Learning and Machine Learning in Hydrological Processes Climate Change and Earth Systems a Systematic Review. In Lecture Notes in Networks and Systems, Proceedings of the Engineering for Sustainable Future; Várkonyi-Kóczy, A.R., Ed.; Springer International Publishing: Cham, Germany, 2020; pp. 52–62. [Google Scholar]
- Kumar, A.; Ramsankaran, R.; Brocca, L.; Muñoz-Arriola, F. A Simple Machine Learning Approach to Model Real-Time Streamflow Using Satellite Inputs: Demonstration in a Data Scarce Catchment. J. Hydrol. 2021, 595, 126046. [Google Scholar] [CrossRef]
- Meng, E.; Huang, S.; Huang, Q.; Fang, W.; Wu, L.; Wang, L. A Robust Method for Non-Stationary Streamflow Prediction Based on Improved EMD-SVM Model. J. Hydrol. 2019, 568, 462–478. [Google Scholar] [CrossRef]
- Samantaray, S.; Sahoo, A.; Ghose, D.K. Assessment of Sediment Load Concentration Using SVM, SVM-FFA and PSR-SVM-FFA in Arid Watershed, India: A Case Study. KSCE J. Civ. Eng. 2020, 24, 1944–1957. [Google Scholar] [CrossRef]
- Xingpo, L.; Muzi, L.; Yaozhi, C.; Jue, T.; Jinyan, G. A Comprehensive Framework for HSPF Hydrological Parameter Sensitivity, Optimization and Uncertainty Evaluation Based on SVM Surrogate Model- A Case Study in Qinglong River Watershed, China. Environ. Model. Softw. 2021, 143, 105126. [Google Scholar] [CrossRef]
- Grabowski, R.C.; Surian, N.; Gurnell, A.M. Characterizing Geomorphological Change to Support Sustainable River Restoration and Management. Wiley Interdiscip. Rev. Water 2014, 1, 483–512. [Google Scholar] [CrossRef]
- Gao, G.; Ning, Z.; Li, Z.; Fu, B. Prediction of Long-Term Inter-Seasonal Variations of Streamflow and Sediment Load by State-Space Model in the Loess Plateau of China. J. Hydrol. 2021, 600, 126534. [Google Scholar] [CrossRef]
- Tarar, Z.R.; Ahmad, S.R.; Ahmad, I.; Majid, Z. Detection of Sediment Trends Using Wavelet Transforms in the Upper Indus River. Water 2018, 10, 918. [Google Scholar] [CrossRef] [Green Version]
- Yaseen, Z.M.; Awadh, S.M.; Sharafati, A.; Shahid, S. Complementary Data-Intelligence Model for River Flow Simulation. J. Hydrol. 2018, 567, 180–190. [Google Scholar] [CrossRef]
- Ganguly, A.; Goswami, K.; Kumar, A. Sil WANN and ANN Based Urban Load Forecasting for Peak Load Management. In Proceedings of the 2020 IEEE Calcutta Conference (CALCON), Kolkata, India, 28 February 2020; pp. 402–406. [Google Scholar]
- Kaveh, K.; Kaveh, H.; Bui, M.D.; Rutschmann, P. Long Short-Term Memory for Predicting Daily Suspended Sediment Concentration. Eng. Comput. 2021, 37, 2013–2027. [Google Scholar] [CrossRef]
- Kim, T.-W.; Valdes, J. Nonlinear Model for Drought Forecasting Based on a Conjunction of Wavelet Transforms and Neural Networks. J. Hydrol. Eng. 2003, 8, 319–328. [Google Scholar] [CrossRef] [Green Version]
- Sharghi, E.; Nourani, V.; Najafi, H.; Molajou, A. Emotional ANN (EANN) and Wavelet-ANN (WANN) Approaches for Markovian and Seasonal Based Modeling of Rainfall-Runoff Process. Water Resour. Manag. 2018, 32, 3341–3356. [Google Scholar] [CrossRef]
- Drisya, J.; Kumar, D.S.; Roshni, T. Hydrological Drought Assessment through Streamflow Forecasting Using Wavelet Enabled Artificial Neural Networks. Environ. Dev. Sustain. 2021, 23, 3653–3672. [Google Scholar] [CrossRef]
- Nourani, V.; Molajou, A.; Uzelaltinbulat, S.; Sadikoglu, F. Emotional Artificial Neural Networks (EANNs) for Multi-Step Ahead Prediction of Monthly Precipitation; Case Study: Northern Cyprus. Theor. Appl. Climatol. 2019, 138, 1419–1434. [Google Scholar] [CrossRef]
- Shukla, R.; Kumar, P.; Vishwakarma, D.K.; Ali, R.; Kumar, R.; Kuriqi, A. Modeling of Stage-Discharge Using Back Propagation ANN-, ANFIS-, and WANN-Based Computing Techniques. Theor. Appl. Climatol. 2021, 147, 687–889. [Google Scholar] [CrossRef]
- Zakhrouf, M.; Bouchelkia, H.; Stamboul, M.; Kim, S.; Heddam, S. Time Series Forecasting of River Flow Using an Integrated Approach of Wavelet Multi-Resolution Analysis and Evolutionary Data-Driven Models. A Case Study: Sebaou River (Algeria). Phys. Geogr. 2018, 39, 506–522. [Google Scholar] [CrossRef]
- Karran, D.J.; Morin, E.; Adamowski, J. Multi-Step Streamflow Forecasting Using Data-Driven Non-Linear Methods in Contrasting Climate Regimes. J. Hydroinform. 2014, 16, 671–689. [Google Scholar] [CrossRef] [Green Version]
- Tikhamarine, Y.; Souag-Gamane, D.; Kisi, O. A New Intelligent Method for Monthly Streamflow Prediction: Hybrid Wavelet Support Vector Regression Based on Grey Wolf Optimizer (WSVR–GWO). Arab. J. Geosci. 2019, 12, 540. [Google Scholar] [CrossRef]
- Suykens, J.A.; Vandewalle, J. Least Squares Support Vector Machine Classifiers. Neural Processing Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Understanding Water Levels of the River Shannon. Available online: //Shannoncframstudy.Jacobs.Com/Docs/Understanding%20water%20levels%20of%20the%20River%20Shannon_120814.Pdf (accessed on 20 May 2021).
- Kelly, M.; Reid, A.; Quinn-Hosey, K.; Fogarty, A.; Roche, J.; Brougham, C. Investigation of the Estrogenic Risk to Feral Male Brown Trout (Salmo Trutta) in the Shannon International River Basin District of Ireland. Ecotoxicol. Environ. Saf. 2010, 73, 1658–1665. [Google Scholar] [CrossRef]
- Gharbia, S.; Gill, L.; Johnston, P.; Pilla, F. GEO-CWB: A Dynamic Water Balance Tool for Catchment Water Management. In Proceedings of the 5th International Multidisciplinary Conference on Hydrology and Ecology (HydroEco’ 2015), Vienna, Austria, 13–16 April 2015; pp. 1–8. [Google Scholar]
- Gharbia, S.; Gill, L.; Johnston, P.; Pilla, F. Multi-GCM Ensembles Performance for Climate Projection on a GIS Platform. Modeling Earth Syst. Environ. 2016, 2, 102. [Google Scholar] [CrossRef] [Green Version]
- Masters, T. Practical Neural Network Recipes in C++; Morgan Kaufmann Publisher: San Francisco, CA, USA, 1993; ISBN 0-12-479040-2. [Google Scholar]
- Haykin, S. Neural Networks, a Comprehensive Foundation; Prentice-Hall Inc.: Upper Saddle River, NJ, USA, 1999; Volume 7458, pp. 161–175. [Google Scholar]
- Schmitz, J.E.; Zemp, R.J.; Mendes, M.J. Artificial Neural Networks for the Solution of the Phase Stability Problem. Fluid Phase Equilibria 2006, 245, 83–87. [Google Scholar] [CrossRef]
- Hofmann, M.; Klinkenberg, R. RapidMiner: Data Mining Use Cases and Business Analytics Applications; CRC Press: Boca Raton, FL, USA, 2016; ISBN 1-4987-5986-6. [Google Scholar]
- Drucker, H.; Burges, C.J.; Kaufman, L.; Smola, A.; Vapnik, V. Support Vector Regression Machines. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 1996; Volume 9. [Google Scholar]
- Burges, C.J.; Schölkopf, B. Improving the Accuracy and Speed of Support Vector Machines. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 1997; pp. 375–381. [Google Scholar]
- Hsu, C.-W.; Chang, C.-C.; Lin, C.-J. A Practical Guide to Support Vector Classification; University of National Taiwan: Taipei, Taiwan, 2003. [Google Scholar]
- Schölkopf, B.; Smola, A.J.; Williamson, R.C.; Bartlett, P.L. New Support Vector Algorithms. Neural Comput. 2000, 12, 1207–1245. [Google Scholar] [CrossRef] [PubMed]
- Smola, A.J.; Schölkopf, B. A Tutorial on Support Vector Regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Addison, P.S. The Illustrated Wavelet Transform Handbook: Introductory Theory and Applications in Science, Engineering, Medicine and Finance; CRC Press: Boca Raton, FL, USA, 2017; ISBN 1-315-37255-X. [Google Scholar]
- Murtagh, F.; Starck, J.-L.; Renaud, O. On Neuro-Wavelet Modeling. Decis. Support Syst. 2004, 37, 475–484. [Google Scholar] [CrossRef]
- Lee, G.R.; Gommers, R.; Wasilewski, F.; Wohlfahrt, K.; O’Leary, A. PyWavelets: A Python Package for Wavelet Analysis. J. Open Source Softw. 2019, 4, 1237. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe Jr, G.J. Evaluating the Use of “Goodness-of-fit” Measures in Hydrologic and Hydroclimatic Model Validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Szwitzerland, 2014. [Google Scholar]
- Adopted, I. Climate Change 2014 Synthesis Report; IPCC: Geneva, Szwitzerland, 2014. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).