Sharing the Burdens of Climate Mitigation and Adaptation: Incorporating Fairness Perspectives into Policy Optimization Models

Abstract

Mitigation of, and adaptation to, climate change can be addressed only through the collective action of multiple agents. The engagement of involved agents critically depends on their perception that the burdens and benefits of collective action are distributed fairly. Integrated Assessment Models (IAMs), which inform climate policies, focus on the minimization of costs and the maximization of overall utility, but they rarely pay sufficient attention to how costs and benefits are distributed among agents. Consequently, some agents may perceive the resultant model-based policy recommendations as unfair. In this paper, we propose how to adjust the objectives optimized within IAMs so as to derive policy recommendations that can plausibly be presented to agents as fair. We review approaches to aggregating the utilities of multiple agents into fairness-relevant social rankings of outcomes, analyze features of these rankings, and associate with them collections of properties that a model’s objective function must have to operationalize each of these rankings within the model. Moreover, for each considered ranking, we propose a selection of specific objective functions that can conveniently be used for generating this ranking in a model. Maximizing these objective functions within existing IAMs allows exploring and identifying climate polices to which multiple agents may be willing to commit.

1. Introduction

The Paris Agreement aims to keep any increase in the global average surface temperature to well below 2 °C above the pre-industrial level, with a further ambition to limit it to 1.5 °C [1]. At the same time, the Paris Agreement seeks to increase the capability of countries to adapt to unavoidable climate change and to deal with its impacts. The pursuit of these interlinked goals is based on the voluntary pledges of individual countries to reduce greenhouse gas (GHG) emissions. Alarmingly, even if nationally determined contributions (NDCs), pledged as of 2021, are fully implemented, they are expected to put the world on track towards a 2.7 °C increase in global average temperature by the end of the century—far above the targets of the Paris Agreement [2].

1.1. Fairness as a Critical Factor in Successful Climate Mitigation and Adaptation Action

The insufficient level of mobilization on the part of the international community to mitigate global warming is largely due to the stark disparities between the historical contributions of countries to climate change and their exposure to its effects. These differences have resulted in countries having a diversity of perspectives on the climate issue [3]. Developed countries, which are historically responsible for the bulk of GHG emissions and have economically benefited from them, face the exceptionally expensive challenge of massively decarbonizing their economies by the middle of the century. As a result, they are seeking a globally cost-efficient way of mitigating climate change and sharing related costs. Developing countries, on the other hand, face the overwhelming challenges of adapting to climate change impacts that are already severe and to which they have contributed little. For them, climate change mitigation and adaptation are about avoiding harm to humans and preserving opportunities for future development. These different ways of framing the climate issue make it extremely difficult for the international community to agree on a set of principles to determine the contributions of countries to concerted climate action. Indeed, given the experiences with climate negotiations so far, a climate treaty based on a set of commonly accepted principles appears to be infeasible, while its opposite—a principles-free bargaining among nations regarding their individual contributions—is not likely to bring about the level of commitments necessary to avert catastrophic climate change [4,5]. The willingness of countries to make more substantial contributions to climate action critically depends on whether they perceive their share of burdens as fair [6,7].

Fairness is closely related to justice and equity, and there is no clear-cut demarcation between these notions. Consequently, in the literature on climate change, these three terms are understood somewhat differently by different authors and are sometimes used interchangeably. In this paper, we follow Grasso [3], who proposes the following disambiguation. “Justice” refers to principles that existed independently before the process of judging the outcomes of climate policies began. The two most common theories of justice appearing in the context of climate negotiations are the Rawlsian principles of justice as fairness [8] and Sen’s capability approach [9]. “Equity” refers to normative criteria used to orient and implement principles of justice in a specific judgement process. For instance, in the context of sharing burdens of climate change mitigation, the relevant equity criteria being discussed are responsibility, capability (or ability-to-pay), equality, and right to development [10]. “Fairness” refers to perceptions of the judgement process and its result. The judgement process can be deemed legitimate if the criteria used to assess policy outcomes are relevant to the circumstances of the countries in question and representative of them and, further, if those criteria have been applied correctly and impartially. The outcome of the policy selected through the judgement process is understood to be fair if (1) equals are treated equally and (2) “unequals” are treated differently, according to the relevant differences among them [11,12]. In this paper, we focus on climate policies that are outcome-fair, by which we mean that the outcomes of these policies can be presented to each country, from the perspective of its own interests, as satisfying criteria (1) and (2).

1.2. Lacking Representation of Fairness in Integrated Assessment Models

The main tools for exploring possible outcomes of climate policies are Integrated Assessment Models (IAMs). To produce insights relevant to the fairness of outcomes of climate policies, IAMs must include a representation of possible policy options and their effects at a national or regional level. A variety of regionally explicit IAMs are available in the literature, ranging from stylized benefit-cost-optimizing (BC) IAMs to highly complex and detailed process-based (DP) IAMs [13]. Although both types of IAMs could, in principle, support the evaluation of climate policies from the perspective of outcome fairness, to our knowledge neither of them has been satisfactorily employed in this way. One of the possible obstacles to doing so lies in the mechanics of these models.

Regionally explicit BC IAMs such as RICE [14] or AD-RICE [15] seek optimal climate policies that balance the marginal costs of the last ton of GHG emissions being avoided against the marginal damages resulting from that last ton being emitted. This is achieved through maximizing, over a certain period, the sum of regional utilities, which are assumed to be functions of regional consumption. The regional consumption is assumed to be reduced by the costs of mitigation and by adaptation measures, as well as by climate-related damages resulting from the cumulative production-driven GHG emissions of all regions. The optimal policy that merely maximizes the sum of regional utilities is, however, problematic from the perspective of outcome fairness. To allow for economically meaningful comparisons between regional utilities, in a way that supports an analysis of the benefits and costs of policies, regional weights are used for aggregating regional consumption, regional mitigation costs, and regional climate-induced damages. How these regional weights are chosen has a significant influence on the distribution of utility across regions, but the legitimacy of the choices is often weak [16,17,18]. On a more fundamental level, the logic of benefit–cost analyses based on maximizing the sum of utilities is not satisfactory from the perspective of outcome fairness, as explained by the critique of Adler [19].

Regionally explicit DP IAMs are used to explore possible scenarios of climate action and their impacts on the environment and economy at a disaggregated (i.e., regional and/or sectoral) level. Each scenario is generated under a coherent and internally consistent set of assumptions about key driving forces (e.g., future population dynamics or rates of technological change) and socioeconomic processes. The internal representation of economic mechanisms in DP IAMs is usually based on the same economic theory as that of BC IAMs and often involves maximizing the sum of regional utilities. For instance, in the MACRO economic module of the MESSAGE model, the demands for, and resultant prices of, different types of energy are determined by maximizing the overall utility of consumption of all regions [20,21]. Comparable optimization mechanisms in BC IAMs and DP IAMs lead to similar concerns about how fair, based on their construction, the outcomes resulting from their solutions can be.

Questions of equity and fairness of scenarios, if dealt with at all, are therefore addressed only ex post, outside of the DP IAMs used to compute them. For instance, du Pont et al. [22] have proposed top-down allocations of GHG emissions to individual countries under globally cost-efficient mitigation scenarios according to various principles of equitable burden sharing. On the other hand, Meinshausen et al. [23] have presented a bottom-up scheme whereby shares of the GHG emissions pool are allocated to different countries in line with a globally cost-efficient mitigation scenario and based on principles of equity in burden sharing chosen by the country in question. Whether such allocations of emission quotas to countries translate into fair outcomes, however, is not self-evident because the aforementioned studies do not take into account the impact of these allocations on the economies of the countries affected by them. This underexplored knowledge gap was partly addressed by Underdal et al. [12], who used the GRACE model to assess the implications of the two most widely discussed principles of equity in the emission quota allocation, namely “capability” and “responsibility”, for the gross domestic product (GDP) of eight large world regions. The authors did not, however, recommend any particular allocation leading to an outcome that could be regarded as fair.

Fairness of a climate policy outcome is a matter of subjective and very diverse perceptions on the part of individual countries or regions, and these perceptions do not easily lend themselves to quantitative representation within IAMs. This does not mean that IAMs are inherently ill-suited to offering meaningful insights into how fair climate policies should look like. What limits the current generation of IAMs most severely in that regard is their focus on maximizing the sum of regional utilities. Even though aggregating regional utilities into a single objective function by adding them up is a natural extension of the objective functions used in the representative-agent utility-maximizing framework common in economics, it unfortunately is insensitive to how overall utility is distributed among regions. This is raising serious problems from the perspective of outcome fairness, as we shall explain in detail in Section 3.

1.3. Can IAMs Be Made Fairness-Relevant?

In this paper, we discuss the theoretical and practical aspects of replacing in IAMs the sum of the utilities of agents, such as countries or regions, with alternative, fairness-relevant objective functions. Our aims are (1) to highlight the important potential of existing IAMs to address the question of fairness and (2) to suggest to IAM modelers specific types of functions that have proven useful in solving practical multi-objective optimization problems and whose maximization leads to outcomes that can plausibly be presented as fair.

Employing only a single type of function we discuss in this paper is unlikely to result in policy recommendations that all countries would commonly accept as fair, given the diversity of their perspectives. It is therefore crucial to use multiple types of functions that represent different notions of fairness. It is this approach that can help build an understanding of what fair outcomes of climate policies look like and eliminate clearly unfair proposals, thus fostering convergence of climate negotiations on a course of climate action by which all countries are treated fairly.

In Section 2, we make the case for our claim that IAMs are an important and useful platform for exploring questions surrounding the fairness of climate policies. Because the pursuit of fairness is an ethical choice, and because countries perceive the fairness of climate policies through the lens of how the outcomes of these policies affect their interests, an appropriate approach to tackle questions of outcome fairness is welfarism—a strand of normative ethics that evaluates the worthiness of outcomes on the basis of interests of considered agents. We briefly introduce elements of the welfarist framework and discuss how they are implemented in IAMs. We also explain how the key element of the welfarist framework—the social welfare function—maps agent utilities onto a social ranking of outcomes of the considered policies. Next, we briefly discuss the minimal requirements that must be satisfied by a welfarist social ranking of outcomes. This leads us to closing Section 2 by observing that the social ranking of outcomes is generated in IAMs by aggregating agent utilities, which implies that an appropriate choice of the method of utility aggregation may lead to a welfarist social ranking of outcomes that can be presented to agents as fair.

In Section 3, we review several major philosophical concepts that can guide the aggregation of agent utilities into a social ranking of outcomes. We begin with classical utilitarian and egalitarian approaches, which are based on the premise that certain aggregate properties of outcomes have intrinsic ethical merit that ought to be promoted. Next, we discuss several more modern approaches to building social rankings of outcomes that operationalize the notion called the separateness of persons, thus allowing social preferences to be justified to each agent from their own perspective. We also explain how the considered aggregation methods relate to the notion of outcome fairness.

Next, in Section 4, we discuss how to formalize various fairness-relevant notions as properties of functions that can be used for aggregating utilities of agents into social rankings of outcomes. We also associate collections of these properties with approaches to building the aggregation-based social rankings of outcomes presented in Section 3. This allows us to build a taxonomy of fairness-relevant aggregating functions. We populate this taxonomy with specific examples of aggregating functions used in various fields of science and interpret their features from the perspective of outcome fairness.

In Section 5, we discuss practical aspects of employing fairness-relevant aggregating functions within existing IAMs, to explore what the outcomes of fair climate policies might look like. We also propose possible modifications to optimization problems solved within IAMs that may improve perceptions of fairness not only across regions but also across generations.

Finally, in the concluding Section 6 of this paper, we offer compact guidance for modelers who may wish to explore questions of fairness in the context of their own models.

2. Welfarist Framework of IAMs as a Platform for the Ethical Evaluation of Climate Policies

Designing a mitigation and adaptation policy is a challenging ethical problem. The dominant approach to the ethical appraisal of different policy options is consequentialism [24], whereby each policy is judged by its expected outcome. While there is a growing appreciation in the international community that any viable climate policy must also protect common goods such as biodiversity and ecosystems services and that climate-related challenges need to be solved collectively, most (if not all) countries participating in the climate negotiations are still primarily driven by their own interests. This reality is reflected well by the welfarist approach, adopted in modern IAMs, as it postulates that the only legitimate yardstick for comparing policy outcomes is the profile of utilities attained by the concerned agents ([11], Ch. 3).

A welfarist framework for policy evaluation consists of four elements: (1) a group of agents whose interests are being considered; (2) a set of policy options, each of which is characterized by its outcome in terms of factors relevant to the interests of the agents under consideration; (3) a set of agent-specific utility functions, each of which ranks outcomes by assigning to them utilities reflecting how well the interests of the considered agents are being served; and (4) a social welfare function mapping agent utilities to a social ranking of outcomes.

Regionally explicit IAMs effectively implement the welfarist framework, with the agents involved being the countries or regions resolved in the model. The policy options considered in these IAMs act upon different parts of the feedback loop that determines how humans affect the climate and how the climate in turn affects humans. The policy options are expressed in terms of sets of decision variables, which represent different types of action that regions may take to promote their development and to combat climate change. An IAM’s complexity is strongly influenced by the level of detail of the policy options it examines: DP IAMs may specify policy options in terms of technologies in the energy sector or land-use choices, crop types, or cultivation methods in the agriculture sector, whereas BC IAMs may specify them in terms of overall investments in adaptation measures or technologies that reduce greenhouse gas (GHG) emissions. In both types of models, policy options may also describe the economic decisions of regions regarding their levels of investment (saving) and consumption. Regardless of technical differences among individual models, all IAMs eventually translate policy options into their outcomes in terms of the model’s state variables, such as the levels of global warming, climate-related damages, and regional per capita consumption.

Regional per capita consumption is considered a good proxy for the standard of living attained through access to material goods and services. It is commonly used in IAMs as a basis for calculating regional utilities, which provide quantitative representations of the regional interests. How well the interests of region $i$ are served across all possible outcomes is described by its utility function $u_i$, which is usually assumed to be a concave function of regional per capita consumption. Ultimately, each policy outcome $x$ is characterized by its utility profile $u\left(x\right)=\left(u_1\left(x\right),\dots , u_N\left(x\right)\right)$, which is a vector consisting of the utilities $u_i\left(x\right)$ attained by all regions $i=1,\dots , N$. When a considered policy option leads to an outcome $x$ and this outcome leads to a utility profile $u\left(x\right)$, the latter is called attainable.

The last element of the welfarist framework is the social welfare function (SWF). Its purpose is to reconcile the interests of agents striving to improve their interests, as quantified by their utilities, which are bound to clash in a world of limited resources. A SWF generates a social ranking of policy outcomes by applying a certain rule for comparing the utility profiles of outcomes [19,25,26]. This may be a social choice rule such as a bargaining scheme or voting procedure, or a heuristic rule such as the “leximin” rule [11,19,27]. In the context of IAMs, the rule for comparing utility profiles is typically based on an aggregate numerical score defined by a scalar function $g: {ℝ}^N\mapsto ℝ$. An SWF applying such a rule generates a social ranking of outcomes through the following pairwise comparisons: outcome $x$ is socially at least as good as outcome $y$ if and only if $g\left(u\left(x\right)\right)\ge g\left(u\left(y\right)\right)$. The resulting social ranking is conveniently expressed in terms of the social utility function $x\mapsto g\left(u\left(x\right)\right)$, which, for each policy outcome $x$, aggregates the utility profile $u\left(x\right)$ into a numerical score $g\left(u\left(x\right)\right)$. Importantly, a social utility function defines a SWF, but not every SWF can be defined through a social utility function. This highlights that SWFs are providing more general descriptions of social choice than social utility functions, even though IAMs are commonly using the latter.

Not every rule for comparing outcomes defines a welfarist SWF. The social rankings of outcomes generated by a welfarist SWF are commonly required to satisfy three minimal conditions ([19], p. 53): (i) impartiality, which requires that the identity of agents must play no role in comparisons of outcomes; (ii) Pareto indifference, which requires that any two outcomes having the same utility profiles are considered socially as equally good; and (iii) Pareto superiority, which requires that if a change from outcome $y$ to outcome $x$ increases the utility of one or more agents without decreasing the utility of the others, then $x$ is considered socially at least as good as $y$. Indeed, all three conditions are necessary from the welfarist perspective. Impartiality is a basic requirement of any ethical, and thus also of any welfarist, judgement, which must not change when applied to different agents under the same circumstances. Pareto indifference reflects the basic premise of welfarism, namely that the only legitimate yardstick for comparing outcomes are agent utilities. Lastly, Pareto superiority is a logical conclusion of this premise: if all agents in outcome $x$ fare no worse than in outcome $y$ and some of them fare better, then $x$ must not be considered to be worse than $y$.

A ranking of outcomes satisfying the three minimal conditions (i)–(iii) is called a Pareto ordering. Outcomes for which there are no Pareto-superior alternatives are called Pareto-optimal or Pareto-nondominated, and the set of all such outcomes is called the Pareto front. In Pareto-optimal outcomes, i.e., along the Pareto front, no possibility of improving agent utilities is wasted. For this reason, Pareto optimality is often called Pareto efficiency, and from the welfarist standpoint, it is an indispensable property of socially optimal outcomes.

Pareto optimality is also a desirable property from the perspective of outcome fairness. In an outcome that is not Pareto-optimal, some agents are denied the opportunity to increase their utilities, even though doing so would not compromise the interests of other agents: accordingly, the former agents may raise justified objections that they are not treated fairly. Pareto optimality alone is not, however, a sufficient condition of fairness. Indeed, an outcome in which all available resources were spent to maximize the utility of just one agent is Pareto-optimal (as it is not possible to maintain the utility of the best-off agent while increasing the utility of other agents), but it cannot plausibly be presented to worse-off agents as fair. Thus, although Pareto ordering is helpful in identifying outcomes that are not satisfactory from the perspective of outcome fairness (i.e., those not belonging to the Pareto front), it offers no relevant information regarding the fairness of Pareto-optimal outcomes. In fact, according to Pareto ordering, all points on the Pareto front are Pareto-incomparable, which means that the Pareto ordering offers no residual information that could be used for their differential ranking.

Consequently, any fairness-relevant welfarist ranking of outcomes must extend Pareto ordering to allow for the differential ranking of Pareto-optimal outcomes. Such a ranking is called Pareto-inclusive, which means that it agrees with Pareto ordering on all pairs of Pareto-comparable outcomes ([26], p. 30). In this paper, we focus on possibilities for extending Pareto ordering based on outcome comparisons derived with the help of aggregating functions—which can be implemented within the frameworks of existing IAMs. Specifically, we use an aggregating function $g$ to define a social utility function $g\left(u(\cdot )\right)$, which allows for comparing any two outcomes $x$ and $y$ by applying the following rule: $x$ is ranked at least as high as $y$ if and only if $g\left(u\left(x\right)\right)\ge g\left(u\left(y\right)\right)$. The social utility function most used in IAMs is the sum of regional utilities, $g\left(u(\cdot )\right)={{\displaystyle \sum }}_{i=1}^N{u}_i(\cdot )$. As we explain in Section 4, if a social utility function $g\left(u(\cdot )\right)$ is to generate a Pareto-inclusive ranking of outcomes, it is necessary for the aggregating function $g$ to be strictly increasing. Nevertheless, aggregating functions that do not have this property can still be used to extend the Pareto ordering, albeit in a more restricted way. Specifically, if $g$ is not strictly increasing, the social utility function $g\left(u(\cdot )\right)$ can be used as an auxiliary numerical score for comparisons between Pareto-optimal outcomes (even though the most preferable outcome according to the ranking generated by $g\left(u(\cdot )\right)$ need not be Pareto-optimal).

To summarize, the welfarist framework implemented by IAMs is a convenient platform for fairness considerations, and it is possible to build a fairness-relevant welfarist social ranking of outcomes with the help of an aggregating function. A necessary condition for the success of this approach, however, is that the chosen function must aggregate agent utilities in a way that can be presented to them as fair—a requirement we address in the next section.

3. Approaches to Fair Utility Aggregation

The scholarship on normative ethics offers several approaches to constructing a social ranking of outcomes through aggregating agent utilities. In this section, we present a brief overview of these approaches and discuss how they relate to outcome fairness.

Two distinct ways of building aggregation-based social rankings of outcomes can be distinguished, as shown in Figure 1. The first is to use an aggregation reflecting those properties of a utility profile that are deemed to possess an intrinsic moral value and thus are meant to be promoted through the social ranking of outcomes. The second is to use an aggregation operationalizing the notion of the separateness of persons.

The notion of the separateness of persons—which in our present context would more generally and aptly be called the notion of the separateness of agents—requires that, in the process of evaluating the utility profiles describing the outcomes of the considered policies, equal concern is given to the interests of all agents and that, in the conclusion of this process of evaluating, the result can be explained to each agent from the agent’s own perspective ([19], pp. 314–317). We discuss the operationalization of this important notion through utility aggregation later in this section (Section 3.2), but first we turn to the aggregation-based social rankings that reflect intrinsic ethical values of outcomes (Section 3.1).

3.1. Aggregation-Based Social Ranking of Outcomes That Reflect Intrinsic Ethical Values of Outcomes

Historically, the first approach to ranking public policies was utilitarianism, founded by Jeremy Bentham in the late 18^th century. The basic premise of utilitarianism is that the ultimate goal of public policies is to promote the happiness of the members of a society and that each person’s happiness, as measured by their utility, is equally important. Consequently, in the utilitarian view, the sum of agent utilities, in which “all interests count for the same, weighted only by their strength” (i.e., by the potential utility gains) has an intrinsic ethical value ([28], p. 3). Accordingly, the aim of public policies should be to maximize the sum of agent utilities, which is often called the overall or total welfare or utility. Policies that achieve this goal are seen as efficient. Potential inequalities resulting from the maximization of the sum of utilities—which, by construction, is entirely insensitive to the patterns of utility distribution—are not a prime concern from the utilitarian standpoint.

In contrast, the axiological–egalitarian ranking of outcomes focuses on reducing inequalities among agents [28]. The premise of axiological egalitarianism is that all human beings have an equal moral worth and thus an equal entitlement to happiness. On this basis, axiological egalitarianism posits that equality has an intrinsic moral value and that outcomes delivering more equal distributions of utility are thus more desirable. Typically, the level of equality in a utility distribution is measured using an aggregate inequality index (Section 4) that quantifies the ethical value of equality and is used to rank possible outcomes.

An axiological–egalitarian ranking that evaluates all attainable outcomes exclusively in accordance with an aggregate inequality index may be inconsistent with the welfarist framework. Such a ranking evaluates all possible outcomes characterized by the same inequality index as equally good, regardless of how much or how little total utility they deliver to all concerned agents. This may lead to leveling-down effects, through which a more equal Pareto-inferior outcome is ranked higher than a less equal Pareto-superior alternative, which may thus violate the welfarist requirement that social rankings of outcomes must be Pareto-inclusive. Nevertheless, an axiological–egalitarian ranking can be used in a more restricted way that is consistent with the welfarist framework: if applied as an auxiliary ranking restricted to comparisons between Pareto-optimal outcomes, it extends the Pareto ordering and allows the most equitable outcome to be found among those belonging to the Pareto front.

Social rankings of outcomes of the Paretian–egalitarian type balance the egalitarian preference for equality in utility distribution with the utilitarian strive for efficiency [28]. This combined design allows the pitfalls of leveling-down effects—the major downside of axiological–egalitarian rankings—to be avoided. Indeed, if outcome $x$ is Pareto-superior to outcome $y$, total utility is higher in $x$ than in $y$, i.e., $x$ is more efficient than $y$. Now, if both $x$ and $y$ realize the same level of equality in utility distribution, they are equally preferable from the axiological–egalitarian standpoint, but as $x$ is more efficient, it is ranked higher than $y$ by Paretian–egalitarian ranking.

The aforementioned social rankings of outcomes based on utility aggregations that reflect intrinsic ethical values can be plausibly presented as fair in situations in which all considered agents are relatively homogenous, i.e., in which they have similar utility functions and comparable initial levels of utility. In such a setup, outcome fairness comes down to ensuring that equals are treated equally. The utilitarian premise that all utility gains of equal magnitude are equally socially desirable can be interpreted in terms of the equal and impartial treatment of homogenous agents. This argument is even stronger when agent utilities are strictly concave functions of their consumption levels, reflecting the assumption, commonly made in IAMs, that marginal increases in consumption imply diminishing utility returns. Then, realizing the utilitarian goal of maximizing total utility leads to outcomes in which consumption, and consequently utility, is evenly distributed among agents. This, however, is a consequence of the additional assumption of diminishing returns, not a property of utilitarian social rankings, which are, by construction, insensitive to any variations in patterns of utility distribution as long as total utility stays the same. In the axiological–egalitarian and Paretian–egalitarian approaches, all agents are considered to be fundamentally equal and, “by design,” are treated equally.

The argument in support of evaluating outcome fairness through of the aforementioned approaches is weaker, however, when agents differ significantly, e.g., when they have different utility functions, different initial utilities, or unequal opportunities to improve their initial utilities. Then, the utilitarian rule of comparing outcomes, which treats all utility gains of equal magnitude as equally good, disregards any differences among the agents. The egalitarian emphasis on the fundamental equality of agents may have a similar effect. By striving to achieve an even distribution of utility among agents, all of which are assumed to be equally deserving, insufficient attention may be given to existing differences among those agents. Consequently, both aforementioned types of aggregation-based social ranking of outcomes may fail to satisfy the second aspect of outcome fairness, namely that “unequals” are treated in accordance with their relevant differences.

3.2. Aggregation-Based Social Ranking of Outcomes That Operationalize the Separateness of Persons

To be able to convincingly take into account the relevant differences among agents, a social ranking of outcomes must be able to distinguish between the interests of individual agents in the first place. In other words, such a ranking must satisfy the requirements of the so-called separateness of persons: (A) the ranking must give equal and individual attention to the interests of every agent, and (B) it must be possible to explain the ranking to each agent from the agent’s own perspective. The social rankings based on intrinsic ethical values of outcomes we have discussed so far all fail to satisfy both of these requirements. This is because, first, the utilitarian ranking based on the sum of agent utilities allows for a utility loss of one agent to be compensated for by an equal (or greater) gain on the part of another agent—a situation that is clearly difficult to justify from the perspective of the first agent and thus fails to satisfy requirement (B). Second, the egalitarian rankings discussed above fail at requirement (A), as they strive to improve some aggregate inequality index rather than the utility of individual agents. The literature offers three main approaches to constructing social rankings of outcomes that operationalize the notion of the separateness of persons (Figure 1).

Historically, the earliest idea for operationalizing the separateness of persons was based on the concept of original position [8]. Original position is a hypothetical situation in which a group of agents decide on principles that regulate the distribution of utility within their group. To insulate this decision process from existing inequalities and power structures, agents are assumed to make this decision behind a “veil of ignorance,” that is, as if they did not know their social positions, i.e., their initial utilities. Rawls [8] argues that, in the original position, in order to protect themselves from unfavorable outcomes, should they end up at the bottom of the social hierarchy once the social contract is struck and the veil of ignorance is lifted, all agents would agree to the principles of a utility distribution that maximizes the utility of the worst-off among them.

A social ranking that aggregates the utilities of all agents to the level of utility attained by the worst-off agent and evaluates outcomes on that basis is often associated in the literature with Rawls’s approach to the separateness of persons (e.g., [29]). For brevity, we call it the Rawlsian–egalitarian ranking of outcomes. Such ranking indeed operationalizes the notion of the separateness of persons: when assessing the lowest level of utility attained in an outcome, the utility of each agent receives individual attention, which fulfills requirement (A), and ranking outcomes according to the utility of the worst-off agent can be explained to all agents, as this is the principle upon which all have agreed, which fulfills requirement (B). It is important to highlight that a Rawlsian–egalitarian ranking of outcomes may not be Pareto-inclusive when applied to the full set of attainable outcomes. If an outcome $x$ is Pareto-superior to outcome $y$ but the lowest attained utilities are equal in both outcomes, then both outcomes are equally good according to Rawlsian–egalitarian ranking. Thus, similarly to the axiological–egalitarian ranking, the Rawlsian–egalitarian ranking should be applied to comparisons between Pareto-optimal outcomes to ensure its consistency with the welfarist framework.

Rawls’s approach to building social rankings of outcomes is deontological, which means that it is based on principles—in this case, on the principles derived with the help of an argument based on a hypothetical original position [8]. In contrast, the other two ways of operationalizing the separateness of persons—one proposed by Temkin [30] and the other by Nagel [31]—are teleological, which means they are based solely on facts about outcomes, such as how agents fare in relative or absolute terms.

In the view of Temkin, the key feature on which social rankings should focus is how agents fare relative to each other within an outcome [30]. He points out that, within each outcome, certain agents will complain that they are worse-off than other agents because of the policy that has been adopted. On this premise, outcome $x$ is considered socially better than outcome $y$ if $x$ gives rise to fewer complaints than $y$ ([19], p. 328). Establishing a procedure of accounting for the overall level of complaints within an outcome involves three steps: (1) deciding which complaints are legitimate (e.g., in relation to the best-off agent), (2) determining the strengths of these legitimate complaints (e.g., in proportion to utility differences), and (3) aggregating these strengths of legitimate complaints (e.g., adding them up). Such a procedure of building social rankings of outcomes is called a complaints-within-outcome approach, and it operationalizes the separateness of persons. Indeed, in the process of collecting complaints, equal and impartial attention is given to the complaints raised by agents, which fulfills requirement (A), and the resulting social ranking of outcomes can be justified to agents on the basis of their own complaints, which fulfills requirement (B). Importantly, the claims-within-outcome type of social ranking is based on differences between agent utilities. Thus, such rankings may not agree with Pareto ordering, which is based on agent utilities measured in absolute terms. Extending a Pareto ordering through the application of a complaints-within-outcomes ranking restricted to comparisons among Pareto-optimal outcomes is, however, consistent with the welfarist framework.

In contrast to Temkin’s approach, Nagel proposes building social rankings of outcomes based on how agents fare in each outcome relative to how they would fare across all alternative outcomes [31]. He points out that, given two alternative outcomes $x$ and $y$, agents have claims in favor of $x$ over $y$ if they are better-off in $x$ than in $y$. Such a procedure of building social rankings of outcomes is called a claims-across-outcomes approach, which ranks $x$ higher than $y$ if the aggregated claims of all agents in favor of $x$ over $y$ are stronger than those in favor of $y$ over $x$. As the procedure of collecting and aggregating claims is similar to that used in the complaints-within-outcome approach, an analogous argument can be used to justify that the claims-across-outcomes approach implements the separateness of persons, with complaints replaced by claims. Importantly, unlike the Rawlsian–egalitarian and complaints-within-outcome social rankings of outcomes, all rankings following the claims-across-outcomes approach are Pareto-inclusive, and thus they are consistent with the welfarist framework. Indeed, if outcome $x$ is Pareto-superior to outcome $y$, at least some agents are better-off in $x$ than in $y$ and thus have claims in favor of $x$ over $y$. At the same time, no agent has a claim in favor of $y$ over $x$ because none of them fare better in $y$ than in $x$. Consequently, claims in favor of $x$ outweigh claims in favor of $y$, and thus $x$ is considered to be socially better. It is also important to note that claims are properties of pairs of outcomes rather than of individual outcomes and that their strengths depend on comparing absolute agent utilities across such pairs. Depending on how the strengths of claims are determined, different variants of claims-across-outcomes rankings are possible. Here we describe two variants that are dominant in the literature: sufficientism and prioritarianism.

The sufficientist approach is based on the notion that the strengths of claims can be determined only in reference to the so-called compassion threshold defined by the utility that allows a satisfactory life to be lived [32,33]. The sufficientist premise is that doing worse than others does not always mean doing badly in absolute terms. Consequently, “being worse-off than…” loses any ethical significance above the compassion threshold. Accordingly, only the claims of agents below the compassion threshold are of primary importance to the social ranking of outcomes, with improvements to the overall utility of agents above this threshold being of secondary importance.

The prioritarian approach is based on the notion of the diminishing ethical value of marginal improvements to agent utilities [34]. In the prioritarian view, the same absolute utility improvement has a greater ethical value to a worse-off agent than to a better-off agent. Thus, improving the utilities of the worse-off agents should be given priority over improving the utilities of the better-off ones. Accordingly, an agent’s claim is assumed to be stronger the higher its utility improvement and, for the same utility improvement, the lower its initial utility.

The aforementioned three types of social rankings of outcomes based on utility aggregations operationalizing the notion of the separateness of persons can convincingly be presented as “outcome-fair.” First, equal and impartial consideration is given to the utilities of individual agents. This ensures that equals are treated equally and thus fulfills condition (1) of outcome fairness. Second, these rankings are built on appraising the relevant differences among agents, be it in utilities (as in the Rawlsian–egalitarian and complaints-within-outcomes approaches) or in potentials for improving utilities (as in the claims-across-outcomes approach). This ensures that “unequals” are treated in accordance with their relevant differences and thus fulfills condition (2) of outcome fairness.

As mentioned in Section 2, IAMs generate social rankings of outcomes by applying a social utility function $g\left(u(\cdot )\right)$ that enables pairwise comparisons: outcome $x$ is socially at least as good as outcome $y$ if $g\left(u\left(x\right)\right)\ge g\left(u\left(y\right)\right).$ In the next section, we focus on the properties an aggregating function $g$ should have to reflect each of the aforementioned approaches to utility aggregation.

4. Properties and Classification of Fairness-Relevant Aggregating Functions

An array of fairness-relevant properties of aggregating functions can be found in the literature [11,19]. In Section 4.1, we provide a survey of these properties. Importantly, there is no simple, one-to-one mapping between these properties and the approaches to fair utility aggregation described in Section 3. Rather, as we explain in Section 4.2, each of these approaches can be associated with a combination of properties of aggregating functions. These combinations are common, but not defining, features of types of aggregating functions that operationalize the described approaches to fair utility aggregation. They are, however, sufficiently specific to allow us to build a taxonomy of types of aggregating functions that represent the described approaches to fair utility aggregation. We present this taxonomy in Figure 2 and populate it with specific types of aggregating functions that have proven useful in solving multi-objective optimization problems across various fields of science and engineering. Table 1, Table 2, Table 3, Table 4 and Table 5 provide definitions of these types of aggregating functions, highlight their technical details, and discuss how they operationalize fair utility aggregation.

Before proceeding to the survey of the fairness-relevant properties of aggregating functions, we state a condition that is desirable, but not strictly necessary, from the perspective of outcome fairness.

Definition 1.

Ratio-rescaling invariance (RRI): An aggregatingfunction $g$ is ratio-rescaling-invariant if and only if, for any scaling factor $r>0$ and pair of utility profiles $u^{\prime }$ and $u^{″}$,

$$g\left(u^{\prime }\right)\ge g\left(u^{″}\right) \Rightarrow g\left(r{u}^{\prime }\right)\ge g\left(r{u}^{″}\right).$$

(1)

RRI of an aggregating function $g$ means that the social utility function $g\left(u(\cdot )\right)$ generates the same social ranking of outcomes regardless of the choice of the common scale, or unit, according to which agent utilities are measured. This useful feature of the social ranking of outcomes is often called independence of common scale [11].

4.1. Fairness-Relevant Properties of Aggregating Functions

Impartiality is one of the three minimal conditions a welfarist social ranking of outcomes must satisfy, according to condition (i) stated in Section 2. It requires that such a ranking must not be influenced by the identity of agents. In terms of properties of aggregating functions, this condition may be stated as follows.

Definition 2.

Impartiality: An aggregating function $g$ satisfies the condition of impartiality if and only if, for any permutation $\pi$ of the set $\left\{1, \dots , N\right\}$,

$$g\left(u_1, \dots , u_N\right)=g\left(u_{\pi \left(1\right)}, \dots , u_{\pi \left(N\right)}\right).$$

(2)

Permutation invariance of an aggregating function $g$ ensures that the social rank $g\left(u\left(x\right)\right)$ of outcome $x$ depends only on the pattern of agent utilities in $x$ and not on the indices $i=1,\dots ,N$ through which individual agents are identified. This implies that equals, i.e., agents with the same utilities, are treated equally, which fulfills condition (1) of outcome fairness stated in Section 1.

Sensitivity to the patterns of utility distribution within outcomes allows relevant utility differences among agents to be recognized, which, in turn, is a prerequisite for condition (2) of outcome fairness stated in Section 1, which requires “unequals” to be treated according to their relevant differences. The property of an aggregating function implying its sensitivity to patterns of distribution most often encountered in the literature is the Pigou–Dalton condition [11,19,26,29,35].

Definition 3.

Pigou–Dalton (PD) condition: An aggregating function $g$ satisfies the PD condition if and only if

$$g\left(u_1, \dots , u_i-\epsilon , \dots , u_j+\epsilon , \dots ,u_N\right)>g\left(u_1, \dots , u_N\right)$$

(3)

for any $i, j=1, \dots , N$ such that $u_i>u_j$ and any $0<\epsilon <u_i-u_j$.

The PD condition being fulfilled by an aggregating function $g$ means that any transfer of utility from a better-off agent to a worse-off agent increases the value of the social utility function $g\left(u(\cdot )\right)$ as long as the beneficiary of such a transfer does not end up being better-off than its benefactor. Any such transfer of utility, which results in a more even utility distribution while preserving total utility and the relative utility ranking of agents, is called a Pigou–Dalton (PD) transfer. The PD condition can thus be expressed by stating that all PD transfers increase $g\left(u(\cdot )\right)$.

As discussed in Section 3, certain types of aggregation-based social rankings of outcomes (axiological–egalitarian, Rawlsian–egalitarian, and complaints-within-outcome) are prone to leveling-down effects, i.e., to disagreements between the social preferences and interests of all agents. Such disagreements are problematic from the perspective of outcome fairness, which is a question of how agents perceive outcomes. Indeed, if all agents perceive an outcome $x$ to be at least as good as an outcome $y$, i.e., if they attain at least as high a utility in $x$ as in $y$, while some agents fare better in $x$ than in $y$, it is difficult to justify why choosing $y$ over $x$ should be fair or socially more desirable. It is therefore important to recognize that a ranking of outcomes generated by a social utility function $g\left(u(\cdot )\right)$ does not suffer from leveling-down effects if the aggregating function $g$ is strongly increasing.

Definition 4.

Strong increase (SI): An aggregating function $g$ is strongly increasing if and only if $g\left(u^{\prime }\right)>g\left(u^{″}\right)$ whenever $u_i^{\prime }\ge u_i^{″}$ for all $i=1,\dots , N$ and $u_j^{\prime }>u_j^{″}$ for some $j=1,\dots ,N$.

The SI property of an aggregating function $g$ implies that the ranking of outcomes generated by the social utility function $g\left(u(\cdot )\right)$ is Pareto-inclusive. Indeed, if outcome $x$ is Pareto-superior to outcome $y$, i.e., if $u_i\left(x\right)\ge u_i\left(y\right)$ for all $i=1,\dots ,N$ and $u_j\left(x\right)>u_j\left(y\right)$ for some $j=1,\dots N$, then $g\left(u\left(x\right)\right)>g\left(u\left(y\right)\right)$, and $x$ is thus socially more desirable than $y$. Consequently, the outcome deemed the most socially desirable according to such a ranking must be Pareto-optimal.

Another property enhancing the perception of agents of being treated fairly is the possibility of demonstrating to each of them that their individual interests contribute to the formation of the social ranking of outcomes without being entangled or confused with the interests of other agents. A social ranking of outcomes generated by a social utility function $g\left(u(\cdot )\right)$ has this property if the aggregating function $g$ is additive.

Definition 5.

Additivity: An aggregating function $g$ is additive if and only if it is of the form $g\left(u\right)={{\displaystyle \sum }}_{i=1}^N{h}_i\left(u\right)$.

For each $i=1,\dots ,N$, the function $h_i(\cdot )$ describes how the interests of agent $i$ contribute to the social ranking generated by $g\left(u(\cdot )\right)$. Importantly, this contribution may depend not only on the utility attained by agent $i$ but also on other information contained in the utility profile $u$, e.g., on how well agent $i$ fares in comparison to other agents.

The latter dependence may lead to situations in which the interests of agent $i$ are served equally well in two outcomes $x$ and $y$, i.e., $u_i\left(x\right)=u_i\left(y\right)$, but the contributions of its interests to the social rankings of $x$ and $y$ differ, i.e., $h_i\left(u\left(x\right)\right)\ne h_i\left(u\left(y\right)\right)$, due to differences in the utilities of other agents. The following tighter property of separability, which implies additivity and is not to be confused with the separateness of persons, is sufficient to prevent such effects.

Definition 6.

Separability: An aggregating function $g$ is separable if and only if it is of the form $g\left(u\right)={{\displaystyle \sum }}_{i=1}^{N}h\left(u_i\right)$, where $h$ is an increasing function.

Separability of an aggregating function $g$ implies that the ranking of outcomes generated by the social utility function $g\left(u(\cdot )\right)$ is independent of unconcerned agents ([11], p. 67), i.e., the social ranks generated by $g\left(u\left(x\right)\right)$ and $g\left(u\left(y\right)\right)$ for outcomes $x$ and $y$ are not influenced by agents whose utilities do not change when $x$ is changed to $y$, since $u_i\left(x\right)=u_i\left(y\right)$ implies $h\left(u_i\left(x\right)\right)=h\left(u_i\left(y\right)\right)$.

4.2. Classification of Fairness-Relevant Aggregating Functions

The fairness-relevant properties of an aggregating function $g$ imply certain features of the ranking of outcomes generated by the social utility function $g\left(u(\cdot )\right)$, which we discuss in this subsection. For each approach to the aggregation-based social ranking of outcomes described in Section 3, some of the properties of aggregating functions described in Section 4 are strictly required, while others are too strong or unnecessary. Thus, with each of the approaches discussed in Section 3 we can associate a collection of properties described in Section 4.1. 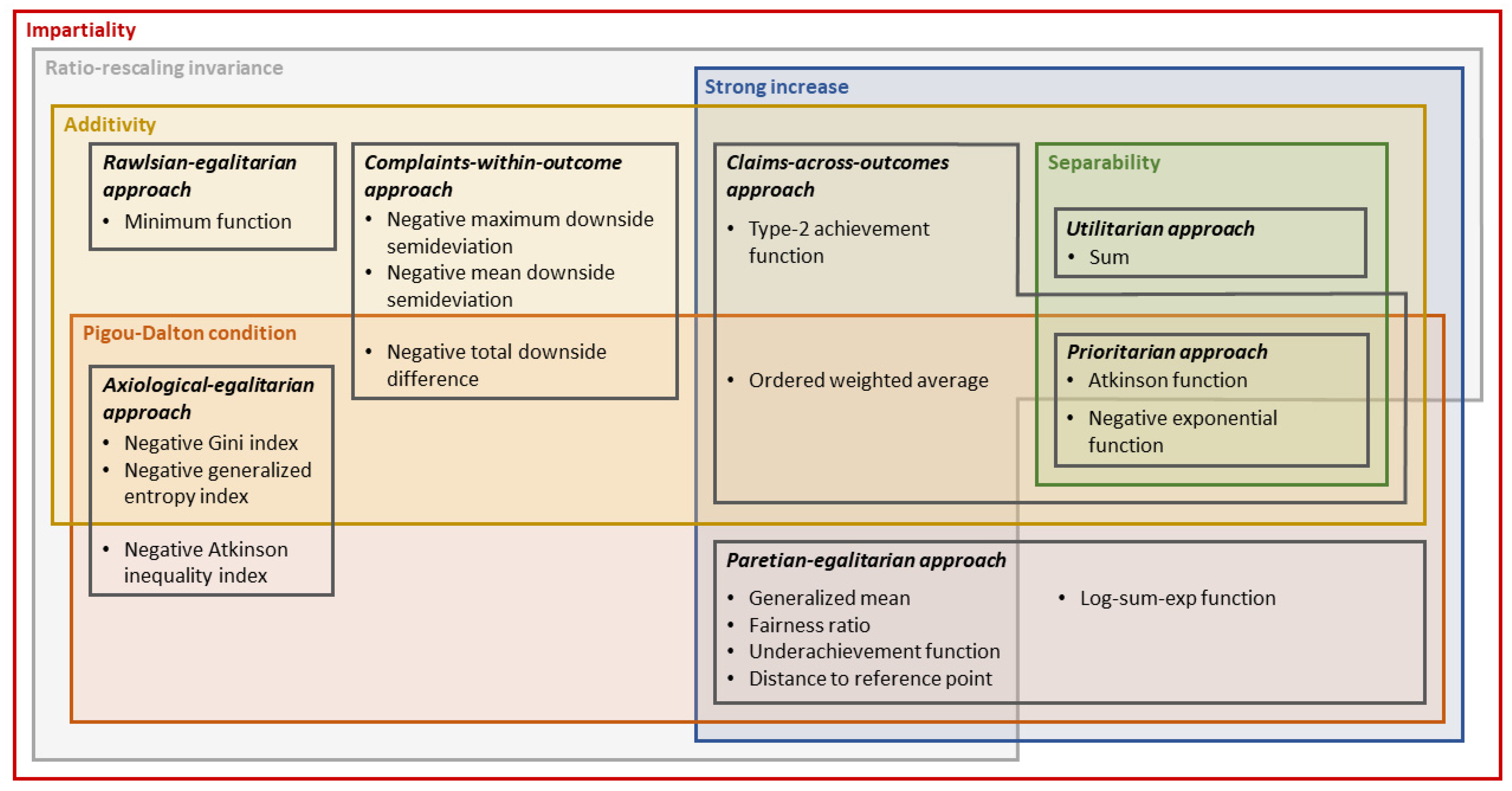These collections of properties are specific enough for a taxonomy of aggregating functions to be built, which we present in Figure 2. Moreover, in Table 1, Table 2, Table 3, Table 4 and Table 5, we provide an overview of several useful types of aggregating functions together with information on their fairness-relevant properties and on how they can be associated with the approaches described in Section 3.

Figure 2. Taxonomy of fairness -relevant aggregating functions. Boxes outlined in color (with bold labels) indicate fairness-relevant properties of aggregating functions described in Section 4.1. Boxes outlined in black (with italic labels) indicate approaches to utility aggregation described in Section 3 and shown in Figure 1. Notice that the sufficientist approach is not included here since it cannot be operationalized with a single aggregating function Bullet points (with regular labels) indicate exemplary types of aggregating functions described in Section 4.2. Function types shown within an approach can be associated with that approach. Approaches shown within a property can be associated with function types possessing that property. Accordingly, approaches can be characterized by the collections of properties within which they are shown. Formulas and details specifying the shown exemplary types of aggregating functions are provided in Table 1, Table 2, Table 3, Table 4 and Table 5. Notice that, for consistency with Figure 1, the sum, representing the utilitarian approach, is shown here as part of the presented taxonomy. This helps to place the shown fairness-relevant aggregating functions in relation to the sum of agent utilities, which is commonly used in IAMs. However, the sum itself is not a fairness-relevant aggregating function. As discussed in Section 3, the utilitarian approach, represented by the sum of agent utilities, has serious deficiencies from the perspective of outcome fairness.

Figure 2. Taxonomy of fairness -relevant aggregating functions. Boxes outlined in color (with bold labels) indicate fairness-relevant properties of aggregating functions described in Section 4.1. Boxes outlined in black (with italic labels) indicate approaches to utility aggregation described in Section 3 and shown in Figure 1. Notice that the sufficientist approach is not included here since it cannot be operationalized with a single aggregating function Bullet points (with regular labels) indicate exemplary types of aggregating functions described in Section 4.2. Function types shown within an approach can be associated with that approach. Approaches shown within a property can be associated with function types possessing that property. Accordingly, approaches can be characterized by the collections of properties within which they are shown. Formulas and details specifying the shown exemplary types of aggregating functions are provided in Table 1, Table 2, Table 3, Table 4 and Table 5. Notice that, for consistency with Figure 1, the sum, representing the utilitarian approach, is shown here as part of the presented taxonomy. This helps to place the shown fairness-relevant aggregating functions in relation to the sum of agent utilities, which is commonly used in IAMs. However, the sum itself is not a fairness-relevant aggregating function. As discussed in Section 3, the utilitarian approach, represented by the sum of agent utilities, has serious deficiencies from the perspective of outcome fairness.

Impartiality is a property inherent to all approaches to utility aggregation described in Section 3. Approaches that reflect certain intrinsic ethical values of outcomes are impartial because these values exist independently of any particular group of agents and their identities and because the moral judgements based on these values do not change when applied to another group of agents with different identities experiencing the same circumstances. Impartiality is also one of the requirements of the separateness of persons, which calls for equal and individual attention to be given to the interests of all agents according to condition (i) for the separateness of persons as stated in Section 3. Consequently, approaches to operationalizing the notion of the separateness of persons are impartial. Thus, all aggregating functions implementing any of the approaches to utility aggregation described in Section 3 satisfy the condition of impartiality.

The PD condition is often interpreted in the literature as an aversion to inequality ([11], p. 67). It is also one of the defining features of aggregate inequality measures. Because the reduction of inequalities in utility distribution is the sole objective of axiological–egalitarian social rankings of outcomes, various types of inequality measures can be used to define social utility functions that generate this type of ranking. Importantly, values of any aggregate inequality measure are bounded from below by zero, and this lower bound is attained for utility profiles which are perfectly equitable, and thus also socially most desirable in the axiological-egalitarian ranking. Therefore, to be consistent with the convention applied throughout this paper that a social utility function $g\left(u(\cdot )\right)$ takes higher values for socially more desirable outcomes, aggregating functions g we associate with the axiological–egalitarian approach are defined as negatives of inequality measures. Examples of types of such aggregating functions are presented in Table 1. The selection of inequality measures used there is not exhaustive but contains the most popular options.

Table 1. Examples of types of aggregating functions that can be associated with the axiological–egalitarian approach.

Type of Function	Properties	Comments and References
Negative Gini index $g\left(u\right)=-\frac{{{\displaystyle \sum }}_{i=1}^N{{\displaystyle \sum }}_{j=1}^N\left|u_i-u_j\right|}{2N{{\displaystyle \sum }}_{j=1}^N{u}_j}$	RRI, Impartiality, PD, Additivity	Gini index can be interpreted geometrically as the ratio between the area under the Lorenz curve of the utility profile $u$ (given by the cumulative utility of the $k$ worst-off agents as a function of $k=1,\dots , N)$ and the area under the Lorenz curve representing a perfectly equal distribution (given by the 45° line). Reference: [36].
Negative generalized entropy index $g_{\alpha }\left(u\right)=\{\begin{array}{ll} \frac{1}{N}{\displaystyle \sum _{i=1}^N}\ln \frac{u_i}{\mu \left(u\right)}\hfill & \mathrm{for} \alpha =0\hfill \\ -\frac{1}{N}{\displaystyle \sum _{i=1}^N}\frac{u_i}{\mu \left(u\right)}\ln \frac{u_i}{\mu \left(u\right)}\hfill & \mathrm{for} \alpha =1\hfill \\ \frac{-1}{N\alpha \left(\alpha -1\right)}{\displaystyle \sum _{i=1}^N}\left({\left(\frac{u_i}{\mu \left(u\right)}\right)}^{\alpha }-1\right)\hfill & \mathrm{for} \alpha \ne 0, 1\hfill \end{array}$ where $\mu \left(u\right)=\frac{1}{N}{{\displaystyle \sum }}_{i=1}^N{u}_i$	RRI, Impartiality, PD, Additivity	The parameter $-\infty \le \alpha \le \infty$ determines the sensitivity to changes in different segments of the utility profile: lower values imply higher sensitivity to changes in the lower tail of the utility profile, while higher values imply higher sensitivity to changes in the upper tail. Special cases: $g_0(\cdot )$ is the mean log deviation or Theil $L$ index $g_1(\cdot )$ is the Theil $T$ index, and $g_2(\cdot )$ is half the squared coefficient of variation. Reference: [37].
Negative Atkinson inequality index $I_{\gamma }\left(u\right)=\{\begin{array}{ll}\left(\frac{N}{{{\displaystyle \sum }}_{i=1}^N{u}_i}\right){\left({\displaystyle \prod _{i=1}^N}{u}_i\right)}^{\frac{1}{N}}-1\hfill & \mathrm{for} \gamma =1\hfill \\ \left(\frac{N}{{{\displaystyle \sum }}_{i=1}^N{u}_i}\right){\left(\frac{{{\displaystyle \sum }}_{i=1}^N{u}_i^{1-\gamma }}{N}\right)}^{\frac{1}{1-\gamma }}-1\hfill & \mathrm{for} \gamma \ne 1, \gamma \ge 0\hfill \end{array}$	RRI, Impartiality, PD	The parameter $0\le \gamma \le \infty$ determines the social aversion to inequality, with $\gamma =0$ corresponding to no aversion and $\gamma =\infty$ to infinite aversion. The utility profile that maximizes this function may be neither unique nor Pareto-optimal. References: [19,38].

Table 1. Examples of types of aggregating functions that can be associated with the axiological–egalitarian approach.

Type of Function	Properties	Comments and References
Negative Gini index $g\left(u\right)=-\frac{{{\displaystyle \sum }}_{i=1}^N{{\displaystyle \sum }}_{j=1}^N\left|u_i-u_j\right|}{2N{{\displaystyle \sum }}_{j=1}^N{u}_j}$	RRI, Impartiality, PD, Additivity	Gini index can be interpreted geometrically as the ratio between the area under the Lorenz curve of the utility profile $u$ (given by the cumulative utility of the $k$ worst-off agents as a function of $k=1,\dots , N)$ and the area under the Lorenz curve representing a perfectly equal distribution (given by the 45° line). Reference: [36].
Negative generalized entropy index $g_{\alpha }\left(u\right)=\{\begin{array}{ll} \frac{1}{N}{\displaystyle \sum _{i=1}^N}\ln \frac{u_i}{\mu \left(u\right)}\hfill & \mathrm{for} \alpha =0\hfill \\ -\frac{1}{N}{\displaystyle \sum _{i=1}^N}\frac{u_i}{\mu \left(u\right)}\ln \frac{u_i}{\mu \left(u\right)}\hfill & \mathrm{for} \alpha =1\hfill \\ \frac{-1}{N\alpha \left(\alpha -1\right)}{\displaystyle \sum _{i=1}^N}\left({\left(\frac{u_i}{\mu \left(u\right)}\right)}^{\alpha }-1\right)\hfill & \mathrm{for} \alpha \ne 0, 1\hfill \end{array}$ where $\mu \left(u\right)=\frac{1}{N}{{\displaystyle \sum }}_{i=1}^N{u}_i$	RRI, Impartiality, PD, Additivity	The parameter $-\infty \le \alpha \le \infty$ determines the sensitivity to changes in different segments of the utility profile: lower values imply higher sensitivity to changes in the lower tail of the utility profile, while higher values imply higher sensitivity to changes in the upper tail. Special cases: $g_0(\cdot )$ is the mean log deviation or Theil $L$ index $g_1(\cdot )$ is the Theil $T$ index, and $g_2(\cdot )$ is half the squared coefficient of variation. Reference: [37].
Negative Atkinson inequality index $I_{\gamma }\left(u\right)=\{\begin{array}{ll}\left(\frac{N}{{{\displaystyle \sum }}_{i=1}^N{u}_i}\right){\left({\displaystyle \prod _{i=1}^N}{u}_i\right)}^{\frac{1}{N}}-1\hfill & \mathrm{for} \gamma =1\hfill \\ \left(\frac{N}{{{\displaystyle \sum }}_{i=1}^N{u}_i}\right){\left(\frac{{{\displaystyle \sum }}_{i=1}^N{u}_i^{1-\gamma }}{N}\right)}^{\frac{1}{1-\gamma }}-1\hfill & \mathrm{for} \gamma \ne 1, \gamma \ge 0\hfill \end{array}$	RRI, Impartiality, PD	The parameter $0\le \gamma \le \infty$ determines the social aversion to inequality, with $\gamma =0$ corresponding to no aversion and $\gamma =\infty$ to infinite aversion. The utility profile that maximizes this function may be neither unique nor Pareto-optimal. References: [19,38].

Strong increase (SI) is a necessary condition for a social utility function to generate a Pareto-inclusive ranking of outcomes. SI also implies that such a ranking gives preference to outcomes that are overall more efficient, in the sense that they deliver a higher total utility. Indeed, if outcome $x$ is Pareto-superior to outcome $y$, i.e., if $u_i\left(x\right)\ge u_i\left(y\right)$ for all $i=1, \dots , N$ and $u_j\left(x\right)\ge u_j\left(y\right)$ for some $1\le j\le N$, then ${{\displaystyle \sum }}_{i=1}^N{u}_i\left(x\right)>{{\displaystyle \sum }}_{i=1}^N{u}_i\left(y\right)$. Consequently, if an aggregating function $g$ satisfies both the PD and the SI conditions, the social utility function $g\left(u(\cdot )\right)$ generates a ranking of outcomes that balances social preferences for equality (according to the PD condition) and for efficiency (according to the SI condition). Thus, aggregating functions possessing both the PD and the SI properties can be associated with the Paretian–egalitarian approach to building aggregation-based social rankings of outcomes. Examples of types of aggregating functions we can associate with the Paretian–egalitarian approach are presented in Table 2. While these types of functions satisfy only the PD and the SI conditions, other types that additionally are additive or separable can also be considered as realizing the Paretian–egalitarian approach. Accounting for these additional properties, however, we associate such functions with other approaches to building aggregation-based social rankings of outcomes, as shown in Figure 2.

Table 2. Examples of types of aggregating functions that can be associated with the Paretian–egalitarian approach.

Type of Function	Properties	Comments and References
Generalized mean $g_p\left(u\right)=\{\begin{array}{ll}{\left(\frac{1}{N}{\displaystyle {\displaystyle \sum }_{i=1}^N}{u}_i^p\right)}^{1/p}\hfill & \mathrm{for} p\ne 0\hfill \\ {\left({\displaystyle {\displaystyle \prod }_{i=1}^N}{u}_i\right)}^{1/N}\hfill & \mathrm{for} p=0\hfill \end{array}$	RRI, Impartiality, PD (for $p<1)$, SI	The parameter $-\infty \le p\le 1$ determines the trade-off between equality (egalitarianism for $p=-\infty$) and efficiency (utilitarianism for $p=1$). For $p>1$, this function is convex and does not satisfy the PD condition. For $p=0$, this function is the Nth root of the exponent of the Nash social welfare function, maximization of which by a utility profile $u$ yields the solution to the Nash bargaining problem [39,40]. Maximization of this function with parameter $p$ is equivalent to maximization of the Atkinson function (Table 5) with parameter $\gamma =1-p$. Reference: [41].
Fairness ratio $g\left(u\right)=\underset{1\le i\le N}{\min }\frac{{\overline{\theta }}_i\left(u\right)}{P_i^{*}}$ where ${\overline{\theta }}_i\left(u\right)={{\displaystyle \sum }}_{k=1}^i{u}_{\left(k\right)}$ for $i=1,\dots ,N$, $u_{\left(k\right)}$ is the $k$th-smallest element of u, $P_i^{*}=\underset{u\in \mathcal{U}}{\max }{\overline{\theta }}_i\left(u\right)$ for $i=1,\dots ,N$, and $\mathcal{U}$ is the set of all attainable utility profiles $u$	RRI, Impartiality, PD, SI	Maximization of this function leads to the most even distribution of agent utilities with respect to their maximal attainable utilities. A utility profile that maximizes this function is Lorenz-nondominated. Reference: [35].
Underachievement function $g_{\alpha }\left(u\right)=\mu \left(u\right)-\alpha \rho \left(u\right)$ where $\mu \left(u\right)=\frac{1}{N}{{\displaystyle \sum }}_{i=1}^N{u}_i$ and $\rho \left(u\right)$ is an inequality measure	RRI, Impartiality, PD, SI	As a mixture of the average utility $\mu \left(u\right)$ and an inequality measure $\rho \left(u\right)$, this function explicitly represents a Paretian–egalitarian trade-off between efficiency and equality. The parameter $0<\alpha <{\overline{\alpha }}_{\rho }$ determines the balance in this trade-off, with smaller values of $\alpha$ favoring efficiency and larger values of $\alpha$ favoring equality. The upper bound ${\overline{\alpha }}_{\rho }$ depends on the choice of the inequality measure $\rho \left(u\right)$. For $\alpha \ge {\overline{\alpha }}_{\rho }$ this function may not satisfy the PD or SI conditions. References: [29,42].
Distance to reference point $g_{p,z}\left(u\right)=-{\left({\displaystyle \sum _{i=1}^N}{\left|u_i-A\right|}^p\right)}^{1/p}$	RRI, Impartiality, PD, SI	The parameter $A<\infty$ determines an aspiration level for agent utilities, although it may potentially be unattainable for some or all agents. The parameter $1\le p\le \infty$ determines the type of distance, which also determines the trade-off between equality (egalitarianism for $p=\infty$) and efficiency (utilitarianism for $p=1$). Reference: [43].
Log-sum-exp function $g\left(u\right)=-\ln \left({\displaystyle \sum _{i=1}^N}{e}^{-u_i} \right)$	Impartiality, PD, SI	This function is also known as “soft min”, as its value is predominantly determined by the smallest element of the utility profile. This function generates a social ranking of outcomes that is close in spirit to Rawlsian–egalitarian ranking, but which is also Pareto-inclusive. Reference: [44].

Table 2. Examples of types of aggregating functions that can be associated with the Paretian–egalitarian approach.

Type of Function	Properties	Comments and References
Generalized mean $g_p\left(u\right)=\{\begin{array}{ll}{\left(\frac{1}{N}{\displaystyle {\displaystyle \sum }_{i=1}^N}{u}_i^p\right)}^{1/p}\hfill & \mathrm{for} p\ne 0\hfill \\ {\left({\displaystyle {\displaystyle \prod }_{i=1}^N}{u}_i\right)}^{1/N}\hfill & \mathrm{for} p=0\hfill \end{array}$	RRI, Impartiality, PD (for $p<1)$, SI	The parameter $-\infty \le p\le 1$ determines the trade-off between equality (egalitarianism for $p=-\infty$) and efficiency (utilitarianism for $p=1$). For $p>1$, this function is convex and does not satisfy the PD condition. For $p=0$, this function is the Nth root of the exponent of the Nash social welfare function, maximization of which by a utility profile $u$ yields the solution to the Nash bargaining problem [39,40]. Maximization of this function with parameter $p$ is equivalent to maximization of the Atkinson function (Table 5) with parameter $\gamma =1-p$. Reference: [41].
Fairness ratio $g\left(u\right)=\underset{1\le i\le N}{\min }\frac{{\overline{\theta }}_i\left(u\right)}{P_i^{*}}$ where ${\overline{\theta }}_i\left(u\right)={{\displaystyle \sum }}_{k=1}^i{u}_{\left(k\right)}$ for $i=1,\dots ,N$, $u_{\left(k\right)}$ is the $k$th-smallest element of u, $P_i^{*}=\underset{u\in \mathcal{U}}{\max }{\overline{\theta }}_i\left(u\right)$ for $i=1,\dots ,N$, and $\mathcal{U}$ is the set of all attainable utility profiles $u$	RRI, Impartiality, PD, SI	Maximization of this function leads to the most even distribution of agent utilities with respect to their maximal attainable utilities. A utility profile that maximizes this function is Lorenz-nondominated. Reference: [35].
Underachievement function $g_{\alpha }\left(u\right)=\mu \left(u\right)-\alpha \rho \left(u\right)$ where $\mu \left(u\right)=\frac{1}{N}{{\displaystyle \sum }}_{i=1}^N{u}_i$ and $\rho \left(u\right)$ is an inequality measure	RRI, Impartiality, PD, SI	As a mixture of the average utility $\mu \left(u\right)$ and an inequality measure $\rho \left(u\right)$, this function explicitly represents a Paretian–egalitarian trade-off between efficiency and equality. The parameter $0<\alpha <{\overline{\alpha }}_{\rho }$ determines the balance in this trade-off, with smaller values of $\alpha$ favoring efficiency and larger values of $\alpha$ favoring equality. The upper bound ${\overline{\alpha }}_{\rho }$ depends on the choice of the inequality measure $\rho \left(u\right)$. For $\alpha \ge {\overline{\alpha }}_{\rho }$ this function may not satisfy the PD or SI conditions. References: [29,42].
Distance to reference point $g_{p,z}\left(u\right)=-{\left({\displaystyle \sum _{i=1}^N}{\left|u_i-A\right|}^p\right)}^{1/p}$	RRI, Impartiality, PD, SI	The parameter $A<\infty$ determines an aspiration level for agent utilities, although it may potentially be unattainable for some or all agents. The parameter $1\le p\le \infty$ determines the type of distance, which also determines the trade-off between equality (egalitarianism for $p=\infty$) and efficiency (utilitarianism for $p=1$). Reference: [43].
Log-sum-exp function $g\left(u\right)=-\ln \left({\displaystyle \sum _{i=1}^N}{e}^{-u_i} \right)$	Impartiality, PD, SI	This function is also known as “soft min”, as its value is predominantly determined by the smallest element of the utility profile. This function generates a social ranking of outcomes that is close in spirit to Rawlsian–egalitarian ranking, but which is also Pareto-inclusive. Reference: [44].

Additivity is an indispensable but not a defining feature of aggregating functions associated with approaches to utility aggregation that operationalize the notion of the separateness of persons. Indeed, some inequality measures representing the axiological–egalitarian approach as well as the utilitarian total utility are additive (Figure 2). In the context of the separateness of persons, however, an additive form of the aggregating function makes it possible to demonstrate to each agent not only that their interests have received individual consideration but also how they have influenced the social ranking of outcomes, which fulfills conditions (i) and (ii) of the separateness of agents in Section 3.

Rawls’s idea for operationalizing the separateness of persons is based on the concept of original position in which all agents agree to act in a way that benefits the worst-off one among them. Accordingly, in the Rawlsian–egalitarian approach, the utility of each agent is considered individually; however, it determines the social rank of an outcome only if it is the lowest utility attained in that outcome. Formally, the contribution of the interests of agent $i$ to the Rawlsian–egalitarian rank of outcome $x$ can be expressed as $h_i\left(u\left(x\right)\right)=u_i\left(x\right){\delta }_{ij}$, where $j={\mathrm{argmin}}_{i=1,\dots ,N}{u}_i\left(x\right)$ is the index of the agent with the lowest utility in the utility profile $u\left(x\right)$ and ${\delta }_{ij}$ is the Kronecker delta, which equals 1 for $i=j$ and 0 otherwise. The social rank of $x$ can then be generated by an additive aggregating function $g\left(u\left(x\right)\right)={{\displaystyle \sum }}_{i=1}^N{h}_i\left(u\left(x\right)\right)={\min }_{i=1,\dots ,N}{u}_i\left(x\right)$. Thus, we can associate the minimum function with the Rawlsian–egalitarian approach to building a social ranking of outcomes (Table 3).

Table 3. Example of an aggregating function that can be associated with the Rawlsian–egalitarian approach.

Type of Function	Properties	Comments and References
Minimum function $g\left(u\right)=\underset{i=1,\dots ,N}{\min }{u}_i$	RRI, Impartiality, Additivity	The utility profile that maximizes this function may be neither unique nor Pareto-optimal. References: [19,26].

Table 3. Example of an aggregating function that can be associated with the Rawlsian–egalitarian approach.

Type of Function	Properties	Comments and References
Minimum function $g\left(u\right)=\underset{i=1,\dots ,N}{\min }{u}_i$	RRI, Impartiality, Additivity	The utility profile that maximizes this function may be neither unique nor Pareto-optimal. References: [19,26].

In the complaints-within-outcome approach to operationalizing the separateness of persons, an outcome is considered socially more desirable if it gives rise to fewer complaints among all agents. The additive form of the social utility function $g\left(u(\cdot )\right)=-{{\displaystyle \sum }}_{i=1}^N{h}_i\left(u(\cdot )\right)$ representing such social preferences has a natural interpretation. For each outcome $x$, the value $h_i\left(u\left(x\right)\right)$ represents the strength of the complaint agent $i$ may have regarding outcome $x$ together with the weight given to agent $i$’s complaint. Different choices can be made regarding what constitutes a legitimate basis for complaints. For instance, an agent may have a complaint regarding outcome $x$ if its utility $u_i\left(x\right)$ is lower than the average utility among agents realized in $x$. Alternatively, an agent may have a complaint against all agents who are better-off within outcome $x$ or against the best-off agent. The weight given to a complaint depends on a decision on how complaints are to be aggregated. For example, in the case of a summative rule, all complaints have equal weights, e.g., a weight of 1. If all complaints are collapsed into the single strongest complaint, all weaker complaints receive a weight of 0. Examples of types of additive aggregating functions we can associate with the complaints-within-outcome approach are presented in Table 4.

Table 4. Examples of types of aggregating functions that can be associated with the complaints-within-outcome approach.

Type of Function	Properties	Comments and References
Negative maximum downside semideviation $g\left(u\right)=\underset{i=1,\dots ,N}{-\max }\left(\mu \left(u\right)-u_i\right)$ where $\mu \left(u\right)=\frac{1}{\mathrm{N}}{{\displaystyle \sum }}_{i=1}^N{u}_i$	RRI, Impartiality, Additivity	Complaints are formulated by each agent in reference to the average utility within an outcome and are aggregated by selecting the one complaint with the highest strength. References: [29,42].
Negative mean downside semideviation $g\left(u\right)=-\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\left(\mu \left(u\right)-u_i\right)}_{+}$ where $\mu \left(u\right)=\frac{1}{\mathrm{N}}{{\displaystyle \sum }}_{i=1}^N{u}_i$ and ${(\cdot )}_{+}=\max \left(\cdot , 0\right)$	RRI, Impartiality, Additivity	Complaints are formulated by each agent in reference to the average utility within an outcome and are aggregated by averaging the strengths of all positive complaints. References: [29,42].
Negative total downside difference $g\left(u\right)=-{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1,j\ne i}^N}{\left(u_j-u_i\right)}_{+}$ where ${(\cdot )}_{+}=\max \left(\cdot , 0\right)$	RRI, Impartiality, PD, Additivity	Complaints are formulated by each agent in reference to the utilities of all better-off agents and are aggregated by summing their strengths.

Table 4. Examples of types of aggregating functions that can be associated with the complaints-within-outcome approach.

Type of Function	Properties	Comments and References
Negative maximum downside semideviation $g\left(u\right)=\underset{i=1,\dots ,N}{-\max }\left(\mu \left(u\right)-u_i\right)$ where $\mu \left(u\right)=\frac{1}{\mathrm{N}}{{\displaystyle \sum }}_{i=1}^N{u}_i$	RRI, Impartiality, Additivity	Complaints are formulated by each agent in reference to the average utility within an outcome and are aggregated by selecting the one complaint with the highest strength. References: [29,42].
Negative mean downside semideviation $g\left(u\right)=-\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\left(\mu \left(u\right)-u_i\right)}_{+}$ where $\mu \left(u\right)=\frac{1}{\mathrm{N}}{{\displaystyle \sum }}_{i=1}^N{u}_i$ and ${(\cdot )}_{+}=\max \left(\cdot , 0\right)$	RRI, Impartiality, Additivity	Complaints are formulated by each agent in reference to the average utility within an outcome and are aggregated by averaging the strengths of all positive complaints. References: [29,42].
Negative total downside difference $g\left(u\right)=-{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1,j\ne i}^N}{\left(u_j-u_i\right)}_{+}$ where ${(\cdot )}_{+}=\max \left(\cdot , 0\right)$	RRI, Impartiality, PD, Additivity	Complaints are formulated by each agent in reference to the utilities of all better-off agents and are aggregated by summing their strengths.

In the claims-across-outcomes approach to operationalizing the separateness of persons, a social ranking of outcomes is built on pairwise comparisons: outcome $x$ is considered socially more desirable than outcome $y$ if the claims of agents in favor of $x$ over $y$ outweigh the claims in favor of $y$ over $x$. If the social utility function $g\left(u(\cdot )\right)$ is additive, then the balance of claims in favor of $x$ and claims in favor of $y$ is conveniently expressed by the difference $g\left(u\left(x\right)\right)-g\left(y\left(y\right)\right)={{\displaystyle \sum }}_{i=1}^N\left(h_i\left(u\left(x\right)\right)-h_i\left(u\left(y\right)\right)\right)$, where the value $h_i\left(u\left(x\right)\right)-h_i\left(u\left(y\right)\right)$ is interpreted, if positive, as the strength of the claim of agent $i$ in favor of $x$ over $y$ and, if negative, as the strength of the claim of agent $i$ in favor of $y$ over $x$. What distinguishes additive aggregating functions that can be associated with the claims-across-outcomes approach from aggregating functions that can be associated with the Rawlsian–egalitarian and complaints-within-outcome approaches is the SI property. Indeed, as explained in Section 3, any social ranking of outcomes based on a claims-across-outcomes approach is Pareto-inclusive, while rankings of the other two types may disagree with Pareto ordering, and the SI property of an aggregating function $g$ ensures that the social utility function $g\left(u(\cdot )\right)$ generates a Pareto-inclusive ranking of outcomes. Examples of types of additives and strictly increasing aggregating functions we can associate with the claims-across-outcomes approach are presented in Table 5.

Table 5. Examples of types of aggregating functions that can be associated with the claims-across-outcomes approach. Notice that the sufficientist approach is not included here since it cannot be operationalized with a single aggregating function.

Type of Function	Properties	Comments and References
Type-2 achievement function $g_{\alpha , A}\left(u\right)=\underset{1\le i\le N}{\min }\left(u_i-A\right)+\alpha {\displaystyle \sum _{i=1}^N}(u_i-A)$	RRI, Impartiality, SI, Additivity	The parameter $A<\infty$ determines an aspiration level for agent utilities, in relation which to agents are formulating their claims, although it may potentially be unattainable for some or all agents. To keep inequality in check, a preferential relative weight of $1+1/\alpha$ is given to the claim of the worst-off agent. References: [45,46].
Ordered weighted average (OWA) $g_w\left(u\right)={\displaystyle \sum _{i=1}^N}{w}_i{u}_{\left(i\right)}$ where $w_1>w_2>\dots >w_N>0$ and $u_{\left(i\right)}$ is the ith-smallest element of $u$	RRI, Impartiality, PD, SI, Additivity	This function represents a claims-across-outcomes approach in which the strength of an agent’s claim is determined by their utility multiplied by a weight depending on the position of their utility in the ordered utility profile. The parameter $w=\left(w_1,\dots ,w_N\right)$ with ${{\displaystyle \sum }}_{i=1}^N{w}_i=1$ is a vector of decreasing weights $w_1>w_2>\dots >w_N>0$ determining how decreasing priority is given to the utilities of better-off agents. In some definitions of OWA functions, the weights $w_1,\dots ,w_N$ must belong to the interval $\left[0, 1\right]$, need not be positive, and/or need not be arranged in a strictly decreasing sequence. However, OWA functions with some weights equal to zero fail to satisfy the SI condition, while OWA functions with weights not arranged in a strictly decreasing sequence fail to satisfy the PD condition. Reference: [47].
Atkinson function $g_{\gamma }\left(u\right)={\displaystyle \sum _{i=1}^N}{h}_{\gamma }\left(u_i\right)$ where $h_{\gamma }\left(u_i\right)=\{\begin{array}{ll}\ln u_i\hfill & \mathrm{for} \gamma =1\hfill \\ {\left(1-\gamma \right)}^{-1}{u}_i^{1-\gamma }\hfill & \mathrm{for} \gamma \ne 1, \gamma >0\hfill \end{array}$	RRI, Impartiality, PD, SI, Additivity, Separability	This function is a prioritarian aggregating function. The parameter $\gamma$ determines the tolerable degree of losses involved in utility transfers from better-off to worse-off agents. For $\gamma =1$, this function is the Nash social welfare function, maximization of which by a utility profile $u$ yields the solution to the Nash bargaining problem [39,40]. References: [11,19,48].
Negative exponential function $g\left(u\right)=-{\displaystyle \sum _{i=1}^N}{e}^{-u_i}$	Impartiality, PD, SI, Additivity, Separability	This function is a prioritarian aggregating function giving a very high strength to the claim of the worst-off agent. This function is particularly sensitive to small utility values, with sensitivity quickly diminishing for larger utility values. Reference: [19].

Table 5. Examples of types of aggregating functions that can be associated with the claims-across-outcomes approach. Notice that the sufficientist approach is not included here since it cannot be operationalized with a single aggregating function.

Type of Function	Properties	Comments and References
Type-2 achievement function $g_{\alpha , A}\left(u\right)=\underset{1\le i\le N}{\min }\left(u_i-A\right)+\alpha {\displaystyle \sum _{i=1}^N}(u_i-A)$	RRI, Impartiality, SI, Additivity	The parameter $A<\infty$ determines an aspiration level for agent utilities, in relation which to agents are formulating their claims, although it may potentially be unattainable for some or all agents. To keep inequality in check, a preferential relative weight of $1+1/\alpha$ is given to the claim of the worst-off agent. References: [45,46].
Ordered weighted average (OWA) $g_w\left(u\right)={\displaystyle \sum _{i=1}^N}{w}_i{u}_{\left(i\right)}$ where $w_1>w_2>\dots >w_N>0$ and $u_{\left(i\right)}$ is the ith-smallest element of $u$	RRI, Impartiality, PD, SI, Additivity	This function represents a claims-across-outcomes approach in which the strength of an agent’s claim is determined by their utility multiplied by a weight depending on the position of their utility in the ordered utility profile. The parameter $w=\left(w_1,\dots ,w_N\right)$ with ${{\displaystyle \sum }}_{i=1}^N{w}_i=1$ is a vector of decreasing weights $w_1>w_2>\dots >w_N>0$ determining how decreasing priority is given to the utilities of better-off agents. In some definitions of OWA functions, the weights $w_1,\dots ,w_N$ must belong to the interval $\left[0, 1\right]$, need not be positive, and/or need not be arranged in a strictly decreasing sequence. However, OWA functions with some weights equal to zero fail to satisfy the SI condition, while OWA functions with weights not arranged in a strictly decreasing sequence fail to satisfy the PD condition. Reference: [47].
Atkinson function $g_{\gamma }\left(u\right)={\displaystyle \sum _{i=1}^N}{h}_{\gamma }\left(u_i\right)$ where $h_{\gamma }\left(u_i\right)=\{\begin{array}{ll}\ln u_i\hfill & \mathrm{for} \gamma =1\hfill \\ {\left(1-\gamma \right)}^{-1}{u}_i^{1-\gamma }\hfill & \mathrm{for} \gamma \ne 1, \gamma >0\hfill \end{array}$	RRI, Impartiality, PD, SI, Additivity, Separability	This function is a prioritarian aggregating function. The parameter $\gamma$ determines the tolerable degree of losses involved in utility transfers from better-off to worse-off agents. For $\gamma =1$, this function is the Nash social welfare function, maximization of which by a utility profile $u$ yields the solution to the Nash bargaining problem [39,40]. References: [11,19,48].
Negative exponential function $g\left(u\right)=-{\displaystyle \sum _{i=1}^N}{e}^{-u_i}$	Impartiality, PD, SI, Additivity, Separability	This function is a prioritarian aggregating function giving a very high strength to the claim of the worst-off agent. This function is particularly sensitive to small utility values, with sensitivity quickly diminishing for larger utility values. Reference: [19].

As mentioned above, if a social utility function is of the additive form $g\left(u(\cdot )\right)={{\displaystyle \sum }}_{i=1}^N{h}_i\left(u(\cdot )\right)$, the strength of the claim of agent $i$ in favor of $x$ over $y$ is given by the value $h_i\left(u\left(x\right)\right)-h_i\left(u\left(y\right)\right)$, with negative values quantifying the strength of claims in the opposite direction. In this general form, the strength of agent $i$’s claim may depend not only on the utilities agent $i$ attains in $x$ and y but also on the utilities attained by other agents. For instance, when the social utility function is given by an OWA function (Table 5), the strength of each agent’s claim depends both on its utility in the considered outcome and on how well it fares relative to the other agents. This may lead to situations in which an agent has the same basis for two claims in favor of outcomes $x$ and $x\prime$ over an alternative outcome $y$ because $u_i\left(x\right)=u_i\left(x^{\prime }\right)$ but in which the strengths of these two claims differ because of differences in the utilities attained by other agents in $x$ and $x\prime$. Consequently, a ranking of outcomes generated by an additive social utility function in its general form may be shaped not only by the utilities of agents who make claims but also by social preferences for certain properties of outcomes considered to have intrinsic ethical value, e.g., equality of utility distribution.

Promoting values other than the utility of agents is, however, contrary to the premise of both the sufficientist and the prioritarian approaches to operationalizing the separateness of persons, namely that the strength of the claim of any agent should be a function of that agent’s utility alone. Thus, any aggregating function we can associate with these two approaches must be separable. Indeed, if a social utility function is to be impartial, SI, and of additive form $g\left(u(\cdot )\right)={{\displaystyle \sum }}_{i=1}^N{h}_i\left(u_i(\cdot )\right)$, it follows that $h_1=\dots =h_N=h$, where $h$ is a strictly increasing function.

The sufficientist ranking of outcomes is based on a two-tier system of primary and secondary claims defined in relation to a reference utility $C$, called the compassion threshold. Each agent is entitled to a primary claim for one of the alternative outcomes $x$ and $y$ over the other if, in at least one of these outcomes, the agent’s utility falls below the compassion threshold $C$—and the farther below this threshold it falls, the stronger the agent’s claim is considered to be. Thus, the strength of the primary claim of agent $i$ for $x$ over $y$ is given by the difference $h\left(\min \left(u_i\left(x\right), C\right)\right)-h\left(\min \left(u_i\left(y\right), C\right)\right)$, where $h(\cdot )$ is a strictly increasing and strictly concave function. The total strength of primary claims of all agents for $x$ over $y$ is given by $g_{\mathrm{p}}\left(x\right)-g_{\mathrm{p}}\left(y\right)$, where $g_{\mathrm{p}}(\cdot )={{\displaystyle \sum }}_{i=1}^{N}h\left(\min \left(u_i(\cdot ), C\right)\right)$ is the primary outcome score of separable form. In the sufficientist ranking, the outcome $x$ is preferred over $y$ if and only if $g_{\mathrm{p}}\left(x\right)>g_{\mathrm{p}}\left(y\right)$. When $g_{\mathrm{p}}\left(x\right)=g_{\mathrm{p}}\left(y\right)$, each agent with a utility above the compassion threshold is entitled to a secondary claim for resolving the tie. The strength of the secondary claim of agent $i$ for $x$ over $y$ is given by the difference $\max \left(u_i\left(x\right),C\right)-\max \left(u_i\left(y\right), C\right)$, and the total strength of secondary claims for $x$ over $y$ is given by $g_{\mathrm{s}}\left(x\right)-g_{\mathrm{s}}\left(y\right)$, where $g_{\mathrm{s}}(\cdot )={{\displaystyle \sum }}_{i=1}^N\max \left(u_i(\cdot ), C\right)$ is the secondary outcome score. The tie is resolved in favor of $x$ if and only if $g_{\mathrm{s}}\left(x\right)>g_{\mathrm{s}}\left(y\right)$, i.e., if $x$ delivers a higher total utility than $y$ to agents with utilities above the compassion threshold. To summarize, the sufficientist ranking of outcomes is generated not by a single social utility function but by a pair of separable outcome scores: the primary outcome score $g_{\mathrm{p}}(\cdot )$, which is a type of prioritarian aggregating function (discussed below), applied to utility profiles truncated above the compassion threshold and the secondary outcome score $g_{\mathrm{s}}(\cdot )$, which is the utilitarian aggregating function, applied to utility profiles truncated below the compassion threshold. Note that the primary outcome score $g_{\mathrm{p}}(\cdot )$ alone may not agree with the Pareto ranking for outcomes in which some agents attain utilities higher than the compassion threshold, but that in such cases the secondary outcome score $g_{\mathrm{s}}(\cdot )$ ensures the Pareto inclusiveness of the sufficientist ranking. Since the sufficientist ranking of outcomes cannot be operationalized with a single aggregating function (it requires two functions $g_{\mathrm{p}}$ and $g_{\mathrm{s}}$ to be applied in a lexicographic order), this approach is omitted from Figure 2 and Table 5.

The core premise of the prioritarian ranking of outcomes is that improving the utilities of agents with low utilities is ethically more important than improving the utilities of agents with high utilities. Accordingly, in the prioritarian approach, the strength of the claim of agent $i$ for an outcome $x$ over an alternative outcome $y$ is given by the difference $h\left(u_i\left(x\right)\right)-h\left(u_i\left(y\right)\right)$, where $h$ is a strictly increasing and strictly concave function. Then, the total strength of claims among all agents $i=1,\dots ,N$ in favor of $x$ over $y$ can be expressed as ${{\displaystyle \sum }}_{i=1}^N\left(h\left(u_i\left(x\right)\right)-h\left(u_i\left(y\right)\right)\right)=g\left(u\left(x\right)\right)-g\left(u\left(y\right)\right)$, where $g\left(u(\cdot )\right)={{\displaystyle \sum }}_{i=1}^{N}h\left(u_i(\cdot )\right)$ and negative values quantify the strength of claims in the opposite direction. Outcome $x$ is preferred in the prioritarian ranking over outcome $y$ if the total strength of claims for $x$ outweigh the total strength of claims for $y$, i.e., if $g\left(u\left(x\right)\right)>g\left(u\left(y\right)\right)$. Thus, we can associate a separable aggregating function $g\left(u\right)={{\displaystyle \sum }}_{i=1}^{N}h\left(u_i\right)$ with the prioritarian approach because it defines a social utility function $g\left(u(\cdot )\right)={{\displaystyle \sum }}_{i=1}^{N}h\left(u_i(\cdot )\right)$ that generates a prioritarian ranking of outcomes.

The prioritarian aggregating function $g\left(u\right)={{\displaystyle \sum }}_{i=1}^{N}h\left(u_i\right)$ has several convenient properties that have important interpretations. As $h(\cdot )$ is strictly increasing, $g(\cdot )$ has the SI property, thus ensuring that the social utility function $g\left(u(\cdot )\right)$ generates a Pareto-inclusive ranking of outcomes. Moreover, the permutation invariance of $g(\cdot )$ and the strict concavity of $h(\cdot )$ imply that $g(\cdot )$ is Schur-concave and thus has the PD property. Consequently, whenever it is possible to reduce the utility of a better-off agent by a given amount and transfer it to a worse-off agent without losses and without reversing the utility ranking of the agents involved in the transfer, the resultant utility profile is always preferred in the prioritarian ranking over the original utility profile. Such loss-free transfers are not always possible, e.g., due to the shape of the set of attainable utility profiles; thus, making the distribution of utility among agents more equal may come at the price of reducing total utility. The prioritarian ranking generated by the social utility function $g\left(u(\cdot )\right)={{\displaystyle \sum }}_{i=1}^{N}h\left(u_i(\cdot )\right)$ allows specifying how much of total utility can be forfeited for attaining a higher equality of the utility distribution, or, conversely, how high an increase in inequality can be accepted for improving efficiency, i.e., total utility. Indeed, it can be shown that for any prioritarian aggregating function $g$ there exists an inequality measure $I_g$ such that the ranking based on the following rule—outcome $x$ is at least as socially preferred as outcome $y$ if $\left(1-I_g\left(u\left(x\right)\right)\right){{\displaystyle \sum }}_{i=1}^N{u}_i\left(x\right)\ge \left(1-I_g\left(u\left(y\right)\right)\right){{\displaystyle \sum }}_{i=1}^N{u}_i\left(y\right)$—is equivalent to prioritarian ranking, which based on the following rule—$x$ is socially at least as good as $y$ if $g\left(u\left(x\right)\right)\ge g\left(u\left(y\right)\right)$ ([19], p. 120).

If, in addition to the properties discussed above, the prioritarian aggregating function $g\left(u\right)={{\displaystyle \sum }}_{i=1}^{N}h\left(u_i\right)$ also has the RRI property, it can be shown that it then must belong to the class of so-called Atkinson functions, which are presented in Table 5 ([11], p. 68). The shape parameter $\gamma >0$ of the Atkinson function $g_{\gamma }$ can be interpreted as the “marginal rate of moral substitution”, which quantifies the critical tolerable loss in transfers of utility from better-off to worse-off agents ([19], p. 385). The parameter $\gamma$ can thus also be understood to quantify the degree of “inequality aversion.” Indeed, it can be shown that the ranking of outcomes generated by the social utility function $g_{\gamma }\left(u(\cdot )\right)$ is equivalent to the ranking generated by the social utility function $\left(1+I_{\gamma }\left(u(\cdot )\right)\right){{\displaystyle \sum }}_{i=1}^N{u}_i(\cdot )$, where $I_{\gamma }$ is the negative Atkinson inequality index (Table 1) with the inequality aversion parameter $\gamma$ ([19], p. 121).

5. Discussion

In Section 2, we have made a case for IAMs being a convenient framework for exploring questions of fairness of climate mitigation and adaptation policies. In Section 3, we have described various approaches to building fairness-relevant social rankings of outcomes that can be used for this purpose. In Section 4, we have proposed specific types of aggregating functions that can be associated with those approaches. What remains to be considered is the practical feasibility of employing these aggregating functions as replacements for objective functions used in existing IAMs.

Typically, regionally explicit IAMs are set up to solve the problem of maximizing the sum of the present values of regional utilities over a certain time horizon $T\mathsf{\Delta }t$. The time interval from 0 until $T\mathsf{\Delta }t$ is divided into a number of shorter time periods $\mathsf{\Delta }t$, e.g., with durations of 5 or 10 years, indexed by $t=1,\dots ,T$. At the beginning of each period $t$, a decision $d_t$ is made about the values of control variables represented in the model, which typically include determinants of consumption (affecting the utility of regions within period $t)$ and savings (invested in capital stocks affecting the utility of regions at times after period $t$). Technically, this problem can be expressed as ${\max }_{d_t, 1\le t\le T}{{\displaystyle \sum }}_{t=1}^T{{\displaystyle \sum }}_{i=1}^N{u}_{i,t}{R}_t$ subject to certain constraints (representing, e.g., the availability of assets and/or the dynamics of capital accumulation and depreciation), where $u_{i,t}$ is the utility of region $i$ in period $t$ (affected by the vector of control variables $d_t$ and state variables of the model in period $t$, with the latter typically including capital stocks and the level of global warming) and $R_t$ is a social discount factor.

This formulation, in which decisions $d_t$ are made with “perfect foresight” (i.e., taking into account actions planned for all future periods) can be found in IAMs such as RICE [14] and AD-RICE [15]. There are also “myopic” IMAs (e.g., [49]), in which decisions are optimized in the short term, planning for only a few periods ahead. In any case, maximizing the discounted sum of regional utilities within a certain time horizon requires optimal values of control variables to be chosen at once for all regions and for all periods. This computationally difficult problem is usually solved efficiently through the use of dynamic optimization techniques, which reformulate multi-period optimization problem in terms of a series of consecutive single-period optimization steps (see, e.g., [50], Ch. 6). The same dynamic programming methods can be applied to solve maximization problems of the more general form ${\max }_{d_t, 1\le t\le T}{{\displaystyle \sum }}_{t=1}^{T}g\left(u_{1, t},\dots ,u_{N,t}\right)R_t$, provided the aggregation function $g$ is strongly increasing and concave.

Consequently, for any Paretian–egalitarian or prioritarian aggregating function $g$ (which must be permutation invariant, SI, and PD, and thus also concave; Figure 2), existing IAMs can readily solve the problem ${\max }_{d_t, 1\le t\le T}{{\displaystyle \sum }}_{t=1}^{T}g\left(u_{1, t},\dots ,u_{N,t}\right)R_t.$ The resulting optimal outcome—characterized by the utilities $u_{i,t}$ of all regions across all periods—is Pareto-optimal. Moreover, it can be presented as fair to each region in each period.

While intragenerational fairness across regions is determined by the aggregating function $g$, intergenerational fairness across periods is determined by the social discounting factor $R_t$. Discounting the utilities of future generations does, however, raise numerous concerns from methodological, ethical, and intergenerational fairness perspectives [51]. The complex and hotly debated issue of intergenerational fairness is, in its full breadth, beyond the scope of this paper.

Nevertheless, the approaches to building social rankings of outcomes in IAMs and associated aggregating functions we have considered for addressing intragenerational outcome fairness across regions could conceivably be applied also for addressing intergenerational outcome fairness across periods. Such an application could help moving beyond the controversies involved in choosing and using specific social discount factors. One may, for instance, aggregate the utilities $u_{i,t}$ attained by the regions $i=1,\dots ,N$ in the periods $t=1,\dots ,T$ into a temporally aggregated utility $U_i=g_i\left(u_{i,1}, \dots , u_{i,T}\right)$, where $g_i$ is a fairness-relevant nondecreasing aggregating function that is reflective of how the region $i$ values the interests of its present and future inhabitants. This is a simple operation that does not involve changes to the setup of existing IAMs.

Finding an optimal policy resulting in a distribution of utility that is satisfactory from the perspectives of both interregional and intergenerational fairness may, however, require the optimization problem solved by the model to be redefined. In general, the problem can be formulated, using an appropriate fairness-relevant aggregating function $g$, as ${\max }_{d_t, 1\le t\le T}g\left(U_1,\dots , U_N\right)$ subject to the same model constraints as in the problem of maximizing the discounted sum of regional utilities solved in existing IAMs.

Depending on the form of the function $g$, to solve this new maximization problem, one may use either dynamic optimization methods already implemented in IAMs or other standard optimization algorithms that would take advantage of the fact that $g$ is a concave scalar-valued function of a vector-valued argument—in this case, of a vector $d=(d_1,\dots ,d_T)$ representing the concatenated decision vectors $d_t$ for periods $1\le t\le T$.

The choice of the specific method for solving the problem ${\max }_{d_t, 1\le t\le T}g\left(U_1,\dots , U_N\right)$ depends on whether the fairness-relevant aggregating function $g$ is strongly increasing or not. If $g$ is strongly increasing, the profile of temporally aggregated utilities $\left(U_1,\dots , U_N\right)$ that maximizes this function is Pareto-optimal, as required by both welfarist and fairness perspectives. If $g$ is not strongly increasing, its maximization may result in an outcome that is not Pareto-optimal. In this case, to ensure Pareto optimality, $g$ should be maximized only over the set of Pareto-optimal outcomes, i.e., over the Pareto front. In practice, it is rarely possible to describe the Pareto front analytically, but it can be efficiently mapped using multi-objective optimization techniques or genetic algorithms [46,52]. Once the Pareto front is mapped by a sufficiently dense set of Pareto-optimal outcomes, $g$ can be evaluated for each of them, and the outcome with the highest value of $g$ can be picked as a Pareto-optimal solution to the problem ${\max }_{d_t, 1\le t\le T}g\left(U_1,\dots , U_N\right)$.

6. Conclusions

In this paper, we have provided guidelines for using integrated assessment models (IAMs) as tools for identifying optimal climate change mitigation and adaptation policies that could be presented to multiple regions as fair. We have built a rationale for using the welfarist framework of IAMs for addressing questions of outcome fairness, and we have presented a theoretical framework of different utility-aggregation approaches for generating welfarist rankings of policy outcomes that could be presented to multiple regions as fair. Finally, we have discussed how these fairness-relevant approaches to selecting optimal policies can be operationalized within existing and future IAMs through the suitable choice of their objective function and have proposed a selection of aggregating functions that would be appropriate for this purpose.

Importantly, the optimal climate policies resulting from maximizing aggregating functions in an IAM can be presented as fair only to the regions represented in the model, and there is no guarantee that any of these policies would be unanimously accepted as fair by all regions. Nevertheless, application of various fairness-relevant aggregating functions as objective functions maximized within IAMs may improve our understanding of how fair climate policies look like and which policies cannot plausibly be contemplated as being fair in any sense. In future research, it will be promising to use fairness-relevant aggregating functions to better understand properties of “plausibly fair” Pareto-optimal outcomes of climate policies.