A New Cooperative Game—Theoretic Approach for Customer-Owned Energy Storage

Abstract

The increasing demand for energy storage systems (ESSs) alongside the continuous enhancements to storage technology have been of great positive impact on the electric grid. Their unceasing development has been driven by the need to accommodate increased penetration of renewable energy resources and defer capital investments, among other benefits. Moreover, ESSs have played a key role in the grid’s ability to cope with its ever-shifting load profiles, resulting in large economic gain for ESS owners. For this reason, this prospective study was designed to investigate privately-owned energy storage hubs (ESHs) and their interactions with potential customers as well as with the electric grid. This research examined two contrasting interaction approaches for customer-owned stationary energy storage hubs: a cooperative and a non-cooperative game-theoretic approach. The goal of the cooperative technique is to conduce to a correlated equilibrium increasing the social welfare of all players involved using a regret matching algorithm. On the other hand, in the non-cooperative approach, modeled as an ascending price-clinching auction, each player acts greedily, maximizing only their individual welfare. Implementing both case studies resulted in important insights into ESH players’ interactions and provided contrasting methods of modeling their behaviors. Finally, depending on the application at hand, the choice of one approach may be more realistic than the other.

1. Introduction

The advancements made in smart grid technologies over the past few years have paved the way for numerous different developments in the power and energy industry. These include an increase in the dispatch of renewable energy resources. With this increased renewable penetration, several problems arise due to the intermittent nature of these resources. Furthermore, with the continuous growth in the world population, the constant changes in global weather conditions, and the increase in electricity-dependent technologies ranging from small home appliances to electric vehicles, the electricity demand has also grown [1]. The issues presented above put additional strain on the current electrical system. Therefore, they must be addressed. For this reason, electric grid operators and consumers have explored ways to reduce or regulate electricity consumption, thereby extending the life of the power distribution system and delaying the need for expensive expansions. As a result, energy storage has received a lot of attention as a potential beneficial solution due to its countless advantages, continuous innovation, and increased availability with time.

As discussed above, the interest in energy storage has been on the rise. The sales of energy storage technologies sales have increased exponentially throughout the last decade, while their prices have dropped significantly [2]. Due to these promising trends alongside the advantageous nature of energy storage technologies, such as their ability to reduce peak loads, aid with voltage and frequency regulation, improve networks’ hosting capacities, and much more, numerous business owners are currently studying the energy storage market and looking to enter it. Additionally, a growing number of electric grids worldwide are now considering shutting down their peaking power plants (the third and highest level of power plants, also the most expensive and environmentally destructive) and replacing them with energy storage devices [3]. However, to shut down these plants, the grids must be able to supply their peak loads from elsewhere; otherwise, the whole system would be unbalanced, leading to failure and possibly a cascaded blackout. Hence, in order to lower the reliance on peaking power plants, the electric grids need to either acquire energy storage systems or become customers of energy storage suppliers.

All the aforementioned aspects have led researchers to delve into the idea of developing a hub composed of numerous energy storage devices of varying capacities that provide energy services to a range of customers due to the diversity of energy storage and its relevance. Investments in energy storage hubs, allocation, and pricing strategies, as well as determining the optimal energy mix are drawing a lot of attention. Several works have tackled the energy storage problem from an optimization perspective [4,5,6]. In [4], the authors solved the optimization problem using a similar decoupled form (SDF) approach, while in [5] and [6], the hub’s structural and operational linear optimization was tackled to understand the energy hubs. While optimization approaches are quite practical and advantageous, their major limitation is their inability to model and analyze situations with interdependence and interactions amongst players. For this reason, game-theoretic approaches are the prime candidate in energy storage hub analysis as well as in multiple other fields due to their superior ability to model competition, interdependence, conflicts of interest, and more [7,8,9,10].

Game-theoretic approaches have been significant in modeling real-life decision making as shown in [11,12,13,14,15]. The construction and waste management industry developed an evolutionary game to study the decision-making process of producing and recycling items under the government’s reward-penalty mechanism, as shown in [11]. Due to its strengths, evolutionary game theory was also utilized by the authors in [12]. While the work in [11] discussed that the government may be able to effectively stimulate the growth of the construction and demolition wastes’ reproduction market if it actively increases government rewards, punishments, and subsidies, corporate leadership was first introduced in [12], hence enriching the decision making process. Additionally, the applications of game theory are widespread across other industries such as cybersecurity [13], economics [10], supply chain [14], and political disputes [15], among others.

Game-theoretic approaches have also proven quite beneficial in the energy industry specifically [16,17,18,19]. In [18], the authors studied a scenario where two business owners who own the same energy storage technology want to enter the market together and attempt to develop a decision mechanism concerning who will participate in the energy market and who will participate in the ancillary service market. This can be modeled as a simple competition game and the results were found. The aforementioned approach would be valuable to study multiple energy storage hub owners attempting to enter the electricity market; however, when studying one storage hub, its development, and its consumers and interactions, optimization problems and competing strategies would be impractical as the interaction of the players would not be as straightforward.

Other forms of interaction are discussed in the literature. The authors in [17] studied coalitions of homes as well as the grid, and how they interact with each other, i.e., how the grid prices energy while the homes purchase it. This was modeled as a Stackelberg game. The Stackelberg game was also utilized in [19] to develop renewable subsidization strategies as well as to optimize the multi-energy system design. Finally, in [16], the authors discussed that the energy market could hypothetically be modeled using a Vickrey-Clarke-Groves (VCG) auction model, though no methodology was presented. Hence, it is apparent that the energy storage problem is of interest to researchers for multiple reasons and is being resolved using multiple methodologies. However, the interactions of the ESH owners with their consumers have not been studied. For this reason, the main focus of this work was to model the interactions of an energy storage hub, to model methodologies through which the users can interact with the hub, energy allocation techniques, and, finally, pricing techniques.

There exists a lot of potential for energy storage problems to be modeled using several game-theoretic approaches; however, it is unclear which one is best. Hence, in this work, two approaches were used: the first approach is a cooperative one that strives to achieve a correlated equilibrium with the help of a regret matching algorithm, and the second is the clinching-auction approach. The former cooperative approach has been used in several works such as [20] and in the demand side management context in the power industry; however, it has not been used in energy storage discussion as per the authors’ knowledge. Cooperative games are a set of games that aim to achieve a common benefit or maximize the social welfare of all players as studied in [21], while non-cooperative games involve players with greedier tendencies of improving their personal benefit.

This work did not aim to conclude whether the cooperative or the non-cooperative modeling is superior; rather, the aim was to observe how both approaches behave and which one could be further expanded on depending on the application for which it is intended. Both cooperative and non-cooperative techniques have been extensively utilized in the literature and proved countless times, though never in the context of energy storage, particularly in the context of developing a stationary energy storage hub. Finally, when modeling problems in a game-theoretic framework, the development of utility functions is a crucial step in ensuring the practicality of the problem at hand. Due to the limited availability of research carried out on energy storage, particularly hub design, utility functions have not been developed in the literature to accurately describe the behavior of an energy seller and their customers. For the scope of this paper, it was assumed that a business owner (the ESH owner) has developed a stationary energy hub, with a predetermined energy mix and a predetermined capacity. The hub has three categories of consumers: the electric grid, residential consumers, and industrial consumers, each with their unique needs and behaviors. A regret matching algorithm, which is a cooperative approach, was first applied followed by a non-cooperative interaction approach modeled as an ascending price-clinching auction. To the authors’ knowledge, the modeling of the interactions between an energy storage hub’s owner and its customers has never been studied.

Hence, the contributions of this work can be summarized as follows:

• Building a fundamental game with multiple energy storage technologies which can be easily expanded and adapted. In this game, multiple modes of operation were modeled: normal and emergency conditions. The players’ utility functions to reflect their satisfaction level with the outcomes were also developed for each player, ensuring that they were not modeled in a simplified linear structure, but rather the risk-averse human nature was considered in the modeling of utility functions. Additionally, the utility functions were modeled for each mode, normal and emergency, considering realistic consequences that each player would face under emergency circumstances and their realistic response to these conditions.
• Studying a cooperative and non-cooperative approach for the energy storage hub problem. While energy storage hubs are a unique concept, the main focus is usually energy allocation modeled as optimization problems. However, the interaction of the owner with the consumers in a realistic manner has not been tackled in the literature. The cooperative approach applied was the regret matching algorithm, which allowed for the improvement of the social welfare of every player involved in the game. Additionally, the non-cooperative approach utilized was the ascending price-clinching auction. Both methodologies produced pricing schemes as well as decisions on which consumers’ needs will be served by the hub.

The rest of this paper is organized as follows: Section 2 discusses the modeling of the problem. Section 3 and Section 4 entail an in-depth explanation of the cooperative and the non-cooperative approaches respectively. These are followed by the case study results and discussion in Section 5, and this topic is then concluded in Section 6.

2. Game Model

As mentioned earlier, this work aimed to study the behavior of energy hub owners and customers as realistically as possible using a game-theoretic approach. We describe the game’s setup in this section.

2.1. System Overview

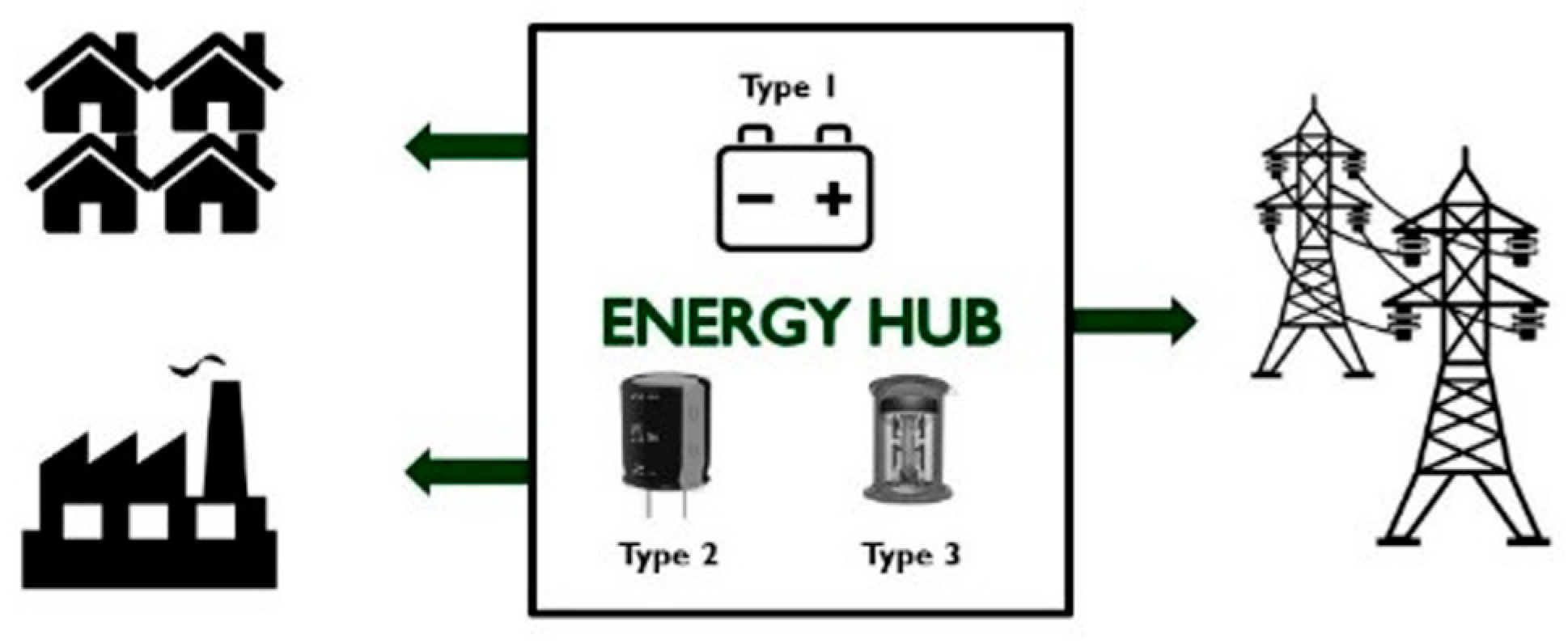
In this work, the energy storage hub was modeled as a collection of three different types of energy storage technologies: batteries, supercapacitors (SCs), and flywheels, each with unique electrical characteristics such as charge and discharge time, capacity, and ramp rate. Batteries, for example, are characterized by low power density but a high energy density, while supercapacitors are the reverse. Thus, batteries, SCs, and flywheels each respond to a specific consumer need because of their complementary qualities. An overall view of the system can be seen in Figure 1.

In this model, each customer has one of three energy needs: reducing peak demand, power quality improvement, and, finally, voltage regulation. Consumers may have additional requirements, while the hub may host far more technologies, but this model can easily be expanded on.

An energy storage management platform (ESMP) is assumed to enable communications between all end-users and the grid, as well as between all end-users and the ESH. In order for the game to begin, consumers must submit their forecasted energy needs for the next 24 h to the ESMP (day before) for an internal optimization problem to determine the optimal charging schedule of the energy storage technologies to incur minimal costs while meeting the predicted demand for the following day. Once that is done, the consumer’s needs during the day may differ from their forecasted needs. Consumers were penalized if their consumption changed drastically; however, if they change within acceptable limits, they must inform the hub every time the system’s power flow is calculated and optimized. This system is run in hourly time slots; hence, every hour, a game is played to determine how the energy hub and its users will behave. Two very different approaches are considered in the coming sections, each yielding interesting results.

2.2. Players and Actions

As discussed above, in this game, two types of players were defined: the hub’s owner and the hub’s customers. The hub’s customers could then be classified into three major groups: the electric grid, aggregated residential customers, and industrial customers, where each group behaves differently and has unique energy storage requirements. Accordingly, energy need i is modeled by energy type i, with i = 1,2,3. As a further clarification, this means that there are three possible energy demands and three possible energy sources to meet those demands. Due to the scope of this work, no matching algorithm is provided to match each need with the appropriate technology, hence the aforementioned assumption. Lastly, j refers to the player number in this work, where player 1 is the hub owner, 2 is the grid, 3 is the residential customer, and 4 is the industrial customer. In summary, the energy hub has a single owner and three major consumer categories which will be discussed in further depth in the remainder of this section (the electric grid, residential customers, and industrial customers).

2.2.1. Energy Hub Owner

The owner of the hub, as the energy seller, has one major responsibility: to determine the cents per kilo-Watt hour (c/kWh) price for every type of energy sold. Therefore, they make a determination: ${\mathrm{p}}_{\mathrm{i}}$, which is the price in cents of 1 kilowatt-hour of energy resource type $\mathrm{i}$. The goal of this player is to maximize profit.

2.2.2. Energy Hub Customers: The Electric Grid

In this work, the electric grid operates in two modes. Firstly, there is the normal mode of operation, in which the grid operator requests energy from the ESH to improve voltage profiles, reduce renewable curtailment, or serve any other standard purpose that enhances the current system. A failure to obtain the full amount of energy requested would not lead to system collapse; it would simply result in higher operational costs.

The second possible mode of operation is the emergency mode. This mode is crucial for distribution networks since it involves service restoration. After an interruption, a self-healing distribution network would need to identify the fault and then restore service. Our study does not cover the fault identification process or restoration details, as our objective was to model the need to restore service in terms of an energy request. Promptly restoring service is a crucial part of enhancing the resilience of distribution networks, so the operator’s energy requests under emergency mode (during restoration) must be met in a timely manner [22]. Hence, the game must be designed so that the electric grid is the hub’s most important customer, thereby guaranteeing that the network operator’s needs are always met.

Under normal and emergency conditions, the grid must perform internal power flow analysis (not covered here) and report hourly on the maximum possible demand for energy as well as the actual energy demanded from each energy resource, ${\mathrm{e}}_{\mathrm{j},\mathrm{i}}^{\max }$ and ${\mathrm{e}}_{\mathrm{j},\mathrm{i}}$ respectively. The following sections include a discussion on how to find the latter by evaluating utility functions in different ways. Lastly, they should identify whether they are operating in emergency conditions or under normal circumstances.

2.2.3. Energy Hub Customers: Residential

Residential customers can only operate under one mode: normal mode. By purchasing energy under normal mode, they can improve their operational conditions and generate profits. The residential consumer can benefit, for instance, if energy is used for peak shaving, as this will decrease their electric utility bills since they are dependent on the peak energy consumed. Moreover, they could request energy to enhance the power quality of their system.

Additionally, residential consumers are also required to report the maximum possible energy demanded as well as the actual energy demanded from each energy resource, ${\mathrm{e}}_{\mathrm{j},\mathrm{i}}^{\max }$ and ${\mathrm{e}}_{\mathrm{j},\mathrm{i}}$.

2.2.4. Energy Hub Customers: Industrial

For industrial customers, the same values must be reported as for residential customers. In addition, another value must be reported: the cost of service failure, which is specific to every industry and is a function of the duration of service interruption, ${\mathrm{cf}}_{\mathrm{j},\mathrm{i}}$, [23]. Accordingly, industrial customers have two utility functions, one for each mode of operation depending on the type of industry and the type of costs incurred due to failures in the system.

2.3. Utility Functions

Following discussion of the actions and goals of all the players, it is necessary to model their utility or payoff functions. In this subsection, all utility functions are listed in accordance with the user’s behavior as described earlier.

2.3.1. Energy Hub Owner

A utility or a payoff function describes the mapping of real-life outcomes of the game to numbers. According to the seller, the goal is to maximize profit; hence, increasing profit would increase their satisfaction. For this reason, the ESH’s owner’s utility function can be defined as the revenue made from selling the different energy resources, ${\mathrm{e}}_{\mathrm{j},\mathrm{i}}$, to the different consumers, at a price of ${\mathrm{p}}_{\mathrm{i}}$, minus the cost of operating the facility, $\mathrm{OPEX}$, as shown in (1).

$${\mathrm{u}}_1={\displaystyle \sum }_{\mathrm{j}\ne 1}{\displaystyle \sum }_{\mathrm{i}}\left({\mathrm{p}}_{\mathrm{i}}\times {\mathrm{e}}_{\mathrm{j},\mathrm{i}}\right)-\mathrm{OPEX}$$

(1)

2.3.2. Energy Hub Customers: The Electric Grid

A consumer’s utility is represented by the monetary gain generated from satisfying an energy need through the ESH. If, for instance, a consumer was to contract the hub to supply energy for peak shaving purposes, the utility function would describe the benefit to the consumer from reducing their peak energy charges while deducting the price of the purchased energy. Equation (2) describes the electric grid’s utility function, where ${\mathrm{B}}_{\mathrm{j},\mathrm{i}}$ is consumer’s price sensitivity coefficient per consumer j and energy type i [24]. This coefficient varies with time depending on the user’s need for energy type i. The first term refers to the benefit the player receives from acquiring a specific amount of energy. Furthermore, the second term illustrates the concave nature of the user’s behavior, which represents a rational game player, while the last term describes the loss the consumer would incur as a result of the price of the energy resources they purchase.

$${\mathrm{u}}_2=\max \left(0, {\displaystyle \sum }_{\mathrm{i}}\left({\mathrm{B}}_{2,\mathrm{i}}\times {\mathrm{e}}_{2,\mathrm{i}}-\left(\frac{{\mathrm{B}}_{2,\mathrm{i}}}{2}\times \frac{{\mathrm{e}}_{2,\mathrm{i}}{}^2}{{\mathrm{e}}_{2,\mathrm{i}}^{\max }}\right)-{ \mathrm{p}}_{\mathrm{i}}\times {\mathrm{e}}_{2,\mathrm{i}}\right) \right)$$

(2)

2.3.3. Energy Hub Customers: Residential

The residential customers have the same behavior as the electric grid. Constraints are added in order to ensure that any player’s utility function is always non-negative.

2.3.4. Energy Hub Customers: Industrial

Under normal conditions, industrial customers behave in the same manner as the residential customers as well as the grid; however, under emergency conditions, the utility function is modified as shown in Equation (3). Adding the coefficient cf_j,i to the equation indicates that if there is some kind of disconnection from the grid, which leads to a failure in the industrial customer’s plant, the customer now values the energy resource even more than they did before. As an example, loss of service in the telecommunications industry is critical; therefore, their factor would be a high value, indicating the significance of the energy received to the continuity of service.

$${\mathrm{u}}_4=\max \left(0, {\displaystyle \sum }_{\mathrm{i}}\left({\mathrm{cf}}_{4,\mathrm{i}}\times {\mathrm{B}}_{4,\mathrm{i}}\times {\mathrm{e}}_{4,\mathrm{i}}-\left(\frac{{\mathrm{B}}_{4,\mathrm{i}}}{2}\times \frac{{\mathrm{e}}_{4,\mathrm{i}}{}^2}{{\mathrm{e}}_{4,\mathrm{i}}^{\max }}\right)-{ \mathrm{p}}_{\mathrm{i}}\times {\mathrm{e}}_{4,\mathrm{i}}\right) \right)$$

(3)

The above equations all describe how the users behave, while

Table 1. Game sets, parameters, and descriptions.

Parameter	Parameter Description
i	$\mathrm{Energy} \mathrm{resource} \mathrm{type}. I=\{1, \dots , \mathrm{i}, \dots , {\mathrm{N}}_{\mathrm{i}}$$\}, |I|={\mathrm{N}}_{\mathrm{i}}=$3
j	$\mathrm{Game} \mathrm{player}, \mathrm{where} \mathrm{player} 1 \mathrm{is} \mathrm{the} \mathrm{ESH} \mathrm{owner} \mathrm{and} \mathrm{the} \mathrm{remaining} \mathrm{players} \mathrm{are} \mathrm{energy} \mathrm{consumers}. J=\{1, \dots , \mathrm{j}, \dots , {\mathrm{N}}_{\mathrm{j}}\}, \left|J\right|={\mathrm{N}}_{\mathrm{j}}=4$
${\mathrm{p}}_{\mathrm{i}}$	Price of one unit of energy type i, in cents per kilowatt hour.
${\mathrm{e}}_{\mathrm{j},\mathrm{i}}^{\max }$	Maximum possible demand for energy based on historical data.
${\mathrm{B}}_{\mathrm{j},\mathrm{i}}$	Price sensitivity coefficient of player j, in cents per kilo-Watt hour to energy type i.
${\mathrm{cf}}_{\mathrm{j},\mathrm{i}}$	Continuity of service coefficient for player, j, and energy resource, i.

provides a summary of the sets and parameters used in the aforementioned equations. Upon analysis, it is evident that all of the utility functions except for that of the ESH’s owner’s, (1), behave in a quasilinear manner, allowing us to reach appropriate conclusions.

In summary, the following is the game amongst users:

• Players: The hub’s owner and the hub’s customers. The hub’s customers are the electric grid, aggregated residential customers, and industrial customers.
• Strategies: The hub’s owner selects how much energy it is supplying to each customer. Each consumer selects its energy consumption in either a cooperative or a greedy manner and that is decided based on the type of game they will play, as discussed in the following sections.
• Utility or payoff functions: ${\mathrm{u}}_{\mathrm{j}}$, where all the players’ utilities are shown in Equations (1)–(3).

At this stage, all the information necessary for the game to begin is available. While we know who the players are, their strategies, and their utilities, we do not know how they interact with one another. The outcome would be substantially different if they interacted cooperatively as opposed to acting greedily. Specifically, Section 3 and Section 4 explain two opposing interaction approaches used to model the ESH while Section 5 presents the results of applying the two approaches.

3. Cooperative Correlated Equilibrium Game Approach

In this approach, the players cooperate and play the game with the goal of achieving the maximum possible social welfare and social fairness. The adaptive learning algorithm utilized here to reach a correlated equilibrium is the regret matching algorithm. There are several steps involved in this iterative approach, the first of which is to adjust the utility functions of all players by adding a global term to every player’s utility function. This additional global term is the utility of the most dissatisfied player, meaning the player with the lowest utility value. Each player’s utility function represents their satisfaction level and adjusting these functions so they incorporate the aforesaid global term would enhance everyone’s overall satisfaction. Rather than every player striving to enhance their own utility (improve their satisfaction), they will now also improve the utility of the least satisfied player. The expected result of this algorithm is that the most selfish player becomes less greedy while all players maintain a reasonable satisfaction level. As proved in [25], the achieved result of the regret matching algorithm will be a correlated equilibrium. A correlated equilibrium describes a probability distribution over a set of strategies and by playing according to this probability distribution; if no other players change their actions, one has no incentive to deviate, hence achieving the necessary game results.

Regret Matching Algorithm

At the very beginning of the game, each player randomly chooses an action from their set of strategies and evaluates their utility for that action. The regret matching algorithm consists of a series of steps. First, each player’s utility function is normalized as follows:

$${\mathrm{u}}_{\mathrm{j}}^{\mathrm{norm}}\left(\mathrm{i},\mathrm{j}\right)=\frac{{\mathrm{u}}_{\mathrm{j}}\left(\mathrm{i},\mathrm{j}\right)-{ \mathrm{u}}_{\mathrm{j}}^{\min }\left(\mathrm{i},\mathrm{j}\right) }{{\mathrm{u}}_{\mathrm{j}}^{\max }\left(\mathrm{i},\mathrm{j}\right)-{ \mathrm{u}}_{\mathrm{j}}^{\min }\left(\mathrm{i},\mathrm{j}\right)}$$

(4)

To perform this normalization, it is clear that at every iteration of the game, the players’ actions must be stored as well as the history of their utility functions. Once this normalization is complete, it is then important to identify the worst-off player within all players. The worst-off player is the one with the lowest value utility function; this player is then identified as seen in Equation (5).

$$\mathrm{F}= \min \left({\mathrm{u}}_1^{\mathrm{norm}}\left(\mathrm{i},\mathrm{j}\right),{ \mathrm{u}}_2^{\mathrm{norm}}\left(\mathrm{i},\mathrm{j}\right),{ \mathrm{u}}_3^{\mathrm{norm}}\left(\mathrm{i},\mathrm{j}\right),{\mathrm{u}}_4^{\mathrm{norm}}\left(\mathrm{i},\mathrm{j}\right)\right)$$

(5)

Once this player is identified, the utility functions of all players are modified for the very last time to include the worst-off player’s utility as seen in (6). In this way, social welfare is improved.

$${\mathrm{u}}_{\mathrm{j}}^{\mathrm{mod}}\left(\mathrm{i},\mathrm{j}\right)={ \mathrm{w}}_1{\mathrm{u}}_{\mathrm{j}}^{\mathrm{norm}}\left(\mathrm{i},\mathrm{j}\right)+{ \mathrm{w}}_2\mathrm{F}$$

(6)

$${\mathrm{w}}_1+{ \mathrm{w}}_2=1$$

(7)

In this work, w₁ and w₂ were chosen to be of equal weight, 0.5 each, to emphasize both each player’s own utility as well as the overall welfare of all other players. As soon as all this is carried out, the game is now ready to be played to achieve a correlated equilibrium. As mentioned earlier, this game is modified at every iteration as the players learn from their previous actions and observe how to improve their own happiness as well as that of others. To achieve this, first, a value called the difference value is calculated. This difference value can be described as such: if player 1 plays action 1, while all other players play their randomly selected actions, player 1 must calculate the difference in their utility if they had played any other action in her action set other than action 1, while all other players did not change their actions, as seen in (8). The current iteration is denoted as n, ${\mathrm{S}}_{\mathrm{j}}$ describes player j’s chosen action at iteration k, while all other actions that player j did not choose at iteration k are denoted as ${\mathrm{S}}_{\mathrm{j}}^{\prime }$. Finally, all other player’s actions at iteration k are represented as ${\mathrm{S}}_{-\mathrm{j}}^{\mathrm{k}}$.

$${\mathrm{D}}_{\mathrm{j}}^{\mathrm{n}}\left({\mathrm{S}}_{\mathrm{j}},{\mathrm{S}}_{\mathrm{j}}^{\prime }\right)=\frac{1}{\mathrm{n}}{{\displaystyle \sum }}_{\mathrm{k}=1}^{\mathrm{n}}\left({\mathrm{u}}_{\mathrm{j}}\left({\mathrm{S}}_{\mathrm{j}}^{\prime },{\mathrm{S}}_{-\mathrm{j}}^{\mathrm{k}}\right)-{ \mathrm{u}}_{\mathrm{j}}\left({\mathrm{S}}_{\mathrm{j}},{\mathrm{S}}_{-\mathrm{j}}^{\mathrm{k}}\right)\right)$$

(8)

Next, once this difference is calculated, it is now easy to calculate regret. This can be seen by the following: if player 1 calculates their difference D(1,2), this means that they are calculating the utility that they would achieve had they played action 2, less the utility they actually achieved.

$${\mathrm{R}}_{\mathrm{j}}^{\mathrm{n}}\left({\mathrm{S}}_{\mathrm{j}},{\mathrm{S}}_{\mathrm{j}}^{\prime }\right)= \max \left\{{\mathrm{D}}_{\mathrm{j}}^{\mathrm{n}}\left({\mathrm{S}}_{\mathrm{j}},{\mathrm{S}}_{\mathrm{j}}^{\prime }\right), 0\right\}$$

(9)

If this is positive, it means that they “regret” not playing action 2; if it is negative, they have no regrets, and regret is stored as 0 as seen in (9). Finally, this regret is then transformed into a probability distribution that defines how the player would play their next move at the next iteration as seen in (10). This is carried out by every player at every iteration where $\mathsf{\mu }$ is a constant that ensures that all probabilities add up to 1.

$$\mathsf{\pi } =\{\begin{array}{c}{\mathrm{p}}_{\mathrm{j}}^{\mathrm{n}+1}\left({\mathrm{S}}_{\mathrm{j}}^{\prime }\right)=\frac{{\mathrm{R}}_{\mathrm{j}}^{\mathrm{n}}\left({\mathrm{S}}_{\mathrm{j}},{\mathrm{S}}_{\mathrm{j}}^{\prime }\right)}{\mathsf{\mu }},\text{for} \mathrm{all}{\mathrm{S}}_{\mathrm{j}}^{\prime }\ne {\mathrm{S}}_{\mathrm{j}}\\ {\mathrm{p}}_{\mathrm{j}}^{\mathrm{n}+1}\left({\mathrm{S}}_{\mathrm{j}}\right)=1-{\displaystyle {\displaystyle \sum }_{{\mathrm{S}}_{\mathrm{j}}^{\prime }\ne {\mathrm{S}}_{\mathrm{j}}}}{\mathrm{p}}_{\mathrm{j}}^{\mathrm{n}+1}\left({\mathrm{S}}_{\mathrm{j}}^{\prime }\right)\end{array}$$

(10)

Once this is completed and each player identifies their new action, and all the utilities are calculated once more, the worst-off utility F at the current iteration is compared to the one at the previous iteration and if it is less (meaning that some player is doing even worse than the worst-off player in the previous iteration), F is found as in (5); however, if F is more (all the players are doing better off than the worst-off player before), F is set as 1 to indicate a direction of improvement. This process is then repeated until a correlated equilibrium is reached.

An argument may arise against this approach, since the energy consumers may not care for each other’s well-being or each other’s satisfaction levels, hence making this approach unreasonable. However, it may be significant to note that this approach can be beneficial because, in reality, all electricity consumers are either directly or indirectly interconnected. Therefore, improving the behavior of one can improve the overall system. For example, if the residential consumer is capable of peak shaving by obtaining energy from the energy hub at the time of peak demand, this means that they would be satisfied because their bills are now decreasing. Moreover, at the same time, this benefits the grid as it reduces the maximum peak, hence reducing the network’s peak charges and delaying the need for equipment upgrades. So, overall, if one user aims to improve their behavior, all users benefit from those actions. Moreover, to further expand on this thought, one of the major challenges with regards to energy storage systems is the issue of ownership; hence, when considering a grid-owned ESH, this cooperative approach is a reasonable methodology. Hence, this approach was taken into consideration in this work.

4. Non-Cooperative Correlated Equilibrium Game Approach

In this section, the same game setup, with the same utility functions, is modeled as an ascending price-clinching auction. It is interesting to note that the following auction framework is based on the concept that each player ends up obtaining what they need at prices reasonable with their valuations. Moreover, the way that this auction is designed entails that every player who “clinches” an item pays a price that is not based on their valuation alone, but rather is also based on all other player’s valuations, allowing for this auction to be a truthful auction as valuation manipulation or covering would lead to no added benefit, as proved by Ausubel in [26].

Auction Framework

Similar to the previous modeling, the main challenges that this auction tries to tackle are the price selection for the energy resources as well as energy allocation. The ascending price-clinching auction mechanism is described in this section to develop answers for the above-posed questions.

As a starting point, all the players in this formulation are limited to integer actions, meaning price is incremented in integer steps by the ESH owner and users bid on integer items (bundles of energy). Each energy resource is auctioned separately. Note also that since each energy request is independent of the other, a combinatorial auction is not required. The next steps describe a simplified version of this procedure. At the beginning of the auction, the auctioneer sets a starting price, ${\mathrm{p}}_{\mathrm{i}}$, and once that has been completed, every bidder then uses the price the auctioneer has announced as a parameter to determine the optimal energy mix they will request at that price. Each player solves an optimization problem that aims to maximize their utility as seen in the following equations:

$$\underset{{\mathrm{e}}_{\mathrm{j},\mathrm{i}}}{\max }{\mathrm{u}}_{\mathrm{j}} , \mathrm{j}=2, 3, 4$$

(11)

$$\mathrm{s}.\mathrm{t}. {\mathrm{e}}_{\mathrm{j},\mathrm{i}}\ge 0$$

(12)

The result of each problem is the optimal energy mix required by each player at the price established by the auctioneer. The budget of each bidder is modeled as an additional constraint to the problem above to ensure that they never exceed their maximum budget. Once each player determines the optimal energy mix to be requested, the auctioneer checks to see if the total demand exceeds or equals the total supply. If there is more demand than the supply, it is necessary to decide which bidders, if any, will clinch items.

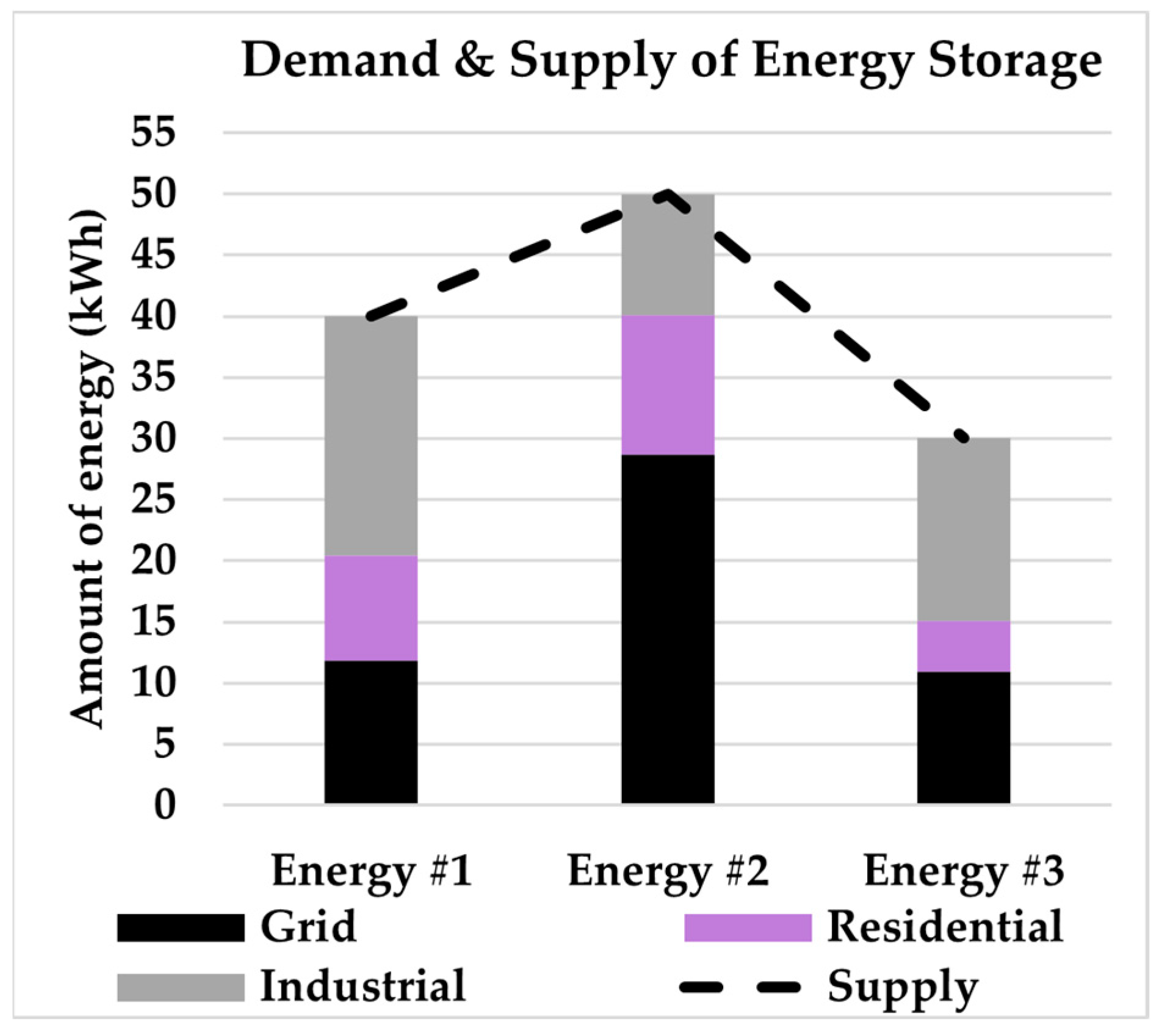
To further clarify, consider the game where the total supply of energy type 1 available is 1000 kWh, at a price of 3 cents/kWh. Every bidder then solves their optimization problem to determine how much energy of type 1 they should request at this price.

Consider the following results are obtained from the optimization problem above: the grid (player 2) requests 600 kWh, the residential customers (player 3) 700 kWh, and the industrial customers (player 4) 300 kWh. The way in which it is determined if anyone is going to clinch any units is as follows. For player j, consider the same game with the same demand levels if j was not participating, and the total demand is calculated. If that total demand exceeds supply, then player j does not clinch any units. However, if the total demand excluding player j is less than the supply, player j then clinches the difference between the supply and that demand at the price the auctioneer has at this stage. So, if the above values are observed, it can be determined that player 3 is the only player who clinches at this round. This player clinches 100 kWh of energy at the price of 3 cents/kWh.

Lastly, the auctioneer increases the price by one (integer) increment and the game is repeated. Once the demand becomes less than the supply, the game is stopped. This is not the only method for conducting auctions; however, this is a simple and reasonable approach for this case. It can be argued that, in this context, the ESH should not be selling the same products or services for different prices. However, this situation is in fact quite reasonable, since an industrial customer, for example, will pay far more than a residential customer to avoid expensive service interruptions; thus, the player who values the item most will receive it. For this reason, during the grid’s emergency mode of operation, the problem is handled differently. When the grid is in a state of emergency, the entire system (all users included) might be impacted, so when the grid is under emergency, whatever energy they need is given to them but for a price that was found using a different approach and the game continues with whatever energy supply is left, and the other users can bid for it. Finally, it is interesting to note that this auction yields the same results as the Vickrey auction.

5. Results

5.1. Cooperative Correlated Equilibrium Approach

To implement both games, ${\mathrm{B}}_{\mathrm{j},\mathrm{i}}$ was identified for each player and each energy type along with the discrete possible action sets allowable for each player. When the cooperative correlated equilibrium approach was implemented, the results obtained are displayed in Figure 2 and Figure 3. The individual utilities of each player are cost values calculated in cents; however, due to the normalization, their global utilities are unitless.

Figure 2 displays the local utilities of each player and how they change with each iteration. As can be seen from the figure above, due to the limited nature of the possible action sets taken by each player, it can be seen that within less than 30 iterations of the game, a correlated equilibrium is reached, and the players continue to change their actions but only slightly. It is also quite visible that all the utilities are maintained as non-negative as per the game specifications. It is significant to note that player 1’s local utility, hence profit, started off as the highest and as it decreased, the other player’s utility functions improved. This is because player 1 is the hub owner: at first the prices start off exceptionally large to maximize individual utility, but as the game proceeds, it is clear that the most selfish player (player 1) becomes less greedy, and the social welfare of the overall system is improved. Figure 3 shows the global utilities of this same game: the global utilities are the normalized, and then the utilities of each player, which include the utility of the worst-off player at every iteration, are modified. It can be seen that as the game progresses, these global utilities continue to change to reach the correlated equilibrium. Once this equilibrium is reached, no player has an incentive to deviate.

5.2. Non-Cooperative Ascending Price Clinching Auction Approach

In this approach, the auctioneer’s energy supply per resource is displayed in

Table 2. Ascending price-clinching auction auctioneer’s supply.

Energy Type i	i = 1	i = 2	i = 3
Maximum Supply Available	40 kWh	50 kWh	30 kWh

. With a starting price of 10 cents/kWh, the auction begins. The auction then proceeds in the manner described earlier and the results are displayed in Figure 4. It can be seen that the aggregate demand of each energy type is equal to the supply, which is exactly what this auction should result in.

A comparison of results obtained from both approaches shows that the hub’s revenue was approximately 11% larger using the auction approach, while each player’s utilities for the two different approaches varied within ±8% of each other for both approaches. However, the allocations differed in both approaches.

This shows that the results were not too different from each other; once again, this may be due to the small size of the simulated system and the fact that multiple technical and physical constraints were not studied. However, the results produced reasonably describe a real-world scenario in terms of the allocations and the final utilities. Finally, since both approaches used are well established, they were thoroughly proved and defended in [25,26]. Hence, the focus of this work was on applying these approaches to the energy storage market and observing their behavior.

6. Conclusions

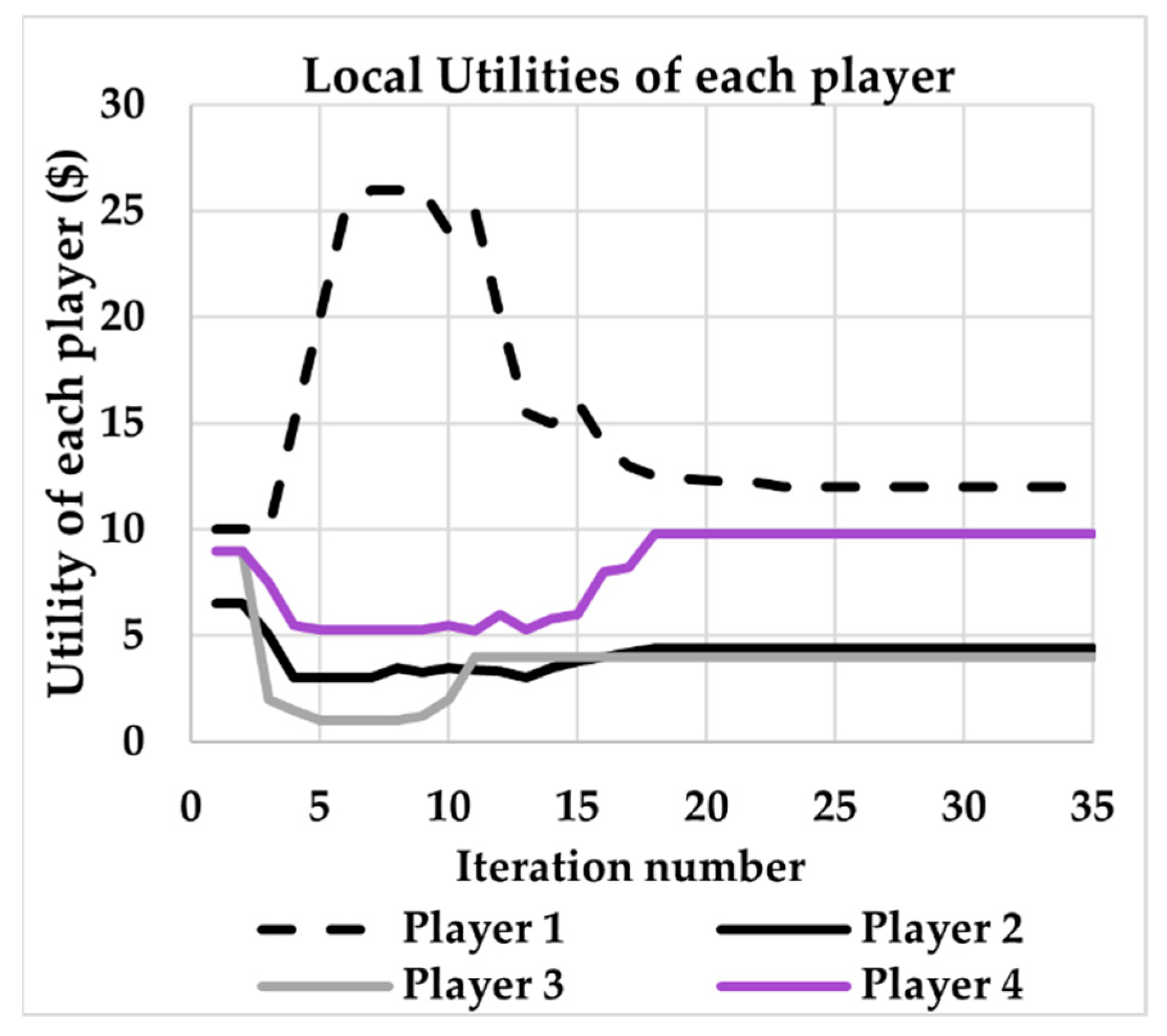
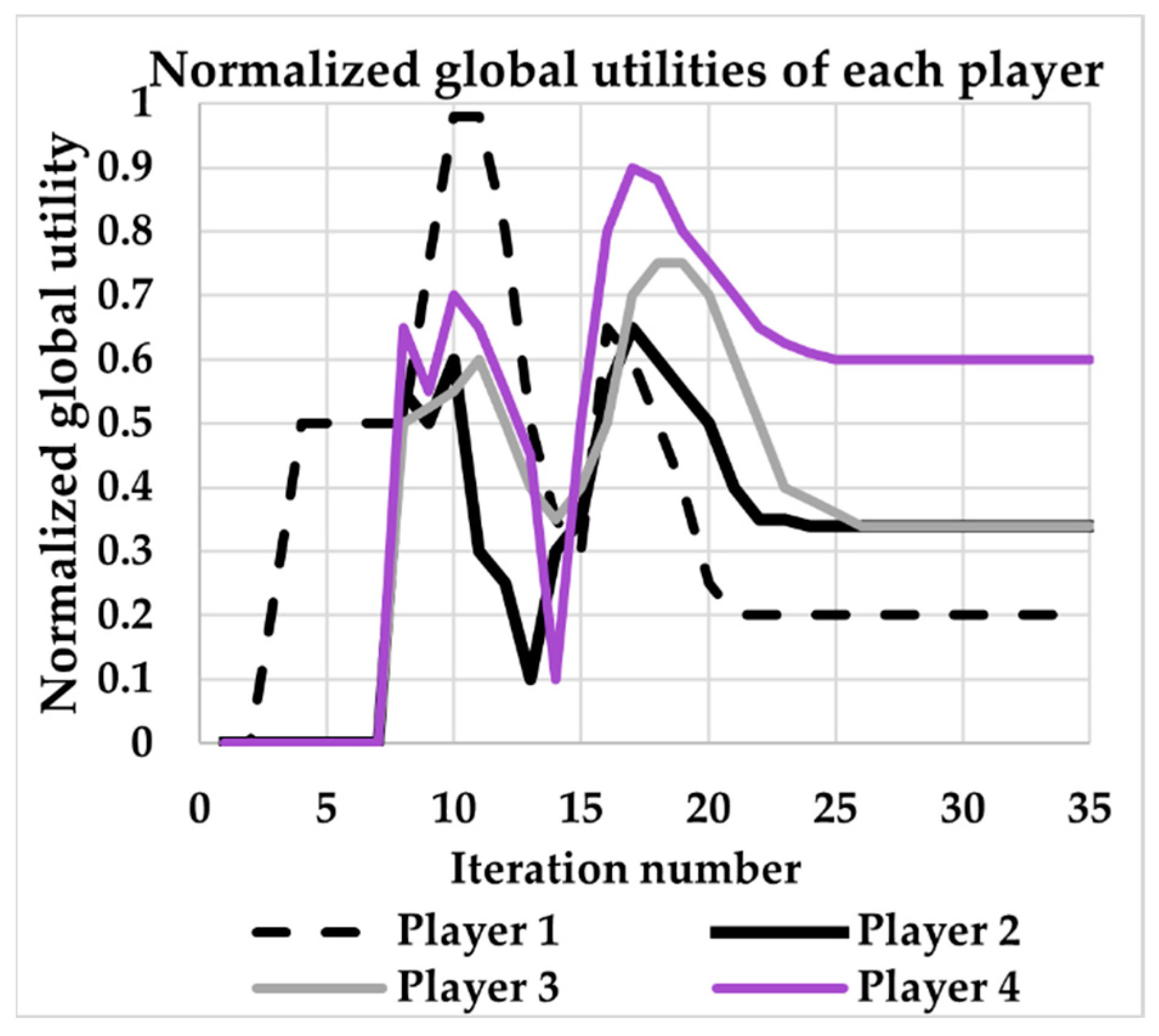
In this work, an energy storage hub was modeled to have three categories of customers: the electric grid, residential, and industrial customers. The interaction was modeled by using two methods, i.e., a cooperative approach and a non-cooperative approach: the regret matching algorithm and the clinching auction. It should be noted that while both approaches discussed above are well-established, they have never been used to model an energy storage hub or any work related to energy storage trading. In the first approach, the cooperative methodology, the greedy player, which is the energy hub owner, reduced their profits; however, the other players were all positively impacted. Despite being independent from each other as entities, these player consumers are still indirectly reliant on each other, especially the grid, so if the grid fails the entire connected system is negatively impacted. Accordingly, it may be beneficial to the hub to work towards improving the grid’s behavior and utility even if it means reducing profits. As for the second approach, the non-cooperative methodology, it was readily evident that this is a reasonable model for the energy hub storage system, as it makes the energy available to the player who values the energy most.

Both approaches are quite different and yielded distinct results. When embedded in a complete system that includes a detailed power system, the comparison would be more comprehensive. The games both describe a one-time representation of the functionality of an actual power system. Consequently, to expand on this work, a year-long simulation involving both methodologies would provide more practical and informative results; however, this is beyond the scope of this study. As observed through the results, both approaches performed as expected in terms of allocation as well as pricing. As this system continues to be expanded on an electrical basis, and as the number of players and available energy resources expands, more constraints and complexity will arise, so both approaches can be more comprehensively compared. Each approach has the potential to provide meaningful results; hence, this work aimed to show how two conflicting methods of interaction can be implemented and the choice of methodology depends on the application at hand. Finally, the cooperative versus non-cooperative approaches can also be expanded upon to address the issue of energy storage ownership.