Predictive Maintenance Planning for Industry 4.0 Using Machine Learning for Sustainable Manufacturing
Abstract
1. Introduction
- The future condition of the components for PdM planning is predicted using optimized deep learning.
- To improve the prediction in PdM planning, support vector machine (SVM) classification, rather than machine learning algorithms that face complexity when prediction values vary, is used to configure a recurrent neural network (RNN) network for each range of prediction.
- To overcome the problem of overfitting and data redundancy, optimal feature selection is performed using the proposed Jaya-based Sea Lion Optimization (J-SLnO) algorithm. The objective considered for optimal feature selection is to minimize the correlation between two selected features.
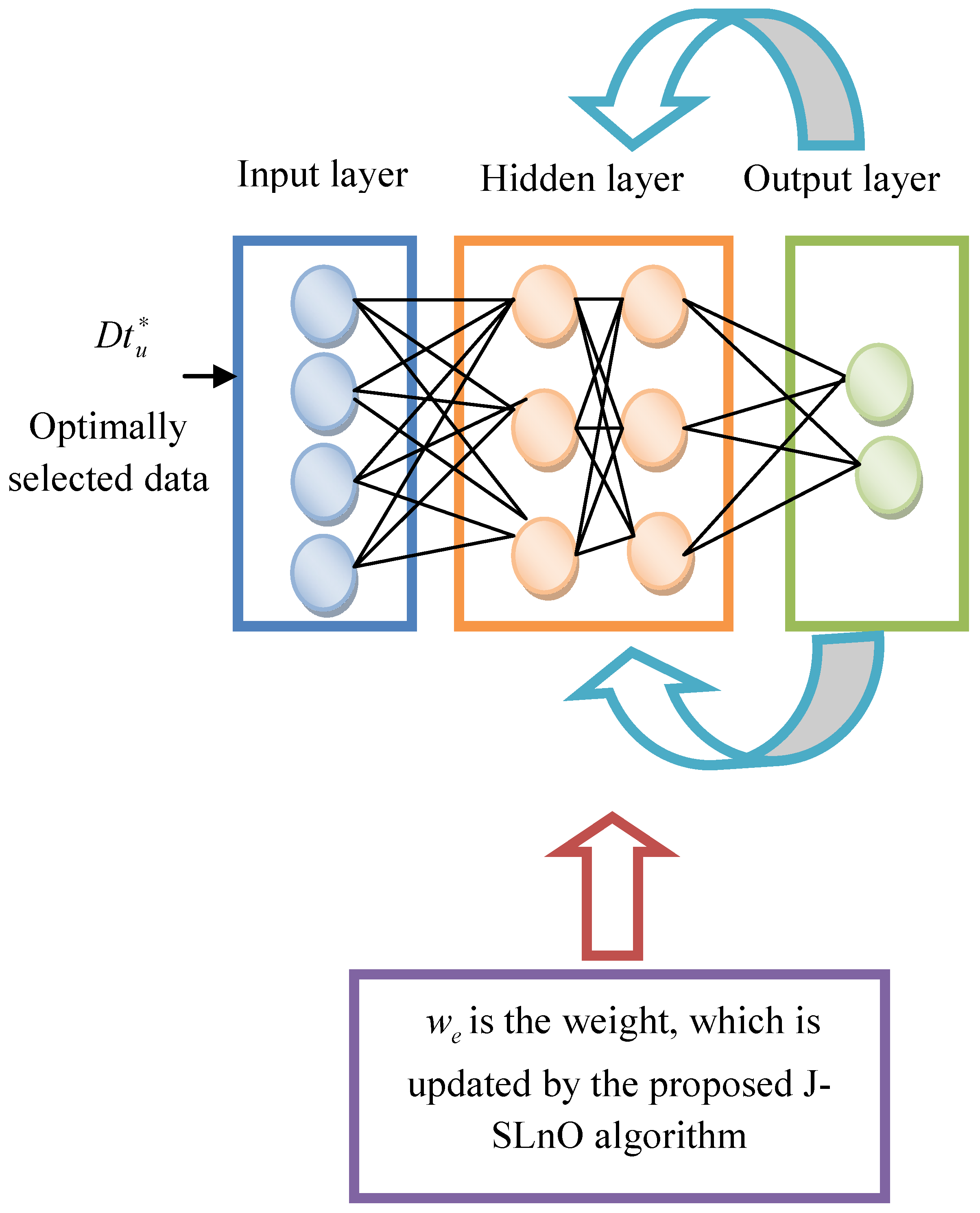
- PdM planning performance is improved by modifying an RNN, in which the weight is updated by the proposed J-SLnO algorithm.
2. Literature Review
3. Procedures for Predictive Maintenance Planning
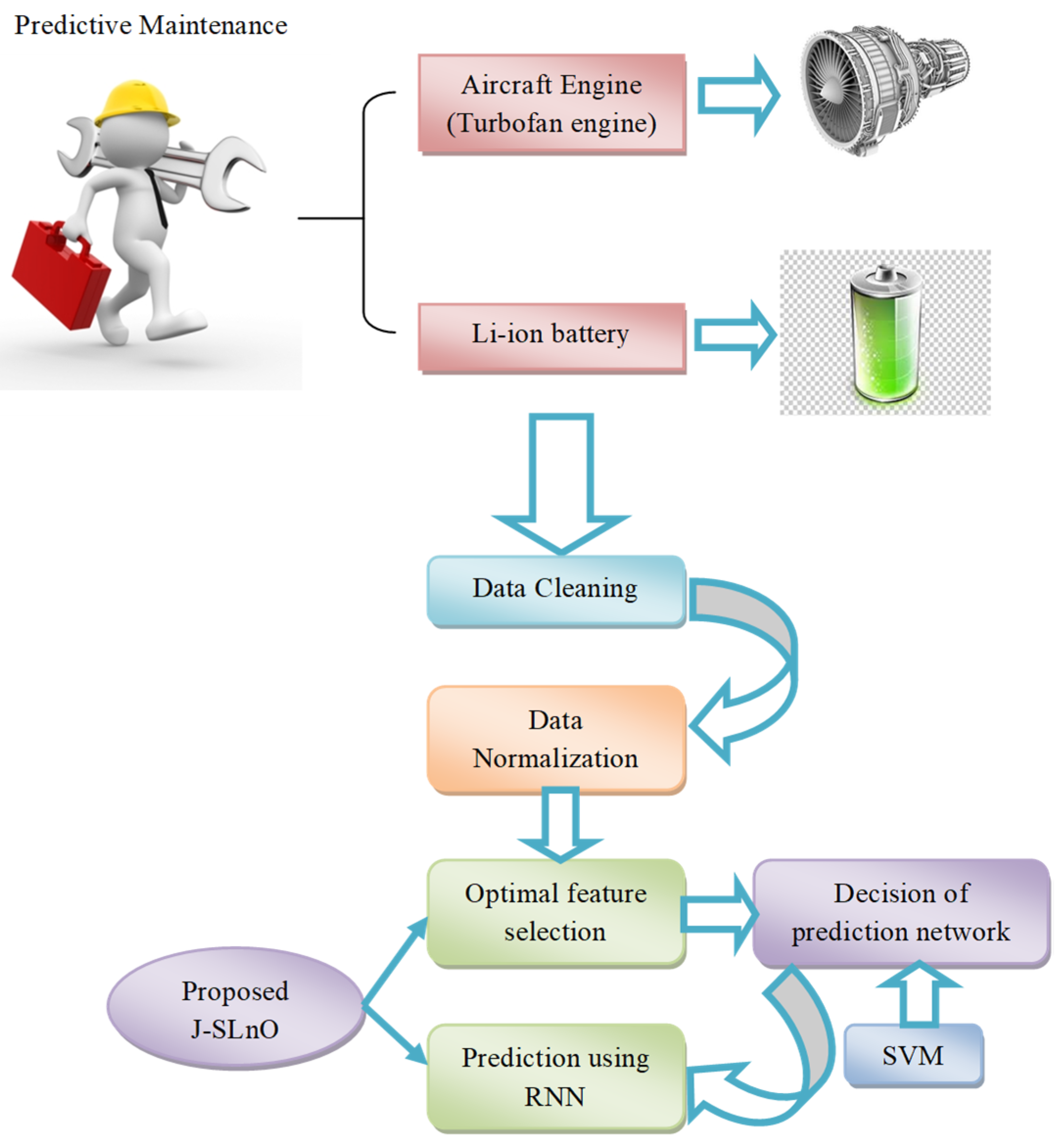
3.1. Developed Architecture
3.2. Data Cleaning
3.3. Data Normalization
4. Objective Model and Optimal Feature Selection
4.1. Objective Model
4.2. Optimal Feature Selection
4.3. SVM-Based RNN Range Classification
5. Hybrid Metaheuristic Algorithms for Optimal Feature Selection and Classification
5.1. Conventional Jaya Algorithm
| Algorithm 1.Pseudocode of conventional JA [38]. | |
| Initialize the size of population | |
| Find the best and worst solutions | |
| Based on best and worst solutions, modify the solutions using Equation (17). | |
| If
| |
| Update the solutions using Equation (17) | |
| Accept and replace the existing solution | |
| Else | |
| Maintain the previous solution | |
| End if | |
| If (termination criteria is met) | |
| Return the optimal solution | |
| Else | |
| Find best and worst solutions | |
| End | |
5.2. Conventional Sea Lion Optimization Algorithm (SLnO)
| Algorithm 2.SLnO Algorithm [39]. | |||
| Start | |||
| Population initialization | |||
| Choose | |||
| Compute fitness function for each search agent | |||
| The best candidate search agent that has best fitness is the X | |||
| while (t < maximum number of iterations) | |||
| Compute using Equation (20) | |||
| if | |||
| If | |||
| Update the location of the current search agent by Equation (18) | |||
| Else | |||
| Choose a random search agent | |||
| Update the location of the current search agent by Equation (25) | |||
| Else | |||
| Update the location of the current search agent by Equation (23) | |||
| Compute the fitness function for each search agent | |||
| Update X if there exists any better solution | |||
| Return X as the best solution | |||
| end while | |||
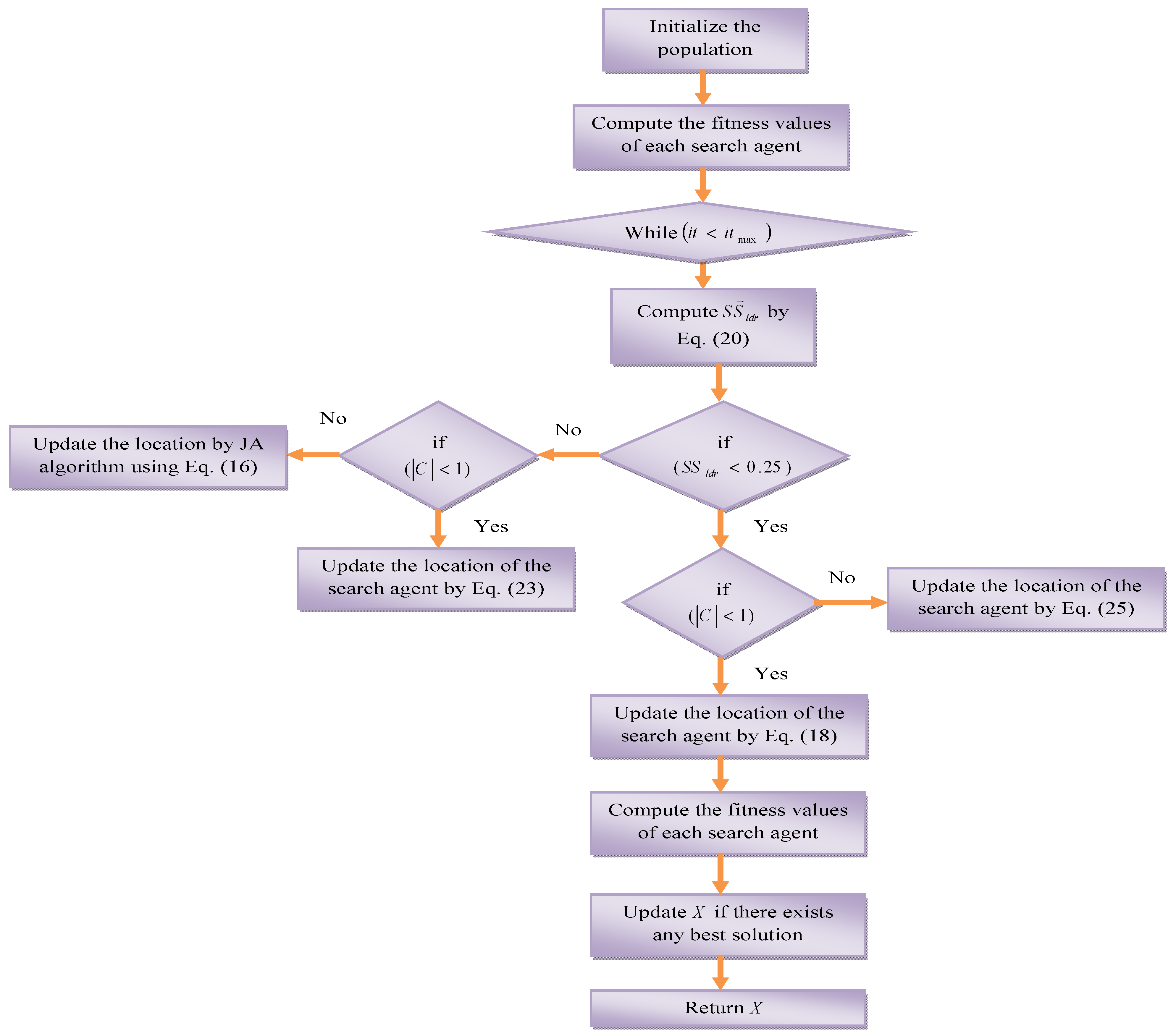
5.3. Proposed J-SLNO Algorithm
| Algorithm 3.J-SLnO Algorithm. | |||
| Start | |||
| Population initialization | |||
| Choose | |||
| Compute fitness function for each search agent | |||
| The best candidate search agent that has the best fitness is the X | |||
| while (t < maximum number of iterations) | |||
| Compute using Equation (20) | |||
| if | |||
| if | |||
| Update the location of the current search agent by Equation (18) | |||
| Else | |||
| Choose a random search agent | |||
| Update the location of the current search agent by Equation (25) | |||
| Else | |||
| if | |||
| Update the location of the current search agent by Equation (23) | |||
| Else | |||
| Update the position by Jaya algorithm using Equation (16) | |||
| Compute the fitness function for each search agent | |||
| Update X if there exists any better solution | |||
| Return X as the best solution | |||
| end while | |||
5.4. Recurrent Neural Network
6. Results and Discussion
6.1. Experimental Setup
6.2. Error Measures
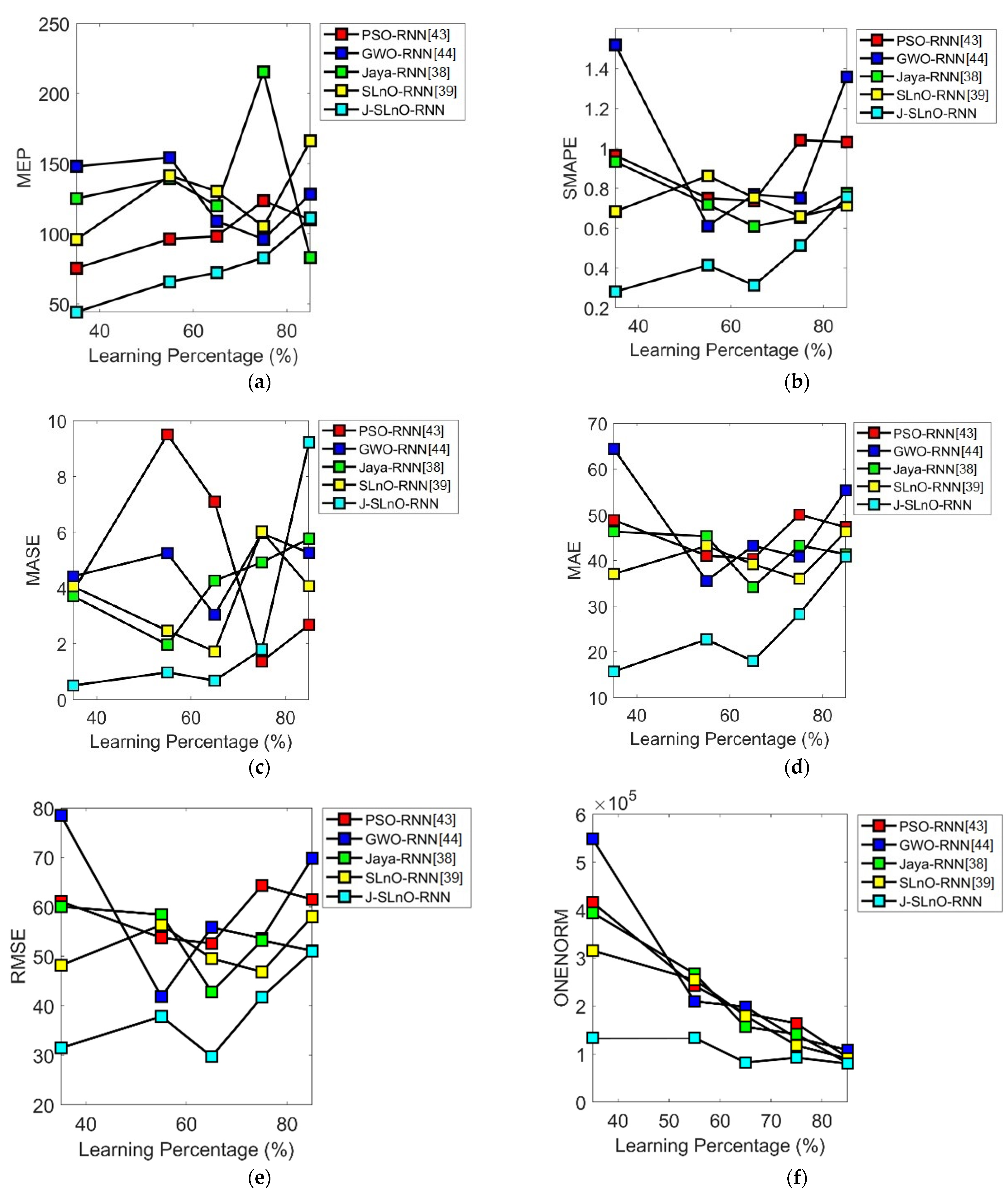
6.3. Meta-Heuristics-Based RNN for PdM Planning
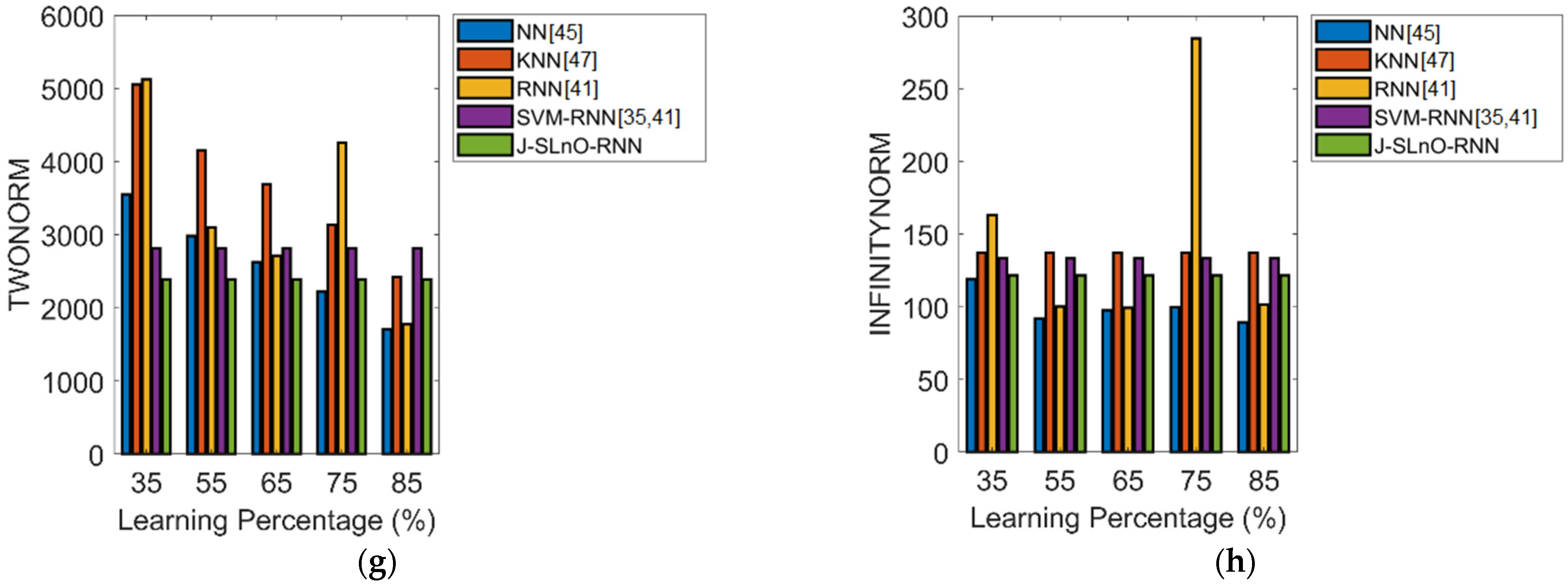
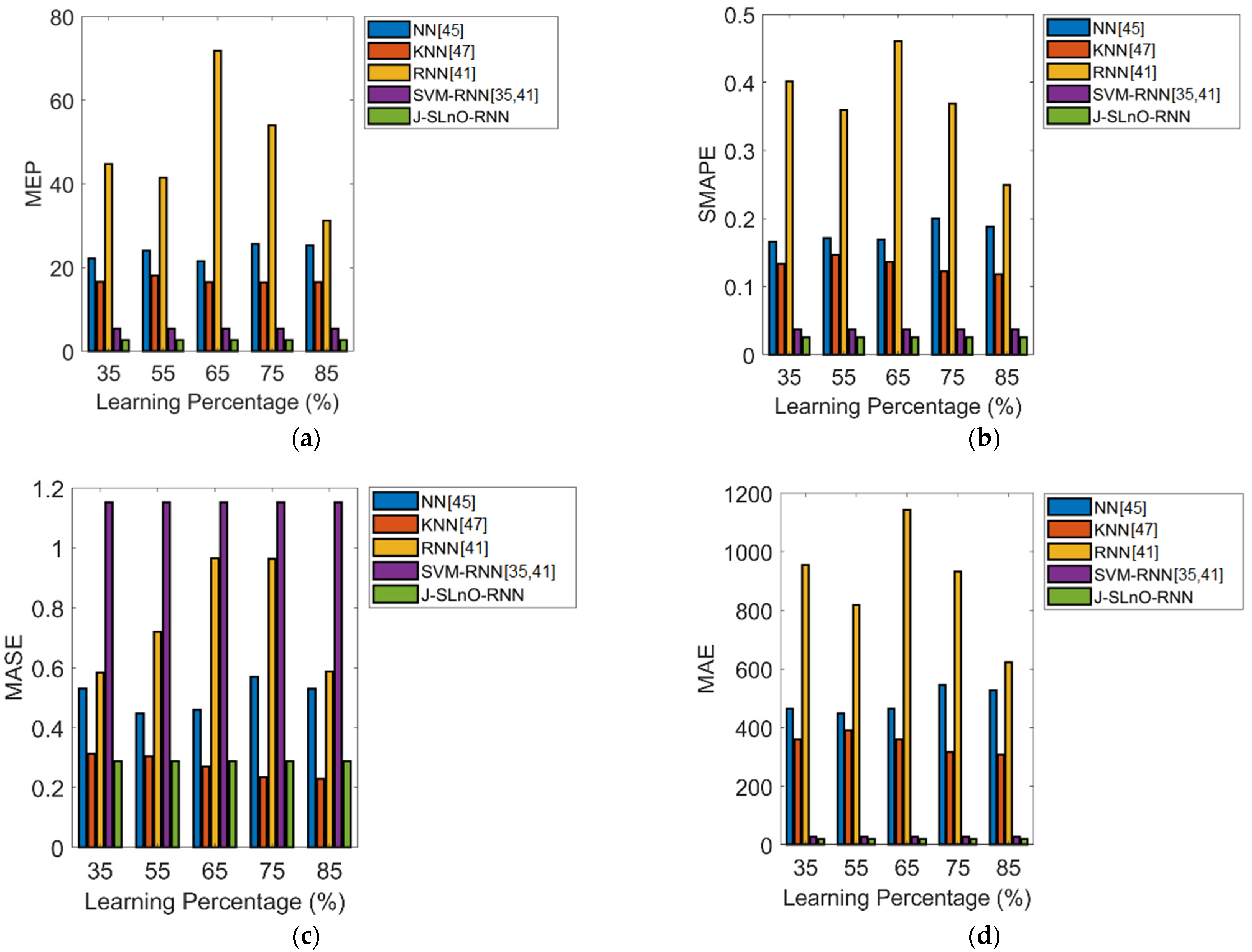
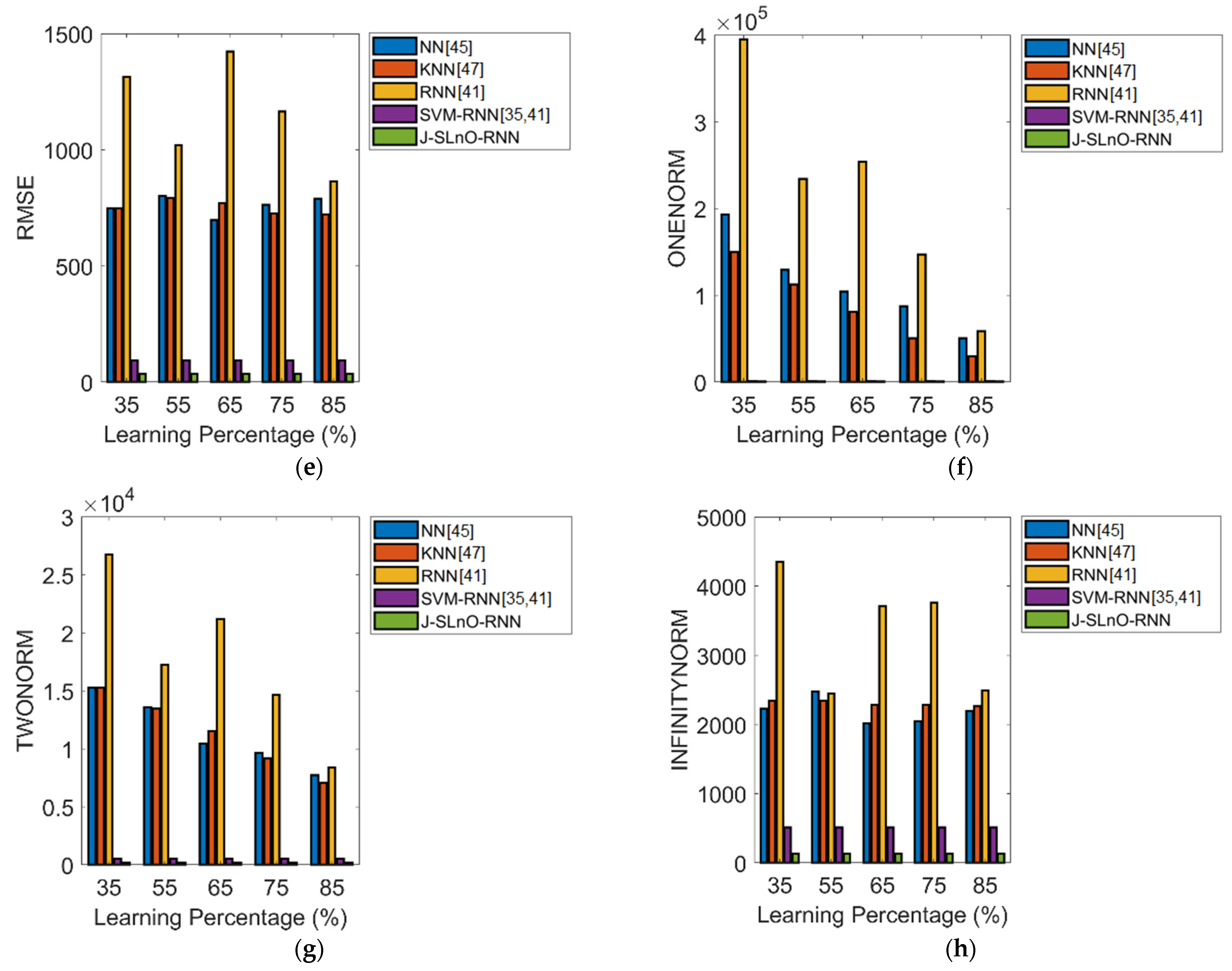
6.4. Machine Learning Algorithms for PdM Planning
6.5. Analysis on K-Fold Validation for PdM Planning
7. Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviations | Descriptions |
| PdM | Predictive Maintenance |
| MEP | Mechanical, Electrical and Plumbing |
| JA | Jaya Algorithm |
| SLnO | Sea Lion Optimization |
| J-SLnO | Jaya-based SLnO |
| SVM | Support Vector Machine |
| RNN | Recurrent Neural Network |
| FM | Facility Management |
| SMAPE | Symmetric Mean Absolute Percentage Error |
| FMM | Facility Maintenance Management |
| CAFM | Computerized Aided Facility Management systems |
| CMMS | Computerized Maintenance Management Systems |
| BIM | Building Information Modelling |
| IoT | Internet of Things |
| RFID | Radio Frequency Identification |
| MASE | Mean Absolute Scaled Error |
| CoxPHDL | Cox Proportional Hazard Deep Learning |
| TBF | Time-Between-Failure |
| CoxPHM | Cox Proportional Hazard Model |
| LSTM | Long Short-Term Memory |
| RMSE | Root Mean Square Error |
| MCC | Matthew’s Correlation Coefficient |
| ANN | Artificial Neural Network |
| LR | Logistic Regression |
| RF | Random Forest |
| GRU | Gated Recurrent Unit |
| MAE | Mean Absolute Error |
| QP | Quadratic Programming |
| MEP | Mean Error Percentage |
References
- Abidi, M.H.; Alkhalefah, H.; Umer, U. Fuzzy harmony search based optimal control strategy for wireless cyber physical system with industry 4.0. J. Intell. Manuf. 2021. [Google Scholar] [CrossRef]
- Maddikunta, P.K.R.; Pham, Q.-V.; Prabadevi, B.; Deepa, N.; Dev, K.; Gadekallu, T.R.; Ruby, R.; Liyanage, M. Industry 5.0: A survey on enabling technologies and potential applications. J. Ind. Inf. Integr. 2021, 26, 100257. [Google Scholar] [CrossRef]
- Baruah, P.; Chinnam, R.B. HMMs for diagnostics and prognostics in machining processes. Int. J. Prod. Res. 2005, 43, 1275–1293. [Google Scholar] [CrossRef]
- Prytz, R.; Nowaczyk, S.; Rögnvaldsson, T.; Byttner, S. Predicting the need for vehicle compressor repairs using maintenance records and logged vehicle data. Eng. Appl. Artif. Intell. 2015, 41, 139–150. [Google Scholar] [CrossRef]
- Aremu, O.O.; Hyland-Wood, D.; McAree, P.R. A Relative Entropy Weibull-SAX framework for health indices construction and health stage division in degradation modeling of multivariate time series asset data. Adv. Eng. Inform. 2019, 40, 121–134. [Google Scholar] [CrossRef]
- Susto, G.A.; Schirru, A.; Pampuri, S.; McLoone, S.; Beghi, A. Machine Learning for Predictive Maintenance: A Multiple Classifier Approach. IEEE Trans. Ind. Inform. 2015, 11, 812–820. [Google Scholar] [CrossRef]
- Malhi, A.; Yan, R.; Gao, R.X. Prognosis of Defect Propagation Based on Recurrent Neural Networks. IEEE Trans. Instrum. Meas. 2011, 60, 703–711. [Google Scholar] [CrossRef]
- Yuan, M.; Wu, Y.; Lin, L. Fault diagnosis and remaining useful life estimation of aero engine using LSTM neural network. In Proceedings of the 2016 IEEE International Conference on Aircraft Utility Systems (AUS), Beijing, China, 10–12 October 2016; pp. 135–140. [Google Scholar]
- Vianna, W.O.L.; Yoneyama, T. Predictive Maintenance Optimization for Aircraft Redundant Systems Subjected to Multiple Wear Profiles. IEEE Syst. J. 2018, 12, 1170–1181. [Google Scholar] [CrossRef]
- Ding, H.; Yang, L.; Yang, Z. A Predictive Maintenance Method for Shearer Key Parts Based on Qualitative and Quantitative Analysis of Monitoring Data. IEEE Access 2019, 7, 108684–108702. [Google Scholar] [CrossRef]
- Alvares, A.J.; Gudwin, R. Integrated System of Predictive Maintenance and Operation of Eletronorte Based on Expert System. IEEE Lat. Am. Trans. 2019, 17, 155–166. [Google Scholar] [CrossRef]
- Huynh, K.T.; Grall, A.; Bérenguer, C. A Parametric Predictive Maintenance Decision-Making Framework Considering Improved System Health Prognosis Precision. IEEE Trans. Reliab. 2019, 68, 375–396. [Google Scholar] [CrossRef]
- Lin, C.Y.; Hsieh, Y.M.; Cheng, F.T.; Huang, H.C.; Adnan, M. Time Series Prediction Algorithm for Intelligent Predictive Maintenance. IEEE Robot. Autom. Lett. 2019, 4, 2807–2814. [Google Scholar] [CrossRef]
- Suzuki, T.; Yamamoto, H.; Oka, T. Advancement in maintenance operation for managing various types of failure and vastly ageing facilities. Cired—Open Access Proc. J. 2017, 2017, 929–933. [Google Scholar] [CrossRef][Green Version]
- Abidi, M.H.; Alkhalefah, H.; Mohammed, M.K.; Umer, U.; Qudeiri, J.E.A. Optimal Scheduling of Flexible Manufacturing System Using Improved Lion-Based Hybrid Machine Learning Approach. IEEE Access 2020, 8, 96088–96114. [Google Scholar] [CrossRef]
- Abidi, M.H.; Alkhalefah, H.; Umer, U.; Mohammed, M.K. Blockchain-based secure information sharing for supply chain management: Optimization assisted data sanitization process. Int. J. Intell. Syst. 2021, 36, 260–290. [Google Scholar] [CrossRef]
- Brown, M.S.; Shah, S.K.; Pais, R.C.; Lee, Y.Z.; McNitt-Gray, M.F.; Goldin, J.G.; Cardenas, A.F.; Aberle, D.R. Database design and implementation for quantitative image analysis research. IEEE Trans. Inf. Technol. Biomed. 2005, 9, 99–108. [Google Scholar] [CrossRef]
- Carter, J. Maintenance management—computerised systems come of age. Comput. Aided Eng. J. 1985, 2, 182–185. [Google Scholar] [CrossRef]
- Uhlmann, E.; Pontes, R.P.; Geisert, C.; Hohwieler, E. Cluster identification of sensor data for predictive maintenance in a Selective Laser Melting machine tool. Procedia Manuf. 2018, 24, 60–65. [Google Scholar] [CrossRef]
- Xie, Q.; Zhou, X.; Wang, J.; Gao, X.; Chen, X.; Liu, C. Matching Real-World Facilities to Building Information Modeling Data Using Natural Language Processing. IEEE Access 2019, 7, 119465–119475. [Google Scholar] [CrossRef]
- Sacks, R.; Eastman, C.; Lee, G.; Teicholz, P. BIM Handbook: A Guide to Building Information Modeling for Owners, Designers, Engineers, Contractors, and Facility Managers, 3rd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2018; p. 688. [Google Scholar]
- Chen, X.; Feng, D.; Takeda, S.; Kagoshima, K.; Umehira, M. Experimental Validation of a New Measurement Metric for Radio-Frequency Identification-Based Shock-Sensor Systems. IEEE J. Radio Freq. Identif. 2018, 2, 206–209. [Google Scholar] [CrossRef]
- Hao, Q.; Xue, Y.; Shen, W.; Jones, B.; Zhu, J. A Decision Support System for Integrating Corrective Maintenance, Preventive Maintenance, and Condition-Based Maintenance. In Proceedings of the Construction Research Congress 2010, Banff, AB, Canada, 8–10 May 2010; pp. 470–479. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Maddikunta, P.K.R.; Meenakshisundaram, I.; Gadekallu, T.R.; Sharma, S.; Alkahtani, M.; Abidi, M.H. Deep Neural Networks Based Approach for Battery Life Prediction. Comput. Mater. Contin. 2021, 69, 2599–2615. [Google Scholar] [CrossRef]
- Ch, R.; Gadekallu, T.R.; Abidi, M.H.; Al-Ahmari, A. Computational System to Classify Cyber Crime Offenses using Machine Learning. Sustainability 2020, 12, 4087. [Google Scholar] [CrossRef]
- Chen, C.; Liu, Y.; Wang, S.; Sun, X.; Di Cairano-Gilfedder, C.; Titmus, S.; Syntetos, A.A. Predictive maintenance using cox proportional hazard deep learning. Adv. Eng. Inform. 2020, 44, 101054. [Google Scholar] [CrossRef]
- Cheng, J.C.P.; Chen, W.; Chen, K.; Wang, Q. Data-driven predictive maintenance planning framework for MEP components based on BIM and IoT using machine learning algorithms. Autom. Constr. 2020, 112, 103087. [Google Scholar] [CrossRef]
- Gohel, H.A.; Upadhyay, H.; Lagos, L.; Cooper, K.; Sanzetenea, A. Predictive maintenance architecture development for nuclear infrastructure using machine learning. Nucl. Eng. Technol. 2020, 52, 1436–1442. [Google Scholar] [CrossRef]
- Traini, E.; Bruno, G.; D’Antonio, G.; Lombardi, F. Machine Learning Framework for Predictive Maintenance in Milling. Ifac-Pap. 2019, 52, 177–182. [Google Scholar] [CrossRef]
- Zenisek, J.; Holzinger, F.; Affenzeller, M. Machine learning based concept drift detection for predictive maintenance. Comput. Ind. Eng. 2019, 137, 106031. [Google Scholar] [CrossRef]
- Markiewicz, M.; Wielgosz, M.; Bocheński, M.; Tabaczyński, W.; Konieczny, T.; Kowalczyk, L. Predictive Maintenance of Induction Motors Using Ultra-Low Power Wireless Sensors and Compressed Recurrent Neural Networks. IEEE Access 2019, 7, 178891–178902. [Google Scholar] [CrossRef]
- Abidi, M.H.; Umer, U.; Mohammed, M.K.; Aboudaif, M.K.; Alkhalefah, H. Automated Maintenance Data Classification Using Recurrent Neural Network: Enhancement by Spotted Hyena-Based Whale Optimization. Mathematics 2020, 8, 2008. [Google Scholar] [CrossRef]
- Singh, K.; Upadhyaya, S. Outlier Detection: Applications And Techniques. Int. J. Comput. Sci. 2012, 9, 307–323. [Google Scholar]
- Deng, W.; Guo, Y.; Liu, J.; Li, Y.; Liu, D.; Zhu, L. A missing power data filling method based on improved random forest algorithm. Chin. J. Electr. Eng. 2019, 5, 33–39. [Google Scholar] [CrossRef]
- Martens, D.; Baesens, B.B.; Gestel, T.V. Decompositional Rule Extraction from Support Vector Machines by Active Learning. IEEE Trans. Knowl. Data Eng. 2009, 21, 178–191. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory, 2nd ed.; Springer: New York, NY, USA, 1999; p. 314. [Google Scholar]
- Steinwart, I.; Scovel, C. Mercer’s Theorem on General Domains: On the Interaction between Measures, Kernels, and RKHSs. Constr. Approx. 2012, 35, 363–417. [Google Scholar] [CrossRef]
- Rao, R.V. Jaya: A simple and new optimization algorithm for solving constrained and unconstrained optimization problems. Int. J. Ind. Eng. Comput. 2016, 7, 19–34. [Google Scholar] [CrossRef]
- Masadeh, R.; Mahafzah, B.A.; Sharieh, A. Sea Lion Optimization Algorithm. Int. J. Adv. Comput. Sci. Appl. 2019, 10, 388–395. [Google Scholar] [CrossRef]
- Beno, M.M.; R, V.I.; M, S.S.; Rajakumar, B.R. Threshold prediction for segmenting tumour from brain MRI scans. Int. J. Imaging Syst. Technol. 2014, 24, 129–137. [Google Scholar] [CrossRef]
- Li, F.; Liu, M. A hybrid Convolutional and Recurrent Neural Network for Hippocampus Analysis in Alzheimer’s Disease. J. Neurosci. Methods 2019, 323, 108–118. [Google Scholar] [CrossRef]
- Arch. Predictive Maintenance (PdM) of Aircraft Engine, Github, Ed. 2020. Available online: https://github.com/archd3sai/Predictive-Maintenance-of-Aircraft-Engine (accessed on 1 February 2022).
- Pedersen, M.E.H.; Chipperfield, A.J. Simplifying Particle Swarm Optimization. Appl. Soft Comput. 2010, 10, 618–628. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Fernández-Navarro, F.; Carbonero-Ruz, M.; Alonso, D.B.; Torres-Jiménez, M. Global Sensitivity Estimates for Neural Network Classifiers. IEEE Trans. Neural Netw. Learn. Syst. 2017, 28, 2592–2604. [Google Scholar] [CrossRef]
- Preetha, N.; Sreedharan, N.; Ganesan, B.; Raveendran, R.; Sarala, P.; Dennis, B.; Boothalingam, R.R. Grey Wolf optimisation-based feature selection and classification for facial emotion recognition. IET Biom. 2018, 7, 490–499. Available online: https://digital-library.theiet.org/content/journals/10.1049/iet-bmt.2017.0160 (accessed on 1 February 2022).
- Chen, Y.; Hu, X.; Fan, W.; Shen, L.; Zhang, Z.; Liu, X.; Du, J.; Li, H.; Chen, Y.; Li, H. Fast density peak clustering for large scale data based on kNN. Knowl. Based Syst. 2020, 187, 104824. [Google Scholar] [CrossRef]

| Author [Citation] | Methodology | Features | Challenges |
|---|---|---|---|
| Chen et al. [26] | LSTM | High performance. Designed to store long-term and short-term pattern data. | Requires more time to train. |
| Cheng et al. [27] | SVM | Requires less time to solve the problem. More effective than ANNs. | Inappropriate for huge datasets. |
| Gohel et al. [28] | SVM | Attempts to maximize margin among closest support vectors. High performance. | Does not perform well if the dataset includes noise. |
| Susto et al. [6] | SVM | Best accuracy. Powerful but complex relative to analysis. | Selecting the kernel function is difficult. |
| Traini et al. [29] | NN | Best performance. High system reliability. | Hardware dependent. |
| Uhlmann et al. [19] | Elbow Method | Used to determine cluster count. Reduces distortion and provides precise cluster count. | Performance can be improved. |
| Zenisek et al. [30] | RF | High performance. Ensembles uncorrelated regression trees provided at random using bagging and boosting to fit the provided information. | Very complex to implement and consumes more time. |
| Markiewicz et al. [31] | RNN | Reduces computational complexity. Power consumption is reduced. | Computation is quite slow. |
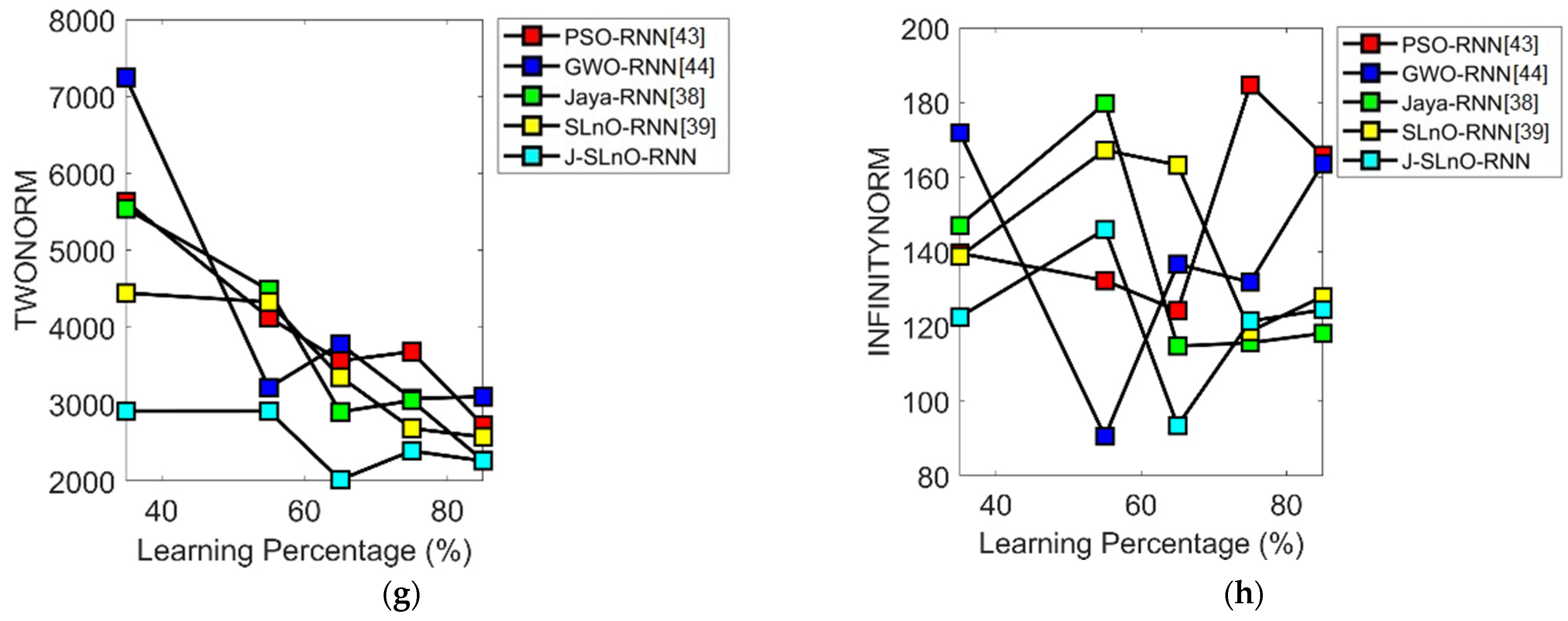
| Error Measures | PSO-RNN [43] | GWO-RNN [44] | JA-RNN [38] | SLnO-RNN [39] | J-SLnO-RNN |
|---|---|---|---|---|---|
| MEP | 123.47 | 96.037 | 215.55 | 105.05 | 82.84 |
| SMAPE | 1.0408 | 0.75052 | 0.65396 | 0.65884 | 0.51309 |
| MASE | 1.3655 | 5.9667 | 4.9249 | 6.0355 | 1.7978 |
| MAE | 50.058 | 40.795 | 43.281 | 36.004 | 28.296 |
| RMSE | 64.307 | 53.641 | 53.204 | 46.857 | 41.742 |
| L1 Norm | 1.64 × 105 | 1.34 × 105 | 1.42 × 105 | 1.18 × 105 | 92,643 |
| L2 Norm | 3679.6 | 3069.2 | 3044.3 | 2681.1 | 2388.4 |
| L-Infinity Norm | 184.72 | 131.9 | 115.64 | 118.7 | 121.45 |
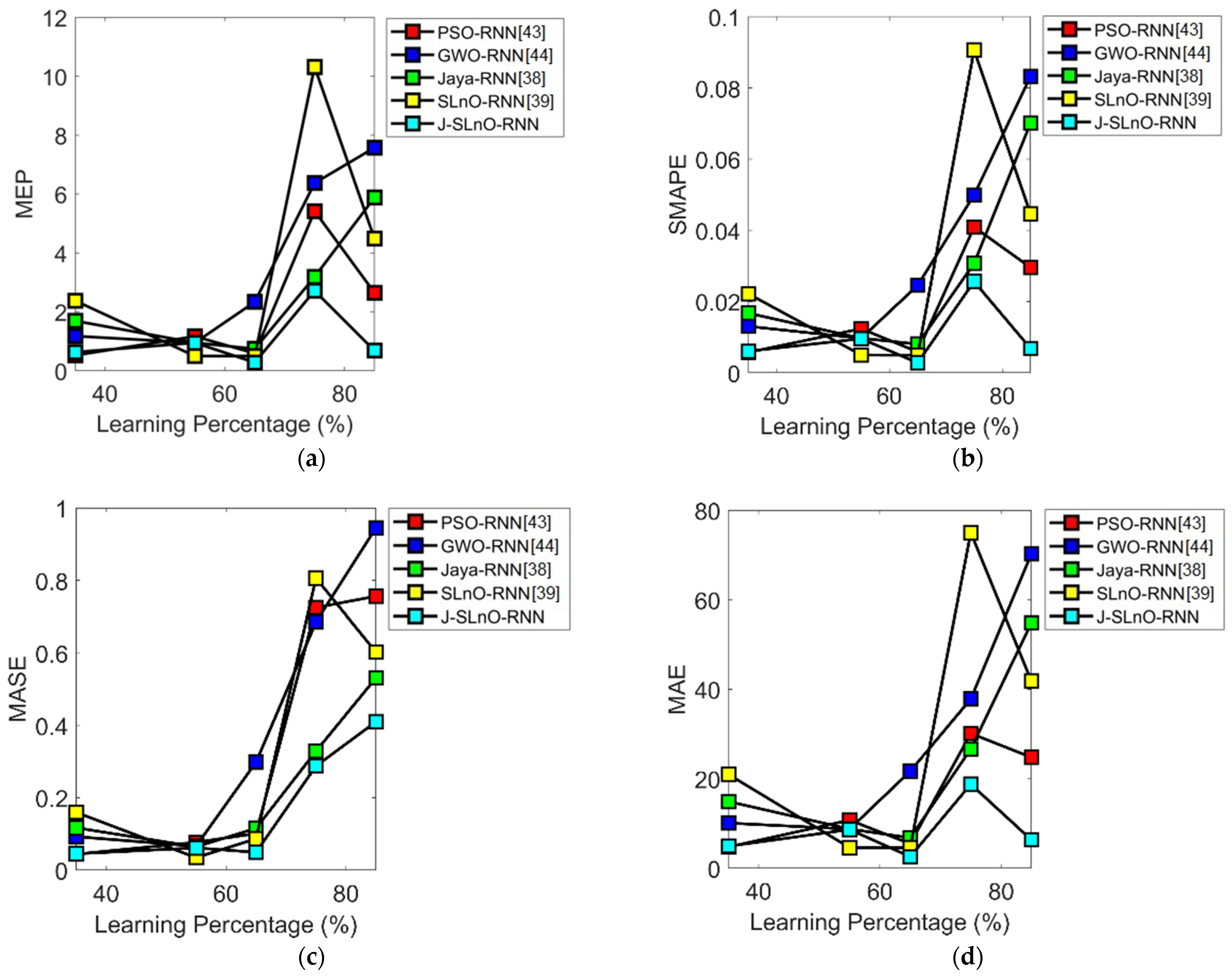
| Error Measures | PSO-RNN [43] | GWO-RNN [44] | JA-RNN [38] | SLnO-RNN [39] | J-SLnO-RNN |
|---|---|---|---|---|---|
| MEP | 5.4193 | 6.3721 | 3.1873 | 10.32 | 2.7151 |
| SMAPE | 0.040926 | 0.049924 | 0.030704 | 0.090627 | 0.025625 |
| MASE | 0.7249 | 0.68541 | 0.32876 | 0.80602 | 0.28758 |
| MAE | 30.152 | 37.854 | 26.658 | 74.992 | 18.781 |
| RMSE | 83.115 | 89.443 | 48.334 | 114.59 | 35.396 |
| L1 Norm | 9.35 × 102 | 1.17 × 103 | 8.26 × 102 | 2.32 × 103 | 582.22 |
| L2 Norm | 462.76 | 498 | 269.11 | 638 | 197.08 |
| L-Infinity Norm | 434.65 | 455.95 | 214.22 | 443.43 | 136.02 |
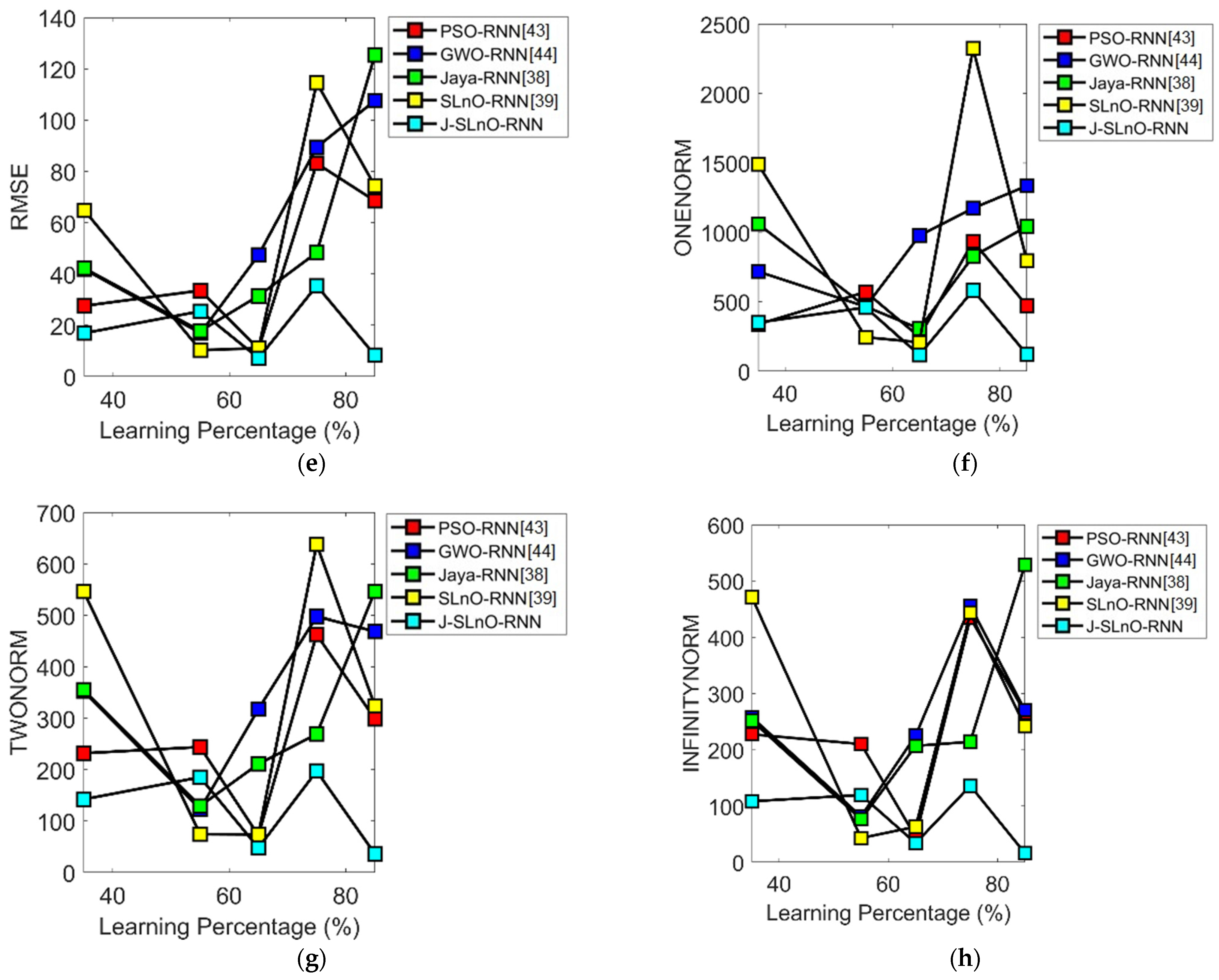
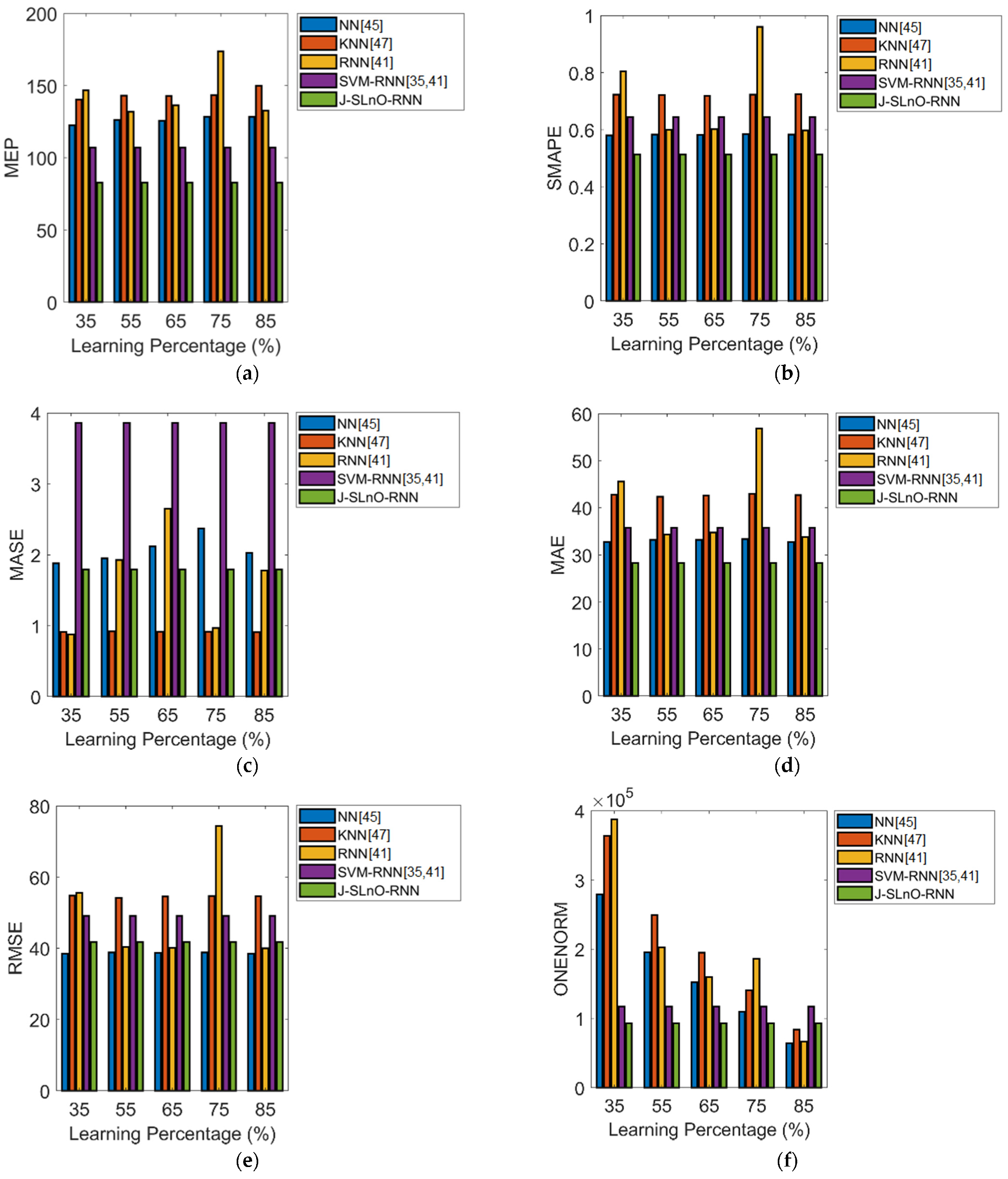
| Error Measures | NN [45] | KNN [47] | RNN [41] | SVM-RNN [35,41] | J-SLnO-RNN |
|---|---|---|---|---|---|
| MEP | 128.31 | 143.48 | 173.64 | 106.95 | 82.84 |
| SMAPE | 0.58454 | 0.72322 | 0.96011 | 0.64453 | 0.51309 |
| MASE | 2.3749 | 0.91535 | 0.96928 | 3.8597 | 1.7978 |
| MAE | 33.419 | 42.884 | 56.886 | 35.794 | 28.296 |
| RMSE | 38.837 | 54.74 | 74.34 | 49.105 | 41.742 |
| L1 Norm | 1.09 × 105 | 1.40 × 105 | 1.86 × 105 | 1.17 × 105 | 92,643 |
| L2 Norm | 2222.2 | 3132.2 | 4252.3 | 2809.7 | 2388.4 |
| L-Infinity Norm | 99.519 | 137 | 284.49 | 133.34 | 121.45 |
| Error Measures | NN [45] | KNN [47] | RNN [41] | SVM-RNN [35,41] | J-SLnO-RNN |
|---|---|---|---|---|---|
| MEP | 25.723 | 16.429 | 54.028 | 5.4725 | 2.7151 |
| SMAPE | 0.20028 | 0.12222 | 0.36893 | 0.037398 | 0.025625 |
| MASE | 0.57038 | 0.23407 | 0.96412 | 1.153 | 0.28758 |
| MAE | 546.08 | 316.3 | 931.43 | 27.119 | 18.781 |
| RMSE | 762.47 | 724.61 | 1164.4 | 92.844 | 35.396 |
| L1 Norm | 87,373 | 50,608 | 1.47 × 105 | 840.7 | 582.22 |
| L2 Norm | 9.64 × 103 | 9.17 × 103 | 1.46 × 104 | 5.17 × 102 | 197.08 |
| L-Infinity Norm | 2044.2 | 2284 | 3759.9 | 509.26 | 136.02 |
| Error Measures | PSO-RNN [43] | GWO-RNN [44] | JA-RNN [38] | SLnO-RNN [39] | J-SLnO-RNN |
|---|---|---|---|---|---|
| Aircraft Dataset | |||||
| MEP | 1.8765 | 1.8345 | 1.7773 | 1.7868 | 1.6914 |
| SMAPE | 0.021446 | 0.020966 | 0.020312 | 0.020421 | 0.01933 |
| MASE | 0.026873 | 0.025767 | 0.025107 | 0.025299 | 0.024076 |
| MAE | 1.2525 | 1.2044 | 1.1728 | 1.1848 | 1.1259 |
| RMSE | 5.3746 | 5.249 | 5.1909 | 5.1776 | 5.0895 |
| L1 Norm | 16,403 | 15,773 | 15,359 | 15,517 | 14,745 |
| L2 Norm | 615.06 | 600.68 | 594.04 | 592.51 | 582.44 |
| L-Infinity Norm | 22.58 | 24.69 | 32.71 | 19.45 | 15.62 |
| Li-ion battery Dataset | |||||
| MEP | 1.9501 | 1.8721 | 1.8331 | 1.7551 | 1.6381 |
| SMAPE | 0.022287 | 0.021395 | 0.020949 | 0.020058 | 0.018721 |
| MASE | 0.049074 | 0.049092 | 0.045265 | 0.044557 | 0.04046 |
| MAE | 56.975 | 57.66 | 53.047 | 51.514 | 47.221 |
| RMSE | 218.81 | 222.43 | 212.05 | 211.73 | 196.02 |
| L1 Norm | 36,521 | 36,960 | 34,003 | 33,021 | 30,269 |
| L2 Norm | 5539.9 | 5631.6 | 5368.8 | 5360.6 | 4962.8 |
| L-Infinity Norm | 966 | 967.25 | 966.25 | 967.25 | 965.25 |
| Error Measures | NN [45] | KNN [47] | RNN [41] | SVM-RNN [35,41] | J-SLnO-RNN |
|---|---|---|---|---|---|
| Aircraft Dataset | |||||
| MEP | 1.9739 | 2.0865 | 1.9911 | 2.0197 | 1.6914 |
| SMAPE | 0.022559 | 0.023846 | 0.022755 | 0.023082 | 0.01933 |
| MASE | 0.027648 | 0.030027 | 0.029407 | 0.028053 | 0.024076 |
| MAE | 1.2914 | 1.4027 | 1.3717 | 1.3104 | 1.1259 |
| RMSE | 5.3765 | 5.6753 | 5.6403 | 5.4632 | 5.0895 |
| L1 Norm | 16,913 | 18,369 | 17,964 | 17,161 | 14,745 |
| L2 Norm | 615.27 | 649.46 | 645.46 | 625.2 | 582.44 |
| L-Infinity Norm | 26.28 | 27.31 | 36.25 | 22.54 | 18.21 |
| Li-ion battery Dataset | |||||
| MEP | 1.9111 | 2.0281 | 1.9501 | 2.0281 | 1.6381 |
| SMAPE | 0.021841 | 0.023178 | 0.022287 | 0.023178 | 0.018721 |
| MASE | 0.048692 | 0.052466 | 0.047627 | 0.049824 | 0.04046 |
| MAE | 57.209 | 60.038 | 55.99 | 58.299 | 47.221 |
| RMSE | 219.16 | 224.91 | 214.64 | 222.39 | 196.02 |
| L1 Norm | 36671 | 38484 | 35890 | 37370 | 30269 |
| L2 Norm | 5548.6 | 5694.2 | 5434.2 | 5630.5 | 4962.8 |
| L-Infinity Norm | 975 | 970.5 | 973.75 | 973.75 | 965.25 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abidi, M.H.; Mohammed, M.K.; Alkhalefah, H. Predictive Maintenance Planning for Industry 4.0 Using Machine Learning for Sustainable Manufacturing. Sustainability 2022, 14, 3387. https://doi.org/10.3390/su14063387
Abidi MH, Mohammed MK, Alkhalefah H. Predictive Maintenance Planning for Industry 4.0 Using Machine Learning for Sustainable Manufacturing. Sustainability. 2022; 14(6):3387. https://doi.org/10.3390/su14063387
Chicago/Turabian StyleAbidi, Mustufa Haider, Muneer Khan Mohammed, and Hisham Alkhalefah. 2022. "Predictive Maintenance Planning for Industry 4.0 Using Machine Learning for Sustainable Manufacturing" Sustainability 14, no. 6: 3387. https://doi.org/10.3390/su14063387
APA StyleAbidi, M. H., Mohammed, M. K., & Alkhalefah, H. (2022). Predictive Maintenance Planning for Industry 4.0 Using Machine Learning for Sustainable Manufacturing. Sustainability, 14(6), 3387. https://doi.org/10.3390/su14063387







