Development of Novel Hybrid Models for Prediction of Drought- and Stress-Tolerance Indices in Teosinte Introgressed Maize Lines Using Artificial Intelligence Techniques
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Collection
2.2. Artificial Intelligence Techniques
2.3. Hybrid Artificial Intelligence Algorithm Based on GA (Genetic Algorithm)
2.4. Statistical Indices
- Root Mean Square Error
- 2.
- Root Mean Square Error
- 3.
- Coefficient of Efficiency
- 4.
- Willmott’s Index of Agreement
3. Results and Discussion
3.1. Gamma Test (GT)
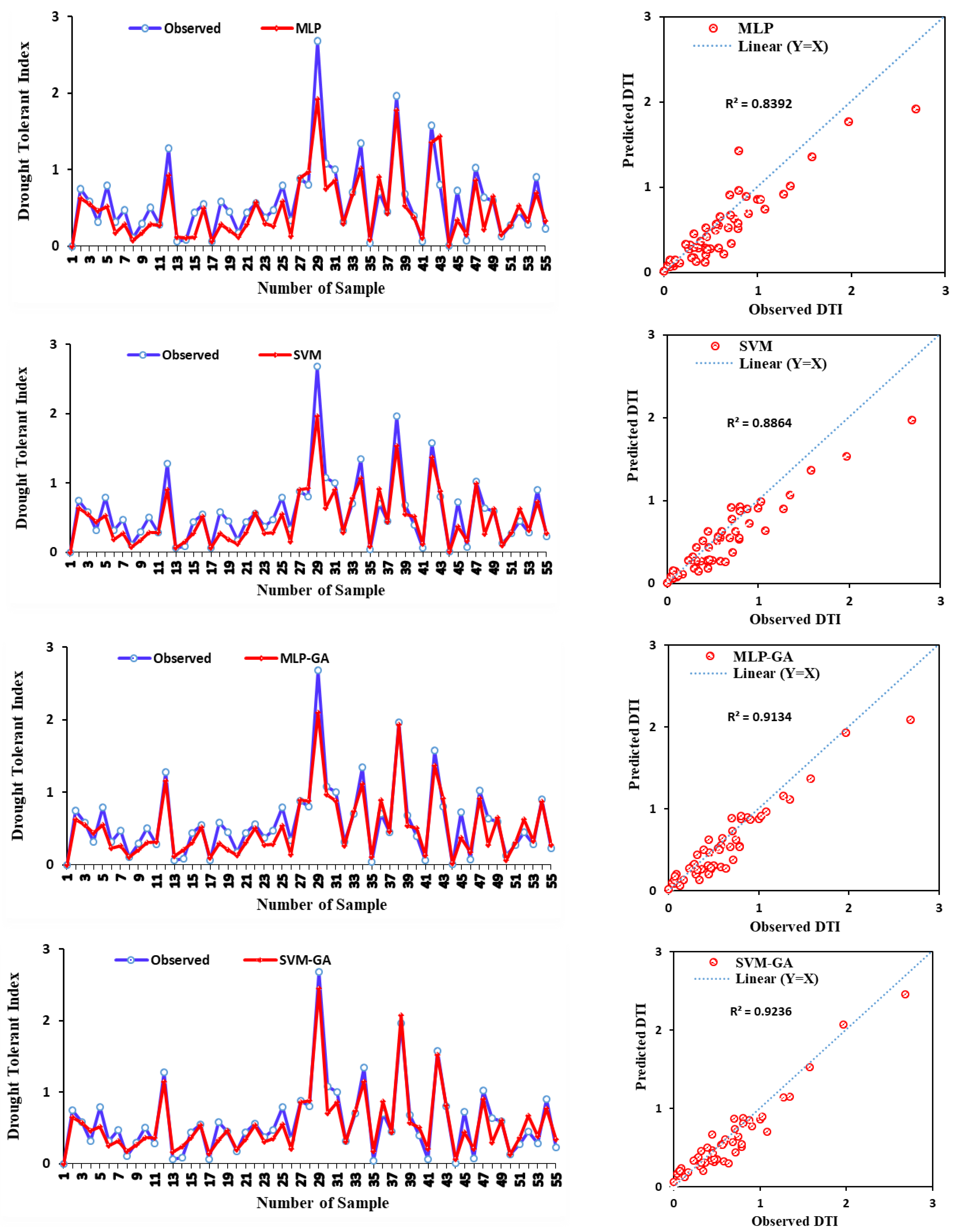
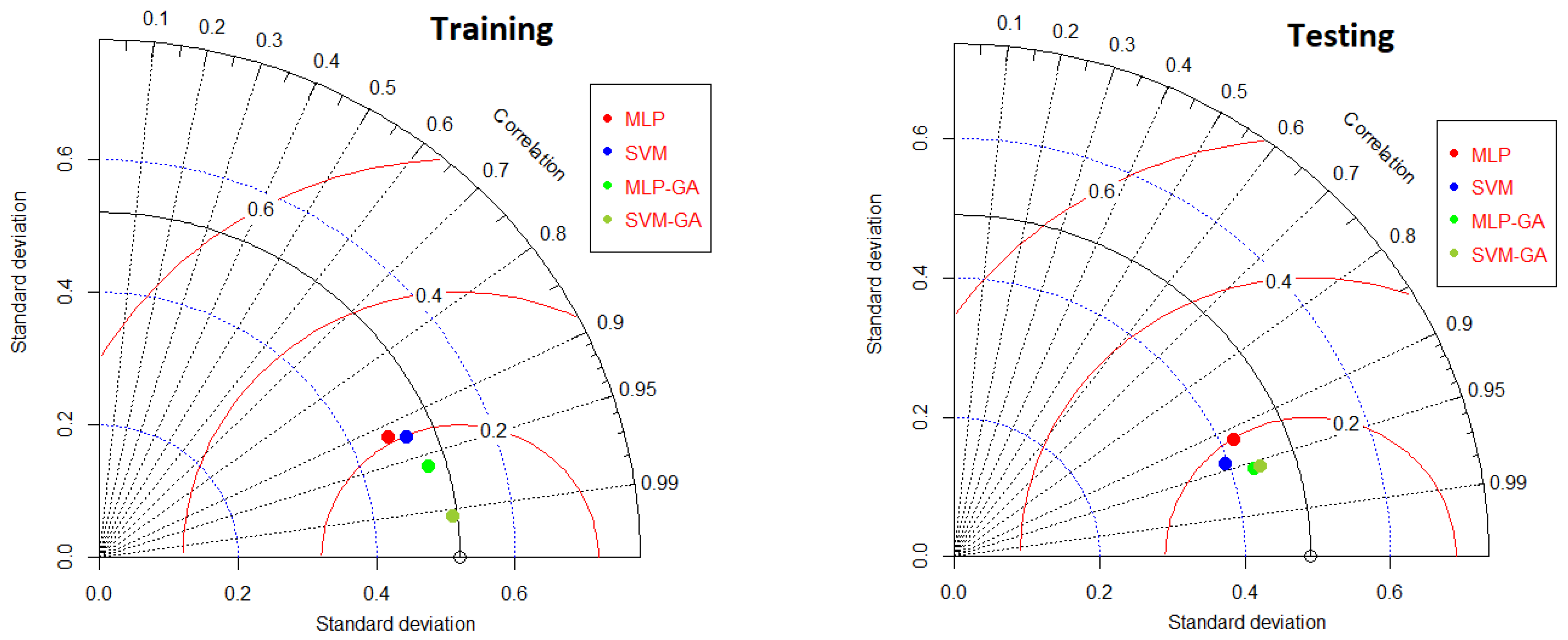
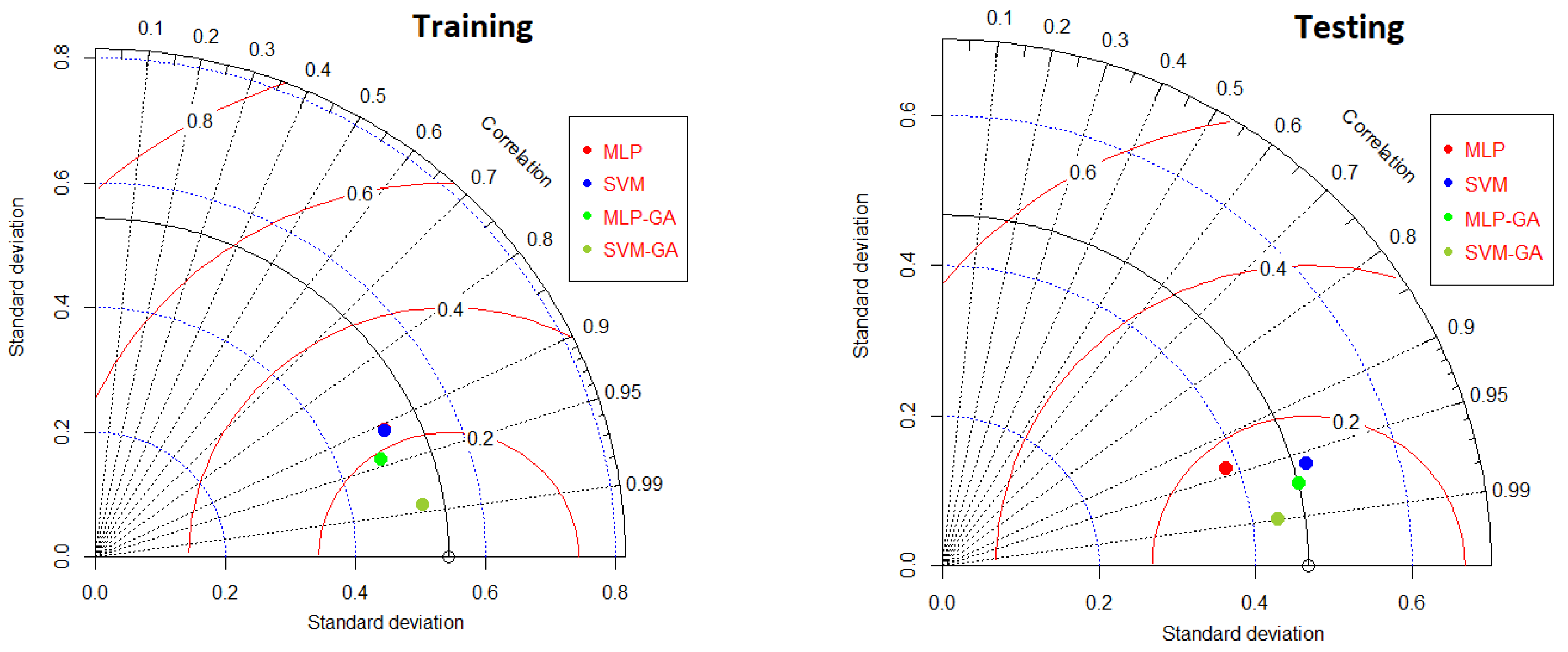
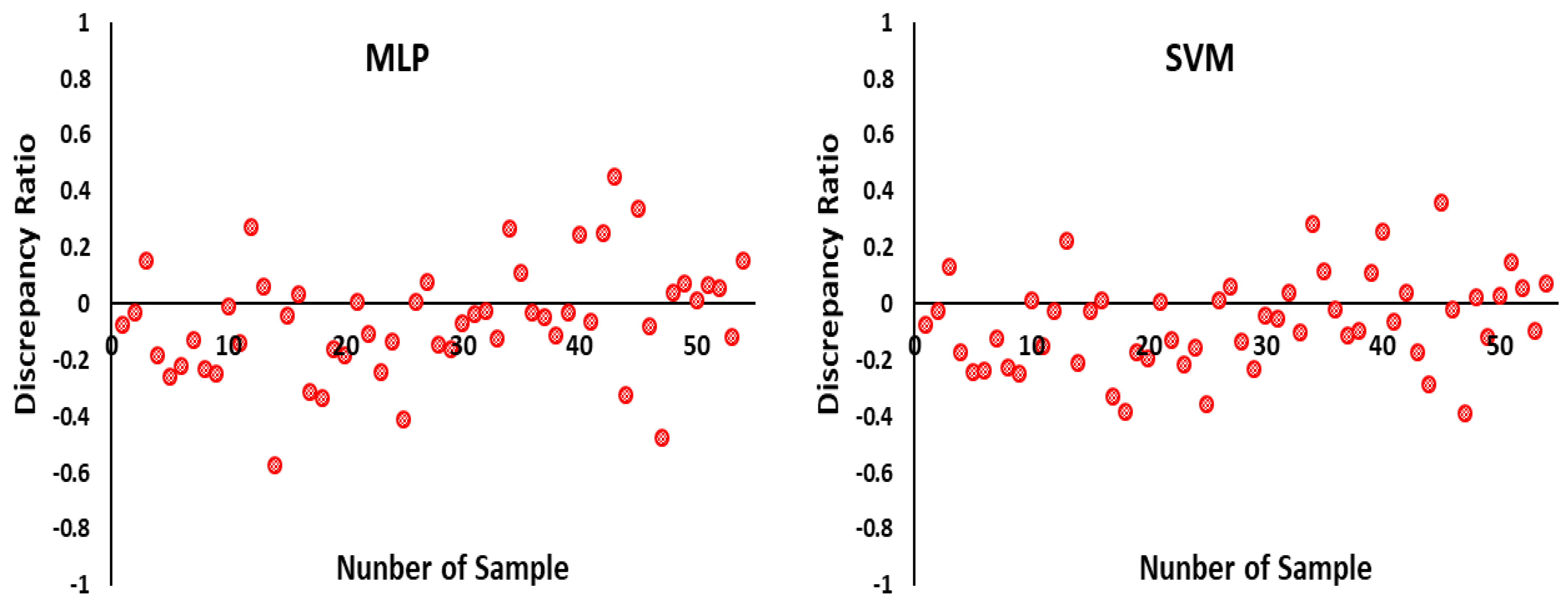
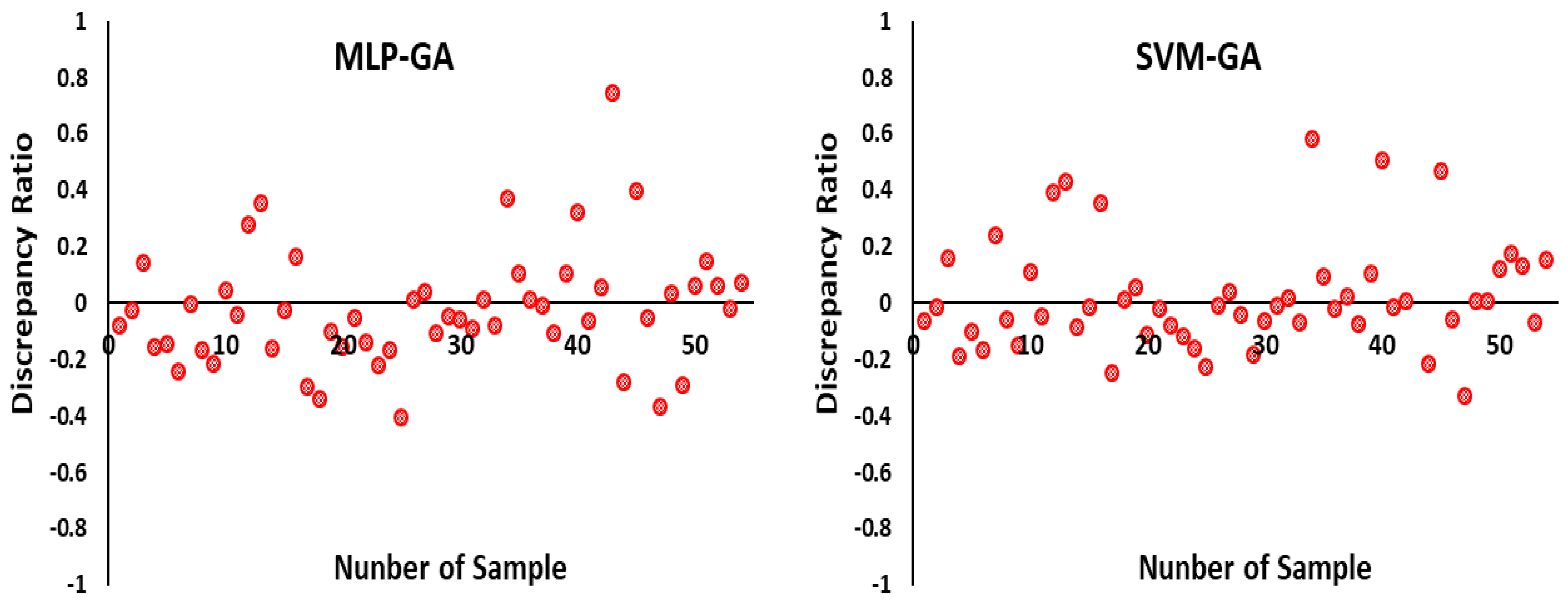
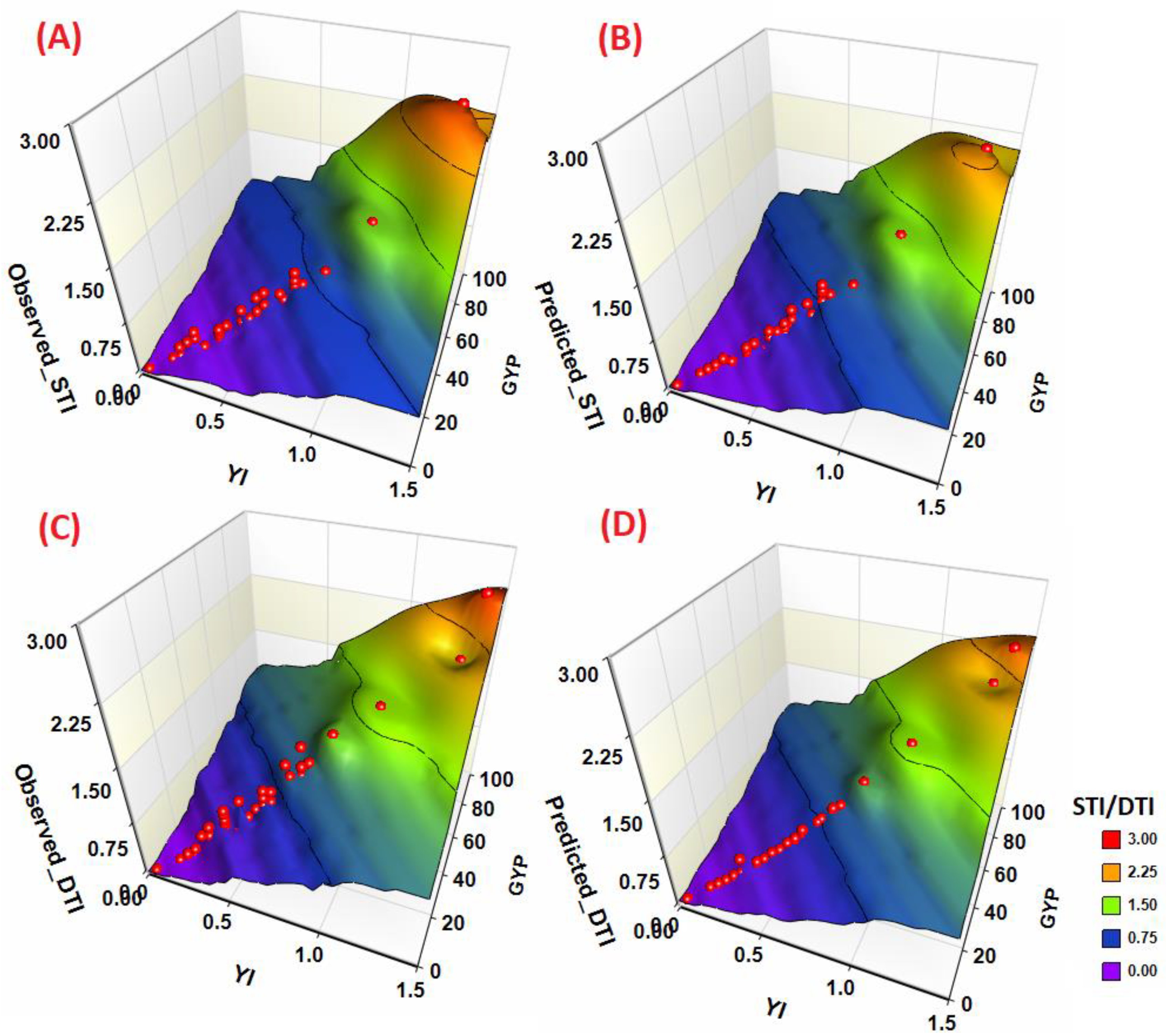
3.2. Artificial Intelligence Techniques
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kumar, A.; Singh, N.K.; Adhikari, S.; Joshi, A. Morphological and molecular characterization of teosinte derived maize population. Indian J. Genet. Plant Breed. 2019, 79, 670–677. [Google Scholar] [CrossRef]
- Alahdadi, I.; Oraki, H.; Khajani, F.P. Effect of water stress on yield and yield components of sunflower hybrids. Afr. J. Biotechnol. 2011, 10, 6504–6509. [Google Scholar] [CrossRef]
- Golbashy, M.; Ebrahimi, M.; Khorasani, S.K.; Choukan, R. Evaluation of drought tolerance of some corn (Zea mays L.) hybrids in Iran. Afr. J. Agric. Res. 2010, 5, 2714–2719. [Google Scholar] [CrossRef]
- FAO Crop Water Information: Maize. Available online: http://www.fao.org/nr/water/cropinfo-maize.html (accessed on 30 January 2022).
- Passioura, J.B. Roots and drought resistance. In Developments in Agricultural and Managed Forest Ecology; Elsevier: Amsterdam, The Netherlands, 1983; Volume 12, pp. 265–280. ISBN 0166-2287. [Google Scholar]
- Messmer, R.E. The Genetic Dissection of Key Factors Involved in the Drought Tolerance of Tropical Maize (Zea mays L.). Ph.D. Thesis, ETH, Zurich, Switzerland, 2006. [Google Scholar]
- Fischer, R.A.; Maurer, R. Drought resistance in spring wheat cultivars. I. Grain yield responses. Aust. J. Agric. Res. 1978, 29, 897–912. [Google Scholar] [CrossRef]
- Ghorbani, M.A.; Shamshirband, S.; Haghi, D.Z.; Azani, A.; Bonakdari, H.; Ebtehaj, I. Application of firefly algorithm-based support vector machines for prediction of field capacity and permanent wilting point. Soil Tillage Res. 2017, 172, 32–38. [Google Scholar] [CrossRef]
- Kim, S.; Singh, V.P. Modeling daily soil temperature using data-driven models and spatial distribution. Theor. Appl. Climatol. 2014, 118, 465–479. [Google Scholar] [CrossRef]
- Singh, V.K.; Singh, B.P.; Kisi, O.; Kushwaha, D.P. Spatial and multi-depth temporal soil temperature assessment by assimilating satellite imagery, artificial intelligence and regression based models in arid area. Comput. Electron. Agric. 2018, 150, 205–219. [Google Scholar] [CrossRef]
- Gu, Z.; Zhu, T.; Jiao, X.; Xu, J.; Qi, Z. Neural network soil moisture model for irrigation scheduling. Comput. Electron. Agric. 2021, 180, 105801. [Google Scholar] [CrossRef]
- Bhagwat, S.; Kashyap, P.S.; Singh, B.P.; Singh, V.K. Daily pan evaporation modeling in hilly region of Uttarakhand using artificial neural network. Indian J. Ecol. 2017, 44, 467–473. [Google Scholar]
- Keshtegar, B.; Piri, J.; Kisi, O. A nonlinear mathematical modeling of daily pan evaporation based on conjugate gradient method. Comput. Electron. Agric. 2016, 127, 120–130. [Google Scholar] [CrossRef]
- Khosravi, K.; Daggupati, P.; Alami, M.T.; Awadh, S.M.; Ghareb, M.I.; Panahi, M.; Pham, B.T.; Rezaie, F.; Qi, C.; Yaseen, Z.M. Meteorological data mining and hybrid data-intelligence models for reference evaporation simulation: A case study in Iraq. Comput. Electron. Agric. 2019, 167, 105041. [Google Scholar] [CrossRef]
- Kushwaha, N.L.; Rajput, J.; Elbeltagi, A.; Elnaggar, A.Y.; Sena, D.R.; Vishwakarma, D.K.; Mani, I.; Hussein, E.E. Data Intelligence Model and Meta-Heuristic Algorithms-Based Pan Evaporation Modelling in Two Different Agro-Climatic Zones: A Case Study from Northern India. Atmosphere 2021, 12, 1654. [Google Scholar] [CrossRef]
- Ramdas, S.; Singh, R.; Sharma, I. Exploring the performance of wheat production in India. J. Wheat Res. 2020, 4, 37–44. [Google Scholar]
- Sihag, P.; Tiwari, N.K.; Ranjan, S. Prediction of unsaturated hydraulic conductivity using adaptive neuro-fuzzy inference system (ANFIS). ISH J. Hydraul. Eng. 2019, 25, 132–142. [Google Scholar] [CrossRef]
- Tang, D.; Feng, Y.; Gong, D.; Hao, W.; Cui, N. Evaluation of artificial intelligence models for actual crop evapotranspiration modeling in mulched and non-mulched maize croplands. Comput. Electron. Agric. 2018, 152, 375–384. [Google Scholar] [CrossRef]
- Singh, V.K.; Kumar, D.; Kashyap, P.S.; Kisi, O. Simulation of suspended sediment based on gamma test, heuristic, and regression-based techniques. Environ. Earth Sci. 2018, 77, 708. [Google Scholar] [CrossRef]
- Citakoglu, H. Comparison of artificial intelligence techniques via empirical equations for prediction of solar radiation. Comput. Electron. Agric. 2015, 118, 28–37. [Google Scholar] [CrossRef]
- Esmaeilbeiki, F.; Nikpour, M.R.; Singh, V.K.; Kisi, O.; Sihag, P.; Sanikhani, H. Exploring the application of soft computing techniques for spatial evaluation of groundwater quality variables. J. Clean. Prod. 2020, 276, 124206. [Google Scholar] [CrossRef]
- Shukla, R.; Kumar, P.; Vishwakarma, D.K.; Ali, R.; Kumar, R.; Kuriqi, A. Modeling of stage-discharge using back propagation ANN-, ANFIS-, and WANN-based computing techniques. Theor. Appl. Climatol. 2021, 147, 867–889. [Google Scholar] [CrossRef]
- Singh, V.K.; Singh, B.P.; Kumar, A. A Comparative Study of Artificial Intelligence and Conventional Techniques for Rainfall-Runoff Modeling. Int. J. Agric. Eng. 2017, 10, 441–449. [Google Scholar] [CrossRef]
- Ryabchuk, N.; Grishko, N.; Grishko, V.; Rudenko, A.; Petryk, V.; Bapiyev, I.; Fedushko, S. Artificial Intelligence Technologies Using in Social Engineering Attacks. In Proceedings of the International Workshop on Cyber Hygiene (CybHyg-2019) [CEUR Workshop Proceedings], Kyiv, Ukraine, 30 November 2020; Volume 2654, pp. 546–555. [Google Scholar]
- Tahir, N.M.T.; Ausat, A.N.; Bature, U.I.; Abubakar, K.A.; Gambo, I. Off-line Handwritten Signature Verification System: Artificial Neural Network Approach. Int. J. Intell. Syst. Appl. 2021, 13, 45–57. [Google Scholar] [CrossRef]
- Singh, V.K.; Kumar, P.; Singh, B.P.; Malik, A. A comparative study of adaptive neuro fuzzy inference system (ANFIS) and multiple linear regression (MLR) for rainfall-runoff modelling. Int. J. Nat. Sci. 2016, 7, 714–723. [Google Scholar]
- Singh, V.K.; Kumar, P.; Singh, B.P. Rainfall-runoff modeling using artificial neural networks (ANNs) and multiple linear regression (MLR) techniques. Indian J. Ecol. 2016, 43, 436–442. [Google Scholar]
- Darbandi, S.; Pourhosseini, F.A. River flow simulation using a multilayer perceptron-firefly algorithm model. Appl. Water Sci. 2018, 8, 85. [Google Scholar] [CrossRef] [Green Version]
- Heddam, S.; Sanikhani, H.; Kisi, O. Application of artificial intelligence to estimate phycocyanin pigment concentration using water quality data: A comparative study. Appl. Water Sci. 2019, 9, 164. [Google Scholar] [CrossRef] [Green Version]
- de Oliveira, M.F.; dos Santos, A.F.; Kazama, E.H.; de Souza Rolim, G.; da Silva, R.P. Determination of application volume for coffee plantations using artificial neural networks and remote sensing. Comput. Electron. Agric. 2021, 184, 106096. [Google Scholar] [CrossRef]
- Özger, M.; Başakın, E.E.; Ekmekcioğlu, Ö.; Hacısüleyman, V. Comparison of wavelet and empirical mode decomposition hybrid models in drought prediction. Comput. Electron. Agric. 2020, 179, 105851. [Google Scholar] [CrossRef]
- Sayari, S.; Mahdavi-Meymand, A.; Zounemat-Kermani, M. Irrigation water infiltration modeling using machine learning. Comput. Electron. Agric. 2021, 180, 105921. [Google Scholar] [CrossRef]
- Tabari, H.; Kisi, O.; Ezani, A.; Talaee, P.H. SVM, ANFIS, regression and climate based models for reference evapotranspiration modeling using limited climatic data in a semi-arid highland environment. J. Hydrol. 2012, 444, 78–89. [Google Scholar] [CrossRef]
- Tabari, H.; Martinez, C.; Ezani, A.; Hosseinzadeh Talaee, P. Applicability of support vector machines and adaptive neurofuzzy inference system for modeling potato crop evapotranspiration. Irrig. Sci. 2013, 31, 575–588. [Google Scholar] [CrossRef]
- Wen, X.; Si, J.; He, Z.; Wu, J.; Shao, H.; Yu, H. Support-Vector-Machine-Based Models for Modeling Daily Reference Evapotranspiration with Limited Climatic Data in Extreme Arid Regions. Water Resour. Manag. 2015, 29, 3195–3209. [Google Scholar] [CrossRef]
- Shiri, J.; Nazemi, A.H.; Sadraddini, A.A.; Landeras, G.; Kisi, O.; Fakheri Fard, A.; Marti, P. Comparison of heuristic and empirical approaches for estimating reference evapotranspiration from limited inputs in Iran. Comput. Electron. Agric. 2014, 108, 230–241. [Google Scholar] [CrossRef]
- Seifi, A.; Soroush, F. Pan evaporation estimation and derivation of explicit optimized equations by novel hybrid meta-heuristic ANN based methods in different climates of Iran. Comput. Electron. Agric. 2020, 173, 105418. [Google Scholar] [CrossRef]
- Oh, M.S.; Chen, Z.; Jahanshiri, E.; Isa, D.; Wong, Y.W. An economic feasibility assessment framework for underutilised crops using Support Vector Machine. Comput. Electron. Agric. 2020, 168, 105116. [Google Scholar] [CrossRef]
- Pourmohammadali, B.; Salehi, M.H.; Hosseinifard, S.J.; Boroujeni, I.E.; Shirani, H. Studying the relationships between nutrients in pistachio leaves and its yield using hybrid GA-ANN model-based feature selection. Comput. Electron. Agric. 2020, 172, 105352. [Google Scholar] [CrossRef]
- Vishwakarma, D.K.; Pandey, K.; Kaur, A.; Kushwaha, N.L.; Kumar, R.; Ali, R.; Elbeltagi, A.; Kuriqi, A. Methods to estimate evapotranspiration in humid and subtropical climate conditions. Agric. Water Manag. 2022, 261, 107378. [Google Scholar] [CrossRef]
- Singh, V.K.; Kumar, D.; Kashyap, P.S.; Singh, P.K.; Kumar, A.; Singh, S.K. Modelling of soil permeability using different data driven algorithms based on physical properties of soil. J. Hydrol. 2020, 580, 124223. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar] [CrossRef] [Green Version]
- Stamenković, L.J. Application of ANN and SVM for prediction nutrients in rivers. J. Environ. Sci. Health Part A 2021, 56, 867–873. [Google Scholar] [CrossRef]
- Rahgoshay, M.; Feiznia, S.; Arian, M.; Hashemi, S.A.A. Modeling daily suspended sediment load using improved support vector machine model and genetic algorithm. Environ. Sci. Pollut. Res. 2018, 25, 35693–35706. [Google Scholar] [CrossRef]
- Massah, J.; Vakilian, K.A.; Shabanian, M.; Shariatmadari, S.M. Design, development, and performance evaluation of a robot for yield estimation of kiwifruit. Comput. Electron. Agric. 2021, 185, 106132. [Google Scholar] [CrossRef]



| Model | Output/Input Combination | Gamma | Gradient | SE |
|---|---|---|---|---|
| D-1 | DTI = f (DOA, DOS, DTS, PHt, EL, NK, GYP) | 0.0085 | 0.0470 | 0.0029 |
| D-2 | DTI = f (DOA, DOS, DTS, EL, NK, GYP) | 0.0071 | 0.0466 | 0.0020 |
| D-3 | DTI = f (DOA, DOS, DTS, EL, GYP) | 0.0060 | 0.0427 | 0.0045 |
| D-4 | DTI = f (DOA, DOS, DTS, EL, NK,) | 0.0077 | 0.0538 | 0.0021 |
| D-5 | DTI = f (DOA, DTS, PHt, EL, NK, GYP) | 0.0093 | 0.0468 | 0.0041 |
| D-6 | DTI = f (DOA, DOS, YI, GYP) | 0.0042 | 0.0452 | 0.0016 |
| D-7 | STI = f (PHt, EL, NK, YI, GYP) | 0.0056 | 0.0508 | 0.0035 |
| S-1 | STI = f (DOA, DOS, DTS, PHt, EL, NK, GYP) | 0.0026 | 0.0550 | 0.0041 |
| S-2 | STI = f (DOA, DOS, DTS, EL, NK, GYP) | 0.0071 | 0.0497 | 0.0037 |
| S-3 | STI = f (DOA, DOS, DTS, EL, GYP) | 0.0042 | 0.0689 | 0.0033 |
| S-4 | STI = f (DOA, DOS, DTS, EL, NK,) | 0.0038 | 0.0810 | 0.0027 |
| S-5 | STI = f (DOA, DTS, PHt, EL, NK, GYP) | 0.0053 | 0.0791 | 0.0035 |
| S-6 | STI = f (DOA, DOS, YI, GYP) | 0.0021 | 0.0434 | 0.0026 |
| S-7 | STI = f (PHt, EL, NK, YI, GYP) | 0.0062 | 0.0561 | 0.0037 |
| Model | Parameters of the Algorithms for DTI | Parameters of the Algorithms for STI |
|---|---|---|
| MLP | The transfer function is tan hyperbolic; Learning rule is delta bar delta; Rate of learning is 0.2; Number of momentum values is 0.1; Neurons in the hidden layer = 19; Iteration is 1000; Hidden layers in the structure = 1. | The transfer function is tan hyperbolic; Learning rule is delta bar delta; Rate of learning is 0.2; Number of momentum values is 0.1; Neurons in the hidden layer = 23; Iteration is 1000; Hidden layers in the structure = 1. |
| SVM | SVM type: regression; Kernel function: Radial; Cast: 11; Gamma: 0.25. | SVM type: regression; Kernel function: Radial; Cast: 13; Gamma: 0.25. |
| MLP-GA | GA (Population size: 30; Generation: 100; Crossover: 0.9; Mutation: 0.001). MLP (Rate of learning is 0.2; Number of momentum values is 0.1; Neurons in the hidden layer = 32; Iteration is 1000; Hidden layers in the structure = 1). | GA (Population size: 32; Generation: 100; Crossover: 0.9; Mutation: 0.001). MLP (Rate of learning is 0.2; Number of momentum values is 0.1; Neurons in the hidden layer = 51; Iteration is 1000; Hidden layers in the structure = 1). |
| SVM-GA | GA (Population size: 30; Generation: 100; Crossover: 0.90; Mutation: 0.001). SVM (Kernel function: Radial; Cast: 31; Gamma: 0.1). | GA (Population size: 40; Generation: 100; Crossover: 0.90; Mutation: 0.001). SVM (Kernel function: Radial; Cast: 18; Gamma: 0.1). |
| Model | Training | Testing | ||||||
|---|---|---|---|---|---|---|---|---|
| RMSE | R2 | NSE | WI | RMSE | R2 | NSE | WI | |
| MLP | 0.041 | 0.839 | 0.836 | 0.946 | 0.025 | 0.839 | 0.799 | 0.932 |
| SVM | 0.038 | 0.855 | 0.855 | 0.957 | 0.023 | 0.886 | 0.830 | 0.936 |
| MLP-GA | 0.028 | 0.921 | 0.921 | 0.978 | 0.020 | 0.910 | 0.890 | 0.964 |
| SVM-GA | 0.013 | 0.984 | 0.984 | 0.996 | 0.018 | 0.916 | 0.892 | 0.966 |
| Model | Training | Testing | ||||||
|---|---|---|---|---|---|---|---|---|
| RMSE | R2 | NSE | WI | RMSE | R2 | NSE | WI | |
| MLP | 0.044 | 0.824 | 0.824 | 0.946 | 0.023 | 0.884 | 0.815 | 0.933 |
| SVM | 0.044 | 0.826 | 0.826 | 0.946 | 0.017 | 0.919 | 0.898 | 0.976 |
| MLP-GA | 0.037 | 0.885 | 0.878 | 0.959 | 0.015 | 0.944 | 0.928 | 0.982 |
| SVM-GA | 0.018 | 0.972 | 0.970 | 0.991 | 0.009 | 0.978 | 0.973 | 0.992 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, A.; Singh, V.K.; Saran, B.; Al-Ansari, N.; Singh, V.P.; Adhikari, S.; Joshi, A.; Singh, N.K.; Vishwakarma, D.K. Development of Novel Hybrid Models for Prediction of Drought- and Stress-Tolerance Indices in Teosinte Introgressed Maize Lines Using Artificial Intelligence Techniques. Sustainability 2022, 14, 2287. https://doi.org/10.3390/su14042287
Kumar A, Singh VK, Saran B, Al-Ansari N, Singh VP, Adhikari S, Joshi A, Singh NK, Vishwakarma DK. Development of Novel Hybrid Models for Prediction of Drought- and Stress-Tolerance Indices in Teosinte Introgressed Maize Lines Using Artificial Intelligence Techniques. Sustainability. 2022; 14(4):2287. https://doi.org/10.3390/su14042287
Chicago/Turabian StyleKumar, Amarjeet, Vijay Kumar Singh, Bhagwat Saran, Nadhir Al-Ansari, Vinay Pratap Singh, Sneha Adhikari, Anjali Joshi, Narendra Kumar Singh, and Dinesh Kumar Vishwakarma. 2022. "Development of Novel Hybrid Models for Prediction of Drought- and Stress-Tolerance Indices in Teosinte Introgressed Maize Lines Using Artificial Intelligence Techniques" Sustainability 14, no. 4: 2287. https://doi.org/10.3390/su14042287
APA StyleKumar, A., Singh, V. K., Saran, B., Al-Ansari, N., Singh, V. P., Adhikari, S., Joshi, A., Singh, N. K., & Vishwakarma, D. K. (2022). Development of Novel Hybrid Models for Prediction of Drought- and Stress-Tolerance Indices in Teosinte Introgressed Maize Lines Using Artificial Intelligence Techniques. Sustainability, 14(4), 2287. https://doi.org/10.3390/su14042287








