Intelligent Data Analysis for Infection Spread Prediction
Abstract
:1. Introduction
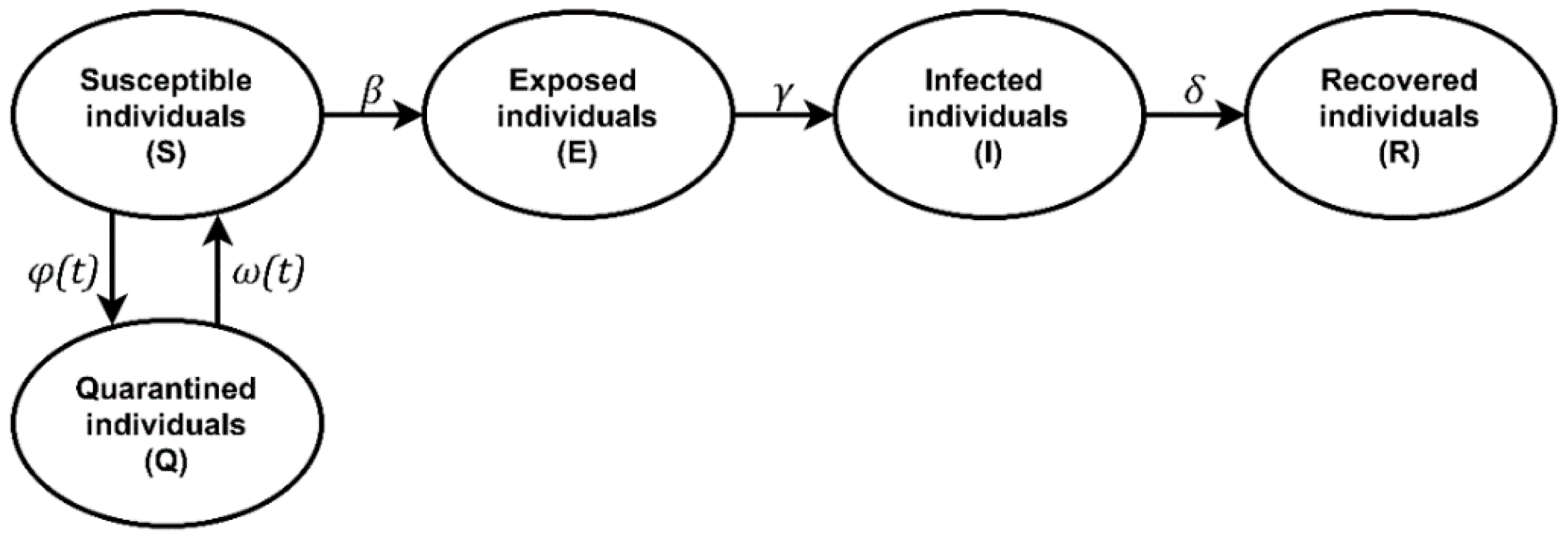
2. Materials and Methods
2.1. Simulation Tools
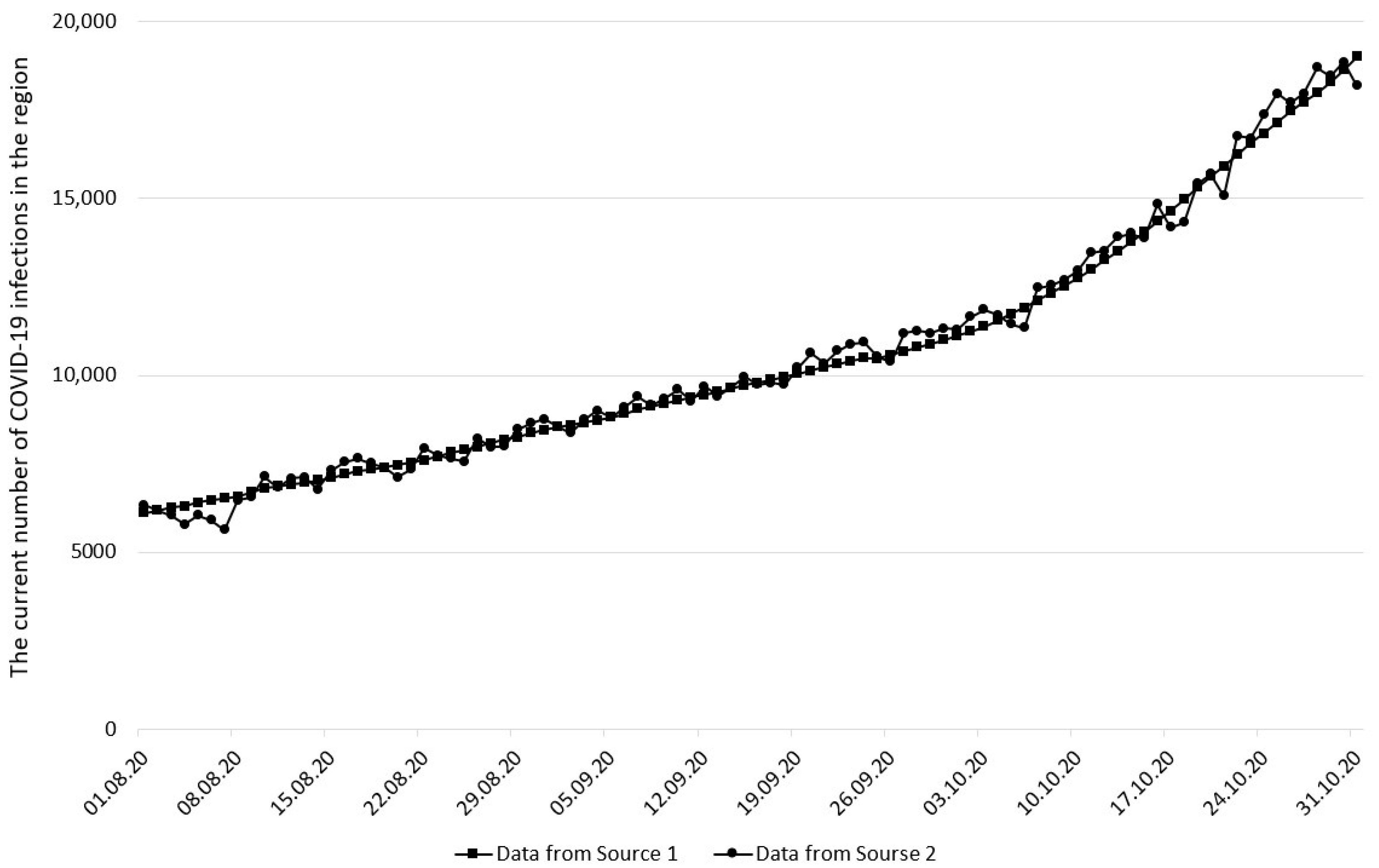
2.2. Input Data
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ali, I.; Alharbi, O.M.L. COVID-19: Disease, management, treatment, and social impact. Sci. Total Environ. 2020, 728, 138861. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Fan, C.; Li, M.; Nie, H.L.; Wang, F.B.; Wang, H.; Wang, R.; Xia, J.; Zheng, X.; Zuo, X.; et al. COVID-19: A Call for Physical Scientists and Engineers. ACS Nano 2020, 14, 3747–3754. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Berawi, M.A. Empowering Healthcare, Economic and Social Resilience during Global Pandemic Covid-19. Int. J. Technol. 2020, 11, 436. [Google Scholar] [CrossRef]
- Rothan, H.A.; Byrareddy, S.N. The epidemiology and pathogenesis of coronavirus disease (COVID-19) outbreak. J. Autoimmun. 2020, 109, 102433. [Google Scholar] [CrossRef] [PubMed]
- Sohrabi, C.; Alsafi, Z.; O’Neill, N.; Khan, M.; Kerwan, A.; Al-Jabir, A.; Iosifidis, C.; Agha, R. World Health Organization declares global emergency: A review of the 2019 novel coronavirus (COVID-19). Int. J. Surg. 2020, 76, 71–76. [Google Scholar] [CrossRef]
- Peeri, N.C.; Shrestha, N.; Rahman, M.S.; Zaki, R.; Tan, Z.; Bibi, S.; Baghbanzadeh, M.; Aghamohammadi, N.; Zhang, W.; Haque, U. The SARS, MERS and novel coronavirus (COVID-19) epidemics, the newest and biggest global health threats: What lessons have we learned? Int. J. Epidemiol. 2020, 49, 717–726. [Google Scholar] [CrossRef] [Green Version]
- Narayan, P.K.; Phan, D.H.B.; Liu, G. COVID-19 lockdowns, stimulus packages, travel bans, and stock returns. Financ. Res. Lett. 2021, 38, 101732. [Google Scholar] [CrossRef]
- Bol, D.; Giani, M.; Blais, A.; Loewen, P.J. The effect of COVID-19 lockdowns on political support: Some good news for democracy? Eur. J. Political Res. 2021, 60, 497–505. [Google Scholar] [CrossRef]
- Akhtaruzzaman, M.; Boubaker, A.; Sensoy, A. Financial contagion during COVID-19 crisis. Financ. Res. Lett. 2021, 38, 101604. [Google Scholar] [CrossRef]
- Wang, J. Fast Identification of Possible Drug Treatment of Coronavirus Disease-19 (COVID-19) through Computational Drug Repurposing Study. J. Chem. Inf. Modeling 2020, 60, 3277–3286. [Google Scholar] [CrossRef]
- Patchsung, M.; Jantarug, K.; Pattama, A.; Aphicho, K.; Suraritdechachai, S.; Meesawat, P.; Sappakhaw, K.; Leelahakorn, N.; Ruenkam, T.; Wongsatit, T.; et al. Clinical validation of a Cas13-based assay for the detection of SARS-CoV-2 RNA. Nat. Biomed. Eng. 2020, 4, 1140–1149. [Google Scholar] [CrossRef] [PubMed]
- Linka, K.; Peirlinck, M.; Sahli Costabal, F.; Kuhl, E. Outbreak dynamics of COVID-19 in Europe and the effect of travel restrictions. Comput. Methods Biomech. Biomed. Eng. 2020, 23, 710–717. [Google Scholar] [CrossRef]
- Ahmed, N.; Michelin, R.A.; Xue, W.; Ruj, S.; Malaney, R.; Kanhere, S.S.; Seneviratne, A.; Hu, W.; Janicke, H.; Jha, S.K. A Survey of COVID-19 Contact Tracing Apps. IEEE Access 2020, 8, 134577–134601. [Google Scholar] [CrossRef]
- Lampos, V.; Majumder, M.S.; Yom-Tov, E.; Edelstein, M.; Moura, S.; Hamada, Y.; Rangaka, M.X.; McKendry, R.A.; Cox, I.J. Tracking COVID-19 using online search. Digit. Med. 2021, 4, 17. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; Chen, H. Modeling the epidemic dynamics and control of COVID-19 outbreak in China. Quant. Biol. 2020, 8, 11–19. [Google Scholar] [CrossRef] [Green Version]
- Nikolopoulos, K.; Punia, S.; Schäfers, A.; Tsinopoulos, C.; Vasilakis, C. Forecasting and planning during a pandemic: COVID-19 growth rates, supply chain disruptions, and governmental decisions. Eur. J. Oper. Res. 2021, 290, 99–115. [Google Scholar] [CrossRef]
- Naudé, W. Artificial intelligence vs COVID-19: Limitations, constraints and pitfalls. AI Soc. 2020, 35, 761–765. [Google Scholar] [CrossRef]
- Ozturk, T.; Talo, M.; Yildirim, E.A.; Baloglu, U.B.; Yildirim, O.; Rajendra Acharya, U. Automated detection of COVID-19 cases using deep neural networks with X-ray images. Comput. Biol. Med. 2020, 121, 103792. [Google Scholar] [CrossRef]
- Loey, M.; Smarandache, F.; M. Khalifa, N.E. Within the Lack of Chest COVID-19 X-ray Dataset: A Novel Detection Model Based on GAN and Deep Transfer Learning. Symmetry 2020, 12, 651. [Google Scholar] [CrossRef] [Green Version]
- Ardabili, S.F.; Mosavi, A.; Ghamisi, P.; Ferdinand, F.; Varkonyi-Koczy, A.R.; Reuter, U.; Rabczuk, T.; Atkinson, P.M. COVID-19 Outbreak Prediction with Machine Learning. Algorithms 2020, 13, 249. [Google Scholar] [CrossRef]
- Zheng, N.; Du, S.; Wang, J.; Zhang, H.; Cui, W.; Kang, Z.; Yang, T.; Lou, B.; Chi, Y.; Long, H.; et al. Predicting COVID-19 in China Using Hybrid AI Model. IEEE Trans. Cybern. 2020, 50, 2891–2904. [Google Scholar] [CrossRef] [PubMed]
- Currie, C.S.M.; Fowler, J.W.; Kotiadis, K.; Monks, T.; Onggo, B.S.; Robertson, D.A.; Tako, A.A. How simulation modelling can help reduce the impact of COVID-19. J. Simul. 2020, 14, 83–97. [Google Scholar] [CrossRef] [Green Version]
- Peter, O.; Shaikh, A.; Ibrahim, M.; Sooppy Nisar, K.; Baleanu, D.; Khan, I.; Abioye, A. Analysis and Dynamics of Fractional Order Mathematical Model of COVID-19 in Nigeria Using Atangana-Baleanu Operator. Comput. Mater. Contin. 2021, 66, 1823–1848. [Google Scholar] [CrossRef]
- Small, M.; Cavanagh, D. Modelling Strong Control Measures for Epidemic Propagation with Networks—A COVID-19 Case Study. IEEE Access 2020, 8, 109719–109731. [Google Scholar] [CrossRef] [PubMed]
- Cuevas, E. An agent-based model to evaluate the COVID-19 transmission risks in facilities. Comput. Biol. Med. 2020, 121, 103827. [Google Scholar] [CrossRef] [PubMed]
- Hernandez-Vargas, E.A.; Velasco-Hernandez, J.X. In-host Mathematical Modelling of COVID-19 in Humans. Annu. Rev. Control 2020, 50, 448–456. [Google Scholar] [CrossRef]
- Redko, S.G.; Shadrin, A.D. Quality Assessment in cyber-physical systems. In Cyber-Physical Systems and Control; Arseniev, D.G., Overmeyer, L., Kälviäinen, H., Katalinić, B., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 124–130. [Google Scholar]
- Santosh, K.C. COVID-19 Prediction Models and Unexploited Data. J. Med. Syst. 2020, 44, 170. [Google Scholar] [CrossRef]
- Taylor, L. The price of certainty: How the politics of pandemic data demand an ethics of care. Big Data Soc. 2020, 7, 1–7. [Google Scholar] [CrossRef]
- Chowdhury, M.J.M.; Ferdous, M.S.; Biswas, K.; Chowdhury, N.; Muthukkumarasamy, V. COVID-19 Contact Tracing: Challenges and Future Directions. IEEE Access 2020, 8, 225703–225729. [Google Scholar] [CrossRef]
- Ahmad, N.; Chauhan, P. State of Data Privacy During COVID-19. Computer 2020, 53, 119–122. [Google Scholar] [CrossRef]
- Upadhyay, R.K.; Roy, P. Spread of a disease and its effect on population dynamics in an eco-epidemiological system. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 4170–4184. [Google Scholar] [CrossRef]
- Tsvetkova, N.A.; Tukkel, I.L.; Ablyazov, V.I. Simulation modeling the spread of innovations. In Proceedings of the XX IEEE International Conference on Soft Computing and Measurements (SCM), Saint Petersburg, Russia, 24–26 May 2017; pp. 675–677. [Google Scholar]
- García- García, J.A.; Enríquez, J.G.; Ruiz, M.; Arévalo, C.; Jiménez-Ramírez, A. Software Process Simulation Modeling: Systematic literature review. Comput. Stand. Interfaces 2020, 70, 103425. [Google Scholar] [CrossRef]
- Silva, P.L.C.; Batista, P.V.C.; Lima, H.S.; Alves, M.A.; Guimarães, F.G.; Silva, R.C.P. COVID-ABS: An agent-based model of COVID-19 epidemic to simulate health and economic effects of social distancing interventions. Chaos Solitons Fractals 2020, 139, 110088. [Google Scholar] [CrossRef] [PubMed]
- Shamil, M.S.; Farheen, F.; Ibtehaz, N.; Khan, I.M.; Rahman, M.S. An Agent-Based Modeling of COVID-19: Validation, Analysis, and Recommendations. Cogn. Comput. 2021, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Cotfas, L.A.; Delcea, C.; Milne, R.J.; Salari, M. Evaluating Classical Airplane Boarding Methods Considering COVID-19 Flying Restrictions. Symmetry 2020, 12, 1087. [Google Scholar] [CrossRef]
- Milne, R.J.; Delcea, C.; Cotfas, L.A.; Ioanas, C. Evaluation of Boarding Methods Adapted for Social Distancing When Using Apron Buses. IEEE Access 2020, 8, 151650–151667. [Google Scholar] [CrossRef]
- Chen, D.; Yang, Y.; Zhang, Y.; Yu, W. Prediction of COVID-19 spread by sliding mSEIR observer. Sci. China Inf. Sci. 2020, 63, 222203. [Google Scholar] [CrossRef]
- Crokidakis, N. Modeling the early evolution of the COVID-19 in Brazil: Results from a Susceptible–Infectious–Quarantined–Recovered (SIQR) model. Int. J. Mod. Phys. C 2020, 31, 2050135. [Google Scholar] [CrossRef]
- Ma, W.; Song, M.; Takeuchi, Y. Global stability of an SIR epidemic model with time delay. Appl. Math. Lett. 2004, 17, 1141–1145. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Xu, Z.; Wu, Z.; Bai, Y. COVID-19 Spreading Prediction with enhanced SEIR model. In Proceedings of the International Conference on Artificial Intelligence and Computer Engineering (ICAICE), Beijing, China, 23–25 October 2020; 2020; pp. 383–386. [Google Scholar]
- Mohammed, M.B.; Salsabil, L.; Tanaaz, S.S.; Shahriar, M.; Fahmin, A. An Extensive Analysis of the Effect of Social Distancing in Transmission of COVID-19 in Bangladesh by the Aid of a Modified SEIRD Model. In Proceedings of the 2020 2nd International Conference on Advanced Information and Communication Technology (ICAICT), Dhaka, Bangladesh, 28–29 November 2020; pp. 422–427. [Google Scholar]
- Calafiore, G.C.; Novara, C.; Possieri, C. A time-varying SIRD model for the COVID-19 contagion in Italy. Annu. Rev. Control 2020, 50, 361–372. [Google Scholar] [CrossRef]
- Sakib, N.; Tian, S.; Haque, M.M.; Khan, R.A.; Ahamed, S.I. SepINav (Sepsis ICU Navigator): A data-driven software tool for sepsis monitoring and intervention using Bayesian Online Change Point Detection. SoftwareX 2021, 14, 100689. [Google Scholar] [CrossRef]
- Salman, A.M.; Ahmed, I.; Mohd, M.H.; Jamiluddin, M.S.; Dheyab, M.A. Scenario analysis of COVID-19 transmission dynamics in Malaysia with the possibility of reinfection and limited medical resources scenarios. Comput. Biol. Med. 2021, 133, 104372. [Google Scholar] [CrossRef] [PubMed]
- Borovkov, A.I.; Bolsunovskaya, M.V.; Gintciak, A.M.; Kudryavtseva, T.J. Simulation Modelling Application for Balancing Epidemic and Economic Crisis in the Region. Int. J. Technol. 2020, 11, 1579. [Google Scholar] [CrossRef]
- Jinjarak, Y.; Ahmed, R.; Nair-Desai, S.; Xin, W.; Aizenman, J. Accounting for Global COVID-19 Diffusion Patterns, January–April 2020. Econ. Disasters Clim. Chang. 2020, 4, 515–559. [Google Scholar] [CrossRef] [PubMed]
- Ramaci, T.; Barattucci, M.; Ledda, C.; Rapisarda, V. Social Stigma during COVID-19 and its Impact on HCWs Outcomes. Sustainability 2020, 12, 3834. [Google Scholar] [CrossRef]
- Shevlin, M.; Nolan, E.; Owczarek, M.; McBride, O.; Murphy, J.; Gibson Miller, J.; Hartman, T.K.; Levita, L.; Mason, L.; Martinez, A.P.; et al. COVID-19-related anxiety predicts somatic symptoms in the UK population. Br. J. Health Psychol. 2020, 25, 875–882. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Pan, R.; Wan, X.; Tan, Y.; Xu, L.; Ho, C.S.; Ho, R.C. Immediate Psychological Responses and Associated Factors during the Initial Stage of the 2019 Coronavirus Disease (COVID-19) Epidemic among the General Population in China. Int. J. Environ. Res. Public Health 2020, 17, 1729. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lai, J.; Ma, S.; Wang, Y.; Cai, Z.; Hu, J.; Wei, N.; Wu, J.; Du, H.; Chen, T.; Li, R.; et al. Factors Associated with Mental Health Outcomes Among Health Care Workers Exposed to Coronavirus Disease 2019. JAMA Netw. Open 2020, 3, e203976. [Google Scholar] [CrossRef]
- Tosepu, R.; Gunawan, J.; Effendy, D.S.; Ahmad, L.O.A.I.; Lestari, H.; Bahar, H.; Asfian, P. Correlation between Weather and Covid-19 Pandemic in Jakarta, Indonesia. Sci. Total Environ. 2020, 725, 138436. [Google Scholar] [CrossRef]
- Liu, J.; Zhou, J.; Yao, J.; Zhang, X.; Li, L.; Xu, X.; He, X.; Wang, B.; Fu, S.; Niu, T.; et al. Impact of Meteorological Factors on the COVID-19 Transmission: A Multi-City Study in China. Sci. Total Environ. 2020, 726, 138513. [Google Scholar] [CrossRef]
- Lurie, N.; Saville, M.; Hatchett, R.; Halton, J. Developing Covid-19 Vaccines at Pandemic Speed. N. Engl. J. Med. 2020, 382, 1969–1973. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Huang, T.; Wang, Y.; Wang, Z.; Liang, Y.; Huang, T.; Zhang, H.; Sun, W.; Wang, Y. COVID-19 Patients’ Clinical Characteristics, Discharge Rate, and Fatality Rate of Meta-analysis. J. Med. Virol. 2020, 92, 577–583. [Google Scholar] [CrossRef] [PubMed]
- Lazarus, J.V.; Ratzan, S.C.; Palayew, A.; Gostin, L.O.; Larson, H.J.; Rabin, K.; Kimball, S.; El-Mohandes, A. A Global Survey of Potential Acceptance of a COVID-19 Vaccine. Nat. Med. 2021, 27, 225–228. [Google Scholar] [CrossRef] [PubMed]
- Siegenfeld, A.F.; Taleb, N.N.; Bar-Yam, Y. Opinion: What Models Can and Cannot Tell Us about COVID-19. Proc. Natl. Acad. Sci. USA 2020, 117, 16092–16095. [Google Scholar] [CrossRef] [PubMed]
- Mahmud, S.G.; Mishu, M.C.; Nandi, D. Predicting Spread, Recovery and Death Due to COVID-19 Using a Time-Series Model (Prophet). AIUB J. Sci. Eng. 2021, 20, 71–76. [Google Scholar] [CrossRef]
- Giordano, G.; Blanchini, F.; Bruno, R.; Colaneri, P.; Di Filippo, A.; Di Matteo, A.; Colaneri, M. Modelling the COVID-19 Epidemic and Implementation of Population-Wide Interventions in Italy. Nat. Med. 2020, 26, 855–860. [Google Scholar] [CrossRef]
- Anastassopoulou, C.; Russo, L.; Tsakris, A.; Siettos, C. Data-Based Analysis, Modelling and Forecasting of the COVID-19 Outbreak. PLoS ONE 2020, 15, e0230405. [Google Scholar] [CrossRef] [Green Version]
| Model Based on Data Source 1 | Model Based on Data Source 2 | |
|---|---|---|
| Individuals’ contact rate | 3.64 × 10−2 | 3.58 × 10−2 |
| Isolation efficiency | −3.45 × 10−3 | −3.43 × 10−3 |
| Determination coefficient (on calibration data) | 99.21% | 98.39% |
| Forecast of Model 1 | Forecast of Model 2 | Observed Data | |
|---|---|---|---|
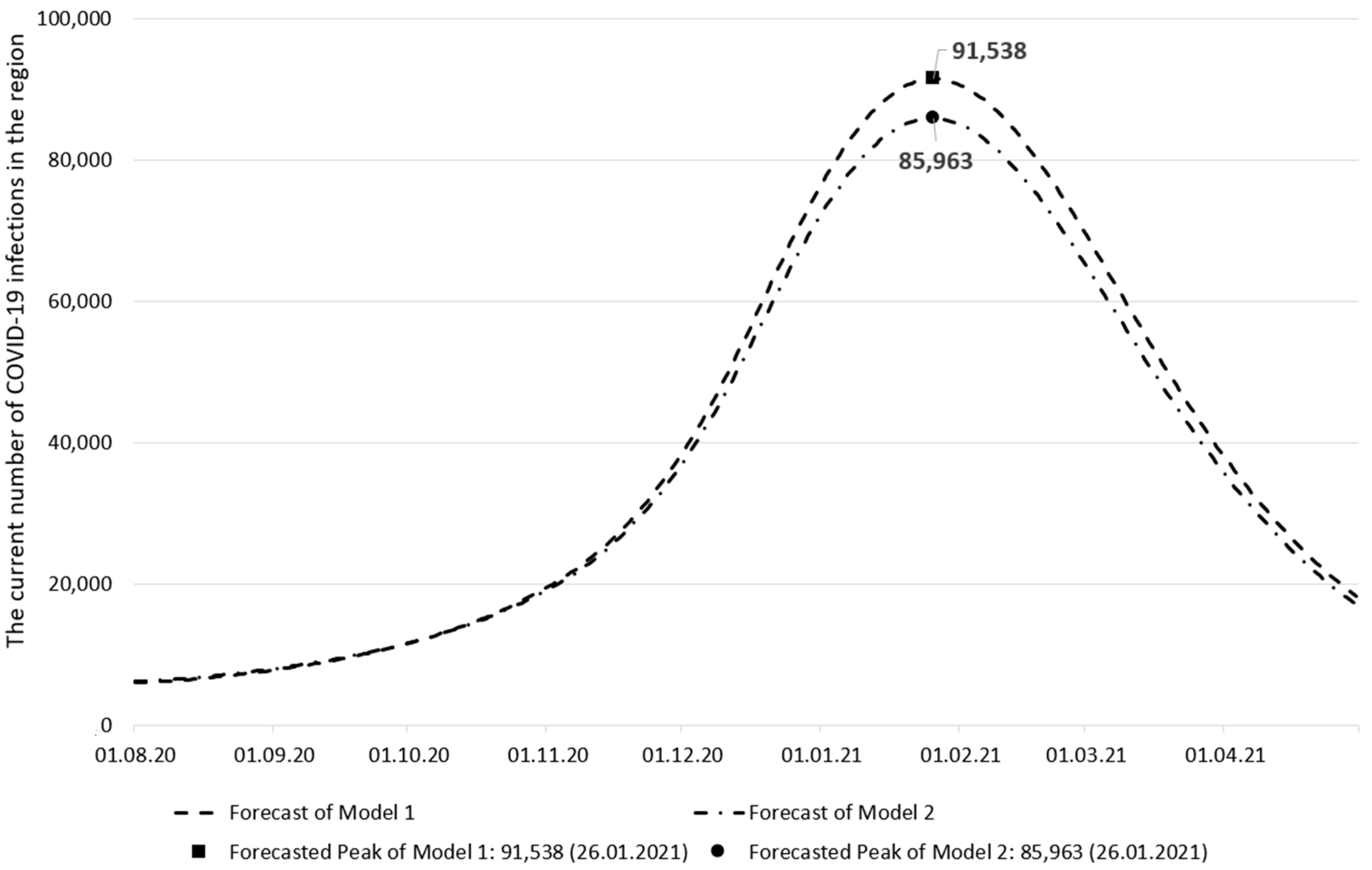
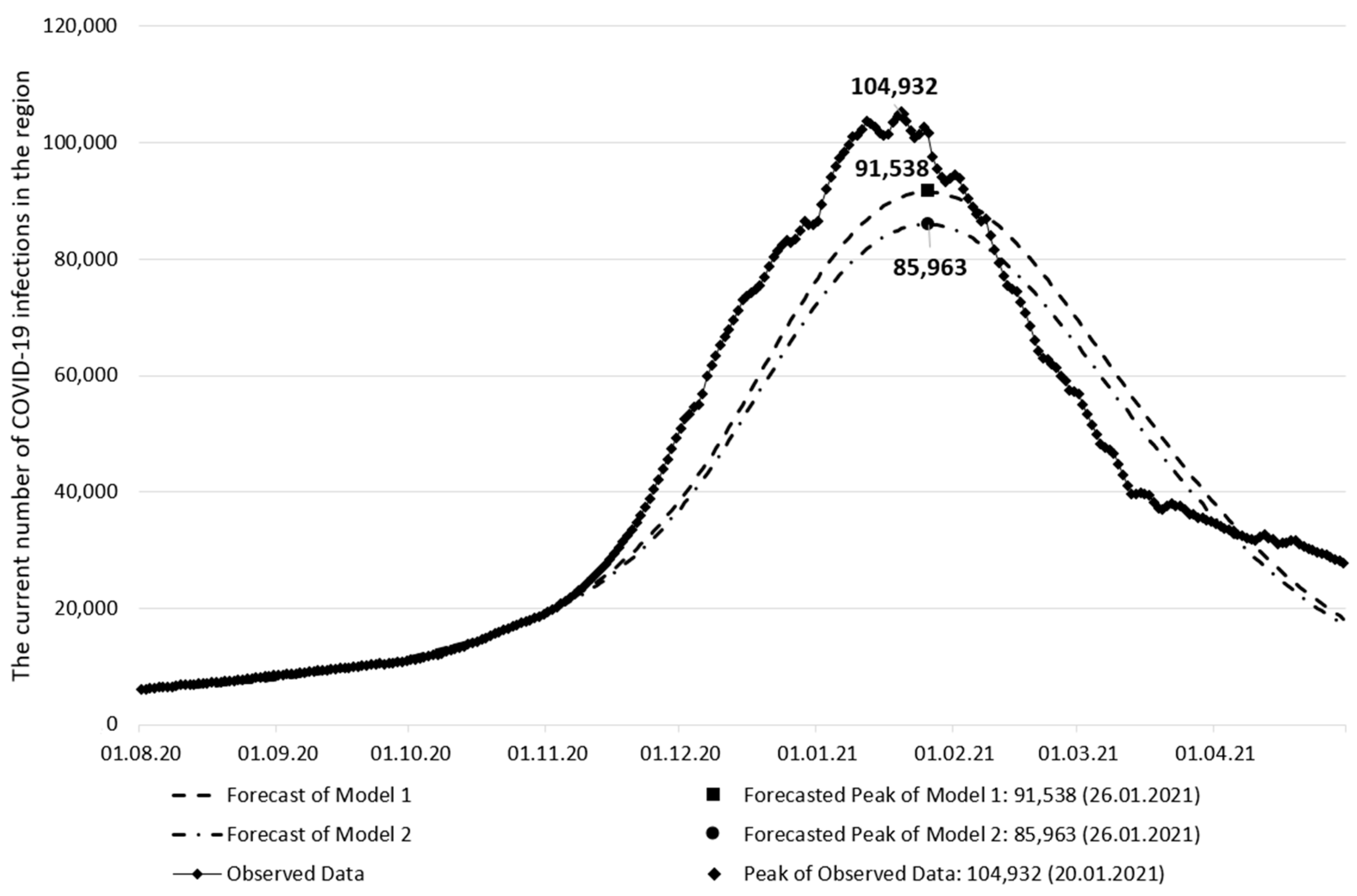
| The peak date of the current number of infections | 26 January 2021 | 26 January 2021 | 20 January 2021 |
| The current number of infections on the peak date | 91,538 | 85,963 | 104,932 |
| The peak date forecast error (days) | 6 | 6 | - |
| The current number of infections forecast error | 12.76% | 18.08% | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borovkov, A.I.; Bolsunovskaya, M.V.; Gintciak, A.M. Intelligent Data Analysis for Infection Spread Prediction. Sustainability 2022, 14, 1995. https://doi.org/10.3390/su14041995
Borovkov AI, Bolsunovskaya MV, Gintciak AM. Intelligent Data Analysis for Infection Spread Prediction. Sustainability. 2022; 14(4):1995. https://doi.org/10.3390/su14041995
Chicago/Turabian StyleBorovkov, Alexey I., Marina V. Bolsunovskaya, and Aleksei M. Gintciak. 2022. "Intelligent Data Analysis for Infection Spread Prediction" Sustainability 14, no. 4: 1995. https://doi.org/10.3390/su14041995
APA StyleBorovkov, A. I., Bolsunovskaya, M. V., & Gintciak, A. M. (2022). Intelligent Data Analysis for Infection Spread Prediction. Sustainability, 14(4), 1995. https://doi.org/10.3390/su14041995








