A Mixed Ensemble Learning and Time-Series Methodology for Category-Specific Vehicular Energy and Emissions Modeling
Abstract
:1. Introduction
- (1)
- To achieve acceptable prediction accuracies in the absence of precise engine-state measurements (a requirement for instrument-independent models) while addressing the serial correlation and the lagged impact of variables on FCR and ERs, we utilize a state-of-the-art Machine Learning (ML) technique of Recurrent Neural Networks (RNN) to keep the models’ architecture in alignment with the nature of the observed vehicular operation data.
- (2)
- The fact that the order of lagged effects of variables on FCR and ERs is not necessarily constant has never been questioned in the literature. Hence, we use an Ensemble Learning (EL) approach to tackle such uncertainty and dynamicity.
- (3)
- Unlike the vast majority of the previous studies that are confined to vehicle-specific modeling, we consider the need for category-specific FCR and ER models; hence, we introduce a generalization methodology (from vehicles to categories) founded upon well-recognized forecast-combination techniques.
2. Literature Review
3. Methodology
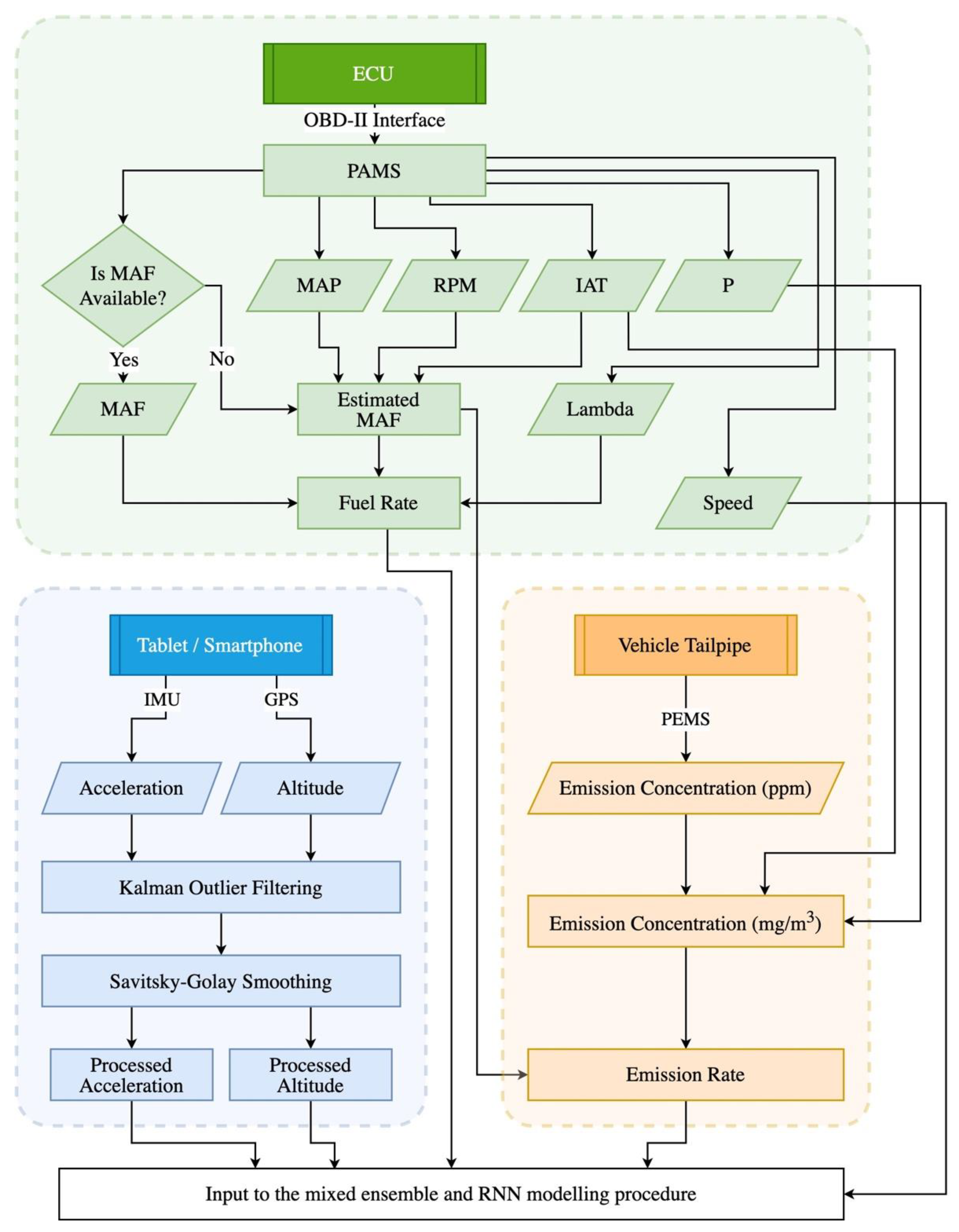
3.1. On-Road Experiments
3.2. Data Preparation
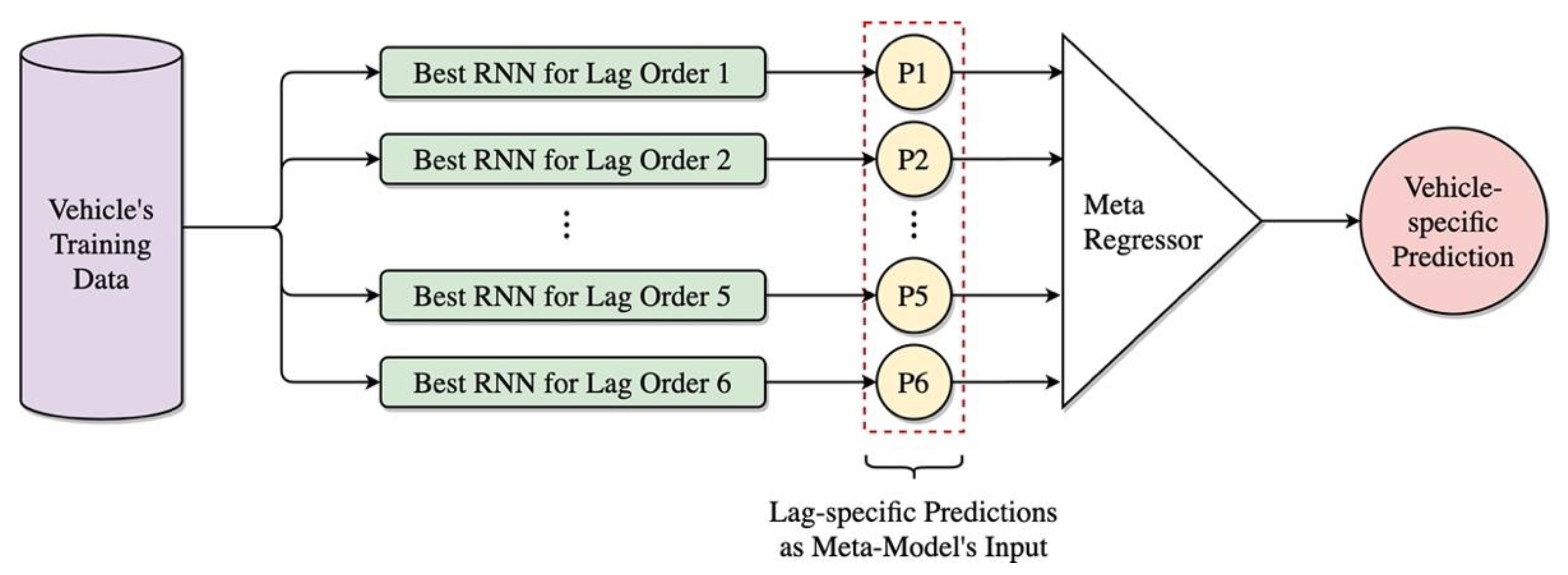
3.3. Vehicle-Specific RNN Modeling
3.4. Primary Forecast Combination for Lag-Specific RNNs
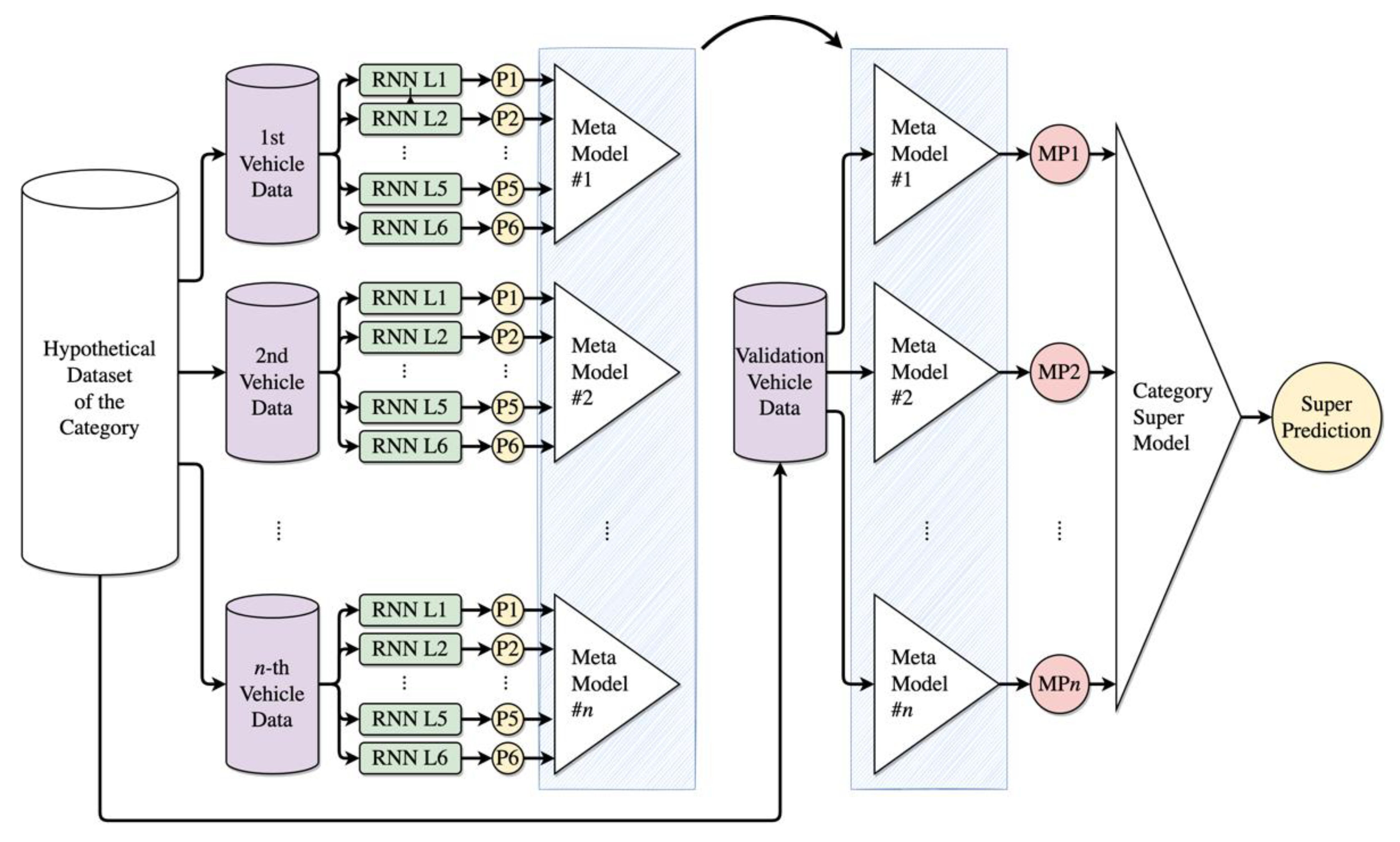
3.5. Category-Specific Ensemble Modeling
4. Results and Discussion
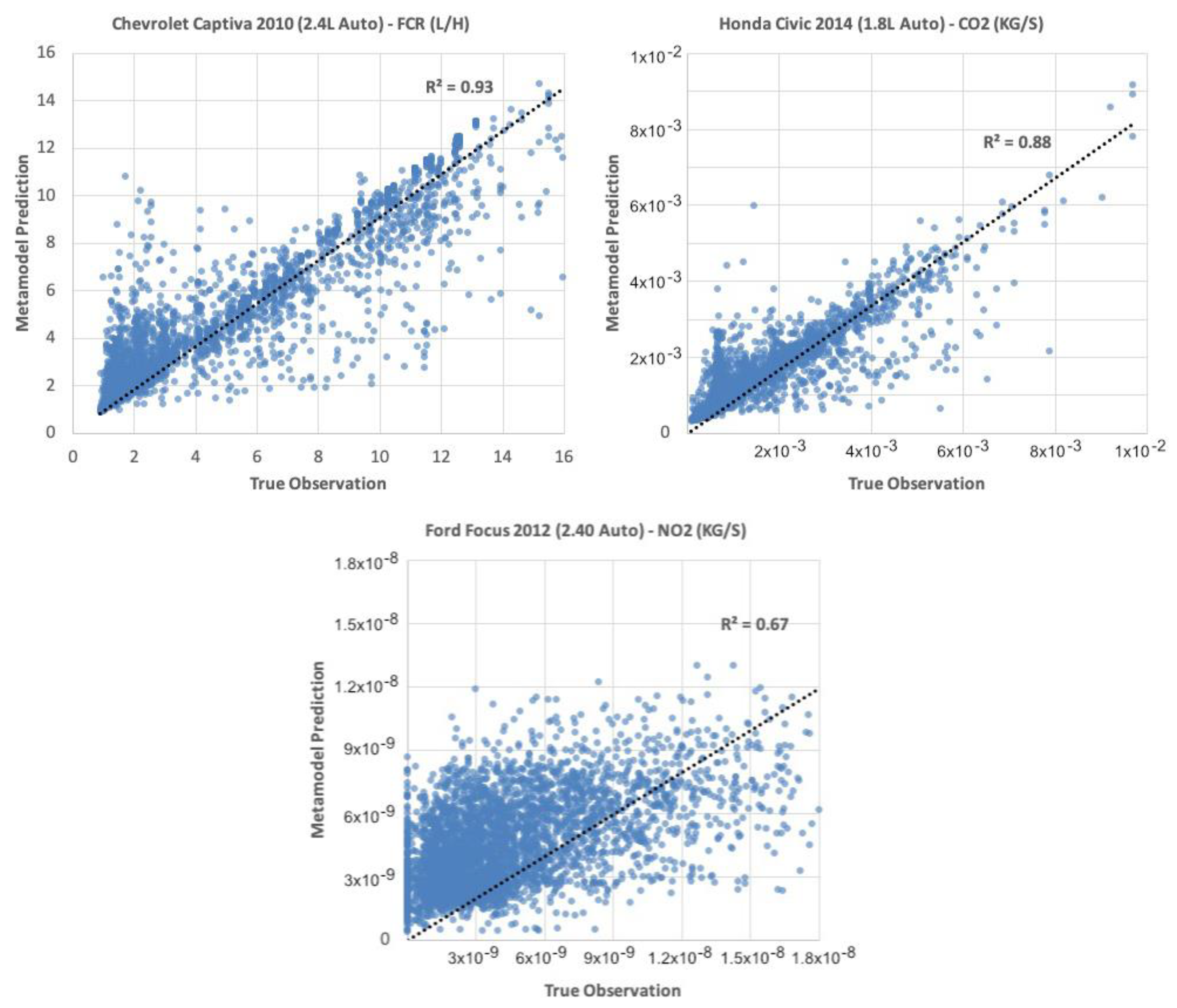
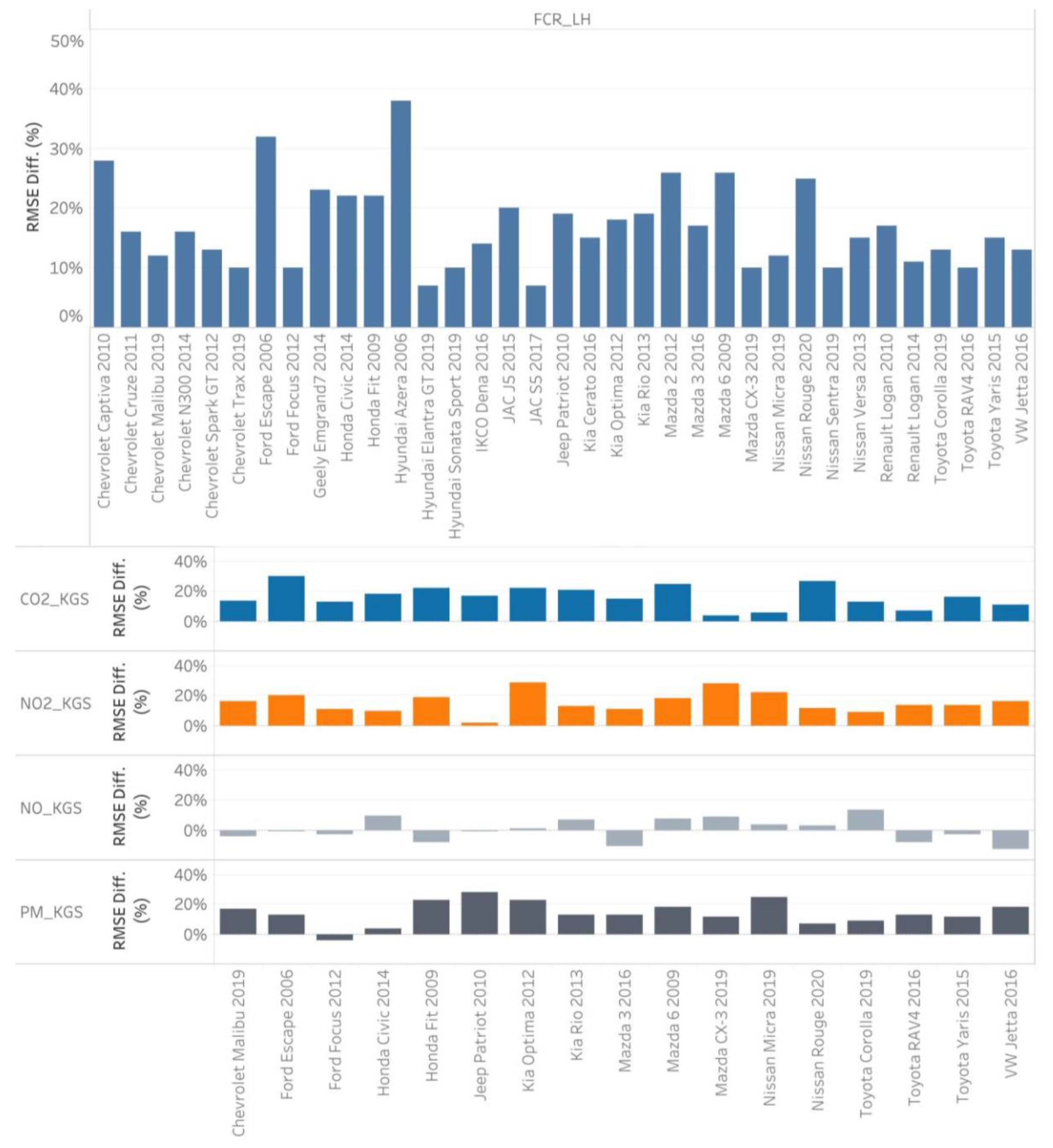
4.1. Metamodel Development Results
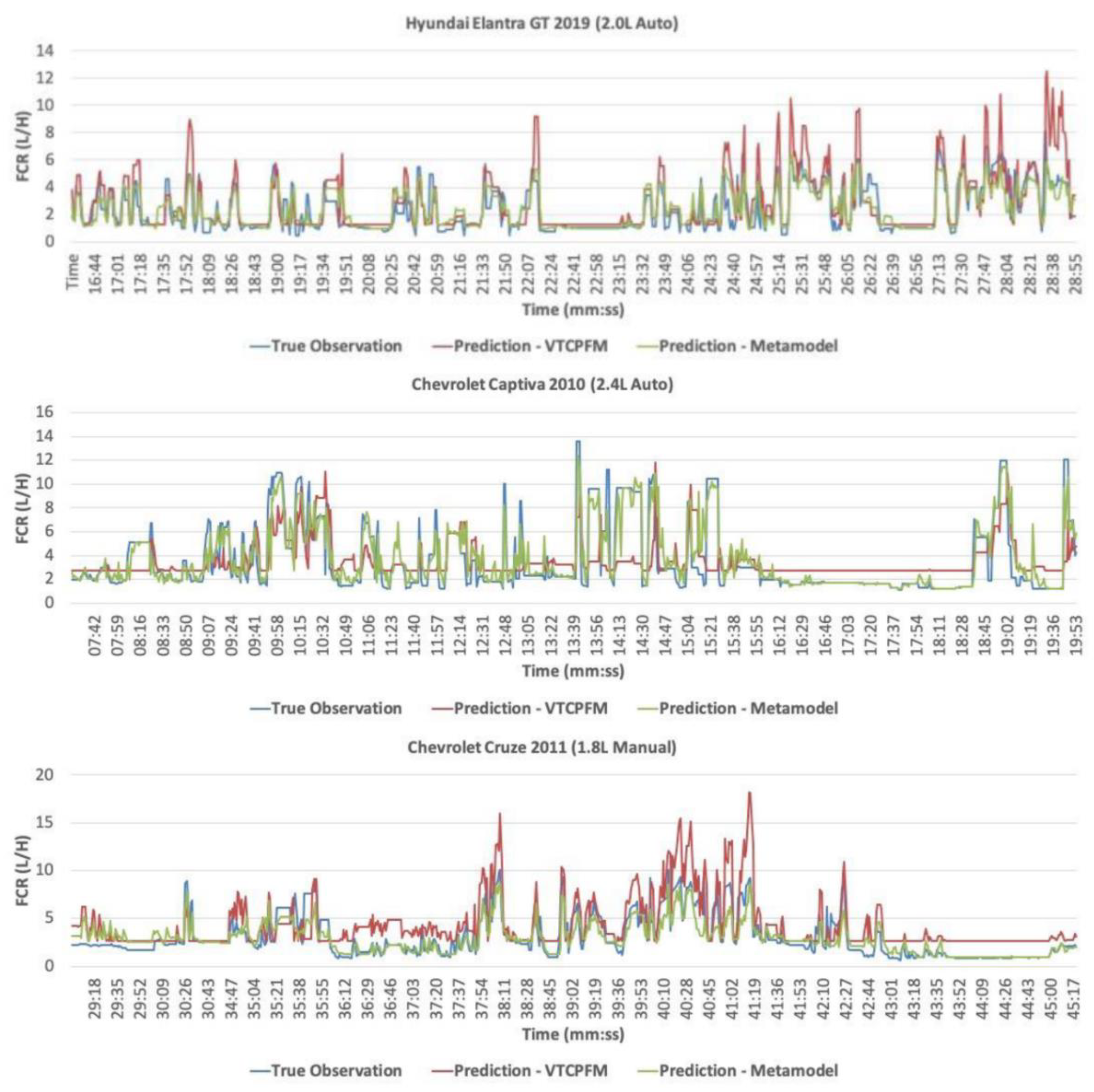
4.2. Validating Metamodels
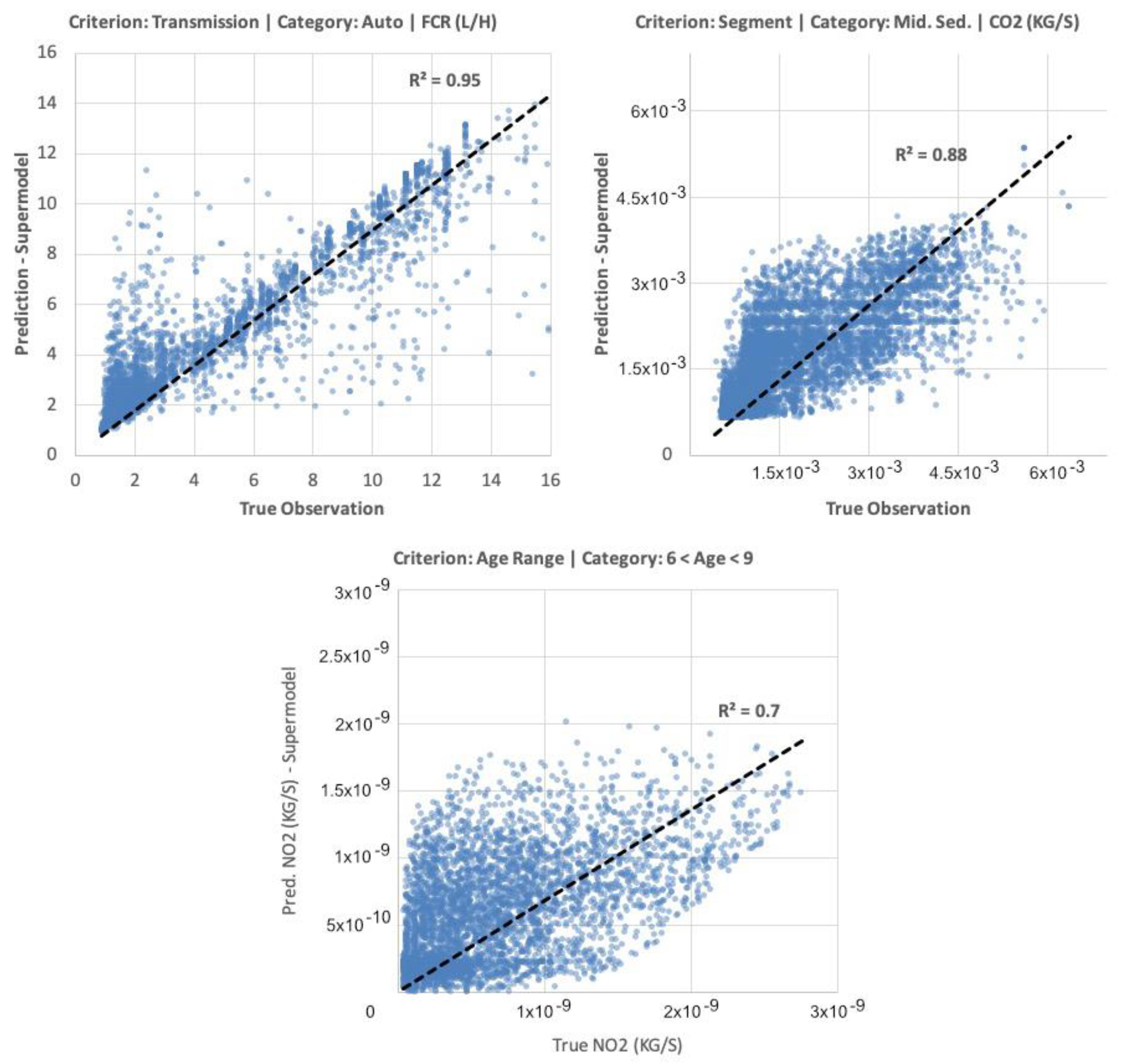
4.3. Supermodel Development Results
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bifulco, G.N.; Galante, F.; Pariota, L.; Spena, M.R. A Linear Model for the Estimation of Fuel Consumption and the Impact Evaluation of Advanced Driving Assistance Systems. Sustainability 2015, 7, 14326–14343. [Google Scholar] [CrossRef] [Green Version]
- Çapraz, A.G.; Özel, P.; Sevkli, M.; Beyca Ömer, F. Fuel Consumption Models Applied to Automobiles Using Real-time Data: A Comparison of Statistical Models. Procedia Comput. Sci. 2016, 83, 774–781. [Google Scholar] [CrossRef] [Green Version]
- Frey, H.C.; Zhang, K.; Rouphail, N. Vehicle-Specific Emissions Modeling Based upon on-Road Measurements. Environ. Sci. Technol. 2010, 44, 3594–3600. [Google Scholar] [CrossRef] [PubMed]
- Nie, Y.; Li, Q. An eco-routing model considering microscopic vehicle operating conditions. Transp. Res. Part B Methodol. 2013, 55, 154–170. [Google Scholar] [CrossRef]
- Rakha, H.A.; Ahn, K.; Moran, K.; Saerens, B.; Van Den Bulck, E. Virginia Tech Comprehensive Power-Based Fuel Consumption Model: Model development and testing. Transp. Res. Part D Transp. Environ. 2011, 16, 492–503. [Google Scholar] [CrossRef]
- Saerens, B.; Rakha, H.; Ahn, K.; Bulck, E.V.D. Assessment of Alternative Polynomial Fuel Consumption Models for Use in Intelligent Transportation Systems Applications. J. Intell. Transp. Syst. 2012, 17, 294–303. [Google Scholar] [CrossRef]
- Zhou, Q.; Gullitti, A.; Xiao, J.; Huang, Y. Neural network-based modeling and optimization for effective vehicle emission testing and engine calibration. Chem. Eng. Commun. 2008, 195, 706–720. [Google Scholar] [CrossRef]
- Koupal, J.; Cumberworth, M.; Michaels, H.; Beardsley, M.; Brzezinski, D. Design and Implementation of MOVES: EPA’s New Generation Mobile Source Emission Model. Int. Emiss. Invent. Conf. 2003, 1001, 105. [Google Scholar]
- Scora, G.; Barth, M. Comprehensive Modal Emissions Model (CMEM), Version 3.01 User’s Guide; University of California: Riverside, CA, USA, 2006; p. 1070. [Google Scholar]
- Guensler, R.; Liu, H.; Xu, X.; Xu, Y.; Rodgers, M.O. MOVES-Matrix: Setup, implementation, and application. In Proceedings of the 95th Annual Meeting of the Transportation Research Board, Washington, DC, USA, 10–14 January 2016. [Google Scholar]
- Ntziachristos, L.; Gkatzoflias, D.; Kouridis, C.; Samaras, Z. COPERT: A European Road Transport Emission Inventory Model. In Information Technologies in Environmental Engineering; Springer: Berlin/Heidelberg, Germany, 2009; pp. 491–504. [Google Scholar]
- Stockholm Environment Institute. Low Emissions Analysis Platform (LEAP). 2020. Available online: https://leap.sei.org/default.asp?action=home (accessed on 22 September 2021).
- Moradi, E.; Miranda-Moreno, L. On-road vs. Software-based Measurements: On Validity of Fuel, CO2, NOx, and PM Predictions by US EPA’s MOVES. In Proceedings of the Transportation Research Board 100th Annual Meeting, Washington, DC, USA, 9–13 January 2021. [Google Scholar]
- Duarte, G.; Gonçalves, G.; Baptista, P.; Farias, T. Establishing bonds between vehicle certification data and real-world vehicle fuel consumption—A Vehicle Specific Power approach. Energy Convers. Manag. 2015, 92, 251–265. [Google Scholar] [CrossRef]
- Kayes, D.; Hochgreb, S. Mechanisms of Particulate Matter Formation in Spark-Ignition Engines. 3. Model of PM Formation. Environ. Sci. Technol. 1999, 33, 3978–3992. [Google Scholar] [CrossRef]
- Zhai, H.; Frey, H.C.; Rouphail, N. A Vehicle-Specific Power Approach to Speed- and Facility-Specific Emissions Estimates for Diesel Transit Buses. Environ. Sci. Technol. 2008, 42, 7985–7991. [Google Scholar] [CrossRef] [PubMed]
- Moradi, E.; Miranda-Moreno, L. Vehicular fuel consumption estimation using real-world measures through cascaded machine learning modeling. Transp. Res. Part D Transp. Environ. 2020, 88, 102576. [Google Scholar] [CrossRef]
- Arrègle, J.; López, J.J.; Guardiola, C.; Monin, C. Sensitivity Study of a NOx Estimation Model for On-Board Applications; SAE International: Washington, DC, USA, 2008. [Google Scholar]
- Demesoukas, S. 0D/1D Combustion Modeling for the Combustion Systems Optimization of Spark Ignition Engines; Université d′Orléans: Montpellier, France, 2015. [Google Scholar]
- Payri, F.; Arrègle, J.; López, J.J.; Mocholí, E. Diesel NOx Modeling with a Reduction Mechanism for the Initial NOx Coming from EGR or Re-Entrained Burned Gases; SAE International: Warrendale, PA, USA, 2008. [Google Scholar]
- Saerens, B.; Diehl, M.; Bulck, E.V.D. Optimal Control Using Pontryagin’s Maximum Principle and Dynamic Programming. In Automotive Model Predictive Control; Springer: Berlin/Heidelberg, Germany, 2010; pp. 119–138. [Google Scholar] [CrossRef]
- Tauzia, X.; Karaky, H.; Maiboom, A. Evaluation of a semi-physical model to predict NOx and soot emissions of a CI automotive engine under warm-up like conditions. Appl. Therm. Eng. 2018, 137, 521–531. [Google Scholar] [CrossRef]
- Anetor, L.; Odetunde, C.; Osakue, E.E. Computational Analysis of the Extended Zeldovich Mechanism. Arab. J. Sci. Eng. 2014, 39, 8287–8305. [Google Scholar] [CrossRef]
- Blauwens, J.; Smets, B.; Peeters, J. Mechanism of “prompt” no formation in hydrocarbon flames. Symp. Combust. 1977, 16, 1055–1064. [Google Scholar] [CrossRef]
- Rakha, H.A.; Ahn, K.; Faris, W.; Moran, K.S. Simple Vehicle Powertrain Model for Modeling Intelligent Vehicle Applications. IEEE Trans. Intell. Transp. Syst. 2012, 13, 770–780. [Google Scholar] [CrossRef]
- Du, Y.; Wu, J.; Yang, S.; Zhou, L. Predicting vehicle fuel consumption patterns using floating vehicle data. J. Environ. Sci. 2017, 59, 24–29. [Google Scholar] [CrossRef]
- Kim, D.; Lee, J. Application of Neural Network Model to Vehicle Emissions. Int. J. Urban Sci. 2010, 14, 264–275. [Google Scholar] [CrossRef]
- Li, Q.; Qiao, F.; Yu, L. A Machine Learning Approach for Light-Duty Vehicle Idling Emission Estimation Based on Real Driving and Environmental Information. Environ. Pollut. Clim. Change 2017, 1, 106. [Google Scholar] [CrossRef]
- Wu, J.-D.; Liu, J.-C. A forecasting system for car fuel consumption using a radial basis function neural network. Expert Syst. Appl. 2012, 39, 1883–1888. [Google Scholar] [CrossRef]
- Ajtay, D.; Weilenmann, M. Static and dynamic instantaneous emission modelling. Int. J. Environ. Pollut. 2004, 22, 226–239. [Google Scholar] [CrossRef]
- Jaikumar, R.; Nagendra, S.S.; Sivanandan, R. Modeling of real time exhaust emissions of passenger cars under heterogeneous traffic conditions. Atmos. Pollut. Res. 2017, 8, 80–88. [Google Scholar] [CrossRef]
- Adhikari, R. A neural network based linear ensemble framework for time series forecasting. Neurocomputing 2015, 157, 231–242. [Google Scholar] [CrossRef]
- Bianchi, F.M.; Maiorino, E.; Kampffmeyer, M.C.; Rizzi, A.; Jenssen, R. An overview and comparative analysis of recurrent neural networks for short term load forecasting. arXiv 2017, arXiv:1705.04378. [Google Scholar]
- Kourentzes, N.; Barrow, D.K.; Crone, S.F. Neural network ensemble operators for time series forecasting. Expert Syst. Appl. 2014, 41, 4235–4244. [Google Scholar] [CrossRef] [Green Version]
- Kang, D.; Lv, Y.; Chen, Y.-Y. Short-term traffic flow prediction with LSTM recurrent neural network. In Proceedings of the 2017 IEEE 20th International Conference on Intelligent Transportation Systems (ITSC), Yokohama, Japan, 16–19 October 2017; IEEE Press: Piscataway, NJ, USA, 2017; pp. 1–6. [Google Scholar]
- Lee, Y.-J.; Min, O. Long Short-Term Memory Recurrent Neural Network for Urban Traffic Prediction: A Case Study of Seoul. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; IEEE Press: Piscataway, NJ, USA, 2018; pp. 1279–1284. [Google Scholar]
- Han, S.; Zhang, F.; Xi, J.; Ren, Y.; Xu, S. Short-term vehicle speed prediction based on Convolutional bi-directional LSTM networks. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; pp. 4055–4060. [Google Scholar]
- Wang, H.; Luo, H.; Zhao, F.; Qin, Y.; Zhao, Z.; Chen, Y. Detecting transportation modes with low-power-consumption sensors using recurrent neural network. In Proceedings of the 2018 IEEE SmartWorld, Ubiquitous Intelligence & Computing, Advanced & Trusted Computing, Scalable Computing & Communications, Cloud & Big Data Computing, Internet of People and Smart City Innovation (SmartWorld/SCALCOM/UIC/ATC/CBDCom/IOP/SCI), Guangzhou, China, 8–12 October 2018; pp. 1098–1105. [Google Scholar]
- Luo, D.; Lu, J.; Guo, G. Road Anomaly Detection Through Deep Learning Approaches. IEEE Access 2020, 8, 117390–117404. [Google Scholar] [CrossRef]
- Bai, M.; Lin, Y.; Ma, M.; Wang, P. Travel-Time Prediction Methods: A Review. In Proceedings of the 3rd International Conference on Smart Computing and Communication, Tokyo, Japan, 10–12 December 2018; pp. 67–77. [Google Scholar]
- Duan, Y.; Yisheng, L.V.; Wang, F.-Y. Travel time prediction with LSTM neural network. In Proceedings of the 2016 IEEE 19th International Conference on Intelligent Transportation Systems (ITSC), Rio de Janeiro, Brazil, 1–4 November 2016; IEEE Press: Piscataway, NJ, USA, 2016; pp. 1053–1058. [Google Scholar]
- Jakteerangkool, C.; Muangsin, V. Short-Term Travel Time Prediction from GPS Trace Data using Re-current Neural Networks. In Proceedings of the 2020 Asia Conference on Computers and Communications (ACCC), Singapore, 4–6 December 2020; pp. 62–66. [Google Scholar]
- Lee, E.H.; Kho, S.-Y.; Kim, D.-K.; Cho, S.-H. Travel time prediction using gated recurrent unit and spatio-temporal algorithm. Proc. Inst. Civ. Eng.-Munic. Eng. 2021, 174, 88–96. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y.; Yang, X.; Zhang, L. Short-term travel time prediction by deep learning: A comparison of different LSTM-DNN models. In Proceedings of the 2017 IEEE 20th International Conference on Intelligent Transportation Systems (ITSC), Yokohama, Japan, 16–19 October 2017; Available online: https://ieeexplore.ieee.org/document/8317886 (accessed on 15 September 2021).
- Ran, X.; Shan, Z.; Fang, Y.; Lin, C. An LSTM-based method with attention mechanism for travel time prediction. Sensors 2019, 19, 861. [Google Scholar] [CrossRef] [Green Version]
- Zhao, J.; Gao, Y.; Qu, Y.; Yin, H.; Liu, Y.; Sun, H. Travel Time Prediction: Based on Gated Recurrent Unit Method and Data Fusion. IEEE Access 2018, 6, 70463–70472. [Google Scholar] [CrossRef]
- Kanarachos, S.; Mathew, J.; Fitzpatrick, M.E. Instantaneous vehicle fuel consumption estimation using smartphones and recurrent neural networks. Expert Syst. Appl. 2019, 120, 436–447. [Google Scholar] [CrossRef]
- Jose, V.R.; Winkler, R.L. Simple robust averages of forecasts: Some empirical results. Int. J. Forecast. 2008, 24, 163–169. [Google Scholar] [CrossRef]
- Wu, M. Trimmed and Winsorized Estimators; Michigan State University: East Lansing, MI, USA, 2006. [Google Scholar]
- Chan, L.-W. Weighted least square ensemble networks. In Proceedings of the IJCNN’99—International Joint Conference on Neural Networks, Washington, DC, USA, 10–16 July 1999. [Google Scholar]
- Ferreira, W.G.; Serpa, A.L. Ensemble of metamodels: The augmented least squares approach. Struct. Multidiscip. Optim. 2016, 53, 1019–1046. [Google Scholar] [CrossRef]
- Hansen, B.E. Least-squares forecast averaging. J. Econ. 2008, 146, 342–350. [Google Scholar] [CrossRef] [Green Version]
- Ren, Y.; Zhang, L.; Suganthan, P. Ensemble Classification and Regression-Recent Developments, Applications and Future Directions. IEEE Comput. Intell. Mag. 2016, 11, 41–53. [Google Scholar] [CrossRef]
- Sagi, O.; Rokach, L. Ensemble learning: A survey. WILEY Interdiscip. Rev. Data Min. Knowl. Discov. 2018, 8, e1249. [Google Scholar] [CrossRef]
- Agamennoni, G.; Nieto, J.I.; Nebot, E. An outlier-robust Kalman filter. In Proceedings of the 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 1551–1558. [Google Scholar]
- Press, W.; Teukolsky, S.A. Savitzky-Golay Smoothing Filters. Comput. Phys. 1990, 4, 669. [Google Scholar] [CrossRef]
- Lambda and Engine Performance. Available online: https://x-engineer.org/automotive-engineering/internal-combustion-engines/performance/air-fuel-ratio-lambda-engine-performance/ (accessed on 18 October 2021).
- Che, Z.; Purushotham, S.; Cho, K.; Sontag, D.; Liu, Y. Recurrent Neural Networks for Multivariate Time Series with Missing Values. Sci. Rep. 2018, 8, 6085. [Google Scholar] [CrossRef] [Green Version]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to Forget: Continual Prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef] [PubMed]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Lipton, Z.C.; Berkowitz, J.; Elkan, C. A Critical Review of Recurrent Neural Networks for Sequence Learning. arXiv 2015, arXiv:1506.00019. [Google Scholar]
- Alcan, G.; Yilmaz, E.; Unel, M.; Aran, V.; Yilmaz, M.; Gurel, C.; Koprubasi, K. Estimating Soot Emission in Diesel Engines Using Gated Recurrent Unit Networks. IFAC-PapersOnLine 2019, 52, 544–549. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Gated feedback recurrent neural networks. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A system for large-scale machine learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation, Savannah, GA, USA, 2–4 November 2016. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Behan, M.; Moradi, E.; Miranda-Moreno, L. A Comparative Analysis of the Vehicular Emissions Generated as a Results of Different Intersection Controls. In Proceedings of the Transportation Research Board 99th Annual Meeting, Washington, DC, USA, 12–16 January 2020. [Google Scholar]
- Jimenez-Palacios, J.L. Understanding and Quantifying Motor Vehicle Emissions with Vehicle Specific Power and TILDAS Remote Sensing. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1998. [Google Scholar]









| Attribute | City | ||
|---|---|---|---|
| Montreal | Bucaramanga | Tehran | |
| Total Trip Length (km) | 1804 | 291 | 255 |
| Total Trip Time (Minutes) | 5224 | 825 | 444 |
| Number of Test Vehicles | 22 | 7 | 6 |
| Criterion | Category | Count |
|---|---|---|
| Vehicle Segments | SUV | 8 |
| Sedan | 19 | |
| Van | 1 | |
| Hatchback | 7 | |
| Engine Types | Regular | 31 |
| Turbo-Charged | 4 | |
| Transmission Types | Manual | 6 |
| Automatic | 19 | |
| Dual-Clutch (Auto) | 2 | |
| CVT (Auto) | 8 |
| Algorithm | Settings | |
|---|---|---|
| Attribute | Value | |
| Linear Regression | Feature Scaling * | Active |
| Ridge Regression | Regularization Strength | = {0.1, 1.0} |
| Support Vector Regression (SVR) | Kernel | Radial Basis Function (RBF) |
| Gamma | Scale | |
| Epsilon | 0.1 | |
| Regularization Parameter | C = {1.0, 10.0} | |
| Decision Tree | Splitting Criterion | Mean Squared Error (MSE) |
| Splitting Strategy at Nodes | {Best, Random} | |
| Maximum Tree Depth | Unbounded | |
| Gradient Boosting | Loss Function | Least Squares Regression |
| Splitting Criterion | Mean Squared Error (MSE) | |
| Learning Rate | 0.1 | |
| Number of Boosting Stages | {10, 100} | |
| AdaBoost | Base Estimator | Decision Tree Regressor |
| Loss Function | Linear | |
| Learning Rate | 1.0 | |
| Number of Boosting Stages | {10, 100} | |
| Random Forest | Number of Trees | {10, 100} |
| Splitting Criterion | Mean Squared Error (MSE) | |
| Maximum Forest Depth | Unbounded | |
| Fully-Connected ANN | Number of Hidden Layers | {1, 2} |
| Layer Size (No. of Neurons) | 100 | |
| Activation Function | ReLU | |
| Optimizer | Adam | |
| Learning Rate | 0.001 | |
| Maximum No. of Iterations | 200 | |
| Vehicle | Model Score (R-Squared) | |
|---|---|---|
| Metamodel | VT-CPFM | |
| Hyundai Elantra GT 2019 (2.0 L Auto) | 0.72 | 0.57 |
| Chevrolet Captiva 2010 (2.4 L Auto) | 0.86 | 0.26 |
| Chevrolet Cruze 2011 (1.8 L Manual) | 0.77 | 0.52 |
| Vehicle | Temporal Scale/Model Type | |||||
|---|---|---|---|---|---|---|
| 1-s | 5-s | 10-s | ||||
| ARIMA | Metamodel | ARIMA | Metamodel | ARIMA | Metamodel | |
| Hyundai Elantra GT 2019 (2.0 L Auto) | 0.53 | 0.69 | 0.66 | 0.83 | 0.71 | 0.84 |
| Chevrolet Captiva 2010 (2.4 L Auto) | 0.11 | 0.86 | 0.25 | 0.92 | 0.23 | 0.94 |
| Chevrolet Cruze 2011 (1.8 L Manual) | 0.56 | 0.77 | 0.67 | 0.83 | 0.7 | 0.84 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moradi, E.; Miranda-Moreno, L. A Mixed Ensemble Learning and Time-Series Methodology for Category-Specific Vehicular Energy and Emissions Modeling. Sustainability 2022, 14, 1900. https://doi.org/10.3390/su14031900
Moradi E, Miranda-Moreno L. A Mixed Ensemble Learning and Time-Series Methodology for Category-Specific Vehicular Energy and Emissions Modeling. Sustainability. 2022; 14(3):1900. https://doi.org/10.3390/su14031900
Chicago/Turabian StyleMoradi, Ehsan, and Luis Miranda-Moreno. 2022. "A Mixed Ensemble Learning and Time-Series Methodology for Category-Specific Vehicular Energy and Emissions Modeling" Sustainability 14, no. 3: 1900. https://doi.org/10.3390/su14031900
APA StyleMoradi, E., & Miranda-Moreno, L. (2022). A Mixed Ensemble Learning and Time-Series Methodology for Category-Specific Vehicular Energy and Emissions Modeling. Sustainability, 14(3), 1900. https://doi.org/10.3390/su14031900






