Abstract
Economic growth, energy prices, technological innovations, and financial depth all play a vital role in sectoral energy consumption. Early studies have extensively examined the interactions among these variables, which are important in developing policies on energy consumption. However, to date, most studies have estimated energy consumption in a linear fashion. If the actual relationship is non-linear or asymmetric, then the inferences drawn from a linear framework may be misleading. Hence, in this study, we employed a non-linear autoregressive distributed lag (NARDL) approach to analyse Malaysian sectoral energy consumption from 1978 to 2016. We found that the bounds test of the NARDL indicates the presence of cointegration among the variables. The key findings include: (1) a rise in income increases energy consumption throughout all sectors, but sectoral energy consumption does not respond significantly to a fall in income; (2) both increases and decreases in energy prices reduce industrial energy consumption, but residential and commercial sectors’ energy consumption react positively to price falls; (3) technological advancement increases transportation energy consumption; and (4) both an increase and decrease of credit availability to private sectors reduce industrial energy consumption, but transportation energy consumption reacts positively to financial deepening. Moreover, the effects at the sectoral level were asymmetrical. The findings indicate that the changes in selected macroeconomic variables were found to have a Granger causality effect on sectoral energy consumption. Given these findings, our study offers empirical support for the inclusion of non-linearity or asymmetric effects when modelling sectoral energy consumption.
1. Introduction
Concerns over climate changes have spawned a greater interest in national energy consumption and energy policy. As a result, there is an urgent need for empirical research to be done in all countries, including Malaysia, regarding national energy issues [1]. Extant empirical studies on sectoral energy consumption have found that economic growth, energy prices, financial depth and technological innovation have a decisive impact on sectoral energy consumption [2].
Early empirical studies examined interactions between these variables in a linear fashion. These studies assumed that variations in economic activities have symmetrical effects on energy consumption. Faced with economic events such as recessions, structural changes may occur in macroeconomic data, thereby inducing asymmetries in the relationships between the variables [3]. For instance, energy users are typically more sensitive towards economic recession compared to economic expansion [4]. In terms of pricing, energy consumers might react more strongly to increasing rather than decreasing prices. Accordingly, it is important to employ asymmetry modelling for energy consumption since a positive or negative change in a given variable does not necessarily have the same impact on energy consumption. However, to date, the bulk of empirical studies have estimated the demand for energy in a linear fashion. If the actual relationship is non-linear or asymmetric, then the inferences drawn from a linear framework may be misleading.
While economic growth, energy prices, financial depth and technological innovation have significant effects on energy consumption, little effort has been directed at examining these relationships in the Malaysian economy at a sectoral level. In this paper, we propose that these relationships can be analysed if different economic sectors are taken into consideration. For instance, end-users of energy can be divided into agricultural, industrial, residential, commercial, transportation, and non-energy using sectors. This research aims to address a gap in the extant empirical literature by examining the non-linear impact of these macroeconomic variables on sectoral energy consumption in Malaysia from 1978 to 2016.
The remainder of this paper is divided into five main parts. Section 2 provides a brief description of energy consumption in Malaysia over time. Section 3 offers a synoptic summary of the empirical literature on energy consumption relevant to the empirical thrust of the paper. Section 4 presents the data set and methodology employed, whereas Section 5 discusses the empirical findings of the study. The paper ends with Section 6, with a brief discussion of the implications of its major findings.
2. Energy Consumption in Malaysia
As one of the fastest-growing economies in the ASEAN region, Malaysia has seen its energy consumption grow in line with rising per capita income. Prior to 1970, when Malaysia was in the initial stages of industrialisation, energy consumption was comparatively low since the primary sector played a dominant role in economic activity. However, as the secondary sector gradually replaced the primary sector, energy consumption rose in line with industrialisation and urbanisation [5]. Additionally, the pattern of energy usage varied according to the economic sector. As shown in Figure 1, the industrial sector consumed almost half of the energy sources in 1978. A subsequent shift from the manufacturing sector to the service sector reduced industrial energy consumption. However, population growth fuelled the demand for energy.
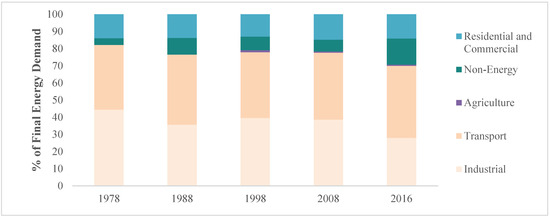
Figure 1.
Composition of Malaysian final energy demand by sector. Source: Malaysia Energy Information Hub.
Energy consumption is commonly influenced by both income and energy prices [6]. A shift in the structure of an economy towards the industrial sector, which tends to be energy-intensive, causes energy consumption to rise. As industrialisation evolves, more energy is required to boost production, particularly in heavy industries that specialise in petroleum refining, metals, cement, and chemicals. In most cases, the more developed a country, the higher is its energy consumption per capita. Thus in 2016, North America had the highest energy consumption per capita (242.65 GJ/head), whereas Africa ranked the lowest (15.24 GJ/head).
3. Empirical Analysis of Energy Consumption
The energy–growth nexus has received considerable empirical attention. In essence, empirical research into the interaction between economic growth and energy consumption rests upon four testable hypotheses: growth, conservation, feedback, and neutrality [1,7,8,9,10,11,12,13]. The growth hypothesis postulates that economic growth fuels higher energy consumption [13]. Accordingly, any interruption in the supply of energy would restrain economic growth [14]. In regions such as Sub-Saharan Africa [15] and Korea [16], the conservation hypothesis has been verified. This hypothesis emphasises that an economy is not dependent on its energy resources for growth, but rather it is economic progress that spurs energy consumption 10]. The feedback hypothesis suggests that higher energy consumption may boost economic growth, and the resultant increase in economic capacity leads to higher energy consumption [9,11]. Studies by [17,18,19] and others have validated this hypothesis. Finally, the neutrality hypothesis rests on the assumption that no causality exists between the variables in either direction [20,21,22].
The increase in energy demand is underpinned by declining costs. From a supply perspective, higher energy prices generate higher revenue and possibly higher energy consumption [23]. Energy prices pose difficulties when undertaking empirical research since accurate data is often not available for most developing countries, including Malaysia [2]. In the case of Italy, [24] used oil price as an indicator of the energy price and found that there was a 0.32% fall in energy consumption after a 1% rise in the oil price. In Malaysia, [25] used the consumer price index (CPI) as a proxy. Their long-run estimation suggested that CPI had a neutral effect on energy consumption. Instead of using the CPI as a proxy, [26] used an energy price index to study the energy–growth nexus in African countries. Unlike the CPI, their index covered only the price of fossil fuels and thus more accurately reflected supply and demand in the energy market. They found a bi-directional causality between both variables in Angola, Morocco, Ethiopia and Mozambique. Since the CPI does not account for all energy prices in Malaysia, [2] utilised the relative price of energy to non-energy goods and concluded that the energy price had a profound negative effect on energy consumption, thereby contradicting the findings of [25]. The selection of the relative price proxy is based on the theory of consumer behaviour, which holds that consumers base their decisions not only on the price of the goods in question but also on substitute goods.
It has been argued that as the demand for energy increases and the supply of natural resources diminishes, the price of energy will eventually rise [27]. A higher energy price will induce the development of more energy-efficient technology. Ref. [28] contended that technological development influenced energy consumption. Their empirical analysis revealed that trade-induced technological change lowered China’s energy intensity through the imports of more advanced equipment. Technological innovation is, therefore, crucial for energy saving. For example, electric vehicles (EVs) can be much cleaner than petroleum-fuelled internal combustion engines, depending on how the electricity is generated. However, the measurement of technological improvement is problematic in most countries, making it difficult to analyse the impact of technological progress on energy demand. Due to this, multiple studies used patent applications as a proxy [29,30]. A study by [30] found that technological development improved energy productivity. In light of this finding, energy consumption should have fallen in proportion to the degree of technological improvement. However, energy demand has increased in most countries, a phenomenon known as the “rebound effect”.
The fourth interesting strand in the empirical literature on energy consumption is the influence of financial deepening on energy consumption that occurs through several mechanisms. Firstly, the inflow of foreign direct investment (FDI) typically benefits key infrastructural sectors, often involving energy-related services. Some scholars have emphasised the role of FDI in financing energy-efficient solutions to reduce the consumption of fossil fuels [31,32]. However, a study by [33] found a negative association between FDI and electricity demand in Malaysia. Secondly, increased lending encourages the purchase of energy-consuming items [34]. Ref. [35] examined the long-run relationship between energy consumption, economic growth, financial depth and population growth in Malaysia from 1971 to 2009, where financial depth was measured by domestic credit to the private sector. A positive relationship was found; that is, a 1% increase in financial depth led to a 0.07% increase in energy consumption.
4. Data and Methodology
4.1. Data
In this study, sectoral energy consumption covers three major energy consumers in Malaysia: the residential and commercial, industrial, and transportation sectors. We employed time series data over the period of 1978 to 2016. Annual data on sectoral energy consumption were obtained from the Malaysia Energy Information Hub and measured in kilotonnes of oil equivalent (ktoe). We used the gross domestic product (GDP) measured at constant 2010 local currency prices to capture economic growth, which was obtained from the World Development Indicators (WDIs). In Malaysia, data on energy prices are not available over a longer time horizon. Moreover, the nation’s energy prices do not adequately reflect supply and demand in the energy market due to fuel subsidies. Most importantly, electricity tariffs for both households and commercial entities are price-controlled, and the effective price of electricity is not freely set by the energy producers. In view of this, we utilised the energy price from the World Bank Commodity Price Outlook as a proxy. This is a weighted index of the price of the energy commodities, which include crude oil, coal and natural gas. As contended by [36], we employed the number of patent applications drawn from the World Intellectual Property Organization to represent technological innovation in Malaysia. To measure financial depth, data on the ratio of domestic credit to the private sector (as a share of GDP) were sourced from WDIs. All variables are expressed in the natural logarithm form.
4.2. Methodology
Following conventional microeconomics, the energy demand function is expressed in terms of income and the energy price, assuming energy demand equals energy consumption [37]. The energy consumption function at time is written as:
where is the sectoral energy consumption at time ; is the economic growth at time ; and is the energy price at time . As we have seen, energy consumption can be related to technological innovation () and financial depth (). The extended energy consumption function is thus expressed as:
Before analysing the relationship between the variables, we sought to determine whether the variables series have a unit root using the Augmented Dickey-Fuller (ADF) and Phillips-Perron (PP) tests. To improve robustness, a breakpoint unit root test was applied to identify possible structural breaks. Although the PP test accounts for the breaks, [38] argued that the exogeneity assumption of the breakpoints would not remove shocks from the noise functions in a series. With respect to the cointegration test, a majority of past empirical studies adopted an assumption of linearity between the variables. A linear model may have neglected potential asymmetries in the energy consumption dynamics, which was described earlier. Furthermore, the inferences drawn from the linear model may be misleading, given that the variables represent all the elements of a cyclical business fluctuation. Based on [3], asymmetric long-run equations of sectoral energy consumption were modelled as follows:
where is sectoral energy consumption, which is divided into industrial, transportation, and residential and commercial consumption; is the real gross domestic product; is the energy price index; is the number of patent applications; is measured by domestic credit to the private sector as a percentage to GDP. is the dummy variable of crises, with “1” for crisis and “0” otherwise, i.e., 1980–1981 oil crisis, 1985–1986 commodity crisis, 1997–1998 Asian financial crisis and 2008–2009 global financial crisis [39,40]. is the usual error term. is a vector of long-run parameters that are estimated.
The key strength of the non-linear autoregressive distributed lag (NARDL) model developed by [3] is that it includes a decomposition of the regressor into its positive and negative changes. The model demonstrates that the magnitude of a rise or fall in the regressor is not identical. This is not the case in the standard ARDL model, whereby the degree of impact of regressor on the regressand is identical, whether increases or decreases. Furthermore, the model contains similar characteristics as the typical ARDL model, whereby the model can be utilised for a combination of variables with different orders of integration, or and their relationship can be estimated using ordinary least squares. Similar to a standard ARDL model, the NARDL model is divided into two components: short-run and long-run. Therefore, we are able to make inferences on the short- and long-run dynamics of sectoral energy consumption. The NARDL bounds test approach may also be viewed as an unrestricted error correction model since the long-run terms are clearly specified and not restricted. Following [41], we did not undertake a non-linearity check prior to the NARDL bounds test. If the null hypothesis of no asymmetric cointegrating relationship is rejected, then the variables are non-linearly or asymmetrically cointegrated. To this end, the rejection of the null of bounds F-test, , verifies the existence of an asymmetric long-run relationship, and the asymmetric long-run parameters, and , reveals how much of the variation in sectoral energy consumption is explained by the rise or fall in the independent variables.
According to [3], a time series can be broken down to its initial value and its cumulative sum of positive and negative components. Independent variables from Equations (3)–(6) were thus decomposed using a zero threshold, thereby distinguishing these positive and negative changes in their rate of growth. The following formulas more precisely describe this modelling approach:
where represents the logarithmic (L) transformation of the independent variables , and .
Based on these equations, the long-run relationship between sectoral energy consumption and a rise in income is in Equation (3), which is expected to be positive. captures the long-run correlation between sectoral energy consumption and income reduction. Following the conventional demand curve, lower incomes tend to reduce the demand for energy as consumers are less willing to spend more. is thus expected to be negative in value. In Equation (4), we anticipate a negative value for and a positive value for due to the price–consumption inverse relationship. We further posit that technological innovation negatively influences energy consumption, i.e., and in Equation (5). According to [42], financial depth accompanies economic growth through investment, thus increasing energy consumption. Therefore, and are expected to be positive and negative in Equation (6). By associating Equations (3)–(6) to the ARDL setting, the following asymmetric ARDL models are formed:
Note that is the constant term; is the first difference operator; and are the short-run coefficients; and are the long-run parameters with ; , and are the optimal lag length for dependent and independent variables to eliminate serial correlation in the errors; is the coefficient of dummy variable; is the error term.
For each equation, different specifications were applied, distinguished by the changes in the independent variable. The first specification (S1) includes only the changes in real income; the second specification (S2) includes only the changes in energy price; the third specification (S3) includes only the changes in technological innovation, while the fourth specification (S4) contains only the changes in financial depth. This study emphasised the asymmetric influences of the respective variables on sectoral energy consumption, but the impact of other independent variables was measured as well. Hence, for the long-run parameters, and in S1; and in S2; and in S3; and in S4. The NARDL model clearly distinguishes the long-run and short-run effects, as well as between positive and negative changes, within a single estimated model.
The bounds testing approach was used to discover the presence of asymmetric cointegration amongst the variables. This involves the Wald test (-statistic) of the null hypothesis, , against the alternative hypothesis, . Moreover, the unrestricted specification of the NARDL model from Equations (9)–(12) involves two types of asymmetries—the long run and short run. The rejection of a long-run symmetry can be tested through while the presence of short-run asymmetry can be verified by rejecting the null hypothesis, which is for the income variable; for the price variable; for the technology variable, and for the financial variable.
Finally, the asymmetric causal effect from changes in the independent variables on sectoral energy consumption was estimated using stepwise least squares augmented with Wald statistics. Equations (9)–(12) can then be rewritten as:
For short-run causality to exist, the null hypothesis of no causality must be rejected. More precisely, economic expansion or contraction is expected to Granger cause , if or is rejected; price rise or fall is expected to Granger cause , if or is rejected; the changes in technological innovation are expected to Granger cause , if or is rejected, and, finally, the changes in financial depth are expected to Granger cause , if or is rejected.
5. Empirical Results
Table 1 reports the results from the hypothesis of unit root validation without structural breaks. The hypotheses of a unit root were not rejected by the unit root tests, except for . By excluding , unit root tests were carried out at the first difference to ensure the stationarity of the other series. All variables, except for , were variables. With respect to the unit root test with breaks, as shown in Table 2, the rejection of the null hypothesis was only found for and . In the first difference, all variables, excluding and , were variables. Some of the break dates coincided with economic events, such as the global financial crisis.

Table 1.
Stationarity test without breaks.

Table 2.
Breakpoint unit root test.
The estimated -statistic for each specification in Table 3 was higher than the upper bound critical value at the 1% level. Hence, economic growth, energy prices, technological innovation, financial depth and sectoral energy consumption are asymmetrically associated in the long run. Before inferences were drawn, model adequacy was assessed based on various diagnostic tests. The results are reported in Table 4. In all test runs of the residuals, there was strong evidence of no serial correlation and heteroscedasticity.

Table 3.
NARDL bounds test.

Table 4.
Diagnostic tests.
Nevertheless, at the time of writing, the dataset used was from 1978 to 2016. To address the issue of outdated data, we provided validation to ensure the predictability of the performance of the proposed models. Therefore, in addition to the model adequacy measures, we also performed out-of-sample validation over the in-sample observations for the period 1978–2016 and evaluated the accuracy of the forecasts. In this study, one-step-ahead and two-step-ahead forecasts were carried out. The idea of minimising the sum of squared residuals is to minimise the in-sample and out-of-sample forecast errors, such as the root mean squared error (RMSE), mean absolute error (MAE), and mean absolute percentage error (MAPE). Moreover, a combination of more than one metric gives a better evaluation of the overall performance [43]. The performance of the model is measured by lowering RMSE, MAE or MAPE [44]. By this means, a model will be optimised, with its predicted values closer to the actual values in the sample. Looking at just in-sample forecast errors are inadequate to judge the model’s overall performance. By comparing out-of-sample forecast performance to that of in-sample, out-of-sample forecast errors turn out to be slightly higher, as shown in Table 5, Table 6 and Table 7. Arguably, there is no significant divergence between actual and the forecasted sectoral energy consumption. We also noticed that one-step-ahead forecasts have better performance than two-step-ahead forecasts for most models. Based on these results, the proposed models show a fairly good performance in predicting energy consumption. Accordingly, the long-run equations were then estimated.

Table 5.
Forecasting performance of industrial energy consumption models.

Table 6.
Forecasting performance of transportation energy consumption models.

Table 7.
Forecasting performance of residential and commercial energy consumption models.
Economic expansion has increased energy consumption in all sectors during the study period (Table 8). More precisely, any positive shock in income increases energy demand in the industrial, transportation, and residential and commercial sectors, with a coefficient of 1.259, 0.913 and 1.039, respectively. This is partially supported by the empirical findings of [4] for Brazil and Russia and [45] for non-OECD countries. Both studies demonstrate that energy consumption responds positively to positive income shocks. According to [18,46], economic expansion drives energy consumption via industrialisation and urbanisation. Malaysia, as a newly industrialised economy, needs energy for economic development. Its economic growth has been driven mostly by energy-intensive industries, including steel, cement, oil, gas and electricity. Therefore, higher GDP translates into higher growth of industrial activities and higher energy consumption. Industrialisation and urbanisation emphasise the need for more energy and fossil fuels, the most economical fuels, to meet the growth of energy demand in each sector (i.e., petroleum for transportation and electricity for households and buildings). Note that income elasticity was close to unity for transportation energy consumption, and it exceeded unity for industrial as well as residential and commercial energy consumption. It is worth noting that industrial energy consumption is more sensitive to an increase in income compared with other sectors. Specifically, economic growth of 1% increases industrial energy consumption by 1.26%. This corroborates the findings of [47,48] that industrial energy consumption tends to have higher income elasticity. The result suggests that industrial energy consumption and the increase in income are strongly linked. There is a desire for more wealth and more resource consumption for an ever-growing population.

Table 8.
NARDL long-run estimation.
We also found that industrial energy consumption reduced, regardless of increases and decreases in energy prices. In particular, a 1% increase in energy prices will reduce industrial energy consumption by 0.47% and, unexpectedly, a 1% decrease in energy prices will reduce industrial energy demand by 0.97%. This finding is consistent with the outcome stated by [49], in that oil consumption in Tunisia is more responsive to price declines (than to rises). The price effect might thus induce energy-saving technological changes. Rising energy prices could induce efficiency improvement, such as the installation of insulation and the retrofitting of industrial machinery, to reduce the cost of energy utilised per unit of output. These energy-saving innovations are not discarded when prices fall, and thus energy consumption will not increase. In line with these developments, emissions from the manufacturing and construction industries have dropped since 2008 due to a shift from the consumption of coal to electricity and a concomitant increase in energy efficiency [50]. Furthermore, the declining contribution of these industries to national income compounds the downward pressure on prices. However, a price fall increases residential and commercial energy consumption by 1.06%. A growing population and a higher standard of living will continue to drive energy demand in the energy-intensive modern sector. Low electricity tariffs coupled with a lack of efficiency in electricity usage explains why its consumption keeps growing [51].
It has been argued that technological innovation improves energy efficiency and thus reduces energy demand. However, the data shown in Table 8 suggest that technological advancement increases energy consumption in the transportation sector with a coefficient of 0.063, suggesting that a 1% increase in technological innovation will increase transportation energy consumption by roughly 0.06%. This finding implies that the developments in transportation over the last 40 years have done little in improving energy efficiency. As more and more people travel extensively, energy consumption takes on even greater importance. However, the ratio of energy-efficient vehicles (EEVs) to private vehicles only accounted for 32.6% in 2015 [52]. Thus, any fuel efficiency improvement in EEVs is offset by the surging fuel consumption in non-efficient internal combustion engine vehicles, which explains the continuous rise in energy consumption associated with transportation.
The proposition that financial deepening boosts energy demand from the industrial sector is not accepted in this study. By contrast, increasing credit availability to the private sector helps to reduce industrial energy consumption. More precisely, a 1% increase in credit availability will reduce industrial energy consumption by 0.98%. The result is unexpectedly consistent with the findings of [53], in that an increase in bank deposits and broad money reduces non-renewable energy consumption by 0.011% and 1.071%, respectively. Financial institutions have made great contributions towards maintaining the sustainable development of the Malaysian industrial sector. Increasing credit enables the sector to install more energy-efficient machinery or equipment and, at the same time, lower energy bills. Alternatively, the producers might opt for green technology such as solar energy, given the credit availability, and reduce the consumption of conventional fuel or electricity, which is generated mainly by non-renewable energy in the country. On the other hand, a negative shock to the domestic credit will reduce industrial energy consumption, conferring that a 1% fall in the credit will reduce industrial energy consumption by 1.67%. This finding is in line with [54], which suggest that a negative shock to financial deepening reduces energy consumption. Our findings reveal that a decrease in the volume of credit could slow down economic activity through reduced consumer expenditure and this will, in turn, affect energy demand. For example, a negative credit shock would result in a fall in industrial energy consumption. The inhibitory effect of an economic contraction compounds the positive impact of the finance-induced energy-saving measures to reduce the demand for industrial energy.
It would be naïve to cease estimation at this point, as was done by previous researchers, and simply conclude that as an economy develops, energy consumption will increase symmetrically. However, it is important to determine the validity of this assumption through empirical energy analysis. Table 9 provides evidence of long-run and short-run asymmetries. If the null hypothesis of a long-run symmetry or short-run symmetry is rejected, it means that economic expansion and contraction have dissimilar effects on sectoral energy consumption in the long-run or short-run, respectively. Although the estimated long-run parameters are not statistically different from zero, they are statistically different from each other.

Table 9.
NARDL symmetry test.
As shown in Table 9, income effects are asymmetric only in the long run for industrial and transportation energy consumption. In the industrial sector, this reflects that producers are reluctant to change their energy consumption immediately according to changes in income due to uncertainties in the underlying business conditions and the high costs of production modifications in the short run. In the transportation sector, petroleum products, such as diesel, are necessities for vehicles. It is thus not easy to make substantial changes in the short run. Over a longer time scale, economic expansion and contraction will lead to changes in energy consumption. By contrast, income affects residential and commercial energy consumption asymmetrically only in the short run. Unlike the industrial sector, which is highly capital intensive and diversified and utilises a range of primary energy sources, electricity is the main source of energy for the residential and commercial sectors [55].
Most of the observations indicate that the energy price asymmetrically affects sectoral energy consumption. This is in line with some previous findings of [49,56]. The asymmetrical price response can be explained in several ways. For instance, the changes in energy consumption to a rise in the energy price is not necessarily and perfectly reversed by a comparable fall in price, nor are the effects of all price decreases necessarily the same [57]. Price hikes can have a positive impact on the energy sector, but a fall in energy prices does not necessarily generate a favourable effect. Uncertainties about energy prices may induce firms and consumers to invest in energy-saving equipment, such as insulation. However, these installations will not be removed when prices drop. Moreover, automobile technology has advanced considerably; hence when fuel price increases are reversed, fuel efficiency continues to improve.
It is worth noting that financial depth asymmetrically affects transportation energy consumption and residential and commercial energy consumption only in the short run. Consumers who are ignorant about energy-saving technologies are more likely to purchase less energy-efficient appliances. Over a longer time horizon, when users become more aware, they might appreciate the benefits of these technologies. In fact, photovoltaic (PV) cells were introduced in Malaysia in the 1980s. However, the utilisation of solar energy remains low due to a lack of awareness and high initial costs. To increase the adoption of solar panels in the residential and commercial sectors, the Malaysian government introduced the Malaysia Building Integrated Photovoltaic (MBIPV) project in 2005. In an effort to reduce cost, the government implemented Equated Monthly Instalment (EMI) schemes to repay loans for PV panel systems [58].
Our empirical analysis concludes with non-linear causality testing on sectoral energy consumption. The results are presented in Table 10. In most tests, the Wald test rejects the null hypothesis of no Granger causality, indicating the importance of economic growth, energy prices, technological innovation and financial depth in influencing the changes in sectoral energy consumption in Malaysia.

Table 10.
Non-linear causality test.
6. Conclusions
As we have seen, the bulk of the empirical literature has assumed that the dynamic relationship between energy consumption and its determining factors are symmetrical. Model specification errors can have adverse effects if they generate fallacious policy proposals. In line with our findings, energy consumers were found to react differently towards an increase or decrease in the contributing factors under different time horizons using the NARDL model. This paper points to the need of establishing conservation policies oriented towards reducing energy intensity in the industrial sector by implementing energy-efficient financing schemes, together with a relatively higher energy price. Investing in energy-efficient appliances and machinery is costly, and the government, together with local financial institutions and banks, has introduced specific financing programmes to address these financial obstacles. To date, there are limited financing schemes available for the purchase of energy-efficient equipment in the industrial sector, probably due to the increasing rate of loan defaults. Indeed, much of the financing is devoted to energy-saving projects in households and buildings as well as the adoption of renewable energy. Our findings show that the energy savings in the industrial sector are greater than in other sectors. Therefore, financial support such as grants and subsidies are encouraged in order to eradicate financial barriers and push the uptake of energy-efficient projects. On the other hand, energy prices (or at least electricity tariffs) should be gradually increased in order to realise the potential of energy savings in the industrial sector and to reduce the upward pressure of the income-increase effect.
In the residential and commercial sectors, subsidised electricity tariffs have encouraged inefficient patterns of energy demand. The unintended consequence of this policy has led to overconsumption, which is inconsistent with the National Environmental Policy. Most electrical appliances are energy-efficient today, but due to the fallacy of composition, the effort towards reducing energy consumption has been diminished. It is often mistakenly assumed that what is true for a given community also holds true for an entire population [59]. The microeconomic effect of purchasing energy-efficient items is that consumers utilise less energy for each unit of energy generated. However, the overall energy consumption will rise because lower electricity bills induce the use of more electricity. There is yet an indication that renewable energy can replace fossil fuels in the near future as a main source of energy. Hence, the possible solution rests on rationalising and phasing out inefficient fuel subsidies while incentivising investments in energy-efficient projects.
With respect to the transportation sector, our findings show that rising incomes and population, coupled with financial deepening, increase transportation energy consumption, and inefficient private vehicles and the high initial cost of EVs lead to the use of more petroleum. The magnitude of the financial effect is greater than the technological effect (0.56 versus 0.06); hence, more attention can be directed to tightening the credit allowed to purchase inefficient vehicles and easing the financing for the purchase of energy-efficient vehicles.
The findings presented in this paper have certain limitations. The unavailability of accurate data to represent the technological variable is one of them. The World Intellectual Property Organization (WIPO) divides technology into eight sections, from A to H. Since patent documents related to clean energy can be found in many areas of technology, they do not fall under any single section. Correspondingly, a new section, Section Y, was introduced to file documents related to climate change mitigation technology. However, there are no statistics for this patent document in Malaysia. In addition, statistics on the patents granted for electric and electronic elements (Section H—electricity), provided by the Intellectual Property Corporation of Malaysia (MyIPO), are limited to 26 years, i.e., from 1993 to 2018. Under these circumstances, future research can replace patent data with other proxies of technological innovation for better estimation. The sample period is another limitation of this study, and it provides justification for the continuation of studies in this area. Additionally, in line with the government’s effort to combat climate change and global warming, future research may focus on renewable energy to assist in the drafting of clear policy recommendations on how industrial and household activities affect the consumption of green energy.
Author Contributions
Writing—original draft preparation, C.-S.T.; model validation, C.-S.T. and M.K.; writing—review and editing, M.K., J.A. and B.D.; supervision, M.K. and J.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no funding, but the APC was funded by Universiti Malaysia Sabah.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: https://meih.st.gov.my/statistics, accessed on 17 January 2022 (data on sectoral energy consumption); https://data.worldbank.org/, accessed on 17 January 2022 (data on real national income, commodity prices, number of patent applications and domestic credit to private sector).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kahouli, B. The short and long run causality relationship among economic growth, energy consumption and financial development: Evidence from South Mediterranean Countries (SMCs). Energy Econ. 2017, 68, 19–30. [Google Scholar] [CrossRef]
- Tang, C.F.; Tan, B.W. The linkages among energy consumption, economic growth, relative price, foreign direct investment, and financial development in Malaysia. Qual. Quant. 2014, 48, 781–797. [Google Scholar] [CrossRef]
- Shin, Y.; Yu, B.; Greenwood-Nimmo, M. Modelling Asymmetric Cointegration and Dynamic Multipliers in a Nonlinear ARDL Framework. In Festschrift in Honor of Peter Schmidt: Econometric Methods and Applications; Springer: New York, NY, USA, 2014; pp. 281–314. [Google Scholar]
- Shahbaz, M.; Shahzad, S.J.H.; Alam, S.; Apergis, N. Globalization, economic growth and energy consumption in the BRICS region: The importance of asymmetries. J. Int. Trade Econ. Dev. Int. Comp. Rev. 2018, 27, 985–1009. [Google Scholar] [CrossRef] [Green Version]
- Chong, C.H.; Ni, W.; Ma, L.; Liu, P.; Li, Z. The Use of Energy in Malaysia: Tracing Energy Flows from Primary Source to End Use. Energies 2015, 8, 2828–2866. [Google Scholar] [CrossRef]
- Gyamfi, S.; Krumdieck, S.; Urmee, T. Residential peak electricity demand response—Highlights of some behavioural issues. Renew. Sustain. Energy Rev. 2013, 25, 71–77. [Google Scholar] [CrossRef] [Green Version]
- Saatci, M.; Dumrul, Y. The relationship between energy consumption and economic growth: Evidence from a structural break analysis for Turkey. Int. J. Energy Econ. Policy 2013, 3, 20–29. [Google Scholar]
- Shahateet, M. Modelling economic growth and energy consumption in Arab countries: Cointegration and causality analysis. Int. J. Energy Econ. Policy 2014, 3, 349–359. [Google Scholar]
- Le, H.P.; Sarkodie, S.A. Dynamic linkage between renewable and conventional energy use, environmental quality and economic growth: Evidence from Emerging Market and Developing Economies. Energy Rep. 2020, 6, 965–973. [Google Scholar] [CrossRef]
- Aslan, A.; Gozbasi, O.; Altinoz, B.; Altuntas, M. Impact of financial development and economic growth on energy consumption: A panel vector autoregressive analysis for the comparison of G7 and top 10 emerging market economies. Energy Environ. 2021, 32, 1315–1330. [Google Scholar] [CrossRef]
- Magazzino, C.; Mutascu, M.; Mele, M.; Sarkodie, S.A. Energy consumption and economic growth in Italy: A wavelet analysis. Energy Rep. 2021, 7, 1520–1528. [Google Scholar] [CrossRef]
- Shakeel, M. Analyses of energy-GDP-export nexus: The way-forward. Energy 2021, 216, 119280. [Google Scholar] [CrossRef]
- Yilanci, V.; Haouas, I.; Ozgur, O.; Sarkodie, S.A. Energy Diversification and Economic Development in Emergent Countries: Evidence From Fourier Function-Driven Bootstrap Panel Causality Test. Front. Energy Res. 2021, 9, 95. [Google Scholar] [CrossRef]
- Esen, Ö.; Bayrak, M. Does more energy consumption support economic growth in net energy-importing countries? J. Econ. Finance Adm. Sci. 2017, 22, 75–98. [Google Scholar] [CrossRef]
- Akinlo, A.E. Energy consumption and economic growth: Evidence from 11 Sub-Saharan African countries. Energy Econ. 2008, 30, 2391–2400. [Google Scholar] [CrossRef]
- Oh, W.; Lee, K. Energy consumption and economic growth in Korea: Testing the causality relation. J. Policy Model. 2004, 26, 973–981. [Google Scholar] [CrossRef]
- Shahbaz, M.; Zeshan, M.; Afza, T. Is energy consumption effective to spur economic growth in Pakistan? New evidence from bounds test to level relationships and Granger causality tests. Econ. Model. 2012, 29, 2310–2319. [Google Scholar] [CrossRef] [Green Version]
- Shahbaz, M.; Loganathan, N.; Sbia, R.; Afza, T. The effect of urbanization, affluence and trade openness on energy consumption: A time series analysis in Malaysia. Renew. Sustain. Energy Rev. 2015, 47, 683–693. [Google Scholar] [CrossRef] [Green Version]
- Osigwe, A.C.; Arawomo, D.F. Energy consumption, energy prices and economic growth: Causal relationships based on error correction model. Int. J. Energy Econ. Policy 2015, 5, 408–414. [Google Scholar]
- Yıldırım, E.; Aslan, A.; Ozturk, I. Energy consumption and gdp in asean countries: Bootstrap-corrected panel and time series causality tests. Singap. Econ. Rev. 2014, 59, 1450010. [Google Scholar] [CrossRef]
- Rezitis, A.N.; Ahammad, S.M. The relationship between energy consumption and economic growth in South and Southeast Asian countries: A panel vector autoregression approach and causality analysis. Int. J. Energy Econ. Policy 2015, 5, 704–715. [Google Scholar]
- Liu, W.-C. The Relationship between Primary Energy Consumption and Real Gross Domestic Product: Evidence from Major Asian Countries. Sustainability 2020, 12, 2568. [Google Scholar] [CrossRef] [Green Version]
- Fuinhas, J.A.; Marques, A.C. Rentierism, energy and economic growth: The case of Algeria and Egypt (1965–2010). Energy Policy 2013, 62, 1165–1171. [Google Scholar] [CrossRef]
- Magazzino, C. GDP, energy consumption and financial development in Italy. Int. J. Energy Sect. Manag. 2018, 12, 28–43. [Google Scholar] [CrossRef] [Green Version]
- Abarahan, A.; Masih, M. Is Energy a Stimulus for Economic Growth? A Focused Study on Malaysia Using the Auto Regressive Distributed Lag Technique; University Library of Munich: Munich, Germany, 2016. [Google Scholar]
- Sharmin, F.; Khan, M.R.A. Causal relationship between energy consumption, energy prices and economic growth in Africa. Int. J. Energy Econ. Policy 2016, 6, 477–494. [Google Scholar]
- Hicks, J.R. The Theory of Wages; Palgrave Macmillan: London, UK, 1963. [Google Scholar]
- Jiang, L.; Ji, M. China’s Energy Intensity, Determinants and Spatial Effects. Sustainability 2016, 8, 544. [Google Scholar] [CrossRef] [Green Version]
- Sohag, K.; Begum, R.; Abdullah, S.M.S.; Jaafar, M. Dynamics of energy use, technological innovation, economic growth and trade openness in Malaysia. Energy 2015, 90, 1497–1507. [Google Scholar] [CrossRef]
- Yan, Z.; Shi, R.; Yang, Z. ICT Development and Sustainable Energy Consumption: A Perspective of Energy Productivity. Sustainability 2018, 10, 2568. [Google Scholar] [CrossRef] [Green Version]
- Hang, L.; Tu, M. The impacts of energy prices on energy intensity: Evidence from China. Energy Policy 2007, 35, 2978–2988. [Google Scholar] [CrossRef]
- Kuo, K.C.; Sue, L.L.; Chancham, K.; Liu, M. Energy consumption, GDP and foreign direct investment. Appl. Mech. Mater. 2014, 675, 1797–1809. [Google Scholar] [CrossRef]
- Tang, C.F. Electricity consumption, income, foreign direct investment, and population in Malaysia: New evidence from multivariate framework analysis. J. Econ. Stud. 2009, 36, 371–382. [Google Scholar] [CrossRef]
- Chang, S.-C. Effects of financial developments and income on energy consumption. Int. Rev. Econ. Financ. 2015, 35, 28–44. [Google Scholar] [CrossRef] [Green Version]
- Islam, F.; Shahbaz, M.; Ahmed, A.U.; Alam, M. Financial development and energy consumption nexus in Malaysia: A multivariate time series analysis. Econ. Model. 2013, 30, 435–441. [Google Scholar] [CrossRef] [Green Version]
- Kumaresan, N.; Miyazaki, K. An integrated network approach to systems of innovation—the case of robotics in Japan. Res. Policy 1999, 28, 563–585. [Google Scholar] [CrossRef]
- Ibrahim, B.I.; Hurst, C. Estimating energy and oil demand functions: A study of thirteen developing countries. Energy Econ. 1990, 12, 93–102. [Google Scholar] [CrossRef]
- Zivot, E.; Andrews, D.W.K. Further evidence on the great crash, the oil price shock, and the unit root hypothesis. J. Bus. Econ. Stat. 1992, 10, 251–270. [Google Scholar]
- Cheng, M.-Y.; Tan, H.-B. Inflation in Malaysia. Int. J. Soc. Econ. 2002, 29, 411–425. [Google Scholar] [CrossRef]
- Yusof, Z.A.; Bhattasali, D. Economic Growth and Development in Malaysia: Policy Making and Leadership; The World Bank: Washington, DC, USA, 2008. [Google Scholar]
- Greenwood-Nimmo, M.; Shin, Y.; Van Treeck, T. The Asymmetric ARDL Model with Multiple Unknown Threshold Decompositions: An Application to the Philips Curve in Canada; Mimeo; Leeds University Business School: Leeds, UK, 2011. [Google Scholar]
- Sbia, R.; Shahbaz, M.; Ozturk, I. Economic growth, financial development, urbanization and electricity consumption nexus in UAE. Econ. Res. 2017, 30, 527–549. [Google Scholar]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef] [Green Version]
- Alexander, C. Market Risk Analysis, Practical Financial Econometrics; John Wiley & Sons, Ltd.: West Sussex, UK, 2008; Volume II. [Google Scholar]
- Liddle, B.; Sadorsky, P. How much do asymmetric changes in income and energy prices affect energy demand? J. Econ. Asymmetries 2020, 21, e00141. [Google Scholar] [CrossRef]
- Shahbaz, M.; Lean, H.H. Does financial development increase energy consumption? The role of industrialization and urbanization in Tunisia. Energy Policy 2012, 40, 473–479. [Google Scholar] [CrossRef] [Green Version]
- Howarth, N.; Galeotti, M.; Lanza, A.; Dubey, K. Economic development and energy consumption in the GCC: An international sectoral analysis. Energy Transit. 2017, 1, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Liddle, B. Accounting for Nonlinearity, Asymmetry, Heterogeneity, and Cross-Sectional Dependence in Energy Modeling: US State-Level Panel Analysis. Economies 2017, 5, 30. [Google Scholar] [CrossRef] [Green Version]
- Uche, E.; Ihezukwu, V.A.; Osunkwo, F.O.C.; Okoronkwo, C. Does oil consumption respond asymmetrically to oil price, exchange rate and income differentials? J. Ekon. Malays. 2021, 55, 51–63. [Google Scholar]
- MESTECC. Malaysia: Third National Communication and Second Biennial Update Report to the UNFCCC; Ministry of Energy, Science, Technology, Environment and Climate Change: Putrajaya, Malaysia, 2018; Available online: https://unfccc.int/sites/default/files/resource/Malaysia%20NC3%20BUR2_final%20high%20res.pdf (accessed on 16 December 2021).
- KeTTHA. National Energy Efficiency Action Plan; Ministry of Energy, Green Technology and Water: Putrajaya, Malaysia, 2015. Available online: https://www.pmo.gov.my/wp-content/uploads/2019/07/National-Energy-Efficiency-Action-Plan.pdf (accessed on 16 December 2021).
- Kondo, H.; Kutani, I. Sustainable Development of the Transport Sector: Malaysia; Economic Research Institute for ASEAN and East Asia: Jakarta, Indonesia, 2018. [Google Scholar]
- Lei, W.; Ozturk, I.; Muhammad, H.; Ullah, S. On the asymmetric effects of financial deepening on renewable and non-renewable energy consumption: Insights from China. Econ. Res. 2021. [Google Scholar] [CrossRef]
- Benkraiem, R.; Lahiani, A.; Miloudi, A.; Shahbaz, M. The asymmetric role of shadow economy in the energy-growth nexus in Bolivia. Energy Policy 2019, 125, 405–417. [Google Scholar] [CrossRef]
- Energy Commission (EC). National Energy Balance; Energy Commission: Putrajaya, Malaysia, 2016. [Google Scholar]
- He, L.; Ding, Z.; Yin, F.; Wu, M. The impact of relative energy prices on industrial energy consumption in China: A consideration of inflation costs. SpringerPlus 2016, 5, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Gately, D.; Huntington, H.G. The Asymmetric Effects of Changes in Price and Income on Energy and Oil Demand. Energy J. 2002, 23, 19–55. [Google Scholar] [CrossRef] [Green Version]
- Jayaraman, K.; Paramasivan, L.; Kiumarsi, S. Reasons for low penetration on the purchase of photovoltaic (PV) panel system among Malaysian landed property owners. Renew. Sustain. Energy Rev. 2017, 80, 562–571. [Google Scholar] [CrossRef]
- Finocchiaro, M.A. Debts, Oligarchies, and Holisms: Deconstructing the Fallacy of Composition. Informal Log. 2013, 33, 143–147. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).