Intensity-Duration-Frequency Curves at Ungauged Sites in a Changing Climate for Sustainable Stormwater Networks
Abstract
1. Introduction
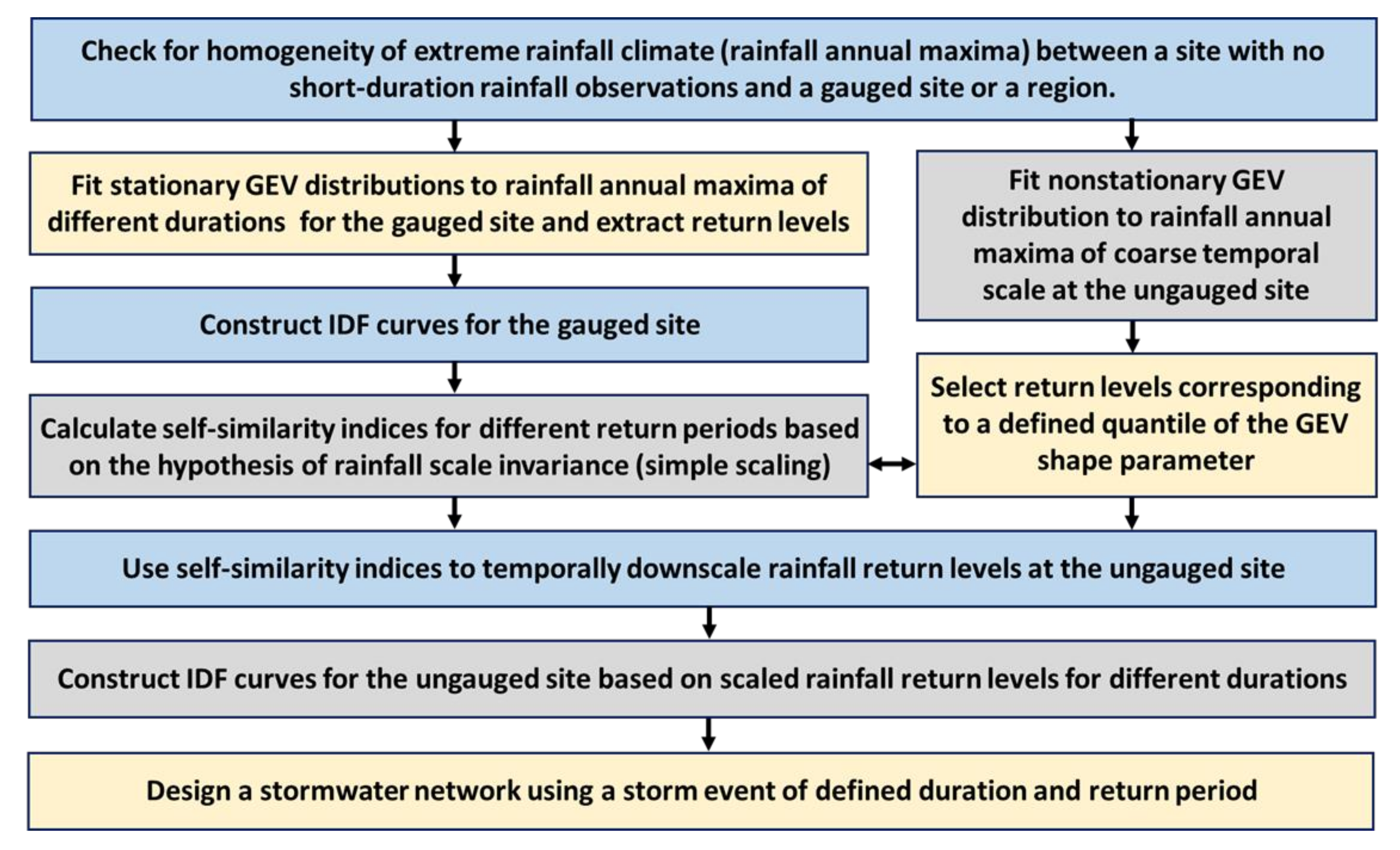
2. Methodology of the Research
2.1. The Nonstationary GEV Distribution Function
2.2. Scaling of Rainfall Intensities
2.3. Rainfall IDF Curves
2.4. Stormwater Network Modelling and Management
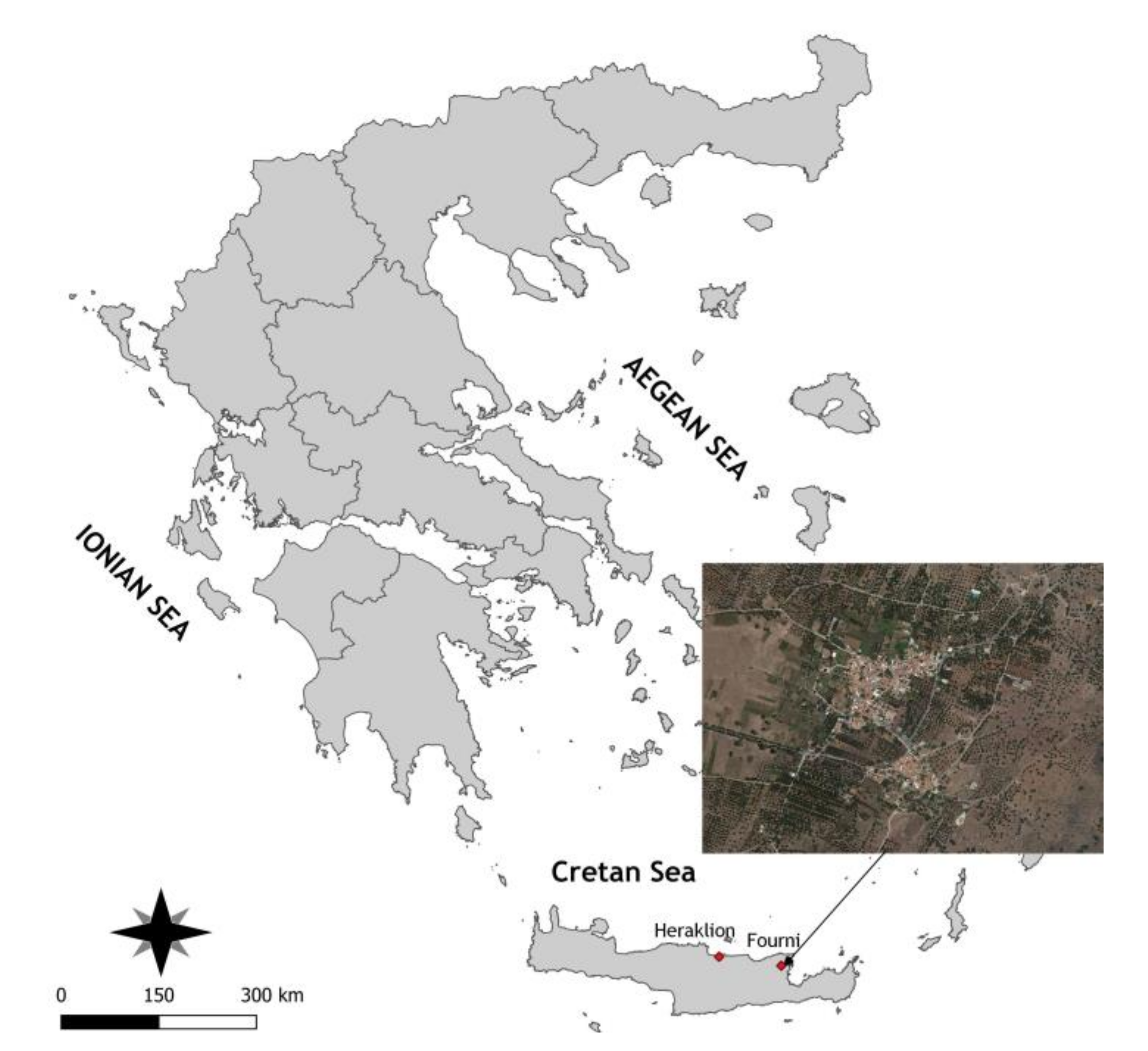
3. Study Area and Available Data
4. Results and Discussion
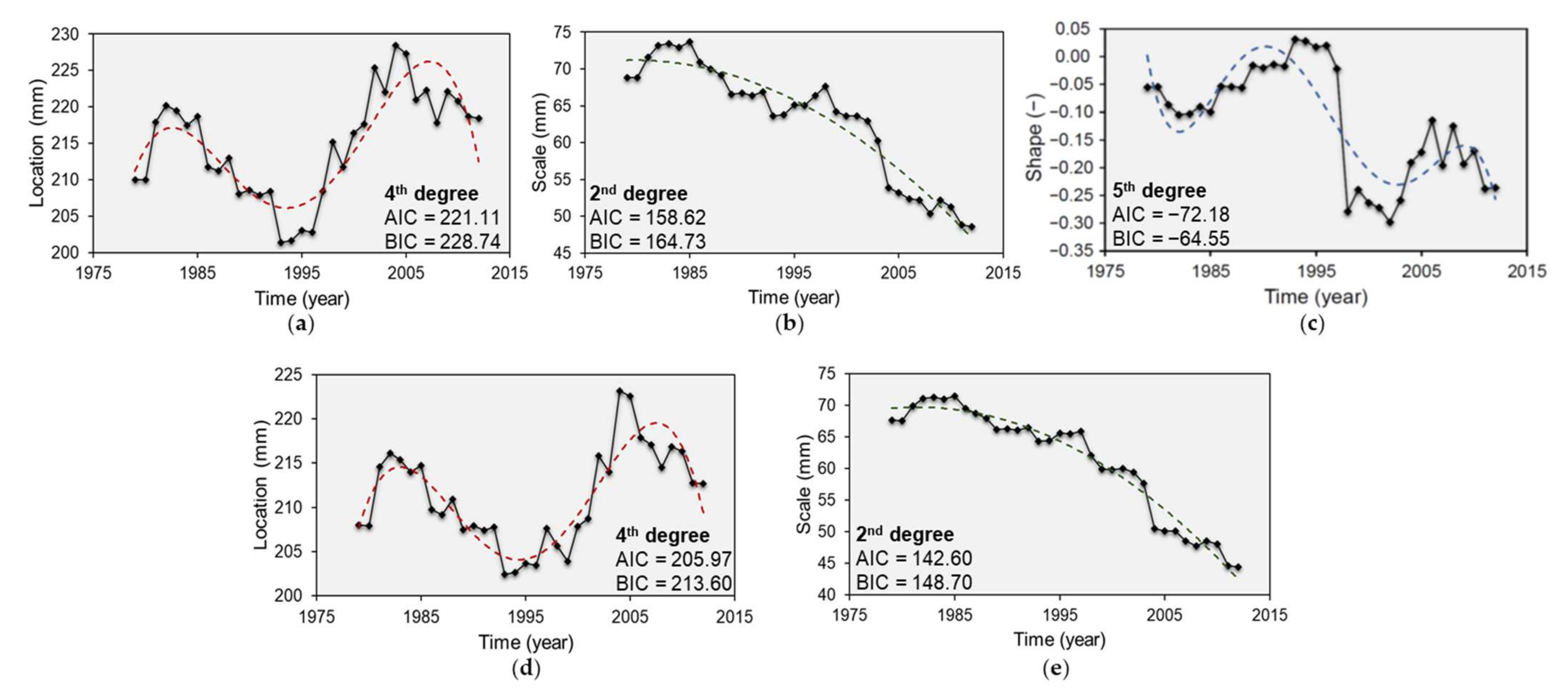
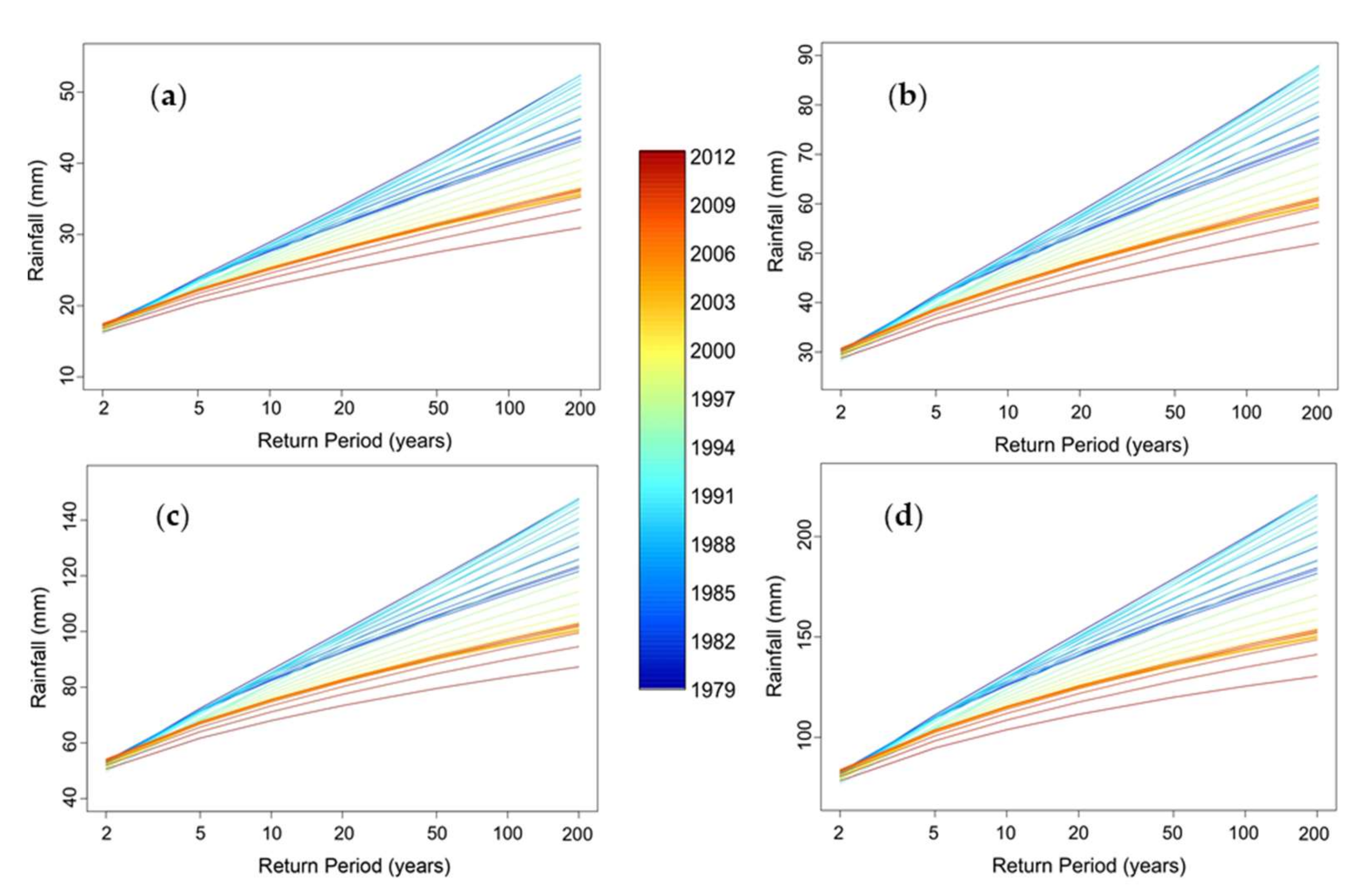
4.1. Nonstationary Analysis of Long-Duration Rainfall Maxima
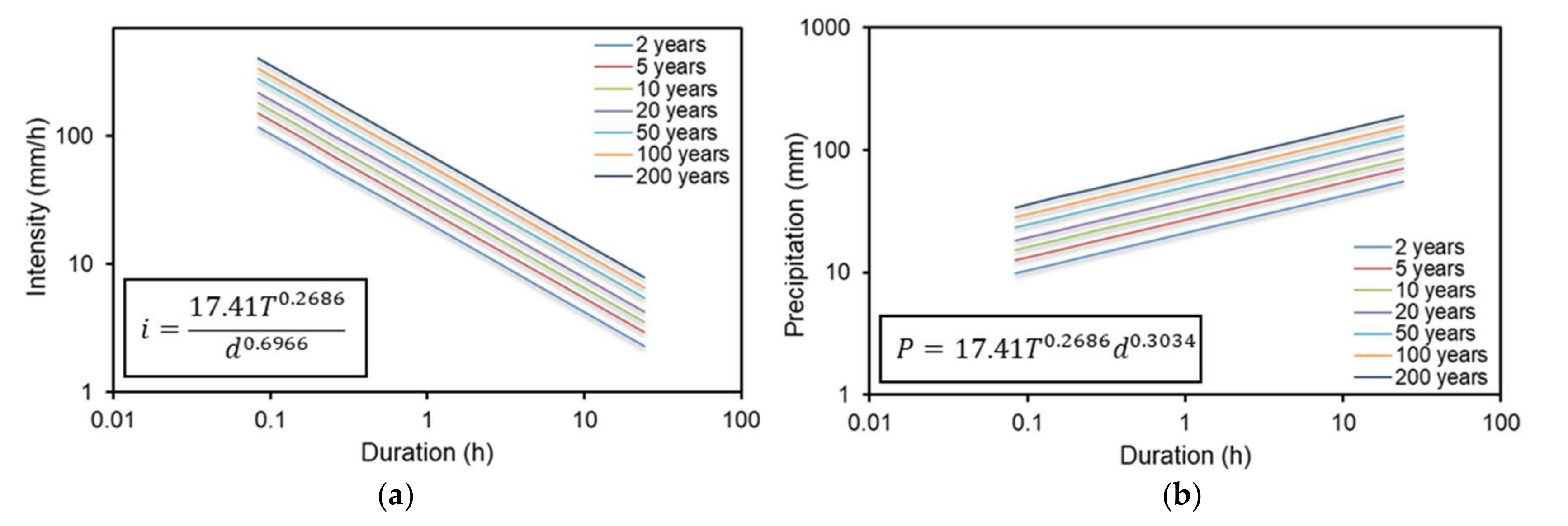
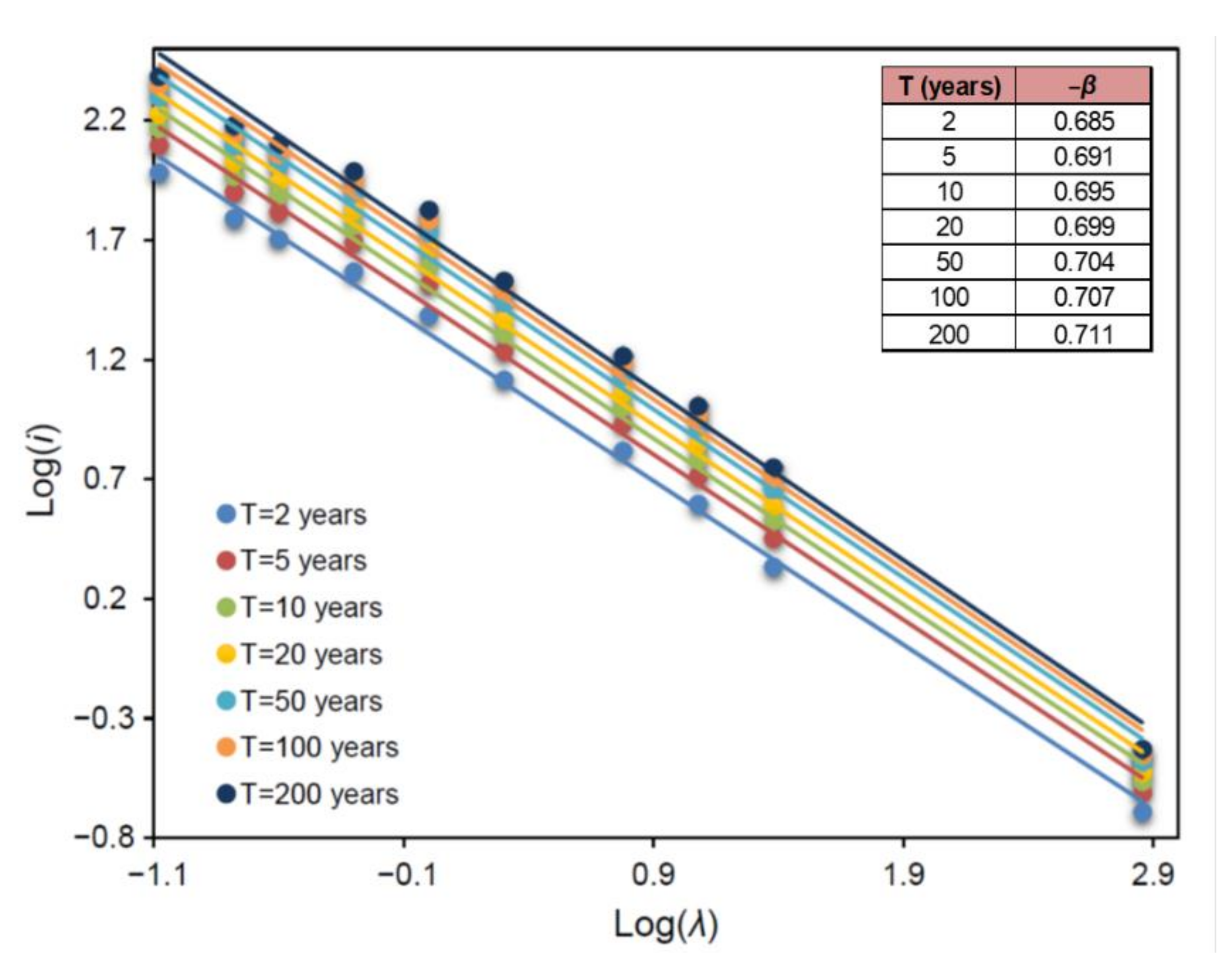
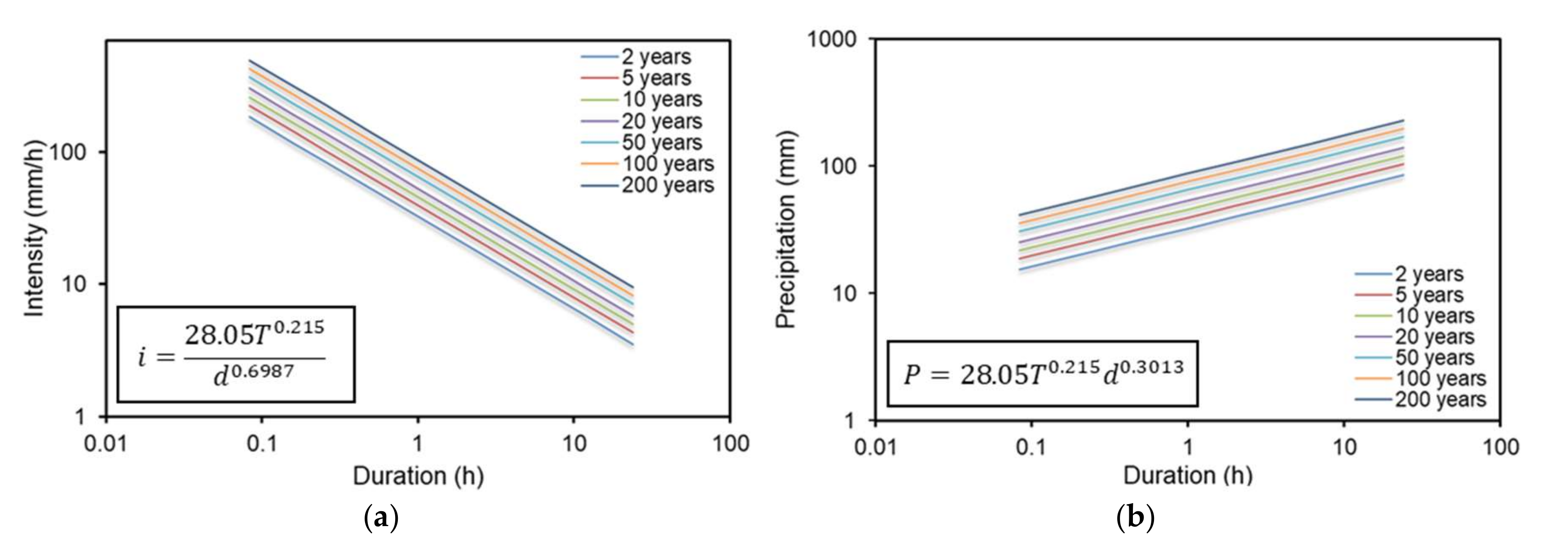
4.2. Rainfall Scaling and Construction of IDF Curves at the Ungauged Site
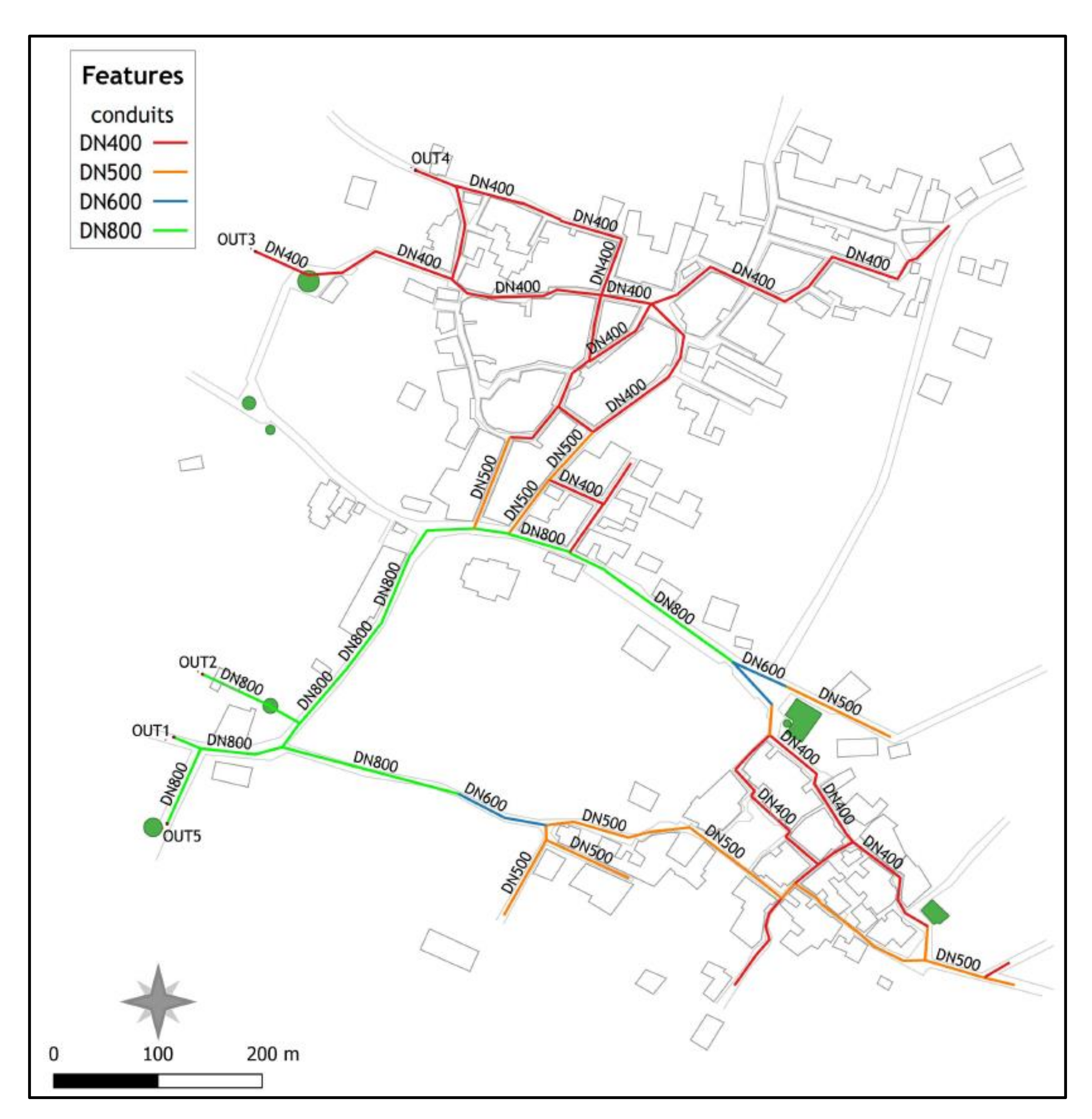
4.3. Design of a Stormwater Network in a Changing Climate
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Norbiato, D.; Borga, M.; Sangati, M.; Zanon, F. Regional frequency analysis of extreme precipitation in the eastern Italian Alps and the 29 August 2003 flash flood. J. Hydrol. 2007, 345, 149–166. [Google Scholar] [CrossRef]
- Morita, M. Flood risk analysis for determining optimal flood protection levels in urban river management. J. Flood Risk Manag. 2008, 1, 142–149. [Google Scholar] [CrossRef]
- Fontanazza, C.M.; Freni, G.; La Loggia, G.; Notaro, V. Uncertainty evaluation of design rainfall for urban flood risk analysis. Water Sci. Technol. 2011, 63, 2641–2650. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Q.; Mikkelsen, P.S.; Halsnæs, K.; Arnbjerg-Nielsen, K. Framework for economic pluvial flood risk assessment considering climate change effects and adaptation benefits. J. Hydrol. 2012, 414, 539–549. [Google Scholar] [CrossRef]
- Cheng, L.; AghaKouchak, A. Nonstationary precipitation intensity-duration-frequency curves for infrastructure design in a changing climate. Sci. Rep. 2014, 4, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Da Silva, C.V.F.; Schardong, A.; Garcia, J.I.B.; Oliveira, C.D.P.M. Climate change impacts and flood control measures for highly developed urban watersheds. Water 2018, 10, 829. [Google Scholar] [CrossRef]
- Yan, H.; Sun, N.; Wigmosta, M.; Skaggs, R.; Hou, Z.; Leung, L.R. Next-generation intensity–duration–frequency curves to reduce errors in peak flood design. J. Hydrol. Eng. 2019, 24, 04019020. [Google Scholar] [CrossRef]
- Yan, H.; Sun, N.; Wigmosta, M.; Leung, L.R.; Hou, Z.; Coleman, A.; Skaggs, R. Evaluating next-generation intensity–duration–frequency curves for design flood estimates in the snow-dominated western United States. Hydrol. Process. 2020, 34, 1255–1268. [Google Scholar] [CrossRef]
- Wallis, J.; Schaefer, M.; Baker, B.; Taylor, G. Regional precipitation-frequency analysis and spatial mapping for 24- and 2-h durations for Washington State. Hydrol. Earth Syst. Sci. Dis. 2007, 11, 415–442. [Google Scholar] [CrossRef]
- Renard, B.; Lall, U. Regional frequency analysis conditioned on large-scale atmospheric or ocean fields. Water Resour. Res. 2014, 50, 9536–9554. [Google Scholar] [CrossRef]
- Devkota, S.; Shakya, N.M.; Sudmeier-Rieux, K.; Jaboyedoff, M.; Van Westen, C.J.; Mcadoo, B.G.; Adhikari, A. Development of monsoonal rainfall intensity-duration-frequency (IDF) relationship and empirical model for data-scarce situations: The case of the Central-Western Hills (Panchase region) of Nepal. Hydrology 2018, 5, 27. [Google Scholar] [CrossRef]
- El-Sayed, E.A.H. Generation of rainfall intensity duration frequency curves for ungauged sites. Nile Basin Water Sci. Eng. J. 2011, 4, 112–124. [Google Scholar]
- Liew, S.C.; Raghavan, S.V.; Liong, S.Y. How to construct future IDF curves, under changing climate, for sites with scarce rainfall records? Hydrol. Process. 2014, 28, 3276–3287. [Google Scholar] [CrossRef]
- Rodriguez, R.D.; Singh, V.P.; Pruski, F.F.; Calegario, A.T. Using entropy theory to improve the definition of homogeneous regions in the semi-arid region of Brazil. Hydrol. Sci. J. 2016, 61, 2096–2109. [Google Scholar] [CrossRef]
- Ouali, D.; Chebana, F.; Ouarda, T.B. Non-linear canonical correlation analysis in regional frequency analysis. Stoch. Environ. Res. Risk Assess. 2016, 30, 449–462. [Google Scholar] [CrossRef]
- Pandey, G.R.; Nguyen, V.T.V. A comparative study of regression-based methods in regional flood frequency analysis. J. Hydrol. 1999, 225, 92–101. [Google Scholar] [CrossRef]
- Ouarda, T.B.; Cunderlik, J.M.; St-Hilaire, A.; Barbet, M.; Bruneau, P.; Bobée, B. Data-based comparison of seasonality-based regional flood frequency methods. J. Hydrol. 2006, 330, 329–339. [Google Scholar] [CrossRef]
- Cannon, A.J. An intercomparison of regional and at-site rainfall extreme value analyses in southern British Columbia, Canada. Can. J. Civ. Eng. 2015, 42, 107–119. [Google Scholar] [CrossRef]
- Ouali, D.; Chebana, F.; Ouarda, T.B. Fully nonlinear statistical and machine-learning approaches for hydrological frequency estimation at ungauged sites. J. Adv. Model. Earth Syst. 2017, 9, 1292–1306. [Google Scholar] [CrossRef]
- Ouali, D.; Chebana, F.; Ouarda, T.B. Quantile regression in regional frequency analysis: A better exploitation of the available information. J. Hydrometeorol. 2016, 17, 1869–1883. [Google Scholar] [CrossRef]
- Cannon, A.J. Quantile regression neural networks: Implementation in R and application to precipitation downscaling. Comput. Geosci. 2011, 37, 1277–1284. [Google Scholar] [CrossRef]
- Ouali, D.; Cannon, A.J. Estimation of rainfall intensity–duration–frequency curves at ungauged locations using quantile regression methods. Stoch. Environ. Res. Risk Assess. 2018, 32, 2821–2836. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Kozonis, D.; Manetas, A. A mathematical framework for studying rainfall intensity-duration-frequency relationships. J. Hydrol. 1998, 206, 118–135. [Google Scholar] [CrossRef]
- Veneziano, D.; Furcolo, P. Multifractality of rainfall and scaling of intensity-duration-frequency curves. Water Resour. Res. 2002, 38, 42-1. [Google Scholar] [CrossRef]
- Singh, V.P.; Zhang, L. IDF curves using the Frank Archimedean copula. J. Hydrol. Eng. 2007, 12, 651–662. [Google Scholar] [CrossRef]
- Ganguli, P.; Coulibaly, P. Does nonstationarity in rainfall require nonstationary intensity–duration–frequency curves? Hydrol. Earth Syst. Sci. 2017, 21, 6461–6483. [Google Scholar] [CrossRef]
- Salas, J.D.; Obeysekera, J. Revisiting the concepts of return period and risk for nonstationary hydrologic extreme events. J. Hydrol. Eng. 2014, 19, 554–568. [Google Scholar] [CrossRef]
- Kharin, V.V.; Zwiers, F.W. Estimating extremes in transient climate change simulations. J. Clim. 2005, 18, 1156–1173. [Google Scholar] [CrossRef]
- El Adlouni, A.; Ouarda, T.B.M.; Zhang, X.; Roy, R.; Bobee, B. Generalized maximum likelihood estimators for the nonstationary generalized extreme value model. Water Resour. Res. 2007, 43, W03410. [Google Scholar] [CrossRef]
- Cooley, D. Extreme value analysis and the study of climate change. Clim. Change 2009, 97, 77–83. [Google Scholar] [CrossRef]
- Towler, E.; Rajagopalan, B.; Gilleland, E.; Summers, R.S.; Yates, D.; Katz, R.W. Modeling hydrologic and water quality extremes in a changing climate: A statistical approach based on extreme value theory. Water Resour. Res. 2010, 46, W11504. [Google Scholar] [CrossRef]
- Cheng, L.; AghaKouchak, A.; Gilleland, E.; Katz, R.W. Non-stationary extreme value analysis in a changing climate. Clim. Chang. 2014, 127, 353–369. [Google Scholar] [CrossRef]
- Sarhadi, A.; Soulis, E.D. Time-varying extreme rainfall intensity-duration-frequency curves in a changing climate. Geophys. Res. Lett. 2017, 44, 2454–2463. [Google Scholar] [CrossRef]
- Agilan, V.; Umamahesh, N.V. Modelling nonlinear trend for developing non-stationary rainfall intensity–duration–frequency curve. Int. J. Climatol. 2017, 37, 1265–1281. [Google Scholar] [CrossRef]
- Ouarda, T.B.; Charron, C. Nonstationary temperature-duration-frequency curves. Sci. Rep. 2018, 8, 1–8. [Google Scholar] [CrossRef]
- Silva, D.F.; Simonovic, S.P.; Schardong, A.; Goldenfum, J.A. Assessment of non-stationary IDF curves under a changing climate: Case study of different climatic zones in Canada. J. Hydrol. Reg. Stud. 2021, 36, 100870. [Google Scholar] [CrossRef]
- Yan, L.; Xiong, L.; Jiang, C.; Zhang, M.; Wang, D.; Xu, C.Y. Updating intensity–duration–frequency curves for urban infrastructure design under a changing environment. WIREs Water 2021, 8, e1519. [Google Scholar] [CrossRef]
- Nguyen, V.T.V.; Nguyen, T.D.; Wang, H. Regional estimation of short duration rainfall extremes. Water Sci. Technol. 1998, 37, 15–19. [Google Scholar] [CrossRef]
- Yu, P.S.; Yang, T.C.; Lin, C.S. Regional rainfall intensity formulas based on scaling property of rainfall. J. Hydrol. 2004, 295, 108–123. [Google Scholar] [CrossRef]
- Bougadis, J.; Adamowski, K. Scaling model of a rainfall intensity-duration-frequency relationship. Hydrol. Process. 2006, 20, 3747–3757. [Google Scholar] [CrossRef]
- Sun, Y.; Wendi, D.; Kim, D.E.; Liong, S.Y. Deriving intensity–duration–frequency (IDF) curves using downscaled in situ rainfall assimilated with remote sensing data. Geosci. Lett. 2019, 6, 1–12. [Google Scholar] [CrossRef]
- Burlando, P.; Rosso, R. Scaling and muitiscaling models of depth-duration-frequency curves for storm precipitation. J. Hydrol. 1996, 187, 45–64. [Google Scholar] [CrossRef]
- Langousis, A.; Carsteanu, A.A.; Deidda, R. A simple approximation to multifractal rainfall maxima using a generalized extreme value distribution model. Stoch. Environ. Res. Risk Assess. 2013, 27, 1525–1531. [Google Scholar] [CrossRef]
- Bara, M.; Gaal, L.; Kohnova, S.; Szolgay, J.; Hlavcova, K. On the use of the simple scaling of heavy rainfall in a regional estimation of IDF curves in Slovakia. J. Hydrol. Hydromech. 2010, 58, 49. [Google Scholar] [CrossRef]
- Ghanmi, H.; Bargaoui, Z.; Mallet, C. Estimation of intensity-duration-frequency relationships according to the property of scale invariance and regionalization analysis in a Mediterranean coastal area. J. Hydrol. 2016, 541, 38–49. [Google Scholar] [CrossRef]
- Yeo, M.H.; Nguyen, V.T.V.; Kpodonu, T.A. Characterizing extreme rainfalls and constructing confidence intervals for IDF curves using Scaling-GEV distribution model. Int. J. Climatol. 2021, 41, 456–468. [Google Scholar] [CrossRef]
- Willems, P.; Arnbjerg-Nielsen, K.; Olsson, J.; Nguyen, V.T.V. Climate change impact assessment on urban rainfall extremes and urban drainage: Methods and shortcomings. Atmos. Res. 2012, 103, 106–118. [Google Scholar] [CrossRef]
- Arnbjerg-Nielsen, K.; Willems, P.; Olsson, J.; Beecham, S.; Pathirana, A.; Bulow Gregersen, I.; Madsen, H.; Nguyen, V.T.V. Impacts of climate change on rainfall extremes and urban drainage systems: A review. Water Sci. Technol. 2013, 68, 16–28. [Google Scholar] [CrossRef]
- Langeveld, J.G.; Schilperoort, R.P.S.; Weijers, S.R. Climate change and urban wastewater infrastructure: There is more to explore. J. Hydrol. 2013, 476, 112–119. [Google Scholar] [CrossRef]
- Willems, P. Revision of urban drainage design rules after assessment of climate change impacts on precipitation extremes at Uccle, Belgium. J. Hydrol. 2013, 496, 166–177. [Google Scholar] [CrossRef]
- Moore, T.L.; Gulliver, J.S.; Stack, L.; Simpson, M.H. Stormwater management and climate change: Vulnerability and capacity for adaptation in urban and suburban contexts. Clim. Change 2016, 138, 491–504. [Google Scholar] [CrossRef]
- Kumar, S.; Agarwal, A.; Ganapathy, A.; Villuri, V.G.K.; Pasupuleti, S.; Kumar, D.; Kaushal, D.R.; Gosain, A.K.; Sivakumar, B. Impact of climate change on stormwater drainage in urban areas. Stoch. Hydrol. Hydraul. 2021, 36, 77–96. [Google Scholar] [CrossRef]
- Huq, E.; Abdul-Aziz, O.I. Climate and land cover change impacts on stormwater runoff in large-scale coastal-urban environments. Sci. Total Environ. 2021, 778, 146017. [Google Scholar] [CrossRef]
- Kourtis, I.M.; Tsihrintzis, V.A. Adaptation of urban drainage networks to climate change: A review. Sci. Total Environ. 2021, 771, 145431. [Google Scholar] [CrossRef] [PubMed]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer: London, UK, 2001; p. 208. [Google Scholar]
- Galiatsatou, P.; Prinos, P. Modeling non-stationary extreme waves using a point process approach and wavelets. Stoch. Environ. Res. Risk Assess. 2011, 25, 165–183. [Google Scholar] [CrossRef]
- Hosking, J.R. L-moments: Analysis and estimation of distributions using linear combinations of order statistics. J. R. Stat. Soc. Ser. B (Methodol.) 1990, 52, 105–124. [Google Scholar] [CrossRef]
- Galiatsatou, P.; Prinos, P. Bivariate analysis of extreme wave and storm surge events. Determining the failure area of structures. Open Ocean Eng. J. 2011, 4, 3–14. [Google Scholar] [CrossRef][Green Version]
- Galiatsatou, P.; Makris, C.; Prinos, P.; Kokkinos, D. Nonstationary joint probability analysis of extreme marine variables to assess design water levels at the shoreline in a changing climate. Nat. Hazards 2019, 98, 1051–1089. [Google Scholar] [CrossRef]
- Galiatsatou, P.; Makris, C.; Krestenitis, Y.; Prinos, P. Nonstationary Extreme Value Analysis of Nearshore Sea-State Parameters under the Effects of Climate Change: Application to the Greek Coastal Zone and Port Structures. J. Mar. Sci. Eng. 2021, 9, 817. [Google Scholar] [CrossRef]
- Gupta, V.K.; Waymire, E. Multiscaling properties of spatial rainfall and river flow distributions. J. Geophys. Res. Atmos. 1990, 95, 1999–2009. [Google Scholar] [CrossRef]
- Veneziano, D.; Lepore, C.; Langousis, A.; Furcolo, P. Marginal methods of intensity-duration-frequency estimation in scaling and nonscaling rainfall. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Innocenti, S.; Mailhot, A.; Frigon, A. Simple scaling of extreme precipitation in North America. Hydrol. Earth Syst. Sci. 2017, 21, 5823–5846. [Google Scholar] [CrossRef]
- Van de Vyver, H. Bayesian estimation of rainfall intensity–duration–frequency relationships. J. Hydrol. 2015, 529, 1451–1463. [Google Scholar] [CrossRef]
- Raudkivi, A.J. Hydrology: An Advanced Introduction to Hydrological Processes and Modelling; Pergamon Press: New York, NY, USA, 1979. [Google Scholar]
- Chow, V.T. Handbook of Applied Hydrology; McGraw-Hill Book: New York, NY, USA, 1988. [Google Scholar]
- Singh, V.P. Elementary Hydrology; Prentice Hall: Englewood Cliffs, NJ, USA, 1992. [Google Scholar]
- Shaw, E.M.; Beven, K.J.; Chappell, N.A.; Lamb, R. Hydrology in Practice; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Chen, C. Rainfall Intensity-Duration-Frequency Formulas. J. Hydraul. Eng. 1983, 109, 1603–1621. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Statistical Hydrology; National Technical University: Athens, Greek, 1997. [Google Scholar] [CrossRef]
- James, W.; Huber, W.C.; Dickinson, R.E.; Pitt, R.E.; James, W.R.C.; Roesner, L.A.; Aldrich, J.A. User’s Guide to SWMM5-CHI Publications, 13th ed.; CHI Water: Guelph, ON, Canada, 2011. [Google Scholar]
- Rossman, L.A. Storm Water Management Model User’s Manual Version 5.1; United States Environmental Protection Agency (USEPA): Cincinnati, OH, USA, 2015. [Google Scholar]
- Rossman, L.A.; Huber, W.C. Storm Water Management Model Reference Manual Volume I—Hydrology (Revised); EPA/600/R-15/162A; National Risk Management Laboratory Office of Research and Development; United States Environmental Protection Agency (USEPA): Cincinnati, OH, USA, 2016. [Google Scholar]
- Niazi, M.; Nietch, C.; Maghrebi, M.; Jackson, N.; Bennett, B.R.; Tryby, M.; Massoudieh, A. Storm water management model: Performance review and gap analysis. J. Sustain. Water Built. Environ. 2017, 3, 04017002. [Google Scholar] [CrossRef] [PubMed]
- Shao, Z.; Zhang, X.; Li, S.; Deng, S.; Chai, H. A novel SWMM based algorithm application to storm sewer network design. Water 2017, 9, 747. [Google Scholar] [CrossRef]
- Markonis, Y.; Batelis, S.C.; Dimakos, Y.; Moschou, E.; Koutsoyiannis, D. Temporal and spatial variability of rainfall over Greece. Theor. Appl. Climatol. 2017, 130, 217–232. [Google Scholar] [CrossRef]
- Serinaldi, F.; Kilsby, C.G. Rainfall extremes: Toward reconciliation after the battle of distributions. Water Resour. Res. 2014, 50, 336–352. [Google Scholar] [CrossRef]
- Scholz, F.W.; Stephens, M.A. K-sample Anderson–Darling tests. J. Am. Stat. Assoc. 1987, 82, 918–924. [Google Scholar]
- Durbin, J.; Knott, M. Components of Cramér–von Mises statistics. I. J. R. Stat. Soc. Ser. B (Methodol.) 1972, 34, 290–307. [Google Scholar] [CrossRef]



| Rainfall Maxima | Descriptive Statistics | ||||||
|---|---|---|---|---|---|---|---|
| Mean (mm) | Median (mm) | Max (mm) | Min (mm) | Range (mm) | St. Dev. (mm) | Skewness (−) | |
| Annual max | 816.3 | 782.0 | 1296.5 | 411.5 | 885.0 | 185.2 | 0.517 |
| Monthly max | 245.2 | 239.3 | 498.5 | 112.7 | 385.8 | 69.9 | 0.731 |
| Duration | Stationary GEV | Nonstationary GEV | |||||||
|---|---|---|---|---|---|---|---|---|---|
| T (Years) | 20 | 50 | 100 | 200 | 20 | 50 | 100 | 200 | |
| 10 min | P (mm) | 30.06 | 34.73 | 38.24 | 41.74 | 32.23 | 38.97 | 44.42 | 50.21 |
| i (mm/h) | 180.35 | 208.37 | 229.42 | 250.42 | 193.36 | 233.81 | 266.54 | 301.28 | |
| 1 h | P (mm) | 51.56 | 59.05 | 64.61 | 70.10 | 55.28 | 66.27 | 75.07 | 84.34 |
| i (mm/h) | 51.56 | 59.05 | 64.61 | 70.10 | 55.28 | 66.27 | 75.07 | 84.34 | |
| 24 h | P (mm) | 134.29 | 151.43 | 163.85 | 175.85 | 143.99 | 169.92 | 190.36 | 211.57 |
| i (mm/h) | 5.60 | 6.31 | 6.83 | 7.33 | 6.00 | 7.08 | 7.93 | 8.82 | |
| Duration | Stationary GEV | Nonstationary GEV | |||||||
|---|---|---|---|---|---|---|---|---|---|
| T (Years) | 20 | 50 | 100 | 200 | 20 | 50 | 100 | 200 | |
| 10 min | P (mm) | 35.13 | 40.74 | 45.03 | 49.37 | 42.02 | 53.39 | 63.38 | 74.64 |
| i (mm/h) | 210.76 | 244.42 | 270.18 | 296.23 | 252.11 | 320.35 | 380.29 | 447.82 | |
| 1 h | P (mm) | 59.53 | 68.75 | 75.82 | 82.97 | 71.21 | 90.11 | 106.72 | 125.42 |
| i (mm/h) | 59.53 | 68.75 | 75.82 | 82.97 | 71.21 | 90.11 | 106.72 | 125.42 | |
| 24 h | P (mm) | 151.73 | 173.96 | 191.05 | 208.33 | 181.50 | 228.00 | 268.91 | 314.94 |
| i (mm/h) | 6.32 | 7.25 | 7.96 | 8.68 | 7.56 | 9.50 | 11.20 | 13.12 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galiatsatou, P.; Iliadis, C. Intensity-Duration-Frequency Curves at Ungauged Sites in a Changing Climate for Sustainable Stormwater Networks. Sustainability 2022, 14, 1229. https://doi.org/10.3390/su14031229
Galiatsatou P, Iliadis C. Intensity-Duration-Frequency Curves at Ungauged Sites in a Changing Climate for Sustainable Stormwater Networks. Sustainability. 2022; 14(3):1229. https://doi.org/10.3390/su14031229
Chicago/Turabian StyleGaliatsatou, Panagiota, and Christos Iliadis. 2022. "Intensity-Duration-Frequency Curves at Ungauged Sites in a Changing Climate for Sustainable Stormwater Networks" Sustainability 14, no. 3: 1229. https://doi.org/10.3390/su14031229
APA StyleGaliatsatou, P., & Iliadis, C. (2022). Intensity-Duration-Frequency Curves at Ungauged Sites in a Changing Climate for Sustainable Stormwater Networks. Sustainability, 14(3), 1229. https://doi.org/10.3390/su14031229







