CA Energy Saving Joint Resource Optimization Scheme Based on 5G Channel Information Prediction of Machine Learning
Abstract
1. Introduction
- (1)
- A mathematical model for the optimal CA energy-efficient resources allocation is established, which comprehensively considers many factors, including the carrier aggregation capability of different users, the delayed channel information, and the selection of MCS, CC, RB, and power allocation. Since the established energy-efficient optimization model is a mixed-integer nonlinear programming (MINLP), the power, RB allocation sub-algorithm, and CC allocation sub-algorithm of energy efficiency optimization are designed to solve the problem iteratively.
- (2)
- Aiming at the problem that CQI with delayed feedback causes the resource allocation performance to be worse, the random forest algorithm is used to predict the SINR online to obtain the current SINR and its corresponding real-time CQI and MCS.
- (3)
- Under the assumption that both the CC allocation and the predicted channel information are known, the energy-efficiency optimized RB and power allocation algorithms (ERPA) are proposed. The ERPA algorithm transforms RB and power allocation problem into a fractional programming problem P3 by introducing relaxation variables. The Dinkelbach theory and Lagrangian dual method are applied to solve P3. The sufficient and necessary conditions for obtaining the maximum energy efficiency are proved and P3 is converted to non-fractional subtraction P4−1 and we obtain P4−1 as the corollary of convex optimization.
- (4)
- The CC allocation algorithm (DDJBNBC) is proposed, which combines the iterative pruning method and the algorithm to avoid the frequent handover of narrowband users and then the criteria for CC deletion and the energy-efficient CC handover of narrowband users is formulated. Based on ERPA and DDJBNBC sub algorithms, an energy efficiency joint resource allocation algorithm (PEJA) based on channel information prediction is proposed.
2. Energy-Efficient Optimization Model
3. Fast Channel Information Prediction Based Random Forest
3.1. Basis for Channel Information Prediction
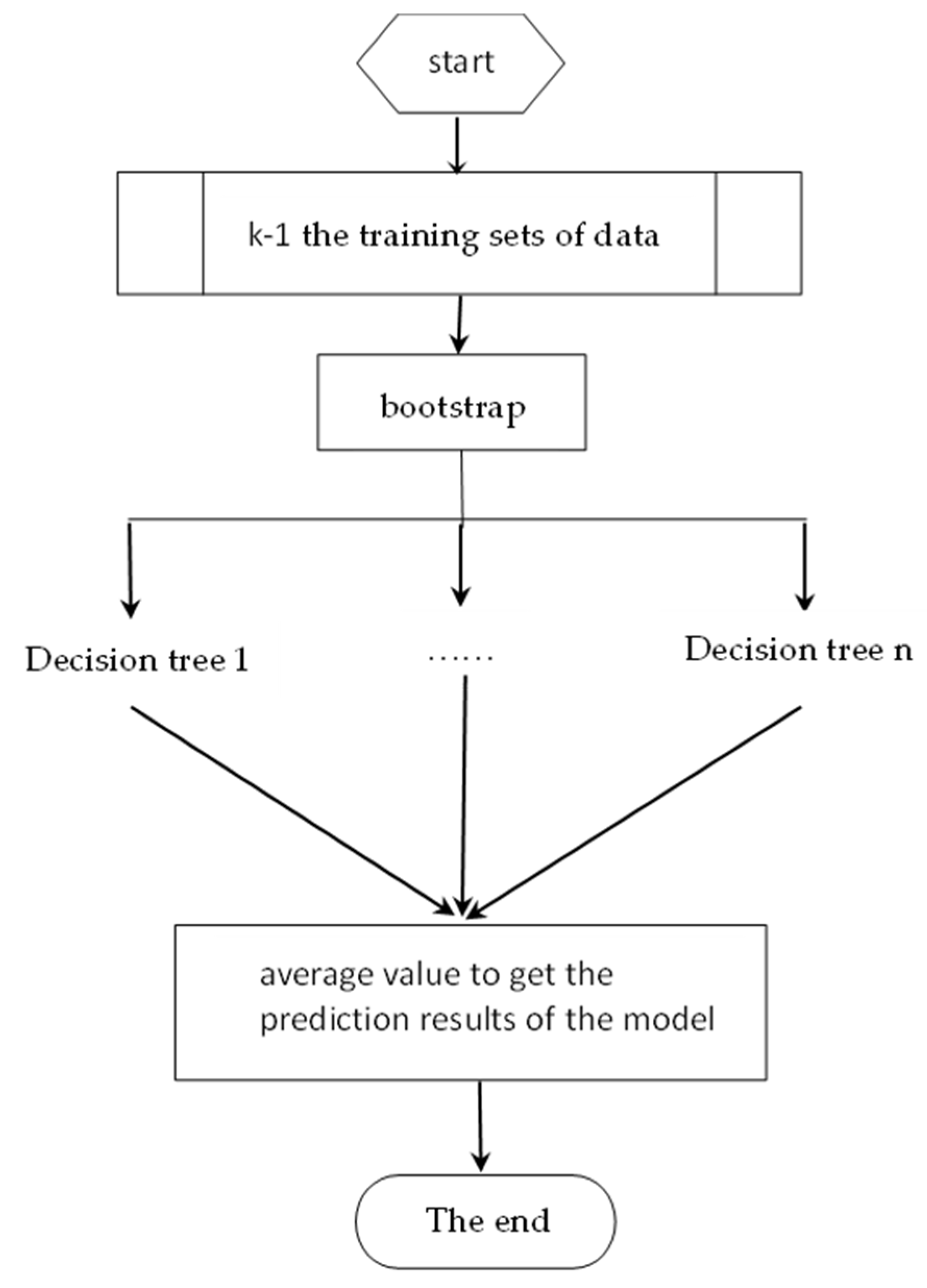
3.2. Random Forest Prediction SINR
| Algorithm 1: Random forest prediction channel SINR |
|
4. Energy-Efficient Resource Optimization Allocation Algorithm Based on Channel Information Prediction
4.1. RB and Power Allocation Algorithm for Energy-Efficient Optimization
| Algorithm 2: Dinkelbach algorithm |
|
| Algorithm 3: ERPA Algorithm |
| Input: the set of component carrier assigned to each user; obtained CQI index and MCS by predicted SINR in Section 3.2;;; Output: RB allocation scheme , power allocation scheme |
|
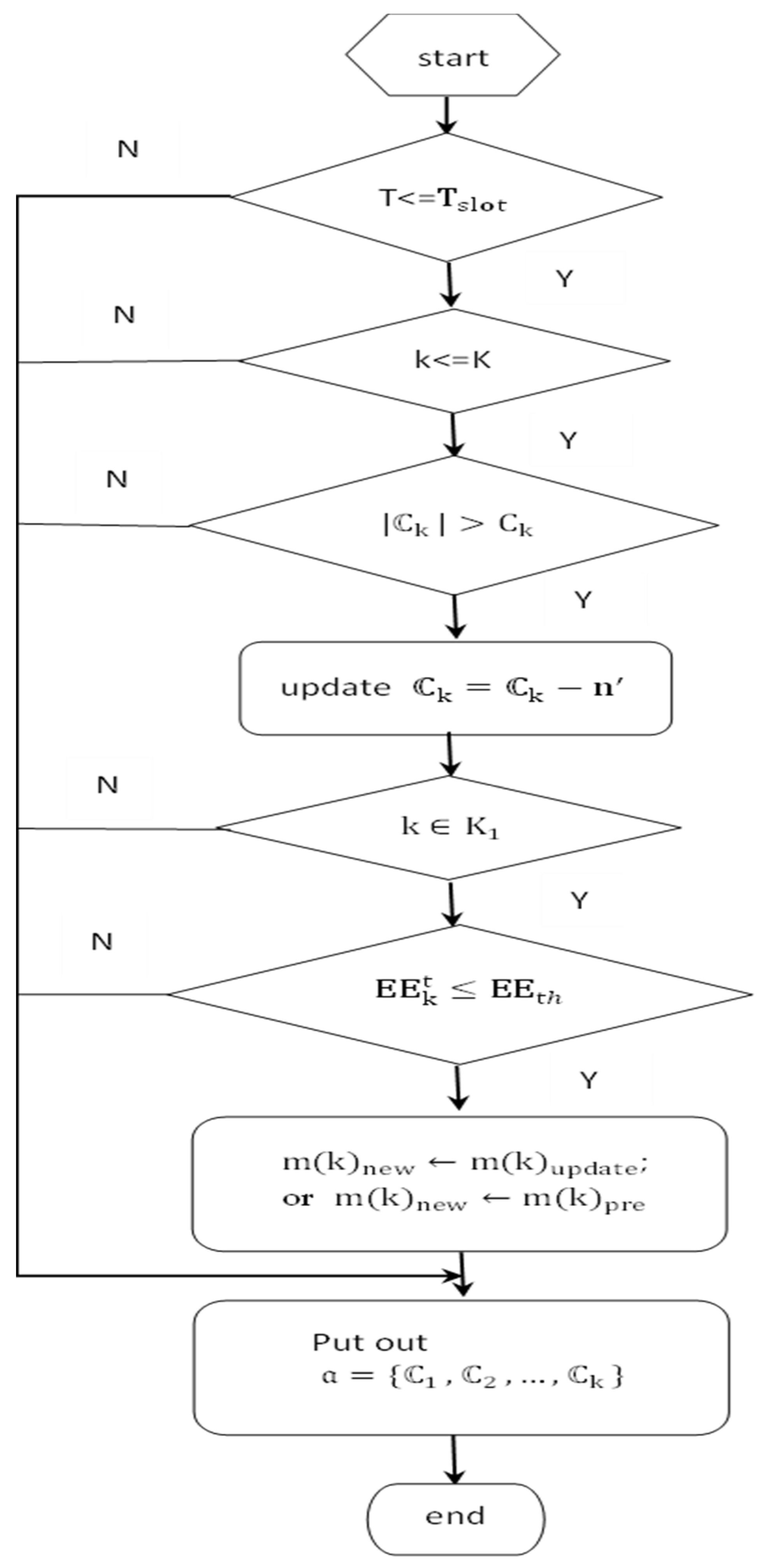
4.2. CC Allocation Algorithm for Energy-Efficient Optimization
| Algorithm 4: DDJBNBC Algorithm |
|
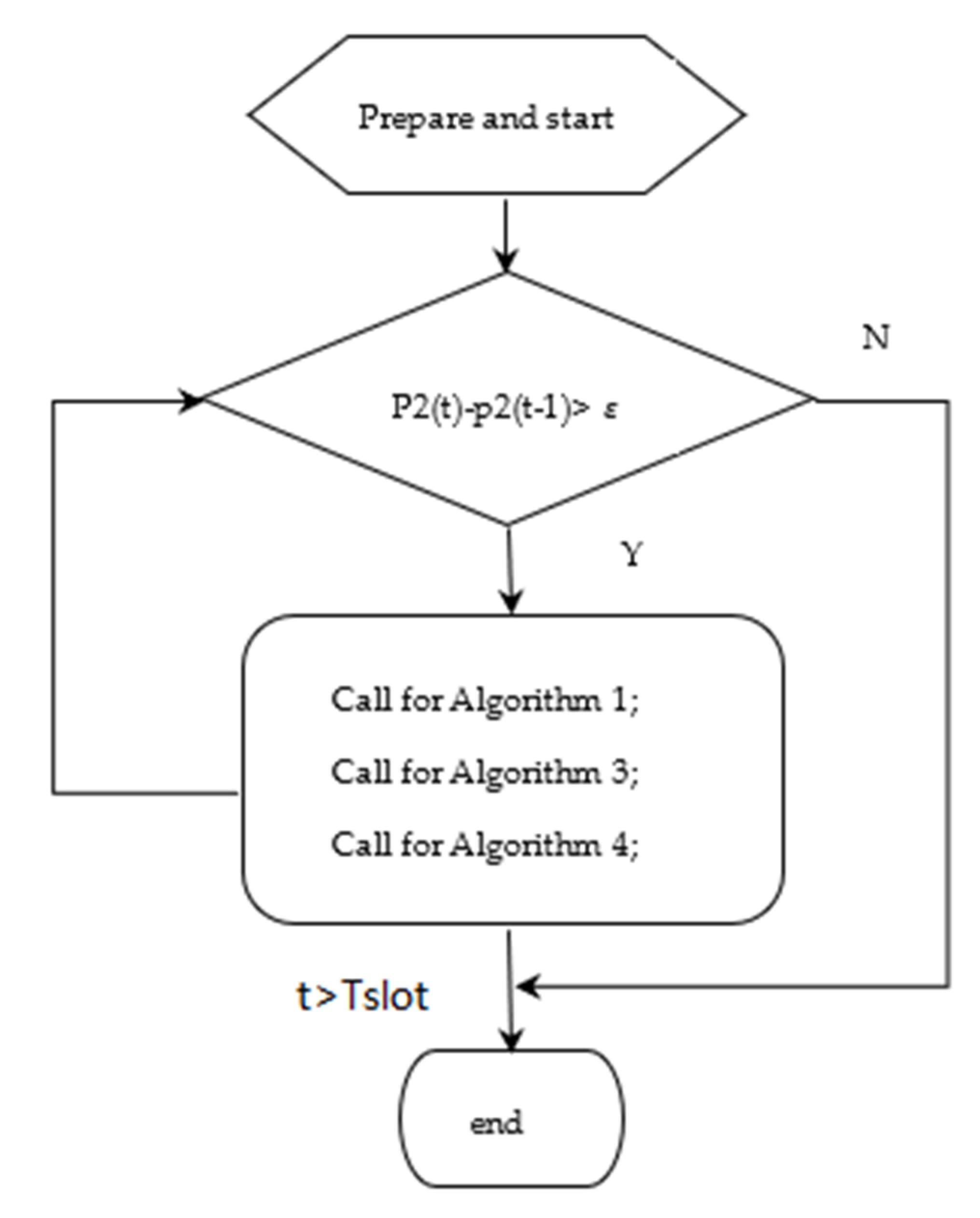
4.3. Energy-Efficient Optimization Joint Resource Allocation Algorithm (PEJA) Based on Channel Information Prediction
| Algorithm 5: PEJA algorithm |
| Input: the random set ; user number n; maximum slot Output: CC allocation scheme ; RB allocation scheme ; power allocation scheme ; maximal . |
| ① do
② slot) do ③ do ④ call for Algorithm 1 ⑤ call for Algorithm 3 ERPA algorithm; ⑥ call for Algorithm 4 DDJBNBC algorithm; ⑦ end for ⑧ end while ⑨ end for. |
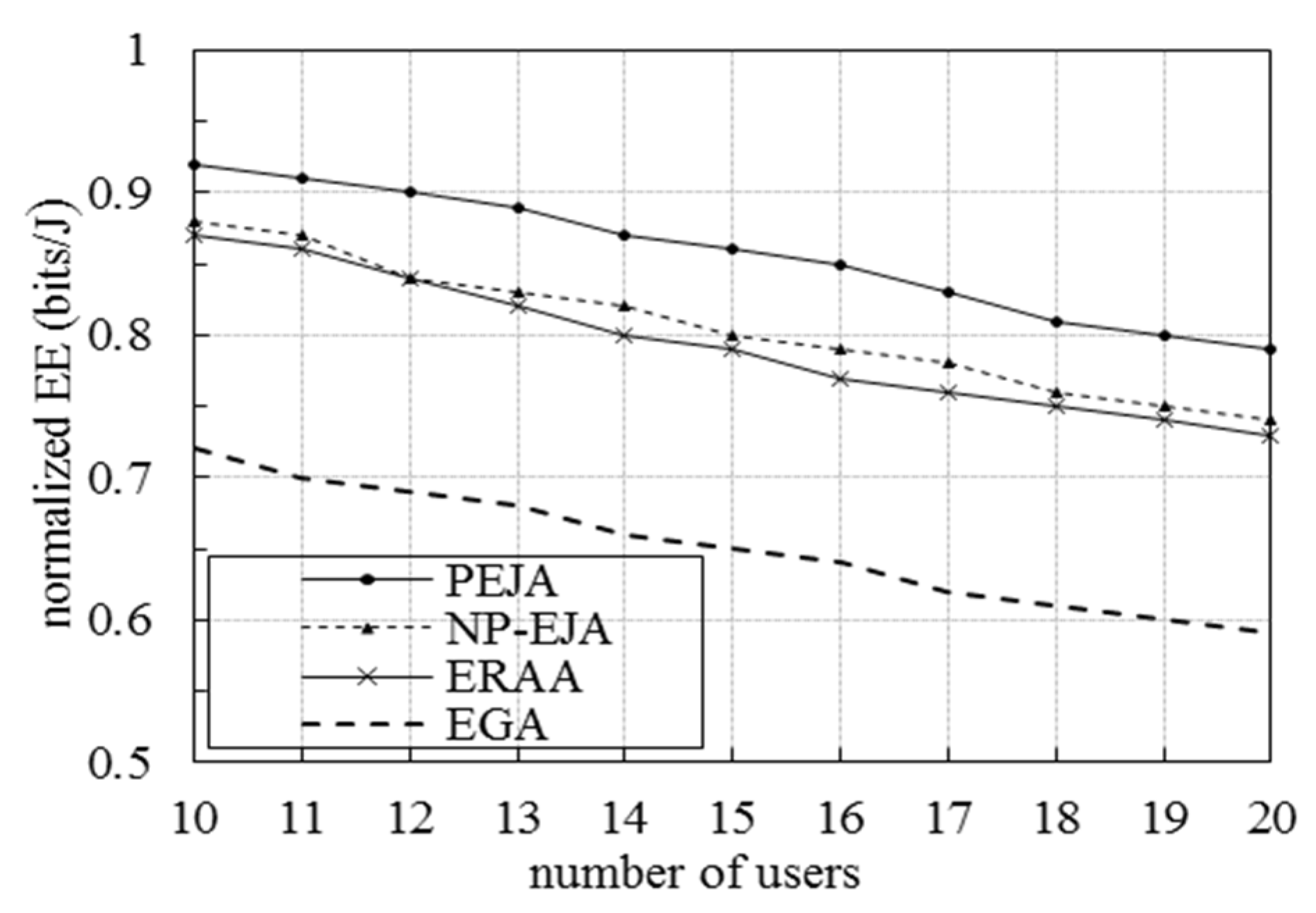
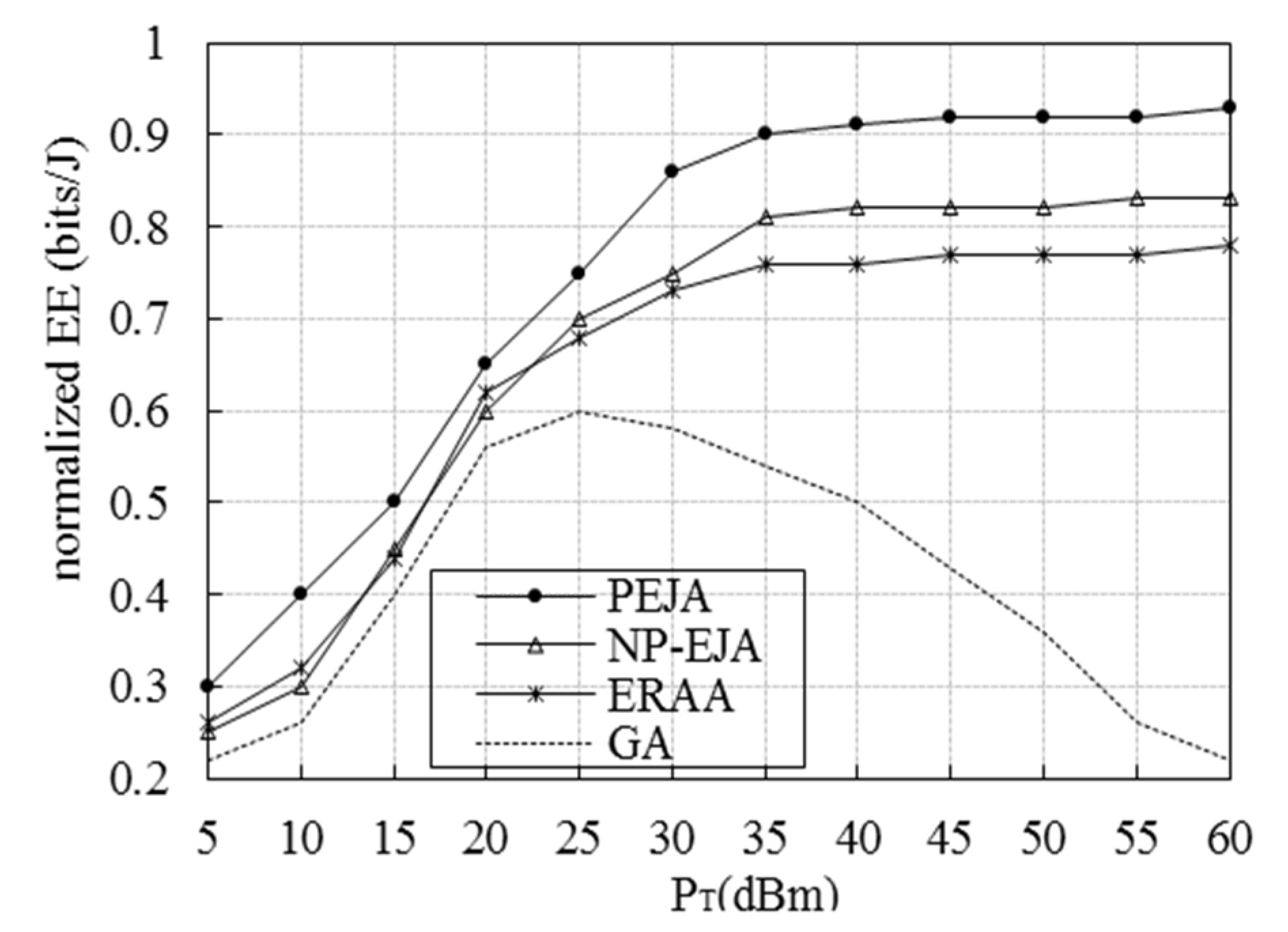
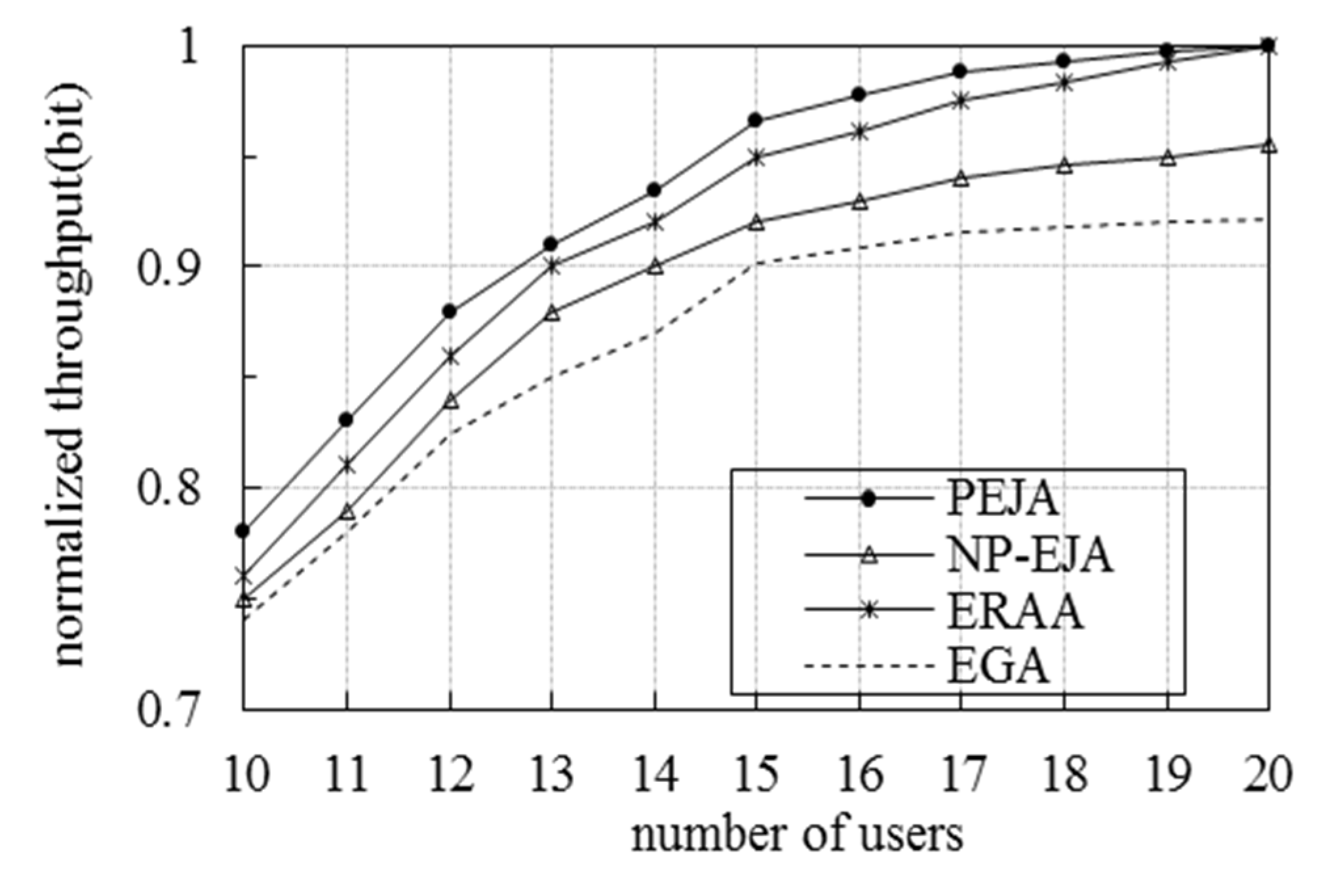
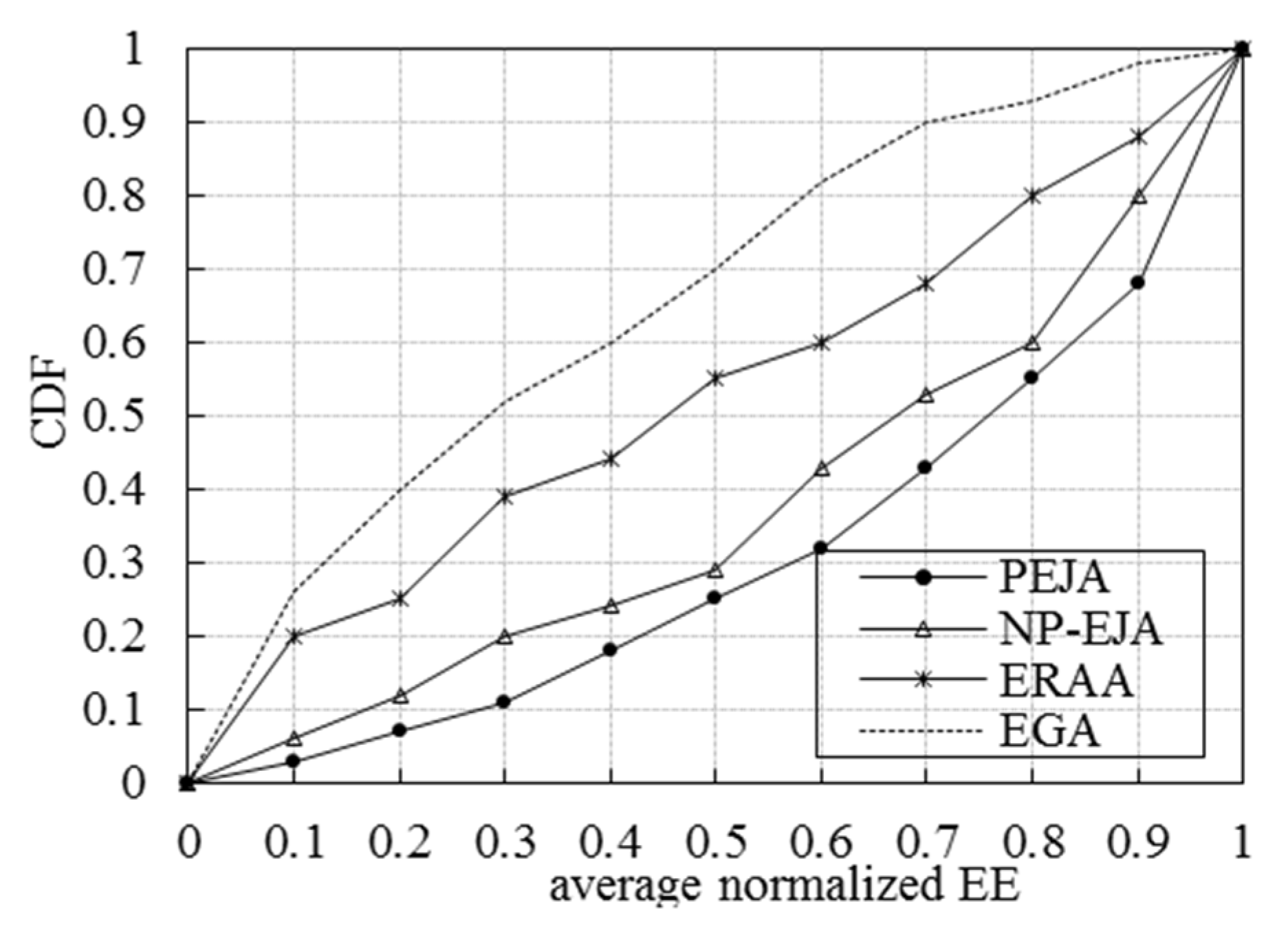
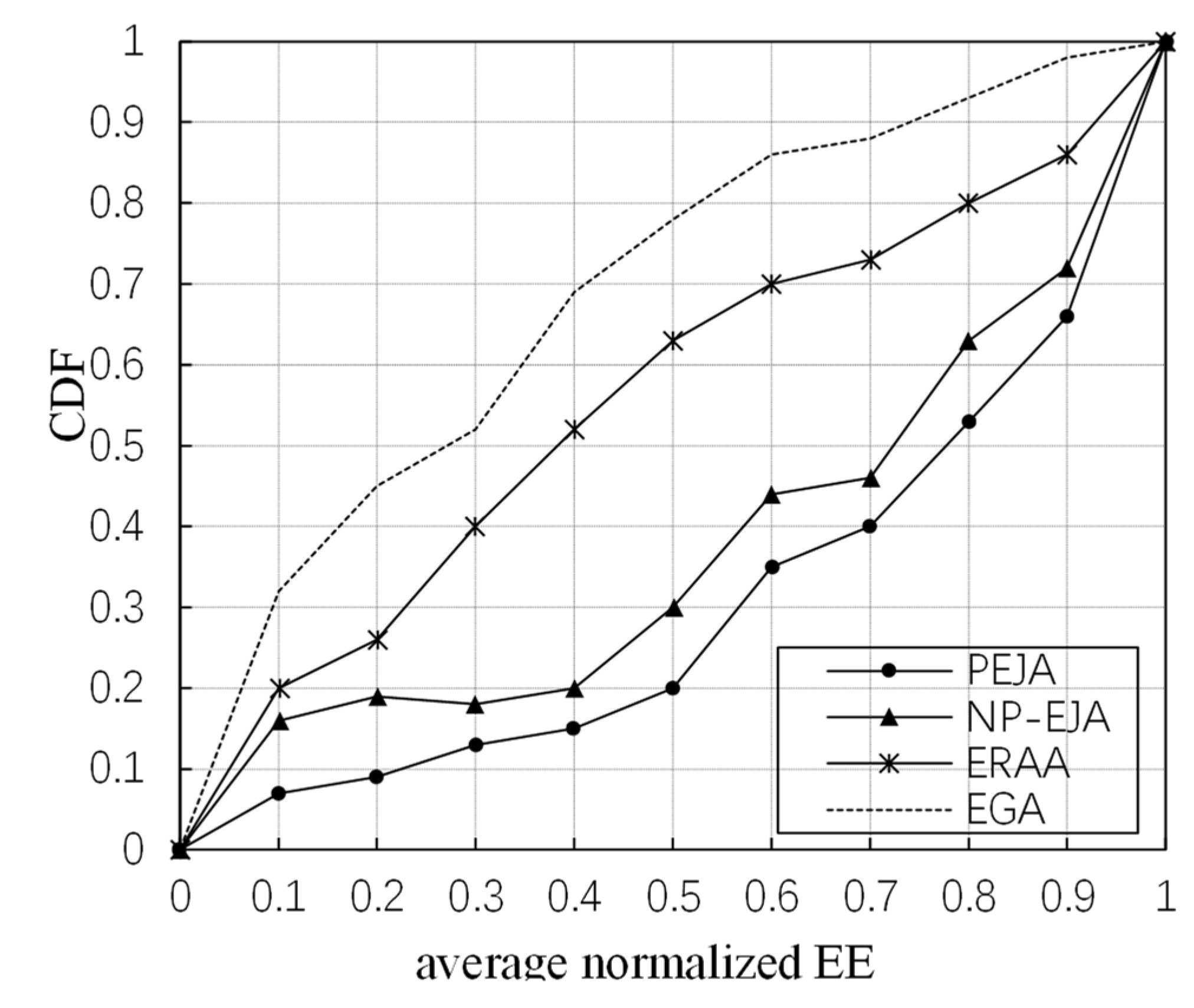
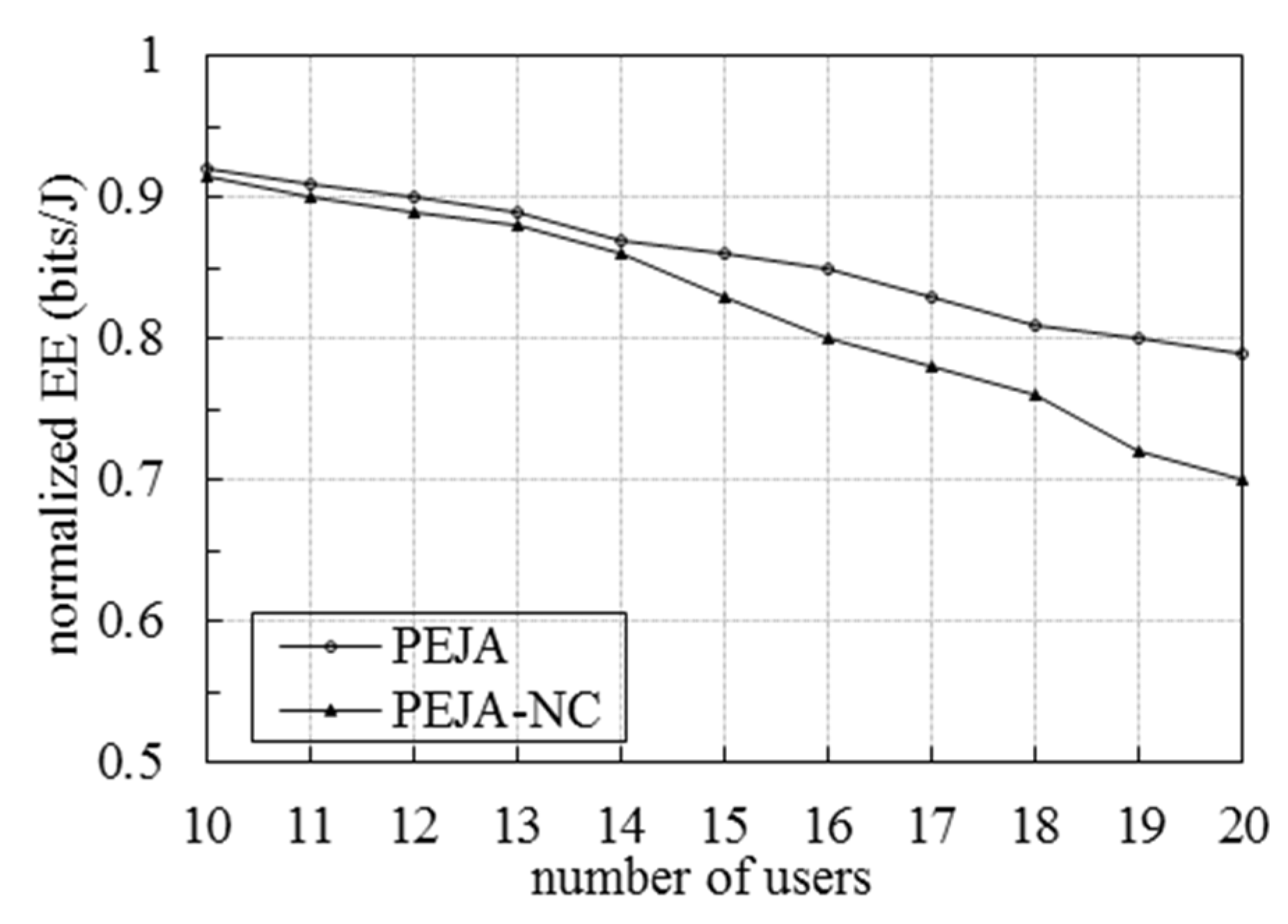
5. Experiment Results and Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Symbol | Series Definition |
|---|---|
| when the mth RB in the nth component carrier is allocated to user k, the rate that user k can achieve in time slot t | |
| the transmission power allocated on the resource block when the mth RB in the nth CC is allocated to user k in time slot t | |
| represents the channel state information when the mth Rb in the nth component carrier of time slot t is allocated to user k | |
| resource block allocation identifier, the value is {0,1} | |
| CC allocation identifier, the value is {0,1} | |
| the total power transmitted by the base station. | |
| the transmit power that the mth resource block on the nth CC is allocated to user k using MCSj in the time slot | |
| the total rate obtained by user k in time slot t | |
| the energy-efficient (EE) in the downlink of the LTE/5G system using CA technology | |
| the optimization model for maximizing the energy efficiency of the system | |
| the CC allocation scheme and t | |
| the RB allocation scheme | |
| the power allocation scheme | |
| the set of users with MCS allocated carrier n is defined | |
| the CQI index set allocated on the available RB | |
| and | the slack variable |
| the maximum energy efficiency | |
| λ | λ≥0 is the Lagrangian multiplier related to the constraint of |
| is the Lagrangian multipliers related to the constraint conditions | |
| the set of CC allocated to each user is randomly generated in the interval [1,5] | |
| the energy efficiency in time slot t-1 of narrowband user k calculated at time slot t. | |
| carrier aggregation capabilities |
References
- Tong, E.; Ding, F.; Pan, Z.; You, X. An energy minimization algorithm based on distributed dynamic clustering for long term evolution (LTE) heterogeneous networks. Sci. China Inf. Sci. 2015, 58, 1–12. [Google Scholar] [CrossRef]
- Tu, Y.; Yang, Z.; Fu, S.; Qin, Y. Latency-efficient code-division multiplexing (CDM) based carrier aggregation for 5G NR mobile fronthaul. Opt. Commun. 2020, 472, 126051. [Google Scholar] [CrossRef]
- Yuan, G.; Zhang, X.; Wang, W.; Yang, Y. Carrier Aggregation for LTE-Advanced Mobile Communication Systems. IEEE Commun. Mag. 2010, 48, 88–93. [Google Scholar] [CrossRef]
- Lee, H.; Vahid, S.; Moessner, K. A survey of radio resource management for spectrum aggregation in LTE-advanced. IEEE Commun. Surv. Tutor. 2014, 16, 745–760. [Google Scholar] [CrossRef]
- Lauridsen, M.; Wang, H.; Mogensen, P. LTE UE energy saving by applying carrier aggregation in a HetNet scenario. In Proceedings of the IEEE 77th Vehicular Technology Conference (VTC Spring), Dresden, Germany, 2–5 June 2013; pp. 1–5. [Google Scholar]
- Lin, Z.; Niu, H.; An, K.; Wang, Y.; Zheng, G.; Chatzinotas, S.; Hu, Y. Refracting RIS aided hybrid satellite-terrestrial relay networks: Joint beamforming design and optimization. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 3717–3724. [Google Scholar] [CrossRef]
- Lin, Z.; An, K.; Niu, H.; Hu, Y.; Chatzinotas, S.; Zheng, G.; Wang, J. SLNR-based secure energy efficient beamforming in multibeam satellite systems. IEEE Trans. Aerosp. Electron. Syst. 2022, 1–4. [Google Scholar] [CrossRef]
- Sokun, H.U.; Bedeer, E.; Gohary, R.H.; Yanikomeroglu, H. Optimization of discrete power and resource block allocation for achieving maximum energy efficiency in OFDMA networks. IEEE Access 2017, 5, 8648–8658. [Google Scholar] [CrossRef]
- Liu, Z.; Kang, G.; Lei, L.; Zhang, N.; Zhang, S. Power allocation for energy efficiency maximization in downlink CoMP systems with NOMA. In Proceedings of the IEEE Wireless Communications and Networking Conference (WCNC), San Francisco, CA, USA, 19–22 March 2017; pp. 1–6. [Google Scholar]
- Chen, H.; Li, G.; Cai, J. Spectral–energy efficiency tradeoff in full-duplex two-way relay networks. IEEE Syst. J. 2017, 12, 583–592. [Google Scholar] [CrossRef]
- Lin, Z.; Lin, M.; Wang, J.B.; Cola, T.; Wang, J.Z. Joint beamforming and power allocation for satellite-terrestrial integrated networks with non-orthogonal multiple access. IEEE J. Sel. Top. Signal Process. 2019, 13, 657–670. [Google Scholar] [CrossRef]
- Zappone, A.; Jorswieck, E.; Leshem, A. Distributed resource allocation for energy efficiency in MIMO OFDMA wireless networks. IEEE J. Sel. Arears Commun. 2016, 34, 3451–3465. [Google Scholar] [CrossRef]
- Lin, Z.; Lin, M.; Cola, T.; Wang, J.B.; Zhu, W.P.; Cheng, J. Supporting IoT with rate-splitting multiple access in satellite and aerial-integrated networks. IEEE Internet Things J. 2021, 18, 11123–11134. [Google Scholar] [CrossRef]
- Sundaresan, K.; Rangarajan, S. Energy efficient carrier aggregation algorithms for next generation cellular networks. In Proceedings of the 21st IEEE International Conference on Network Protocols (ICNP), Goettingen, Germany, 7–10 October 2013; pp. 1–10. [Google Scholar]
- Li, P.; Kuo, C.; Feng, K.; Chang, T.S. Joint base station association and radio resource allocation for downlink carrier aggregation in LTE-advanced systems. In Proceedings of the IEEE 81st Vehicular Technology Conference (VTC Spring), Glasgow, UK, 11–14 May 2015; pp. 1–5. [Google Scholar]
- Liu, X.Y.; Guo, W.B.; Wang, L.H.; Quan, Q.Y. Energy-efficient algorithm for carrier aggregation and cognitive radio based TD-LTE system. In Proceedings of the 2014 International Conference on Information and Communications Technologies (ICT 2014), Nanjing, China, 15–17 May 2014; pp. 4–108. [Google Scholar]
- Rostami, S.; Arshad, K.; Rapajic, P. Energy-efficient resource allocation for LTE-A networks. IEEE Commun. Lett. 2016, 20, 1429–1432. [Google Scholar] [CrossRef]
- Du, J.; Zhao, L.; Feng, J.; Xin, J.; Wang, Y. Enhanced PSO based energy-efficient resource allocation and CQI based MCS selection in LTE-A heterogeneous system. China Commun. 2016, 13, 197–204. [Google Scholar] [CrossRef]
- Xiao, X.; Tao, X.; Lu, J. Energy-efficient resource allocation in LTE based MIMO-OFDMA systems with user rate constraints. IEEE Trans. Veh. Technol 2015, 64, 185–197. [Google Scholar] [CrossRef]
- Liao, H.S.; Chen, P.Y.; Chen, W.T. An efficient downlink radio resource allocation with carrier aggregation in LTE-advanced networks. IEEE Trans. Mob. Comput. 2014, 13, 2229–2239. [Google Scholar] [CrossRef]
- Rostami, S.; Arshad, K.; Rapajic, P. Optimum radio resource management in carrier aggregation based LTE-advanced systems. IEEE Trans. Veh. Technol. 2018, 67, 580–589. [Google Scholar] [CrossRef]
- Joda, R.; Elsayed, M.; Abou-Zeid, H.; Atawia, R.; Sediq, A.B.; Boudreau, G.; Erol-Kantarci, M. QoS-aware joint component carrier selection and resource allocation for carrier aggregation in 5G. In Proceedings of the 2021 IEEE International Conference on Communications (ICC), Montreal, QC, Canada, 14–23 June 2021; pp. 1–6. [Google Scholar]
- Liu, F.; Zheng, K.; Wei, X.; Zhao, H. Design and performance analysis of an energy-efficient uplink carrier aggregation scheme. IEEE J. Sel. Areas Commun. 2014, 32, 197–207. [Google Scholar]
- Yu, G.; Chen, Q.; Yin, R.; Zhang, H.; Li, G.Y. Joint downlink and uplink resource allocation for energy-efficient carrier aggregation. IEEE Trans. Wirel. Commun. 2015, 14, 3207–3218. [Google Scholar] [CrossRef]
- ETSI. Feasibility Study for Further Advancements for E-UTRA (Release 10), 3GPP TR 36.912 Version 10.0.0, April 2011. Available online: https://www.etsi.org/deliver/etsi_tr/136900_136999/136912/10.00.00_60/tr_136912v100000p.pdf (accessed on 21 November 2022).
- ETSI. Medium Access Control (MAC) Protocol Specification (Release 10), 3GPP TS 36.321 Version 10.10.0, January 2014. Available online: https://www.etsi.org/deliver/etsi_ts/136300_136399/136321/10.10.00_60/ts_136321v101000p.pdf (accessed on 21 November 2022).
- Ni, M.; Xu, X.; Mathar, R. A channel feedback model with robust SINR prediction for LTE systems. In Proceedings of the 2013 European Conference on Antennas and Propagation (EuCAP), Gothenburg, Sweden, 8–12 April 2013; pp. 1866–1870. [Google Scholar]
- Zhang, H.; Li, J.; Xu, X.; Svensson, T.; Botella, G.; Lee, S. Channel allocation based on Kalman filter prediction for downlink OFDMA systems. In Proceedings of the IEEE 70th Vehicular Technology Conference Fall, Anchorage, AK, USA, 20–23 September 2009; pp. 1–4. [Google Scholar]
- Wu, B.; Mi, Z.-k.; Wang, W.N.; Lu, Y.C.; Zhu, Z.W. A LTE downlink scheduling based on CQI predicted by neural network. J. Beijing Univ. Posts Telecommun. 2013, 36, 45–49. [Google Scholar]
- Abdulhasan, M.Q.; Salman, M.I.; Ng, C.K.; Noordin, N.K. A channel quality indicator (CQI) prediction scheme using feed forward neural network (FF-NN) technique for MU-MIMO LTE system. In Proceedings of the IEEE 2nd International Symposium on Telecommunication Technologies (ISTT), Langkawi, Malaysia, 24–26 November 2015; pp. 17–22. [Google Scholar]
- Zhou, K.; Zhang, L.; Jiang, M. Enhanced effective SNR prediction for LTE downlink. In Proceedings of the 2015 IEEE/CIC International Conference on Communications in China (ICCC), Shenzhen, China, 2–4 November 2015; pp. 1–6. [Google Scholar]
- Liaw, A.; Wiener, M. Classification and regression by random forest. R News 2002, 23, 18–22. [Google Scholar]
- Wei, Y.; Lui, R. Dual methods for nonconvex spectrum optimization of multicarrier systems. IEEE Trans. Commun. 2006, 54, 1310–1322. [Google Scholar] [CrossRef]

| Parameter | Settings |
|---|---|
| Number of CCs; bandwidth per CC | 3 CCs; bandwidth of each CC is 10MHz |
| Subcarrier spacing | 15KHz |
| Carrier frequency | 3.5GHz |
| Path loss | PL(d) = 137.74 + 5.22log(d) |
| Thermal noise power spectral density | −174 dBm/Hz |
| Standard deviation of shadow fading | 7 db |
| Small-scale fading distribution | Rayleigh fading |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Liu, W. CA Energy Saving Joint Resource Optimization Scheme Based on 5G Channel Information Prediction of Machine Learning. Sustainability 2022, 14, 17012. https://doi.org/10.3390/su142417012
Liu J, Liu W. CA Energy Saving Joint Resource Optimization Scheme Based on 5G Channel Information Prediction of Machine Learning. Sustainability. 2022; 14(24):17012. https://doi.org/10.3390/su142417012
Chicago/Turabian StyleLiu, Junxia, and Wen Liu. 2022. "CA Energy Saving Joint Resource Optimization Scheme Based on 5G Channel Information Prediction of Machine Learning" Sustainability 14, no. 24: 17012. https://doi.org/10.3390/su142417012
APA StyleLiu, J., & Liu, W. (2022). CA Energy Saving Joint Resource Optimization Scheme Based on 5G Channel Information Prediction of Machine Learning. Sustainability, 14(24), 17012. https://doi.org/10.3390/su142417012









