Group-Sparse Feature Extraction via Ensemble Generalized Minimax-Concave Penalty for Wind-Turbine-Fault Diagnosis
Abstract
1. Introduction
2. Basic Theory
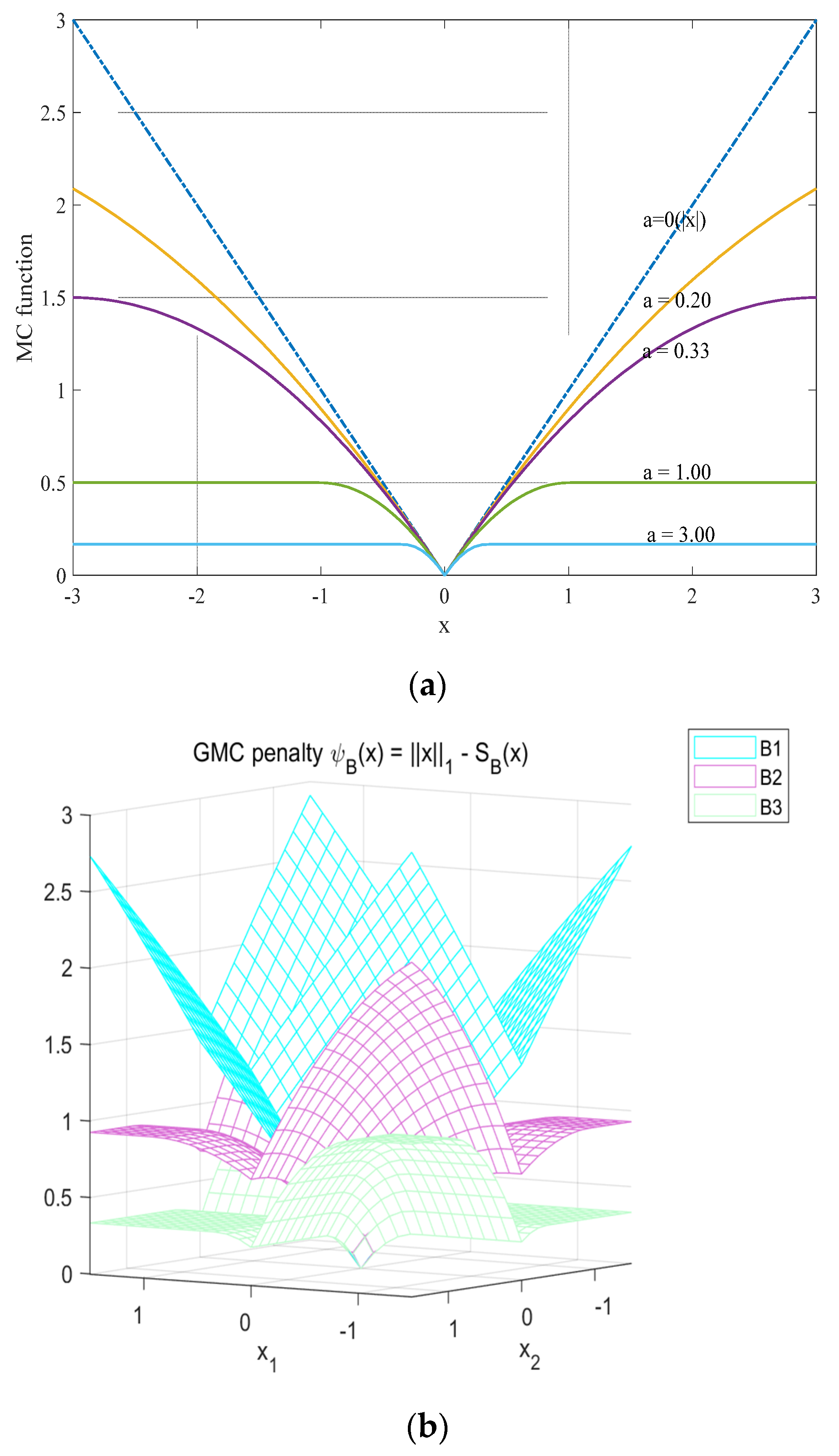
2.1. GMC Penalty
2.2. Overlapping Group Shrinking Algorithm
3. The Proposed Group-Sparse Feature Extraction Method Based on Ensemble GMC
3.1. Optimization Problem Formulation
3.2. Convexity Condition
3.3. Algorithm Implementation
| Algorithm 1 FBGFE: Forward–backward group feature extraction algorithm |
| Input:,,, |
| Initialization:, |
| For end where is the iteration counter. Return: |
3.4. Remark of the Proposed Algorithm
4. Simulation Study
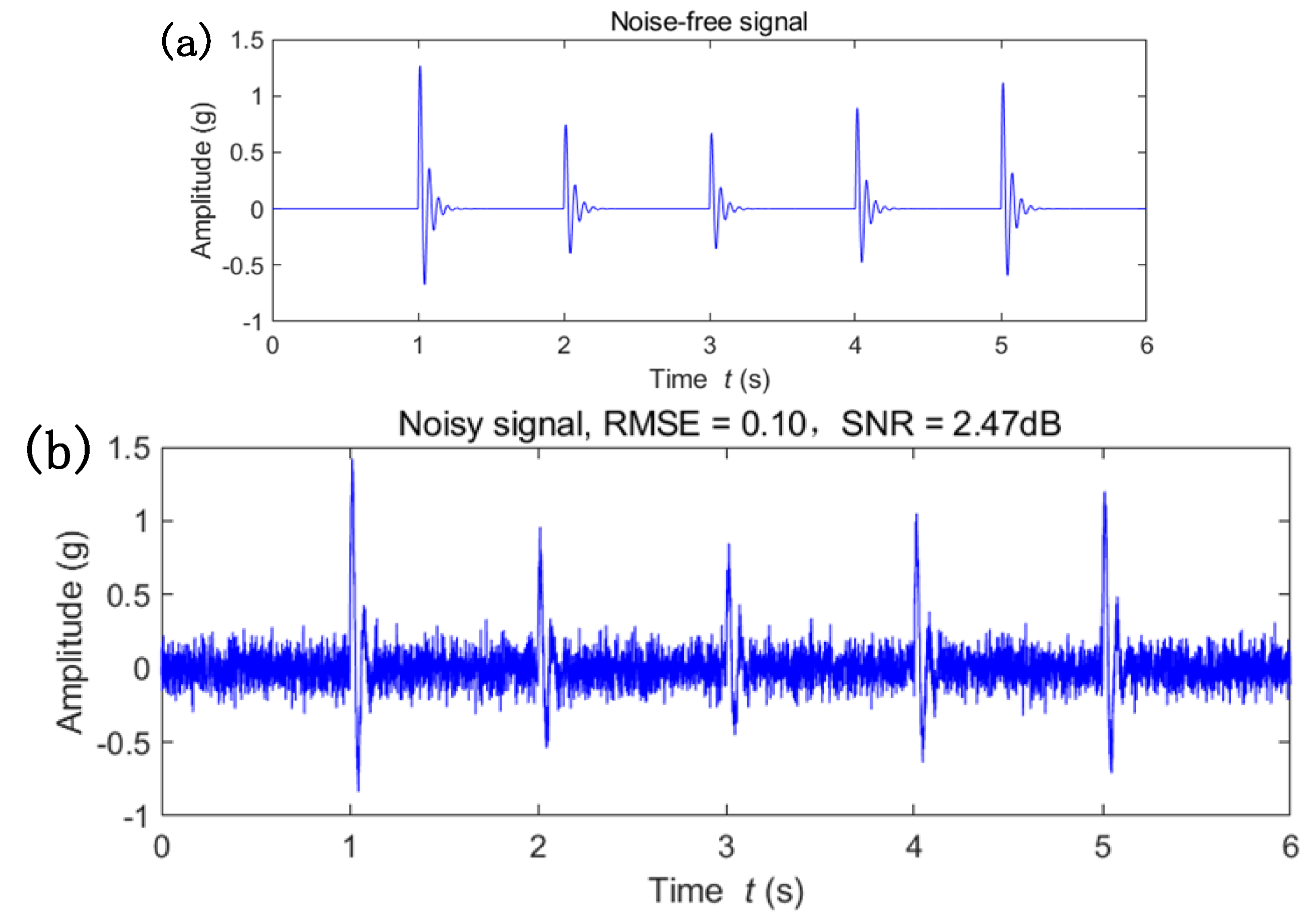
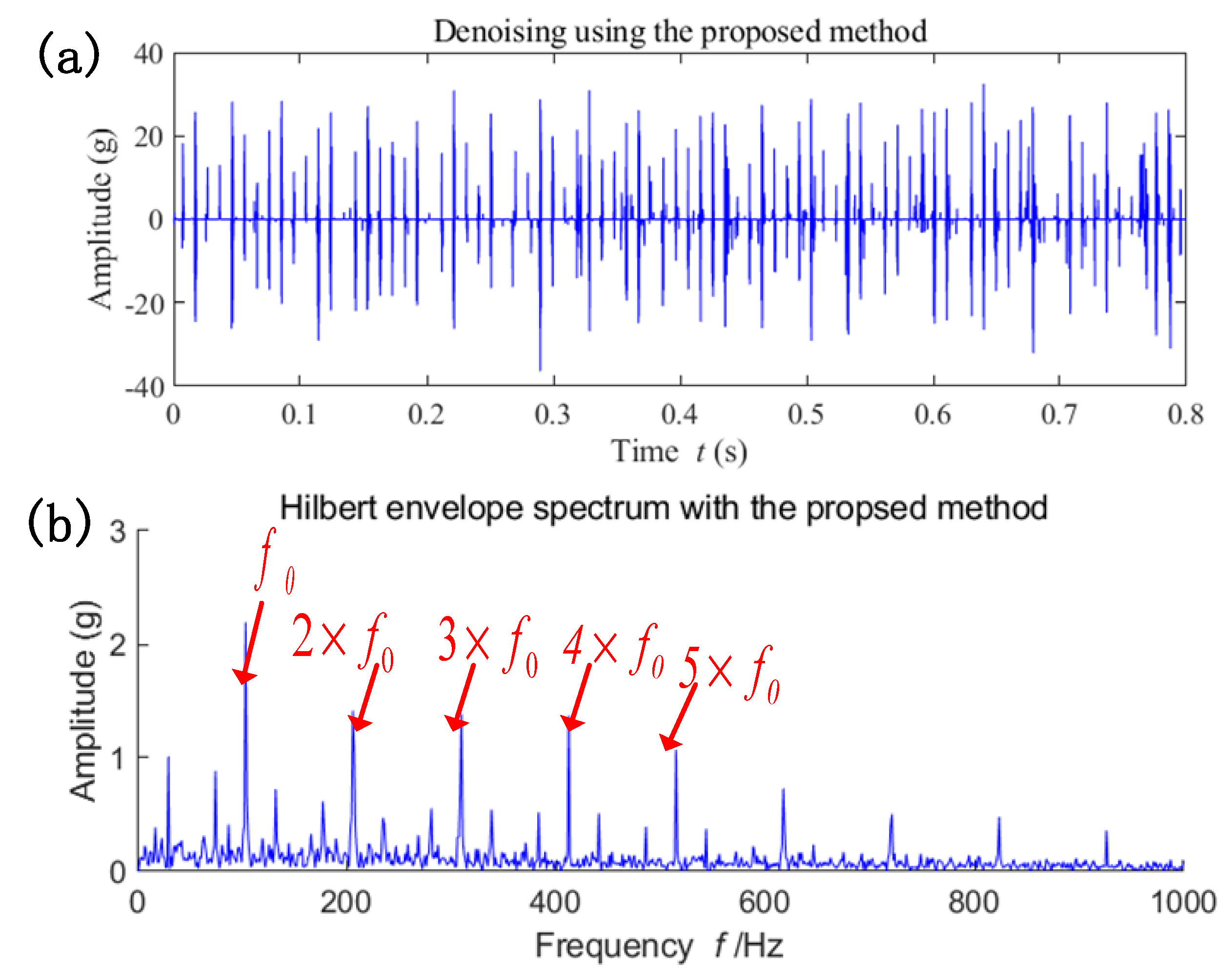
4.1. Simulation Validation
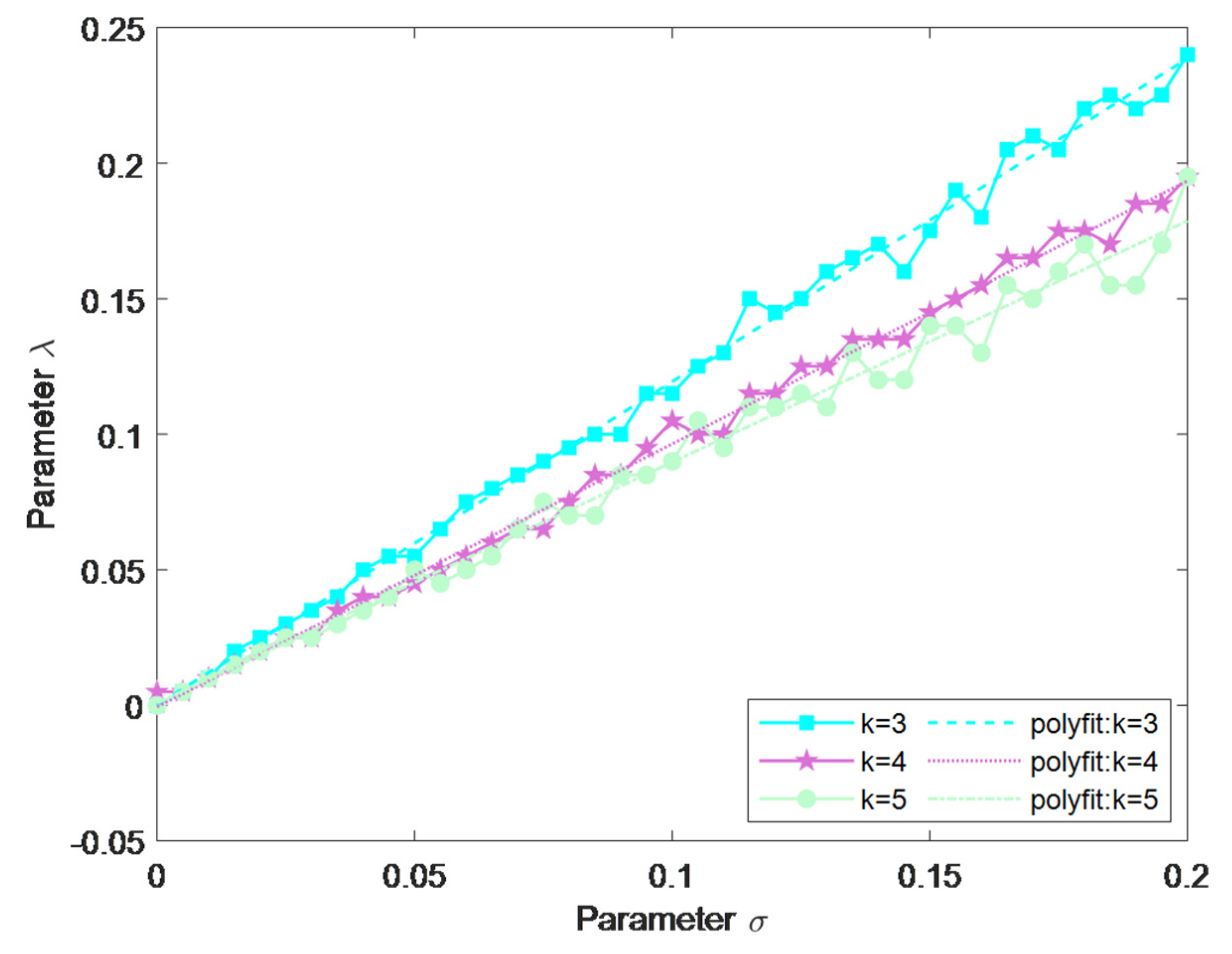
4.2. Selection of Regularization Parameter
5. Experimental Validation
5.1. Case 1: High-Speed Bearing Outer-Race Fault
5.2. Case 2: Fault Diagnosis of a Wind Turbine Pinion Gear
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, M.-H.; Lu, S.-D.; Hsieh, C.-C.; Hung, C.-C. Fault Detection of Wind Turbine Blades Using Multi-Channel CNN. Sustainability 2022, 14, 1781. [Google Scholar] [CrossRef]
- Wang, X.; Tang, G.; Wang, T.; Zhang, X.; Peng, B.; Dou, L.; He, Y. Lkurtogram Guided Adaptive Empirical Wavelet Transform and Purified Instantaneous Energy Operation for Fault Diagnosis of Wind Turbine Bearing. IEEE Trans. Instrum. Meas. 2020, 70, 1–19. [Google Scholar] [CrossRef]
- Liu, X.; Ma, H.; Liu, Y. A Novel Transfer Learning Method Based on Conditional Variational Generative Adversarial Networks for Fault Diagnosis of Wind Turbine Gearboxes under Variable Working Conditions. Sustainability 2022, 14, 5441. [Google Scholar] [CrossRef]
- Yang, S.; Wang, Y.; Li, C. Wind turbine gearbox fault diagnosis based on an improved supervised autoencoder using vibration and motor current signals. Meas. Sci. Technol. 2021, 32, 114003. [Google Scholar] [CrossRef]
- He, W.; Guo, B.; Chen, B.; Ye, J.; Bechhoefer, E. A data-driven group-sparse feature extraction method for fault detection of wind turbine trans-mission system. Meas. Sci. Technol. 2020, 31, 074008. [Google Scholar] [CrossRef]
- Wang, C.; Gan, M.; Zhu, C. Intelligent fault diagnosis of rolling element bearings using sparse wavelet energy based on over-complete DWT and basis pursuit. J. Intell. Manuf. 2017, 28, 1377–1391. [Google Scholar] [CrossRef]
- He, Q.; Wang, X. Time-frequency manifold correlation matching for periodic fault identification in rotating machines. J. Sound Vib. 2013, 332, 2611–2626. [Google Scholar] [CrossRef]
- Zhang, D. Wavelet transform. In Fundamentals of Image Data Mining; Springer: Cham, Switzerland, 2019; pp. 35–44. [Google Scholar]
- Pathak, R.S. The Wavelet Transform; Springer Science & Business Media: Cham, Switzerland, 2009. [Google Scholar]
- Liu, C.-L. A Tutorial of the Wavelet Transform; NTUEE: Taiwan, China, 2010. [Google Scholar]
- Wang, L.-H.; Zhao, X.P.; Wu, J.X.; Xie, Y.-Y.; Zhang, Y.-H. Motor fault diagnosis based on short-time Fourier transform and convolutional neural network. Chin. J. Mech. Eng. 2017, 30, 1357–1368. [Google Scholar] [CrossRef]
- Zhong, J.; Huang, Y. Time-Frequency Representation Based on an Adaptive Short-Time Fourier Transform. IEEE Trans. Signal Process. 2010, 58, 5118–5128. [Google Scholar] [CrossRef]
- Li, Z.; Jiang, Y.; Guo, Q.; Hu, C.; Peng, Z. Multi-dimensional variational mode decomposition for bearing-crack detection in wind turbines with large driving-speed variations. Renew. Energy 2016, 116, 55–73. [Google Scholar] [CrossRef]
- Li, Z.; Liu, F.; Sun, S.; Sarkodie-Gyan, T.; Li, W. Decoupling of Multiple Concurrent Faults for Diagnosing Coal-cutter Gearboxes: An Extensive Ex-perimental Investigation with Multi-Channel Sensor Measurements. Nondestruct. Eval. Diagn. Progn. Eng. Syst. 2019, 2, 041001. [Google Scholar]
- Xiang, J.; Zhong, Y.; Gao, H. Rolling element bearing fault detection using PPCA and spectral kurtosis. Measurement 2015, 75, 180–191. [Google Scholar] [CrossRef]
- Liu, W.Y.; Gao, Q.W.; Ye, G.; Ma, R.; Lu, X.N.; Han, J.G. A novel wind turbine bearing fault diagnosis method based on Integral Extension LMD. Measurement 2015, 74, 70–77. [Google Scholar] [CrossRef]
- Lei, Y.; Qiao, Z.; Xu, X.; Lin, J.; Niu, S. An underdamped stochastic resonance method with stable-state matching for incipient fault diagnosis of rolling element bearings. Mech. Syst. Signal Process. 2017, 94, 148–164. [Google Scholar] [CrossRef]
- He, Q.; Wu, E.; Pan, Y. Multi-Scale Stochastic Resonance Spectrogram for fault diagnosis of rolling element bearings. J. Sound Vib. 2018, 420, 174–184. [Google Scholar] [CrossRef]
- Buzzoni, M.; Antoni, J.; d’Elia, G. Blind deconvolution based on cyclostationarity maximization and its application to fault iden-tification. J. Sound Vib. 2018, 432, 569–601. [Google Scholar] [CrossRef]
- Wan, S.; Zhang, X.; Dou, L. Compound fault diagnosis of bearings using improved fast spectral kurtosis with VMD. J. Mech. Sci. Technol. 2018, 32, 5189–5199. [Google Scholar] [CrossRef]
- Wang, Y.; Xiang, J.; Markert, R.; Liang, M. Spectral kurtosis for fault detection, diagnosis and prognostics of rotating machines: A review with applications. Mech. Syst. Signal Process. 2016, 66–67, 679–698. [Google Scholar] [CrossRef]
- Tsai, T.C.; Wang, C.N. Acoustic-based method for identifying surface damage to wind turbine blades by using a convolutional neural network. Meas. Sci. Technol. 2022, 33, 085601. [Google Scholar] [CrossRef]
- Ding, C.; Zhao, M.; Lin, J. Sparse feature extraction based on periodical convolutional sparse representation for fault detection of rotating machinery. Meas. Sci. Technol. 2020, 32, 015008. [Google Scholar] [CrossRef]
- Song, Z.; Huang, W.; Liao, Y.; Mao, L.; Shi, J.; Wang, J.; Shen, C.; Zhu, Z. Sparse representation based on generalized smooth logarithm regularization for bearing fault diagnosis. Meas. Sci. Technol. 2021, 32, 105003. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, X.; Liu, Z.; Wang, J. Sparsity-based fractional spline wavelet denoising via overlapping group shrinkage with non-convex regularization and convex optimization for bearing fault diagnosis. Meas. Sci. Technol. 2019, 31, 055003. [Google Scholar] [CrossRef]
- Hai, B.; Jiang, H.; Yao, P.; Wang, K.; Yao, R. Rolling bearing fault feature extraction using non-convex periodic group sparse method. Meas. Sci. Technol. 2021, 32, 105005. [Google Scholar] [CrossRef]
- Xia, Y.; Lu, S. Convolutional sparse coding with periodic overlapped group sparsity for rolling element bearing fault diagnosis. Meas. Sci. Technol. 2018, 29, 115103. [Google Scholar] [CrossRef]
- Chen, P.Y.; Selesnick, I.W. Translation-invariant shrinkage/thresholding of group sparse signals. Signal Process. 2014, 94, 476–489. [Google Scholar] [CrossRef]
- Chen, P.Y.; Selesnick, I.W. Group-sparse signal denoising: Non-convex regularization, convex optimization. IEEE Trans. Signal Process. 2014, 62, 3464–3478. [Google Scholar] [CrossRef]
- Huang, W.; Sun, H.; Wang, W. Resonance-Based Sparse Signal Decomposition and Its Application in Mechanical Fault Diagnosis: A Review. Sensors 2017, 17, 1279. [Google Scholar] [CrossRef]
- Fan, W.; Cai, G.; Huang, W.; Shang, L.; Zhu, Z. Sparse Representation of Transients Based on Wavelet Basis and Majorization-Minimization Algorithm for Machinery Fault Diagnosis. Math. Probl. Eng. 2014, 2014, 696051. [Google Scholar] [CrossRef]
- He, W.; Ding, Y.; Zi, Y.; Selesnick, I.W. Repetitive transients extraction algorithm for detecting bearing faults. Mech. Syst. Signal Process. 2017, 84, 227–244. [Google Scholar] [CrossRef]
- Selesnick, I. Sparse Regularization via Convex Analysis. IEEE Trans. Signal Process. 2017, 65, 4481–4494. [Google Scholar] [CrossRef]
- He, W.; Hu, J.; Chen, B.; Guo, B. GMC sparse enhancement diagnostic method based on the tunable Q-factor wavelet transform for detecting faults in rotating machines. Measurement 2021, 174, 109001. [Google Scholar] [CrossRef]
- Liu, J.; Qiao, B.; He, W.; Yang, Z.; Chen, X. Impact force identification via sparse regularization with generalized minimax-concave penalty. J. Sound Vib. 2020, 484, 115530. [Google Scholar] [CrossRef]
- He, W.; Chen, B.; Zeng, N.; Zi, Y. Sparsity-based signal extraction using dual Q-factors for gearbox fault detection. ISA Trans. 2018, 79, 147–160. [Google Scholar] [CrossRef]
- Randall, R.B.; Antoni, J. Rolling element bearing diagnostics—A tutorial. Mech. Syst. Signal Process. 2011, 25, 485–520. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, W.; Zhang, P.; Liu, X.; Chen, B.; Guo, B. Group-Sparse Feature Extraction via Ensemble Generalized Minimax-Concave Penalty for Wind-Turbine-Fault Diagnosis. Sustainability 2022, 14, 16793. https://doi.org/10.3390/su142416793
He W, Zhang P, Liu X, Chen B, Guo B. Group-Sparse Feature Extraction via Ensemble Generalized Minimax-Concave Penalty for Wind-Turbine-Fault Diagnosis. Sustainability. 2022; 14(24):16793. https://doi.org/10.3390/su142416793
Chicago/Turabian StyleHe, Wangpeng, Peipei Zhang, Xuan Liu, Binqiang Chen, and Baolong Guo. 2022. "Group-Sparse Feature Extraction via Ensemble Generalized Minimax-Concave Penalty for Wind-Turbine-Fault Diagnosis" Sustainability 14, no. 24: 16793. https://doi.org/10.3390/su142416793
APA StyleHe, W., Zhang, P., Liu, X., Chen, B., & Guo, B. (2022). Group-Sparse Feature Extraction via Ensemble Generalized Minimax-Concave Penalty for Wind-Turbine-Fault Diagnosis. Sustainability, 14(24), 16793. https://doi.org/10.3390/su142416793







