Shark Skin—An Inspiration for the Development of a Novel and Simple Biomimetic Turbulent Drag Reduction Topology
Abstract
1. Introduction
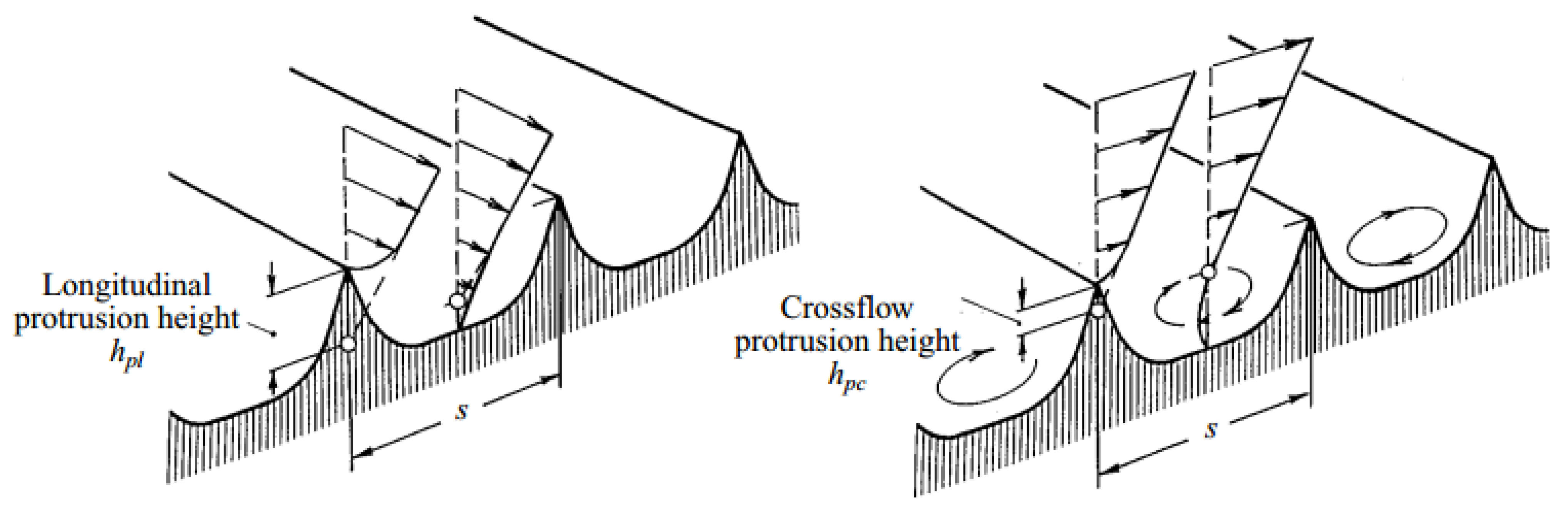
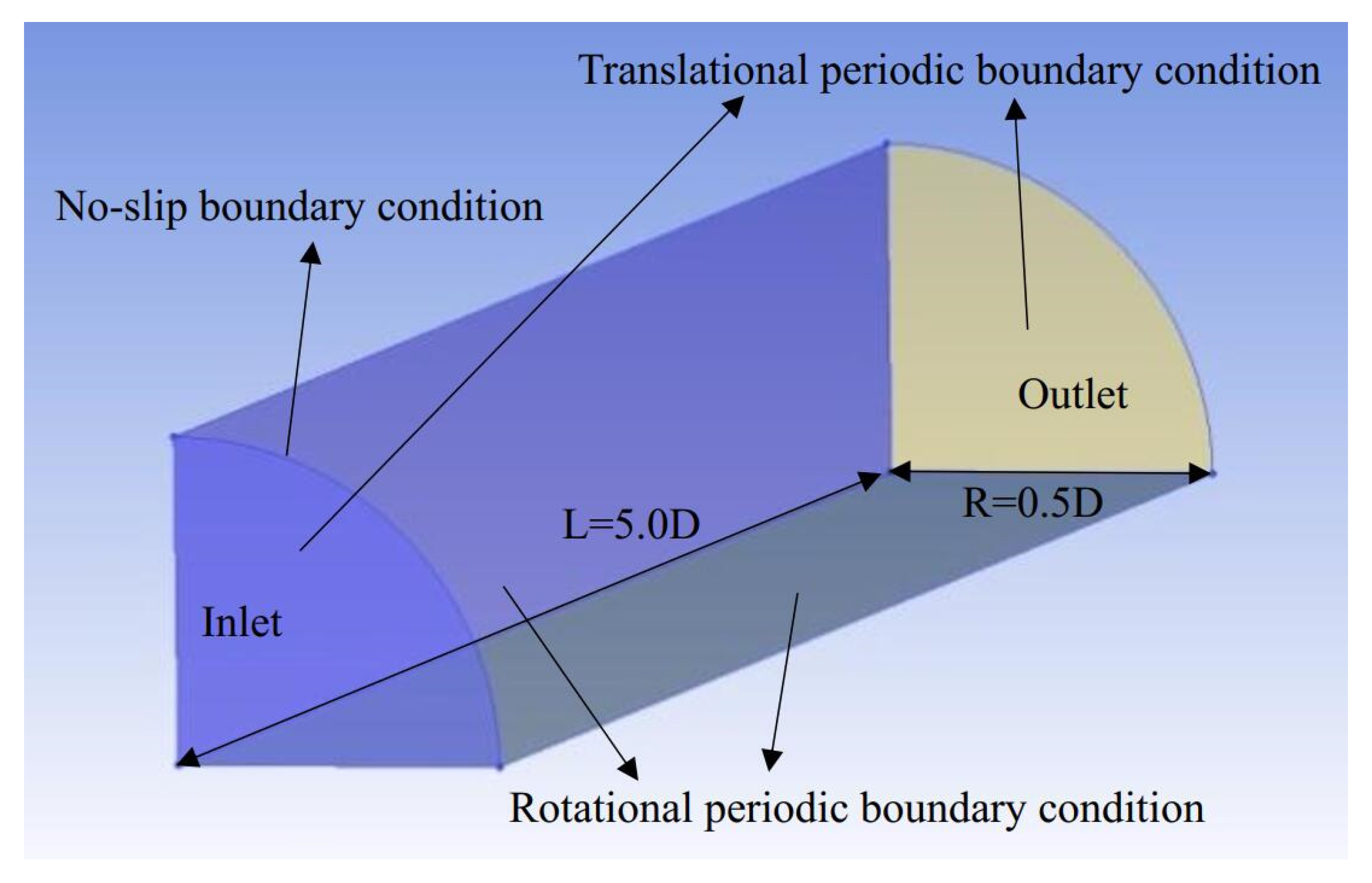
2. Materials and Methods
3. Results and Discussion
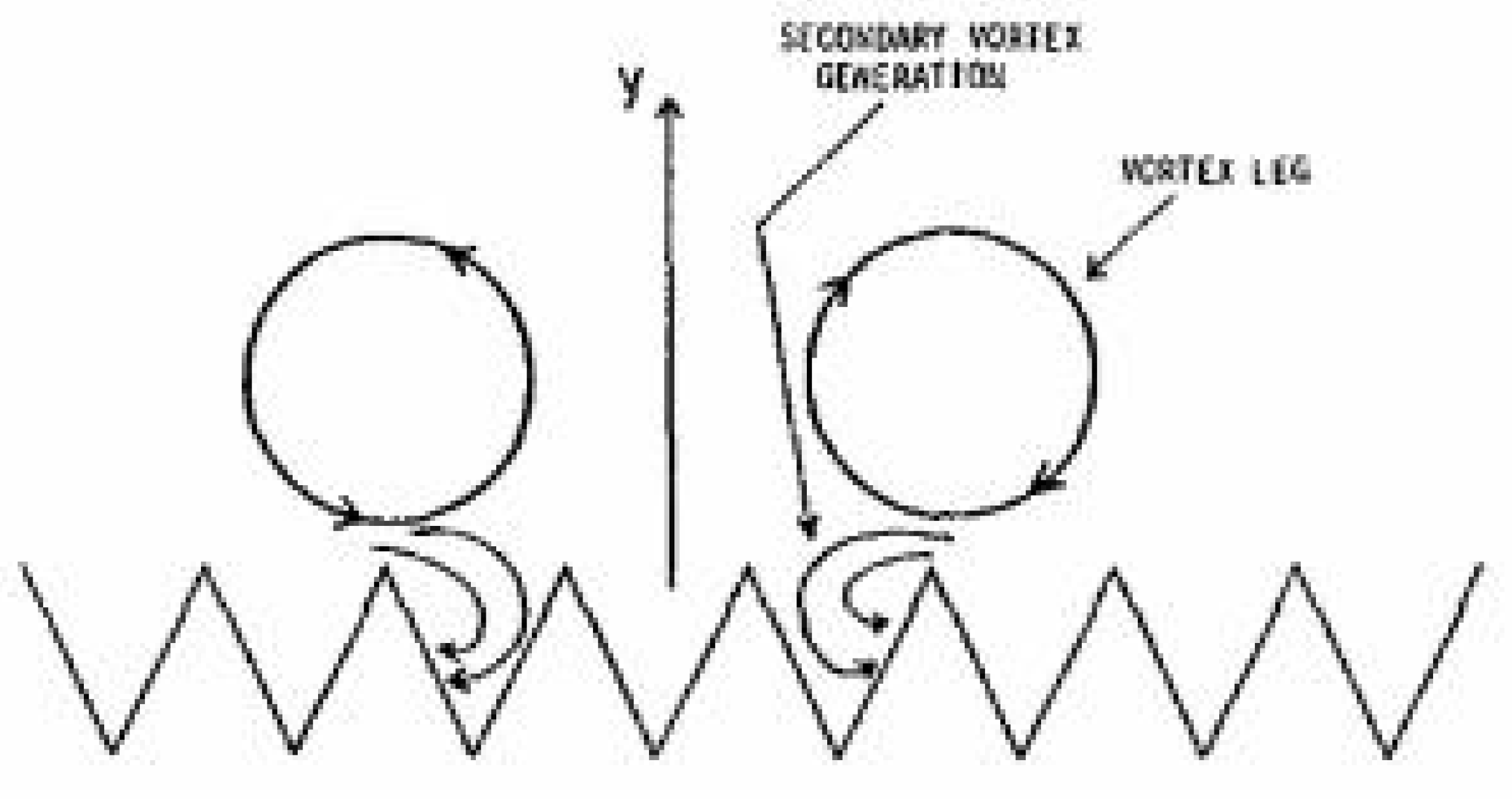
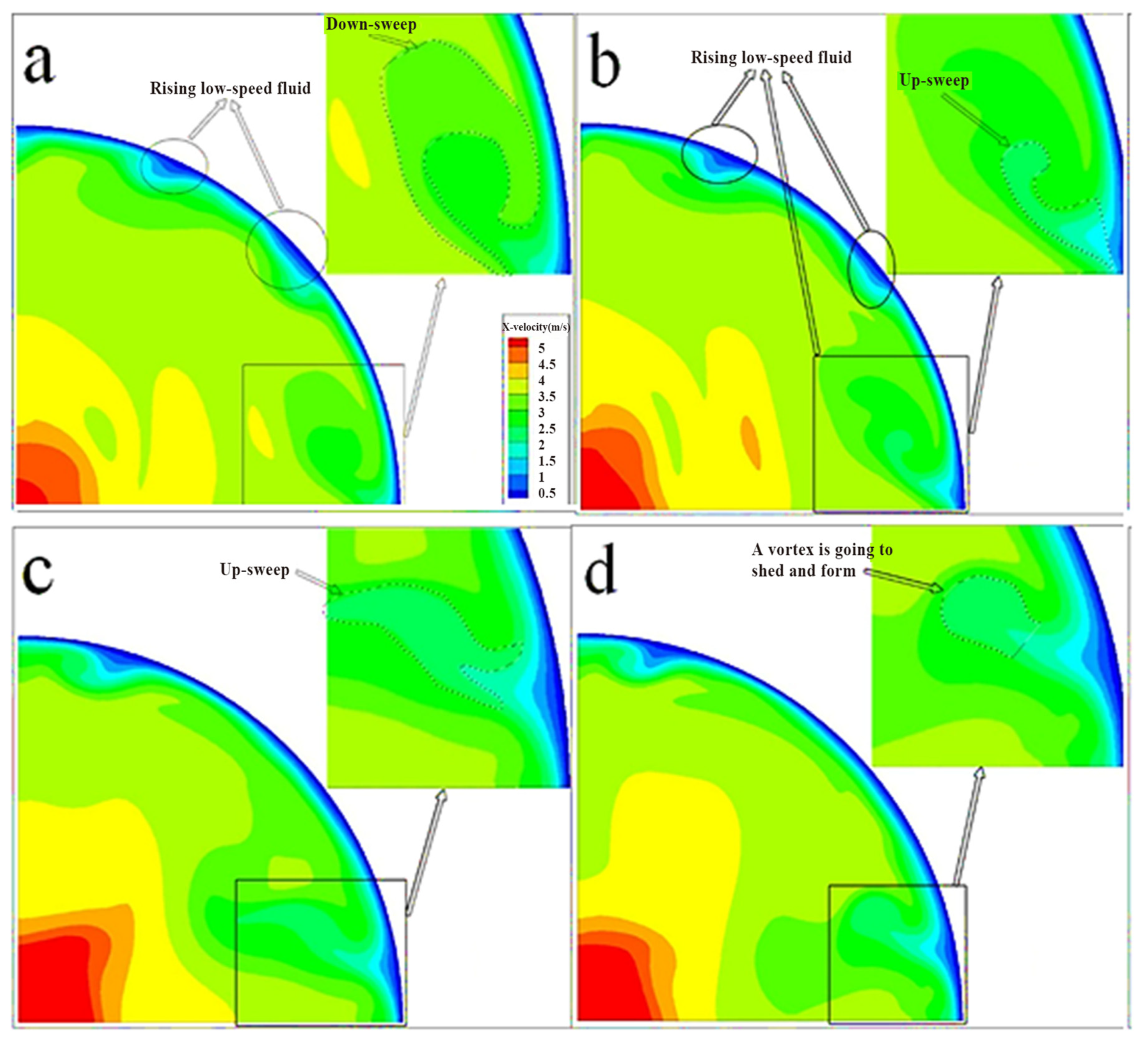
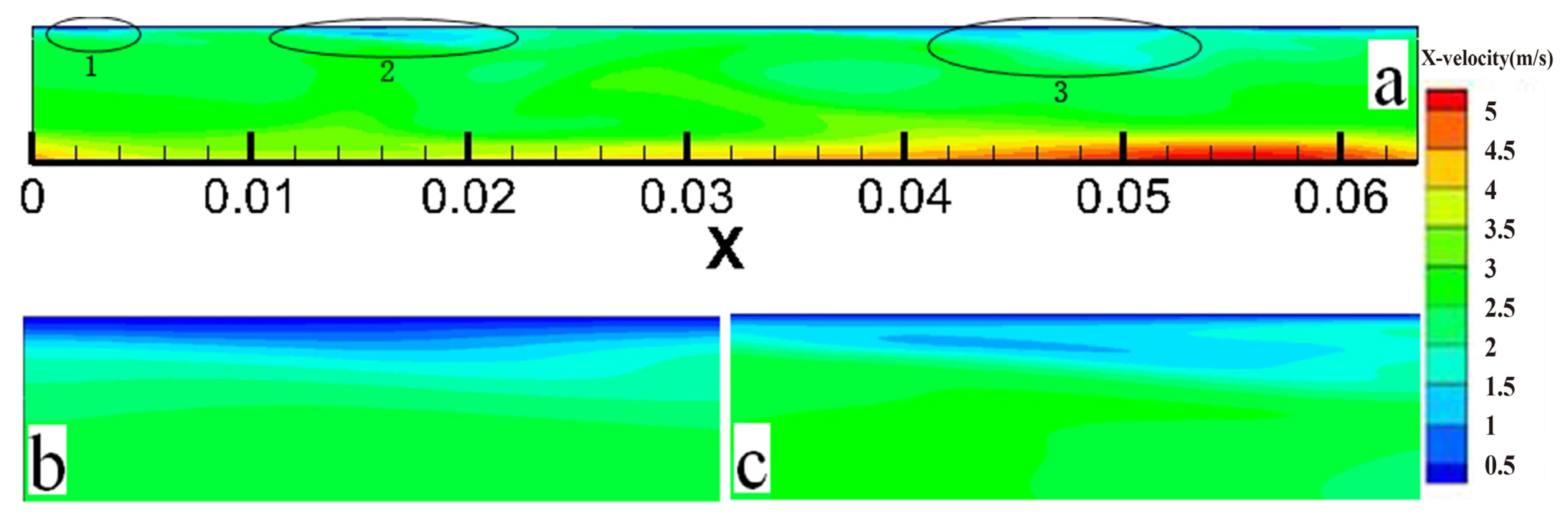
3.1. Evolution of a Coherent Structure near the Wall
3.2. Turbulent Drag
3.3. Thickness of Viscous Sublayer
3.4. Analysis of Turbulent Flow Field
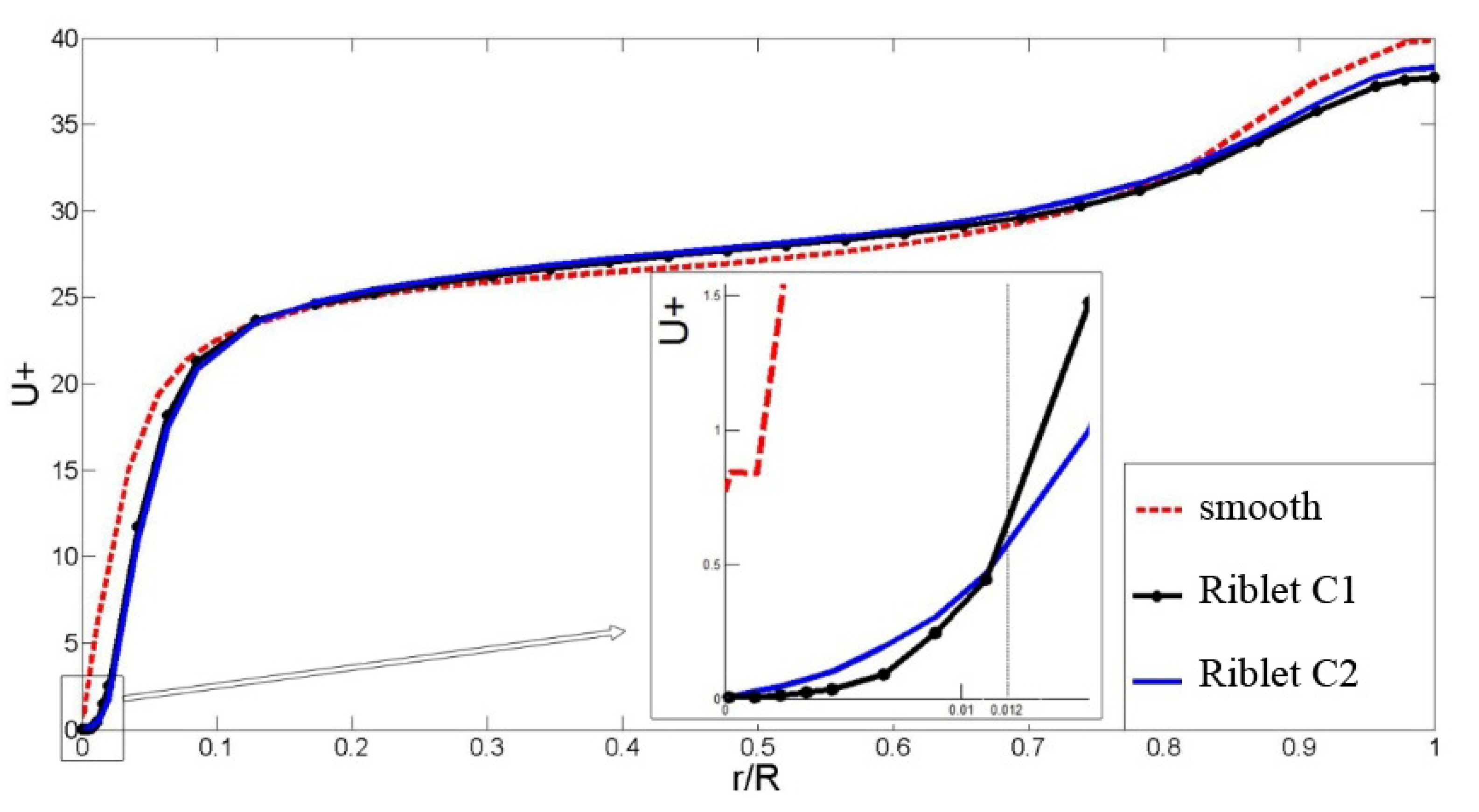
3.4.1. Velocity Profiles
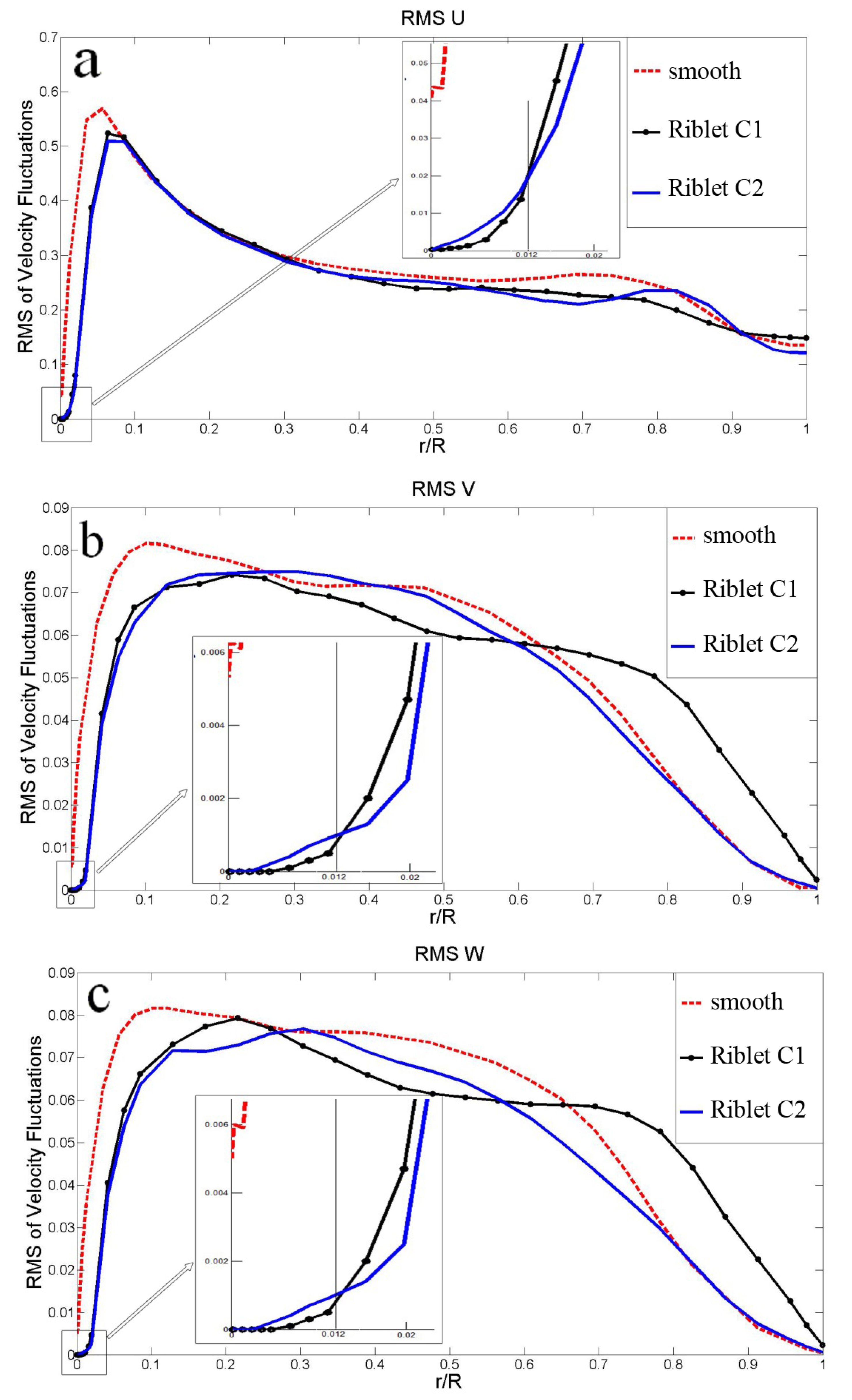
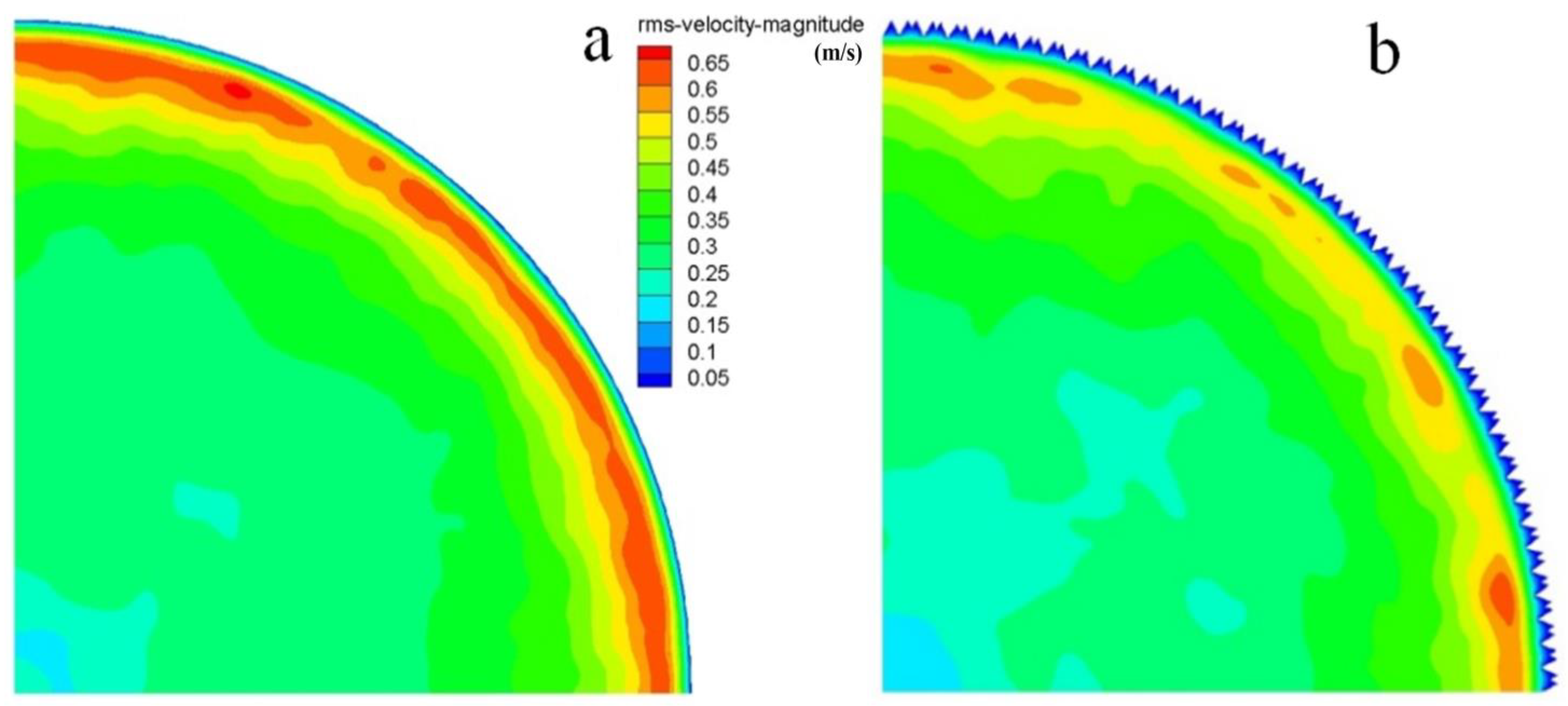
3.4.2. Velocity Fluctuation
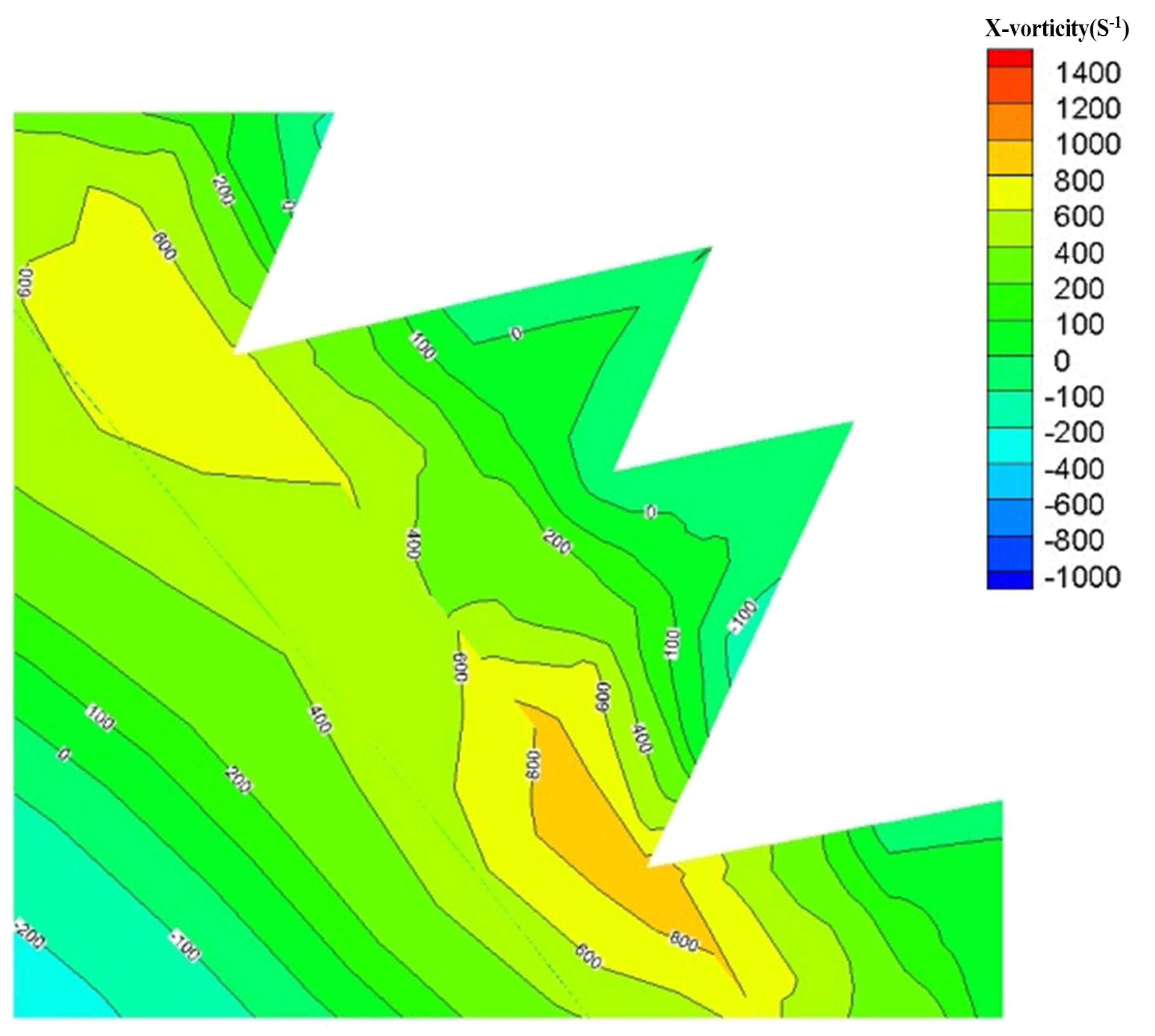
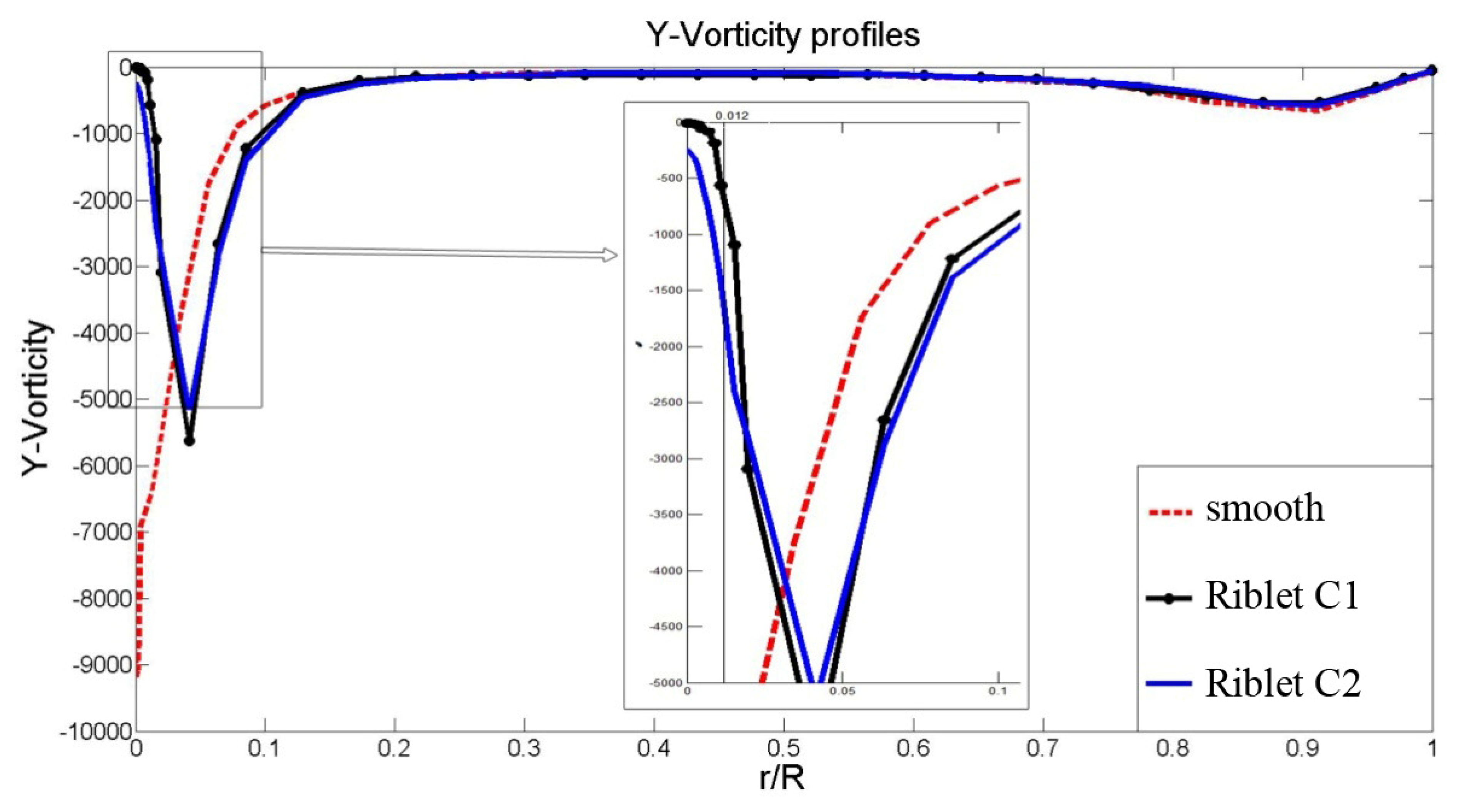
3.4.3. Streamwise Vorticity Distribution
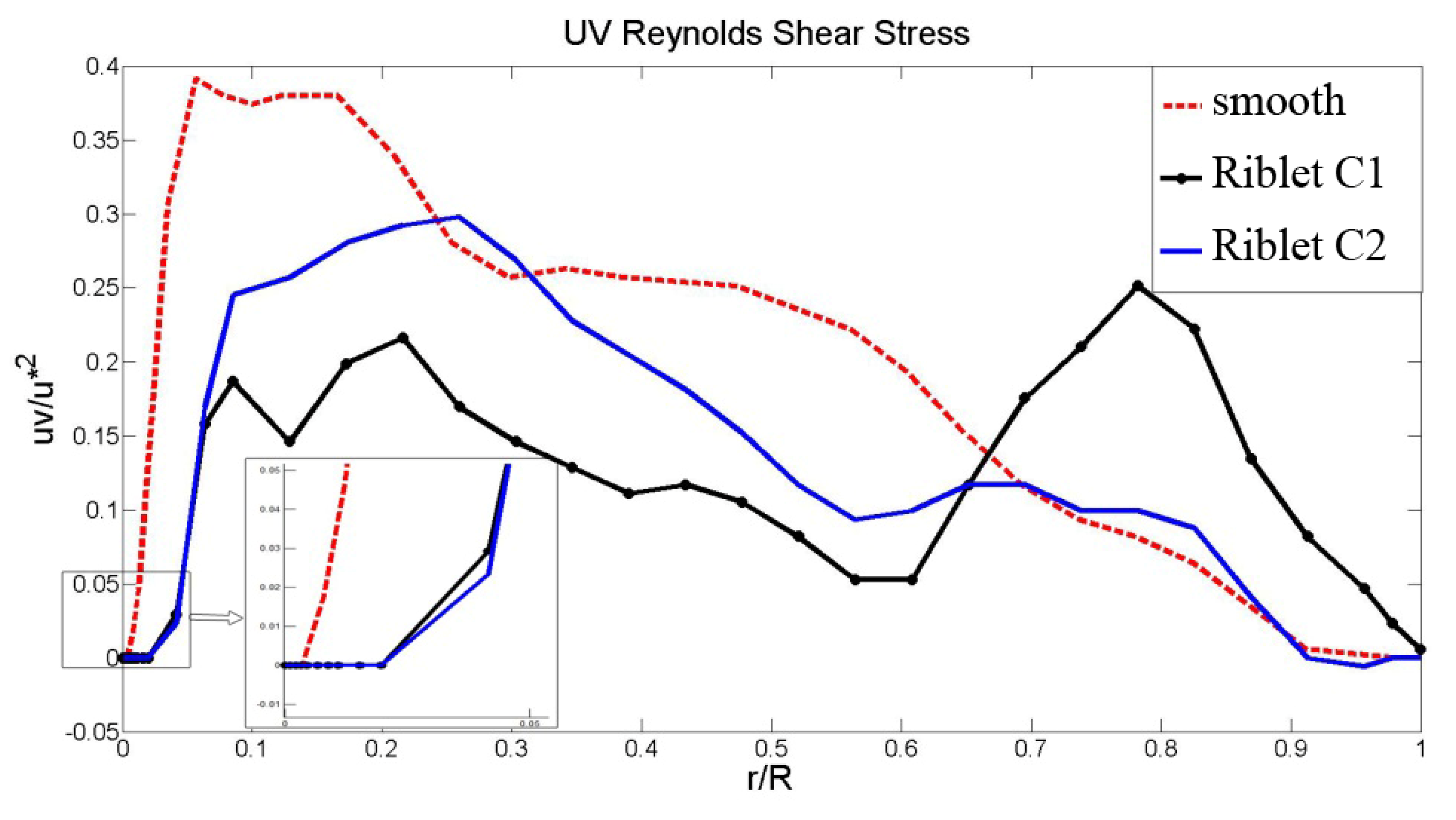
3.4.4. Reynolds Shear Stress
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| U | Mean streamwise velocity |
| τw | Wall shear stress |
| u* | Friction velocity |
| U+ | Non-dimensional mean streamwise velocity |
| Non-dimensional riblet spacing | |
| Non-dimensional riblet height | |
| γ | Angle between the flow direction and riblets |
| Cs | Smagorinsky constant |
| D | External diameter of non-smooth pipe |
| A | Cross-sectional area of non-smooth pipe |
| Drag reduction efficiency |
References
- Bechert, D.W.; Bruse, M.; Hage, W. Experiments on drag-reducing surfaces and their optimization with an adjustable geometry. J. Fluid Mech. 1997, 33, 59–87. [Google Scholar] [CrossRef]
- Bechert, D.W.; Bruse, M.; Hage, W. Experiments with three-dimensional riblets as an idealized model of shark skin. Exp. Fluids. 2000, 28, 403–412. [Google Scholar] [CrossRef]
- Bechert, D.W.; Bruse, M.; Hage, W.; Meyer, R. Fluid mechanics of biological surfaces and their technological application. Naturwissenschaften 2000, 87, 157–171. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.J.; Lee, S.H. Flow field analysis of a turbulent boundary layer over a riblet surface. Exp. Fluids 2001, 30, 153–166. [Google Scholar] [CrossRef]
- Djenidi, L.; Antonia, R.A. Laser Doppler anemometer measurements of turbulent boundary layer over a riblet surface. AIAA J. 1996, 34, 1007–1012. [Google Scholar] [CrossRef]
- Rapp, H.; Zoric, I.; Kasemo, B. Microstructured surfaces for drag reduction purposes: Experiments and simulation on rectangular 2D riblets. Mater. Res. Soc. 2006, 899, 808. [Google Scholar] [CrossRef]
- Wang, J.J.; Lan, S.L.; Miao, F.Y. Drag-reduction characteristics of turbulent boundary layer flow over riblets surfaces. Shipbuild. China 2001, 42, 1–5. [Google Scholar]
- Cong, Q.; Feng, Y.; Ren, L.Q. Affecting of riblets shape of nonsmooth surface on drag reduction. J. Hydrodyn. Ser. B 2006, 21, 232–238. [Google Scholar]
- Choi, K.S. Effects of longitudinal pressure gradients on turbulent drag reduction with riblets. In Turbulent Control by Passive Means; Coustols, E., Ed.; Springer: Dordrecht, The Netherlands, 1990; Volume 3, pp. 109–122. [Google Scholar]
- Debisschop, J.P.; Nieuwstadt, T.M. Turbulent boundary layer in an adverse pressure gradient: Effectiveness of riblets. AIAA J. 1996, 34, 932–937. [Google Scholar] [CrossRef]
- Wang, A.W.; Motta, P.; Hidalgo, P.; Westcott, M. Bristled shark skin: A microgeometry for boundary layer control? Bioinsp. Biomim. 2008, 3, 046005. [Google Scholar] [CrossRef]
- Cong, Q.; Feng, Y. Numerical simulation of turbulent flow over triangle riblets. J. Ship Mech. 2006, 10, 11–16. [Google Scholar]
- Luchini, P.; Manzo, F.; Pozzi, A. Resistance of a grooved surface to parallel flow and cross-flow. J. Fluid Mech. 1991, 228, 87–109. [Google Scholar] [CrossRef]
- Fukagata, K. Drag reduction by wavy surfaces. J. Fluid Sci. Technol. 2011, 6, 2–13. [Google Scholar] [CrossRef][Green Version]
- Nitschke, P. Experimental Investigation of the Turbulent Flow in Smooth and Longitudinal Grooved Pipes Dissertation. Available online: https://ntrs.nasa.gov/api/citations/19880017231/downloads/19880017231.pdf (accessed on 24 October 2014).
- Chen, J.J.J.; Leung, Y.C. Drag reduction in a longitudinally grooved flow channel. Ind. Eng. Chem. Fundam. 1986, 25, 741–745. [Google Scholar] [CrossRef]
- Reidy, L.W.; Anderson, G.W. Drag reduction for external and internal boundary layers using riblets and polymers. In Proceedings of the AIAA 26th Aerospace Sciences Meeting, Reno, NV, USA, 11–14 January 1988. [Google Scholar]
- Enyutin, G.V.; Lashkov, Y.A.; Samoilova, N.V. Drag reduction in riblet-lined pipes. Fluid Dyn. 1995, 30, 45–48. [Google Scholar] [CrossRef]
- Shiki, O.; Takashi, Y.; Masato, K. Drag reduction in pipe flow with riblet. Trans. Jpn. Soc. Mech. Eng. 2002, 68, 1058–1064. [Google Scholar]
- Koeltzsch, K.; Dinkelacker, A.; Grundmann, R. Flow over convergent and divergent wall riblets. Exp. Fluids. 2002, 33, 346–350. [Google Scholar] [CrossRef]
- Auteri, F.; Baron, A.; Belan, M. Campanardi G and Quadrio M Experimental assessment of drag reduction by traveling waves in a turbulent pipe flow. Phys. Fluids 2010, 22, 115103. [Google Scholar] [CrossRef]
- Tang, F.; Yan, Z.L.; Wang, X.H. Experimental research on lift up and drag reduction effect of streamwise travelling wave wall. Key Eng. Mater. 2011, 483, 721–726. [Google Scholar] [CrossRef]
- Ahn, J.; Choi, H.; Lee, J.S. Large eddy simulation of flow and heat transfer in a channel roughened by square or semicircle ribs. J. Turbomach. 2005, 127, 263–269. [Google Scholar] [CrossRef]
- Peet, Y.; Sagaut, P. Turbulent drag reduction using sinusoidal riblets with triangular cross-section. In Proceedings of the 38th AIAA Fluid Dynamics Conference and Exhibit, Seattle, WA, USA, 23–26 June 2008. [Google Scholar]
- Martin, S.; Bhushan, B. Fluid flow analysis of continuous and segmented riblet structures. Rsc. Adv. 2016, 6, 10962–10978. [Google Scholar] [CrossRef]
- Martin, S.; Bhushan, B. Modeling and optimization of shark-inspired riblet geometries for low drag applications. J. Colloid Interface Sci. 2016, 474, 206–215. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, M.D.; Amran, S.N.A.; Yunos, Y.S.; Ramham, M.R.A.; Mohtar, M.Z.; Wong, L.K.; Zulakharmain, A. The study of drag reduction on ships inspired by simplified shark skin imitation. Appl. Bionics Biomechan. 2018, 2018, 7854321. [Google Scholar] [CrossRef] [PubMed]
- Du Clos, K.T.; Lang, A.; Devey, S.; Motta, P.J.; Habegger, M.L.; Gemmell, B.J. Passive bristling of mako shark scales in reversing flows. J. R. Soc. Interface 2018, 15, 20180473. [Google Scholar] [CrossRef]
- Lloyd, C.J.; Peakall, J.; Burns, A.D.; Keevil, G.M.; Dorrell, R.M.; Wignall, P.B.; Fletcher, T.M. Hydrodynamic efficiency in sharks: The combined role of riblets and denticles. Bioinspir. Biomim. 2021, 16. [Google Scholar] [CrossRef]
- Genc, M.S.; Kemal, K.; Acikel, H.H. Investigation of pre-stall flow control on wind turbine blade airfoil using roughness element. Energy 2019, 176, 320–334. [Google Scholar] [CrossRef]
- Koca, K.; Genç, M.S.; Özkan, R. Mapping of laminar separation bubble and bubble-induced vibrations over a turbine blade at low Reynolds numbers. Ocean Eng. 2021, 239. [Google Scholar] [CrossRef]
- Koca, K.; Genç, M.S.; Veerasamy, D.; Özden, M. Experimental flow control investigation over suction surface of turbine blade with local surface passive oscillation. Ocean Eng. 2022, 266, 113024. [Google Scholar] [CrossRef]
- Pan, J. The experimental approach to drag reduction of the transverse ribbons on turbulent flow. ACTA Aerodyn. Sin. 1996, 14, 304–310. [Google Scholar]
- Bacher, E.V.; Smith, C.R. A combined visualization-anemometry study of the turbulent drag reducing mechanisms of triangular micro-groove surface modifications. In Proceedings of the AIAA Shear Flow Control Conference, Boulder, CO, USA, 12–14 March 1985. [Google Scholar]
- Schumann, U. Subgrid scale model for finite difference simulations of turbulent flows in plane channels and annuli. J. Comput. Phys. 1975, 18, 376–404. [Google Scholar] [CrossRef]
- Smagorinsky, J. General circulation experiments with the primitive equations. I. The basic experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Liu, K.N.; Christodoulou, C.; Riccius, O.; Joseph, D.D. Drag reduction in pipes lined with riblets. AIAA 1990, 28, 1697–1698. [Google Scholar] [CrossRef]
- Byun, D. Drag reduction on micro-structured super-hydrophobic surface. IEEE Int. Conf. Robot. Biomim. 2006, 818–823. [Google Scholar] [CrossRef]
- Wu, N. Study on Turbulent Drag Characteristics of Non-Smooth Surfaces Using Large Eddy Simulation MEng Dissertation. Master’s Thesis, South China University of Technology, Guangzhou, China, 1 June 2012. (In Chinese). [Google Scholar]
- Wu, X.H.; Moin, P. A direct numerical simulation study on the mean velocity characteristics in turbulent pipe flow. J. Fluid Mech. 2008, 608, 81–112. [Google Scholar] [CrossRef]
- Vijiapurapu, S.; Cui, J. Large eddy simulation of fully developed turbulent pipe flow. In Proceedings of the ASME Heat Transfer/Fluids Engineering Summer Conference, Charlotte, NC, USA, 11–15 July 2004. [Google Scholar]
- Zhang, D.Y.; Luo, Y.H.; Li, X.; Chen, H.W. Numerical simulation and experimental study of drag reducing surface of a real shark skin. J. Hydrodyn. 2011, 23, 204–211. [Google Scholar] [CrossRef]
- Wu, N.; Tang, Y.; Zhao, C.; Lin, W.; Chen, X.; Li, R. Numerical investigation of a blade riblet surface for drag reduction applications with large eddy simulation method. Appl. Mech. Mater. 2012, 187, 315–319. [Google Scholar] [CrossRef]
- Choi, H.; Moin, P.; Kim, J. Direct numerical simulation of turbulent flow over riblets. J. Fluid Mech. 1993, 255, 503. [Google Scholar] [CrossRef]

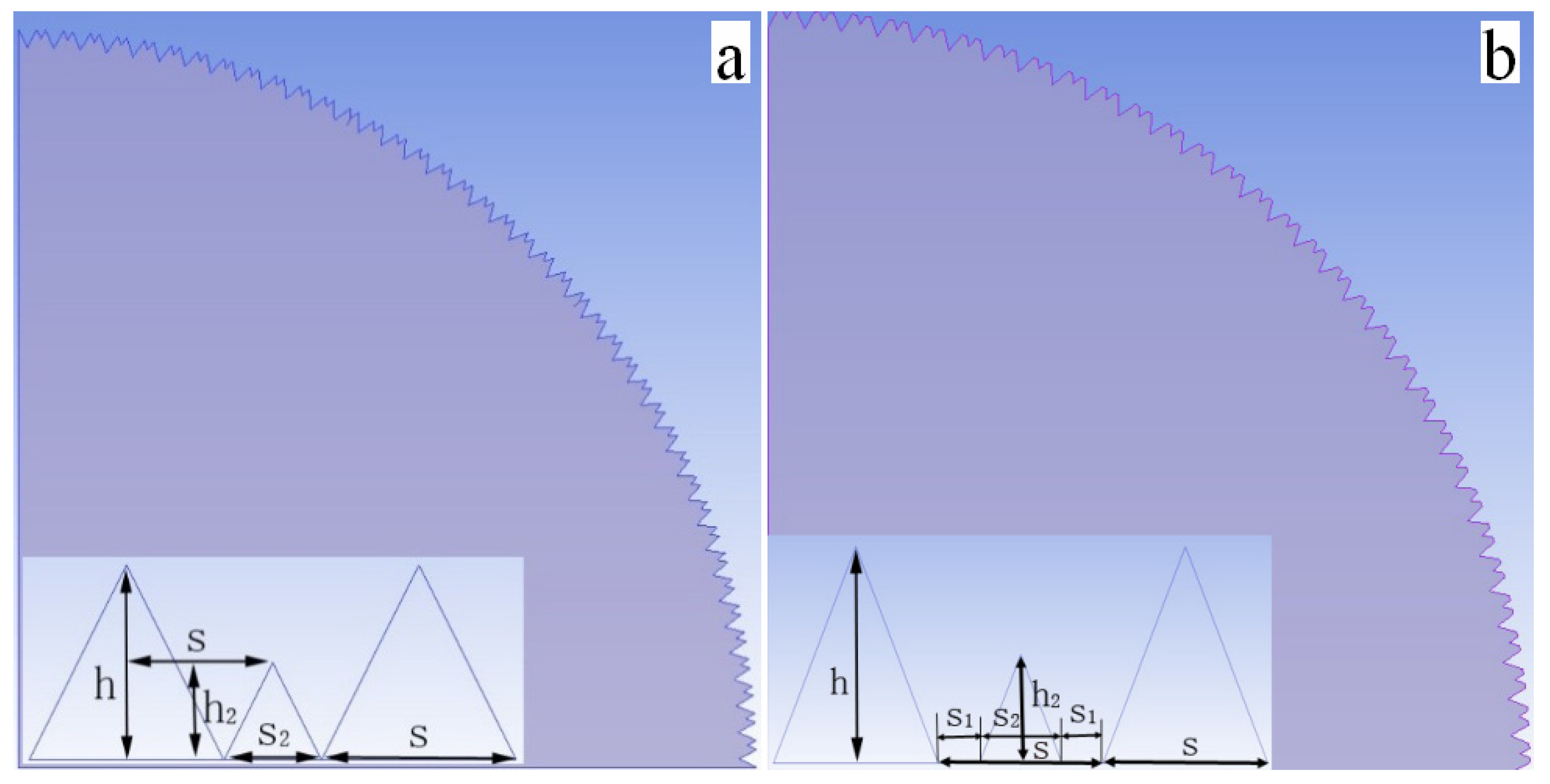



| s | h | s1 | s2 | h2 | D | dr | L | |
|---|---|---|---|---|---|---|---|---|
| riblet C1 (mm) | 0.1524 | 0.1524 | —— | 0.0762 | 0.0762 | 12.7 | 12.5718 | 63.5 |
| riblet C2 (mm) | 0.1524 | 0.1524 | 0.0381 | 0.0762 | 0.0762 | 12.7 | 12.6039 | 63.5 |
| Riblet Form | Flow Rate of the Whole Pipe | Flow Rate of the Quarter of Pipe | A (mm2) | dr (mm) | ρ (kg/m3) | ν (m2/s) | Re | |
|---|---|---|---|---|---|---|---|---|
| riblet C1 | 0.4 kg/s | 0.1 kg/s | 124.1323 | 12.5718 | 1000 | 3.2224 | 10−6 | ≈40,459 |
| riblet C2 | 0.4 kg/s | 0.1 kg/s | 124.7670 | 12.6039 | 1000 | 3.2060 | 10−6 | ≈40,459 |
| Re = 10,115 | Re = 40,459 | |||||
|---|---|---|---|---|---|---|
| Smooth | Riblet C1 | Riblet C2 | Smooth | Riblet C1 | Riblet C2 | |
| s+ | 0 | 6.9601 | 6.9601 | 0 | 18.9737 | 18.9737 |
| s1+ | 0 | 0 | 1.74 | 0 | 0 | 4.7434 |
| s2+ | 0 | 3.4801 | 3.4801 | 0 | 9.4869 | 9.4869 |
| Turbulent drag | 0.0013 | 0.0011 | 0.001061 | 0.0107 | 0.0086 | 0.008327 |
| % DR | — | 15.3846 | 18.3462 | — | 19.6262 | 21.4475 |
| Ref. | Shape of Riblet | Domains | % DR |
|---|---|---|---|
| [1] | Longitudinal blade-shaped ribs with slits | Oil channel experiment | 9.9 at fully developed turbulent state |
| [2] | Fins | Flat plate flow experiment | 7.3 at fully developed turbulent state |
| [3] | Individual movable scales | Surface flow experiment | 3 at fully developed turbulent state |
| [7] | Trapezoidal riblet | Flat plate flow experiment | 26 at Re = 31406 |
| [15] | Longitudinal grooves | Tubes flow experiment | 3 at moderate Re |
| [18] | Triangular riblet | Pipe flow experiment | 6 at Re = 3.0 × 105 − 4.0 × 105 |
| [19] | Isosceles-shaped V-groove riblet | Pipe flow experiment | 8 at Re = 3.0 × 105 − 8.0 × 105 |
| [42] | Real shark skin | Water tunnel experiment | 13.63 at fully developed turbulent state |
| [43] | Blade-shaped riblet | Channel flow simulation | 9 at Re = 210 |
| Present | Riblet C1 | Pipe flow simulation | 19.63 at Re = 40,459 |
| Present | Riblet C2 | Pipe flow simulation | 21.45 at Re = 40,459 |
| Re = 10,115 | Re = 40,459 | |||||
|---|---|---|---|---|---|---|
| Smooth | Riblet C1 | Riblet C2 | Smooth | Riblet C1 | Riblet C2 | |
| Thickness of viscous layer | 1.0948 × 10−4 | 1.749 × 10−4 | 1.8426 × 10−4 | 3.84 × 10−5 | 6.4253 × 10−5 | 7.157 × 10−5 |
| Increment (%) | — | 59.755 | 68.303 | — | 67.417 | 83.278 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, S.; Han, X.; Tang, Y.; Wang, Y.; Kong, X. Shark Skin—An Inspiration for the Development of a Novel and Simple Biomimetic Turbulent Drag Reduction Topology. Sustainability 2022, 14, 16662. https://doi.org/10.3390/su142416662
Fan S, Han X, Tang Y, Wang Y, Kong X. Shark Skin—An Inspiration for the Development of a Novel and Simple Biomimetic Turbulent Drag Reduction Topology. Sustainability. 2022; 14(24):16662. https://doi.org/10.3390/su142416662
Chicago/Turabian StyleFan, Shaotao, Xiangxi Han, Youhong Tang, Yiwen Wang, and Xiangshao Kong. 2022. "Shark Skin—An Inspiration for the Development of a Novel and Simple Biomimetic Turbulent Drag Reduction Topology" Sustainability 14, no. 24: 16662. https://doi.org/10.3390/su142416662
APA StyleFan, S., Han, X., Tang, Y., Wang, Y., & Kong, X. (2022). Shark Skin—An Inspiration for the Development of a Novel and Simple Biomimetic Turbulent Drag Reduction Topology. Sustainability, 14(24), 16662. https://doi.org/10.3390/su142416662











