Metaheuristics Based Energy Efficient Task Scheduling Scheme for Cyber-Physical Systems Environment

Abstract

The widespread applicability of cyber-physical systems (CPS) necessitates efficient schemes to optimize the performance of both computing units and physical plant. Task scheduling (TS) in CPS is of vital importance to enhance resource usage and system efficiency. Traditional task schedulers in embedded real-time systems are unable to fulfill the performance requirements of CPS because of the task diversity and system heterogeneities. In this study, we designed a new artificial rabbit optimization enabled energy-efficient task-scheduling scheme (ARO-EETSS) for the CPS environment. The presented ARO-EETSS technique is based on the natural survival practices of rabbits, comprising detour foraging and arbitrary hiding. In the presented ARO-EETSS technique, the TS process is performed via the allocation of $n$ autonomous tasks to $m$ different resources. In addition, the objective function is based on the reduction of task completion time and the effective utilization of resources. In order to demonstrate the higher performance of the ARO-EETSS system, a sequence of simulations was implemented. The comparison study underlined the improved performance of the ARO-EETSS system in terms of different measures.

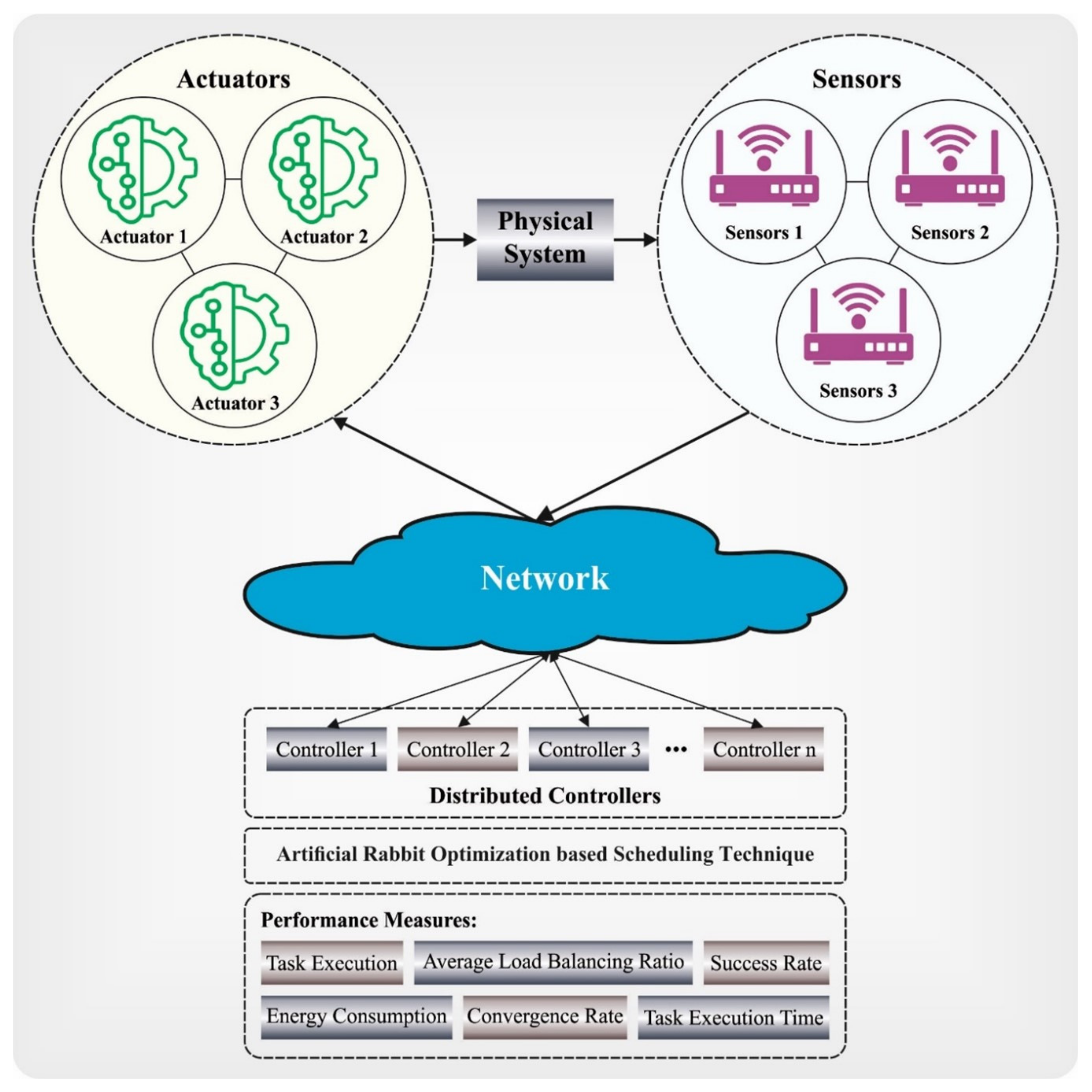
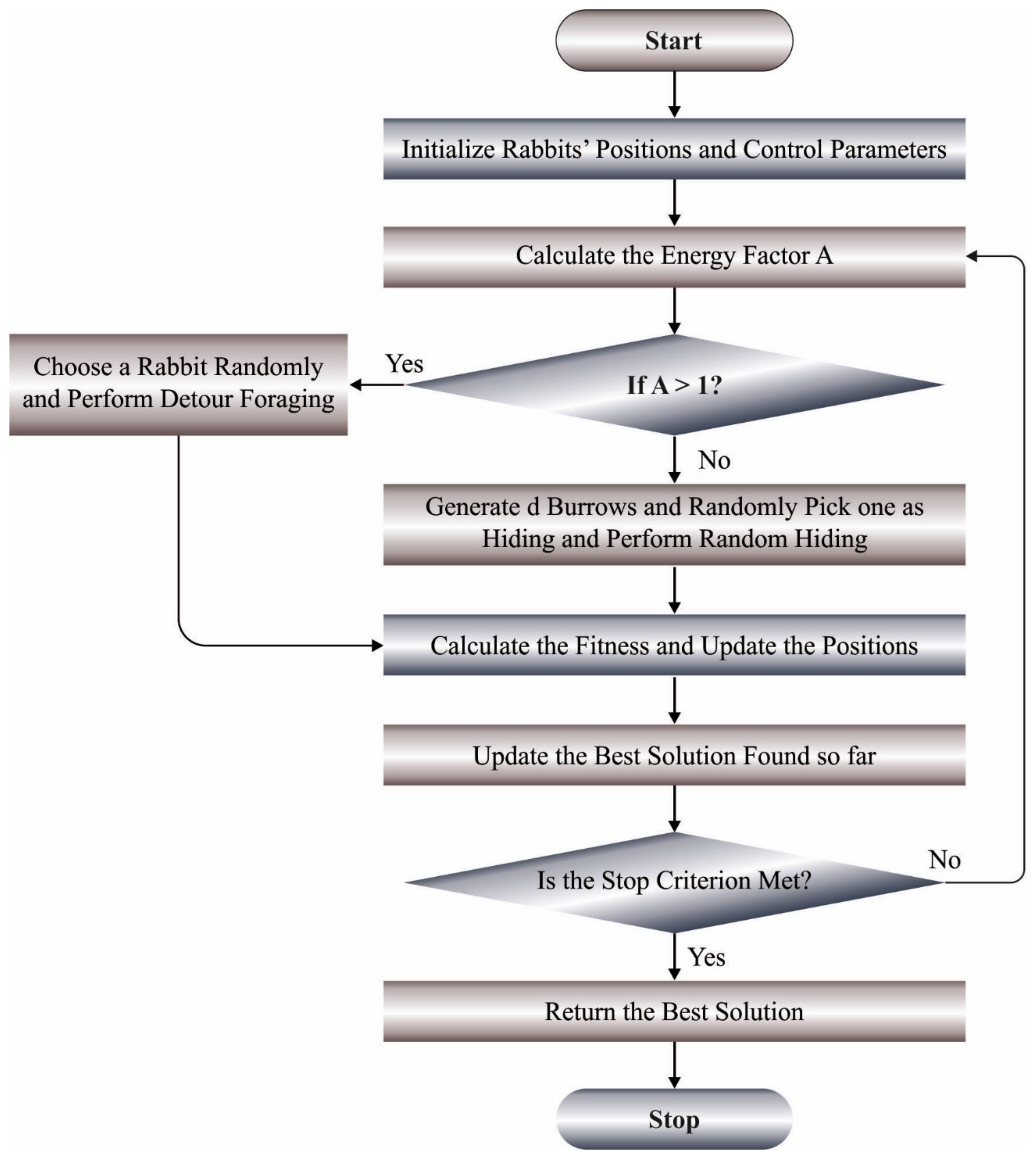
1. Introduction

Technological revolutions have intensely transformed customs within society, in which humans are irreversibly coupled with countless interlinked electronic gadgets and their cyber methods. This procedure is still ongoing, offering novel application scenarios and the continually arising novel scientific difficulties involved in the research fields of cyber-physical systems (CPS) and the Internet of Things (IoT) [1]. The application scenarios involve the fields of manufacturing, assisted living, telerehabilitation, e-health, automotive and smart environments. Certainly, by utilizing these mechanisms, both industry and users obtain a wide range of advantages in relation to their requirements that involve performance enhancement, security, low cost, and comfort [2]. The first and foremost objective is to enable users, machines, and applications to communicate and understand their surrounding atmosphere. By addressing the fundamental needs of users, such as communication, and mobility, water provisioning, and assistive monitoring, different communities (for instance embedded and intelligent) debate to support their views, technologies, and approaches [3]. These solutions can typically be, inappropriately, technically based, while the actual requirements of the particular application domain and its users may be ignored.

CPS range from comparatively small mechanisms, such as automobiles and aircraft, to large mechanisms such as the national power grid [4]. The physical features of these mechanisms will be regulated well by controllers by placing algorithms and computers into a loop; however, to attain the complete advantage of compiling CPS, power consumption, control, and computing can no longer be maximized distinctly [5]. The dynamics of physical systems and the dynamics of computers communicate in ways that need basically novel design techniques. Principally, they involve mechanisms with distinct performances, hardware, and time limitations which have direct communication with the atmosphere, such as a transportation system, a control system, a robotic system, and many more [6]. Each requirement arises from various kinds of applications; therefore, numerous types of scheduling systems are required.

A flexible scheduling policy that alters in accordance with different needs indicates a desideratum in many cases [7]. Handling such complicated difficulties has led to the advancement of novel ideas and a novel class of models: the mixed criticality system [8], which is “an embedded computing platform where application functions of various criticality share computation and or transmission resources” [9]. In numerous cases, the safety and real-time needs should match the limited resources, minimum cost, and small power limitations, which raises the difficulty level in CPS cases. The method of utilizing mixed criticality scheduling in CPS was mostly application based, resulting in a variety of specific task methods having a multitude of system performance limitations [10]. These techniques, while featuring higher real-world relevance, have inadequacies when it comes to interaction and scalability in an unpredictable atmosphere.

In this study, we propose a new artificial rabbit optimization enabled energy-efficient task-scheduling scheme (ARO-EETSS) for the CPS environment. The goal of the presented model is to allocate $n$ autonomous tasks to $m$ different resources, and thus the entire task completion period is minimized and resources totally exploited. To demonstrate the higher efficiency of the ARO-EETSS system, a sequence of simulations was performed. In summary, the paper’s contribution is given as follows.

• Propose a new ARO-EETSS technique for scheduling tasks in the CPS environment. To the best of our knowledge, none of the existing task schedulers are based on the ARO algorithm and the ARO-EETSS technique does not exist in the literature.
• Derive a task scheduler to assign $n$ autonomous tasks to $m$ different resources.
• Validate the performance of the ARO-EETSS technique under different aspects.

2. Related Works

In [11], the authors modelled an energy-aware CPS (E-CPS) for Big Data analysis and recessive construction anomaly detection. The proposed model included a data association and data reduction study, which was devised for examining manufactured data in E-CPS. An energy Big Data-driven recessive production anomaly study technique was devised on the basis of DBN by consideration of the dynamics and complexity of the manufacturing procedure. In [12], the authors initially developed the mobile CPS (MCPS) security maximized issue as a mixed integer nonlinear programming (MINLP) issue and next converted it as an MILP issue without efficiency degradations. To resolve the converted MILP issue proficiently, the researchers suggested a decomposed technique for deriving the optimal task scheduling (TS) solution as an alternative utilizing MILP resolvers that might be time-consuming for MCPS of huge granularity.

Energy-aware and service-level agreements (SLAs) determining the job schedule structure based on MapReduce were proposed in [13]. The main objective of this modelled structure was to sightsee task-to-slot or container map issues as a unique case of energy-aware scheduling from deadline-limited cases. Therefore, this complexity was extracted as a complicated multi-objective issue that has various limitations. For solving this issue proficiently, it was divided into three sub-problems (SPs), such as deadline segregation, mapping, and minimizing stage energy-aware scheduling. In [14], the researchers studied the issue of TS in a heterogeneous multi-processor mechanism on chip (MPSoC) positioned in the IoT to optimize the security quality in energy, real-time, and task-precedence limitations. The authors initially offered an MILP design to schedule and allocate reliant on tasks having energy and real-time limitations on the heterogeneous MPSoC mechanism for maximizing security quality.

Tang et al. [15] presented an effectual scheduling technique that gratified cost and functional reliability limitations in multi-functional mixed-criticality task replication executing cases. Utilizing the modelled fault-tolerant hardware cost-aware multi-functional safety assurance (FT_HCMSA) technique could minimize DMR of higher criticality purpose suggestively when meeting the automotive functional security. Hossain et al. [16] presented an energy-aware CPS therapy mechanism (T-CPS) that inculcated smart gadgets and things in both the cyber and physical worlds for a therapy system. In [17], the authors recommended an energy aware meta-heuristic technique related to a Harris Hawks optimized technique related to local search strategy (HHOLS) for TS in fog computing (FC) (TSFC) for enhancing the quality of service offered to users from Industrial-Internet-of-Things (IIoT) applications. Firstly, the authors explained the higher virtual layered FC method considering its varied structure. The scaling and normalization stage helped the HHO to solve the TSFC, which would be discrete.

Ghobaei-Arani et al. [18] examined a TS technique dependent upon the moth-flame optimized (MFO) technique for assigning a better group of tasks to fog node for meeting the approval of the service quality requirements of CPS applications so that the entire execution time of tasks is minimized. The minimized task execution and transmission time in the presented technique were assumed the main functions. In [19], the authors examined energy-efficient and contention-aware static TS with priority and deadline constraints on intelligent edge devices utilizing heterogeneous VFI-based NoC-MPSoCs (VFI-NoC-HMPSoC) with DVFS-enabled processors. Different from the existing population-based optimized systems, the authors presented a new population-based technique named ARSH-FATI which is dynamically switched betwixt exploitative and explorative searching modes at run-time. Xu et al. [20] defined a new method for reducing thermally induced damage from CPS processors by targeting dynamic voltage and frequency scaling (DVFS) to high activity task stages. Specifically, by preferably slowing down high activity task stages, major extra savings in energy and thermal stress were obtained to provide a count of computational slowdowns; this method demonstrated that higher than typical approaches utilize DVFS without regard to activity level.

3. The Proposed Model

In this study, an ARO-EETSS system could be introduced for TS from the CPS situation. The presented ARO-EETSS technique depends upon the natural survival practices of rabbits, encompassing detour foraging and random hiding. In the presented ARO-EETSS technique, the TS process was carried out via the allocation of $n$ autonomous tasks to $m$ dissimilar resources, and thus the entire task completion period is minimized and resources are totally exploited. Figure 1 demonstrates the overall procedure of ARO-EETSS system.

3.1. Algorithmic Steps of ARO Technique

The ARO algorithm is based on the foraging and hiding practices of real rabbits and energy shrink [21]. The ARO algorithm has the following merits. It exhibits competitive performance over other metaheuristic algorithms. It avoids local extremum and carries out a global search. It maintains a balanced transition from exploration to exploitation throughout the iterations. Finally, the algorithm is effective and easy to implement. The mathematical modeling of the ARO algorithm is discussed in the following:

3.1.1. Detour Foraging (Exploration)

During the time of foraging, the rabbit looks further away and neglects what exists closer at hand. It can eat grass arbitrarily in the other area rather than its individual region; the foraging behavior can be defined as detour foraging. In the ARO algorithm, consider that every individual rabbit from the colony has its individual area of grass around the burrows, and the rabbits continually arbitrarily stray to the location of every other one to forage. In fact, at the time of foraging, the rabbits are likely to cause disturbance over the food source in order to obtain adequate food. So, the detour foraging nature of the ARO algorithm signifies that every searching individual tends to upgrade its position in the direction of another arbitrarily selected individual in the colony and inflict disturbance.

The detour foraging process of rabbits can be defined as follows [21]:

$${\overrightarrow{v}}_{\mathrm{i}}\left(t+1\right)={\overrightarrow{x}}_{\mathrm{j}}\left(t\right)+R·\left(\overrightarrow{x}\left(t\right)-{\overrightarrow{x}}_{\mathrm{j}}\left(t\right)\right)+ronnd\left(0.5·\left(0.05+r_1\right)\right)·n_1, i,j=1, \dots ,n and j\ne i,$$

(1)

$$R=L·c,$$

(2)

$$L=\left(e-e^{{(\frac{t-1}{T})}^2}\right)· \sin \left(2\pi r_2\right),$$

(3)

$$c\left(k\right)=\left\{\begin{array}{l}1 if k==g\left(l\right)\hfill \\ 0 else\hfill \end{array}\right.k=1, \dots ,d and l=1\dots ,r_3·d,$$

(4)

$$g=rand perm\left(d\right),$$

(5)

$$n_1\sim N\left(0,1\right),$$

(6)

where ${\overrightarrow{v}}_{\mathrm{i}}\left(t+1\right)$ denotes the candidate’s place of $i\mathrm{th}$ rabbit at the time $t+1,$ ${\overrightarrow{x}}_{\mathrm{i}}\left(t\right)$ defines place of ith rabbit at the time $t,$ $n$ implies rabbit population size, $d$ is the dimension, round determines rounding to the adjoining integer, randperm provides an arbitrary permutation of the integers, $r_1,$ $r_2$ and $r_3$ are arbitrary numbers in zero and one, $L$ refers to the running length representing the movement pace at the time of detour foraging, and $n_1$ defines the subject to normal distribution.

Equation (1) defines that the searching population carries out an arbitrary searching process for food based on the location. It enables a rabbit to move away from its original area to the areas of others. These peculiar characteristics of rabbits considerably contributed to the exploration and promise of the global searching ability of the ARO technique.

3.1.2. Random Hiding (Exploitation)

To escape from predators, a rabbit usually digs roughly diverse burrows over the nest to hide. In the ARO algorithm, at every round, the rabbit generally creates $d$ burrows over every individual dimension of the searching area, and it arbitrarily selects one from every burrow for hiding and thereby minimizes the likelihood of being preyed upon. The jth burrow of the $i\mathrm{th}$ rabbit can be determined as follows [21]:

$${\overrightarrow{b}}_{i,j}\left(t\right)={\overrightarrow{x}}_{\mathrm{i}}\left(t\right)+H·g·{\overrightarrow{x}}_{\mathrm{i}}\left(t\right),\hspace{1em}i=1\dots ,n and j=1,\dots d,$$

(7)

$$H=\frac{T-t+1}{T}·r_4,$$

(8)

$$g\left(k\right)=\left\{\begin{array}{l}1 if k==j\hfill \\ 0 else\hfill \end{array},\right. k=1,\dots ,d,$$

(9)

where the $d$ burrows are produced from the neighboring area of rabbits over each dimension. $H$ denotes hiding variable that is linearly reduced in 1 to 1/T with an arbitrary perturbation over several iterations. Based on this, the burrows are produced from a larger region of a rabbit. With a rise in iterations, this neighboring area gets reduced.

As aforementioned, rabbits are frequently exposed to pursuing and attacking predators. For survival, the rabbits require a safe location for hiding. So, it can be reduced to arbitrarily selecting a burrow from its burrows to shelter in to avoid getting caught. In order find to mathematical system for this arbitrary hiding approach, the formulas are presented as:

$${\overrightarrow{v}}_{\mathrm{i}}\left(t+1\right)={\overrightarrow{x}}_{\mathrm{i}}\left(t\right)+R·\left(r_4·{\overrightarrow{b}}_{i,r}\left(t\right)-\overrightarrow{x}\left(t\right)\right), i=1,\dots ,n,$$

(10)

$$g_r\left(k\right)=\left\{\begin{array}{ll}1& ifk==\lceil r_5·d\lceil \hfill \\ 0\hfill & else\hfill \end{array}\right.k=1,\dots ,d,$$

(11)

$${\overrightarrow{b}}_{i,r}\left(t\right)={\overrightarrow{x}}_{\mathrm{i}}\left(t\right)+H·g_r·{\overrightarrow{x}}_{\mathrm{i}}\left(t\right),$$

(12)

where ${\overrightarrow{b}}_{i,r}$ defines the arbitrarily selected burrow to hide in of their $d$ burrows, and, $r_4$ and $r_5$ represent the 2 arbitrary numbers from zero and one. According to Equation (10), the ith search separately is the attempt to update their position only after selecting the burrow in their $d$ burrows.

Afterward, once the detoured foraging and arbitrary hide were obtained, the place upgrade of ith rabbit is given as follows [21]:

$${\overrightarrow{x}}_{\mathrm{i}}\left(t+1\right)=\left\{\begin{array}{ll}\overrightarrow{x}\left(t\right)& f\left(\overrightarrow{x}\left(t\right)\right)\le f\left({\overrightarrow{v}}_{\mathrm{i}}\left(t+1\right)\right)\hfill \\ \overrightarrow{v}\left(t+1\right)\hfill & f\left({\overrightarrow{x}}_{\mathrm{i}}\left(t\right)\right)>f({\overrightarrow{v}}_{\mathrm{i}}\left(t+1\right))\hfill \end{array},\right.$$

(13)

This formula represents that when the fitness of candidate places of the ith rabbit was superior to that of the present one, the rabbit gene abandons the present location and stops at the candidate place created.

3.1.3. Energy Shrink (Switch from Exploration to Exploitation)

In ARO, rabbits are continuously inclined to often carry out detour foraging at an early stage of iterations but often implement arbitrary hiding at the later stage of iterations. This outcome of this search process is that the energy of the rabbits is shrinking slowly with the lapse of time. Thus, an energy factor was planned for modeling the switch from exploration to exploitation. The energy influence in ARO was determined as:

$$A\left(t\right)=4\left(1-\frac{t}{T}\right)\ln \frac{1}{r},$$

(14)

in which r denotes the arbitrary number from zero and one. The big value of energy factors defines that the rabbit is reaching appropriate energy and physical strength levels to resume detour foraging. Figure 2 showcases the flowchart of ARO technique.

Conversely, the smaller value of energy factors represents that the rabbit is less active; therefore it needs to remain arbitrarily hidden. Thus, in ARO, once the energy factor $A\left(t\right)>1$, the rabbit is prone to arbitrarily explore the area of other various rabbits to forage from the exploration stage; thus, detour foraging occurs; once the energy influence $A\left(t\right)\le 1$, the rabbit then arbitrarily exploits its individual burrows during the exploitation stage, so, arbitrary hiding takes place. According to the value of the energy influence A, ARO is switched between detour foraging and arbitrary hiding. Specifically, exploration takes place once $A\left(\mathrm{t}\right)>1$, but exploitation occurs once $A\left(t\right)\le 1$.

To investigate the impact of the energy factor on the search performance of the technique, the probability of $A>1$ was computed. Assume that $=2·\left(1-\frac{t}{T}\right)$, afterward $A\left(t\right)=2· \ln \frac{1}{r}·\theta$, the probability of $A>0$ was computed as:

$$P\left\{A\left(t\right)>1\right\}=\frac{{{\displaystyle \int }}_0^2{{\displaystyle \int }}_0^{e^{-\frac{1}{2k}}}drd\theta }{1·2}=\frac{1}{4}·{{\displaystyle \int }}_{-\infty }^{-\frac{1}{4}}\frac{e^t}{t}dt+e^{-\frac{1}{4}}\approx 0.5177,$$

(15)

Therefore, the action of detour foraging was about 0.5 during the iterative procedure of carrying out the action; the ARO technique is nearly the same for carrying out either detour foraging or arbitrary hiding under the iterative procedure that gives consideration for the balance of exploration and exploitation as explained in Algorithm 1 below.

Algorithm 1: Pseudocode of ARO algorithm.

Input: Parameter initialization

Arbitrarily prepare a group of rabbit $X_i$ (solutions) and evaluate its fitness $Fi{t}_i,$$and X_{best}$ is the optimum solution created so far.

While the termination condition is not fulfilled do

For all the individuals $X_i$ do

Compute the energy factor $A$ utilizing in Equation (14).

$IfA>1$

Select a rabbit arbitrarily in other individuals.

Compute $R$ utilizing in Equations (2) $–\left(6\right)$.

Implement detour foraging utilizing in Equation (1).

Compute the fitness $Fi{t}_i$.

Upgrade the position of present individual utilizing Equation (13).

Else

Create $d$ burrows and arbitrarily choose one as hide utilizing in Equation (12).

Execute arbitrary hiding utilizing Equation (10).

Compute the fitness $Fi{t}_i$.

Upgrade the position of individuals utilizing Equation (13).

End If

Upgrade the optimum solution create so far $X_{best}$

End For

End While

Return $X_{best}$

Output: Scheduled Tasks

3.2. Process Involved in Scheduling Process

In the presented ARO-EETSS technique, the scheduling process is performed in the CPS environment. The rule of the presented system is assigning $n$ independent tasks to $m$ heterogeneous accessible resources, therefore the complete task completion duration is minimized and resources have been used entirely [22]. During the distributing method, $n$ sub-tasks $Task=\left\{T_1, T_2, \dots , T_n\right\}$ were allotted to $m$ processors $C=$ $\left\{C_1, C_2, \dots , C_{\mathfrak{m}}\right\}.$ $R=\left\{R_1, R_2, \dots , R_{\mathfrak{m}}\right\}$ denotes the maximum resource quantity group of every processor, $R_j$ implies the higher source count of processors $C_j$, and the count of resources required for every task execution is $H=\left\{H_1, H_2, \dots , H\right\}$. $T_j={{\displaystyle \sum }}_i^{ }{X}_{ij}=t_i/v_j$ demonstrates the number of execution times (ETs) of all tasks scheduled on processors $j$, whereas $t_i$ illustrates the ET of tasks $i$ on minimal processors and $v_j$ represents the processing speed of processors $j$.

$$f\left(X\right)=\min \left(A{\displaystyle \sum }_{j=1}^m{t}_j^d+B{\displaystyle \sum }_{i=1}^m{\displaystyle \sum }_{j=1}^m{\displaystyle \sum }_{p=1}^m{\displaystyle \sum }_{q=1}^m{\omega }_{ijpq}{X}_{ij}{X}_{pq}\right),$$

(16)

$${{\displaystyle \sum }}_{j=1}^{\mathfrak{m}}{X}_{ij}=1,i=1,2,\dots ,n,$$

(17)

$${{\displaystyle \sum }}_{i=1}^m{H}_i{X}_{ij}\le R_j,j=1,2,\dots ,m,$$

(18)

in which, $A$ and $B\left(A+B=1\right)$ imply the comparative importance of total end time and communication cost in the objective purpose, $w_{ijpq}$ represents the task $i$ scheduling on processors $j$ and task $p$ carried out on processors $q$.

$$T=\left[\begin{array}{llll}tim{e}_{11}\hfill & tim{e}_{12}\hfill & \cdots \hfill & tim{e}_{1m}\hfill \\ tim{e}_{21}\hfill & tim{e}_{22}\hfill & \cdots \hfill & tim{e}_{2\mathfrak{m}}\hfill \\ ⋮\hfill & ⋮\hfill & ⋮\hfill & ⋮\hfill \\ tim{e}_{n1}\hfill & tim{e}_{n1}\hfill & \cdots \hfill & tim{e}_{nm}\hfill \end{array}\right],$$

(19)

in which $tim{e}_{ij}$ denotes the ET required for virtual machine (VM) $v_j$ to process the task $t_i$, and $tim{e}_{ij}=M{I}_i/MIP{S}_j.$ The evaluated time for computing of $n$ tasks on $m$ effectual resources, defined as $E,$ $E$ is a $n\times m$ matrix. $E_{ij}$ implies the time required for $T_i$ to run in the VM, $E_{ij}=c_{ij}+e_{ij}$. Next, the VM applies the allocated task gathering time expressed as $E_j$. While the tasks assigned for every VM resource can be applied separately, the ET essential to all the tasks to the whole is the higher value array $E$ represented as $E_{total}$:

$$E_j={\displaystyle \sum }_{i\in Taskj} e_{ij}+{\displaystyle \sum }_{i\in Tas{k}_j} t_{ij},$$

(20)

whereas $Tas{k}_j$ stands for a set of tasks executed on VM. The matrix $x\left[i\right]\left[j\right]$ is established dependent upon the equal linking betwixt the VM and the task, denoting once the task $t_i$ is assigned to VM $v_j$, it is defined as:

$$x\left[i\right]\left[\mathrm{j}\right]=\left\{\begin{array}{l}1, is assigned to V_j\hfill \\ 0, Otherwise\hfill \end{array}\right.,$$

(21)

4. Results and Discussion

This section assesses the TS performance of the ARO-EETSS model in the CPS environment. The proposed model was simulated using MATLAB tool.

Table 1. TET analysis of ARO-EETSS system with recent algorithms in different iterations.

Task Execution (ms)
No. of Iterations	EDD	EDF	ACOTS	QIWO-EATS	ARO-EETSS
I-20	782	773	655	548	451
I-40	773	744	627	496	414
I-60	753	677	591	481	403
I-80	722	667	573	448	380
I-100	691	644	537	427	361
I-120	680	596	510	405	332
I-140	663	599	490	388	322
I-160	639	571	459	368	298
I-180	596	557	442	364	287
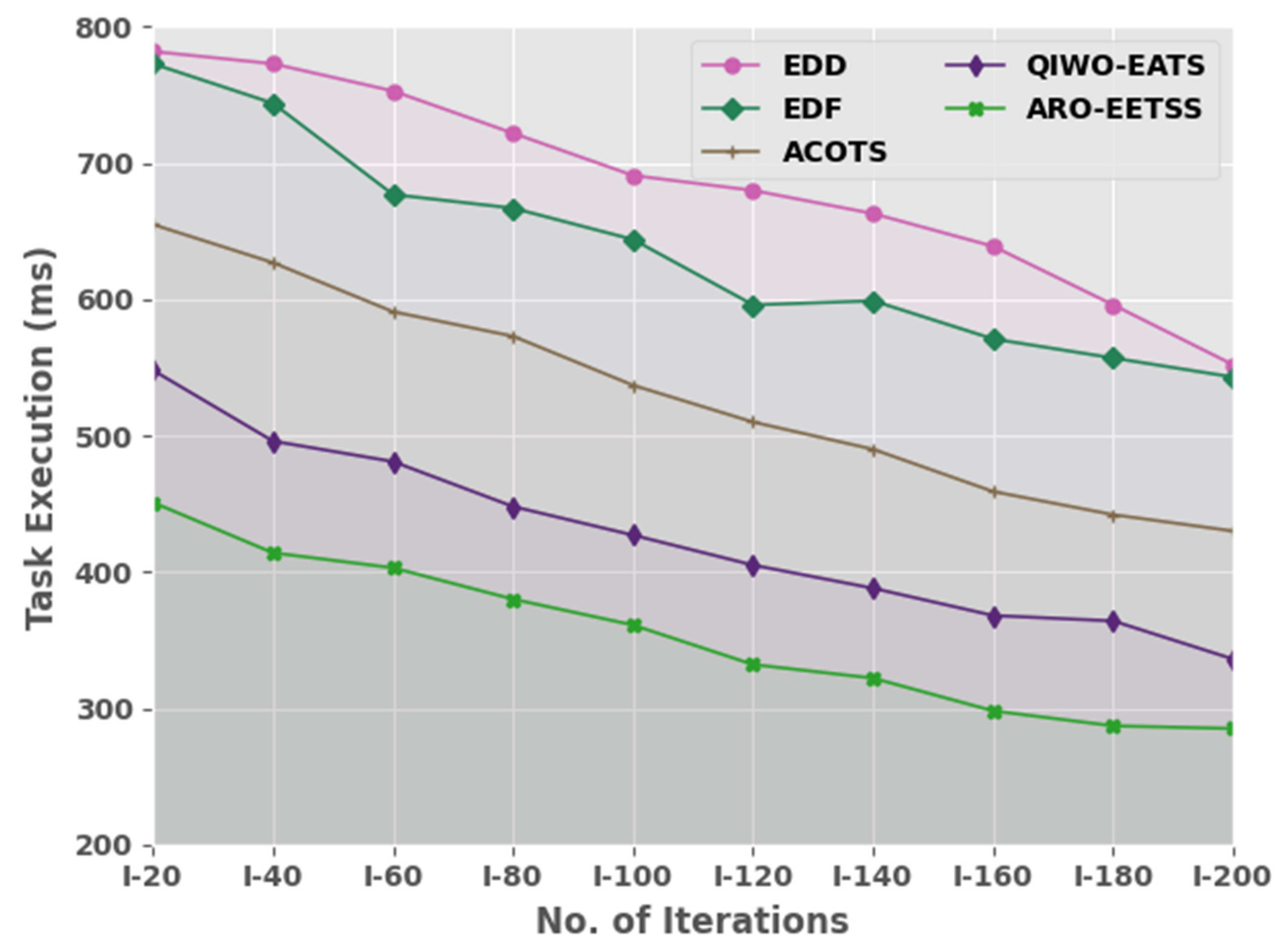
I-200	552	543	430	336	285

and Figure 3 compare the task execution time (TET) examination of the ARO-EETSS method with current approaches such as earliest due date (EDD), earliest deadline first (EDF), ant colony optimization-based task scheduler (ACOTS), and quantum invasive weed optimization-based energy-aware scheduling (QIWO-EATS) [4]. The experimental values suggested the ARO-EETSS method reached least TET values under all iterations. For instance, on I-20 iterations, the ARO-EETSS model showed the lowest TET of 451 ms whereas the EDD, EDF, ACOTS, and QIWO-EATS models demonstrated higher TETs of 782, 773, 655, and 548 ms, respectively. Along with that, on I-100 iterations, the ARO-EETSS method displayed the lowest TET of 361 ms where the EDD, EDF, ACOTS, and QIWO-EATS methods showed increased TETs of 691, 644, 537, and 427 ms, correspondingly.

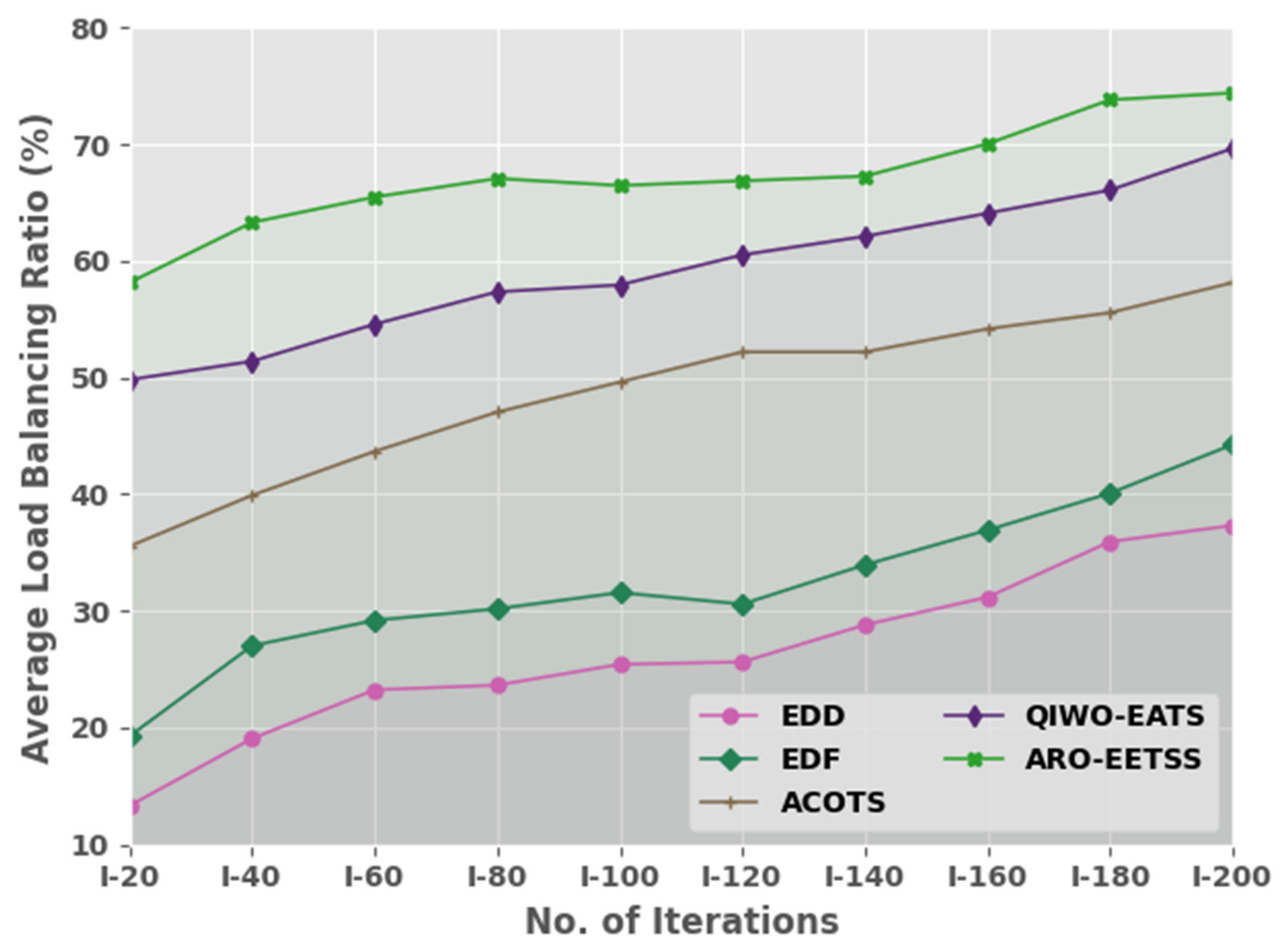
An average load balancing ratio (ALBR) of the ARO-EETSS method with current methodologies is investigated in

Table 2. ALBR analysis of ARO-EETSS system with recent algorithms in different iterations.

Average Load Balancing Ratio (%)
No. of Iterations	EDD	EDF	ACOTS	QIWO-EATS	ARO-EETSS
I-20	13.32	19.27	35.54	49.83	58.16
I-40	19.07	27.01	39.91	51.41	63.32
I-60	23.24	29.19	43.68	54.59	65.50
I-80	23.64	30.18	47.05	57.37	67.09
I-100	25.42	31.57	49.63	57.96	66.49
I-120	25.62	30.58	52.21	60.54	66.89
I-140	28.80	33.95	52.21	62.13	67.29
I-160	31.18	36.93	54.19	64.11	70.07
I-180	35.94	40.10	55.58	66.10	73.84
I-200	37.33	44.27	58.16	69.67	74.43

and Figure 4. The outcomes denoted the ARO-EETSS method gained improved outcomes in all iterations. For example, on I-20 iterations, the ARO-EETSS method offered a maximum ALBR of 58.16% whereas the EDD, EDF, ACOTS, and QIWO-EATS models depicted higher ALBRs of 13.32, 19.27, 35.54, and 49.83% respectively. In addition, on I-100 iterations, the ARO-EETSS method presented a maximum ALBR of 66.49% whereas the EDD, EDF, ACOTS, and QIWO-EATS methods portrayed higher ALBRs of 25.42, 31.57, 49.63, and 57.96%, correspondingly.

Table 3. CR analysis of ARO-EETSS system with recent algorithms under varying iterations.

Convergence Rate (ms)
No. of Iterations	EDD	EDF	ACOTS	QIWO-EATS	ARO-EETSS
I-20	660	659	660	656	657
I-40	636	621	613	602	594
I-60	615	604	587	571	559
I-80	604	584	571	551	535
I-100	593	576	560	539	524
I-120	586	568	554	533	519
I-140	581	562	551	530	515
I-160	577	560	543	527	511
I-180	570	555	543	525	510
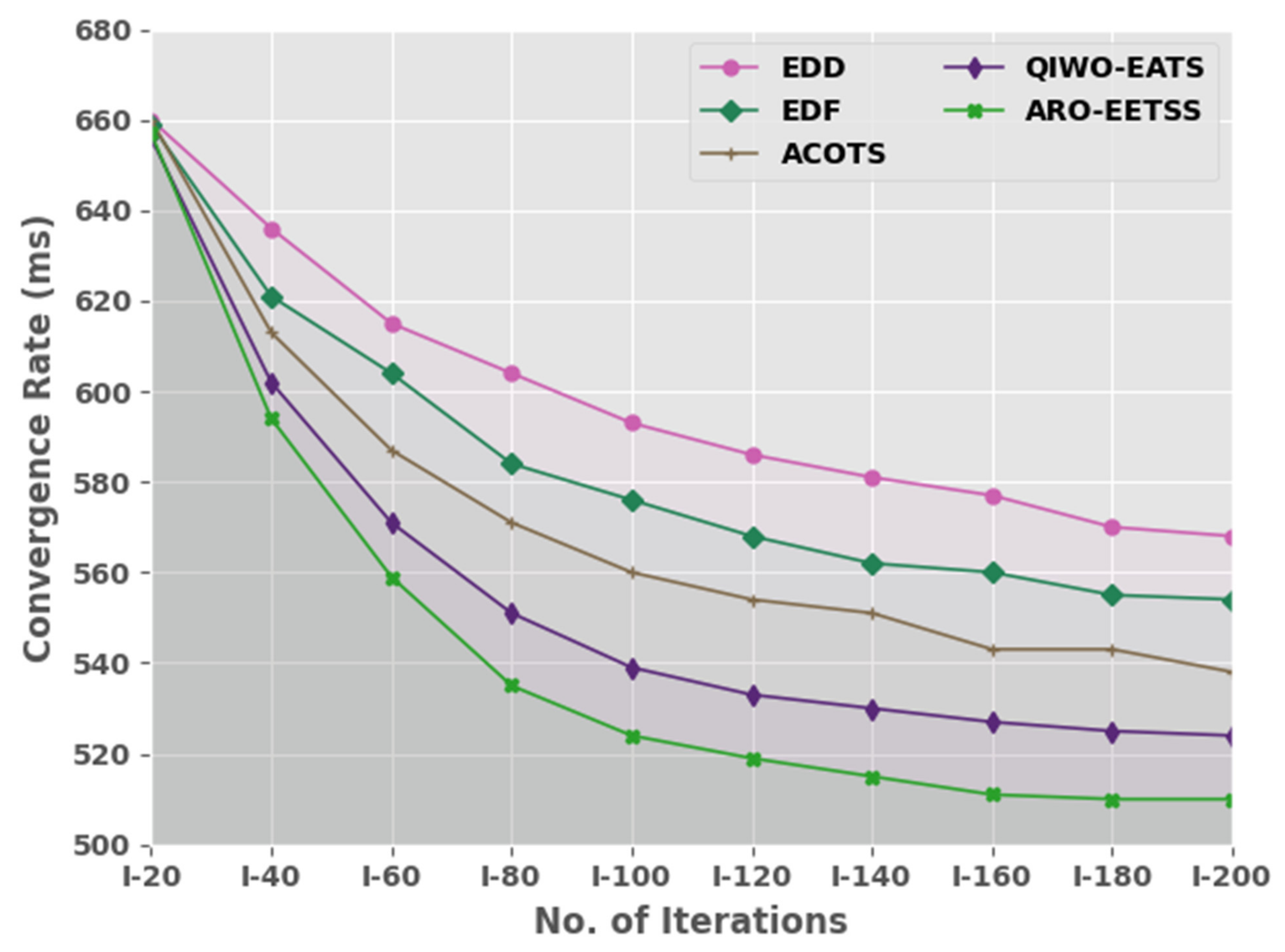
I-200	568	554	538	524	510

and Figure 5 compare the task convergence rate (CR) inspection of the ARO-EETSS method with recent methods. The experimental values denoted by the ARO-EETSS method reached lowest CR values under all iterations. For example, on I-20 iterations, the ARO-EETSS approach displayed a minimal CR of 657 ms whereas the EDD, EDF, ACOTS, and QIWO-EATS methods demonstrated increased CRs of 660, 659, 660, and 656 ms, correspondingly. Similarly, on I-100 iterations, the ARO-EETSS method exhibited the lowest CR of 524 ms whereas the EDD, EDF, ACOTS, and QIWO-EATS methods demonstrated increased CRs of 593, 576, 560, and 539 ms, correspondingly.

Table 4. ECON analysis of ARO-EETSS system with recent algorithms under varying iterations.

Energy Consumption (Wh)
No. of Physical Machines	EDD	EDF	ACOTS	QIWO-EATS	ARO-EETSS
PM-20	1657	3146	4717	665	417
PM-40	3229	5255	6868	1947	1285
PM-60	4593	7364	9018	3229	2236
PM-80	6578	9225	10,961	5379	2815
PM-100	8439	11,127	12,533	7033	3435
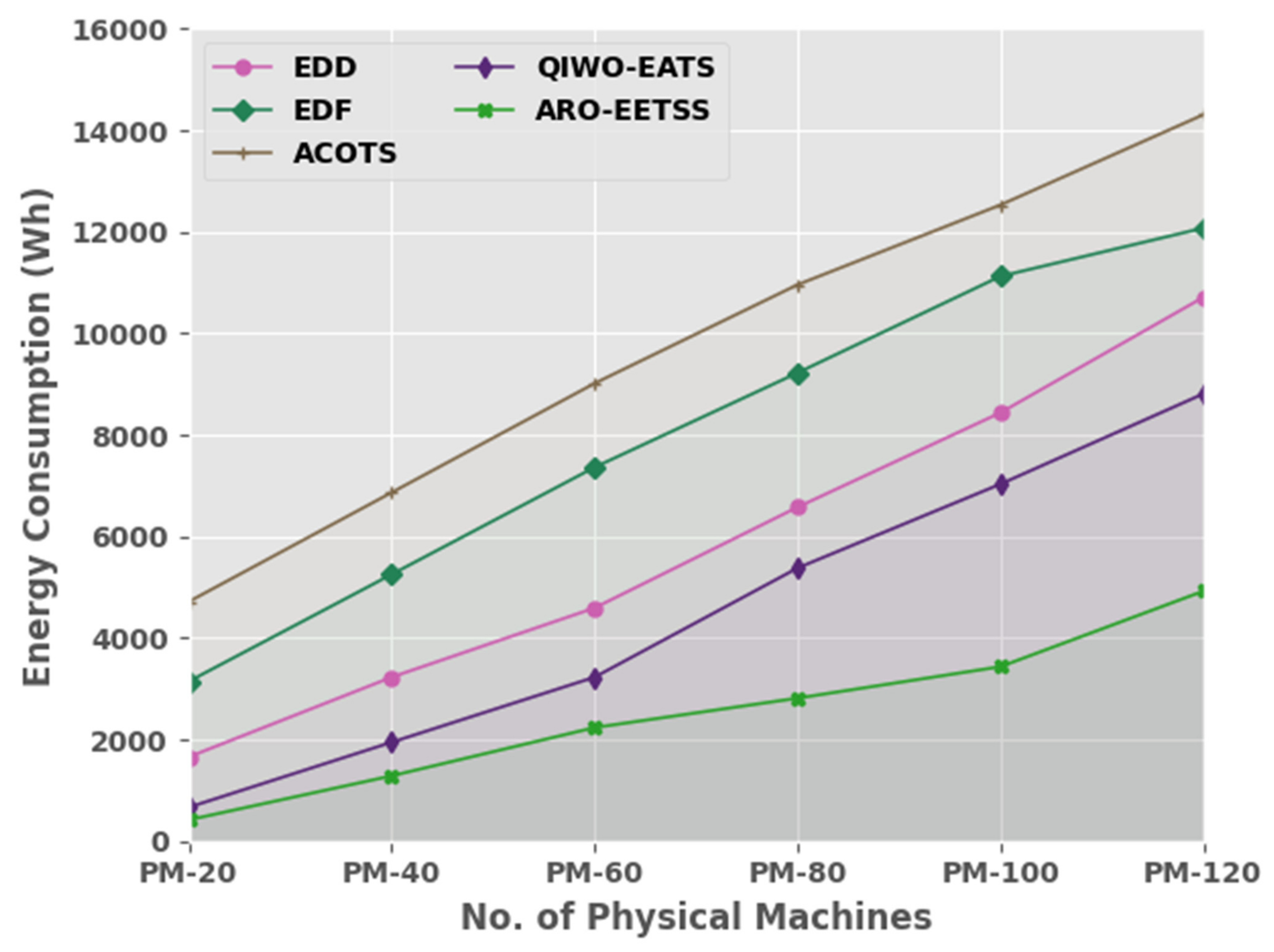
PM-120	10,713	12,078	14,311	8811	4924

and Figure 6 compare the task energy consumption (ECON) inspection of ARO-EETSS method with recent methods. The experimental values denoted by the ARO-EETSS approach reached the least ECON values under all iterations. For example, on PM20, the ARO-EETSS technique showed a reduced ECON of 417 Wh whereas the EDD, EDF, ACOTS, and QIWO-EATS approaches illustrated higher ECONs of 1657, 3146, 4717, and 665 Wh, correspondingly. Moreover, on PM-100, the ARO-EETSS method exemplified a reduced ECON of 3435 Wh, for which the EDD, EDF, ACOTS, and QIWO-EATS methods demonstrated higher ECONs of 8439, 11,127, 12,533, and 7033 Wh, correspondingly.

Table 5. TET analysis of ARO-EETSS system with recent algorithms under varying tasks.

Task Execution Time (ms)
No. of Tasks	EDD	EDF	ACOTS	QIWO-EATS	ARO-EETSS
T-200	228	170	115	79	49
T-400	346	239	159	134	90
T-600	470	349	231	156	107
T-800	597	440	310	219	134
T-1000	726	564	407	283	181
T-1200	812	663	478	335	206
T-1400	947	779	583	393	219
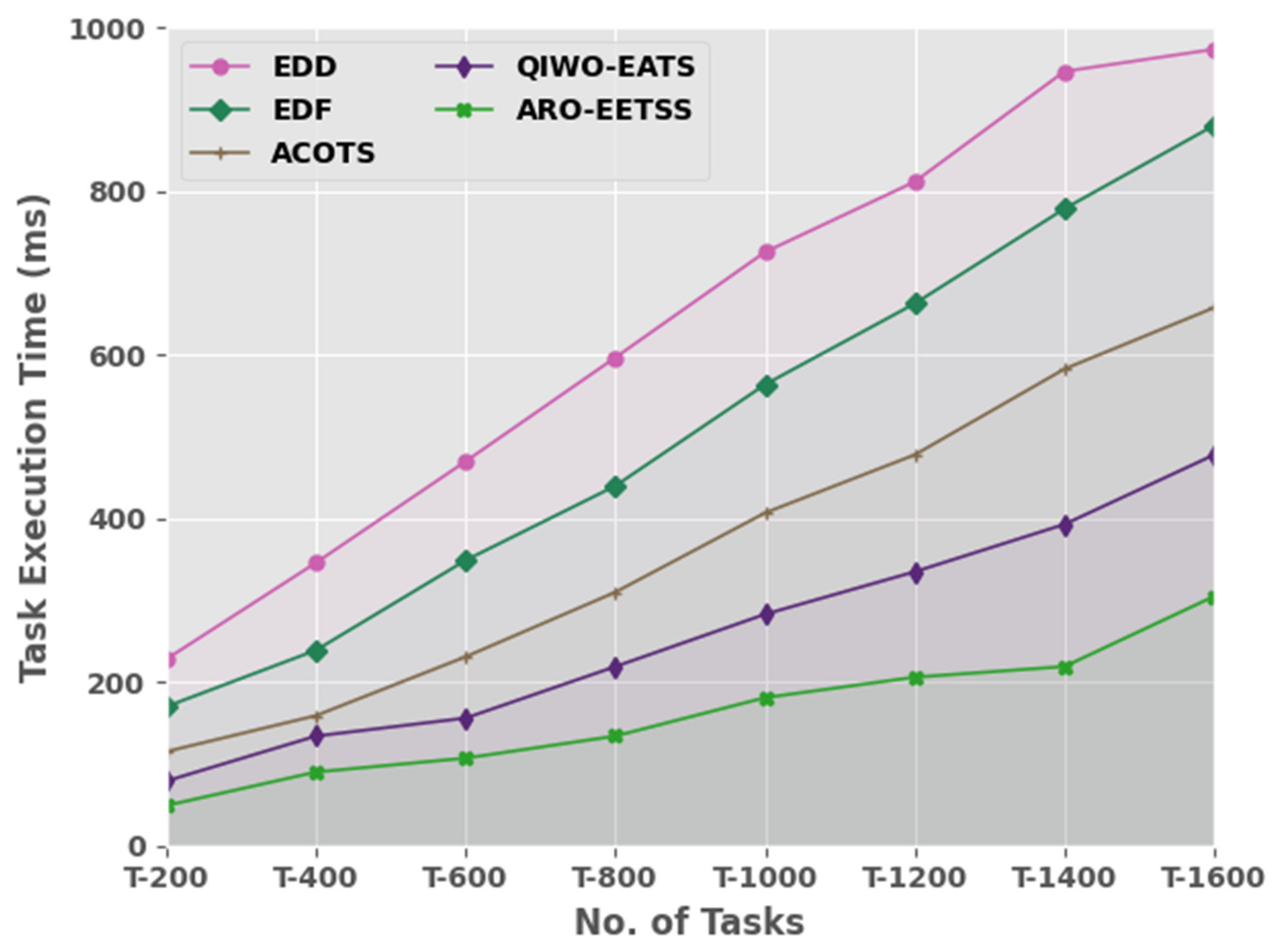
T-1600	974	881	658	478	305

and Figure 7 compare the TET inspection of the ARO-EETSS method with recent methods. The experimental values denoted by the ARO-EETSS approach reached the lowest TET values under all iterations. For example, on T-200 tasks, the ARO-EETSS technique displayed a minimal TET of 49 ms, whereas the EDD, EDF, ACOTS, and QIWO-EATS models demonstrated higher TETs of 228, 170, 115, and 79 ms, correspondingly. Further, on T-1000 tasks, the ARO-EETSS method showed a reduced TET of 181 ms but the EDD, EDF, ACOTS, and QIWO-EATS methods established increased TETs of 726, 564, 407, and 283 ms, correspondingly.

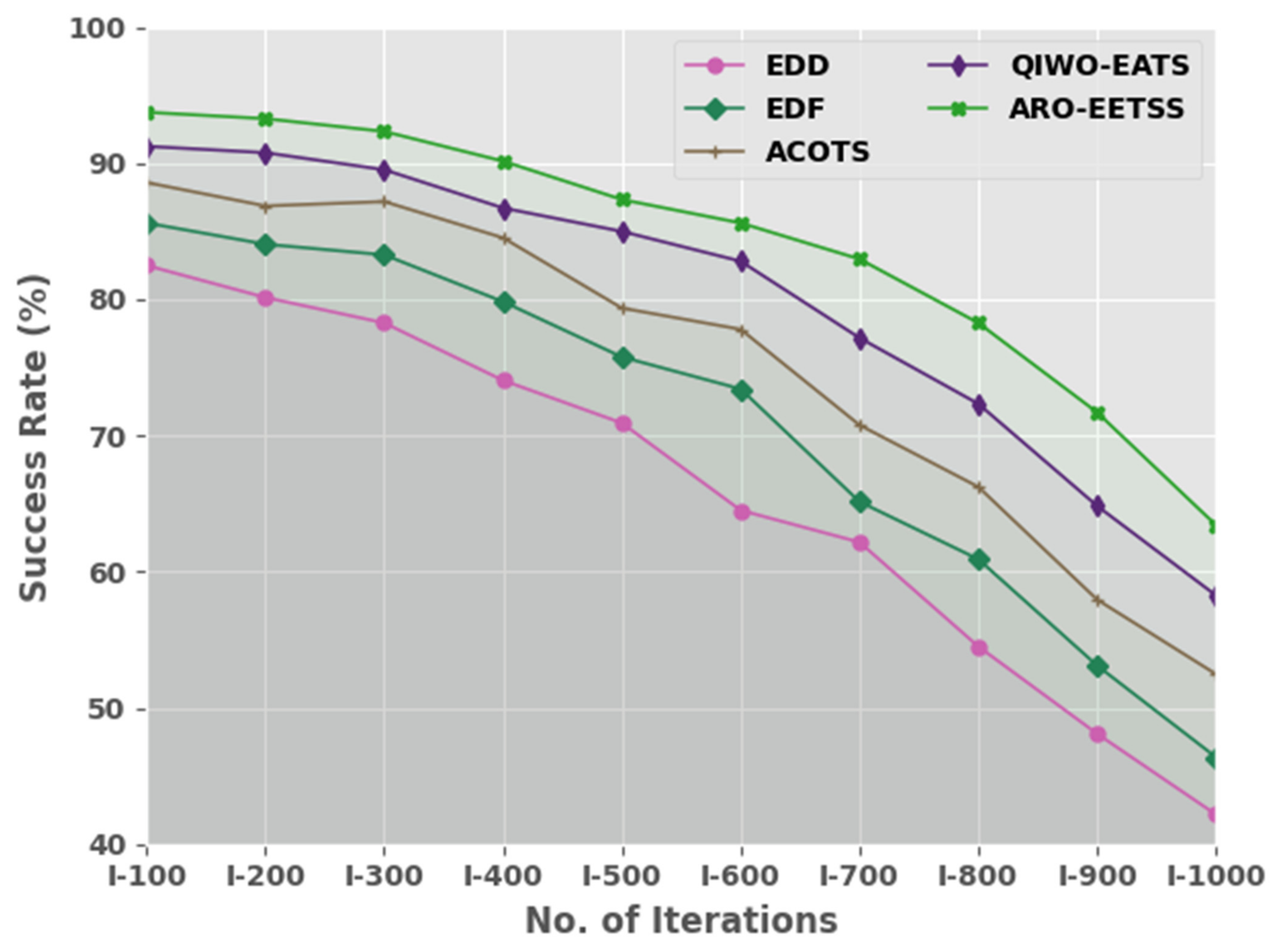
The success rate (SR) of the ARO-EETSS method against recent models is shown in

Table 6. SR analysis of ARO-EETSS system with recent algorithms in different iterations.

Success Rate (%)
No. of Iterations	EDD	EDF	ACOTS	QIWO-EATS	ARO-EETSS
I-100	82.48	85.60	88.57	91.23	93.73
I-200	80.13	84.04	86.85	90.76	93.26
I-300	78.26	83.26	87.17	89.51	92.32
I-400	74.04	79.82	84.51	86.70	90.14
I-500	70.91	75.76	79.35	84.98	87.32
I-600	64.50	73.41	77.79	82.79	85.60
I-700	62.16	65.13	70.76	77.16	82.95
I-800	54.50	60.91	66.22	72.32	78.26
I-900	48.09	53.10	57.94	64.82	71.69
I-1000	42.16	46.37	52.47	58.25	63.41

and Figure 8. The outcomes denoted that the ARO-EETSS approach obtained improved outcomes in every iteration. For example, on I-100 iterations, the ARO-EETSS method offered a maximum SR of 93.73%, where the EDD, EDF, ACOTS, and QIWO-EATS approaches showed maximum SRs of 82.48, 85.60, 88.57, and 91.23%, correspondingly.

Furthermore, on I-500 iterations, the ARO-EETSS method presented a maximum SR of 87.32%, whereas the EDD, EDF, ACOTS, and QIWO-EATS methods gave SRs of 70.91, 75.76, 79.35, and 84.98%, correspondingly. These results show that the presented method has enhanced performance over other existing methods.

5. Conclusions

In this article, a novel ARO-EETSS system was introduced for TS from the CPS environment. The presented ARO-EETSS system depends upon the existing natural practices of rabbits, encompassing detour foraging and random hiding. In the presented ARO-EETSS technique, the TS process was carried out via the allocation of $n$ autonomous tasks to $m$ dissimilar resources, and thus the entire task completion period was minimized and resources were totally exploited. To demonstrate the higher efficiency of the ARO-EETSS system, a sequence of experiments was performed. The comparison study underlined the higher performance of the ARO-EETSS technique with respect to several measures.

In future, the outcomes of ARO-EETSS system will be improved by the use of hybrid metaheuristic optimization algorithms. Furthermore, in future, data deduplication mechanisms can be designed to improve network efficiency. Though adequate discussions and assessments have already been made in this work, some future work is discussed here. Flexible and dynamic TS can improve the schedulability of the CPS environment by the use of statistical learning techniques for supervision and cloud computing facilities for adaptively managing resource reclamation. In addition, a scheduler that better matches the dual-period model also deserves to be explored. An accurate timing analysis will be utilized for the effective analysis of resource utilization. Moreover, a real-world case study would provide stronger support for the usability of the framework. To transform the proposed method into a real-world application, some details related to software development, kernel modification, and communication with the cloud need to be formalized in future.