Multi-Objective Optimization of Ultra-Low Energy Consumption Buildings in Severely Cold Regions Considering Life Cycle Performance
Abstract
1. Introduction
- The potential of XGBoost for building performance optimization design is explored by constructing a high-precision meta-model for optimization.
- A new building performance optimization strategy is proposed from the life cycle perspective to reduce the GWP, GC, and OE of the ULEB in severely cold regions.
- Sensitivity analysis is used to obtain variables with a significant impact on the target so that architects or engineers can pay more attention to them in the design phase.
2. Materials and Methods
2.1. Definition of Optimization Variables
2.2. Definition of Optimization Objectives
2.2.1. OE
2.2.2. GC
2.2.3. GWP
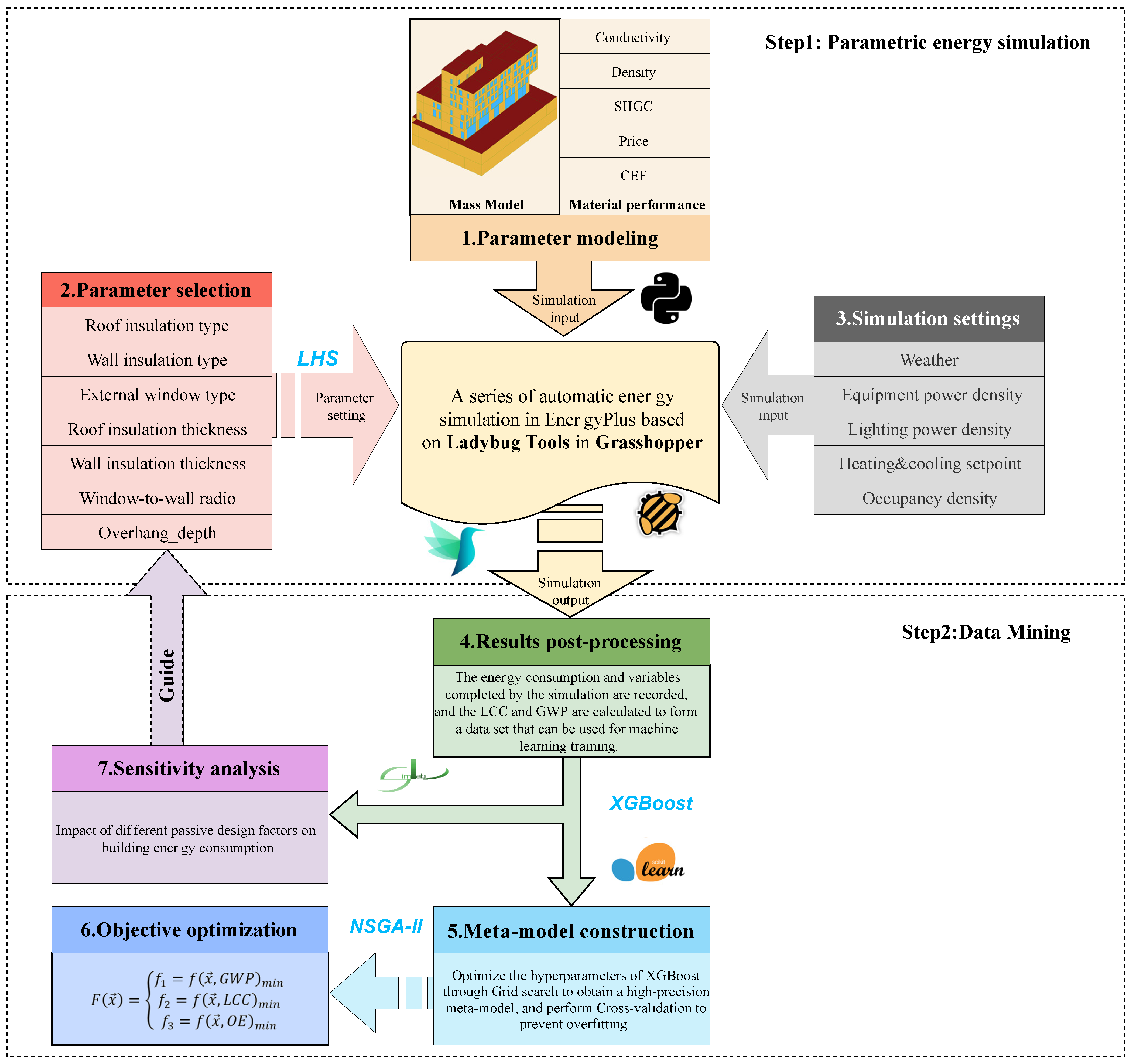
2.3. Optimization Procedure
2.3.1. Building Simulation
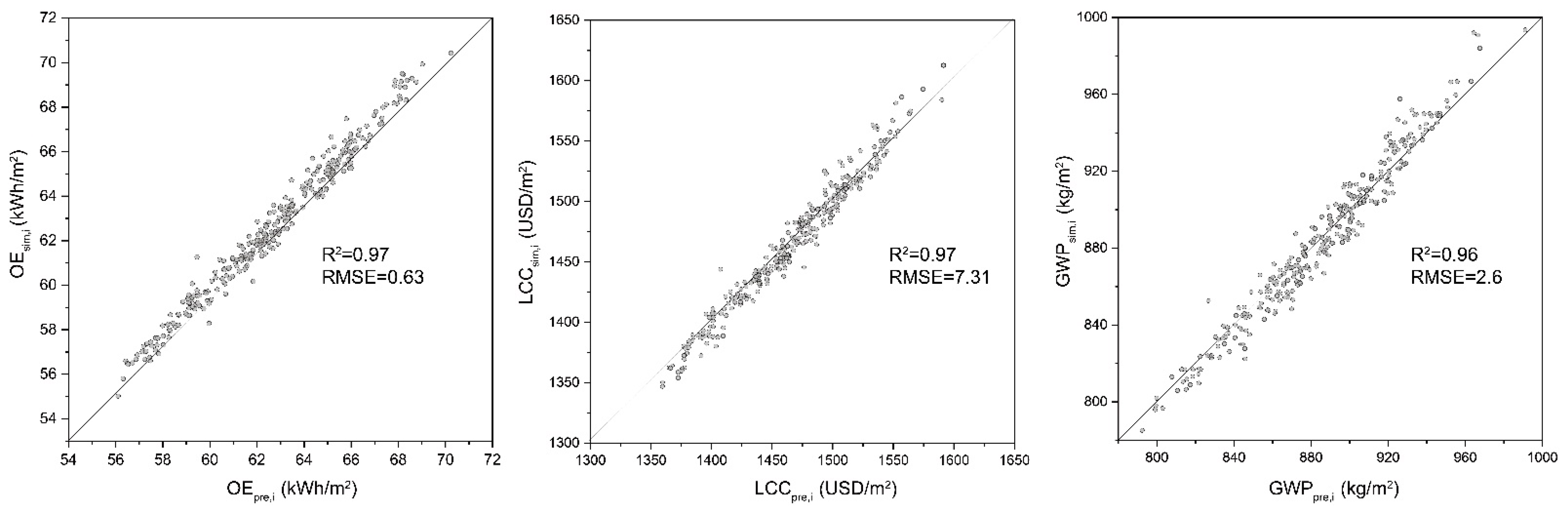
2.3.2. Meta-Model Construction
2.3.3. Objective Optimization
2.3.4. Sensitivity Analysis
3. The Base-Case Building Model
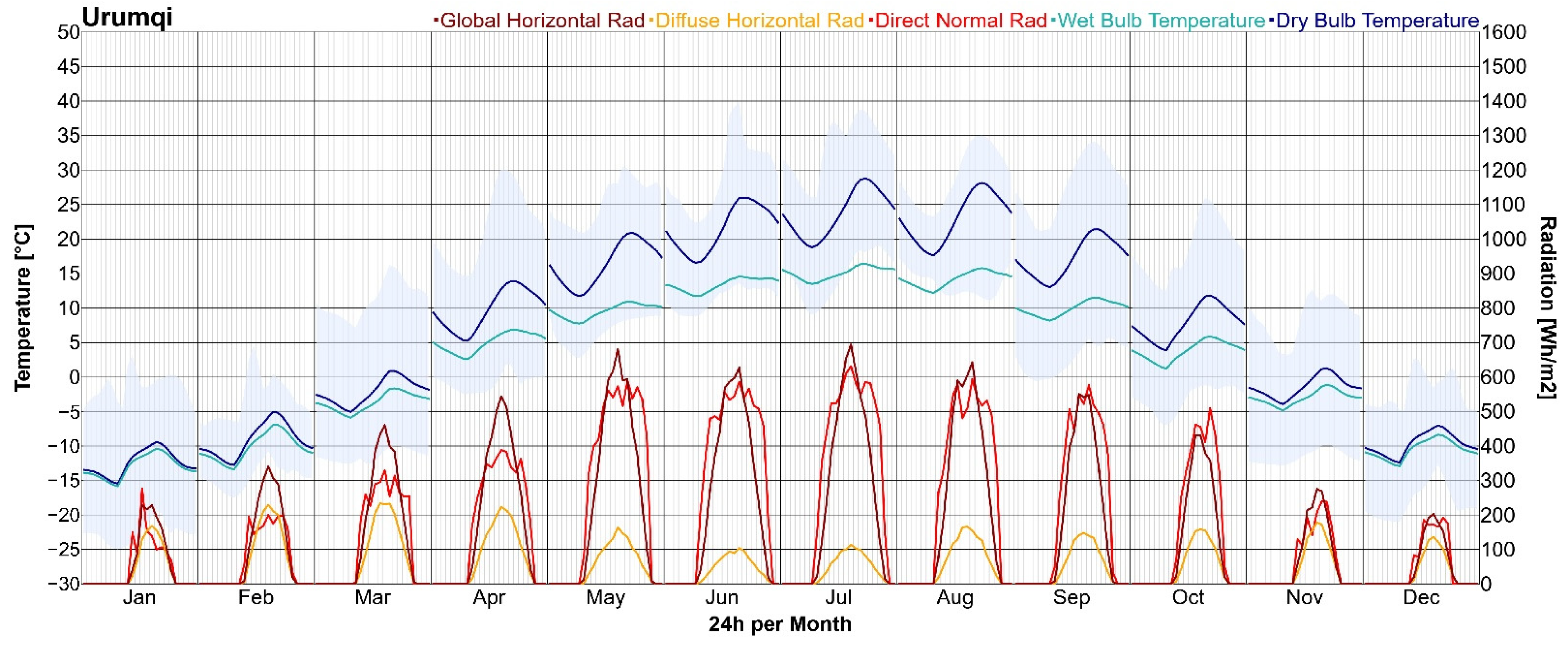
3.1. Weather Conditions
3.2. Building Modeling
4. Results
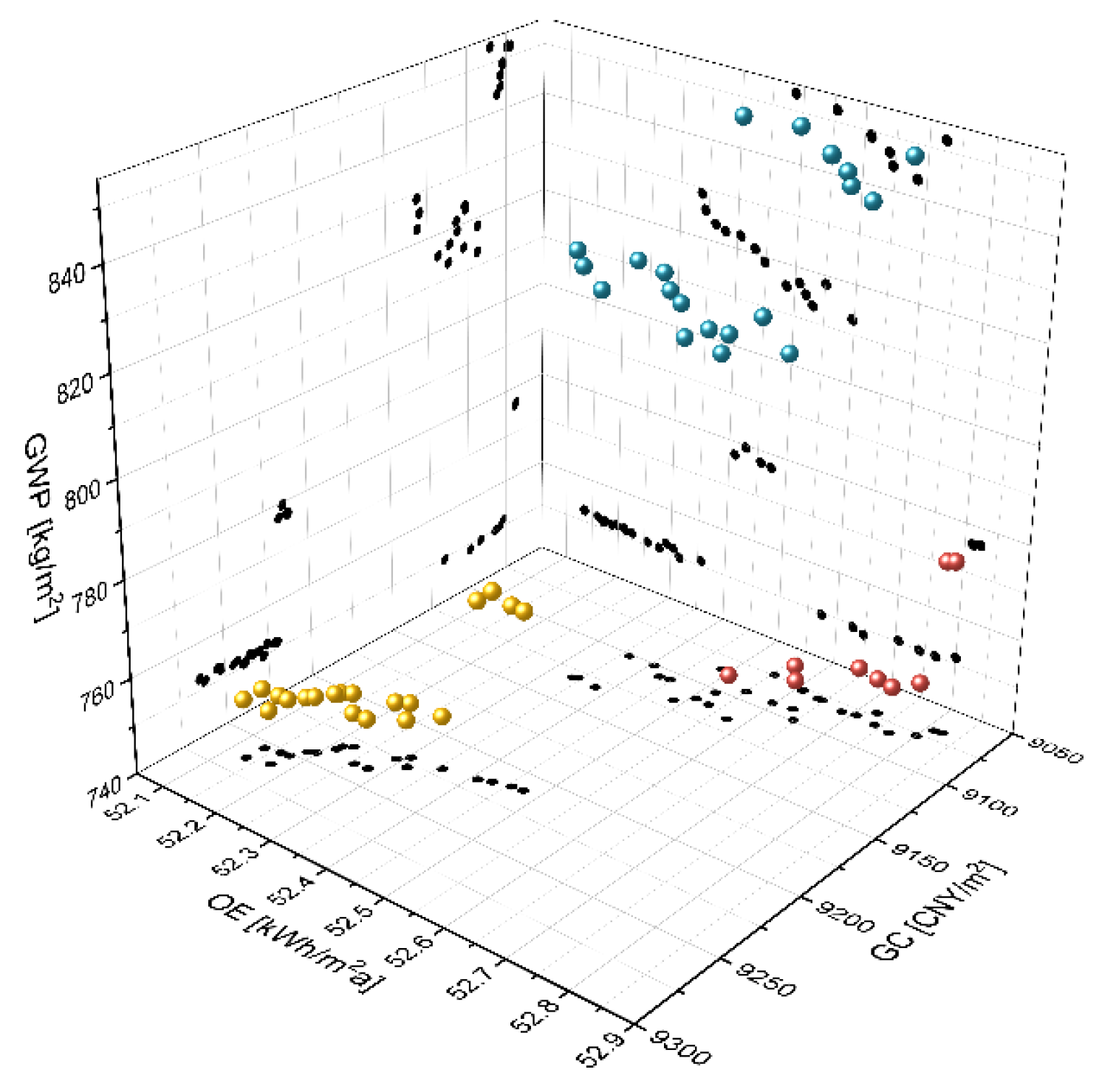
4.1. Analysis of Optimization Results
4.2. Comparison between the Optimal Solutions
5. Discussion
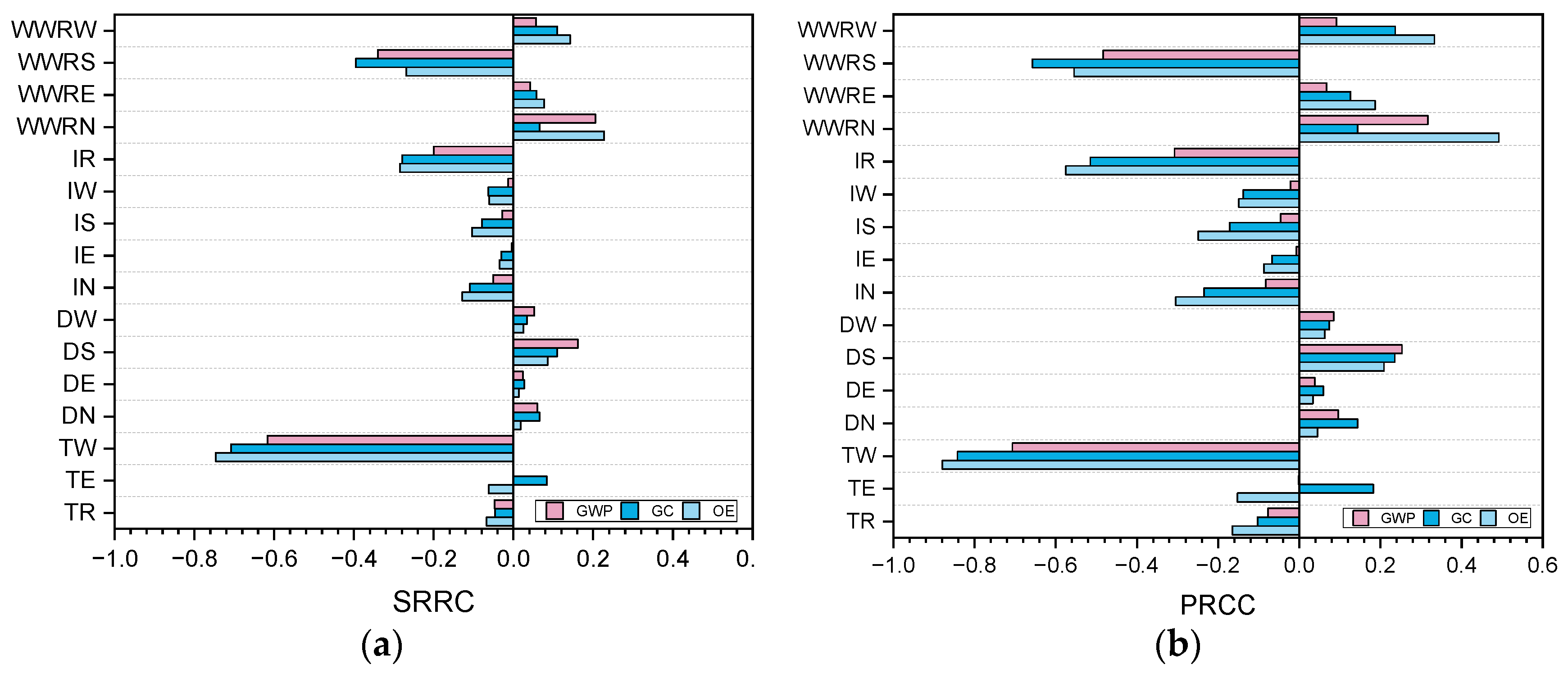
5.1. Analysis the Result of Sensitivity Analysis
5.2. The Limit and Future Research
6. Conclusions
- (1)
- The application of this framework still enhances the carbon reduction potential of ULEBs. The three optimization targets, GWP, GC, and OE, have a maximum increase of 12.7%, 6.7%, and 7.4%. Each optimal indicators generated during optimization are 748.6 kg/m2, 1295.5 USD/m2, and 4.2 kWh/m2, respectively.
- (2)
- After optimization, the most suitable types of roof insulation in severely cold areas are XPS and PU, and the types of external wall insulation are EPS, XPS, and PU. Insulation thickness on roofs and north walls should be adjusted to the maximum. The window type selection of Triple pane, Low-E, and argon is most beneficial to the life-cycle targets.
- (3)
- This study provides the optimal solution set and the range of values of geometric variables can provide a reference for designers. Firstly, the length of shading members: DN ≤ 0.1, 0.2 ≤ DE ≤ 0.6, 0.1 ≤ DS ≤ 0.2, 0.3 ≤ DW ≤ 0.4. For insulation thickness: 0.25 ≤ IN ≤ 0.33, 0.21 ≤ IE ≤ 0.30, 0.2 ≤ IS ≤ 0.27, 0.19 ≤ IW ≤ 0.32, 0.32 ≤ IR ≤ 0.33. For window wall area ratio: 0.18 ≤ WWRN ≤ 0.4, 0 ≤ WWRE ≤ 0.02, WWRS = 0.9, 0 ≤ WWRW ≤ 0.01.
- (4)
- Through sensitivity analysis, it can be seen that: for GWP, the top four sensitivities are: TW > WWRS > IR > WWRN; for GC, the top four sensitivities are: TW > WWRS > IR > WWRW; for OE, the top four sensitivities are: TW > IR > WWRS > WWRN.
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
References
- MOHURD. Technical Guidelines for Passive Ultra-Low Energy Green Buildings; Ministry of Housing and Urban-Rural Development of China: Beijing, China, 2015. (In Chinese) [Google Scholar]
- GB/T 51350-2019; Technical Standard for Nearly Zero Energy Buildings. Ministry of Housing and Urban-Rural Development of China: Beijing, China, 2019. (In Chinese)
- CABEE. 2021 China Building Energy Consumption and Carbon Emission Research Report: Assessment of Provincial Building Carbon Peak Situation. Available online: https://www.baogaoting.com/artical/10390 (accessed on 31 December 2021).
- Wang, X.; Guo, Z.; Zhang, Z.; Li, B.; Su, C.; Sun, L.; Wang, S. Game Analysis of the Evolution of Energy Structure Transition Considering Low-Carbon Sentiment of the Decision-Makers in the Context of Carbon Neutrality. Processes 2022, 10, 1650. [Google Scholar] [CrossRef]
- Resende, J.; Monzón-Chavarrías, M.; Corvacho, H. The applicability of nearly/net zero energy residential buildings in Brazil—A study of a low standard dwelling in three different Brazilian climate zones. Indoor Built Environ. 2020, 30, 1693–1713. [Google Scholar] [CrossRef]
- Walter Costa, J.F.; David Amorim, C.N.; Ribeiro Silva, J.C. Retrofit guidelines towards the achievement of net zero energy buildings for office buildings in Brasilia. J. Build. Eng. 2020, 32, 101680. [Google Scholar] [CrossRef]
- Aram, K.; Taherkhani, R.; Šimelytė, A. Multistage Optimization toward a Nearly Net Zero Energy Building Due to Climate Change. Energies 2022, 15, 983. [Google Scholar] [CrossRef]
- Eloranta, V.; Grönman, A.; Woszczek, A. Case Study and Feasibility Analysis of Multi-Objective Life Cycle Energy System Optimization in a Nordic Campus Building. Energies 2021, 14, 7742. [Google Scholar] [CrossRef]
- Tagliabue, L.C.; Di Giuda, G.M.; Villa, V.; De Angelis, E.; Ciribini, A.L.C. Techno-economical Analysis based on a Parametric Computational Evaluation for decision process on envelope technologies and configurations. Energy Build. 2018, 158, 736–749. [Google Scholar] [CrossRef]
- Lolli, N.; Lien, A.; Rønneseth, Ø. Cost Optimization of a Zero-Emission Office Building. Buildings 2020, 10, 222. [Google Scholar] [CrossRef]
- Jin, Y.; Wang, L.; Xiong, Y.; Cai, H.; Li, Y.H.; Zhang, W.J. Feasibility studies on net zero energy building for climate considering: A case of “All Green House” for Datong, Shanxi, China. Energy Build. 2014, 85, 155–164. [Google Scholar] [CrossRef]
- Ni, S.; Zhu, N.; Zhang, Z.; Hou, Y.; Li, S. The operational performance of net zero energy wooden structure building in the severe cold zone: A case study in Hailar of China. Energy Build. 2022, 257, 111788. [Google Scholar] [CrossRef]
- Pallis, P.; Gkonis, N.; Varvagiannis, E.; Braimakis, K.; Karellas, S.; Katsaros, M.; Vourliotis, P.; Sarafianos, D. Towards NZEB in Greece: A comparative study between cost optimality and energy efficiency for newly constructed residential buildings. Energy Build. 2019, 198, 115–137. [Google Scholar] [CrossRef]
- Rezaee, R.; Vakilinezhad, R.; Haymaker, J. Parametric framework for a feasibility study of zero-energy residential buildings for the design stage. J. Build. Eng. 2021, 35, 101960. [Google Scholar] [CrossRef]
- Abdou, N.; El Mghouchi, Y.; Hamdaoui, S.; El Asri, N.; Mouqallid, M. Multi-objective optimization of passive energy efficiency measures for net-zero energy building in Morocco. Build. Environ. 2021, 204, 108141. [Google Scholar] [CrossRef]
- Li, H.; Wang, S. New challenges for optimal design of nearly/net zero energy buildings under post-occupancy performance-based design standards and a risk-benefit based solution. Build. Simul. 2021, 15, 685–698. [Google Scholar] [CrossRef]
- Gupta, R.; Gregg, M. Assessing energy use and overheating risk in net zero energy dwellings in UK. Energy Build. 2018, 158, 897–905. [Google Scholar] [CrossRef]
- Feng, W.; Zhang, Q.; Ji, H.; Wang, R.; Zhou, N.; Ye, Q.; Hao, B.; Li, Y.; Luo, D.; Lau, S.S.Y. A review of net zero energy buildings in hot and humid climates: Experience learned from 34 case study buildings. Renew. Sustain. Energy Rev. 2019, 114, 109303. [Google Scholar] [CrossRef]
- CAOBEE. China Building Energy Consumption Annual Report 2020. J. Build. Energy Effic. 2021, 49, 1–6. [Google Scholar]
- GB 50189-2015; Design Standard for Energy Efficiency of Public Buildings. Ministry of Housing and Urban-Rural Development of China: Beijing, China, 2015. (In Chinese)
- Jiang, W.; Ju, Z.; Tian, H.; Liu, Y.; Arıcı, M.; Tang, X.; Li, Q.; Li, D.; Qi, H. Net-zero energy retrofit of rural house in severe cold region based on passive insulation and BAPV technology. J. Clean. Prod. 2022, 360, 132198. [Google Scholar] [CrossRef]
- Zhou, Z.; Anwar, G.A.; Dong, Y. Performance-Based Bi-Objective Retrofit Optimization of Building Portfolios Considering Uncertainties and Environmental Impacts. Buildings 2022, 12, 85. [Google Scholar] [CrossRef]
- Wang, M.; Cao, S.; Chen, D.; Ji, G.; Ma, Q.; Ren, Y. Research on Design Framework of Middle School Teaching Building Based on Performance Optimization and Prediction in the Scheme Design Stage. Buildings 2022, 12, 1897. [Google Scholar] [CrossRef]
- Chaturvedi, S.; Rajasekar, E.; Natarajan, S. Multi-objective Building Design Optimization under Operational Uncertainties Using the NSGA II Algorithm. Buildings 2020, 10, 88. [Google Scholar] [CrossRef]
- GB 50176-2016; Code for Thermal Design of Civil Building. Ministry of Housing and Urban-Rural Development of China: Beijing, China, 2016. (In Chinese)
- Yu, H.; Yang, W.; Li, Q.; Li, J. Optimizing Buildings’ Life Cycle Performance While Allowing Diversity in the Early Design Stage. Sustainability 2022, 14, 8316. [Google Scholar] [CrossRef]
- Longo, S.; Montana, F.; Riva Sanseverino, E. A review on optimization and cost-optimal methodologies in low-energy buildings design and environmental considerations. Sustain. Cities Soc. 2019, 45, 87–104. [Google Scholar] [CrossRef]
- Zhang, H.; Hewage, K.; Prabatha, T.; Sadiq, R. Life cycle thinking-based energy retrofits evaluation framework for Canadian residences: A Pareto optimization approach. Build. Environ. 2021, 204, 108115. [Google Scholar] [CrossRef]
- GB/T 2589-2020; General Principles of Comprehensive Energy Consumption Calculation. State Administration for Market Regulation: Beijing, China, 2020. (In Chinese)
- GB/T 51366-2019; Building Carbon Emission Calculation Standard. Ministry of Housing and Urban-Rural Development of China: Beijing, China, 2019. (In Chinese)
- Xue, Y.; Liu, W. A Study on Parametric Design Method for Optimization of Daylight in Commercial Building’s Atrium in Cold Regions. Sustainability 2022, 14, 7667. [Google Scholar] [CrossRef]
- Zhang, T.; Hu, Q.; Ding, Q.; Zhou, D.; Gao, W.; Fukuda, H. Towards a Rural Revitalization Strategy for the Courtyard Layout of Vernacular Dwellings Based on Regional Adaptability and Outdoor Thermal Performance in the Gully Regions of the Loess Plateau, China. Sustainability 2021, 13, 13074. [Google Scholar] [CrossRef]
- Besbas, S.; Nocera, F.; Zemmouri, N.; Khadraoui, M.A.; Besbas, A. Parametric-Based Multi-Objective Optimization Workflow: Daylight and Energy Performance Study of Hospital Building in Algeria. Sustainability 2022, 14, 12652. [Google Scholar] [CrossRef]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code. Technometrics 1979, 21, 239–245. [Google Scholar] [CrossRef]
- Tian, W. A review of sensitivity analysis methods in building energy analysis. Renew. Sustain. Energy Rev. 2013, 20, 411–419. [Google Scholar] [CrossRef]
- GB 55015-2021; General Code for Energy Efficiency and Renewable Energy Application in Buildings. Ministry of Housing and Urban-Rural Development of China: Beijing, China, 2022. (In Chinese)
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Alshboul, O.; Shehadeh, A.; Almasabha, G.; Almuflih, A.S. Extreme Gradient Boosting-Based Machine Learning Approach for Green Building Cost Prediction. Sustainability 2022, 14, 6651. [Google Scholar] [CrossRef]
- Ding, Z.; Wang, Z.; Hu, T.; Wang, H. A Comprehensive Study on Integrating Clustering with Regression for Short-Term Forecasting of Building Energy Consumption: Case Study of a Green Building. Buildings 2022, 12, 1701. [Google Scholar] [CrossRef]
- Mohammadiziazi, R.; Bilec, M. Application of Machine Learning for Predicting Building Energy Use at Different Temporal and Spatial Resolution under Climate Change in USA. Buildings 2020, 10, 139. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Ghaderian, M.; Veysi, F. Multi-objective optimization of energy efficiency and thermal comfort in an existing office building using NSGA-II with fitness approximation: A case study. J. Build. Eng. 2021, 41, 102440. [Google Scholar] [CrossRef]
- Si, B.; Wang, J.; Yao, X.; Shi, X.; Jin, X.; Zhou, X. Multi-objective optimization design of a complex building based on an artificial neural network and performance evaluation of algorithms. Adv. Eng. Inform. 2019, 40, 93–109. [Google Scholar] [CrossRef]
- Harkouss, F.; Fardoun, F.; Biwole, P.H. Multi-objective optimization methodology for net zero energy buildings. J. Build. Eng. 2018, 16, 57–71. [Google Scholar] [CrossRef]
- China Meteorological Bureau; Climate Data Office And Tsinghua University; Department of Building Science And Technology. China Standard Weather Data for Analyzing Building Thermal Conditions; China Architecture & Building Press: Beijing, China, 2005. [Google Scholar]
- Ganjehkaviri, A.; Mohd Jaafar, M.N.; Hosseini, S.E.; Barzegaravval, H. Genetic algorithm for optimization of energy systems: Solution uniqueness, accuracy, Pareto convergence and dimension reduction. Energy 2017, 119, 167–177. [Google Scholar] [CrossRef]
- Alghamdi, S.; Tang, W.; Kanjanabootra, S.; Alterman, D. Effect of Architectural Building Design Parameters on Thermal Comfort and Energy Consumption in Higher Education Buildings. Buildings 2022, 12, 329. [Google Scholar] [CrossRef]
- Jiang, W.; Liu, B.; Zhang, X.; Zhang, T.; Li, D.; Ma, L. Energy performance of window with PCM frame. Sustain. Energy Technol. Assess. 2021, 45, 101109. [Google Scholar] [CrossRef]
- Wu, W.; Skye, H.M.; Domanski, P.A. Selecting HVAC systems to achieve comfortable and cost-effective residential net-zero energy buildings. Appl. Energy 2018, 212, 577–591. [Google Scholar] [CrossRef]
- Sun, Y. Sensitivity analysis of macro-parameters in the system design of net zero energy building. Energy Build. 2015, 86, 464–477. [Google Scholar] [CrossRef]

| Categories | Names | Transmittance [W/(m2·K)] | Specific Heat Capacity [J/kg·K] |
|---|---|---|---|
| Insulation | RW EPS XPS PU | 0.044 0.037 0.030 0.024 | 1220 1380 1380 1380 |
| Categories | Names | Conductivity [W/(m·K)] | SHGC |
| Window | Double pane Double pane, low-e Double pane, low-e, argon Triple pane, low-e Triple pane, low-e, argon | 2.3 1.8 1.5 1.0 0.8 | 0.7 0.62 0.62 0.57 0.57 |
| No. | Categories | Symbol | Unit | Range |
|---|---|---|---|---|
| 1 | Roof insulation type | TR | / | [0–3] |
| 2 | Exterior Wall insulation type | TE | / | [0–5] |
| 3 | Window type | TW | / | [0–5] |
| 4 | Roof insulation thickness | IR | m | [0:0.33] |
| 5 | Insulation thickness of the north wall | IN | m | [0:0.33] |
| 6 | Insulation thickness of the east wall | IE | m | [0:0.33] |
| 7 | Insulation thickness of the south wall | IS | m | [0:0.33] |
| 8 | Insulation thickness of the west wall | IW | m | [0:0.33] |
| 9 | Window-to-wall radio of north wall | WWRN | / | [0:0.9] |
| 10 | Window-to-wall radio of east wall | WWRE | / | [0:0.9] |
| 11 | Window-to-wall radio of south wall | WWRS | / | [0:0.9] |
| 12 | Window-to-wall radio of west wall | WWRW | / | [0:0.9] |
| 13 | Horizontal overhang depth in north | DN | m | [0:1.5] |
| 14 | Vertical fin depth in the east | DE | m | [0:1.5] |
| 15 | Horizontal overhang depth in the south | DS | m | [0:1.5] |
| 16 | Vertical fin depth in the west | DW | m | [0:1.5] |
| Categories | Names | No. | Cost | CEF |
|---|---|---|---|---|
| Insulation | RW EPS XPS PU | 0 | 48.6 USD/m3 | 2.4 kgCO2/kg |
| 1 | 60 USD/m3 | 5.7 kgCO2/kg | ||
| 2 | 74.3 USD/m3 | 20.1 kgCO2/kg | ||
| 3 | 150 USD/m3 | 5.1 kgCO2/kg | ||
| Window | Double pane Double pane, Low-E Double pane, Low-E, argon Triple pane, Low-E Triple pane, Low-E, argon | 0 | 48.6 USD/m2 | 92 kgCO2/m2 |
| 1 | 61.4 USD/m2 | 101 kgCO2/m2 | ||
| 2 | 88.6 USD/m2 | 130 kgCO2/m2 | ||
| 3 | 105.7 USD/m2 | 141 kgCO2/m2 | ||
| 4 | 118.6 USD/m2 | 150 kgCO2/m2 | ||
| Overhang | \ | \ | 11.4 USD/m2 | 110 kgCO2/m2 |
| Categories | Names | No. | Cost | CEF |
| Energy | Gas | \ | 0.064 USD/kg | 2.62 kg/m3 |
| Electricity | \ | 0.069 USD/kWh | 0.61 kg/kWh |
| N_Estimators | Max_Depth | Learning_Rate | Gamma | Subsample | R2 |
|---|---|---|---|---|---|
| 700 | 3 | 0.05 | 0.0 | 0.7 | 0.967 |
| Component | Construction Practices | Conductivity |
|---|---|---|
| Roof | 100 mm Reinforced concrete + 300 mm XPS board | 0.1 |
| Exterior wall | 200 mm Aerated concrete blocks + 300 mm EPS board | 0.15 |
| Interior wall | 200 mm Aerated concrete blocks | 1.056 |
| Exterior floor | 100 mm Reinforced concrete + 300 mm EPS board | 0.1 |
| Interior wall | 100 mm Reinforced concrete + 250 mm glass wool heat insulating material | 0.1 |
| Window | 5 + 6A + 5+7A + 5low-E | 0.8 |
| Item | Value |
|---|---|
| Location | Chongqing, China (106.44 °E, 29.49 °N) |
| Orientation | South |
| Solar distribution | Full interior and exterior (with reflections) |
| Occupancy density | 0.125 m2/person |
| Lighting power density | 9 W/m2 |
| Electric equipment power density | 15 W/m2 |
| Heating setpoint | 18 °C |
| Cooling setpoint | 26 °C |
| Infiltration | 0.0006 m3/s per m2 façade |
| Minimum ventilation | 0.0083 m3/h· person |
| Natural ventilation |  |
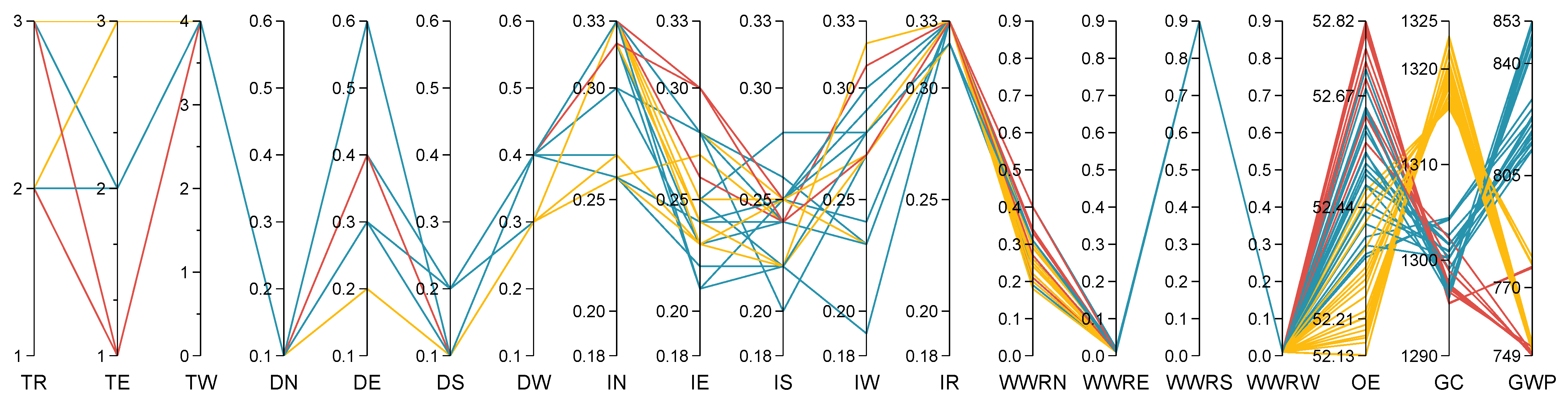
| Categories | UP-OPTIMAL | GWP-OPTIMAL | GC-OPTIMAL | OE-OPTIMAL |
|---|---|---|---|---|
| TR | PU | PU | XPS | PU |
| TE | EPS | EPS | EPS | PU |
| TW | Triple pane, Low-E, argon | Triple pane, Low-E, argon | Triple pane, Low-E, argon | Triple pane, Low-E, argon |
| DN | 0.1 | 0.1 | 0.1 | 0.1 |
| DE | 0.4 | 0.2 | 0.4 | 0.3 |
| DS | 0.1 | 0.1 | 0.1 | 0.1 |
| DW | 0.4 | 0.3 | 0.4 | 0.4 |
| IN | 0.32 | 0.33 | 0.33 | 0.33 |
| IE | 0.3 | 0.24 | 0.3 | 0.28 |
| IS | 0.24 | 0.25 | 0.25 | 0.25 |
| IW | 0.27 | 0.27 | 0.27 | 0.27 |
| IR | 0.33 | 0.33 | 0.33 | 0.33 |
| WWRN | 0.27 | 0.25 | 0.34 | 0.18 |
| WWRE | 0.01 | 0.01 | 0.01 | 0.01 |
| WWRS | 0.9 | 0.9 | 0.9 | 0.9 |
| WWRW | 0.01 | 0.01 | 0.01 | 0.01 |
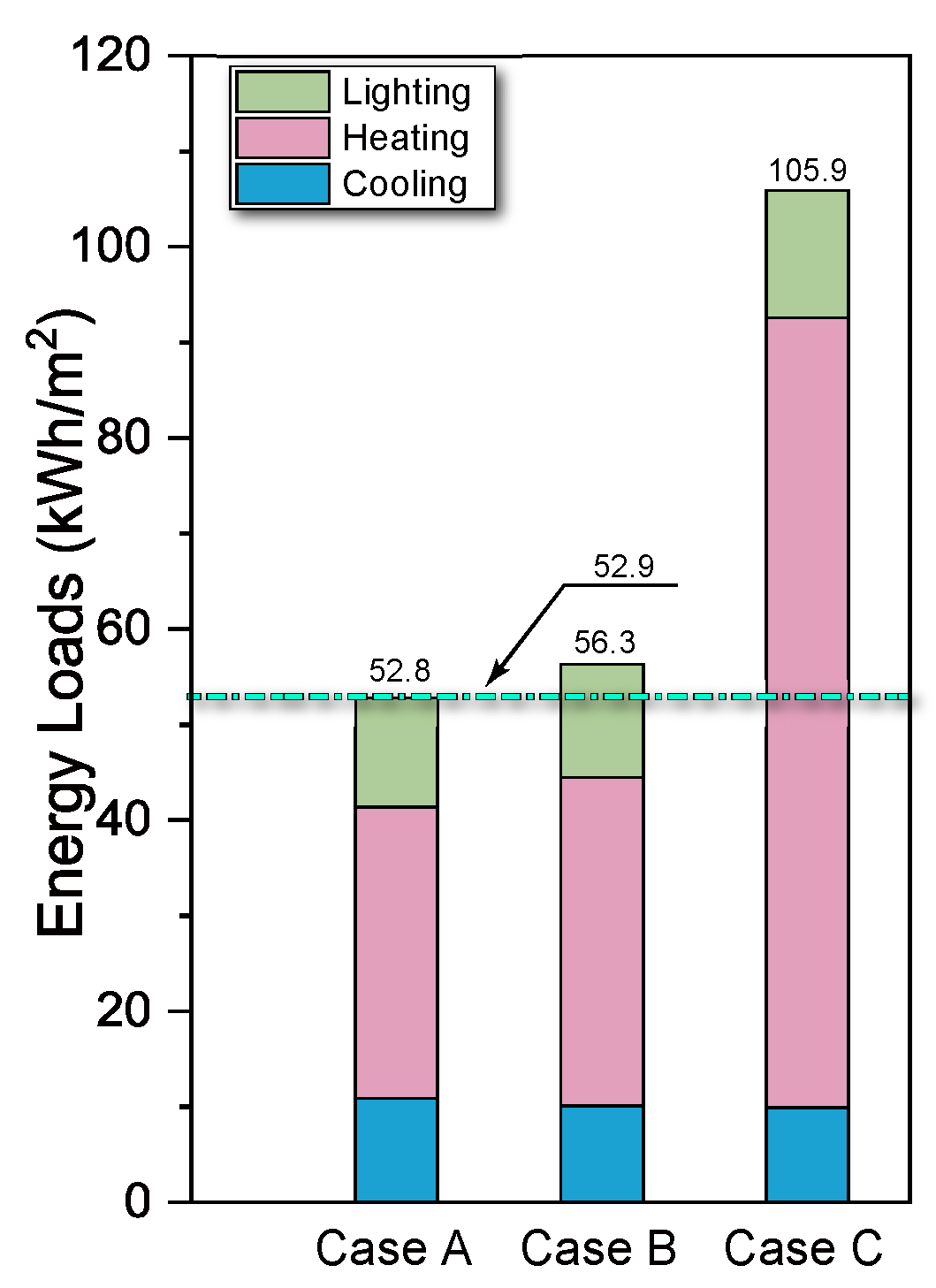
| OE | 52.6 | 52.7 | 52.8 | 52.1 |
| GC | 1298.9 | 1300.0 | 1295.4 | 1323.4 |
| GWP | 749.5 | 748.6 | 776.5 | 752.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Wang, W.; Song, J.; Wang, Z.; Wang, W. Multi-Objective Optimization of Ultra-Low Energy Consumption Buildings in Severely Cold Regions Considering Life Cycle Performance. Sustainability 2022, 14, 16440. https://doi.org/10.3390/su142416440
Zhang Z, Wang W, Song J, Wang Z, Wang W. Multi-Objective Optimization of Ultra-Low Energy Consumption Buildings in Severely Cold Regions Considering Life Cycle Performance. Sustainability. 2022; 14(24):16440. https://doi.org/10.3390/su142416440
Chicago/Turabian StyleZhang, Zihan, Wanjiang Wang, Junkang Song, Zhe Wang, and Weiyi Wang. 2022. "Multi-Objective Optimization of Ultra-Low Energy Consumption Buildings in Severely Cold Regions Considering Life Cycle Performance" Sustainability 14, no. 24: 16440. https://doi.org/10.3390/su142416440
APA StyleZhang, Z., Wang, W., Song, J., Wang, Z., & Wang, W. (2022). Multi-Objective Optimization of Ultra-Low Energy Consumption Buildings in Severely Cold Regions Considering Life Cycle Performance. Sustainability, 14(24), 16440. https://doi.org/10.3390/su142416440





