Compensation of Distributed Generations Outage Using Controlled Switched Capacitors

Abstract

Researchers recently came up with innovative ways to generate enough electricity to meet the rising demand through establishing an electricity distribution system and enhancing power quality on the customer side. One of these innovative ways is the installation of distributed generation (DG). DG is widely used in modern networks due to its great benefits of improving the voltage profile and the system’s power quality. Additionally, DGs are ideally placed near the end user in distribution systems to improve the system’s performance while minimizing power losses and enhancing voltage profile in the grid. DG recently grew in importance, and its penetration increased in most distribution systems. Due to the spreading of DG in the power system, the dynamic performance of the system is affected. This paper studies the system’s performance and behavior under condition of DG outage from the system. The model of DGs in this study assumes two cases of the power provided to the network; the first case considered DG units injecting active power only to the grid (unity power factor). In the second case, DG injects both active and reactive power to the system. After that, outage of DG units is fixed by injecting a reactive power source using a capacitor with a controlled switch to compensate the outage of DGs from the distribution system and to reduce the outage’s negative effect on the network. The sizing of capacitors is optimized using a harmony search algorithm (HSA) in the same location of the DG units.

1. Introduction

With the initiation of employing distributed generation (DG) technologies, the need for using transmission systems decreased. This is due to the availability of generated power at the distribution level with a satisfactory amount to supply the end user. Furthermore, since most of this power is generated from renewable resources, DG can have a lower environmental impact [1]. This renewable energy-based DGs can be installed as small power plants directly near loads, or can be built on the rooftops of some buildings, unlike conventional stations that should be installed in large capacities and have allocation restrictions. However, installing DGs in the power system caused some changes in the power flow to customers, where the customer can receive power from two sources: the utility and DG units. That is why DGs must be wisely allocated in the distribution system, as well as why the proper size must be chosen. Proper sizing and siting of DGs can improve the system’s performance by improving power quality, voltage profile, reliability, and minimizing power losses [2,3,4]. They can also be easily installed near customers because they emit no pollution, take less time to build, and are noiseless [4,5,6]. This ideality will cause a revolution and open new avenues for research into the behavior of the power system after the addition of DGs on the customer side. Several researchers investigated the size and placement of DGs in distribution systems, as well as their impact on the grid (voltage profile, reliability, and power losses) [4]. They also investigated the impact on the system’s security [7]. The concept of generating electricity is not limited to centralized plants; it can also be produced on the customer side and injected directly into the distribution system to loads without the need for a transmission system; this is an economical method because it does not require expanding the transmission system to generate more power on the distribution side.

Until now, there was no agreed-upon definition of DG or distributed energy resource (DER). Some researchers believe that the DG generates electrical power at or near the site while it is in use. Furthermore, DG is linked to the utility distribution system medium voltage and low voltage (MV and LV) on a scale ranging from few KWs up to 20 MW. Furthermore, several researchers [8,9,10,11] regarded DG as an essential source of electric power from renewable or sustainable resources, such as wind, solar, or water resources. Because of its proximity to customers, it must not emit or make noise to avoid significant environmental impacts. While conventional power plants have a huge negative impact on the environment, they should be installed in a remote area from the end user. Furthermore, due to the massive size of wind turbines, some types may produce some noise, which is unacceptable in a populated area. Additionally, some suggested using a small wind turbine to reduce noise [12]. Most DG types are typically linked via inverters to provide either active power or both active and reactive power. Using a lower power electronics element and inverter size as a wind turbine (typically DFIG) reduces costs. Other types of DGs are directly connected to the grid as combined heat and power (CHP) units, which can be considered as co-generation units because they generate both electrical power and heat. This type has a low environmental impact because the exhaust gases from the generator can be used for heating [1].

Many researchers investigated the effects of DG units on the distribution system. DG has both positive and negative effects on system performance, voltage profile, losses (active and reactive power), and protective devices [13,14].

The effect of DG on system performance is determined by the position and size of DG units. The energy produced close to the loads makes installing PV-DG units near the customer very appealing to utilities and consumers [15]. The primary goals [2] of installing DG near customers are:

• Reducing the transmission line losses;
• Improving the voltage profile on the system;
• Reducing the emission from centralized plant;
• Low operating cost due to peak shaving;
• Reduced or deferred investment in generation, transmission, transformers, and distribution infrastructure upgraded due to relieved transmission and distribution congestion [3].

The main contribution of this paper is studying the effect of the gradual outage of DGs in a power system under different loading conditions, and different modes of operation of DGs (unity power factor, or DGs supplying active and reactive power), as well as investigating the effect of adding capacitors with controlled switches (CSCs), for compensation of DGs outage, under different loading conditions and modes of operation.

Unlike previous research studies related to the size and site of DGs, this research is focused on enhancing the performance of the electric power system after DG outage.

2. Simulation Scenarios

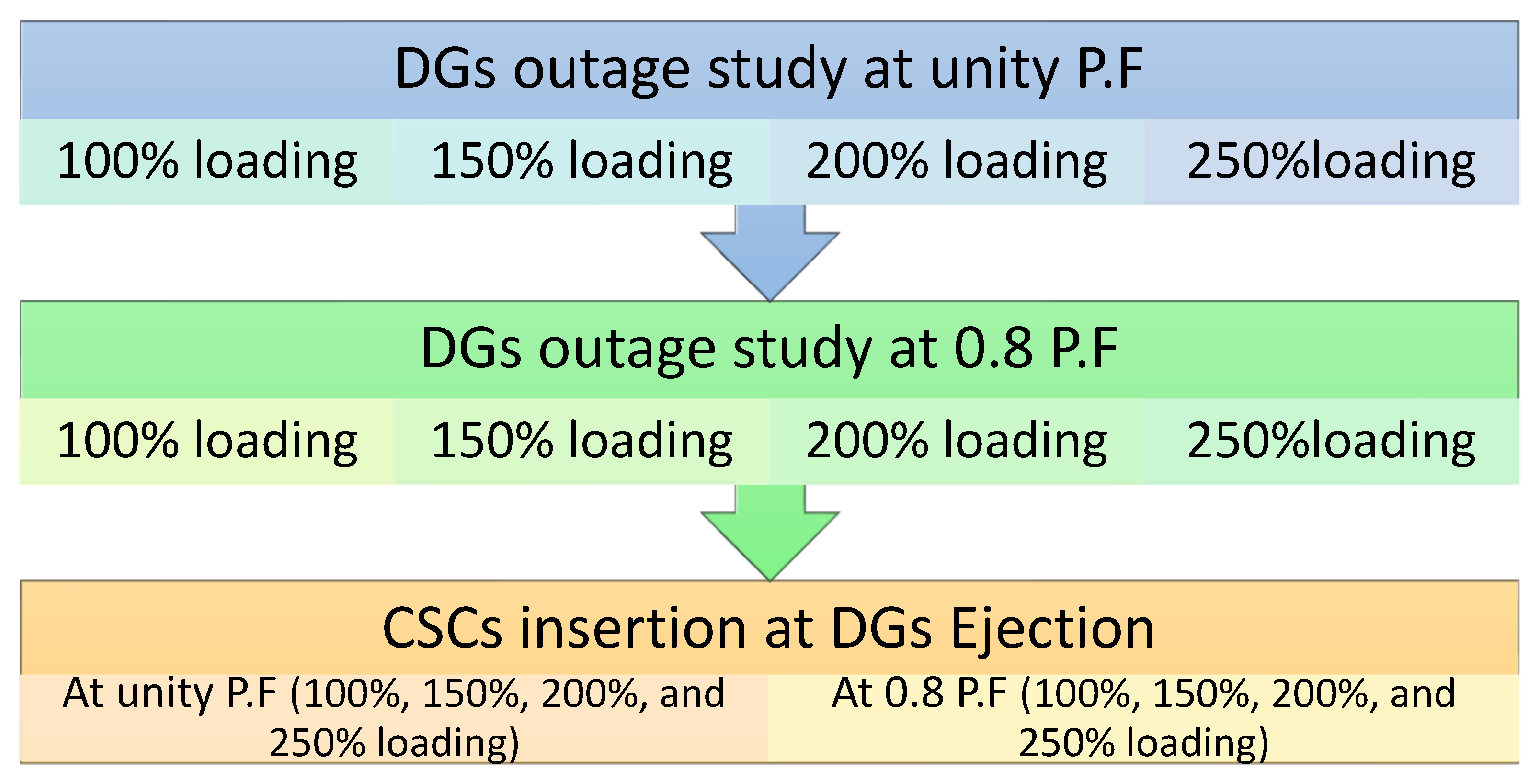
The different simulation scenarios are depicted in Figure 1. The simulation starts with studying the gradual DG outage effects on the system then studying the recovery of the system by adding optimized switched capacitor. As seen in Figure 1, the DG outages are carried out at different power factors, being the first study at unity power factor, while the second study is when DGs are supplying active and reactive powers at 0.8 power factor. Furthermore, the third study considered the insertion of an optimized switched capacitor as a cure for DG outage for different levels of DG ejection. In this paper, different levels of DG ejection are considered (25%, 50%, and 75% of DG output power is ejected/off). The optimized switched capacitor injection is conducted for both power factor cases (unity and 0.8 P.F). It should be noted that for each power factor case, the system is studied under different loading conditions. The loading condition is increased in steps from 100% of the nominal system loading to 250%, in steps of 50%.

For each of the above-mentioned studies, the voltage profile, as well as active and reactive power losses are recorded to assess the power system performance.

3. System Modeling

3.1. IEEE 33-Bus System

In this paper, the IEEE-33 bus system is used to test the system’s performance by gradual ejection of DGs. This system is widely used in the sizing and placement of DG units [16,17]. The 33-bus distribution system provided a primary distribution system via overhead transmission lines with a voltage of 11 kV and a total load of 2000 kVA (3581 kW and 1745 kVAr).

3.2. Backward/Forward Sweep Method

The backward/forward sweep method is a load flow method that can be used to iteratively calculate the real and reactive power at each branch and the voltage at each bus using two sets of repetitive equations. The first step backward direction is used to find the power flows to the system from the system’s last branch until it reaches the source node. The second step equations set is used to obtain the voltage and angle for each bus node in the forward direction starting from the source node and ending at the last node. Forward sweep is used to calculate the voltage drop for each bus node from the source node to the last bus; the main feeder voltage was set to its actual value. During the forward sweep, the effective power in each branch is held constant to the value obtained from the backward sweep calculations. While the backward sweep function is to calculate the power flow in the reverse direction from the last branch to the source feeder, the power flow is calculated using the previous voltage node iteration, which is conducted in forward sweep [18].

3.3. Type of DG Used in This Work

PV panels, micro gas turbines, and micro wind turbines are examples of DGs with a unity power factor. All types are assumed to be connected to the grid via inverters, which only supply active power. In steady state, the PV-DG is regarded as a negative load connected to the system buses. In the case of an inverter system, this PV-DG model injects reactive power into the grid where the inverter can produce both active and reactive powers to improve the power quality and enhance the voltage profile of the power system. This type of inverter-based DG is shown in Figure 2.

Several researchers are studying the impact of PV-DG on the distribution system in steady-state and transient cases to study any voltage and power fluctuations that occur in this generator [19,20,21].

In this study, DGs are implemented in the IEEE 33-bus system to observe the insertion effect on the system’s performance, then these DGs are gradually ejected (25%, 50%, and 75% of DG size) and more observations are recorded. The methodology used for ejecting DGs is based on many possible trials of DG outages and selecting the worst case in each situation. When ejecting these DGs from the system, the DG outage is clearly affecting the voltage profile and the system losses. In the first case, the system is operating without DGs, and then, full rated DG units are injected. The implemented size of DG units is calculated for the standard 33-bus system from previous studies. The following step is to eject 25% of DGs and allow 75% of the DGs in operation. In the second case, 50% of the DGs are ejected and 50% of the DGs continue to operate. In the last case, 75% of the DGs are ejected and only 25% of the DGs are in operation. These three cases are simulated under 100%, 150%, 200%, and 250% of the normal load.

3.4. Harmony Search Algorithm (HSA)

Geem Z.W. and others published the first harmony search algorithm in 2001 [22,23]. This method was developed to find the best water distribution network solution. It recently became popular in mechanical engineering, electrical engineering, and other fields. In contrast to most emerging nature-inspired computing NIC algorithms, the inspiration for HSA is not a natural phenomenon, such as a bird swarm, column ants, coco search, and so on. However, the musical process is conceived to seek the perfect state of harmony within the constraints of aesthetic standards. When creating a new harmony or performing a musical recital, the musician tries many different combinations of the music in their head or memory to find the best harmony. Finding the optimal results or solution to engineering problems is similar to finding the optimal harmony. The frank rules of harmony improvisation inspired the harmony search method.

3.5. Dynamic Loads

The power absorbed by dynamic loads is independent of the magnitude of the voltage. That is, the variation in voltage is unaffected by dynamic loads, which absorb constant power without considering the variation in voltage with time as rotational loads do (inductive loads). This type of load will be considered in all studied cases.

4. Load Flow Results for DGs Partial Outages

This section contains the results obtained from the system’s partial outage of the distributed generation. The first type of DG produces only active power to the grid. The second type of DG generates both active and reactive power with a power factor of 0.8 before injecting it into the grid.

4.1. DGs Supplying Active Power Only (Unity Power Factor)

The results of the IEEE 33-bus system at the proposed loading cases (100%, 150%, 200%, and 250%) are carried out with the unity power factor DGs as (PV-DG), or any DG producing active power only. The dynamic load type is used and the criteria of the DG installation are at the minimum voltage buses criteria, which are explained in the previous sections where the system loads are (3581 kW and 1745 kVAr).

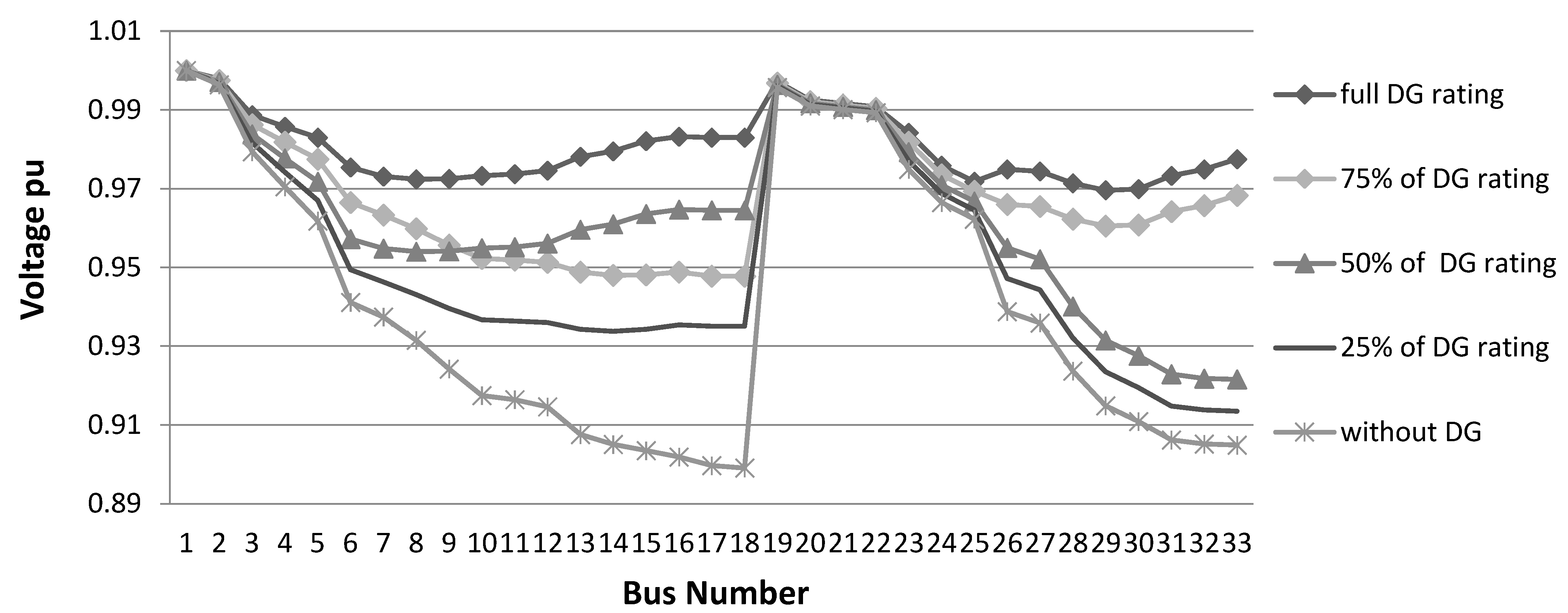
4.1.1. Unity Power Factor DGs Outage Study at 100% Loading

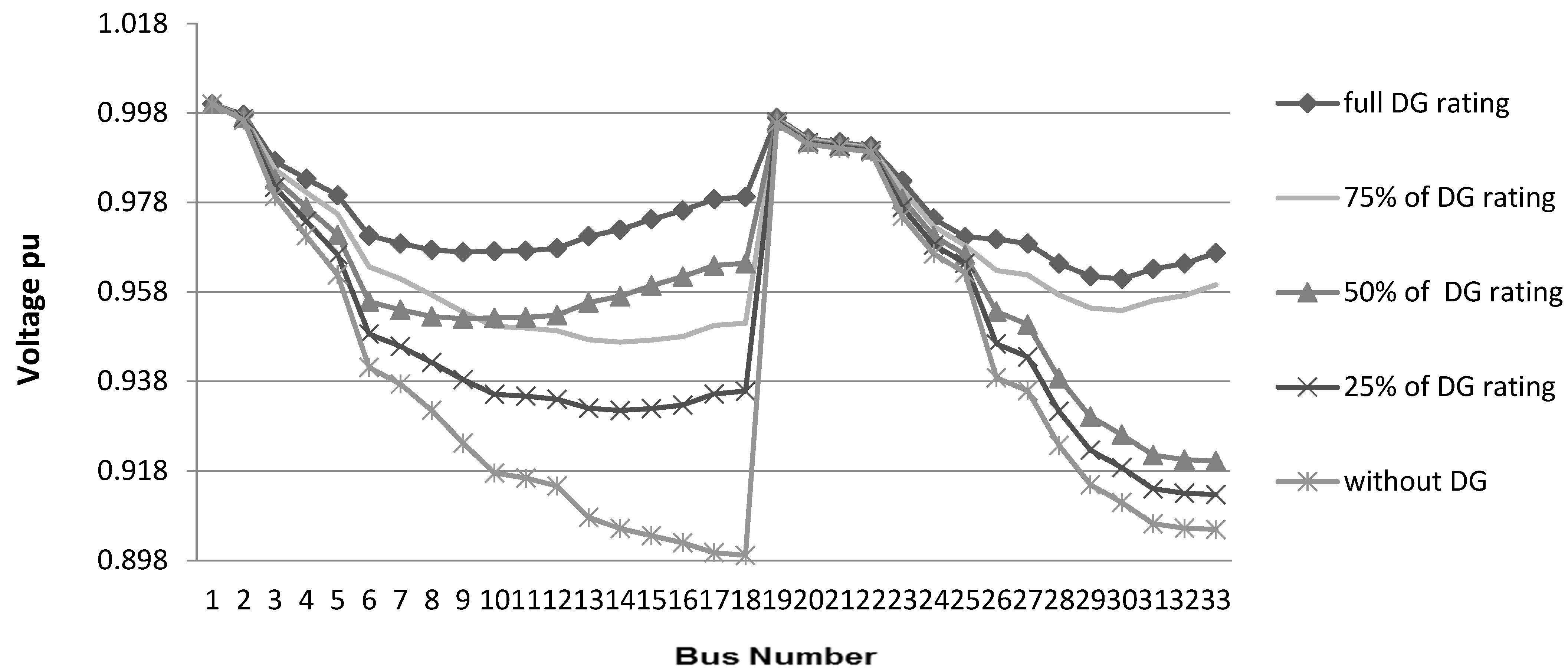
For the first case, the loading is set to 100% the system’s normal load with no DG existence. The active power losses are determined to be 211 kW at about 5.89% of the system load, the reactive power losses are 140 kvar at about 8% from reactive power and the minimum voltage is 0.899 pu. After the insertion of the DGs, it is noted that the performance of the system is improved. Where the active power losses are reduced to 72 kW (2% of the system losses), and the reactive power losses are reduced to 51.55 kVAr (2.95% of the system losses), while the voltage profile is increased where the minimum voltage at the system after the insertion of the DGs became 0.97 pu.

In the next step when ejecting 25% of the DGs (DGs outages in buses 15 and 17), the active power losses are increased from 2% to 2.4% and the reactive power losses are raised from 2.95% to 3.49%, while the voltage profile falls to 0.947 pu. When moving to the next step, which is ejecting 50% of the DGs (DG outage in bus 33), the active and reactive power losses are increased to 3.57% and 4.86%, respectively, and the voltage profile is reduced to 0.922 pu.

For the last step, when ejecting 75% of DGs (DGs outages in buses 15 and 33) the active and reactive power losses are raised to 4.33% and 5.82%, respectively. Additionally, the minimum voltage drops to 0.9135 pu. This indicates the increasing harmful effect on the system’s performance with the rise of DG outage percentage.

The recorded results of the first case are introduced in

Table 1. IEEE 33-bus load flow results for 100% loading with DG ratings found by HSA (unity PF).

Branch		Power Loss (KW)	Reactive Loss (KVAr)	Bus
From Bus No.	To Bus No.			No.	Voltage (pu)	DG Rating kW
1	2	5.18	2.64	1	1.000	0
2	3	18.48	9.41	2	0.998	0
3	4	4.28	2.18	3	0.988	0
4	5	3.67	1.87	4	0.986	0
5	6	7.26	6.27	5	0.983	0
6	7	0.31	1.01	6	0.975	0
7	8	0.54	0.18	7	0.973	0
8	9	0.65	0.46	8	0.972	0
9	10	0.79	0.56	9	0.972	0
10	11	0.19	0.06	10	0.973	0
11	12	0.41	0.14	11	0.974	0
12	13	2.00	1.57	12	0.975	0
13	14	0.91	1.20	13	0.978	0
14	15	1.49	1.33	14	0.980	0
15	16	0.29	0.22	15	0.982	387
16	17	0.03	0.04	16	0.983	232
17	18	0.01	0.01	17	0.983	65
2	19	0.21	0.20	18	0.983	102
19	20	1.07	0.97	19	0.997	0
20	21	0.13	0.15	20	0.992	0
21	22	0.06	0.07	21	0.992	0
3	23	3.77	2.57	22	0.990	0
23	24	6.08	4.80	23	0.984	0
24	25	1.52	1.18	24	0.976	0
6	26	0.60	0.30	25	0.971	0
26	27	0.79	0.40	26	0.975	0
27	28	2.85	2.52	27	0.974	0
28	29	2.18	1.90	28	0.971	0
29	30	1.42	0.72	29	0.969	0
30	31	2.11	2.08	30	0.970	0
31	32	1.10	1.28	31	0.973	0
32	33	2.09	3.25	32	0.975	0
				33	0.978	900

, which represents the IEEE 33 bus with the DG siting and sizing at 100% loading.

Table 2. Results of system at 100% loading (unity PF).

Case	Minimum Voltage (pu)	Total Active Losses (kW)		Total Reactive Losses (kVAr)
Without DG	0.899	211.01	5.89%	140.17	8.02%
With full DG (40% of loading)	0.970	72.45	2.01%	51.55	2.95%
With 75% of DG	0.948	87.73	2.4%	60.94	3.49%
With 50% of DG	0.922	128.14	3.57%	84.97	4.86%
With 25% of DG	0.914	155.06	4.33%	101.67	5.82%

shows the results of the gradual outage of DG (25%, 50%, and 75%). Moreover, Figure 3 demonstrates the voltage at each bus in each step.

Referring to Table 1 it can be found that:

• Total system losses = (72.44 + j51.55) kVA;
• Lowest nodal voltage = 0.97 pu;
• Total power of DG used = 1686 kW.

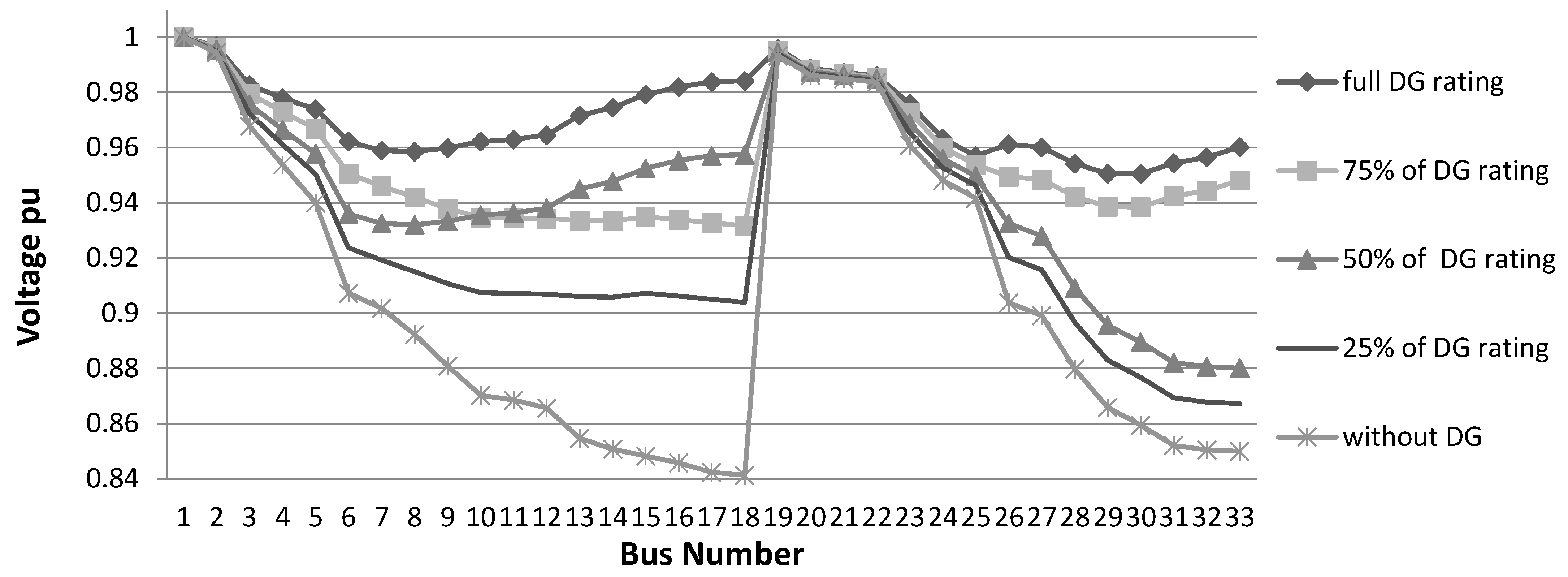
4.1.2. Unity Power Factor DGs Outage Study at 150% Loading

In this case, the loading percentage is raised to 150% of the nominal loading condition. It is noted that the system is seriously affected in the case of absence of DG and after increasing the load to 150%. Where the voltage is dropped to 0.841 pu, which means quite a high depression in the voltage. Additionally, the active and reactive power losses increased to 9.73% and 19.9% from the load (5370 kW active load and 2617 kVAr reactive load), respectively, which shows that the system needs to inject more power to improve the quality of the system. By the insertion of DGs to the system (DG full rating is 2491 kW), the system is relatively restored. Where the minimum voltage is raised to 0.951 pu, the active power losses drop to 3.16% and the reactive power losses are reduced to 6.84%, which assures the system improvement after adding DGs.

As the gradual DG outage starts, the losses and the voltage are affected as follows: For the 25% DG outage (buses 16 and 18), the voltage profile dropped to 0.932 pu, while the active and reactive power losses increased to 3.53% and 7.42%, respectively. Then, the DG outage is raised to 50% (bus 33). This will result in a rise in active and reactive power losses to 5.61% and 11.5%, respectively. As well as the drop in the voltage profile to 0.880 pu. At this point, the system is in the disturbance zone. In the last stage, 75% of DGs are ejected (buses 16, 18 and 33). The voltage dips to 0.867 pu and the active and the reactive power losses are raised to 6.64% and 13.4%, respectively.

Table 3. IEEE 33-bus load flow results for 150% loading with DG ratings found by HSA (unity PF).

Branch		Power Loss (kW)	Reactive Loss (kVAr)	Bus
From Bus No.	To Bus No.			No.	Voltage (pu)	DG Rating kW
1	2	12.06	6.15	1	1.000	0
2	3	43.22	22.01	2	0.997	0
3	4	9.99	5.0	3	0.983	0
4	5	8.55	4.36	4	0.978	0
5	6	16.92	14.61	5	0.974	0
6	7	0.59	1.94	6	0.962	0
7	8	1.19	0.39	7	0.959	0
8	9	1.98	1.42	8	0.959	0
9	10	2.49	1.76	9	0.96	0
10	11	0.59	0.19	10	0.962	0
11	12	1.29	0.42	11	0.963	0
12	13	6.17	4.85	12	0.965	0
13	14	2.77	3.64	13	0.972	0
14	15	4.32	3.85	14	0.975	0
15	16	1.46	1.07	15	0.979	530
16	17	0.50	0.67	16	0.982	350
17	18	0.07	0.05	17	0.984	191
2	19	0.47	0.45	18	0.984	220
19	20	2.43	2.19	19	0.996	0
20	21	0.29	0.34	20	0.989	0
21	22	0.13	0.17	21	0.988	0
3	23	8.71	5.95	22	0.987	0
23	24	14.07	11.11	23	0.976	0
24	25	3.51	2.75	24	0.963	0
6	26	1.43	0.73	25	0.957	0
26	27	1.84	0.94	26	0.961	0
27	28	6.41	5.65	27	0.960	0
28	29	4.71	4.11	28	0.954	0
29	30	2.82	1.44	29	0.951	0
30	31	3.20	3.16	30	0.950	0
31	32	1.82	2.12	31	0.954	0
32	33	3.78	5.88	32	0.957	0
				33	0.960	1200

shows the DG size at each bus.

Table 4. Results of system at 150% loading (unity PF).

Case	Minimum Voltage (pu)	Total Active Losses (kW)		Total Reactive Losses (kVAr)
Without DG	0.841	522.97	9.73%	348.00	19.9%
With full DG (46% from load)	0.950	169.77	3.16%	119.46	6.84%
With 75% of DG	0.932	189.74	3.53%	129.60	7.42%
With 50% of DG	0.880	301.69	5.61%	201.57	11.5%
With 25% of DG	0.867	356.77	6.64%	234.20	13.4%

shows the behavior of the system when the outage of the DGs is complete. Additionally, Figure 4 shows the voltage in each situation.

Referring to Table 3 it can be found that:

• Total system losses = (169.7 + j119.45) kVA;
• Lowest nodal voltage = 0.95 pu;
• Total power of the DG used = 2491 kW.

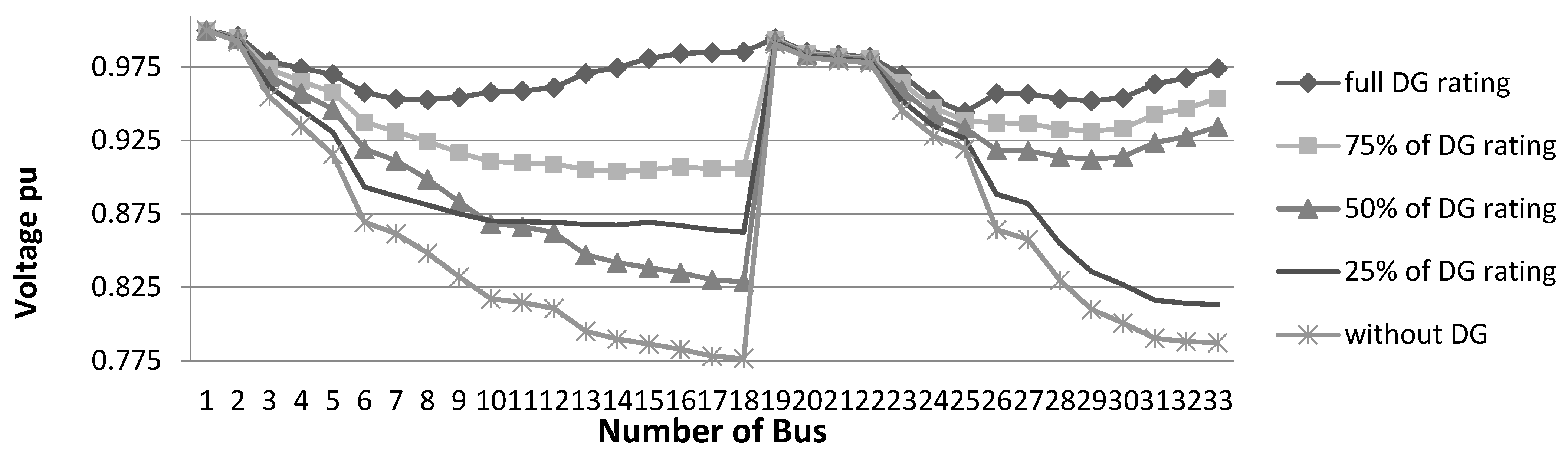
4.1.3. Unity Power Factor DGs Outage Study at 200% Loading

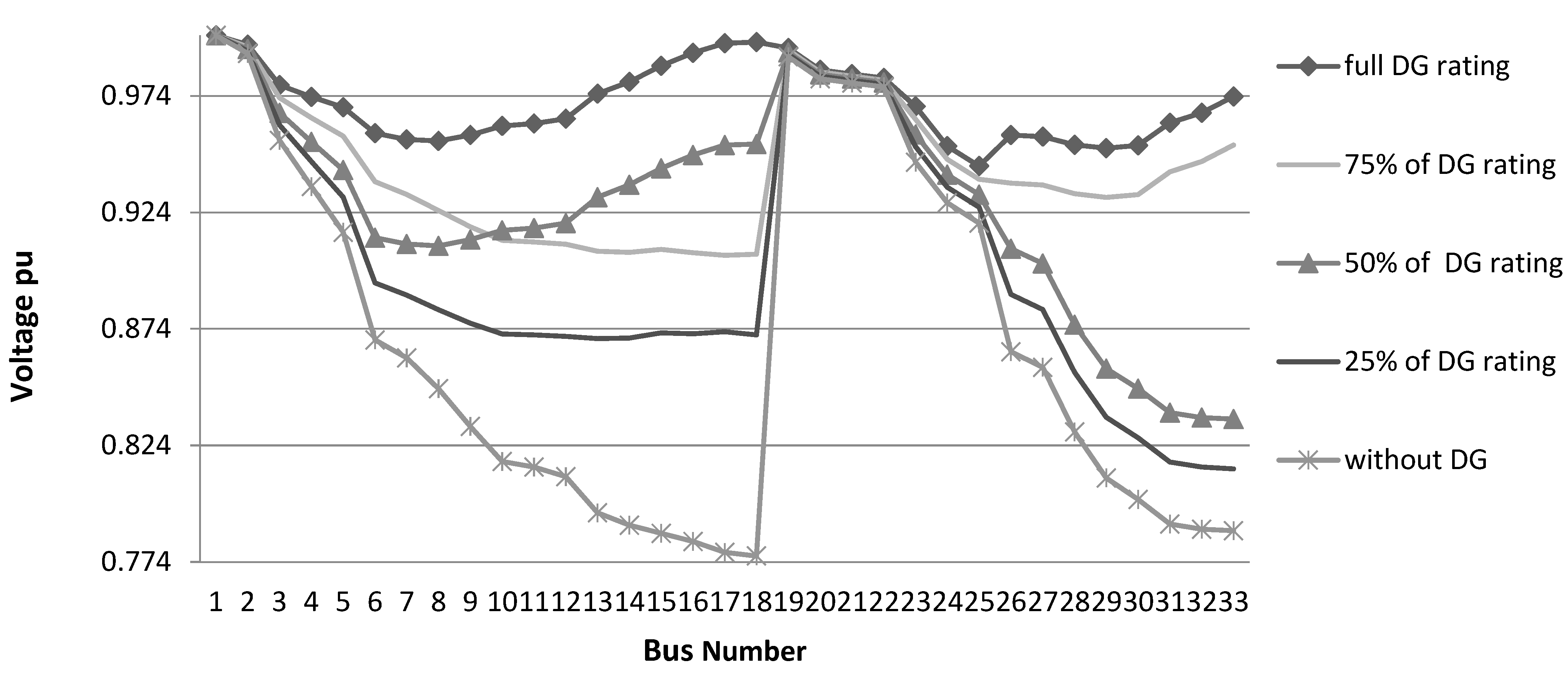
In the third case, the system is overloaded by 200%, compared to the normal load (7160 kW, 3460 kVAr). Without DGs, the value of the minimum voltage is determined to be 0.776 pu, whereas the active and reactive power losses are 14.5% and 19.9% of the load, respectively. These recorded values show poor system performance.

According to the above data, the system needs more power to improve it. The suggested solution is to add DGs with suitable sizing to improve the quality of the network. Once DG units are added, the minimum voltage in the system will restore to 0.950 pu, whereas active and reactive power losses drop to 4.15% and 6.23%. The total size of added DG to the grid is 3708 kW, which represents 51% of the load in this case (200% of normal loading). As presented in

Table 5. IEEE 33-bus load flow results for 200% loading with DG ratings found by HSA (unity PF).

Branch		Power Loss (kW)	Reactive Loss (kVAr)	Bus
From Bus No.	To Bus No.			No.	Voltage (pu)	DG Rating kW
1	2	12.06	6.15	1	1.000	0
2	3	43.22	22.01	2	0.997	0
3	4	9.99	5.0	3	0.983	0
4	5	8.55	4.36	4	0.978	0
5	6	16.92	14.61	5	0.974	0
6	7	0.59	1.94	6	0.962	0
7	8	1.19	0.39	7	0.959	0
8	9	1.98	1.42	8	0.959	0
9	10	2.49	1.76	9	0.96	0
10	11	0.59	0.19	10	0.962	0
11	12	1.29	0.42	11	0.963	0
12	13	6.17	4.85	12	0.965	0
13	14	2.77	3.64	13	0.972	0
14	15	4.32	3.85	14	0.975	0
15	16	1.46	1.07	15	0.979	530
16	17	0.50	0.67	16	0.982	350
17	18	0.07	0.05	17	0.984	191
2	19	0.47	0.45	18	0.984	220
19	20	2.43	2.19	19	0.996	0
20	21	0.29	0.34	20	0.989	0
21	22	0.13	0.17	21	0.988	0
3	23	8.71	5.95	22	0.987	0
23	24	14.07	11.11	23	0.976	0
24	25	3.51	2.75	24	0.963	0
6	26	1.43	0.73	25	0.957	0
26	27	1.84	0.94	26	0.961	0
27	28	6.41	5.65	27	0.960	0
28	29	4.71	4.11	28	0.954	0
29	30	2.82	1.44	29	0.951	0
30	31	3.20	3.16	30	0.950	0
31	32	1.82	2.12	31	0.954	0
32	33	3.78	5.88	32	0.957	0
				33	0.960	1200

, on the ejection of 25% of DG (buses 15 and 17) the disturbance raised shortly in the system’s performance. The minimum voltage is dropped to 0.900 pu, whereas the active and reactive power losses are increased to 4.88% and 7.12%, respectively. Subsequently, 50% of DG size is removed (buses 15, 16, 17, and 18). This resulted in a drop in the minimum voltage to 0.830 pu and an increase in the active and reactive power losses up to 7.28% and 10.6%, respectively. Finally, 75% of DGs are installed at buses 16, 18, and 33. The system becomes unstable due to the minimum voltage reduction to 0.813 pu and the rise of active and reactive power losses to 9.72% and 13.1%, respectively.

Table 5 shows the sizing, allocation DG units, the voltage at each bus, and the losses at each branch.

Table 6. Results of system at 200% loading (unity PF).

Case	Minimum Voltage (pu)	Total Active Losses (kW)		Total Reactive Losses (kVAr)
Without DG	0.777	1.045 × 103	14.5%	696.57	19.9%
With full DG (46% from load)	0.952	297.15	4.15%	217.72	6.23%
With 75% of DG	0.904	350.09	4.88%	248.82	7.12%
With 50% of DG	0.829	521.78	7.28%	371.59	10.6%
With 25% of DG	0.814	696.37	9.72%	457.98	13.1%

depicts the results of DG outages. Additionally, Figure 5 describes the voltage at each bus for all states at 200% loading.

Referring to Table 5, it can be found that:

• Total system losses = (291.15 + j217.71) kVA;
• Lowest nodal voltage = 0.944 pu;
• Total power of the DG used = 3708 kW.

4.1.4. Unity Power Factor DGs Outage Study at 250% Loading

In the last case, when increasing the load to 250% (8952.5 kW and 4362.5 kVAr), the minimum voltage on the system is recorded to be 0.704 pu and the losses are 21.1% and 28.9% for active and the reactive power losses, respectively. The size of the inserted DG units to improve the system’s performance is 5027 kW, which is limited by the harmony search algorithm (HSA). The inserted DG raised the minimum voltage to 0.942 pu and reduced the active and the reactive power losses to 5.41% and 8.27%, respectively. The system is improved but still in the critical zone and tends to lose its stability. As a result of ejecting 25% of the DGs (buses 16 and 18), the voltage is dipped to 0.903 pu and the losses increase to reach 5.71% and 8.37% for the active and the reactive power, respectively. Then, 50% of the DGs are removed (buses 15, 16, 17, and 18), leading to the reduction in voltage to 0.777 pu, whereas the active and the reactive power losses increased to 9.7% and 14.1%, respectively. Finally, 75% of the DGs are ejected (on buses 16, 18, and 33), leading to the reduction in the voltage to 0.759 pu and the rise in active and reactive power losses to 12.9% and 17.6%, respectively.

Table 7. IEEE 33-bus load flow results for 250% loading with DG ratings found by HSA (unity PF).

Branch		Power Loss (kW)	Reactive Loss (kVAr)	Bus
From Bus No.	To Bus No.			No.	Voltage (pu)	DG Rating kW
1	2	27.09	13.81	1	1	0
2	3	94.01	47.88	2	0.995	0
3	4	21.56	10.98	3	0.975	0
4	5	19.1	9.73	4	0.971	0
5	6	38.85	33.54	5	0.967	0
6	7	1.24	4.11	6	0.955	0
7	8	3.91	1.29	7	0.95	0
8	9	9.45	6.79	8	0.952	0
9	10	11.81	8.37	9	0.958	0
10	11	2.71	0.9	10	0.966	0
11	12	5.88	1.94	11	0.968	0
12	13	27.4	21.56	12	0.972	0
13	14	11.88	15.64	13	0.99	0
14	15	17.42	15.5	14	0.997	0
15	16	6.62	4.83	15	1.007	1000
16	17	2.15	2.87	16	1.014	736
17	18	0.53	0.41	17	1.019	291
2	19	1.33	1.27	18	1.021	500
19	20	6.88	6.19	19	0.994	0
20	21	0.83	0.97	20	0.982	0
21	22	0.36	0.48	21	0.979	0
3	23	25.35	17.32	22	0.977	0
23	24	41.04	32.41	23	0.964	0
24	25	10.29	8.05	24	0.942	0
6	26	3.68	1.87	25	0.942	0
26	27	5.07	2.58	26	0.954	0
27	28	19.09	16.83	27	0.954	0
28	29	15.13	13.18	28	0.95	0
29	30	10.46	5.33	29	0.949	0
30	31	18.56	18.34	30	0.952	0
31	32	9.09	10.59	31	0.964	0
32	33	16.3	25.35	32	0.969	0
				33	0.978	2500

shows the system at 250% supported by the DG units on the buses (15, 16, 17, 18, and 33), as well as the voltage in each bus and the losses.

Table 8. Results of system at 250% loading (unity PF).

Case	Minimum Voltage (pu)	Total Active Losses (kW)		Total Reactive Losses (kVAr)
Without DG	0.704	1.89 × 103	21.1%	1.26 × 103	28.9%
With full DG (56.1%)	0.942	485.07	5.41%	360.92	8.27%
With 75% of DG	0.903	511.26	5.71%	365.28	8.37%
With 50% of DG	0.777	868.50	9.70%	618.96	14.1%
With 25% of DG	0.759	1.167 × 103	12.9%	769.45	17.6%

describes the results of the DGs outages in the system at 250% loading. Figure 6 shows the voltage at each bus for all states at 250% loading.

Referring to Table 7 it can be found that:

• Total system losses = (485.06 + j360.92) kVA;
• Lowest nodal voltage = 0.942 pu;
• Total power of DG used = 5027 kW.

4.2. DGs Supplying Active and Reactive Powers (0.8 Power Factor)

In this section, the results of IEEE 33-bus system at the proposed loading cases (100%, 150%, 200%, and 250%) are carried out with DGs supplying active and reactive powers, at 0.8 power factor.

4.2.1. DG Supplying Active and Reactive Powers Outage Study at 100% Loading

For the first case, the loading is set to 100% of the system’s normal load with no DG existence. The minimum voltage is 0.899 pu, while the active and reactive power losses are determined to be 211 kW and 140 kVAr at about 5.89% and 8.02% of the system load, respectively. After the insertion of the DGs, it is noted that the performance of the system is improved. Where the optimal inserted DG rating is 1581 kVA with a 0.8 power factor. In this case, the power losses are reduced to 64.52 kW and 43.29 kVAr (1.8% and 2.48% of the system losses), respectively, while the voltage profile is increased to where the minimum voltage at the system after the insertion of the DGs is 0.961 pu.

In the next step, when ejecting 25% of the DGs (DG outages in buses 15 and 16), the power losses are increased to 85.38 kW and 56.91 kVAr (2.28% and 3.26%), respectively, while the voltage profile falls to 0.948 pu. When moving to the next step, which is ejecting 50% of the DGs (DG outage in bus 33), the active and reactive power losses are increased to 128.43 kW and 84.58 kVAr (3.58% and 4.84%), respectively, and the voltage profile is reduced to 0.920 pu.

For the last step, when ejecting 75% of DGs (DGs outages in buses 15, 16, and 33) the active and reactive power losses are raised to 159.83 kW and 105.023 kVAr (4.46% and 6.01%), respectively. Additionally, the minimum voltage drops to 0.913 pu.

Table 9. IEEE 33-bus load flow for 100% loading with DG ratings found by HSA (0.8 PF).

Branch		Power Loss (kW)	Reactive Loss (kVAr)	Bus
From Bus No.	To Bus No.			No.	Voltage (pu)	KVA Ratting of DG at 0.8 Power Factor
1	2	5.93	3.02	1	1	0
2	3	21.29	10.84	2	0.998	0
3	4	4.4	2.24	3	0.987	0
4	5	3.6	1.83	4	0.983	0
5	6	6.86	5.92	5	0.98	0
6	7	0.33	1.08	6	0.971	0
7	8	0.36	0.12	7	0.969	0
8	9	0.04	0.03	8	0.967	0
9	10	0.05	0.03	9	0.967	0
10	11	0.03	0.01	10	0.967	0
11	12	0.08	0.02	11	0.967	0
12	13	0.55	0.43	12	0.968	0
13	14	0.33	0.44	13	0.97	0
14	15	0.77	0.68	14	0.972	0
15	16	0.51	0.38	15	0.974	195
16	17	0.34	0.46	16	0.976	198
17	18	0.04	0.03	17	0.979	192
2	19	0.21	0.2	18	0.979	196
19	20	1.07	0.97	19	0.997	0
20	21	0.13	0.15	20	0.992	0
21	22	0.06	0.07	21	0.991	0
3	23	3.78	2.58	22	0.991	0
23	24	6.1	4.81	23	0.981	0
24	25	1.52	1.19	24	0.974	0
6	26	0.46	0.23	25	0.97	0
26	27	0.54	0.27	26	0.97	0
27	28	1.66	1.46	27	0.969	0
28	29	1.09	0.94	28	0.964	0
29	30	0.51	0.26	29	0.962	0
30	31	0.45	0.44	30	0.961	0
31	32	0.4	0.47	31	0.963	0
32	33	1.07	1.67	32	0.964	0
				33	0.967	800

shows the IEEE 33-bus system with 100% loading supported with the DG units, the voltage at each bus, and the losses at each branch.

Table 10. Results of system at 100% loading with DGs 0.8 PF.

Case	Minimum Voltage (pu)	Total Active Losses (kW)		Total Reactive Losses (kVAr)
Without DG	0.899	211.01	5.89%	140.18	8.02%
With full DG	0.961	64.52	1.80%	43.29	2.48%
With 75% of DG	0.948	85.39	2.28%	56.92	3.26%
With 50% of DG	0.920	128.43	3.58%	84.58	4.84%
With 25% of DG	0.913	159.84	4.46%	105.02	6.01%

shows the results of the outage of the DG from the system at 100% loading. Figure 7 displays the voltage at each bus for all steps.

Referring to Table 9, it can be found that:

• Total system losses = (64.52 + j43.29) kVA;
• Lowest nodal voltage = 0.960 pu;
• Total power of the DG used = 158 kVAr.

4.2.2. DG Supplying Active and Reactive Powers Outage Study at 150% Loading

In this section, the system loading is raised to 150% compared to the nominal loading condition (5371 kW and 2617 kVAr). Additionally, more DG units are added to compensate for the new loading condition (2837 kVA).

It is noted that the system is seriously affected in case of the absence of DG and after increasing the load to 150%. Where the voltage is dropped to 0.841 pu, which means quite a high depression in the voltage. Additionally, the active and reactive power losses increased to 522 kW and 348 kVAr (9.73% and 19.9%), respectively, which designates that the system needs to inject more power to improve the quality of the system. By the insertion of DGs to the system (the DG full rating to is 2837 kVA), the system is relatively restored. Where the minimum voltage is raised to 0.951 pu, the active power losses are dropped to 2.5% and the reactive power losses are reduced to 3.58%, which assures the system improvement after adding DGs. As the gradual DG outage starts, the losses and the voltage are affected as follows: For the 25% DG outage (buses 15 and 18), the voltage profile dropped to 0.933 pu, while the active and reactive power losses are increased to 3.17% and 4.36%, respectively. Then, the DG outage is raised to be 50% (buses 18 and 33). This will result in the rise of active and reactive power losses to 5.74% and 7.75%, respectively, as well as the drop of the voltage profile to 0.875 pu. At this point, the system is in the disturbance zone. In the last stage, 75% of DGs are ejected (buses 16, 17, and 33). The voltage drops to 0.866 pu and the active and the reactive power losses are raised to 6.67% and 8.98%, respectively.

Table 11. IEEE 33-bus load flow for 150% loading with DG ratings found by HSA (0.8 PF).

Branch		Power Loss (kW)	Reactive Loss (kVAr)	Bus
				No.	Voltage (pu)	KVA Ratting of DG at 0.8 Power Factor
From Bus No.	To Bus No.
1	2	11.30	5.76	1	1.000	0
2	3	39.07	19.90	2	0.997	0
3	4	6.69	3.41	3	0.983	0
4	5	5.20	2.65	4	0.978	0
5	6	9.69	8.36	5	0.974	0
6	7	0.26	0.86	6	0.963	0
7	8	0.12	0.04	7	0.962	0
8	9	0.67	0.48	8	0.961	0
9	10	1.17	0.83	9	0.964	0
10	11	0.34	0.11	10	0.967	0
11	12	0.85	0.28	11	0.967	0
12	13	4.59	3.61	12	0.969	0
13	14	2.23	2.94	13	0.978	0
14	15	3.87	3.45	14	0.982	0
15	16	2.62	1.91	15	0.987	387
16	17	1.81	2.41	16	0.992	392
17	18	0.19	0.15	17	0.997	389
2	19	0.47	0.45	18	0.999	371
19	20	2.43	2.19	19	0.996	0
20	21	0.29	0.34	20	0.989	0
21	22	0.13	0.17	21	0.987	0
3	23	8.71	5.95	22	0.986	0
23	24	14.07	11.11	23	0.976	0
24	25	3.511	2.75	24	0.963	0
6	26	0.90	0.46	25	0.957	0
26	27	1.05	0.53	26	0.962	0
27	28	3.29	2.90	27	0.961	0
28	29	2.20	1.92	28	0.955	0
29	30	1.12	0.57	29	0.952	0
30	31	1.55	1.53	30	0.951	0
31	32	1.18	1.38	31	0.955	0
32	33	2.90	4.51	32	0.958	0
				33	0.962	1298

shows the DG size at each bus.

Table 12. Results of system at 150% loading with DGs 0.8 PF.

Case	Minimum Voltage (pu)	Total Active Losses (kW)		Total Reactive Losses (kVAr)
Without DG	0.841	522.97	9.73%	348.00	19.9%
With full DG	0.951	134.45	2.50%	93.90	3.58%
With 75% of DG	0.933	170.57	3.17%	114.16	4.36%
With 50% of DG	0.875	308.47	5.74%	202.91	7.751%
With 25% of DG	0.867	358.68	6.67%	235.14	8.98%

shows the behavior of the system when the outage of the DGs is complete. Additionally, Figure 8 shows the voltage in each situation.

Referring to Table 11, it can be found that:

• Total system losses = (134.45 + j93.9) kVA;
• Lowest nodal voltage = 0.951 pu;
• Total power of the DG used = 2837 kVAr.

4.2.3. DG Supplying Active and Reactive Powers Outage Study at 200% Loading

In the third case, the system is overloaded by 200% of the normal load (7162 kW and 3490 kVAr). Without DGs, the value of the minimum voltage is determined to be 0.776 pu, whereas the active and reactive power losses are 14.5% and 19% of the load, respectively. These recorded values show a poor system performance.

According to the above data, the system needs more power to improve it. The suggested solution is to add DGs with suitable sizing to improve the quality of the network. Once DG units are added, the minimum voltage in the system will be restored to 0.9439 pu, whereas active and the reactive power losses are dipped to 3.05% and 4.54%. The total size of added DG to the grid is 4191 kVA. As presented in

Table 13. IEEE 33-bus load flow for 200% loading with DG ratings found by HSA (0.8 PF).

Branch.		Power Loss (kW)	Reactive Loss (kVAr)	Bus
From Bus No.	To Bus No.			No.	Voltage (pu)	KVA Ratting of DG at 0.8 Power Factor
1	2	17.83	9.09	1	1.000	0
2	3	59.89	30.50	2	0.996	0
3	4	8.76	4.46	3	0.979	0
4	5	6.55	3.34	4	0.974	0
5	6	12.04	10.39	5	0.969	0
6	7	0.54	1.80	6	0.958	0
7	8	0.26	0.09	7	0.955	0
8	9	0.94	0.67	8	0.955	0
9	10	1.73	1.22	9	0.957	0
10	11	0.52	0.17	10	0.961	0
11	12	1.33	0.44	11	0.962	0
12	13	7.33	5.77	12	0.964	0
13	14	3.62	4.76	13	0.975	0
14	15	6.42	5.70	14	0.980	0
15	16	3.56	2.60	15	0.987	595
16	17	0.98	1.31	16	0.992	689
17	18	0.02	0.02	17	0.997	438
2	19	0.84	0.81	18	0.997	277
19	20	4.36	3.93	19	0.995	0
20	21	0.53	0.62	20	0.985	0
21	22	0.23	0.31	21	0.983	0
3	23	15.86	10.84	22	0.982	0
23	24	25.65	20.26	23	0.969	0
24	25	6.42	5.02	24	0.952	0
6	26	0.97	0.49	25	0.944	0
26	27	1.22	0.62	26	0.957	0
27	28	4.30	3.79	27	0.956	0
28	29	3.39	2.95	28	0.953	0
29	30	2.52	1.28	29	0.952	0
30	31	7.52	7.43	30	0.953	0
31	32	4.24	4.94	31	0.962	0
32	33	8.43	13.11	32	0.967	0
				33	0.974	2195

, on the ejection of 25% of DG (buses 16 and 17) the disturbance raised shortly in the system’s performance. Where the minimum voltage is dropped to 0.905 pu, whereas the active and reactive power losses are increased to 4.11% and 5.92%, respectively. Subsequently, 50% of DG size is removed (bus 33). This resulted in a drop in the minimum voltage to 0.835 pu and an increase in the active and reactive power losses up to 7.58% and 10.3%, respectively. Finally, 75% of DG is emitted. The system becomes unstable due to the minimum voltage reduction to 0.814 pu and the rise of active and reactive power losses to 9.63% and 12.9%, respectively.

Table 13 shows the sizing, allocation DG units, the voltage at each bus, and the losses at each branch.

Table 14. Results of system at 200% loading with DGs 0.8 PF.

Case	Minimum Voltage (pu)	Total Active Losses (kW)		Total Reactive Losses (kVAr)
Without DG	0.777	1.045 × 103	14.5%	696.57	19.9%
With full DG	0.944	218.74	3.05%	158.69	4.54%
With 75% of DG	0.906	297.01	4.11%	206.70	5.92%
With 50% of DG	0.835	543.23	7.58%	361.61	10.3%
With 25% of DG	0.814	689.85	9.63%	452.83	12.9%

depicts the results of DG outages. Additionally, Figure 9 describes the voltage at each bus for all states at 200% loading.

Referring to Table 13 it can be found that:

• Total system losses = (218.73 + j158.6) kVA;
• Lowest nodal voltage = 0.943 pu;
• Total power of the DG used = 4191 kVAr.

4.2.4. DG Supplying Active and Reactive Powers Outage Study at 250% Loading

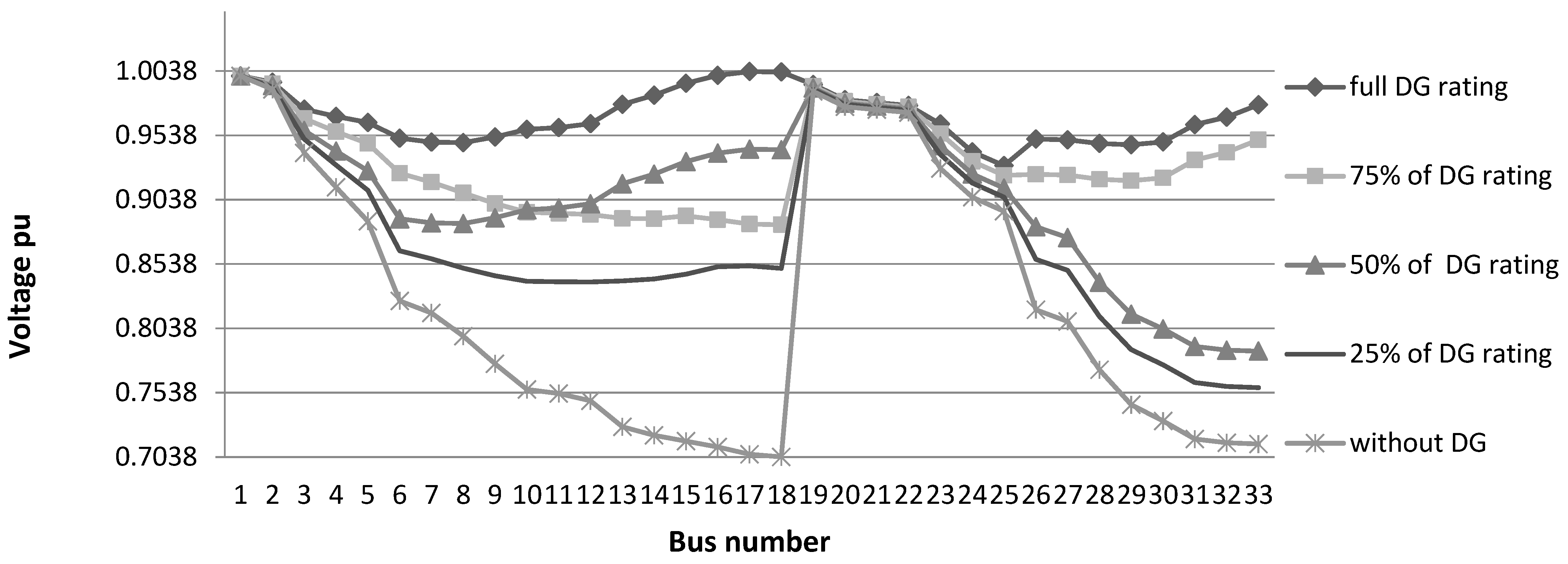
In the last case, when increasing the load to 250% (8952.5 kW and 4362 kVAr), the minimum voltage of the system is recorded to be 0.704 pu and the losses are 21.1% and 28.9% for active and the reactive power losses, respectively. The size of the inserted DG units to improve the system’s performance is 5521 kVA, which is limited by HSA. The inserted DG raised the minimum voltage to 0.9303 pu and reduced the active and the reactive power losses to 3.79% and 5.73%, respectively. The system is improved but is still in the critical zone and tends to lose its stability. As a result of ejecting 25% of the DGs (buses 16 and 17), the voltage is dipped to 0.884 pu and the losses are increased to reach 5.09% and 7.37% for the active and the reactive power, respectively. Then, 50% of the DGs are removed (bus 33), leading to the reduction in voltage to 0.786 pu, whereas the active and the reactive power losses increased to 10.1% and 14.8%, respectively. Finally, 75% of the DGs are ejected (on buses 15, 18, and 33), leading to the reduction in the voltage to 0.758 pu and the rise in active and reactive power losses to 12.8% and 17.2%, respectively.

Table 15. IEEE 33-bus load flow for 250% loading with DG ratings found by HSA (0.8 PF).

Branch		Power Loss (kW)	Reactive Loss (kVAr)	Bus
From Bus No.	To Bus No.			no.	Voltage (p.u)	kVA Ratting of DG at 0.8 Power Factor
1	2	26.39	13.45	1	1.00	0
2	3	87.31	44.47	2	0.995	0
3	4	11.66	5.94	3	0.974	0
4	5	8.56	4.36	4	0.968	0
5	6	15.65	13.51	5	0.964	0
6	7	0.67	2.20	6	0.952	0
7	8	0.29	0.10	7	0.949	0
8	9	2.18	1.58	8	0.948	0
9	10	3.70	2.62	9	0.953	0
10	11	1.05	0.35	10	0.959	0
11	12	2.60	0.86	11	0.960	0
12	13	13.92	10.95	12	0.963	0
13	14	6.69	8.81	13	0.978	0
14	15	11.42	10.17	14	0.985	0
15	16	4.56	3.36	15	0.994	971
16	17	0.49	0.66	16	1.000	961
17	18	0.02	0.02	17	1.003	503
2	19	1.33	1.27	18	1.003	194
19	20	6.88	6.2	19	0.993	0
20	21	0.83	0.97	20	0.981	0
21	22	0.36	0.48	21	0.979	0
3	23	25.42	17.37	22	0.977	0
23	24	41.15	32.50	23	0.963	0
24	25	10.32	8.08	24	0.941	0
6	26	1.38	0.70	25	0.930	0
26	27	1.80	0.92	26	0.951	0
27	28	6.69	5.90	27	0.950	0
28	29	5.52	4.81	28	0.947	0
29	30	4.39	2.24	29	0.946	0
30	31	14.13	13.97	30	0.949	0
31	32	7.62	8.88	31	0.962	0
32	33	14.63	22.75	32	0.968	0
				33	0.977	2892

shows the system at 250% supported by the DG units, as well as the voltage in each bus and the losses.

Table 16. Results of system at 250% loading with DGs 0.8 PF.

Case	Minimum Voltage (pu)	Total Active Losses (kW)		Total Reactive Losses (kVAr)
Without DG	0.704	1.89 × 103	21.1%	1.26 × 103	28.9%
With full DG	0.930	339.68	3.79%	250.41	5.73%
With 75% of DG	0.884	456.49	5.09%	321.95	7.37%
With 50% of DG	0.786	905.11	10.1%	603.99	14.8%
With 25% of DG	0.758	1.15 × 103	12.8%	753.95	17.2%

describes the results of the DGs outages in the system at 250% loading. Figure 10 shows the voltage at each bus for all states at 250% loading.

Referring to Table 15, it can be found that:

• Total system losses = (339.6 + j250.4) kVA;
• Lowest nodal voltage = 0.93 pu;
• Total power of the DG used = 5521 kVAr.

4.3. Discussion on DGs Outages for the Unity and 0.8 Power Factor Cases

By observing the unity power factor results, increasing the loading level from 100% to 150%, 200%, and 250% of the nominal loading of the IEEE 33-bus system (Section 4.1), the DG outage causes a perceptible impact, especially on the voltage profile and the losses. This effect is increased by increasing the loading conditions. The voltage falls to a reasonable value in the first two steps of DG ejection (25% and 50%), while the losses do not noticeably increase until the ejection reaches 50%. When DG outages are raised to 75%, the voltage and the losses are abruptly affected. At this point, the system becomes unstable and needs to be recovered.

By observing the results of the DGs with 0.8 power factor operation at 100%, 150%, 200%, and 250% loading conditions (Section 4.2), it is found that DG outage from the system caused a negative impact, especially on the voltage profile and the losses. For instance, at 250% loading, the voltage considerably dropped from 0.93 pu at fully rated DG to 0.758 pu when 25% of the DG was in service. For the same condition, the active and reactive power losses increased from 339.68 kW to 1150 kW, and from 250.41 kVAr to 753.95 kVAr, respectively. This effect was increased by increasing the system load from 100% to 250%, as can be seen in Table 10, Table 12, Table 14 and Table 16.

To improve the voltage profile of the IEEE 33-bus system and reduce the active and reactive power losses, controlled switched capacitors (CSCs) are proposed, as discussed in the following section.

5. DGs Outage Compensation Using Controlled Switched Capacitors (CSCs)

In this section, it is suggested to insert controlled switched capacitors (CSCs) or shunt capacitor banks with a controller to support the network for recovering and compensating the power losses due to the outage of DGs. In this regard, the CSCs are inserted gradually to the network instead of the DGs. At fully rated DGs, no CSCs are inserted to the grid since the system does not need it. When partial outage of DGs occurs, the system performance changes and the voltage starts to decrease, whereas the power losses increase. This will affect the quality of the system. To cure this problem, CSC is inserted, and its size is optimized using HSA.

5.1. CSC Optimization for DGs Supplying Active Power Only (Unity Power Factor)

In this subsection, the CSCs are optimized and inserted as compensation the DG outages, for different loading levels of 100%, 150%, 200%, and 250% of the nominal system load. The DGs are assumed to only supply active power, or unity power factor operation.

5.1.1. CSC Optimization for Unity Power Factor DGs at 100% Loading

At 100% loading conditions without the insertion of DGs, the minimum voltage is 0.899 pu and the active and the reactive power losses are 211 kW and 140.1 kVAr, respectively, as shown in

Table 17. Results of the system at 100% loading (unity PF) after CSC insertion.

Case	Minimum Voltage (pu)	Total Active Losses (kW)		Total Reactive Losses (kVAr)
Without DG	0.899	211.01	5.89%	140.18	8.02%
With full DG (40%)	0.970	72.45	2.01%	51.55	2.95%
With 75% of DG	0.948	87.73	2.4%	60.94	3.49%
With 50% of DG	0.922	128.14	3.57%	84.97	4.86%
With 25% of DG	0.914	155.06	4.33%	101.67	5.82%
With 75% of DG + CSC	0.968	72.28	2.01%	51.42	2.95%
With 50% of DG + CSC	0.899	211.01	5.89%	140.18	8.02%
With 25% of DG + CSC	0.970	72.45	2.01%	51.55	2.95%

. When inserting a full rate of the DGs of 1686 kW, it causes an increase in the voltage to 0.97 pu and a reduction in the power losses up to 2% and 2.9% for both the active and the reactive power. When ejecting 25% of DGs from the grid the losses increase and there is a drop in the voltage to compensate this defect and insert a reactive power source CSC (460 kVAr), which represent 26.3% from the reactive load that produces an increase in the voltage up to 0.9675 pu, and reduces the losses to 2% and 2.95% for both the active and the reactive power. The second state ejects 50% of the DGs and recovers them by CSC (700 kVAr), which represents around 40% of the reactive loads in the same places of the outage DG. The power losses are reduced to 2.72% and 3.93% for the active and the reactive power and the voltage is improved to reach 0.9521 pu. Additionally, in the last state, when removing 75% of the DGs and inserting CSC (1050 kVAr), which represented 60% of the reactive loads, the increase in the voltage is up to 0.9512 pu and the losses are reduced to 3.33% and 4.65%. The system data is improved, and the difference is clear when the comparison is between case 100% without DG in Table 2 and with CSC in Table 17.

5.1.2. CSC Optimization for Unity Power Factor DGs at 150% Loading

In the second case, 150% of the loading system, compared to

Table 18. Results of system at 150% loading (unity PF) after CSC insertion.

Case	Minimum Voltage (pu)	Total Active Losses (kW)		Total Reactive Losses (kVAr)
Without DG	0.841	522.97	9.73%	348.00	19.9%
With full DG (46%)	0.951	169.77	3.16%	119.46	6.84%
With 75% of DG	0.932	189.74	3.53%	129.60	7.42%
With 50% of DG	0.880	301.70	5.61%	201.57	11.5%
With 25% of DG	0.867	356.77	6.64%	234.20	13.4%
With 75% of DG + CSC	0.950	164.69	3.06%	118.35	4.521%
With 50% of DG + CSC	0.950	236.07	4.39%	174.64	6.67%
With 25% of DG + CSC	0.950	279.67	5.20%	201.28	7.6%

after inserting CSC to the system, the difference appears in the third state when removing 25% of the DG and it is replaced by the reactive power source CSC (980 kVAr), which represents 37.44% of the reactive load that the additional reactive power causes, increasing the minimum voltage to reach 0.950 pu and reducing the power losses to 3.06% and 4.52% for the active and the reactive power. Additionally, the fourth state ejects about 50% of the DGs, which is replaced by CSC (1557 kVAr), which represents 59.49%, causing a rise in the minimum voltage to 0.950 pu and helping to reduce the losses to 4.39% and 6.67% for both the real and the reactive power. The last state is when removing 75% of the DG can be compensated by inserting CSC (2072 kVAr), which represents 79.17% from the reactive load to boost the minimum voltage to 0.950 pu and decreases the losses to 5.20% and 7.6% for the active and the reactive power. Table 18 describes the comparison and the difference between the two cases on the minimum voltage and the total active and reactive power losses by looking in Table 4 and Table 18.

5.1.3. CSC Optimization for Unity Power Factor DGs at 200% Loading

The third case is at 200% when removing 25% of the distributed generation and compensating it by inserting CSC (982 kVAr), which represented 28.1% from the reactive power loads that caused a boost in the voltage to reach 0.942 pu and reduced in the losses to 3.92% and 5.91% for both the active and the reactive power. The third state is ejecting 50% of the DG and is replaced with CSC (1842 kVAr), which represented 52.7% from the reactive power loads that cause a rise in the minimum voltage to reach 0.941 pu and a decrease in both the active and the reactive power losses to 6.25% and 9.66%. The last case is ejecting 75% of the DGs and inserting CSC (2790 kVAr), which represented 80% of the reactive power load that improved the minimum voltage to reach 0.9461 kVAr and reduced the power losses to 7.45% and 11% for the active and the reactive power.

Table 19. Results of system at 200% loading (unity PF) after CSC insertion.

Case	Minimum Voltage (pu)	Total Active Losses (kW)		Total Reactive Losses (kVAr)
Without DG	0.777	1.045 × 103	14.5%	696.57	19.9%
With full DG (51%)	0.953	297.15	4.15%	217.72	6.23%
With 75% of DG	0.904	350.09	4.88%	248.82	7.12%
With 50% of DG	0.829	521.78	7.28%	371.59	10.6%
With 25% of DG	0.813	696.37	9.72%	457.98	13.1%
With 75% of DG + CSC	0.942	281.36	3.92%	206.48	5.91%
With 50% of DG + CSC	0.941	448.19	6.25%	337.39	9.66%
With 25% of DG + CSC	0.946	533.97	7.45%	385.87	11.0%

displays the system data after and before the insertion of CSC compared to Table 6.

5.1.4. CSC Optimization for Unity Power Factor DGs at 250% Loading

In the fourth case, with 250% loading system, by looking to

Table 20. Results of system at 250% loading (unity PF) after CSC insertion.

Case	Minimum Voltage (pu)	Total Active Losses (kW)		Total Reactive Losses (kVAr)
Without DG	0.704	1.89 × 103	21.1%	1.26 × 103	28.9%
With full DG (56%)	0.942	485.07	5.41%	360.92	8.27%
With 75% of DG	0.903	511.26	5.71%	365.28	8.37%
With 50% of DG	0.777	868.50	9.70%	618.96	14.1%
With 25% of DG	0.759	1.17 × 103	12.9%	769.45	17.6%
With 75% of DG + CSC	0.940	446.94	4.99%	342.01	4.84%
With 50% of DG + CSC	0.931	779.23	8.7%	605.58	13.8%
With 25% of DG + CSC	0.930	994.22	11.1%	737.78	16.9%

after inserting the CSC to the system, the difference appeared in the third state when removing 25% of the DG and was replaced by CSC (1700 kVAr), which represented 40% of the reactive power load, the addition of which caused an increase in the minimum voltage to reach 0.940 pu and reduce both the active and the reactive power losses to 4.99% and 4.84%. The third state ejects 50% of the DG and replaces it with CSC (4894 kVAr), which represents (112.1% of reactive load) that produces a rise in the minimum voltage to 0.931 pu and decrease the losses to 8.7% and 13.8% for the active and the reactive power. The last case is ejecting 75% of the DGs and inserting CSC (5239 kVAr), which represents 121.3% of the reactive power load to improve the minimum voltage to reach 0.930 pu and to reduce the power losses to 11.1% and 16.9% for the active and the reactive power. System data at Table 20 can be compared to Table 8. From this comparison, in the case of 250%, there is a very high rating of CSC, which is needed to compensate the outage of the DGs where it is considered as a difficult case, and it rarely happens to have an increase of 250% loading without a change in the infrastructure.

5.2. CSC Optimization for DGs Supplying Active and Reactive Powers (0.8 Power Factor)

In this subsection, the CSCs are optimized and inserted as a compensation of DG outages, for different loading levels of 100%, 150%, 200%, and 250% of the nominal system load. The DGs are assumed to supply active and reactive powers at a 0.8 power factor.

5.2.1. CSC Optimization for DG Supplying Active and Reactive Powers at 100% Loading

At 100% loading condition, as presented in

Table 21. Results of system at 100% loading at DG 0.8 PF after CSC insertion.

Case	Minimum Voltage (pu)	Total Active Losses (kW)		Total Reactive Losses (kVAr)
Without DG	0.899	211.0103	5.89%	140.18	8.02%
With full DG	0.961	64.52	1.80%	43.29	2.48%
With 75% of DG	0.948	85.388	2.28%	56.92	3.26%
With 50% of DG	0.920	128.43	3.58%	84.58	4.84%
With 25% of DG	0.913	159.84	4.46%	105.02	6.01%
With 75% of DG + CSC	0.960	76.69	2.1%	51.77	2.96%
With 50% of DG + CSC	0.950	102.87	2.87%	70.22	4.02%
With 25% of DG + CSC	0.950	128.05	3.57%	87.71	5.02%

, the first case 75% of the DGs are at work in the system, the minimum voltage is 0.9480 pu after the insertion of the CSC around 338 kVAr, and the minimum voltage will be increased to 0.960 pu, and both the active and the reactive power losses will be decreased from 85.3871 kW and 56.9171 kVAr to 76.69 kW and 51.77 kVAr. For the second step, when ejecting 50% of the DGs and compensating it by CSC, which is injected around 600 kVAr reactive power to the system, the minimum voltage to 0.95 pu is improved and decreases the losses to 2.87% and 4.02% of the normal load. The last state removes 75% from the DG units, which causes a high drop in the voltage and increases the power losses. To improve the system’s performance as usual, the insertion of the CSC reactive power source around 1015 kVAr is carried out. This causes the voltage to reach 0.950 pu and decreases the active and reactive losses to 3.57% and 5.02% of the normal load.

5.2.2. CSC Optimization for DG Supplying Active and Reactive Powers at 150% Loading

The second case is when the system loading is increased by 150% from the normal load. The first step is when the outage is around 25% from the DGs, which causes the voltage to be dropped and the losses to be increased. When adding CSC around (700 kVAr), which represents 26.7% from the reactive power load as a solution for compensating this outage, the minimum voltage is raised from 0.933 pu to 0.946 pu, and both the active and the reactive power losses are reduced to around 2.97% and 4.26% of the normal load. Additionally, when ejecting 50% of the DGs rating that leads to an increase in the CSC ratings to 1888 kVAr, which represents 72.1% from the reactive power load that caused the minimum voltage to be raised from 0.875 pu to 0.950 pu, both the real and the reactive power losses are reduced to 4.82% and 7.15% of the normal load. For the last stage, when ejecting around 75% of the DG units, the CSC rating is suggested by the HSA optimization around (2323 kVAr), which represents 88.7% from the reactive power load that made the minimum voltage increase from 0.867 pu to 0.950 pu, and the active and the reactive power losses are reduced to 5.55% and 8.17% of the normal load.

Table 22. Results of system at 150% loading with DGs 0.8 PF after CSC insertion.

Case	Minimum Voltage (pu)	Total Active Losses (kW)		Total Reactive Losses (kVAr)
Without DG	0.841	522.97	9.73%	348.00	19.9%
With full DG	0.951	134.45	2.50%	93.90	3.58%
With 75% of DG	0.933	170.56	3.17%	114.16	4.36%
With 50% of DG	0.875	308.47	5.74%	202.91	7.751%
With 25% of DG	0.867	358.68	6.67%	235.14	8.98%
With 75% of DG + CSC	0.946	159.80	2.97%	111.59	4.26%
With 50% of DG + CSC	0.950	259.26	4.82%	187.29	7.15%
With 25% of DG + CSC	0.950	298.47	5.55%	214.05	8.17%

displays the system performance after inserting CSC to compensate for the outage of the distributed generation.

5.2.3. CSC Optimization for DG Supplying Active and Reactive Powers at 200% Loading

As shown in

Table 23. Results of system at 200% loading with DGs 0.8 PF after CSC insertion.

Case	Minimum Voltage (pu)	Total Active Losses (kW)		Total Reactive Losses (kVAr)
Without DG	0.777	1.045 × 103	14.5%	696.57	19.9%
With full DG	0.944	218.74	3.05%	158.69	4.54%
With 75% of DG	0.906	297.01	4.11%	206.70	5.92%
With 50% of DG	0.835	543.23	7.58%	361.61	10.3%
With 25% of DG	0.814	689.85	9.63%	452.83	12.9%
With 75% of DG + CSC	0.944	277.21	3.86%	203.03	5.81%
With 50% of DG + CSC	0.941	426.54	5.95%	314.10	8.99%
With 25% of DG + CSC	0.940	564.50	7.88%	411.16	11.7%

at 200% loading with the outage of the distributed generation from the system, at outage 25% of DGs directly at the HSA optimization suggest the insertion of (CSC) around 1010 kVAr, which represents 28.9% from the reactive power load, which causes improvement in the minimum voltage up to 0.944 pu, also reducing both the real and the reactive power losses to 3.86% and 5.81% of its normal load. In the second stage, when ejecting 50% of DGs the minimum voltage is reached to 0.941 pu after the insertion of CSC around (2113 kVAr) 60.5% from the reactive power load into the system and that also caused reduction in the real and the reactive power losses to 5.95% and 8.99% of its normal load. The last state, due to the outage of 75% of DGs, the HSA optimization suggested the insertion of the reactive power source CSC around (3151 kVAr), which represents 90.2% from the reactive power load which supports the minimum voltage to rise from 0.814 pu to 0.94 pu and the active and the reactive power losses to be reduced from 9.63% and 12.9% to 7.88% and 11.7% of its normal load.

5.2.4. CSC Optimization for DG Supplying Active and Reactive Powers at 250% Loading

The last case presented the results of the 250% loading condition with the outage 25% of the distributed generation from the system with the reactive power compensation, which will be inserted through the CSC around 1994 kVAr, which represented 45.7% from the reactive load. This caused improvement in the minimum voltage up to 0.930 pu, and also reduction in both the real and the reactive power losses to 5.54% and 8.67%. The second step is ejecting 50% of the DG and compensating it by CSC around 3100 kVAr, which represents 71% from the reactive power load to the system, which improves the minimum voltage to 0.930 pu and decreases the losses to 7.85% and 12.2% in the main load active and reactive power. The last stage is ejecting around 75% of the DG units, and the CSC suggested is (5018 kVAr), which represents 115% from the reactive power load, which increases the minimum voltage from 0.7578 pu to 0.930 pu and the active and the reactive power losses are reduced from 12.8% and 17.2% to 11.1% and 17.1%.

Table 24. Results of system at 250% loading with DGs 0.8 PF after CSC insertion.

Case	Minimum Voltage (pu)	Total Active Losses (kW)		Total Reactive Losses (kVAr)
Without DG	0.7039	1.8893 × 103	21.1%	1.2632 × 103	28.9%
With full DG	0.9303	339.6773	3.79%	250.4097	5.73%
With 75% of DG	0.8844	456.4934	5.09%	321.9534	7.37%
With 50% of DG	0.7861	905.1130	10.1%	603.9933	14.8%
With 25% of DG	0.7578	1.1460 × 103	12.8%	753.9540	17.2%
With 75% of DG+ CSC	0.9300	496.5871	5.54%	378.5022	8.67%
With 50% of DG + CSC	0.9300	703.6191	7.85%	532.9129	12.2%
With 25% of DG + CSC	0.9300	998.2163	11.1%	747.7663	17.1%

displays the compression after and before inserting the CSC to the system below.

5.3. Discussion on CSCs Optimization for the Unity and 0.8 Power Factor Cases

In the unity power factor operation results, the controlled switched capacitors (CSCs) are inserted to compensate for the partial outage of DGs at different loading levels (100%, 150%, 200%, and 250% of the nominal load). Table 17, Table 18, Table 19 and Table 20 show the improvement of the IEEE 33-bus system in terms of minimum voltage and power losses after the insertion of CSCs. For instance, for the 250% loading condition (Table 20), the minimum voltage for 25% of DGs in service and the minimum voltage increased from 0.759 pu to 0.93 pu when inserting optimally sized CSCs to the system. Additionally, the active and reactive power losses decreased to 11.1% and 16.9%, respectively.

The results for the CSC insertion at different loading conditions for the 0.8 power factor are given in Table 21, Table 22, Table 23 and Table 24. Again, the insertion of optimally sized CSCs has a positive impact on the system performance (minimum bus voltage and power losses). For instance, as seen Table 24, the minimum bus voltage increased to 0.93 pu with the insertion of CSCs at 25% of DGs in service. The active and reactive power losses decreased to 11.1% and 17.1%, respectively.

From the above results, it is observed that inserting optimally sized CSCs has a favorable impact on the power system in case of partial outage of DGs.

6. Conclusions

This paper presents a full study on the impact of inserting DG units in the system under different loading condition, as well as the gradual ejection of DGs and its impact on the system. Moreover, a suggested solution for DG outages is presented. Adding optimally sized CSC (using the harmonic search algorithm) to the system as a cure for the DG outage problem is suggested.

The DG outage has a noticeable effect, especially on the voltage profile and the losses, as can be seen by looking at both the unity power factor DGs and DGS with active and reactive power values and raising the loading level from 100% to 150%, 200%, and 250% of the normal loading of the IEEE 33-bus system. When the loading conditions are increased, this effect is amplified. In the first two steps of DG ejection (25% and 50%), the voltage decreases considerably, while until the expulsion hits 50%, the losses are not expected to rise. The voltage and losses suddenly change when DG outages are increased to 75%. The system needs to be recovered because it becomes unstable at this point.

The controlled switched capacitors (CSCs) are introduced to make up for a partial failure of the DGs at different loading levels (100%, 150%, 200%, and 250% of the nominal load) to compensate for the unity power factor DGs. The addition of CSCs improved the IEEE 33-bus system in terms of minimal voltage and power losses, according to the results. When adding optimally sized CSCs to the system under 250% loading conditions, the minimum voltage increased from 0.759 pu (25% of DGs in service) to 0.93 pu (fully rated DGs in service). Additionally, the losses of both active and reactive power dropped to 11.1% and 16.9%, respectively.

Once more, the findings for the CSC insertions under various loading scenarios for the 0.8 power factor show that the performance of the system (minimum bus voltage and power losses) is improved by the insertion of optimally sized CSCs. Moreover, results show that when CSCs were installed in 25% of the operational DGs, the minimum bus voltage increased to 0.93 pu. Additionally, the reduction in the active and reactive power losses to 11.1% and 17.1%, respectively, were achieved.

According to the aforementioned findings, inserting CSCs of the ideal size has a positive effect on the power system in the event of a partial DG loss.

Future work might include studying practical distribution systems. Additionally, the stochastic nature of the renewable DGs (as wind or solar energy generators) could be taken into consideration.