Quantum Key Distribution Protocol Selector Based on Machine Learning for Next-Generation Networks

Abstract

In next-generation networks, including the sixth generation (6G), a large number of computing devices can communicate with ultra-low latency. By implication, 6G capabilities present a massive benefit for the Internet of Things (IoT), considering a wide range of application domains. However, some security concerns in the IoT involving authentication and encryption protocols are currently under investigation. Thus, mechanisms implementing quantum communications in IoT devices have been explored to offer improved security. Algorithmic solutions that enable better quantum key distribution (QKD) selection for authentication and encryption have been developed, but having limited performance considering time requirements. Therefore, a new approach for selecting the best QKD protocol based on a Deep Convolutional Neural Network model, called Tree-CNN, is proposed using the Tanh Exponential Activation Function (TanhExp) that enables IoT devices to handle more secure quantum communications using the 6G network infrastructure. The proposed model is developed, and its performance is compared with classical Convolutional Neural Networks (CNN) and other machine learning methods. The results obtained are superior to the related works, with an Area Under the Curve (AUC) of 99.89% during testing and a time-cost performance of 0.65 s for predicting the best QKD protocol. In addition, we tested our proposal using different transmission distances and three QKD protocols to demonstrate that the prediction and actual results reached similar values. Hence, our proposed model obtained a fast, reliable, and precise solution to solve the challenges of performance and time consumption in selecting the best QKD protocol.

1. Introduction

The sixth-generation (6G) mobile communication network will have the capacity to improve the reliability and performance of the entire network in terms of latency, security, spectrum, and energy consumption, among other requirements. The Internet of Things (IoT) is responsible for connecting various devices through network communication. Its growing popularity has awakened many security concerns [1], in addition to existing problems, such as limited battery energy, lack of proper encryption, insufficient privacy protection, and application vulnerabilities, among other issues [2].

Currently, because these network standards work in a flexible environment and an interoperable setting, IoT device usage is becoming more widespread on next-generation networks (NGN). The 6G networks aim to offer a more robust harmonization to the co-existence of current networks and their predecessors [3,4] by providing a more compatible working environment for IoT devices operating in different network generations. As a result, to provide the responsiveness desired in this connected heterogeneous network, fast information processing capacity combined with high-security functionalities is in high demand [5].

In recent decades, there has been a surge in demand for fast, secure, and dependable data connections. To this end, it is necessary to enhance the computational capability of network systems with high-performance [6]. By utilizing quantum computing (QC), a technology that has shown a clear potential to outperform the majority of traditional computing systems [7,8], this phenomenon can be achieved. QC combines the ideas of computer science and quantum mechanics to design more complex systems capable of handling sophisticated computational tasks. The elementary operational unit of QC is the quantum cubit (qubit) [9] and involves fundamental concepts of superposition and matching in quantum scenarios [10] that have accounted for its high performance. QC and QC-assisted communications are increasingly gaining an audience among the scholarly community and have been investigated in the literature [11,12,13,14]. QC-communication has promising abilities to offer improved communication and security in the 6G networks [15]. To this end, reliable communication of quantum channel implementation has been investigated in the literature [16,17,18].

The QC, a branch of computing that employs quantum mechanical features to enable efficient and faster task processing, is currently being challenged by the issues associated with cryptographic algorithms. Some asymmetric cryptographic algorithms, such as the Rivest–Shamir–Adleman (RSA) algorithm, one of the most widely used cryptographic algorithms, have some inefficiencies in offering highly rated security. As a result, the development of a new cryptographic algorithm called Quantum Cryptography that offers unconditional security independent of the current computing power [19] and has given rise to the use of quantum key distribution (QKD). QKD is one of the most popular applications in the quantum cryptographic research area as it offers an information-theoretically secure (i.e., a system that offers high-level of security against intruders with unlimited computing resources and time) solution to the challenge of the key exchange between communicating devices [20].

In QKD, the majority of the schemes provide security based on two main principles: the Heisenberg uncertainty and the no-cloning paradigm of quantum mechanics. The first paradigm makes it impossible for an eavesdropper to measure the quantum information without disturbing the system [21]. In contrast, the latter makes an eavesdropper in a quantum channel unable to copy, let alone tamper with the information without revealing its presence to the parties involved in the communication. QKD operates using a secret key that originates from the combination of random choices performed by two trusted communicating parties [22] in the communication channel. Although this method provides a secure communication mechanism between end devices, some issues must be addressed.

One of the major issues confronting the QKD protocol implementation is the difficulty of utilizing the protocol in a real-life scenario. Although significant improvements have been made in this regard, the cost of practical implementation of an optimal QKD system is still significantly high. Thus, it is essential to study how to develop and implement better QKD protocols depending on a determined scenario.

In [23], a QKD protocol selector based on a Random Forest (RF) classifier is proposed to increase the security in communication systems. The authors aim to optimize system resource configuration while providing high-level security. We used the RF model as a baseline to evaluate the performance of our model because of its lightweight nature, which makes it easily adaptable to IoT environments.

In quantum communications, security challenges related to IoT devices have received top concern from several researchers, ensuring that these systems are well-protected from quantum computing adversaries [24,25]. In the case of a distributed IoT network, mobility management, security, and location awareness as well as geo-distribution and scalability mechanisms are paramount. In this architecture, determined servers can manage the security-concerned tasks. There are few studies that present solutions for selecting the best QKD among the devices of communication through a fast and reliable model. For this reason, we propose a solution based on Tree-CNN and TanhExp activation functions.

In this work, we present a machine-learning-based solution to the quantum cryptographic challenges. The proposed solution offers better performance, thereby enhancing the protection of IoT devices and ensuring that the devices handle quantum communications by themselves. IoT controllers have many functions, such as collecting, aggregating, and processing data from different IoT sensors. The data are transferred over the network and stored on servers where further processing and analysis are performed. Meanwhile, because the controllers have more computing power, they can securely communicate with the servers, exchanging cryptographic information.

These controllers perform the QKD and distribute the generated keys to the IoT devices, which are applied to the data to encrypt it over traditional radio frequency (RF) communication links. In order to defend the IoT devices and the controller link from potential attackers, the controllers can finally run the QKD. Therefore, in this regard, a new approach for selecting an optimal QKD protocol is proposed. A Deep Convolutional Neural Network method, the Tree-CNN, is used in this work using the Tanh Exponential Activation Function (TanhExp) [26], achieving an efficient optimal QKD protocols selector with an AUC of 99.89%. Other algorithms used for comparison purposes presented lower performance accuracy than the Tree-CNN. The authors [27,28] also proposed a similar algorithm for different applications, not exploring the TanhExp on this type of model, i.e., the deep neural model.

Furthermore, we perform a simulation of the proposed QKD process to evaluate and validate the effectiveness of the proposed framework. The contributions of this work are the following:

• A Deep Convolutional Neural Network method for determining appropriate QKD protocols with good accuracy in contrast to previous machine learning models is proposed.
• We show that the Tree-CNN architecture can present an improved performance with the Tanh Exponential Activation Function (TanhExp).
• The proposed QKD is tested in a scenario that takes into account three different quantum cryptography algorithms in order to achieve highly secure communication between the IoT devices and the controllers of an NGN, such as 6G.

Three transmission distance ranges in conjunction with three QKD protocols, including the decoy-state Bennett Brassard 1984 (BB84) [29], the Measurement-Device-Independent (MDI) [30], and the Twin-Field (TF) [31], were used to evaluate the effectiveness of the QKD protocol selector in different network settings. The experimental results showed a high accuracy of the protocol prediction.

This article is structured in the following sections. Section 2 provides an overview of Quantum Key Distribution. Following that, we present the security problems in 6G networks in Section 3. The proposed framework is explained in Section 4. We present the results analysis and discussions with a comparison with other conventional approaches in Section 5. Finally, Section 6 concludes the study and highlights some future research directions.

2. Quantum Key Distributions

QKD revolutionarily provides an information-theoretic secure way for distant parties to transmit information. In a QKD-based cryptographic scheme, the QKD implements the laws of quantum physics to distribute unconditionally secured symmetric secret keys between the parties involved in the communication. It is important to note that the elements of a QKD system include a transmitter, a receiver, and a QKD link connecting the communicating entities. The combination of these is known as the QKD transceiver. The QKD link constitutes a quantum and classical channel. The quantum channel is responsible for transmitting quantum signals by quantum states with the polarization of a single photon, while the classical channel is responsible for exchanging the classical data for synchronization and key distillation between the devices. If someone captures some quantum states of photons in the quantum channel, the quantum states will not be used to distill the secret keys because the other party in the communication channel will not receive them. This will lead to the exposure of any potential eavesdropping on the QKD.

The QKD helps to facilitate key establishment through an untrusted network by producing a secret key, which contains random photons (Qubit) carried in the end communication. The QKD needs two parties on the communication channel to exchange a symmetric key. Thus, if an attacker tries to pick up the key contained in a QKD protocol, then the communicators can use some quantum rules to detect such an attempt [32].

A common pair of conventional techniques for achieving information security is presented in Figure 1a,b. In Figure 1a, two communicating entities use a public-key cryptosystem to distribute keys and a symmetric-key cryptosystem to encrypt messages, where plaintext is transformed into ciphertext. In Figure 1b, which involves a physical-layer security (PLS) cryptographic mechanism, the parties can generate the secret keys directly from their channel, and afterward, the generated secret keys are used by the symmetric-key cryptosystem for encrypting the messages. In Figure 1c, a QKD-based cryptographic scheme is presented, in which the QKD implements the laws of quantum physics for distributing unconditionally secure symmetric secret keys between the parties.

The problem with a traditional Vernam one-time pad cryptosystem is that, in the case where a secret key is delivered to two legitimate parties, there are possibilities of security compromise. Quantum cryptography treats this fact by providing a key that must be secret to the two people present in the communication for the cryptosystem [33]. Thus, a quantum mechanism can provide a guarantee of distributed-key security. The QKD protocols available in the literature that perform this task are BB84, E91, B92, and BBM92, among which the BB84 protocol is the most widely used in QKD schemes.

The BB84, proposed by Charles Bennett and Gilles Brassard in 1984 [29], is the first and most widely used QKD protocol, often implemented with decoy-state methods [34]. The BB84 protocol has some drawbacks, such as the difficulty of detecting particular attacks and the presence of a side channel. Again, there exists the disadvantage of being unable to generate keys that can operate over a long distance. Such drawbacks are solved by other protocols, such as the measurement-device-independent quantum key distribution (MDI-QKD) protocol [30] that is known for promptly detecting an attack and, afterward, shutting down the detected channels, including the undiscovered ones. The MDI-QKD creates the possibility that allows two communicating parties to have access to keys created and transmitted over a longer distance. Recently, the TF-QKD protocol has been proposed to enable long-distance communication with the keys [31]. As this protocol can overcome the various limitations associated with security key capacities (SKC), it becomes unnecessary to have quantum repeaters on the SKC path.

Miniaturization, chip integration, and cyberization are the current trends in QKD because technological advancements nowadays have the capacity to enhance the realization of this scenario. This has increased the chances of implementing QKD in networks. However, it is necessary to have an allocation of real-time resources, such as the possibility of having a fast decision for selecting parameters. A Local Search Algorithm (LSA) [35] can be used to improve the process, but this process consumes time and is not recommended for applications with a large volume of data. Thus, various studies have tried to solve the issue of time consumption and other problems related to the fast selection of parameters of the protocols by proposing different machine learning approaches [36,37,38].

In [37], the authors proposed a neural-network-based approach to directly predict the optimal parameters necessary for key distribution for the QKD scheme. The proposed machine learning algorithm was tested on the Raspberry Pi 3 single-board computer hardware interface and a mobile phone, both having a power consumption of fewer than 5 watts. The authors also used a speedup mechanism to improve the magnitude when compared to standard local search algorithms. On evaluation, the model achieved 95% accuracy in providing an optimal secure key selection rate for a given protocol. The method proposed by the authors uses a simple neural network that has the drawback of high training loss and overfitting. In addition, in [38], a random forest (RF) approach was proposed to optimize the process of selecting the best QKD protocol for IoT security. In contrast to traditional random forest implementation, the authors carried out some preprocessing to improve the performance of their model and tested the model on a hardware system.

In [23], a machine learning method based on RF is implemented for selecting better parameters of a QKD protocol, achieving a faster parameter selection process. It is important to note that this work was used for comparison to our model, as it is a lightweight model.

Nevertheless, there are few works that handle the issues of performing a fast and simple selection of the most appropriate protocol for a QKD. Hence, in this research, a new method is proposed for selecting the best protocol for QKD using a Deep Convolutional Neural Network using the TanhExp activation function.

3. Security Problems in 6G Networks

As 6G networks present many opportunities to enable quick, easy, and reliable communication between IoT systems in solving security challenges, there exist some concerns about its deployment [39,40]. In [39], four different important areas of concern were examined in securing the 6G network. They include: the communication issues in multi-sensory virtual reality (VR) applications, which present threats to the dynamics of the network to improve communication; malicious behavior and encryption challenges of Blockchain and distributed ledger technologies, including wireless brain–computer interactions; and the authentication issues in connected robotics and intelligent systems. The authors of [40] provided a thorough overview of the topic and predicted that a number of technologies, including distributed ledger (DL) technologies such as Blockchain, enhanced edge computing, molecular communication, terahertz (THz), visible light communication (VLC), and artificial intelligence (AI), will form the basis of 6G networks. According to the authors, novel authentication, communication, encryption, access control, and malicious activity detection are some of the serious security concerns that need an urgent response before the deployment of the network.

In Figure 2, we present the architectural representation of a future 6G network, including applications, services, and management protocols. It can be observed that the applications and services cover many aspects of human life, involving gestures, minds, and other communication protocols for interacting with mobile users [41] and devices, including hologram videos. Thus, immersive experiences and smart verticals based on IoT are allowed by the 6G era, which can incorporate many innovative technologies, such as space–air–ground–underwater communication, sea networks, and cloud technologies. This integration of space, air, ground, and underwater/sea networks constitutes a large-dimensional 6G network that provides unlimited connectivity. The full spectra featured by this kind of network architecture are capable of achieving good network capacity and data rates. Considering all these new network capabilities, a security system with high performance needs to be considered in the NGN.

Meanwhile, the usage of the terahertz spectrum has led to a denser nature of the 6G network space, thereby presenting a more concentrated challenge in the implementation of emerging technology. Once more, integrating a variety of IoT devices and other customized systems may lead to information compromise; thus, security systems with a fast response are mandatory in these network scenarios to future 6G systems communication. It is anticipated that better network management can be achieved over the wide, complicated, intelligent, and dispersed network topology by adding some techniques such as machine learning, Blockchain technology, and Software-Defined Network/Network Functions Virtualization (SDN/NFV).

Quantum cryptography enhances the protection of IoT devices in the 6G era. Currently, IoT devices have limited processing power and computational capabilities. Hence, it becomes necessary that IoT devices be capable of handling complex algorithms more easily, thereby facilitating more rapid quantum communication between them. Quantum communication commonly uses more robust algorithms present in the IoT controllers to collect, aggregate, and process data from different IoT sensors before delivering the data over to the network of remote servers [42]. It is therefore necessary that models which are to be used in the 6G network should perform quantum cryptography mechanisms in an intelligent and fast manner.

4. Proposed Method

In this section, the parameter section for QKD, the proposed method, data treatment, and IoT configurations are explained.

4.1. Parameters for the QKD Selection

The performance of the QKD design is a function of the parameters affecting its working mode. In general, some variables need to be specified for choosing the rate of a QKD protocol, which include the variables of count rate ($D_0$), which is the rate of photon detection; the efficiency of the photon detector ($pd$); transmission distance ($TD$); error rate ($m{e}_d$) for finding the overall communication error; and pulse number ($pn$). According to [43], to set up a real-time simulation of QKD to obtain a more precise output, the parameters to be used are necessarily set to the ranges defined as:

• $D_0$ = ${10}^{-10}$ to ${10}^{-5}$;
• $m{e}_d$ = 0.00 to 0.06;
• $pd$ = 0.1 to 0.9;
• $pn$ = ${10}^6$ to ${10}^{16}$;
• $TD$ = 1 to 600 km.

These features are used as input to the proposed classifier c represented by the Equation (1):

$$\mathbf{c}=[D_0,m{e}_d,pd,pn,TD]$$

(1)

The data transmission rates used for generating the keys for the MDI-QKD, BB84, and TF-QKD protocols are conducted for each scenario, $\mathbf{c}$. The simulation phase includes data generation, where a dataset was generated for the training of the proposed model. It contains a total of 80,962 instances. In this work, we have used 80% of the data for the training, and the remaining 20% for the testing phase. Thus, the testing and training set includes scenarios of 17,028 and 63,934 sets, respectively. A dimension-reduction method called principal component analysis (PCA) was applied to the training set to obtain a reduced dataset for the training of the model to achieve a faster and more precise result.

The dataset has some imbalances as some features are higher than others in dimension. To overcome this drawback, which can negatively influence the performance of the model, the Tomek algorithm based on Synthetic Minority Oversampling Technique (SMOTE-Tomek) is applied to the dataset. This helps to generate synthetic data for the minority class using the existing minority data. Thus, a balanced dataset containing the same amount of information for all the different labels present in the dataset is obtained. The algorithms are implemented using Mathematical Laboratory (MATLAB) software and the QKD simulator [44].

In the simulator, both the sender and receiver communicate through two channels. While one is represented by a quantum channel, the other is performed using a classical channel. In this communication, the quantum channel sends photons through a quantum scheme. In it, the photons are polarized randomly. Furthermore, through the classical channel, both the sender and the receiver can compare each received photon during the communication. In the end, some flaws observed during the transmission in classical communication can be corrected.

4.2. Deep Convolutional Neural Network, Tree-CNN

A Convolutional Neural Network (CNN) is a deep learning algorithm characterized by the presence of multiple hidden layers, which differentiates it from other artificial neural networks. It has been applied to image detection, segmentation, and computer vision. A traditional CNN has three main layers: the convolutional layer, the pooling layer, and the output layers. These traditional CNN models are utilized to generate detection at the top of the networks. A more complex CNN that is considered hierarchical, called the Tree-CNN model, has recently been used due to its great potential.

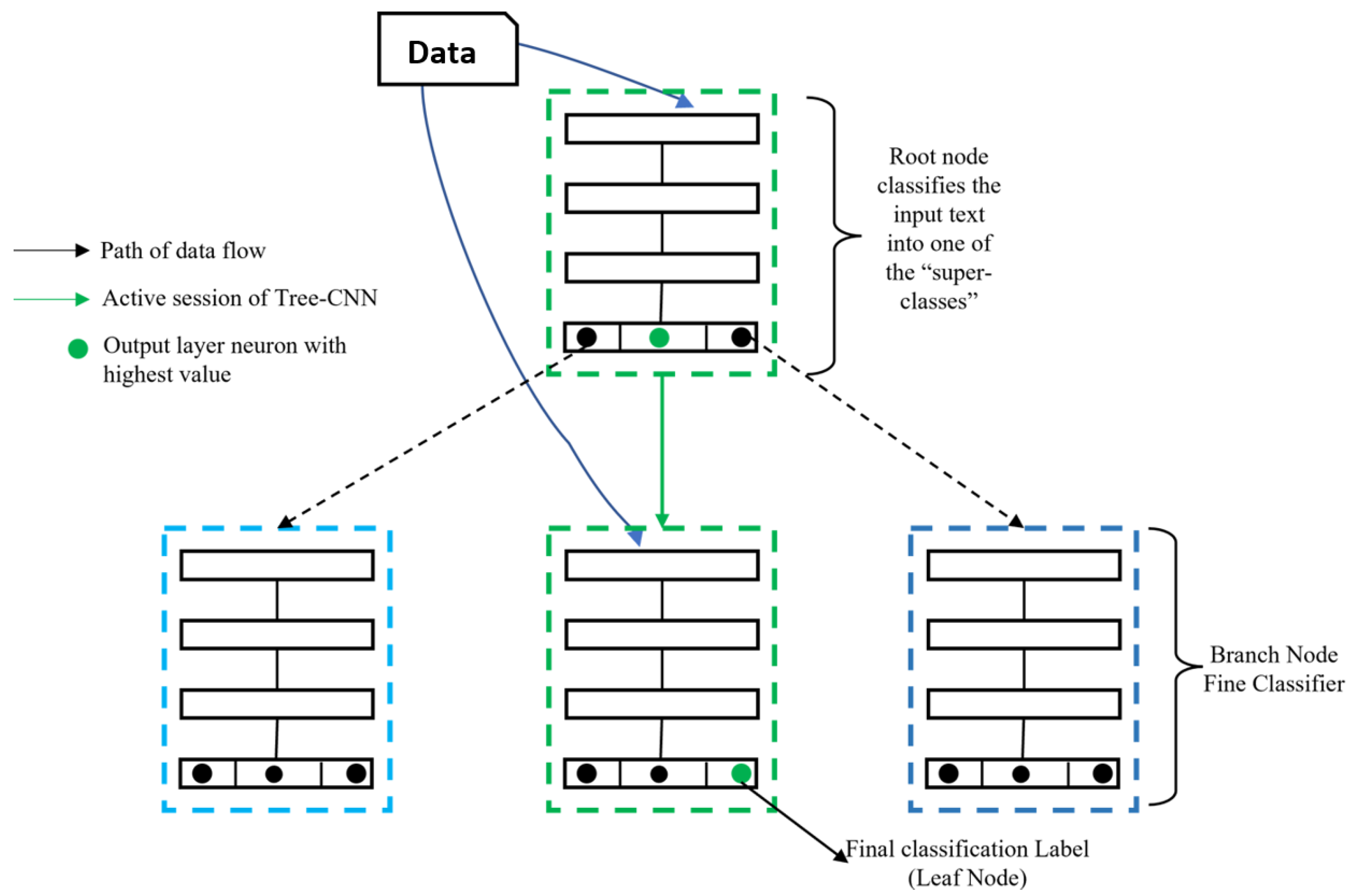
The Tree-CNN is a variant of CNN with higher nodes in the tree position, thereby requiring fewer resources to train and hence minimizing the complexity of the training phase. In the Tree-CNN topology, the network begins as the main node, and below it, new formations appear in which the new classes are accommodated at the end. Figure 3 shows a generic model of a 2-level Tree-CNN for classification tasks [45]. The special capabilities of the Tree-CNN are adapted in this work and tested in quantum communication for IoT scenarios. It is important to note that diverse levels of Tree-CNN were tested and that the 2-level Tree-CNN showed better results of classification for the QKD.

In the model, $\mathit{F}({\mathit{x}}_{\mathit{s}},\mathit{Sr})$ represents the function of the probability that the data used as entrance can be correctly classified in a class in the trunk structure $\mathit{Sr}$. $\mathit{F}({\mathit{C}}_{\mathit{i}},\mathit{Sr})$ refers to the chance that the data used as entrance are correctly classified in an $\mathit{i}$ class, where $\mathit{F}({\mathit{x}}_{\mathit{s}},\mathit{Br})$ represents the chance in which the data that are used as entrance are correctly classified as being of an $\mathit{i}$ class in the branch of the network, $\mathit{Br}$. In the case where $\mathit{F}({\mathit{x}}_{\mathit{s}},\mathit{Br})>\mathit{F}({\mathit{x}}_{\mathit{s}},\mathit{Sr})$, then the branch differentiates the $\mathit{i}$ class from other classes that can be seen as equal or similar, diverging from the trunk in the network. In a situation where $\mathit{F}({\mathit{C}}_{\mathit{i}},\mathit{Sr})$ is close to the value of 1, then the chance of the proposed model $\mathit{F}({\mathit{x}}_{\mathit{s}},\mathit{Br})\mathit{F}({\mathit{C}}_{\mathit{i}},\mathit{Sr})$ correctly hitting the class in a branch A is higher than $\mathit{F}({\mathit{x}}_{\mathit{s}},\mathit{Sr})$.

The activation function plays a crucial role in determining the performance of the model in terms of loss and weight update. The rectified linear unit (ReLU) and Softmax are the most widely used activation functions in deep neural networks. However, the Tanh Exponential Activation Function (TanhExp) has also presented superior results to the other activation functions in deep learning models. The TanhExp is shown in Equation (2):

$$\mathit{f}\left(\mathit{x}\right)=\mathit{x}\times \mathit{tanh}\left({\mathit{e}}^{\mathit{x}}\right)$$

(2)

where the hyperbolic tangent function is represented by tanh. It represents a smooth function, extending below zero when applied in a negative part with a larger gradient. It is important to note that the TanhExp requires fewer calculations.

The Tree-CNN used in this work has 15 layers, which are built based on the generic architecture shown in Figure 3, in which four convolutional blocks are present. Each of these blocks contains two groups of 3 × 3 convolutional kernels, some pooling layers, and some batch normalization layers, which are used to tune the model to achieve faster and more precise performance at a reduced time. A momentum of 0.8 and a weight decay of 0.0001 is achieved. The model is trained for 200 epochs, and the accuracy, loss, and validation are recorded.

After the training, our model was tested on the test dataset to ensure that consistent results for both the training and testing sets are obtained. In addition, we evaluate and compare the performance of our Tree-CNN model using some machine learning algorithms such as the K-nearest neighbors algorithm (KNN), a simple convolutional neural network (CNN), and also the supporting vector machine (SVM).

4.3. Evaluation Metrics

The evaluation metrics used in this work to measure the performance of the model are the accuracy, sensitivity (also called recall), F1-measure, and the performance metric G-mean. These metrics are used with the aim to evaluate the effectiveness of the proposed model and other machine learning approaches in performing the QKD selection:

$$\mathrm{Accuracy}=\frac{\mathrm{TPos}+\mathrm{TNeg}}{\mathrm{TPos}+\mathrm{TNeg}+\mathrm{FPos}+\mathrm{FNeg}}$$

(3)

$$\mathrm{Sensitivity}=\frac{\mathrm{TPos}}{\mathrm{TPos}+\mathrm{FNeg}}$$

(4)

$$\mathrm{F1-measure}=\frac{\mathbf{2}\times \left(\mathrm{precision}\times \mathrm{recall}\right)}{\mathrm{precision}+\mathrm{recall}}$$

(5)

$$\mathrm{G-mean}=\sqrt{{\mathrm{TPos}}_{\mathrm{rate}}\times {\mathrm{TNeg}}_{\mathrm{rate}}}$$

(6)

where TPos, TNeg, FPos, and FNeg are the true positive, the true negative, the false positive, and the false negative cases, respectively.

The performance metric G-mean, also known as geometric mean, represents a score that helps to understand the specificity of the measured information.

The Area Under the Curve (AUC) is also calculated to indicate a decided classifier’s capacity to differentiate between the various classes used.

The receiver Operating Characteristic (ROC) curve is analyzed and represented graphically, where the x-axis represents information about specificity and the y-axis represents sensitivity.

4.4. IoT Scenario

We appropriately configured the IoT test environment to obtain our dataset and evaluate the model. The major components of the IoT test scenario are the server, the IoT controllers, and the IoT devices. We used three IoT controllers, one server, and various IoT devices in the experimental setup to evaluate the developed model.

These component systems are connected to several IoT sensors to exchange information with the server. The initial number of quantum bits sent to the controllers for producing the secret key qubit was 1000 photons, as suggested by the authors in [46]. Afterward, we increased the flexibility of our mechanism by enhancing the number of photons to 1500. In order to achieve comprehensive communication between the devices, various IoT sensors were used to send the measured data to the IoT controller, which then transmits the data between the devices using 6G communication to an access point (AP). Progressively, the data are transferred to the server in the cloud for analysis, processing, and storage. The QKD was used between the AP and the controller as a means of protection against possible attackers. Free space optics communication occurs in the quantum channel. Hence, the keys used in the communication help to encrypt the data in the radio frequency channel of the 6G communication.

5. Results and Discussions

In this section, we present and discuss the experimental results obtained. The proposed model was developed and tested using a computer system having a CPU Intel Core i7-8750H@ with 2.20 GHz, using GPU, a GeForce 1070ti video card, and RAM of 8 GB. In addition, we perform a comparison of some machine learning models used to implement the QKD, specifically similar solutions based on RF [23].

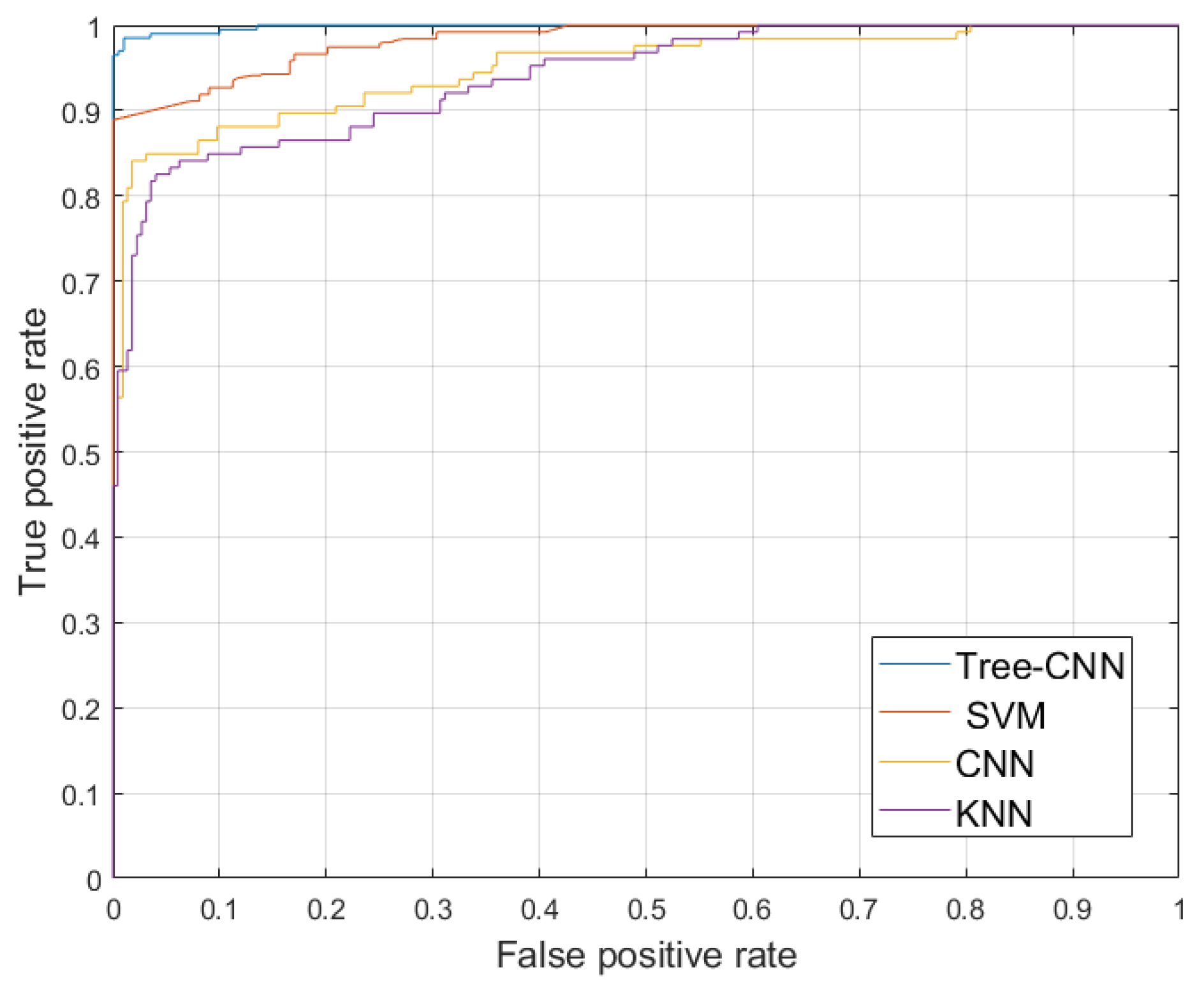
Figure 4 shows the robustness and precision of each algorithm through the receiver operating curves (ROC), which are used to analyze the results of each algorithm. The Tree-CNN model almost reached the 1.00 value, proving that it is a robust model. Additionally, the curve of the Tree-CNN is above that of the SVM, CNN, and KNN, suggesting that the Tree-CNN has good behavior in generalization. As a result, the findings show that our proposed model performs better in terms of robustness and precision.

Table 1. AUC Results of the algorithms for all protocols.

	Tree-CNN	SVM	CNN	KNN
AUC	99.89	98.17	97.02	95.76

presents the AUC results of the algorithms for all protocols showing that the Tree-CNN has the value of 99.89%, followed by the SVM model with an AUC of 98.17%, normal CNN model that achieved an AUC of 97.02%, and the kNN model with the AUC of 95.76%.

Table 2. Performance parameter results for the Tree-CNN model and related studies.

Model	Sensitivity	F1-Measure	G-Mean
Proposed	0.9913	0.9895	0.9906
RF [23]	0.9814	0.9726	0.9801

shows the performance comparison in terms of sensitivity, F1-measure, and G-mean of the proposed solution and another solution obtained using the RF algorithm in [23]. From the results, it can be observed that while the model proposed with RF achieved 98.14%, 97.26%, and 98.01% for sensitivity, F1-measure, and G-mean, respectively, our proposed model obtained 99.13% sensitivity, 98.95% F1-measure, and 99.06% G-mean. Hence, our model outperforms the existing model in this regard.

This research also determined which algorithm met the requirements for real-time optimization on a large-sized QKD network. As a result, a time test was run for each algorithm that produced improved AUC values, which were the Tree-CNN, SVM, and CNN.

Table 3. Time Cost Performance in seconds for Predicting the Optimal Protocol.

	Tree-CNN	CNN	SVM	B [23]
Time Cost	0.65	2.3	3.1	0.65

shows that the Tree-CNN presents an efficient result concerning the timing test. This performance rate occurred because the Tree-CNN with the TanhExp-based activation function presents a low complexity mechanism when in comparison to others, except for the model using RF [23], which serves to demonstrate that although we used a more complex model with Tree-CNN, we still generated a light and efficient model. Thus, the TanhExp has the property of having better information dissemination and also makes it possible to have a model with better learning speed than other functions. A more concise normalization approach is used, which increases the throughput of the deep learning model’s training process.

To demonstrate that the prediction performed by Tree-CNN can be used in real situations, we measured the relationship between the actual and predicted values for BB84, MDI, and TF-QKD protocols for different distances. Thus, we implemented and tested the Tree-CNN (T-CNN), SVM, CNN, and KNN machine learning algorithms.

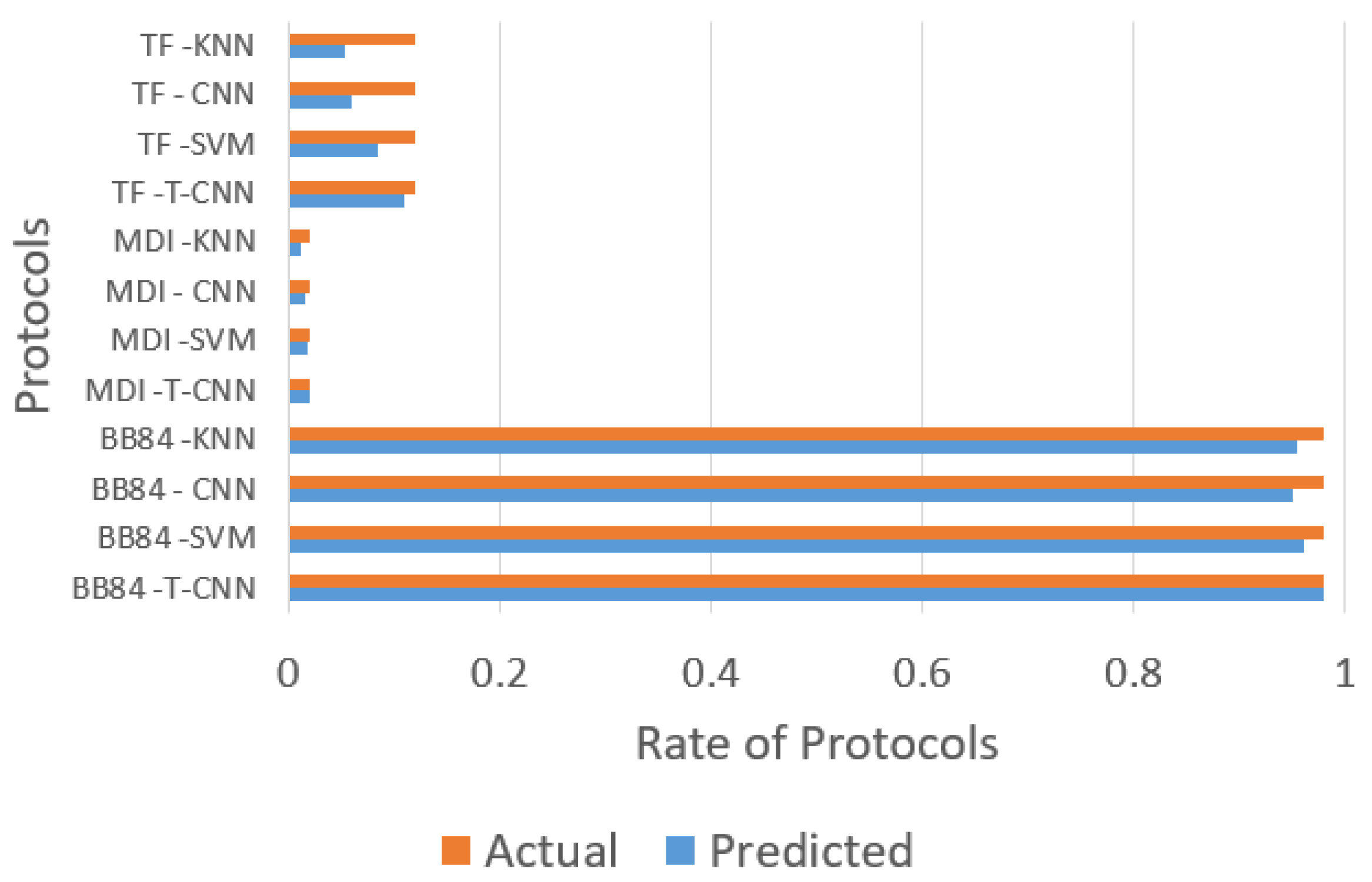
In Figure 5, the results obtained for a transmission distance range of 0 to 250 Km are presented.

As depicted in Figure 5, the BB84 protocol reached the best results because of the short transmission distances, as concluded in different works [47].

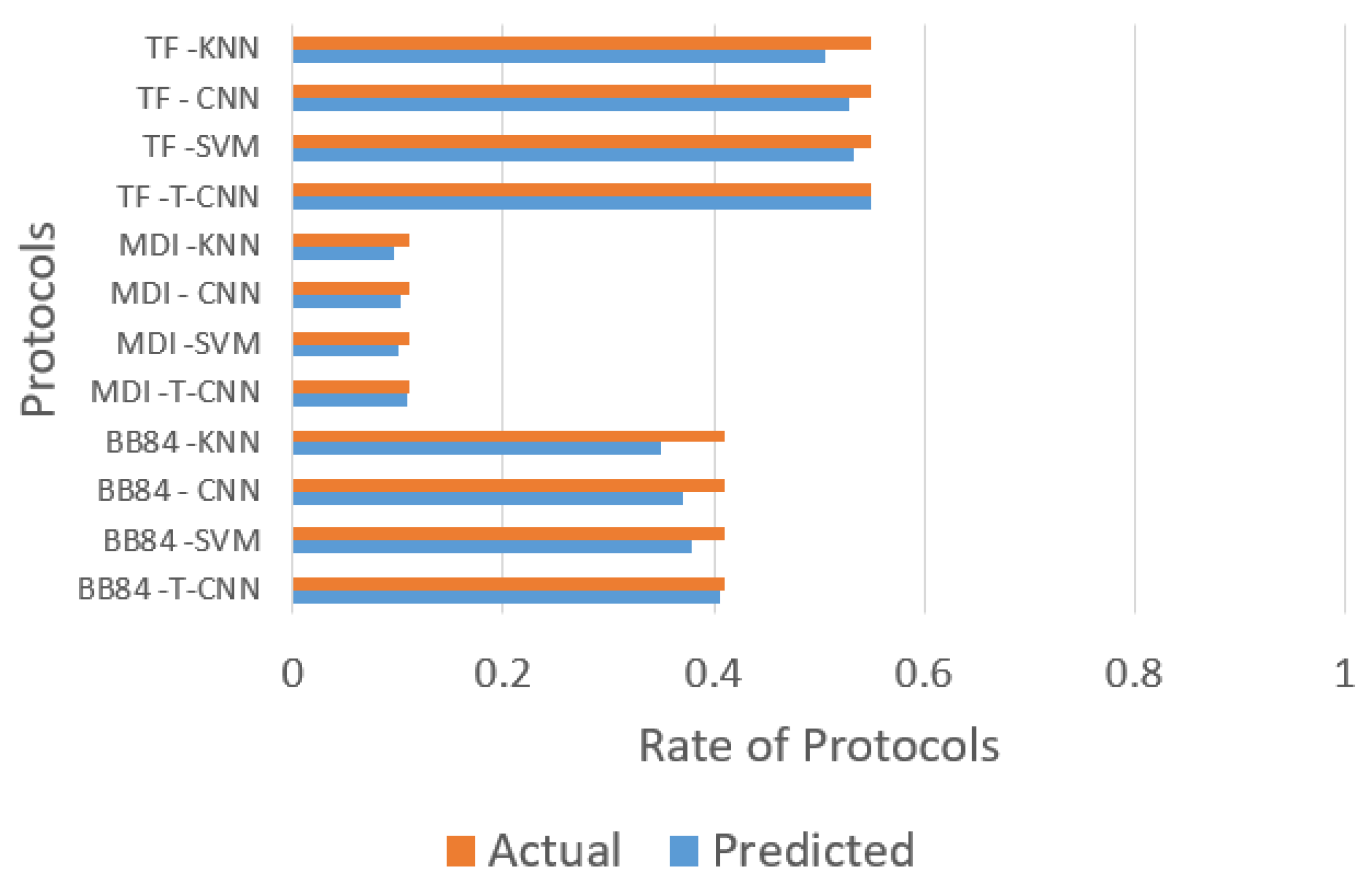
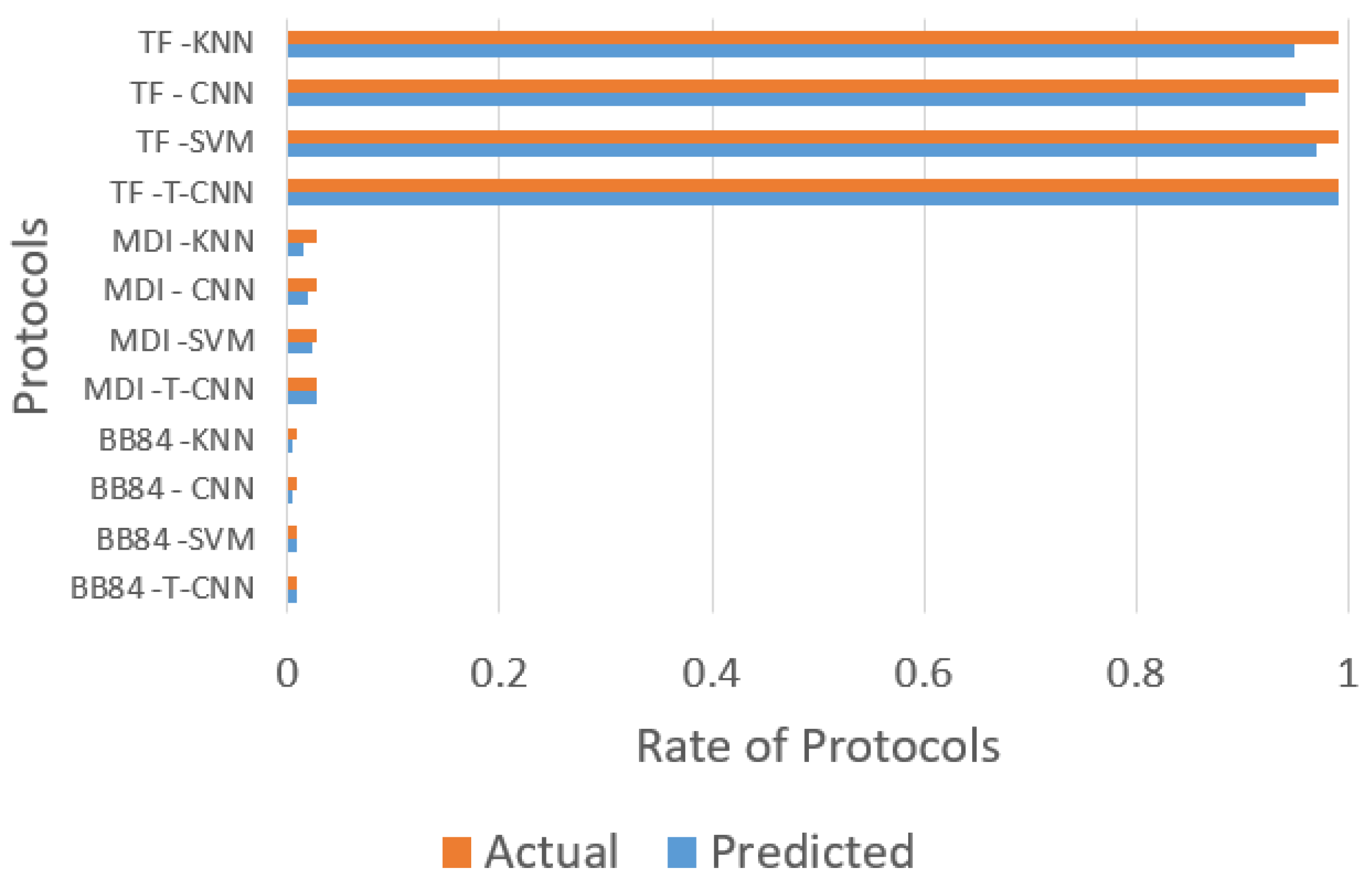
In Figure 6, the results obtained for a transmission distance range of 250 to 500 km are presented. In Figure 7, the results obtained for a transmission distance range of 250 to 500 km are presented. As can be observed, the best performance results are obtained by the TF protocol.

Figure 5, Figure 6 and Figure 7 show that the performance of the QKD selection protocols varies greatly at different transmission distances. The protocol BB84 presents better results for a short distance, in scenarios of 1 to 200 km. On the other hand, the TF-QKD presented better results for long distances. In addition, it is worth noting that the predicted result values obtained by the Tree-CNN algorithm reached the highest level of agreement with the actual values.

6. Conclusions

In order to increase the security of communication in next-generation networks, for instance, communication between servers and IoT controllers in 5G or 6G networks, our research suggested a novel way of selecting an optimal QKD protocol. The Deep Convolutional Neural Network, Tree-CNN, using the TanhExp activation function outperformed the other methods in the experimental testing and hence has higher advantages in terms of precision, robustness, and efficiency in handling scenarios of long or short distances. Tree-CNN maintained that the proposed algorithm offers personalized ideas for communication to users by obtaining an AUC of 99.89% during testing. In comparison to other algorithms, Tree-CNN also shows a quicker prediction speed. In determining the best QKD protocol, it calculated the time cost as 0.65 s. The outcome, therefore, demonstrates that the Tree-CNN is a fast method for selecting the ideal QKD and other system parameters in real-time communication for upcoming large-scale communications. Additionally, it performs a classification with high AUC, according to the obtained results. The experimental findings in this study demonstrated that the smoothness, nonmonotonicity, and delimitation qualities of the Tree-CNN algorithm are useful performance indices in choosing the best QKD protocol. As a result, the data-forgetting problem in the retraining phase of new models is not an issue with the suggested strategy. The technique has minimal computing cost, which makes it simple to implement the model in IoT controllers without overtaxing the IoT devices. Future research will put the suggested approach for detecting an attacker during the distribution of quantum keys between communicating devices.