Abstract
Even though organic farming is perceived worldwide as the most eco-friendly agricultural method, its significantly lower yield compared to conventional farming poses a major challenge in ensuring food security for the ever-increasing world population. On the other hand, the adverse environmental impacts of conventional agriculture due to the uncontrolled use of key farm inputs like fertilizer and irrigation water cannot be overlooked. In this context, we develop a new eco-label to promote an efficient agricultural method that provides the right balance between yield and environmental impacts through the optimal use of these farm inputs. The proposed eco-label is applied to a game-theoretic model of a farmer-retailer supply chain under demand and yield uncertainties. We consider the demand as a function of the product’s retail price, greenness, and quality; and model yield using a crop-response function. The analytical results derived help optimize the farm inputs, retail prices, and order quantity so that the stakeholders’ profits are maximized. We also investigate the effects of yield information sharing in this supply chain and find that the stakeholders must share yield information when environmentally conscious consumers dominate the market.
1. Introduction
The increasing world population and the associated need for ensuring food security using limited resources have forced agricultural communities around the world to rely on high-yield farming techniques which depend on excessive fertilization, which adversely affects the environment in numerous ways. The life cycle assessment of a wheat-to-bread supply chain reveals that the use of ammonium nitrate fertilizers accounts for 41.9% of the total Human Toxicity Potential of the supply chain [1]. Today’s consumer is conscious and vocal about health and environmental concerns. Therefore, there is an increasing importance for sustainable practices in agriculture to ensure safe and healthy food for human consumption. The emergence of various farming practices like Good Agricultural Practices (GAP) [2], Three Controls Technology [3], System of Rice Intensification [4], and organic farming [5] are some examples of this development. Among all the farming methods developed, organic farming has been identified by most consumers as the most eco-friendly mode of agriculture [6,7] as it completely avoids the use of synthetic fertilizers. The premium prices that the consumers are willing to pay for organic farm products support this observation. However, many scientific studies across the world point out a significant reduction in yield in organic farms due to the non-usage of fertilizers [7,8]. These studies highlight that the environmental impact measured per hectare of cultivated land was less for organic farming when compared to conventional farming. However, this impact was higher when the impacts were measured per tonne of farm output, primarily because of the low yield from the organic farming practices. This means that organic farming would require more land area than conventional farming to produce the same output (yield) as that of conventional farming. This can significantly affect land use patterns, which in turn causes severe environmental impacts. Moreover, attempts to increase the yield in organic farming would require high compost quality and improved quality of organic fertilizers, which in turn would increase the investment in time, money, and effort. All of this may make organic farming economically less viable [5]. In fact, it is with this issue in mind Stubenrauch et al. [9] developed a legal framework to merge the conventional and organic agricultural systems. Such a transformation is necessary for the present-day agricultural settings to ensure safe and high-quality food for the masses.
Another important aspect that has a major impact on the yield and sustainability of agricultural practices is the type of irrigation facilities used. It is observed that the yield of mostly all agricultural products are dependent on the type of irrigation facilities used [10], and many of these products have a very high water footprint [11]. Hence, the excessive water consumption is a matter of grave concern.
Given the above discussion, we identify the need for promoting an agricultural practice that is more efficient in terms of output and resource usage. Specifically, the focus should be on improving the farm yield while minimizing the product’s environmental impacts per unit quantity. This requires optimizing the primary farm inputs like fertilizer and irrigation water, as these are the key factors that influence the yield when adequately applied but create severe environmental impacts when overused. Since eco-labels play a crucial role in promoting green approaches, we argue that these labeling schemes should consider quantities of fertilizer and irrigation water used while determining the greenness of an agri-food product. While numerous eco-labels are prevalent worldwide for agri-food products, they fall short of meeting this requirement (www.ecolabelindex.com; Accessed on 20 April 2021). To bridge this gap, in this work, we develop a new eco-labeling scheme for agri-food supply chains. Our labeling scheme opens up the possibility of incorporating yield considerations while certifying agri-food products, which is crucial considering the rising challenge of feeding the growing world population. On the practical side, the proposed scheme can be applied in various agricultural settings with little modifications due to its coherent nature.
To demonstrate the effectiveness of the proposed eco-label, we model a two-echelon green agri-food supply chain consisting of a farmer and a retailer. Such supply chains are typical in supermarket contracts where the supermarket procures fresh agricultural products directly from the farmer [12,13]. The farmer and the retailer enter into a contract where the farmer agrees to supply a fixed quantity of green products to the retailer at a fixed price for a period of time as mentioned in the contract. The farmer is expected to replenish the retailer’s inventory at fixed intervals. While it is common in the literature to consider the demand at the retailer for any green product to be dependent on its retail price and greenness level [14,15], a third factor in the form of product quality needs to be considered in the case of agricultural products [16]. As the quality of these products decreases over time due to physical deterioration, the consumers refrain from buying them when their expiry dates grow nearer [17]. In addition, it is necessary to consider uncertainties in some form (due to the availability of alternative products, other consumer preferences, etc.) as the fourth factor affecting the demand for these products. There is a dearth of supply chain models in the literature that account for all these factors while modeling product demand. To address this gap, we model the retailer’s demand as a function of these four factors.
The proposed eco-labeling scheme, which considers a reduction in fertilizer and irrigation water usage, is used to certify the farmer’s products. The retailer decides the order quantity and the retail price of the product, while the farmer chooses the amount of fertilizer and irrigation water to be used so that his yield will be sufficient to meet the retailer’s demand. In this sense, this is a typical futures contract where the retailer is deciding on an order quantity for the future, and the farmer is planning for the present. As his yield is uncertain, the farmer forecasts the yield before sowing seeds. This forecast information, along with the retailer’s order quantity information, is then used to decide the farm inputs. By considering uncertainties in yield and demand together in our supply chain model, we explore some critical areas that are rarely studied in the sustainable agri-food supply chain literature. We derive closed-form solutions for the farmer’s and retailer’s problems under different market settings to aid them in decision-making.
Finally, through rigorous numerical analysis, we study the effects of yield information sharing on the stakeholder’s profits. While researchers have conducted extensive studies on the effects of demand information sharing, the topic of yield information sharing has remained less explored in the context of sustainable agri-food supply chains. Our study provides some valuable insights to the stakeholders by helping them identify the scenarios where it is beneficial to share the yield information.
The remainder of this paper is organized as follows: In Section 2, a literature review is conducted to discuss the existing works in this area and identify the research gaps. Section 3 details our model and the associated assumptions, and in Section 4, the model is analyzed to obtain closed-form solutions for the farmer’s and retailer’s problems. In Section 5, a numerical study is conducted to study the effects of information sharing. The significance of the results obtained is discussed in Section 6, and finally, the conclusions are drawn.
2. Literature Review
Recognizing the pivotal role of sustainable agricultural supply chains in shaping the future of humanity, the scientific community has conducted extensive research in this field. Some of the most recent studies in this direction include the impact of COVID-19 on these supply chains [18,19], drivers and barriers to sustainability [20,21,22], sustainable supply chain logistics [23,24], stakeholders’ contributions to improving sustainability [25], etc. Another exciting but not intensely explored area in the literature is the effect of knowledge management on the internationalization of green agri-food industries [26]. A wide array of review articles [27,28,29,30,31,32,33,34] dealing with various aspects of these supply chains have been published recently. In particular, Nematollahi and Tajbakhsh [28] stress the importance of developing new solution approaches to deal with the agri-food supply chain problems, which are complicated due to the presence of demand and yield uncertainties and sustainability issues. Nematollahi and Tajbakhsh [28] also highlights the limited number of studies investigating the effect of product perishability in these supply chains. Although there has been considerable attention to modeling the perishability of goods in supply chains [35,36,37], most of these models do not consider the sustainability aspects in defining the demand function. While Song et al. [38] address the perishability aspect by using a demand function that depends on the greenness and freshness of the product, they fail to incorporate the uncertainties in their model.
It is also important to consider the factors like the amount of fertilizer and water used during cultivation while determining the greenness level of an agri-food product, as these factors have a significant impact on the environment [1,11]. Excessive use of synthetic nitrogen fertilizers results in high greenhouse gas emissions, which must be avoided. However, avoiding their use entirely, as in the case of organic farming, is not advisable as it results in significant yield losses. To counter this, Stubenrauch et al. [9] demand amending the organic farming provisions by permitting the controlled use of synthetic fertilizers and pesticides. Similarly, Karamian et al. [39] stress the importance of reducing water consumption to improve the sustainability of agricultural systems. The research aimed at optimizing fertilizer and water usage is mostly case-study based (e.g., [40,41,42,43]), and there exists a need for a standard way to handle such problems. It is in this context that we develop a new green labeling scheme based on the ideas of Stubenrauch et al. [9] and Karamian et al. [39].
The yield in agricultural systems has been modeled using various crop response functions like the von Liebig [44], Mitscherlich–Baule [45], etc. However, these functions are not invoked often in the context of agricultural supply chains. In addition, Peng et al. [46] discuss yield uncertainties in a contract farming supply chain by studying the effects of government subsidies and the level of uncertainties on the supply chain performance. Zare et al. [47] point out the importance of risk-sharing in a cocoa-beans supply chain in the Ivory Coast. Behzadi et al. [48] developed a stochastic model for an agribusiness supply chain to investigate the effect of various strategies on managing yield disruptions. The major highlight of their work was the consideration of the perishability aspect of the product alongside yield uncertainties. Combined analysis of perishability, demand, and yield uncertainties together are sparse in the literature. Golmohammadi et al. [49] discuss the importance of considering supply and demand uncertainties jointly to make efficient decisions. An equally important aspect to consider is the sharing of yield information. While the supply chain literature is rich with studies on cost and demand information sharing, only a few studies consider the sharing of yield information [50]. Table 1 compares our model with the most relevant previous studies in the field of agri-food supply chains.

Table 1.
Comparison with Previous Studies.
Our work contributes to the literature in many ways. Firstly, the proposed eco-labeling scheme is a unique approach that promises an improvement in agricultural sustainability by assuring good crop yields while limiting the adverse environmental impacts of uncontrolled fertilizer and irrigation water usage. Secondly, the use of the crop-response function (von Liebig Production Function) in our supply chain design helps to model crop yield more realistically. This approach, which is unprecedented in the supply chain literature, has a remarkable advantage. Since such functions quantify crop yield based on the main farm inputs such as fertilizer and irrigation water, their usage in a supply chain model helps us optimize these farm inputs for good yields. Thirdly, our work adds to the sparse literature dealing with combined aspects of perishability, demand, and yield uncertainties in sustainable agri-food supply chains. Finally, the literature on yield information sharing is extended by conducting numerical studies to identify instances where sharing yield information benefits the stakeholders in the context of the farmer-retailer supply chain.
3. Model Formulation and Assumptions
We consider a two-echelon agri-food supply chain problem in which a farmer signs a supermarket contract with the retailer. The model is described in Figure 1 and a comprehensive list of decision variables and parameters used in the model is given in Table 2. In the beginning, the farmer forecasts the uncertainty in his (Without loss of generality, we refer to the farmer as ‘he’, and the retailer as ‘she’) yield () and decides whether to share the forecast information with the retailer. Since it is almost impossible to predict the exact yield accurately, we associate an error () with his forecast. The retailer chooses her order quantity (Q) based on the available information on yield uncertainty and shares her requirements with the farmer. In case of a discouraging forecast, information sharing helps the farmer avoid shortages by forcing the retailer to reduce the quantity of her order. On the other hand, when the forecasts are good, sharing yield information encourages the retailer to order more (provided there is demand), resulting in better revenue for both players. In response to the retailer’s requirement, the farmer determines the fertilizer requirement () and irrigation water requirement (). The crops are then allowed to grow with the controlled application of these inputs. We assume that the crops, especially fruits and vegetables, can be harvested multiple times at regular intervals once they are fully grown, [56,57] and hence there is a steady supply of products from the farm throughout the demand season.
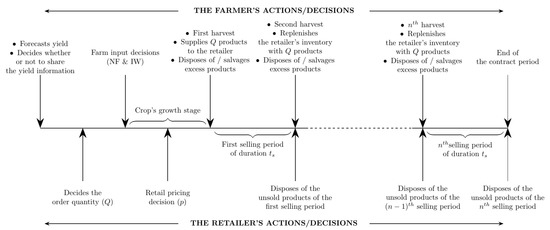
Figure 1.
Timeline of Events.

Table 2.
Notations Used.
Once the crops are fully grown, they start bearing fruits/vegetables, which the farmer harvests at regular intervals of . The number of harvests in a crop season is n. After each harvest, he supplies Q quantity of these products to the retailer, and the remaining are either salvaged or disposed of. He cannot replenish the retailer’s inventory daily, as the choice of maturity stages and harvesting intervals varies across different fruits and vegetables [56,57]. To assure a daily supply of his products, he can preserve the products of a single harvest and sell only a part of it daily until the next harvest. In our study, this possibility is ruled out; instead, we assume that the farmer sells his entire produce soon after each harvest, as it helps eliminate the holding and preservation costs. Due to the consumer’s dependence on the sensory attributes of the agri-products to evaluate freshness [58,59], their perceived value of freshness will be high at the beginning of a selling period. This results in more sales at the onset of each selling period, encouraging the retailer to let the farmer sell his entire production to her at the beginning of each selling period.
The period between each harvest constitutes the retailer’s selling period, and her inventory is replenished at the beginning of each period. There are n such selling periods during the contract duration (Figure 1). Each time the stock replenishment occurs at the retailer, she may have some unsold products from the previous selling period in her inventory. If she does not dispose of these old products during each replenishment, her inventory will have perishable products of the same type but with different ages and quality levels. This makes it difficult for the customers to separate out the fresh products from the old ones and hence impacts the retailer’s profits [60]. To avoid this issue, a rational retailer disposes of the unsold products (at a disposal cost of ) every time the farmer replenishes the stock. In addition, her limited inventory space is another reason for forcing her to dispose of the old products. In cases when she is unable to meet the demand of the consumers, there are chances that her goodwill is affected, and the consumers might approach a different retailer during their next purchase. Therefore, she must minimize the shortage of products. This possibility is modeled by incorporating a shortage cost of for her.
It is assumed that an average-price contract, similar to that employed by retail giants like Walmart, La Colonia, etc. [61] exists between the retailer and the farmer. According to this contract, the retailer pays the average traditional market price (w) to the farmer regardless of whether the market price rises or falls during the demand season. This helps the farmer, for it considerably reduces his risk in terms of price fluctuations. On the other hand, the retailer enjoys an assured supply of quality products throughout the demand season [62].
Generally, in supermarket contracts, the retailer’s order quantity remains fixed throughout the crop season. She terminates the contract of the farmer who is unable to supply products as per requirement. This forces the farmer to compensate for the deficit by getting products from open markets in the event of shortages, which incurs a “shortage cost” () for him [12,13]. When the yield per harvest () is greater than the order quantity per period (Q), the farmer sells the excess products at salvage value () in open markets, which promotes direct interaction between him and the consumers [12,63]. In cases where there are difficulties in accessibility to these open markets due to reasons like remote farm location, high transportation costs, etc., he disposes of the surplus products, at a cost of . Our model considers both of these cases, as explained later in Section 4.2.
The individual rationality constraint ensures the farmer’s participation in the contract, and requires that the wholesale price should be set higher than the salvage value (). Similarly, incentive compatibility constraint forces the farmer to optimize resource utilization, and would demand that the shortage cost is at least equal to the wholesale price (). This constraint makes fetching products from open markets an expensive alternative.
The total yield (Y) of the farmer is determined by the linear von Liebig production function and other external uncertainties. The uncertainties include the factors that are not under the farmer’s direct control, for example, climatic variations. The capability of the linear von Liebig specification in modeling crop response is discussed in detail by Grimm et al. [44] and Holloway [64]. Though non-linear specifications of this function exist, the selection of the most appropriate functional form for a crop response problem must be made after considering the available empirical data [65]. In this work, we limit our interest to the linear model, as many empirical studies [44,66,67] identify the linear formulation as a good fit for the available data. According to the linear von Liebig function, the yield of a crop is given by:
As per this function, the yield potential of a crop is limited by that factor that is not applied to the greatest extent. Here, the limiting factors are either or , which represent the fertilizer and irrigation water requirement, respectively. The variable m, termed as the “yield plateau”, is the maximum possible crop yield that can be achieved by varying and . The expression for m is given as . Furthermore, are constants that are to be determined by field experiments and and are the optimum values of fertilizer and irrigation water that results in maximum yield. The intercept () gives the expected yield when () is the limiting factor, in absence of the fertilizer (irrigation & rainfall). The uncertainty in yield can be modeled using a Gaussian disturbance [44] with the mean of zero and the variance . Let and be the corresponding pdf and CDF of the distribution. Thus, total yield in the presence of uncertainties is given by:
Even though the exact value of is not known to the farmer in advance, he can estimate it before sowing the seeds. This is important for him, as his input decisions are heavily dependent on these forecasts. Denoting the forecast signal obtained by him as , we can write, . Here, captures the noise in the forecast signal, which can be considered to be normally distributed with mean zero and variance . Such an approach is common in literature [68,69] and when both and are normally distributed we have:
Let us use and to define the pdf and CDF of the corresponding posterior distribution of yield uncertainty (). The farmer can decide whether to share the forecast information, which includes the updated distribution parameters ( and ) with the retailer. In such cases, the retailer makes their decisions based on the shared information. However, in the absence of shared information, they depend on their prior beliefs (). Nevertheless, it is assumed that all other information associated with the farmer is known to the retailer. This is a reasonable assumption as the retailer can access the details of the farm parameters () from the farm records used for green certification [70]. Additionally, the production costs () are generally known to everyone through the maximum retail prices set by the suppliers and irrigation costs set by the authorities. The other farmer related costs () are also known to them as they have access to the agri-food markets.
3.1. Green Labeling
Since the consumers are environmentally aware, it is essential to have a labeling scheme that classifies the products into two categories: green and not-green. The primary requirement of such a labeling scheme is to have a greenness function that can measure the product’s environmental sustainability levels. Global Warming Potential (GWP) during a product’s life cycle is considered one of the major indicators of its environmental sustainability [42]. Products with lower values of GWP are generally considered to be green. Since the nitrogen fertilizer application contributes to a high GWP, reducing its usage improves product greenness [71]. The greenness level achieved by adequate fertilizer management is given by:
Another important indicator that determines the greenness level of an agri-food product is the ability to save water during irrigation. Methods such as drip irrigation help in saving water by minimizing water losses due to runoffs or evaporation [11]. The agri-food products can be considered green only if significant water savings are obtained during their cultivation. The greenness level achieved by adequate irrigation water management is given by:
where denotes the efficiency of the irrigation technique employed, and corresponds to the maximum amount of water available for irrigation. When , the irrigation technique employed is highly efficient, and there is no wastage of water. For , the amount of water wasted is , and with the decrease in value of , the wastage increases. In our model, we assume that ). This ensures that the farmer is not constrained due to the unavailability of water even when he aims for the maximum yield of m.
A composite indicator defined as an additive function of fertilizer () and irrigation water management () is used for describing the product’s greenness level ():
where, and . Since, by definition , we have that . Note that can be adjusted depending on the factor to be prioritized. For example, can be assigned a higher value when the farmland considered is in a water-scarce region. This definition of follows a weak sustainability approach where a sufficiently high value of one indicator compensates for the poor performance of the other [72]. This sustainability approach is necessary in agricultural settings where a farmer faces issues such as water scarcity or soil depletion. For example, in areas where is low (water scarce areas), will be low even when efficient irrigation techniques are used (). In this case, a weak sustainability approach rewards the farmer with a high greenness value if his value is high.
To communicate the greenness of the product with consumers, we make use of eco-labels. Since most of the eco-labeling agencies like the EU Organic Product label, India Organic, USDA Organic (See www.ecolabelindex.com for more details; Accessed on 20 April 2021), etc., do not explicitly consider the reduction in fertilizers and water consumption when evaluating product greenness, a new scheme is proposed here. This scheme uses the greenness function defined by Equation (7) and considers the reduction in fertilizer and water usage at its core when evaluating greenness. Additionally, to address the concerns of health-conscious consumers, Integrated Pest Management (IPM) [73] or Agroecological Crop Protection (ACP) [74] are made mandatory requirements to ensure that the products are free of pesticide residues. Thus, according to our scheme, the product is certified green if the IPM or ACP practices are followed and the product greenness () is at least equal to the minimum greenness level required to obtain the green certification ().
Decreasing fertilizer application () improves the product greenness (see Equations (5) and (7)) but at the expense of crop yield (Equation (1)). To balance this tradeoff between yield and greenness, we use the concept of Greenhouse Gas Emission Intensity (GHGI) which measures the Global Warming Potential (GWP) per unit yield of the farmland [75]. A low value of GHGI is always preferred as it ensures minimal emissions per unit yield. As GWP and yield are increasing functions of the fertilization level, GHGI varies at different levels of applied fertilizers. We determine a maximum allowable fertilization level such that GHGI is within the limits of the prevalent emission regulations. As a special case, when the GHGI function is convex, as in Chi et al. [71] and Kim et al. [41], can be determined as the fertilization level that minimizes GHGI. According to the linear von Liebig function, corresponding to this value of , there is a value of irrigation water requirement () such that both and become the limiting factors. Mathematically, this can be expressed as . Now, the minimum greenness level required for certification () can be calculated as:
where and . Note that, represents the maximum greenness level achieved by irrigation water management when and the irrigation efficiency () corresponds to the efficiency of the existing most efficient irrigation technique. The new labeling scheme can be explained using the cases below:
- WhenThis happens only when the farmer’s fertilizer () and irrigation water () usage are precisely equal to their corresponding maximum permissible limits defined by the labeling scheme (). Moreover, the farmer should be using the most efficient irrigation technique (). This results in the GHGI value being at its minimum or the maximum permissible limit depending upon whether it is convex or not. In both cases, the emissions are within limits, and hence the farmer gets a green certification.
- WhenFor this to happen, the farmer should use less quantity of fertilizers and irrigation water than the maximum permissible limits mentioned in the labeling scheme (). When the GHGI function is convex, this results in a higher GHGI value than in the previous case where . Although the GHGI is high, the Global Warming Potential (GWP) in this case will be lesser than that in the scenario due to the reduced fertilizer and irrigation water usage. The reduced GWP helps the farmer obtain green certification, which is justifiable. A non-convex GHGI function will also result in a green certification because GWP is lesser.
- WhenThis scenario is marked by the intense use of fertilizers () and irrigation water (), resulting in and . Here, regardless of the convexity of the GHGI function, the emissions and the emission intensity are on the higher side. According to Carlson et al. [76], it is important to concentrate mitigation efforts on crops and locations that exhibit high emissions and high emission intensities. Moreover, from Equations (6) and (7), it can be understood that a poorly designed irrigation technique with a small value of irrigation efficiency () can also result in even when fertilizer and irrigation water requirement are well within limits (). Here, the farmer is to be penalized for wastage of water stemming from the improper design of the irrigation facility. Therefore, to force farmers to go green, the products with will not receive green certification.
Chen et al. [77] discuss the significance of eco-labels that encourage efficient farm management practices in promoting sustainable agricultural methods among farmers. Due to the flexibility offered by this scheme in terms of fertilizer usage, existing organic consumers may find it unattractive. However, such schemes can target the share of the eco-sensitive population who cannot buy organic products at premium prices, provided that the retail prices are lower [78]. Furthermore, educating the consumers about the importance of promoting sustainable farming techniques that ensure better yield compared to organic farming is critical. This could make more consumers embrace the new labeling scheme.
It should be noted that in our labeling scheme, the greenness is quantified based on only two factors, which are fertilizer and irrigation water consumption. Although adherence to IPM or ACP practices is made mandatory for certification, they are not used in calculating greenness . This approach is justifiable as we attempt to quantify greenness based on the factors that directly influence yield. Although judiciously administered pest control techniques help the farmer prevent yield losses due to pest attacks, there is no significant evidence in the literature that claims an improvement in total yield by using these control techniques. This means that practicing IPM or ACP does not help improve the yield, but it only safeguards the farmer against yield losses.
3.2. Modeling Demand
Since the products are perishable, their quality is expected to deplete with time. According to Chen et al. [37], the quality level of the product as a function of time t can be written as , where is the initial quality, and represents the deterioration rate. Not all vegetables have the same shelf-life, and hence the deterioration rate depends on the type of vegetable under consideration. The demand for the product is a function of the retail price, greenness, and product quality. Since product quality is time-dependent, the demand for the product varies over time. We can write the demand of an agri-food product with deterioration rate and quality function at any time t as [37,79]:
where = Potential Market Size; = Price Sensitivity Factor, ; = Greenness Sensitivity Factor, ; = Quality Sensitivity Factor, . Note that, in this study, we attempt to develop a model in which the farmer is supplying a single type of agri-food product to the retailer.
An environmentally-conscious consumer prefers an eco-labeled product over one without a label. To capture this sensitivity of demand to product greenness, the term is included in the demand function such that:
Thus, a product with an eco-label increases the demand by , in comparison with a product without one. Considering the above factors, demand for the product in the retailer during a selling period of duration is given by:
As consumer demand for agri-food products can continue to vary, it is important to consider the stochastic nature of the demand function. A random variable can represent the stochasticity in demand. This random variable has PDF and CDF as and , respectively, defined over the support with mean and standard deviation [68]. Thus, the demand in each selling period is given by:
where D is the deterministic part of the demand. To ensure a positive value of demand, we impose a condition that on all admissible parameter values. As discussed earlier, there are n selling periods in the entire length of the selling season. To reduce the problem complexity and ensure analytical tractability, we assume that the selling periods are identical in terms of the realized values.
The farmer’s major expenses while growing his crops include the cost of fertilizers, (denoted by per unit quantity of fertilizer used) and that for irrigation (denoted by per unit quantity of water consumed). We assume that all other associated costs are included in this cost component. Any additional expense of the farmer, such as the transportation cost, is assumed to be less significant and therefore not considered.
4. Model Analysis
We aim to determine the equilibrium decisions of the farmer and the retailer so that their profits are maximized. A backward induction approach is used to obtain a solution for our problem [69]. Thus, we begin by solving the retailer’s problem of deciding the retail price and then solve the farmer’s problem of determining the input levels. Finally, we find the solution for the retailer’s order quantity requirement problem. Note that, in our approach, the quantity decision precedes the price decision, but it is immaterial whether the price is decided before or after the realization of the yield. This sequential approach, which is similar to [80], is used to overcome the complexities associated with the determination of closed-form solutions in a joint decision-making case in the presence of uncertainties.
4.1. Determination of Retail Price
The profit function of the retailer in a sales period can be written as:
Depending on whether or not, the retailer will have excess inventory or shortages, respectively. In both cases, we assume that the retailer bears the cost: either the cost to dispose of excess products (at a rate of ) or the shortage cost (at a rate of ). The last term for both cases represents the retailer’s total purchase cost. The terms and are the revenues that the retailer gains in cases 1 and 2, respectively.
For ease of calculation, we represent . Using this expression and Equation (10), the retailer’s profit function can be rewritten as:
Here, D represents the deterministic part of the demand (Equation (9)), and z is the stocking factor. The stocking factor can be a positive or a negative value. It takes a positive value when the demand uncertainty () turns to be positive, thereby compelling the retailer to order more products than D. Alternatively, a negative results in the retailer setting an order quantity less than D, resulting in z being negative. Moreover, if , the retailer will have leftovers; and if , shortages occur. Thus, the selection of z is an optimization problem for the retailer [81,82]. Now, the expected profit function of the retailer is:
Theorem 1.
For following any distribution, the profit function of the retailer is concave in p, and the optimal value of p can be written as a function of z as where, , and
(Proofs for all theories, lemmas, and corollaries are given in Appendix A).
Corollary 1.
The retail price () in the proposed greenness scheme is less than that of an organic labeling scheme () and greater than that in the case of conventional farming (). Mathematically, .
From Corollary 1 it is evident that the new greenness scheme benefits the consumer by providing eco-friendly products at reduced costs in comparison with the organic labeling scheme. Furthermore, it helps the retailer earn better profits by selling products at a higher price compared to the case of conventional farming.
4.2. Determination of Farmer’s Inputs
The retailer transmits the order quantity requirement to the farmer, based on which he has to make his input decisions ( and ). In addition to this, considering the environmental consciousness of the consumers, the retailer can demand the farmer to produce “eco-labeled” products. The profit function of the farmer per harvest can be written as:
where the total yield Y is given by Equation (2). Assuming a steady supply from the farm throughout the selling season, the yield per harvest can be determined as , where n is the number of harvests. Depending on whether or not, the farmer faces a condition of shortage or over-production, respectively. To compensate for the shortage, he purchases products from open markets (at the rate of ), whereas in case of over-production, he sells the excess products in open markets at a salvage value of per unit. If selling in open markets is not profitable, he disposes of excess products at a cost of per unit. To model cases when he earns the salvage revenue, we have to substitute in the profit function. The other terms are the same in both cases. The first, third, and fourth terms represent farmers’ revenue, fertilization costs, and irrigation costs, respectively, during each harvest. Since the fertilizer and irrigation water inputs ( and ) are estimated for the entire crop season, the third and fourth terms are divided by n to obtain the related costs for a single harvest.
Lemma 1.
In the linear von Liebig crop response function, for each value of the ideal yield y, we have a unique set of values of and , which maximizes the farmer’s profit, and these values can be estimated using the relation: .
From Lemma 1, it is clear that and are linear functions of the yield y alone, and thus we can convert the actual farmer’s problem of optimizing and into a new problem of optimizing y. Using Equation (2), the forecast information and Lemma 1, we can rewrite the profit function of the farmer as:
The expected profit function is given by:
Lemma 2.
To obtain a green certification, the farmer should limit his target yield such that , where and is given by Equation (8).
Now, using Equation (12) and Lemma (2), we can write the farmer’s profit maximization problem as:
subject to
In case the farmer does not wish to aim for the eco-label certification, we can replace the above constraint with . Here, the upper limit on the yield is defined by the maximum defined under the von Liebig function. Because of the way is defined, this constraint is always satisfied in the case of green products. We now define a term K, called the cost index, which plays a significant role in the analysis of the farmer’s profit function. Let
Theorem 2.
Based on the presence or absence of open markets and the value of the cost index (K), the farmer’s optimal decisions when he is producing green products are characterized as follows:
- For K , irrespective of the presence or absence of open markets, the profit function of the farmer is concave in y, and the optimal value of y, which maximizes the farmer’s profit, is given by:
- For , and in the absence of open markets, the farmer’s profit function is always monotonically decreasing in y and the optimum value of y for the farmer is .
- For , and in the presence of open markets, the profit function of the farmer is monotonically increasing in y, if for alland the corresponding value of y, which maximizes the farmer’s profit is .
- For , and in the presence of open markets, the profit function of the farmer is monotonically decreasing in y, if for alland the optimum value of y is .
Based on the value of the cost index K, the farmer’s market can be classified as given in Table 3. A high salvage value () such that results in . In this case, statement 3 of Theorem 2 is always satisfied, and the optimal yield for the farmer is . In other words, a higher salvage value encourages the farmer to produce to his maximum allowable capacity as he can sell his excess products in open markets at good prices, helping him earn better profits. This market condition can be considered as a “highly favorable market condition.” A necessary, but not sufficient, condition for is . While in the absence of open markets, this condition is also sufficient, an additional condition is required for sufficiency when open markets are present. Under this setting, according to statement 1 of Theorem 2, the farmer’s profit function is concave in y, and he may not always benefit by carrying out production at his maximum capacity due to the following reasons: (i) In the absence of open markets, he is forced to dispose of his excess products at the cost of which attract revenue losses (ii) When open markets are present, the salvage revenue () is too low that he cannot recover his production costs by selling in these markets. This can be considered as a “favorable market situation” where the farmer benefits only by selling his products to the retailer, but not in open markets. The condition occurs when the production costs are much higher than the shortage costs so that . In such cases, the market condition is “unfavorable” as the production costs exceed the farmer’s wholesale price (as ), and he decides not to use any farm inputs, resulting in a very low yield and subsequently minimal profits. Statements 2 and 4 of Theorem 2 denote these conditions.

Table 3.
Classification of farmer’s markets based on the cost index (K).
The yield under organic farming is generally lower (by about ) than that in conventional agriculture, and this gap is more pronounced in the case of cereals and vegetables (26–33%) [83]. Thus, the maximum possible yield in organic farming () can be represented as a fraction of m, the maximum possible yield in conventional agriculture. In other words, where . Additionally, in the context of production costs, there are no significant differences between organic and conventional agriculture [84]. Considering these factors, the following corollary can be derived from Theorem 2.
Corollary 2.
For a given order quantity Q, when , we have the relation , where is given by Lemma 2 and represents the optimal yield under conventional, proposed, and organic agricultural practices, respectively.
Corollary 2 is significant, especially in cases of vegetable production, where there is a large yield gap (low values) between conventional and organic agricultural methods. In such cases, the yield is highest for conventional agriculture, but it is criticized for its high environmental impacts. On the contrary, the organic scheme, which boasts low ecological impacts, suffers significantly lower yields. Interestingly, the greenness scheme proposed by us provides the right balance between yield and environmental impacts by ensuring a better yield when compared to the organic scheme and lower ecological impacts compared to conventional methods.
Theorem 3.
When the linear von Liebig production function determines the yield of a crop and the farmer aims at maximizing his profit, the optimum quantities of nitrogen fertilizer () and irrigation water () required are and , where is given in Theorem 2.
4.3. Determination of the Order Quantity
Lemma 3.

To ensure that the farmer signs a contract with the retailer to supply green products, the retailer should limit her order quantity (Q) such that , where the expressions for based on the cost index values are given in Table 4.

Table 4.
Expressions for based on the cost index K.
Using the relation , the condition mentioned in Lemma 3 becomes . Using Equation (9) we can rewrite this as . Now, from Theorem 1, we finally have the inequality as . This condition should be satisfied by the retailer when deciding the stocking factor z. Using Theorem 1, we can write the retailer’s expected profit function in terms of the stocking factor z alone, and it will take the form . Now, the retailer’s problem of determining the optimal order quantity becomes a constrained optimization problem as follows:
subject to
As discussed above, the constraint (14), ensures that the farmer signs the contract to sell green products to the retailer. Let correspond to z, which makes the constraint (14) binding.
Theorem 4.
The optimal order quantity of the retailer, which maximizes her profit when selling green products, is given by , where D is given by Equation (9), and is determined as follows:
- If the distribution function G(.) satisfies the condition , for all and , then is given as follows:Here, , and is the largest among the two roots of the equation and is the other root.
- If, along with the conditions given in statement 1, the inequality is also satisfied, then the retailer’s profit function is concave in z, and the value of is given by:where is the solution of equation
- If and G(.) is an arbitrary distribution function, which maximizes the retailer’s profit can be found by an exhaustive search over all z values in the region
- When , irrespective of the distribution of G(.),
It is interesting to note that the term represents the hazard rate of a distribution. All distributions with a non-decreasing hazard rate, which includes the PF2 family of distributions and also the log-normal distribution, satisfy the condition [81].
5. Effects of Information Sharing
Due to the complexities associated with an analytical approach, we numerically study the effects of information sharing on the performance of the supply chain that incorporates the proposed labeling scheme. Specifically, we investigate the sensitivity of the information-sharing decision with respect to (a) varying potential market sizes (); (b) varying greenness level sensitivity factor (); and (c) varying product deterioration rates (). The parameter values used in each case are as follows, unless stated otherwise:
Demand function parameters: Potential market size, ; Price sensitivity factor, ; Greenness level sensitivity factor, ; Quality sensitivity factor, ; Duration of each sale period, ; Initial product quality ; Product deterioration rate, ;
Farm parameters: Production function coefficients, ; Irrigation efficiency, ; Fertilizer requirement for maximum yield, ; Maximum amount of irrigation water available, ; number of harvests,
Farmer’s cost parameters: Salvage value, ; Shortage cost, ; Wholesale price, ; Cost of fertilizers, ; Cost of irrigation water,
Retailer’s cost parameters: Disposal cost, ; Shortage cost,
Greenness function parameters:
The common belief about yield uncertainty before the forecast is that it is normally distributed with a mean of zero and a standard deviation, . The forecast signal noise is normally distributed with a mean of zero and standard deviation, . We have assumed a uniform distribution for the demand uncertainty, such that . This assumption satisfies statement 2 of Theorem 4. The numerical analysis procedure is detailed in Appendix B, and a detailed discussion of the results is given in Section 5.1, Section 5.2 and Section 5.3.
5.1. Varying Potential Market Sizes ()
We consider 30 different problem instances (PI) (numbered 1–30) to study the effects of information sharing under varying potential market sizes (). For problem instances numbered 1–10, is set as 40, while it is equal to 50 for instances from 11–20 and 60 for the remaining ten cases. Additionally, we consider a positive yield forecast () for the first five problem instances in each market size category and a negative forecast () for the remaining five cases. A positive yield forecast denotes favorable conditions where the yield is better than the expected value of y, and a negative forecast indicates unfavorable farming conditions where the yield is less than y. For each problem instance, the order quantities (Q) under different information-sharing scenarios and the corresponding demands are plotted in Figure 2 and the corresponding retail prices are plotted in Figure 3. Similarly, the farmer’s and retailer’s profits associated with each problem instance are also plotted (Figure 4 and Figure 5).
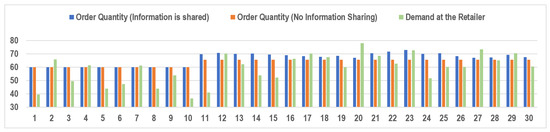
Figure 2.
Plots of order quantity (Q) and demand () under varying potential market sizes () for the eco-labeled product.
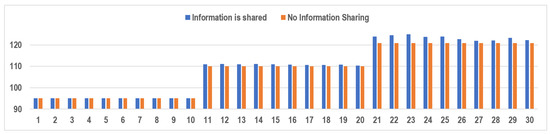
Figure 3.
Retail price (p) under varying potential market sizes () for the eco-labeled product.
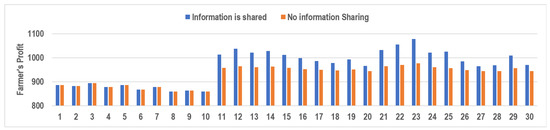
Figure 4.
Farmer’s Profit under varying potential market sizes () for the eco-labeled product.
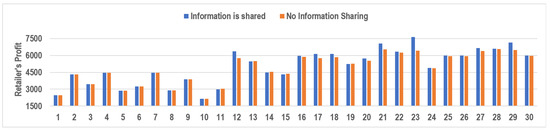
Figure 5.
Retailer’s Profit under varying potential market sizes () for the eco-labeled product.
As seen in Section 4.3, the retailer’s problem of determining the order quantity is a single-constraint optimization problem in z (and therefore in Q). When the retailer’s profit function is concave in Q (or z) (as in our case), it can be solved by first considering it as an unconstrained optimization problem in Q (or z) and then limiting the value of Q thus obtained so that , where is determined by Lemma 3. Note that the value of depends on the information setting (see Lemma 3), but the value of Q is independent of the same. Following the same procedure as in our problem, the retailer’s optimal order quantity turns out to be the maximum allowable value, , when the potential market size is high (). Since the value of varies in different information settings, the retailer’s order quantities vary across these settings, as seen in Figure 2 (PI: 11–30). On the other hand, when the market size is small (), the value of Q obtained by solving the unconstrained optimization problem will be much lesser than irrespective of the information set considered to determine . Thus, Q remains the same regardless of whether the information is shared or not (Figure 2, PI: 1–10). As a result, when the market size is small (), the profit of the farmer and the retailer does not vary across different information settings as seen in Figure 4 and Figure 5 (PI: 1–10).
When the potential market size is large (), sharing the yield forecast with the retailer benefits the farmer (Figure 4, PI: 11–30). By giving a clear yield estimate, he encourages the retailer to order more products that help him earn better profits. This is evident in Figure 2 (PI: 11–30), where the retailer’s order quantity (Q) is always higher under the information-sharing scenario. When information is shared, and the farmer sees a negative forecast signal (), he limits the retailer’s order quantity to avoid shortages (Figure 2, PI: 16–20 & 26–30 ). In contrast, he lets the retailer order more products when (Figure 2, PI: 11–15 & 21–25). Thus in Figure 4, we can see that his profit is higher when the forecast signal is positive () (PI: 11–15 & 21–25) when compared with the cases where it is negative () (PI: 16–20 & 26–30).
The retailer benefits from shared information only when the realized demand () exceeds the maximum order quantity limit () of the no-information sharing case ( Figure 2 and Figure 5, PI: ). The higher inventory levels, resulting from a larger order quantity in the information-sharing case, become useful only when is large. If is low, the large inventory levels result in more unsold products to be disposed of, causing revenue losses to the retailer. In such cases, even though she has to spend more in disposing of excess products, her profits are on par with that of the no-sharing scenario (Figure 5, PI: ). Higher retail prices in the information sharing scenario (Figure 3), as well as the small disposal costs (, in both cases), can be considered as the reasons for this observation. Higher values of may offset the benefits of higher retail prices, and it may result in more revenue losses to the retailer under information sharing when is low. Accurate demand forecasts may help the retailer improve their profits, as it helps them determine the order quantity more precisely, thus reducing the quantity of unsold products at the end of a selling period.
Furthermore, we obtain interesting insights by comparing the cases where the product is eco-labeled and when it is not (conventional products) (Figure 6, Figure 7 and Figure 8). Here, we consider the potential market sizes () to be 50 (PI: 1–8), 60 (PI: 9–16), 70 (PI: 17–24) and 80 (PI: 25–32). The first four problem instances in each category are good yield scenarios (indicated by ), and the remaining four are poor yield scenarios (). Since it has already been shown that when , sharing yield information benefits the farmer, we assume that he always shares the yield information with the retailer.
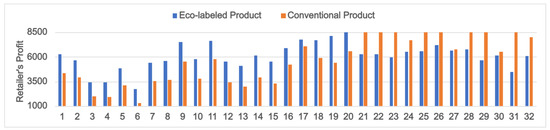
Figure 6.
Retailer’s Profit for different product types under varying potential market sizes ().
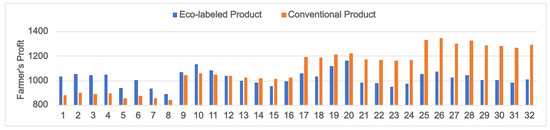
Figure 7.
Farmer’s Profit for different product types under varying potential market sizes ().
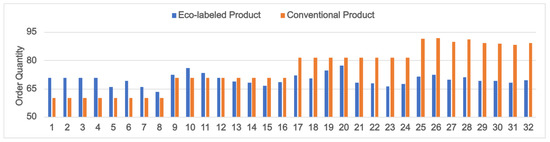
Figure 8.
Retailer’s order quantity (Q) for different product types under varying potential market sizes ().
Figure 6 shows that the retailer makes better profits by selling eco-labeled products when (PI: 1–8) or 60 (PI: 9–16) and also under positive forecasts when (PI: 17–20). For all other instances considered (PI: 21–32), the retailer enjoys better profits on the sale of conventional products. This happens mainly because the term represents the demand quantity ignoring the green label and the quality considerations (see Equation (9)). A high value of compared to and signifies that a considerable number of consumers are insensitive to the labeling or quality attributes of the product. In such cases, it is beneficial for the retailer to overlook the labeling provision, as it helps her lift the constraints on order quantity set by the demands of the labeling scheme (see Lemma 3). This, in turn, helps her gain better profits by reducing product shortages and selling more quantities to consumers. Simultaneously, the farmer, relieved from meeting the labeling requirements, enjoys better profits by supplying more product quantities grown under conventional agricultural methods (Figure 7; PI: 25–32).
On the contrary, when or 60, the retailer’s stocking quantity (Q) requirement, calculated considering the product is eco-labeled, falls within the limiting order quantity requirement () set by Lemma 3. This means that if she opts for an eco-label, she can increase the product demand (by ) without fearing the occurrence of stockouts. Due to the higher demand for eco-labeled products and the corresponding higher retail prices compared to conventional products (see Corollary 1), the retailer enjoys better profits by opting to sell eco-labeled products (Figure 6; PI: 1–16). In such cases, the farmer enjoys better profits by growing his crops following the labeling regulations (see Figure 7; PI: 1–12) as it helps him reduce cultivation costs (due to less fertilization and irrigation costs).
Problem instances 13–16 in Figure 7 show the cases of the farmer benefitting from conventional farming even when . From the model definition (, for PI: 13–16), it is evident that the farmer suffers poor yields in these situations. In such circumstances, a farmer can obtain a reasonable yield only if he aims for a much higher yield during his initial planning. This requires an excessive use of farm inputs, such as fertilizers and irrigation water, which is not allowed in the standards of the proposed labeling scheme. Since the yield forecast information has already been communicated with the retailer, she reduces her order quantity, reducing the farmer’s profit. Conversely, the absence of constraints on the farm inputs in conventional agriculture helps counteract possible yield losses. This allows the farmer to make higher profits by supplying more product quantities (Q) to the retailer, provided that she sells conventional products (Figure 8; PI: 13–16). However, when , the extra quantity that the retailer can sell by opting for conventional products over eco-labeled ones is negligibly small. Considering the higher retail prices of eco-labeled products (see Corollary 1), this small difference will be insufficient to ensure higher retailer profits by selling conventional products over eco-labeled ones. This is evident in Figure 6; (PI: 13–16), where the retailer’s profits are higher when selling eco-labeled products. Hence, in such a scenario, the farmer’s and retailer’s decisions about the type of product will be conflicting. From Figure 6 and Figure 7 (PI: 13–16), it is clear that the effect of the product type decision is more pronounced on the retailer’s profit. Hence, the retailer should incentivize the farmer to cultivate eco-labeled products on his farm. A similar observation can be made for positive yield forecasts with (PI: 17–20).
Finally, for poor yield scenarios () with (PI: 21–24), significantly more quantities of conventional products will be available for sale compared to the eco-labeled ones (Figure 8; PI: 21–24). Since the potential market size () is also large, the difference between the quantities of conventional and eco-labeled products sold will be significant enough to make the sale of conventional products more profitable for the retailer (Figure 6; PI: 21–24). In this scenario, the farmer will also prefer conventional agriculture as it allows him to supply more products, thus, increasing his income (Figure 7; PI: 21–24).
5.2. Varying Greenness Level Sensitivity Factor ()
A market setting in which environmentally conscious consumers are predominant is marked with higher values of and lower values of . Products bearing eco-labels () significantly increase the demand in this environment. This section investigates the effects of information sharing at varying greenness sensitivity levels (). The profits of the farmer and retailer at different values in different information settings are evaluated, and the corresponding plots are developed (Figure 9 and Figure 10). The values considered are 20 (PI: 1–10), 40 (PI: 11–20) and 60 (PI: 21–30). Similarly to Section 5.1, we consider a positive (negative) forecast signal for the first (last) five problem instances in each category.
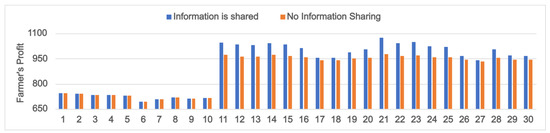
Figure 9.
Farmer’s profit under varying greenness level sensitivity factor () for the eco-labeled product.
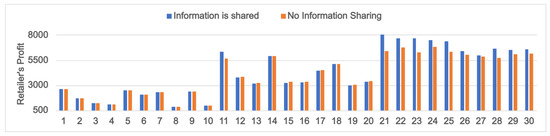
Figure 10.
Retailer’s profit under varying greenness level sensitivity factor () for the eco-labeled product.
The results obtained are similar to the case of varying potential demand sizes (Section 5.1), with both the farmer (Figure 9) and the retailer (Figure 10) benefitting from the sharing of information at high values of (). At low values sharing yield information offers no advantage as the profits of both stakeholders remain the same in both information settings (Figure 9 and Figure 10; PI: 1–10). The explanation for this behavior is similar to that of the low case discussed in Section 5.1.
Importantly, there is a noticeable difference in the farmer’s and retailer’s preference for product types (eco-labeled/conventional) under high values compared with those under high values. For very high values of , both the farmer and retailer were found to benefit from preferring conventional products (Section 5.1). However, when is high compared to and , the farmer and retailer gain good profits only if they prefer eco-labeled products. This is due to the fact that the demand in a high setting can be boosted only if the product is eco-labeled () (see Equation (9)).
5.3. Varying Product Deterioration Rates ()
When quality-conscious consumers dominate the market, we have higher values for the quality sensitivity factor () compared to and . The demand for products in such an environment is highly influenced by the product deterioration rate () (see Equation (9)). In this section, we analyze the effects of information sharing on stakeholders’ profits, considering the perishability attributes of the eco-labeled products. Here, we assume a high value of compared to and . Figure 11 displays the order quantities under different information-sharing scenarios and the corresponding product demand when (PI: 1–10), (PI: 11–20), and (PI: 21–30). Figure 12 shows the related retail prices. The profits of the farmer and the retailer are displayed in Figure 13 and Figure 14, respectively. Similarly to Section 5.1 and Section 5.2, we consider a positive (negative) forecast signal for the first (last) five instances in each category.
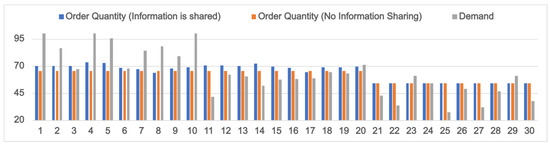
Figure 11.
Plots of order quantity (Q) and demand () under varying product deterioration rates () for the eco-labeled product.
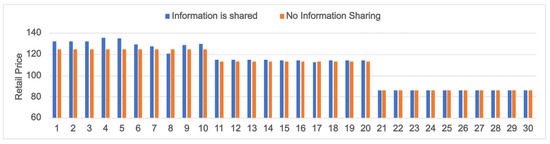
Figure 12.
Retail price (p) under varying product deterioration rates () for the eco-labeled product.
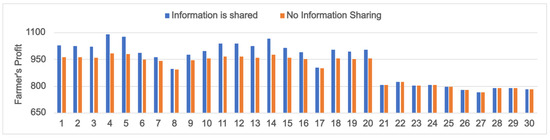
Figure 13.
Farmer’s Profit under varying product deterioration rates () for the eco-labeled product.
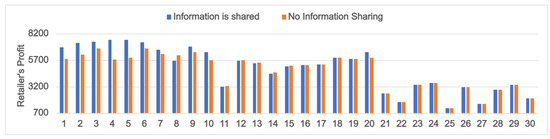
Figure 14.
Retailer’s Profit under varying product deterioration rates () for the eco-labeled product.
When the deterioration rate is low (), the total demand for the product will be high (see Equation (9)), as seen in Figure 11 (PI: 1–10). In this case, the retailer prefers that the farmer shares his yield information so that she can order the maximum possible quantities that the farmer can supply. This is evident in Figure 11 (PI: 1–10), as in almost all instances (except PI: 8), the retailer’s order quantity (Q) under information sharing is higher than that under the no information sharing (In PI: 8, when information is shared, the retailer is forced to restrict her order quantity to a lower value due to a high negative yield forecast by the farmer). Here, the farmer is also at an advantage by sharing the yield information as it enables him to gain better profits (Figure 13; PI: 1–10) by supplying more products to the retailer. Interestingly, in Figure 12, we can find that the retail prices under information-sharing remain fairly high compared to the no information-sharing case for PI: 1–10 (except PI: 8). The sale of more quantities at higher retail prices under the information-sharing scenario results in greater profits for the retailer (Figure 14; PI: 1–10).
Information sharing is not always rewarding for the retailer with higher product deterioration rates (). The high value of results in a decrease in product demand and retail prices, as seen in Figure 11 and Figure 12 (PI: 11–20). However, uncertainties associated with demand and high shortage costs () force the retailer to follow a conservative approach where she stocks more products based on availability. For PI: 11–20, except for PI: 17, the yield information shared by the farmer is such that the product quantity that he can supply is greater than the corresponding value calculated under the no information sharing scenario. This results in the retailer ordering larger quantities when information is shared (Figure 11; PI: 11–20). On the other hand, when the retailer remains uninformed about the yield forecast, she makes her order quantity decision based on her knowledge of yield. The excess quantities ordered, when information is shared, prove useful to her only when the demand exceeds the order quantity of the no information-sharing case, which happens only for PI:20. For all the other instances (PI: 11–19), the total disposal costs for the retailer are higher in the information-shared situation. Low disposal costs per unit quantity and marginally better retail prices under information-sharing (Figure 12; PI: 11–20) are the reasons why the profit in this scenario remains almost the same as in the other case.
Although information sharing may not help the retailer when , the farmer reaps its benefits. It allows him to sell more products to the retailer through which he receives higher profits (Figure 13; PI: 11–20). Finally, for highly perishable products (), the high results in low demand; hence, information-sharing offers no benefits to the stakeholders (PI: 21–30). This can be explained using the same logic discussed in Section 5.1, where information-sharing was found not beneficial for low potential market sizes ().
6. Discussion
This section discusses the significance of the major results obtained for our supply chain model.
6.1. Effectiveness of the Proposed Eco-Labeling Scheme
Among the per unit area and the per unit mass of output measures available for measuring environmental impacts (see Section 1), the latter gains prominence in the interest of ensuring food security with minimal ecological damage. It is already seen in Section 1 that the organic scheme, due to its low yield, performed poorly under this measure. On the contrary, the proposed eco-label is defined to control the fertilizer application such that the greenhouse gas emissions per unit yield are minimal (Section 3.1). Moreover, Corollary 2 proves that the proposed scheme guarantees a better yield than organic farming. Effectively, this proves the superiority of the proposed scheme over the organic one in terms of ensuring agricultural sustainability, as it has minimal environmental impacts per unit yield. Although Corollary 2 points towards a higher yield in the case of conventional farming, its severe environmental impacts due to the uncontrolled use of synthetic fertilizers make it an unsustainable alternative.
Many previous studies [40,41,42,43] stress the importance of optimizing fertilizer usage to balance the yield-emission trade-off. Although all of these studies identify the optimal fertilizer requirement through field experiments, none discusses how observations can be put into practice. However, the proposed eco-label helps the consumer identify agri-products grown using such sustainable practices, creating a demand for such products in the market. This incentivizes the farmer and retailer to implement such practices.
Secondly, Corollary 1 suggests that the retail price under the proposed scheme is lower than that under the organic scheme. This makes the products cultivated under the new scheme affordable to the group of eco-sensitive consumers who find the price of organic products too high. The need for such products and their importance in promoting green agricultural practices are discussed in [78].
6.2. Farmer’s Cost Index (K) and Optimal Input Decisions
As seen in Equation (13), the farmer’s cost index (K) is calculated based on his cost and field parameters. It helps the farmer identify his market setting and the corresponding optimal yield levels (Table 3). Precise knowledge of the market environment helps the farmer identify scenarios where production to his maximum capacity proves beneficial. Moreover, it lets him recognize the cases where he has to avoid overproduction (beyond the retailer’s requirement) to prevent profit losses. Further, using Theorem 3, he can determine the exact amount of fertilizer and irrigation water needed to achieve the required yield. The precise control over the fertilizer and irrigation water application makes the agricultural setting more sustainable as it aids in checking greenhouse gas emissions and conserving water resources.
In existing green agri-food supply chain models like [54,79], attempts are made to determine the optimal greenness levels of the farmers to ensure agricultural sustainability while maximizing farmers’ profits. However, these models fail to explain how to achieve the recommended greenness levels. Our model addresses this issue by creating a clear connection between the greenness levels and the critical farm inputs (Section 3.1).
6.3. Retailer’s Optimal Decisions
Theorems 1 and 4 deal with the optimal retailer decisions on the retail price and order quantities that maximize her profit. These results are applicable in various retailer settings, as no specific distribution of demand uncertainties is considered during their development. They are derived following the seminal work of Petruzzi et al. [81] on pricing and order quantity decisions for a newsvendor problem. An important factor differentiating our work from [81] is the presence of constraints on order quantity (see lemma 3) due to the necessity of meeting the greenness requirement. As a result, the order quantity decisions in our model vary considerably from that of [81] (see Theorem 4).
6.4. Importance of Yield Information Sharing
The effects of yield information sharing in various market settings are detailed in Section 5. It identifies the contexts where information sharing becomes beneficial for both stakeholders and points out the importance of accurate demand forecasting at the retailer’s end. The study offers many practical implications to stakeholders by helping them make crucial decisions in various contexts, some of which are discussed here. In a market dominated by consumers who are less sensitive to eco-labels, the choice of the product type (eco-labeled/conventional) to be sold should depend on the potential market size (). Although a very large potential market size may favor conventional products, opting for eco-labeled products in comparatively smaller markets may prove beneficial to the farmer and the retailer, provided they share the yield information (see Section 5.1). It is advisable that the farmer shares his yield information with the retailer when the market size is large and eco-sensitive consumers dominate the market (Section 5.2). It is always important to share the yield information when the products are less perishable (Section 5.3). For products with high perishability, information sharing does not help improve the stakeholder profits unless the market size is huge. Such an in-depth study on yield information sharing in sustainable agri-food supply chains has not been attempted previously in the literature.
7. Conclusions
The proposed eco-labeling scheme is a novel approach to sustainable agriculture, focusing on balancing the tradeoff between yield and environmental impacts of agriculture. The unique way in which greenness is defined under the scheme ensures that the farmer always uses his key farm inputs (fertilizer and irrigation water) judiciously, thereby ensuring a good yield with minimal ecological consequences. By bringing the considerations of crop yield into the labeling framework, we show a new way to improve agricultural sustainability. This is the first theoretical contribution of our work.
Due to its advantages over the organic and conventional schemes (see Section 6.1), the proposed eco-labeling scheme can potentially bring a positive change in the agricultural sector. Practically, to make this possible, it is vital to make environmentally-conscious consumers aware of the disadvantages of extensive implementation of organic farming practices (discussed in Section 1). Although it may take some time and effort to convince people to think beyond organic farming, an immediate opportunity for a niche market segment that constitutes these uniquely labeled products is identified in Section 6.1.
The farmer-retailer supply chain model, to which the proposed eco-labeling scheme is applied, considers the aspects of demand and yield uncertainties, and product perishability, thereby moving a step closer to a realistic setting. In addition, we prove the existence of closed-form solutions for the farmer’s and retailer’s problems, which is another important theoretical contribution considering the complexity of the problem. On the practical side, by classifying the farmer’s market based on the cost index (K), the model simplifies the farmer’s task of making important production decisions (Section 6.2). As discussed in Section 6.3, the generic nature of the retailer’s closed-form solution extends the applicability of our model across various retailer settings.
Finally, the numerical analysis (Section 5) throws more light on the importance of yield information sharing. Notably, the analysis focuses on identifying the scenarios in which sharing yield information benefits the stakeholders. The consideration of different market types, including the eco-sensitive consumer market, perishable products market, add more value to the analysis. Additionally, the study aids the stakeholders in recognizing scenarios where the production and sale of conventional products gain them better profits. Section 6.4 lists out some practical implications of our numerical study.
Furthermore, studies can be undertaken to extend the present model in various directions. Identification of other production variables with considerable environmental impacts and their incorporation into the eco-labeling scheme is an idea that future researchers can contemplate. It will help to further strengthen the proposed scheme, thus, improving its effectiveness in ensuring agricultural sustainability. Another important step would be to consider other crop-production functions like the Mitscherlich–Baule function, quadratic function, etc., [85] so that the model can be extended to a wide variety of crops. Extending the model by considering a retailer sourcing her products from competing farmers, which is a common scenario for large retail chains, will also be interesting. In such cases, each farmer may have different farm parameters and levels of uncertainties, according to which the production decisions of individual farmers may vary. The retailer has to decide on the quantities to be sourced from each farmer under uncertainties. It will also be interesting to study the effects of product preservation on supply chain decisions. Different preservation levels may result in completely new retailer behavior, and it has to be closely investigated.
Author Contributions
Conceptualization, A.P.; methodology, A.P. and R.R.M.; writing—original draft preparation, A.P.; writing—review and editing, R.R.M.; supervision, R.R.M.; funding acquisition, R.R.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the Robert Bosch Centre for Data Science and Artificial Intelligence (under the grant number CR1718CSE001RBEIBRAV), Indian Institute of Technology Madras, Chennai 600036—India.
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
Not Applicable.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| GAP | Good Agricultural Practices |
| GWP | Global Warming Potential |
| IPM | Integrated Pest Management |
| ACP | Agroecological Crop Protection |
| GHGI | Greenhouse Gas Emission Intensity |
| PI | Problem Instance |
Appendix A. Proof of Theories, Lemmas and Corollaries
Proof of Lemma 1.
Let and be a set of values representing fertilizer () and irrigation water () consumption of a certain crop that follows von Liebig’s law, which is given by Equation (1). Let us assume that . Now, according to the von Liebig law, both and are the limiting factors that determine the crop yield. Let represent the corresponding yield, and using Equation (1), we obtain . It is clear from the definition of the von Liebig function that increasing the value of beyond keeping constant at will not increase the yield beyond . On the other hand, this attempt results in a reduction in the farmer’s profit. This is evident from the observation that each case in the farmer’s profit function contains only one term that involves . This term, which has a negative sign, tends to reduce the farmer’s profit when the value of increases. Attempts to reduce to a value below cause the crop yield to drop below as becomes the new limiting factor. Similar results can be observed if we vary keeping a constant. Based on these observations, it can be concluded that the profit of the farmer is maximized for a given value of yield , when . A generalized form of this statement is presented as Lemma 1. □
Proof of Lemma 2.
Using Lemma 1 and Equation (7) we can write:
To obtain green certification, we should have or in other words,
Upon rearrangement of the terms, we obtain the expression given in Lemma 2. □
Proof of Lemma 3.
Equation (A1) gives greenness in terms of yield y. When the information is shared and , the equilibrium decision of the farmer is . When the yield is , the maximum order quantity that the farmer can provide the retailer during a sales period is . Therefore, the retailer should limit their order quantity by to ensure that the farmer signs the contract.
When and information is shared, the retailer determines the equilibrium decision of the farmer as . When , the greenness function can be written as:
For obtaining green certification, we should have , which means:
OR
Let us represent the RHS of the above inequality as .
According to Lemma 2, is the maximum yield the farmer can achieve while ensuring green certification for his products. When the yield is , the maximum order quantity that the farmer can supply the retailer during a sales period is . In this case, to ensure the farmer’s participation, the retailer should satisfy the condition . Combining the two cases, we can write the general condition for the acceptance of the contract by the farmer as where . Any order quantity greater than may result in a rational farmer rejecting the contract offer, as he will not be able to meet the retailer’s requirements in terms of quantity and greenness simultaneously. Therefore, the retailer should restrict her order quantity by .
Finally, when , the farmer’s optimal decision is . In this case, the farmer is not interested in applying any production inputs such as or due to the high production costs involved. Even then he can have a yield of . Thus, if the retailer’s order quantity is less than this value of yield, the farmer may agree to sign the contract. This completes the first part of the proof.
Similarly, when information is not shared, the retailer determines the equilibrium decision of the farmer using her beliefs about the yield uncertainty factor . The corresponding decisions will be: when and when and when . On proceeding in a way similar to the first part of the proof, we obtain the results listed in the case where no information is shared. □
Proof of Theorem 1.
Since the values of and are always positive, the second derivative of with respect to p is always negative. Thus, according to KKT conditions, is concave in p, and the function attains a maximum at a value of p for which . The corresponding value of p is expressed as in the statement of the theorem. This result is similar to that obtained by [81]. □
Proof of Theorem 2.
Using to represent the updated pdf of , that is, , the above equation can be re-written as:
where is the corresponding CDF. Moreover, we get:
The concavity of the farmer’s profit function can be proved if there exists a such that and . We know that and , so the sign of the second derivative depends on the term . As long as this term remains positive, the second derivative is negative. While always holds a positive value, the sign of depends on the availability of open markets. In the absence of open markets, remains positive as the farmer is forced to dispose of his excess products. This means that is positive, making the second derivative negative. In the presence of open markets, we have , the second derivative remains negative as long as . Our model always satisfies this condition, as we already have (as a combined result of the individual rationality constraint and the incentive compatibility constraint). Equating to zero, we get:
or
Since is a CDF, a solution for exists only when , or in other words, is concave in y when K satisfies this condition. It should be noted that the value of is obtained by relaxing the constraint , or in other words, we have performed an unconstrained optimization of the profit function. As is concave for all values of y, incorporating the constraint leads to the following 3 cases:
- When , the optimal yield is given by
- When , the optimal yield is given by
- When , the optimal yield is given by
This result is summarized as statement 1 of Theorem 2.
In the absence of open markets, all the terms in the equation of K (Equation (13)) are positive, and the condition is satisfied only if
Since is a CDF, we have . Taking into account this result along with the condition derived above, it can be proved that the inequality (A4) is always satisfied when . This means that in the absence of open markets, if , the farmer’s profit function is always monotonically decreasing in y. In such cases, the optimal decision of the farmer is , which is the minimum value of y according to the von Liebig function. This proves statement 2 of the theorem.
When , in the presence of open markets, is replaced by and the slope of the profit function is positive for all when the condition in statement (3) is satisfied. In this case, the profit function is monotonically increasing in y, and the optimal value of y is given by . The corresponding result is given as the third statement of the theorem. The fourth statement can also be proved using similar arguments. □
Proof of Theorem 3.
From Theorem 2, we have obtained the optimum value of yield for maximizing the farmer’s profit as . The optimal amount of nitrogen fertilizer and irrigation water required to obtain this yield can be found directly using Lemma 1, which gives . From this and can be determined as and . In cases when , we obtain a negative value for if () which is trivial. In such cases, the actual value of both and are zero. To accommodate this in the equation, we use and . □
Proof of Theorem 1.
First, it should be noted that the value of limits the maximum allowable stocking factor z in our problem. In the first three statements of the theorem, the condition is commonly mentioned. This is important because only in the cases where can we decide the stocking factor considering the demand uncertainties as the uncertainties vary in the interval . Differentiating with respect to z we get:
Equation (A5) gives the slope of the profit function and lets us use to denote this slope function. Studying the behavior of will shed more light on the nature of the profit function. Differentiating with respect to z, we get:
Moreover,
When , we get
On simplification, this gives:
When , the second derivative of is always zero or negative. This means that is either monotone or concave in z. When is concave, it will have either two roots, or no roots. The presence of two roots means that the slope of the profit function is zero at two values of z. Denoting the corresponding smaller and larger values of z as and , it can be seen that for all , the slope of is positive as is concave. At , the slope again becomes zero, and further beyond it, the slope remains negative. This means is a point of maxima for and using a similar argument, it can be shown that is the point of minima. If this satisfies the constraint (14) of our maximization problem, and then it is the optimal value of z for our problem. On the other hand, if , it is clear that violates the constraint, and hence the best possible solution to our problem is if . Finally, when both of these conditions are not satisfied, the maximum value of occurs at . Moreover, the absence of roots for when it is concave means that is negative for all values of z. When it is, will be a monotonically decreasing function for all . In such cases, it is obvious that is our optimal solution. The above discussion is summarized as statement 1 of the theorem.
On the other hand, the presence or absence of roots for , when it is a monotonic function, depends on the values of and . We can easily see that , which is always negative. This means that will have a root only when . In such cases, R(z) changes sign from positive to negative at its root, which means that has a maximum at that point. Since there is only one point where this happens, we can say that is concave in z. Thus, the conditions required for the concavity of the profit function are: and . Moreover,
For a concave profit function, the maximum value occurs at the point when . If , the constraint (14) is not violated, and hence becomes the optimal solution. On the other hand, violation of the constraint results in becoming the optimal solution. The above discussion is summed up in statement 2 of the theorem.
In cases where does not satisfy the conditions mentioned in statements 1 and 2, we cannot identify any conditions on the profit function. Hence, an exhaustive search is required for all values of z in to find the optimum, which is the third statement in the theorem.
So far, we have discussed cases where . In cases where , the stocking factor is limited by , which means that the retailer cannot stock products to meet the uncertain part of demand. In such cases, the retailer always faces a shortage of products. The smaller the value of , the greater the shortage, and hence the retailer stocks the maximum allowable quantity of . This explains statement 4 of the theorem. □
Proof of Corollary 1.
The absence of synthetic inputs like pesticides and chemical fertilizers during production is the primary attribute that boosts the demand for organic products among health-conscious consumers [86,87,88]. Although synthetic pesticides are not allowed in the new greenness scheme suggested by us, controlled use of synthetic fertilizers is permitted. This may result in a smaller greenness sensitivity () value for our scheme when compared to that of the organic labeling scheme (). Finally, the greenness sensitivity () would be zero for conventional farming techniques where these synthetic inputs are permitted. Mathematically, this can be written as . Using this relationship in Theorem 1 and assuming that all other parameters are common, we obtain . □
Proof of Corollary 2.
From the von Liebig production function, it is evident that the parameter represents the improvement in yield due to the application of synthetic fertilizers. Since we use the same type of fertilizers in conventional and the proposed agricultural methods, this parameter will be the same for both of these methods. On the other hand, the reduced yield in organic farming results from the slower response of the crops towards organic fertilizers, and hence the corresponding parameter, , has a value such that . Moreover, from Equation (13) we have . As there is no significant difference between production costs in these different methods of agriculture [84], the value of K under different schemes is dependent on the parameter , and since , we obtain .
When the optimum yield is decided by statement 1 of Theorem 2, according to the agricultural scheme used, we have the following cases:
- For the proposed scheme:
- For the conventional scheme:
- For the organic scheme:
As we already have , it can be proved that . Moreover, when , from the definitions of m, and , we have . From these observations, it can be concluded that .
The optimum yield for the conventional and proposed schemes are decided by statement 2 of Theorem 2, only when the condition is satisfied (see the proof of Theorem 2) and the corresponding optimal values are . Since we already have , this condition is always satisfied in the organic labeling scheme whenever it is satisfied in the other two schemes. Thus, the optimal yield value in this scenario for the organic scheme is . This gives us the relation , whenever statement 2 determines the yield.
When the condition in statement 3 of Theorem 2 is satisfied, the farmer’s profit function monotonically increases in y, and the farmer attempts to maximize his production to gain higher profits. This results in an optimal yield of in the case of the proposed greenness scheme and in the case of the conventional scheme. On the other hand, the optimal decision under the organic scheme depends on the value of . A small value of might result in the inequality condition being reversed, resulting in a monotonically decreasing profit function. In this case, the optimal decision becomes . The other possible decision for the organic farmer is , which occurs when the condition for monotonically increasing profit function is satisfied for the value of . In any case, we can summarize that as we already know that .
Finally, when the condition in statement 4 of theorem 2 is satisfied in the conventional and proposed schemes, the same is satisfied for the organic scheme as well. This claim is valid as we have . Thus the optimal yield under the three schemes will be .
From the above discussion, we can summarize that the observation is always valid when . □
Appendix B. Procedure for Numerical Analysis
The step-by-step procedure for evaluating each problem instance is given below:
- Assuming a mean of zero and a given variance, a random variate is generated for the normally distributed random variable . This value of gives the actual value of the yield uncertainty for a problem instance. The farmer cannot observe this value directly, but he can make a forecast of this value.
- Assuming a mean of zero and a given variance, a random variate is generated for the normally distributed random variable . This value of gives the noise associated with the forecast signal obtained by the farmer.
- The forecast signal obtained by the farmer is now determined as . In reality, the farmer will be observing only this forecast signal.
- Using this value of obtained, the farmer determines the conditional expectation , the conditional variance , and the corresponding . The farmer, in his decision-making, uses these conditional values.
- The conditional values obtained in the previous step are shared with the retailer when information sharing occurs, and the retailer makes her decisions based on this shared information. The demand uncertainty in the retailer’s problem () is taken into account by randomly generating a value that is uniformly distributed in the interval .
- In cases where information is not shared, the retailer makes her decisions based on common beliefs about yield uncertainties. Here also, is generated similar to the case where information is shared.
- Based on the farmer’s and retailer’s decisions and the actual yield uncertainty determined in step 1, their profits are determined.
The above steps are repeated for each problem instance, and the corresponding graphs are plotted.
References
- Goucher, L.; Bruce, R.; Cameron, D.D.; Koh, S.C.L.; Horton, P. The environmental impact of fertilizer embodied in a wheat-to-bread supply chain. Nat. Plants 2017, 3, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Kılıç, O.; Boz, I.; Eryılmaz, G.A. Comparison of conventional and good agricultural practices farms: A socio-economic and technical perspective. J. Clean. Prod. 2020, 258, 120666. [Google Scholar] [CrossRef]
- Wehmeyer, H.; de Guia, A.H.; Connor, M. Reduction of fertilizer use in South China-Impacts and implications on smallholder rice farmers. Sustainability 2020, 12, 2240. [Google Scholar] [CrossRef]
- Mwalupaso, G.E.; Korotoumou, M.; Eshetie, A.M.; Essiagnon Alavo, J.P.; Tian, X. Recuperating dynamism in agriculture through adoption of sustainable agricultural technology - Implications for cleaner production. J. Clean. Prod. 2019, 232, 639–647. [Google Scholar] [CrossRef]
- Lee, S.; Nguyen, T.T.; Poppenborg, P.; Shin, H.J.; Koellner, T. Conventional, partially converted and environmentally friendly farming in South Korea: Profitability and factors affecting farmers’ choice. Sustainability 2016, 8, 704. [Google Scholar] [CrossRef]
- Foteinis, S.; Chatzisymeon, E. Life cycle assessment of organic versus conventional agriculture. A case study of lettuce cultivation in Greece. J. Clean. Prod. 2016, 112, 2462–2471. [Google Scholar] [CrossRef]
- Tricase, C.; Lamonaca, E.; Ingrao, C.; Bacenetti, J.; Lo Giudice, A. A comparative Life Cycle Assessment between organic and conventional barley cultivation for sustainable agriculture pathways. J. Clean. Prod. 2018, 172, 3747–3759. [Google Scholar] [CrossRef]
- Ronga, D.; Gallingani, T.; Zaccardelli, M.; Perrone, D.; Francia, E.; Milc, J.; Pecchioni, N. Carbon footprint and energetic analysis of tomato production in the organic vs the conventional cropping systems in Southern Italy. J. Clean. Prod. 2019, 220, 836–845. [Google Scholar] [CrossRef]
- Stubenrauch, J.; Ekardt, F.; Heyl, K.; Garske, B.; Schott, V.L.; Ober, S. How to legally overcome the distinction between organic and conventional farming - Governance approaches for sustainable farming on 100% of the land. Sustain. Prod. Consum. 2021, 28, 716–725. [Google Scholar] [CrossRef]
- Taki, M.; Soheili-Fard, F.; Rohani, A.; Chen, G.; Yildizhan, H. Life cycle assessment to compare the environmental impacts of different wheat production systems. J. Clean. Prod. 2018, 197, 195–207. [Google Scholar] [CrossRef]
- Aivazidou, E.; Tsolakis, N.; Vlachos, D.; Iakovou, E. A water footprint management framework for supply chains under green market behaviour. J. Clean. Prod. 2018, 197, 592–606. [Google Scholar] [CrossRef]
- Ochieng, D.O.; Veettil, P.C.; Qaim, M. Farmers’ preferences for supermarket contracts in Kenya. Food Policy 2017, 68, 100–111. [Google Scholar] [CrossRef]
- Ogutu, S.O.; Ochieng, D.O.; Qaim, M. Supermarket contracts and smallholder farmers: Implications for income and multidimensional poverty. Food Policy 2020, 95, 101940. [Google Scholar] [CrossRef]
- Halati, A.; He, Y. Intersection of economic and environmental goals of sustainable development initiatives. J. Clean. Prod. 2018, 189, 813–829. [Google Scholar] [CrossRef]
- Zu, Y.; Chen, L.; Fan, Y. Research on low-carbon strategies in supply chain with environmental regulations based on differential game. J. Clean. Prod. 2018, 177, 527–546. [Google Scholar] [CrossRef]
- Rong, A.; Akkerman, R.; Grunow, M. An optimization approach for managing fresh food quality throughout the supply chain. Int. J. Prod. Econ. 2011, 131, 421–429. [Google Scholar] [CrossRef]
- Avinadav, T.; Herbon, A.; Spiegel, U. Optimal ordering and pricing policy for demand functions that are separable into price and inventory age. Int. J. Prod. Econ. 2014, 155, 406–417. [Google Scholar] [CrossRef]
- Kazancoglu, Y.; Ozbiltekin-Pala, M.; Sezer, M.D.; Ekren, B.Y.; Kumar, V. Assessing the impact of covid-19 on sustainable food supply chains. Sustainability 2022, 14, 143. [Google Scholar] [CrossRef]
- Tansuchat, R.; Suriyankietkaew, S.; Petison, P.; Punjaisri, K.; Nimsai, S. Impacts of COVID-19 on Sustainable Agriculture Value Chain Development in Thailand and ASEAN. Sustainability 2022, 14, 12985. [Google Scholar] [CrossRef]
- Guimarães, Y.M.; Eustachio, J.H.P.P.; Leal Filho, W.; Martinez, L.F.; do Valle, M.R.; Caldana, A.C.F. Drivers and barriers in sustainable supply chains: The case of the Brazilian coffee industry. Sustain. Prod. Consum. 2022, 34, 42–54. [Google Scholar] [CrossRef]
- Amin-Chaudhry, A.; Young, S.; Afshari, L. Sustainability motivations and challenges in the Australian agribusiness. J. Clean. Prod. 2022, 361, 132229. [Google Scholar] [CrossRef]
- Liu, Y.; Wood, L.C.; Venkatesh, V.G.; Zhang, A.; Farooque, M. Barriers to sustainable food consumption and production in China: A fuzzy DEMATEL analysis from a circular economy perspective. Sustain. Prod. Consum. 2021, 28, 1114–1129. [Google Scholar] [CrossRef]
- Paciarotti, C.; Torregiani, F. The logistics of the short food supply chain: A literature review. Sustain. Prod. Consum. 2021, 26, 428–442. [Google Scholar] [CrossRef]
- Galati, A.; Giacomarra, M.; Concialdi, P.; Crescimanno, M. Exploring the feasibility of introducing electric freight vehicles in the short food supply chain: A multi-stakeholder approach. Case Stud. Transp. Policy 2021, 9, 950–957. [Google Scholar] [CrossRef]
- Giacomarra, M.; Crescimanno, M.; Sakka, G.; Galati, A. The contribution of a supplier of the food and beverage industry to the sustainability of the overall supply chain. Glob. Bus. Econ. Rev. 2021, 25, 231–250. [Google Scholar] [CrossRef]
- Thrassou, A.; Vrontis, D.; Crescimanno, M.; Giacomarra, M.; Galati, A. The requisite match between internal resources and network ties to cope with knowledge scarcity. J. Knowl. Manag. 2020, 24, 861–880. [Google Scholar] [CrossRef]
- Kamble, S.S.; Gunasekaran, A.; Gawankar, S.A. Achieving sustainable performance in a data-driven agriculture supply chain: A review for research and applications. Int. J. Prod. Econ. 2020, 219, 179–194. [Google Scholar] [CrossRef]
- Nematollahi, M.; Tajbakhsh, A. Past, present, and prospective themes of sustainable agricultural supply chains: A content analysis. J. Clean. Prod. 2020, 271, 122201. [Google Scholar] [CrossRef]
- Adams, D.; Donovan, J.; Topple, C. Achieving sustainability in food manufacturing operations and their supply chains: Key insights from a systematic literature review. Sustain. Prod. Consum. 2021, 28, 1491–1499. [Google Scholar] [CrossRef]
- Latino, M.E.; Menegoli, M.; De Giovanni, M. Evaluating the sustainability dimensions in the food supply chain: Literature review and research routes. Sustainability 2021, 13, 11816. [Google Scholar] [CrossRef]
- Desiderio, E.; García-Herrero, L.; Hall, D.; Segrè, A.; Vittuari, M. Social sustainability tools and indicators for the food supply chain: A systematic literature review. Sustain. Prod. Consum. 2022, 30, 527–540. [Google Scholar] [CrossRef]
- Tort, Ö.Ö.; Vayvay, Ö.; Çobanoğlu, E. A Systematic Review of Sustainable Fresh Fruit and Vegetable Supply Chains. Sustainability 2022, 14, 1573. [Google Scholar] [CrossRef]
- van Bussel, L.M.; Kuijsten, A.; Mars, M.; van ‘t Veer, P. Consumers’ perceptions on food-related sustainability: A systematic review. J. Clean. Prod. 2022, 341, 130904. [Google Scholar] [CrossRef]
- Kumar, A.; Mangla, S.K.; Kumar, P. An integrated literature review on sustainable food supply chains: Exploring research themes and future directions. Sci. Total. Environ. 2022, 821, 153411. [Google Scholar] [CrossRef]
- Huang, H.; He, Y.; Li, D. Pricing and inventory decisions in the food supply chain with production disruption and controllable deterioration. J. Clean. Prod. 2018, 180, 280–296. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, J.; Tang, W. Joint dynamic pricing and investment strategy for perishable foods with price-quality dependent demand. Ann. Oper. Res. 2015, 226, 397–416. [Google Scholar] [CrossRef]
- Chen, X.; Wu, S.; Wang, X.; Li, D. Optimal pricing strategy for the perishable food supply chain. Int. J. Prod. Res. 2019, 57, 2755–2768. [Google Scholar] [CrossRef]
- Song, Z.; He, S.; Baifeng, A. Decision and Coordination in a Dual-Channel Three-Layered Green Supply Chain. Symmetry 2018, 10, 549. [Google Scholar] [CrossRef]
- Karamian, F.; Mirakzadeh, A.A.; Azari, A. The water-energy-food nexus in farming: Managerial insights for a more efficient consumption of agricultural inputs. Sustain. Prod. Consum. 2021, 27, 1357–1371. [Google Scholar] [CrossRef]
- Zhu, E.; Deng, J.; Wang, H.; Wang, K.; Huang, L.; Zhu, G.; Belete, M.; Shahtahmassebi, A.R. Identify the optimization strategy of nitrogen fertilization level based on trade-off analysis between rice production and greenhouse gas emission. J. Clean. Prod. 2019, 239, 118060. [Google Scholar] [CrossRef]
- Kim, G.W.; Gutierrez-Suson, J.; Kim, P.J. Optimum N rate for grain yield coincides with minimum greenhouse gas intensity in flooded rice fields. Field Crop. Res. 2019, 237, 23–31. [Google Scholar] [CrossRef]
- Li, C.; Xiong, Y.; Huang, Q.; Xu, X.; Huang, G. Impact of irrigation and fertilization regimes on greenhouse gas emissions from soil of mulching cultivated maize (Zea mays L.) field in the upper reaches of Yellow River, China. J. Clean. Prod. 2020, 259, 120873. [Google Scholar] [CrossRef]
- Li, M.; Fu, Q.; Singh, V.P.; Liu, D.; Li, T.; Li, J. Sustainable management of land, water, and fertilizer for rice production considering footprint family assessment in a random environment. J. Clean. Prod. 2020, 258, 120785. [Google Scholar] [CrossRef]
- Grimm, S.S.; Paris, Q.; Williams, W.A. A von Liebig Model for Water and Nitrogen Crop Response. West. J. Agric. Econ. 1987, 12, 182–192. [Google Scholar] [CrossRef]
- Llewelyn, R.V.; Featherstone, A.M. A comparison of crop production functions using simulated data for irrigated corn in Western Kansas. Agric. Syst. 1997, 54, 521–538. [Google Scholar] [CrossRef]
- Peng, H.; Pang, T. Optimal strategies for a three-level contract-farming supply chain with subsidy. Int. J. Prod. Econ. 2019, 216, 274–286. [Google Scholar] [CrossRef]
- Zare, M.; Esmaeili, M.; He, Y. Implications of risk-sharing strategies on supply chains with multiple retailers and under random yield. Int. J. Prod. Econ. 2019, 216, 413–424. [Google Scholar] [CrossRef]
- Behzadi, G.; O’Sullivan, M.J.; Olsen, T.L.; Scrimgeour, F.; Zhang, A. Robust and resilient strategies for managing supply disruptions in an agribusiness supply chain. Int. J. Prod. Econ. 2017, 191, 207–220. [Google Scholar] [CrossRef]
- Golmohammadi, A.; Hassini, E. Review of supplier diversification and pricing strategies under random supply and demand. Int. J. Prod. Res. 2020, 58, 3455–3487. [Google Scholar] [CrossRef]
- Shen, B.; Choi, T.m.; Minner, S. A review on supply chain contracting with information considerations: Information updating and information asymmetry. Int. J. Prod. Res. 2019, 57, 4898–4936. [Google Scholar] [CrossRef]
- Liu, X.; Shen, X.; You, M. Study on Coordination and Optimization of Contract Farming Supply Chain Based on Uncertain Conditions. Sci. Program. 2020, 2020, 8858812. [Google Scholar] [CrossRef]
- Golmohammadi, A.; Hassini, E. Capacity, pricing and production under supply and demand uncertainties with an application in agriculture. Eur. J. Oper. Res. 2019, 275, 1037–1049. [Google Scholar] [CrossRef]
- Ye, F.; Lin, Q.; Li, Y. Coordination for contract farming supply chain with stochastic yield and demand under CVaR criterion. Oper. Res. 2020, 20, 369–397. [Google Scholar] [CrossRef]
- Cao, Y.; Tao, L.; Wu, K.; Wan, G. Coordinating joint greening efforts in an agri-food supply chain with environmentally sensitive demand. J. Clean. Prod. 2020, 277, 123883. [Google Scholar] [CrossRef]
- Fu, H.; Teo, K.L.; Li, Y.; Wang, L. Weather risk-reward contract for sustainable agri-food supply chain with loss-averse farmer. Sustainability 2018, 10, 4540. [Google Scholar] [CrossRef]
- Tran, D.T.; Hertog, M.L.; Tran, T.L.; Quyen, N.T.; Van De Poel, B.; Mata, C.I.; Nicolaï, B.M. Population modeling approach to optimize crop harvest strategy. The case of field tomato. Front. Plant Sci. 2017, 8, 608. [Google Scholar] [CrossRef] [PubMed]
- Ehlenfeldt, M.K. Fruit Firmness and Holding Ability in Highbush Blueberry — Implications for Mechanical Harvesting. Int. J. Fruit Sci. 2005, 5, 83–91. [Google Scholar] [CrossRef]
- Pe, S.; Linke, A.; Escher, F.; Nuessli, J. Freshness of fruits and vegetables: Consumer language and perception. Br. Food J. 2009, 111, 243–256. [Google Scholar] [CrossRef]
- Massaglia, S.; Borra, D.; Peano, C.; Sottile, F.; Merlino, V.M. Consumer Preference Heterogeneity Evaluation in Fruit and Vegetable Purchasing Decisions Using the Best–Worst Approach. Foods 2019, 8, 266. [Google Scholar] [CrossRef]
- Herbon, A. Should retailers hold a perishable product having different ages? The case of a homogeneous market and multiplicative demand model. Int. J. Prod. Econ. 2017, 193, 479–490. [Google Scholar] [CrossRef]
- Michelson, H.; Reardon, T.; Perez, F. Small Farmers and Big Retail: Trade-offs of Supplying Supermarkets in Nicaragua. World Dev. 2012, 40, 342–354. [Google Scholar] [CrossRef]
- Nuthalapati, C.S.R.; Sutradhar, R.; Reardon, T.; Qaim, M. Supermarket procurement and farmgate prices in India. World Dev. 2020, 134, 105034. [Google Scholar] [CrossRef]
- Singh, S. Linking small horticultural producers with markets: Indian experiences and lessons. Acta Hortic. 2010, 880, 75–82. [Google Scholar] [CrossRef]
- Holloway, G. An Old Problem Revisited - and Solved: Upton and Dalton’s Linear Production Response: A Note. J. Agric. Econ. 2003, 54, 487–497. [Google Scholar] [CrossRef]
- Paris, Q. The von Liebig Hypothesis. Am. J. Agric. Econ. 1992, 74, 1019–1028. [Google Scholar] [CrossRef]
- Ackello Ogutu, A.C.; Paris, Q.; Williams, W.A. Testing a von Liebig Crop Response Function against Polynomial Specifications. Am. J. Agric. Econ. 1985, 67, 873–880. [Google Scholar] [CrossRef]
- Kouka, P.J.; Jolly, C.M.; Henao, J. Agricultural response functions for limited resource farmers in Sub-Saharan Africa. Fertil. Res. 1994, 40, 135–141. [Google Scholar] [CrossRef]
- Ding, J.; Wang, W. Information sharing in a green supply chain with promotional effort. Kybernetes 2019, 49, 2683–2712. [Google Scholar] [CrossRef]
- Lai, X.; Tao, Y.; Wang, F.; Zou, Z. Sustainability investment in maritime supply chain with risk behavior and information sharing. Int. J. Prod. Econ. 2019, 218, 16–29. [Google Scholar] [CrossRef]
- Squatrito, S.; Arena, E.; Palmeri, R.; Fallico, B. Public and Private Standards in Crop Production: Their Role in Ensuring Safety and Sustainability. Sustainability 2020, 12, 606. [Google Scholar] [CrossRef]
- Chi, Y.; Yang, P.; Ren, S.; Yang, J. Finding the optimal fertilizer type and rate to balance yield and soil GHG emissions under reclaimed water irrigation. Sci. Total Environ. 2020, 729, 138954. [Google Scholar] [CrossRef]
- Pollesch, N.; Dale, V.H. Applications of aggregation theory to sustainability assessment. Ecol. Econ. 2015, 114, 117–127. [Google Scholar] [CrossRef]
- Lucchi, A.; Benelli, G. Towards pesticide-free farming? Sharing needs and knowledge promotes Integrated Pest Management. Environ. Sci. Pollut. Res. 2018, 25, 13439–13445. [Google Scholar] [CrossRef]
- Deguine, J.p.; Rousse, P.; Atiama-nurbel, T. Agroecological Crop Protection: Concepts and a Case Study from Reunion. In Integrated Pest Management and Pest Control: Current and Future Tactics; IntechOpen: London, UK, 2012; pp. 63–76. [Google Scholar] [CrossRef][Green Version]
- Nie, T.; Chen, P.; Zhang, Z.; Qi, Z.; Lin, Y.; Xu, D. Effects of different types of water and nitrogen fertilizer management on greenhouse gas emissions, yield, and water consumption of paddy fields in cold region of China. Int. J. Environ. Res. Public Health 2019, 16, 1639. [Google Scholar] [CrossRef]
- Carlson, K.M.; Gerber, J.S.; Mueller, N.D.; Herrero, M.; MacDonald, G.K.; Brauman, K.A.; Havlik, P.; O’Connell, C.S.; Johnson, J.A.; Saatchi, S.; et al. Greenhouse gas emissions intensity of global croplands. Nat. Clim. Chang. 2017, 7, 63–68. [Google Scholar] [CrossRef]
- Chen, X.; Gao, Z.; Swisher, M.; House, L.; Zhao, X. Eco-labeling in the Fresh Produce Market: Not All Environmentally Friendly Labels Are Equally Valued. Ecol. Econ. 2018, 154, 201–210. [Google Scholar] [CrossRef]
- Ricci, E.C.; Banterle, A.; Stranieri, S. Trust to Go Green: An Exploration of Consumer Intentions for Eco-friendly Convenience Food. Ecol. Econ. 2018, 148, 54–65. [Google Scholar] [CrossRef]
- Cui, L.; Guo, S.; Zhang, H. Coordinating a green agri-food supply chain with revenue-sharing contracts considering retailers’ green marketing efforts. Sustainability 2020, 12, 1289. [Google Scholar] [CrossRef]
- Hu, B.; Qu, J.; Meng, C. Supply chain coordination under option contracts with joint pricing under price-dependent demand. Int. J. Prod. Econ. 2018, 205, 74–86. [Google Scholar] [CrossRef]
- Petruzzi, N.C.; Dada, M. Pricing and the Newsvendor Problem: A Review with Extensions. Oper. Res. 1999, 47, 183–194. [Google Scholar] [CrossRef]
- Huang, G.; Ding, Q.; Dong, C.; Pan, Z. Joint optimization of pricing and inventory control for dual-channel problem under stochastic demand. Ann. Oper. Res. 2021, 298, 307–337. [Google Scholar] [CrossRef]
- Seufert, V.; Ramankutty, N.; Foley, J.A. Comparing the yields of organic and conventional agriculture. Nature 2012, 485, 229–232. [Google Scholar] [CrossRef] [PubMed]
- Crowder, D.W.; Reganold, J.P. Financial competitiveness of organic agriculture on a global scale. Proc. Natl. Acad. Sci. USA 2015, 112, 7611–7616. [Google Scholar] [CrossRef] [PubMed]
- Frank, M.D.; Beattie, B.R.; Embleton, M.E. A Comparsion of Alternative Crop Models. Am. J. Agric. Econ. 1990, 72, 597–603. [Google Scholar] [CrossRef]
- Rodrigues, D.B.; Dalmarco, D.d.A.S.; Aoqui, C.; Marinho, B.d.L. The meaning of the organic certification label for the consumer: A cluster analysis. REGE-Rev. Gestão 2016, 23, 316–325. [Google Scholar] [CrossRef]
- Singh, A.; Verma, P. Factors influencing Indian consumers’ actual buying behaviour towards organic food products. J. Clean. Prod. 2017, 167, 473–483. [Google Scholar] [CrossRef]
- Kushwah, S.; Dhir, A.; Sagar, M.; Gupta, B. Determinants of organic food consumption. A systematic literature review on motives and barriers. Appetite 2019, 143, 104402. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).