Study on the Impact of Road Traffic Accident Duration Based on Statistical Analysis and Spatial Distribution Characteristics: An Empirical Analysis of Houston
Abstract
1. Introduction
2. Literature Review
3. Data Processing
4. Methodology
5. Results and Discussion
6. Conclusions
- (1)
- The significant influencing elements of heavy traffic accidents and serious traffic accidents were comparable when using general traffic accidents as the reference item. Heavy traffic accidents and serious traffic accidents were significantly influenced by day or night, highway, accident roadside, intersection, crosswalk, traffic signal, and stop sign; serious traffic accidents were significantly influenced by peak hour and weekday; and heavier traffic accidents were significantly influenced by body temperature. Body temperature has a considerable impact on more severe auto accidents. When attempting to minimize the delay brought on by traffic accidents, several considerations should be taken into consideration.
- (2)
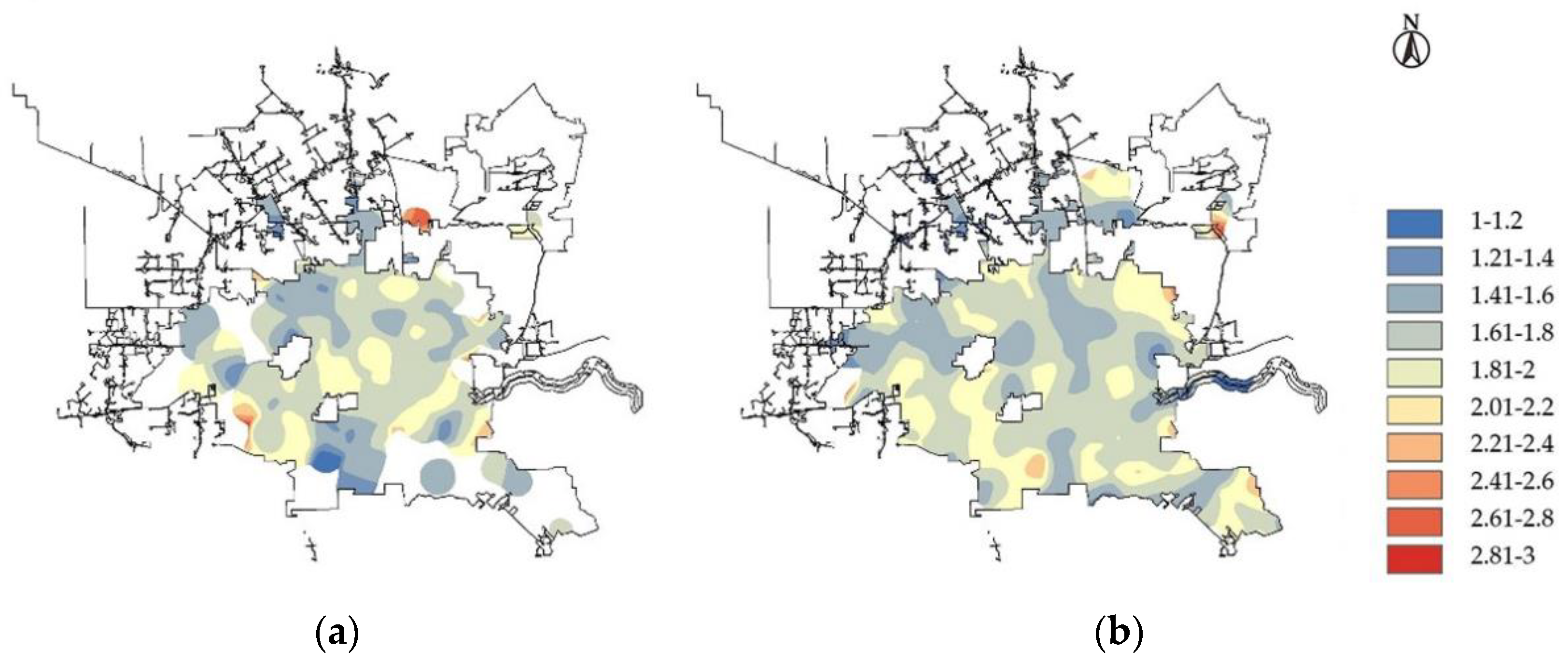
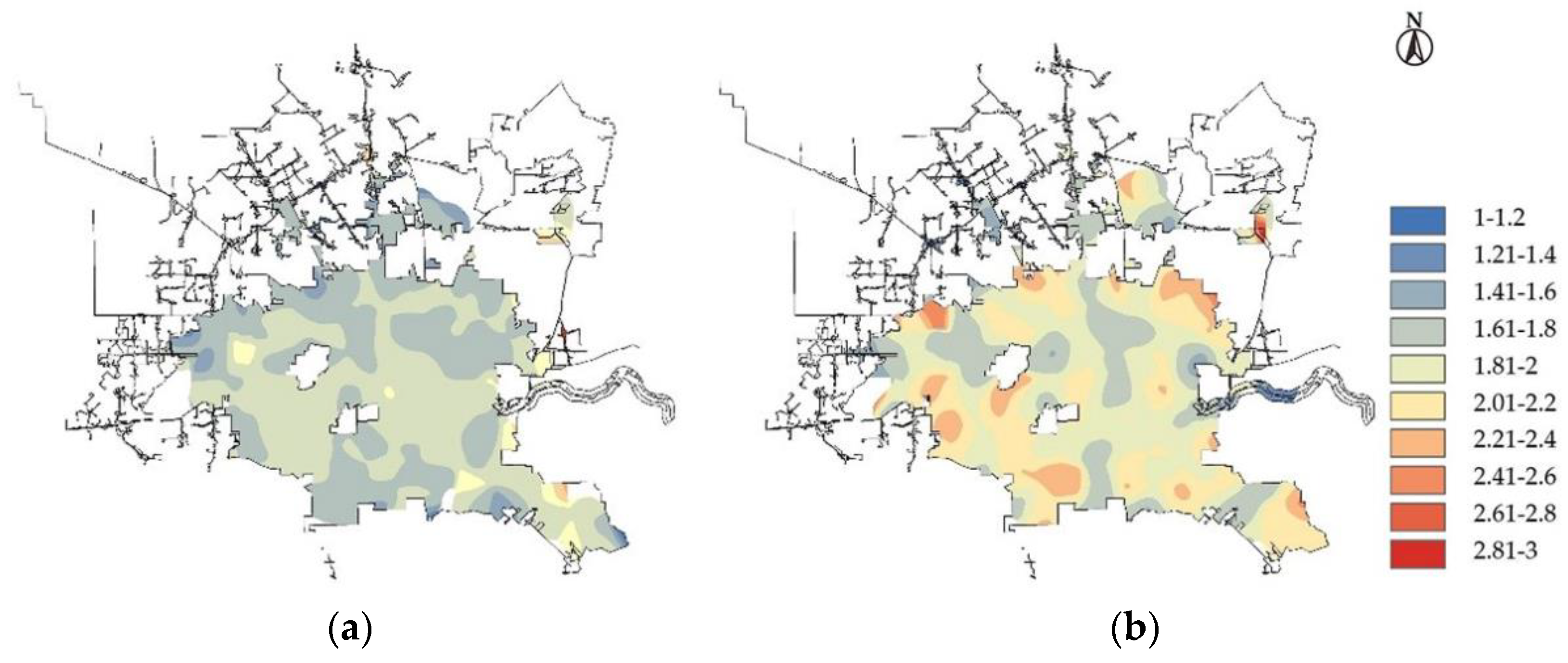
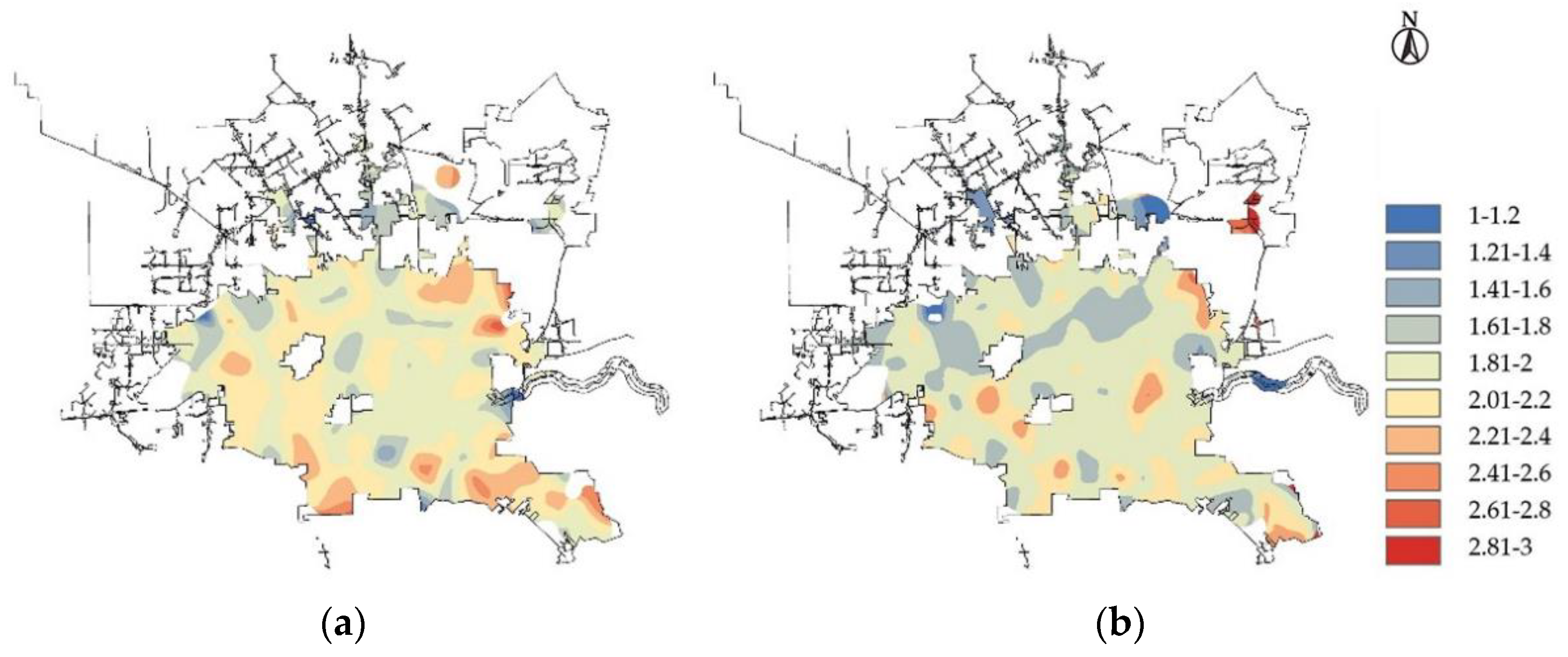
- Through spatial analysis, it has been discovered that traffic accidents generally last longer in residential areas. At the same time, serious accidents are more likely to happen at night and on non-working days, necessitating attention. In order to ensure traffic safety, residential areas’ nighttime lighting conditions should be enhanced, and nighttime and non-working daytime traffic control should be strengthened to increase the response time of crash handling departments.
- (3)
- The study found that the crash durations show different trends near different road facilities. In some road sections, it is necessary to focus on traffic safety issues and take optimization measures, such as: near pedestrian crossings and near stop signs. Traffic crashes with a long duration often occur in the above sections, and traffic safety should be ensured by setting traffic signs, speed limits, and speed bumps.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y. The world health organization released the “2018 Global Road Safety Status Report”. Chin. J. Disaster Med. 2019, 2, 100. [Google Scholar]
- Wang, H.M. Present situation of road traffic accident in China and its characteristics. China Saf. Sci. J. 2009, 10, 121–126. [Google Scholar] [CrossRef]
- Bardal, K.G.; Jorgensen, F. Valuing the risk and social costs of road traffic accidents—Seasonal variation and the significance of delay costs. Transp. Policy 2017, 57, 10–19. [Google Scholar] [CrossRef]
- Zhang, L. Study on the Relationship between Urban Road Traffic Accident Duration Prediction and Accident Influencing Factors. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2021. [Google Scholar] [CrossRef]
- Yang, Y.; He, K.; Wang, Y.P.; Yuan, Z.Z.; Yin, Y.H.; Guo, M.Z. Identification of dynamic traffic crash risk for cross-area freeways based on statistical and machine learning methods. Phys. A Stat. Mech. Its Appl. 2022, 595, 127083. [Google Scholar] [CrossRef]
- Yang, Y.; Yuan, Z.; Meng, R. Exploring Traffic Crash Occurrence Mechanism toward Cross-Area Freeways via an Improved Data Mining Approach. J. Transp. Eng. Part A Syst. 2022, 148, 04022052. [Google Scholar] [CrossRef]
- Wang, J.Y.; Lu, H.P.; Sun, Z.; Wang, T. A method for identifying influencing factors of severity of vehicle crash based on MNL model. J. Highw. Transp. Res. Dev. 2021, 10, 107–113. [Google Scholar]
- Li, G. Highway Traffic Accident Severity Prediction Based on Ordered Logit and Multinomial Logit Model. Master’s Thesis, Chang’an University, Shaanxi, China, 2018. [Google Scholar]
- Celik, A.K.; Oktay, E. A multinomial logit analysis of risk factors influencing road traffic injury severities in the Erzurum and Kars Provinces of Turkey. Accid. Anal. Prev. 2014, 11, 66–77. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, G.H.; Zhu, X.Y. Analysis of driver injury severity in single-vehicle crashes on rural and urban roadways. Accid. Anal. Prev. 2016, 94, 35–45. [Google Scholar] [CrossRef]
- Topuz, K.; Delen, D. A probabilistic bayesian inference model to investigate injury severity in automobile crashes. Decis. Support Syst. 2021, 150, 113557. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, K.; Yuan, Z.; Liu, D. Predicting freeway traffic crash severity using XGBoost-Bayesian network model with consideration of features interaction. J. Adv. Transp. 2022, 2022, 4257865. [Google Scholar] [CrossRef]
- Jeong, H.; Jang, Y.; Bowman, P.J.; Masoud, N. Classification of motor vehicle crash injury severity: A hybrid approach for imbalanced data. Accid. Anal. Prev. 2018, 12, 250–261. [Google Scholar] [CrossRef] [PubMed]
- Erdogan, S.; Yilmaz, I.; Baybura, T.; Gullu, M. Geographical information systems aided traffic accident analysis system case study: City of Afyonkarahisar. Accid. Anal. Prev. 2008, 1, 174–181. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.P.; Luo, S.X.; Li, R.M. GIS-based spatial patterns analysis of urban road traffic crashes in shenzhen. China J. Highw. Transp. 2019, 8, 156–164. [Google Scholar] [CrossRef]
- Singh, N.; Katiyar, S.K. Application of geographical information system (GIS) in reducing accident blackspots and in planning of a safer urban road network: A review. Ecol. Inform. 2021, 66, 101436. [Google Scholar] [CrossRef]
- Rodrigues, D.S.; Ribeiro, P.J.; Nogueira, I.C. Safety classification using GIS in decision-making process to define priority road interventions. J. Transp. Geogr. 2015, 43, 101–110. [Google Scholar] [CrossRef]
- Yang, S.; Lu, S.J.; Wu, Y.J. GIS-based economic cost estimation of traffic accidents in St. Louis, Missouri. Procedia Soc. Behav. Sci. 2013, 96, 2907–2915. [Google Scholar] [CrossRef][Green Version]
- Shafabakhsh, G.A.; Famili, A.; Bahadori, M.S. GIS-based spatial analysis of urban traffic accidents: Case study in Mashhad, Iran. J. Traffic Transp. Eng. 2017, 4, 290–299. [Google Scholar] [CrossRef]
- Al-Aamri, A.K.; Hornby, G.; Zhang, L.C.; Al-Maniri, A.A.; Padmadas, S.S. Mapping road traffic crash hotspots using GIS-based methods: A case study of Muscat Governorate in the Sultanate of Oman. Spat. Stat. 2021, 42, 100458. [Google Scholar] [CrossRef]
- Sun, F.H.; Ban, X.X.; Qi, L.L. The “body sense” temperature calculation method. Meteorol. Sci. Technol. 2002, 5, 282–283+303. [Google Scholar] [CrossRef]
- Jin, A. On methodology of parameter estimation in logit model. J. Transp. Syst. Eng. 2004, 1, 71–75. [Google Scholar] [CrossRef]
- Zou, T.H.; Xie, J.; Liu, J.F.; Chen, P. Analysis on the spatial distribution of junior middle school education resources based on GIS in Neijiang. Geomat. Spat. Inf. Technol. 2022, 6, 8–13. [Google Scholar]
- Chen, J.L. Research on Identifing Hotspots in the Urban Road Networks Based on the Network Kernel Density Estimation Method. Master’s Thesis, Southeast University, Nanjin, China, 2015. [Google Scholar]
- Chen, Y.; Xiangnan, L.I.; Sun, Z. Identification method of factors affecting traffic accident based on Logistics. Technol. Econ. Areas Commun. 2018, 5, 1–5. [Google Scholar] [CrossRef]
- Ding, C.; Ma, X.L.; Wang, Y.H. Exploring the influential factors in incident clearance time: Disentangling causation from self-selection bias. Accid. Anal. Prev. 2015, 85, 58–65. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.K.; Zhang, J. Exploring background risk factors for fatigue crashes involving truck drivers on regional roadway networks: A case control study in Jiangxi and Shaanxi, China. Springer Plus 2016, 5, 582. [Google Scholar] [CrossRef][Green Version]
- Zhang, P.; Wang, C.; Chen, F.; Cui, S.; Cheng, J.; Bo, W. A random-parameter negative binomial model for assessing freeway crash frequency by injury severity: Daytime versus nighttime. Sustainability 2022, 14, 9061. [Google Scholar] [CrossRef]
- Helai, H.; Chor, C.H.; Haque, M.M. Severity of driver injury and vehicle damage in traffic crashes at intersections: A Bayesian hierarchical analysis. Accid. Anal. Prev. 2008, 40, 45–54. [Google Scholar] [CrossRef]
- Nam, D.; Mannering, F. An exploratory hazard-based analysis of highway incident duration. Transp. Res. Part A Policy Pract. 2000, 34, 85–102. [Google Scholar] [CrossRef]
- Yang, Y.; Tian, N.; Wang, Y.; Yuan, Z. A Parallel FP-Growth Mining Algorithm with Load Balancing Constraints for Traffic Crash Data. Int. J. Comput. Commun. Control 2022, 17, 4806. [Google Scholar] [CrossRef]
- Ma, A. Research on the Duration and Influence Scope of Expressway Traffic Accidents. Master’s Thesis, Chang’an University, Shaanxi, China, 2013. [Google Scholar]
- Jin, W.; Chowdhury, M.; Salek, M.S.; Khan, S.M.; Gerard, P. Investigating hierarchical effects of adaptive signal control system on crash severity using random-parameter ordered regression models incorporating observed heterogeneity. Accid. Anal. Prev. 2021, 150, 105895. [Google Scholar] [CrossRef]
- Shi, X. Research on Speed Control and Visual Search Behavior of Drivers at Urban Signalized Intersections. Master’s Thesis, Chang’an University, Shaanxi, China, 2011. [Google Scholar]
- Gao, L. Conflict Analysis and Delay Modeling between Pedestrians and Motor Vehicles at Pedestrian crossing in Urban Road Environment. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2010. [Google Scholar]
- Shao, Z.Q. Analysis and optimization of stop and yield signs at intersections and setting of yield lines. Shandong Transp. Sci. Technol. 2021, 5, 128–131. [Google Scholar] [CrossRef]
- Wang, D.; Li, L.; Wu, Q.; Luan, J. Analysis of the influence of adverse weather conditions on expressway traffic crashes. In Proceedings of the 32nd Annual Meeting of China Meteorological Society, Tianjin, China, 14 October 2015; p. 501. [Google Scholar]
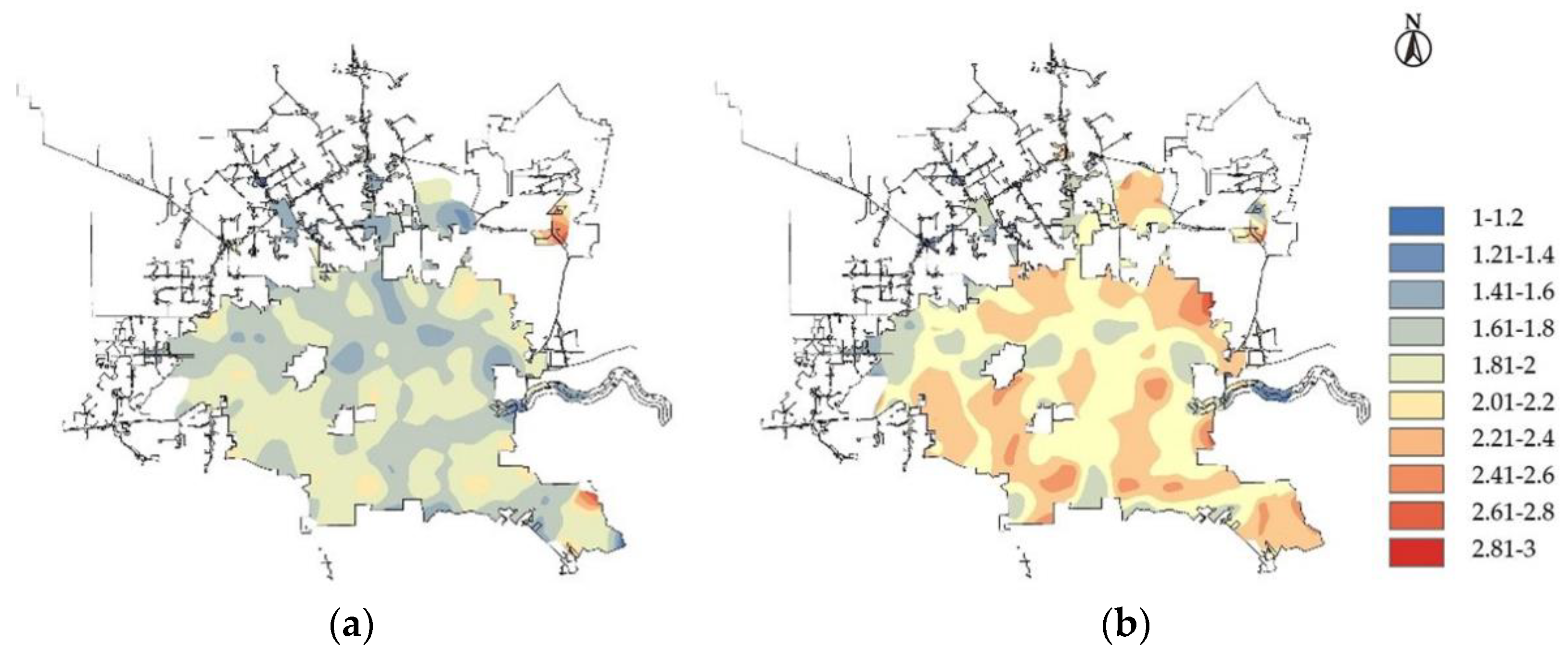
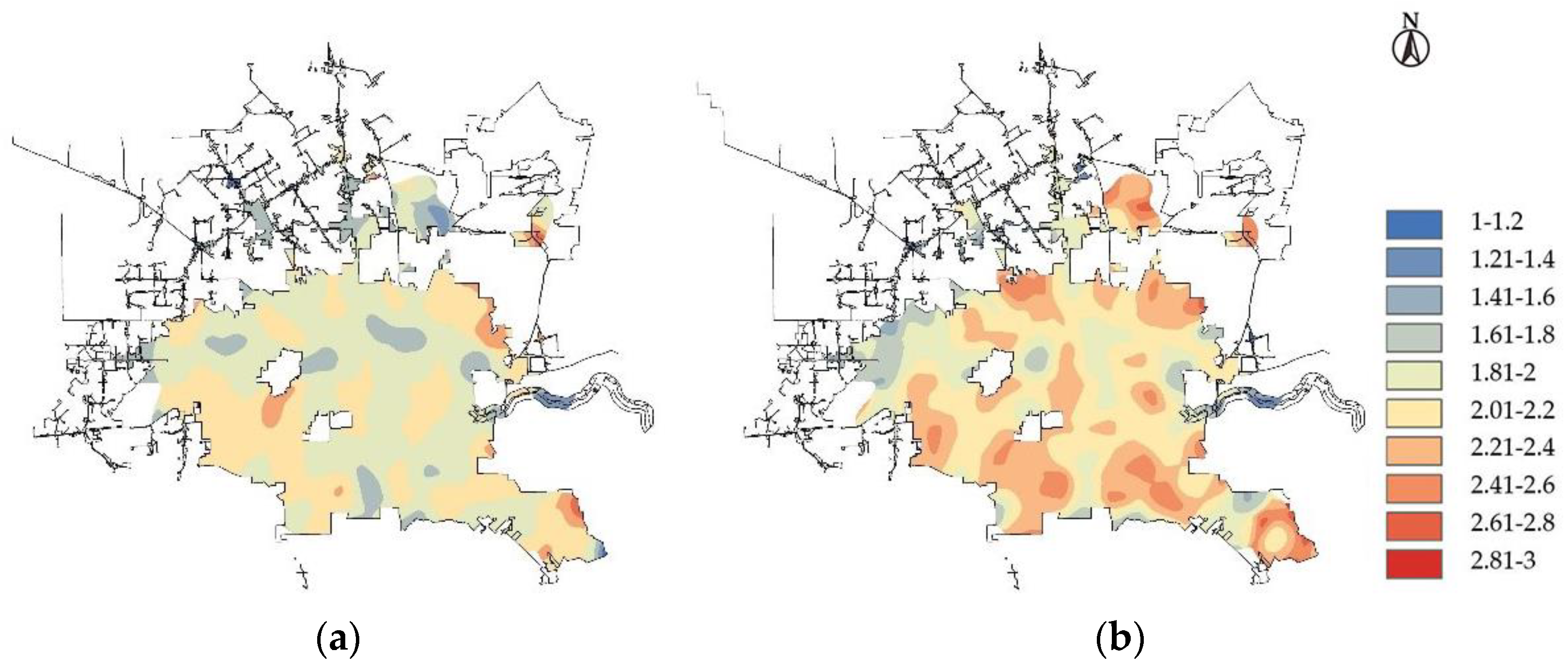

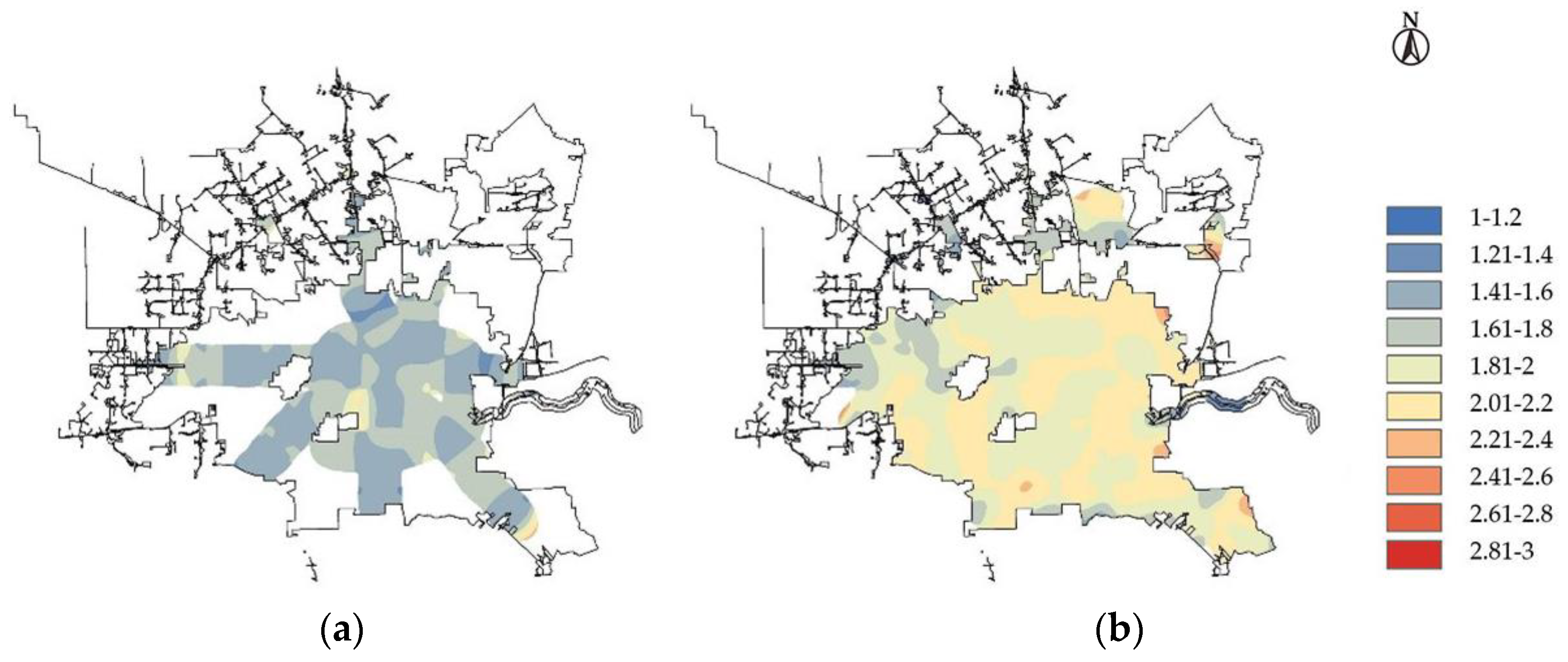
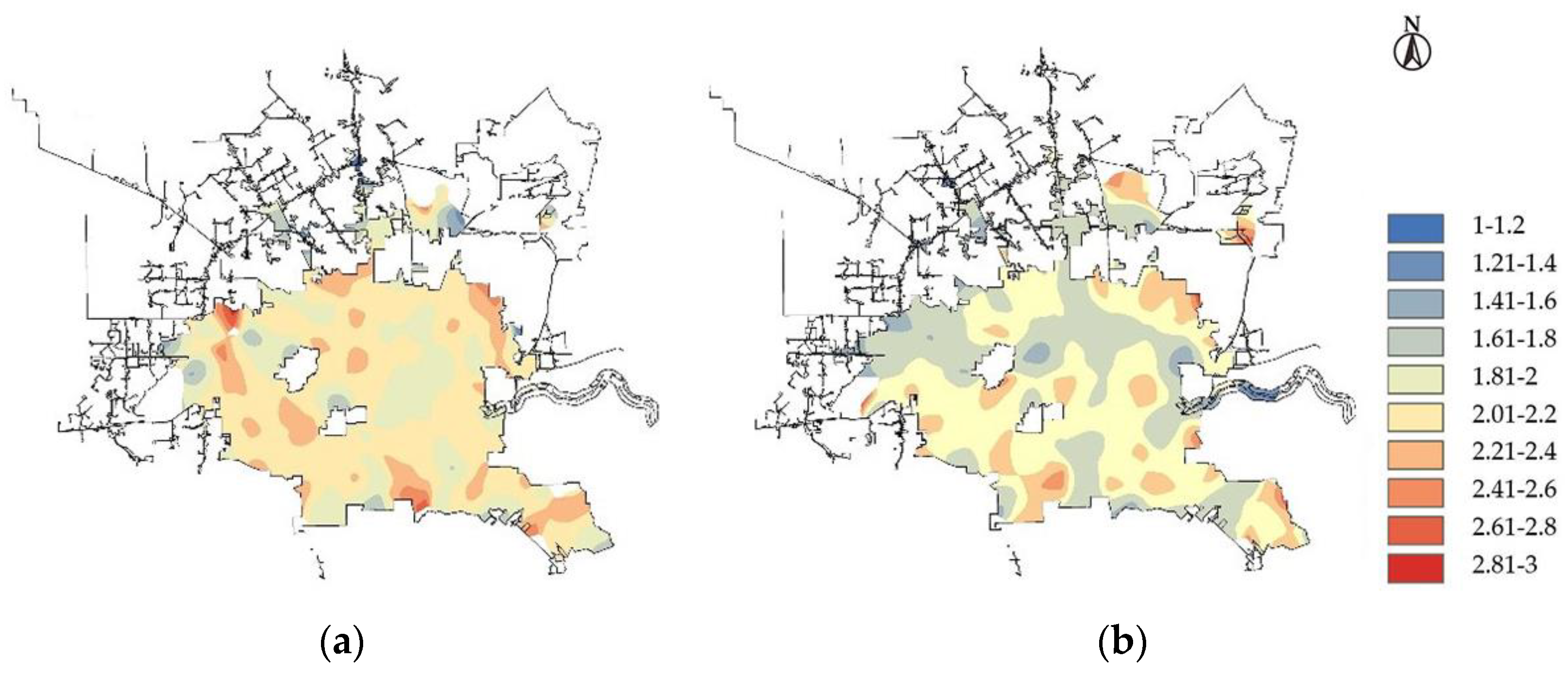


| Variable Category | Variable Name | Variable Assignment and Proportion |
|---|---|---|
| Dependent Variable | Duration | 1 (36%) = general traffic crash (duration ≤ 60 min), 2 (41.9%) = serious traffic crash (60 min < duration ≤ 120 min), 3 (22.1%) = serious traffic crash (duration > 120 min) |
| Time | Peak hours | 1 (40.8%) = occurred during peak hours, 0 (59.2%) = did not occur during peak hours |
| Season | 1 (17.3%) = spring, 2 (16.9%) = summer, 3 (33.6%) = autumn, 4 (32.3%) = winter | |
| Weekday | 0 (86.8%) = occured on a weekday, 1 (13.2%) = did not occur on a weekday | |
| Day or night | 1 (65.3%) = daytime, 0 (34.7%) = nighttime | |
| Roadway | Happens on the highway | 1 (22.3%) = Yes, 0 (77.7%) = No |
| Roadside crash | 1 (24.2%) = Left, 0 (75.8%) = Right | |
| Near the intersection | 1 (3.6%) = Yes, 0 (96.3%) = No | |
| Near the crosswalk | 1 (9.6%) = Yes, 1 (90.4%) = No | |
| Near a stop sign | 1 (6.1%) = Yes, 0 (93.9%) = No | |
| Near traffic lights | 1 (28.1%) = Yes, 0 (71.9%) = No | |
| The Environment | Sensible temperature | 1 (15%) = (sensible temperature < 10 °C), 2 (26%) = (10 °C ≤ sensible temperature ≤ 20 °C), 3 (40.5%) = (20 °C ≤ sensible temperature < 30 °C), 4 (18.6%) = (sensible temperature ≥ 30 °C) |
| Visibility | 1 (88.8%) = high visibility, 2 (3.8%) = average visibility, 3 (7.4%) = poor visibility | |
| Snowy and Rainy | 0 (8.7%) = No, 1 (91.3%) = Yes |
| Model | Model Fit Conditions | Likelihood Ratio Test | ||
|---|---|---|---|---|
| −2 log−Likelihood | Chi−Square | Degrees of Freedom | Significant | |
| Only intercept | 15,855.336 | |||
| In the end | 11,488.435 | 4366.901 | 50 | 0 |
| Category | Effective Factors | Slightly Serious Traffic Crashes | Serious Traffic Crash | ||||||
|---|---|---|---|---|---|---|---|---|---|
| B | Wald | p | OR | B | Wald | p | OR | ||
| Peak hour | - | - | - | - | 0.461 | 96.085 | 0 | 0.631 | |
| Time | Day or night | 0.299 | 54.744 | 0 | 0.742 | 0.771 | 252.942 | 0 | 0.463 |
| Weekdays | - | - | - | - | 0.85 | 186.005 | 0 | 0.427 | |
| The road | Highway | 0.618 | 187.722 | 0 | 0.539 | 1.246 | 393.552 | 0 | 0.288 |
| Side of the road | 0.319 | 53.715 | 0 | 1.375 | 0.497 | 90.189 | 0 | 1.644 | |
| Near the intersection | 0.402 | 20.417 | 0 | 0.669 | 1.03 | 46.697 | 0 | 0.357 | |
| Near a crosswalk | 0.27 | 17.903 | 0 | 1.31 | 0.23 | 7.084 | 0.008 | 1.258 | |
| Near stop signs | 0.331 | 17.394 | 0 | 1.393 | 0.21 | 5.059 | 0.024 | 1.234 | |
| Near traffic signals | 0.169 | 15.722 | 0 | 1.184 | 0.524 | 81.535 | 0 | 0.592 | |
| The environment | Somatosensory temperature level 1 | 0.212 | 6.863 | 0.009 | 1.236 | - | - | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, X.; Hu, H.; Ma, S.; Lin, K.; Wang, J.; Lu, H. Study on the Impact of Road Traffic Accident Duration Based on Statistical Analysis and Spatial Distribution Characteristics: An Empirical Analysis of Houston. Sustainability 2022, 14, 14982. https://doi.org/10.3390/su142214982
Sun X, Hu H, Ma S, Lin K, Wang J, Lu H. Study on the Impact of Road Traffic Accident Duration Based on Statistical Analysis and Spatial Distribution Characteristics: An Empirical Analysis of Houston. Sustainability. 2022; 14(22):14982. https://doi.org/10.3390/su142214982
Chicago/Turabian StyleSun, Xu, Hanxiao Hu, Shuo Ma, Kun Lin, Jianyu Wang, and Huapu Lu. 2022. "Study on the Impact of Road Traffic Accident Duration Based on Statistical Analysis and Spatial Distribution Characteristics: An Empirical Analysis of Houston" Sustainability 14, no. 22: 14982. https://doi.org/10.3390/su142214982
APA StyleSun, X., Hu, H., Ma, S., Lin, K., Wang, J., & Lu, H. (2022). Study on the Impact of Road Traffic Accident Duration Based on Statistical Analysis and Spatial Distribution Characteristics: An Empirical Analysis of Houston. Sustainability, 14(22), 14982. https://doi.org/10.3390/su142214982









