An Integrated Seamless Control Strategy for Distributed Generators Based on a Deep Learning Artificial Neural Network
Abstract
1. Introduction
- No transition between different control schemes is required.
- The strategy enables the DG to be a local load-follower.
- It eliminates harmonics from the utility current in the case of a non-linear local load.
- Moreover, using the DL-ANN controller allows the DG system to overcome sudden changes without the need to change the controller’s parameters.
2. System Model
2.1. Power Stage
2.2. Control Stage
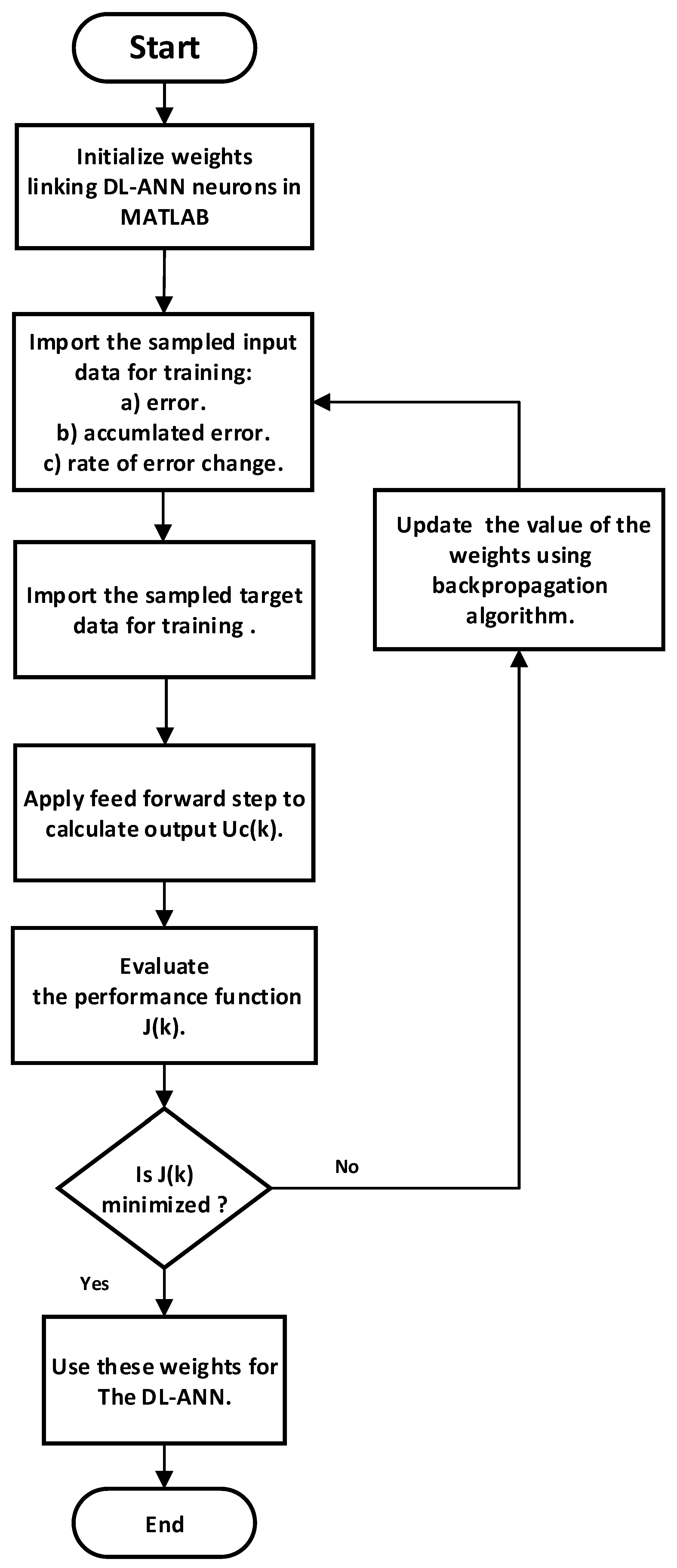
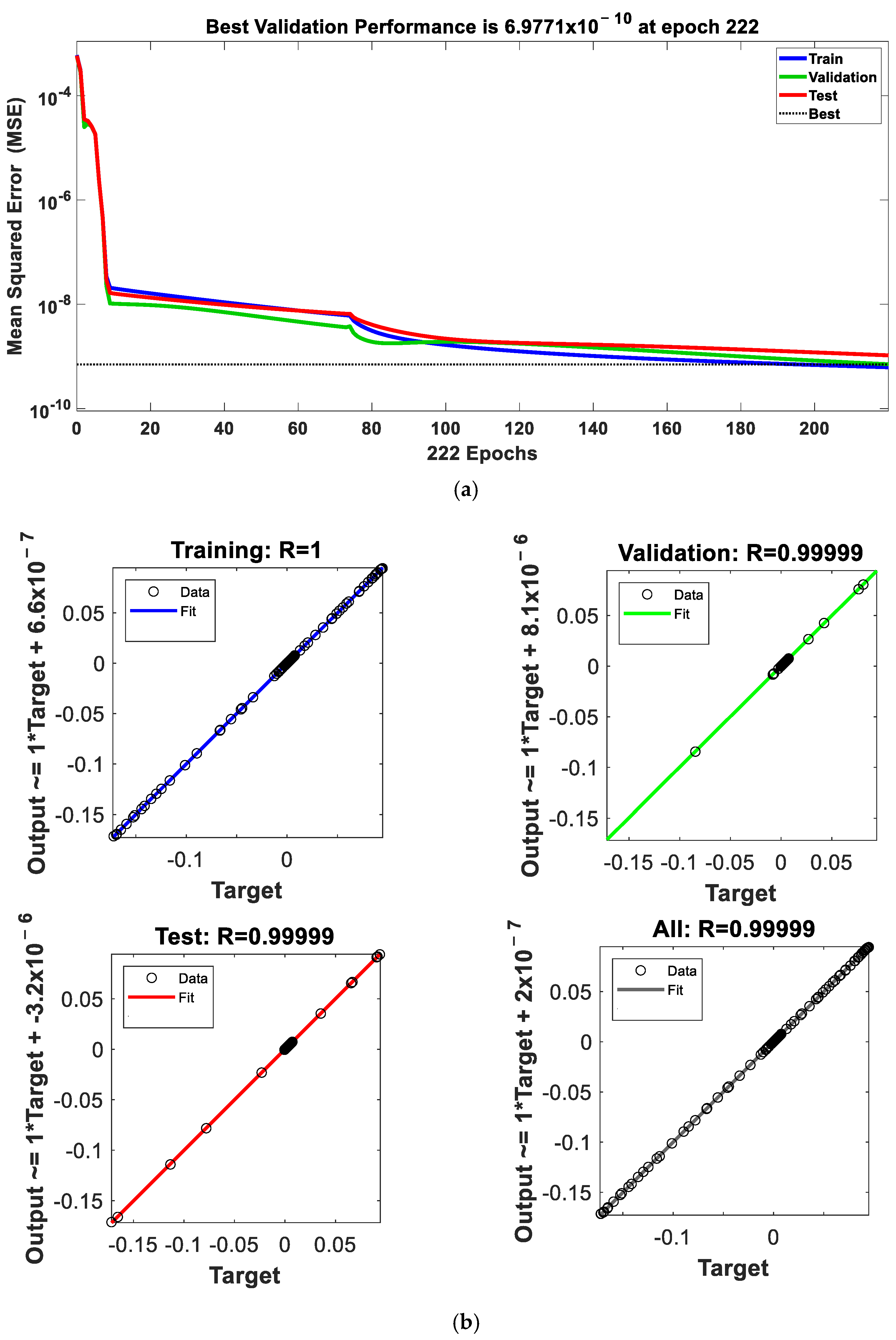
3. The Proposed DL-ANN-Based PID Controller
4. Simulation Results
4.1. Mode of Grid Connection
4.2. Islanding Transition
4.3. Grid-Connected Transition
4.4. Comparison
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jayaram, J.; Srinivasan, M.; Prabaharan, N.; Senjyu, T. Design of Decentralized Hybrid Microgrid Integrating Multiple Renewable Energy Sources with Power Quality Improvement. Sustainability 2022, 14, 7777. [Google Scholar] [CrossRef]
- Wang, J.; Li, D.; Lv, X.; Meng, X.; Zhang, J.; Ma, T.; Pei, W.; Xiao, H. Two-Stage Energy Management Strategies of Sustainable Wind-PV-Hydrogen-Storage Microgrid Based on Receding Horizon Optimization. Energies 2022, 15, 2861. [Google Scholar] [CrossRef]
- Pattabiraman, D.; Lasseter, R.H.; Jahns, T.M. Comparison of grid following and grid forming control for a high inverter penetration power system. In Proceedings of the IEEE Power & Energy Society General Meeting in 2018 (PESGM), Portland, OR, USA, 5–10 August 2018; pp. 1–5. [Google Scholar]
- Omar, O.A.; Badra, N.M.; Attia, M.A. Enhancement of on-grid pv system under irradiance and temperature variations using new optimized adaptive controller. Int. J. Electr. Comput. Eng. 2018, 8, 2650. [Google Scholar] [CrossRef]
- González, I.; Calderón, A.J.; Portalo, J.M. Innovative multi-layered architecture for heterogeneous automation and monitoring systems: Application case of a photovoltaic smart microgrid. Sustainability 2021, 13, 2234. [Google Scholar] [CrossRef]
- Zeng, Q.; Chang, L. Study of advanced current control strategies for three-phase grid-connected pwm inverters for distributed generation. In Proceedings of the 2005 IEEE Conference on Control Applications, Toronto, ON, Canada, 28–31 August 2005; pp. 1311–1316. [Google Scholar]
- Kim, H.; Yu, T.; Choi, S. Indirect current control algorithm for utility interactive inverters in distributed generation systems. IEEE Trans. Power Electron. 2008, 23, 1342–1347. [Google Scholar]
- Li, X.; Zhang, H.; Shadmand, M.B.; Balog, R.S. Model predictive control of a voltage-source inverter with seamless transition between islanded and grid-connected operations. IEEE Trans. Ind. Electron. 2017, 64, 7906–7918. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, J.; Zhao, Y. A unified control strategy for three-phase inverter in distributed generation. IEEE Trans. Power Electron. 2013, 29, 1176–1191. [Google Scholar]
- Singh, M.; Khadkikar, V.; Chandra, A.; Varma, R.K. Grid interconnection of renewable energy sources at the distribution level with power-quality improvement features. IEEE Trans. Power Deliv. 2010, 26, 307–315. [Google Scholar] [CrossRef]
- Rodriguez, P.; Luna, A.; Munoz-Aguilar, R.S.; Etxeberria-Otadui, I.; Teodorescu, R.; Blaabjerg, F. A stationary reference frame grid synchronization system for three-phase grid-connected power converters under adverse grid conditions. IEEE Trans. Power Electron. 2011, 27, 99–112. [Google Scholar] [CrossRef]
- Marei, M.I. A unified control strategy based on phase angle estimation for matrix converter interface system. IEEE Syst. J. 2012, 6, 278–286. [Google Scholar] [CrossRef]
- Gao, F.; Iravani, M.R. A control strategy for a distributed generation unit in grid-connected and autonomous modes of operation. IEEE Trans. Power Deliv. 2008, 23, 850–859. [Google Scholar]
- Yu, T.; Choi, S.; Kim, H. Indirect current control algorithm for utility interactive inverters for seamless transfer. In Proceedings of the 2006 37th IEEE Power Electronics Specialists Conference, Jeju, Korea, 18–22 June 2006; pp. 1–6. [Google Scholar]
- Kwon, J.; Yoon, S.; Choi, S. Indirect current control for seamless transfer of three-phase utility interactive inverters. IEEE Trans. Power Electron. 2012, 27, 773–781. [Google Scholar] [CrossRef]
- Lim, K.; Choi, J. PR based indirect current control for seamless transfer of grid-connected inverter. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016; pp. 3749–3755. [Google Scholar]
- Kim, K.; Kim, H.J.; Shin, D.; Lee, J.P.; Kim, T.J.; Yoo, D.W. A novel seamless transfer control strategy for wide range load. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; pp. 1–5. [Google Scholar]
- Mohamed, Y.A.R.I.; Radwan, A.A. Hierarchical control system for robust microgrid operation and seamless mode transfer in active distribution systems. IEEE Trans. Smart Grid 2011, 2, 352–362. [Google Scholar] [CrossRef]
- Jin, C.; Gao, M.; Lv, X.; Chen, M. A seamless transfer strategy of islanded and grid-connected mode switching for microgrid based on droop control. In Proceedings of the 2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 969–973. [Google Scholar]
- Mansour, A.M.; Arafa, O.M.; Marei, M.I.; Abdelsalam, I.; Aziz, G.A.A.; Sattar, A.A. Hardware-in-the-loop testing of seamless interactions of multi-purpose grid-tied PV inverter based on SFT-PLL control strategy. IEEE Access 2021, 9, 123465–123483. [Google Scholar] [CrossRef]
- Meng, X.; Liu, Z.; Liu, J.; Wu, T.; Wang, S.; Liu, B. A seamless transfer strategy based on special master and slave DGs. In Proceedings of the 2017 IEEE 3rd International Future Energy Electronics Conference and ECCE Asia (IFEEC 2017-ECCE Asia), Kaohsiung, Taiwan, 3–7 June 2017; pp. 1553–1558. [Google Scholar]
- Zhang, W.; Liu, H.; Wang, W.; Loh, P.C. Seamless transfer scheme for parallel PV inverter system. IET Power Electron. 2020, 13, 1051–1058. [Google Scholar] [CrossRef]
- Amin, M.; Zhong, Q.C. Resynchronization of distributed generation based on the universal droop controller for seamless transfer between operation modes. IEEE Trans. Ind. Electron. 2019, 67, 7574–7582. [Google Scholar] [CrossRef]
- Patino, H.D.; Liu, D. Neural network-based model reference adaptive control system. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2000, 30, 198–204. [Google Scholar] [CrossRef]
- Mokhtar, M.; Marei, M.I.; El-Sattar, A.A. A control scheme for islanded and grid-connected DC microgrids. In Proceedings of the 2017 Nineteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 19–21 December 2017; pp. 176–180. [Google Scholar]
- Sameh, M.A.; Badr, M.A.; Mare, M.I.; Attia, M.A. Enhancing the performance of photovoltaic systems under partial shading conditions using cuttlefish algorithm. In Proceedings of the 2019 8th International Conference on Renewable Energy Research and Applications (ICRERA), Brasov, Romania, 3–6 November 2019; pp. 874–885. [Google Scholar]
- Mokhtar, M.; Marei, M.I.; El-Sattar, A.A. Improved current sharing techniques for DC microgrids. Electr. Power Compon. Syst. 2018, 46, 757–767. [Google Scholar] [CrossRef]
- Sefa, I.; Altin, N.E.C.M.İ.; Ozdemir, S.; Kaplan, O.R.H.A.N. Fuzzy PI controlled inverter for grid interactive renewable energy systems. IET Renew. Power Gener. 2015, 9, 729–738. [Google Scholar] [CrossRef]
- Yu, L.; Zhang, J.; Jiang, C. D-STATCOM control based on self-tuning PI with neural networks. In Proceedings of the China International Conference on Electricity Distribution 2012, Shanghai, China, 10–14 September 2012; pp. 1–4. [Google Scholar]
- Zare, A.; Moattari, M.; Melicio, R. Distributed Generation Control Using Modified PLL Based on Proportional-Resonant Controller. Appl. Sci. 2020, 10, 8891. [Google Scholar] [CrossRef]
- Bianchini, M.; Scarselli, F. On the complexity of neural network classifiers: A comparison between shallow and deep architectures. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 1553–1565. [Google Scholar] [CrossRef] [PubMed]
- Marei, M.I.; El-Saadany, E.F.; Salama, M.M. A novel control scheme for STATCOM using space vector modulation-based hysteresis current controller. In Proceedings of the 2004 11th International Conference on Harmonics and Quality of Power (IEEE Cat. No. 04EX951), Lake Placid, NY, USA, 12–15 September 2004; pp. 58–65. [Google Scholar]
- Power Systems Computer Aided Design Software PSCAD/EMTDC Manual; Manitoba HVDC Research Center: Winnipeg, MB, Canada, 1994.
- El-Ebiary, A.H.; Attia, M.A.; Marei, M.I. An Adaptive Unified Seamless Control Strategy for Distributed Generator Inverter. In Proceedings of the 2019 IEEE Conference on Power Electronics and Renewable Energy (CPERE), Aswan, Egypt, 23–25 October 2019; pp. 264–269. [Google Scholar]
- Kotsiantis, S.B.; Zaharakis, I.; Pintelas, P. Supervised machine learning: A review of classification techniques. Emerg. Artif. Intell. Appl. Comput. Eng. 2007, 160, 3–24. [Google Scholar]
- Yang, Q.; Jagannathan, S. Reinforcement learning controller design for affine nonlinear discrete-time systems using online approximators. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2012, 42, 377–390. [Google Scholar] [CrossRef] [PubMed]
- Kumar, R.; Srivastava, S.; Gupta, J.R.P. Artificial neural network based PID controller for online control of dynamical systems. In Proceedings of the 2016 IEEE 1st International Conference on Power Electronics, Intelligent Control and Energy Systems (ICPEICES), Delhi, India, 4–6 July 2016; pp. 1–6. [Google Scholar] [CrossRef]








| Vdc | 600 V |
| Lfilter | 8 mH |
| Cfilter | 15 μF |
| Rload | 60 Ω |
| Lload | 1 mH |
| Frequency | 50 Hz |
| Non-linear Local Load | Three-phase rectifier |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
EL-Ebiary, A.H.; Attia, M.A.; Marei, M.I.; Sameh, M.A. An Integrated Seamless Control Strategy for Distributed Generators Based on a Deep Learning Artificial Neural Network. Sustainability 2022, 14, 13506. https://doi.org/10.3390/su142013506
EL-Ebiary AH, Attia MA, Marei MI, Sameh MA. An Integrated Seamless Control Strategy for Distributed Generators Based on a Deep Learning Artificial Neural Network. Sustainability. 2022; 14(20):13506. https://doi.org/10.3390/su142013506
Chicago/Turabian StyleEL-Ebiary, Ahmed H., Mahmoud A. Attia, Mostafa I. Marei, and Mariam A. Sameh. 2022. "An Integrated Seamless Control Strategy for Distributed Generators Based on a Deep Learning Artificial Neural Network" Sustainability 14, no. 20: 13506. https://doi.org/10.3390/su142013506
APA StyleEL-Ebiary, A. H., Attia, M. A., Marei, M. I., & Sameh, M. A. (2022). An Integrated Seamless Control Strategy for Distributed Generators Based on a Deep Learning Artificial Neural Network. Sustainability, 14(20), 13506. https://doi.org/10.3390/su142013506












