Demand Response Transit Scheduling Research Based on Urban and Rural Transportation Station Optimization

Abstract

To reduce the operating cost and running time of demand responsive transit between urban and rural areas, a DBSCAN K-means (DK-means) clustering algorithm, which is based on the density-based spatial clustering of applications with noise (DBSCAN) and K-means clustering algorithm, was proposed to cluster pre-processing and station optimization for passenger reservation demand and to design a new variable-route demand responsive transit service system that can promote urban–rural integration. Firstly, after preprocessing the reservation demand through DBSCAN clustering algorithm, K-means clustering algorithm was used to divide fixed sites and alternative sites. Then, a bus scheduling model was established, and a genetic simulated annealing algorithm was proposed to solve the model. Finally, the feasibility of the model was validated in the northern area of Yongcheng City, Henan Province, China. The results show that the optimized bus scheduling reduced the operating cost and running time by 9.5% and 9.0%, respectively, compared with those of the regional flexible bus, and 4.5% and 5.1%, respectively, compared with those of the variable-route demand response transit after K-means clustering for passenger preprocessing.

1. Introduction

Due to the low density of passenger travel demand in urban and rural transportation areas, there are fewer bus services between urban and rural areas, and the cost of system operation and maintenance is relatively high. Especially under the influence of the COVID-19 epidemic, the demand for passenger travel has been further reduced due to policies and the closure of bus roads. The traditional bus system has difficulty meeting the travel requirements of passengers and does not meet the sustainable development strategy of urban and rural areas. Demand response transit (DRT) is a new mode of public transportation that can provide customized and high-quality travel services to passengers, among which variable-route DRT is one of its main development directions. It takes into account the advantages of fixed-line bus and DRT system, not only has the advantages of the low cost of the traditional bus system, but also has the advantage of the high flexibility of the DRT system. This study developed a variable-route DRT to satisfy passengers’ demand for public transportation with a lower operating cost and operating time.

For the evolution of the pandemic and its impact on DRT, Schasché and Sposato et al. [1] analyze numerous articles on DRT, outline developments in the research field, uncover conflicting performance expectations for services, and identify the relationship between differential perceptions of DRT services and the empirical design of the study. Campisi and Canale et al. [2] provide some ideas for optimizing integrated public transport services, balancing supply and demand mechanisms and improving service quality through literature and regulatory studies on the implementation of DRT systems in Italy under the influence of the COVID-19 epidemic. Abdullah [3] assessed passenger satisfaction with the services provided by demand response transportation services in Lahore, and through factor analysis of the designed questionnaire data, two basic factors, DRT service attributes and environment, were obtained. Dytckov [4] compares DRT service with regular buses under the same passenger demand and concludes that DRT service is more cost-effective and can significantly reduce CO₂ emissions at lower demand levels.

For rural public transport and urban public transport studies, Xiao [5] explored the urban and rural passenger traffic safety mechanism, investigated the personal attributes of urban and rural bus drivers in different regions, and concluded that the violations of rural bus drivers are significantly higher than those of urban bus drivers. Lu [6] proposed a flexible feeder bus route model that can serve irregularly shaped networks within cities and improve the accessibility of bus systems in urban areas. Wang [7] points out that it may be beneficial for public transport agencies to adapt to changing markets and provide flexible bus services in rural and suburban areas. Das [8] pointed out that rural feeder services between villages and bus stops are largely a missing component, suggesting that planning for feeder services can help bring benefits to rural communities. Wang [9] pointed out that bus services in rural areas are characterized by no transfers, as there is only one bus route per area, and almost all passengers go to the same destination in the city center. Ernesto [10] pointed out that the application of the public transportation system in large cities has the characteristics of complex road network topology, multimodal public transportation system (rapid rail transit system, bus and tram lines), and many-to-many ride demand characteristics.

For the route aspect of variable-route DRT, many studies have considered each reservation demand in planning the optimal route but ignore the uneconomical system-wide response to dispersed demand with a small number of reservation requests. Nourbakhsh and Ouyang et al. [11] pointed out that the route design problem for transit systems in low-traffic corridors is different from that of conventional transit and created a bus system with variable routes. Igor et al. [12] showed that bus operation network design is best when the interests of both passengers and bus operators are considered. Yu et al. [13] used a mixed-integer two-level planning model to optimize a bus route layout with the upper-level objective as total cost of the entire system and the lower-level objective as walking distance of passengers to the bus. Momenitabar [14] comprehensively analyzed the characteristics and advantages of customized buses over conventional buses and concluded that customized buses are more suitable for routes with concentrated passenger trips and moderate operating paths.

In terms of scheduling algorithms for variable-route demand responsive transit, studies have generally modeled bus companies with the goal of responding to most passengers with less passenger waiting time. Huang [15] and Guan [16] established a model for dynamic and static demand response transit scheduling, considering both advance reservation and real-time reservation phases. Sun [17] developed a mixed-integer planning model for DRT path optimization and collaborative scheduling to maximize the benefits to both passengers and bus companies. Jin [18] and Zheng [19] proposed a flexible DRT scheduling system combining multiple bus types and multiple operation modes to solve the uneconomical bus operation in low-density areas. Liu [20] and Shang [21] proposed a real-time bookable and dynamic scheduling bus system for passengers in low-density time windows and areas and demonstrated the effectiveness of the scheduling model through experimental simulations.

In terms of station design and service area scope, studies have mainly focused on intra-city demand response transit for relatively high-demand density and urban road conditions. Qiu [22] and Yue et al. [23] proposed a dynamic station strategy and slack arrival strategy to reduce the impact of uncertain travel demand on the performance of variable-route buses, and verified the utility of the dynamic station and slack arrival strategies. Pratelli and Schoen et al. [24] developed a model to optimize the station layout for DRT operations with an objective of maximizing the benefits to passengers inside and outside the vehicle. Crainic [25] addressed the problem of passenger assignment and station location selection using the relationship between bus service routes and bus station locations. Yu [26] proposes a web-based layout design method to generate tiered service areas and stops for customized transit systems. Daganzo [27] and Diana et al. [28] proposed and verified that demand responsive transit has a higher efficiency ratio and transportation efficiency than conventional transit in low-density areas and concluded that it is more applicable in low-density areas. Quadrifoglio et al. [29] investigated the relationship between the service area characteristics and the system service capacity of demand responsive transit at stations, whereas Wang [30] and Han [31] determined and optimized the flexible transit service area by introducing the concept of Voronoi diagram and “agglomeration effect” theory.

The K-means algorithm has the characteristics of high computational efficiency [32], but the K-means algorithm is highly sensitive to the selection of the initial cluster center and has a poor clustering effect on non-spherical data [33]. DBSCAN is also a common clustering method, the disadvantage of this algorithm is that its execution speed is low [34], and it will reduce the accuracy to a certain extent for high-dimensional data and data that may have different densities [35].

The main objective of this study is to explore the operational cost and efficiency of variable-route bus and regional flexible bus and traditional bus for station optimization between urban and rural areas. We selected the northern part of Yongcheng City, China for research. In the service area between urban and rural areas, most of the passenger demand comes from various rural areas, mainly middle and primary school students who study in cities and laborers who work in cities. Different from the characteristics of demand points in cities, their demands are locally concentrated and overall scattered. According to the characteristics of passenger demand points in urban and rural areas, we introduce an improved DK-means clustering algorithm. First, the DBSCAN algorithm is used to cluster the demand points to preprocess the demand points, and the noise points with far-distribution and less demand are eliminated. The K-means algorithm clusters the remaining demand points to obtain the optimal clustered bus stops. We determine fixed and alternative stations based on the clustering results and location relationship of backbone roads between urban and rural areas (fixed stations when the clustering results are close to the backbone roads and alternative stations, otherwise), which reduces the line offset times, improves the system’s ability to serve passengers, and reduces bus costs and operating times. We compare the operating cost and running time of a station-optimized variable-route transit system with regional flexible transit in the region and variable-route transit by K-means clustering alone. To ensure comparison accuracy, we assume the same amount of demand within the service area. The results show that the variable-route bus system through DK-means clustering has high cost-effectiveness and operational efficiency. The main contributions of this study lie in the following points:

(1)

Considering the distribution characteristics of passenger reservation demand in urban and rural areas, an optimization strategy for bus stops is designed.

(2)

Reducing the number of bus route excursions, improving the efficiency of bus operations and reducing environmental pollution.

(3)

Aiming at the lowest operating cost of public transport enterprises and the lowest cost of travel time for passengers, a variable-route bus scheduling model is established.

The remainder of this paper is organized as follows. Section 2 discusses the model construction by describing the problem and model assumptions. Section 3 presents the solution of the abovementioned model using a genetic simulated annealing algorithm. Section 4 presents a case study and analyzes the results using real urban and rural road scenarios, and Section 5 presents the summary of the study.

2. Model Construction

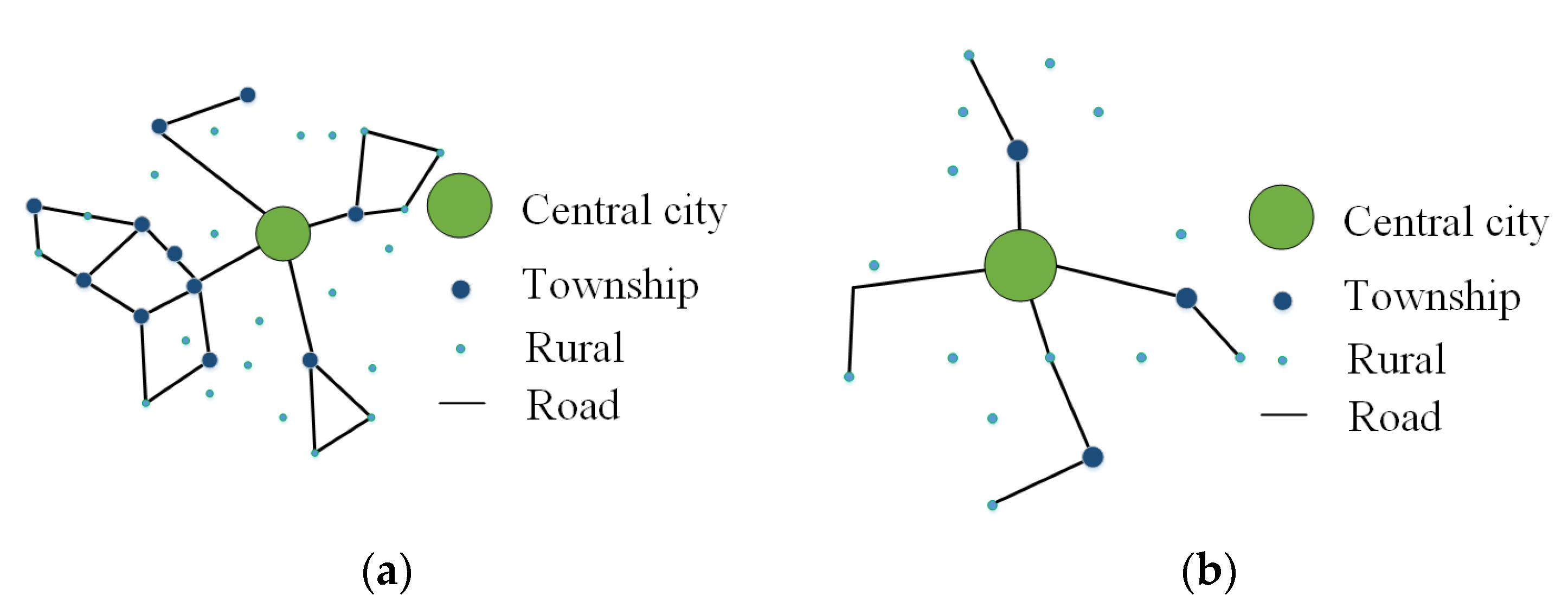
2.1. Problem Description

Different from urban public transportation, urban and rural public transportation demand density is low and scattered, and there is no intermodal transportation with other public transportation systems. Compared with urban areas, the types of passengers are relatively simple, usually students and migrant workers, and the travel time periods are relatively concentrated. Usually, there is only one fixed bus route, and they have to travel a long distance to a fixed bus stop to wait for a response, resulting in longer commute times and limited service areas for passengers. With the improvement of living standards of residents in urban and rural areas, residents in urban and rural areas need a flexible bus scheduling suitable for urban and rural areas to meet the travel requirements. Designing station-optimized variable-route demand response transit can help bring benefits to rural communities, who only need to travel shorter distances to set up temporary or fixed stops to wait for transit response, reducing commute time.

Layouts of transportation networks between urban and rural areas are mainly based on a ring and tree structure, as shown in Figure 1, usually the bus vehicle running along a fixed road, only able to pass through a small number of towns and villages, the vast majority of rural locations from the bus fixed away from the line farther. However, for most passenger demand from rural areas, passengers need to walk a long time to take the bus. At the same time, this increases the demand response transit operation cost and running time owing to longer urban and rural transportation lines and uneven distribution of demand points [36]. This also leads to a poor operational effect on bus enterprises and reduces passenger well-being. To address the abovementioned drawbacks, a variable-route demand response transit service model is proposed, as shown in Figure 2. After processing the reservation passenger information, fixed stations and alternative stations are established. The line connected by the fixed stations is called the base line, and the bus needs to respond to all fixed stations during operation, as shown in Figure 1a. For the base line outside the demand point a and b clustered into alternative sites 6 at 7:00 to respond, but the demand point c is rejected, as shown in Figure 1b. This is because the demand point 7, where the alternative station is located, has a low number of passengers, and shifting past it would produce significant waiting time and operating costs.

Figure 1. Bus route network layout model for rural areas. (a) Ring network structure diagram; (b) tree structure diagram.

Figure 2. Service model. (a) Base operating line; (b) the route with optimized stations visited.

Bus vehicles depart from the parking lot, respond to the reservation demand for some passengers in the service area, determine the DRT driving path, and the expected arrival time at each demand station according to the location of each reservation demand pick-up and drop-off station and the reservation demand ride time, and notify the reservation passenger of the ride time and the expected arrival time to prepare for the ride. The specific reservation travel service flow chart is shown in Figure 3.

Figure 3. Flow of travel reservation services.

2.2. Model Assumptions

This study makes the following basic assumptions for the line-variable route-based demand response transit scheduling model.

(1)

Passenger reservation information is submitted prior to the departure of the bus, and reservation requests are not changed or cancelled after submission.

(2)

Except for requests that have no responses, passengers who respond are expected to board the bus and arrive at the reserved terminal within the agreed time window in accordance with notified information.

(3)

The time required for responding passengers to get on and off the bus remains the same.

(4)

The average speed of a bus vehicle running smoothly on the road does not vary significantly and is not affected by traffic congestion, signals, or other internal and external conditions.

(5)

The bus vehicle models and the rated passenger capacity are known.

(6)

The vehicle departs from the site and returns to the site after completing the demand response.

(7)

To simplify the calculation, the distance travelled by the bus is assumed to be a straight line between two points.

2.3. Scheduling Model

2.3.1. Aiming for the Shortest Running Time

In this study, the running time is divided into two components of passenger boarding and alighting time cost, expressed by Equation (1).

$$t={\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{x}_{ij}\frac{L_{ij}}{\overline{V}}}}+{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{x}_{ij}(o_i+o_j+d_i+d_j)t_c}}$$

(1)

where ${ o}_i$ is the number of passengers boarding at station $i$; $d_i$ is the number of passengers alighting at station $i$; $t_c$ denotes the time required for a passenger to board and exit the bus;$n$ is the set of all stops in the service area; $t$ is the passenger travel time (min); $x_{ij}=1$ when a bus vehicle departs from stop $i$ and arrives at stop $j$, otherwise $x_{ij}=0$; $L_{ij}$ is the straight-line distance from stop $i$ to stop $j$ (km), and $\overline{V}$ is the average bus running speed (km/h).

2.3.2. Achieving Lowest Operating Costs for Urban and Rural Public Transport Enterprises

The costs incurred during the operation of a public transportation vehicle are related to many factors, such as the cost of operating the vehicle and the costs incurred by the denial of reservation demand, expressed in Equation (2).

$$P={\displaystyle \sum }_{i\in n}{\displaystyle \sum }_{j\in n}{c}_0{x}_{ij}{L}_{ij}+\epsilon {\displaystyle \sum }_{i\in n}{\displaystyle \sum }_{j\in n}\left(1-x_{ij}\right)\left(o_i+d_i\right)$$

(2)

where $c_0$ is the cost incurred by the bus for every 1 km traveled (yuan/km); $\epsilon$ denotes the penalty weight coefficient for rejecting a reservation demand; P is the operating cost of urban and rural bus enterprises (yuan).

2.3.3. Multiobjective Analysis

The urban and rural bus operation scheduling must select the corresponding coefficients based on the importance of the two optimization objectives. Because the two optimization objectives are not in the same unit, they need to be normalized. Therefore, when constructing the overall objective function, Equation (3) is used to normalize the two objectives.

$$F=\alpha P+\beta \omega t$$

(3)

where F is the utility function of the overall objective, $\alpha$ is the importance coefficient for the lowest operating cost, $\beta$ is the importance coefficient for the shortest passenger travel time, and $\omega$ is the normalization coefficient (yuan/min) that normalizes the passenger travel time unit to the same unit as the profit unit of urban and rural bus enterprises; the relationship between $\alpha$ and $\beta$ satisfies $\alpha +\beta =1$.

Substituting Equations (1) and (2) into Equation (3), the overall objective function of the urban and rural bus operation scheduling optimization model is expressed in Equation (4).

$$\begin{array}{l}\min F=\alpha \left({\displaystyle {\displaystyle \sum }_{i\in n}}{\displaystyle {\displaystyle \sum }_{j\in n}}{c}_0{x}_{ij}{L}_{ij}+\epsilon {\displaystyle {\displaystyle \sum }_{i\in n}}{\displaystyle {\displaystyle \sum }_{j\in n}}\left(1-x_{ij}\right)\left(o_i+d_i\right)\right)+\\ \beta \omega \left({\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{x}_{ij}\frac{L_{ij}}{\overline{V}}+{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{x}_{ij}(o_i+o_j+d_i+d_j)t_c}}}}\right)\end{array}$$

(4)

2.3.4. Constraints

1.

All vehicles must pass through a fixed station, as expressed in Equations (5) and (6).

$${\displaystyle \sum }_{j\in n}{x}_{ij}=1,\forall i\in G$$

(5)

$${\displaystyle \sum }_{i\in n}{x}_{ij}=1,\forall j\in G$$

(6)

where $G$ is a fixed station.

2.

In all stations in the area served by intercity and rural vehicles, the vehicle arrives and leaves the station at most once, as described in Equations (7) and (8).

$${\displaystyle \sum }_{j\in n}{x}_{ij}\le 1,\forall i\in n$$

(7)

$${\displaystyle \sum }_{j\in n}{x}_{ij}\le 1,\forall j\in n$$

(8)

3.

The actual operating routes of vehicles between urban and rural areas will not be duplicated, as described in Equation (9).

$${\mu }_i-{\mu }_j+M{x}_{ij}⩽M-1,\forall i,j\in V,i\ne j,i\ne 0,j\ne 0$$

(9)

where ${\mu }_i$ and ${\mu }_j$ denote the serial numbers for sites $i$ and $j$, respectively. $M$ denote the total number of all sites.

4.

If there is a succession of bus services between the two sites $i$ and $j$, the time the bus vehicle arrives at site j will not be earlier than the time it leaves at site i; the time spent by passengers getting on and off at bus site $i$ and the sum of the travel times between the two bus sites $i$ and $j$, as expressed in Equation (10).

$${\mu }_i-{\mu }_j+M{x}_{ij}⩽M-1,\forall i,j\in V,i\ne j,i\ne 0,j\ne 0$$

(10)

where t_i and t_j indicate the times at which the bus vehicle arrives at stations $i$ and $j$, respectively.

5.

The number of bus passengers always satisfies the condition that it is less than the rated capacity of the vehicle and greater than the number of passengers boarding at the station, as described in Equation (11).

$$o_i⩽u_i⩽Q,\forall i\in V$$

(11)

where $u_i$ is the total number of passengers on board after leaving station $i$ and $Q$ is the rated capacity of the bus.

6.

The variables are restricted to be assigned with values, as shown in Equation (12).

$$x_{ij}=\left\{0,1\right\},{\mu }_i⩾0,u_i⩾0,t_i⩾0$$

(12)

3. Model Solution

3.1. Clustering Algorithm for Urban and Rural Bus Stops

To filter and cluster all reservation requirements, this study proposed a DK-means clustering algorithm, which combines the DBSCAN clustering and K-means algorithms. This is because the conventional K-means algorithm has difficulty in handling non-spherical clusters, and the clustering results are influenced by extreme values [37]. In this study, the clustering reliability can be substantially improved by using the DBSCAN algorithm to pre-process the passenger reservation demand and divide them into clusterable and noisy points and by using the K-means algorithm to operate on the set of clusterable points to obtain fixed and alternative stations in each location. The steps of the DK-means algorithm are presented below, and the algorithm flow is shown in Figure 4.

Figure 4. DBSCAN K-means (DK-means) algorithm steps.

(1)

Input the dataset A containing travel and reservation histories of the passengers in the region, parameter field radius δ, minimum data point threshold Minpts, and number of parameter clusters k.

(2)

Calculate the distance between each point in the data and the other points.

(3)

Determine whether the number of points in the δ domain of any demand point is greater than the threshold Minpts, mark the point as a core point, and classify the points in its neighborhood as a class; otherwise, mark the point as a noisy point.

(4)

Determine whether all points are classified. Repeat steps (2) and (3) until all points are classified as class or noisy points.

(5)

After eliminating the noisy points in the dataset, select the k points, including the core points, as the initial centroids.

(6)

Calculate the distance between the centroid and other points and assign each point in the new dataset to the class with the closest distance.

(7)

Calculate new centroids in the k classes of data points.

(8)

Determine whether the centroids change. Repeat steps (6) and (7) until the squared distances and convergence between each point, and the centroids and all the data points are classified into a certain class and no longer change.

(9)

Determine the coordinates of the centers of the clusters.

3.2. Genetic Simulated Annealing Algorithm

The above problem is an extension of a vehicle routing problem, and with the increasing number of reservation demand points and buses, it is extremely difficult to solve this type of problem using an exact algorithm [38]. Using a heuristic algorithm to solve this [39], a high-quality approximate optimal solution within a reasonable computation time can be obtained. Because the simulated annealing algorithm has almost no global spatial search capability, its local spatial search capability is strong [40]. In contrast, the genetic algorithm has a strong global search capability but poor local search capability. Thus, a hybrid intelligent algorithm, genetic simulated annealing algorithm, was used to solve the problem.

The specific steps for the design and implementation of the modified genetic simulated annealing algorithm are as follows:

(1)

Coding. The departure frequency and service order were encoded in binary form based on the characteristics of the genetic simulated annealing algorithm.

(2)

Initial solution. The simulated annealing algorithm randomly generated the initial schedules and paths at the initial temperature at the initial temperature.

(3)

Construction of the adaptation function. The smaller the cost incurred by a vehicle as it travels along a path, the easier it is for the cost incurred by that path to be retained across genetic operations, expressed as $f\left(x\right)$, which is generally constructed using the objective function $Z(x$) of the model. The fitness function is represented by Equation (13).

$$f\left(x\right)=\{\begin{array}{l}Z\left(x\right)-G_{\min },\\ 0,\end{array}\begin{array}{l}Z\left(x\right)\ge G_{\min }\\ Z\left(x\right)\le G_{\min }\end{array}$$

(13)

where $G_{\min }$ denotes the individual with the smallest objective function value in the same generation population, $Z(x$) denotes the objective function value of the individual, and $f\left(x\right)$ denotes the fitness function.

(4)

Genetic operator. It includes the selection, crossover, and variation operators. The selection operator uses a combination of the roulette wheel and elite retention strategy, the single-point crossover is used as the crossover operator of the genetic simulated annealing algorithm, and the variation operator is used to maintain the population diversity, which is typically between 0.0001–0.1.

(5)

Simulated annealing operation. To compensate for the poor local search ability of the genetic algorithm, a simulated annealing operation was performed on new individuals derived using the genetic algorithm. The general simulated annealing algorithm operation was divided into two steps: first, the current population was set as $N_c$ and the current temperature as $T_c$, and the individual fitness ${f(x}_c)$ in the current population was calculated; second, the size of the individual fitness was determined. If ${f(x}_c{)>f(x}_{c-1})$, then a new individual was generated to replace the old one; if ${f(x}_c{)<f(x}_{c-1})$, then the generated new individual replaced the old one with the probability of p $=\exp \left\{\left[\frac{Z\left(x_c\right)-Z\left(x_{c-1}\right)}{T_c}\right]\right\}$.

(6)

Cooling operation. The cooling function is expressed in Equation (14).

$$T=T_0{\gamma }^{K^{’}}$$

(14)

where $T_0$ is the initial velocity, $\gamma$ is the cooling coefficient with a value of $\gamma$ ∊ [0,1], $K^{’}$ is the number of iterations of the algorithm, and $T$ is the temperature after cooling.

(7)

Algorithm termination conditions. The algorithm is terminated if the new solution generated at the set end temperature and the number of iterations of the algorithm are not accepted. Here, we used a pre-set number of iterations $K^{’}$ and executed the simulated annealing operation continuously until the pre-set number of iterations was reached, then the loop was stopped, and the algorithm was terminated.

4. Case Study

To verify the effectiveness of this scheduling model, a case study was conducted in the northern part of Yongcheng City in Henan Province, China. The backbone road bus route map is shown in Figure 5. A field study, as shown in Figure 6, was conducted to obtain information on ridership at demand points within the urban and rural bus operating areas. It mainly includes the pick-up and drop-off locations for passengers, as well as the appointment time for pick-up. Five noisy points were screened out using the DBSCAN algorithm, as shown in Figure 7a. Based on the clustering results of the DBSCAN algorithm, the 12 demand focused regions after eliminating noise points are clustered one by one K-means, so k = 12, and the cluster center obtained at this time is the variable-route DRT station, as shown in Figure 7b, combined with the backbone road bus lines, to get the benchmark running line length of 48.4 km, as shown in Figure 8. When there is a need for an alternate station, the vehicle will deviate from the backbone road to respond.

Figure 5. Backbone road bus route map.

Figure 6. Demand point information collection. (a) We conducted a survey of urban commuters to rural and suburban areas, and collected their desired pick-up and drop-off points and desired pick-up times; (b) a survey was conducted among rural commuters to the city to collect their desired boarding and alighting locations and desired boarding times.

Figure 7. DK−means algorithm clustering results. (a) Clustering diagram of passenger demand points; (b) site optimization diagram.

Figure 8. Baseline operation line diagram.

Combining the length of the baseline route and travel reservation demand of passengers from 06:30 to 09:40 a.m., we initially obtained the downward schedule of buses from Yongcheng City to Mangshan Town, as shown in Table 1, and the upward schedule of buses from Mangshan Town to Yongcheng City, as shown in Table 2. We expressed the travel demand of passengers by station serial number, as shown in Table 3.

Table 1. Yongcheng City to Mangshan Town vehicle downstream schedule.

Yongcheng City–Mangshan Town	Downstream Stations
	Site 1	Site 2	Site 3	Site 4	Site 5
First shift	06:30	07:00	07:30	07:50	08:05
Second shift	07:00	07:30	08:00	08:20	08:35
Third shift	07:30	08:00	08:30	08:50	09:05
Fourth shift	08:00	08:30	09:00	09:20	09:35

Table 2. Mangshan Town to Yongcheng City vehicle upward schedule.

Mangshan Town–Yongcheng City	Upstream Sites
	Site 5	Site 4	Site 3	Site 2	Site 1
First shift	06:30	06:45	07:05	07:35	08:05
Second shift	07:00	07:15	07:35	08:05	08:35
Third shift	07:30	07:45	08:05	08:35	09:05
Fourth shift	08:00	08:15	08:35	09:05	09:35

Table 3. Passenger travel demand statistics.

Vehicle Shift	Passenger Travel Station Requirements	Total
First shift	(1,2) 1 (1,3) 1 (1,4) 1 (1,5) 2 (2,1) 2 (2,8) 1 (2,7) 2 (3,6) 3 (3,4) 2 (3,10) 2 (3,11) 3 (3,12) 3 (6,4) 3	26
Second shift	(6,2) 2 (6,5) 3 (6,12) 3 (4,3) 1 (2,3) 1 (2,9) 2 (2,6) 2 (2,1) 1 (7,12) 2 (5,1) 2 (12,1) 2 (7,1) 2 (12,5) 2 (4,5) 2 (8,5) 3 (6,5) 2	32
Third shift	(1,6) 2 (5,1) 1 (5,3) 1 (4,3) 1 (10,4) 1 (10,5) 1 (7,5) 2 (12,9) 3 (8,2) 2 (7,12) 2 (7,8) 4 (3,6) 3 (9,1) 2 (9,3) 2	27
Fourth shift	(2,1) 1 (7,1) 2 (3,4) 1 (8,12) 2 (1,12) 3 (11,7) 2 (9,5) 2 (9,2) 2	15

In Table 1, according to the reservation information of passengers between urban and rural areas (Yongcheng and Mangshan Town), we determine 5 fixed stops during the operation of the bus from Yongcheng to Mangshan Town (passengers clustering results are close to the backbone roads) and four shift schedules. The timetable of the fixed station should be strictly met during the operation of the vehicle.

Similarly, in order to make the scheduling in line with the actual situation of bidirectional bus operation, in Table 2, we also study the scheduling situation from townships to cities based on the reservation information between urban and rural areas.

Table 3 shows the results of our statistics on the passenger travel demand of 100 passengers. We clustered the travel demand of passengers with similar travel time and distance into 1–12 stations, and the numbers inside the brackets represent the pick-up point and the drop-off point of passengers, respectively, and the numbers outside the brackets represent the number of people from that pick-up point to that drop-off point.

Using the demands of 100 passengers, as shown above as an example for analysis, the passenger reservation demand data for each time period were brought into the variable route type DRT dispatching model, assuming that the vehicle travelled at $\overline{V}$ = 20 km/h, the rated passenger capacity was $Q=20$, the variable cost was $c_0=1$ RMB/km, and the required boarding and alighting time for each passenger was t_c = 10 s. For Yongcheng City, we assumed that the normalization coefficient $\omega =0.25$ yuan/min, and the penalty weight coefficient used for the number of rejected reservation demands was $\epsilon =1$. Relevant algorithm parameters were set to solve the model; the values of the parameters are listed in Table 4.

Table 4. Algorithm parameter settings.

Algorithm	Parameters	Values Used
Genetic algorithm	Population size	200
	Turnover probability	0.95
	Mutation probability	0.0005
Simulated annealing algorithm	Number of iterations	200
	Initial temperature	5500
	Cooling factor	0.9

The model was solved in a MATLAB environment using a genetic simulated annealing algorithm, and the results of the operation showed that the objective was optimal when $\alpha =0.5$ and $\beta =0.5$. An iterative optimization run diagram is shown in Figure 9.

Figure 9. Iterative optimization run diagram.

The bus vehicle operating routes and actual dispatching moments are listed in Table 5 and Table 6, respectively, where the bus operation route map is shown in Figure 10, where stations 1–5 indicate fixed stations and 6–12 indicate variable stations. The effects of regional flexible DRT, variable-route DRT with passenger pre-processing using K-means, and variable-route DRT service mode with passenger pre-processing and station optimization using DK-means are shown in Table 7, in which the operating cost is represented by Cost and the operating time is represented by Time. The effects of the DK-means variable-route DRT relative to the regional flexible DRT and K-means variable-route DRT on (a) operating cost and (b) running time for each frequency are shown in Figure 11.

Table 5. Yongcheng City to Mangshan Town downstream schedule.

Downward Shift	First Shift	Second Shift	Third Shift	Fourth Shift
Site 1	06:30	07:00	07:30	08:00
Site 2	06:55	07:32	08:03	08:25
Site 3	07:20	07:58	08:30	08:58
Site 4	07:53	08:26	08:48	09:18
Site 5	08:02	08:33	09:04	09:28
Site 6	—	07:06	07:36	—
Site 7	—	07:14	07:44	—
Site 8	—	07:24	07:54	08:18
Site 9	—	08:04	—	08:45
Site 10	07:45	—	08:40	—
Site 11	07:34	—	—	—
Site 12	—	08:20	08:54	09:12
Running line	1-2-3-11-10-4-5	1-6-7-8-2-3-9-12-4-5	1-6-7-8-2-3-10-4-12-5	1-8-2-9-3-12-4-5

Table 6. Mangshan Town to Yongcheng City upstream schedule.

Upward Shift	First Shift	Second Shift	Third Shift	Fourth Shift
Site 12	—	07:16	07:46	—
Site 11	—	—	—	08:18
Site 10	—	—	—	—
Site 9	—	—	07:56	08:39
Site 8	07:32	—	—	—
Site 7	07:45	08:14	—	09:13
Site 6	07:53	08:22	08:53	—
Site 5	06:30	07:00	07:30	08:00
Site 4	06:40	07:10	07:40	08:10
Site 3	06:58	07:31	08:00	08:28
Site 2	07:25	08:00	08:30	08:58
Site 1	07:59	08:32	09:00	09:32
Running line	5-4-3-2-8-7-6-1	5-4-12-3-2-7-6-1	5-4-12-9-3-2-6-1	5-4-11-3-9-2-7-1

Figure 10. Bus operation route map. (a) Yongcheng City to Mangshan Town downstream route map; (b) Mangshan Town to Yongcheng City upstream route map.

Table 7. Effectiveness of three types of bus service models.

Passenger Service Schedule	Regional Flexible DRT		Variable Route DRT (K-Means)		Variable Route DRT (DK-Means)
	Cost/yuan	Time/min	Cost/yuan	Time/min	Cost/yuan	Time/min
First shift	178.5	216.9	168.3	202. 5	158.6	190.9
Second shift	182.2	220.4	178.5	218.8	173.2	209.8
Third shift	176.8	212.2	171.9	208.9	163.4	195.1
Fourth shift	155.3	174.5	138.1	160.2	132.1	154.2
Total	692.8	824	656.8	790.4	627.3	750

Figure 11. Effects of reduction. (a) Operating costs; (b) running time. (Note: Cost1 and Cost2 indicate the operating cost savings of DK-means variable-route DRT compared to regional flexible DRT and K-means variable-route DRT, respectively; Time1 and Time2 indicate the ride time savings of DK-means variable-route DRT compared to regional flexible DRT and K-means variable-route DRT, respectively).

Table 5 and Table 6 are the time for the four shifts to pass through fixed stations (1, 2, 3, 4, 5) and alternative stations (6, 7, 8, 9, 10, 11, 12), where “—” means that the vehicle does not pass the station.

Table 7 compares the service mode effects of the four shifts of the three types of buses. Among them, the regional flexible DRT is a type of bus that can respond to all reservation demands in the service area. Due to the excessive number of shifts, it often leads to operating costs and time higher. After K-means and DK-means clustering of variable-route DRT through the passenger reservation information processing, the number of bus excursions is reduced, operating costs and time are relatively low, it is intelligent in a certain degree of optimization of fixed stops and alternative stops, but for DK-means clustering of variable-route bus, through two clustering process processing, bus stops achieve optimality.

The example compared the performance of three bus scheduling systems in terms of the operating cost and operating time. Compared with the regional flexible DRT, the total operating cost and time for four bus schedules were reduced by 9.5% and 9.0%, respectively. Compared with the variable-route DRT after pre-processing passengers using K-means, the total operating cost and ride time were reduced by 4.5% and 5.1%, respectively. In summary, the variable-route DRT through station optimization can also serve the majority of travel demand between urban and rural areas under the condition of reducing the number of bus route deviations, and has strong applicability to urban and rural areas with low travel demand density.

5. Conclusions

To solve the limitations of fixed-route bus service passengers between urban and rural areas and to reduce the high cost of picking up and dropping off passengers caused by route deviation of demand response transit, this paper proposes a variable-route demand response transit scheduling optimization model suitable for operation in urban and rural areas based on the demand characteristics of passengers and road network conditions in urban and rural areas. DK-means clustering is performed on passenger demands with similar travel times and locations in urban and rural areas. Compared with buses without passenger clustering and only through K-means clustering, the method proposed in this paper eliminates special demands that are farther distributed and fewer in number through the DBSCAN clustering algorithm, which enables subsequent K-means clustering to obtain the optimal stopping points for buses during operation. This optimizes bus scheduling. It reduces the number of offsets compared with regional flexible bus, improves bus operation efficiency, and reduces environmental pollution and costs for bus companies and passengers.

In future research, due to the increasing passenger demand for travel quality, the focus on passenger evaluation of ridership services should be considered in bus route optimization. In addition, this paper does not consider such passengers for real-time reservations, and it is important to include such passengers in the model for scheduling and route planning. With the rapid development of computer and Internet technology, information on real-time reservation demand is readily available, and the bus can serve more passengers by establishing a two-stage station optimization scheduling model.