Optimization of Snowplow Routes for Real-World Conditions
Abstract
1. Introduction
2. Data Preparation and Processing
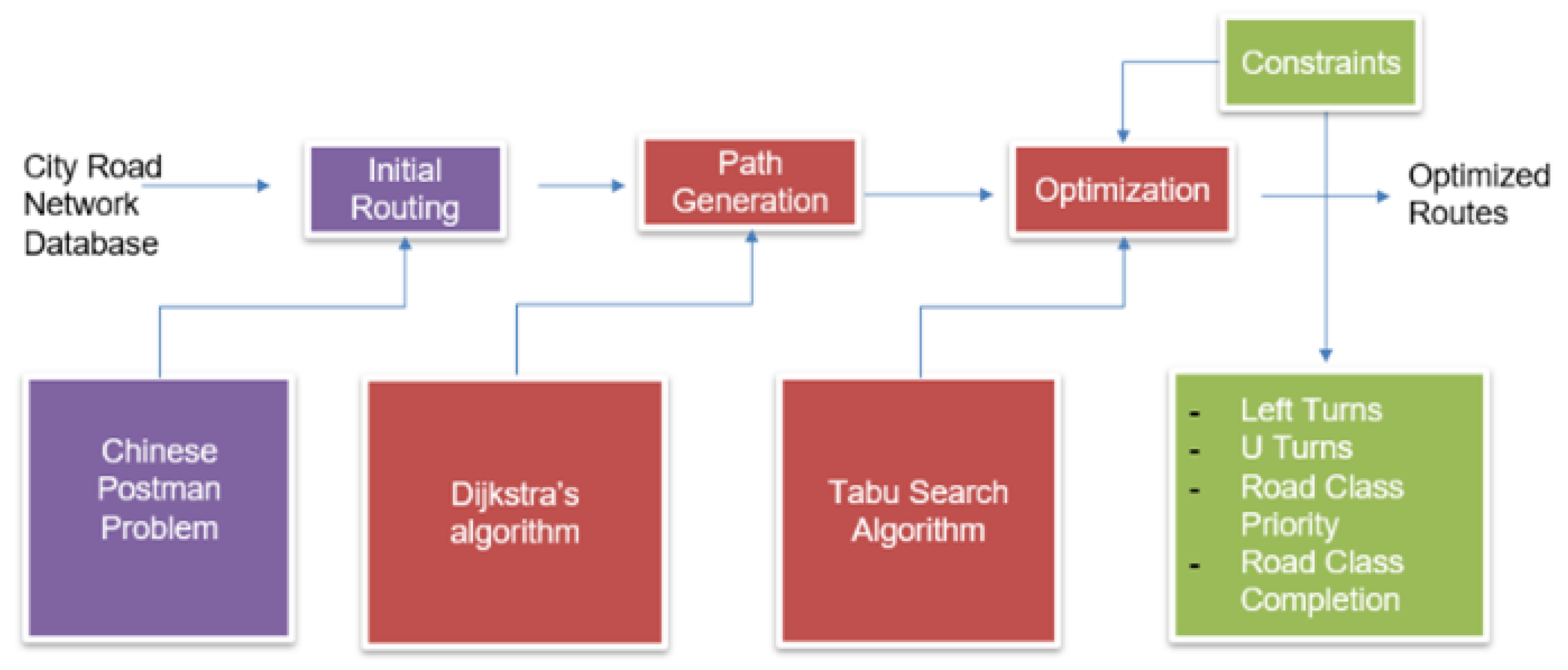
3. Methodology
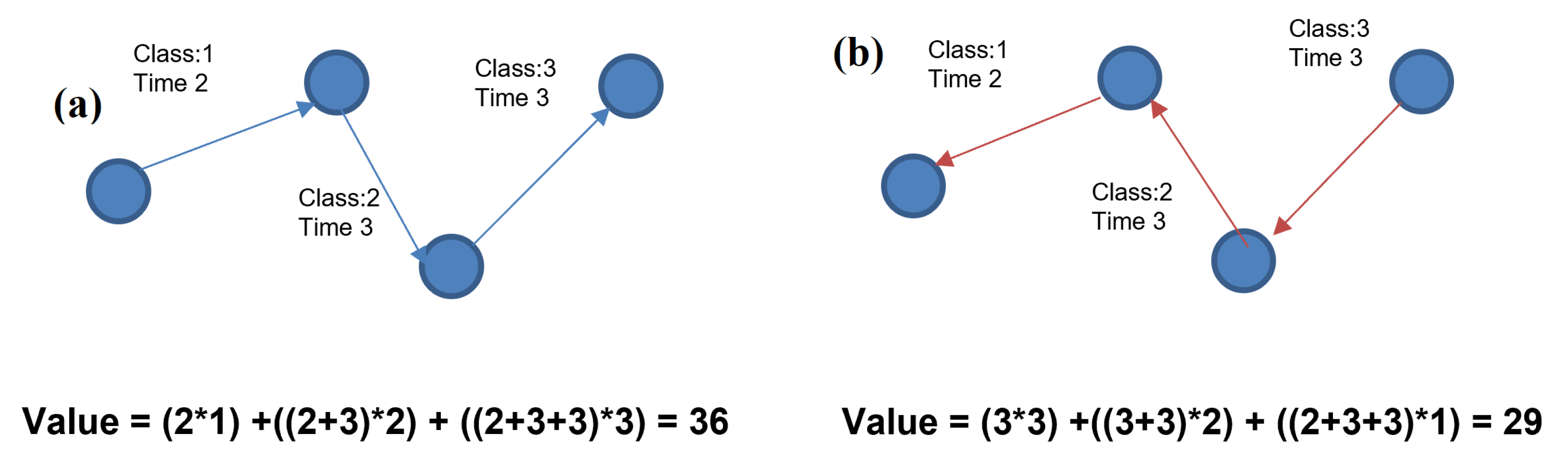
3.1. Problem Description and Objective Function
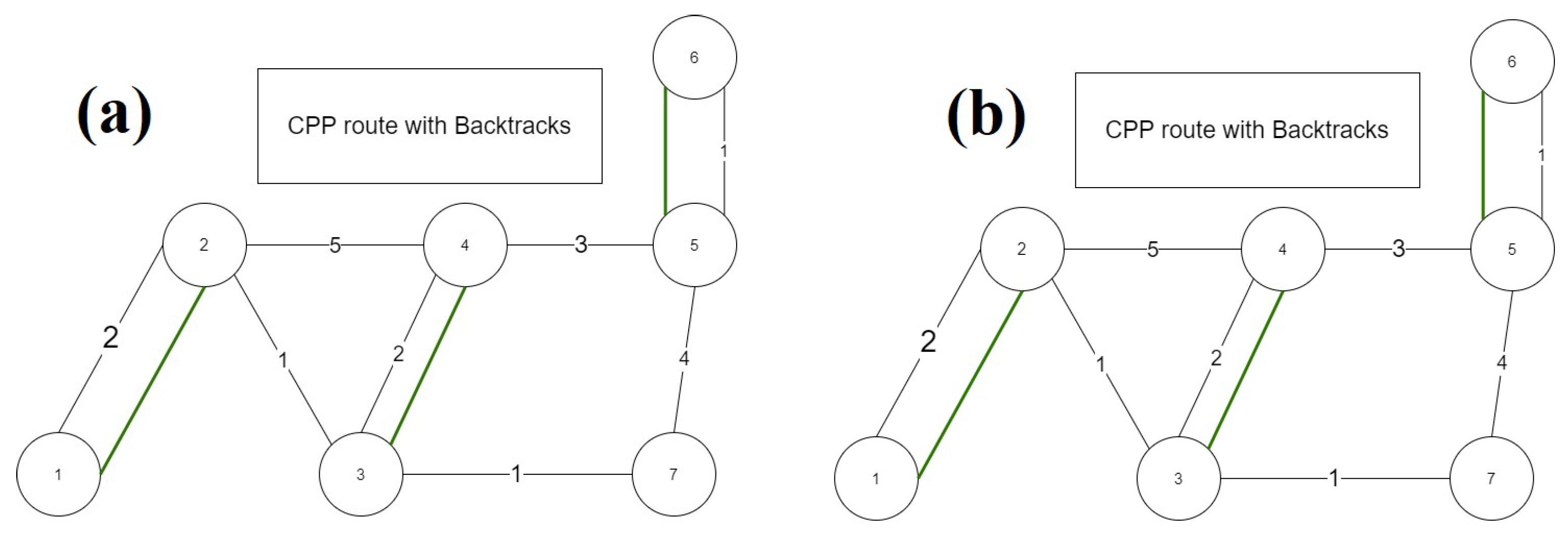
3.2. Chinese Postman Problem
| Algorithm 1 Chinese Postman Problem—Steps |
Input: Output: |
3.3. Dijkstra’s Algorithm
| Algorithm 2 Dijkstra’s Algorithm |
Input: Output:
|
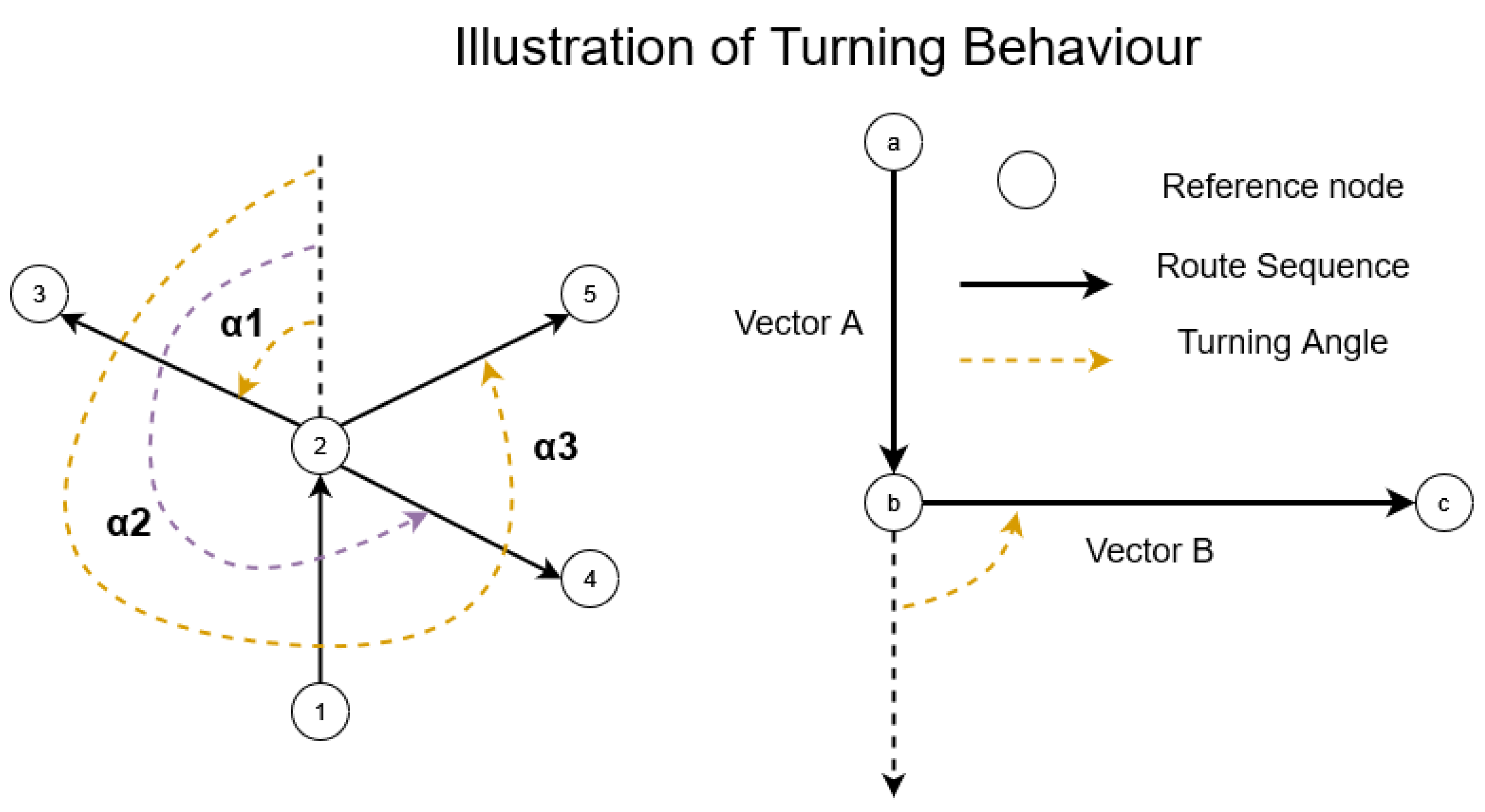
3.4. Tabu Search Algorithm
| Algorithm 3 Tabu Search algorithm |
Input: Output:
|
4. Results and Discussion
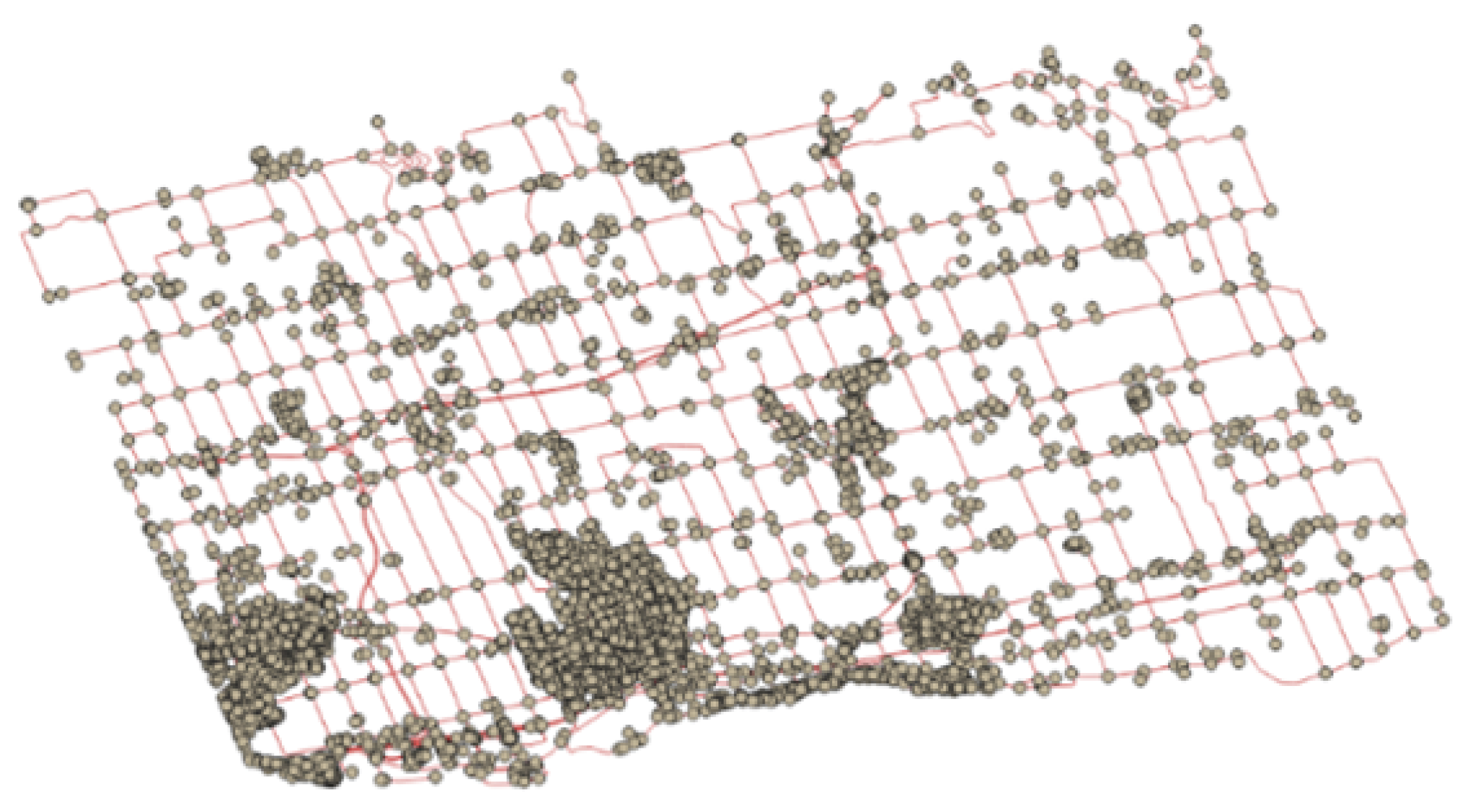
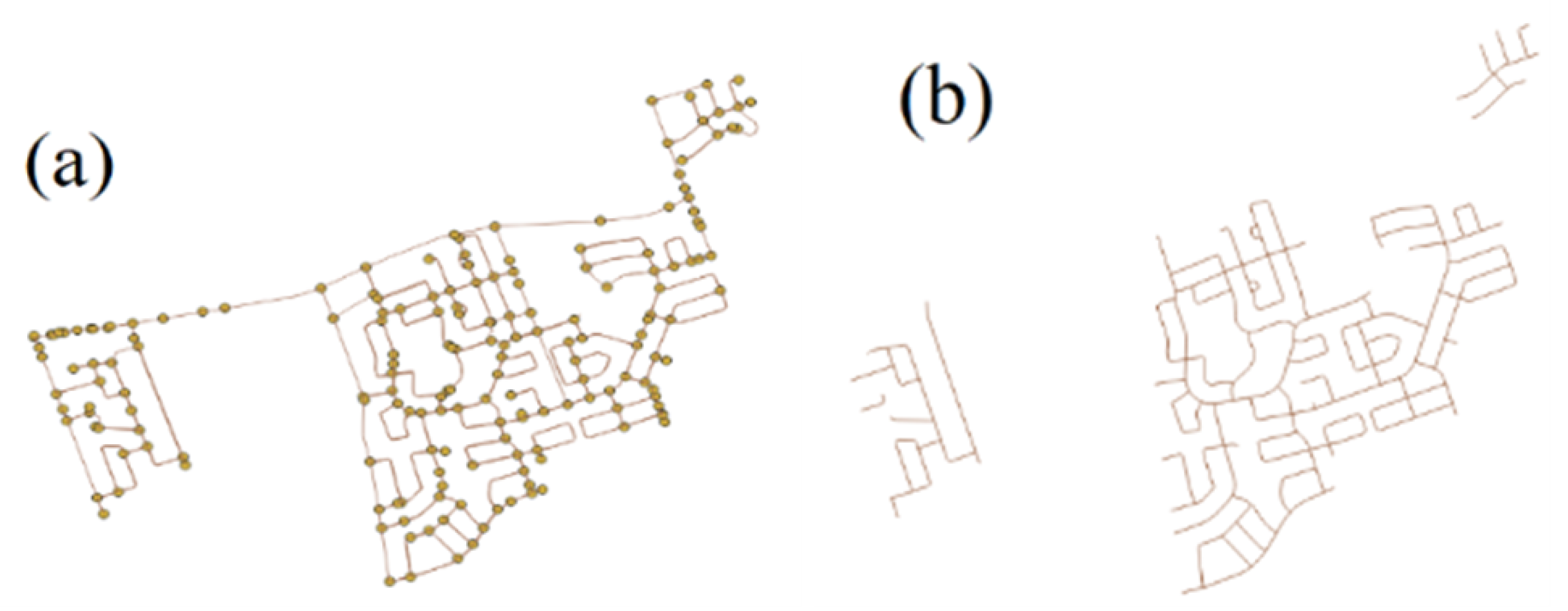
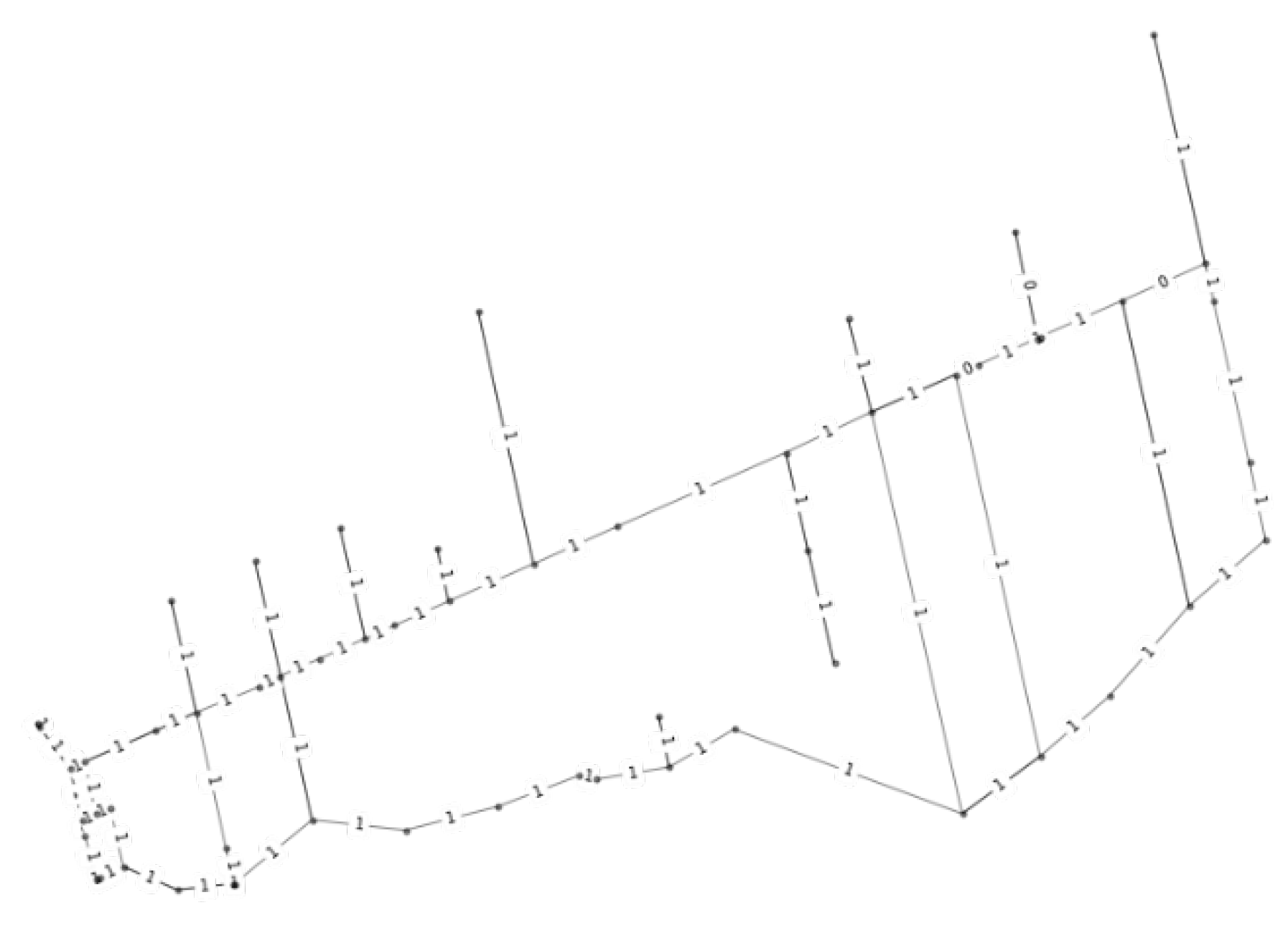
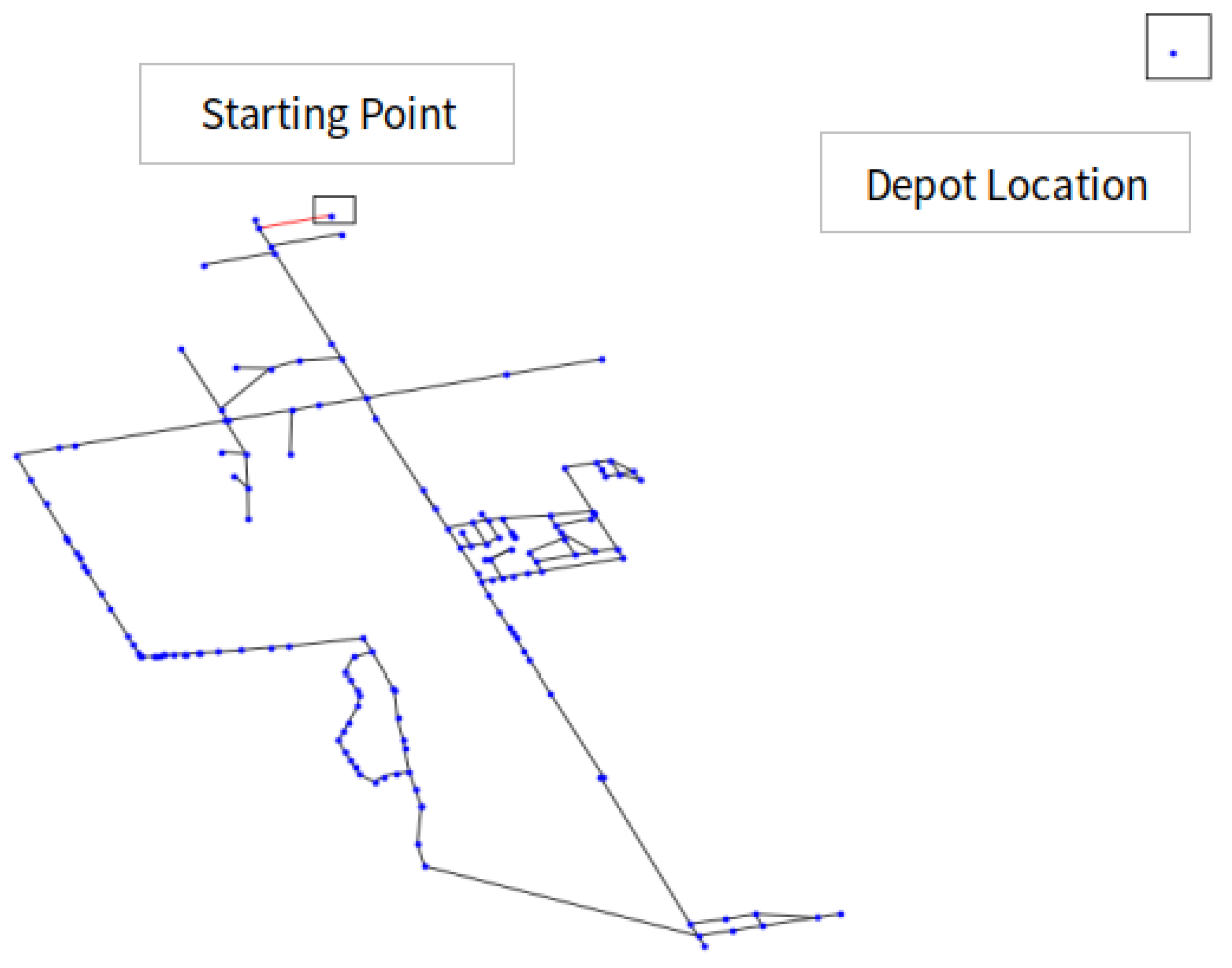
4.1. Network Topology Generation
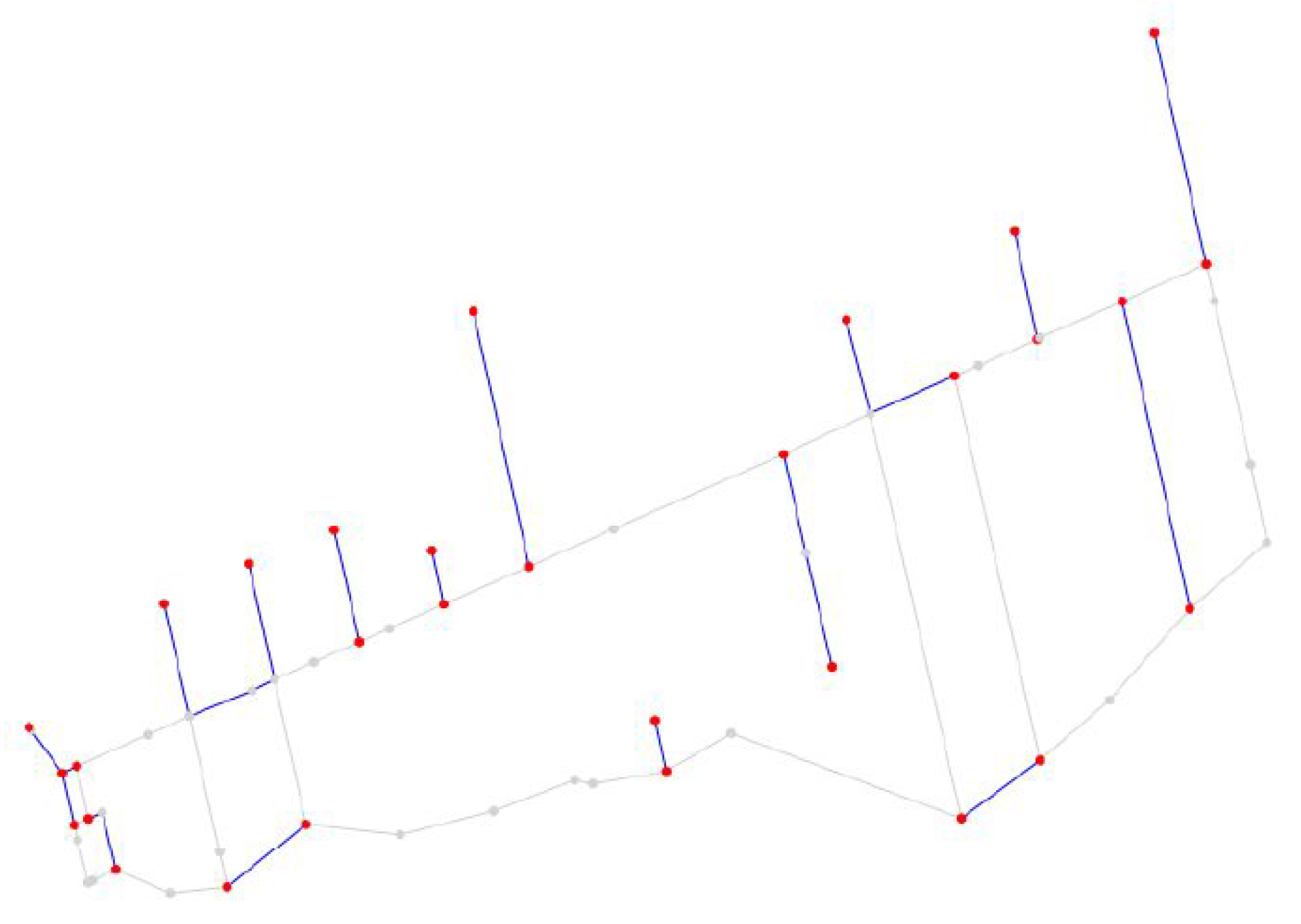
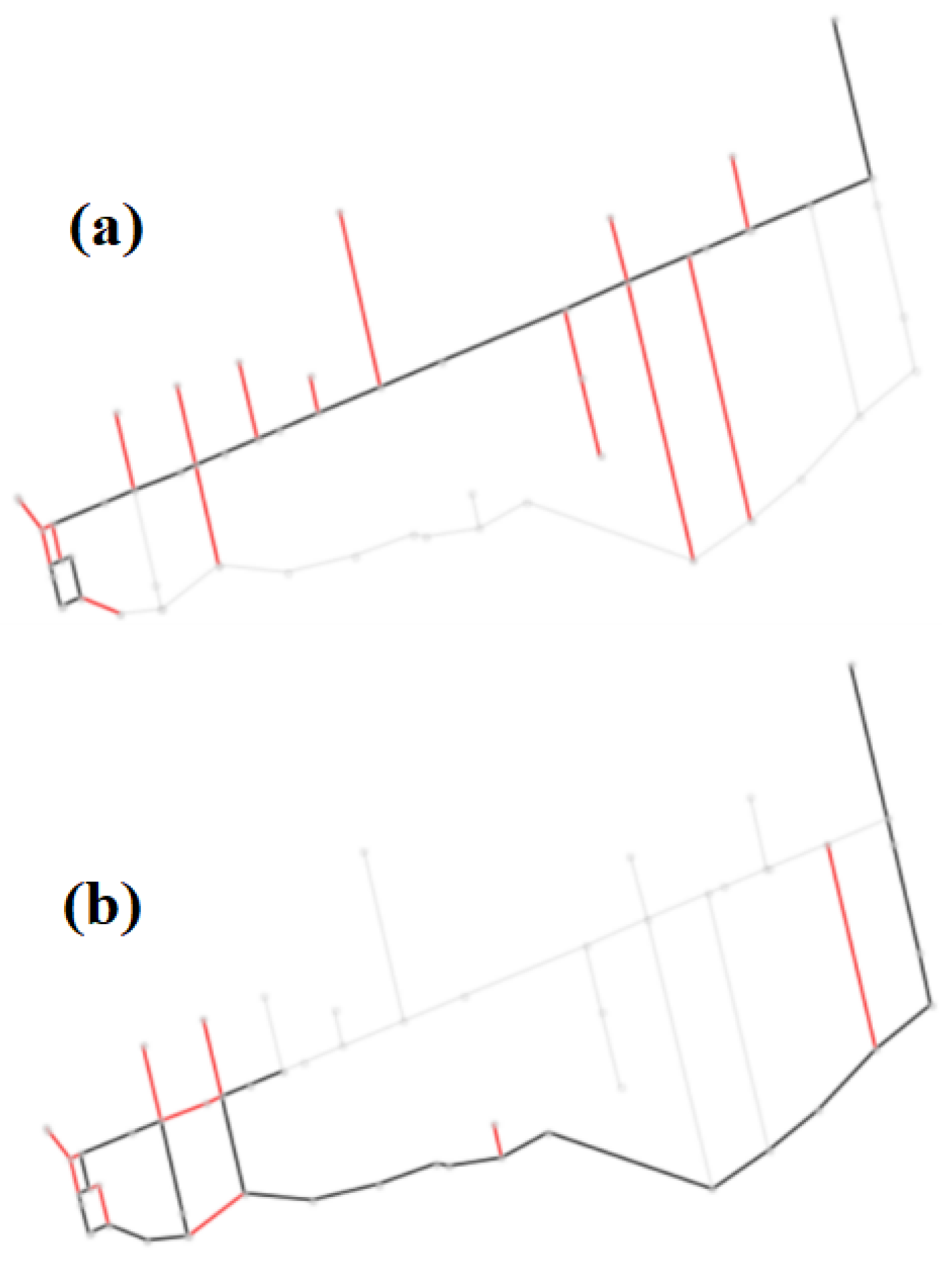
4.2. Results Obtained Using CPP and Dijkstra’s Algorithm
4.3. Results of Optimization Algorithm
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Manual, H.C. Highway Capacity Manual. Washington, DC, USA. 2000. Available online: https://onlinepubs.trb.org/Onlinepubs/trnews/rpo/rpo.trn129.pdf (accessed on 28 July 2022).
- Jean, A.; Brian, M.; Jessica, A. Weather Information and Road Safety; Institute for Catastrophic Loss Reduction: Toronto, ON, Canada, 2001. [Google Scholar]
- Rao, T.; Mitra, S.; Zollweg, J.; Sahin, F. Computing optimal snowplow route plans using genetic algorithms. In Proceedings of the IEEE Systems, Man, and Cybernetics (SMC), Anchorage, AK, USA, 9–12 October 2011; pp. 2785–2790. [Google Scholar]
- Applegate, D.; Bixby, R.; Chvatal, V.; Cook, W. The Traveling Salesman Problem; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
- Rao, T.; Mitra, S.; Zollweg, J. Snow-plow route planning using AI search. In Proceedings of the IEEE Systems, Man, and Cybernetics (SMC), Anchorage, AK, USA, 9–12 October 2011; pp. 2791–2796. [Google Scholar]
- Malandraki, C.; Daskin, M. The maximum benefit Chinese postman problem and the maximum benefit traveling salesman problem. Eur. J. Oper. Res. 1993, 65, 218–234. [Google Scholar] [CrossRef]
- Perrier, N.; Langevin, A.; Amaya, C. Vehicle routing for urban snow plowing operations. Transp. Sci. 2008, 42, 44–56. [Google Scholar] [CrossRef]
- Kinable, J.; van Hoeve, W.; Smith, S. Optimization models for a real-world snowplow routing problem. In Proceedings of the International Conference on AI and OR Techniques in Constraint Programming for Combinatorial Optimization Problems, Banff, AB, Canada, 29 May–1 June 2016; pp. 229–245. [Google Scholar]
- Sullivan, J.; Dowds, J.; Novak, D.; Scott, D.; Ragsdale, C. Development and application of an iterative heuristic for roadway snow and ice control. Transp. Res. Part A Policy Pract. 2019, 127, 18–31. [Google Scholar] [CrossRef]
- Çodur, M.; Yılmaz, M. A time-dependent hierarchical Chinese postman problem. Cent. Eur. J. Oper. Res. 2020, 28, 337–366. [Google Scholar] [CrossRef]
- Korteweg, P.; Volgenant, T. On the hierarchical Chinese postman problem with linear ordered classes. Eur. J. Oper. Res. 2006, 169, 41–52. [Google Scholar] [CrossRef]
- Ahabchane, C.; Langevin, A.; Trépanier, M. Robust optimization for the hierarchical mixed capacitated general routing problem applied to winter road maintenance. Comput. Ind. Eng. 2021, 158, 107396. [Google Scholar] [CrossRef]
- Bopardikar, S.D.; Englot, B.; Speranzon, A. Multiobjective path planning: Localization constraints and collision probability. IEEE Trans. Robot. 2015, 31, 562–577. [Google Scholar] [CrossRef]
- Ontario. Minimum Maintenance Standards for Municipal High-Ways. Available online: https://www.ontario.ca/laws/regulation/020239 (accessed on 23 January 2022).
- Minieka, E. The Chinese postman problem for mixed networks. Manag. Sci. 1979, 25, 643–648. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A note on two problems in connection with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Ahr, D.; Reinelt, G. A Tabu search algorithm for the Min–Max k-Chinese postman problem. Comput. Oper. Res. 2006, 33, 3403–3422. [Google Scholar] [CrossRef]
- OpenStreetMap. OpenStreetMap Data. Available online: https://www.openstreetmap.org (accessed on 23 January 2022).
- Qgis.org. QGIS. Available online: https://www.qgis.org/en/site (accessed on 23 January 2022).
- Sniedovich, M. Dijkstra’s algorithm revisited: The dynamic programming connexion. Control Cybern. 2006, 35, 599–620. [Google Scholar]
- Xu, S.; Kwon, T. Optimizing snowplow routes using all new perspectives: Road users and winter road maintenance operators. Can. J. Civ. Eng. 2020, 48, 1–10. [Google Scholar] [CrossRef]
- Ghiani, G.; Guerriero, F.; Laporte, G.; Musmanno, G. Tabu Search Heuristics for the Arc Routing Problem with Intermediate Facilities under Capacity and Length Restrictions. J. Math. Model. Algorithms 2004, 3, 209–223. [Google Scholar] [CrossRef]
- Glover, F. Tabu Search: A Tutorial. Interfaces 1990, 20, 74–94. [Google Scholar] [CrossRef]
- NetworkX. NetworkX Documentation. Available online: https://networkx.org (accessed on 23 January 2022).
- Rasul, A.; Seo, J.; Xu, S.; Kwon, T.; MacLean, J.; Brown, C. Snowplow route optimization using Chinese postman problem and Tabu search algorithm. In Proceedings of the ISARC 2021, Dubai, United Arab Emirates, 2–4 November 2021; pp. 403–409. [Google Scholar]
- Cormen, T.; Leiserson, C.; Rivest, R.; Stein, C. Introduction to Algorithms; The MIT Press: Cambridge, MA, USA, 2001; pp. 658–664. [Google Scholar]


| Variable | Assumed Value |
|---|---|
| Truck speed | 35 km/h |
| Service area | Clarington |
| Number of trucks | 1 |
| MMS: applicable time for road class 1 | 1 h for simulation (original time: 4 h) |
| MMS: Applicable time for road class 2 | 2 h for simulation (original time: 6 h) |
| MMS: Applicable time for road class 3 | 3 h for simulation (original time: 12 h) |
| MMS: Applicable time for road class 4 | 4 h for simulation (original time: 16 h) |
| MMS: Applicable time for road class 5 | 5 h for simulation (original time: 24 h) |
| Number of lanes | Both single and multi-lanes covered |
| Routes | Route 1: CPP | Route 2: CPP + Optimization |
|---|---|---|
| Fitness | −20 | 60 |
| Total travel Time | 1 h 17 min | 1 h 15 min |
| Total travel distance (km) | 63.4 | 62.9 |
| Left Turns | 21 | 22 |
| U-turns | 12 | 9 |
| Sharp Right Turns | 0 | 0 |
| Number of roads (edges) failing to the MMS | 4 | 3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rasul, A.; Seo, J.; Xu, S.; Kwon, T.J.; MacLean, J.; Brown, C. Optimization of Snowplow Routes for Real-World Conditions. Sustainability 2022, 14, 13130. https://doi.org/10.3390/su142013130
Rasul A, Seo J, Xu S, Kwon TJ, MacLean J, Brown C. Optimization of Snowplow Routes for Real-World Conditions. Sustainability. 2022; 14(20):13130. https://doi.org/10.3390/su142013130
Chicago/Turabian StyleRasul, Abdullah, Jaho Seo, Shuoyan Xu, Tae J. Kwon, Justin MacLean, and Cody Brown. 2022. "Optimization of Snowplow Routes for Real-World Conditions" Sustainability 14, no. 20: 13130. https://doi.org/10.3390/su142013130
APA StyleRasul, A., Seo, J., Xu, S., Kwon, T. J., MacLean, J., & Brown, C. (2022). Optimization of Snowplow Routes for Real-World Conditions. Sustainability, 14(20), 13130. https://doi.org/10.3390/su142013130








