Abstract
The consumption of construction materials and the pollution caused by their production can be reduced by the use of reliable adaptive load-bearing structures. Adaptive load-bearing structures are able to adapt to different load cases by specifically manipulating internal stresses using actuators installed in the structure. One main aspect of quality is reliability. A verification of reliability, and thus the safety of conventional structures, was a design issue. When it comes to adaptive load-bearing structures, the material savings reduce the stiffness of the structure, whereby integrated actuators with sensors and a control take over the stiffening. This article explains why the conventional design process is not sufficient for adaptive load-bearing structures and proposes a method for demonstrating improved reliability and environmental sustainability. For this purpose, an exemplary adaptive load-bearing structure is introduced. A linear elastic model, simulating tension in the elements of the adaptive load-bearing structure, supports the analysis. By means of a representative local load-spectrum, the operating life is estimated based on Woehler curves given by the Eurocode for the critical notches. Environmental sustainability is increased by including reliability and sustainability in design. For an exemplary high-rise adaptive load-bearing structure, this increase is more than 50%.
1. Introduction
As the world population grows [1], living space becomes scarce due to urbanization [2]. The constantly increasing consumption of construction material [3] results in the depletion of natural resources. Furthermore, the construction industry emitted 11% of the global CO2 emissions in 2015 [4], which makes it a significant influencing factor on the world’s climate. One problem is that conventional structural design practice usually ensures that the strength and the deformation capacity of the structure meets the worst load case. Predominantly, such structures are loaded much lower than the design load, meaning they are oversized for most of their operating life.
Saving construction material is possible if the structure is able to adapt to different load cases. That makes a manipulation of internal forces towards a homogenization of the inner stresses to external actions, such as wind, snow, or earthquakes, necessary.
The so-called adaptive structures are able to manipulate the distribution of their internal forces or influence external applied loads by changing form or shape. The adaptation can be in an active way, which needs auxiliary energy, or a passive way [5].
Previous research completed at the “Stuttgart SmartShell” proves that for an adaptive shell structure a reduction in the peak fiber stresses in the wooden structure is achievable. Furthermore, the models show the active supports to be very efficient with respect to counteracting vibrations in the system [6].
To carry out further investigation, the German Research Foundation is funding the Collaborative Research Centre 1244 (CRC 1244) “Adaptive Skins and Structures for Tomorrow’s Built Environment” [7], to which this study contributes by demonstrating reliability and environmental sustainability.
Reliability describes the probability of fulfilling the intended attributes or functions within a defined operating period and under specified operating and environmental conditions [8,9]. At the same time, reliability or its fulfillment is a quality characteristic. According to Garvin [10], reliability is one of eight quality dimensions. Consequently, studies on reliability are also studies of a particular aspect of quality.
Environmental sustainability, here, means minimizing emissions to the environment and responsible use of natural resources. Although the environmental footprint of a product includes multiple impact categories, the focus in this study is on climate change and the reduction in building materials used.
Furthermore, the following investigation is focused on adaptive load-bearing structures in which actuators, installed in the load-bearing structure of the building, take over the adaptation. The research is carried out on a high-rise demonstrator, see Figure 1, explained in detail afterwards.

Figure 1.
High-rise demonstrator with adaptive load-bearing structure (l) and access tower (r) at the University of Stuttgart. Source: Institute for Lightweight Structures and Conceptual Design (ILEK).
2. Problem Formulation
To meet the demand for housing, while preventing the depletion of natural resources and increasing environmental sustainability, the concept of adaptive load-bearing structures involves replacing mass, construction material, with electrical energy. The stiffness of the load-bearing structure is ensured by built-in actuators that allow adaptation to various loads, which requires electrical energy [5]. The expectation is that electrical energy will be available to a large extent in the near future, and the continual switch to renewable energy sources leads to a reduction in CO2 emissions per kWh [11]. Adaptive load-bearing structures, thus, experience an increase in environmental sustainability because of mass savings with the additional effect that greenhouse gas emissions occur slowly over time due to electrical energy, rather than in large quantities due to construction material at the very beginning.
The potential of material savings when it comes to high-rise buildings is shown in Figure 2 according to Khan, cited by Mufti [12]. An ideal structure isolated from lateral loads such as wind and earthquake is only exposed to static loads, whereas a strength-dominated design prevails. For a realistic scenario, the structure undergoes wind and earthquake loads, which results in a stiffness- or fatigue strength-dominated design. In conclusion, a considerable amount of construction material is necessary to withstand lateral loads and achieve sufficient stiffness. This is the so-called “premium for height”, whose influence increases with the number of floors. With adaptive load-bearing structures in high-rises, the stiffening and vibration control can be performed by the actuators using electrical energy. Less construction material is needed, and it is expected that environmental sustainability increases. From Sobek [13], the so-called ultra-lightweight structures become possible. This saves construction material and mass which then reduces the necessary actuator forces but has the side effect of making the load-bearing structure more susceptible to external loads, which in turn requires electrical energy to adapt. The more the material savings, the more the influence of external loads, and thus, the higher the energy consumption. This is the simple relationship of the approach of Senatore [14] or Reksowardojo [15], which is not comprehensive in the design of adaptive load-bearing structures. Further aspects to be considered are dealt with in the next sections.
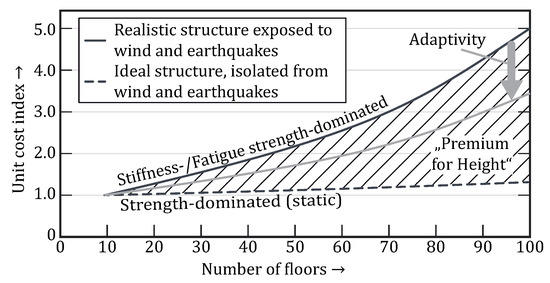
Figure 2.
“Premium for height” with high-rise buildings (similar to [12]).
Another effect to be considered when reducing the cross-sections for saving construction material is the decreasing fatigue strength of the critical notches under the aspect of an increased susceptibility to vibrations of the load-bearing structure. In particular, for loads that are lower and, therefore, do not require an adaptation, reliability needs to be demonstrated. Regardless, the adaptation function requires the integration of mechatronic components such as sensors, actuators, and control, which also require a reliability assurance.
Overall, these factors are interdependent and behave partly oppositely and partly analogously in their relationship. This large number of dependencies in the fields of reliability and environmental sustainability are shown in Figure 3 and must be considered in a comprehensive design of adaptive structures.
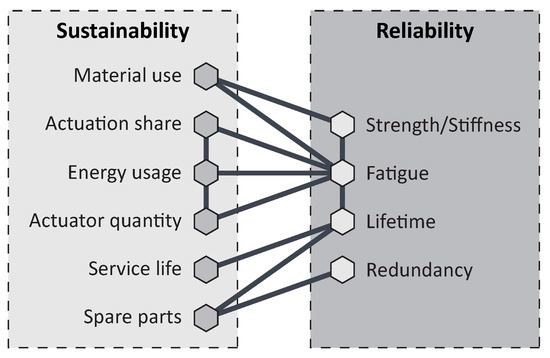
Figure 3.
Factors of reliability and environmental sustainability in the design of adaptive load-bearing structures.
Design of Passive Load-Bearing Structures
Civil Engineering in Europe uses the DIN EN 1990 Eurocode (EC) standard [16] for the reliable and safe design of structures. The standard defines ultimate limit states (ULS) and serviceability limit states (SLS) governed by regional statically simplified loads and partial safety factors. This leads to a reliable and safe design because of conservative safety factors and load assumptions. The admissible deformation of the structure caused by the maximum load, represented by a load combination of, e.g., wind and snow, results from the SLS comfort aspects and determines the slenderness of the structure.
The verification of a reliable design is performed by a comparison of the probability of failure and the reliability index , with a minimum permissible design failure probability , according to Equation (1). equates the distribution function of the standardized normal distribution.
The probability of failure of structural components depends on the probability that action effect E (stress) exceeds resistance R (strength), while variables E and R are described by distribution functions, as shown in Figure 4. The probability corresponds to a reference period , which usually equals the design life.
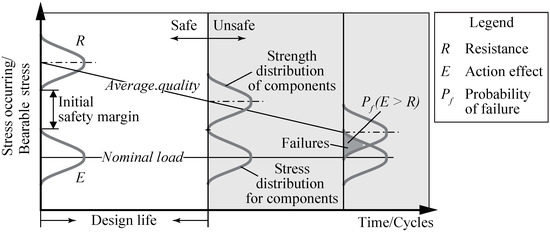
Figure 4.
Stress–strength interference for structural components over time/cycles (based on [17]).
In the EC standard, a stress–strength interference is excluded during design life using partial factors. The partial factors guarantee that statistical variability in action effects and resistances, on the one hand, and uncertainties in modeling, on the other hand, do not affect the reliability and, therefore, safety of the building. The load assumptions are simplified as static loads, whereby this simplification presupposes a load-bearing structure without unusual geometry, stiffness, or mass distribution. For regional loads, the EC is extended by national appendixes, including maps for a rough determination of the local weather conditions such as snow or wind loads.
As a very common approach, the EC standard defines consequence classes related to reliability with minimum values for the reliability index, according to Equation (1). Assuming medium consequences for loss of human life as well as for economic, social, and environmental consequences, the reliability class RC2 is mandatory [18]. The reliability index with the related probability of failure is defined according to Table 1. It needs to be pointed out that these values are notional values and used for the comparison of reliability levels of load-bearing structures. These specifications include the probability of the critical load.

Table 1.
Reliability index and probability of failure for RC2 according to Eurocode [18].
Load assumptions simplified by static loads, as well as partial safety factors of the Eurocodes approach, result in an oversized design of the load-bearing structure. The insufficiency of considering the mechatronic components needed for adaptation in the reliability demonstration emerges. An uneven stiffness distribution for adaptive load-bearing structures using actuators installed in the structure and active damping is not in accordance with the Eurocodes static design methodology [18]. In consequence, a dynamic analysis is required.
3. Limits in Designing Adaptive Load-Bearing Structures
During product design in mechanical engineering, there is usually a reliability estimation. Normally, this estimate is carried out on the basis of tests or prior knowledge. In the worst case, the actual failure distribution occurs before the estimate, which might be a serious problem or at least a warranty issue. Optimally, the distributions coincide, or the estimate is a little conservative. If the actual end of life is considerably after the estimate, the product is highly oversized. Generally, in architecture and civil engineering, the quantity of structures designed is one. Extensive testing is not possible, which is why the structures are oversized to ensure reliability. A reliable and safe design is ensured by a probability of failure, described by the probability that action effect exceeds resistance of the structure, less than a permissible value. Up to now, safety and reliability have therefore been a subject of a safe-life design and are equivalent to each other.
Saving construction material, on the one hand, presupposes a design with more precise location-based load profiles and a more detailed analysis of load cycles than only considering the worst case regarding serviceability and load-bearing capacity. On the other hand, designing adaptive load-bearing structures requires a load spectrum to be defined to analyze the operational as well as the passive behavior of the load-bearing structure. Since the lifetime of a building is very long, a probable failure of the components of the adaptive load-bearing structure, e.g., actuators, sensors, or control needs to be considered, which should not lead to an unsafe state [16]. The safety and reliability of the structure are, therefore, influenced by the faultless function of the adaptation and need to be distinguished.
Reliability describes the ability to perform, e.g., the adaptation function, under given conditions for a given time interval [19]. By contrast, safety evaluates the impact of a failure, considering the probability of occurrence and the severity of the event. This distinction is necessary in design for the SLS and ULS, where a safety analysis becomes necessary.
To guarantee the same reliability comparing conventional to adaptive load-bearing structures, standardized limits of the Eurocode should be adopted. When it comes to safety, the safe-life principle no longer works. The adaptation process is a safety-related function, whereas functional safety standards, as established in mechanical engineering, e.g., EN 61508 [20], need to be considered. The correlation between safety and reliability for conventional and adaptive load-bearing structures under the aspect of environmental sustainability is shown in Figure 5. The qualitative graph shows the reliability of the structure on the vertical axis above the utilization on the horizontal axis. The dashed line represents the reliability of a conventional passive structure, which is high for a low utilization and decreases with increasing utilization of the structure. In practice, there is some minimum reliability ensuring a certain lifetime. For safety reasons, the design of conventional structures, symbolized by the point “today’s design”, aims for a higher reliability, the target reliability. On the point “today’s design”, the gap between the minimum and target reliability is the design safety.
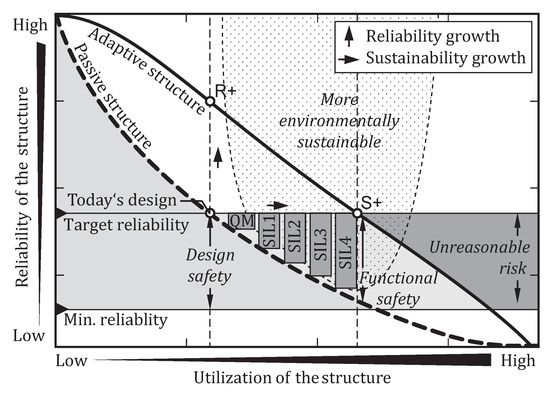
Figure 5.
Reliability and safety under the aspect of environmental sustainability for an adaptive and passive structure (based on [21]).
To the left, the design safety is increasing with reliability, whereas it is decreasing to the right, as highlighted by the area below. Taking the “today’s design” point as reference for environmental sustainability, an increasing safety margin in design, top left, is not sustainable because more construction material is needed. Reducing the design safety (bottom right) leads to a more sustainable design because less construction material is used. Environmental sustainability in this graph defines the ratio of construction material consumption compared to the reference point of “today’s design”. Energy consumption for adapting the structure is neglected here. Analogous to the dashed line, the solid line defines the reliability of an adaptive load-bearing structure. Like a redundancy, the adaptivity of the structure improves the building’s reliability. Reliability growth is described by the vertical arrow, pointing to the point “R+”, marking the reliability by use of an adaptive structure. As previously noted, the new point might be unsustainable, as more material for components is needed to provide the adaptation. Hence, simply adding adaptivity does not serve the purpose, as it increases oversizing. Instead, reliability and lifetime assessment help to achieve an accurate design. Nevertheless, reliability growth can be achieved, which might be interesting as well. An activation of the load-bearing structure of bridges, for example, may extend their lifetime by actively damping vibrations or adapting the bridge to moving loads such as trains in order to reduce the deflection. The extension of the lifetime of a building also promises a positive effect on environmental sustainability. The environmental impact per year of use decreases with an increased lifetime. In addition, new and more efficient construction methods or materials may be available in the future and could be utilized.
Aiming for the same target reliability as today’s design, the horizontal arrow describes the growth of environmental sustainability, leading to point “S+” for an adaptive load-bearing structure. In point “S+”, there is only minimal design safety left, highlighted by the gray area below. If the gap between minimum reliability and target reliability describes the safety margin and a reduction is not acceptable, the safety integrity has to be ensured otherwise. By transferring reliability, respectively, safety-related functions to the adaptation using an adaptive load-bearing structure, the functioning becomes safety relevant. Functional safety standards, such as the EN 61508 [20] in mechanical engineering, have to be applied. Based on the hazard that comes from a malfunction of the safety related function, a safety integrity level (SIL), prescribing risk-reducing measures, needs to be applied. Figure 5 shows the different SILs, reaching from standard quality measures (QM) to the highest requirements on SIL 4. The SIL classification for the safety-related function depends on the safety relevance of the function. This means that the less safety from a safe design, the more safety need to be related to the adaptation function. That does not go arbitrarily far because the risk reduction according to the standard is exploited with SIL 4. An unacceptable residual risk would remain if design safety is further reduced. The optimal design finally depends on the development effort, which is related to the SIL and further risk-reducing measures off-standard.
Depending on the application type for ULS or SLS, a validation of the adaptive load-bearing structure regarding safety and reliability is necessary to, first, ensure that the system does not pose any unreasonable hazard and, second, that the reliability can compete with that of conventional buildings under the aspect of saving building material.
In the following section, the inter-relationship of reliability and safety in the design of adaptive load-bearing structures is shown using the previously introduced high-rise demonstrator, which is explained in more detailed afterwards.
4. Reliability and Safety of Adaptive Load-Bearing Structures
Adaptive load-bearing structures include mechanical components, e.g., actuators with lifetimes less than the design life of conventional structures. This leads to failures and interrupts the adaptation. In addition to the actuators, an intelligent control with sensors is needed, see Figure 6. The controller gathers the information and calculates the response for the actuators to reduce the stress magnitude or the displacement induced by disturbances from external loads on the structure. A diagnostic system detects failures, so that the control strategy can be adapted to the new situation. In comparison to conventional passive structures, where only structural failures can occur, more failures have to be detected and handled.
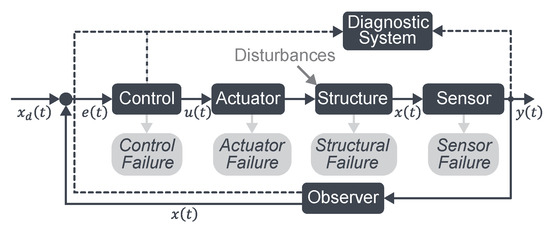
Figure 6.
Control loop with failure modes (based on [22,23]).
According to the Eurocodes, approach safety is guaranteed by ensuring a minimum reliability, given by the standard. The control loop of an adaptive load-bearing structure, as presented in Figure 6, is a mechatronic system with safety-related functions depending on the structural design, which is not covered within the Eurocode (EC). The simple relation between reliability and safety does not apply.
In the following investigations, reliability and safety were contemplated separately, as shown in Figure 7. The procedure for reliability analysis is analogous to mechanical engineering, starting with a system overview, applying qualitative and quantitative methods, and calculating the system availability [8]. The availability is the probability of finding the system in a functional state. Depending on the design for ULS or SLS, a structural failure is probable or at least design limits were exceeded, if the adaption function is not operable while a critical load event happens. The specifications of the EC, such as a maximum probability of failure are considered as limitations. Since buildings are usually built in very small numbers, often with a quantity of one, extensive hardware tests are not possible. Therefore, a simulation model is needed to analyze the capability of the adaptation function to adapt the structure, to investigate the effect of failures to set up the fault tree, and also to analyze fatigue in a nonoperational state of the structure for loads below where an adaptation is needed.
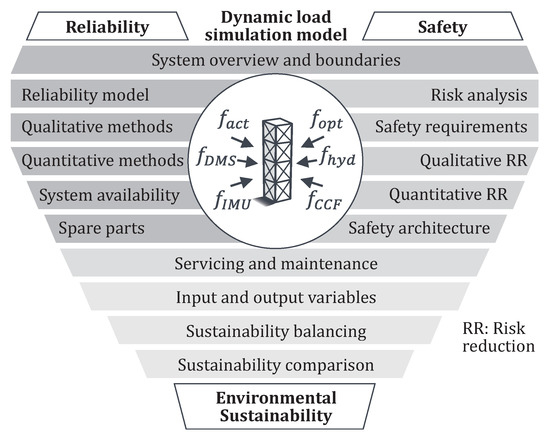
Figure 7.
Procedure for safety and reliability verification and environmental sustainability balancing.
For the safety analysis, a procedure according to the functional safety standard EN 61508 [20] appears to be suitable. This ensures functional safety with a residual risk as low as reasonably possible by a systematic risk mitigation. After a risk analysis, the safety architecture is analyzed, and qualitative and quantitative risk-reducing methods are applied. The procedure is shown in an overview in Figure 7. The safety verification is not the subject of this article, and a reference is made at this point to [24]. Finally, the environmental sustainability assessment provides a comprehensive balancing of inputs and outputs, such as spare parts and hardware architecture, as well as material consumption and energy usage calculated by the simulation.
As the capability to adapt to external loads depends strongly on the design of the load-bearing structure, the design of the adaptation function is related to the design of the structure. This dependency requires the design to be iterative using a dependable load spectrum to consider control dynamics and evaluate the adaptation function to counteract dynamic loads.
5. Introducing the Adaptive High-Rise Demonstrator
In order to do justice to urban migration and the resulting higher population density, a high-rise is considered in the present investigations. Moreover, the mass saving potential is higher compared to, for example, detached houses.
The high-rise demonstrator at the University of Stuttgart, pictured in Figure 1, has an adaptive load-bearing structure and serves to validate the concept for an adaptive structure and to have a testing unit for active structural building components. Over its total height of m, there are 12 floors, which are accessible through an access tower next to the high-rise demonstrator. The access tower also ensures an appropriate power and hydraulic fluid supply for the actuators.
The demonstrator consists of a modular construction repeating four times, each with three floors, eight bracings, and two crossings on each side, as shown in Figure 8. Actuators are placed in the first three modules, eight in the columns, and 16 in the bracings. For experimental investigations, parallel installed actuators in the columns are used for excitation, whereas the serial integrated actuators in the bracings are used to stiffen and dampen the structure.
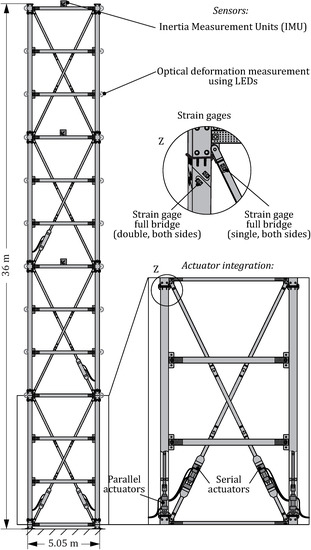
Figure 8.
Adaptive load-bearing structure of the high-rise demonstrator for the CRC 1244 [25].
A deformation, e.g., by wind loads, requires an active counteraction. In a three-dimensional view, torsional deformation is possible. This can be compensated for by activating the bracings diagonally opposite. The actuator placement comes from two different load cases, considering static and dynamic loads as explained in [25] using 24 actuators in total. Several sensors ensure a sufficient controllability and observability. A control system controls the hydraulic actuators and adapts the structure to lateral static as well as dynamic loads.
6. Reliability and Environmental Sustainability Modeling of the Adaptive High-Rise Demonstrator
For reliability analysis, a system overview of the adaptive high-rise demonstrator is illustrated in Figure 9 and explained hereafter. Because of the large forces needed, so far, only hydraulic actuators were considered. A valve, controlled by a process controller in each module, regulates the hydraulic fluid stream. For measuring the tensions full-bridge-strain-gage-setups were placed on each active element as shown in Figure 8. The sensor signal is amplified and passed through a decentralized control installed in each active module to the main control. Depending on the number of actuators, each active module is equipped with a decentralized control. The main control acts as a redundancy. The control response is calculated. The hydraulic pressure comes from a hydraulic pump and to bridge the start-up out of a pressure reservoir. The electronic devices are supplied with electricity, where, in case of a power outage, a backup battery ensures the supply.
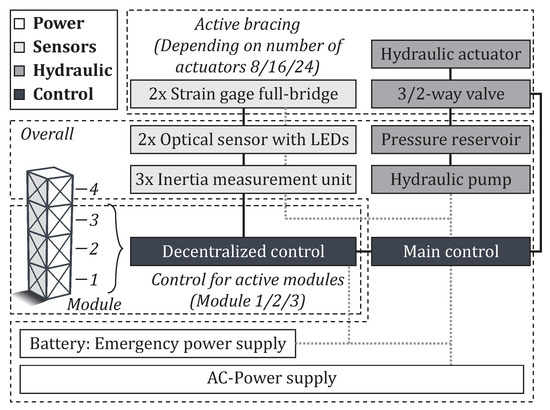
Figure 9.
System layout of the adaptive high-rise demonstrator.
A failure of the adaptation function is only fatal in case of a simultaneous occurrence with the critical load event. To demonstrate the reliability of the adaptation function and calculate the availability to estimate the probability of failure, the influence of component failures of the adaptation must be evaluated.
Furthermore, the structural fatigue needs to be proven, as cross-sections were reduced, and the influence of external loads on the structure increased. To investigate these effects, a simulation model was used in an iterative design approach, introduced in the following section.
6.1. Simulation Model and Iterative Design Approach
The modeling of structures exposed to dynamic loads is a common task in control theory. The expression by the second-order equation of motion (2) has proven to be well suited to this purpose [26,27].
The mass matrix and the stiffness matrix can be determined out of a finite element (FE) analysis, whereas, for the damping matrix , for example, the Rayleigh damping model can be set. Actuator forces are considered within the input matrix , distributing the actuator forces u on the structure. Accordingly, the disturbances v were distributed among the structure by . A modal analysis returns eigenvalues and eigenmodes and allows a characterization and model order reduction for a dynamic analysis [26].
The overall simulation process is shown in Figure 10. A strongly iterative procedure was applied here. Based on the configured models, all load cases were simulated with their proportions. If these investigations are successful for a structure and actuator configuration in all failure combinations, the next step follows. Here, in the major iteration step, it was investigated whether a further reduction in the material cross-sections was permissible.
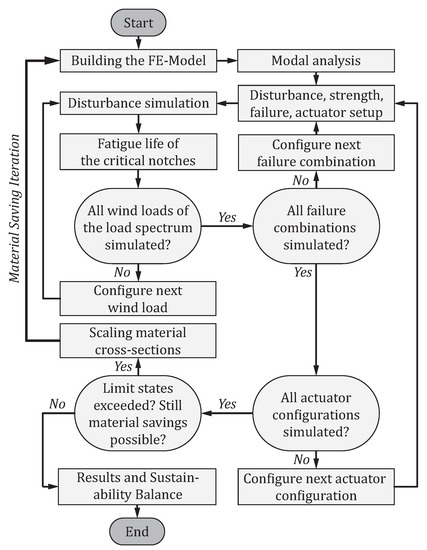
Figure 10.
Iterative design process.
The dynamic analysis presupposes accurate dynamic local load-time histories within a load spectrum, which are not included in the Eurocode. They allow a fatigue life analysis of the structure and an evaluation of failures of the adaptation.
6.2. Local Load Spectrum (Stress Modeling)
As the Eurocodes’ load estimations are static but related to the location of the building, a representative local load-time history as part of a load spectrum is needed. In the investigations in this article, next to earthquake loads, only wind loads were considered. This selection was location specific, and other dynamic loads could be added.
With the classification of suitable locations for wind turbines, much effort was put in mapping the wind load distribution in a very detailed way, at least across Germany. These specifications of the wind classes with the mean wind speed on basis of a 10 year time-period serve as a database for load-time histories within a load spectrum as shown in Figure 11.
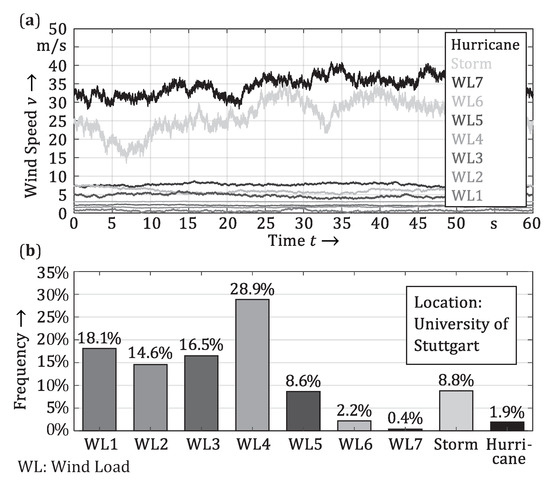
Figure 11.
Load-time histories and frequencies of the local load spectrum using [28] (based on [21]). (a) Wind speed over time for different wind loads; (b) statistical frequency of different wind loads.
The disturbances were calculated according to Gienger [29] by Equation (3). For each floor , a mapping of the wind forces to the nodes on the floor using for each of the four sides takes place. The superposition with the floor loads calculated with mass and gravity g returns the resulting load.
For the investigation of the critical load event, a load combination is assumed. The facade of the structure is considered with 2 kN/m2 and another 2 kN/m2 for the operating loads according to the Eurocode for office and residential buildings. These loads were added to the floor loads.
For lifetime estimation, this load spectrum was used in the simulation. In Figure 11b, the frequency of the different wind speeds is shown. A simulation was performed for every wind speed, calculating the structural fatigue and considering the frequency. The control of the adaptation, according to Figure 6, is conducted by using a Kalman filter and a linear-quadratic regulator (LQR). For further explanations, see [26,29].
6.3. Structural Fatigue (Strength Modeling)
The structural fatigue depends on the scaling of the cross-sections, on the one hand, because the critical notches, such as welding seams were also scaled, on the other hand, because of different load distributions when scaling and adapting the structure. To calculate the structural fatigue, the critical notches needed to be defined and modeled. In this case, the bolts, as well as the welded flange and the welded cross joints, were considered in the fatigue analysis, see Figure 12.
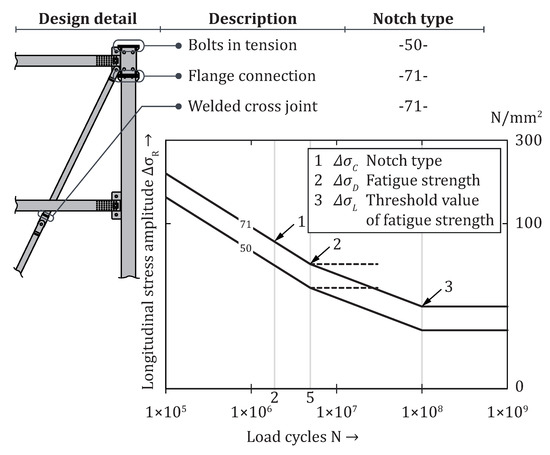
Figure 12.
Critical structural notch types with fatigue curves according to Eurocode [30].
The Eurocodes’ design procedure provides a classification of notch types and related fatigue curves based on a notch type number [30]. The lower the number, the more critical the notch type. The fatigue curves depend on an analysis of several samples and have a reliability of 95%. The amplitudes below the fatigue strength are calculated with a lower slope of the fatigue line and are conservatively included in the total damage calculation. The accumulation of damage is performed by means of rainflow counting and considers mean, amplitude, and frequency. The structural fatigue in this case was assumed to determine the operating life of the load-bearing structure, which is essential for the reference period of the environmental sustainability balancing.
6.4. Reliability and Availability Modeling
As for the reliability demonstration, maintenance needs to be considered; hence, a state-based dynamic modeling is necessary. For this purpose, Petri nets were used to model the system and calculate the probability for unavailability over time, which together with the critical load can result in exceedance of the limit state. Within the Petri net, each state was modeled with state intact/normal and defect/critical. A simplified illustration of the model can be seen in Figure 13. The probability of failure describes the transition to the defect state, which requires a repair described by the time . By means of a Monte Carlo simulation, the frequency of the states and their state probability was calculated.
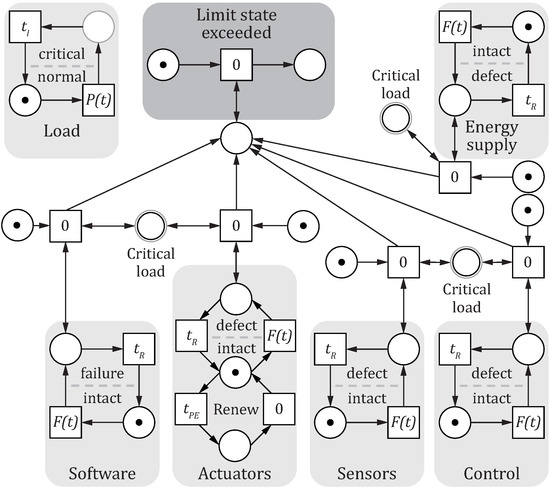
Figure 13.
Simplified Petri net of an adaptive load-bearing structure.
Table 2 contains the reliability data to calculate the systems availability. The sensor system was assumed to be a two-out-of-three system, and as for a sufficient observation and control, at least two sensor principles need to be operable. For the strain gages and the inertia measurement units (IMUs), a minimum of 50% is needed to work properly. A decentralized control in each active module with a central redundancy controls the actuators response to the external loads. Hurricanes usually also trigger damage to overhead power lines, which is why there is no reliance on a main power supply. In the reliability analysis, it is, therefore, not considered as a fallback level. The fault table for the actuators follows out of an analysis of how failures of the actuators affect the overall specifications and was performed using the simulation. The probability of the critical load event was assumed to be a constant 10% to occur, as the frequency in Figure 11 is only a mean value per year. For this example, the critical load event was a hurricane, which needed the adaptation to be operable; otherwise, an irreversible damage state occurred.

Table 2.
Exemplary reliability data for the components of the adaptive high-rise demonstrator according to [31,32,33,34,35].
6.5. Environmental Sustainability Balancing
The basis for the comparison of passive and adaptive load-bearing structures is the environmental sustainability balancing as global warming potential , expressed in terms of greenhouse gas emissions in kg CO2-equivalent. The components were modeled in the professional software suit for life cycle engineering GaBi with the professional database SP39 (July 2019). The life cycle impact assessment (LCIA) was calculated following DIN EN ISO 14040 [36] and 14044 [37]. The modules A1-3 (production), B6 (operational energy use), C1-4 (end of life), and D (benefits beyond the system boundary) according to DIN EN 15804 [38] were considered.
The results are shown in Table 3 and form the basis for the evaluation. The scaling of the load-bearing model defined the emission for structural steel , considering the recycling potential. The components needed for adaptation , including battery, number of actuators and sensors, and the hydraulic oil capacity also influenced the balance. The necessary spare parts, which arose from the simulation performed with the Petri net, were considered by . Energy consumption for the simulation time was calculated according to Equation (4), based on the actuator force and stroke , as well as efficiency in kWh extrapolated to the operating life.

Table 3.
LCIA results of the modeled components.
For the emissions per kWh for production, the German electricity mix was assumed. The change to renewable energy sources causes a further reduction in emissions at this point. The global warming potential out of the greenhouse gas emissions for adaptive load-bearing structures was calculated according to Equation (5):
For a comparable passive load-bearing structure, only the greenhouse gas emissions for the structural steel were considered.
7. Results and Comparison for the Adaptive High-Rise Demonstrator
In the results analysis, several variants of the adaptive high-rise demonstrator were compared to the passive load-bearing structures. Therefore, the same functional and boundary conditions were used.
As stated at the beginning, the design of load-bearing structures can be differentiated in the design for ultimate limit state (ULS) and serviceability limits state (SLS). In this case, the SLS requirement was a displacement below 40 mm, whereas the design for ULS was limited by the material strength to be met. The variants investigated are shown in Table 4 and include a different number of actuators and structural scales. The disturbance simulation resulted in an optimum mass scaling regarding the boundary conditions and the control dynamics of the adaptation. Out of the Petri net simulation, the spare parts and the availability were calculated. For the variants including 8, 16, and 24 actuators, the availability and probability of failure are depicted in Figure 14.

Table 4.
Investigated variants of the adaptive high-rise demonstrator.
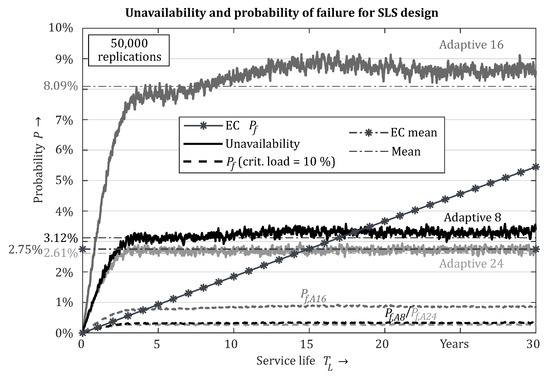
Figure 14.
Unavailability and probability of failure: adaptive variants and Eurocode specification (based on [24]).
In Figure 14, a comparison of the Eurocodes specification for the probability of failure and the result of the Petri net simulation for the SLS design out of 50,000 replications are shown. The Eurocodes probability of failure rises constantly over time and assumes a certain frequency of the critical load. In comparison, the unavailability of the adaptation function can be seen as a limit, representing the maximum probability of failure using this hardware architecture. Assuming a 10% probability of a simultaneous critical load, the probability of failure results. For all variants, the Eurocodes probability of failure was greater, except for variant Adaptive 16, which at the beginning was slightly higher than the other variants, as there was no redundancy for a failure of the actuators. All in all, the specification was met, and it can be stated that the design of adaptive structures can achieve the same high reliability as that of passive structures based on the Eurocode.
Considering the design for ULS, an assumption for the frequency of the critical load is necessary. The result strongly depends on this assumption, which leads to the probability of failure. As the design for ULS is of safety relevance, structural failure can lead to a total collapse of the building. Therefore, a design according to safety standards, e.g., EN 61508 [20], as used in mechanical engineering is proposed. The standards specification includes a differentiated analysis, depending on the operation of the adaptation function as a safety-related function. A distinction is made between continuous and low demand rate. For adaptive load-bearing structures, there are usually only rarely occurring critical loads, as in this example a hurricane, which need an adaptation; therefore, the low demand rate is adequate. This defines a frequency of demand of the maximum once a year and requires qualitative and quantitative methods to be applied. Since the safety-related design of adaptive load-bearing structures is not the focus of this article, and for a detailed analysis, a reference is made to [24].
The environmental sustainability balancing according to the data in Table 3 allows for the comparison of the adaptive variants and the passive load-bearing structure. For environmental sustainability balancing, the construction steel for the structure and the components needed for adaptation were considered. Due to a lack of data and a high recycling rate, supply lines and wires as well as electronic devices such as sensors and control were neglected. The amount of spare parts was considered conservatively as the worst-case scenario out of the 50,000 replications. The data consider production, incineration, and recycling of the materials. Environmental sustainability for the design of both limit states is shown in Figure 15 and the following. For the SLS design, three variants according to Table 4 were compared to the passive variant. On the y-axis, global warming potential (GWP) per year is shown. Depending on the operating life of the structure, the reference period varied. The passive load-bearing structure was designed for a operating life of ten years. For adaptive load-bearing structures, vibration damping and the material savings, resulting in lower mean values, led to a drastically reduced fatigue of the structure even though the mass was significantly reduced. Considering the same load spectrum, the disturbance simulation of the adaptive variants resulted in almost three times the operating life of the passive structure from a fatigue point of view.
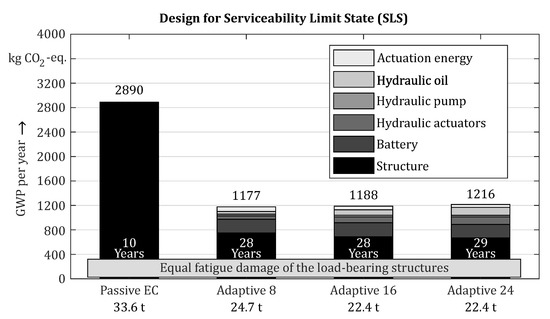
Figure 15.
Environmental sustainability comparison of the adaptive and passive variants when designing for SLS with equal fatigue damage (based on [24]).
Environmental sustainability increased drastically, due to the reference to the operating life, and caused a more than 50% reduction in greenhouse gas emissions than the passive load-bearing structure.
Although more mass savings and a longer operating life are possible, the more actuators are installed in the structure, and the variant Adaptive 8 performed best. The material savings for variants with more actuators were compensated by the additional demand for actuators and hydraulic oil. In addition, variant Adaptive 8 required the least wiring and supply lines.
Nevertheless, the improvements in environmental sustainability for the investigated configurations are only present if the longer operating life is used. Figure 16 illustrates this. None of the adaptive variants compared performed more environmentally sustainably than the passive variant for the same operating life of only 10 years. Although the CO2-equivalent for the load-bearing structures was lower in each case, the effort required for the adaptivity resulted in a poorer balance overall. Furthermore, the battery had a relatively high impact on this, as the comparison shows.
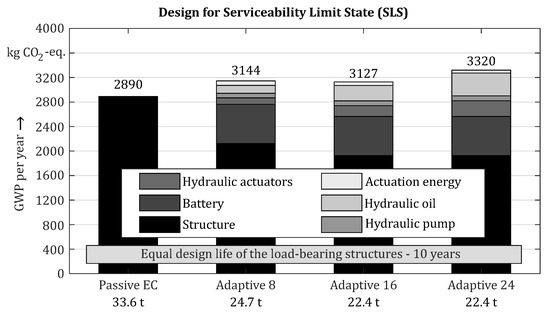
Figure 16.
Environmental sustainability comparison of the adaptive and passive variants when designing for SLS with equal operating life (based on [24]).
The design for ultimate limit state (ULS) is shown in Figure 17. Only the variants with 16 and 24 actuators were able to actively compensate the huge material savings considering the tensions. Because of the drastic reduction in the cross-sections to save construction material, the fatigue strength of the critical notches, e.g., of the welded flange connection, decreased strongly. Therefore, the operating life could not be extended and was ten years, as for the passive load-bearing structure. For comparison, the passive variant according to the Eurocode standard is shown on the left, as well as a theoretical minimal passive variant without design safety to show what the absolute minimum is. In this case, there were only small savings in green-house gas emissions compared to the Eurocodes design and no savings at all compared to the minimal passive structure. In this design, the scaling of the structure is limited by critical notches, which experience a greater fatigue with decreasing cross-sections.
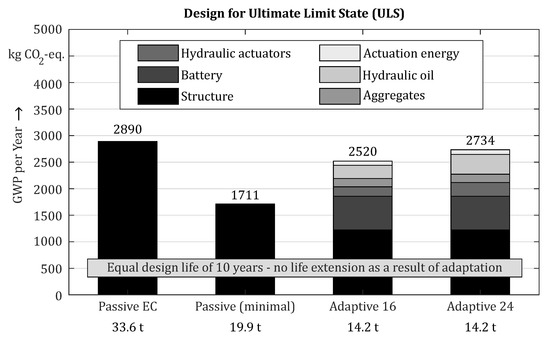
Figure 17.
Environmental sustainability comparison of the adaptive and passive variants when designing for ULS (based on [24]).
In the design for ULS, the safety requirement according to EN 61508 [20] specifies an additional redundancy for the power supply, which is why an emergency power generator was considered beside the hydraulic pump in the share named “Aggregates”.
From the comparison of the two limit states, it can be concluded, that for the adaptive high-rise demonstrator investigated in this article, a design for the SLS is associated with higher greenhouse gas savings. Furthermore, the design for ULS requires a sufficient and extensive safety analysis—an effort that is not reflected in the bar graphs shown.
8. Summary and Outlook
Adaptive load-bearing structures are a promising way to offer living space with low surface sealing while saving construction material and thereby conserving resources and diminishing emissions. As a mechatronic system, the conventional design practice of stress–strength comparison according to the Eurocode is not suitable anymore. A reliability analysis needs to be conducted, first, for the adaptation function and, second, for the structure itself. In addition, a more sustainable design requires load-time histories rather than simplified static load specifications of the Eurocode, as the standard for designing load-bearing structures.
An iterative design approach, as presented within this article, is necessary to demonstrate reliability and to evaluate the environmental sustainability of adaptive load-bearing structures as their intersection needs to be considered. The reliability requirements set with reference to the Eurocode are high, and for components of the adaptation such as actuators, maintenance needs to be considered. Thus, methods of mechanical engineering have to be applied, as this is not considered in the Eurocodes approach. A high availability is necessary because, if a failure occurs, the simultaneous occurrence with the critical load can cause irreversible damage to the load-bearing structure. To cover these events, using safety factors is counterproductive for environmental sustainability as more construction material is consumed. The approach in this article assumes that specifications for reliability have to be necessarily equal to the requirements for conventional passive load-bearing structures. Redundant components and maintenance can be one approach to increase reliability with regard to environmental sustainability. Furthermore, reliability and safety need a clearer distinction insofar as a reliable design also ensures a safe design. Now, the functional safety of the components relevant for adaptation needs to be proven when designing for ultimate limit states. A sufficient environmental sustainability demonstration for adaptive load-bearing structures must finally include the share of construction material, adaptive components, spare parts, energy use, and operating life, determined by fatigue life.
A review of the requirements, especially the uncertainties covered by safety factors and the loads specified in the Eurocode, is generally reasonable and may allow further material savings, as also considered in mechanical engineering [39]. Future investigations could possibly also take into consideration including approaches from research such as [40].
Author Contributions
Conceptualization, B.B., M.D., and S.A.; methodology, A.O., M.D., and D.B.; software, A.O.; investigation, A.O.; resources, S.A. and M.D.; data curation, A.O., D.E., and D.B.; writing—original draft preparation, D.E., A.O., and D.B.; writing—review and editing, D.E., A.O., D.B., M.D., and S.A.; visualization, D.E. and A.O.; supervision, M.D., S.A., and B.B.; project administration, B.B., M.D., and S.A.; funding acquisition, B.B., M.D., and S.A. All authors have read and agreed to the published version of the manuscript.
Funding
This project was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—Project-ID 279064222—SFB 1244.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data supporting the reported results can be obtained from the corresponding author.
Acknowledgments
The authors acknowledge Friederike van den Adel, née Schlegl, (Institute of Acoustics and Building Physics, University of Stuttgart), Andreas Gienger and Julia Heidingsfeld, née Wagner, (both: Institute for System Dynamics, University of Stuttgart). Special gratitude goes to Friederike van den Adel for the work with the LCIA models. Andreas Gienger and Julia Heidingsfeld are especially thanked for their contribution to the system dynamic models of the adaptive high-rise load-bearing structure.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| CRC | Collaborative Research Centre |
| DIN | Deutsches Institut für Normung—German Institute for Standardisation |
| EC | Eurocode |
| EN | Europäische Norm—European Norm |
| eq. | Equivalent |
| FE | Finite Element |
| FIT | Failures in Time—Number of units failing per billion operating hours |
| GWP | Global Warming Potential |
| Hydr. | Hydraulic |
| ILEK | Institute for Lightweight Structures and Conceptual Design |
| IMU | Inertia Measurement Unit |
| ISO | International Organization for Standardization |
| LCIA | Life Cycle Impact Analysis |
| LED | Light-Emitting Diode |
| LQR | Linear–Quadratic Regulator |
| QM | Quality Measures |
| RC | Reliability Class |
| RR | Risk Reduction |
| SIL | Safety Integrity Level |
| SLS | Serviceability Limit States |
| ULS | Ultimate Limit States |
| WL | Wind Load |
References
- Department of Economic and Social Affairs—Population Division. World Population Prospects—Highlights, New York, 2019. Available online: https://population.un.org/wpp/Publications/Files/WPP2019_Highlights.pdf (accessed on 15 September 2021).
- United Nations, Department of Economic and Social Affairs, Population Division, Population Facts. The Speed of Urbanization Around the World. 2018. Available online: population.un.org/wup/Publications/Files/WUP2018-PopFacts2018-1.pdf (accessed on 5 June 2021).
- OECD, Material Resources, Productivity and the Environment. OECD Green Growth Studies; OECD Publishing: Paris, France, 2015; ISBN 978-92-64-19050-4. [Google Scholar] [CrossRef]
- UN Environment and International Energy Agency. Global Status Report 2017—Towards a Zero-Emission, Efficient, and Resilient Buildings and Construction Sector, 2017. Available online: https://globalabc.org/resources/publications/2017-global-status-report-buildings-and-construction (accessed on 28 August 2021).
- Sobek, W. The Future of Sustainable Architecture—Resources, Recyclability and Ultra-Lightweight. A + U-Architecture and Urbanism, 27 May 2014. [Google Scholar]
- Neuhaeuser, S.; Weickgenannt, M.; Witte, C.; Haase, W.; Sawodny, O.; Sobek, W. Stuttgart SmartShell—A Full Scale Prototype of an Adaptive Shell Structure. J. Int. Assoc. Shell Spat. Struct. 2013, 54, 259–270. [Google Scholar]
- Sobek, W.; Daniela, F.; Philip, L. Adaptive Skins and Structures for Tomorrow’s Built Environment; Funding Application; Collaborative Research Centre, German Research Foundation (DFG): Stuttgart, Germany, 2016. [Google Scholar]
- Bertsche, B. Reliability in Automotive and Mechanical Engineering: Determination of Component and System Reliability; Springer: Berlin/Heidelberg, Germany, 2008; ISBN 978-3-540-33969-4. [Google Scholar]
- Neudörfer, A. Konstruieren Sicherheitsgerechter Produkte; Methoden und Systematische Lösungssammlungen zur EG-Maschinenrichtlinie; Springer: Berlin/Heidelberg, Germany, 2014; ISBN 978-3-642-45447-9. [Google Scholar]
- Garvin, D. Managing Quality: The Strategic and Competitive Edge; Free Press: London, UK, 1988; ISBN 978-0-02-911380-6. [Google Scholar]
- Gwinner, D. More than a Dream—A Renewable Electricity Future. NREL Continuum Magazine, 8 March 2013. [Google Scholar]
- Mufti, A.A.; Bakht, B. Fazlur Khan (1929–1982): Reflections on their Life and Works. Can. J. Civ. Eng. 2002, 29, 238–245. [Google Scholar] [CrossRef]
- Sobek, W. Ultra-lightweight construction. Int. J. Space Struct. 2016, 31, 74–80. [Google Scholar] [CrossRef]
- Senatore, G.; Duffour, P.; Winslow, P. Synthesis of Minimum Energy Adaptive Structures. Struct. Multidiscip. Optim. 2019, 60, 849–877. [Google Scholar] [CrossRef] [Green Version]
- Reksowardojo, A.P.; Senatore, G.; Smith, I.F.C. Design of Structures that Adapt to Loads through Large Shape Changes. J. Struct. Eng. 2019, 146, 04020068. [Google Scholar] [CrossRef]
- Ostertag, A.; Toader, T.N.; Bertsche, B.; Sobek, W. System-Safety in the Application of Adaptive Load-Bearing Structures. In Proceedings of the 2019 Annual Reliability and Maintainability Symposium (RAMS), Orlando, FL, USA, 28–31 January 2019. [Google Scholar]
- WOO, S. Reliability Design of Mechanical Systems; Springer International Publishing: Cham, Switzerland, 2017; ISBN 978-92-1-148316-1. [Google Scholar]
- European Committee for Structural Design. EN 1990:2010-12, Eurocode 0: Basis of Structural Design; Beuth Verlag GmbH: Berlin, Germany, 2010. [Google Scholar]
- VDI-Gesellschaft Systementwicklung und Projektgestaltung. VDI 4003:2007-03, Reliability Management; Beuth Verlag GmbH: Berlin, Germany, 2007. [Google Scholar]
- European Committee for Standardization. EN 61508-1:2011-02, Functional Safety of Electrical/Electronic/Programmable Electronic Safety-Related Systems—Part 1: General Requirements; Beuth Verlag GmbH: Berlin, Germany, 2011. [Google Scholar]
- Ostertag, A.; Toader, T.N.; Bertsche, B.; Sobek, W. Reliable Design of Adaptive Load-Bearing Structures with Focus on Sustainability. In Proceedings of the 30th European Safety and Reliability Conference and the 15th Probabilistic Safety Assessment and Management Conference, Venice, Italy, 1–5 November 2020. [Google Scholar]
- Preumont, A. Vibration Control of Active Structures—An Introduction, 4th ed.; Springer International Publishing: Cham, Switzerland, 2018; ISBN 978-3-319-72296-2. [Google Scholar]
- Gienger, A.; Schaut, S.; Sawodny, O.; Tarin, C. Modular Distributed Fault Diagnosis for Adaptive Structures using Local Models. IFAC-PapersOnLine 2020, 53, 13631–13637. [Google Scholar] [CrossRef]
- Ostertag, A. Zuverlässigkeit, Sicherheit und Nachhaltigkeit adaptiver Tragwerke. Ph.D. Thesis, Universität Stuttgart, Stuttgart, Germany, 2021. [Google Scholar] [CrossRef]
- Weidner, S.; Kelleter, C.; Sternberg, P.; Haase, W.; Geiger, F.; Burghardt, T.; Binz, H. The Implementation of Adaptive Elements into an Experimental High-Rise Building. Steel Constr. 2018, 11, 109–117. [Google Scholar] [CrossRef]
- Wagner, J.; Böhm, M.; Sawodny, O. Nonlinear Modelling and Control of Tension-Only Elements in Adaptive Structures. In Proceedings of the IX ECCOMAS Thematic Conference on Smart Structures and Materials, Paris, France, 8–11 July 2019. [Google Scholar]
- Böhm, M.; Wagner, J.; Steffen, S.; Sobek, W.; Sawodny, O. Homogenizability of Element Utilization in Adaptive Structures. In Proceedings of the IEEE 15th International Conference on Automation Science and Engineering (CASE), Vancouver, BC, Canada, 22–26 August 2019; pp. 1263–1268. [Google Scholar]
- LUBW State Institute for the Environment Baden-Württemberg, State Institute for the Environment Baden-Württemberg (LUBW)—Synthetic Representative Dispersion Category Time Series for Wind, 2019. Available online: udo.lubw.baden-wuerttemberg.de/public/ (accessed on 20 November 2019).
- Gienger, A.; Wagner, J.; Böhm, M.; Sawodny, O.; Tarín, C. Robust Fault Diagnosis for Adaptive Structures with Unknown Stochastic Disturbances. IEEE Trans. Control. Syst. Technol. 2021, 29, 1131–1146. [Google Scholar] [CrossRef]
- European Committee. European Committee for Structural Design, EN 1993-1-9:2010-12, Eurocode 3: Design of Steel Structures—Part 1-9—Fatigue; Beuth Verlag GmbH: Berlin, Germany, 2010. [Google Scholar]
- Denson, W.; Chandler, G.; Crowell, W.; Clark, A.; Jaworsky, P. Nonelectronic Parts Reliability Data; Defense Technical Information Center: Rome, Italy, 1995. [Google Scholar]
- Aceinna, OpenIMU330—Triple Redundant 1.5°/Hr SMT IMU, 2020. Available online: navview.blob.core.windows.net/webresources/6020-1800-01%20OpenIMU330BRevE.pdf?t=1593183415710 (accessed on 17 August 2020).
- Berghmans, F.; Eve, S.; Held, M. An Introduction to Reliability of Optical Components and Fiber Optic Sensors. In Optical Waveguide Sensing and Imaging; Springer: Dordrecht, The Netherlands, 2007; Volume 47, pp. 73–100. [Google Scholar]
- Bachmann electronic. Systemübersicht, Österreich, 11/2019. Available online: www.bachmann.info/issuu-pages/systemuebersicht-2020-deutsch/ (accessed on 17 August 2020).
- Texas Instruments. Quality & Reliability—MTBF/FIT Estimator—TMS320F2837xD Dual-Core Microcontroller, Data Sheet, Texas, 1995–2020. Available online: www.ti.com/quality/docs/estimator.tsp (accessed on 3 November 2020).
- Deutsches Institut für Normung e.V. Environmental Management—Life Cycle Assessment—Principles and Framework (ISO 14040:2006 + Amd 1:2020); German Version EN ISO 14040:2006 + A1:2020; Beuth Verlag GmbH: Berlin, Germany, 2021. [Google Scholar]
- Deutsches Institut für Normung e.V. Environmental Management—Life Cycle Assessment—Requirements and Guidelines (ISO 14044:2006 + Amd 1:2017); German Version EN ISO 14044:2006 + A1:2018; Beuth Verlag GmbH: Berlin, Germany, 2019. [Google Scholar]
- Deutsches Institut für Normung e.V. Environmental Sustainability of Construction Works—Environmental Product Declarations—Core Rules for the Product Category of Construction Products; German Version EN 15804:2012+A2:2019; Beuth Verlag GmbH: Berlin, Germany, 2020. [Google Scholar]
- Hanselka, H.; Pelz, H. SFB 805: Control of Uncertainties in Load Carrying Systems in Mechanical Engineering—Project 57157498. DFG Collaborative Research Centres; Technische Universität: Darmstadt, Germany, 2020. [Google Scholar]
- Wang, L.; Liu, Y.; Liu, D.; Wu, Z. A novel dynamic reliability-based topology optimization (DRBTO) framework for continuum structures via interval-process collocation and the first-passage theories. Comput. Methods Appl. Mech. Eng. 2021, 386, 114107. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).