The Casualty Stabilization–Transportation Problem in a Large-Scale Disaster
Abstract
1. Introduction
2. Literature Review
3. The Casualty Pickup and Transport Problem: Description
3.1. Casualty Prioritization
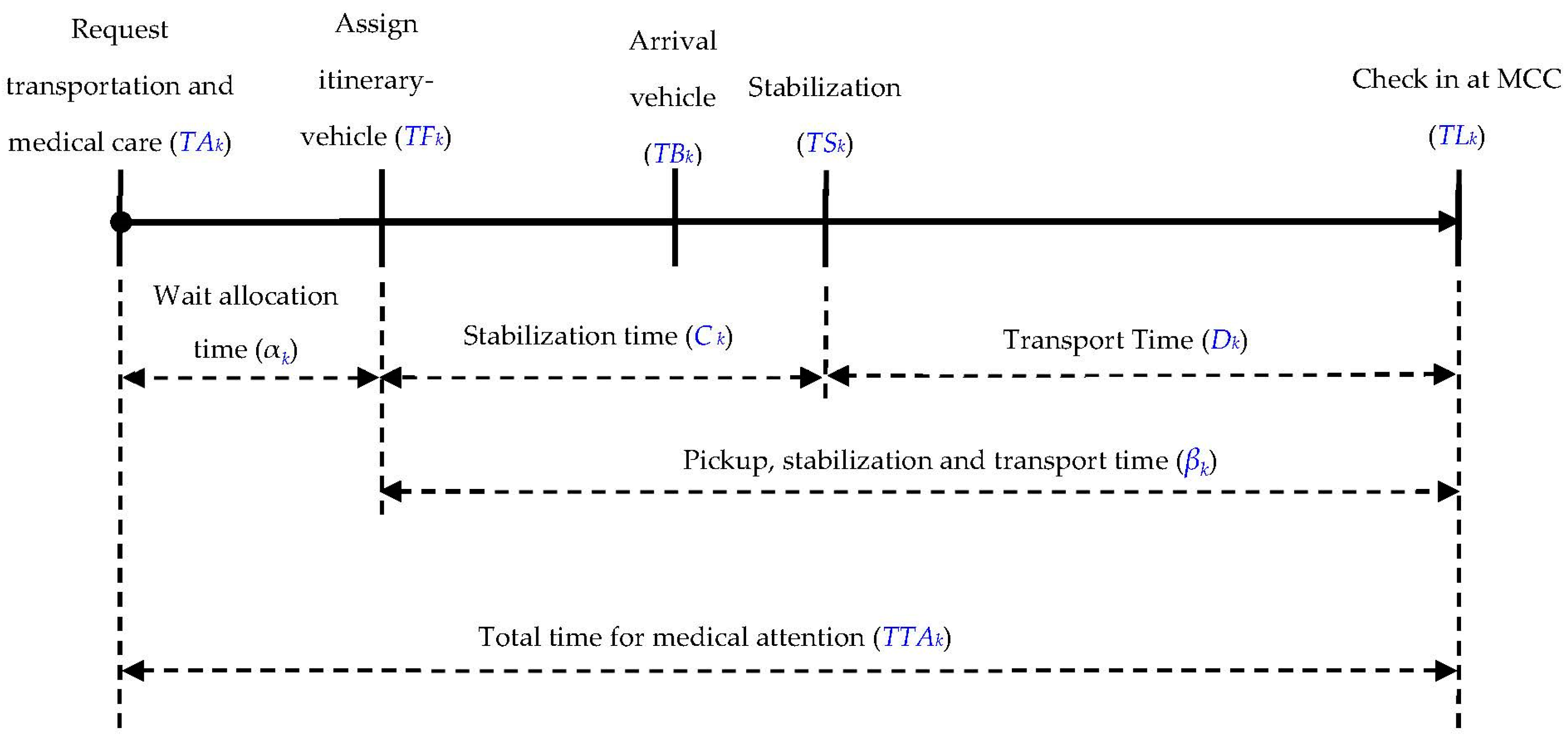
3.2. Total Medical Attention, Waiting, and Stabilization Times for Casualties
4. Proposed Methodology
4.1. Method Description
4.2. Resolution Procedure
- Identification of casualties transported to an MCC and in the process of being transported during the previous period:
- Set of casualties transported to an MCC in period p − 1:
- Casualties who are in the process of being transported in period p − 1:
- Updating the set :For each casualty k∈ proceed as follows:
- Identify PAk and . PA = {PAk /k ∈ }.
- Determine the wait-allocation time of each casualty k at the beginning of period p ∈ P as follows:
- Calculate with Equation (1)
- Sort casualties in ascending order according to their transport priority index .
- (a)
- Identification of the origin node of the vehicle m ∈ M, Om.
- Identify the last trip performed by vehicle m ∈ M (σm) as follows:If , then, otherwise where TTp is the time at which the planning period p∈P begins and Tmv the time needed by vehicle m ∈ M to complete trip v ∈ V.
- (b)
- Update the values of the maximum capacity of patients with g-type LSI ∈L that can be attended by MCC h∈H. Proceed as follows:
- where is the available capacity in MCC h ∈ H to attend casualties of severity g ∈ L at the beginning of the period p ∈ P, and is equal to 1 if vehicle m ∈ M transports the casualty k to medical center h on trip v, and 0 otherwise.
- (c)
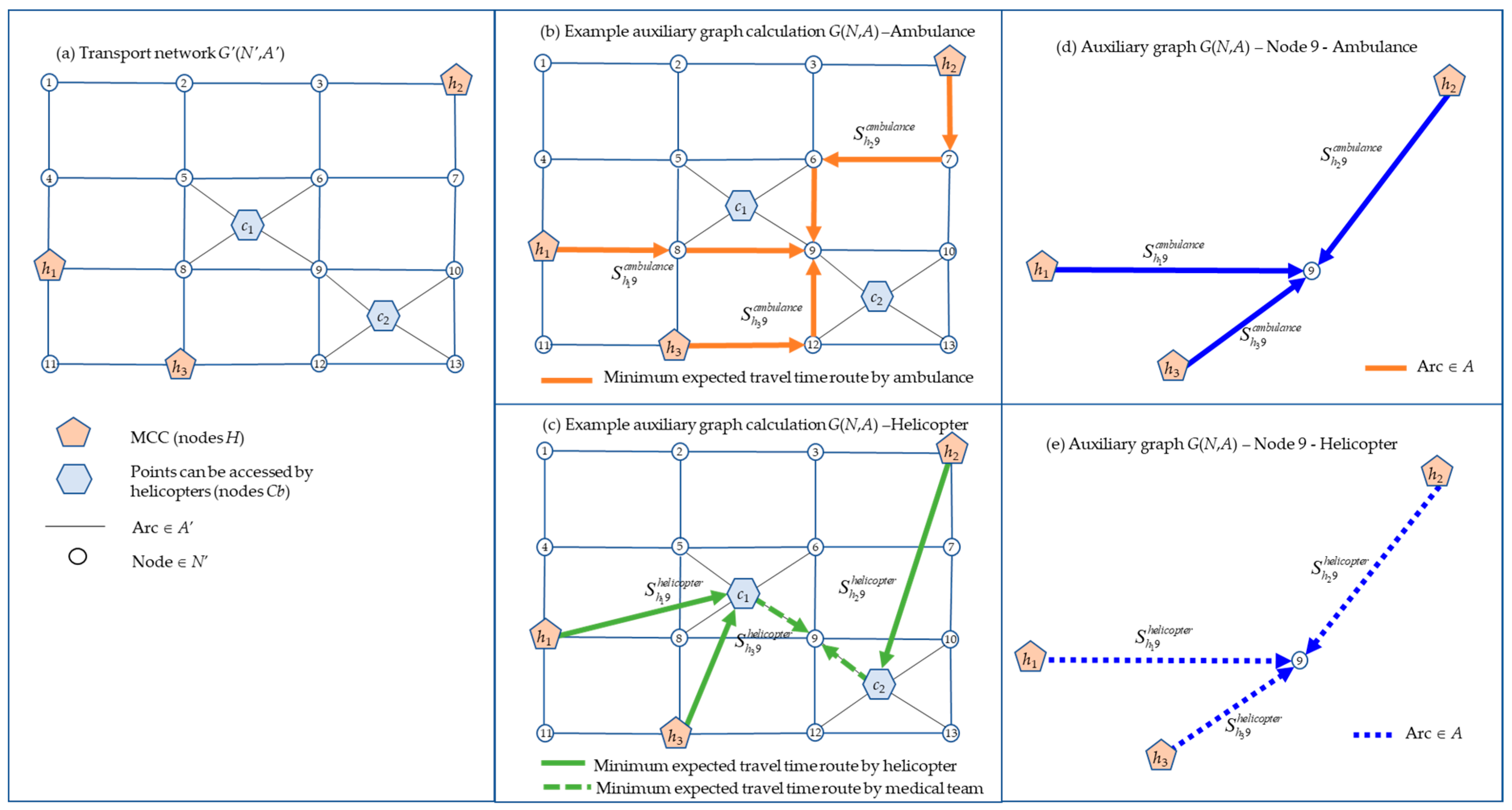
- Perform N = H ∪ PA, build a new auxiliary network G(N,A) and update values .
- (d)
- Update TDme (time required by e-type ∈ E vehicle m ∈ M to start operations) for vehicles in use.
- ∀ e ∈ E1/= 1 proceed as follows:If , then:If not,
- ∀ e ∈ E2/= 1 proceed as follows:If , then:If not,where E1 is the set of land-based vehicles (ambulances), E2 is the set of airborne vehicles (helicopters), and δme is equal to 1 if vehicle m ∈ M is of type e ∈ E, and 0 otherwise.
- (e)
- Availability of emergency vehicles m.Ωmp = 1 if vehicle m ∈ M is available at the beginning of period p ∈ P, and 0 if otherwise. Thus, M = m /Ωmp = 1.
4.3. Casualty Pickup, On-Site Stabilization, and Transport (CPST) Mathematical Model
- ■
- Objective Function:
- ■
- Constraints:
5. Methodology Implementation
5.1. Numerical Example
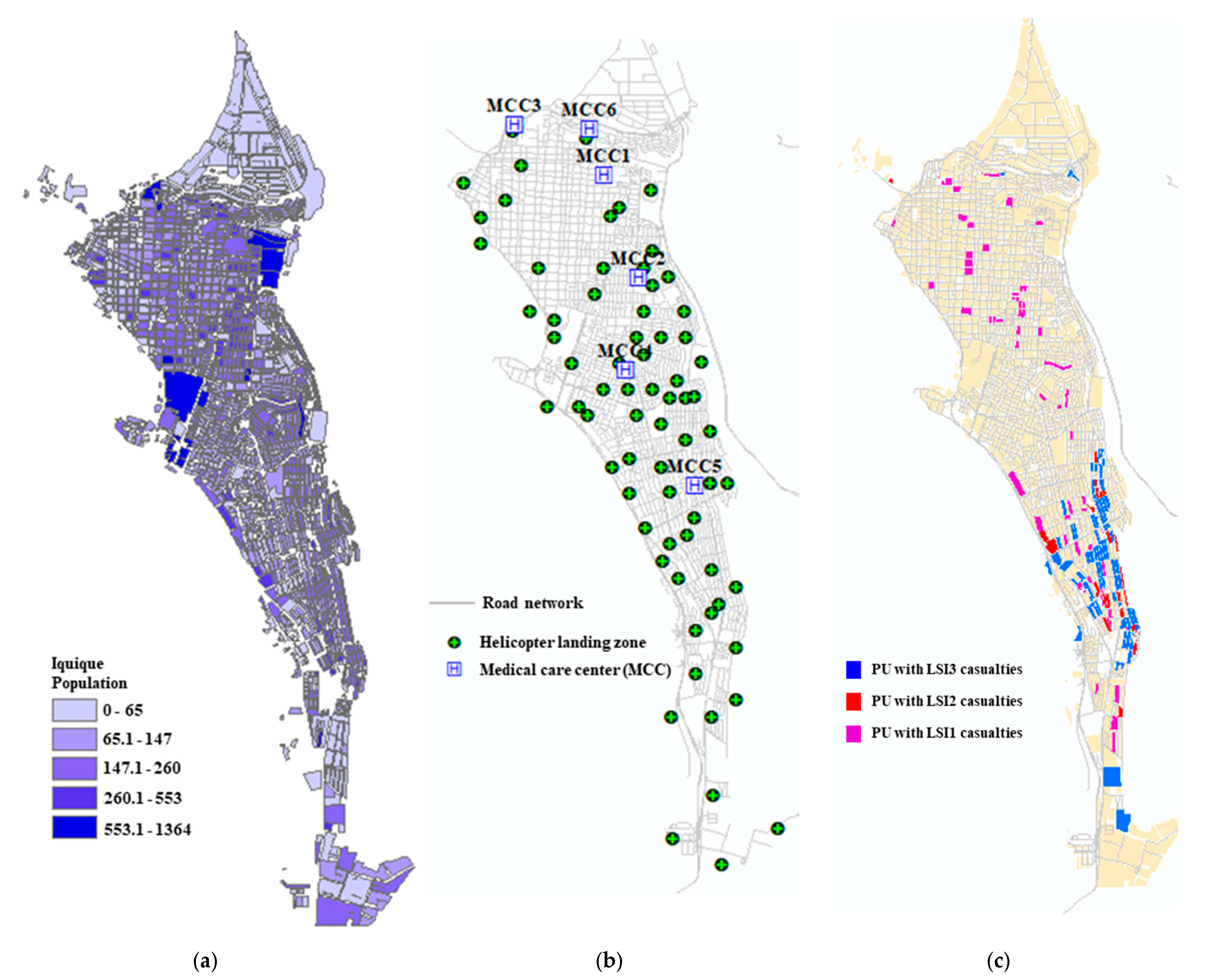
5.2. Case Study: Iquique, Chile
5.3. Iquique Population, Health Network, and Other Modeling Parameters
5.4. Requirements for Pickup, Stabilization, and Transport of Casualties in a Mw 8.95 Scenario
5.5. Methodology Implementation
5.6. Casualty Pickup, Stabilization, and Transport Schedule (CPST Schedule)
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A. Methodology implementation. Casualty Pickup, Stabilization, and Transport Schedule
| Vehicle ID Code | Casualty ID Code | Node ID (li) | Age Range | LSI | Trip (v) | TFk | TBk | TSk | TLk | MCC Assigned | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A1 | V1 | 44030 | 0–14 | 3 | 93.3 | 5.105 | 1 | 7:41:00 | 8:09:28 | 9:42:46 | 10:10:14 | MCC1 |
| V17 | 36020 | 15–59 | 2 | 29.9 | 0.895 | 2 | 7:41:00 | 10:32:51 | 11:02:45 | 11:20:58 | MCC2 | |
| V21 | 38080 | 0–14 | 2 | 42 | 0.895 | 3 | 7:41:00 | 11:38:37 | 12:20:37 | 12:38:16 | MCC2 | |
| V26 | 41050 | 0–14 | 2 | 42 | 0.895 | 4 | 7:41:00 | 12:56:18 | 13:38:18 | 14:09:47 | MCC3 | |
| V45 | 43020 | 15–59 | 1 | 15.04 | 0.372 | 5 | 7:41:00 | 14:38:55 | 14:53:57 | 15:08:53 | MCC2 | |
| V50 | 37040 | 15–59 | 1 | 15.04 | 0.372 | 6 | 7:41:00 | 15:16:26 | 15:31:28 | 15:39:00 | MCC2 | |
| V54 | 10190 | 0–14 | 1 | 14.98 | 0.372 | 7 | 7:41:00 | 15:53:56 | 16:08:55 | 16:23:50 | MCC2 | |
| V64 | 11200 | 15–59 | 1 | 15.04 | 0.372 | 8 | 7:41:00 | 16:27:30 | 16:42:32 | 16:46:11 | MCC2 | |
| V62 | 29080 | 0–14 | 1 | 14.98 | 0.372 | 9 | 7:41:00 | 17:02:28 | 17:17:27 | 17:43:12 | MCC1 | |
| A2 | V5 | 42030 | 15–59 | 3 | 62.14 | 5.105 | 1 | 7:41:00 | 8:06:05 | 9:08:13 | 9:32:17 | MCC1 |
| V11 | 38060 | 15–59 | 2 | 29.9 | 0.895 | 2 | 7:41:00 | 9:57:12 | 10:27:06 | 10:52:00 | MCC1 | |
| V25 | 36020 | 15–59 | 2 | 29.9 | 0.895 | 3 | 7:41:00 | 11:15:18 | 11:45:12 | 12:08:30 | MCC1 | |
| V30 | 44030 | 15–59 | 2 | 29.9 | 0.895 | 4 | 7:41:00 | 12:32:31 | 13:02:25 | 13:26:26 | MCC1 | |
| V34 | 39060 | 15–59 | 1 | 15.04 | 0.372 | 5 | 7:41:00 | 13:51:14 | 14:06:16 | 14:23:11 | MCC2 | |
| V42 | 42050 | 0–14 | 1 | 14.98 | 0.372 | 6 | 7:41:00 | 14:25:53 | 14:40:52 | 14:43:34 | MCC2 | |
| V46 | 42050 | 15–59 | 1 | 15.04 | 0.372 | 7 | 7:41:00 | 14:58:30 | 15:13:32 | 15:42:41 | MCC3 | |
| V60 | 37040 | 15–59 | 1 | 15.04 | 0.372 | 8 | 7:41:00 | 16:16:36 | 16:31:38 | 17:05:33 | MCC3 | |
| A3 | V2 | 36020 | ≥60 | 3 | 65 | 5.105 | 1 | 7:41:00 | 8:04:18 | 9:09:18 | 9:31:36 | MCC1 |
| V14 | 43030 | ≥60 | 2 | 27.6 | 0.895 | 2 | 7:41:00 | 9:53:17 | 10:20:53 | 10:42:34 | MCC1 | |
| V18 | 36020 | 15–59 | 2 | 29.9 | 0.895 | 3 | 7:41:00 | 11:07:28 | 11:37:22 | 12:02:17 | MCC1 | |
| V29 | 44030 | 15–59 | 2 | 29.9 | 0.895 | 4 | 7:41:00 | 12:11:02 | 12:40:56 | 12:53:28 | MCC3 | |
| V33 | 39060 | ≥60 | 1 | 9.3 | 0.372 | 5 | 7:41:00 | 13:25:43 | 13:35:01 | 14:07:16 | MCC3 | |
| V44 | 44020 | 15–59 | 1 | 15.04 | 0.372 | 6 | 7:41:00 | 14:39:39 | 14:54:41 | 15:15:10 | MCC2 | |
| V51 | 42030 | 15–59 | 1 | 15.04 | 0.372 | 7 | 7:41:00 | 15:34:31 | 15:49:33 | 16:08:54 | MCC2 | |
| V59 | 42050 | 15–59 | 1 | 15.04 | 0.372 | 8 | 7:41:00 | 16:27:19 | 16:42:21 | 17:00:45 | MCC2 | |
| A4 | V9 | 42060 | 15–59 | 2 | 29.9 | 0.895 | 1 | 7:41:00 | 8:12:05 | 8:41:59 | 9:00:12 | MCC2 |
| V8 | 42010 | 0–14 | 2 | 42 | 0.895 | 2 | 7:41:00 | 9:18:24 | 10:00:24 | 10:23:02 | MCC1 | |
| V20 | 59088 | 15–59 | 2 | 29.9 | 0.895 | 3 | 7:41:00 | 10:44:43 | 11:14:37 | 11:36:18 | MCC1 | |
| V24 | 41030 | 15–59 | 2 | 29.9 | 0.895 | 4 | 7:41:00 | 12:02:46 | 12:32:40 | 12:54:42 | MCC2 | |
| V32 | 41010 | ≥60 | 2 | 27.6 | 0.895 | 5 | 7:41:00 | 13:12:21 | 13:39:57 | 13:57:36 | MCC2 | |
| V37 | 37040 | 15–59 | 1 | 15.04 | 0.372 | 6 | 7:41:00 | 14:23:42 | 14:38:44 | 15:09:15 | MCC1 | |
| V49 | 42050 | 15–59 | 1 | 15.04 | 0.372 | 7 | 7:41:00 | 15:18:51 | 15:33:53 | 15:43:29 | MCC1 | |
| V56 | 42050 | 15–59 | 1 | 15.04 | 0.372 | 8 | 7:41:00 | 16:14:00 | 16:29:02 | 16:59:33 | MCC1 | |
| H1 | V3 | 39060 | 15–59 | 3 | 62.14 | 5.105 | 1 | 7:41:00 | 7:50:02 | 8:52:10 | 8:57:51 | MCC1 |
| V10 | 42050 | 15–59 | 2 | 29.9 | 0.895 | 2 | 7:41:00 | 9:04:34 | 9:34:28 | 9:40:33 | MCC2 | |
| V15 | 36030 | 15–59 | 2 | 29.9 | 0.895 | 3 | 7:41:00 | 9:45:10 | 10:15:04 | 11:10:36 | MCC2 | |
| V13 | 4030 | 0–14 | 2 | 42 | 0.895 | 3 | 7:41:00 | 10:21:24 | 11:03:24 | 11:10:36 | MCC2 | |
| V16 | 41030 | 15–59 | 2 | 29.9 | 0.895 | 4 | 7:41:00 | 11:15:13 | 11:45:07 | 11:50:51 | MCC3 | |
| V23 | 41020 | 15–59 | 2 | 29.9 | 0.895 | 5 | 7:41:00 | 11:56:51 | 12:26:45 | 12:31:38 | MCC2 | |
| V28 | 36020 | 15–59 | 2 | 29.9 | 0.895 | 6 | 7:41:00 | 12:36:40 | 13:06:34 | 13:11:35 | MCC2 | |
| V31 | 36030 | 15–59 | 2 | 29.9 | 0.895 | 7 | 7:41:00 | 13:16:28 | 13:46:22 | 13:51:15 | MCC2 | |
| V38 | 36020 | 15–59 | 1 | 15.04 | 0.372 | 8 | 7:41:00 | 13:58:27 | 14:13:29 | 14:43:07 | MCC2 | |
| V39 | 36020 | 15–59 | 1 | 15.04 | 0.372 | 8 | 7:41:00 | 14:20:54 | 14:35:56 | 14:43:07 | MCC2 | |
| V43 | 59061 | 0–14 | 1 | 14.98 | 0.372 | 9 | 7:41:00 | 14:50:19 | 15:05:18 | 15:12:29 | MCC2 | |
| V47 | 43030 | 0–14 | 1 | 14.98 | 0.372 | 10 | 7:41:00 | 15:17:24 | 15:32:23 | 15:37:18 | MCC2 | |
| V55 | 42050 | ≥60 | 1 | 9.3 | 0.372 | 11 | 7:41:00 | 15:42:12 | 15:51:30 | 16:22:23 | MCC2 | |
| V52 | 40030 | 15–59 | 1 | 15.04 | 0.372 | 11 | 7:41:00 | 16:00:10 | 16:15:12 | 16:22:23 | MCC2 | |
| V57 | 42050 | 15–59 | 1 | 15.04 | 0.372 | 12 | 7:41:00 | 16:29:35 | 16:44:37 | 16:52:27 | MCC1 | |
| V61 | 37040 | 15–59 | 1 | 15.04 | 0.372 | 13 | 7:41:00 | 16:58:32 | 17:13:34 | 17:20:09 | MCC3 | |
| H2 | V4 | 36020 | 15–59 | 3 | 62.14 | 5.105 | 1 | 7:41:00 | 7:50:02 | 8:52:10 | 8:57:51 | MCC1 |
| V6 | 42060 | 15–59 | 2 | 29.9 | 0.895 | 2 | 7:41:00 | 9:02:18 | 9:32:12 | 10:20:48 | MCC3 | |
| V7 | 41040 | 0–14 | 2 | 42 | 0.895 | 2 | 7:41:00 | 9:33:56 | 10:15:56 | 10:20:48 | MCC3 | |
| V12 | 42010 | 15–59 | 2 | 29.9 | 0.895 | 3 | 7:41:00 | 10:26:20 | 10:56:14 | 11:01:46 | MCC3 | |
| V19 | 36030 | 15–59 | 2 | 29.9 | 0.895 | 4 | 7:41:00 | 11:08:03 | 11:37:57 | 11:44:15 | MCC3 | |
| V22 | 41040 | 0–14 | 2 | 42 | 0.895 | 5 | 7:41:00 | 11:53:00 | 12:35:00 | 12:43:21 | MCC1 | |
| V27 | 41050 | 15–59 | 2 | 29.9 | 0.895 | 6 | 7:41:00 | 12:51:11 | 13:21:05 | 13:28:55 | MCC1 | |
| V35 | 37080 | 15–59 | 1 | 15.04 | 0.372 | 7 | 7:41:00 | 13:35:00 | 13:50:02 | 13:56:07 | MCC1 | |
| V36 | 37070 | 0–14 | 1 | 14.98 | 0.372 | 8 | 7:41:00 | 14:00:34 | 14:15:33 | 14:44:29 | MCC2 | |
| V40 | 41060 | 15–59 | 1 | 15.04 | 0.372 | 8 | 7:41:00 | 14:22:15 | 14:37:17 | 14:44:29 | MCC2 | |
| V41 | 42030 | 15–59 | 1 | 15.04 | 0.372 | 9 | 7:41:00 | 14:51:51 | 15:06:53 | 15:15:17 | MCC3 | |
| V48 | 42050 | 15–59 | 1 | 15.04 | 0.372 | 10 | 7:41:00 | 15:24:03 | 15:39:05 | 15:47:52 | MCC3 | |
| V53 | 10070 | 15–59 | 1 | 15.04 | 0.372 | 11 | 7:41:00 | 15:53:54 | 16:08:56 | 16:14:32 | MCC1 | |
| V58 | 42050 | 15–59 | 1 | 15.04 | 0.372 | 12 | 7:41:00 | 16:19:48 | 16:34:50 | 16:40:06 | MCC1 | |
| V63 | 28060 | 15–59 | 1 | 15.04 | 0.372 | 13 | 7:41:00 | 16:45:35 | 17:00:37 | 17:06:06 | MCC1 |
| Period | Vehicle ID Code | Casualty ID Code | Node ID (li) | Age Range | LSI | Trip (v) | αk | TFk | TBk | TSk | TLk | MCC ASSIGNED | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | A1 | V1 | 44030 | 0–14 | 3 | 93.30 | 5.10 | 1 | 0 | 7:41 | 8:09 | 9:42 | 10:10 | MCC1 |
| A2 | V2 | 36020 | 60+ | 3 | 65.00 | 5.10 | 1 | 0 | 7:41 | 8:04 | 9:09 | 9:31 | MCC1 | |
| A3 | V5 | 42030 | 15–59 | 3 | 62.14 | 5.10 | 1 | 0 | 7:41 | 8:06 | 9:08 | 9:32 | MCC1 | |
| H1 | V3 | 39060 | 15–59 | 3 | 62.14 | 5.10 | 1 | 0 | 7:41 | 7:50 | 8:52 | 8:57 | MCC1 | |
| H2 | V4 | 36020 | 15–59 | 3 | 62.14 | 5.10 | 1 | 0 | 7:41 | 7:50 | 8:52 | 8:57 | MCC1 | |
| A4 | V9 | 42060 | 15–59 | 2 | 29.90 | 0.90 | 1 | 0 | 7:41 | 8:12 | 8:41 | 9:00 | MCC2 | |
| A4 | V8 | 42010 | 0–14 | 2 | 42.00 | 0.90 | 2 | 0 | 7:41 | 9:18 | 10:00 | 10:18 | MCC2 | |
| H1 | V10 | 42050 | 15–59 | 2 | 29.90 | 0.90 | 2 | 0 | 7:41 | 9:04 | 9:34 | 9:40 | MCC2 | |
| H2 | V6 | 42060 | 15–59 | 2 | 29.90 | 0.90 | 2 | 0 | 7:41 | 9:02 | 9:32 | 10:19 | MCC2 | |
| H2 | V7 | 41040 | 0–14 | 2 | 42.00 | 0.90 | 2 | 0 | 7:41 | 9:33 | 10:15 | 10:19 | MCC2 | |
| 2 | H1 | V66 | 40050 | 15–59 | 3 | 62.14 | 5.10 | 3 | 0 | 9:26 | 9:44 | 10:46 | 10:51 | MCC1 |
| A5 | V65 | 40050 | 15–59 | 3 | 62.14 | 5.10 | 1 | 0 | 9:26 | 9:41 | 10:44 | 11:05 | MCC1 | |
| A2 | V11 | 38060 | 15–59 | 2 | 29.90 | 1.35 | 2 | 105 | 7:41 | 9:56 | 10:26 | 10:30 | MCC5 | |
| A3 | V14 | 43030 | ≥ 60 | 2 | 27.60 | 1,35 | 2 | 105 | 7:41 | 9:53 | 10:21 | 10:31 | MCC4 | |
| H2 | V12 | 42010 | 15–59 | 2 | 29.90 | 1.35 | 3 | 105 | 7:41 | 10:23 | 10:53 | 10:56 | MCC5 | |
| A2 | V17 | 36020 | 15–59 | 2 | 29.90 | 1.35 | 3 | 105 | 7:41 | 10:31 | 11:01 | 11:03 | MCC5 | |
| A3 | V20 | 59088 | 15–59 | 2 | 29.90 | 1.35 | 3 | 105 | 7:41 | 10:41 | 11:11 | 11:17 | MCC5 | |
| A1 | V15 | 36030 | 15–59 | 2 | 29.90 | 1.35 | 2 | 105 | 7:41 | 10:40 | 11:10 | 11:20 | MCC5 | |
| H1 | V16 | 41030 | 15–59 | 2 | 29.90 | 1.35 | 4 | 105 | 7:41 | 10:57 | 11:26 | 11:30 | MCC5 | |
| H2 | V19 | 36030 | 15–59 | 2 | 29.90 | 1.35 | 4 | 105 | 7:41 | 11:00 | 11:30 | 11:34 | MCC5 | |
| A4 | V13 | 4030 | 0–14 | 2 | 42.00 | 1.35 | 3 | 105 | 7:41 | 10:44 | 11:26 | 11:37 | MCC5 | |
| A2 | V24 | 41030 | 15–59 | 2 | 29.90 | 1.35 | 4 | 105 | 7:41 | 11:08 | 11:38 | 11:43 | MCC5 | |
| A3 | V25 | 36020 | 15–59 | 2 | 29.90 | 1.35 | 4 | 105 | 7:41 | 11:19 | 11:49 | 11:51 | MCC5 | |
| A5 | V18 | 36020 | 15–59 | 2 | 29.90 | 1.35 | 2 | 105 | 7:41 | 11:30 | 12:00 | 12:04 | MCC5 | |
| A1 | V21 | 38080 | 0–14 | 2 | 42.00 | 1.35 | 3 | 105 | 7:41 | 11:22 | 12:04 | 12:06 | MCC5 | |
| A4 | V30 | 44030 | 15–59 | 2 | 29.90 | 1.35 | 4 | 105 | 7:41 | 11:39 | 12:09 | 12:12 | MCC5 | |
| H2 | V27 | 41050 | 15–59 | 2 | 29.90 | 1.35 | 5 | 105 | 7:41 | 11:40 | 12:10 | 12:16 | MCC5 | |
| H1 | V22 | 41040 | 0–14 | 2 | 42.00 | 1.35 | 5 | 105 | 7:41 | 11:36 | 12:18 | 12:25 | MCC5 | |
| A2 | V26 | 41050 | 0–14 | 2 | 42.00 | 1.35 | 5 | 105 | 7:41 | 11:46 | 12:28 | 12:30 | MCC5 | |
| 3 | A6 | V109 | 45010 | 15–59 | 3 | 62.14 | 5.10 | 1 | 0 | 11:46 | 11:52 | 12:54 | 13:11 | MCC1 |
| H3 | V28 | 36020 | 15–59 | 2 | 29.90 | 2.68 | 1 | 245 | 7:41 | 11:55 | 12:24 | 12:28 | MCC5 | |
| A3 | V31 | 36030 | 15–59 | 2 | 29.90 | 2.68 | 5 | 245 | 7:41 | 11:55 | 12:25 | 12:29 | MCC5 | |
| A7 | V29 | 44030 | 15–59 | 2 | 29.90 | 2.68 | 1 | 245 | 7:41 | 11:57 | 12:27 | 12:31 | MCC6 | |
| A1 | V32 | 41010 | ≥60 | 2 | 27.60 | 2.68 | 4 | 245 | 7:41 | 12:07 | 12:34 | 12:35 | MCC5 | |
| A5 | V23 | 41020 | 15–59 | 2 | 29.90 | 2.68 | 3 | 245 | 7:41 | 12:08 | 12:38 | 12:42 | MCC5 | |
| A4 | V67 | 36020 | 15–59 | 2 | 29.90 | 1.59 | 5 | 140 | 9:26 | 12:18 | 12:48 | 12:54 | MCC5 | |
| H1 | V69 | 4050 | 15–59 | 2 | 29.90 | 1.59 | 6 | 140 | 9:26 | 12:28 | 12:58 | 13:02 | MCC4 | |
| H2 | V68 | 36020 | 0–14 | 2 | 42.00 | 1.59 | 6 | 140 | 9:26 | 12:21 | 13:03 | 13:10 | MCC4 | |
| A2 | V72 | 28060 | 15–59 | 2 | 29.90 | 1.59 | 6 | 140 | 9:26 | 12:34 | 13:04 | 13:16 | MCC4 | |
| H3 | V70 | 4050 | 15–59 | 2 | 29.90 | 1.59 | 2 | 140 | 9:26 | 12:37 | 13:07 | 13:17 | MCC4 | |
| A3 | V71 | 42050 | 0–14 | 2 | 42.00 | 1.59 | 6 | 140 | 9:26 | 12:32 | 13:14 | 13:22 | MCC4 | |
| A1 | V73 | 59049 | 15–59 | 2 | 29.90 | 1.59 | 5 | 140 | 9:26 | 12:42 | 13:12 | 13:25 | MCC4 | |
| A7 | V75 | 42060 | 15–59 | 2 | 29.90 | 1.59 | 2 | 140 | 9:26 | 12:51 | 13:21 | 13:34 | MCC4 | |
| A5 | V74 | 59048 | 15–59 | 2 | 29.90 | 1.59 | 4 | 140 | 9:26 | 12:54 | 13:23 | 13:40 | MCC4 | |
| H1 | V76 | 41040 | 15–59 | 2 | 29.90 | 1.59 | 7 | 140 | 9:26 | 13:09 | 13:39 | 13:46 | MCC4 | |
| H2 | V77 | 41040 | 15–59 | 2 | 29.90 | 1.59 | 7 | 140 | 9:26 | 13:14 | 13:44 | 13:48 | MCC4 | |
| A4 | V79 | 36010 | 0–14 | 2 | 42.00 | 1.59 | 6 | 140 | 9:26 | 12:57 | 13:39 | 13:49 | MCC4 | |
| A6 | V81 | 41050 | 15–59 | 2 | 29.90 | 1.59 | 2 | 140 | 9:26 | 13:16 | 13:46 | 13:51 | MCC6 | |
| H3 | V80 | 36010 | 15–59 | 2 | 29.90 | 1.59 | 3 | 140 | 9:26 | 13:23 | 13:53 | 13:58 | MCC4 | |
| A1 | V83 | 24100 | 15–59 | 2 | 29.90 | 1.59 | 6 | 140 | 9:26 | 13:33 | 14:03 | 14:10 | MCC4 | |
| A3 | V82 | 18030 | 15–59 | 2 | 29.90 | 1.59 | 7 | 140 | 9:26 | 13:32 | 14:02 | 14:11 | MCC4 | |
| A2 | V78 | 41040 | 0–14 | 2 | 42.00 | 1.59 | 7 | 140 | 9:26 | 13:24 | 14:06 | 14:13 | MCC4 | |
| 4 | H1 | V151 | 42050 | 0–14 | 3 | 93.30 | 5.10 | 8 | 0 | 13:26 | 13:49 | 15:22 | 15:28 | MCC1 |
| A7 | V150 | 36020 | 0–14 | 3 | 93.30 | 5.10 | 3 | 0 | 13:26 | 13:41 | 15:14 | 15:31 | MCC1 | |
| A5 | V85 | 23080 | 15–59 | 2 | 29.90 | 2.61 | 5 | 240 | 9:26 | 13:47 | 14:17 | 14:25 | MCC4 | |
| A6 | V86 | 40040 | 15–59 | 2 | 29.90 | 2.61 | 3 | 240 | 9:26 | 13:54 | 14:24 | 14:28 | MCC6 | |
| H2 | V84 | 24040 | 15–59 | 2 | 29.90 | 2.61 | 8 | 240 | 9:26 | 13:53 | 14:23 | 14:28 | MCC4 | |
| A4 | V87 | 59047 | 15–59 | 2 | 29.90 | 2.61 | 7 | 240 | 9:26 | 13:56 | 14:26 | 14:37 | MCC2 | |
| H3 | V88 | 36020 | 15–59 | 2 | 29.90 | 2.61 | 4 | 240 | 9:26 | 14:03 | 14:33 | 14:39 | MCC2 | |
| A2 | V111 | 42060 | 15–59 | 2 | 29.90 | 1.32 | 8 | 100 | 11:46 | 14:24 | 14:54 | 15:04 | MCC4 | |
| A1 | V110 | 42030 | 15–59 | 2 | 29.90 | 1.32 | 7 | 100 | 11:46 | 14:20 | 14:50 | 15:05 | MCC2 | |
| H2 | V117 | 42050 | 15–59 | 2 | 29.90 | 1.32 | 9 | 100 | 11:46 | 14:32 | 15:02 | 15:07 | MCC2 | |
| A5 | V113 | 41030 | ≥60 | 2 | 27.60 | 1.32 | 6 | 100 | 11:46 | 14:33 | 15:00 | 15:11 | MCC2 | |
| A3 | V112 | 42060 | 0–14 | 2 | 42.00 | 1.32 | 8 | 100 | 11:46 | 14:20 | 15:02 | 15:15 | MCC2 | |
| A4 | V115 | 42050 | 15–59 | 2 | 29.90 | 1.32 | 8 | 100 | 11:46 | 14:48 | 15:18 | 15:28 | MCC2 | |
| H3 | V116 | 42050 | 0–14 | 2 | 42.00 | 1.32 | 5 | 100 | 11:46 | 14:44 | 15:26 | 15:30 | MCC2 | |
| A6 | V114 | 41030 | 15–59 | 2 | 29.90 | 1.32 | 4 | 100 | 11:46 | 14:47 | 15:17 | 15:33 | MCC2 | |
| H2 | V118 | 42020 | 15–59 | 2 | 29.90 | 1.32 | 10 | 100 | 11:46 | 15:12 | 15:42 | 15:47 | MCC2 | |
| A2 | V121 | 44020 | 15–59 | 2 | 29.90 | 1.32 | 9 | 100 | 11:46 | 15:12 | 15:42 | 15:53 | MCC2 | |
| A1 | V119 | 42020 | 15–59 | 2 | 29.90 | 1.32 | 8 | 100 | 11:46 | 15:18 | 15:48 | 16:01 | MCC2 | |
| A3 | V120 | 41030 | 15–59 | 2 | 29.90 | 1.32 | 9 | 100 | 11:46 | 15:26 | 15:56 | 16:06 | MCC2 | |
| H1 | V124 | 36020 | 15–59 | 2 | 29.90 | 1.32 | 9 | 100 | 11:46 | 15:36 | 16:05 | 16:13 | MCC1 | |
| H3 | V127 | 36010 | 15–59 | 2 | 29.90 | 1.32 | 6 | 100 | 11:46 | 15:37 | 16:07 | 16:15 | MCC1 | |
| A5 | V122 | 44020 | 0–14 | 2 | 42.00 | 1.32 | 7 | 100 | 11:46 | 15:25 | 16:07 | 16:21 | MCC2 | |
| A6 | V126 | 42010 | 15–59 | 2 | 29.90 | 1.32 | 5 | 100 | 11:46 | 15:42 | 16:12 | 16:21 | MCC2 | |
| A4 | V125 | 42010 | 15–59 | 2 | 29.90 | 1.32 | 9 | 100 | 11:46 | 15:41 | 16:11 | 16:25 | MCC2 | |
| A7 | V123 | 36020 | 15–59 | 2 | 29.90 | 1.32 | 4 | 100 | 11:46 | 15:45 | 16:15 | 16:30 | MCC1 | |
| 5 | H2 | V181 | 41070 | 15–59 | 3 | 62.14 | 5.10 | 11 | 0 | 15:36 | 15:51 | 16:54 | 17:00 | MCC1 |
| A2 | V152 | 42050 | 15–59 | 2 | 29.90 | 1.51 | 10 | 130 | 13:26 | 16:01 | 16:31 | 16:41 | MCC1 | |
| A1 | V153 | 36030 | 15–59 | 2 | 29.90 | 1.51 | 9 | 130 | 13:26 | 16:11 | 16:41 | 16:52 | MCC1 | |
| H1 | V155 | 36020 | 15–59 | 2 | 29.90 | 1.51 | 10 | 130 | 13:26 | 16:18 | 16:48 | 16:54 | MCC1 | |
| H3 | V160 | 42050 | 15–59 | 2 | 29.90 | 1.51 | 7 | 130 | 13:26 | 16:20 | 16:50 | 16:56 | MCC1 | |
| A3 | V154 | 37050 | 0–14 | 2 | 42.00 | 1.51 | 10 | 130 | 13:26 | 16:14 | 16:56 | 17:06 | MCC1 | |
| A6 | V157 | 28040 | 15–59 | 2 | 29.90 | 1.51 | 6 | 130 | 13:26 | 16:29 | 16:59 | 17:09 | MCC1 | |
| A4 | V156 | 42050 | ≥60 | 2 | 27.60 | 1.51 | 10 | 130 | 13:26 | 16:32 | 17:00 | 17:12 | MCC1 | |
| A5 | V158 | 42050 | 0–14 | 2 | 42.00 | 1.51 | 8 | 130 | 13:26 | 16:29 | 17:11 | 17:21 | MCC1 | |
| A7 | V159 | 40040 | 15–59 | 2 | 29.90 | 1.51 | 5 | 130 | 13:26 | 16:43 | 17:13 | 17:26 | MCC1 | |
| A2 | V165 | 42010 | 15–59 | 2 | 29.90 | 1.51 | 11 | 130 | 13:26 | 16:52 | 17:21 | 17:32 | MCC1 | |
| H1 | V162 | 42050 | 15–59 | 2 | 29.90 | 1.51 | 11 | 130 | 13:26 | 17:00 | 17:30 | 17:36 | MCC1 | |
| H3 | V164 | 42050 | 15–59 | 2 | 29.90 | 1.51 | 8 | 130 | 13:26 | 17:02 | 17:32 | 17:38 | MCC1 | |
| H2 | V161 | 42050 | 15–59 | 2 | 29.90 | 1.51 | 12 | 130 | 13:26 | 17:05 | 17:35 | 17:41 | MCC1 | |
| A1 | V163 | 37050 | 0–14 | 2 | 42.00 | 1.51 | 10 | 130 | 13:26 | 17:02 | 17:44 | 17:55 | MCC1 | |
| A3 | V166 | 42010 | 15–59 | 2 | 29.90 | 1.51 | 11 | 130 | 13:26 | 17:16 | 17:46 | 17:56 | MCC1 | |
| A6 | V183 | 42050 | 15–59 | 2 | 29.90 | 0.90 | 7 | 0 | 15:36 | 17:22 | 17:52 | 18:05 | MCC1 | |
| A4 | V184 | 42060 | 15–59 | 2 | 29.90 | 0.90 | 11 | 0 | 15:36 | 17:24 | 17:54 | 18:07 | MCC1 | |
| A5 | V182 | 42030 | 15–59 | 2 | 29.90 | 0.90 | 9 | 0 | 15:36 | 17:33 | 18:02 | 18:14 | MCC1 | |
| H3 | V189 | 36010 | 15–59 | 2 | 29.90 | 0.90 | 9 | 0 | 15:36 | 17:43 | 18:13 | 18:18 | MCC1 | |
| H1 | V187 | 36010 | 15–59 | 2 | 29.90 | 0.90 | 12 | 0 | 15:36 | 17:43 | 18:13 | 18:20 | MCC1 | |
| A2 | V188 | 41050 | 15–59 | 2 | 29.90 | 0.90 | 12 | 0 | 15:36 | 17:43 | 18:13 | 18:24 | MCC1 | |
| A7 | V185 | 42030 | 0–14 | 2 | 42.00 | 0.90 | 6 | 0 | 15:36 | 17:37 | 18:19 | 18:31 | MCC1 | |
| H2 | V190 | 41070 | 0–14 | 2 | 42.00 | 0.90 | 13 | 0 | 15:36 | 17:47 | 18:29 | 18:34 | MCC1 | |
| A1 | V186 | 36020 | 15–59 | 2 | 29.90 | 0.90 | 11 | 0 | 15:36 | 18:08 | 18:38 | 18:51 | MCC1 | |
| A6 | V192 | 42050 | 15–59 | 2 | 29.90 | 0.90 | 9 | 0 | 15:36 | 18:16 | 18:46 | 18:58 | MCC1 | |
| A3 | V191 | 42030 | 0–14 | 2 | 42.00 | 0.90 | 13 | 0 | 15:36 | 18:09 | 18:51 | 19:03 | MCC1 | |
| A4 | V35 | 37080 | 15–59 | 1 | 15.04 | 0.50 | 12 | 475 | 7:41 | 18:17 | 18:32 | 18:33 | MCC5 | |
| A5 | V34 | 39060 | 15–59 | 1 | 15.04 | 0.50 | 10 | 475 | 7:41 | 18:25 | 18:40 | 18:41 | MCC5 | |
| 6 | H3 | V193 | 42060 | 15–59 | 2 | 29.90 | 1.74 | 11 | 160 | 15:36 | 18:23 | 18:53 | 18:58 | MCC6 |
| H1 | V200 | 42010 | 15–59 | 2 | 29.90 | 0.90 | 14 | 0 | 18:16 | 18:25 | 18:55 | 19:00 | MCC6 | |
| A2 | V198 | 42060 | 15–59 | 2 | 29.90 | 0.90 | 15 | 0 | 18:16 | 18:34 | 19:03 | 19:13 | MCC1 | |
| A4 | V199 | 42060 | 15–59 | 2 | 29.90 | 0.90 | 14 | 0 | 18:16 | 18:34 | 19:03 | 19:14 | MCC6 | |
| A7 | V202 | 37080 | 15–59 | 2 | 29.90 | 0.90 | 9 | 0 | 18:16 | 18:40 | 19:10 | 19:20 | MCC6 | |
| H2 | V201 | 36010 | 0–14 | 2 | 42.00 | 0.90 | 16 | 0 | 18:16 | 18:39 | 19:21 | 19:26 | MCC6 | |
| A5 | V203 | 16020 | 15–59 | 2 | 29.90 | 0.90 | 14 | 0 | 18:16 | 18:53 | 19:23 | 19:33 | MCC6 | |
| H3 | V204 | 42050 | 15–59 | 2 | 29.90 | 0.90 | 14 | 0 | 18:16 | 19:06 | 19:36 | 19:44 | MCC6 | |
| A5 | V33 | 39060 | ≥60 | 1 | 9.30 | 0.55 | 11 | 635 | 7:41 | 18:42 | 18:51 | 18:52 | MCC5 | |
| A1 | V42 | 42050 | 0–14 | 1 | 14.98 | 0.55 | 13 | 635 | 7:41 | 18:56 | 19:11 | 19:12 | MCC2 | |
| H1 | V36 | 37070 | 0–14 | 1 | 14.98 | 0.55 | 16 | 635 | 7:41 | 19:05 | 19:20 | 19:23 | MCC5 | |
| A6 | V39 | 36020 | 15–59 | 1 | 15.04 | 0.55 | 11 | 635 | 7:41 | 19:11 | 19:26 | 19:30 | MCC5 | |
| A1 | V45 | 43020 | 15–59 | 1 | 15.04 | 0.55 | 15 | 635 | 7:41 | 19:18 | 19:33 | 19:36 | MCC5 | |
| A3 | V37 | 37040 | 15–59 | 1 | 15.04 | 0.55 | 15 | 635 | 7:41 | 19:17 | 19:32 | 19:36 | MCC5 | |
| A4 | V44 | 44020 | 15–59 | 1 | 15.04 | 0.55 | 16 | 635 | 7:41 | 19:25 | 19:40 | 19:42 | MCC5 | |
| A2 | V38 | 36020 | 15–59 | 1 | 15.04 | 0.55 | 17 | 635 | 7:41 | 19:26 | 19:41 | 19:45 | MCC5 | |
| A7 | V47 | 43030 | 0–14 | 1 | 14.98 | 0.55 | 11 | 635 | 7:41 | 19:30 | 19:45 | 19:47 | MCC5 | |
| A6 | V41 | 42030 | 15–59 | 1 | 15.04 | 0.55 | 13 | 635 | 7:41 | 19:32 | 19:47 | 19:49 | MCC5 | |
| H1 | V40 | 41060 | 15–59 | 1 | 15.04 | 0.55 | 18 | 635 | 7:41 | 19:29 | 19:44 | 19:50 | MCC5 | |
| A5 | V49 | 42050 | 15–59 | 1 | 15.04 | 0.55 | 16 | 635 | 7:41 | 19:36 | 19:51 | 19:53 | MCC3 | |
| H2 | V43 | 59061 | 0–14 | 1 | 14.98 | 0.55 | 18 | 635 | 7:41 | 19:34 | 19:49 | 19:55 | MCC5 | |
| 7 | A3 | V211 | 41030 | ≥60 | 2 | 27.60 | 0.90 | 12 | 0 | 9:36 | 18:20 | 18:47 | 18:58 | MCC6 |
| A1 | V210 | 41030 | 15–59 | 2 | 29.90 | 0.90 | 12 | 0 | 9:36 | 18:19 | 18:49 | 19:00 | MCC6 | |
| A4 | V212 | 41030 | 15–59 | 2 | 29.90 | 0.90 | 13 | 0 | 9:36 | 18:26 | 18:56 | 19:06 | MCC6 | |
| A8 | V50 | 37040 | 15–59 | 1 | 15.04 | 0.58 | 1 | 715 | 7:41 | 18:18 | 18:33 | 18:35 | MCC1 | |
| H3 | V55 | 42050 | ≥60 | 1 | 9.30 | 0.58 | 10 | 715 | 7:41 | 18:29 | 18:39 | 18:43 | MCC5 | |
| A2 | V46 | 42050 | 15–59 | 1 | 15.04 | 0.58 | 13 | 715 | 7:41 | 18:27 | 18:42 | 18:44 | MCC5 | |
| A7 | V51 | 42030 | 15–59 | 1 | 15.04 | 0.58 | 7 | 715 | 7:41 | 18:29 | 18:44 | 18:46 | MCC5 | |
| A6 | V52 | 40030 | 15–59 | 1 | 15.04 | 0.58 | 8 | 715 | 7:41 | 18:32 | 18:47 | 18:51 | MCC5 | |
| H1 | V48 | 42050 | 15–59 | 1 | 15.04 | 0.58 | 13 | 715 | 7:41 | 18:36 | 18:51 | 18:57 | MCC5 | |
| H2 | V53 | 10070 | 15–59 | 1 | 15.04 | 0.58 | 14 | 715 | 7:41 | 18:39 | 18:54 | 18:57 | MCC5 | |
| A8 | V64 | 11200 | 15–59 | 1 | 15.04 | 0.58 | 2 | 715 | 7:41 | 18:38 | 18:53 | 18:59 | MCC6 | |
| A5 | V54 | 10190 | 0–14 | 1 | 14.98 | 0.58 | 12 | 715 | 7:41 | 18:42 | 18:57 | 18:59 | MCC5 | |
| H3 | V58 | 42050 | 15–59 | 1 | 15.04 | 0.58 | 12 | 715 | 7:41 | 18:46 | 19:01 | 19:05 | MCC5 | |
| A2 | V57 | 42050 | 15–59 | 1 | 15.04 | 0.58 | 14 | 715 | 7:41 | 18:48 | 19:03 | 19:06 | MCC5 | |
| A7 | V56 | 42050 | 15–59 | 1 | 15.04 | 0.58 | 8 | 715 | 7:41 | 18:49 | 19:04 | 19:08 | MCC5 | |
| A6 | V61 | 37040 | 15–59 | 1 | 15.04 | 0.58 | 10 | 715 | 7:41 | 18:52 | 19:07 | 19:11 | MCC4 | |
| A5 | V62 | 29080 | 0–14 | 1 | 14.98 | 0.58 | 13 | 715 | 7:41 | 19:00 | 19:15 | 19:19 | MCC4 | |
| H1 | V63 | 28060 | 15–59 | 1 | 15.04 | 0.58 | 15 | 715 | 7:41 | 19:01 | 19:16 | 19:20 | MCC4 | |
| H2 | V60 | 37040 | 15–59 | 1 | 15.04 | 0.58 | 15 | 715 | 7:41 | 19:01 | 19:16 | 19:21 | MCC4 | |
| A3 | V59 | 42050 | 15–59 | 1 | 15.04 | 0.58 | 14 | 715 | 7:41 | 19:07 | 19:22 | 19:23 | MCC5 | |
| A4 | V96 | 24010 | 0–14 | 1 | 14.98 | 0.54 | 15 | 610 | 9:26 | 19:09 | 19:24 | 19:26 | MCC6 | |
| A2 | V89 | 42010 | 0–14 | 1 | 14.98 | 0.54 | 16 | 610 | 9:26 | 19:07 | 19:22 | 19:28 | MCC2 | |
| H3 | V90 | 42010 | 15–59 | 1 | 15.04 | 0.54 | 13 | 610 | 9:26 | 19:08 | 19:23 | 19:28 | MCC4 | |
| A8 | V93 | 42020 | 15–59 | 1 | 15.04 | 0.54 | 3 | 610 | 9:26 | 19:09 | 19:24 | 19:30 | MCC4 | |
| A1 | V91 | 45040 | 15–59 | 1 | 15.04 | 0.54 | 14 | 610 | 9:26 | 19:10 | 19:25 | 19:31 | MCC4 | |
| A7 | V92 | 42020 | 15–59 | 1 | 15.04 | 0.54 | 10 | 610 | 9:26 | 19:11 | 19:26 | 19:31 | MCC4 | |
| A5 | V97 | 42050 | 15–59 | 1 | 15.04 | 0.54 | 15 | 610 | 9:26 | 19:20 | 19:35 | 19:37 | MCC4 | |
| A6 | V94 | 39060 | 0–14 | 1 | 14.98 | 0.54 | 12 | 610 | 9:26 | 19:17 | 19:31 | 19:37 | MCC4 | |
| A3 | V98 | 42050 | 15–59 | 1 | 15.04 | 0.54 | 16 | 610 | 9:26 | 19:23 | 19:38 | 19:43 | MCC4 | |
| H2 | V101 | 41070 | 15–59 | 1 | 15.04 | 0.54 | 17 | 610 | 9:26 | 19:24 | 19:39 | 19:43 | MCC4 | |
| H1 | V95 | 39060 | 15–59 | 1 | 15.04 | 0.54 | 17 | 610 | 9:26 | 19:25 | 19:40 | 19:44 | MCC4 | |
| H3 | V102 | 9040 | 15–59 | 1 | 15.04 | 0.54 | 15 | 610 | 9:26 | 19:31 | 19:46 | 19:50 | MCC2 | |
| A8 | V103 | 9040 | 15–59 | 1 | 15.04 | 0.54 | 4 | 610 | 9:26 | 19:33 | 19:48 | 19:51 | MCC4 | |
| A7 | V108 | 36010 | 15–59 | 1 | 15.04 | 0.54 | 12 | 610 | 9:26 | 19:34 | 19:49 | 19:52 | MCC4 | |
| A1 | V106 | 36020 | 15–59 | 1 | 15.04 | 0.54 | 16 | 610 | 9:26 | 19:34 | 19:50 | 19:54 | MCC2 | |
| A4 | V100 | 36010 | 15–59 | 1 | 15.04 | 0.54 | 17 | 610 | 9:26 | 19:37 | 19:52 | 19:59 | MCC4 | |
| A2 | V99 | 36020 | 0–14 | 1 | 14.98 | 0.54 | 18 | 610 | 9:26 | 19:36 | 19:51 | 20:00 | MCC2 | |
| A6 | V105 | 4230 | 15–59 | 1 | 15.04 | 0.54 | 14 | 610 | 9:26 | 19:40 | 19:55 | 20:00 | MCC2 | |
| A5 | V104 | 9040 | 15–59 | 1 | 15.04 | 0.54 | 17 | 610 | 9:26 | 19:41 | 19:56 | 20:02 | MCC2 | |
| H2 | V107 | 36020 | 15–59 | 1 | 15.04 | 0.54 | 19 | 610 | 9:26 | 19:47 | 20:02 | 20:06 | MCC2 | |
| A1 | V130 | 41070 | 15–59 | 1 | 15.04 | 0.50 | 17 | 470 | 11:46 | 19:56 | 20:11 | 20:12 | MCC2 | |
| H1 | V132 | 41070 | 15–59 | 1 | 15.04 | 0.50 | 19 | 470 | 11:46 | 19:51 | 20:06 | 20:13 | MCC2 | |
| A3 | V131 | 38060 | 15–59 | 1 | 15.04 | 0.50 | 17 | 470 | 11:46 | 19:50 | 20:05 | 20:14 | MCC2 | |
| H3 | V128 | 42050 | 0–14 | 1 | 14.98 | 0.50 | 16 | 470 | 11:46 | 19:55 | 20:10 | 20:15 | MCC2 | |
| A7 | V136 | 42010 | 0–14 | 1 | 14.98 | 0.50 | 13 | 470 | 11:46 | 19:57 | 20:12 | 20:18 | MCC2 | |
| A8 | V129 | 42050 | 0–14 | 1 | 14.98 | 0.50 | 5 | 470 | 11:46 | 19:59 | 20:14 | 20:23 | MCC2 | |
| A2 | V134 | 42010 | 0–14 | 1 | 14.98 | 0.50 | 19 | 470 | 11:46 | 20:06 | 20:21 | 20:27 | MCC2 | |
| A5 | V139 | 41030 | 0–14 | 1 | 14.98 | 0.50 | 18 | 470 | 11:46 | 20:08 | 20:23 | 20:28 | MCC2 | |
| A4 | V137 | 38060 | 15–59 | 1 | 15.04 | 0.50 | 18 | 470 | 11:46 | 20:07 | 20:22 | 20:30 | MCC2 | |
| H2 | V135 | 42010 | 15–59 | 1 | 15.04 | 0.50 | 20 | 470 | 11:46 | 20:11 | 20:26 | 20:31 | MCC2 | |
| A6 | V133 | 47020 | 0–14 | 1 | 14.98 | 0.50 | 15 | 470 | 11:46 | 20:09 | 20:24 | 20:33 | MCC2 | |
| H1 | V138 | 36030 | 15–59 | 1 | 15.04 | 0.50 | 20 | 470 | 11:46 | 20:18 | 20:33 | 20:38 | MCC2 | |
| A1 | V140 | 36020 | 0–14 | 1 | 14.98 | 0.50 | 18 | 470 | 11:46 | 20:18 | 20:33 | 20:39 | MCC2 | |
| A3 | V142 | 24010 | 15–59 | 1 | 15.04 | 0.50 | 18 | 470 | 11:46 | 20:20 | 20:35 | 20:42 | MCC2 | |
| H3 | V141 | 36020 | 0–14 | 1 | 14.98 | 0.50 | 17 | 470 | 11:46 | 20:22 | 20:37 | 20:44 | MCC2 | |
| A7 | V144 | 42050 | 0–14 | 1 | 14.98 | 0.50 | 14 | 470 | 11:46 | 20:27 | 20:42 | 20:52 | MCC1 | |
| A8 | V145 | 42050 | 15–59 | 1 | 15.04 | 0.50 | 6 | 470 | 11:46 | 20:29 | 20:44 | 20:53 | MCC1 | |
| H2 | V147 | 36030 | 15–59 | 1 | 15.04 | 0.50 | 21 | 470 | 11:46 | 20:35 | 20:50 | 20:56 | MCC1 | |
| A2 | V143 | 42050 | 15–59 | 1 | 15.04 | 0.50 | 20 | 470 | 11:46 | 20:33 | 20:48 | 20:56 | MCC1 | |
| A4 | V149 | 24010 | 15–59 | 1 | 15.04 | 0.50 | 19 | 470 | 11:46 | 20:36 | 20:51 | 20:59 | MCC1 | |
| A1 | V169 | 40040 | 15–59 | 1 | 15.04 | 0.47 | 19 | 370 | 13:26 | 20:43 | 20:58 | 21:00 | MCC6 | |
| A5 | V146 | 36030 | 0–14 | 1 | 14.98 | 0.50 | 19 | 470 | 11:46 | 20:38 | 20:53 | 21:02 | MCC2 | |
| H1 | V168 | 42050 | 15–59 | 1 | 15.04 | 0.47 | 21 | 370 | 13:26 | 20:43 | 20:58 | 21:04 | MCC1 | |
| A6 | V148 | 41030 | 0–14 | 1 | 14.98 | 0.50 | 16 | 470 | 11:46 | 20:42 | 20:57 | 21:07 | MCC1 | |
| A3 | V171 | 42010 | 15–59 | 1 | 15.04 | 0.47 | 19 | 370 | 13:26 | 20:47 | 21:02 | 21:11 | MCC1 | |
| H3 | V167 | 28040 | 15–59 | 1 | 15.04 | 0.47 | 18 | 370 | 13:26 | 20:50 | 21:06 | 21:12 | MCC1 | |
| A1 | V179 | 41010 | 15–59 | 1 | 15.04 | 0.47 | 20 | 370 | 13:26 | 21:02 | 21:17 | 21:20 | MCC6 | |
| H2 | V170 | 36020 | 15–59 | 1 | 15.04 | 0.47 | 22 | 370 | 13:26 | 21:02 | 21:17 | 21:24 | MCC1 | |
| A7 | V173 | 36030 | 0–14 | 1 | 14.98 | 0.47 | 15 | 370 | 13:26 | 21:01 | 21:16 | 21:25 | MCC6 | |
| A2 | V174 | 36030 | 15–59 | 1 | 15.04 | 0.47 | 21 | 370 | 13:26 | 21:04 | 21:19 | 21:27 | MCC1 | |
| A8 | V172 | 42040 | 15–59 | 1 | 15.04 | 0.47 | 7 | 370 | 13:26 | 21:04 | 21:19 | 21:29 | MCC1 | |
| A5 | V176 | 42050 | 15–59 | 1 | 15.04 | 0.47 | 20 | 370 | 13:26 | 21:07 | 21:22 | 21:29 | MCC1 | |
| A4 | V177 | 42050 | 15–59 | 1 | 15.04 | 0.47 | 20 | 370 | 13:26 | 21:07 | 21:22 | 21:30 | MCC1 | |
| H1 | V175 | 42050 | 15–59 | 1 | 15.04 | 0.47 | 22 | 370 | 13:26 | 21:10 | 21:25 | 21:31 | MCC1 | |
| H3 | V196 | 36010 | 15–59 | 1 | 15.04 | 0.43 | 19 | 240 | 15:36 | 21:17 | 21:32 | 21:36 | MCC1 | |
| A6 | V178 | 37080 | 0–14 | 1 | 14.98 | 0.47 | 17 | 370 | 13:26 | 21:15 | 21:30 | 21:38 | MCC1 | |
| A3 | V180 | 36010 | 15–59 | 1 | 15.04 | 0.47 | 20 | 370 | 13:26 | 21:19 | 21:34 | 21:41 | MCC1 | |
| H2 | V194 | 42030 | 15–59 | 1 | 15.04 | 0.43 | 23 | 240 | 15:36 | 21:28 | 21:43 | 21:48 | MCC1 | |
| A1 | V195 | 36020 | 15–59 | 1 | 15.04 | 0.43 | 21 | 240 | 15:36 | 21:29 | 21:44 | 21:52 | MCC1 | |
| A7 | V197 | 41050 | 0–14 | 1 | 14.98 | 0.43 | 16 | 240 | 15:36 | 21:34 | 21:49 | 21:57 | MCC1 | |
| H1 | V208 | 42050 | 15–59 | 1 | 15.04 | 0.39 | 23 | 80 | 18:16 | 21:36 | 21:51 | 21:58 | MCC6 | |
| A2 | V207 | 42050 | 15–59 | 1 | 15.04 | 0.39 | 22 | 80 | 18:16 | 21:36 | 21:51 | 22:00 | MCC6 | |
| A5 | V209 | 42050 | 15–59 | 1 | 15.04 | 0.39 | 21 | 80 | 18:16 | 21:37 | 21:52 | 22:00 | MCC6 | |
| A8 | V206 | 38090 | 15–59 | 1 | 15.04 | 0.39 | 8 | 80 | 18:16 | 21:38 | 21:53 | 22:01 | MCC1 | |
| H3 | V214 | 36010 | 15–59 | 1 | 15.04 | 0.37 | 20 | 0 | 19:36 | 21:42 | 21:57 | 22:03 | MCC6 | |
| A4 | V205 | 38090 | 15–59 | 1 | 15.04 | 0.39 | 21 | 80 | 18:16 | 21:40 | 21:55 | 22:06 | MCC6 | |
| A6 | V213 | 37040 | 15–59 | 1 | 15.04 | 0.37 | 18 | 0 | 19:36 | 21:46 | 22:01 | 22:09 | MCC6 |
References
- Wallemacq, P. Economic Losses, Poverty & Disasters: 1998–2017. Cent. Res. Epidemiol. Disasters 2018, 31. [Google Scholar]
- McNicholl, B. The golden hour and pre-hospital trauma care. Injury 1994, 25, 215–254. [Google Scholar] [CrossRef]
- Knight, V.A.; Harper, P.R.; Smith, L. Ambulance allocation for maximal survival with heterogeneous outcome measures. Omega 2012, 40, 918–926. [Google Scholar] [CrossRef]
- McLay, L.A.; Mayorga, M.E. Evaluating emergency medical service performance measures. Health Care Manag. Sci. 2010, 13, 124–136. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Yuan, Y. Emergency logistics in a large-scale disaster context: Achievements and challenges. Int. J. Environ. Res. Public Health 2019, 16, 779. [Google Scholar] [CrossRef]
- Anaya-Arenas, A.M.; Renaud, J.; Ruiz, A. Relief distribution networks: A systematic review. Ann. Oper. Res. 2014, 223, 53–79. [Google Scholar] [CrossRef]
- Hoyos, M.C.; Morales, R.S.; Akhavan-Tabatabaei, R. OR models with stochastic components in disaster operations management: A literature survey. Comput. Ind. Eng. 2015, 82, 183–197. [Google Scholar] [CrossRef]
- Caunhye, A.M.; Nie, X.; Pokharel, S. Optimization models in emergency logistics: A literature review. Socioecon. Plan. Sci. 2012, 46, 4–13. [Google Scholar] [CrossRef]
- Altay, N.; Green, W.G. OR/MS research in disaster operations management. Eur. J. Oper. Res. 2006, 175, 475–493. [Google Scholar] [CrossRef]
- Kovács, G.; Spens, K.M. Humanitarian logistics in disaster relief operations. Int. J. Phys. Distrib. Logist. Manag. 2007, 37, 99–114. [Google Scholar] [CrossRef]
- Simpson, N.; Hancock, P. Fifty years of operational research and emergency response. J. Oper. Res. Soc. 2008, 60, S139. [Google Scholar] [CrossRef]
- Galindo, G.; Batta, R. Review of recent developments in OR/MS research in disaster operations management. Eur. J. Oper. Res. 2013, 230, 201–211. [Google Scholar] [CrossRef]
- Esposito Amideo, A.; Scaparra, M.P.; Kotiadis, K. Optimising shelter location and evacuation routing operations: The critical issues. Eur. J. Oper. Res. 2019, 279, 279–295. [Google Scholar] [CrossRef]
- Farahani, R.Z.; Lotfi, M.M.; Baghaian, A.; Ruiz, R.; Rezapour, S. Mass casualty management in disaster scene: A systematic review of OR&MS research in humanitarian operations. Eur. J. Oper. Res. 2020, 287, 787–819. [Google Scholar] [CrossRef]
- Liberatore, F.; Ortuño, M.T.; Tirado, G.; Vitoriano, B.; Scaparra, M.P. A hierarchical compromise model for the joint optimization of recovery operations and distribution of emergency goods in Humanitarian Logistics. Comput. Oper. Res. 2014, 42, 3–13. [Google Scholar] [CrossRef]
- Nolz, P.C.; Doerner, K.F.; Hartl, R.F. Water distribution in disaster relief. Int. J. Phys. Distrib. Logist. Manag. 2010, 40, 693–708. [Google Scholar] [CrossRef]
- Ozdamar, L. Planning helicopter logistics in disaster relief. OR Spectr. 2011, 33, 655–672. [Google Scholar] [CrossRef]
- Vitoriano, B.; Ortuño, T.; Tirado, G. HADS, a goal programming-based humanitarian aid distribution system. J. Multi-Criteria Decis. Anal. 2009, 16, 55–64. [Google Scholar] [CrossRef]
- Beamon, B.M.; Kotleba, S.A. Inventory management support systems for emergency humanitarian relief operations in South Sudan. Int. J. Logist. Manag. 2006, 17, 187–212. [Google Scholar] [CrossRef]
- Salas, L.C.; Cárdenas, M.R.; Zhang, M. Inventory policies for humanitarian aid during hurricanes. Socioecon. Plan. Sci. 2012, 46, 272–280. [Google Scholar] [CrossRef]
- Rottkemper, B.; Fischer, K.; Blecken, A.; Danne, C. Inventory relocation for overlapping disaster settings in humanitarian operations. OR Spectr. 2011, 33, 721–749. [Google Scholar] [CrossRef]
- Van Hentenryck, P.; Bent, R.; Coffrin, C. Strategic planning for disaster recovery with stochastic last mile distribution. Lect. Notes Comput. Sci. 2010, 6140, 318–333. [Google Scholar] [CrossRef]
- Yan, S.; Shih, Y.L. Optimal scheduling of emergency roadway repair and subsequent relief distribution. Comput. Oper. Res. 2009, 36, 2049–2065. [Google Scholar] [CrossRef]
- Yi, W.; Özdamar, L. A dynamic logistics coordination model for evacuation and support in disaster response activities. Eur. J. Oper. Res. 2007, 179, 1177–1193. [Google Scholar] [CrossRef]
- Barbarosolu, G.; Özdamar, L.; Çevik, A. An interactive approach for hierarchical analysis of helicopter logistics in disaster relief operations. Eur. J. Oper. Res. 2002, 140, 118–133. [Google Scholar] [CrossRef]
- Yi, W.; Kumar, A. Ant colony optimization for disaster relief operations. Transp. Res. Part E Logist. Transp. Rev. 2007, 43, 660–672. [Google Scholar] [CrossRef]
- Özdamar, L.; Yi, W. Greedy neighborhood search for disaster relief and evacuation logistics. IEEE Intell. Syst. 2008, 23, 14–23. [Google Scholar] [CrossRef]
- Özdamar, L.; Demir, O. A hierarchical clustering and routing procedure for large scale disaster relief logistics planning. Transp. Res. Part E Logist. Transp. Rev. 2012, 48, 591–602. [Google Scholar] [CrossRef]
- Najafi, M.; Eshghi, K.; Dullaert, W. A multi-objective robust optimization model for logistics planning in the earthquake response phase. Transp. Res. Part E Logist. Transp. Rev. 2013, 49, 217–249. [Google Scholar] [CrossRef]
- Najafi, M.; Eshghi, K.; de Leeuw, S. A dynamic dispatching and routing model to plan/re-plan logistics activities in response to an earthquake. OR Spectr. 2014, 36, 323–356. [Google Scholar] [CrossRef]
- Fiedrich, F.; Gehbauer, F.; Rickers, U. Optimized resource allocation for emergency response after earthquake disasters. Saf. Sci. 2000, 35, 41–57. [Google Scholar] [CrossRef]
- Jotshi, A.; Gong, Q.; Batta, R. Dispatching and routing of emergency vehicles in disaster mitigation using data fusion. Socioecon. Plan. Sci. 2009, 43, 1–24. [Google Scholar] [CrossRef]
- Jin, S.; Jeong, S.; Kim, J.; Kim, K. A logistics model for the transport of disaster victims with various injuries and survival probabilities. Ann. Oper. Res. 2015, 230, 17–33. [Google Scholar] [CrossRef]
- Salman, F.S.; Gül, S. Deployment of field hospitals in mass casualty incidents. Comput. Ind. Eng. 2014, 74, 37–51. [Google Scholar] [CrossRef]
- Talarico, L.; Meisel, F.; Sörensen, K. Ambulance routing for disaster response with patient groups. Comput. Oper. Res. 2015, 56, 120–133. [Google Scholar] [CrossRef]
- Repoussis, P.P.; Paraskevopoulos, D.C.; Vazacopoulos, A.; Hupert, N. Optimizing emergency preparedness and resource utilization in mass-casualty incidents. Eur. J. Oper. Res. 2016, 255, 531–544. [Google Scholar] [CrossRef]
- Shavarani, S.M.; Vizvari, B. Post-disaster transportation of seriously injured people to hospitals. J. Humanit. Logist. Supply Chain Manag. 2018, 8, 227–251. [Google Scholar] [CrossRef]
- Argon, N.T.; Ziya, S.; Winslow, J.E. Triage in the Aftermath of Mass-Casualty Incidents. Wiley Encycl. Oper. Res. Manag. Sci. 2011, 8, 5611–5620. [Google Scholar] [CrossRef]
- Khajehaminian, M.R.; Ardalan, A.; Keshtkar, A.; Hosseini Boroujeni, S.M.; Nejati, A.; Ebadati, E.O.M.E.; Rahimi Foroushani, A. A systematic literature review of criteria and models for casualty distribution in trauma related mass casualty incidents. Injury 2018, 49, 1959–1968. [Google Scholar] [CrossRef] [PubMed]
- Argon, N.T.; Ziya, S.; Righter, R. Scheduling impatient jobs in a clearing system with insights on patient triage in mass casualty incidents. Probab. Eng. Inf. Sci. 2008, 22, 301–332. [Google Scholar] [CrossRef]
- Jacobson, E.U.; Argon, N.T.; Ziya, S. Priority assignment in emergency response. Oper. Res. 2012, 60, 813–832. [Google Scholar] [CrossRef]
- Zhu, L.; Gong, Y.; Xu, Y.; Gu, J. Emergency relief routing models for injured victims considering equity and priority. Ann. Oper. Res. 2019, 283, 1573–1606. [Google Scholar] [CrossRef]
- Mills, A.F.; Argon, N.T.; Ziya, S. Dynamic distribution of patients to medical facilities in the aftermath of a disaster. Oper. Res. 2018, 66, 716–732. [Google Scholar] [CrossRef]
- Dean, M.D.; Nair, S.K. Mass-casualty triage: Distribution of victims to multiple hospitals using the SAVE model. Eur. J. Oper. Res. 2014, 238, 363–373. [Google Scholar] [CrossRef]
- Mills, A.F.; Argon, N.T.; Ziya, S. Resource-based patient prioritization in mass-casualty incidents. Manuf. Serv. Oper. Manag. 2013, 15, 361–377. [Google Scholar] [CrossRef]
- Liu, K.; Wang, J. Fast dynamic vehicle detection in road scenarios based on pose estimation with convex-hull model. Sensors 2019, 19, 3136. [Google Scholar] [CrossRef]
- Bach, A.J.E.; Maley, M.J.; Minett, G.M.; Stewart, I.B. Occupational cooling practices of emergency first responders in the United States: A survey. Temperature 2018, 5, 348–358. [Google Scholar] [CrossRef]
- Frykberg, E.R. Triage: Principles and practice. Scand. J. Surg. 2005, 94, 272–278. [Google Scholar] [CrossRef]
- Pons, P.T.; Haukoos, J.S.; Bludworth, W.; Cribley, T.; Pons, K.A.; Markovchick, V.J. Paramedic Response Time: Does It Affect Patient Survival? Acad. Emerg. Med. 2005, 12, 594–600. [Google Scholar] [CrossRef] [PubMed]
- Erkut, E.; Ingolfsson, A.; Erdogan, G. Ambulance location for maximum survival. Nav. Res. Logist. 2008, 55, 42–58. [Google Scholar] [CrossRef]
- Blanchard, I.E.; Doig, C.J.; Hagel, B.E.; Anton, A.R.; Zygun, D.A.; Kortbeek, J.B.; Powell, D.G.; Williamson, T.S.; Fick, G.H.; Innes, G.D. Emergency medical services response time and mortality in an urban setting. Prehosp. Emerg. Care 2012, 16, 142–151. [Google Scholar] [CrossRef]
- Borrows, E.L.; Lutman, D.H.; Montgomery, M.A.; Petros, A.J.; Ramnarayan, P. Effect of patient- and team-related factors on stabilization time during pediatric intensive care transport. Pediatr. Crit. Care Med. 2010, 11, 451–456. [Google Scholar] [CrossRef]
- Comte, D.; Pardo, M. Reappraisal of great historical earthquakes in the northern Chile and southern Peru seismic gaps. Nat. Hazards 1991, 4, 23–44. [Google Scholar] [CrossRef]
- Hayes, G.P.; Herman, M.W.; Barnhart, W.D.; Furlong, K.P.; Riquelme, S.; Benz, H.M.; Bergman, E.; Barrientos, S.; Earle, P.S.; Samsonov, S. Continuing megathrust earthquake potential in Chile after the 2014 Iquique earthquake. Nature 2014, 512, 295–298. [Google Scholar] [CrossRef] [PubMed]
- Aguirre, P.; Vásquez, J.; de la Llera, J.C.; González, J.; González, G. Earthquake damage assessment for deterministic scenarios in Iquique, Chile. Nat. Hazards 2018, 92, 1433–1461. [Google Scholar] [CrossRef]
- Gobierno Regional de Tarapacá. Plan de Movilidad Urbana Sostenible Para el Área Metropolitana Iquique—Alto Hospicio. Available online: https://geoportal.goretarapaca.gov.cl/wp-content/uploads/2021/03/3.-Resumen-Ejecutivo-Informe-3-P.M.U.S..pdf (accessed on 20 November 2021).
- ONEMI. Plan Regional de Emergencia Tarapacá. Available online: http://repositoriodigital.onemi.gov.cl/web/bitstream/handle/2012/1812/PRE_Tarapaca_C.pdf (accessed on 20 November 2021).
- Lubillo, S.; Burillo-Putze, G.; Alonso, E.; Herranz, I.; Gomez, A.; Gomez, N. Helicopter emergency medical service in Canary Islands, Spain. Eur. J. Emerg. Med. 2000, 7, 55–59. [Google Scholar] [CrossRef] [PubMed]
- Tijssen, J.A.; Prince, D.K.; Morrison, L.J.; Atkins, D.L.; Austin, M.A.; Berg, R.; Brown, S.P.; Christenson, J.; Egan, D.; Fedor, P.J.; et al. Time on the scene and interventions are associated with improved survival in pediatric out-of-hospital cardiac arrest. Resuscitation 2015, 94, 1–7. [Google Scholar] [CrossRef]
- Lin, M.W.; Wu, C.Y.; Pan, C.L.; Tian, Z.; Wen, J.H.; Wen, J.C. Saving the On-Scene Time for Out-Of-Hospital Cardiac Arrest Patients: The Registered Nurses’ Role and Performance in Emergency Medical Service Teams. BioMed Res. Int. 2017, 2017, 6. [Google Scholar] [CrossRef]
- Drenck, N.; Viereck, S.; Bækgaard, J.S.; Christensen, K.B.; Lippert, F.; Folke, F. Pre-hospital management of acute stroke patients eligible for thrombolysis—An evaluation of ambulance on-scene time. Scand. J. Trauma Resusc. Emerg. Med. 2019, 27, 3. [Google Scholar] [CrossRef]
- Kumar, P.P.; Kumar, C.D.; Shaik, F.; Yadav, S.; Dusa, S.; Venkatlakshmi, A. Transported neonates by a specialist team—How STABLE are they. Indian J. Pediatr. 2011, 78, 860–862. [Google Scholar] [CrossRef]
- Brown, L.; Arthur, A.; Keeling, C.; Yuhas, C.; Thomas, S.H. Establishing Benchmarks for Helicopter EMS Patient Stabilization Times in Interfacility Transport for Primary Percutaneous Coronary Intervention. Int. J. Clin. Med. 2012, 3, 765–768. [Google Scholar] [CrossRef][Green Version]
- Rhodes, M.; Perline, R.; Aronson, J.; Rappe, A. Field triage for on-scene helicopter transport. J. Trauma 1986, 26, 963–969. [Google Scholar] [CrossRef]
- Spaite, D.W.; Tse, D.J.; Valenzuela, T.D.; Criss, E.A.; Meislin, H.W.; Mahoney, M.; Ross, J. The impact of injury severity and prehospital procedures on scene time in victims of major trauma. Ann. Emerg. Med. 1991, 20, 1299–1305. [Google Scholar] [CrossRef]
- Petri, R.W.; Dyer, A.; Lumpkin, J. The Effect of Prehospital Transport Time on the Mortality from Traumatic Injury. Prehosp. Disaster Med. 1995, 10, 24–29. [Google Scholar] [CrossRef] [PubMed]
- Birk, H.O.; Henriksen, L.O. Prehospital interventions: On-scene-Time and ambulance-technicians’ experience. Prehosp. Disaster Med. 2002, 17, 167–169. [Google Scholar] [CrossRef]
- van der Velden, M.W.A.; Ringburg, A.N.; Bergs, E.A.; Steyerberg, E.W.; Patka, P.; Schipper, I.B. Prehospital interventions: Time wasted or time saved? An observational cohort study management in initial trauma care. Emerg. Med. J. 2008, 25, 444–449. [Google Scholar] [CrossRef] [PubMed]
- Kidher, E.; Krasopoulos, G.; Coats, T.; Charitou, A.; Magee, P.; Uppal, R.; Athanasiou, T. The effect of prehospital time related variables on mortality following severe thoracic trauma. Injury 2012, 43, 1386–1392. [Google Scholar] [CrossRef] [PubMed]
- Feng, C.; Wen, C. Traffic control management for earthquake-raided area. J. East. Asia Soc. Transp. Stud. 2003, 5, 3261–3275. [Google Scholar]
- Hara, Y.; Kuwahara, M. Traffic Monitoring immediately after a major natural disaster as revealed by probe data—A case in Ishinomaki after the Great East Japan Earthquake. Transp. Res. Part A Policy Pract. 2015, 75, 1–15. [Google Scholar] [CrossRef]



| Ambulance Travel Times (min) | Helicopter Travel Times (min) | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MCC 1 | MCC 2 | MCC 3 | V1 | V2 | V3 | V4 | V5 | MCC 1 | MCC 2 | MCC 3 | V1 | V2 | V3 | V4 | V5 | ||
| V1 | 29.19 | 23.91 | 36.64 | 0 | 6.67 | 8.33 | 8.33 | 0 | V1 | 7.42 | 6.78 | 7.89 | 0 | 5.46 | 5.51 | 5.51 | 5 |
| V2 | 27.46 | 20.96 | 32.64 | 6.67 | 0 | 6.61 | 6.61 | 6.67 | V2 | 7.1 | 6.47 | 7.51 | 5.46 | 0 | 5.46 | 5.46 | 5.46 |
| V3 | 22.63 | 18.21 | 30.09 | 8.33 | 6.61 | 0 | 0 | 8.33 | V3 | 6.93 | 6.29 | 7.43 | 5.51 | 5.46 | 0 | 0 | 5.51 |
| V4 | 22.63 | 18.21 | 30.09 | 8.33 | 6.61 | 0 | 0 | 8.33 | V4 | 6.93 | 6.29 | 7.43 | 5.51 | 5.46 | 0 | 0 | 5.51 |
| V5 | 29.19 | 23.91 | 36.64 | 0 | 6.67 | 8.33 | 8.33 | 0 | V5 | 7.42 | 6.78 | 7.89 | 0 | 5.46 | 5.51 | 5.51 | 0 |
| ID Age Range | Age Range (Years) | Stabilization Time According to LSI (min) | ||
|---|---|---|---|---|
| LSI 1 | LSI 2 | LSI 3 | ||
| 1 | 0–14 | 14.98 | 42 | 93.3 |
| 2 | 15–59 | 15.04 | 29.9 | 62.14 |
| 3 | 60 or more | 9.3 | 27.6 | 65 |
| Ambulance with 1 patient capacity | Helicopter with capacity for 3 patients | ||||||||||||||||||||
| Min Ck | Min Ck | Minβk | |||||||||||||||||||
| Casualty ID Code | LSI | Age Range | (min) | Trip (v) | TBk(min) | TSk(min) | TLk(min) | Casualty ID Code | LSI | Age Range | (min) | Trip (v) | TBk(min) | TSk(min) | TLk(min) | Trip (v) | TBk(min) | TSk(min) | TLk(min) | ||
| V1 | 3 | 2 | 5.1 | 62.1 | 5 | 482.6 | 544.7 | 573.9 | V1 | 3 | 2 | 5.1 | 62.1 | 1 | 8.1 | 70.3 | 206.3 | 1 | 8.1 | 70.3 | 75.1 |
| V2 | 3 | 2 | 5.1 | 62.1 | 3 | 243.3 | 305.4 | 332.9 | V2 | 3 | 2 | 5.1 | 62.1 | 2 | 213.8 | 275.9 | 357.9 | 4 | 229.4 | 291.6 | 299.0 |
| V3 | 3 | 2 | 5.1 | 62.1 | 1 | 23.6 | 85.8 | 108.4 | V3 | 3 | 2 | 5.1 | 62.1 | 1 | 72.9 | 135.0 | 206.3 | 2 | 80.7 | 142.9 | 148.5 |
| V4 | 3 | 2 | 5.1 | 62.1 | 2 | 131.0 | 193.2 | 215.8 | V4 | 3 | 2 | 5.1 | 62.1 | 1 | 138.5 | 200.7 | 206.3 | 3 | 154.2 | 216.4 | 222.0 |
| V5 | 3 | 2 | 5.1 | 62.1 | 4 | 362.1 | 424.2 | 453.4 | V5 | 3 | 2 | 5.1 | 62.1 | 2 | 285.6 | 347.8 | 357.9 | 5 | 309.1 | 371.3 | 381.4 |
| (a) | |||||||||||||||||||||
| Ambulance with 1 patient capacity | Helicopter with capacity for 3 patients | ||||||||||||||||||||
| Min Ck | Min Ck | Minβk | |||||||||||||||||||
| Casualty ID Code | LSI | Age Range | (min) | Trip (v) | TBk(min) | TSk(min) | TLk(min) | Casualty ID Code | LSI | Age Range | (min) | Trip (v) | TBk(min) | TSk(min) | TLk(min) | Trip (v) | TBk(min) | TSk(min) | TLk(min) | ||
| V1 | 3 | 2 | 5.1 | 62.1 | 4 | 424.4 | 486.5 | 515.7 | V1 | 3 | 2 | 5.1 | 62.1 | 2 | 282.1 | 344.2 | 426.5 | 3 | 219.7 | 281.9 | 286.7 |
| V2 | 3 | 1 | 8.7 | 93.3 | 2 | 167.0 | 260.3 | 287.8 | V2 | 3 | 1 | 8.7 | 93.3 | 1 | 109.5 | 202.8 | 277.3 | 2 | 114.6 | 207.9 | 215.0 |
| V3 | 3 | 1 | 8.7 | 93.3 | 1 | 23.6 | 116.9 | 139.6 | V3 | 3 | 1 | 8.7 | 93.3 | 1 | 9.0 | 102.3 | 277.3 | 1 | 9.0 | 102.3 | 107.5 |
| V4 | 3 | 2 | 5.1 | 62.1 | 3 | 310.4 | 372.6 | 395.2 | V4 | 3 | 2 | 5.1 | 62.1 | 1 | 210.0 | 272.1 | 277.3 | 4 | 291.8 | 354.0 | 359.2 |
| V5 | 3 | 3 | 5.1 | 65.0 | 5 | 544.9 | 609.9 | 639.1 | V5 | 3 | 3 | 5.1 | 65.0 | 2 | 351.3 | 416.3 | 426.5 | 5 | 369.3 | 434.3 | 444.5 |
| (b) | |||||||||||||||||||||
| Ambulance with 1 patient capacity | Helicopter with capacity for 3 patients | ||||||||||||||||||||
| Min Ck | Min Ck | Minβk | |||||||||||||||||||
| Casualty ID Code | LSI | Age Range | (min) | Trip (v) | TBk(min) | TSk(min) | TLk(min) | Casualty ID Code | LSI | Age Range | (min) | Trip (v) | TBk(min) | TSk(min) | TLk(min) | Trip (v) | TBk(min) | TSk(min) | TLk(min) | ||
| V1 | 3 | 2 | 5.1 | 62.1 | 2 | 137.6 | 199.7 | 228.9 | V1 | 3 | 2 | 5.1 | 62.1 | 1 | 8.2 | 70.3 | 175.6 | 1 | 8.2 | 70.3 | 75.1 |
| V2 | 2 | 2 | 0.9 | 29.9 | 4 | 320.6 | 350.5 | 371.5 | V2 | 2 | 2 | 0.9 | 29.9 | 2 | 182.7 | 212.6 | 250.0 | 4 | 193.6 | 223.5 | 230.0 |
| V3 | 2 | 2 | 0.9 | 29.9 | 3 | 251.5 | 281.4 | 299.6 | V3 | 2 | 2 | 0.9 | 29.9 | 1 | 140.5 | 170.4 | 175.6 | 3 | 152.7 | 182.6 | 187.2 |
| V4 | 3 | 2 | 5.1 | 62.1 | 1 | 23.7 | 85.8 | 108.4 | V4 | 3 | 2 | 5.1 | 62.1 | 1 | 74.9 | 137.0 | 175.6 | 2 | 80.3 | 142.4 | 147.6 |
| V5 | 1 | 2 | 0.4 | 15.0 | 5 | 395.4 | 410.4 | 434.3 | V5 | 1 | 2 | 0.4 | 15.0 | 2 | 224.3 | 239.3 | 250.0 | 5 | 239.6 | 254.6 | 264.1 |
| (c) | |||||||||||||||||||||
| Ambulance with 1 patient capacity | Helicopter with capacity for 3 patients | ||||||||||||||||||||
| Min Ck | Min Ck | Minβk | |||||||||||||||||||
| Casualty ID Code | LSI | Age Range | (min) | Trip (v) | TBk(min) | TSk(min) | TLk(min) | Casualty ID Code | LSI | Age Range | (min) | Trip (v) | TBk(min) | TSk(min) | TLk(min) | Trip (v) | TBk(min) | TSk(min) | TLk(min) | ||
| V1 | 3 | 2 | 5.1 | 62.1 | 2 | 168.8 | 230.9 | 260.1 | V1 | 3 | 2 | 5.1 | 62.1 | 1 | 107 | 169.1 | 224.5 | 2 | 112.3 | 174.4 | 179.2 |
| V2 | 2 | 1 | 1.9 | 42.0 | 3 | 287.5 | 329.5 | 350.5 | V2 | 2 | 1 | 1.9 | 42.0 | 1 | 175.4 | 217.4 | 224.5 | 3 | 186.3 | 228.3 | 234.7 |
| V3 | 2 | 2 | 0.9 | 29.9 | 4 | 368.7 | 398.6 | 416.8 | V3 | 2 | 2 | 0.9 | 29.9 | 2 | 229.6 | 259.5 | 289.0 | 4 | 239.3 | 269.2 | 273.7 |
| V4 | 3 | 1 | 8.7 | 93.3 | 1 | 23.6 | 116.9 | 139.6 | V4 | 3 | 1 | 8.7 | 93.3 | 1 | 9 | 102.3 | 224.5 | 1 | 9 | 102.3 | 107.5 |
| V5 | 1 | 3 | 0.4 | 9.3 | 5 | 440.7 | 450.0 | 473.9 | V5 | 1 | 3 | 0.4 | 9.3 | 2 | 269.5 | 278.8 | 289.0 | 5 | 283.2 | 292.5 | 302.0 |
| (d) | |||||||||||||||||||||
| ID Age Range | Age Range (Years) | Population (Persons) |
|---|---|---|
| 1 | 0–14 | 41.163 |
| 2 | 15–59 | 106.744 |
| 3 | 60 or more | 15.374 |
| Medical Care Center ID | Capacity (No. of Beds) | ||
|---|---|---|---|
| LSI1 | LSI2 | LSI3 | |
| MCC1 | 23 | 30 | 20 |
| MCC2 | 24 | 21 | 0 |
| MCC3 | 24 | 21 | 0 |
| MCC4 | 16 | 19 | 0 |
| MCC5 | 24 | 21 | 0 |
| MCC6 | 25 | 22 | 0 |
| Age Range ID | Age Range (Years) | People Injured by LSI | ||
|---|---|---|---|---|
| LSI 1 | LSI 2 | LSI 3 | ||
| 1 | 0–14 | 24 | 23 | 3 |
| 2 | 15–59 | 72 | 75 | 7 |
| 3 | 60 or more | 2 | 5 | 1 |
| Period ID | Period Start Time | Number of Casualties (People) | Availability of the Health Network | % Decrease in Speed | |||||
|---|---|---|---|---|---|---|---|---|---|
| Total | LSI 1 | LSI 2 | LSI 3 | Available MCCS | Ambulances Available | Helicopters Available | |||
| Period 1 | 07:41 | 64 | 32 | 27 | 5 | 3 (MCC1, 2 and 3) | 4 (A1, A2, A3, A4) | 2 (H1, H2) | 70% |
| Period 2 | 09:26 | 44 | 20 | 22 | 2 | 5 (MCC 1, 2, 3, 4, 5) | 5 (A1, A2, A3, A4, A5) | 2 (H1, H2) | 70% |
| Period 3 | 11:46 | 41 | 22 | 18 | 1 | 6 (MCC 1, 2, 3, 4, 5, 6) | 7 (A1, A2, A3, A4, A5, A6, A7) | 3 (H1, H2, H3) | 50% |
| Period 4 | 13:26 | 31 | 14 | 15 | 2 | 6 (MCC 1, 2, 3, 4, 5, 6) | 7 (A1, A2, A3, A4, A5, A6, A7) | 3 (H1, H2, H3) | 50% |
| Period 5 | 15:36 | 17 | 4 | 12 | 1 | 6 (MCC 1, 2, 3, 4, 5, 6) | 7 (A1, A2, A3, A4, A5, A6, A7) | 3 (H1, H2, H3) | 30% |
| Period 6 | 18:16 | 12 | 6 | 6 | 0 | 6 (MCC 1, 2, 3, 4, 5, 6) | 7 (A1, A2, A3, A4, A5, A6, A7) | 3 (H1, H2, H3) | 30% |
| Period 7 | 19:36 | 5 | 2 | 3 | 0 | 6 (MCC 1, 2, 3, 4, 5, 6) | 8 (A1, A2, A3, A4, A5, A6, A7, A8) | 3 (H1, H2, H3) | 10% |
| Vehicle ID Code | Casualty ID Code | Node ID (li) | Age Range | LSI | Trip (v) | TFk | TBk | TSk | TLk | MCC Assigned | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A3 | V2 | 36020 | ≥60 | 3 | 65 | 5.105 | 1 | 7:41:00 | 8:04:18 | 9:09:18 | 9:31:36 | MCC1 |
| H2 | V4 | 36020 | 15–59 | 3 | 62.14 | 5.105 | 1 | 7:41:00 | 7:50:02 | 8:52:10 | 8:57:51 | MCC1 |
| A1 | V17 | 36020 | 15–59 | 2 | 29.9 | 0.895 | 2 | 7:41:00 | 10:32:51 | 11:02:45 | 11:20:58 | MCC2 |
| A3 | V18 | 36020 | 15–59 | 2 | 29.9 | 0.895 | 3 | 7:41:00 | 11:07:28 | 11:37:22 | 12:02:17 | MCC1 |
| A2 | V25 | 36020 | 15–59 | 2 | 29.9 | 0.895 | 3 | 7:41:00 | 11:15:18 | 11:45:12 | 12:08:30 | MCC1 |
| H1 | V28 | 36020 | 15–59 | 2 | 29.9 | 0.895 | 6 | 7:41:00 | 12:36:40 | 13:06:34 | 13:11:35 | MCC2 |
| H1 | V38 | 36020 | 15–59 | 1 | 15.04 | 0.372 | 8 | 7:41:00 | 13:58:27 | 14:13:29 | 14:43:07 | MCC2 |
| H1 | V39 | 36020 | 15–59 | 1 | 15.04 | 0.372 | 8 | 7:41:00 | 14:20:54 | 14:35:56 | 14:43:07 | MCC2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bronfman, A.; Beneventti G., D.; Alvarez, P.P.; Reid, S.; Paredes-Belmar, G. The Casualty Stabilization–Transportation Problem in a Large-Scale Disaster. Sustainability 2022, 14, 621. https://doi.org/10.3390/su14020621
Bronfman A, Beneventti G. D, Alvarez PP, Reid S, Paredes-Belmar G. The Casualty Stabilization–Transportation Problem in a Large-Scale Disaster. Sustainability. 2022; 14(2):621. https://doi.org/10.3390/su14020621
Chicago/Turabian StyleBronfman, Andrés, Diego Beneventti G., Pamela P. Alvarez, Samantha Reid, and Germán Paredes-Belmar. 2022. "The Casualty Stabilization–Transportation Problem in a Large-Scale Disaster" Sustainability 14, no. 2: 621. https://doi.org/10.3390/su14020621
APA StyleBronfman, A., Beneventti G., D., Alvarez, P. P., Reid, S., & Paredes-Belmar, G. (2022). The Casualty Stabilization–Transportation Problem in a Large-Scale Disaster. Sustainability, 14(2), 621. https://doi.org/10.3390/su14020621







