Abstract
The objective of this paper is to study the specifics of the selection of renewables for regions of Azerbaijan with diverse conditions. Information is obtained through the analysis of the regions’ conditions and experts’ opinions. Analysis reveals that geographical position, diversity of natural resources, and a variety of other factors of the five economic regions of the country require subdivision of these regions in the selection of renewables. Given that the selection of renewables is a multi-criteria decision-making (MCDM) task under a high degree of uncertainty, Z-number-based models have been developed, and Z-extension of the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) method has been used. Solutions have been derived based on direct calculations with Z-numbers. In this paper, results obtained for two regions are presented. In the case of one region, for the first part (mountains and foothill) of the Karabakh economic region, renewables are ranked as hydro, solar, and wind. For the second part (plain), the ranking is as follows: solar, hydro, and wind. For the Guba-Khachmaz economic region, the rankings of renewables for parts of the region are also different: the wind is preferable for the seaside, and solar is more appropriate for the foothills. Results show that in the case of uneven distribution of renewables and significant differences in factors influencing decision-making, it is necessary to subdivide economic regions and use different models for the selection of renewables.
1. Introduction
Countries are developing and implementing long-term plans for the gradual replacement of the environmentally unfriendly fossil energy resources. Differences in geographical position, diversity of the natural and economic conditions, and uneven distributions of the resources within the countries and regions require the application of different approaches for the development of renewables in various economic regions.
Azerbaijan is endowed with rich natural resources. The share of oil-gas sector in the GDP is 37 percent, which has decreased significantly from 56 percent in 2006 (when oil rent as a percent of GDP was 39.7 percent), due to reforms on economic diversification [1,2,3]. On the way to achieving sustainable development, shifting from non-renewable energy to renewable energy is dispensable. Azerbaijan has nine climatic zones, and its nature is represented by mountains and foothill zones, plains, semi-deserts, sub-tropics, and seaside areas. The potential of economically viable and technically feasible renewable energy sources of Azerbaijan is estimated at 27,000 MW, including 3000 MW of wind energy, 23,000 MW of solar energy, 380 MW of bioenergy potential, and 520 MW of mountain rivers [4]. Currently, total energy supply is 17,566,600 TOE. The shares of renewable energy supplies of hydropower, biomass, wind power, and solar (photovoltaic) power in total energy consumption are 0.6 percent, 0.6 percent, 0.1 percent, and 0.03 percent, respectively [2]. Potential utilization of rich renewable energy resources of Azerbaijan requires proper evaluation and investment analysis of its economic regions. Therefore, diversity of the natural resources, uneven distribution of the energy resources within the country and regions, and geographical and other peculiarities of the regions must be considered in the model of selecting renewables. Azerbaijan is planning to increase electricity production by renewables up to thirty percent by 2030. This is a challenging task, and to meet this objective, it is necessary to use all available options efficiently [4].
Selection of energy resources is a multi-criteria decision-making task, and various approaches have been used for the problem solution. Comprehensive reviews of the multiple-criteria decision-making (MCDM) method applications in the energy sector are provided in [5,6] and in many other papers. As it is shown in these papers, researchers apply both conventional and fuzzy methods in the energy sector. The renewable selection model, based on fuzzy AHP and a new procedure for the aggregation of experts’ judgements, was developed for Indonesia [7]. The intuitionistic, fuzzy AHP (analytical hierarchy process) method was proposed for sustainable energy planning in Malaysia [8]. A multi-criteria approach, based on an extension of the fuzzy TOPSIS (the Technique for Order of Preference by Similarity to Ideal Solution) for group decision support, for achieving the 2030 target in European member states in the use of renewables, was developed in [9]. The fuzzy AHP method was applied for assessing the potential of renewable energy sources for electricity generation in Serbia [9]. The differences between approaches presented in [5,6,7,8,9,10] lie in the models used, category and number of criteria applied, number of alternatives analyzed, and applications.
In [11,12,13,14,15,16,17,18,19,20], various combinations of AHP, ANP, TOPSIS, G-AHP (grey AHP), WASPAS (weighted aggregates sum product assessment), and SWOT analysis are used for energy policy development, planning, and selection of renewables in Turkey, Taiwan, Vietnam, Saudi Arabia, and Jordan.
An integrated Delphi-AHP and fuzzy TOPSIS methodology was employed by [21] to analyze various renewable resources of Pakistan. Study [22] employed four MCDM methods—WSM (weighted sum method), VIKOR (Visekriterijumsko Kompromisno Rangiranje), TOPSIS, and ELECTRE (elimination et choice translating reality)—to conduct comparative analysis of ranking renewable energy sources for electricity generation in Taiwan. To provide more reliable results and facilitate decision makers, [23] proposed the integrated analytical hierarchy process (AHP)–quality function deployment (QFD) model to determine the most viable renewable energy source for the state of Maharashtra in India.
It is necessary to underline that the fuzzy models presented in these publications only partially resolve issues related to deficiency and subjectivity of the information used in MCDM methods. In the classical version of the fuzzy models, the issue of information reliability is not considered. Proposed by [24], Z-numbers allow us to alleviate this deficiency. Z-numbers operate with fuzzy estimates and a degree of confidence in these estimates. Solutions based on Z-information provide values of fuzzy decision variables and their reliability to decision-makers. At present there are a limited number of publications that make use of Z-numbers in the selection and assessment of energy sources [25,26].
The application of Z-numbers allows researchers to get more relevant estimates from a group of experts. Moreover, their use allows you to reduce the time for Delphi analysis. Thus, the moderator of the Delphi panel, having received the opinions of experts, can evaluate the importance of each criterion by Z-numbers, which contain information about the value of an uncertain variable and the confidence in this value. Next, the experts can express their opinions about the Z-number-based estimations, and the moderator can make certain changes to the Z-numbers. The final Z-evaluations represent the consensus opinion of the panel of experts.
As mentioned, except [23], problem statement and solutions in the previous studies have been provided for a whole country. In our study, we consider the solution of the problem for certain economic regions of a country, with a division of these regions to the subregions according to the specifics of the nature of those regions. To the best of our knowledge, no previous research has been conducted in this direction in the case of Azerbaijan. In this paper, we present MCDM models based on direct calculations with Z-numbers for the assessment and selection of renewable energy resources for two economic regions of Azerbaijan with diverse conditions that have huge potential for the development of its green economy: Karabakh (mountains and foothill, and plain parts) and Guba-Khachmaz (seaside and foothill parts).
2. Theoretical Background and Methods
2.1. Definitions and Operations with Z-Numbers
Definition 1.
Z-number [24]. Continuous or discrete Z-number is an ordered pair (A, B) of fuzzy numbers. Part A is a restriction on the values of the uncertain variable X, and part B is a measure of the reliability or certainty of A.
Definition 2
Arithmetic operations on Z-numbers [27]. If Z1 and Z2 are two Z-numbers with parts A and B expressed as (A1, B1) and (A2, B2), and * is one of the binary arithmetic operations (+, −, ., /), then this operation on Z-numbers is defined by the formula
Part A of Z12 is computed under the rules of arithmetic operations on fuzzy numbers A12 = A1 × A2. To calculate B12, the method described in [27] is used.
Z12(A12, B12) = (A1, B1) × (A2, B2)
Definition 3.
Z-numbers ranking based on the fuzzy Pareto optimality principle [27]. Two Z-numbers are compared as multi-attribute alternatives by calculating the degrees of optimality do(Z1) and do(Z2). These degrees are determined based on the number of components for which one Z-number dominates over another Z-number. Intermediate functions nbest(Zi, Zj), nequal(Zi, Zj), and nworst(Zi, Zj) estimate how much one Z-number is superior, equivalent, or less, with respect to the components A and B, and then d(Zi, Zj) is calculated
If d(Zi,Zj) = 1, then Zi is Pareto-dominated over Zj. If d(Zi,Zj) = 0, Zi is not Pareto-dominated over Zj. Based on the values of the function d, the degree of optimality of Zj is calculated by the formula
do (Zi) determines the degree to which one Z-number is over than another:
do(Zi) = 1 − d(Zi,Zj)
Zi > Zj, if do(Zi) > do(Zj); Zi < Zj, if do(Zi) < do(Zj); and Zi = Zj, if do(Zi) = do(Zj)
Definition 4.
Distance between Z-numbers. The distance between two Z-numbers Z1 and Z2, in case of the triangle or trapezoidal fuzzy numbers, is calculated based on membership function parameters [28]: half of the total sum of the absolute values of the sum of the differences of the A1 and A2 parameters and absolute values of the sum of the differences of the B1 and B2 parameters.
2.2. Z-Extension of the TOPSIS Method
Z-extension of the TOPSIS method requires sequential performance of the following steps:
Step 1. Selection of the criteria.
Step 2. Division of the criteria set into two sub-sets: cost criteria and benefit criteria.
Step 3. Generation of a set of alternatives.
Step 4. Weighting of the criteria and experts.
Step 5. Z-numbers-based decision matrix (ZDMx) construction and normalization: for normalization of part A, the linear scale transformation is applied. Bijnorm of Zij = Bij of Zij
Step 6. Construction of the weighted, normalized decision matrix.
Step 7. Defining of the Z-number-based positive-ideal and negative-ideal solution.
Step 8. Calculation of the distance from each alternative to the ideal-positive and ideal-negative solution [29]. Distances between the ith alternative and the ideal solutions, according to Definition 4, are calculated as
where N is a number of criteria.
Step 9. Calculation of the relative closeness to the best alternative
Step 10. Ranking of the alternatives according to the relative closeness.
3. Results and Discussion
We analyzed the selection and ranking of renewable energy resources in economic regions of Azerbaijan. Capacities of available resources predetermined three alternatives for the renewables that are of interest: solar energy, wind, and hydro.
The Figure 1, Figure 2 and Figure 3 below give information about renewable energy potential in Azerbaijan and its considered regions [30,31,32].
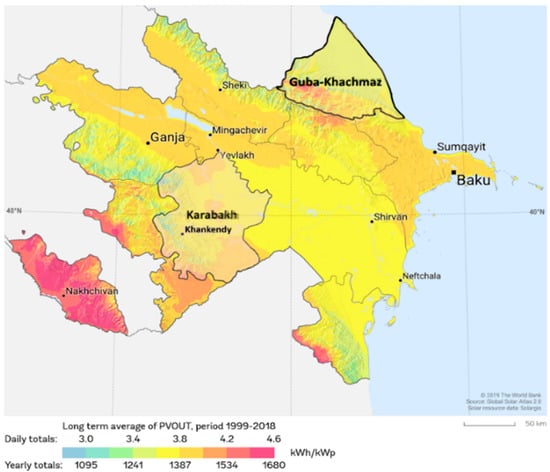
Figure 1.
Photovoltaic power potential of Azerbaijan and its Karabakh and Guba-Khachmaz regions. Source: Global Solar Atlas.
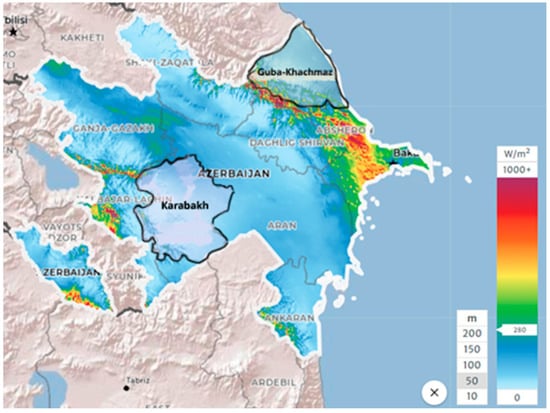
Figure 2.
Mean power density (height 50 m) in Azerbaijan and its Karabakh and Guba-Khachmaz economic regions. Source: Global Wind Atlas.
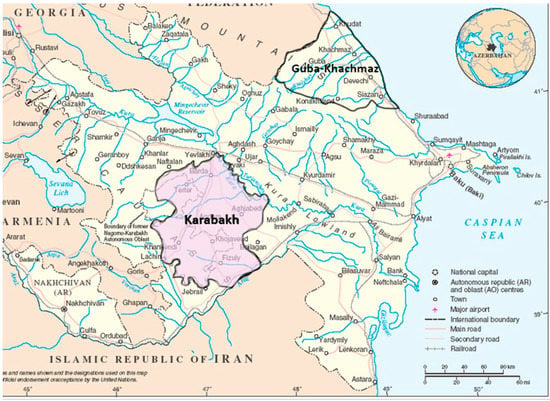
Figure 3.
Rivers of the Azerbaijan Republic. Source: [30]
Alternatives were analyzed with respect to six criteria: government policy and regulation (C1); social acceptance (C2); labor impact (C3); cost efficiency (C4); environmental effect (C5); and resource availability (C6).
As a source of information, we employed experts’ judgement studies. Five experts with more than ten years of experience in economics, energy economics, and decision science provided linguistic estimates of the criteria weights and evaluated alternatives. The discussion was conducted both through a face-to-face meeting and a Zoom conference.
Based on the literature review, a preliminary list of seven criteria (1—government policy and regulation, 2—social acceptance, 3—labor impact, 4—cost efficiency, 5—environmental effect, 6—distance to users, and 7—land availability) was presented as a starting point for discussions to the group of experts. Experts had the opportunity to revise, expand, or shorten the list of criteria. As a result of discussions by experts, two criteria (distance to users, land availability) were rejected and one criterion (resource availability) was proposed. Finally, it was decided to use six criteria (government policy and regulation, social acceptance, labor impact, cost efficiency, resource availability, and environmental effect) for further research. Then, experts were asked to evaluate each of the criterion by linguistic values according to Table 1. The second round of discussions was in the form of the Zoom conference, where the experts presented their estimates. Estimates were processed and finalized by the moderator.

Table 1.
Linguistic terms for alternatives and criteria evaluation.
These estimates contain information about the value of the estimates and their confidence/reliability levels. In this paper, we used seven linguistic terms, and correspondingly, seven Z-numbers that cover the domain of expert judgement [0;1]. These terms overlap and allow experts to select the term that best describes his/her opinion about variables. Z-number-based descriptions of the linguistic terms used for weights, criteria, and evaluation of alternatives are presented in Table 1.
Differences in criteria importance were considered by Z-number-based weights. Weights were assigned by experts and aggregated by applying the Delphi procedure.
3.1. Karabakh Economic Region
Here, we present detailed calculations for one sub-region. Examples of Z-number-based evaluations of the alternatives, with respect to the various criteria for the first part of the Karabakh economic region (mountains and foothill), are shown in Table 2.

Table 2.
Z-number-based aggregated evaluations of alternatives, with respect to various criteria.
After receiving expert assessments, they must be aggregated. One possible approach is to sum up the evaluations (Z-numbers) given by the experts for each alternative for each criterion, and then multiply the resulting Z-number by the scalar value 1/n, where n is the number of experts. In our case, to evaluate the first alternative according to the first criterion, all the corresponding assessments given by five experts were summed up, and the result was multiplied by a scalar value of 0.2 (1/number of experts). Then, according to the TOPSIS procedure, the obtained values were normalized, and in Table 3, the Z-number-based normalized decision matrix is presented. This matrix reflects the aggregated Z-evaluations in the form of fuzzy numbers (parts A and B of Z-numbers).

Table 3.
Z-number-based normalized decision matrix.
Analysis of Table 3 points out the fact that the experts, depending on the criterion, give different priorities to one or another alternative.
As in the case of the values of the alternatives for each criterion, the values of the weights given by five experts should also be aggregated. Table 4 presents the results of the aggregation—Z-number-based weighted criteria.

Table 4.
Z-number based weights of criteria.
According to the expert opinion provided in Table 4, the more important criteria are C1, C6, and C5, followed by C4. Criteria C2 and C3 are less important.
In Table 5, the Z-number-based normalized weighted decision matrix and closeness to ideal solutions are presented. For this step, according to the TOPSIS procedure, the appropriate values of Z-numbers from Table 3 and Table 4 were multiplied, and relative closeness to ideal solutions were calculated based on Definition 4.

Table 5.
Normalized weighted decision matrix and closeness values to ZPIS and ZNIS.
The results of the calculations of the relative closeness based on Formulas (4)–(6) are illustrated in Figure 4.
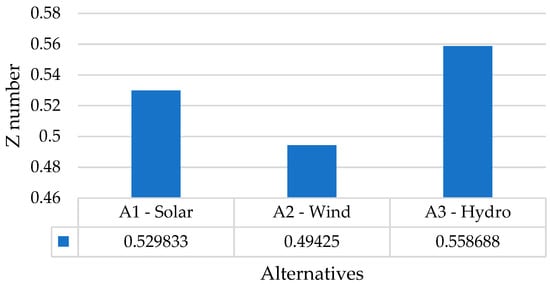
Figure 4.
Relative closeness of alternatives to ideal solutions: the first part of the Karabakh economic region (mountains and foothill). Source: own calculation.
According to the relative closeness provided in Figure 4, the experts generally prioritized alternative A3 (hydro), followed by A1 (solar) and A2 (wind) for the first part of the Karabakh economic region (mountains and foothill).
Similar calculations were carried out for the second part of the Karabakh economic region (plain). Here, we present only final results.
Based on various criteria, Table 6 specifies the aggregation of Z-number based evaluations of alternatives.

Table 6.
Example of Z-number-based aggregated evaluations of alternatives, with respect to various criteria.
After the aggregation of Z-number-based expert evaluations, the resulting Z-number-based normalized decision matrix is presented in Table 7. Aggregation was fulfilled according to the approach mentioned before.

Table 7.
Z-number-based normalized decision matrix.
Z-number-based normalized weighted decision matrix and closeness to ideal solutions are presented in Table 8.

Table 8.
Normalized weighted decision matrix and closeness values to ZPIS and ZNIS.
A simple acquaintance with the opinions of experts, formalized in Table 7 and Table 8, does not allow one to immediately draw an unambiguous conclusion about the best alternative. Only after calculating the relative closeness to positive and negative ideal solutions is it possible to define best alternative.
The relative closeness of alternatives to ideal solution (see Figure 5) are A1 = 0.536833, A2 = 0.507854, A3 = 0.521813. The best alternative is A1 (solar), followed by A3 (hydro) and A2 (wind) for the second part of the Karabakh economic region (plain).
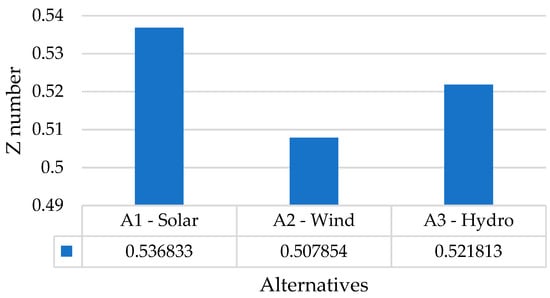
Figure 5.
Relative closeness of alternatives to ideal solutions: the second part of the Karabakh economic region (plain). Source: own calculation.
3.2. Guba-Khachmaz Region
The solution for the Guba-Khachmaz region also provided different rankings of the renewables for the first (seaside) and second (foothill) parts of the region. On the seaside part of Guba-Khachmaz region (see Figure 6), the wind power was much higher than in other parts [32].
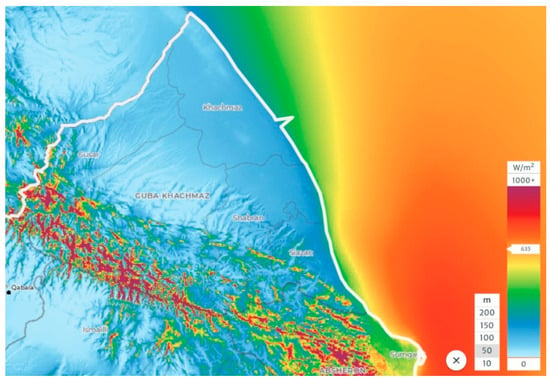
Figure 6.
Mean power density (height 50 m) on the seaside part of the Guba-Khachmaz region. Source: Global Wind Atlas.
The example of expert evaluation for the first and second parts of this region, expressed by the linguistic form of Z-number-based values, is presented in Table 9.

Table 9.
Z-number-based aggregated evaluations for the Guba-Khachmaz region.
As can be seen from Table 9, expert estimates for the two different parts of the same region are different.
Applying the Z-number-based TOPSIS method with the weights of the criteria from Table 4 and the codebook (Table 1), we obtained the next relative closeness of alternatives to ideal solution provided in Figure 7: A1 = 0.55772, A2 = 0.57407, A3 = 0.52763. The best alternative is A2 (wind).
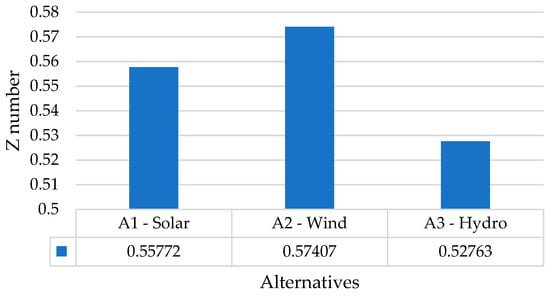
Figure 7.
Relative closeness of the alternatives to the ideal solutions: the first part of the Guba-Khachmaz region economic region (seaside). Source: own calculation.
Similar calculations were carried out for the second part of the region. The values of the relative closeness of the alternatives to the ideal solution are shown in Figure 8: A1 = 0.57758, A2 = 0.50909, and A3 = 0.51997. The best alternative is A1 (solar).
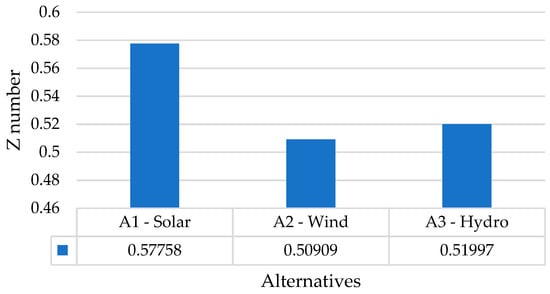
Figure 8.
Relative closeness of the alternatives to the ideal solutions: the second part of the Guba-Khachmaz economic region (foothill). Source: own calculation.
Economic diversification and transition to renewable energy sources are economically as well as environmentally good choices for developing and sustaining Azerbaijan. As this study suggests, before making an effective investment decision, extensive analysis of different parts of economic regions of Azerbaijan should be a prerequisite. In this regard, this study fills in a big knowledge gap on the mentioned topic in the scientific literature. It will serve policymakers as a helpful analytical tool to better address and initiate new policies.
4. Conclusions
Use of the green energy sources is a crucial element of sustainable development. Developers of green energy programs encounter a situation when green energy resources with potentially high production capacities are distributed unevenly within the economic regions of the country characterized by different natural and geographical conditions. In this paper, such a case was considered for the regions of Azerbaijan, and an approach based on the decomposition of the economic regions is proposed for the decision making.
Given that the MCDM task ranks and selects energy resources under high-level uncertainty, a model and decision procedures based on the formation of Z-numbers were developed and evaluated in the cases of two economic regions that have different natural and geographical settings: Karabakh and Guba-Khachmaz regions.
For the problem solution, the Z-TOPSIS method was applied. Solutions obtained for different parts of the same region show that sub-regions with different natural and geographical conditions provided different rankings for renewables. The use of direct calculations with Z-numbers can provide decision-makers with solutions that are based on fuzzy information and information reliability. The rankings of renewables were different in the mountain and foothill areas of the Karabakh region and the plain area. In mountain and foothill areas, hydro had higher priority, followed by solar. In the plain area, solar was followed by hydro. Similar models were developed for Guba-Khachmaz region. Results were also different for seaside and foothill areas. At the seaside, wind had higher priority, followed by solar, and in the foothill area, the solar and hydro, respectively.
Results obtained show that Z-extensions of the MCDM methods, based on direct calculations with Z-numbers, efficiently solved the renewable selection task and can be applied for the solution of the other MCDM tasks in the energy sector and other fields.
The results of this research are of extreme importance for policy makers and investors in the decision-making process on the way to the sustainable development of Azerbaijan.
Author Contributions
Conceptualization, M.N. and J.M. (Jeyhun Mammadov); methodology, A.N.; software, J.M. (Joshgun Mammadov); validation, M.N., J.M. (Jeyhun Mammadov), A.N., and J.M. (Joshgun Mammadov); formal analysis, M.N., J.M. (Jeyhun Mammadov), A.N., and J.M. (Joshgun Mammadov); investigation, M.N., and J.M. (Jeyhun Mammadov); resources, M.N.; data curation, A.N.; writing—original draft preparation, M.N. and A.N.; writing—review and editing, J.M. (Joshgun Mammadov); supervision, M.N.; project administration, J.M. (Jeyhun Mammadov). All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Ethical review and approval were waived for this study due to due to non-existence of ethical concerns and conflicts of interests.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Information was obtained through the analysis of the regions’ conditions and experts’ opinions. The data are available on request from the corresponding authors.
Conflicts of Interest
The authors declare no conflict of interest.
References
- The State Statistical Committee of the Republic of Azerbaijan (SSC). GDP Production in the Section of Oil and Non-Oil of Economy. Available online: https://stat.gov.az/source/system_nat_accounts/en/007_1en.xls (accessed on 21 September 2022).
- The State Statistical Committee of the Republic of Azerbaijan (SSC). Renewable Energy Supply, Thousand TOE. Available online: https://stat.gov.az/source/balance_fuel/en/001_5en.xls (accessed on 21 September 2022).
- The World Development Indicators, the World Bank. Available online: https://api.worldbank.org/v2/en/country/AZE?downloadformat=excel (accessed on 21 September 2022).
- The Ministry of Energy of the Republic of Azerbaijan. Available online: https://minenergy.gov.az/en/alternativ-ve-berpa-olunan-enerji/azerbaycanda-berpa-olunan-enerji-menbelerinden-istifade (accessed on 21 September 2022).
- Kaya, I.; Çolak, M.; Yildiz, F.T. A comprehensive review of fuzzy multi criteria decision making methodologies for energy policy making. Energy Strategy Rev. 2019, 24, 207–228. [Google Scholar] [CrossRef]
- Kaya, I.; Çolak, M.; Yildiz, F.T. Use of MCDM techniques for energy policy and decision-making problems: A review. Int. J. Energy Res. 2018, 42, 2344–2372. [Google Scholar] [CrossRef]
- Tasri, A.; Susilawati, A. Selection among renewable energy alternatives based on a fuzzy analytic hierarchy process in Indonesia. Sustain. Energy Technol. Assess. 2014, 7, 34–44. [Google Scholar] [CrossRef]
- Abdullah, L.; Najib, L. Sustainable energy planning decision using the intuitionistic fuzzy analytic hierarchy process: Choosing energy technology in Malaysia. Int. J. Sustain. Energy Novemb. 2014, 35, 360–377. [Google Scholar] [CrossRef]
- Papapostolou, A.; Karakosta, C.; Doukas, H. Analysis of policy scenarios for achieving renewable energy sources targets: A fuzzy TOPSIS approach. Energy Environ. 2017, 28, 88–109. [Google Scholar] [CrossRef]
- Pavlović, B.; Ivezić, D.; Živković, M. A multi-criteria approach for assessing the potential of renewable energy sources for electricity generation: Case Serbia. Energy Rep. 2021, 7, 8624–8632. [Google Scholar] [CrossRef]
- Afsordegan, A.; Sánchez, M.; Agell, N.; Zahedi, S.; Cremades, L.V. Decision making under uncertainty using a qualitative TOPSIS method for selecting sustainable energy alternatives. Int. J. Environ. Sci. Technol. 2016, 13, 1419–1432. [Google Scholar] [CrossRef]
- Cengiz, M.T.; Taşkin, H. A fuzzy hybrid decision model for renewable energy sources selection. Int. J. Comput. Exp. Sci. Eng. 2018, 4, 6–10. [Google Scholar] [CrossRef]
- Çolak, M.; Kaya, İ. Prioritization of renewable energy alternatives by using an integrated fuzzy MCDM model: A real case application for Turkey. Renew. Sustain. Energy Rev. 2017, 80, 840–853. [Google Scholar] [CrossRef]
- Das, A.; Shabbiruddin. Renewable energy source selection using analytical hierarchy process and quality function deployment: A case study. In Proceedings of the 2016 Second International Conference on Science Technology Engineering and Management (ICONSTEM), Chennai, India, 30–31 March 2016. [Google Scholar] [CrossRef]
- Erdogan, M.; Kaya, I. An integrated multi-criteria decision-making methodology based on type-2 fuzzy sets for selection among energy alternatives in Turkey. Iran. J. Fuzzy Syst. 2015, 12, 1–25. [Google Scholar] [CrossRef]
- Ervural, B.C.; Zaim, S.; Demirel, O.F.; Aydin, Z.; Delen, D. An ANP and fuzzy TOPSIS-based SWOT analysis for Turkey’s energy planning. Renew. Sustain. Energy Rev. 2017, 82, 1538–1550. [Google Scholar] [CrossRef]
- Kang, H.; Hung, M.; Pearn, W.; Lee, A.; Kang, M. An Integrated Multi-Criteria Decision Making Model for Evaluating Wind Farm Performance. Energies 2011, 4, 2002–2026. [Google Scholar] [CrossRef]
- Şengül, Ü.; Eren, M.; Shiraz, S.; Gezder, V.; Şengül, A. Fuzzy TOPSIS method for ranking renewable energy supply systems in Turkey. Renew. Energy 2015, 75, 617–625. [Google Scholar] [CrossRef]
- Shatnawi, N.; Abu-Qdais, H.; Qdais, F.A. Selecting renewable energy options: An application of multi-criteria decision making for Jordan. Sustain. Sci. Pract. Policy 2021, 17, 209–219. [Google Scholar] [CrossRef]
- Wang, C.-N.; Kao, J.-C.; Wang, Y.-H.; Nguyen, V.T.; Nguyen, V.T.; Husain, S.T. A Multicriteria Decision-Making Model for the Selection of Suitable Renewable Energy Sources. Mathematics 2021, 9, 1318. [Google Scholar] [CrossRef]
- Solangi, Y.A.; Tan, Q.; Mirjat, N.H.; Valasai, G.D.; Khan, M.W.; Ikram, M. An Integrated Delphi-AHP and Fuzzy TOPSIS Approach toward Ranking and Selection of Renewable Energy Resources in Pakistan. Processes 2019, 7, 118. [Google Scholar] [CrossRef]
- Lee, H.C.; Chang, C.-T. Comparative analysis of MCDM methods for ranking renewable energy sources in Taiwan. Renew. Sustain. Energy Rev. 2018, 92, 883–896. [Google Scholar] [CrossRef]
- Andejany, M. Ranking Renewable Energy Sources in Saudi Arabia. Int. J. Eng. Res. Technol. 2021, 14, 569–581. Available online: http://www.irphouse.com/ijert21/ijertv14n6_12.pdf (accessed on 14 September 2022).
- Zadeh, L.A. A note on Z-numbers. Inf. Sci. 2011, 181, 2923–2932. [Google Scholar] [CrossRef]
- Nuriyev, M. Z-numbers Based Hybrid MCDM Approach for Energy Resources Ranking and Selection. Int. J. Energy Econ. Policy 2020, 10, 22–30. [Google Scholar] [CrossRef]
- Rathore, N.; Debasis, K.; Singh, M.P. Selection of Optimal Renewable Energy Resources Using TOPSIS-Z Methodology. In Advances in Communication and Computational Technology: Select Proceedings of ICACCT 2019; Springer: Singapore, 2020; pp. 967–975. [Google Scholar]
- Aliev, R.A.; Huseynov, O.H.; Aliyev, R.R.; Alizadeh, A.A. The Arithmetic of Z-Numbers: Theory and Applications; World Scientific: Singapore, 2015. [Google Scholar] [CrossRef]
- Aliev, R.A.; Pedrycz, W.; Huseynov, O.H.; Eyupoglu, S.Z. Approximate reasoning on a basis of Z-number valued If-then rules. IEEE Trans. Fuzzy Syst. 2017, 25, 1589–1600. [Google Scholar] [CrossRef]
- Chen, C.T. Extensions of the TOPSIS for group decision-making under fuzzy environment. Fuzzy Sets Syst. 2000, 114, 1–9. [Google Scholar] [CrossRef]
- Howard, K.; Israfilov, R.; Rashidov, T.; Griffith, A.; Ismailova, M.; Rashidov, T. Use of groundwater models for managing serious urban water issues in Baku, the capital city of Azerbaijan. In Proceedings of the International Symposium on New Directions in Urban Water Management, Paris, France, 12–14 September 2007. [Google Scholar]
- Global Solar Atlas. Available online: https://globalsolaratlas.info/map?c=39.956912,47.04895,7&r=AZE (accessed on 15 September 2022).
- Global Wind Atlas. Available online: https://globalwindatlas.info (accessed on 15 September 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).