Dynamic Response Analysis on Stress and Displacement of the Shield Tunnel Structure and Soil Layer under Train-Induced Vibration in Xiamen Metro Line 6

Abstract

Tunnel engineering develops rapidly. To study the dynamic response of shield tunnel structure and its bottom soil layer caused by metro train operation, a three-dimensional finite-difference dynamic calculation method is used to establish a shield tunnel-soil layer coupling model based on the shield tunnel project of Maluan Central Station-Jimei Island Station of Xiamen Metro Line 6, and the dynamic response of tunnel structure and its bottom soil layer caused by metro train operation is calculated. The results show that: Under the action of train-induced vibration, the shield tunnel structure mainly bears compressive stress and generates compressive deformation. The dynamic response of tunnel structure represents a significant increasing trend with the enhancement of train-induced vibration load. Under the same load strength, dynamic response change amplitude of structure is not obvious with tunnel structural stiffness, stress is gradually increasing, and displacement is weakening. The deeper the soil depth at the bottom of the shield tunnel structure, the weaker the dynamic response of the soil layer. The stress response of the soil layer at the same depth is increasing with the train-induced vibration load improving, but the displacement response has a stage characteristic. The dynamic response of the soil layer at the same depth does not change obviously with the increase in shield tunnel structural stiffness, but the stress response gradually increases, and the displacement response becomes weak. In general, investigation of the dynamic response of the subway shield tunnel under train-induced vibration has important practical significance for maintaining the long-term safe operation of subway tunnels.

1. Introduction

In recent years, with the rapid and efficient development of the global economy and urbanization, the urban population has grown rapidly, resulting in increasingly serious urban traffic congestion. The construction of urban rail transit can effectively relieve urban traffic pressure. At present, the subway has become one of the main means of urban rail transit because of its advantages, such as fast driving speed, large carrying capacity, clean and comfortable riding environment, and more safety and punctuality compared with ordinary traffic tools. By the end of 2021, 541 cities in 79 countries and regions opened urban rail transit and have put their urban rail transit lines into operation, with a total length of 36,854.20 km. Among them, 188 cities in 62 countries and regions have opened metro lines (excluding light rail, trams, and others), with a total length of 18,952.29 km. Shanghai (851.63 km), Beijing (824.20 km), and Chengdu (612.70 km) rank among the top three in the 2021 rankings of metro operating mileage in cities around the world [1]. Although the construction of the subway makes it more convenient for urban residents to travel, there is also an urgent need to address some problems in subway projects. The construction of urban subways primarily adopts the shield tunneling method. The shield tunnel is not only affected by the multi-directional stress of the surrounding rock but also faces the long-term effect of the vibration load of the train during the operation period. The train-induced vibration load is the load that can be generated by a dynamic interaction between rough wheels and uneven rail tracks, and it can induce the dynamic response of the tunnel structure and surrounding environment [2]. The dynamic response of the shield tunnel structure and its surrounding soil layer is complicated and varied under train-induced vibration loading due to the subway having a large passenger capacity and a long running time during operation. Under the action of the long-term vibration load, the tunnel lining structure may crack, peel off the concrete at the top of the tunnel, or even bulge and deform at the bottom, which will lead to water leakage and other problems. In addition, the surrounding soil will also experience sand liquefaction, uneven settlement, and ground collapse under the long-term train-induced vibration load [3,4,5,6]. The initial damage during tunnel construction is accumulated during operation, which can ultimately result in a decrease in structure resistance and loss of function due to the long-term repeated function of the vibration effect [7]. Therefore, research into the dynamic response characteristics and rules of shield tunnel structure and its surrounding environment under train-induced vibration loading also plays a pivotal role in the subway project. The findings will provide a theoretical basis for shield tunnel safety assessment and the design of structural vibration reduction methods.

A series of problems caused by train-induced vibrations has attracted widespread attention in society. The study and discussion are gradually increasing about the influence of train-induced vibration load on tunnel structure and surrounding environment. Currently, domestic and foreign scholars have carried out some related research in this field. Based on the similarity theory of model test, Yuan (2014) carried out the subway-soil interaction model test under train-induced vibration load and analyzed the dynamic response characteristics of tunnel lining structure and surrounding rock soil [8]. Lei et al. (2015) used a dynamic finite difference method and investigated the dynamic response of tunnel structures and accumulated foundation deformation under train vibration loads [9]. Yuan et al. (2015,2017) utilized the finite element method to establish the tunnel structure–saturated soil coupling analysis model and researched the time-domain response and spatial distribution of the shield tunnel and saturated soil under subway train loads [10,11]. He et al. (2015) conducted a numerical simulation of soil around the tunnel and analyzed its variations of the acceleration and displacement response under vibration loads of the subway [12]. Saba Gharehdash and Milad Barzegar (2015) utilized a complex elastoplastic 3D dynamic finite-difference model to study the dynamic response of the shield tunnel structure under the vibrating load of the metro train [13]. Shi et al. (2015) established a vehicle-track coupling and tunnel-soil coupling model to predict the displacement of the soil below the tunnel due to train vibration during metro operation [14]. Huang et al. (2015) conducted a similarity ratio dynamic model test to study the dynamic response characteristics of the tunnel invert and its foundation soil under different train operating speeds and investigated the relation between dynamic stress distribution and train speed [15]. Luo et al. (2016) analyzed the dynamic characteristics and estimated settlement of soft soil under subway vibration loading through the finite element simulation of subway foundation [16]. Lai et al. (2016) investigated the characteristics and the spreading rules of vibration response of the metro train load to the structure of a shield tunnel by applying the three-dimensional dynamic finite element model [7]. Huang et al. (2017) through soil-water full coupling dynamic finite method investigated dynamic response and long-term settlement of a metro tunnel due to train vibration load based on DBLEAVES [17]. Yang et al. (2018) presented a series of physical model tests aimed at researching the influence of train loads on the dynamic response of stagger-jointed and uniform tunnel lining and surrounding soil [18]. Yan et al. (2018, 2020) used the finite element software ABAQUS and established a three-dimensional numerical model of shield tunnels, to reveal the vibration features of the overlapped shield tunnels under the action of different train speeds and vibration loads [19,20]. Yang et al. (2019) conducted an experiment, established a tunnel model applied train loads, and measured the dynamic response of the tunnels and the soils [21]. Pan et al. (2020) developed the train-tunnel-soil finite element model to analyze the dynamic responses of acceleration, displacement, and strain of the soils around the tunnel under train dynamic load [22]. Yang et al. (2020) conducted a systematic study that consist of numerical simulation and fatigue damage experiment and researched fatigue damage caused by the long-term dynamic load from a running train, in order to ensure the safety and serviceability of the cross tunnel lining [23]. Tian et al. (2021) built a three-dimensional numerical model of shield tunnel lining structure to study its dynamic reaction and fatigue crack propagation under the train vibration load [24]. Yang et al. (2021) established the three-dimensional finite element model for calculating the vibration response of railway to conclude the response rules of the displacement, speed, and acceleration of surrounding soil [25]. Li et al. (2021) established the model of vehicle-tunnel coupling vibration and studied the identification and location of the subway tunnel structural damage by using train vibration response [26]. Yang et al. (2021) studied the dynamic response characteristics of shield tunnels and surrounding soil under train vibration load through the method of model test combined with numerical simulation based on the time domain and frequency domain analysis [27]. Maziyar Bahri et al. (2022) simulated Line 1 of the metro in the city of Seville by numerical methods using FLAC^3D software and evaluated the surface settlements by taking the characteristics of the soil in Seville [28]. Jin et al. (2022) proposed a three-dimensional numerical model to evaluate the short-term and long-term displacement of the soft soil strata under the shield tunnel after construction [29]. Masoud Forsat et al. (2022) investigated the three-dimensional modeling of the metro tunnel for the case of the Tehran metro line and studied the factors influencing the stress and displacement of soil [30].

These results provide important insights into the research of the dynamic response of tunnel structure or its surrounding soil under the vibration load of the metro train. Researchers mainly analyzed shield tunnel structure, but have not treated the dynamic response characteristics of the soil layer at the bottom of the shield tunnel in much detail. Furthermore, few writers have been able to draw any systematic research into distinct rules in the dynamic response of shield tunnel structure and soil layer of its bottom with different train vibrations and different tunnel structural stiffness. Therefore, this paper adopts a three-dimensional finite-difference dynamic calculation method to establish a shield-tunnel coupling model based on the shield tunnel project between Maluan Central Station and Jimei Island Station of Xiamen Metro Line 6. The excitation force function was conducted at the bottom of the shield tunnel via stress loading. The displacement and stress response of the shield tunnel structure and its bottom soil layer were studied with four different train speeds and four different tunnels structural stiffness, respectively. It reveals the influence law of train speed and structural stiffness on the dynamic response of the tunnel structure and its bottom soil layer. This article aims to provide a significant reference value for the dynamic stability of the tunnel structure and its bottom soil layer and tunnel structural security design.

2. Dynamic Calculation Model and Parameters

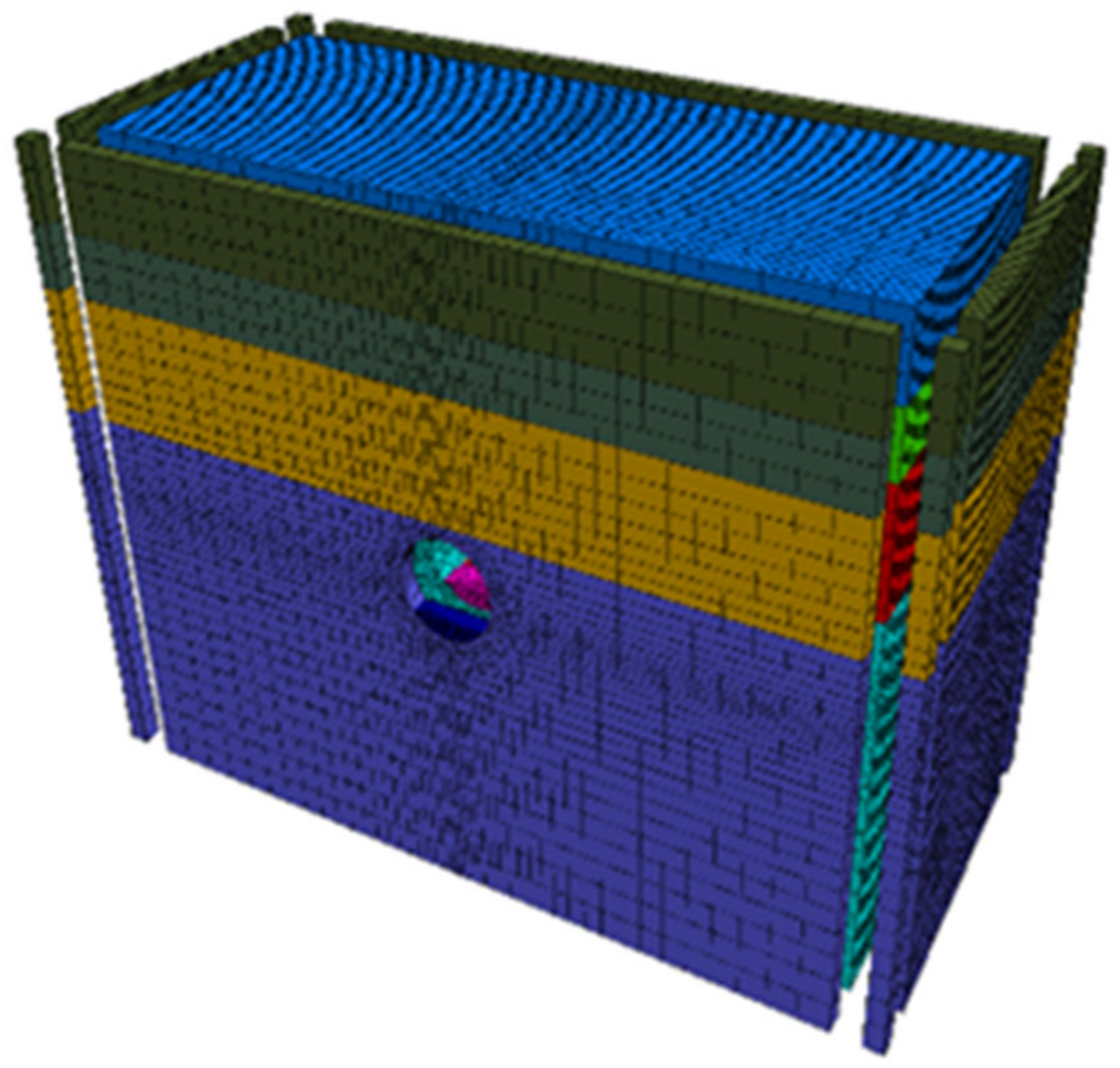
2.1. Establishment of Calculation Model and Determination of Parameters

To meet the requirements of the model size for dynamic calculation, based on the Saint–Venant principle and the influence range of tunnel excavation, fully considering geological conditions of the tunnel’s surrounding rock, the size of the three-dimensional dynamic numerical calculation solid model is 50 m × 20 m × 40 m, and the specific size of the tunnel structure is 6.2 m in outer diameter, 5.6 m in inner diameter, and 0.3 m in segment thickness. The buried depth of the tunnel is 16.8 m. According to geological survey data, the surrounding soil layer is composed of a silt layer, medium-coarse sand, residual sandy clay, and fully weathered granite from top to bottom. Since the vibration load of the train passing through once has little effect on the deformation of the tunnel structure, the tunnel structure in the numerical model employs the elastic constitutive relation, and the soil layer adopts the Mohr–Coulomb constitutive relation. Because this paper focuses on the dynamic response of tunnel structure and surrounding soil under train load, the shield tunnel lining structure is considered a homogeneous cylinder, ignoring the influence of segment joints. Additionally, the three-dimensional shell structure is used to simulate the segment in the shield tunnel. The tunnel structure model and physical and mechanical parameters of each stratum are shown in

Table 1. Model material parameters of numerical calculation.

Type	Density (kg/m3)	Dynamic Elastic Modulus (MPa)	Dynamic Shear Modulus (MPa)	Poisson Ratio	Internal Friction Angle (°)	Cohesion (kPa)
Silt layer	1580	81.2	28.3	0.47	7.1	9
Medium-coarse sand layer	1960	242.7	110.4	0.46	30	0
Residual sandy cohesive soil	1810	206.3	100.2	0.46	17.9	29
Fully weathered granite	1840	300.6	155.0	0.45	21.2	31
C35	2400	31,500	12,600	0.2	-	-
C45	2500	33,500	13,400	0.2	-	-
C50	2600	34,500	13,800	0.2	-	-
C55	2700	35,500	14,200	0.2	-	-

. The parameter was set by the properties of the saturated soil. C35, C40, C45, and C50 are the strength grades of segment concrete in the shield tunnel. Soil properties are shown in

Table 2. The mainly characteristic of soil layer.

Soil Layer	State	Main Engineering Geological Characteristics
Silt	flow plasticity	It is mainly composed of clay, containing organic matter and humic substances, with high natural water content.
Medium-coarse sand	medium dense	It mainly contains quartz medium and coarse sand.
Residual sandy cohesive soil	hard plasticity	It is mainly composed of weathered clay, silt, and quartz.
Fully weathered granite	state of hard soil	The original rock structure has been basically destroyed and weathered into soil except for quartz.

.

When meshing in FLAC^3D dynamic calculation, it is necessary to consider the size of the model grid. To achieve calculation accuracy, it should be ensured that the grid size Δ l is smaller than 1/8 to 1/10 of the wavelength λ corresponding to the highest frequency in the input wave. The train-induced vibration load frequency is in the range of 0~60 Hz, the shortest wavelength of the input vibration wave can be calculated according to the running speed of the subway train and the relevant physical and mechanical parameters. To meet the requirements, it shall be ensured that the grid size used in the calculation using the vibration wave is less than 1/10 of λ. If the load frequency is 60 Hz, the minimum shear wave velocity in the soil layer is v = 106 m/s, 1/10 λ= 0.177 m. The maximum grid size of the numerical calculation model is 0.05 m < 1/10 λ. The dynamic response characteristics of shield tunnel structure and surrounding soil layer are the main points studied. Then, the grid size of the calculation model is gradually enlarged from 0.05 m in the middle to 1 m on both sides in the horizontal and vertical directions to reduce the calculation time. The grid division is shown in Figure 1.

2.2. Train Loads and Monitoring Points Arrangement

2.2.1. Train Loads in Subway

Train-induced vibration load is transmitted through the wheel to the rail, and then from the rail to the tunnel structure. In order to obtain the dynamic response of the model under different train speed loads, the excitation force function is usually used to represent the vertical excitation load generated by train-induced vibration [31]. Its expression is:

$$\mathrm{F}\left(t\right)=P_0+P_1\sin {\omega }_{1}t+P_2\sin {\omega }_{2}t+P_3\sin {\omega }_{3}t,$$

(1)

where $P_0$ is the wheel self-weight load; $P_1$, $P_2$, and $P_3$ are vibration loads, so that the mass under spring of the train is $M_0$, and the corresponding vibration load amplitude is:

$$P_i=M_0{\alpha }_i{\omega }_i^2\left(i=1,2,3\right),$$

(2)

where $M_0$ is the unsprung mass under the train; ${\alpha }_i$ is a typical vector height; ${\omega }_i^2$ is the circular frequency of the non-uniform vibration wavelength at the corresponding speed. The expression is:

$${\omega }_i=2\pi v/L_i\left(i=1,2,3\right),$$

(3)

where $v$ is the running speed of the train; $L_i$ is the typical wavelength.

This paper selects the maximum train axle load 17 t, $M_0$ = 750 kg, irregularity vibration wavelength and vector height: $L_1$ = 10.0 m, ${\alpha }_1$ = 3.5 mm; $L_2$ = 2.0 m, α₂ = 0.4 mm; $L_2$ = 0.5 m, α₂ = 0.08 mm [19], the vertical excitation load is calculated when the train speed is 40 km/h, 60 km/h, 80 km/h and 100 km/h. The time history curve of train-induced vibration load is obtained through numerical processing, as shown in Figure 2.

The dynamic load is directly applied to the internal node of the model by APPLY interior. In order to obtain the dynamic response of the model under different train-induced loads, the load is expressed by the excitation force function, and it is applied to the bottom of the shield tunnel structure in the form of stress loading. After the dynamic response amplitude of each monitoring point is stable, the time-history curves of each monitoring point are derived, namely, the time-history curves of tunnel structure and bottom vibration load under different train speed loads are obtained.

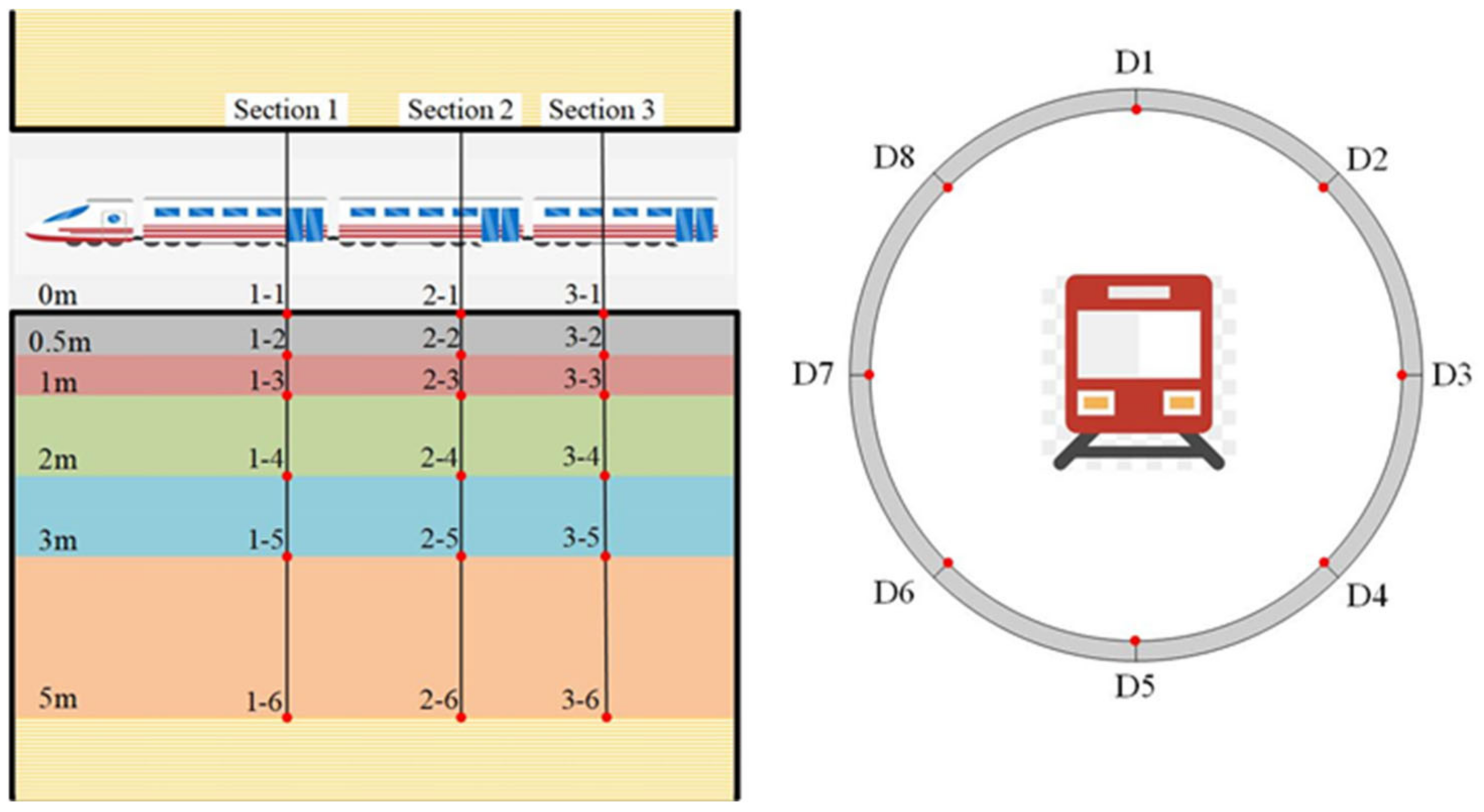
2.2.2. Monitoring Points Arrangement

The tunnel sections D1 (vault), D2 and D8 (spandrel), D3 and D7 (arch waist), D4 and D6 (arch foot), D5 (arch bottom), and the 0 m, 0.5 m, 1 m, 2 m, 3 m, and 5 m of the bottom soil layer are selected as monitoring points as shown in Figure 3.

2.3. Boundary Conditions and Damping Parameters

The actual engineering environment is a semi-infinite body, and the size of the model established in the numerical simulation is very limited. Therefore, in the dynamic analysis, there is a big difference between the influence of the model boundary on the wave propagation and the actual project. In order to ensure the accuracy of simulation, the boundary conditions of dynamic calculation in this paper are free field boundary conditions. The premise of using free field boundary in FLAC^3D is that the model is based on the horizontal and vertical direction is basically normal direction. The boundary is vertical around, and its normal direction is the x-axis or y-axis.

The condition imposed by the free field boundary is that the model is in a static equilibrium state, and the command of the free field boundary condition is invoked through the APPLY ff command.

In order to ensure the assumption of infinite extension around the model, the nodes on the free surface must be two-dimensional, the angular grid must be one-dimensional, and both of the grids are standard FLAC^3D domains. The free boundary effect of the model is shown in Figure 4. In the dynamic analysis, the correct selection of damping is the key to ensuring the reliability of numerical simulation. The Rayleigh damping provided by FLAC^3D difference calculation software is more consistent with the actual monitoring results [32,33]. The value of the minimum critical damping ratio is 0.05. The minimum center frequency is based on the velocity time history curve, adjusting f_min makes the energy mainly concentrated in the range of f_min–3f_min, at this time f_min is the minimum center frequency.

3. Analysis of Dynamic Response Characteristics of Shield Tunnel Structure

In order to study the dynamic response characteristics of subway tunnel structures under various train speed loads and the influence of the changeable segment concrete strength, under the premise of maintaining the same other influencing factors, the dynamic response of tunnel structures with four train speeds of 40 km/h, 60 km/h, 80 km/h, 100 km/h and four concrete strength grade of shield tunnel segment, C35, C45, C50, and C55 were compared.

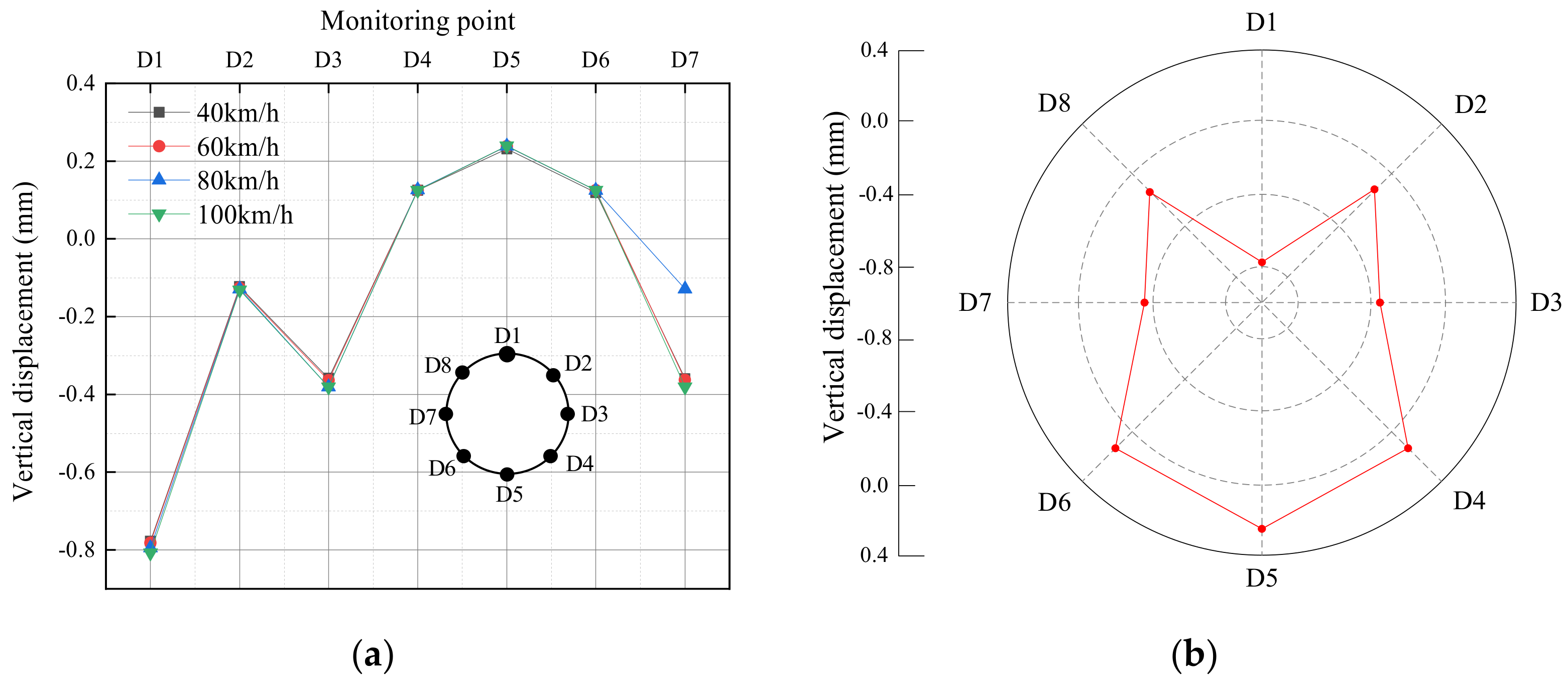
3.1. Dynamic Response of Tunnel Structures under Different Train-Induced Vibration Load

This section mainly analyzes the dynamic response characteristics of subway shield tunnel structure under different train-induced vibration loads (40 km/h, 60 km/h, 80 km/h, and 100 km/h) and its variation with the increase in train speed.

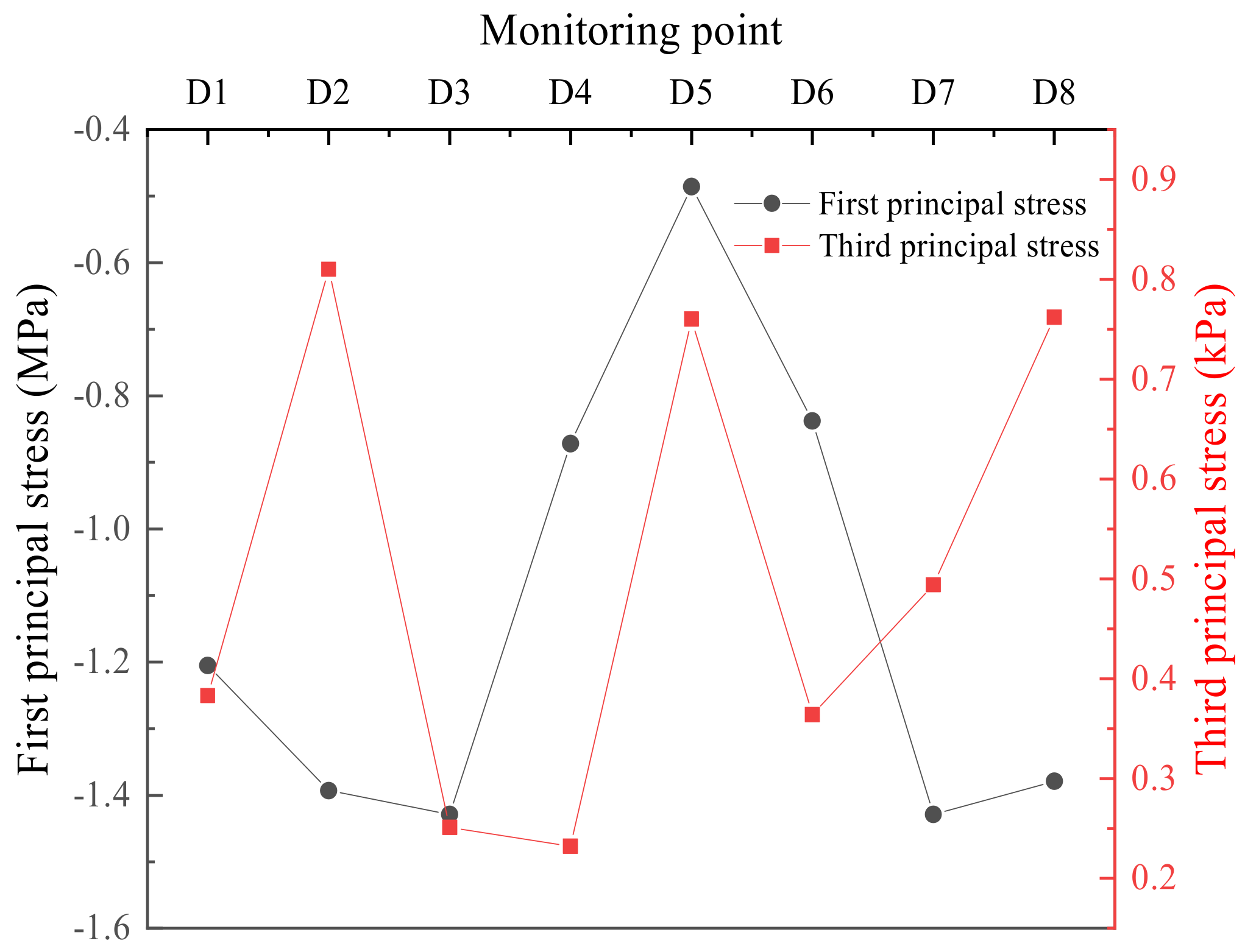
3.1.1. Dynamic Stress Response

Firstly, it is monitored that the stress of tunnel structure under 40 km/h train-induced vibration load, and the response curve of first principal and third principal stress are shown in Figure 5.

Through analyzing the vibration load when the train speed is 40 km/h, it can be seen that: The stress response of the subway shield tunnel structure is mainly the first principal stress, and the response value of the third principal stress is generally small. The two main characteristics are as follows: The value of the first principal stress is mainly negative, namely compressive stress. The stress value of the first principal stress at vault (D1) and arch waist (D3, D7) is relatively larger, and the peak value of the maximum first principal stress appears at the arch waist of the tunnel structure, which is −1.429 MPa. The value of the third principal stress is mainly positive, and the stress peak value is generally small, so the tensile stress on the tunnel structure has little effect on the tunnel structure. For example, at monitoring points D1, D5, D7, and D8, the peak values of the first principal stress of the subway shield tunnel are 1.205 MPa, 0.501 MPa, 1.429 MPa, and 1.393 MPa, respectively, and the peak values of the third principal stress are 0.383 kPa, 0.751 kPa, 0.512 kPa, and 0.762 kPa, respectively. Under the vibration load with a train speed of 40 km/h, the response of the tunnel structure is dominated by the first principal stress. In order to further study the influence of train-induced vibration load on the stress response of shield tunnel structure, the response laws of the first principal stress of shield tunnel structure under different train speeds (60 km/h, 80 km/h, 100 km/h) are studied, and the results are shown in Figure 6.

It can be seen from Figure 6 that under the vibration loads of various train speeds, the peak value of the maximum first principal stress in the subway shield tunnel structure appears at the arch waist (D3 and D7) of the tunnel structure, while the peak value of the first principal stress at the arch bottom (D5) of the tunnel is relatively smaller. When the train speed is 80 km/h, the first principal stress at D3 and D7 is 1.447 MPa and 1.458 MPa, and the first principal stress at D5 is 0.510 MPa. Figure 7 is the curve of the first principal stress at the representative measuring point varying with the train speed.

It can be seen from Figure 7 that the dynamic stress response of the shield tunnel structure under the vibration load of different train speeds shows the following laws: the variation range of the first principal stress at different monitoring points of the shield tunnel structure with the increase in train speed is slightly various, but the overall variation law is basically the same. The variation range of the first principal stress of the shield tunnel structure under the action of train-induced vibration is low when the train speed is small. When the train time is in a high range (60 km/h to 80 km/h), the response of the first principal stress of each monitoring point is more obvious. When the train speed is 40 km/h, the peak values of the first principal stress at D1, D5, D7, and D8 are 1.192 MPa, 0.454 MPa, 1.424 MPa, and 1.375 MPa, respectively. When the train speed is 60 km/h, the peak value of the first principal stress at the four monitoring points is 1.198 MPa, 0.464 MPa, 1.429 MPa, and 1.384 MPa. When the train speed is 80 km/h, the peak value of the first principal stress at the four monitoring points is 1.232 MPa, 0.510 MPa, 1.456 MPa, and 1.436 MPa. When the train speed increases from 40 km/h to 60 km/h, the variation amplitudes of the peak values of the first principal stress are 6 kPa, 10 kPa, 5 kPa, and 9 kPa, respectively. When the train speed increases from 60 km/h to 80 km/h, the variation amplitude of the peak values of the first principal stress are 34 kPa, 46 kPa, 27 kPa, and 52 kPa. This phenomenon indirectly shows that the higher the running speed of the subway train, the greater the impact on the shield tunnel structure.

3.1.2. Vertical Displacement Response

The vertical displacement of each monitoring point of the tunnel structure is monitored under the action of four train-induced vibration loads. The vertical displacement change curve of the representative monitoring point under different train speeds is shown in Figure 8. The variation curve of vertical displacement is shown in Figure 9.

It can be seen from Figure 8 that the peak value of displacement response of tunnel structure basically occurs at the moment when the train load acts, then tends to a relatively stable fluctuation, and finally reaches the equilibrium state. However, with the increase in train speed, the displacement fluctuation range of each monitoring point of tunnel structure will gradually expand, and the relative displacement between vault and arch bottom will also increase. Figure 9 shows that under the action of various train-induced vibration loads (the train speed is 40 km/h, 60 km/h, 80 km/h, and 100 km/h, respectively), the peak value of displacement at the five monitoring points of tunnel structure vault (D1), spandrel (D2 and D8), and arch waist (D3 and D7) is negative. The peak value of displacement at the arch foot (D4 and D6) and the arch bottom (D5) is positive, so the shield tunnel structure has compression deformation as a whole. At different train speeds, when the train-induced vibration load passes only once, the displacement response curves of each monitoring point of the tunnel structure are not significantly different. When the train speed is 40 km/h, 60 km/h, 80 km/h, and 100 km/h, respectively, the peak value of displacement of the shield tunnel vault (D1) is −0.778 mm, −0.782 mm, −0.795 mm and −0.808 mm; the displacements at the arch bottom (D5) of the shield tunnel are 0.231 mm, 0.238 mm, 0.238 mm and 0.239 mm, and the relative displacements between the vault and the arch bottom are 1.009 mm, 1.02 mm, 1.033 mm and 1.047 mm.

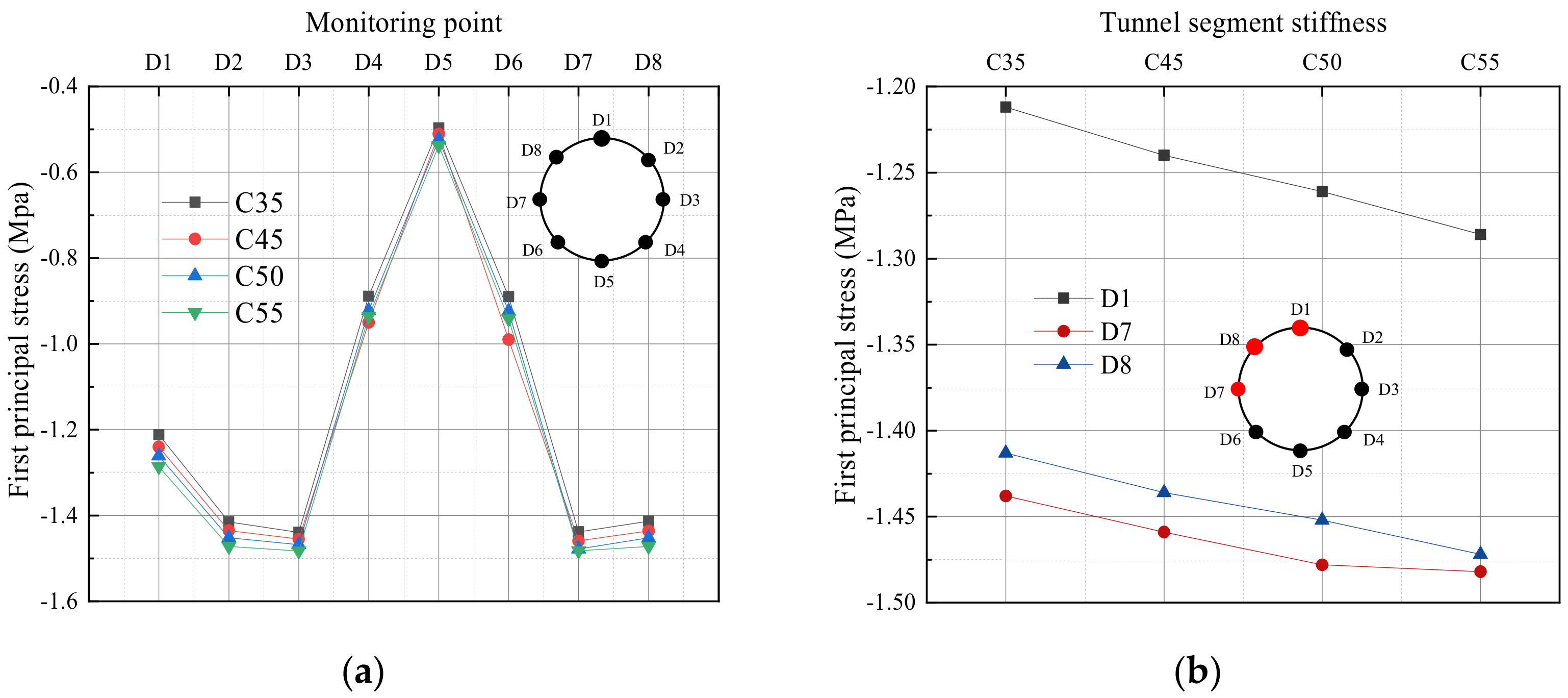
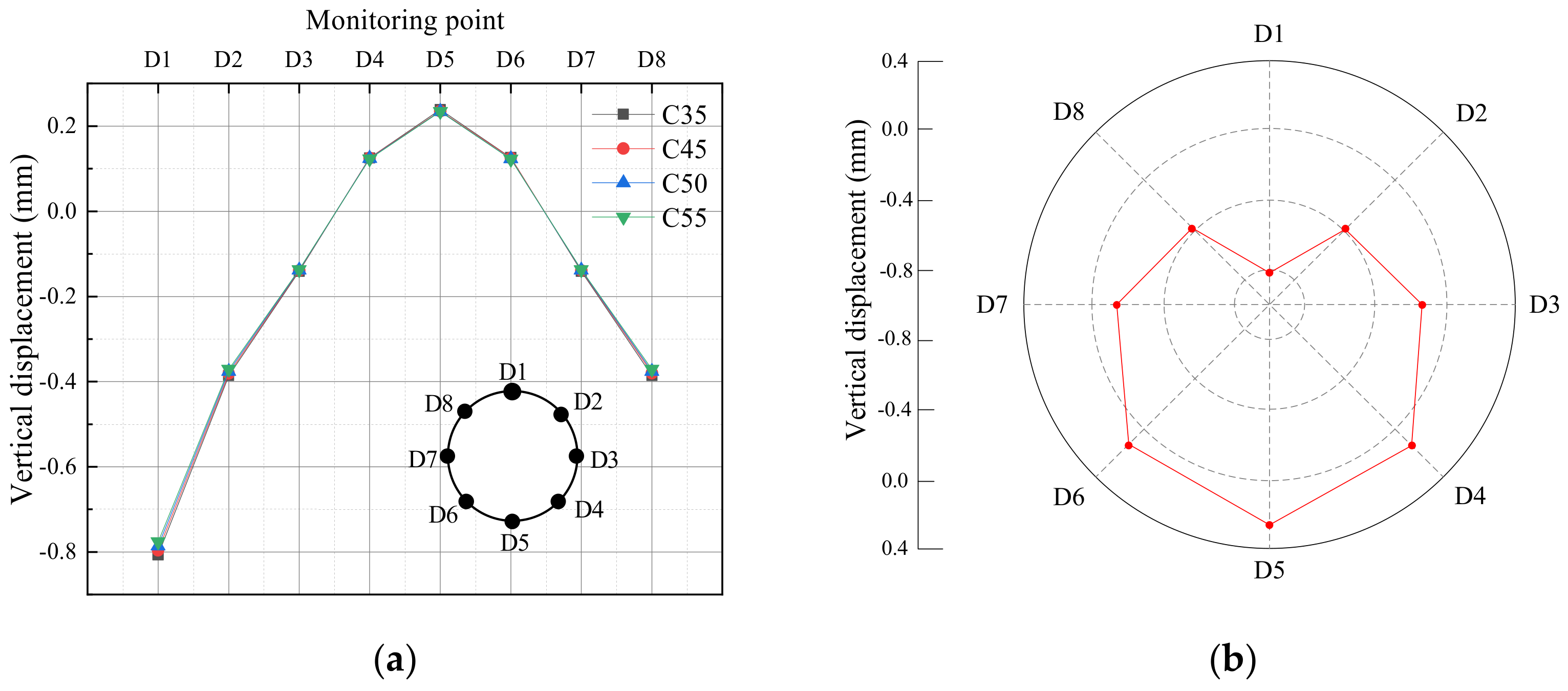
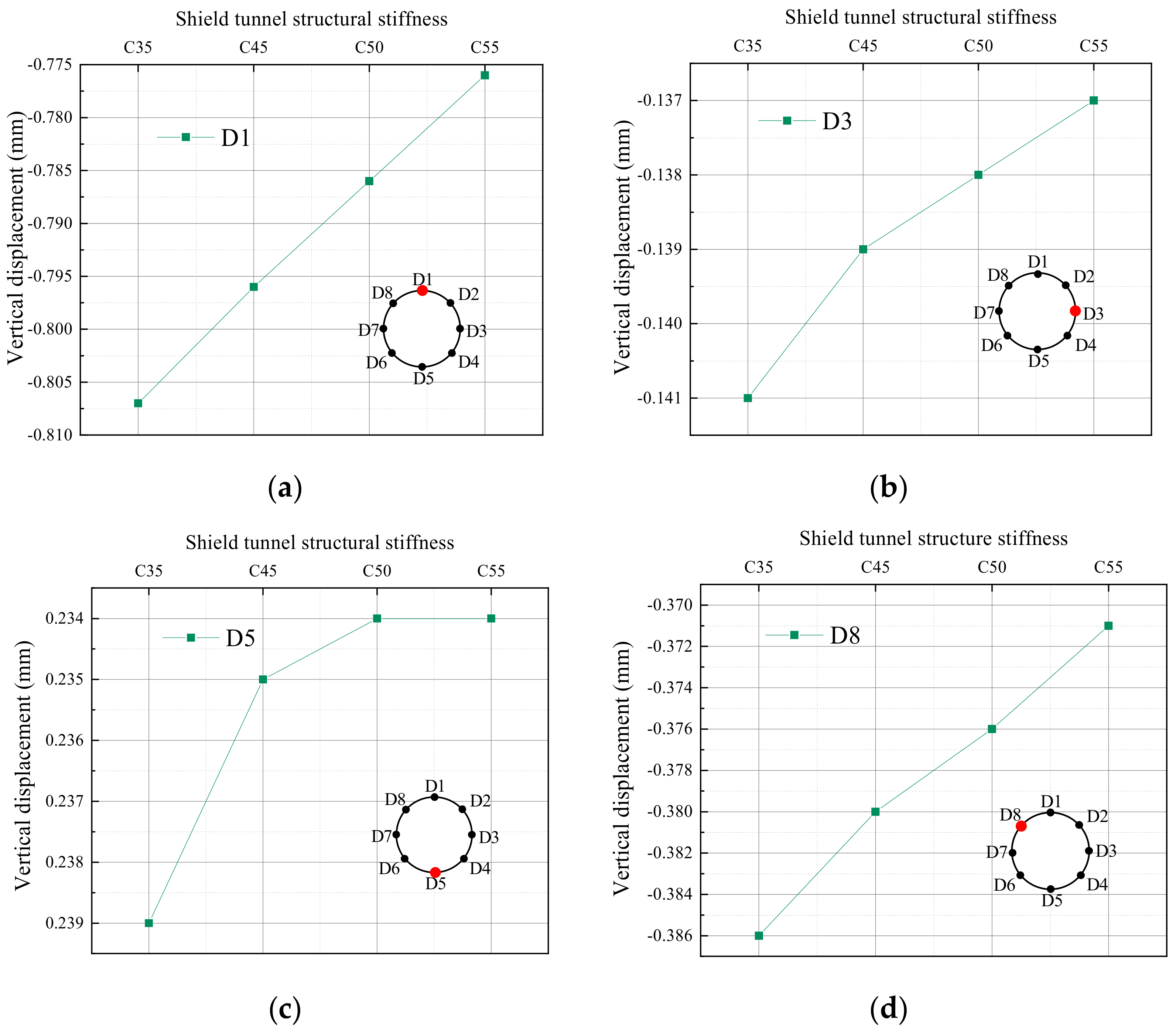
3.2. Dynamic Response of Tunnel Structures with Different Stiffness

The vibration load with a train speed of 80 km/h was applied at the bottom of the tunnel structure to explore the influence of the change in tunnel structure stiffness on the dynamic response characteristics of the tunnel structure.

3.2.1. First Principal Stress Response

Figure 10 shows the response characteristics of the first principal stress at each monitoring point of the shield tunnel structure under different structural stiffness (the strength grades of segment concrete are C35, C45, C50, and C55, respectively) when the train speed is 80 km/h.

It can be seen from Figure 10 that the maximum first principal stress peak value of the tunnel structure appears at the arch waist (D3, D7) when the train-induced vibration load is applied to the shield tunnel structure with different stiffness. With the increase in structural stiffness of the shield tunnel, the peak value of the first principal stress of each monitoring point shows an increasing trend, but the enhancement is not obvious, and the amplitude has a decreasing trend.

When the structural stiffness of the shield tunnel is C35, C45, C50, and C55, the peak value of the first principal stress at the D1 monitoring point is 1.212 MPa, 1.240 MPa, 1.261 MPa, and 1.280 MPa, and the growth is 0.028 MPa, 0.021 MPa, and 0.019 MPa, respectively. The peak value of the first principal stress at the D7 monitoring point is 1.438 MPa, 1.459 MPa, 1.478 MPa, and 1.482 MPa, and the growth is 0.021 MPa, 0.019 MPa, and 0.004 MPa, respectively. The peak value of the first principal stress at the D8 monitoring point is 1.413 MPa, 1.436 MPa, 1.452 MPa, and 1.469 MPa, and the growth is 0.023 MPa, 0.016 MPa, and 0.017 MPa, respectively. Thus, the influence of shield segment concrete strength grade on the first principal stress response of tunnel structure is not significant. In the design of tunnel structure, considering the material performance and economic applicability, it is not the case that the higher the concrete strength grade, the better the safety of the tunnel structure.

3.2.2. Vertical Displacement Response

The vibration load is applied at the bottom of the tunnel structure, and the variation curve of vertical displacement at tunnel structure with different structural stiffness (the strength grades of segment concrete are C35, C45, C50, and C55, respectively) are shown in Figure 11. The vertical displacement curves of the representative monitoring point are shown in Figure 12.

What can be clearly seen in Figure 11 is the phenomenon of the displacement peaks at the shield tunnel arch bottom (D5) and arch feet (D4, D6) are all negative, and the displacement responses of the other measuring points are positive with various shield tunnel structural stiffness. Therefore, the tunnel structure as a whole produces compression deformation. It can be seen from Figure 12 that with the enhancement of structural stiffness, the peak value of vertical displacement of each monitoring point of the shield tunnel structure shows a decreasing trend, and the relative displacement between the vault and the arch bottom of the tunnel structure also gradually decreases, but the change amplitude is weakening. It can be concluded that the change in tunnel structure stiffness has a certain influence on the peak value in the displacement of the tunnel structure. When the concrete strength grade is improved, the elastic modulus is increasing, so the deformation of materials will decline. Therefore, with the increase in tunnel structure stiffness, the bearing capacity is stronger, and the deformation performance of response will be weakened. When the strength grade of the shield tunnel structural segment is C35, C45, C50, and C55, the displacement peak values at D3 monitoring points are 0.141 mm, 0.139 mm, 0.138 mm, and 0.137 mm, respectively. With the increase in stiffness, the change amplitude is 0.002 mm, 0.001 mm, and 0.001 mm. The peak values of displacement at the D8 monitoring point are 0.386 mm, 0.38 mm, 0.376 mm, and 0.371 mm, respectively, and the change amplitudes are 0.006 mm, 0.004 mm, and 0.005 mm, respectively. The relative displacements between the vault and the arch bottom under the four stiffness grades are 1.046 mm, 1.004 mm, 1.020 mm, and 1.010 mm, respectively, and the variation amplitudes are 0.042 mm, 0.016 mm, and 0.010 mm, respectively.

4. Analysis of Dynamic Response Characteristics of Soil Layer at the Bottom of Tunnel

In order to study the dynamic response characteristics of the soil layer at the bottom of the shield tunnel under different train speed loads and the influence of the change in the tunnel structure stiffness, under the premise of maintaining the same other influencing factors, four train speeds of 40 km/h, 60 km/h, 80 km/h and 100 km/h and four structural stiffness of C35, C45, C50, and C55 are selected for comparative study of the dynamic response.

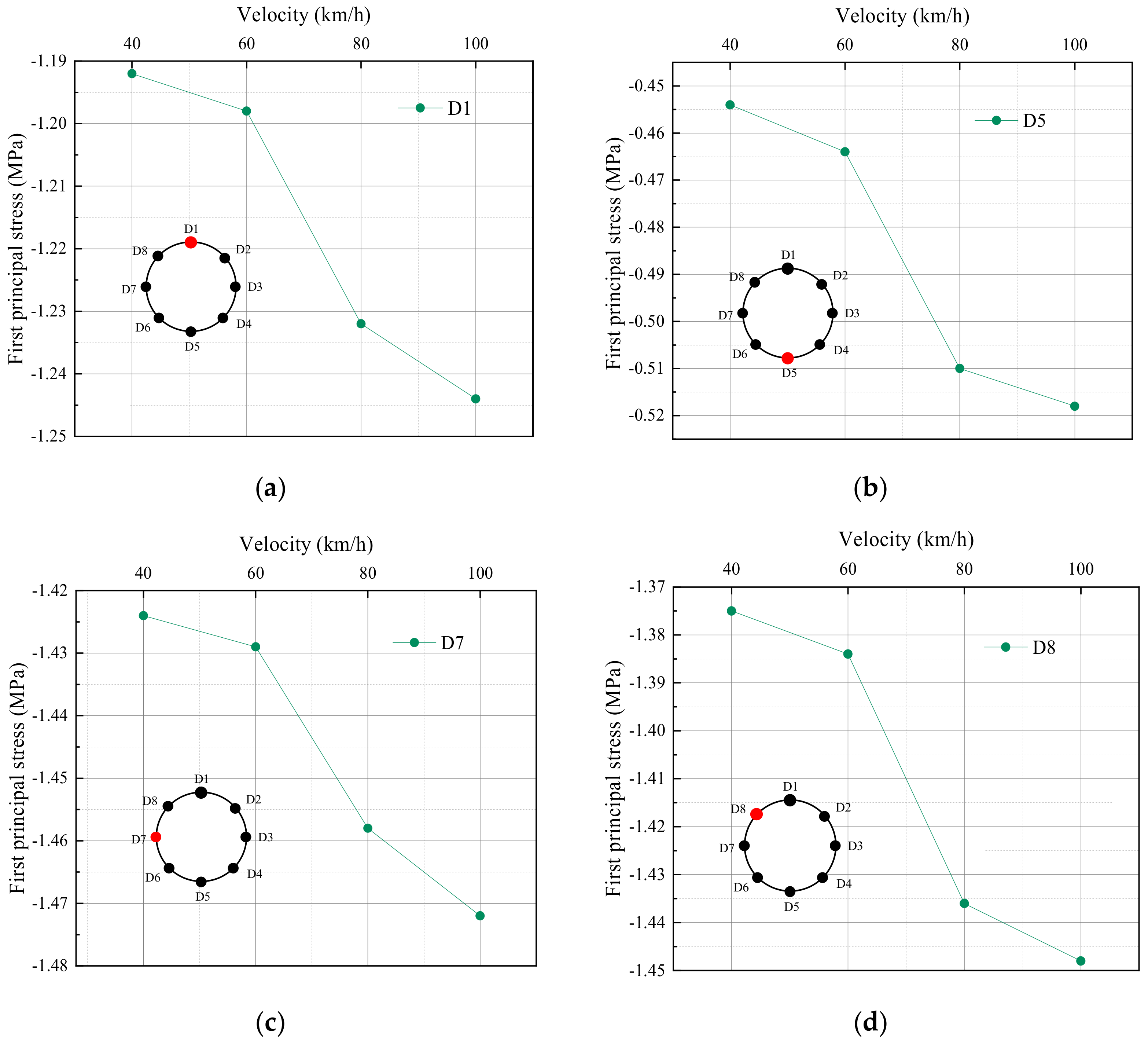
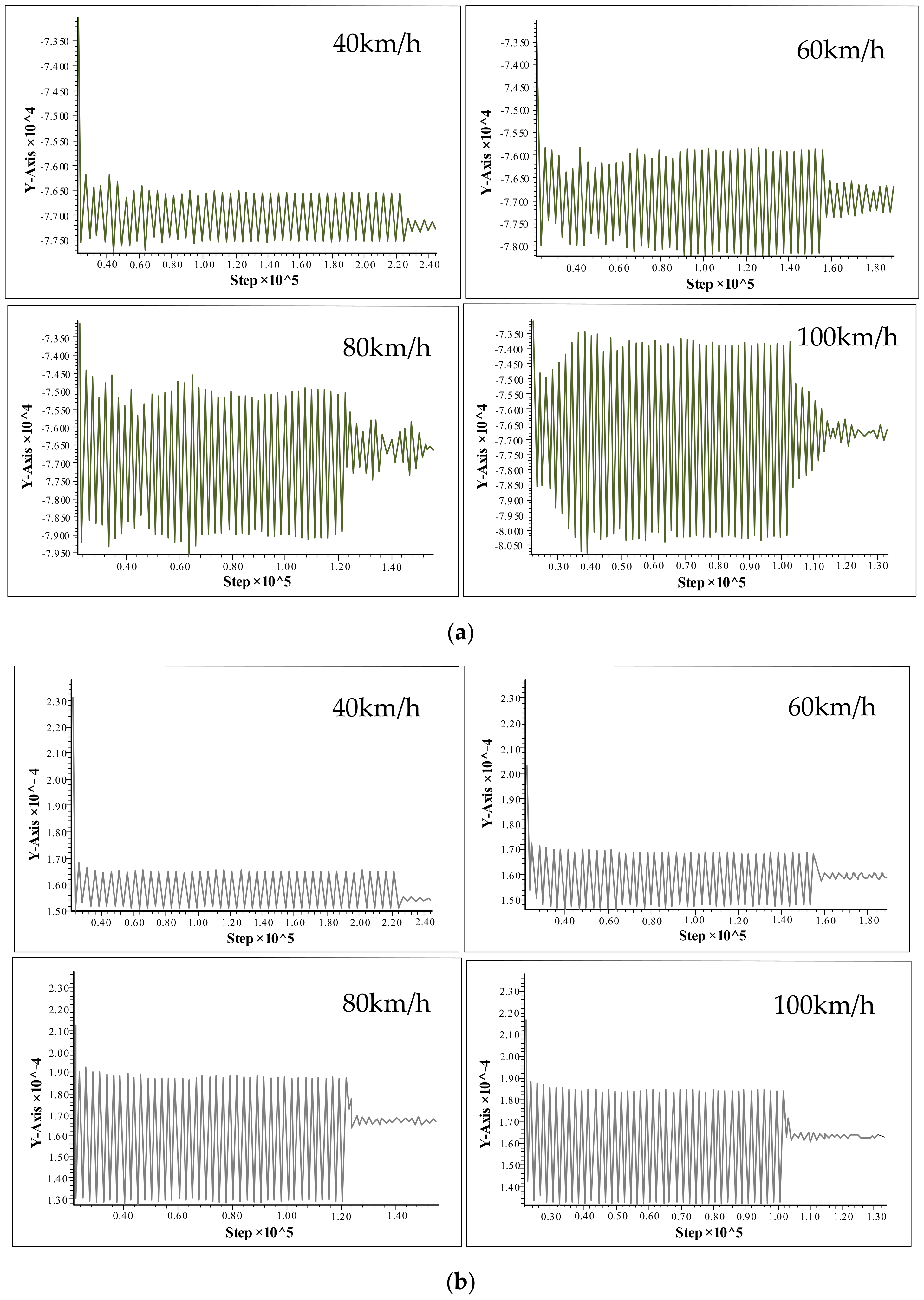
4.1. Dynamic Response of Soil Layer under Different Train Speed

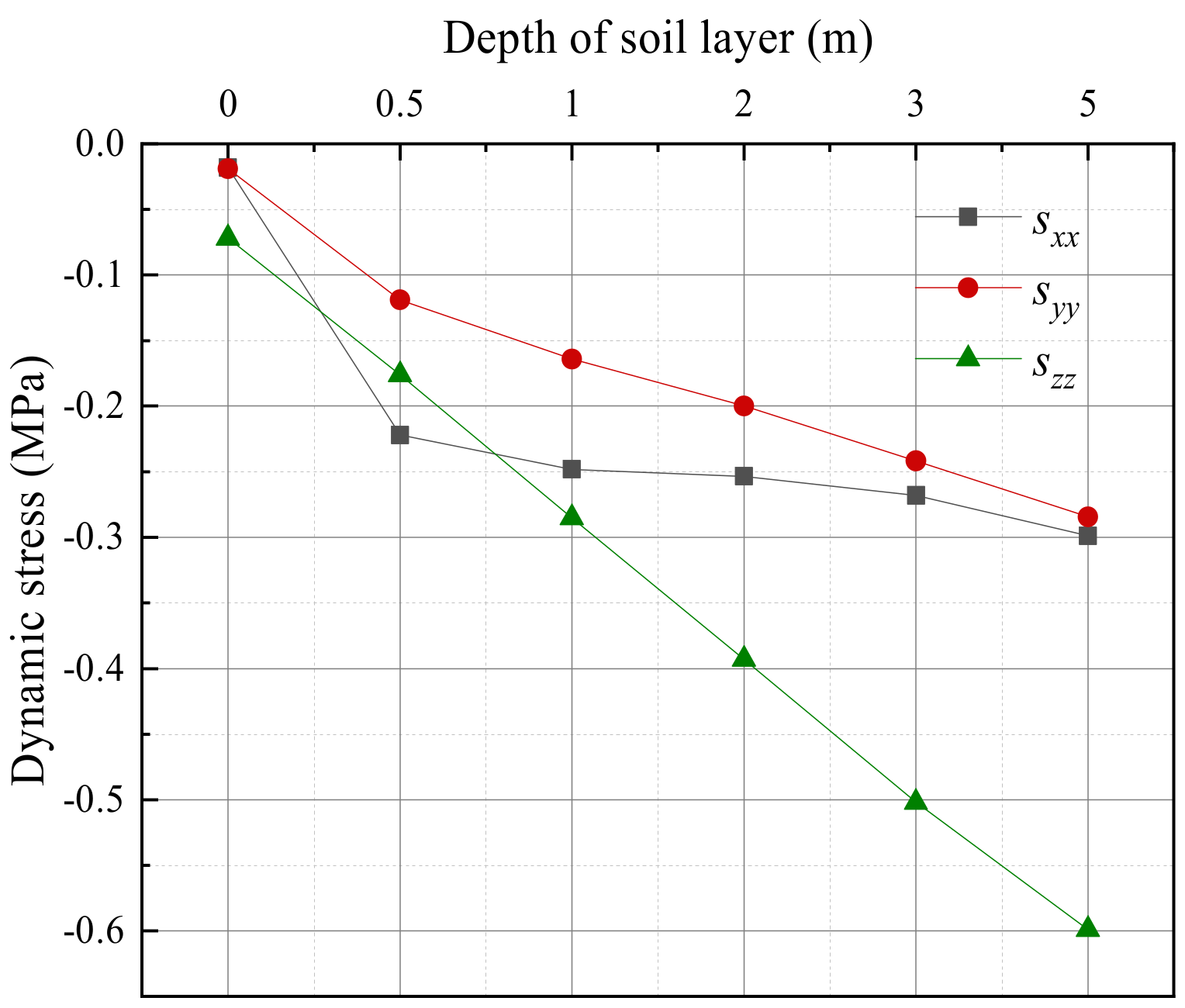
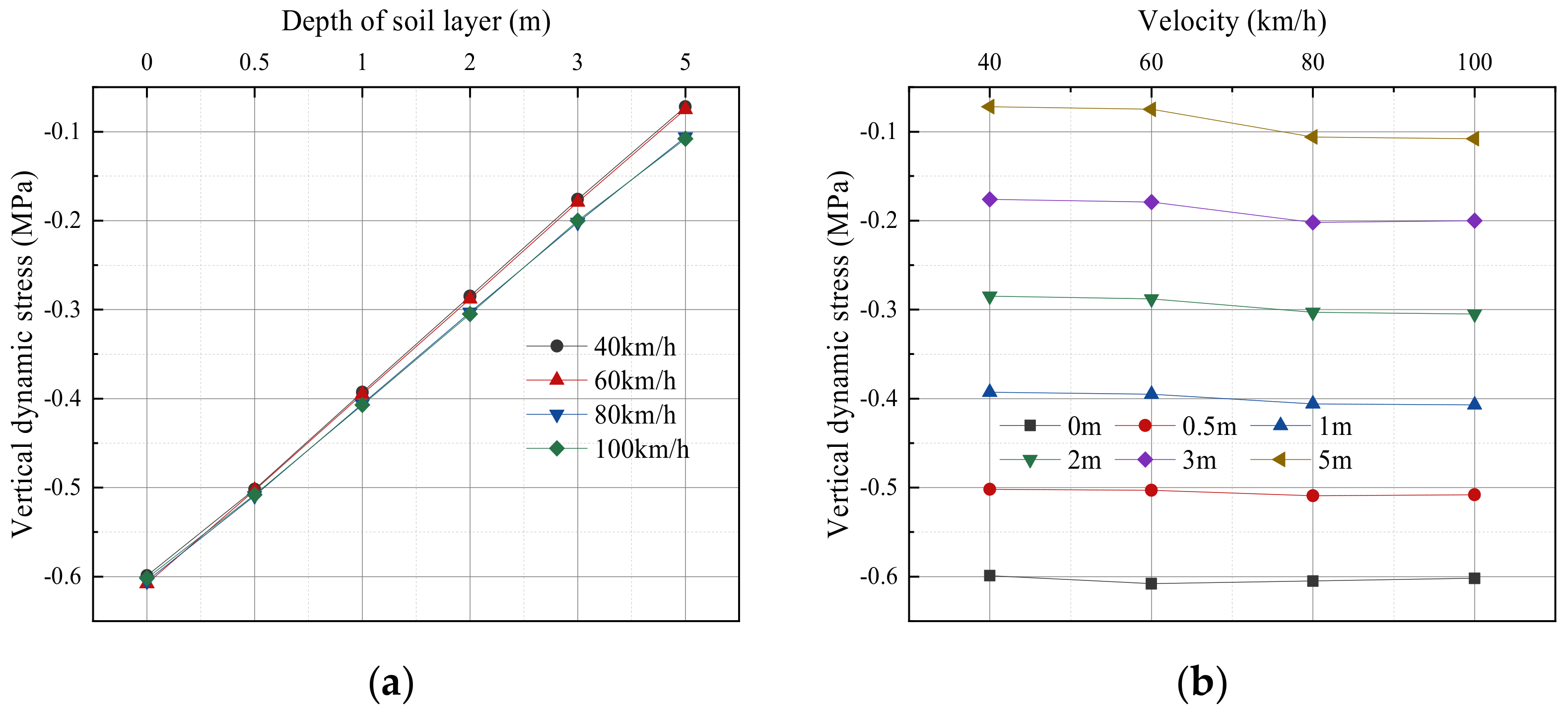
4.1.1. Vertical Dynamic Stress Response

This section studies the dynamic stress response of the soil layer at the bottom of the tunnel when train speeds are 40 km/h, 60 km/h, 80 km/h, and 100 km/h. Firstly, the dynamic stress changes of s_xx, s_yy, and s_zz at each monitoring point in the bottom soil layer of the tunnel structure are monitored and analyzed under the train speed is 40 km/h. The stress curve is shown in Figure 13.

Figure 13 shows that with the rise of the depth of the soil layer from the bottom of the shield tunnel, the dynamic stress in the x, y, and z directions of each measuring point in the soil layer increases gradually. However, the stress values in the x and y direction of each monitoring point are much smaller than the stress values in the z-direction. Therefore, the train-induced vibration has the greatest influence on the vertical stress of the bottom soil layer of the subway shield tunnel. The magnitudes of the dynamic stress downward from the z-direction at the bottom of the tunnel are 0.072 MPa, 0.176 MPa, 0.285 MPa, 0.393 MPa, 0.502 MPa, 0.599 MP, and the growth rate gradually slows down to 168.25%, 62.72%, 39.64%, 28.91%. The dynamic stress response of the soil layer at the bottom under the vibration load is mainly vertical stress. In order to further study the impact of the train on the dynamic stress of the soil layer at the bottom, the research on the vertical dynamic stress response of the soil layer under different train-induced vibration loads (40 km/h, 60 km/h, 80 km/h and 100 km/h, respectively) has been carried out. The results are shown in Figure 14 and Figure 15.

Figure 14 shows that under the different vibration loads, the variation law of the vertical stress of each monitoring point in the soil layer at the same depth below the shield tunnel structure is basically consistent. For example, at the depth of 0 m below the shield tunnel structure, the vertical stress is growing with the increase in train-induced vibration. When the soil depth is 1 m, the change rule is consistent. Additionally, at the beginning of the train-induced vibration load, the vertical stress time-history curve rapidly increases to the peak, and then gradually tends to a relatively stable fluctuation, which oscillates near the horizontal line of the peak stress.

From Figure 15, under different train running speeds, with the rise of the depth of the soil layer from the bottom of the shield tunnel, the vertical stress of the soil layer decreases. Taking the train speed of 60 km/h as an example, when the distance between the soil monitoring point and the bottom of the shield tunnel changes from 0 to 5 m, the vertical dynamic stress changes from 0.608 MPa to 0.075 MPa, a decrease of 87.66%. With the enhancement of train speed, the peak value of vertical dynamic stress and its fluctuation range at different soil layers are gradually increasing, but the variation range is not large. However, when the train speed increases from 60 km/h to 80 km/h, the amplitude increases slightly. The vertical dynamic stress of the soil layer farther from the bottom of the shield tunnel has a smaller increase rate with the improvement of the train-induced vibration load. When the train speed increases from 40 km/h to 100 km/h, the vertical dynamic stress increases by 50% at 0 m from the bottom of the shield tunnel. At 0.5 m from the bottom of the shield tunnel, the increase rate of vertical dynamic stress of the soil layer with train speed is 13.63%. At 3 m from the bottom of the shield tunnel structure, the increase rate of vertical dynamic stress of the soil layer with the change in train speed is 1.19%. Overall, the change in train speed does not influence in change pattern of the vertical stress of the bottom soil layer of the tunnel structure at different soil distances, but it will have a certain impact on the peak value of vertical dynamic stress and its fluctuation range.

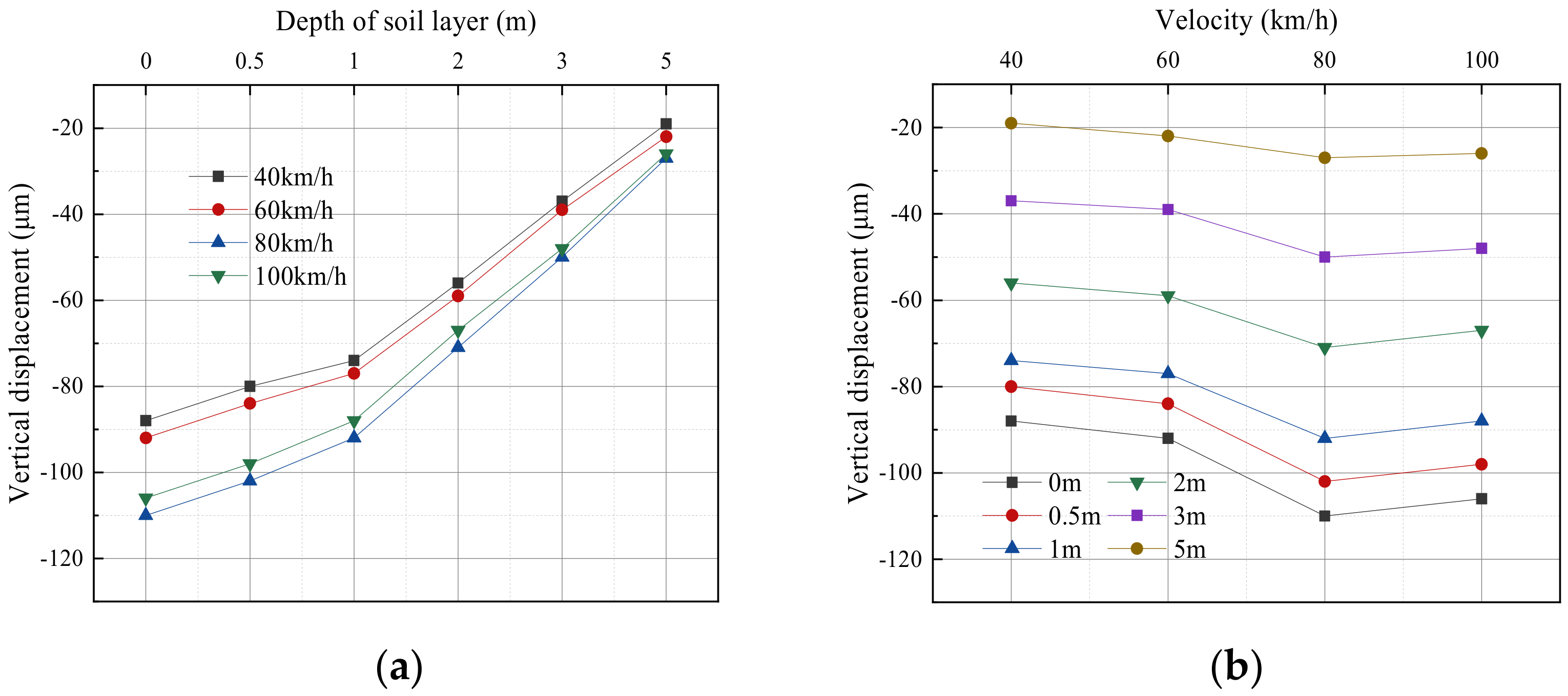
4.1.2. Vertical Displacement Response

The vertical displacement changes of the soil layer at the bottom of the tunnel were monitored when the train speed was 40 km/h, 60 km/h, 80 km/h, and 100 km/h, respectively. Figure 16 shows the comparison of the vertical displacement of each monitoring point of the soil layer at the bottom of the tunnel structure under the above four train speed loads.

According to Figure 16, under the same train-induced vibration load, the vertical displacement of the soil layer at the bottom decreases with the enhancement of the depth of the soil layer, but the decreasing rate is rising. Taking the train speed of 80 km/h as an example, the vertical displacements of the bottom soil layer at 0 m, 0.5 m, 2 m, and 5 m from the bottom soil layer of the shield tunnel are 110 μm, 102 μm, 71 μm, and 27 μm, respectively, and the reduction rates are 7.27%, 30.39%, and 61.97%, respectively. With the increase in train-induced vibration load, the vertical displacement of each monitoring point at the soil layer of the bottom rises significantly. Additionally, the increase in vertical displacement presents periodic characteristics with the increase in train-induced vibration load. When the train speed rises from 60 km/h to 80 km/h, the increase in vertical displacement is the largest. When the train speed rises from 80 km/h to 100 km/h, the increase in vertical displacement of the soil layer is significantly reduced. The soil layer closer to the bottom of the shield tunnel has a larger vertical displacement increase with the increase in train speed. When the train speed is increased from 60 km/h to 80 km/h, the vertical displacement at 0 m at the bottom of the shield tunnel structure increases by 18 μm, and at 1 m from the bottom of the shield tunnel structure, the vertical displacement increases by 15 μm, the vertical displacement growth amplitude of 3 m from the bottom of the shield tunnel structure is 11 μm.

4.2. Dynamic Response of Soil Layer at the Bottom of Tunnel Structure with Different Stiffness

The vibration load with a train speed of 80 km/h was applied at the bottom of the tunnel structure to explore the influence of the change in tunnel structure stiffness on the dynamic response characteristics of the soil layer at the bottom of the shield tunnel structure.

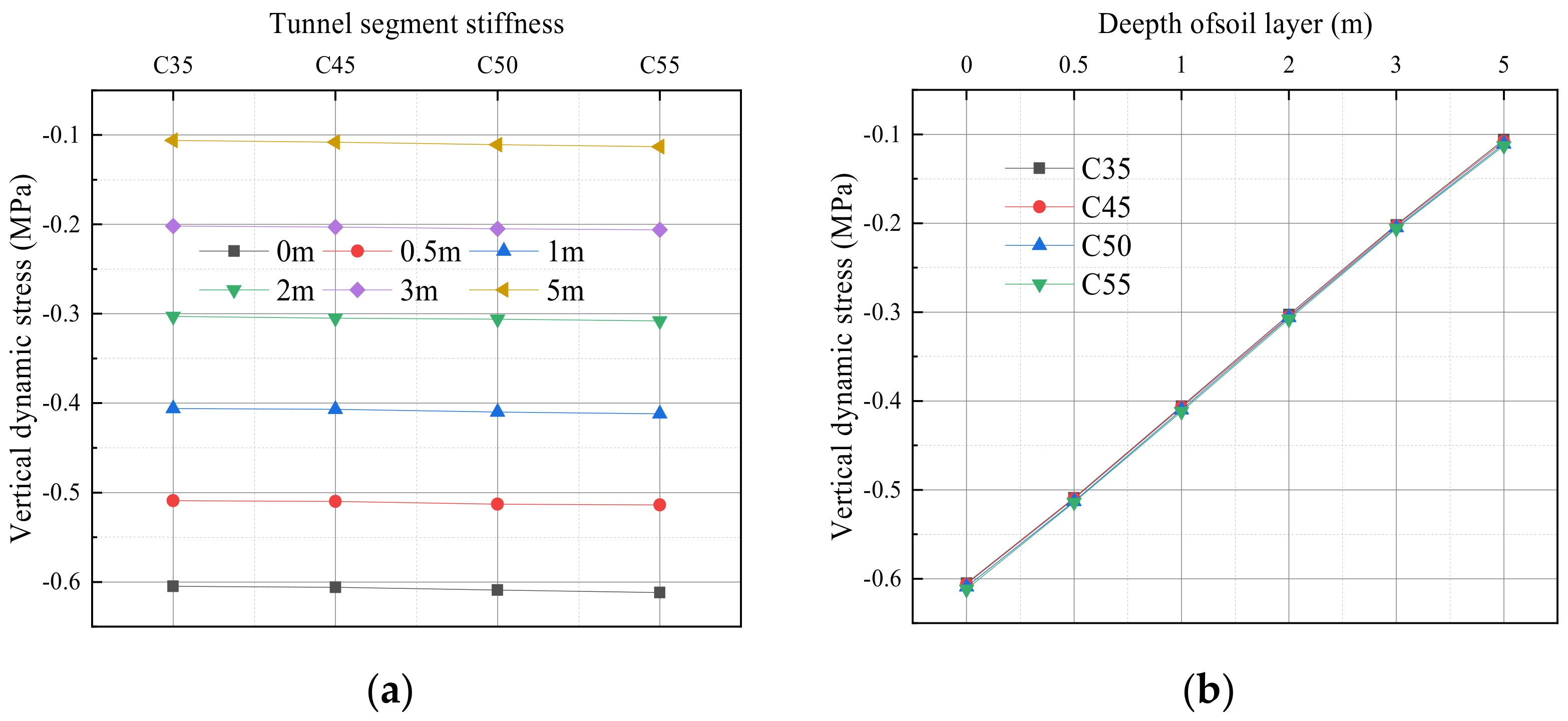
4.2.1. Vertical Stress Response

Under the train-induced vibration load with the speed of 80 km/h, the dynamic stress of the soil layer at the bottom of the shield tunnel structure with different stiffness (the strength grades of tunnel segment concrete are C35, C45, C50, and C55, respectively) is shown in Figure 17.

It can be seen from Figure 17 that under different stiffness, the variation law of vertical dynamic stress of the soil layer at the bottom with the increase in soil depth is basically the same. With the improvement of the depth of the soil layer from the bottom of the shield tunnel, the vertical stress of each measuring point declines under different structural stiffness conditions, but the change rate is gradually increasing. When the segment concrete grade is C35, the vertical dynamic stress peak values of 0 m, 0.5 m, 1 m, and 2 m away from the bottom of the shield tunnel are 0.605 MPa, 0.509 MPa, 0.406 MPa, and 0.303 MPa, respectively, and the reduction rates are 15.86%, 20.23%, and 25.36%, respectively.

The higher the stiffness of the shield tunnel structure, the greater the peak value of vertical dynamic stress of the soil layer at the same depth from the shield tunnel, but the variation range is not significant. For example, at the soil layer of 1 m away from the shield tunnel bottom, when the structural stiffness of the shield tunnel is C35, the vertical dynamic stress of the soil layer is 0.406 MPa. When the structural stiffness is C45, the vertical dynamic stress is 0.407 MPa. When the structural stiffness is C50, the vertical dynamic stress is 0.410 MPa. When the structural stiffness is C55, the vertical dynamic stress is 0.412 MPa. The growth amplitude is 1 kPa, 3 kPa, and 2 kPa, respectively. It can be seen that under the same train load, the change in tunnel structure stiffness has little effect on the vertical stress of the soil layer at the bottom of the tunnel structure.

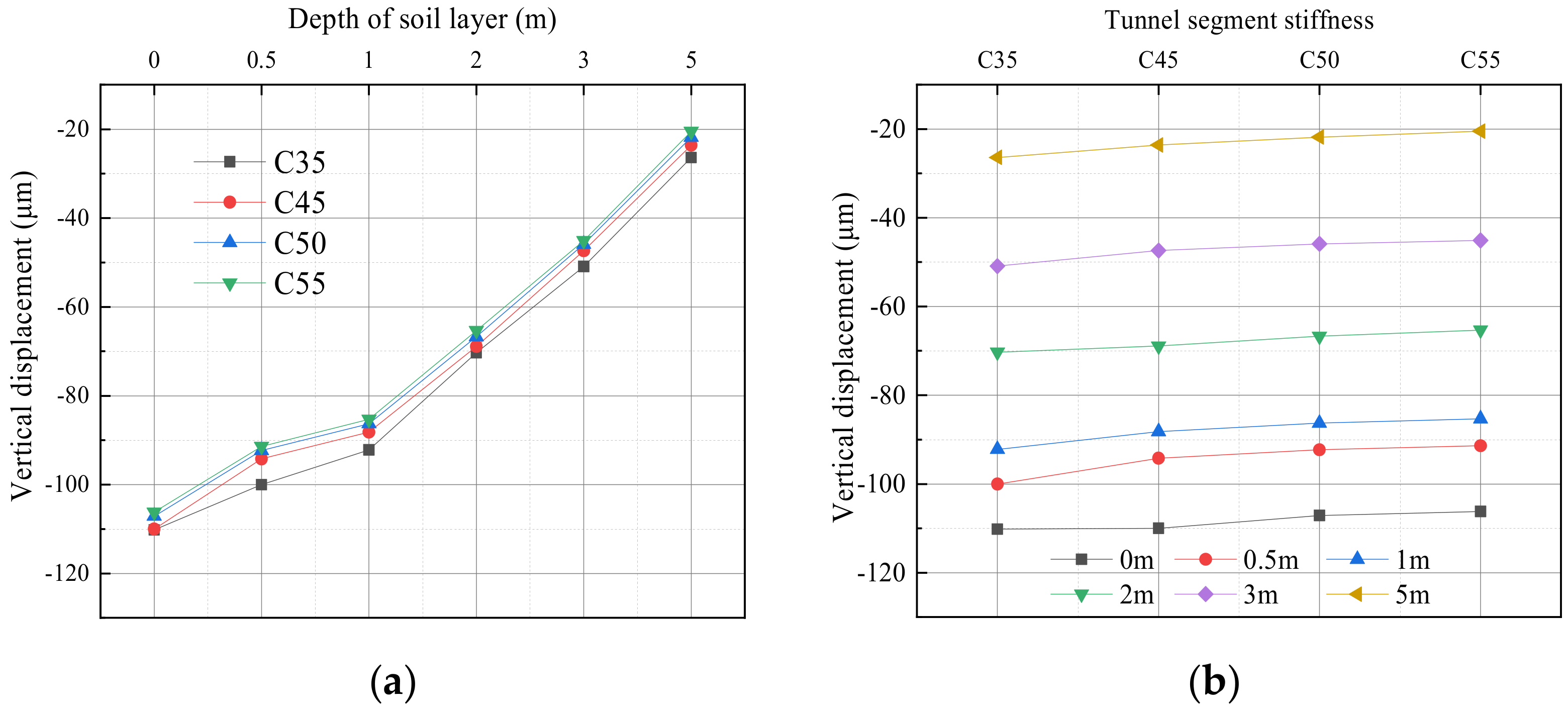
4.2.2. Displacement Response

Under the train load with the train speed of 80 km/h, the vertical displacement response characteristics of the soil layer at the bottom of the shield tunnel under different stiffness (C35, C45, C50, and C55) are studied. The variation curve of the peak vertical displacement is shown in Figure 18.

Through the analysis of Figure 18, it can be seen that under different structural stiffness conditions of shield tunnels, the variation law of every monitoring point’s vertical displacement with the increase in soil depth at the bottom of the tunnel is basically the same. With the increase in soil depth from the bottom, the peak value of vertical displacement of the soil layer continues to decrease, and the reduction rate gradually rises. Taking the stiffness of tunnel structure C45 as an example, the vertical displacement peak values of the soil layer at 0 m, 1 m, 2 m, and 3 m away from the bottom are 110.0 μm, 68.9 μm, and 47.4 μm, and the change rates are 19.78%, 21.88%, and 31.20%, respectively. In addition, the vertical displacement of the soil layer at the same distance from the bottom of the shield tunnel is decreasing with the stiffness increases, but the overall decreased range is very small. For example, at the soil layer 0 m away from the bottom of the shield tunnel, when the tunnel structural stiffness is C35, the peak value of vertical displacement is 110.2 μm. When the structural stiffness is C55, the vertical displacement is 106.2 μm, and the change amplitude is only 4.0 μm. It can be seen from Figure 18 that at the same depth of soil layer from the bottom of the shield tunnel, the influence of the concrete strength grade from C35 to C45 on the vertical displacement is notable, and when the structural stiffness increases from C50 to C55, it has little impact on the vertical displacement of the soil layer at the bottom. Therefore, the change in the stiffness has a certain effect on the vertical displacement of the soil layer at the bottom, but it is not always unchanged. It cannot simply improve the concrete strength of the tunnel structure to enhance the stability of the structure.

5. Conclusions

In this paper, based on the subway shield tunnel project between Maluan Central Station and Jimei Island Station of Xiamen Metro Line 6, the shield tunnel-soil numerical calculation model by using the three-dimensional finite difference method to research the dynamic response characteristics of shield tunnel structure and soil layer at its bottom. The main conclusions are as follows:

(1)

When the subway train is running, the stress response of the shield tunnel structure is dominated by the first principal stress, which is mainly subjected to compressive stress and generates compressive deformation. The maximum stress peak of the tunnel structure appears at the arch waist of the shield tunnel structure at different train speed vibration loads. The stress and displacement responses of the shield tunnel structure show an improving trend with the increase in the train speed. The change in train speed has less effect on the displacement response but has a significant effect on the dynamic stress response. In the design of the shield tunnel structure, the reinforcement measures at the arch waist should be fully considered.

(2)

The influence of shield segment concrete strength grade on the first principal stress of tunnel structure is not obvious under train-induced vibration load. With the enhancement of structural stiffness, the first principal stress rises but the increased amplitude is gradually reduced. With the increase in the stiffness level of the shield tunnel structure, the relative displacement and its variation range between the vault and the bottom of the tunnel structure are gradually reduced, and the displacement response is gradually weakened. It is not significant for enhancing the structural stability to improve the strength grade of concrete.

(3)

When the soil depth increases, the dynamic response of the soil layer at the bottom of the shield tunnel structure is consistent under different train-induced vibration loads. With the increase in the depth of the soil layer from the tunnel bottom, the stress and displacement responses decrease, and the change rate increases gradually. At the same distance, with the increase in train-induced vibration load, the stress of soil gradually enhances. However, the farther away from the bottom of the shield tunnel, the smaller the increase rate of the soil stress. The displacement response presents periodic characteristics. With the increase in depth from the bottom of the shield tunnel, the influence of the train speed change on the vertical displacement of soil layer gradually disappears.

(4)

With the increase in the depth of the soil layer from the tunnel bottom, the stress and displacement response of the soil layer decrease, and the decline rate increases under different tunnel stiffness conditions. At the same depth from the bottom, with the increase in structural stiffness, the stress response of the soil layer increases slightly, and the displacement response decreases gradually, but the changes are not obvious. The changes in tunnel structural stiffness have a certain influence on the dynamic response of the soil layer at the bottom, but the influence gradually disappears with the increase in structural stiffness. It is important to pay continuous attention to the dynamic response of stress and displacement caused by train-induced vibration for the safe operation of the subway.