Energy-Saving Manufacturing System Design with Two Geometric Machines
Abstract
:1. Introduction
2. Literature Review
3. System Model and Problem Formulation
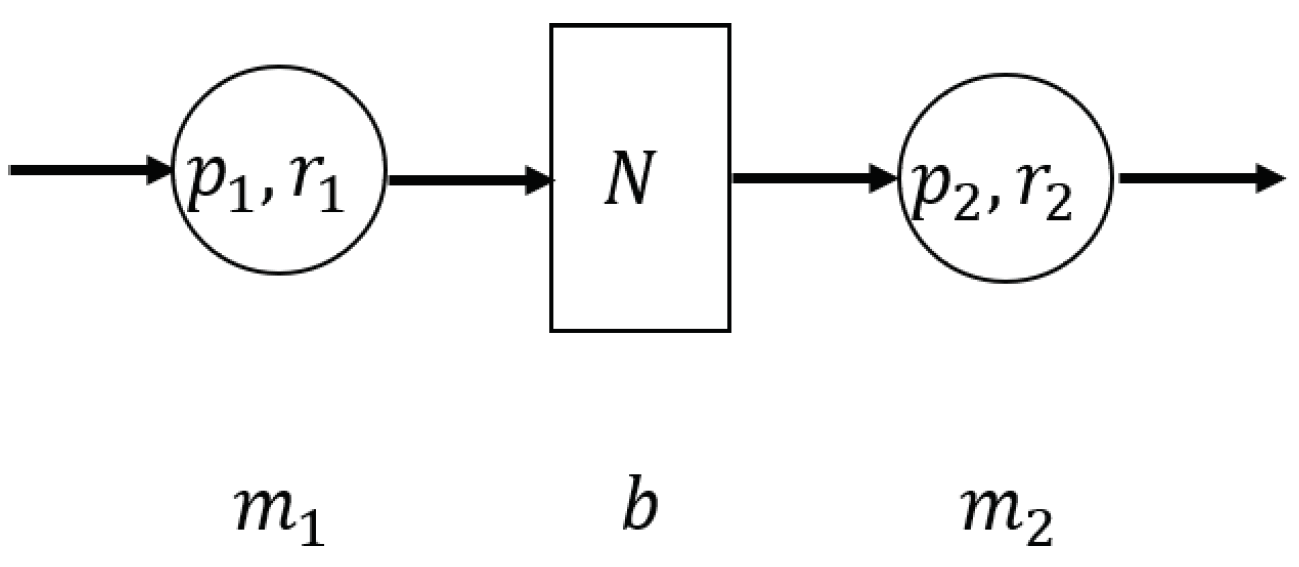
3.1. System Model
- (i)
- Machine and have identical cycle time . During each time slot, where the time slot is also called the cycle time, if the machine is up, it will produce one part, otherwise, there will be no throughput. The state of the machines is determined at the beginning of each time slot.
- (ii)
- These two machines, , where , obey the geometric reliability model, where and are breakdown and repair probabilities, respectively. The state of a machine is denoted by at time slot t. Then, the transition probabilities are as follows:Note that the average up- and downtime of the machines can be obtained by and . Then, the machine efficiency is . Both two machines are independent of each other.
- (iii)
- Buffer b has a finite capacity . The state of the buffer is determined at the end of each time slot.
- (iv)
- Machine is never starved; it will be blocked if it is up and the buffer b is full at the beginning of the time slot. Machine is never blocked; it will be starved if it is up and the buffer b is empty at the beginning of the time slot.
- (v)
- When the machine , where , is working, the energy consumption is . When the machine is idle, the energy consumption is . When the machine starts up from the down state, the energy consumption is .
- (vi)
- The resulting productivity of the production system must meet the target, .
3.2. Problem Formulation
- Both two machines are up with probability ; the energy consumption is ;
- Machine is up and is down with probability ; the energy consumption is ;
- Machine is down and is up with probability ; the energy consumption is ;
- Both two machines are down with probability ; no energy consumption occurs.
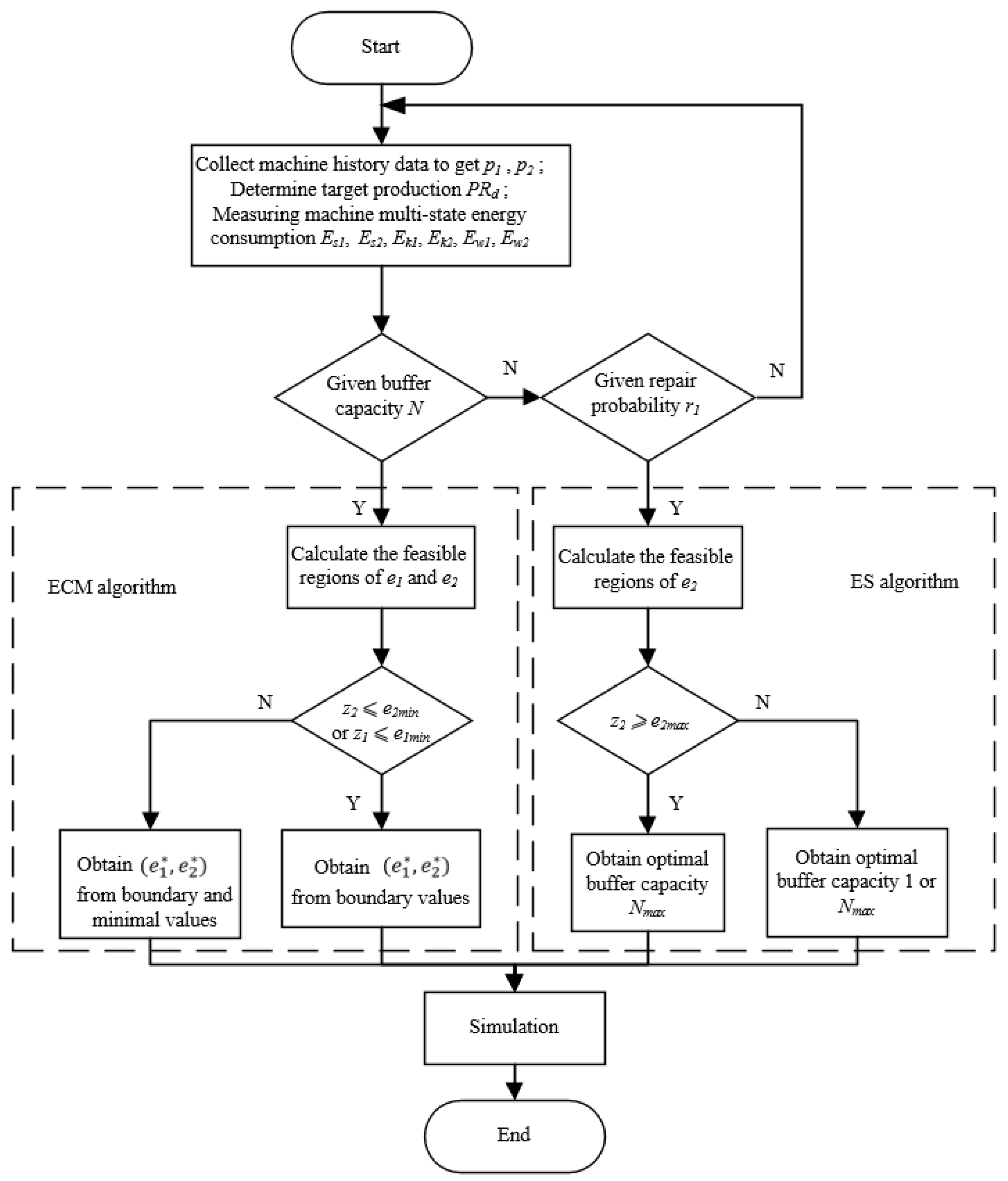
4. The ECM Algorithm
4.1. The ECM Algorithm
- (i)
- .
- (ii)
- (iii)
- .
- (i)
- When ;
- (ii)
- When , stands for the left limit of ;
- (iii)
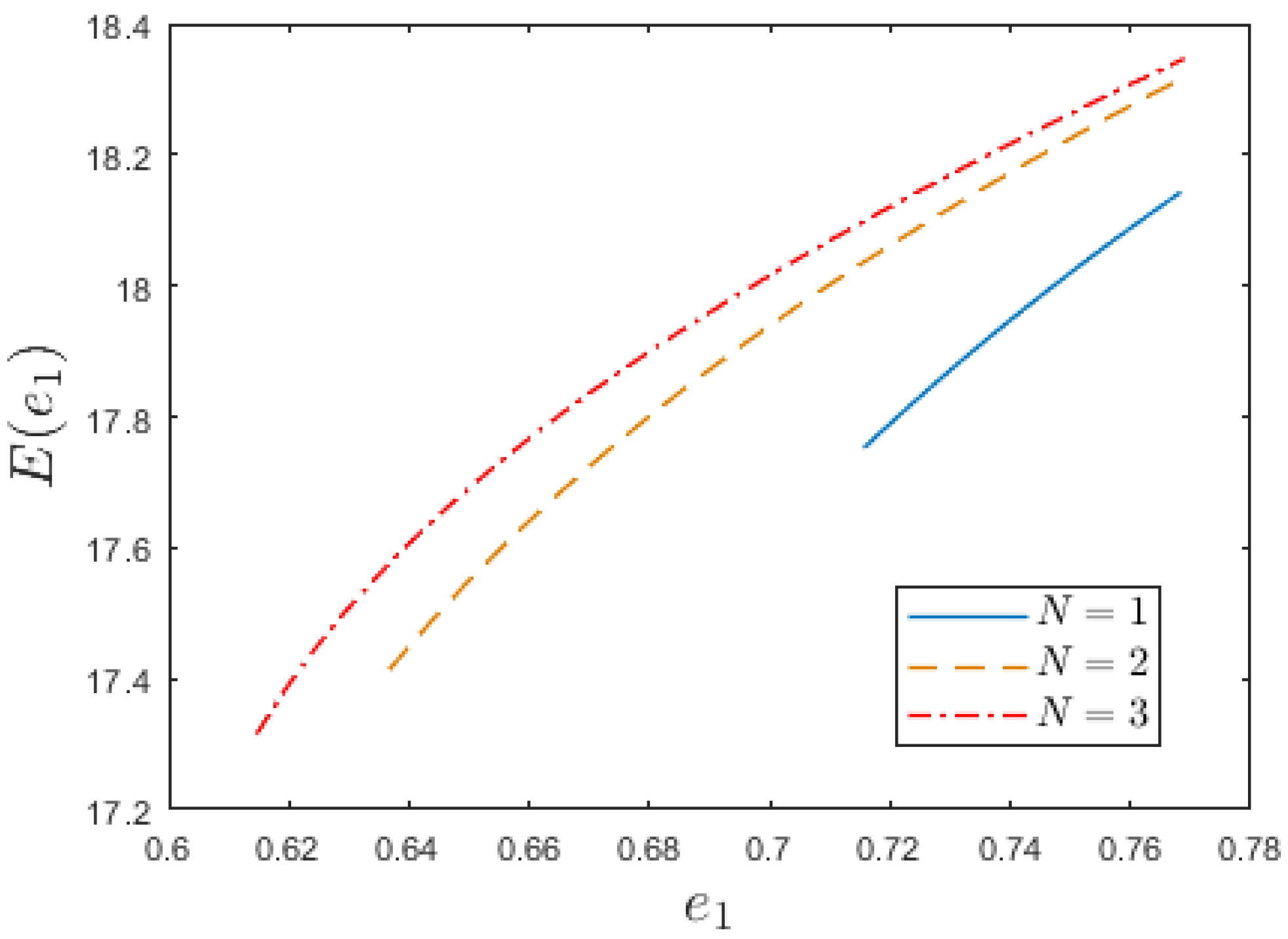
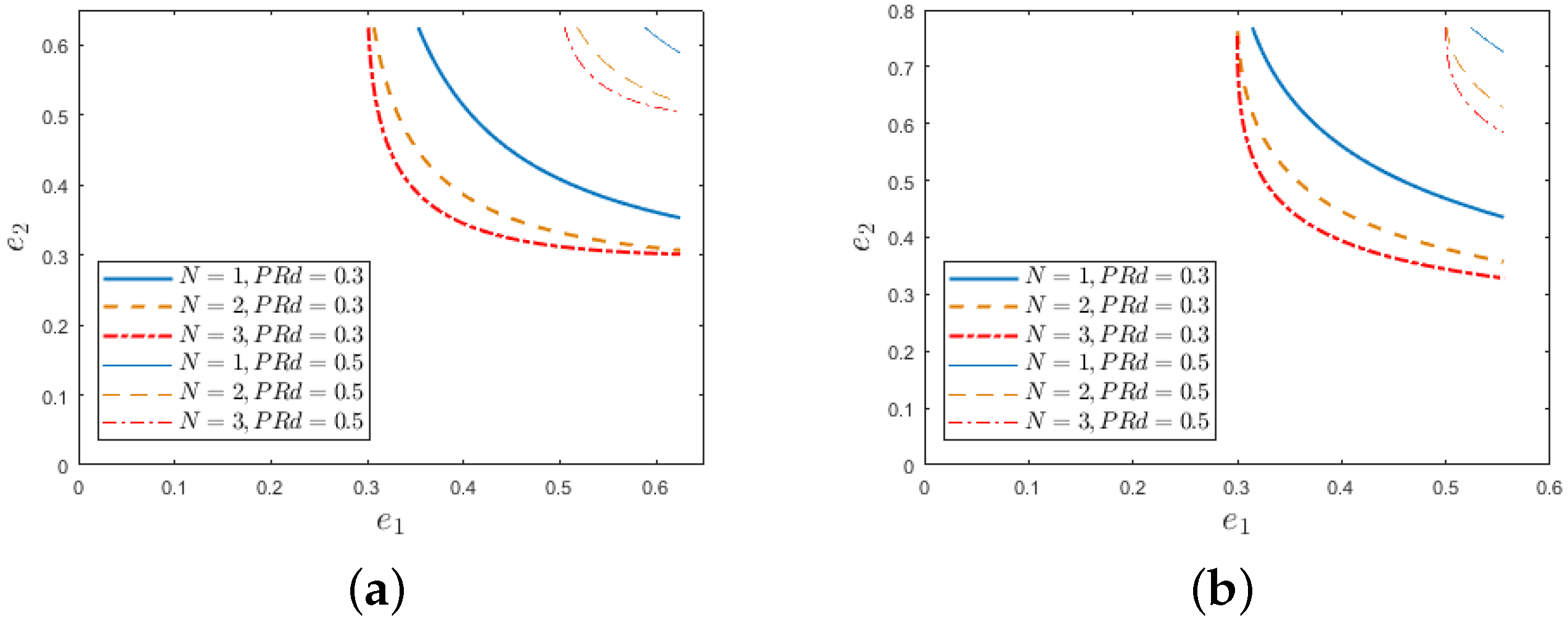
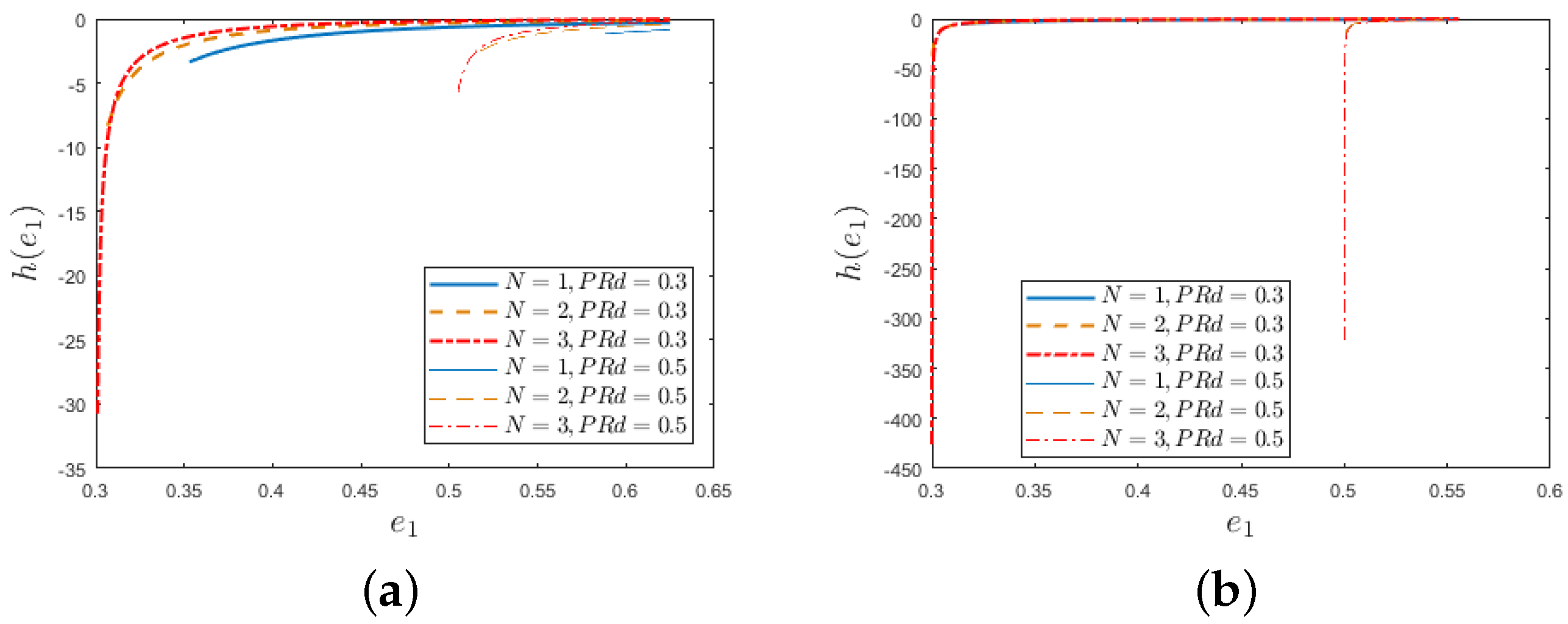
- When , is monotonically decreasing (see Figure 6).

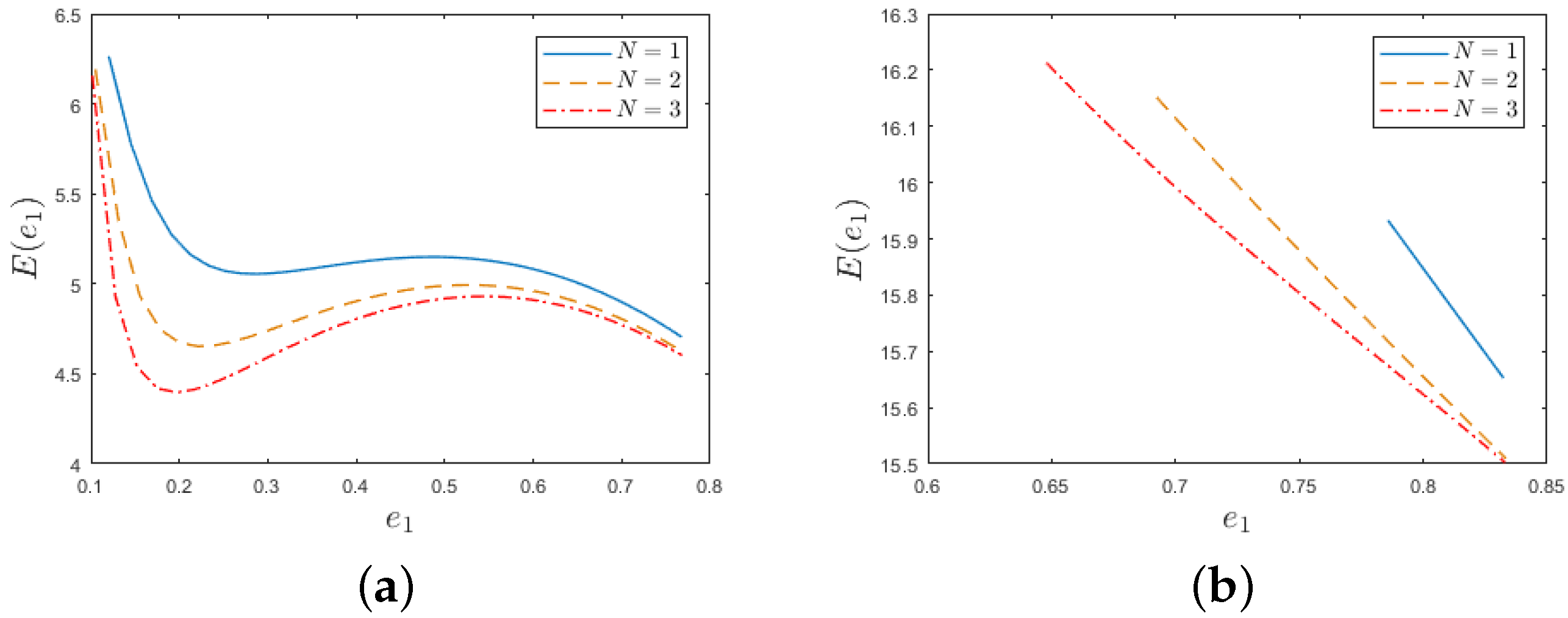
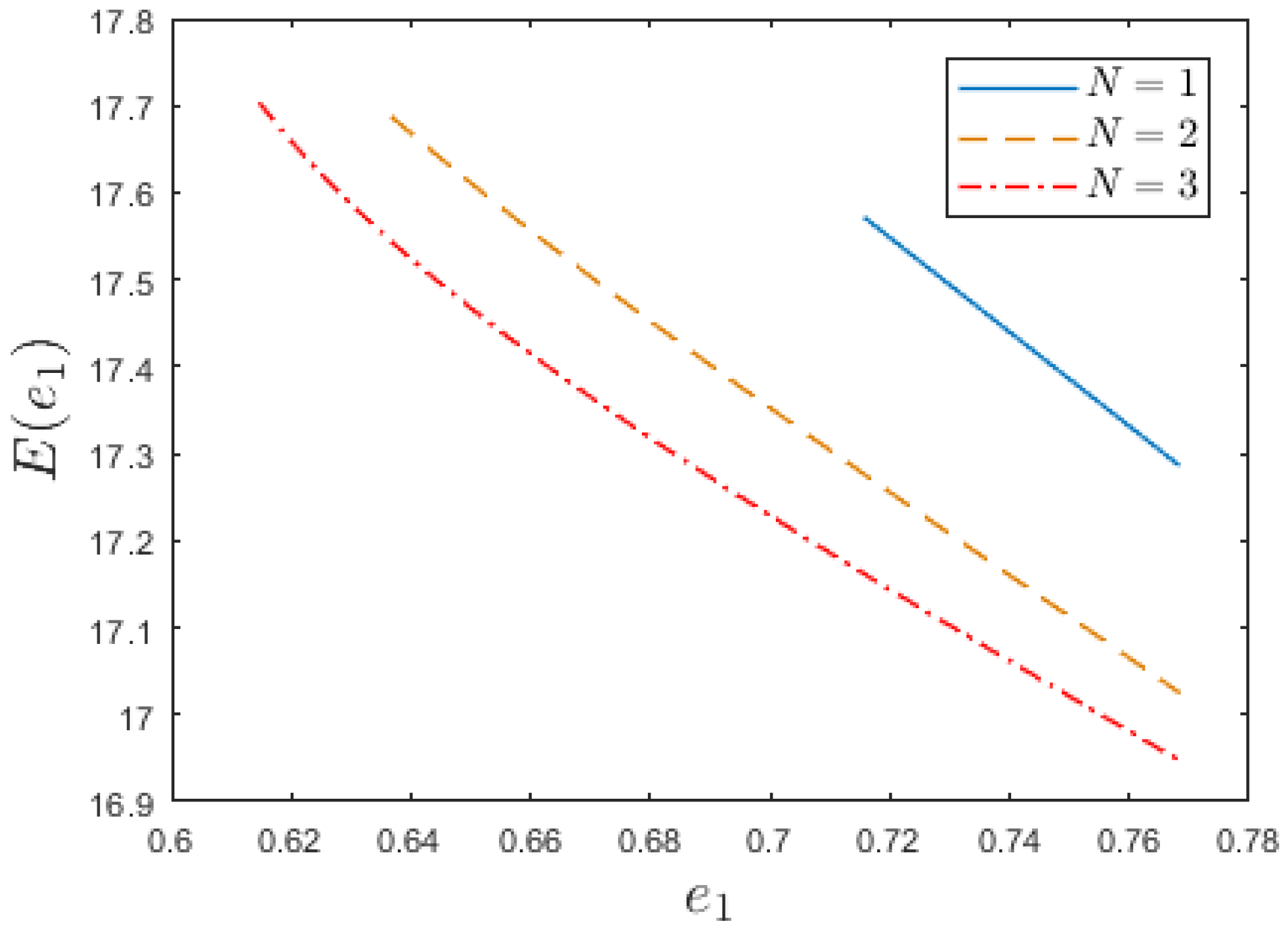
- (i)
- when ;
- (ii)
- When , and stand for the left and right limits of ;
- (iii)
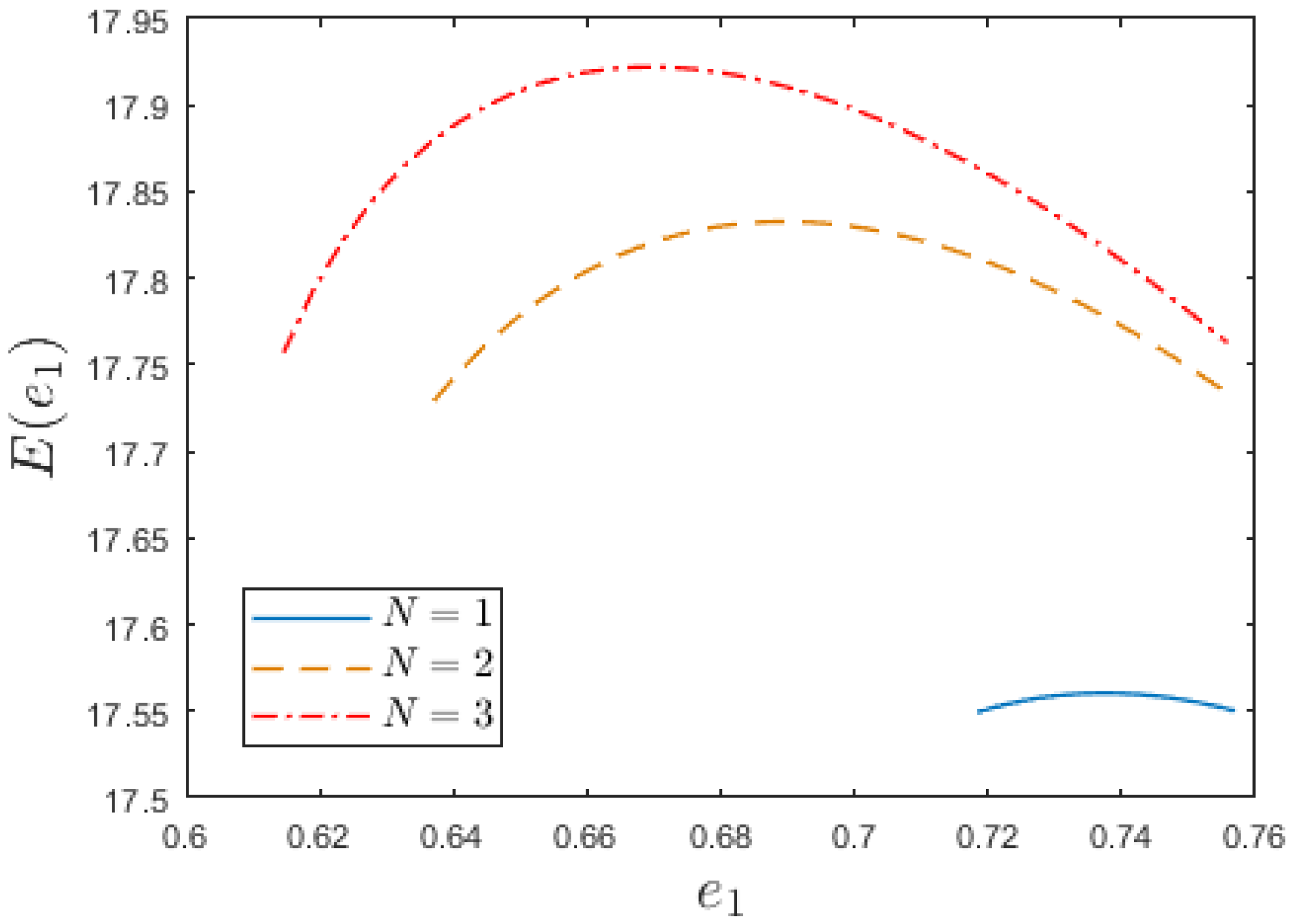
- When , has one local maximum (see Figure 9).
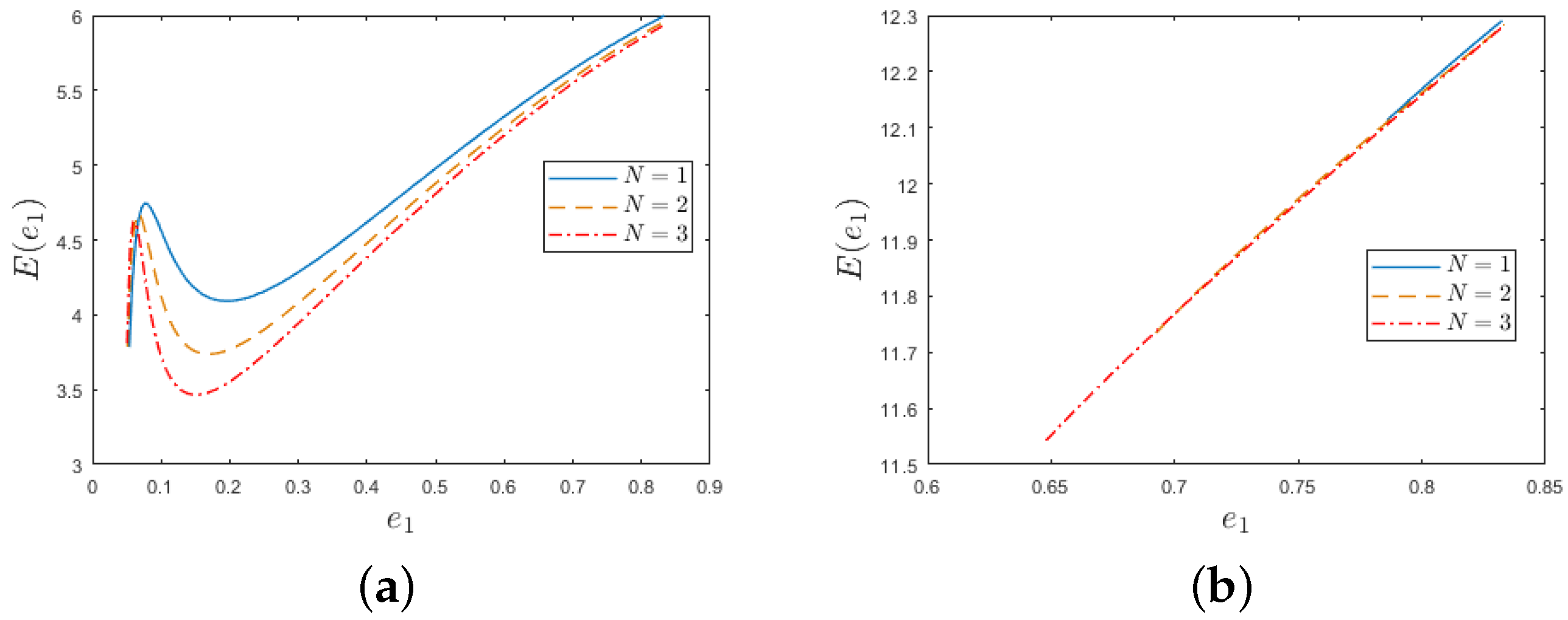
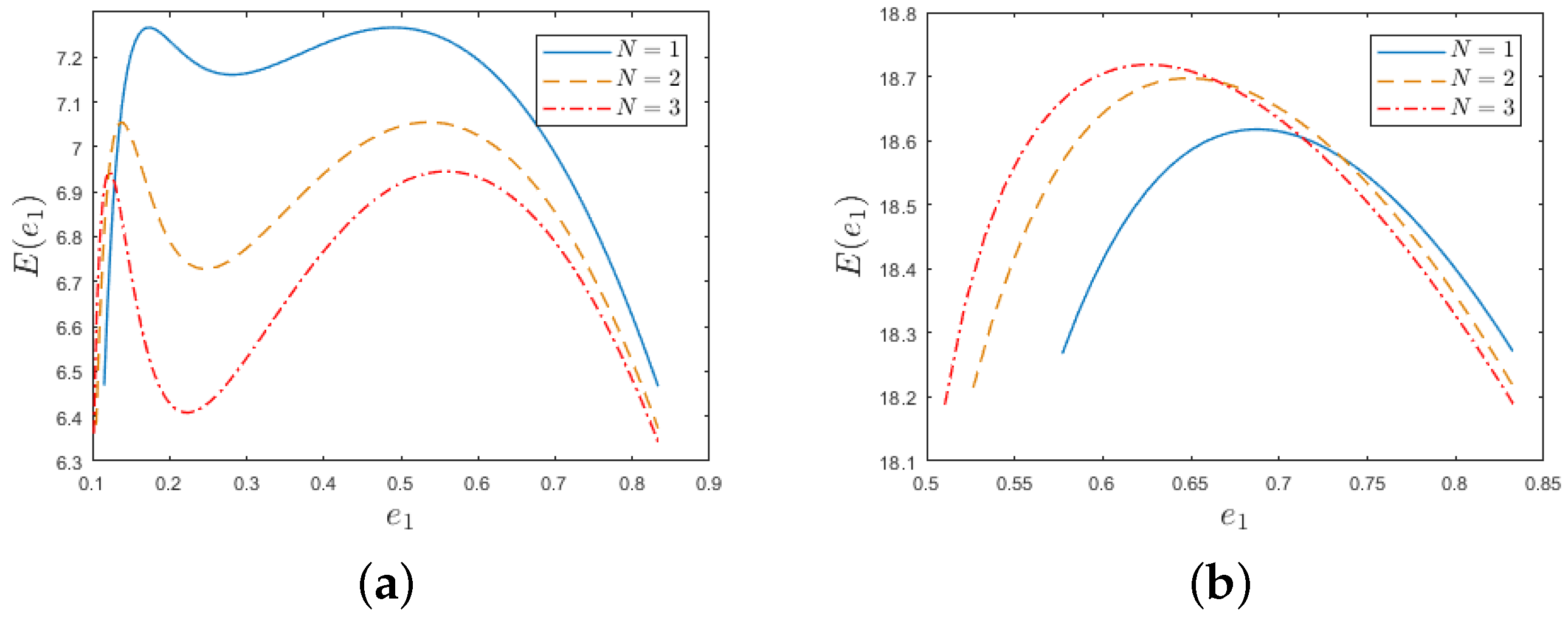


| Algorithm 1: Energy consumption minimization (ECM) algorithm. |
|
4.2. The ES Algorithm
| Algorithm 2: Energy-saving (ES) algorithm. |
Input:
Output: The optimal solution , the candidate solution and the total energy consumption E. |
5. Numerical and Sensitivity Analysis
5.1. Sensitivity Analysis of Energy Consumption Parameters
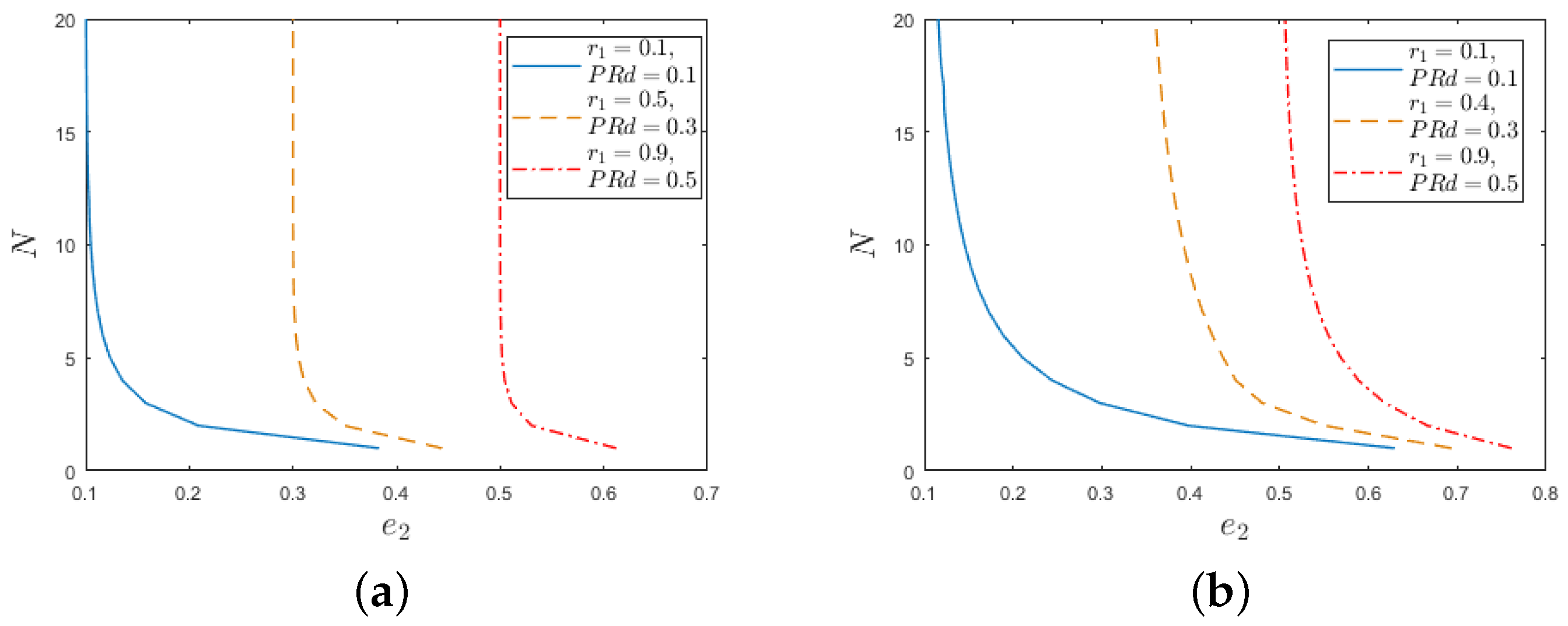
5.2. Sensitivity Analysis of Buffer Capacity
5.3. Sensitivity Analysis of
5.4. Sensitivity Analysis of
5.5. ES Algorithm and Simulation Comparison
5.6. Discussion and Imitations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Proof of Theorem 1
Appendix B
| N | Case | ECM Algorithm | Simulation | Gap | ||||
|---|---|---|---|---|---|---|---|---|
| 1 | 1-1 | 0.4463 | 0.4375 | 0.4716 | 0.4667 | 6.7982 | 7.0813 ) | 3.9974% |
| 2-1 | 0.2813 | 1 | 0.3600 | 0.6667 | 10.6249 | 10.5496 | 0.7142% | |
| 3-1 | 1 | 0.2813 | 0.6667 | 0.3600 | 9.7438 | 9.7030 | 0.4207% | |
| 4-1 | 1 | 0.2813 | 0.6667 | 0.3600 | 12.5565 | 12.4680 | 0.7105% | |
| 2 | 1-1 | 0.3559 | 0.3434 | 0.4158 | 0.4072 | 6.3019 | 6.4776 | 2.7125% |
| 2-1 | 0.2249 | 1 | 0.3103 | 0.6667 | 10.3266 | 9.8413 | 4.9316% | |
| 3-1 | 1 | 0.2249 | 0.6667 | 0.3103 | 9.4294 | 9.0171 | 4.5729% | |
| 4-1 | 1 | 0.2249 | 0.6667 | 0.3103 | 12.2760 | 11.7154 | 4.7848% | |
| 3 | 1-1 | 0.3175 | 0.3083 | 0.3884 | 0.3814 | 6.0620 | 6.0774 | 0.2526% |
| 2-1 | 0.2165 | 1 | 0.3022 | 0.6667 | 10.2767 | 9.7356 | 5.5581% | |
| 3-1 | 1 | 0.2165 | 0.6667 | 0.3022 | 9.3765 | 8.9209 | 5.1077% | |
| 4-1 | 1 | 0.2165 | 0.6667 | 0.3022 | 12.2267 | 11.5895 | 5.4984% | |
| Case | ECM Algorithm | Simulation | Gap | |||||
|---|---|---|---|---|---|---|---|---|
| 0.05 | 1-1 | 0.0840 | 0.0764 | 0.1438 | 0.1325 | 1.9963 | 1.9659 | 1.5439% |
| 2-1 | 0.0850 | 0.0755 | 0.1453 | 0.1312 | 3.1876 | 3.1425 | 1.4361% | |
| 3-1 | 0.0890 | 0.0725 | 0.1511 | 0.1267 | 2.9249 | 2.9003 | 0.8492% | |
| 4-1 | 0.0810 | 0.0790 | 0.1394 | 0.1365 | 3.7612 | 3.6787 | 2.2440% | |
| 0.3 | 1-1 | 0.4463 | 0.4375 | 0.4716 | 0.4667 | 6.7982 | 7.0813 | 3.9974% |
| 2-1 | 0.2813 | 1 | 0.3600 | 0.6667 | 10.6249 | 10.5496 | 0.7142% | |
| 3-1 | 1 | 0.2813 | 0.6667 | 0.3600 | 9.7438 | 9.7030 | 0.4207% | |
| 4-1 | 1 | 0.2813 | 0.6667 | 0.3600 | 12.5565 | 12.4680 | 0.7105% | |
| 0.55 | 1-1 | 0.9706 | 1 | 0.6600 | 0.6667 | 9.7221 | 9.5312 | 2.0029% |
| 2-1 | 0.9706 | 1 | 0.6600 | 0.6667 | 16.1065 | 15.6774 | 2.7373% | |
| 3-1 | 1 | 0.9706 | 0.6667 | 0.6600 | 15.2203 | 14.8304 | 2.6287% | |
| 4-1 | 1 | 0.9706 | 0.6667 | 0.6600 | 18.6585 | 18.0036 | 3.6376% | |
| Case | ECM Algorithm | Simulation | Gap | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.2 | 0.1 | 1-1 | 0.1944 | 0.1304 | 0.4911 | 0.5660 | 7.2895 | 7.0010 | 4.1211% |
| 2-1 | 0.0957 | 1 | 0.3236 | 0.9087 | 9.6389 | 9.4890 | 1.5797% | ||
| 3-1 | 1 | 0.0545 | 0.8333 | 0.3528 | 9.2826 | 8.9229 | 4.0315% | ||
| 4-1 | 1 | 0.0545 | 0.8333 | 0.3528 | 12.1015 | 11.6417 | 3.9495% | ||
| 0.5 | 0.5 | 1-1 | 0.4463 | 0.4375 | 0.4716 | 0.4667 | 6.7982 | 7.0813 | 3.9974% |
| 2-1 | 0.2813 | 1 | 0.3600 | 0.6667 | 10.6249 | 10.5496 | 0.7142% | ||
| 3-1 | 1 | 0.2813 | 0.6667 | 0.3600 | 9.7438 | 9.7030 | 0.4207% | ||
| 4-1 | 1 | 0.2813 | 0.6667 | 0.3600 | 12.5565 | 12.4680 | 0.7105% | ||
| 0.8 | 0.9 | 1-1 | 0.5595 | 0.5646 | 0.4116 | 0.3855 | 6.1833 | 6.0434 | 2.3155% |
| 2-1 | 0.3965 | 1 | 0.3314 | 0.5263 | 10.4181 | 10.2493 | 1.6471% | ||
| 3-1 | 1 | 0.4119 | 0.5554 | 0.3140 | 9.5154 | 9.2318 | 3.0717% | ||
| 4-1 | 1 | 0.4119 | 0.5554 | 0.3140 | 12.2984 | 11.9102 | 2.4197% | ||
References
- Kolta, T. Selecting Equipment to Control Air Pollution from Automotive Painting Operations. In Technical Report; SAE Technical Paper; Auto. Eng.: Warrendale, PA, USA, 1992. [Google Scholar]
- Galitsky, C.; Worrell, E. Energy Efficiency Improvement and Cost Saving Opportunities for the Vehicle Assembly Industry: An Energy Star Guide for Energy and Plant Managers. In Technical Report; Lawrence Berkeley National Lab. (LBNL): Berkeley, CA, USA, 2008. [Google Scholar]
- Altiok, T. Performance Analysis of Manufacturing Systems; Springer: Belin, Germany, 1997. [Google Scholar]
- Askin, R.G.; Standridge, C.R. Modeling and Analysis of Manufacturing Systems; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Li, J.; Meerkov, S.M. Production Systems Engineering; Springer: New York, NY, USA, 2009. [Google Scholar]
- Pei, Z.; Lu, H.; Jin, Q.; Zhang, L. Target-based distributionally robust optimization for single machine scheduling. Eur. J. Oper. Res. 2022, 299, 420–431. [Google Scholar] [CrossRef]
- Kim, W.S.; Morrison, J.R. The throughput rate of serial production lines with deterministic process times and random setups: Markovian models and applications to semiconductor manufacturing. Comput. Oper. Res. 2015, 53, 288–300. [Google Scholar] [CrossRef]
- Pei, Z.; Wan, M.; Jiang, Z.Z.; Wang, Z.; Dai, X. An approximation algorithm for unrelated parallel machine scheduling under tou electricity tariffs. IEEE Trans. Autom. Sci. Eng. 2020, 18, 743–756. [Google Scholar] [CrossRef]
- Tu, J.; Zhang, L. Performance analysis and optimisation of Bernoulli serial production lines with dynamic real-time bottleneck identification and mitigation. Int. J. Prod. Res. 2022, 60, 3989–4005. [Google Scholar] [CrossRef]
- Arinez, J.; Biller, S.; Meerkov, S.M.; Zhang, L. Quality/quantity improvement in an automotive paint shop: A case study. IEEE Trans. Autom. Sci. Eng. 2009, 7, 755–761. [Google Scholar] [CrossRef]
- Hillier, M. Designing unpaced production lines to optimize throughput and work-in-process inventory. IIE Trans. 2013, 45, 516–527. [Google Scholar] [CrossRef]
- Biller, S.; Meerkov, S.M.; Yan, C.B. Raw material release rates to ensure desired production lead time in Bernoulli serial lines. Int. J. Prod. Res. 2013, 51, 4349–4364. [Google Scholar] [CrossRef]
- Shen, X.; Li, N. Scheduling policies analysis for matching operations in bernoulli selective assembly lines. Int. J. Prod. Res. 2022, 60, 3965–3988. [Google Scholar] [CrossRef]
- Menghi, R.; Papetti, A.; Germani, M.; Marconi, M. nergy efficiency of manufacturing systems: A review of energy assessment methods and tools. J. Clean. Prod. 2019, 240, 118276. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, J.; Liu, M. Enterprises’ energy-saving capability: Empirical study from a dynamic capability perspective. Renew. Sustain. Energy Rev. 2022, 162, 112450. [Google Scholar]
- Li, L.; Sun, Z. Dynamic Energy Control for Energy Efficiency Improvement of Sustainable Manufacturing Systems Using Markov Decision Process. IEEE Trans. Syst. Man Cybern. Syst. 2013, 43, 1195–1205. [Google Scholar] [CrossRef]
- Mashaei, M.; Lennartson, B. Energy Reduction in a Pallet-Constrained Flow Shop Through On–Off Control of Idle Machines. IEEE Trans. Autom. Sci. Eng. 2013, 1, 45–56. [Google Scholar] [CrossRef]
- Cui, P.H.; Wang, J.Q.; Li, Y.; Yan, F.Y. Energy-efficient control in serial production lines: Modeling, analysis and improvement. J. Manuf. Syst. 2021, 60, 11–21. [Google Scholar] [CrossRef]
- Frigerio, N.; Matta, A. Analysis on Energy Efficient Switching of Machine Tool With Stochastic Arrivals and buffer information. IEEE Trans. Autom. Sci. Eng. 2016, 1, 238–246. [Google Scholar] [CrossRef]
- Renna, P.; Materi, S. Switch off policies in job-shop manufacturing systems including workload evaluation. Int. J. Manag. Sci. Eng. Manag. 2021, 16, 254–263. [Google Scholar] [CrossRef]
- Jia, Z.; Zhang, L.; Arinez, J.; Xiao, G. Performance analysis for serial production lines with Bernoulli machines and real-time WIP-based machine switch-on/off control. Int. J. Prod. Res. 2016, 54, 6285–6301. [Google Scholar] [CrossRef]
- Li, Y.; Cui, P.H.; Wang, J.Q.; Chang, Q. Energy-saving control in multistage production systems using a state-based method. IEEE Trans. Autom. Sci. Eng. 2021. [Google Scholar] [CrossRef]
- Chen, G.; Zhang, L.; Arinez, J.; Biller, S. Energy-efficient production systems through schedule-based operations. IEEE Trans. Autom. Sci. Eng. 2013, 1, 27–37. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, Q.; Feng, Y.; Zheng, H.; Zheng, B.; Tan, J. An energy-saving optimization method of dynamic scheduling for disassembly line. Energies 2018, 11, 1261. [Google Scholar] [CrossRef]
- Li, S.; Liu, F.; Zhou, X. Multi-objective energy-saving scheduling for a permutation flow line. Proc. Inst. Mech. Eng. Part J. Eng. Manuf. 2018, 232, 879–888. [Google Scholar] [CrossRef]
- Su, W.; Xie, X.; Li, J.; Zheng, L. Improving energy efficiency in Bernoulli serial lines: An integrated model. Int. J. Prod. Res. 2016, 54, 3414–3428. [Google Scholar] [CrossRef]
- Yan, C.B.; Cheng, X.; Gao, F.; Guan, X. Formulation and Solution Methodology for Reducing Energy Consumption in Two-Machine Bernoulli Serial Lines. IEEE Trans. Autom. Sci. Eng. 2022, 19, 522–530. [Google Scholar] [CrossRef]
- Yan, C.B. Analysis and Optimization of Energy Consumption in Two-Machine Bernoulli Lines with General Bounds on Machine Efficiency. IEEE Trans. Autom. Sci. Eng. 2021, 18, 151–163. [Google Scholar] [CrossRef]
- Su, W.; Xie, X.; Li, J.; Zheng, L.; Feng, S.C. Reducing energy consumption in serial production lines with Bernoulli reliability machines. Int. J. Prod. Res. 2017, 55, 7356–7379. [Google Scholar] [CrossRef]
- Yan, C.B.; Zheng, Z. Problem Formulation and Solution Methodology for Energy Consumption Optimization in Bernoulli Serial Lines. IEEE Trans. Autom. Sci. Eng. 2021, 18, 776–790. [Google Scholar] [CrossRef]
- Yan, C.B.; Zheng, Z. An effective and efficient divide-and-conquer algorithm for energy consumption optimisation problem in long Bernoulli serial lines. Int. J. Prod. Res. 2021, 59, 7018–7036. [Google Scholar] [CrossRef]
- Cheng, X.; Yan, C.B.; Gao, F. Energy cost optimisation in two-machine Bernoulli serial lines under time-of-use pricing. Int. J. Prod. Res. 2022, 60, 3948–3964. [Google Scholar] [CrossRef]
- Yan, C.B.; Liu, L. Energy Consumption Optimization in Two-Machine Geometric Serial Lines. In Proceedings of the 2020 IEEE 16th International Conference on Automation Science and Engineering (CASE), Hong Kong, China, 20–21 August 2020; pp. 830–835. [Google Scholar]
- Pei, Z.; Yang, P.; Wang, Y.; Yan, C.B. Energy consumption control in the two-machine Bernoulli serial production line with setup and idleness. Int. J. Prod. Res. 2022, 1–20. [Google Scholar] [CrossRef]
- Li, J. Production Variability in Manufacturing Systems: A Systems Approach; University of Michigan: Ann Arbor, MI, USA, 2000. [Google Scholar]
- Yan, C.B.; Liu, L.; Derivatives of Key Functions w.r.t. Machine Efficiencies in Two-Machine Geometric Line. 2020. Available online: http://gr.xjtu.edu.cn/web/chaoboyan/reports (accessed on 1 April 2020).
| Case | Machine 1 | Machine 2 | |||||
|---|---|---|---|---|---|---|---|
| 1-1 | 2 | 4 | 5 | 3 | 4 | 9 | |
| 1-2 | 3 | 4 | 9 | ||||
| 1-3 | 2 | 4 | 5 | ||||
| 2-1 | 3 | 5 | 8 | 9 | 2 | 15 | |
| 2-2 | 9 | 2 | 15 | ||||
| 2-3 | 3 | 5 | 8 | ||||
| 3-1 | 7 | 1 | 12 | 4 | 5 | 10 | |
| 3-2 | 4 | 5 | 10 | ||||
| 3-3 | 7 | 1 | 12 | ||||
| 4-1 | 9 | 2 | 14 | 8 | 3 | 12 | |
| 4-2 | 8 | 3 | 12 | ||||
| 4-3 | 9 | 2 | 14 | ||||
| Case | ECM Algorithm | Simulation | Gap | ||||
|---|---|---|---|---|---|---|---|
| 1-1 | 0.4463 | 0.4375 | 0.4716 | 0.4667 | 6.7982 | 7.0813 () | 3.9974% |
| 1-2 | 0.2813 | 1 | 0.3600 | 0.6667 | ( | 0.1681% | |
| 1-3 | 1 | 0.2813 | 0.6667 | 0.3600 | ( | 2.0415% | |
| 2-1 | 0.2813 | 1 | 0.3600 | 0.6667 | 10.6249 | 10.5496 ( | 0.7142% |
| 2-2 | 0.2813 | 1 | 0.3600 | 0.6667 | 1.4672% | ||
| 2-3 | 1 | 0.2813 | 0.6667 | 0.3600 | 3.3325% | ||
| 3-1 | 1 | 0.2813 | 0.6667 | 0.3600 | 9.7438 | 9.7030 ( | 0.4207% |
| 3-2 | 0.2813 | 1 | 0.3600 | 0.6667 | 4.2099% | ||
| 3-3 | 1 | 0.2813 | 0.6667 | 0.3600 | 1.7876% | ||
| 4-1 | 1 | 0.2813 | 0.6667 | 0.3600 | 12.5565 | 12.4680 ( | 0.7105% |
| 4-2 | 0.2813 | 1 | 0.3600 | 0.6667 | 3.4456% | ||
| 4-3 | 1 | 0.2813 | 0.6667 | 0.3600 | 2.3537% | ||
| Case | ES Algorithm | Simulation | Gap | |||||
|---|---|---|---|---|---|---|---|---|
| 0.3 | 0.4 | 1-1 | 0.0732 | 0.4226 | 20 | 6.0002 | 5.6751 ( | 5.7281% |
| 2-1 | 0.4000 | 0.8000 | 1 | 10.1733 | 10.1246 | 0.4810% | ||
| 3-1 | 0.0732 | 0.4226 | 20 | 9.7779 | 9.5336 | 2.5629% | ||
| 4-1 | 0.0732 | 0.4226 | 20 | 12.1865 | 12.9396 | 5.8204% | ||
| 0.4 | 0.6 | 1-1 | 0.1123 | 0.5290 | 20 | 7.4676 | 7.0791 | 5.4878% |
| 2-1 | 0.5719 | 0.8512 | 1 | 12.1200 | 12.0232 | 0.8047% | ||
| 3-1 | 0.1123 | 0.5290 | 20 | 12.1846 | 11.7161 | 3.9991% | ||
| 4-1 | 0.5719 | 0.8512 | 1 | 15.0282 | 14.7474 | 1.9039% | ||
| 0.5 | 0.9 | 1-1 | 0.1267 | 0.5588 | 20 | 8.5907 | 8.7511 | 1.8332% |
| 2-1 | 0.6835 | 0.8724 | 1 | 14.1413 | 12.7798 | 4.3490% | ||
| 3-1 | 0.1267 | 0.5588 | 20 | 14.0535 | 14.4791 | 2.9396% | ||
| 4-1 | 0.6835 | 0.8724 | 1 | 17.3089 | 17.4639 | 0.8875% | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, P.; Pei, Z. Energy-Saving Manufacturing System Design with Two Geometric Machines. Sustainability 2022, 14, 11448. https://doi.org/10.3390/su141811448
Yang P, Pei Z. Energy-Saving Manufacturing System Design with Two Geometric Machines. Sustainability. 2022; 14(18):11448. https://doi.org/10.3390/su141811448
Chicago/Turabian StyleYang, Peiqi, and Zhi Pei. 2022. "Energy-Saving Manufacturing System Design with Two Geometric Machines" Sustainability 14, no. 18: 11448. https://doi.org/10.3390/su141811448
APA StyleYang, P., & Pei, Z. (2022). Energy-Saving Manufacturing System Design with Two Geometric Machines. Sustainability, 14(18), 11448. https://doi.org/10.3390/su141811448





