Effects of Temperature Rise on Clean Energy-Based Capital Market Investments: Neural Network-Based Granger Causality Analysis
Abstract
:1. Introduction
2. Literature Review
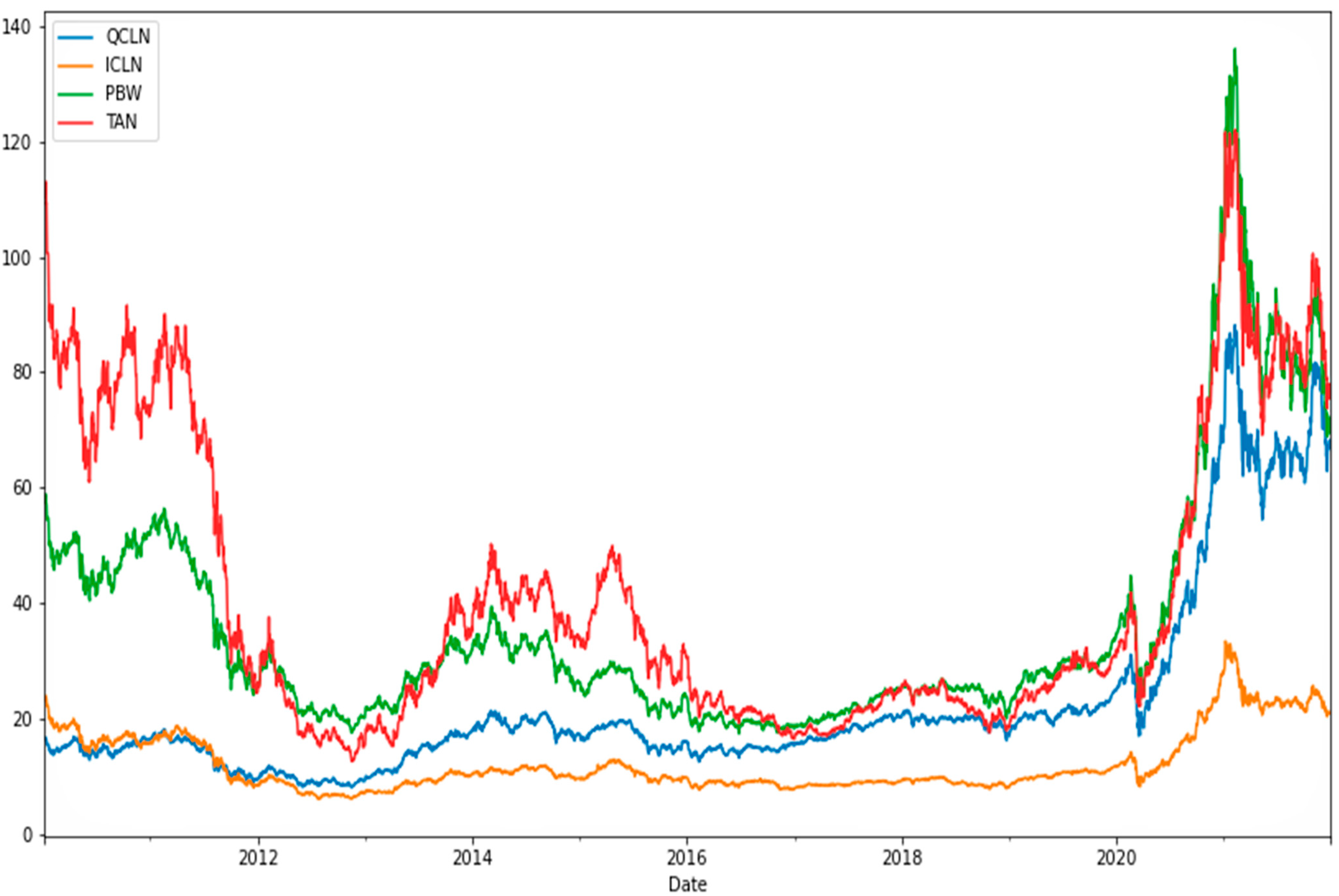
3. Data and Methodology
4. Results
5. Discussions and Policy Implications
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ETF | Exchange Traded Funds |
| ANN | Artificial Neural Network |
| MLP | Multi-Layer Perceptron |
| LSTM | Long Short-Term Memory |
| GRU | Gated Recurrent Unit |
| QCLN | First Trust NASDAQ Clean Edge Green Energy Index Fund |
| ICLN | iShares Global Clean Energy |
| PBW | Invesco WilderHill Clean Energy ETF |
| TAN | Invesco Solar ETF |
| NCEI | National Centre for Environmental Information |
| IPCC | Intergovernmental Panel on Climate Change |
| COP | Conference of the Parties |
| ADB | Asian Development Bank |
| GARCH | Generalized Auto-Regressive Conditional Heteroscedasticity |
References
- Warner, K.; Hamza, M.; Oliver-Smith, A.; Renaud, F.; Julca, A. Climate change, environmental degradation and migration. Nat. Hazards 2010, 55, 689–715. [Google Scholar] [CrossRef]
- Dell, M.; Jones, B.F.; Olken, B.A. Temperature shocks and economic growth: Evidence from the last half century. Am. Econ. J. Macroecon. 2012, 4, 66–95. [Google Scholar] [CrossRef]
- Hsiang, S.M. Temperatures and cyclones strongly associated with economic production in the Caribbean and Central America. Proc. Nat. Acad. Sci. USA 2010, 107, 15367–15372. [Google Scholar] [CrossRef] [PubMed]
- Schlenker, W.; Roberts, M.J. Nonlinear temperature effects indicate severe damages to US crop yields under climate change. Proc. Nat. Acad. Sci. USA 2009, 106, 15594–15598. [Google Scholar] [CrossRef] [PubMed]
- Heyes, A.; Saberian, S. Temperature and decisions: Evidence from 207,000 court cases. Am. Econ. J. Appl. Econ. 2019, 11, 238–265. [Google Scholar] [CrossRef]
- Khan, Z.; Iyer, G.; Patel, P.; Kim, S.; Hejazi, M.; Burleyson, C.; Wise, M. Impacts of long-term temperature change and variability on electricity investments. Nat. Commun. 2021, 12, 1–12. [Google Scholar] [CrossRef]
- Fisher, A.C.; Hanemann, W.M.; Roberts, M.J.; Schlenker, W. The economic impacts of climate change: Evidence from agricultural output and random fluctuations in weather: Comment. Am. Econ. Rev. 2012, 102, 3749–3760. [Google Scholar] [CrossRef]
- Reichelt, H. Green bonds: A model to mobilise private capital to fund climate change mitigation and adaptation projects. In EuroMoney Environmental Finance Handbook; The World Bank: Washington, DC, USA, 2010; pp. 1–7. [Google Scholar]
- Liu, X.; Zeng, M. Renewable energy investment risk evaluation model based on system dynamics. Renew. Sustain. Energy Rev. 2017, 73, 782–788. [Google Scholar] [CrossRef]
- Krueger, P.; Sautner, Z.; Starks, L.T. The importance of climate risks for institutional investors. Rev. Financ. Stud. 2020, 33, 1067–1111. [Google Scholar] [CrossRef]
- Chen, A.S.; Leung, M.T.; Daouk, H. Application of neural networks to an emerging financial market: Forecasting and trading the Taiwan Stock Index. Comput. Oper. Res. 2003, 30, 901–923. [Google Scholar] [CrossRef]
- Fahmy, H. The rise in investors’ awareness of climate risks after the Paris Agreement and the clean energy-oil-technology prices nexus. Energy Econ. 2022, 106, 105738. [Google Scholar] [CrossRef]
- Hansen, J.; Sato, M.; Ruedy, R. Perception of climate change. Proc. Nat. Acad. Sci. USA 2012, 109, E2415–E2423. [Google Scholar] [CrossRef] [PubMed]
- Pryor, S.C.; Scavia, D.; Downer, C.; Gaden, M.; Iverson, L.; Nordstrom, R.; Robertson, G.P. Midwest. Climate Change Impacts in the United States: The Third National Climate Assessment; Melillo, J.M., Richmond, T.C., Yohe, G.W., Eds.; National Climate Assessment Report; US Global Change Research Program: Washington, DC, USA, 2014; pp. 418–440.
- Xu, A.; Tian, M.W.; Firouzi, B.; Alattas, K.A.; Mohammadzadeh, A.; Ghaderpour, E. A New Deep Learning Restricted Boltzmann Machine for Energy Consumption Forecasting. Sustainability 2022, 14, 10081. [Google Scholar] [CrossRef]
- Şenhaz, Z.; Katircioglu, S.; Katircioglu, S. Dynamic effects of shadow economy and environmental pollution on the energy stock prices: Empirical evidence from OECD countries. Environ. Sci. Pollut. Res. 2021, 28, 8520–8529. [Google Scholar] [CrossRef]
- Tufan, E.; Hamarat, B. Do cloudy days affect stock exchange returns: Evidence from Istanbul stock exchange. J. Nav. Sci. Eng. 2004, 2, 117–126. [Google Scholar]
- Levy, T.; Yagil, J. Air pollution and stock returns in the US. J. Econ. Psychol. 2011, 32, 374–383. [Google Scholar] [CrossRef]
- Teng, M.; He, X. Air quality levels, environmental awareness and investor trading behavior: Evidence from stock market in China. J. Clean. Prod. 2020, 244, 118663. [Google Scholar] [CrossRef]
- Howarth, E.; Hoffman, M.S. A multidimensional approach to the relationship between mood and weather. Br. J. Psychol. 1984, 75, 15–23. [Google Scholar] [CrossRef]
- Addoum, J.M.; Ng, D.T.; Ortiz-Bobea, A. Temperature shocks and establishment sales. Rev. Financ. Stud. 2020, 33, 1331–1366. [Google Scholar] [CrossRef]
- Burke, M.; Hsiang, S.M.; Miguel, E. Global non-linear effect of temperature on economic production. Nature 2015, 527, 235–239. [Google Scholar] [CrossRef]
- Colacito, R.; Hoffmann, B.; Phan, T. Temperature and growth: A panel analysis of the United States. J. Money Credit Bank. 2019, 51, 313–368. [Google Scholar] [CrossRef]
- Cao, M.; Wei, J. Stock market returns: A note on temperature anomaly. J. Bank. Financ. 2005, 29, 1559–1573. [Google Scholar] [CrossRef]
- Balvers, R.; Du, D.; Zhao, X. Temperature shocks and the cost of equity capital: Implications for climate change perceptions. J. Bank. Financ. 2017, 77, 18–34. [Google Scholar] [CrossRef]
- Bansal, R.; Ochoa, M.; Kiku, D. Climate Change and Growth Risks (No. w23009); National Bureau of Economic Research: Cambridge, MA, USA, 2017. [Google Scholar]
- Baker, M.; Wurgler, J. Investor sentiment and the cross-section of stock returns. J. Financ. 2006, 61, 1645–1680. [Google Scholar] [CrossRef]
- He, J.; Ma, X. Extreme temperatures and firm-level stock returns. Int. J. Environ. Res. Public Health 2021, 18, 2004. [Google Scholar] [CrossRef] [PubMed]
- Yan, Y.; Xiong, X.; Li, S.; Lu, L. Will temperature change reduce stock returns? Evidence from China. Int. Rev. Financ. Anal. 2022, 81, 102112. [Google Scholar] [CrossRef]
- Lohrmann, C.; Lohrmann, A. Accuracy and Predictive Power of Sell-Side Target Prices for Global Clean Energy Companies. Sustainability 2021, 13, 12746. [Google Scholar] [CrossRef]
- Ben-David, I.; Franzoni, F.; Moussawi, R. Exchange-traded funds. Annu. Rev. Financ. Econ. 2017, 9, 169–189. [Google Scholar] [CrossRef]
- Kosev, M.; Williams, T. Exchange-traded funds. RBA Bull. 2011, 51–59. Available online: https://www.rba.gov.au/publications/bulletin/2011/mar/pdf/bu-0311.pdf#page=53 (accessed on 10 July 2022).
- Mendelsohn, M.; Feldman, D. Financing US Renewable Energy Projects through Public Capital Vehicles: Qualitative and Quantitative Benefits (No. NREL/TP-6A20-58315); National Renewable Energy Lab. (NREL): Golden, CO, USA, 2013. [Google Scholar]
- Agreement, P. Paris agreement. In Proceedings of the Conference of the Parties to the United Nations Framework Convention on Climate Change (21st Session), Paris, France, 30 November–3 December 2015; Volume 4, p. 2017. [Google Scholar]
- La Monaca, S.; Assereto, M.; Byrne, J. Clean energy investing in public capital markets: Portfolio benefits of yieldcos. Energy Policy 2018, 121, 383–393. [Google Scholar] [CrossRef]
- Ibikunle, G.; Steffen, T. European green mutual fund performance: A comparative analysis with their conventional and black peers. J. Bus. Eth. 2017, 145, 337–355. [Google Scholar] [CrossRef]
- Pavlova, I.; de Boyrie, M.E. ESG ETFs and the COVID-19 stock market crash of 2020: Did clean funds fare better? Financ. Res. Lett. 2022, 44, 102051. [Google Scholar] [CrossRef]
- Kumar, S.; Managi, S.; Matsuda, A. Stock prices of clean energy firms, oil and carbon markets: A vector autoregressive analysis. Energy Econ. 2012, 34, 215–226. [Google Scholar] [CrossRef]
- Broadstock, D.C.; Cao, H.; Zhang, D. Oil shocks and their impact on energy related stocks in China. Energy Econ. 2012, 34, 1888–1895. [Google Scholar] [CrossRef]
- Kocaarslan, B.; Soytas, U. Asymmetric pass-through between oil prices and the stock prices of clean energy firms: New evidence from a nonlinear analysis. Energy Rep. 2019, 5, 117–125. [Google Scholar] [CrossRef]
- Dutta, A.; Jana, R.K.; Das, D. Do green investments react to oil price shocks? Implications for sustainable development. J. Clean. Prod. 2020, 266, 121956. [Google Scholar] [CrossRef]
- Nasreen, S.; Tiwari, A.K.; Eizaguirre, J.C.; Wohar, M.E. Dynamic connectedness between oil prices and stock returns of clean energy and technology companies. J. Clean. Prod. 2020, 260, 121015. [Google Scholar] [CrossRef]
- Ferrer, R.; Shahzad, S.J.H.; López, R.; Jareño, F. Time and frequency dynamics of connectedness between renewable energy stocks and crude oil prices. Energy Econ. 2018, 76, 1–20. [Google Scholar] [CrossRef]
- Elie, B.; Naji, J.; Dutta, A.; Uddin, G.S. Gold and crude oil as safe-haven assets for clean energy stock indices: Blended copulas approach. Energy 2019, 178, 544–553. [Google Scholar] [CrossRef]
- Sadorsky, P. The Impact of Market Uncertainty on the Systematic Risk of Clean Energy Stocks. In Applications in Energy Finance; Palgrave Macmillan: Cham, Germany, 2022; pp. 171–193. [Google Scholar]
- Wang, J.; Ma, F.; Bouri, E.; Zhong, J. Volatility of clean energy and natural gas, uncertainty indices, and global economic conditions. Energy Econ. 2022, 108, 105904. [Google Scholar] [CrossRef]
- Baek, E.G.; Brock, W.A. A nonparametric test for independence of a multivariate time series. Stat. Sin. 1992, 2, 137–156. [Google Scholar]
- Lusch, B.; Maia, P.D.; Kutz, J.N. Inferring connectivity in networked dynamical systems: Challenges using Granger causality. Phys. Rev. E 2016, 94, 032220. [Google Scholar] [CrossRef] [PubMed]
- Hiemstra, C.; Jones, J.D. Testing for linear and nonlinear Granger causality in the stock price-volume relation. J. Financ. 1994, 49, 1639–1664. [Google Scholar]
- Bergmann, T.O.; Hartwigsen, G. Inferring causality from noninvasive brain stimulation in cognitive neuroscience. J. Cogn. Neurosc. 2021, 33, 195–225. [Google Scholar] [CrossRef] [PubMed]
- Popken, D.A.; Cox, L.A., Jr. Quantifying Human Health Risks Caused by Toxoplasmosis from Open System Production of Swine. Hum. Ecol. Risk Assess. Int. J. 2015, 21, 1717–1735. [Google Scholar] [CrossRef]
- Henderson, J.; Michailidis, G. Network reconstruction using nonparametric additive ode models. PLoS ONE 2014, 9, e94003. [Google Scholar] [CrossRef]
- Hastie, T.J. Generalized additive models. In Statistical Models in S; Routledge: New York, NY, USA, 2017; pp. 249–307. [Google Scholar]
- Tabari, N.; Seyeditabari, A.; Peddi, T.; Hadzikadic, M.; Zadrozny, W. A comparison of neural network methods for accurate sentiment analysis of stock market tweets. In ECML PKDD 2018 Workshops; Springer: Cham, Germany, 2018; pp. 51–65. [Google Scholar]
- Zhang, G.P. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Zhang, G.P.; Qi, G.M. Neural network forecasting for seasonal and trend time series. Eur. J. Oper. Res. 2005, 160, 501–514. [Google Scholar] [CrossRef]
- Kashei, M.; Bijari, M. An artificial neural network (p, d, q) model for time series forecasting. Expert Syst. Appl. 2010, 37, 479–489. [Google Scholar] [CrossRef]
- Tank, A.; Cover, I.; Foti, N.J.; Shojaie, A.; Fox, E.B. An interpretable and sparse neural network model for nonlinear granger causality discovery. arXiv 2017, arXiv:1711.08160. [Google Scholar]
- Marcinkevičs, R.; Vogt, J.E. Interpretable models for granger causality using self-explaining neural networks. arXiv 2021, arXiv:2101.07600. [Google Scholar]
- Maciej, R.; Mlynczak, M.; Cybulski, G. Granger causality test with nonlinear neural-network-based methods: Python package and simulation study. Comput. Methods Progr. Biomed. 2021, 216, 1–16. [Google Scholar]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to forget: Continual prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef]
- Kao, E.H.; Fung, H.G. Intraday trading activities and volatility in round-the-clock futures markets. Int. Rev. Econ. Financ. 2012, 21, 195–209. [Google Scholar] [CrossRef]
| Return_Qcln | Return_Icln | Vol_Qcln | Vol_Icln | Temp_NY | Temp_L | Temp_T | |
|---|---|---|---|---|---|---|---|
| N | 4376 | 4376 | 4376 | 4376 | 4376 | 4376 | 4376 |
| Mean | 0.0317 | −0.0176 | 70,662.3 | 72,002.6 | 55.6 | 51.4 | 62.3 |
| Median | 0.1389 | 0.0000 | 14,830 | 25,445 | 55.5 | 51.3 | 63 |
| Std | 1.7893 | 1.6175 | 145,349.6 | 139,501.2 | 16.5 | 11.3 | 13.9 |
| Min | −13.9 | −13.7 | 100 | 1010 | 8.5 | 11.4 | 34.1 |
| Max | 13.6 | 10.8 | 999,810 | 991,680 | 90.1 | 83.4 | 90.3 |
| Skew | −0.4139 | −0.5235 | 3.3958 | 3.7514 | −0.1744 | −0.1980 | −0.0133 |
| Kurtosis | 4.4585 | 5.5627 | 12.6491 | 15.4445 | −0.9641 | −0.2615 | −1.1707 |
| Lag Value | Granger Causality | MLP | AR |
|---|---|---|---|
| 30 | return_qcln | 3.300 × 10−85 ** | 0.9586 |
| return_qcln | 0.1558 | 0.7259 | |
| return_qcln | 0.00181 ** | 0.3639 | |
| return_icln | 0.0004598 ** | 0.9693 | |
| return_icln | 3.02839 × 10−52 ** | 0.6994 | |
| return_icln | 0.02819 * | 0.2961 | |
| 60 | return_qcln | 1.189715 × 10−28 ** | 0.8919 |
| return_qcln | 6.802304 × 10−13 ** | 0.5499 | |
| return_qcln | 1.066786 × 10−13 ** | 0.5741 | |
| return_icln | 3.579381 × 10−05 ** | 0.9281 | |
| return_icln | 2.161692 × 10−49 ** | 0.3977 | |
| return_icln | 1.197499 × 10−40 ** | 0.3111 |
| Lag Value | Granger Causality | MLP | AR |
|---|---|---|---|
| 30 | vol_qcln | 2.073000 × 10−36 ** | 0.0507 * |
| vol_qcln | 4.015626 × 10−09 ** | 0.0383 * | |
| vol_qcln | 3.122777 × 10−108 ** | 0.6730 | |
| vol_icln | 4.050622 × 10−49 ** | 0.3861 | |
| vol_icln | 1.890867 × 10−68 ** | 0.9022 | |
| vol_icln | 2.989957 × 10−77 ** | 0.0974 * | |
| 60 | vol_qcln | 6.542931 × 10−16 ** | 0.0452 ** |
| vol_qcln | 2.369952 × 10−13 ** | 0.0668 * | |
| vol_qcln | 1.797172 × 10−50 ** | 0.1938 | |
| vol_icln | 6.052480 × 10−62 ** | 0.6370 | |
| vol_icln | 1.858961 × 10−68 ** | 0.1864 | |
| vol_icln | 0.630244 | 0.0703 * |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Swarup, S.; Singh Kushwaha, G. Effects of Temperature Rise on Clean Energy-Based Capital Market Investments: Neural Network-Based Granger Causality Analysis. Sustainability 2022, 14, 11163. https://doi.org/10.3390/su141811163
Swarup S, Singh Kushwaha G. Effects of Temperature Rise on Clean Energy-Based Capital Market Investments: Neural Network-Based Granger Causality Analysis. Sustainability. 2022; 14(18):11163. https://doi.org/10.3390/su141811163
Chicago/Turabian StyleSwarup, Shivam, and Gyaneshwar Singh Kushwaha. 2022. "Effects of Temperature Rise on Clean Energy-Based Capital Market Investments: Neural Network-Based Granger Causality Analysis" Sustainability 14, no. 18: 11163. https://doi.org/10.3390/su141811163
APA StyleSwarup, S., & Singh Kushwaha, G. (2022). Effects of Temperature Rise on Clean Energy-Based Capital Market Investments: Neural Network-Based Granger Causality Analysis. Sustainability, 14(18), 11163. https://doi.org/10.3390/su141811163






