A Cooperative Merging Control Method for Freeway Ramps in Connected and Autonomous Driving

Abstract

The highway on-ramp merging area is one of the major sections that form traffic bottlenecks. In a connected vehicle environment, V2V and V2I technologies enable real-time exchange of information, including position, speed, and acceleration. To improve the efficiency of vehicle merging at the on-ramp, this study proposes a cooperative merging control strategy for network-connected autonomous vehicles. First, the central controller designs the merging sequence and safety space for vehicles passing through the confluence point. Then, a trajectory optimization model was constructed based on vehicle longitudinal dynamics, and the PMP algorithm was used to determine the optimal control input. Finally, all vehicles follow the optimal trajectory so that the ramp vehicles merge smoothly into the mainline. Simulations verify that the proposed algorithm performs better than FIFO, with 13.2% energy savings, 41.4% increase in average speed, and 50.4% reduction in travel time over the uncontrolled merging scenario. The method is further applied to different traffic flow conditions and the results show that it can significantly improve traffic safety and mobility, while effectively reducing vehicle energy consumption. However, the traffic operation improvement is not satisfactory under low traffic demand.

1. Introduction

The ramp merging area formed at the junction of the freeway mainline and on-ramps causes traffic bottlenecks for the following main reasons: (1) In the highway on-ramp merging area, potential conflicts between ramp vehicles and mainline vehicles may occur from time to time, and (2) uncontrolled inflow of traffic can cause congestion when the downstream highway capacity is exceeded. In addition, due to the limited field of view and the uncoordinated behavior of merging vehicles with mainline vehicles, a driver may unnecessarily accelerate or decelerate, resulting in additional energy consumption and pollutant emissions.

In connected and autonomous driving, vehicles can exchange information in real time through V2V and V2I technologies, which enable ramp vehicles to collaborate with mainline vehicles. In addition to communication devices, self-driving vehicles are capable of precise trajectory planning control, further facilitating cooperative merging. Based on this, we propose a ramp merging method for CAVs, including the sequence of merging between vehicles and the corresponding trajectory control. Vehicle maneuvers directly affect traffic efficiency and energy emissions, so this approach has great potential to improve traffic operations and the transportation environment. The main contributions of this paper can be divided into the following points. (1) The method considers the time optimization problem in the ramp merging process. It increases the throughput by minimizing the merging time and reduces the cross-merging by constraint, thus achieving the goal of improving the merging efficiency and safety. (2) Numerical simulations were carried out to validate the method under different traffic flow conditions to evaluate the performance and applicability of the method. The remainder of this paper is organized as follows. Section 2 presents a review of existing research. In Section 3, the system framework and modeling scheme of the cooperative merging control method are described. Section 4 presents the simulation process and a discussion of the results. Section 5 shows the simulation results applied to different traffic flows. Finally, Section 6 gives some concluding remarks.

2. Literature Review

The traditional ramp control method is to control the ramp vehicles with the help of signal lights (ramp metering [1] (RM)); or control the mainline vehicles by setting speed limit signs (variable speed limit [2] (VSL)). Currently, the most widely used ramp control method is ALINEA [3], which calculates the ramp flow merging into the mainline from the traffic occupancy observed on the mainstream, downstream of the ramp. METALIENE [4] is an extension of the single-point ramp control ALINEA algorithm which enables the coordinated control of ramps within a traffic network. Stephanedes [5] proposed the ZONE algorithm, which decomposes the mainline into multiple control zones to ensure smooth traffic flow by balancing the input and output traffic volumes. Subsequently, algorithms such as HERO [6], SZM [7], and SWARM [8] were proposed to continuously enrich and improve the control of ramp flow regulation. Traditional ramp control methods do not consider the complex driving behavior in the confluence area, especially the forced lane change behavior taken by ramp vehicles in the process of merging into the mainline, which interferes with the normal operation of the mainline traffic flow.

In recent years, the technology of connected autonomous vehicles (CAV) has been continuously developed to improve traffic safety, mobility, and environmental impact. CAV can shorten the interval between vehicles and decrease the reaction time, thereby improving highway capacity [9]. Given the CAV capabilities, automated on-ramp merging strategies can be broadly classified into two categories: centralized control and distributed control. An excellent survey of proposed approaches may be found in reference [10].

Centralized control is present if the system’s tasks and control commands need to be executed by the road infrastructure or the traffic management center (TMC) for all CAVs on a global scale [11]. In some centralized methods, CAV collaborative merging can also be modeled as an optimization problem solved by a centralized controller. Raravi et al. [12] proposed an optimization problem with the goal of minimizing the vehicle-to-intersection time (DTTI) and ensuring safety under certain constraints. Awal et al. [13] proposed an optimization problem whose goal is to reduce the merging time at ramps, thereby mitigating the bottleneck character of the confluence area. Rios-Torres et al. [14] formulated an unconstrained optimal control problem with the goal of reducing fuel consumption and driving time. They use a centralized controller to optimize the trajectory of each vehicle and consider hard constraints to avoid collisions.

Distributed control makes local coordinated decisions between different CAVs through vehicle-to-vehicle (V2V) communication. Compared with centralized control relying on V2V and V2I technology, distributed control can reduce communication requirements and increase flexibility. Uno et al. [15] propose to use the vehicles on the ramp as virtual vehicles mapped to the main road before the actual merge occurs, allowing for a safer and smoother merge operation. Lu et al. [16] put forward a new concept of virtual queuing in the merging problem with similar ideas and established a unified longitudinal control model for different road layouts. In addition to the idea of virtual vehicles, there are other distributed methods to control the longitudinal movement of the CAV on the ramp. Ntousakis et al. [17] proposed a cooperative merging system to efficiently handle the gap between vehicles and evaluated its performance and impact on highway capacity. Dao et al. [18] presented a distributed control strategy to select lanes for platoons using inter-vehicle communication. Ntousakis et al. [19] proposed a longitudinal trajectory optimization method for a pair of cooperating vehicles, including the merged vehicle and its hypothetical leader. Zhou et al. [20] proposed a vehicle trajectory planning method for automated on-ramp merging. Trajectory planning tasks of an on-ramp merging vehicle and a mainline facilitating vehicle are formulated as two related distributed optimization problems.

There are hierarchical control methods where upper-level tasks are obtained by a centralized controller and then locally coordinated by a distributed control method. Schmidt et al. [21] proposed a coupled two-layer control scheme. The upper layer is responsible for merging sequence control, and the lower layer is responsible for vehicle motion control. Ran et al. [22] also proposed a centralized multi-layer automatic ramp merging system and established a microscopic simulation model to verify its characteristics. A cooperative multi-player game-based optimization framework and a corresponding algorithm are presented to coordinate vehicles by Jing et al. [23] First, it determines the confluence sequence of vehicles based on game theory and then optimizes the trajectories with the goals of fuel consumption mitigation and passenger comfort.

Based on the above research status, most of the current methods focus on discussing the trajectory optimization of vehicles, but rarely consider the timing and sequence of vehicles through the merging zone. The sequence of vehicles through the merging zone corresponds to different trajectories, which can also have an impact on energy consumption and traffic efficiency. Existing merging sequence optimization methods consider only fuel consumption as an objective and require a high computational cost, which is limited in terms of real-time implementation. In this paper, we propose a systematic approach that considers the merging sequence and trajectory control, with optimization goals that also include improving the merging efficiency and safety. Moreover, unlike previous simple case studies, we tested the applicability of the method under different traffic flow conditions.

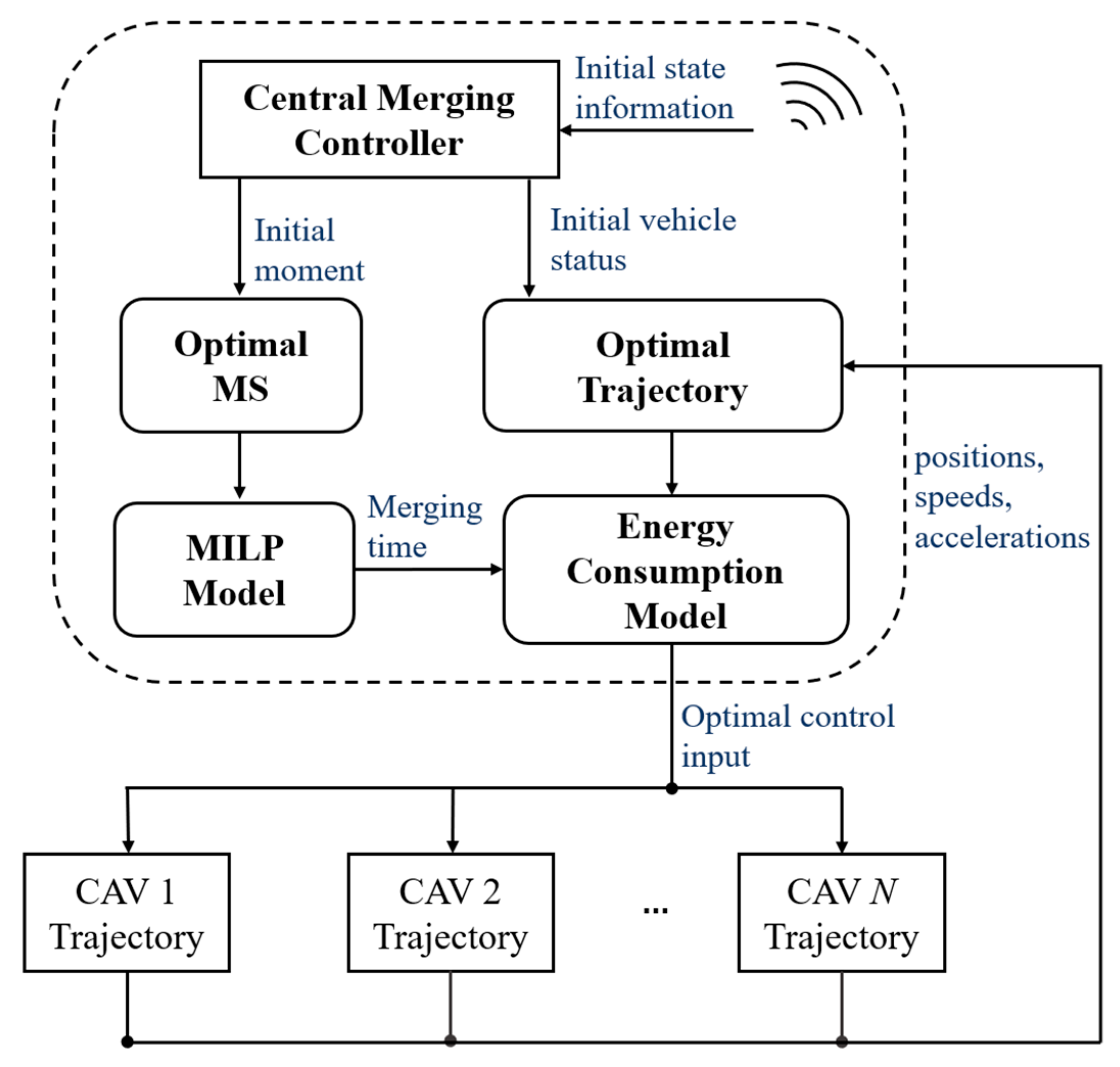
3. System Framework and Methodology

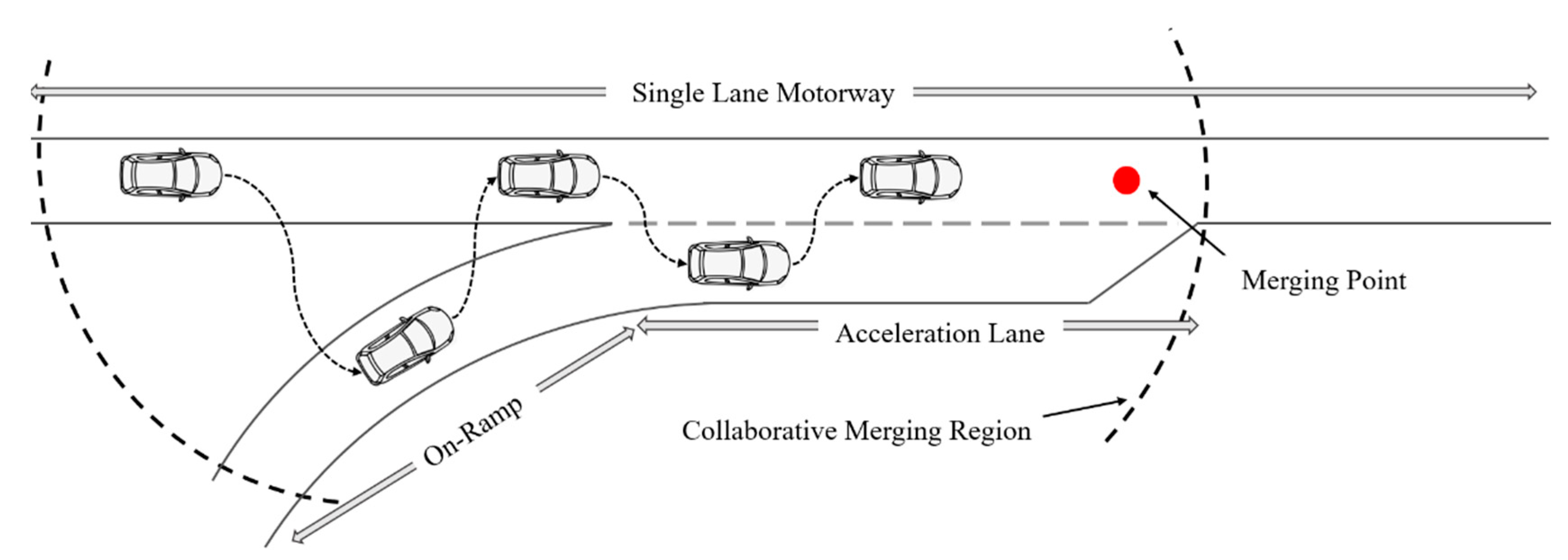
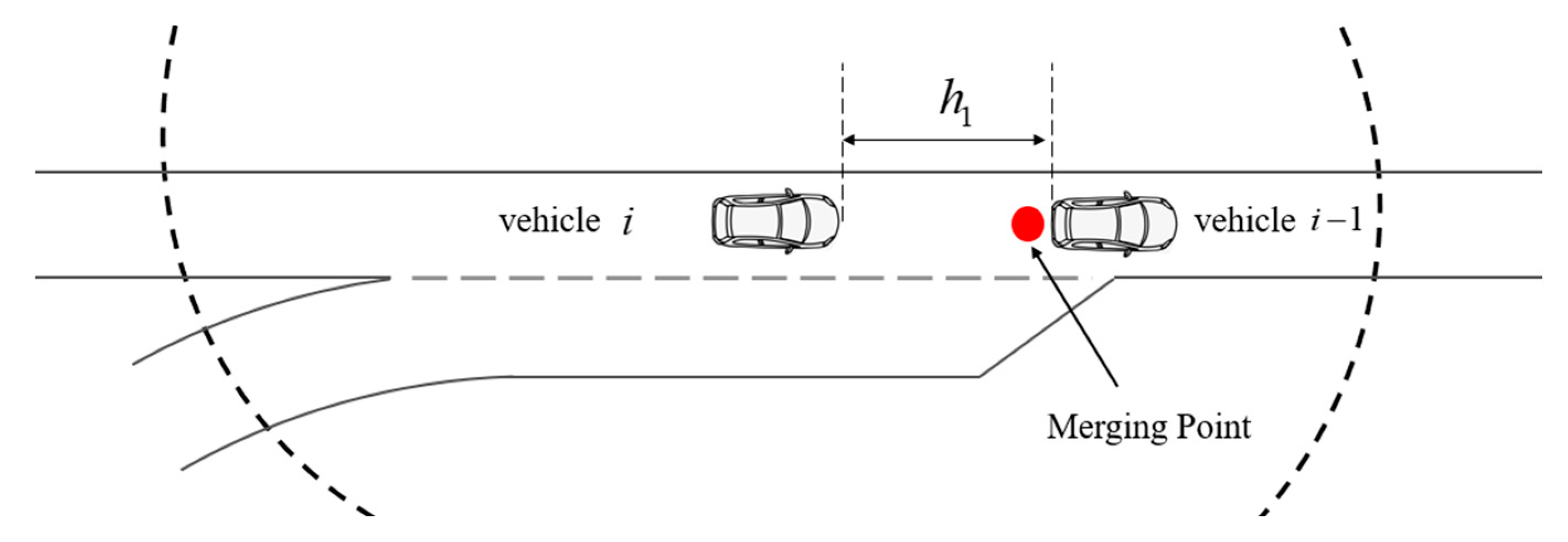
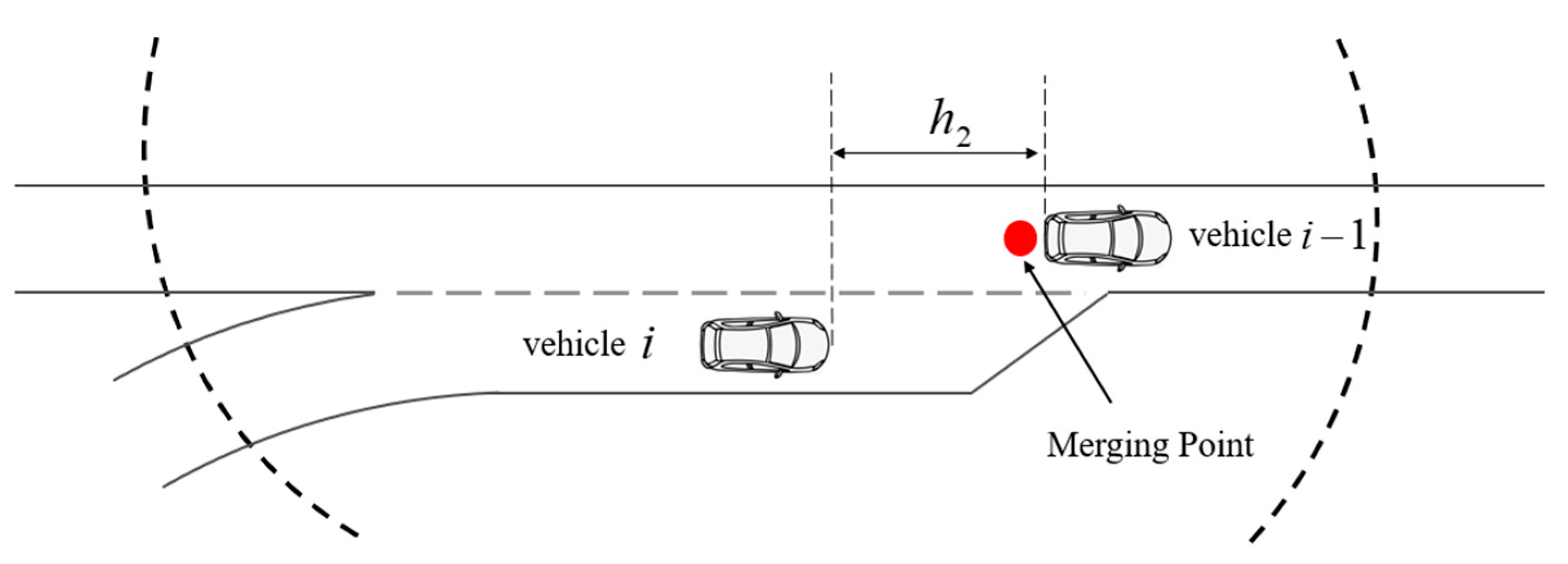
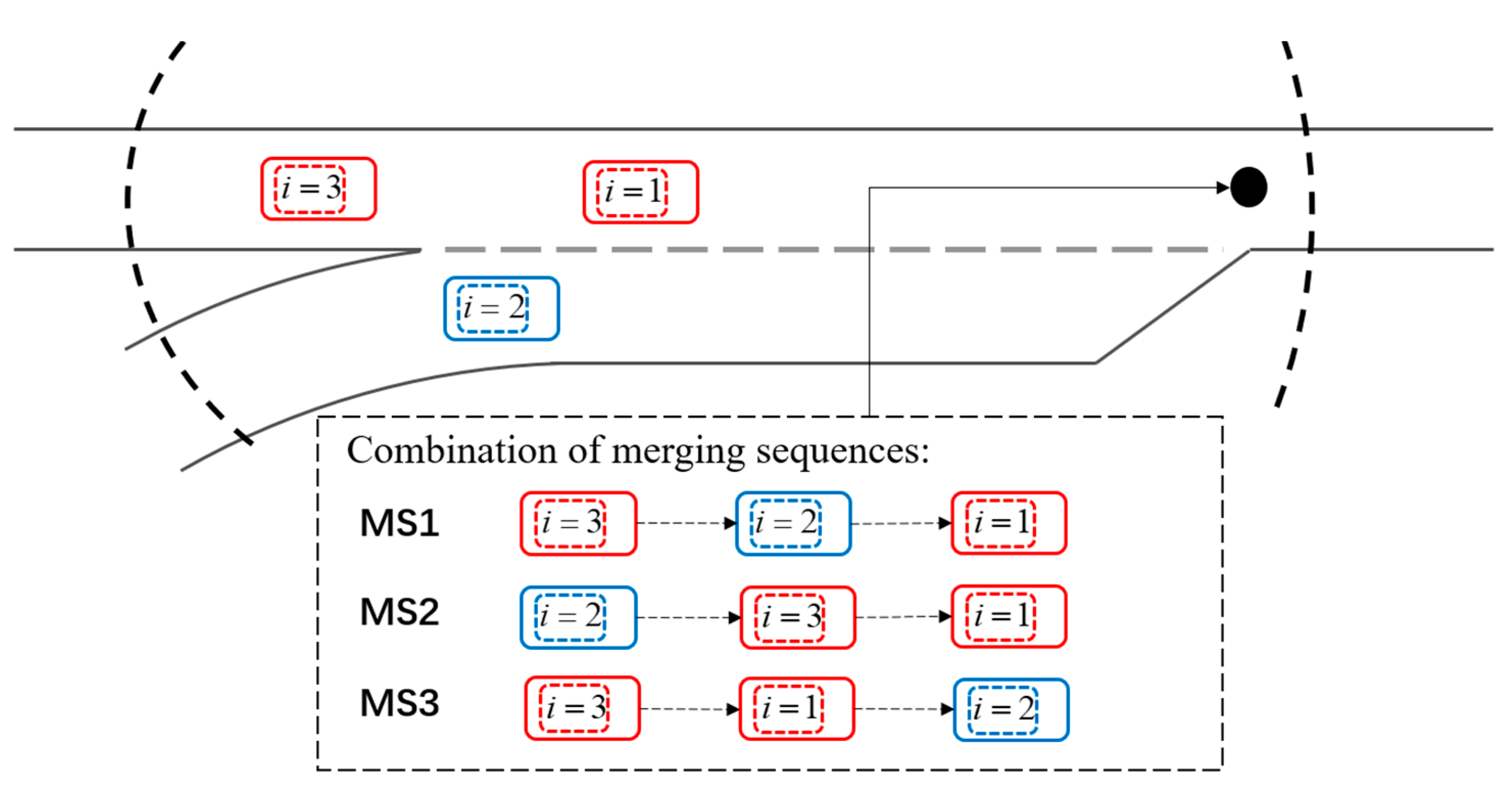
3.1. Problem Formulation

In common freeway ramp scenarios, vehicles on the outside of the mainline and ramp always slow down or accelerate to maintain safe spacing and thus avoid collisions. As ramp vehicles suddenly merge into the mainline fleet, the traffic density on the mainline increases dramatically, causing traffic congestion as well as energy waste. To improve the ramp merging efficiency and save energy, this paper proposed a cooperative merging control method for freeway ramp in connected and autonomous driving. A typical freeway single-lane ramp merging situation is considered in this paper, as shown in Figure 1.

A merging point is defined at the end of the confluence area, where the mainline and the entrance ramp meet. A collaborative merging area is defined within 300 m upstream area of the merging point, which covers the onramp and the rightmost lane of the mainline (Figure 1). All vehicles in the collaborative merging area are connected autonomous vehicles, equipped with on-board units (OBU) to communicate and interconnect with the roadside unit (RSU). Therefore, the central controller can obtain the traffic state information of the controlled vehicles and return corresponding input signals to control the vehicles.

This study assumes that all mainline vehicles will not change lane after entering the collaborative merging area and hence that all vehicles in the ramp and the rightmost lane of the mainline participate in the merging procedure. As shown in Figure 2, the vehicles in the cooperative merging area switch the automatic mode to the unified centralized control mode and send their own traffic status information to the central controller. The central controller collects the information and optimizes the merging sequence (MS) and control inputs using the mixed integer planning model (MILP) and energy consumption model described below. This problem does not consider the lateral lane change maneuver of ramp vehicles, but all vehicles adjust their longitudinal trajectory according to the optimal control input. Following the optimized trajectory, vehicles can pass the merging point in sequence and safely without any traffic conflicts.

Assume that at time $t$, the number of vehicles in the collaborative merging control area is $N\left(t\right)$. The central controller assigns a unique number i to the vehicles in the order in which they enter, $i\in N\left(t\right)$. The calculation of the optimal vehicle trajectories requires previous determination of the merging sequence of the vehicles [24]. At first, first-in-first-out (FIFO) is used to determine the sequence of vehicles arriving at the merging point. It means that the smaller $i$ is, the earlier vehicle $i$ has entered the collaborative merging area, and the earlier it will reach the merging point. As mentioned, the driving state of each vehicle $i$ is only referring to the longitudinal movement, which is described by the third-order equation of motion:

$${\dot{x}}_i=f\left(x_i\left(t\right),u_i\left(t\right),t\right)=A{x}_i\left(t\right)+B{u}_i\left(t\right)$$

(1)

where $f$ is the state variable function, $x_i\left(t\right)$ is the state variable, $u_i\left(t\right)$ is the control input variable, $t$ is the time, $A=\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ 0& 0& 0\end{array}\right]$, $B=\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$. More specifically, we have

$${\dot{x}}_i\left(t\right)=\left[\begin{array}{c}{\dot{p}}_i\left(t\right)\\ {\dot{v}}_i\left(t\right)\\ {\dot{a}}_i\left(t\right)\end{array}\right]=\left[\begin{array}{c}{v}_i\left(t\right)\\ a_i\left(t\right)\\ u_i\left(t\right)\end{array}\right]$$

(2)

where $p_i\left(t\right)$, $v_i\left(t\right)$ and $a_i\left(t\right)$ are the position, speed, and acceleration of vehicle $i$ at time $t$, respectively, and $u_i\left(t\right)$ is the control input of vehicle i at time $t$.

3.2. Optimization Model

In this paper, the cooperative merging problem of mainline and ramp vehicles is developed as an optimal control problem. As demonstrated in the fuel consumption model presented in [25], the energy consumption during vehicle travel is a function of speed and acceleration, which has a positive correlation. In general, by minimizing acceleration, unnecessary engine running can be reduced, which helps improve fuel economy. Thus, fuel minimization in vehicle trajectories may be achieved with excellent accuracy via minimization of the square-of-acceleration over time. In addition, the control input (rate of change of acceleration) that indicates sudden vehicle motion can be used as an important indicator of passenger ride comfort. Therefore, to minimize the energy consumption and vehicle bumps during the process of vehicle $i$ from initial state $x_i(t_i^0)$ to end state $x_i(t_i^f)$, the cost function of the vehicle trajectory optimization model is constructed as follows:

$$\min {\displaystyle {\int }_{t_i^0}^{t_i^f}{\omega }_1{a}_i{\left(t\right)}^2+{\omega }_2{u}_i{\left(t\right)}^2}dt$$

(3)

where $t_i^0$ is the moment the vehicle $i$ enters the collaborative merging area, $t_i^f$ is the moment vehicle $i$ reaches the merging point, ${\omega }_1$ and ${\omega }_2$ are the weighting factors.

When the vehicle $i$ is driving in the cooperative merging area, the state variables and control input should be limited to a reasonable range with the following constraints:

$$\begin{array}{l}{v}_{\min }\le v_i\left(t\right)\le v_{\max }\\ a_{\min }\le a_i\left(t\right)\le a_{\max }\\ u_{\min }\le u_i\left(t\right)\le u_{\max },t\in \left[t_i^0,t_i^f\right]\end{array}$$

(4)

where $v_{\min }$ and $v_{\max }$ are the minimum and maximum velocity of the vehicle in the cooperative merging area, respectively; $a_{\min }$ and $a_{\max }$ are the minimum and maximum acceleration of the vehicle in the cooperative merging area, respectively; and $u_{\min }$ and $u_{\max }$ are the minimum and maximum input of the vehicle in the cooperative merging area, respectively.

Once a vehicle enters the control area, in addition to the optimal trajectory, the central controller needs to establish the optimal merging sequence. Often, the criterion for establishing the merging sequence is first-in-first-out (FIFO), that is, the vehicles that enter the control area earlier have priority to pass the merging point over vehicles entered later [17]. Alternatively, there are control strategies based on the priority of main-road vehicles over ramp vehicles. We define the time from when a vehicle enters the control area to when it passes the merging point as the merging time, which refers to the concept of the time when a vehicle passes an intersection in [26]. In addition to the trajectory optimization model mentioned above, we also aim to improve the merging efficiency and safety. As much as possible, vehicles in the same lane (including those from the ramp or mainline) pass the merge point together, thus reducing cross merging.

Since the terminal moment $t_i^f$ is variable, it can be a series of different values. In the optimization scheme proposed in this paper, $t_i^f$ will be used as a variable. To reduce the waste of gaps between vehicles to increase the throughput of the main road, we set the optimization objective to minimize the merging time as follows:

$$\min {\displaystyle \sum _{i=1}^n{t}_i^f-t_i^0}$$

(5)

where $i\in \mathbb{N}(t)=\left\{1,...,n\right\}$ is the vehicle under the FIFO order, and we also defined two different subsets: (1) ${\mathbb{S}}_i(t)$ are all vehicles in the same lane as $i$; (2) ${\mathbb{Z}}_i(t)$ are all vehicles in a different lane than $i$.

When the traffic density is too small, the headway between vehicle i and the preceding vehicle may be very large, while the allocated arrival time causes their headway to decrease sharply, or the allocated arrival time exceeds the vehicle dynamics constraint, and to avoid such unreasonable phenomena, the allocated arrival time needs to be further calculated as:

$$\begin{array}{l}{t}_i^f\ge \max \left\{t_{i-1}^f+h_d,t_i^{\min }\right\}\\ t_i^{\min }=t_i^0+\min \left(\frac{v_{\max }-v_i^0}{a_{\max }},\frac{\sqrt{{(v_i^0)}^2+2a_{\max }L}-v_i^0}{a_{\max }}\right)\end{array}$$

(6)

where $h_d$ is the headway between vehicle $i$ and the preceding vehicle $i-1$, and $L$ is length of the control zone.

In order to avoid traffic conflicts while driving vehicles, the constraints are discussed in the following two scenarios:

Scenario 1: As represented in Figure 3, vehicle $i$ enters the control area keeping in the same lane as vehicle $i-1$, which means that both vehicles are on the main road or both are on the ramp. Since the single lane cannot change lanes, vehicle $i-1$ will have priority over vehicle $i$ through the merging point. To ensure that two adjacent vehicles in the same lane can safely pass the merging point, it is necessary to satisfy the time interval between the preceding vehicle and the following vehicle is not less than $h_1$, and the constraint can be expressed as follows:

$$t_i^f-t_{i-1}^f\ge h_1,\forall i\in {\mathbb{S}}_{i-1}(t)$$

(7)

Scenario 2: As represented in Figure 4, vehicle $i$ enters the control area in a different lane from vehicle $i-1$; that is, one vehicle is on the main road while the other is on the ramp. The situation requires avoiding not only longitudinal traffic conflicts, but also lateral collisions due to vehicles changing from the ramp to the main road. Therefore, the minimum time interval $h_2$ that needs to be satisfied by two adjacent vehicles in different lanes when passing the merging point should logically be greater than $h_1$. This constraint can be expressed as:

$$\left|t_i^f-t_{i-1}^f\right|\ge h_2,\forall i\in {\mathbb{Z}}_{i-1}(t)$$

(8)

3.3. Optimization Analysis Solving

The control method of the trajectory optimization model allows to constrain the final state of the vehicle, such as the final moment, as well as the speed and acceleration of the vehicle at the final moment. The speed and acceleration of all vehicles at the final moment can be unified to a constant value, but the final moment of the vehicle needs to be assigned artificially. Therefore, the first problem to be solved is to assign the arrival moment of vehicles at the merging point, that is, the primary task of the central controller is to optimize the sequence of vehicles through the merging point. As a simple example to illustrate the optimization sequence, we assume that two vehicles on the main road and one vehicle on the ramp enter the control area, and then number them sequentially in the order in which they enter. According to the enumeration method, it is known that there exist three merging sequences, as shown in Figure 5. However, as the number of vehicles increases, it is known from the knowledge of permutations and combinations that the number of sequential species will continue to grow.

Therefore, we transform the optimal sequence problem into the arrival moment of vehicles at the merging point as an optimization variable in this paper. According to the problem description in the previous subsection, we transform it into a mixed integer linear programming model and solve it using the solver in MATLAB. Additionally, to improve the solving speed, we set the optimization time window to T = 10 s. For vehicles within the optimization time window, i.e., $(k-1)T+1\le t\le kT$, the specific model is as follows:

$$\min {\displaystyle \sum _{i=n}^{N(kT)}{t}_i^f-t_i^0}$$

(9)

$$t_i^f-t_{i-1}^f\ge h_1,\forall i\in {\mathbb{S}}_{i-1}(t)$$

(10)

$$B_i\times M+t_i^f-t_{i-1}^f\ge h_2,\forall i\in {\mathbb{Z}}_{i-1}(t)$$

(11)

$$\left(1-B_i\right)\times M+t_{i-1}^f-t_i^f\ge h_2,\forall i\in {\mathbb{Z}}_{i-1}(t)$$

(12)

$$t_i^f\ge \max \left\{t_i^f+h_d,t_i^{\min }\right\},\forall i\in \left[n,N\left(kT\right)\right]$$

(13)

where $n$ is the is the first vehicle in the k time window, M is an extreme value, $B_i$ is a 0–1 variable. $B_i$ equal to 1 indicates that vehicles on the main road have priority in passing, while $B_i$ equal to 0 indicates that vehicles on the ramp have priority in passing.

In addition to the merging sequence, the central controller also needs to optimize the vehicle trajectory using the energy consumption optimal model. For simplicity of solution, we consider the problem as an unconstrained optimization problem as long as the state variables of the vehicle do not exceed the dynamic limits in (4) to (5). Combining the objective function (3) and the state Equation (1), the analytical solution can be found quickly according to Pontryagin’s minimum principle. For each controlled vehicle in the cooperative region, the Hamiltonian function of the optimal control problem is:

$$H_i\left[x_i\left(t\right),u_i\left(t\right),t\right]=L\left[x_i\left(t\right),u_i\left(t\right),t\right]+{\lambda }_i^{T}f\left[x_i\left(t\right),u_i\left(t\right),t\right]$$

(14)

where $L$ is the function of $x_i\left(t\right)$ and $u_i\left(t\right)$, and ${\lambda }_i$ is the co-states vector.

Substituting state space Equation (1) and cost function (3) into Equation (14), we obtain:

$$H_i={\lambda }_i^1{v}_i+{\lambda }_i^2{a}_i+{\lambda }_i^3{u}_i+\frac{1}{2}{\omega }_1{a}_i^2+\frac{1}{2}{\omega }_2{u}_i^2$$

(15)

where, ${\lambda }_1^i$, ${\lambda }_2^i$, and ${\lambda }_3^i$ are the co-states of the vehicle; $v_i$, $a_i$, and $u_i$ are the velocity, acceleration, and control inputs of the vehicle, respectively.

Let $u^{*}\left(t\right)$ and $x^{*}\left(t\right)$ respectively be the optimal control input and the optimal trajectory, where $x^{*}\left(t\right)={\left\{p^{*}\left(t\right),v^{*}\left(t\right),a^{*}\left(t\right)\right\}}^T$, $p^{*}\left(t\right)$, $v^{*}\left(t\right)$, $a^{*}\left(t\right)$ are optimal position, optimal velocity, and optimal acceleration trajectories, respectively. According to the Pontryagin minimal value principle, the following equations and equations hold under appropriately chosen Lagrange multipliers.

Control equation:

$$\frac{\partial H_i}{\partial u_i}={\lambda }_3^i+{\omega }_2{u}_i^{*}=0$$

(16)

Co-states equation:

$${\dot{\lambda }}_1^i=-\frac{\partial H_i}{\partial p_i}=0$$

(17)

$${\dot{\lambda }}_2^i=-\frac{\partial H_i}{\partial v_i}=-{\lambda }_1^i$$

(18)

$${\dot{\lambda }}_3^i=-\frac{\partial H_i}{\partial a_i}=-{\omega }_1{a}_i^{*}-{\lambda }_2^i$$

(19)

Solving from Equation (17) yields ${\lambda }_1^i=c_1$; then, substitute it into Equations (18) and (19) to obtain ${\dot{\lambda }}_3^i=-{\omega }_1{a}_i^{*}+c_{1}t-c_2$. Combining Equation (16) yields:

$${\omega }_2{u}_i^{*}-{\omega }_1{a}_i^{*}+c_{1}t-c_2=0$$

(20)

where $c_1$ and $c_2$ are constants of integration. The optimal control input can be obtained immediately after the solution of Equation (20) in conjunction with the state space equation, i.e.,

$$u_i^{*}\left(t\right)=c_3\sqrt{\frac{{\omega }_1}{{\omega }_2}}{e}^{\sqrt{\frac{{\omega }_1}{{\omega }_2}}t}-c_4{e}^{-\sqrt{\frac{{\omega }_1}{{\omega }_2}}t}+\frac{c_1}{{\omega }_1}$$

(21)

where $c_3$ and $c_4$ are constants of integration. Ultimately, the optimal trajectory of the state variables is as follows:

$$p_i^{*}\left(t\right)=c_3\frac{{\omega }_2}{{\omega }_1}{e}^{\sqrt{\frac{{\omega }_1}{{\omega }_2}}t}+c_4\frac{{\omega }_2}{{\omega }_1}{e}^{-\sqrt{\frac{{\omega }_1}{{\omega }_2}}t}+\frac{c_1}{6{\omega }_1}{t}^3-\frac{c_2}{2{\omega }_1}{t}^2+c_{5}t+c_6$$

(22)

$$v_i^{*}\left(t\right)=c_3\sqrt{\frac{{\omega }_2}{{\omega }_1}}{e}^{\sqrt{\frac{{\omega }_1}{{\omega }_2}}t}+c_4\sqrt{\frac{{\omega }_2}{{\omega }_1}}{e}^{-\sqrt{\frac{{\omega }_1}{{\omega }_2}}t}+\frac{c_1}{2{\omega }_1}{t}^2-\frac{c_2}{{\omega }_1}t+c_5$$

(23)

$$a_i^{*}\left(t\right)=c_3{e}^{\sqrt{\frac{{\omega }_1}{{\omega }_2}}t}+c_4{e}^{-\sqrt{\frac{{\omega }_1}{{\omega }_2}}t}+\frac{c_1}{{\omega }_1}t-\frac{c_2}{{\omega }_1}$$

(24)

where $c_5$ and $c_6$ are constants of integration.

To solve for the vector a consisting of six integration constants $C=\left\{c_1,c_2,...,c_6\right\}$, the vehicle initial state $x_i\left(t_i^0\right)$, the end state $x_i\left(t_i^f\right)$, the initial moment $t_i^0$, and the end moment $t_i^f$ are used. To calculate the optimal trajectory of vehicle $i$ online, the vehicle state obtained through V2X communication at each sampling moment $t$, will be used as the initial state to update the constants. Then the initial state value of the vehicle and the state value at the merge point are substituted into (22)–(24) to solve the linear equation system to obtain the coefficients.

It is worth noting that when the vehicle $i$ enters the control area, if it does not fall within the optimization time window, the moment of arrival at the merging point is temporarily assumed to be $t_i^f=t_{i-1}^f+h,h\in \left\{h_1,h_2\right\}$. Then, after sequential optimization, the state information of vehicle $i$ (including current position, speed, and acceleration) and the moment of scheduled arrival at the merging point $t_i^f$ are resent to calculate the optimal trajectory for the subsequent time period.

4. Simulation Results and Discussion

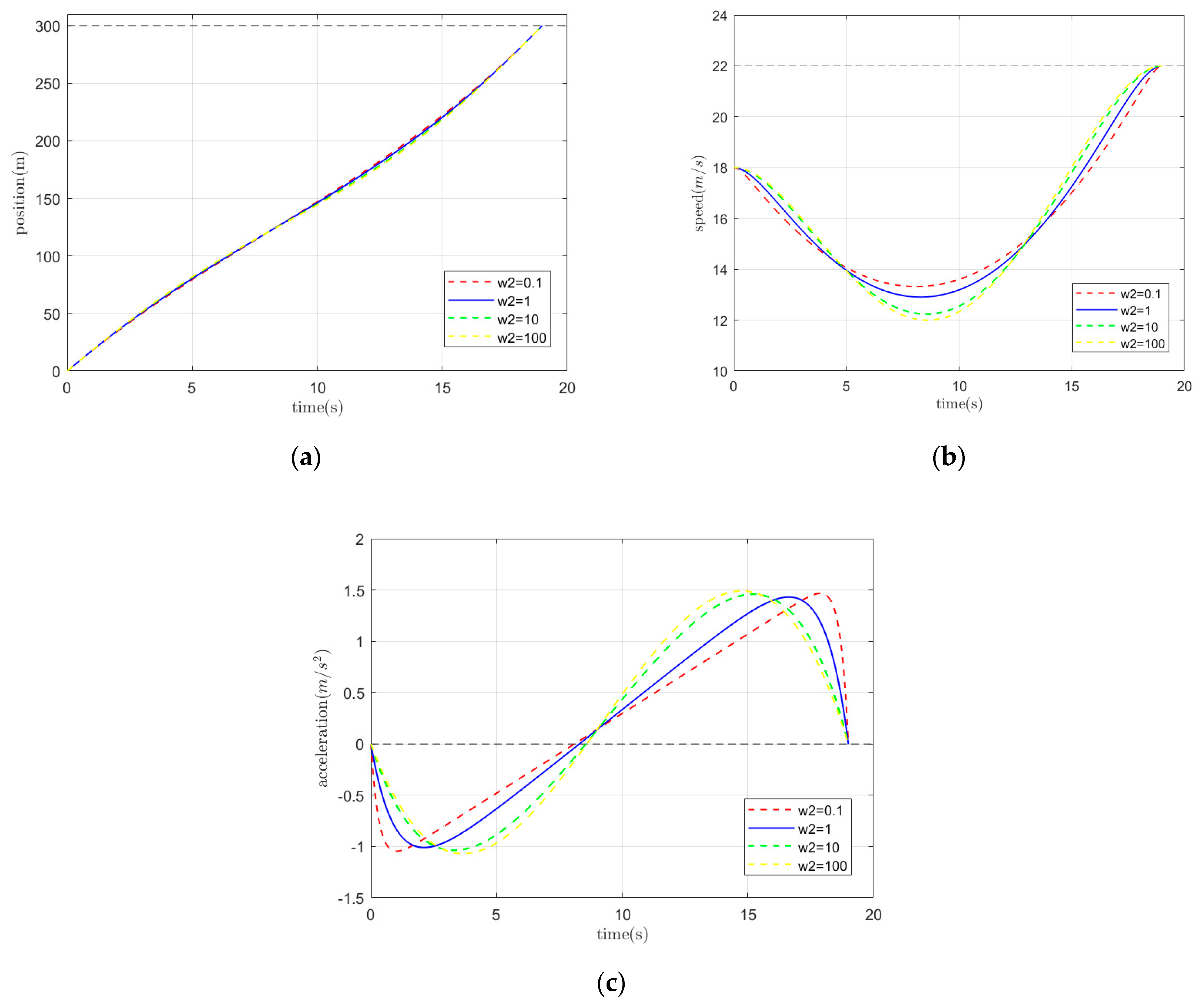
4.1. The Choice of Weights

In this model, the cost function contains the acceleration of the vehicle and the rate of change of acceleration. When multiple weighting terms are included in the cost function, the choice of weight values plays an important role in the shape of the optimal trajectory. Additionally, it has a direct impact on the vehicle fuel economy and ride comfort. The selection of appropriate weight values can also control acceleration and input variables within extreme values. The weight values can be adjusted according to the driver’s driving style or automatically using machine learning techniques.

To illustrate the effect of weight values on the optimal trajectory, the trajectory of a single vehicle is simulated. Keep the weighting factor ${\omega }_1$ constant (${\omega }_1=1$) and change the value of the weighting factor ${\omega }_2$ (${\omega }_2=0.1,1,10,100$). The corresponding results are shown in Figure 6. It can be found that the spatial–temporal trajectory and velocity profiles are less affected when the weighting factor ${\omega }_2$ is taking different values, and especially the position does not differ much. When ${\omega }_2$ takes the value of 0.1, the vehicle has a steeper acceleration change after entering the cooperative merging area and when reaching the merging point, which greatly reduces passenger comfort. Therefore, in the case considered in this paper, it is not appropriate to take too small a value for ${\omega }_2$. Of course, a large number of different merging examples may be needed to understand the impact of weights and related possibilities.

4.2. Experiment Design

To verify the effectiveness of the collaborative merging method in real traffic scenarios, this paper utilizes NGSIM data for simulation [27]. These data were collected on the I-80 freeway in California, with a section that includes six freeway lanes and one ramp. Since the ramp merging scenario in this paper includes only single-lane mainline and single-lane ramps of the freeway, the raw NGSIM data are cleaned and filtered. Therefore, we selected the vehicle trajectory data on the mainline lane 6 and the ramps for the study. The merging point is set at the junction of the mainline lane 6 and the end of the ramp. With the merging point as the center of the circle, the road section within a radius of 300 m is set as the collaborative merging control area. The moment and speed of each vehicle entering the collaborative merging area are used as a reference state to initialize the MATLAB cooperative merging simulation.

In the MATLAB simulation, vehicles are set to enter the main road or ramp randomly, and the initial state is kept consistent with the NGSIM trajectory data. In this simulation, unlike human-driven vehicles, the connected autonomous vehicles are under the unified control of a central controller upon entering the collaborative merging area. As with the NGSIM trajectory data, the control time range is 15 min with a control time step of 0.1 s. According to the test results in the previous section, the weighting factors are taken as ${\omega }_1=1$, ${\omega }_2=1$ and the remaining parameters in the simulation are set as follows: $v_f=18$, $a_f=0$, $h_1=1.5$, $h_2=2$.

4.3. Analysis of Results

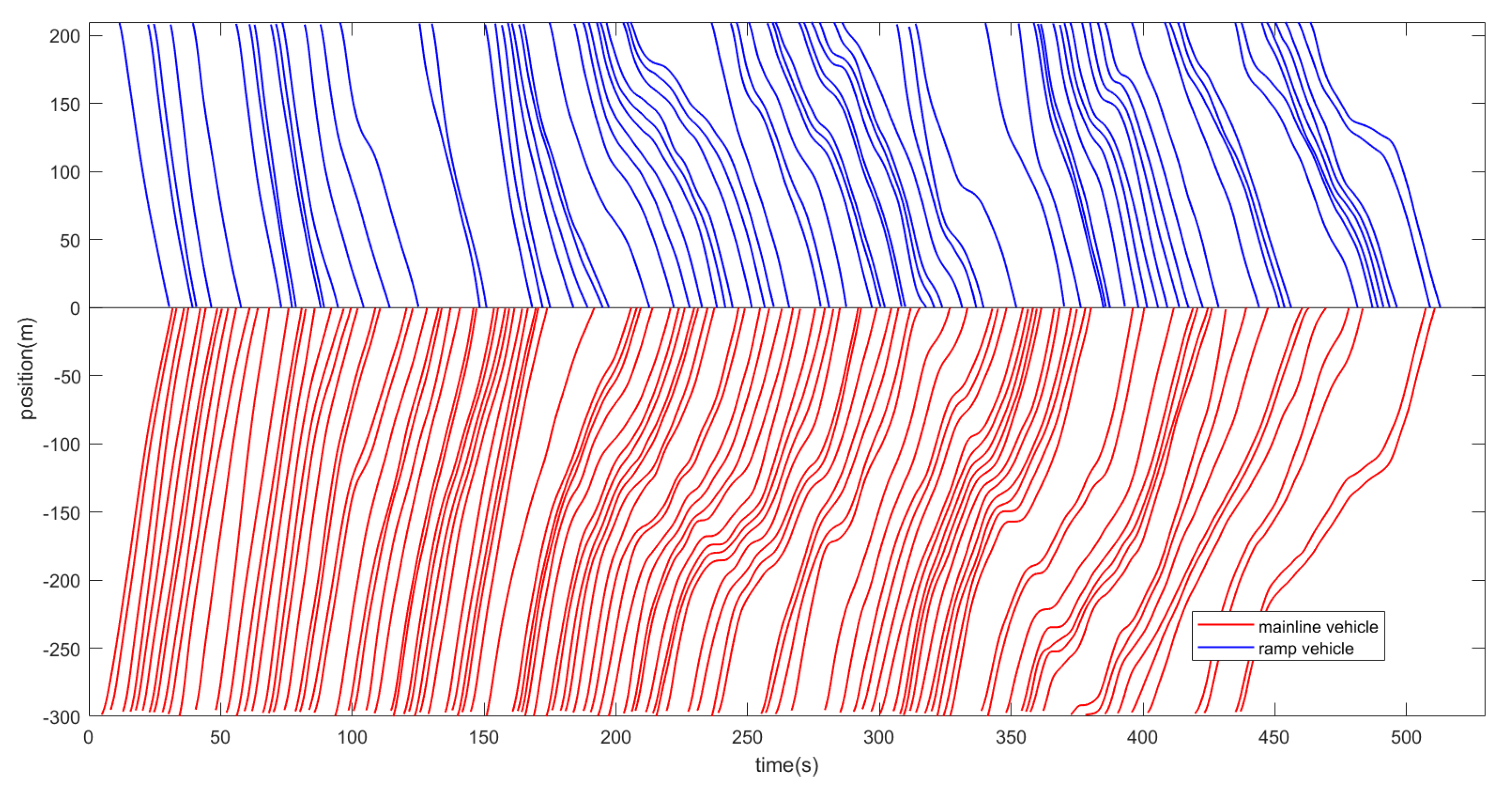
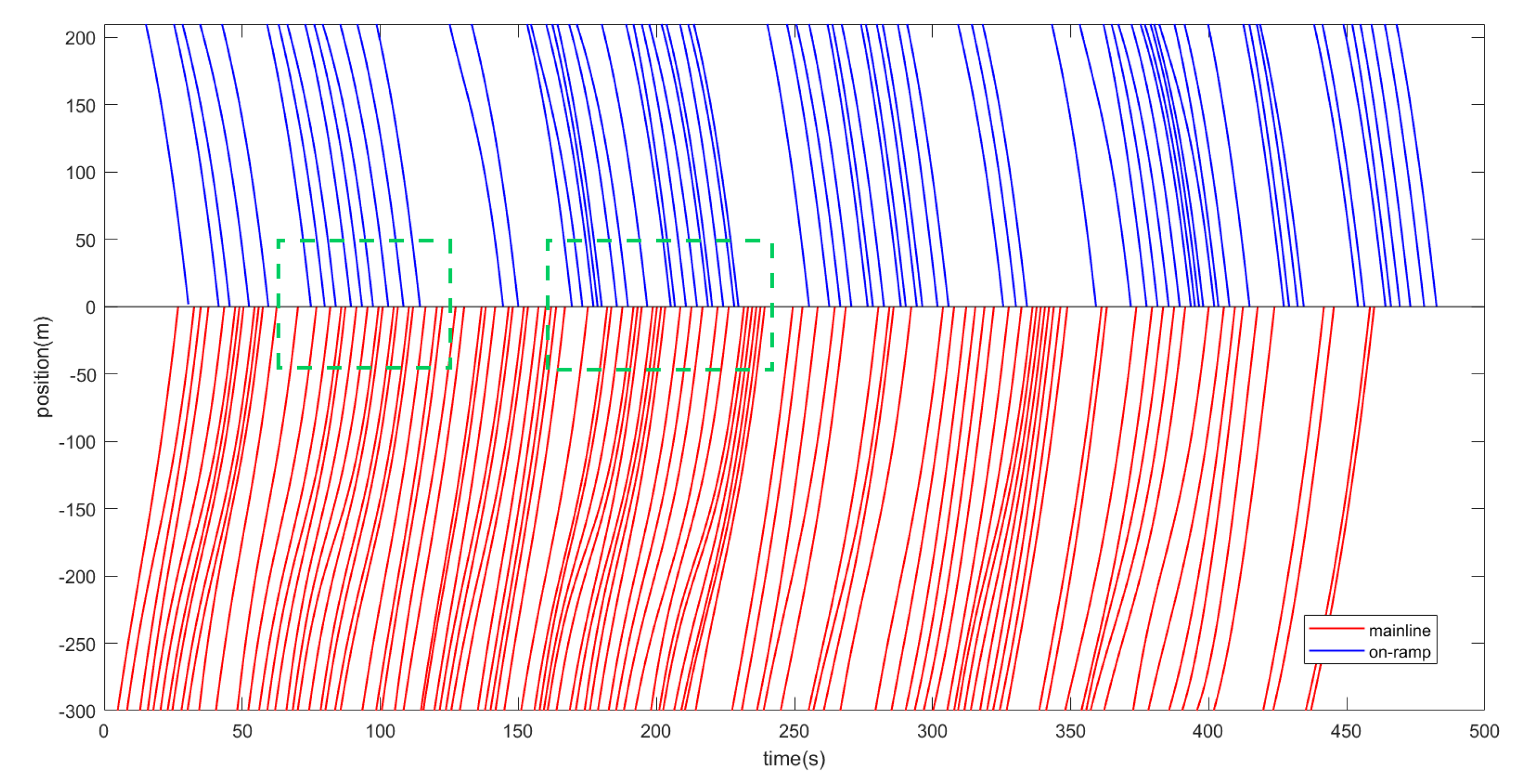
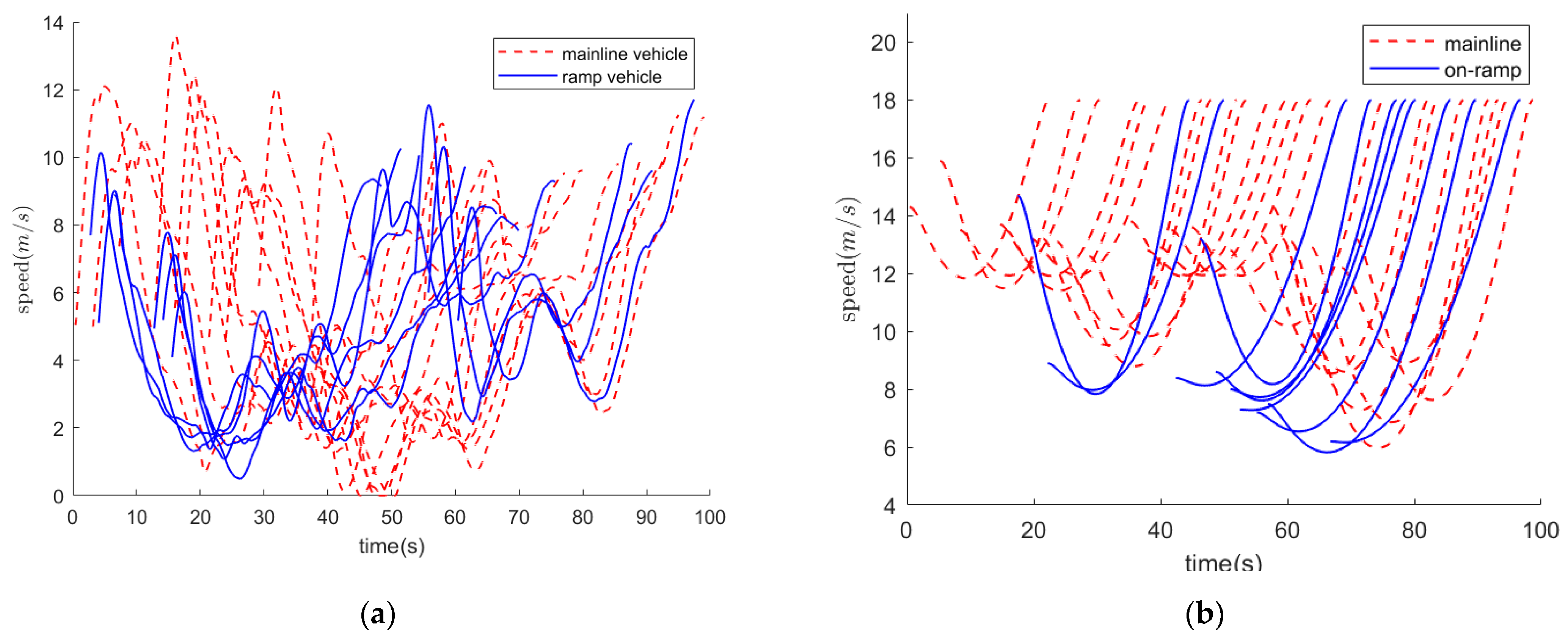
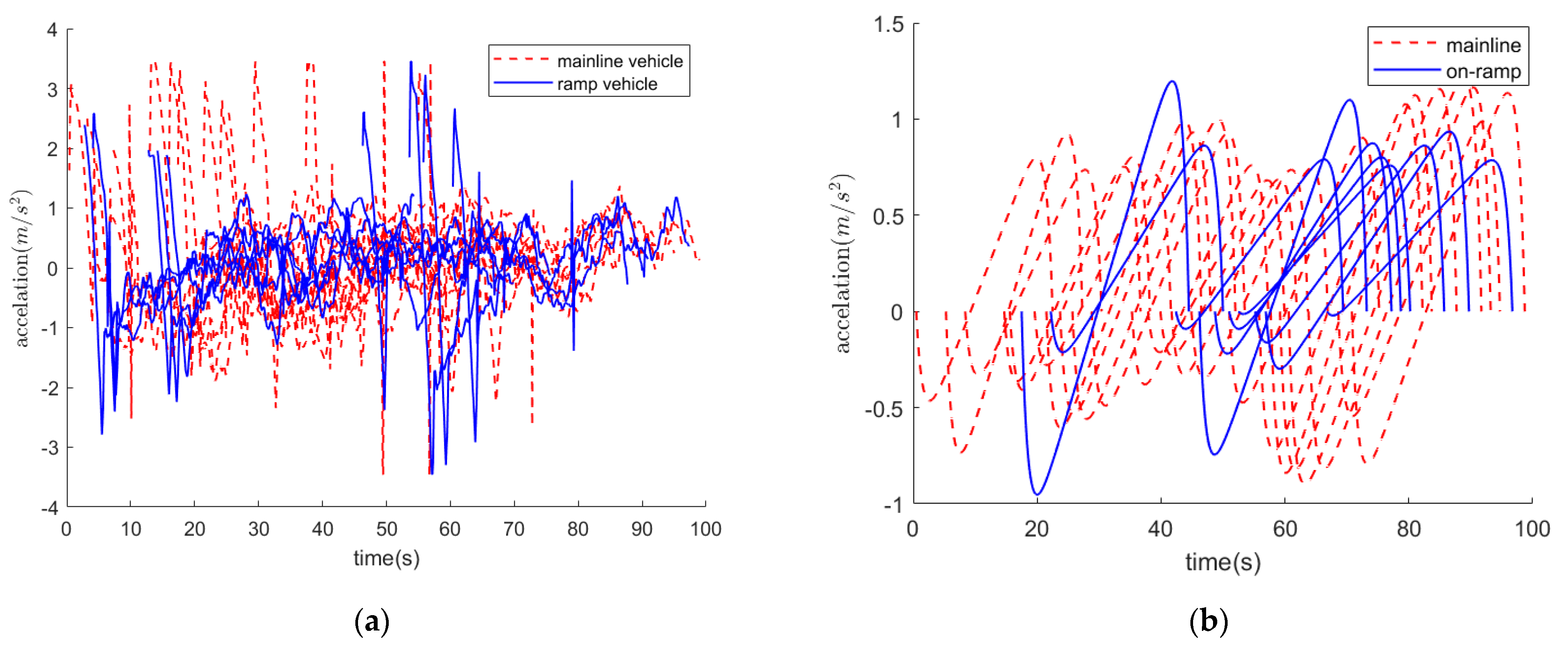
4.3.1. Vehicle Trajectory Evaluation

As shown in Figure 7, near the merging point, it is difficult for human drivers on the ramp vehicles to find a suitable traffic gap to insert because they cannot accurately judge the driving status of the mainline vehicles. Similarly, when there are more vehicles traveling on the ramp, for reasons such as courtesy or conservative driving style, human drivers of mainline vehicles will slow down to give way, which results in delays. Especially when the traffic volume is high, this shock wave is transmitted downstream, which will cause a traffic congestion phenomenon. Figure 8 shows the trajectory of the collaborative merging according to the FIFO principle, but without optimization of the merging order. The analysis was carried out in other traffic scenarios using the FIFO coordination model [26,28]. And it can be found that all vehicles pass the merging point sequentially under the coordination of the central controller. In contrast, ramp vehicle queues and mainline traffic flow congestion no longer occur. The cooperative merging method avoids collisions of adjacent vehicles, so the collision rate in studies [29,30] are not used as an indicator in this paper.

The model proposed in this paper further optimizes the merging sequence of vehicles, as shown in Figure 9. For example, as shown in the area inside the green box in Figure 8 and Figure 9. When the merging sequence is not optimized in Figure 8, vehicles from different merging directions, such as from the main road or the ramp, respectively, will cross through the merging point according to the first-in-first-out strategy. When traffic volumes are high, the scenario may lead to more traffic conflicts, which often occur on ramp bottlenecks [31]. The timing optimization in Figure 9 can minimize the number of vehicles crossing the merging point in conflicting directions, while increasing the number of vehicle groups formed by vehicles of the same lane passing the merging point, thus reducing traffic conflicts, and improving the efficiency of the merging.

As shown in Figure 10a, due to the sudden merging of vehicles on the ramp, the mainline vehicles must slow down and even appear to have zero speed. The acceleration and deceleration process are shown in Figure 11a, both mainline and ramp vehicles are frequently accelerating or decelerating sharply, and the peak is close to 4 m/s². The frequent sharp braking behavior of the previous vehicle directly affects the driving decisions of the following vehicle, which greatly reduces the comfort of the passengers. At the same time, the rate of change of acceleration is fluctuating rapidly, which not only consumes too much energy but also is very likely to cause rear-end accidents. The velocity and acceleration profile curves under the cooperative merging method are shown in Figure 10b and Figure 11b, respectively. Although a large acceleration is required to bring the vehicle to its final speed, the method reduces the acceleration range of the vehicle, especially the deceleration, to some extent. Compared with the original trajectory data, the velocity and acceleration profiles under this method are smoother. It is easy to see that the vehicles from the mainline and the ramps eventually converge into a uniform velocity flow, and the acceleration of the vehicles is zero when they reach the merging point.

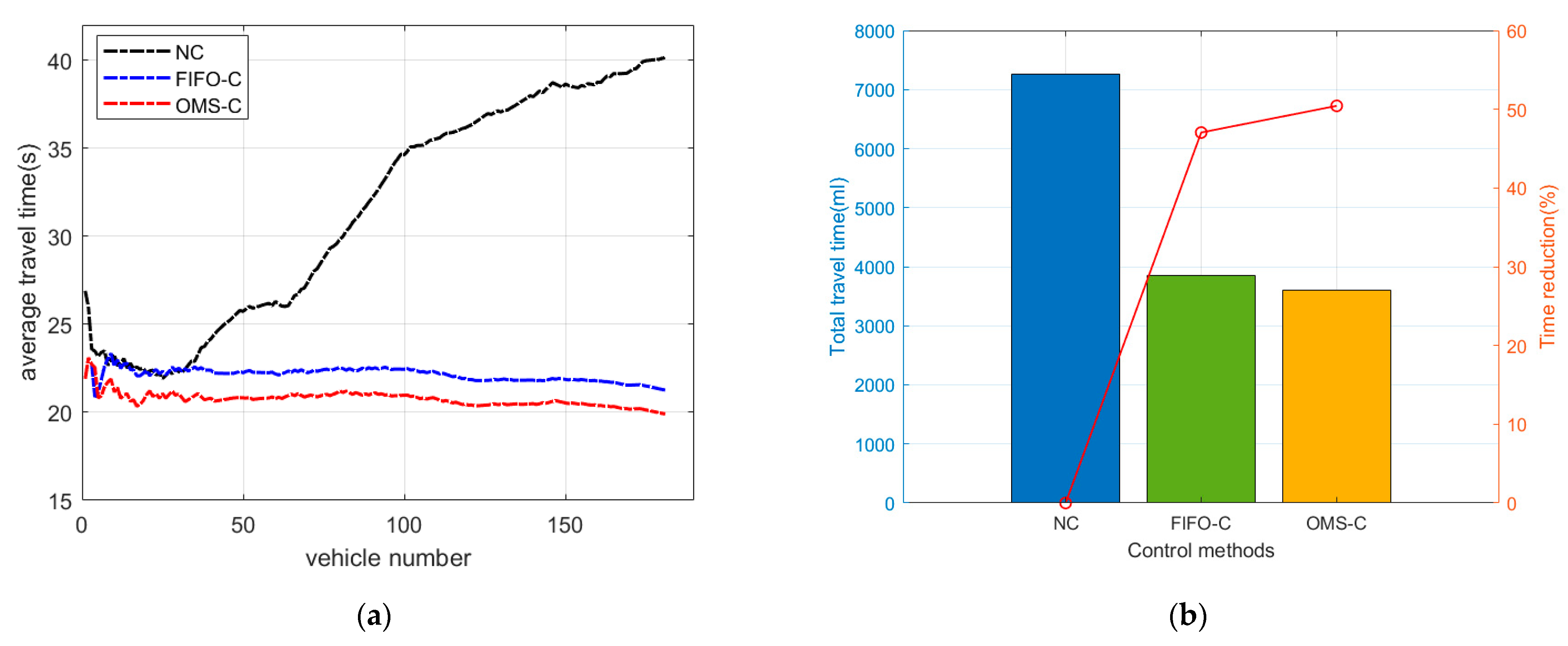
4.3.2. Traffic Indicators Evaluation

To visualize the energy consumption during vehicle driving, this paper uses the fuel consumption model proposed in study [32]. The model represents fuel consumption as a function of speed and acceleration with time as follows:

$$\begin{array}{c}f=f_{cruise}+f_{accel}\\ f_{cruise}=b_0+b_{1}v+b_2{v}^2+b_3{v}^3\\ f_{accel}=a\left(c_0+c_{1}v+c_2{v}^2\right)\end{array}$$

(25)

For a typical vehicle, the fuel consumption parameters are: $b_0=0.1569$, $b_1=2.450\times {10}^{-2}$, $c_0=0.07224$, $c_1=9.681\times {10}^{-2}$, and $c_2=1.075\times {10}^{-3}$.

As shown in Figure 12, compared to the natural traffic flow under no control (NC), the final energy consumption is reduced for both the non-optimized merging sequence (FIFO) and the optimized sequence (OC) control conditions. Among them, using FIFO resulted in energy savings of 9.3%, and using OC resulted in energy savings of 13.2%. As shown by existing studies, the energy consumption of a vehicle is related to the magnitude and duration of acceleration and deceleration. The control method OC optimizes the merging sequence and increases the number of vehicle groups in the same direction, with correspondingly smaller changes in acceleration and deceleration during vehicle following. Therefore, the use of OC may consume less energy than FIFO.

Additionally, as shown in Figure 13, it can be clearly observed in the natural merging case that the speed of subsequent vehicles close to the ramp merging area decreases significantly with time, which is caused by the transmission of traffic waves formed in the upstream area to the downstream area. Under the cooperative control, the average speed of all vehicles always fluctuates within a controlled range, which facilitates the formation of a stable traffic flow. Although the average speed of MOS-C is slightly higher than that of FIFO-C, the difference between them is not significant.

It has been shown in the literature [32] that minimizing the total time in a freeway network is equivalent to maximizing the time weight of the total exit traffic. Therefore, in this paper, the travel time is used as a measure of the exit flow, which is the time from the vehicle entering the collaborative merging area to leaving the merging point. That is, the shorter the total travel time in the network, the higher the exit flow in the confluence region.

In Figure 14a, the average vehicle travel time under uncontrolled continues to increase as the number of vehicles increases, which is one of the important reasons to explain the congestion. In Figure 14b, FIFO-C reduces the travel time by 47% compared to NC, while OMS-C reduces the travel time by 50.4%. This results in a greater reduction in vehicle travel time during the merging process compared to the method proposed in the literature [14,33]. The average travel time is the same for FIFO-C and OMS-C in the first period, but as the number of vehicles accumulates, it is clear that OMS-C can reduce the headway time wastage due to cross convergence and thus increase the road throughput.

5. Application to Traffic Flow Simulation

In this section, to better evaluate the performance of the proposed algorithm, three traffic demands (low, medium, and high) are designed using VISSIM simulation software. The traffic volumes are 800, 1000, and 1200 veh/h for the main road and 300, 500, and 700 veh/h for the on-ramp. The effectiveness measures used for comparison are energy consumption, average speed, and travel time. The parameter selection remains the same as in the model validation in the previous section, but to improve the throughput at middling and high traffic flows, we set the safe headway as $h_1=1,h_2=1.5$.

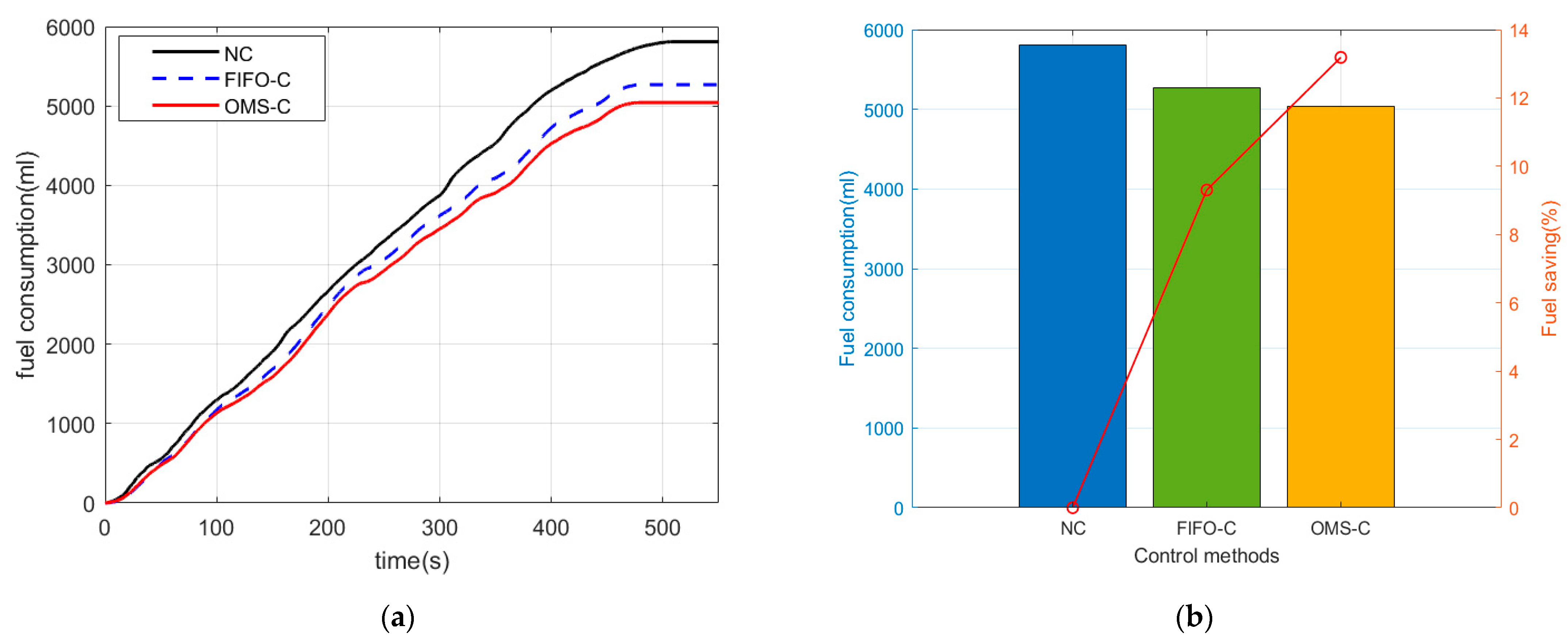
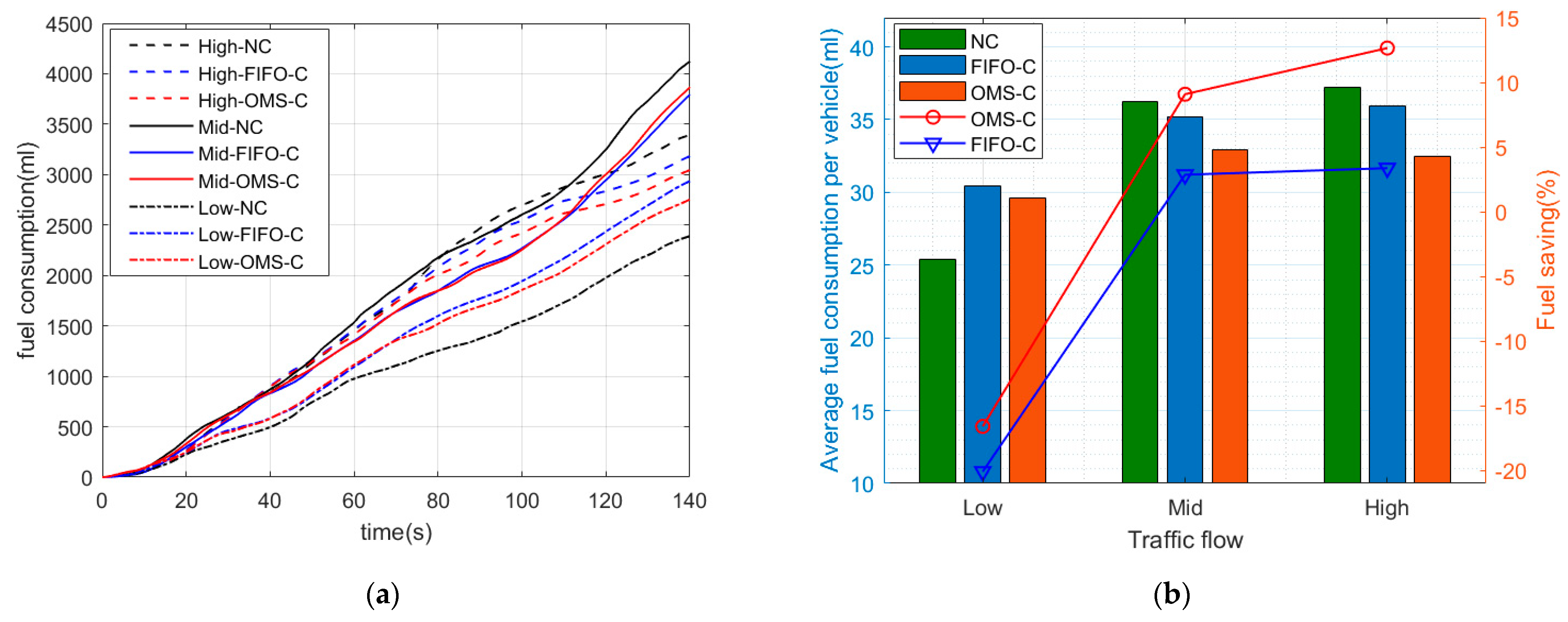
5.1. Energy Consumption

As shown in Figure 15, the final average fuel consumption decreases under both high and medium traffic flow conditions. In particular, OMS-C saves more fuel consumption than FIFO-C under high traffic demand conditions. The decrease in energy consumption under high traffic flow compared to middle traffic flow is due to the fact that traffic congestion reduces the number of vehicles passing. However, when the traffic flow is low, the fuel consumption due to cooperative control does not decrease but increases compared to no control. This suggests that the collaborative merge control method may not be advantageous in terms of energy savings in low traffic flow situations.

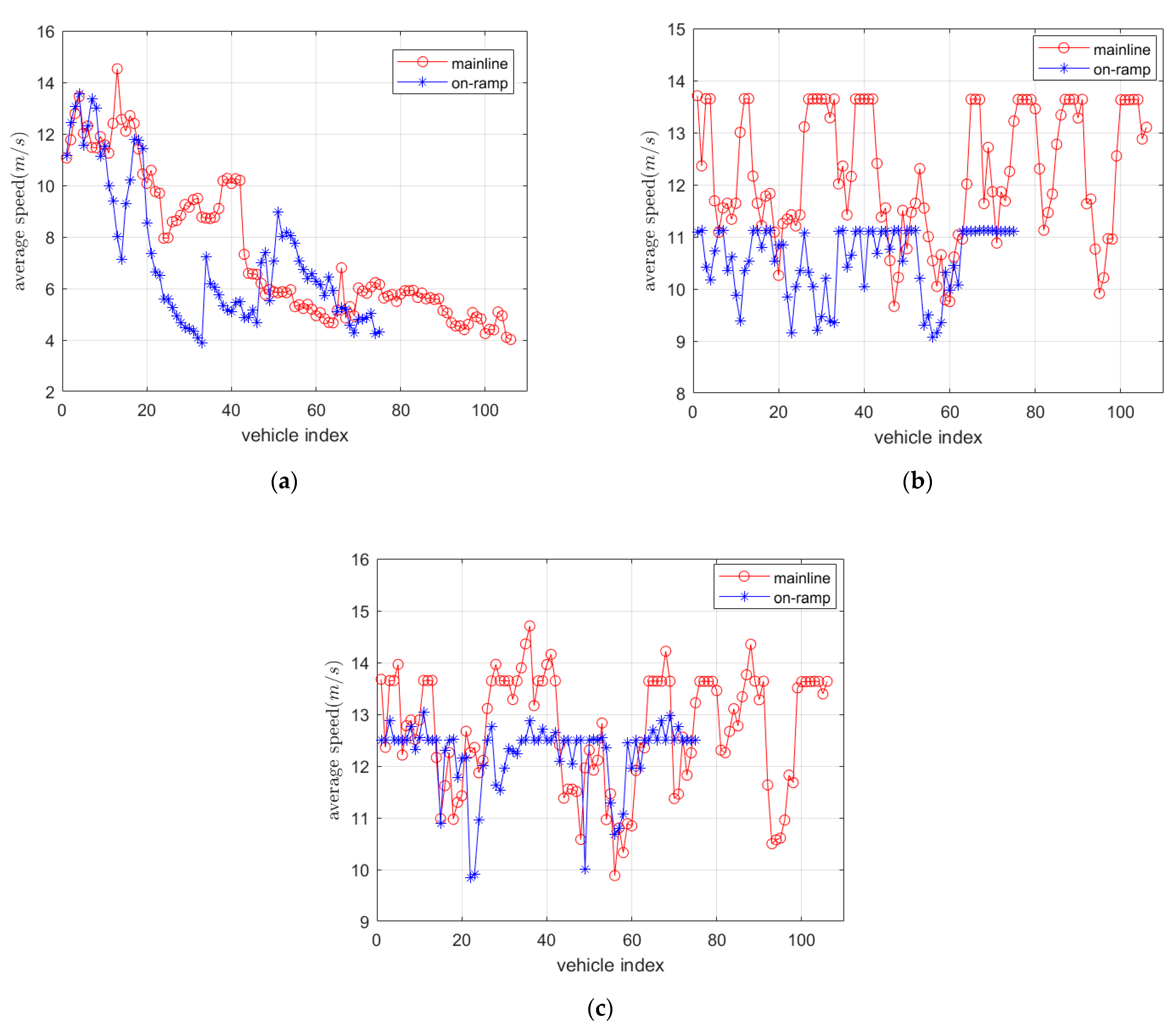
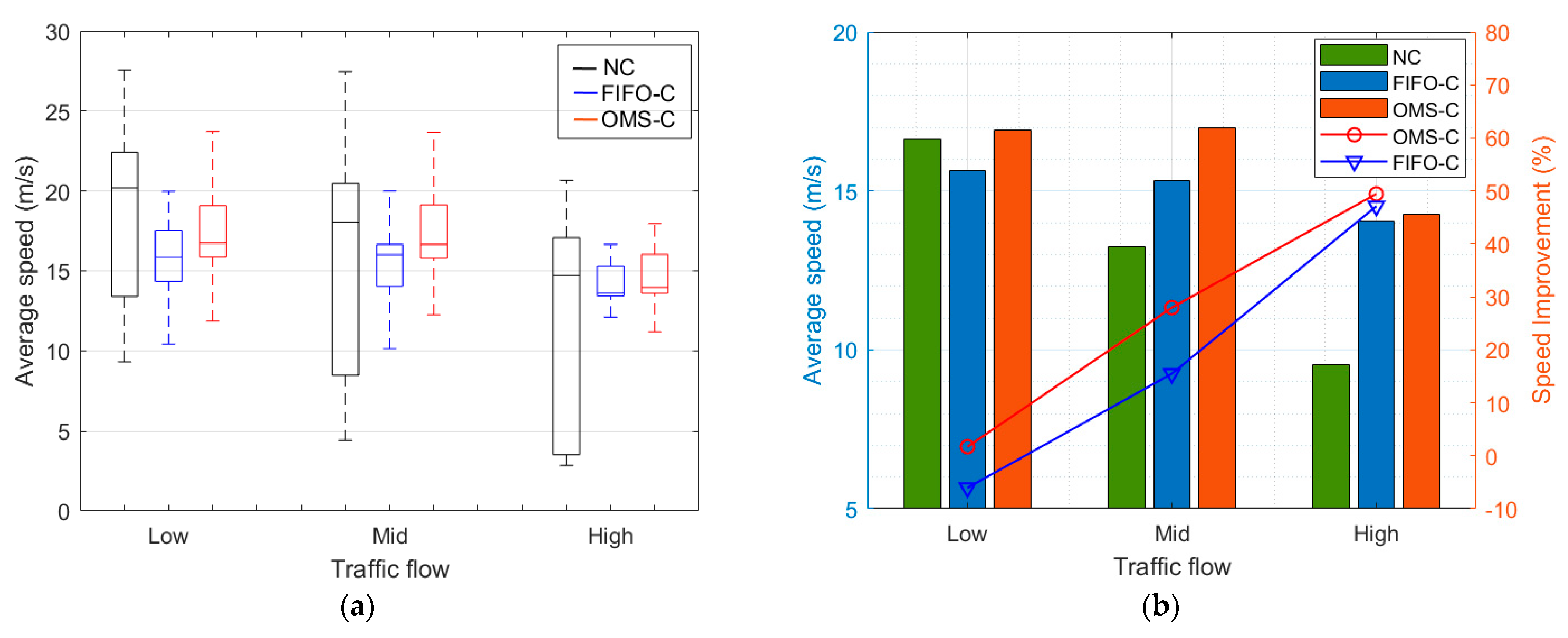
5.2. Average Speed

As shown in Figure 16, the cooperative merging control approach results in increased speeds regardless of the traffic flow. The lower speeds are mainly for ramp vehicles, which have to slow down significantly to wait for the convergence at higher traffic flows. In particular, traffic conflicts often occur at high traffic volumes, allowing traffic waves to propagate upstream and create traffic congestion. In contrast, in the case of cooperative control, all vehicles reach the final desired speed under the unified control of the central controller. As a result, this leads to an increase in the average speed of the entire network. The speed of OMS-C is always higher than that of FIFO, which also demonstrates the need for vehicle merging sequence optimization.

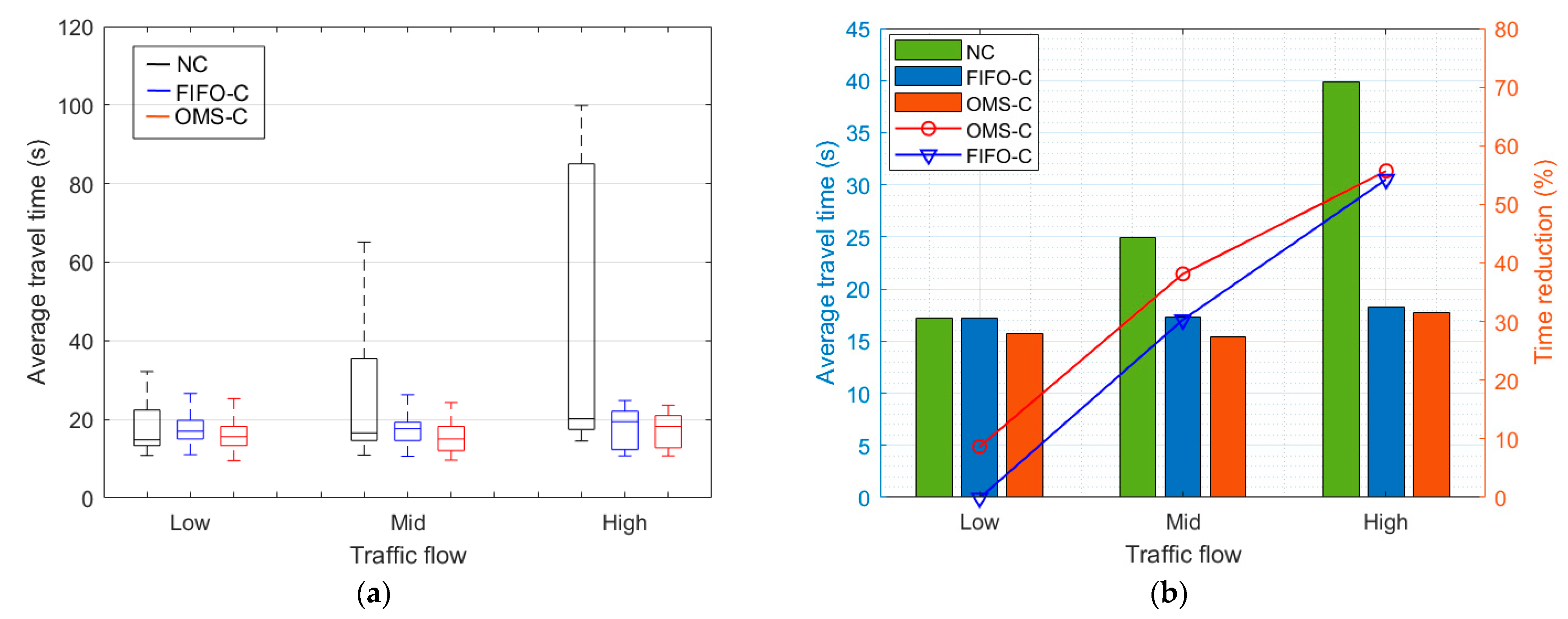
5.3. Travel Time

As shown in Figure 17, the reduction in average travel time is not significant under the low traffic demand. However, the rate of reduction is larger under medium and high traffic demand, especially more than 50% under high demand. This is because the ramp vehicles merge into the mainline in an orderly manner under the coordination of the central controller, avoiding traffic conflicts and thus achieving an effective reduction in vehicle delays. This shows that the proposed control method can take advantage of improving traffic throughput only when the traffic flow is relatively high.

6. Conclusions

In this paper, a collaborative merging control strategy for entrance ramps based on optimal control was proposed and verified by simulation. Firstly, the MILP model was used to optimize the merging sequence and improve the traffic efficiency, while the constraints also improve the safety to some extent. Then the vehicle trajectory was constructed as an optimal control problem with the optimization objectives of reducing energy consumption and improving passenger comfort and is solved using the PMP algorithm. The model coordinates the longitudinal motion of the vehicle by optimizing control inputs based on the spatial state of the vehicle, including position, velocity, and acceleration.

The results of the study show that the proposed strategy results in a significant improvement in energy economy and traffic efficiency compared to uncontrolled natural confluence. Under medium and high traffic flow conditions, energy consumption can be saved by 4–15%, speed can be increased by 15–50%, and travel time can be reduced by 30–60%. At the same time, the vehicle trajectory has been optimized to improve ride comfort by smoothing out the speed and acceleration profiles. In addition, the proposed method performs better in terms of energy saving, speed, and travel time compared to FIFO. Among them, the proposed method saves 17.8% of energy, increases speed by 11%, and reduces travel time by 11% over the maximum improvement of FIFO. Furthermore, the method reduces wasted headway to increase roadway throughput. It also increases the number of vehicles passing the merge point in the same direction, which helps improve traffic safety.

However, the study also found that the method is not as energy efficient when the highway traffic volume is low. This result is similar to that of the literature [9], where the proposed method does not improve significantly in all indicators under low traffic demand. This is also because the ramp traffic itself merges well into the mainline when traffic volumes are low, and when the traffic volume on the mainline is too high, the method does not seem to guarantee traffic safety, which is because the trajectory optimization will be constrained by the terminal moment. If the trajectory is always made optimal, the headway between terminal moments, the safety constraint will be difficult to ensure. Therefore, how to better combine the merging sequence and trajectory optimization problems to adapt to different traffic flow scenarios will be the key research direction in the future.