Neuro-Cybernetic System for Forecasting Electricity Consumption in the Bulgarian National Power System
Abstract
:1. Introduction
2. Predicting Electricity Consumption—State of the Art
3. Materials and Methods
3.1. Forecasting Process
3.2. Multifactor Forecasting System through Automated Selection of the Best Methods
- mechanisms for integrating different forecasting methods into the system;
- potential to work with a different number of factors;
- automated search and selection of effective forecasting methods when solving a specific task.
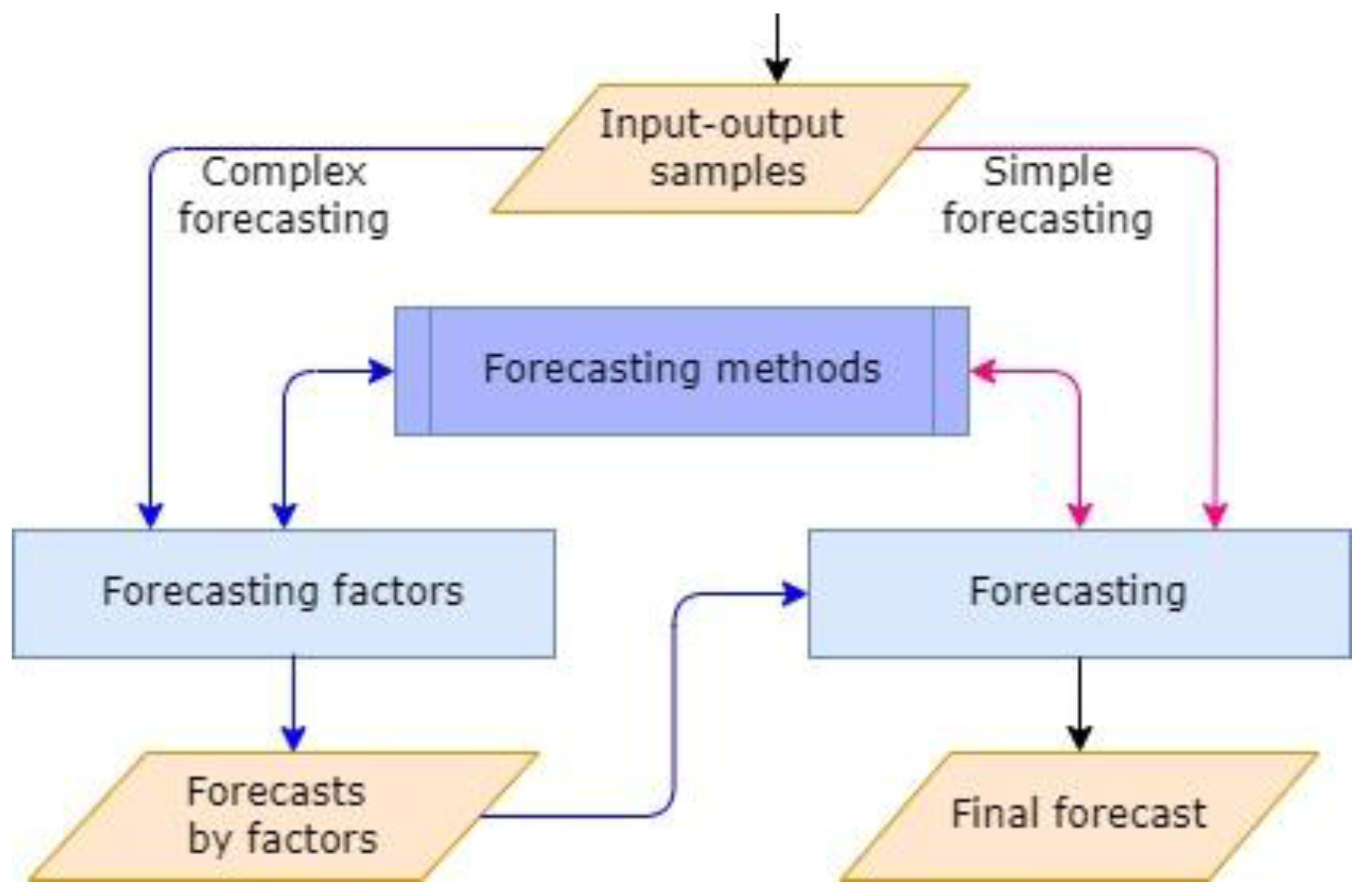
- Complex forecasting, which is multivariate time series forecasting. It is applicable to multifactor forecasting, in which preliminary forecasting of individual factors is performed;
- Simple forecasting, which is univariate time series forecasting.
3.3. Mathematical Model of the Forecasting Task
- (1)
- Automatically searches for and constructs a neural network NN with input vectors , approximating with minimal error ;
- (2)
- Based on the samples forecasts the future behavior of the factors using in a number of different factors ;
- (3)
- For each of the factors the efficiency of the used forecasting methods is compared separately;
- (4)
- For the final forecast value of , the forecast of the respective most effective method is selected;
- (5)
- Through the forecasted values of the factors and the method M, the outcome of the event is predicted.
- is the actual value of the measured value,
- is the predicted value proposed by the method used.
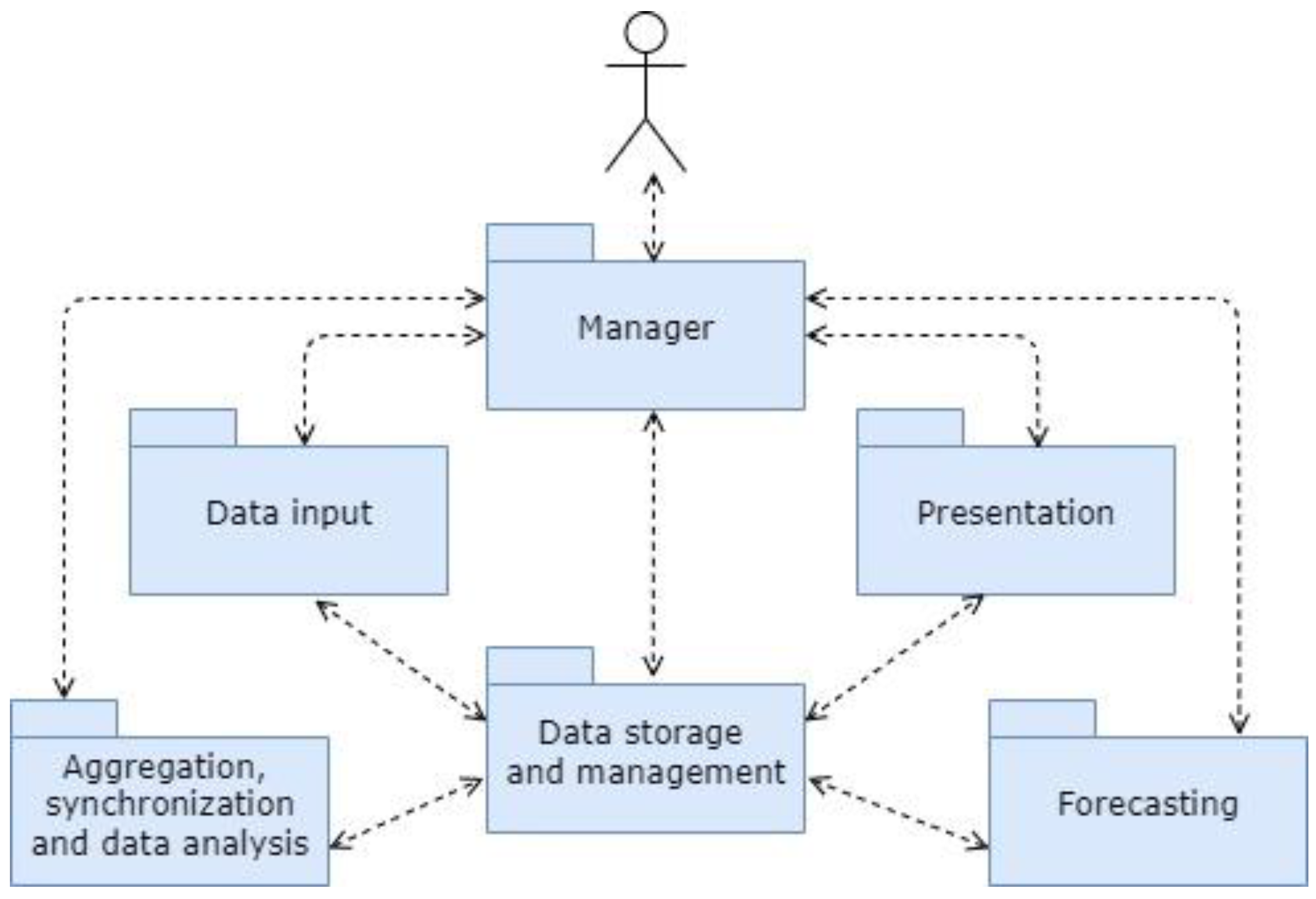
3.4. System Architecture
- primary input–output data and initial parameters;
- data models used by forecasting methods;
- maximum permissible error criteria set by the users;
- number and type of methods used;
- errors obtained in each of the methods;
- identifier of the most effective method;
- results from forecasting tasks, etc.
3.5. Multifactorial Multi-Step Forecasts
- simple forecasting—direct forecasting with known behavior of the factors, or if we consider the values of the target variable as a time series;
- complex forecasting—the forecasting of the target value is based on additionally created forecast data for the individual factors.
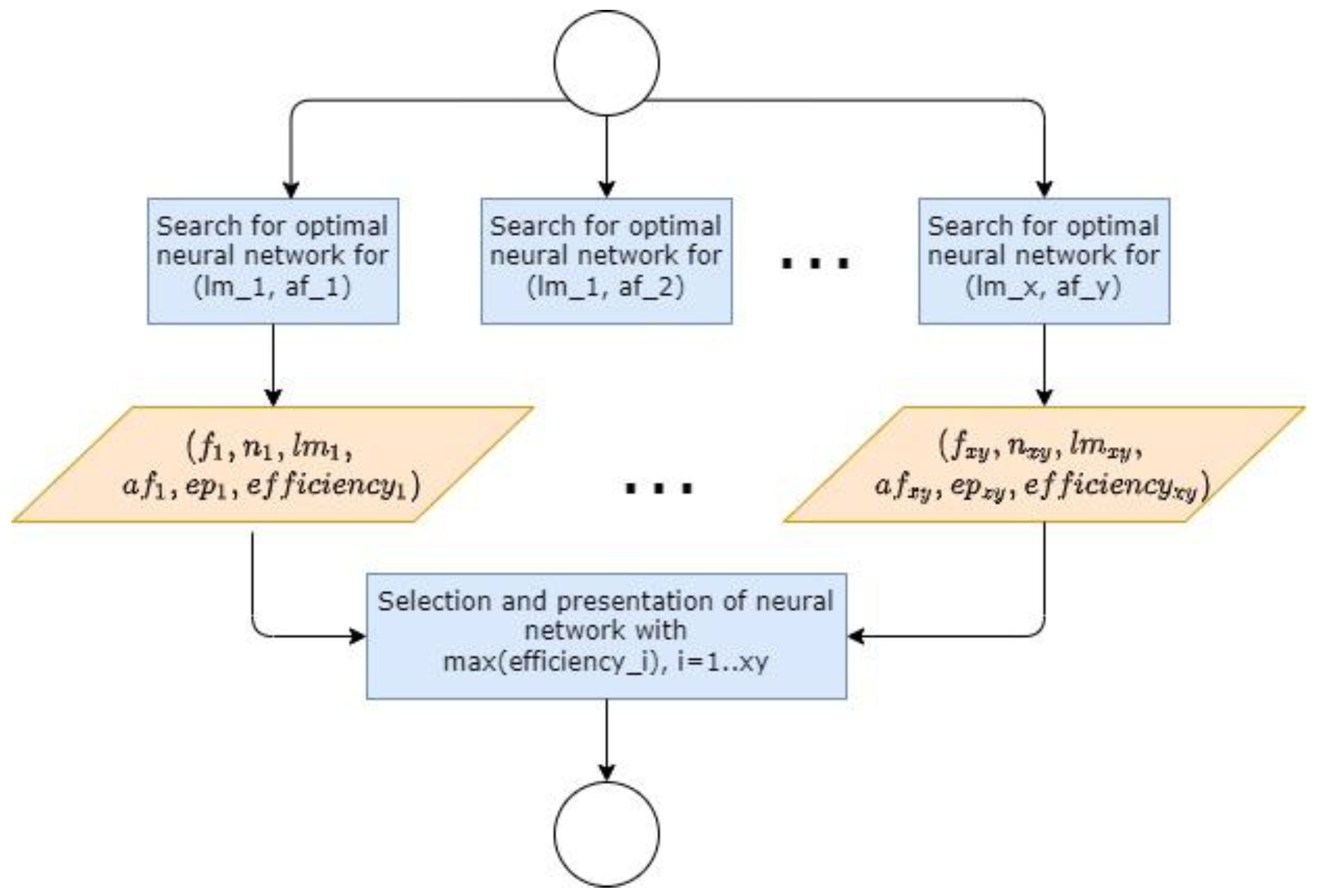
3.6. Algorithm for Searching for an Optimal Artificial Neural Network
- Indication of parameters for changing the number of neurons. Reducing the limits of variation in the number of neurons will reduce the total number of iterations in the algorithm and therefore will accelerate the achievement of the final result—the creation of an optimal neural network. In some cases, the expected number of neurons can be justified mathematically [40,41].
- Arrangement of the used training methods and activation functions. Different activation functions are suitable for different tasks. To solve problems requiring the application of mathematical logic, we included the hard-limit transfer function and its variant—the Symmetric hard-limit transfer function. These functions provide an interrupted binary signal along the axon of neurons and are suitable in case there is a need to solve problems requiring binary logical thinking. On the other hand, to forecast the future development of continuous processes, we used a large number of efficient and convenient transfer functions. Priority in the order of use is given to those with a sigmoid character such as hyperbolic tangent sigmoid transfer function and log-sigmoid transfer function, useful in a very wide range of problems [42].
- Necessity to change the number of learning epochs. Sometimes, to reach the optimal neural network it is only necessary to change the number of training epochs. Increasing the iterations slows down the neural network learning process, but often even a slight change in this parameter leads to a surprising overcoming of a small plateau of neural network errors and leads to a sharp improvement in the final approximation.
- (1)
- Preparation of input data:
- Tensor data—input data for the factors, which are usually in the form of a one-dimensional——or two-dimensional array—.
- Number of forecasted results——which is 1 for single-point forecasts or a larger integer for multi-step forecasts.
- Desired efficiency——of the trained neural network.
- (2)
- Preparation of the parameters on which iteration is performed:
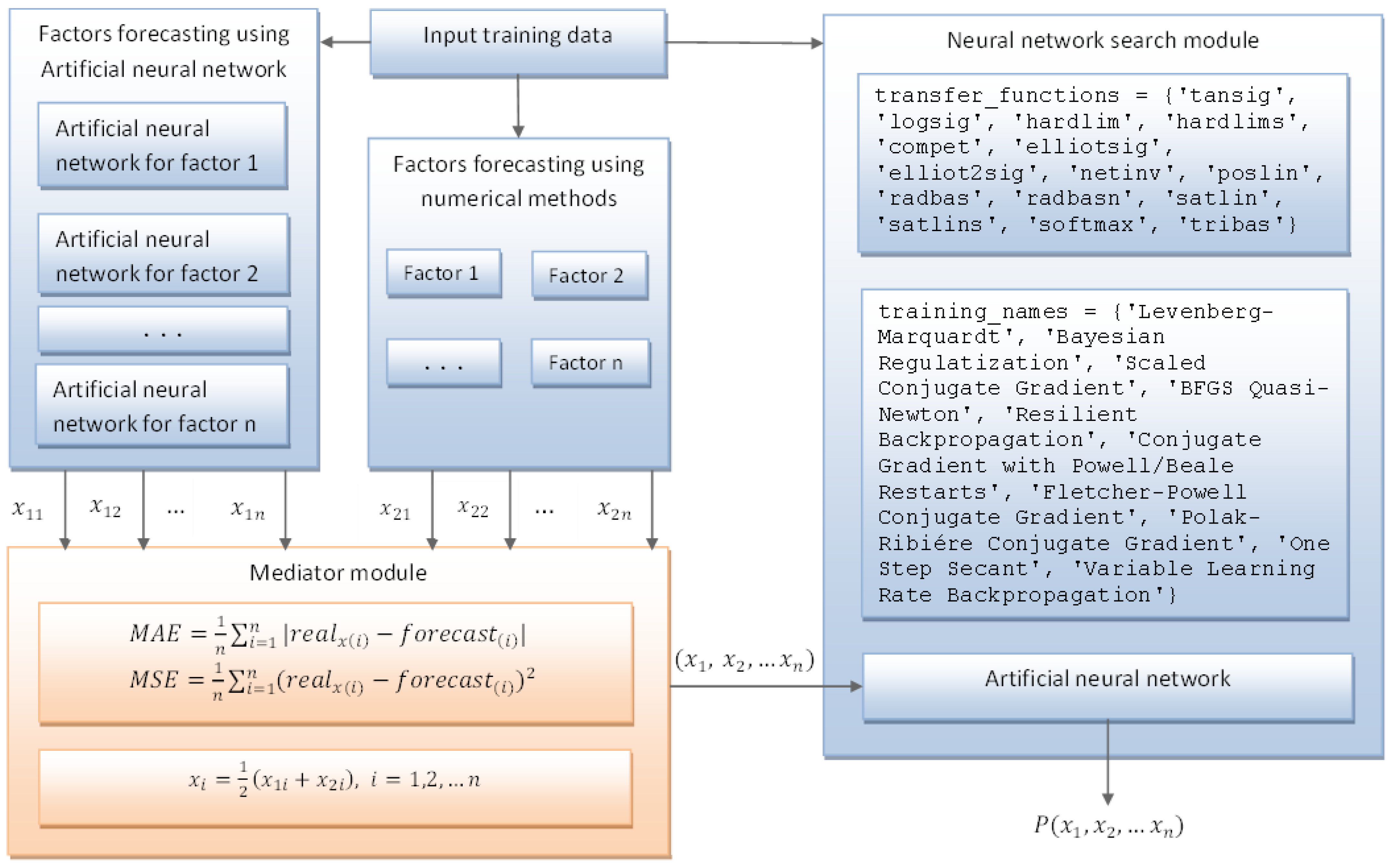
- List of training methods , where varies from 1 to the number of methods (Table 2). Depending on the task, to achieve the desired result faster, it is possible to arrange the methods in the list according to the expected efficiency, and some of them may even be excluded if they are considered inappropriate.
- List of activation functions , where varies from 1 to the number of functions (Table 1). Here, too, the functions can be arranged at the discretion of the appropriateness of their use in the specific task.
- Minimal and maximal number of neurons— u , as well as a step by which neurons change—. The current number of neurons we denote by . For more elementary tasks, the number of neurons may start from 1 () and the step by which their number increases is also 1. The maximum number limits the possible iterations related to the number of neurons.
- The epochs change from to with a step . Values we have experimented with are , where usually 3–4 iterations are enough to assess whether the change of epochs affects the efficiency of the trained neural network.
- By iterating over the number of neurons, training methods and activation functions, a neural network with their current values is created—the ordered triple and the input data. The nesting of the loops for the specific task is a matter of judgment, which determines the sequence of the parameters change. In the experiments, we chose to increase the number of neurons in the outermost loop, as we wanted to find a neural network with the lowest number of neurons. Training methods and activation functions change in inner loops.
- (3)
- After the creation of the current neural network, it is trained, tested, and validated.
- (4)
- The desired efficiency is compared to the efficiency of the current neural network, and then:
- If the neural network meets the condition, its data is saved and the task is completed;
- Otherwise, attempts are made to increase the efficiency of the neural network by increasing the number of learning epochs. The information about the most efficient neural network found (with the smallest error) is saved, and it can be current or obtained in a previous iteration.
- (5)
- The end result of the algorithm is a trained neural network having the closest possible to the specified efficiency, as well as parameters for its architecture and training—efficiency, number of neurons n, training method lm, activation function af, and epochs ep.
4. Results and Discussion
4.1. Setup of the Experiment
- (1)
- Total final consumption in the national power system;
- (2)
- Electricity consumption in the industry, the public sector, and services;
- (3)
- Electricity consumption in households.
- (1)
- Gross domestic product (GDP);
- (2)
- Energy intensity (EI);
- (3)
- Population;
- (4)
- Income of the population;
- (5)
- Energy efficiency;
- (6)
- Price of electricity.
- (1)
- Modules for factor forecasting, respectively through time series and neural networks;
- (2)
- Error estimation module (mediator module) for the various methods and parameters;
- (3)
- Consumption forecasting module.
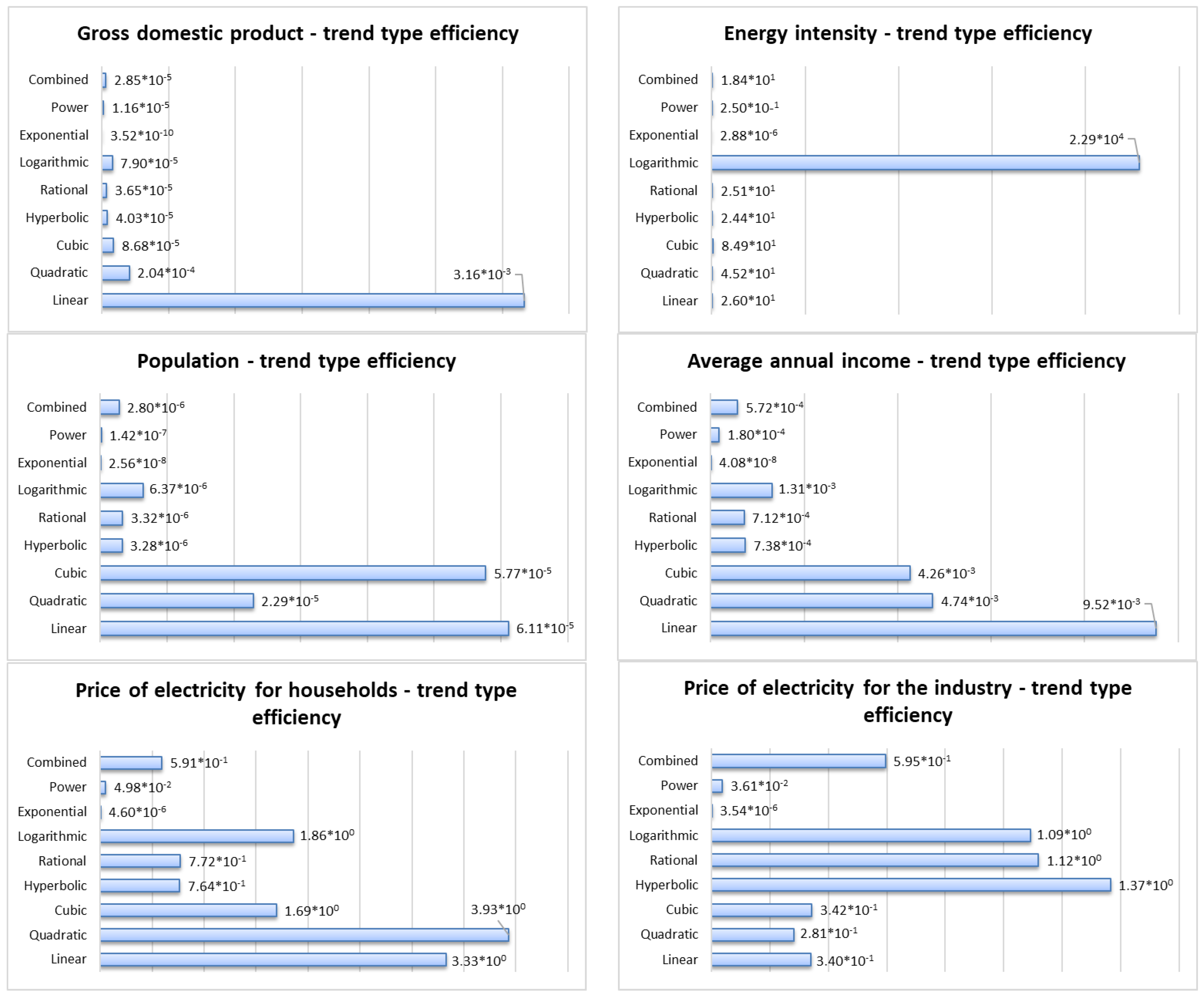
4.2. Single-Point Forecasts for the Factors
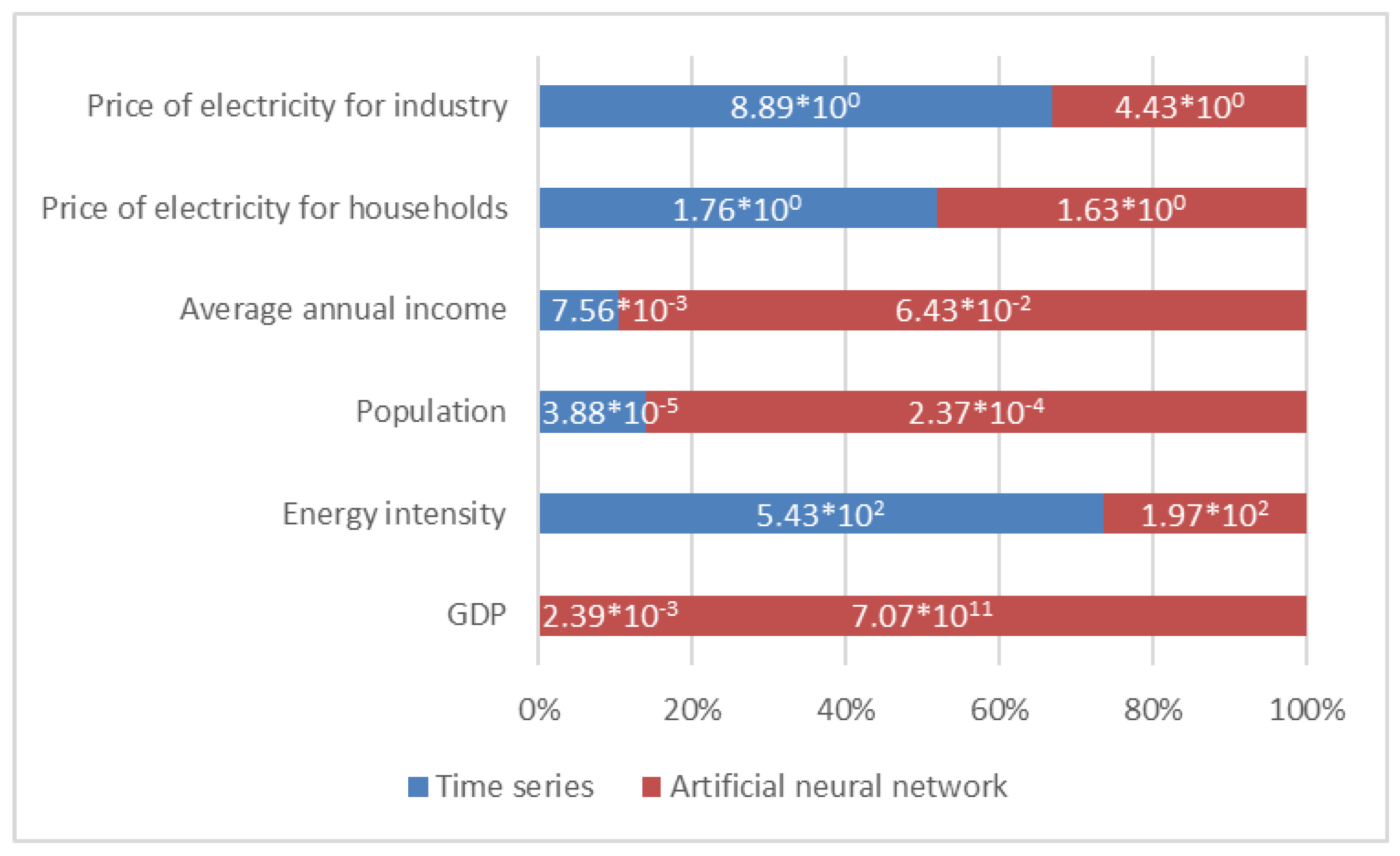
4.3. Multifactor Single-Point Forecasts of Target Values
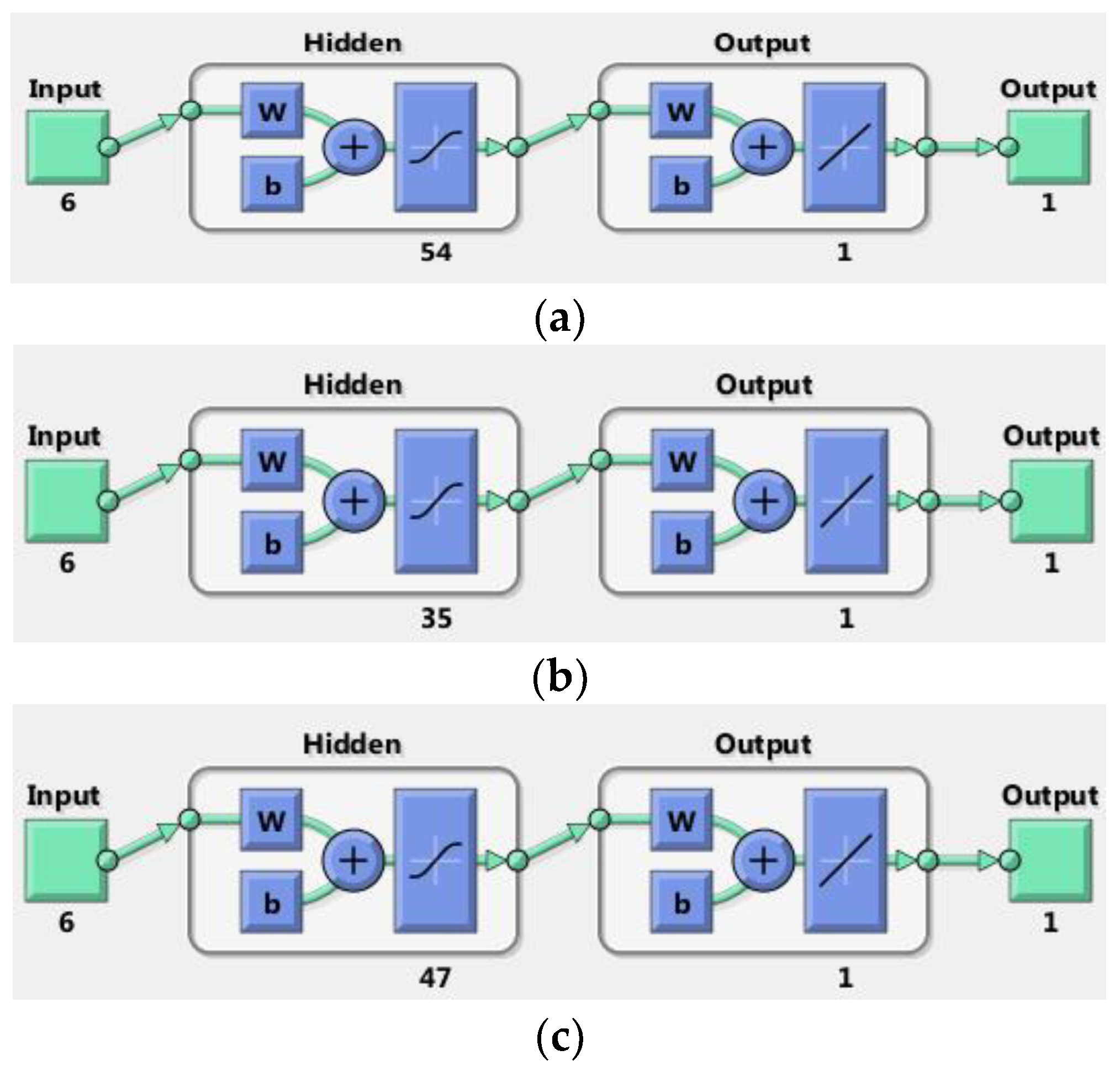
- (1)
- Total final consumption in the National Power System—the neural network named Net_Nees, with 54 neurons in the hidden layer;
- (2)
- Electricity consumption in industry, public sector and services—Net_Industry neural network with 35 neurons in the hidden layer;
- (3)
- Electricity consumption on households—Net_Household neural network with 47 neurons in the hidden layer.
4.4. Multi-Step Forecasts
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- ReferencesHyndman, R.; Athanasopoulos, G. Forecasting: Principles and Practice; OTexts: Melbourne, Australia, 2021. [Google Scholar]
- Slavova, I. Forecasting and Planning; New Bulgarian University: Sofia, Bulgaria, 2012. [Google Scholar]
- Skiadas, C.H.; Bozeman, J. Data Analysis and Applications 1: Clustering and Regression, Modeling-Estimating, Forecasting and Data Mining; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2019; Volume 2. [Google Scholar]
- Brockwell, P.; Davis, R. Introduction to Time Series and Forecasting; Springer: Berlin/Heidelberg, Germany, 2016; ISBN 9783319298528. [Google Scholar]
- Agung, I.G. Advanced Time Series Data Analysis: Forecasting Using EViews; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2019; ISBN 978-1-119-50471-9. [Google Scholar]
- Ostertagová, E.; Ostertag, O. Forecasting Using Simple Exponential Smoothing Method. Acta Electrotech. Inform. 2012, 12, 64–66. [Google Scholar] [CrossRef]
- Chen, T.; Honda, K. Fuzzy Collaborative Forecasting and Clustering: Methodology, System Architecture, and Applications; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Lazzeri, F. Machine Learning for Time Series Forecasting with Python; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2020; ISBN 1119682363. [Google Scholar]
- Gridin, I. Time Series Forecasting using Deep Learning: Combining PyTorch, RNN, TCN, and Deep Neural Network Models to Provide Production-Ready Prediction Solutions; BPB Publications: Noida, India, 2021; ISBN 9391392571. [Google Scholar]
- BAS Strategy. Preparation of the National Strategy in the Field of Energy; BAS: Sofia, Bulgaria, 2017. [Google Scholar]
- Risk Management Lab. Forecast of the Electricity Balance of the Republic of Bulgaria 2025. 2014. Available online: https://www.bia-bg.com/uploads/files/events/Energy_balans_BG2025.pdf (accessed on 15 July 2022).
- Mohamed, Z.; Bodger, P. Forecasting electricity consumption in New Zealand using economic and demographic variables. Energy 2005, 30, 1833–1843. [Google Scholar]
- Lee, Y.; Gaik, T.; Yee, C.H. Forecasting Electricity Consumption Using Time Series Model. Int. J. Eng. Technol. 2018, 7, 218–223. [Google Scholar]
- Sun, T.; Zhang, T.; Teng, Y.; Chen, Z.; Fang, J. Monthly Electricity Consumption Forecasting Method Based onX12 and STL Decomposition Model in an Integrated Energy System. Math. Probl. Eng. 2019, 2019, 9012543. [Google Scholar]
- Chou, J.S.; Tran, D.S. Forecasting energy consumption time series using machine learning techniques based on usage patterns of residential householders. Energy 2018, 165, 709–726. [Google Scholar] [CrossRef]
- Ding, S.; Hipel, K.; Dang, Y. Forecasting China’s electricity consumption using a new grey prediction model. Energy 2018, 149, 314–328. [Google Scholar] [CrossRef]
- Lee, Y.S.; Tong, L.T. Forecasting energy consumption using a grey model improved by incorporating genetic programming. Energy Convers. Manag. 2011, 52, 147–152. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, C.; Dang, H.; Lai, S. Evaluating performance of the DGM(2,1) model and its modified models. Appl. Sci. 2016, 6, 73. [Google Scholar] [CrossRef]
- Chung, Y. Electricity consumption prediction using a neural-network-based grey forecasting approach. J. Oper. Res. Soc. 2017, 68, 1259–1264. [Google Scholar]
- Chernykh, I.; Chechushkov, D.; Panikovskaya, T. Prediction of electrical loads in operational control of power systems based on neural network structures. WIT Trans. Ecol. Environ. 2014, 190, 109–117. [Google Scholar]
- Khosravani, H.; Castilla, M.; Berenguel, M.; Ruano, A.; Ferreira, P. A Comparison of Energy Consumption Prediction Models Based on Neural Networks of a Bioclimatic Building. Energies 2016, 9, 57. [Google Scholar]
- Yoo, S.; Myriam, H.A. Predicting residential electricity consumption using neural networks: A case study. J. Phys. Conf. Ser. 2018, 1072, 012005. [Google Scholar] [CrossRef]
- Jahn, M. Artificial Neural Network Regression Models: Predicting GDP Growth; HWWI Research Paper, No. 185; Hamburg Institute of International Economics (HWWI): Hamburg, Germany, 2018.
- Bouktif, S.; Fiaz, A.; Ouni, A.; Serhani, M.A. Optimal Deep Learning LSTM Model for Electric Load Forecasting using Feature Selection and Genetic Algorithm: Comparison with Machine Learning Approaches. Energies 2018, 11, 1636. [Google Scholar] [CrossRef]
- Alamaniotis, M.; Bargiotas, D.; Tsoukalas, L.H. Towards smart energy systems: Application of kernel machine regression for medium term electricity load forecasting. Springer Plus 2016, 5, 58. [Google Scholar] [CrossRef]
- Alamaniotis, M. Synergism of Deep Neural Network and ELM for Smart Very-Short-Term Load Forecasting. In Proceedings of the 2019 IEEE PES Innovative Smart Grid Technologies Europe (ISGT-Europe), Novi Sad, Serbia, 10–12 October 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Chou, J.S.; Truong, D.N. Multistep energy consumption forecasting by metaheuristic optimization of time-series analysis and machine learning. Energy Res. 2021, 45, 4581–4612. [Google Scholar] [CrossRef]
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-Term Residential Load Forecasting Based on LSTM Recurrent Neural Network. IEEE Trans. Smart Grid 2019, 10, 841–851. [Google Scholar] [CrossRef]
- Moradzadeh, A.; Moayyed, H.; Zakeri, S.; Mohammadi-Ivatloo, B.; Aguiar, A.P. Deep Learning-Assisted Short-Term Load Forecasting for Sustainable Management of Energy in Microgrid. Inventions 2021, 6, 15. [Google Scholar] [CrossRef]
- Khwaja, A.S.; Anpalagan, A.; Naeem, M.; Venkatesh, B. Joint bagged-boosted artificial neural networks: Using ensemble machine learning to improve short-term electricity load forecasting. Electr. Power Syst. Res. 2020, 179, 106080. [Google Scholar] [CrossRef]
- Khwaja, A.S.; Zhang, X.; Anpalagan, A.; Venkatesh, B. Boosted neural networks for improved short-term electric load forecasting. Electr. Power Syst. Res. 2017, 143, 431–437. [Google Scholar] [CrossRef]
- Cao, Z.; Wan, C.; Zhang, Z.; Li, F.; Song, Y. Hybrid Ensemble Deep Learning for Deterministic and Probabilistic Low-Voltage Load Forecasting. IEEE Trans. Power Syst. 2020, 35, 1881–1897. [Google Scholar] [CrossRef]
- Karatasou, S.; Santamouris, M.; Geros, V. Modeling and predicting building’s energy use with artificial neural networks: Methods and results. Energy Build. 2008, 38, 949–958. [Google Scholar] [CrossRef]
- Cervená, M.; Schneider, M. Short-term forecasting of GDP with a DSGE model augmented by monthly indicators. Int. J. Forecast. 2014, 30, 498–516. [Google Scholar] [CrossRef]
- Farsi, B.; Amayri, M.; Bouguila, N.; Eicker, U. On Short-Term Load Forecasting Using Machine Learning Techniques and a Novel Parallel Deep LSTM-CNN Approach. IEEE Access 2021, 9, 31191–31212. [Google Scholar] [CrossRef]
- Chung, W.; Gu, Y.H.; Yoo, S.J. District heater load forecasting based on machine learning and parallel CNN-LSTM attention. Energy 2022, 246, 123350. [Google Scholar] [CrossRef]
- Sajjad, M.; Khan, Z.A.; Ullah, A.; Hussain, T.; Ullah, W.; Lee, M.Y.; Baik, S.W. A Novel CNN-GRU-Based Hybrid Approach for Short-Term Residential Load Forecasting. IEEE Access 2020, 8, 143759–143768. [Google Scholar] [CrossRef]
- Alamo, D.H.; Medina, R.N.; Ruano, S.D.; García, S.S.; Moustris, K.P.; Kavadias, K.K.; Zafirakis, D.; Tzanes, G.; Zafeiraki, E.; Spyropoulos, G.; et al. An Advanced Forecasting System for the Optimum Energy Management of Island Microgrids. Energy Procedia 2019, 159, 111–116. [Google Scholar] [CrossRef]
- Botchkarev, A. A New Typology Design of Performance Metrics to Measure Errors in Machine Learning Regression Algorithms. Interdiscip. J. Inf. Knowl. Manag. 2019, 14, 45–76. [Google Scholar] [CrossRef]
- Sheela, K.; Deepa, S.N. Review on Methods to Fix Number of Hidden Neurons in Neural Networks. Math. Probl. Eng. 2013, 2013, 425740. [Google Scholar] [CrossRef] [Green Version]
- Lörke, A.; Schneider, F.; Heck, J.; Nitter, P. Cybenko’s Theorem and the Capability of a Neural Network as Function Approximator. 2019. Available online: https://www.mathematik.uni-wuerzburg.de/fileadmin/10040900/2019/Seminar__Artificial_Neural_Network__24_9__.pdf (accessed on 15 July 2022).
- National Statistical Institute. Available online: https://www.nsi.bg/ (accessed on 15 July 2022).
- INFOSTAT Information System. Available online: https://infostat.nsi.bg/infostat/pages/external/login.jsf (accessed on 15 July 2022).
- Electricity System Operator. Available online: http://www.eso.bg/ (accessed on 15 July 2022).
- The World Bank Group. Available online: https://www.worldbank.org (accessed on 15 July 2022).
- Eurostat. Your Key to European Statistic. Available online: https://ec.europa.eu/eurostat (accessed on 15 July 2022).


| Function |
|---|
| Hyperbolic tangent sigmoid transfer function |
| Log-sigmoid transfer function |
| Hard-limit transfer function |
| Symmetric hard-limit transfer function |
| Competitive transfer function |
| Elliot symmetric sigmoid transfer function |
| Elliot 2 symmetric sigmoid transfer function |
| Inverse transfer function |
| Positive linear transfer function |
| Radial basis transfer function |
| Normalized radial basis transfer function |
| Saturating linear transfer function |
| Symmetric saturating linear transfer function |
| Soft max transfer function |
| Triangular basis transfer function |
| Method |
|---|
| Levenberg–Marquardt |
| Bayesian Regularization |
| Scaled Conjugate Gradient |
| BFGS Quasi-Newton |
| Resilient Backpropagation |
| Conjugate Gradient with Powell/Beale Restarts |
| Fletcher-Powell Conjugate Gradient |
| Polak–Ribiére Conjugate Gradient |
| One Step Secant |
| Variable Learning Rate Backpropagation |
| Levenberg–Marquardt |
| Bayesian Regularization |
| Factor | Predicted Value | The Most Effective Method | SMAPE (%) |
|---|---|---|---|
| GDP | 102,954.73 | Neural network | 0.15 |
| Energy intensity of the economy | 0.42 | Time series with logarithmic trend | 3.65 |
| Population | 7,006,425.85 | Neural network | 0.65 |
| Average annual income | 6196.5 | Neural network | 1.57 |
| Price of electricity for households | 22.56 | Time series with quadratic trend | 4.98 |
| Price of electricity for the industry | 21.77 | Time series with hyperbolic trend | 4.8 |
| Neural Network | Actual Value | Predicted Value | Absolute Error | SMAPE (%) |
|---|---|---|---|---|
| Net_Nees | 9737.9 | 9745.1 | 7.2 | 0.04 |
| Net_Industry | 2721.3 | 2679.8 | 41.48 | 0.77 |
| Net_Households | 2318.7 | 2318.0 | 0.7 | 0.02 |
| Consumption | Method Type | Method | Absolute Error (Thousand Toe) | SMAPE (%) |
|---|---|---|---|---|
| Total final consumption in the National Power System | Time series | Cubic trend | 199.33 | 1.01 |
| Neural network | Net_Nees | 7.2 | 0.04 | |
| Electricity consumption in industry, public sector and services | Time series | Combined trend | 111.16 | 2 |
| Neural network | Net_Industry | 41.48 | 0.77 | |
| Electricity consumption in households | Time series | Linear trend | 24.47 | 0.52 |
| Neural network | Net_House holds | 0.7 | 0.02 |
| Factor | 2021 | 2022 | 2023 | 2024 | 2025 | 2026 | 2027 |
|---|---|---|---|---|---|---|---|
| GDP (Million levs) | 102,932 | 106,693 | 110,455 | 114,217 | 117,978 | 121,740 | 125,501 |
| Energy intensity of the economy | 0.400 | 0.395 | 0.390 | 0.385 | 0.380 | 0.376 | 0.371 |
| Population | 6,804,441 | 6,746,144 | 6,687,847 | 6,629,550 | 6,571,253 | 6,512,956 | 6,454,659 |
| Average annual income | 6671 | 6798 | 6942 | 7013 | 7105 | 7241 | 7339 |
| Price of electricity for industry (in stotinki per kWh and without VAT) | 26.79 | 27.62 | 28.46 | 29.29 | 30.12 | 30.96 | 31.79 |
| Price of electricity for households (in stotinki per kWh and without VAT) | 19.22 | 19.35 | 19.47 | 19.58 | 19.69 | 19.79 | 19.89 |
| Consumption | 2021 | 2022 | 2023 | 2024 | 2025 | 2026 | 2027 |
|---|---|---|---|---|---|---|---|
| Total final consumption in the National Power System | 13,832 | 13,856 | 13,858 | 13,858 | 13,858 | 13,858 | 13,858 |
| Electricity consumption in industry, public sector and services | 3103 | 3101 | 3100 | 3099 | 3099 | 3098 | 3098 |
| Electricity consumption in households | 2800 | 2800 | 2800 | 2800 | 2800 | 2800 | 2800 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yotov, K.; Hadzhikolev, E.; Hadzhikoleva, S.; Cheresharov, S. Neuro-Cybernetic System for Forecasting Electricity Consumption in the Bulgarian National Power System. Sustainability 2022, 14, 11074. https://doi.org/10.3390/su141711074
Yotov K, Hadzhikolev E, Hadzhikoleva S, Cheresharov S. Neuro-Cybernetic System for Forecasting Electricity Consumption in the Bulgarian National Power System. Sustainability. 2022; 14(17):11074. https://doi.org/10.3390/su141711074
Chicago/Turabian StyleYotov, Kostadin, Emil Hadzhikolev, Stanka Hadzhikoleva, and Stoyan Cheresharov. 2022. "Neuro-Cybernetic System for Forecasting Electricity Consumption in the Bulgarian National Power System" Sustainability 14, no. 17: 11074. https://doi.org/10.3390/su141711074
APA StyleYotov, K., Hadzhikolev, E., Hadzhikoleva, S., & Cheresharov, S. (2022). Neuro-Cybernetic System for Forecasting Electricity Consumption in the Bulgarian National Power System. Sustainability, 14(17), 11074. https://doi.org/10.3390/su141711074








