Analysis of Lane-Changing Decision-Making Behavior and Molecular Interaction Potential Modeling for Connected and Automated Vehicles
Abstract
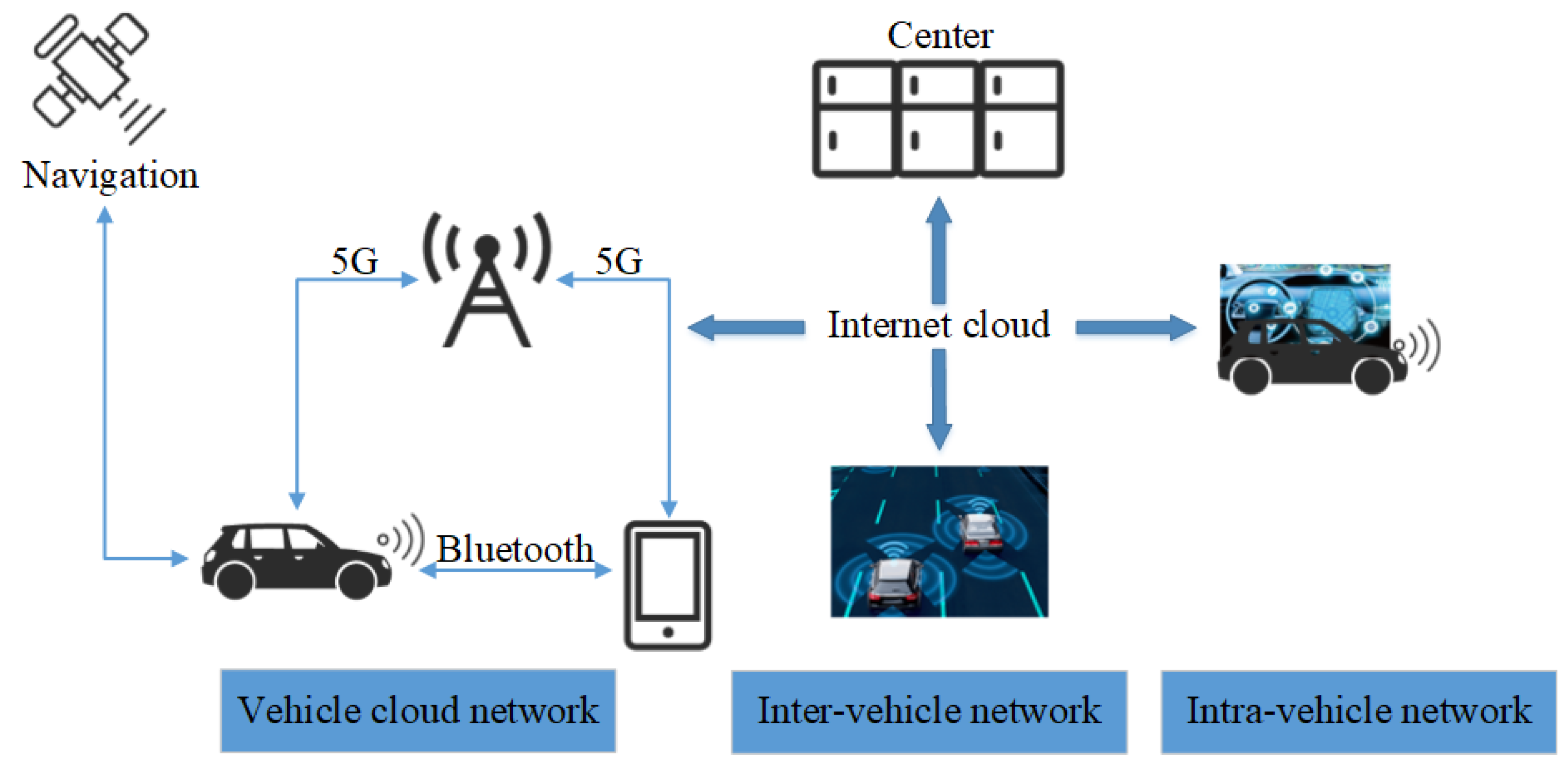
:1. Introduction
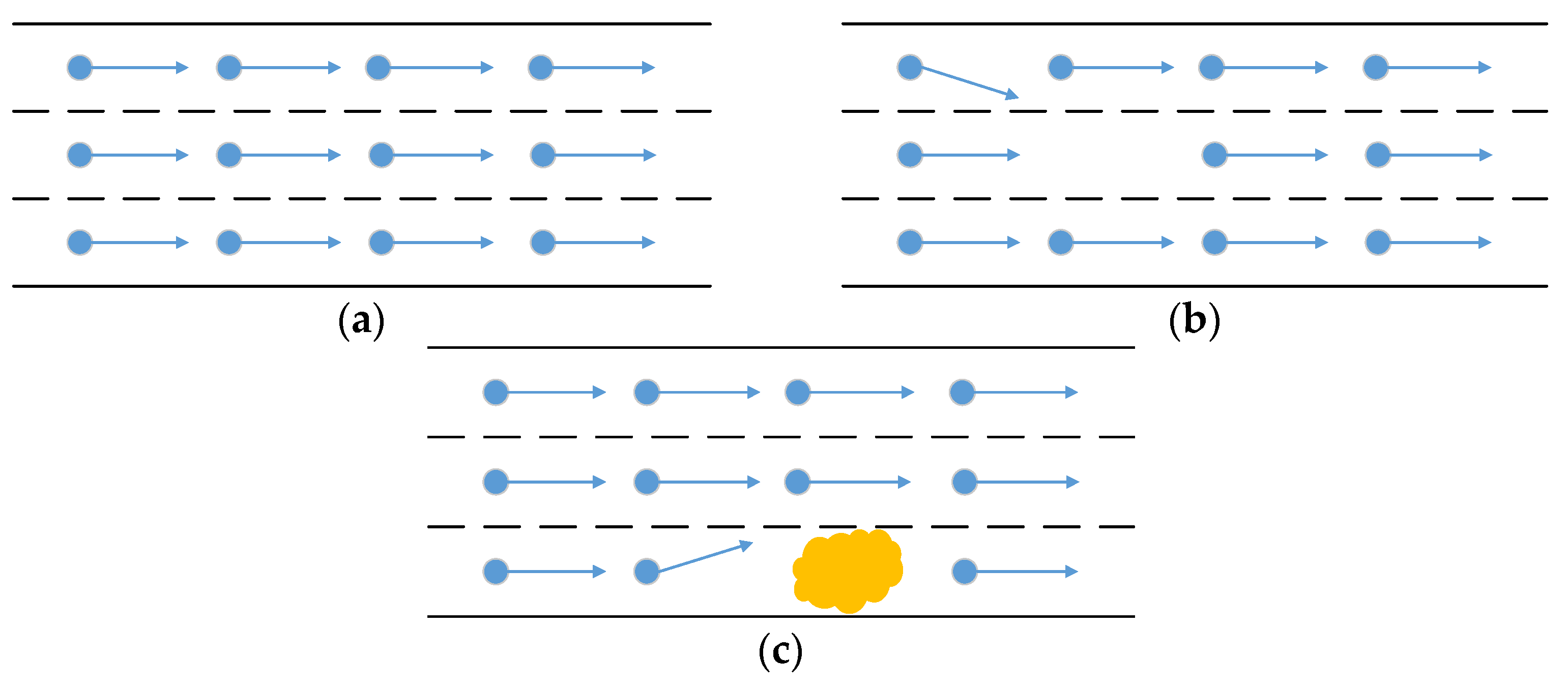
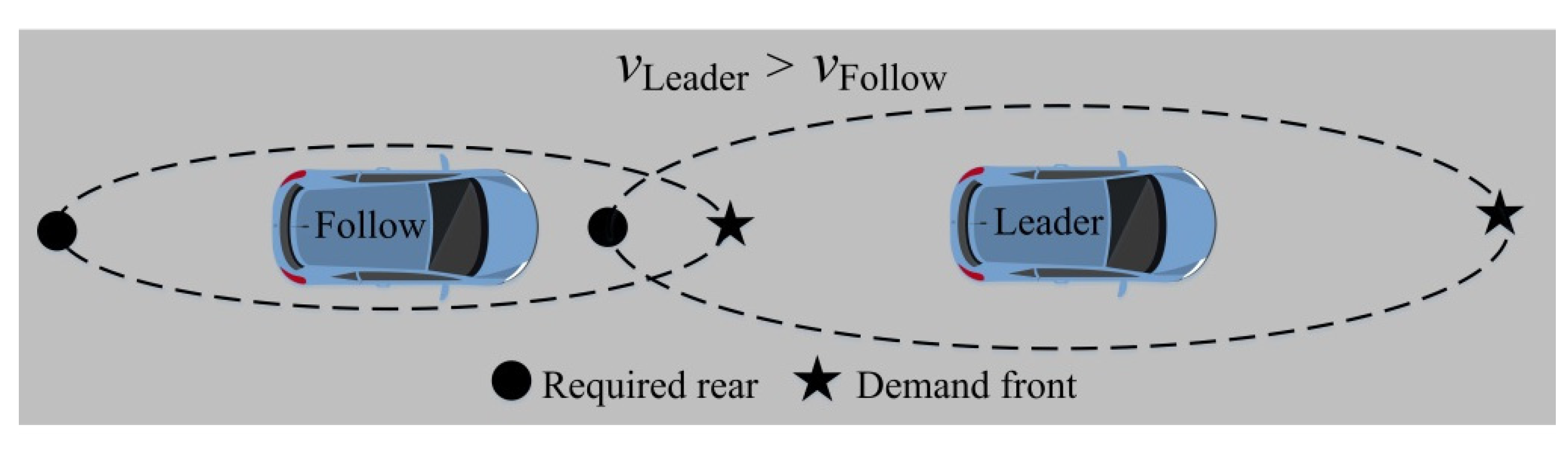
2. Analysis of Lane-Changing Behavior
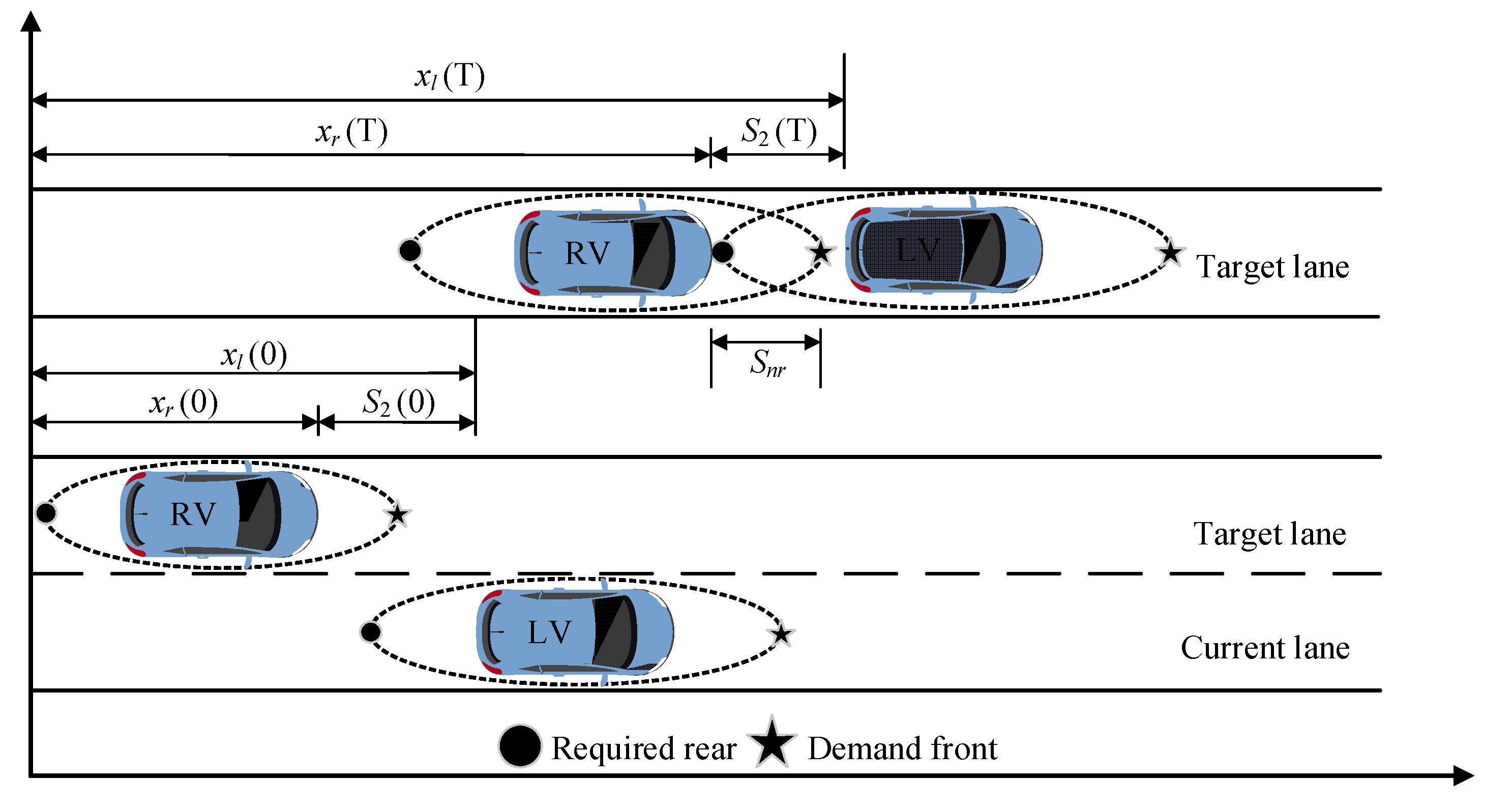
3. Similarity Analysis of System
4. Construction of Lane-Changing Decision-Making Behavior Model Based on Molecular Interaction Potential
- The automation level of the Connected and Automated Vehicles is high, and the vehicle can complete the driving operation by itself;
- The Connected and Automated Vehicles can obtain the position and speed of themselves and surrounding vehicles in real time;
- The Connected and Automated Vehicles are unified standard cars and can communicate with each other.
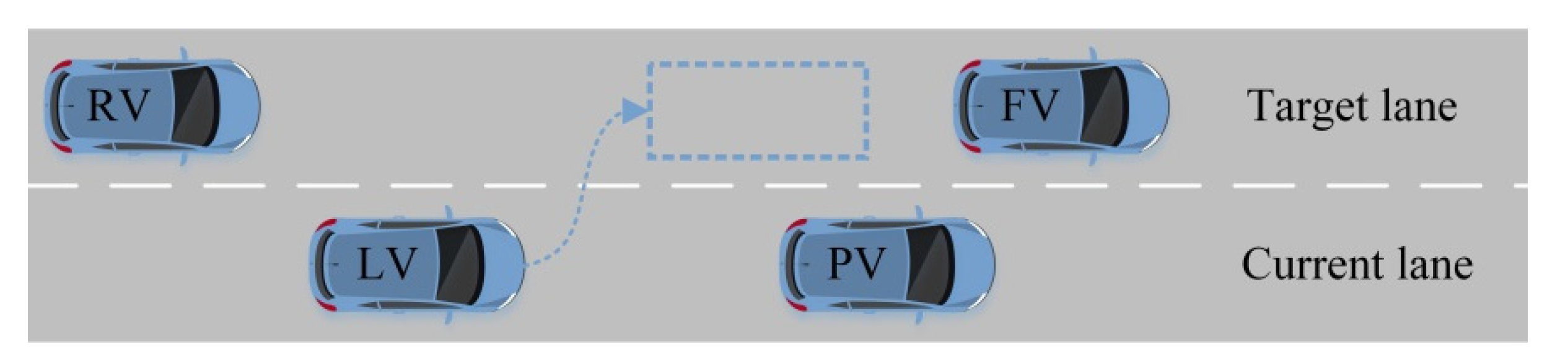
4.1. Generation of Lane-Changing Intention
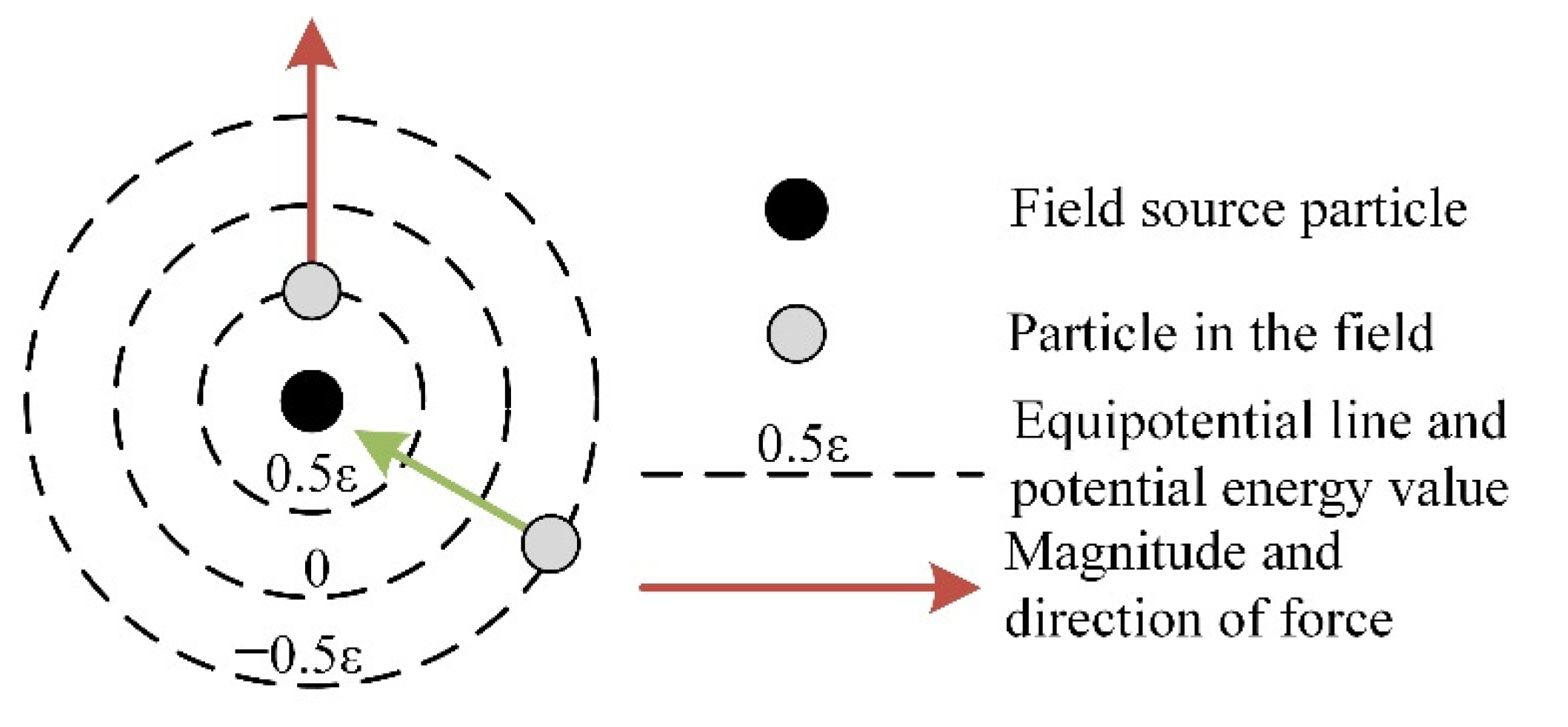
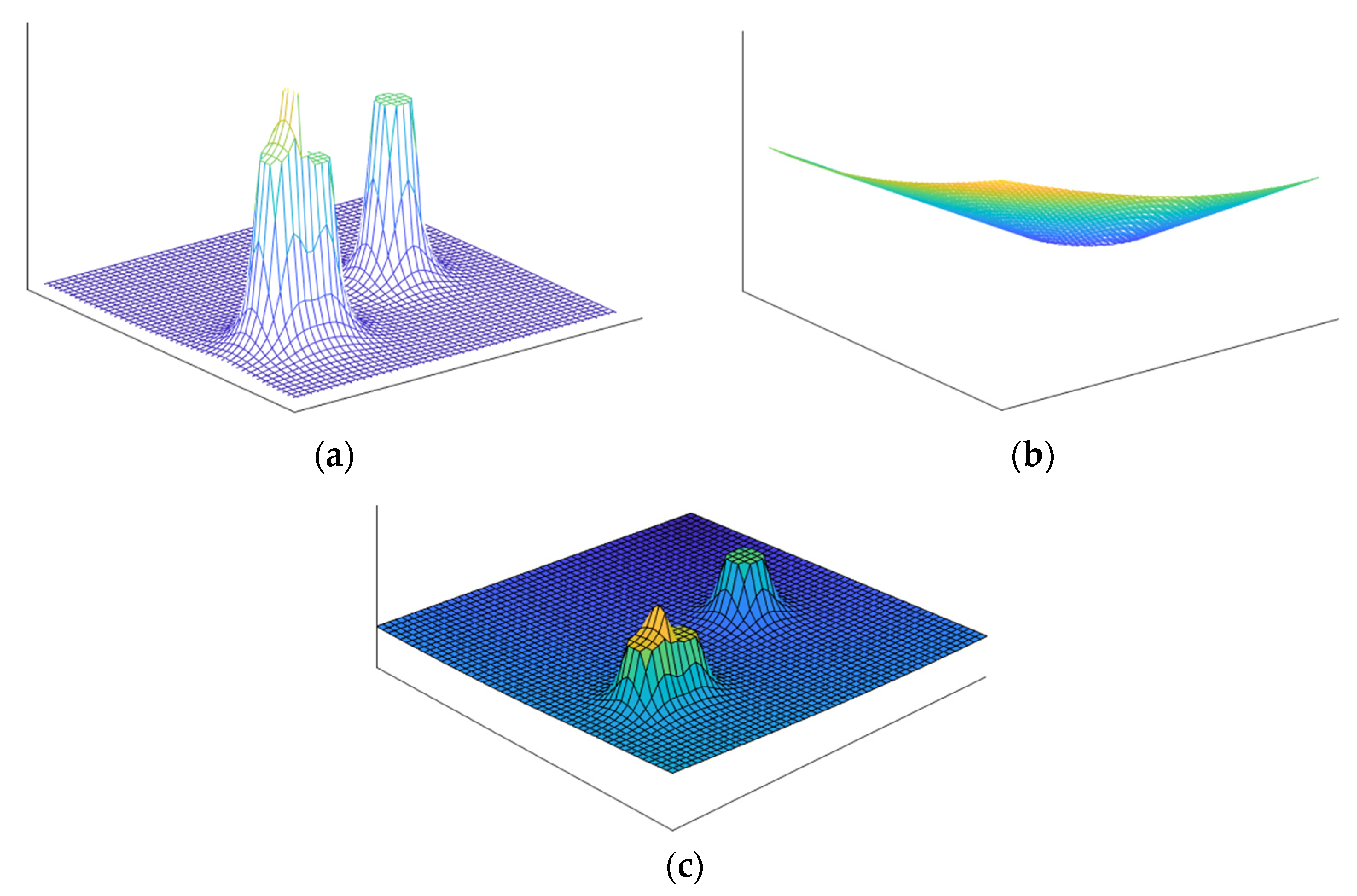
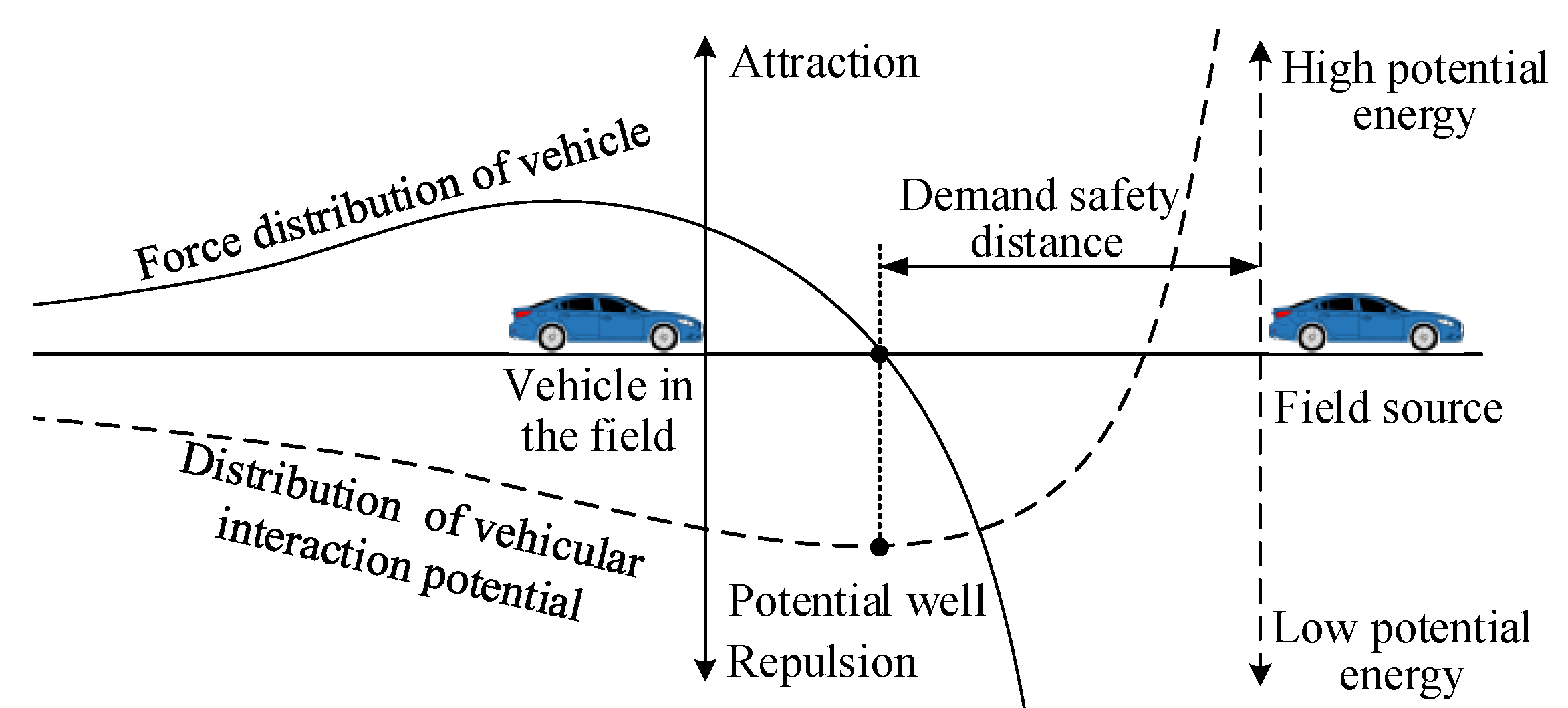
4.2. Explanation of Molecular Interaction Potential
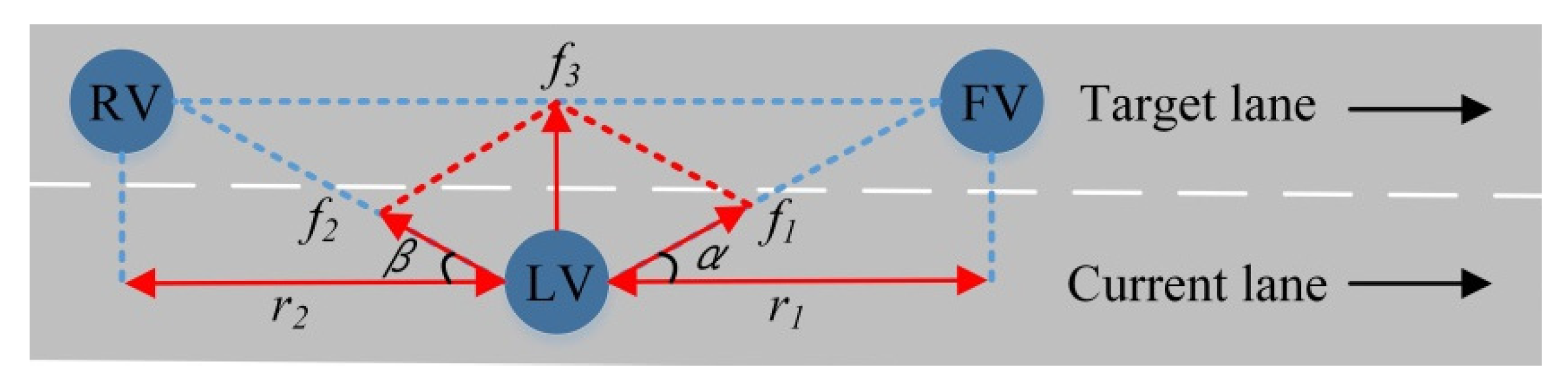
4.3. Establishment of Molecular Interaction Potential Lane-Changing Model
5. Experimental Verification and Discussion
5.1. Platform and Environment of Simulation
5.2. Analysis of Lane-Changing Data
- (1)
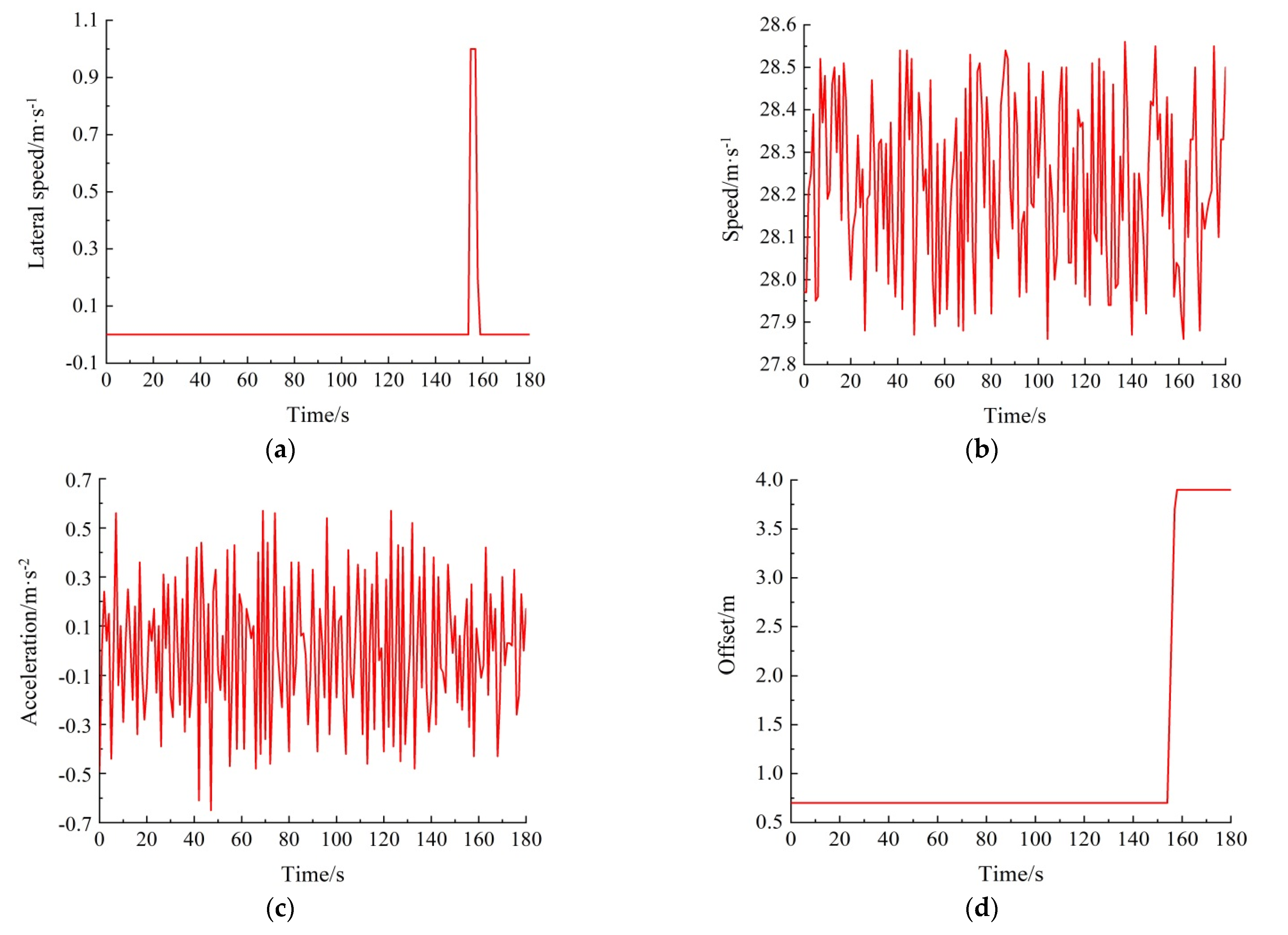
- Figure 15a shows the variation of lateral speed for the lane-changing vehicle. At first, when the vehicle does not change lanes, its lateral speed is zero, and the vehicle keeps driving along the center of the current lane. In the process of lane-changing, the lateral speed of the vehicle begins to change, and the change is to accelerate first and then decelerate. After arriving at the center of the target lane, the lateral speed of the lane-changing vehicle returns to zero. Finally, the vehicle drives in the target lane. It can be seen from the figure that the lane-changing vehicle only changes the lane once.
- (2)
- Figure 15b shows the variation of speed for the lane-changing vehicle. Sometimes the lane-changing vehicle accelerates and sometimes decelerates. Because the vehicle runs on the high-speed road with relatively few obstacles, its speed fluctuation range is relatively small, and it can finally run in a more stable state.
- (3)
- Figure 15c shows the variation of acceleration for the lane-changing vehicle. During the process of lane-changing, the acceleration of the vehicle fluctuates up and down near zero. It can be seen from the figure that the variation range of acceleration is −0.7 m/s2~0.7 m/s2, which enables the vehicle to drive stably with small speed fluctuation. Moreover, the information shown in Figure 15b,c can be mutually verified.
- (4)
- Figure 15d shows the variation of the offset of the right side of the lane-changing vehicle relative to the right side of the road. This offset actually represents the lateral position of the vehicle and can directly reflect the lane-changing information. When the vehicle drives in the current lane, the offset does not change. When the vehicle changes the lane, the offset will change, and the final change is the width of the single lane. It can be seen from the figure that the lane-changing vehicle only changes the lane once. In addition, the information shown in Figure 15a,d can be mutually verified.
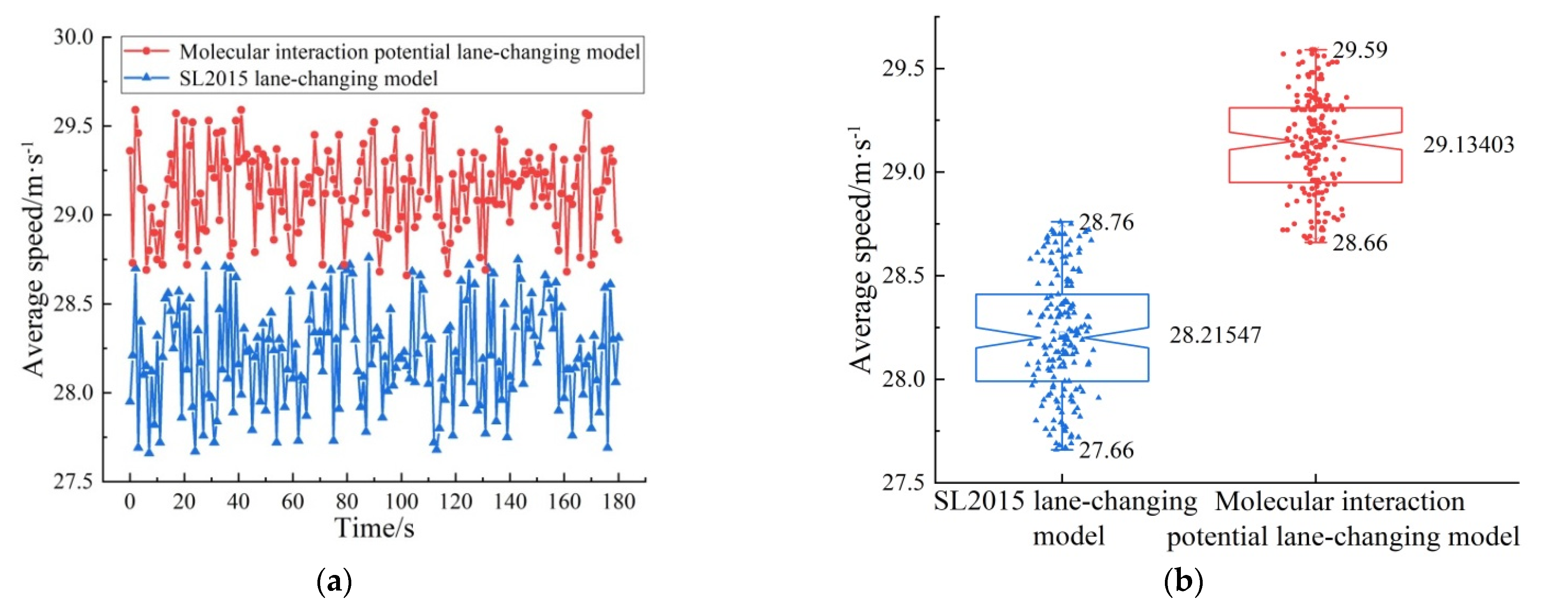
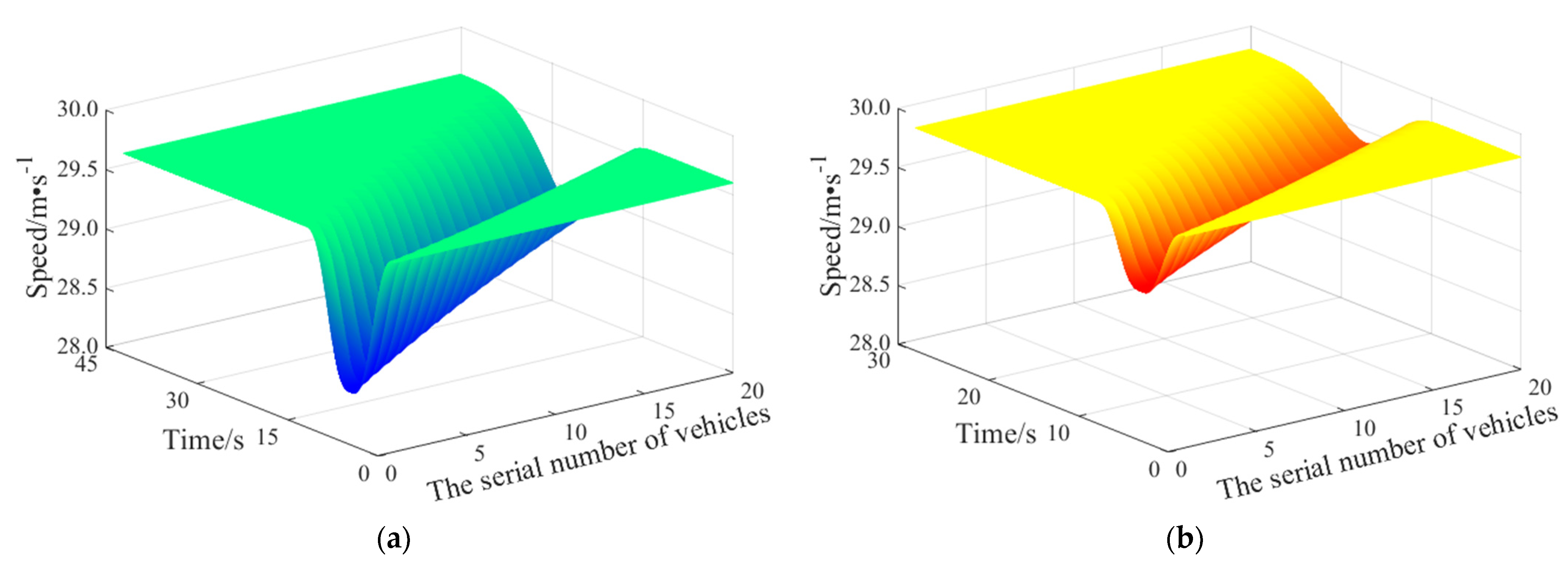
5.3. Evaluation of Molecular Interaction Potential Lane-Changing Model
6. Conclusions
- Connected and Automated Vehicles have the characteristics of interactivity and dynamics. By analyzing its similarity with molecules, the molecular interaction potential theory is applied to the lane-changing scene, and the molecular interaction potential lane-changing model is established, which scientifically shows the lane-changing characteristics of the Connected and Automated Vehicles.
- The molecular interaction potential lane-changing model unifies the attraction and repulsion into a whole while considering the dynamic influencing factors, so as to form the reasonable lane-changing decision-making mechanism, so that the Connected and Automated Vehicles can implement lane-changing safely and efficiently. The experimental results show that, compared with the SL2015 lane-changing model, the average speed under the molecular interaction potential lane-changing model is increased by 3.26%, the speed fluctuation is reduced by 15.5%, and the number of passed vehicles is increased by 3.26%. In addition, there is no collision accident and the perturbation of lane-changing vehicle to the traffic flow of the target lane is small. Therefore, the molecular interaction potential lane-changing model has good safety, stability, and road utilization.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ali, Y.; Zheng, Z.; Haque, M.M.; Yildirimoglu, M.; Washington, S. A Complete Lane-changing Decision Modeling Framework for the Connected and Traditional Environments. Transp. Res. Part C Emerg. Technol. 2021, 128, 103162. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, F.; Wang, W.; Meng, F.; Zhang, D.; Wang, H. Prediction of Clearance Vibration for Intelligent Vehicles Motion Control. Sustainability 2022, 14, 6698. [Google Scholar] [CrossRef]
- Wei, J.; Dolan, M.; Litkouhi, B. A Prediction and Cost Function-Based Algorithm for Robust Autonomous Freeway Driving. In Proceedings of the 2010 IEEE Intelligent Vehicles Symposium, La Jolla, CA, USA, 21–24 June 2010. [Google Scholar]
- Stefan, H.; Hermann, W.; Sven, B. A Maneuver-based Lane Change Assistance System. In Proceedings of the 2011 IEEE Intelligent Vehicles Symposium, Baden, Germany, 5–9 June 2011. [Google Scholar]
- Kim, D.; Moon, S.; Park, J. Design of an Adaptive Cruise Control/Collision Avoidance with Lane Change Support for Vehicle Autonomous Driving. In Proceedings of the 2009 ICCAS-SICE, Fukuoka, Japan, 18–21 August 2009. [Google Scholar]
- Sayanan, S.; Mohan, T. Dynamic Probabilistic Drivability Maps for Lane Change and Merge Driver Assistance. IEEE Trans. Intell. Transp. 2014, 15, 2063–2073. [Google Scholar]
- Bi, L.; Wang, C.; Yang, X. Detecting Driver Normal and Emergency Lane-Changing Intentions with Queuing Network-Based Driver Models. Int. J. Hun. Comput. Int. 2015, 31, 139–145. [Google Scholar] [CrossRef]
- Hidas, P. Modelling Lane Changing and Merging in Microscopic Traffic Simulation. Transp. Res. C Emer. 2002, 10, 351–371. [Google Scholar] [CrossRef]
- Gipps, P. A Model for the Structure of Lane Changing Decisions. Transp. Res. B Meth. 1986, 20, 403–414. [Google Scholar] [CrossRef]
- Yang, Q.; Koutsopoulos, H. A Microscopic Traffic Simulator for Evaluation of Dynamic Traffic Management Systems. Transp. Res. C Emer. Technol. 1996, 4, 113–129. [Google Scholar] [CrossRef]
- Ahmed, I. Modeling Drivers’ Acceleration and Lane Change Behavior. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1999. [Google Scholar]
- Kanaris, A.; Kosmatopoulos, B.; Loannou, A. Strategies and Spacing Requirements for Lane Changing and Merging in Automated Highway Systems. IEEE Trans. Veh. Technol. 2001, 50, 1568–1581. [Google Scholar] [CrossRef]
- Wang, R.-B.; You, F.; Cui, G.-J. Analysis on Lane-Changing Safety of Vehicle. J. Jilin Univ. Technol. 2005, 2, 179–182. [Google Scholar]
- Qu, D.-Y.; Hei, K.-X.; Guo, H.-B. Game Behavior and Model of Lane-Changing on the Internet of Vehicles Environment. J. Jilin Univ. 2021, 1, 1–11. [Google Scholar]
- Schubert, R.; Schulze, K.; Wanielik, G. Situation Assessment for Automatic Lane-Change Maneuvers. IEEE Trans. Intell. Transp. Syst. 2010, 11, 607–616. [Google Scholar] [CrossRef]
- Ulbrich, S.; Maurer, M. Situation Assessment in Tactical Lane Change Behavior Planning for Automated Vehicles. In Proceedings of the 2015 IEEE 18th International Conference on Intelligent Transportation Systems, Gran Canaria, Spain, 15–18 September 2015. [Google Scholar]
- Wang, J.-Q.; Chai, R.; Cao, N. Modeling Highway Lane Changing Using Bayesian Networks. Mat. Sci. Eng. R 2014, 505, 1143–1147. [Google Scholar] [CrossRef]
- Mccall, C.; Wipf, P.; Trivedi, M. Lane Change Intent Analysis Using Robust Operators and Sparse Bayesian Learning. IEEE Trans. Intell. Transp. 2007, 8, 431–440. [Google Scholar] [CrossRef] [Green Version]
- Maurer, M.; Ulbrich, S. Probabilistic Online POMDP Decision Making for Lane Changes in Fully Automated Driving. In Proceedings of the 2013 IEEE 16th International Conference on Intelligent Transportation Systems, The Hague, The Netherlands, 6–9 October 2013. [Google Scholar]
- Brechtel, S.; Gindele, T.; Dillmann, R. Probabilistic Decision-Making under Uncertainty for Autonomous Driving Using Continuous POMDPs. In Proceedings of the 2014 IEEE 17th International Conference on Intelligent Transportation Systems, Qingdao, China, 8–11 October 2014. [Google Scholar]
- Nilsson, J.; Silvlin, J.; Brannstrom, M. If, When, and How to Perform Lane Change Maneuvers on Highways. IEEE Intel. Transp. Syst. 2016, 8, 68–78. [Google Scholar] [CrossRef]
- Toledo, T.; Koutsopoulos, N.; Ben, M. Estimation of an Integrated Driving Behavior Model. Transport. Res. C Emer. 2009, 17, 365–380. [Google Scholar] [CrossRef]
- Zheng, H.; Rong, J.; Ren, F. A Lane Change Model Based on Utility Selection. J. Highw. Transp. Res. Dev. 2004, 21, 88–91. [Google Scholar]
- Feng, Y.; Pei, Y.; Zhang, Y. Calibration of Selective Lane Change Model Based on Close-range Photogrammetry. J. Harbin Inst. Technol. 2007, 39, 1292–1296. [Google Scholar]
- Long, X.; Tan, Y. Microscopic Simulation of Autonomous Lane Transformation Model. J. Highw. Transp. Res. Dev. 2012, 29, 115–119. [Google Scholar]
- Guo, H.-B.; Qu, D.-Y.; Hong, J.-L. Vehicle Lane Changing Interaction Behavior and Decision Model Based on Utility Theory. Sci. Technol. Eng. 2020, 20, 12185–12190. [Google Scholar]
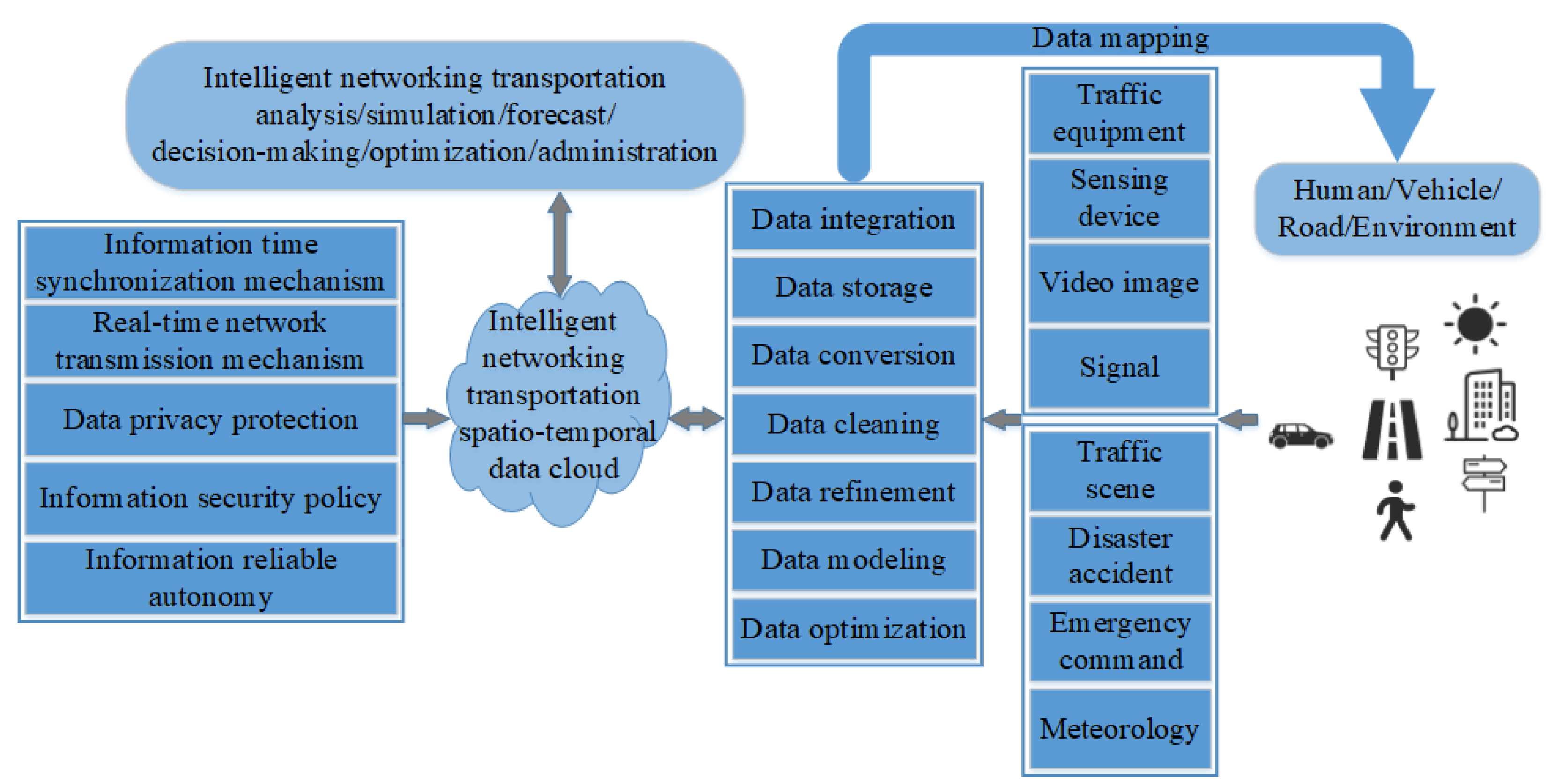
- Zhang, L.; Shen, G.; Qin, X. Information Physics Mapping and System Construction in Intelligent Network Transportation System. J. Tongji Univ. 2022, 50, 79–86. [Google Scholar]
- Luo, Q.; Zang, X.; Cai, X.; Gong, H.; Yuan, J.; Yang, J. Vehicle Lane-Changing Safety Pre-Warning Model under the Environment of the Vehicle Networking. Sustainability 2021, 13, 5146. [Google Scholar] [CrossRef]
- Yang, J.-R. Driving Behavior Characteristics and Models under Vehicle-Infrastructure Cooperation. Master’s Thesis, Qingdao University of Technology, Qingdao, China, 2019. [Google Scholar]
- Li, L.-H.; Gan, J.; Zhou, K. A Novel Lane-Changing Model of Connected and Automated Vehicles: Using the Safety Potential Field Theory. Physica A 2020, 559, 125039. [Google Scholar] [CrossRef]
- Sun, Y.-Q.; Ge, H.-X.; Cheng, R.-J. An Extended Car-Following Model Considering Driver’s Memory and Average Speed of Preceding Vehicles with Control Strategy. Physica A 2019, 521, 752–761. [Google Scholar] [CrossRef]
- Hung, X.-C.; Tang, Y.-S.; Liu, G.-J. Analysis of Driver Lane Change Behavior. Aut. Appl. Technol. 2017, 18, 147–148. [Google Scholar]
- Hei, K.-X.; Qu, D.-Y.; Guo, H.-B. Modeling Lane-Changing Behavior in Mixed Traffic Flow Connected Environment Based on Game Behavior. Sci. Technol. Eng. 2021, 21, 2495–2501. [Google Scholar]
- Wen, C. Coupled Game Theory-Kinematics Decision Making for Automatic Driving Lane Change. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2019. [Google Scholar]
- Pan, W.; Xue, Y.; He, H.-D. Impacts of Traffic Congestion on Fuel Rate, Dissipation and Particle Emission in a Single Lane Based on Nasch Model. Physica A 2018, 503, 154–162. [Google Scholar] [CrossRef]
- Fu, D.-J.; Li, Q.-L. Statistical Analysis of Velocity and Vehicle Spacing in Synchronous Flow Region. J. Anqing Norm. Univ. 2022, 28, 19–25. [Google Scholar]
- Zhou, T.; Zheng, L.-J.; Liu, W.-N. Congestion Control Car-Following Model Considering the Steady-State Expected Speed Effect of Multiple Vehicles. J. Chongqing Univ. 2018, 41, 51–60. [Google Scholar]
- Ou, H.; Tang, T.-Q. Impacts of Moving Bottlenecks on Traffic Flow. Physica A 2018, 500, 131–138. [Google Scholar] [CrossRef]
- Yu, S.-W.; Zhao, X.-M.; Xu, Z.-G. The Effects of Velocity Difference Changes with Memory on the Dynamics Characteristics and Fuel Economy of Traffic Flow. Physica A 2016, 461, 613–628. [Google Scholar] [CrossRef]
- Chen, D.; Hou, L.; Zhu, Q.-Y. Tire-ground Interaction Force Model and Its Parameter Identification Considering Tire Geometry and Pressure. J. Mech. Eng. 2020, 56, 174–183. [Google Scholar]
- Yang, L.-H.; Wang, H.; Li, S. Car-Following Model with Improved Molecular Dynamics. J. Chongqing Univ. 2021, 44, 26–33. [Google Scholar]
- Geng, Z.-F.; Wu, Y.-G. Motion Path Planning Based on Potential Field. Robot 1992, 5, 38–43. [Google Scholar]
- Reuschel, A. Vehicle Movements in a Platoon. Oes. Ing-Atchir. 1950, 4, 193–215. [Google Scholar]
- Li, Y.-K.; Liu, Y. Development Status and Suggestions of Domestic Intelligent Connected Vehicles. Aut. Parts 2016, 41, 56–59. [Google Scholar]
- Meng, X. Research on the Simulation of the Weaving Area on the Urban Expressway under the Mixed Traffic Environment. Master’s Thesis, Jilin University, Changchun, China, 2019. [Google Scholar]
- Ma, G.-Q.; Niu, R.-X.; Li, L.-L. Non-Degree Gradient Ratio Function of Gravity and Magnetic Data for Field-Source Correlation Imaging Method Study. Prog. Geophys. 2021, 36, 2062–2068. [Google Scholar]
- Khatib, O. Real-Time Obstacle Avoidance for Manipulators and Mobile Robots. Ind. Robot 1986, 5, 90–98. [Google Scholar]
- Jia, Y.-F.; Qu, D.-Y.; Zhao, Z.-X. Car-Following Behavior Decision and Model of Networked Autonomous Vehicle Based on Safety Potential Field. J. Transp. Syst. Eng. Inf. Technol. 2022, 22, 85–97. [Google Scholar]
- Qu, D.-Y.; Li, J.; Liu, C. Dynamic Characteristics and Model of Vehicle Flow Based on Molecular Dynamics. J. Transp. Syst. Eng. Inf. Technol. 2017, 17, 188–194. [Google Scholar]
- Li, L.-H.; Gan, J.; Qu, X.; Ran, B. Vehicle Lane Change Model Based on Safety Potential Field Theory in Intelligent Network Environment. China J. Highw. Transp. 2021, 34, 184–195. [Google Scholar]
- Zhao, Z.-X.; Jia, Y.-F. Car-Following Dynamics Characteristics and Model Based on Lennard-Jones Potential. J. Jilin Univ. 2022, 1, 5274056. [Google Scholar]
- Liang, W.-B. Research on Lane-Changing Decision of Autonomous Vehicles in the Connected Environment. Master’s Thesis, Dalian University of Technology, Dalian, China, 2018. [Google Scholar]
- Shi, B.-Y.; Yang, X.-G.; Yu, X.-F. Modeling and Simulation of Discretionary Lane-Change Considering the Combination with the Car-Following Model. J. Transp. Sci. Eng. 2009, 25, 91–96. [Google Scholar]
- Qiu, X.-P.; Ma, L.; Zhou, X.-X.; Yang, D. Study on Mixed Traffic Flow of Manual-Automatic Driving Based on Safety Distance. J. Transp. Syst. Eng. Inf. Technol. 2016, 16, 101–108. [Google Scholar]
- Bing, Q.-C. Molecular Dynamics Characteristics and Models of Vehicle Lane Changing Interaction Behavior. J. Transp. Syst. Eng. Inf. Technol. 2019, 19, 68–74. [Google Scholar]
- Li, J.; Liu, C. Car-Following Characteristics and Its Models Based on Molecular Dynamics. J. Highw. Transp. Res. Dev. 2018, 35, 126–131. [Google Scholar]
- Martin, T.; Arne, K. Estimating Acceleration and Lane-Changing Dynamics from Next Generation Simulation Trajectory Data. Transport. Res. Rec. 2008, 1, 90–101. [Google Scholar]
- Li, J. Study on Traffic Flow Characteristics and Its Model Based on Molecular Dynamics. Master’s Thesis, Qingdao University of Technology, Qingdao, China, 2018. [Google Scholar]
- Qu, D.-Y.; Yang, J.; Chen, X.-F. Molecular Kinetics Behavior of Car-Following and Its Model. J. Jilin Univ. 2012, 42, 1198–1202. [Google Scholar]





| Parameters | Value |
|---|---|
| α | 0.0546 |
| β | 0.0514 |
| μ | 0.0056 |
| Additional Parameters | Range |
|---|---|
| LcSublane | [0, inf] |
| LcPushy | [0, 1] |
| LcAssertive | [0, 1] |
| LcImpatience | [−1, 1] |
| Parameters | SL2015 Lane-Changing Model | Molecular Interaction Potential Lane-Changing Model |
|---|---|---|
| Vehicle length (m) | 4.8 | 4.8 |
| Vehicle width (m) | 1.8 | 1.8 |
| Vehicle color | blue | red |
| Maximum speed (m/s) | 33.33 | 33.33 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, K.; Qu, D.; Song, H.; Wang, T.; Dai, S. Analysis of Lane-Changing Decision-Making Behavior and Molecular Interaction Potential Modeling for Connected and Automated Vehicles. Sustainability 2022, 14, 11049. https://doi.org/10.3390/su141711049
Zhang K, Qu D, Song H, Wang T, Dai S. Analysis of Lane-Changing Decision-Making Behavior and Molecular Interaction Potential Modeling for Connected and Automated Vehicles. Sustainability. 2022; 14(17):11049. https://doi.org/10.3390/su141711049
Chicago/Turabian StyleZhang, Kekun, Dayi Qu, Hui Song, Tao Wang, and Shouchen Dai. 2022. "Analysis of Lane-Changing Decision-Making Behavior and Molecular Interaction Potential Modeling for Connected and Automated Vehicles" Sustainability 14, no. 17: 11049. https://doi.org/10.3390/su141711049
APA StyleZhang, K., Qu, D., Song, H., Wang, T., & Dai, S. (2022). Analysis of Lane-Changing Decision-Making Behavior and Molecular Interaction Potential Modeling for Connected and Automated Vehicles. Sustainability, 14(17), 11049. https://doi.org/10.3390/su141711049








