1. Introduction
In 2020, electric buses were fully popularized in Guangzhou. With the popularization of electrified vehicles, electronic in-vehicle devices with real-time monitoring functions are also gradually popularizing in road transportation vehicles. With the continuous expansion of social construction needs, the number of trucks and their transportation mileage continue to increase. According to statistics [
1], 11,128,000 trucks were owned as of 2020. Although road traffic continues to develop, the safety situation is not optimistic. According to statistics [
1], 244,700 traffic accidents occurred in 2020. To eliminate potential accidents fundamentally, the management department attaches great importance to the supervision of the whole process of traffic operation during the construction of intelligent transportation system. “Two passengers, one danger, and one cargo” refers to chartered vehicles for tourism; three or more class of bus to work; special road vehicles and heavy trucks for transporting hazardous chemicals, fireworks and firecrackers; and civilian explosives. “Two passengers, one danger and one cargo” vehicle accidents are often accompanied by serious losses and are an important supervision object for road transportation production.
To formulate scientific safety improvement programs, exploring the causes of truck traffic accidents is an important issue in the field of traffic safety research. There have been a lot of research results in the analysis of the causes of truck driver accidents. The data sources of related research are mainly divided into three categories: One is to conduct driving experiments based on simulated drivers [
2] or simulation programs [
3] and collect physiological indicators of drivers under hypothetical conditions and corresponding driving behavior. For example, through the collision procedure, experiments with different truck weights and bumper heights were carried out at different speeds to estimate the throw distance after collision with pedestrians [
4]. The second is to analyze the influence of road, environment, traffic flow, and other factors within the research scope by building a statistical model based on historical collision data. Risky driving behaviors, such as aggressive driving, failure to keep to the proper lane [
5], speeding, drowsiness and fatigue, distraction [
6], and inattention have been shown to significantly affect the likelihood of a crash. As expected, seat belt use significantly decreases the severity of a run-off-road crash [
7]. The environment, such as severe weather [
8], wind speed, rainfall, humidity, air temperature [
9], midnight [
10], and other factors, significantly affects the accident rate. Influencing factors also include the driver’s own characteristics, such as age [
11], gender [
12], and weight [
13]. The third is to design a questionnaire that collects the behavioral intentions and personal characteristics of a certain group of truck drivers. For example, with the mediation of attitude toward risky driving, risk perception had a negative influence on the intention, and attitude toward risky driving had a positive influence on the intention [
14]. Factors such as angry driving [
15], compensation [
16], and personality [
14] have all been shown to influence truck drivers’ risky driving behavior.
However, the cost of data collection for simulation experiments is high, and detailed data on historical accidents are generally not available to the public. The lack of third-party management companies with the above data makes it difficult to optimize risky driving-monitoring systems to strengthen the dynamic supervision of road transport vehicles, and prevent and reduce road transport accidents. Guangdong Province has formulated management measures for vehicles with “two passengers, one danger, and one cargo”. First, road transportation enterprises need to install and use intelligent video monitoring and alarm devices that meet the technical standards of Guangdong Province for their passenger vehicles, dangerous goods vehicles, and heavy vehicles and report the monitoring data to the intelligent supervision system in real time through the main link of the equipment. The second is to encourage third-party monitoring agencies to provide professional monitoring services for road transport enterprises. A series of intelligent supervision systems is constructed to reduce the operational risk of road transport vehicles. The intelligent video monitoring and alarm device has functions such as satellite positioning, vehicle video monitoring, advanced driving assistance, and driver status monitoring.
When the vehicle is running, the system can monitor driving risks and bad driving behaviors in real time and issue warnings to the driver. Status warning identification is mainly through preset scenarios, and each warning factor is a separate identification module. When the warning is triggered, the warning event itself has occurred, such as changing lanes across a solid line. The electrified supervision system is part of an advanced driver assistance system (ADAS). Based on the results of one-way analysis of variance, most warnings from ADAS positively affected commercial truck drivers’ behaviors [
17], for example, on safety headway improvement, compliance with lane departure, keeping to the speed limit, and collision avoidance under high-speed driving conditions. The intervention of in-vehicle monitoring system (IVMS) has also been proven to be beneficial to reducing risky driving behavior [
18]. The results showed that the combination of risk training can optimize the intervention effect of driving warning on risky driving. However, different alarming behaviors are always classified as risky behaviors, and the internal correlation between them lacks research.
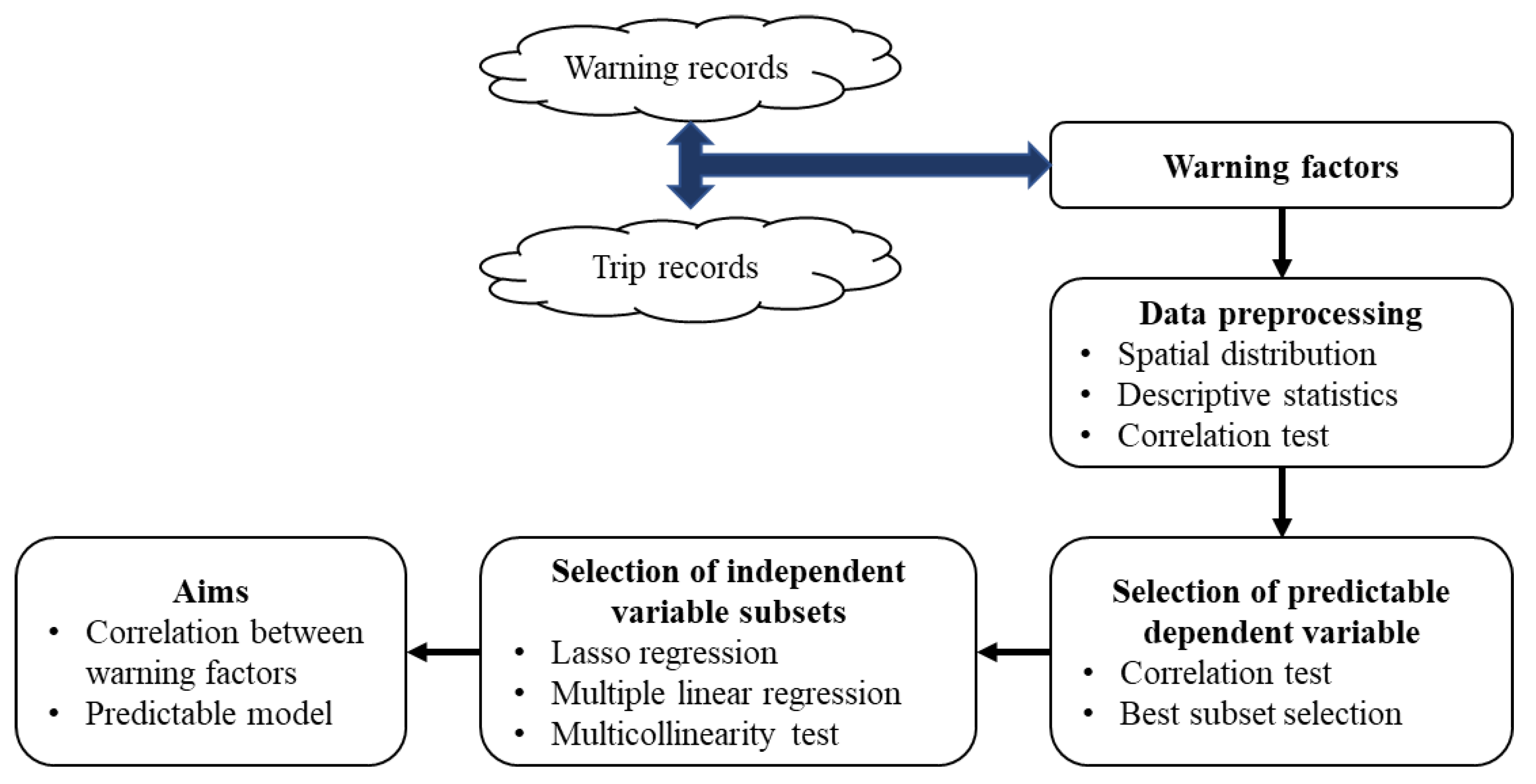
To further optimize the warning system, it is necessary to explore more factors that lead to the occurrence of warnings, rather than relying only on identifying whether the event has occurred. The third-party supervision platform needs to regularly provide feedback on the operation report to the operating company based on the historical warning records. The purpose of this paper is to analyze the internal correlation between different warning behaviors based on the existing large number of alarm records and trip records of third-party-platform companies. The model was constructed using multiple linear regression equations that can intuitively explain the influence between variables. The optimal subset method was used to discover potential combinations of variables that could be used to build a model, and Lasso regression was used to reduce the number of model variables.
Figure 1 is the framework of the research.
2. Literature Review
Heavy construction trucks generally refers to heavy trucks that transport soil and stone and other infrastructure materials for construction sites. Wages for such drivers are calculated by the number of trips and weight. Excessive driving and speeding are rampant for better pay. Due to the serious traffic accident losses of heavy construction trucks, the insurance of the vehicles is much higher than that of ordinary vehicles [
19]. Research on heavy construction trucks is mainly divided into two categories. One is to study the optimization of scheduling to improve engineering efficiency [
20]. Among them, the “Truck+” platform integrates a global positioning system (GPS) and geographic information system (GIS) through intelligent vehicle-mounted equipment. Implemented monitoring and forecasting productivity function for project teams [
21]. Shehadeh et al. built an earthwork model based on a genetic algorithm to reduce the time and cost of earthwork [
22]. The second is to study the impact of the driving process of heavy construction trucks on the health of drivers [
23]. Burgess-Limerick and Lynas [
24] confirmed that operators of dozers and off-road haul trucks in use at surface coal mines are frequently exposed to vertical whole-body vibration levels that lie within or above the Health Guidance Caution Zone defined by ISO2631.1.
With the popularity of driver-assistance systems, research has expanded to geospatial analysis based on geographic information data. A comparative analysis found that road sections greater than 20 miles from a rest area were more prone to accidents [
25]. Compared with natural driving, the data obtained based on collision reconstruction has inherent limitations [
26], and historical collision data are prone to missing records of key information. By loading the natural driving data collected by intelligent vehicle equipment, not only is the information collected when the event occurs, but the most realistic driving state can also be restored. Research in natural driving has shown that the warning of rear-end collisions by in-vehicle collision warning systems enables drivers to react faster in the face of conflicts than without warning [
27].
Due to the randomness and variability of collision accidents, scholars search for more frequent and more observable traffic characteristics than collision accidents for safety analysis. For example, the occurrence of accidents is predicted by building a traffic conflict index model, such as time-to-collision (TTC), post-encroachment time (PET), and other indicators. The analysis found that the Pearson correlation coefficient between the recurrence level of millions of lane-change accidents and the number of real traffic accident was significantly correlated (β = 0.77). It proved the effectiveness of traffic conflict technology in predicting accidents [
28]. Although there is no direct evidence for the predictive effectiveness of warning frequency on accidents, there is no doubt that research is necessary.
In terms of model methods, statistical models are mainly constructed based on discrete variables. Most of these studies classify the response variables reflecting collisions as categorical variables. For example, truck drivers are divided into three categories, namely, “middle-aged and elderly drivers with low risk of driving violations and high historical accident records”, “high risk of driving violations and high historical accident records”, and “middle-aged drivers with no record of driving violations and historical accident records” to construct an ordered logit model [
29] or classify by accident severity, such as dividing truck drivers into three categories of injury levels [
30]. Various logistic regression models [
31,
32] are commonly used models. Further studies have shown that complex models have better performance. For example, the mixed logit model has better performance than the polynomial logit model [
12]. There is also a model combined with machine learning models, such as a complementary model of random parameter binary logit (RPBL) and support vector machine (SVM) [
33]. The same variable has different importance in different models, and complementary models make the model more applicable. Chen et al. [
30] regarded that a disadvantage of finite mixture models is that they neglect the observation heterogeneity within each data group due to the assumption of observation homogeneity in each group. A hierarchical Bayesian multinominal logit model with a random intercept setting was utilized to effectively examine attribute influence as well as the unobserved variance in multi-level data analyses. The results of the regression model can directly reflect the influence of different factors on the collision and have strong interpretability.
Compared with the frequency of traffic accidents, the risk warning of heavy construction trucks occurs more frequently and is easier to observe. However, there are no fixed routes for heavy construction trucks in the city, and the corresponding road attributes are also difficult to obtain. To this end, this paper conducted factor correlation analysis based on the warning records and trip records of a third-party supervision platform in the second half of 2021. The warning records were labelled according to the number of running trips. A regression model was established to quantitatively explain the relationship between the occurrence frequencies of various types of warnings. When there is a causal relationship between different warning factors, the early warning platform needs to consider adjusting the triggering principle of the warning factors. At the same time, it provides a reference for the formulation of the driver evaluation system.
3. Materials and Methods
3.1. Data Preprocessing
This study selected the warning records and trip records of 17 heavy construction trucks from July to December 2021. The 17 heavy construction trucks came from two small earth and stone transportation enterprises in Guangzhou and covered the intelligent supervision system according to the management measures. Through the third-party supervision platform, not only can real-time data be obtained, but historical monitoring data can also be traced back. From the platform’s Evidence Center, the information in
Table 1 was obtained. The table of warning records contains 20 fields, and the table of trip records contains 12 fields. Among them, there are 24 types of warning, with a total of 279,798 warning records. The details are shown in
Table 2. The personal information of the drivers of each vehicle is not available and is not considered in this paper, although they may lead to differences in behavior, such as the driver’s age, gender, and driving experience.
In principle, the system will record the corresponding evidence as pictures or videos. After deleting the false warning records, 279,424 pieces of data remained. According to the evidence, it was found that there were several warning factors that had no actual significance to warn, and four invalid warning factors were deleted. Specifically, most of the data of “pedestrian collision” and “driver behavior monitoring function fails” were missing. “Driver abnormal” means that the driver leaves the monitoring view due to device movement, which is meaningless. “Right rear approach” had a very high error rate in identifying objects and could only be judged manually. Eight factors without data were deleted, namely, “frequent lane changes”, “road sign overrun”, “obstacle”, “assisted-driving fails”, “pedestrian detection in carriageway”, “driver mismatch (platform)”, “overtime driving”, and “infrared-blocking sunglasses fail”. In the end, there were 12 effective warning factors, with a total of 88,841 warning records, which are divided into two categories: trajectory abnormality and driving behavior abnormality.
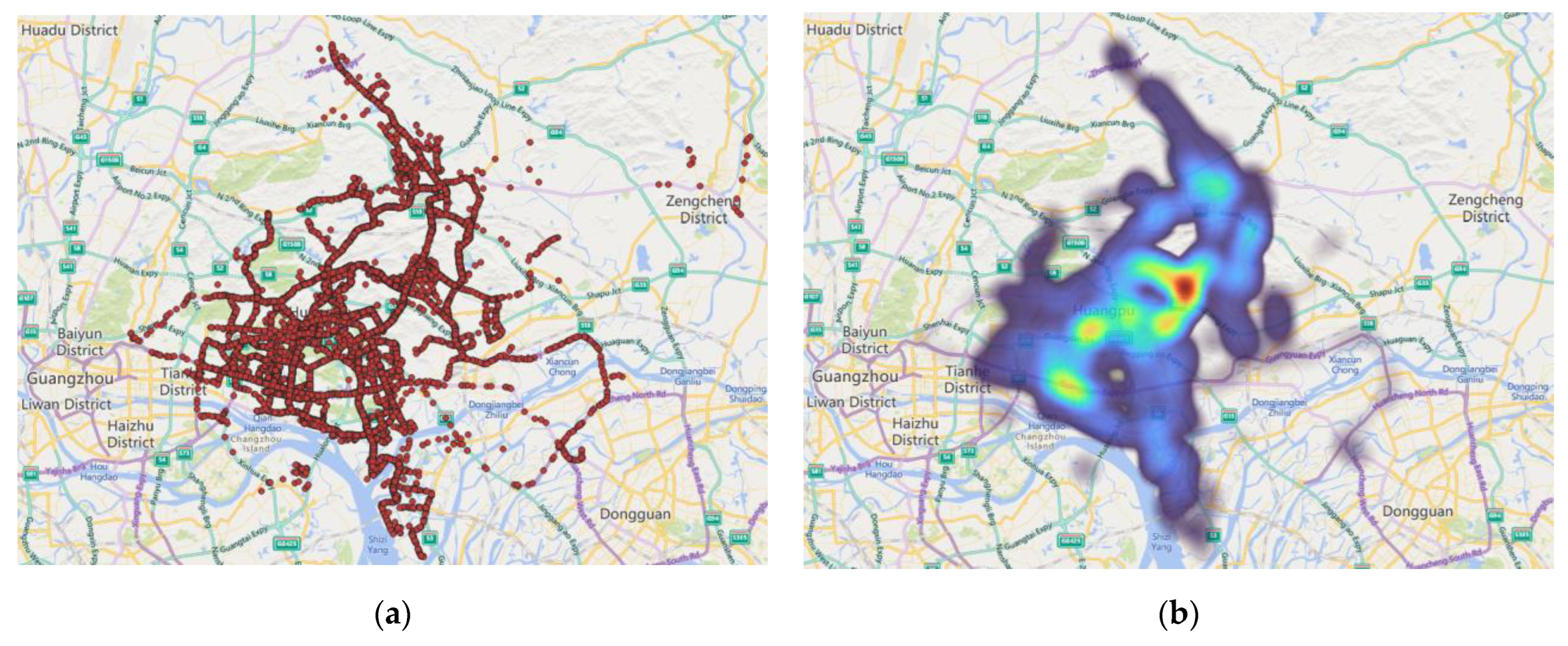
According to the latitude and longitude of the warning records, it was found that 22 records were not in line with reality, so they were deleted. As shown in
Figure 2, QGIS3.20.2 was used to draw a spatial distribution map and heat map based on the latitude and longitude. Due to the lack of information on road attributes, spatial correlation analysis was not carried out in this study. To perform correlation analysis between different factors, it is necessary to merge the data in two tables. In this paper, a trip is taken as the sample collection unit. First, trips with no warning, trips lack of speed information, and trips with abnormal speed were deleted. The number of remaining samples was 1033. According to research experience, the number of samples should be greater than 10 times the number of variables [
34]. According to the central limit theorem, each group of samples should be greater than 30. There were 1033 valid samples for 17 vehicles, and each vehicle had more than 30 samples. This sample size can be considered reasonable. The second step was to add the corresponding trip label to each warning record by comparing the license plate and time. The third step was to count the occurrences of different warning factors for each trip. In the end, three variables representing vehicle operation and 12 variables representing warning factors were obtained, and all were considered continuous variables. As mentioned in the literature review, many factors (such as traffic flow density, road type, driving speed, etc.) may have an influence on certain behaviors of drivers. During the whole trip of a heavy truck, the traffic flow density and road type are always changing. The average speed and maximum speed of the operation are considered, but other factors will not be considered in this article.
Descriptive statistical analysis was performed on the sorted data, as shown in
Table 3. The median and minimum values of most warning factors were basically the same, and both were 0. From the counts of each variable, “lane change across solid line” was the most, followed by “too close distance” and “not wearing seat belt” the least. It reflected the actual situation that the driver competed for the right of way on the premise of shortening the journey. Obviously, the warning variable contained many zero values and did not conform to the normal distribution. Therefore, the Spearman correlation coefficient was used for binary correlation analysis. The Spearman correlation coefficient uses the rank of the original value to calculate the product-difference correlation coefficient. The correlation test of these explanatory variables was carried out by SPSS 26, and the results are shown in
Table 4. The results showed that the absolute values of the Spearman correlation coefficients between t1 (forward collision) and t3 (too close distance), and t3 and t4 (lane change across solid line) were greater than 0.6. That is, there was a large linear correlation between these variables. When constructing regression models, it is important to focus on collinearity between these variables to avoid significant correlations that negatively affect coefficient estimates.
3.2. Multiple Linear Regression
Due to the lack of research about relevant data for reference, this paper conducted a series of exploratory studies. The multiple linear regression model is used to study the relationship between dependent variables and multiple explanatory variables, and its general form is as in Formula (1). The model estimation method adopts the least square method. Multiple linear regression is based on the following assumptions:
There is a linear relationship between the dependent and explanatory independent variables.
The independent variables are not highly correlated with each other.
The variance of the residuals is constant.
The observations should be independent of one another.
Multivariate normality occurs when residuals are normally distributed.
In Formula (1), y is the dependent or predictor variable and are the explanatory variables, k is the number of explanatory variables, are the corresponding coefficients, is the intercept, and is the random error term.
Let ω = [
], X = [
]; it can also be expressed as the following matrix form:
3.3. Variable Selection
In machine learning, variable selection, also known as feature selection, is the process of selecting a subset of relevant features from a given set of features. Among them, the attributes that are useful for the current learning task are called “relevant features”, otherwise they are called “irrelevant features”. The purpose of feature selection is to reduce the complexity of the model and improve the generality of the model. This paper used best subset selection and least absolute shrinkage and selection operator (Lasso) regression methods for feature selection. Feature selection mainly has the following four steps:
Generating a candidate set of features subsets;
Evaluation function to evaluate the performance of different feature subsets;
Setting a threshold and stopping when the evaluation function value reaches the threshold;
Verifying the validity of the optimal feature subset.
3.3.1. Best Subset Selection
Optimal subset selection is a basic method for independent variable selection of multiple linear regression equations. The selection process is as follows:
Step 1: Assuming that there are k features, start from the null model M0 with only the intercept term.
Step 2: Fit the model with different feature combinations. When the number of variables is fixed, there are the best combinations of factors corresponding to the number of variables is achieved. Models M1, M2, …, Mk are obtained by calculating the best combination of the number of variables from 1 to k. The model is optimal when the degree of freedom adjustment complex decision coefficient ( is the largest in this paper.
Step 3: Generally, the cross-check error, the Bayesian information criterion (BIC), Cp [
35], or adjusted R
2 are used to select the optimal model among the k + 1 models obtained in step 1. In this paper,
was used to determine the optimal model. The formula for
is shown in Equation (3).
In Formula (3), n is the sample size, k is the number of explanatory variables, TSS is the total sum of squares, RSS is the residual sum of squares, is the observations of y, is the predicted value of y, and is the mean of the observations of y.
The advantage of this method is that the principle is simple and the result is globally optimal. The disadvantage is that 2 to the power of k models need to be fitted, and the amount of calculation increases exponentially.
3.3.2. Lasso Regression
The Lasso regression method is a compressed estimation method proposed by [
36] to replace the least squares method. Lasso regression prevents overfitting by adding an L1 penalty term to the regression coefficients, reducing the degree of variation and improving the accuracy of linear regression models. Due to the penalty value, some parameter estimation results are 0, which achieves the purpose of feature selecting. The objective function of its minimization is shown in Formula (3).
In Formula (3), n is the sample size, λ is the shrinkage parameter, and . When λ is larger, the penalty is stronger and fewer variables will be retained in the model. As λ decreases, more and more variables are retained in the model until significant variables appear sequentially.
3.4. Multicollinearity Test
From the binary correlation test, we can know that there was a significant correlation between some independent variables. If an independent variable is a linear organization of one or several other independent variables, there is multicollinearity among those independent variables. To reduce the influence of multicollinearity on the coefficient estimates, we needed to test the model for collinearity. Variance inflation factor (VIF) can characterize the degree of collinearity between independent variables, and its value can reflect whether there is multicollinearity between the investigated variables. A VIF value above 10 is usually referred to as an indication that multicollinearity exists [
37]. However, the VIF values of all investigated variables in the models were less than three, indicating no multicollinearity problem. The calculation formula of VIF is shown in Formula (4).
In Formula (4), is the square of the complex correlation coefficient of to the remaining p-1 independent variables .
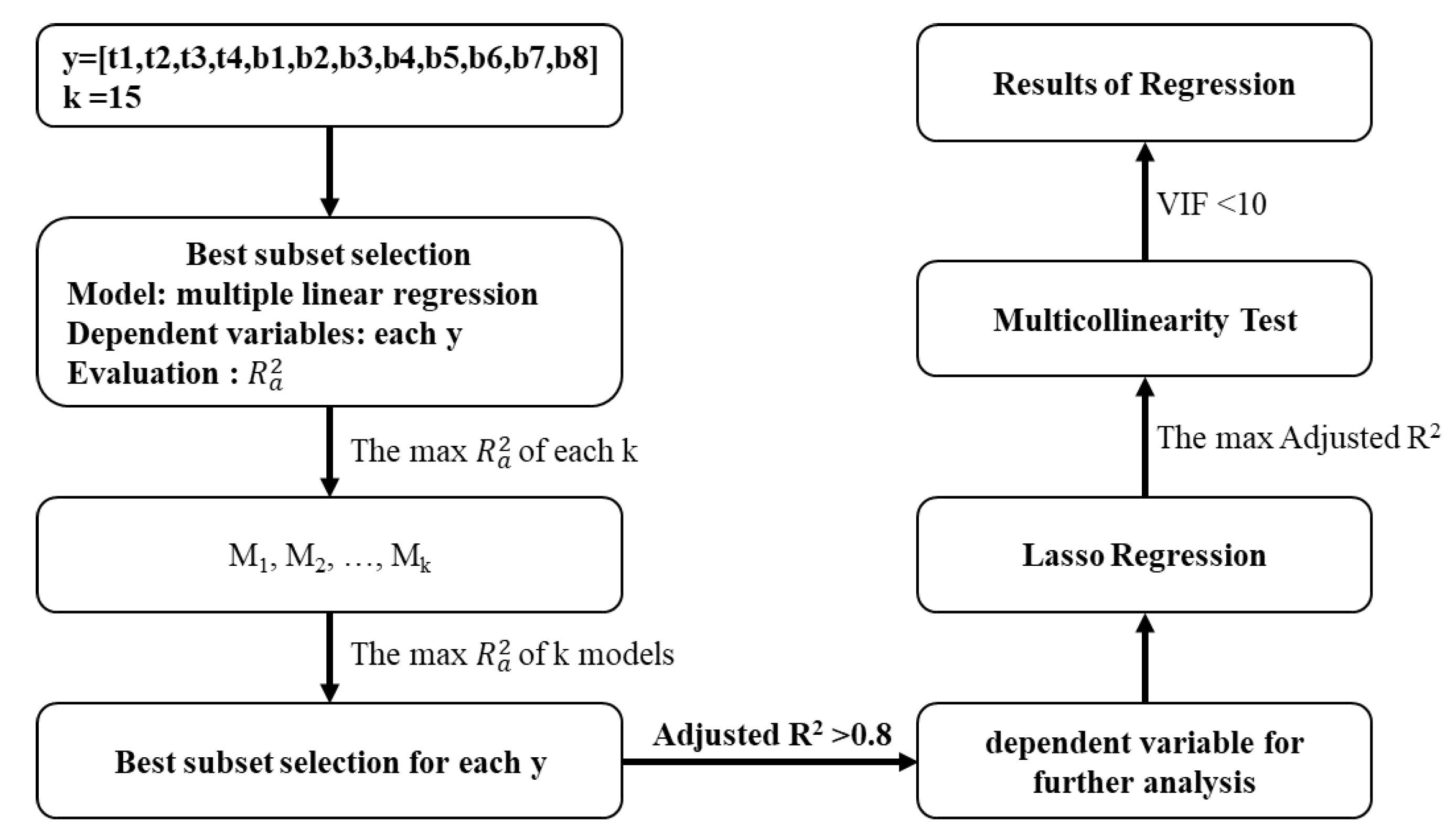
From the results in
Table 4, there was a weak correlation between multiple groups of variables. To further analyze the correlation between variables, a multiple regression model was constructed according to the process in
Figure 3. Firstly, 12 warning variables were set as dependent variables, and the best explanatory variable combination for each dependent variable was screened out by the optimal subset method. Secondly, the adjusted R-square was used to determine the dependent variable for further analysis. Thirdly, Lasso regression was used to screen the explanatory variables for the dependent variables selected in the previous step. Finally, the VIF coefficient was used to judge the collinearity among the explanatory variables.
In Formula (6), n is the sample size, and k is the number of explanatory variables.
5. Discussion
5.1. Too Close Distance
The study showed that following too closely significantly increased the odds of being involved in a crash by 1.34 times for truck drivers [
26]. It is very necessary to strengthen the management of the “too close distance” behavior. According to
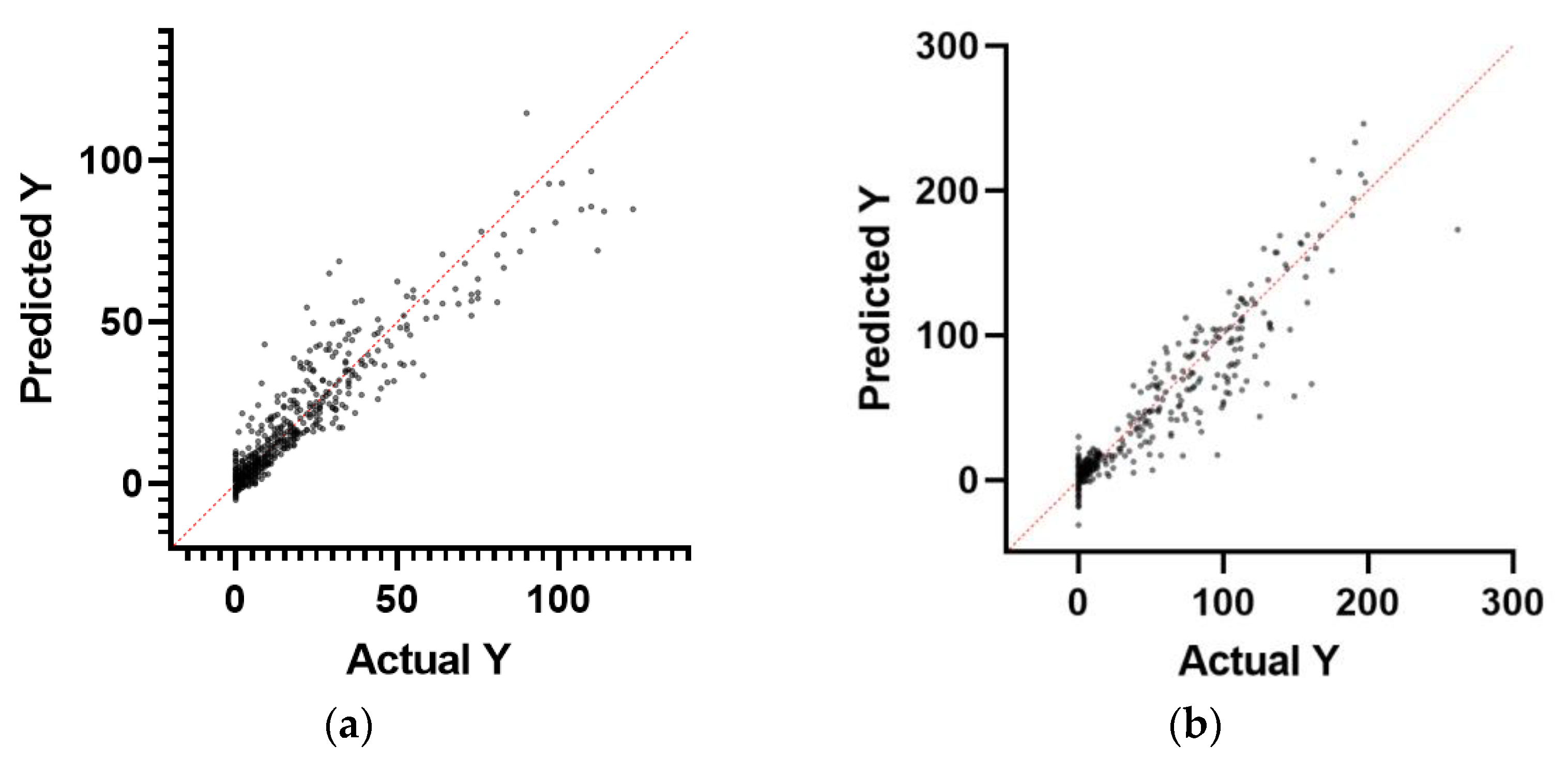
Table 7, max speed, t1 (forward collision), t4 (lane change across solid line), and b2 (answering calls) were positively correlated with t3 (too close distance). The largest regression coefficients were b2 (0.773), followed by t1 (0.622) and t4 (0.429). Due to multivariate effects, the positive and negative regression coefficients differed from those in the binary correlation analysis.
“Too close distance” is one of the embodiments of aggressive driving behavior [
39]. Research shows that angry driving [
40] and neuroticism [
41] are positively correlated with aggressive driving behavior. This result showed that when drivers compete for the right of way to shorten the travel time, they will frequently illegally change lanes and accelerate frequently. The forward collision warning is determined according to the collision time between the two vehicles. When the driver ignores the forward collision warning and does not slow down, the “too close warning” will be triggered. When the driver answers the phone, the driver’s attention will be distracted. The study showed that more mobile phone use causes more driving errors like speeding and collisions [
42]. It is difficult to maintain a safe distance from the vehicle in front.
Average speed, b1 (fatigue), and b3 (smoking) were negatively correlated with t3. Since urban roads are often crowded, the average speed drops when vehicles travel in congested traffic. At the same time, in order not to be cut in the queue, the distance at which it is difficult to be overtaken is maintained, which often triggers an “too close distance” warning. When the driver smokes or is in a state of fatigue, the attention is relaxed, and the awareness of competing for the right of way decreases. The initiative of the vehicle in front decreases, and the situation that the distance between the vehicles is too close is reduced. If the driver of t3 often occurs in the past driving, but suddenly does not occur in one instance of driving, it is worth paying attention to whether the driver is driving while fatigued.
5.2. Lane Change across Solid Line
“Lane change across solid line” is also one of the embodiments of aggressive driving behavior [
39]. According to
Table 8, average speed, t3 (too close distance), b3 (smoking), and b7 (hands-off driving) were positively correlated with t4 (lane change across solid line). The largest regression coefficients were t3 (1.918), followed by b3 (1.089) and average speed (0.233). Solid lines are usually set on road sections where interweaving traffic should be avoided for safety, such as ramps, tunnels, entry lanes, and single lanes. These sections also often have speed limits. The study showed that higher average speeds increased risk of inattention [
43]. To shorten the travel time, the driver must take the risk of being too close and having a higher speed to complete the lane change and overtaking. Surprisingly, behaviors such as “smoking” and “hands-off driving” led to more “lane change across solid line”. Drivers who smoke or take their hands away while driving are always confident in their driving.
Max speed, t1 (forward collision), t2 (lane departure), b2 (answering calls), b5 (probe occlusion), and b8 (playing phone) were negatively correlated with t4. T1 (−1.155) had the largest negative influence on t4, followed by b8 (−1.094) and b5 (0.826). “Lane change across solid line” is a behavior of drivers to actively change the original trajectory, which requires a certain amount of attention to complete such planned behavior. The study showed that most non-distracted single drivers were more likely to perceive their behavior as aggressive, as opposed to distracted drivers, who were overall less likely to perceive that they drove aggressively. Obviously, behaviors such as playing phones, answering calls, and blocking probes affect the driver’s concentration, and it is difficult to consider the lane changing behavior at the same time. The negative effects of “forward collision” warning and “lane departure” on t4 are difficult to explain. However, when the driver is unwilling to reduce the speed to safely follow the vehicle in front after the forward collision warning occurs, changing lanes is one way to stop the forward collision warning from continuing.
In addition, in practical work, we focus not only on the frequency of warnings, but also on whether warning events will occur. In this paper, the regression model was used to estimate the occurrence frequency of warning events. The frequency of most warnings was 0. In further research, this problem can be transformed into a binary classification problem, that is, of whether the warning event will occur.
6. Conclusions
Since the popularization of electrified supervision system has just begun, there is still little research on the internal correlation of warning behaviors recorded by supervision systems. The research in this paper attempts to fill the gaps. Firstly, the visualization of the spatial distribution of early warning points was carried out. Secondly, the construction of multivariate linear model and variable screening was carried out. Lane changing across a solid line is a driving violation, and if the distance between vehicles is too close, the probability of accidents will be greatly increased. The occurrence of “answering calls” and “forward collision” will be accompanied mainly by more occurrence of “too close distance”. The occurrence of “too close distance” is reduced when behaviors indicative of decreased attention, such as “fatigue” and “smoking”, are engaged in The occurrence of “too close distance” and “smoking” will be accompanied mainly by more occurrence of “lane change across solid line”, and the occurrence of “lane change across solid line” is reduced when behaviors indicative of decreased attention, such as “probe occlusion”, “answering calls”, and “playing with phone”, occur. Overall, distracted behaviors had a significant impact on aggressive driving behavior. Subsequent studies investigating aggressive driving behavior need to consider more historical monitoring or self-reported distracted behavior.
Based on the above results and analysis, the mechanism for triggering t3 (too close distance) and t4 (lane change across solid line) warnings should consider other relevant warning factors. For example, based on the cumulative warning frequency of related warning factors, when the predicted value of the dependent variable is greater than a threshold (such as 1), the driver can be reminded to reduce the occurrence of warnings. When formulating the driver evaluation system, the weight of the factors that bring concurrent warning should be increased. The specific implementation needs more analysis and testing. The causes of warning factors should include the driver’s own characteristics and road attributes. The correlation of early warning behavior studied in this paper has information limitations.