Genetic Algorithm-Optimized Adaptive Network Fuzzy Inference System-Based VSG Controller for Sustainable Operation of Distribution System

Abstract

To achieve a more sustainable supply of electricity and reduce dependency on fuels, the application of renewable energy sources-based distribution systems (DS) is stimulating. However, the intermittent nature of renewable sources reduces the overall inertia of the power system, which in turn seriously affects the frequency stability of the power system. A virtual synchronous generator can provide inertial response support to a DS. However, existing active power controllers of VSG are not optimized to react to the variation of frequency changes in the power system. Hence this paper introduces a new controller by incorporating GA-ANFIS in the active power controller to improve the performance of the VSG. The advantage of the proposed ANFIS-based controller is its ability to optimize the membership function in order to provide a better range and accuracy for the VSG responses. Rate of change of frequency (ROCOF) and change in frequency are used as the inputs of the proposed controller to control the values of two swing equation parameters, inertia constant (J) and damping constant (D). Two objective functions are used to optimize the membership function in the ANFIS. Transient simulation is carried out in PSCAD/EMTDC to validate the performance of the controller. For all the scenarios, VSG with GA-ANFIS (VOFIS) managed to maintain the DS frequency within the safe operating limit. A comparison between three other controllers proved that the proposed VSG controller is better than the other controller, with a transient response of 22% faster compared to the other controllers.

1. Introduction

The desire to “Go Green”due to worries about the shrinking non-renewable energy sources and the preservation of the environment has substantially increased the use of renewable energy sources (RES) for electric power generation. In addition, to be in line with United Nations Sustainable Development Goal (SDG) and ensure access to affordable, reliable, sustainable, and modern energy for all, the use of RES is increasing [1]. In this regard, most countries have set a target to achieve a renewable energy mix in their total generation by 2030, which has resulted in an increase in the level of distributed generation (DG). For instance, Malaysia has given the regulations to realize a 31% objective from the entire share of energy from RES [2] by 2025. DG has been the impetus in the transformation of the traditional distribution scheme to a much more green, sustainable, flexible, reliable, and efficient power distribution scheme known as distributed system (DS). The introduction of DS into the power system helps to promote the usage of RES. Furthermore, power losses in the system could be reduced with power generation closer to the load points. Moreover, DS can reduce peak power generation from the centralized coal-fired power plant. Thus, reducing the emission of greenhouse gases.

Nevertheless, DS has many issues that need to be addressed pertaining to their voltage and frequency standard [3], especially during islanding. For DS to be independent of the main grid, it needs to solve the lack of power inertia problem in its power system [4]. The main sources of power generation in a DS come from solar power, small wind turbines, a battery energy storage system, and mini hydro power, all of which have little to no inertia reserve. During islanding, DS based on RES could not react to any sudden changes during the inertial period of frequency responses. DS-based RESs are connected to the power system via a power converter that does not offer inertia support like a conventional synchronous generator (SG). Even the process of (sudden) islanding for a low inertia DS would cause spikes in frequency and risk damaging critical equipment in the DSs. One way to maintain the stability of the DS is to introduce ancillary service that can inject artificial inertia into the network.

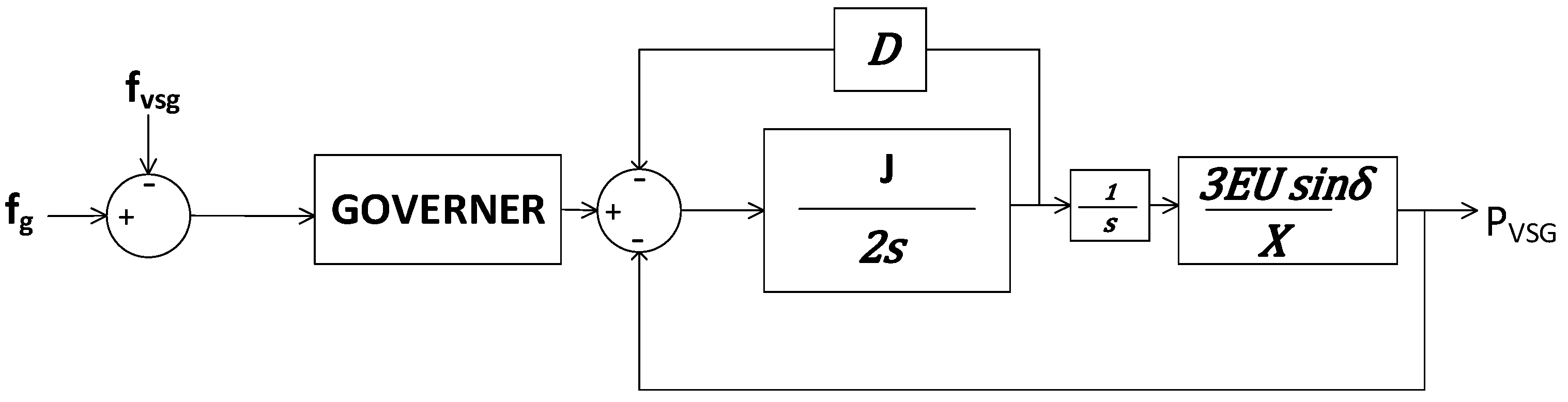
A few solutions were introduced to mitigate low inertia power systems, namely virtual synchronous generator (VSG). VSG is a concept that modeled a cylindrical-rotor-type SG architecture. It was first proposed in the European project “VSYNC” [3]. The swing equation in SG is used to calculate the VSG inertial response. In an SG, these parameters are determined by the rotational kinetic energy stored in the rotor at a certain rated speed. These parameters cannot be changed unless one changes the physical component of the rotor. However, in a VSG controller, these parameters are not constrained to any physical limitation. Therefore, they can be adjusted in real-time to improve and optimize the controller performance. A variety of VSG controller methods have been reviewed, ranging from conventional to intelligence techniques [5]. Initially, VSG used a droop controller to regulate the inertia response [6]. An improved droop controller was introduced, which helped to reduce the frequency nadir, but the droop controller alone could not solve the oscillation problem that occurs after each VSG injection.

Alternating methods were proposed to improve the dynamic performance of VSG inertial response. Large inertia is needed to overcome the high rate of change of frequency (ROCOF), while low inertia is needed to subdue the oscillation. By adjusting the key parameters in the VSG controller, the oscillation problem is reduced. Thus, VSG with an alternating moment of inertia was introduced to compensate for the problem from the droop controller by damping the power oscillation after each VSG response. However, the proposed technique switched between small and big virtual inertia value [7], which limit the range of the VSG inertia support. Another concept to mitigate the power oscillation problem is by alternating the damping constant of the VSG controller. However, it does not reduce the frequency of nadir during high ROCOF [8]. The time for the frequency to recover to its nominal frequency is too long. Although it helps reduce the oscillation, it takes a longer time to stabilize and return to nominal frequency. Consequently, the addition of a fuzzy inference system (FIS) in the VSG controller was proposed to regulate the alternating value of inertia. A variety of FIS techniques have been used to improve the VSG concept. FIS in [9] regulated the VSG output only from the ROCOF value. With a fixed range of membership functions (MF), the FIS proposed was unable to cover a wide range of over- and under-frequency events. In [10], optimization of FIS was applied to regulate only the oscillation of VSG injection. In contrast, FIS in [11] was used to generate active and reactive power references for VSG according to the DS connection mode. However, the FIS design had too many inputs and the input MF were not optimized, resulting limited VSG range response.

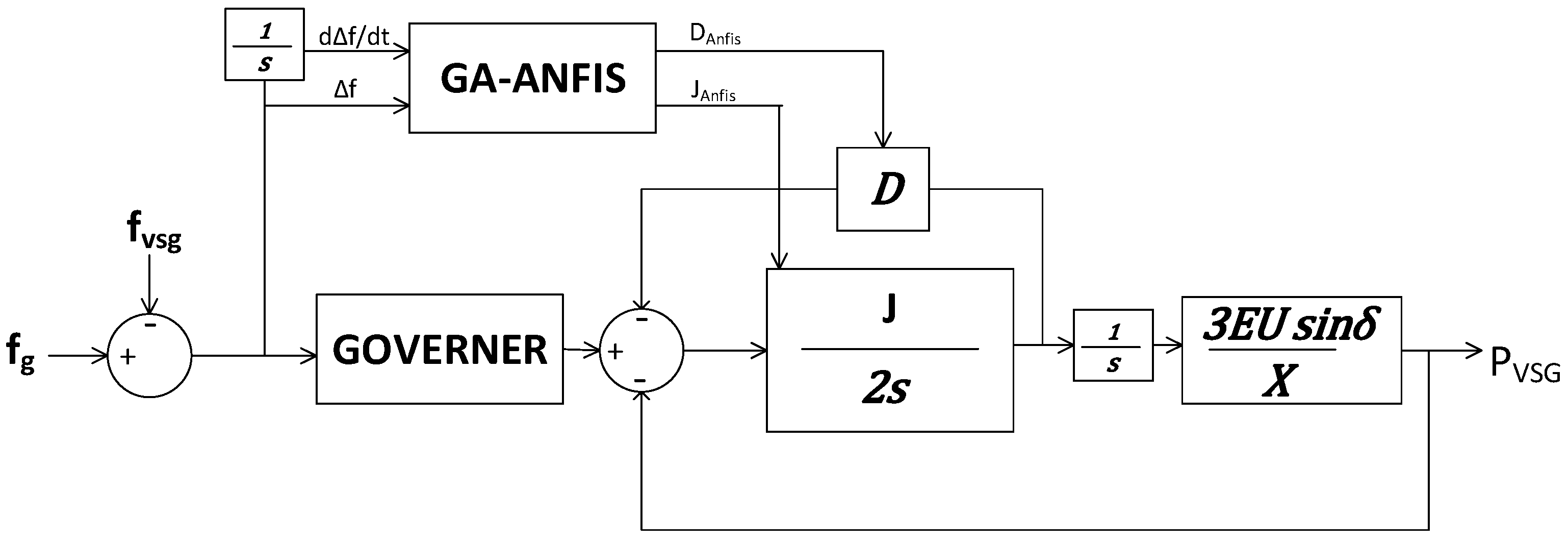
There is no work being carried out to optimize the membership function of a fuzzy inference system (FIS) for the active power controller in VSG. Either the input MF or the output MF. By optimizing both the input and output MF, a wide range of responses and input scenarios could be managed in real-time by scheduling through FIS. FIS will optimize and update the MF whenever the system responses are out of the safe operating region. Instead of continuous MF optimization, most controllers change the values of J and D in a linear or flip-flop manner.

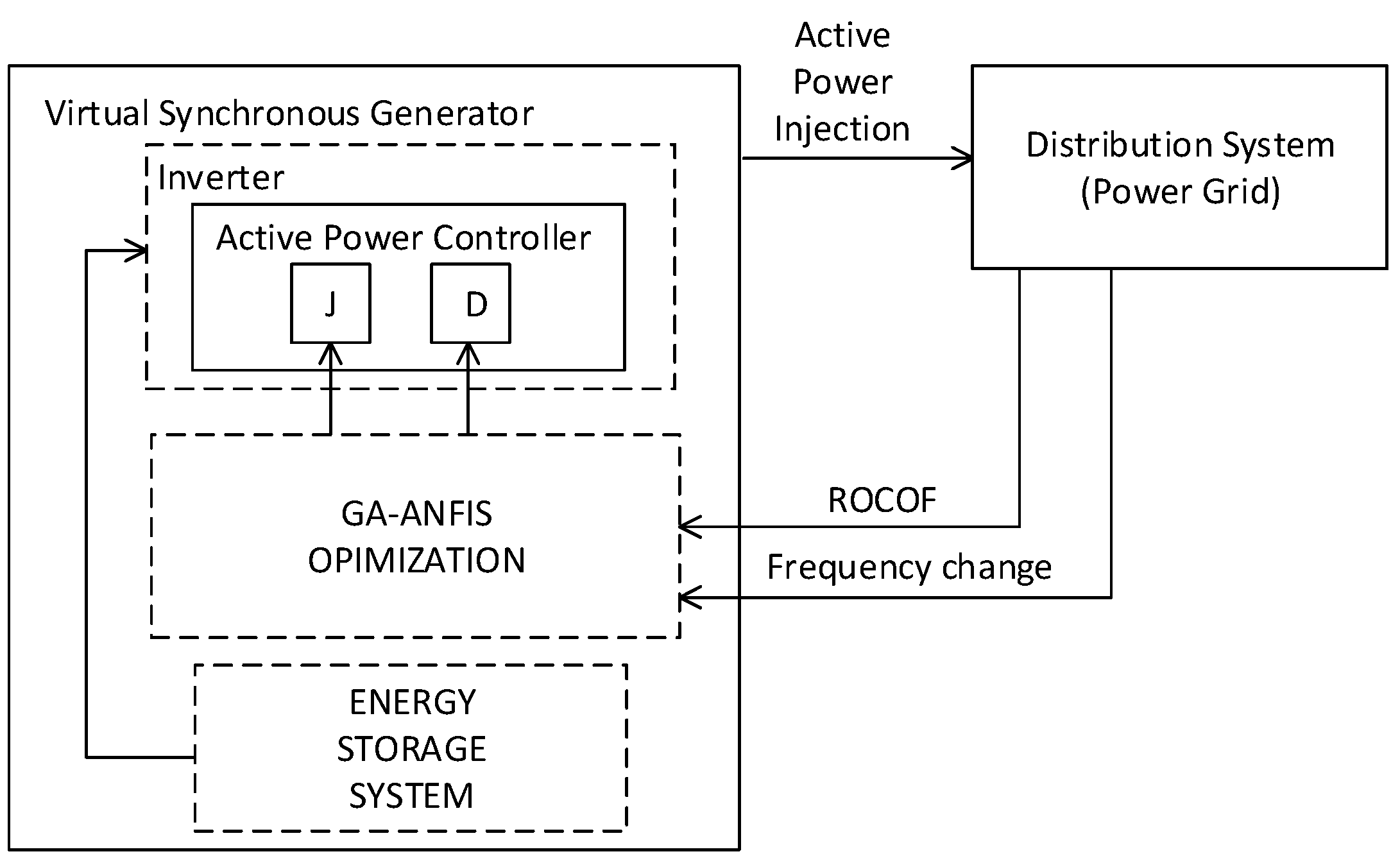
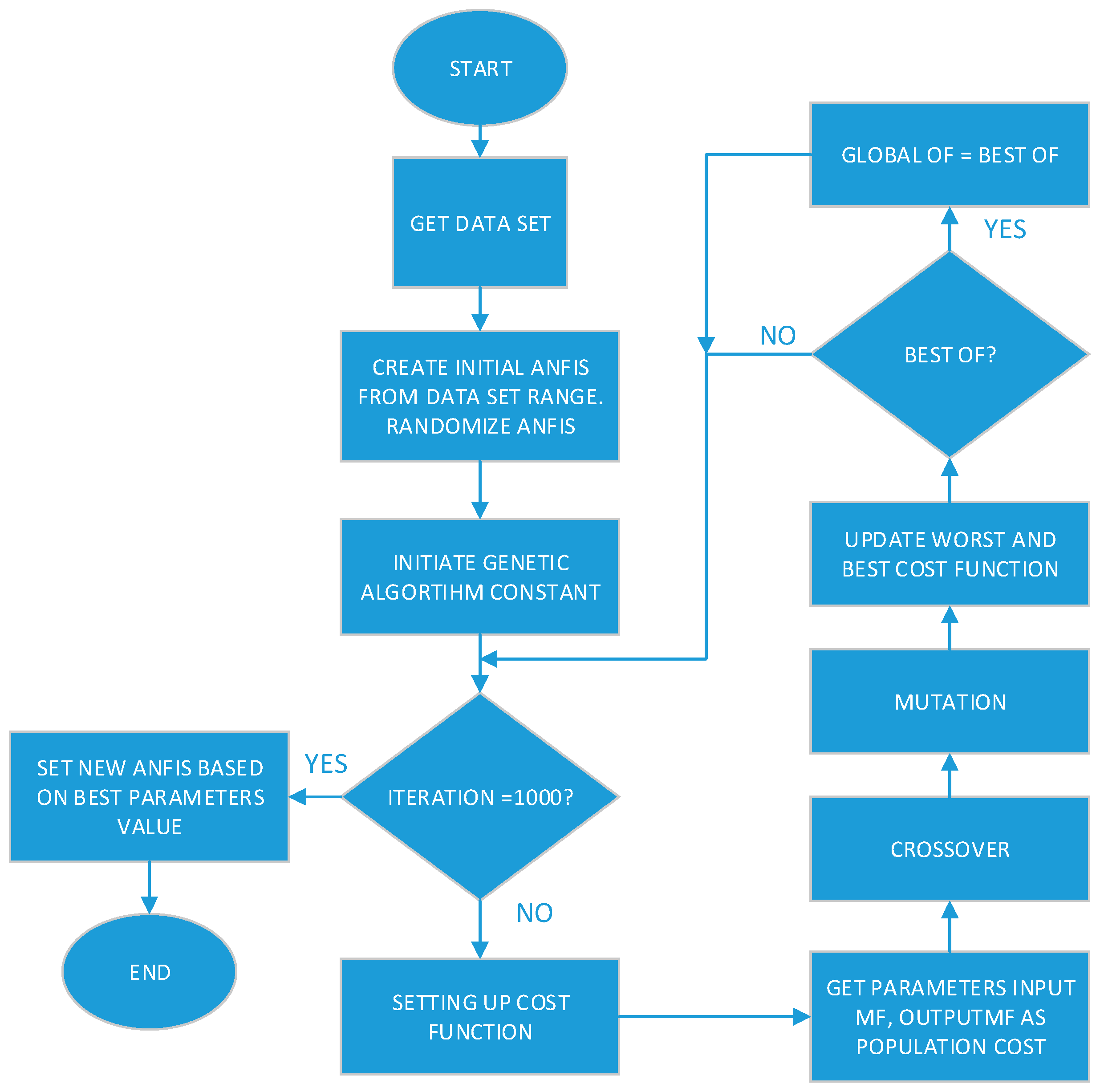
Considering the limitations of the previous VSG controllers, this paper proposes a new controller, which incorporates a genetic algorithm (GA) optimized adaptive network-based fuzzy inference system (ANFIS) to improve the performance of the active power controller in VSG. Two parameters of VSG’s swing equation, namely inertia constant, J, and damping constant, D, are optimized to give a wide range of VSG responses. The input parameters for ANFIS are the rate of change of frequency (ROCOF) and the change in frequency. While the output parameters for ANFIS are inertia constant, J, and damping constant, D. Membership function (MF) used for both the input and output are gauss MF. GA is used to optimize the MF for both the input and output of ANFIS. As a result, both input and output MF are heuristically designed to manage a wide range of interruptions and responses.

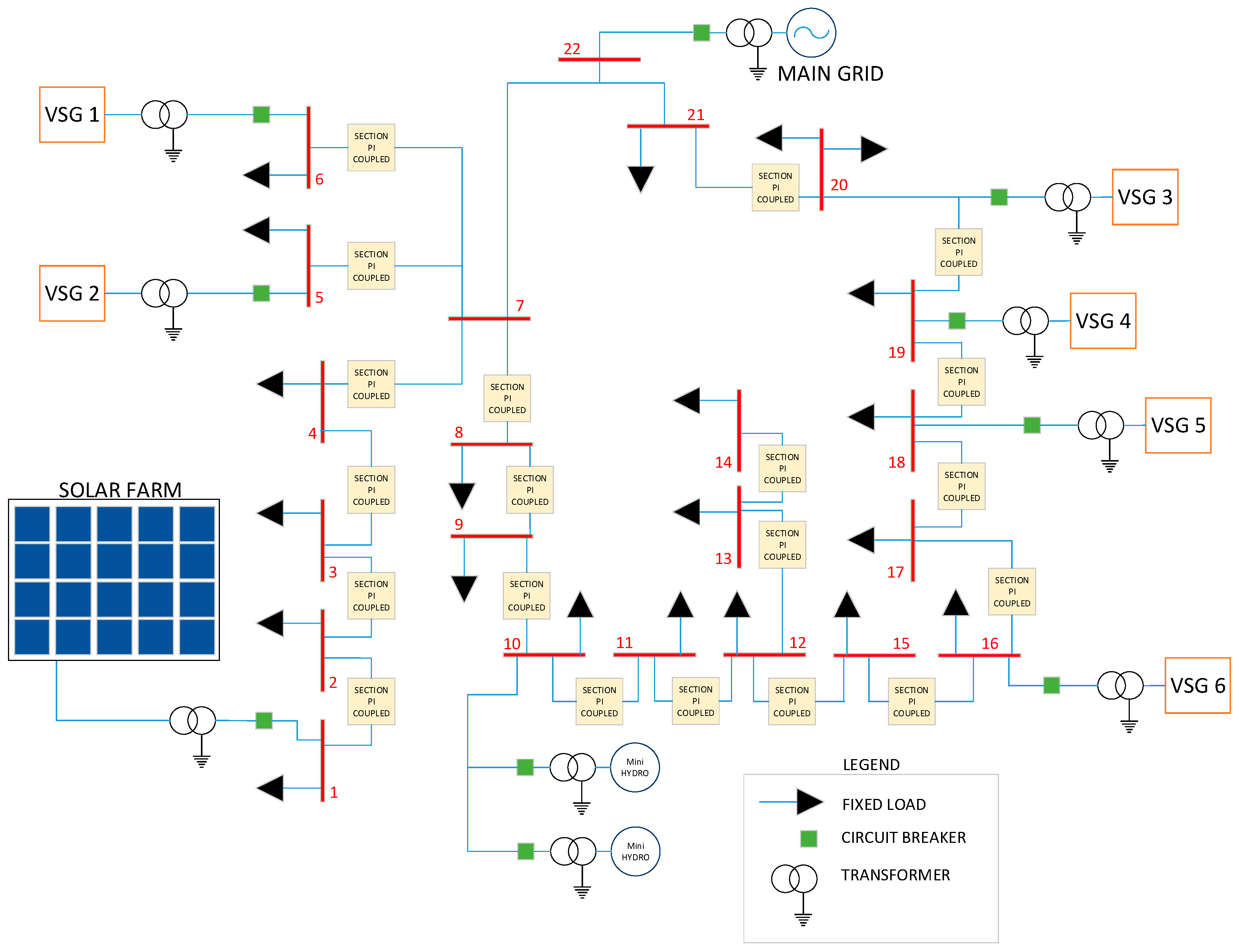
Optimization of the ANFIS using GA has given the controller an optimized range of inertial responses based on real-world simulation. This concept improves both the transient and the oscillation damping of the inertial response of the VSG, which ensures the sustainable and reliable operation of the RES-based DS. The performance of the proposed VSG controller is verified on an 11 kV, 22 bus Malaysian distribution system consisting of two mini hydro and one solar farm. Further, a comparative study has been conducted between the optimized and non-optimized VSG controllers presented to prove the superiority of the proposed controller. The main contribution of this paper is as follows:

• Proposed a new way of VSG active power injection through optimizing both the input and output MF of ANFIS.
• Through the optimizations, real-time scheduling of values J and D is produced. It managed to cover a wide range of interruptions and able to give appropriate active power responses.

The rest of the paper is arranged as follows. Section 2 is the methodology for the controller and test system used, Section 3 is the verification of the controller effectiveness by simulation using PSCAD EMTDC, and finally, Section 4 concludes the findings of the paper.

2. Optimized Adaptive Network-Based Fuzzy Inference System Using Genetic Algorithm

2.1. VSG Active Power Controller

The common topology of VSG consists of three major components: the inverter, controller, and energy storage system, as shown in Figure 1. The well-known swing Equation (1) is used as the basic component for the VSG controller.

$$P_{in}-P_{out}=J{\omega }_o\frac{{\omega }_m}{dt}+D∆\omega$$

(1)

where $P_{in}, P_{out}, J$, ${\omega }_o, \mathrm{and} D$ are the input power (similar to prime mover power in an SG), the output power of the VSG, the moment of inertia of the virtual rotor, the virtual velocity of the virtual rotor, and the damping factor, respectively. $∆\omega$ is the difference between the grid frequency and the reference frequency. Figure 2 shows the active power control structure for a VSG. The controller mimics the ability of an SG by using the swing equation in (1). In this paper, a similar approach to VSYNC is applied, where the frequency changes are used as the input reference. In VSYNC, the phase-locked loop is designed to produce the changes in frequency and ROCOF. Both of these parameters are vital to the GA-ANFIS design. In VSYNCH, the inertial power is calculated linearly as in Equation (2), where $∆\omega$ is the change in frequency and $\frac{d∆\omega }{dt}$ is the ROCOF. GA-ANFIS is inspired by the controller method used in VSYNCH and the traditional swing equation. Frequency and ROCOF are used as the input to the GA-ANFIS. As shown in Figure 3, both inputs will affect the value of inertia constant, J, and damping constant, D, subsequently help the VSG injects and absorbs the right amount of active power into the power system.

$$P_{inertia}=K_{SOC}∆SOC+K_p∆\omega +K_i\frac{d∆\omega }{dt}$$

(2)

2.2. Adaptive Network Fuzzy Inference System

The evolutionary adaptive neuro-fuzzy inference system (ANFIS) is a kind of artificial neural network that is based on the Takagi-Sugeno fuzzy inference system (FIS). This technique was developed in 1990. It has five layers of a fuzzy inference system. ANFIS used a data set of inputs and outputs to create the rules and membership function. In this paper, as shown in Figure 4 and Figure 5, the ANFIS structure has two inputs and two outputs. It is composed of six membership functions and six rules.

The first layer is the fuzzification layer. It uses MF to obtain fuzzy clusters from the input data set. {a, b} is the premise parameters that shape the Gauss membership function (GMF). For this work, GMF is selected. It is selected for the simplicity of the MF equation, where it depends on two parameters, which represent the center and the width. GMF is also the basis for the connection between the fuzzy system and radial basis function neural networks. uA_i and uB_j, are the membership degrees of the linguistic label, A and B, as given in Equations (3) and (5). For this ANFIS design, I is set to 7 because each linguistic label has seven MF.

$$\mu A_i\left(x\right)=gaussmf\left(a,b\right)=e^{-\frac{1}{2}{\left(\frac{x-a}{b}\right)}^2}$$

(3)

$$O_i^1=\mu A_i\left(x\right)$$

(4)

$$\mu B_i\left(x\right)=gaussmf\left(a,b\right)=e^{-\frac{1}{2}{\left(\frac{x-a}{b}\right)}^2}$$

(5)

$$O_i^2=\mu B_i\left(x\right)$$

(6)

The second layer is called the rule layer. Firing strengths, w_i, of each rule are generated by using membership degrees in layer 1. w_i values are calculated as the following.

$$O_i^2=w_i=\mu A_i\left(x\right)·\mu B_i\left(y\right) i=1,2$$

(7)

The third layer is called the normalization layer. Normalized firing strength to each rule is calculated. The normalized value is the ratio of the firing strength, w_i to the total of all firing strengths as given in Equation (8).

$$O_i^3=\overline{w_i}=\frac{w_i}{w_1+w_2+w_3+w_4} i\in \left\{1,2,3,4\right\}$$

(8)

The fourth layer is the defuzzification layer. Weighted values of rules are calculated in each node shown in Equation (9). {p, q, r} is the parameter set. These are called the consequence parameters.

$$O_i^4=\overline{w_i}{f}_{ij}=\overline{w_{ij}}\left(p_{ij}x+q_{ij}y+r_{ij}\right)$$

(9)

The fifth layer is the summation. The output of the ANFIS is produced by summing the output obtained for each rule in the fuzzification layer.

$$O_i^5={{\displaystyle \sum }}_i\overline{w_i}=\frac{{\sum }_i{w}_i{f}_i}{{\sum }_i{w}_i}$$

(10)

Initially, the membership function (MF) for the inputs and outputs are randomized within pre-set ranges. GA will sort the output and input values according to the data set. At every iteration, input MF and the output MF will be optimized, and a new fuzzy set is created. The new fuzzy set will be tested in the Simulink model, which is created to mimic the VSG response in the PSCAD simulation. At every iteration, an error from the Simulink model is produced and fed to the GA optimization to observe the accuracy of the fuzzy set.

2.3. Genetic Algorithm

Genetic algorithm (GA) is an optimization method that models the evolution process in nature. This optimization technique aims to achieve the best population by using the processes such as reproduction, crossover, and mutation. GA has been used in numerous problems in the fields [12]. In the case of GA-ANFIS, all parts of the ANFIS can be trained [13]. However, in this paper, multi-objective GA is used to optimize the gauss MF parameters {a,b} of ANFIS. The input MF and output MF parameters are set as the population cost. Figure 6 shows the flowchart of the implemented GA optimization to form the MF.

$$OF=Min\left\{{\alpha }_{1}O{F}_1+{\alpha }_{2}O{F}_2\right\} , where OF>0;$$

(11)

$$O{F}_1=Min\left\{\left|f_c-f_i\right|\right\} , f_c=60 \mathrm{Hz}$$

(12)

$$O{F}_2=0.75-\frac{ln\frac{x_n}{x_0}}{{\left(2\pi n\right)}^2+\left(ln\frac{x_n}{x_0}\right)} , n=4$$

(13)

The objective of GA optimization is to minimize the objective function (11) by accurately designing parameters of ANFIS input MF and output MF. ${\alpha }_1$ and ${\alpha }_2$ are the normalization constants. Normalization by weighted sum is used to calculate ${\alpha }_1$ and ${\alpha }_2$. It is normalized by the optimum value of each OF₁ and OF₂.

$${\alpha }_1=\frac{1}{O{V}_1}$$

(14)

$${\alpha }_2=\frac{1}{O{V}_2}$$

(15)

where OV₁ and OV₂ is the optimum value for OF₁ and OF₂. For this work, OV₁ is equal to 60, and OV₂ is equal to 0.75. Objective function 1 (OF₁) in (12) is the frequency difference produced during each iteration. $f_c$ is the reference frequency and $f_i$ is the maximum output frequency for each iteration. OF₁ aims to minimize the frequency difference at every response. In contrast, objective function 2 (OF₂) in (13) is the damping ratio calculation of each response. The target for OF₂ is to obtain a response close to the optimal damping ratio, which is set at 0.75. $x_n$ is the peak response value at n period, $x_0$ is the peak response value for the first period. Once GA has optimized the ANFIS, GA-ANFIS will be used in the PSCAD simulation. A new data set from the PSCAD simulation will be used to improve the GA-ANFIS if the VSG response does not meet a certain minimum setpoint. A total of 70% of the PSCAD simulation data set is used as a training set, while 30% is used as a testing set. The number of iterations for GA optimization is set at 100 iterations. GA-ANFIS rules surface generated from MATLAB is shown in Figure 7.

3. Test System Structure and Scale

The proposed VSG controller is verified in PSCAD/EMTDC software, where GA-ANFIS is first optimized in MATLAB/SIMULINK. An existing 11 kV Malaysian actual distribution network was used as the test system shown in Figure 8. The system consists of 21 lumped loads. The base load is provided by 2 mini hydro and a solar farm powering up the distribution system. The voltage of the mini hydro is stepped up using a 1 MVA, 3.3/11 kV transformer. DS is also connected to the main grid via a two-step-down 132/11 kV, 30 MVA transformer. Initially, from time 0 to 1.5 s, DS was connected to the main grid for the mini hydro initialization process. At time t = 1.5 s, DS was islanded. A total of 6 VSGs connected at buses 5, 6, 16, 18, 19, and bus 20. Each of the VSGs uses super magnetic energy storage (SMES) as the energy source. The PV farm is rated at 1.3 MW, connected at bus no. 1. A dc-dc converter with maximum power point tracking and a voltage source converter is used to control the solar power. The parameters of the VSG-SME are listed in

Table 1. Parameters for VSG-SME.

Parameters	Value
SME power	0.95 MW
SME storage capacity	0.95 MWh
DC link voltage	600 V
Line voltage	400 V
Inverter switching frequency	2 kHz
LCL filter	11 mH, 0.62 µF, 6.6 mH
Line reactance, resistance	0.0238 Ohm/km, 0.342 Ohm/km

,

Table 2. Parameters for mini hydro generator.

Parameters	Value
Rated power	1 MVA
Rated voltage	11 kV
Inertia constant	0.2 s
Neutral series resistance	10,000 (pu)
Neutral series reactance	0 (pu)
Iron loss resistance	300 (pu)

and

Table 3. Parameters for solar power.

Parameters	Value
Number of modules connected in series per array	20
Number of module strings in parallel per array	20
Number of cells connected in series per module	108
Number of cell strings in parallel per module	4
Reference irradiation	1000 W/m2
Reference cell temperature	25 °C
Effective area per cell	0.01 m2
Series resistance per cell	0.02 Ohm
Shunt resistance per cell	1000 Ohm
Band gap energy	1.103 eV
Saturation current at reference conditions per cell	1 × 10−12 kA
Short circuit current at reference conditions per cell	0.0025 kA

.

4. Results and Discussions

The performance of the controllers was assessed through PSCAD/EMTDC software. The dynamic performance is evaluated using frequency metrics, such as the frequency nadir (FN), frequency spikes, and the damping ratio (DR). The peak-to-peak value for each frequency response should lie within the safe operating frequency of 60 Hz ± 3% Hz [14]. DR is the measure of the oscillation of a system response. For this simulation, the logarithmic decrement method was used to calculate DR. The best value of DR is known to be $\frac{1}{\sqrt{2}}$ equals 0.7071, where the response is neither too slow nor too oscillatory [15]. System response with DR < 0.7071 will generate under damped response. While a system with DR > 0.7071 will generate an overdamped response. Under damped response could cause the system to have a prolonged oscillation and cause instability to the system. Comparisons between 4 VSG controllers were made for all scenarios. The controllers are; (i) NO VSG support (NV), (ii) VSG with a fixed value of J and D (VF), (iii) VSG with fuzzy inference system controller (VFIS), and (iv) VSG with GA-optimized fuzzy inference system controller (VOFIS). The method used for each controller is shown in

Table 4. Controller method comparison.

Controllers	Method
VSG with fixed value of J and D (VF)	The value of J and D is fixed to two constants. Both constants are deduced from a unit pulse interruption response.
VSG with fuzzy inference system for J and D (VFIS)	Value of J and D are scheduled in the form of a fuzzy inference system (FIS). The only input for the FIS is the ROCOF. The uniform triangle membership function is used for the FIS. The range of each MF is fixed.
VSG with GA-ANFIS for J and D (VOFIS)	For the ANFIS, two input MF and two output MFs are set. Change in frequency and ROCOF as the input while constant J and D as the output. Both input and output MF are optimized using a genetic algorithm. From the optimization, input and output MF are heuristically designed to manage a wide range of interruptions and responses.

.

4.1. Scenario 1: Solar Drop 100% for 0.2 s

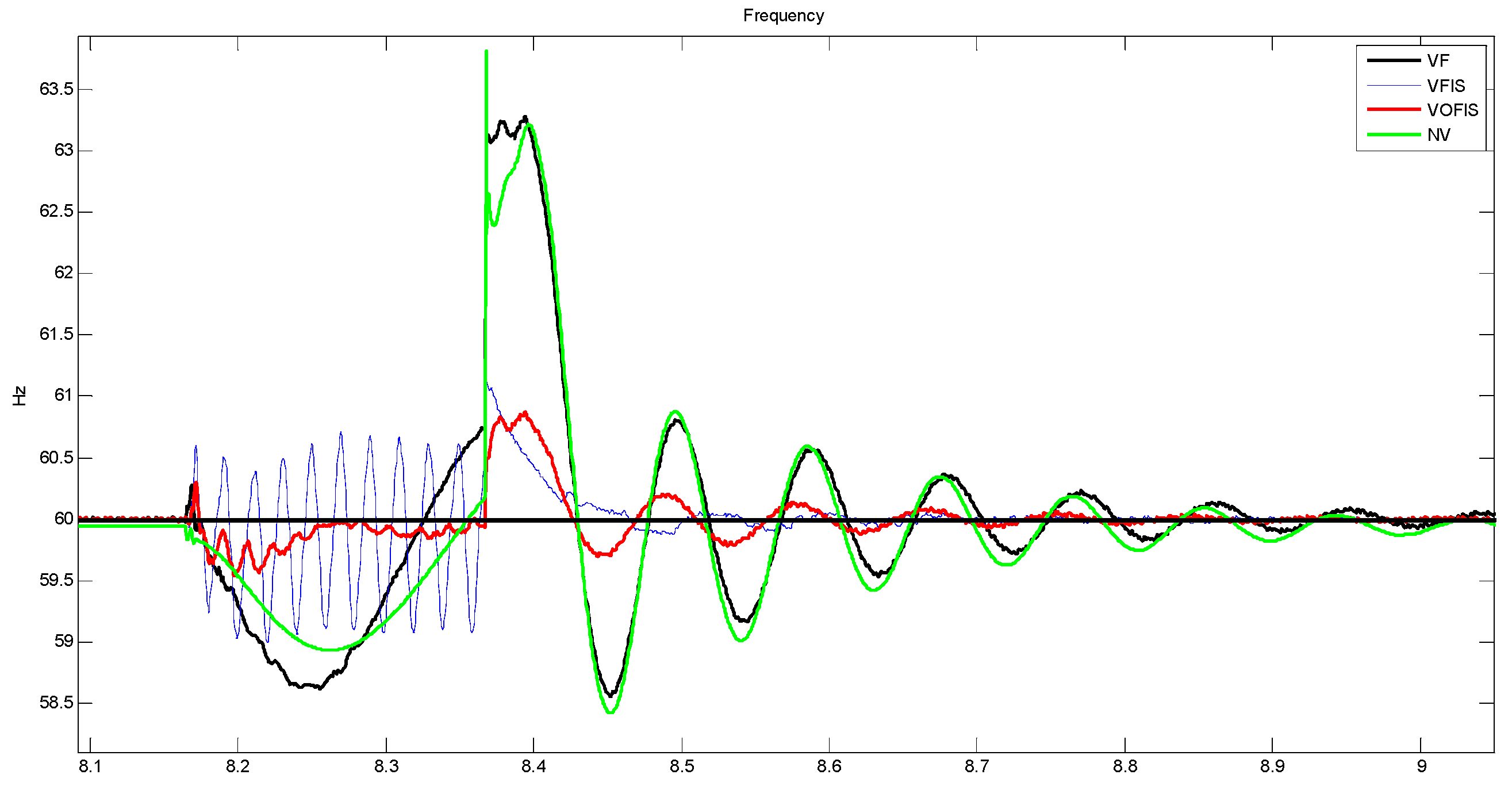
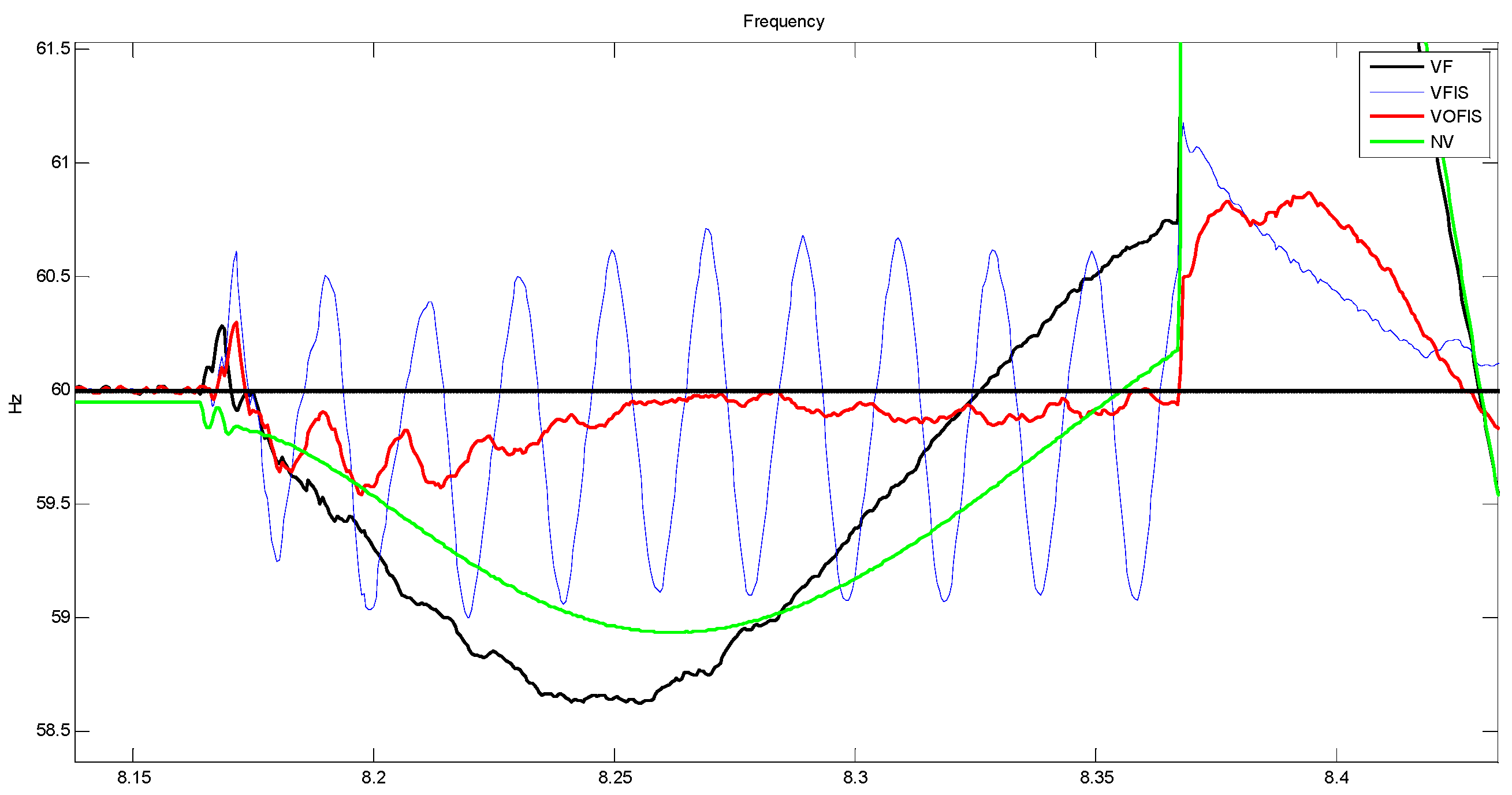
For the first scenario, the performance of the system was analyzed by turning off the solar power. At the time, t = 8.16 s, solar power was switched OFF for 0.2 s, and solar was switched back ON at t = 8.36 s to mimic the sudden loss of solar power generation. The first transition at t = 8.16 s created an under-frequency event. The second transition at t = 8.36 s was caused by the sudden reconnection of solar power to the DS and created an over-frequency event. During an under-frequency event, energy stored in the VSG was used to minimize the frequency change. During an over-frequency event, VSG absorbed excess power and charged the energy storage in the VSG.

The results in the Figure 9 and Figure 10 below show the effect of the sudden switch-off of solar power. Figure 10 is the zoomed-out version of the result in Figure 9. From figures, FN for VFIS is 59.09 Hz. Whereas the FN for VOFIS is 59.4 Hz. While FN for both VF and NV are well beyond 48 Hz. Although both the FN for VFIS and VOFIS do not differ much, from a frequency recovery point of view, VOFIS has faster recovery at 70 ms compared to VFIS at 90 ms. The damping ratio (DR) value for VOFIS is 0.856 while VFIS 0.1858. From the results, VOFIS is the best DR value and the highest FN.

At t = 8.36 s, solar power was reconnected and caused an over-frequency event due to the sudden injection of power. VOFIS controller was able to reduce the frequency spike to 60.68 Hz, while the frequency for the VFIS controller spiked up to 62.12 Hz, well beyond the safe frequency operation. During over-frequency events, excess power generated was used to charge the energy storage. It can be concluded that the VOFIS controller was able to absorb more excess power because the controller was optimized to manage a larger range of frequency changes. Besides reducing the peak frequency, VOFIS has the best DR, at 0.8133, as compared to the other controllers in

Table 5. Frequency nadir, peak, and damping ratio comparison for scenario 1.

Controller Strategies	Frequency Nadir, FN (Hz)	1st Transition Damping Ratio, DR (%)	Frequency Peak, FP (Hz)	2nd Transition Damping Ratio, DR (%)
NV	53.68	<0.01	67.31	3.7169
VF	59.06	0.2536	63.91	5.3174
VFIS	59.09	0.1858	62.12	2.8827
VOFIS	59.40	0.8560	60.68	0.8133

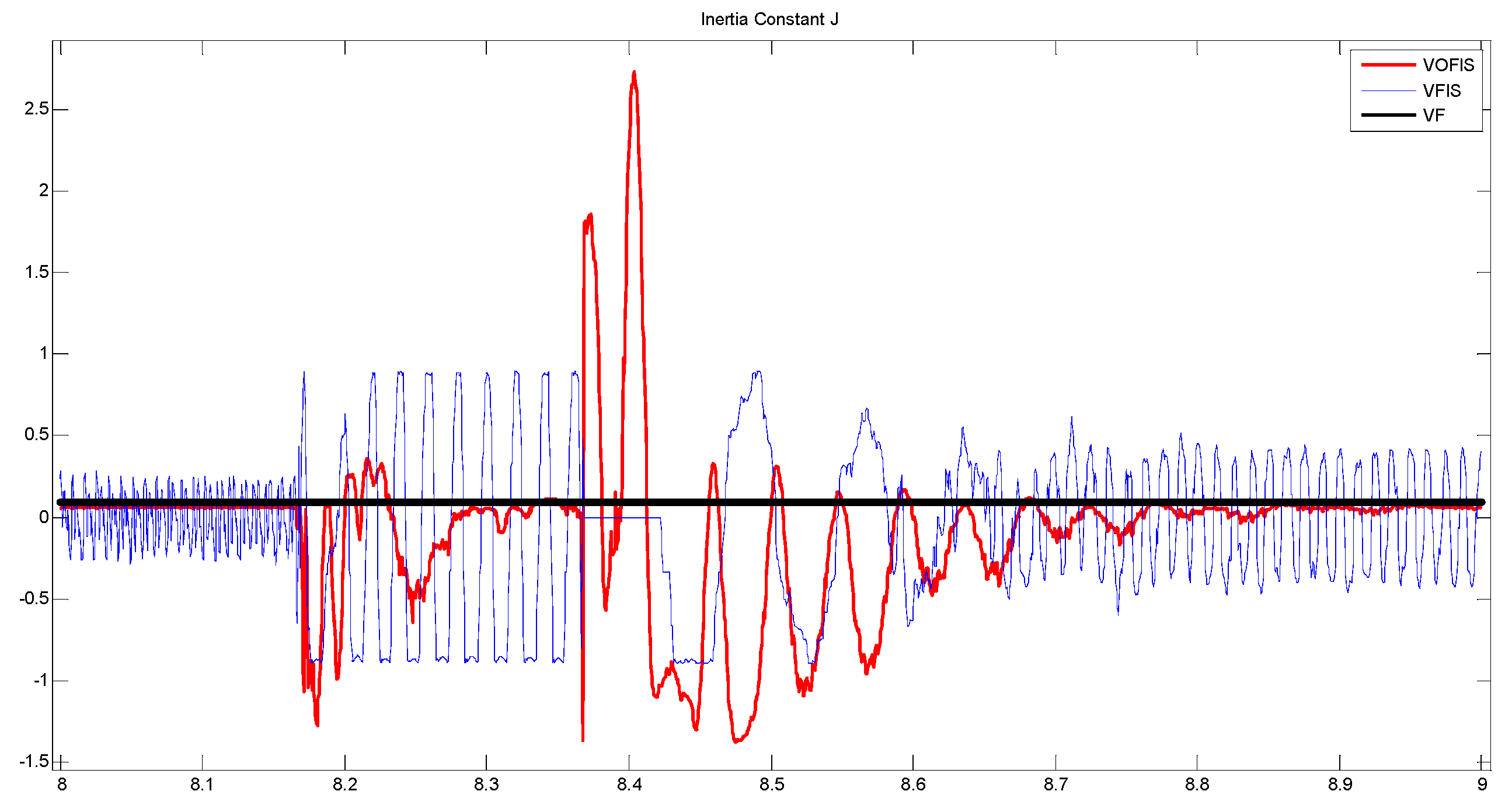
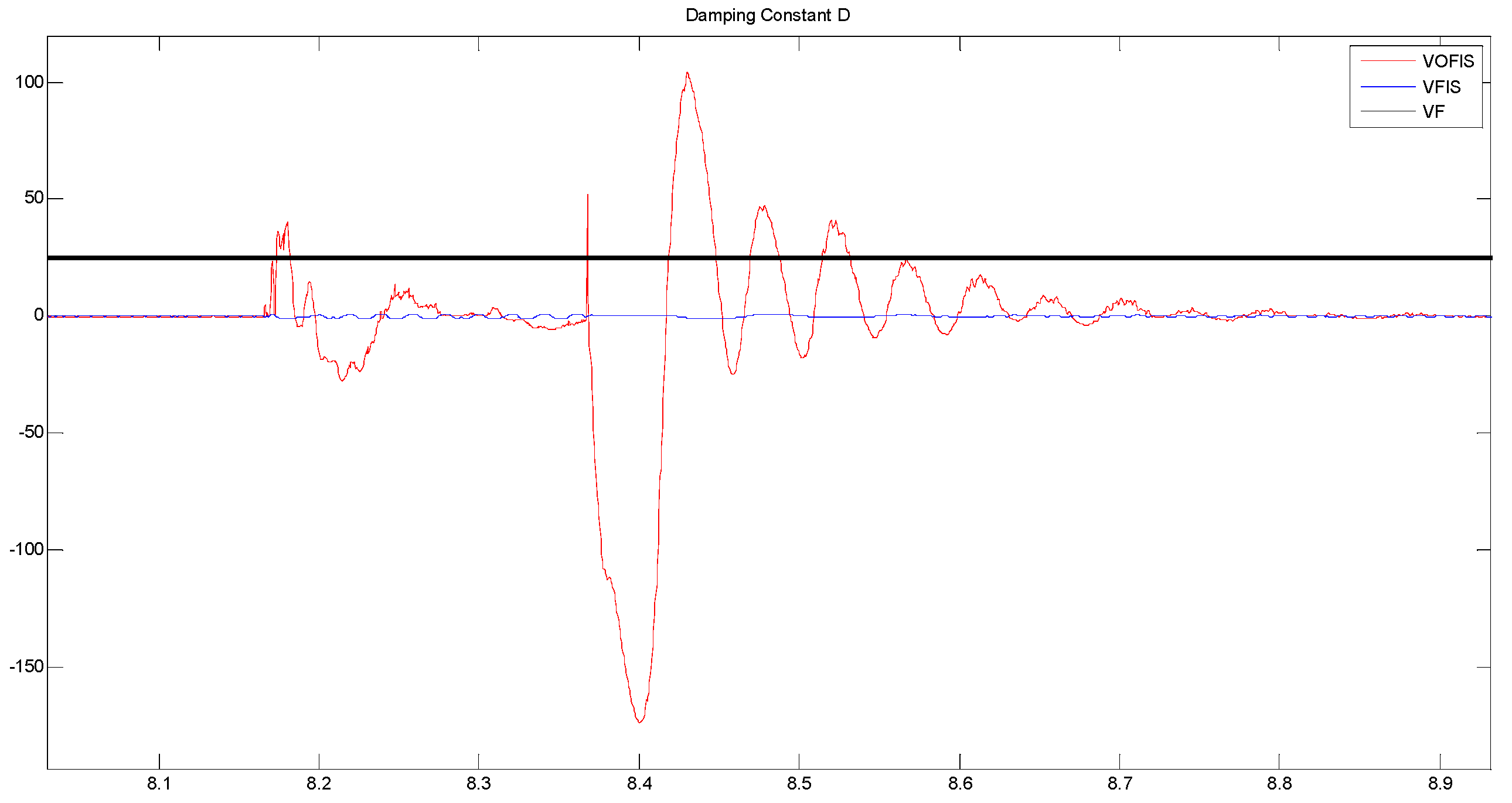
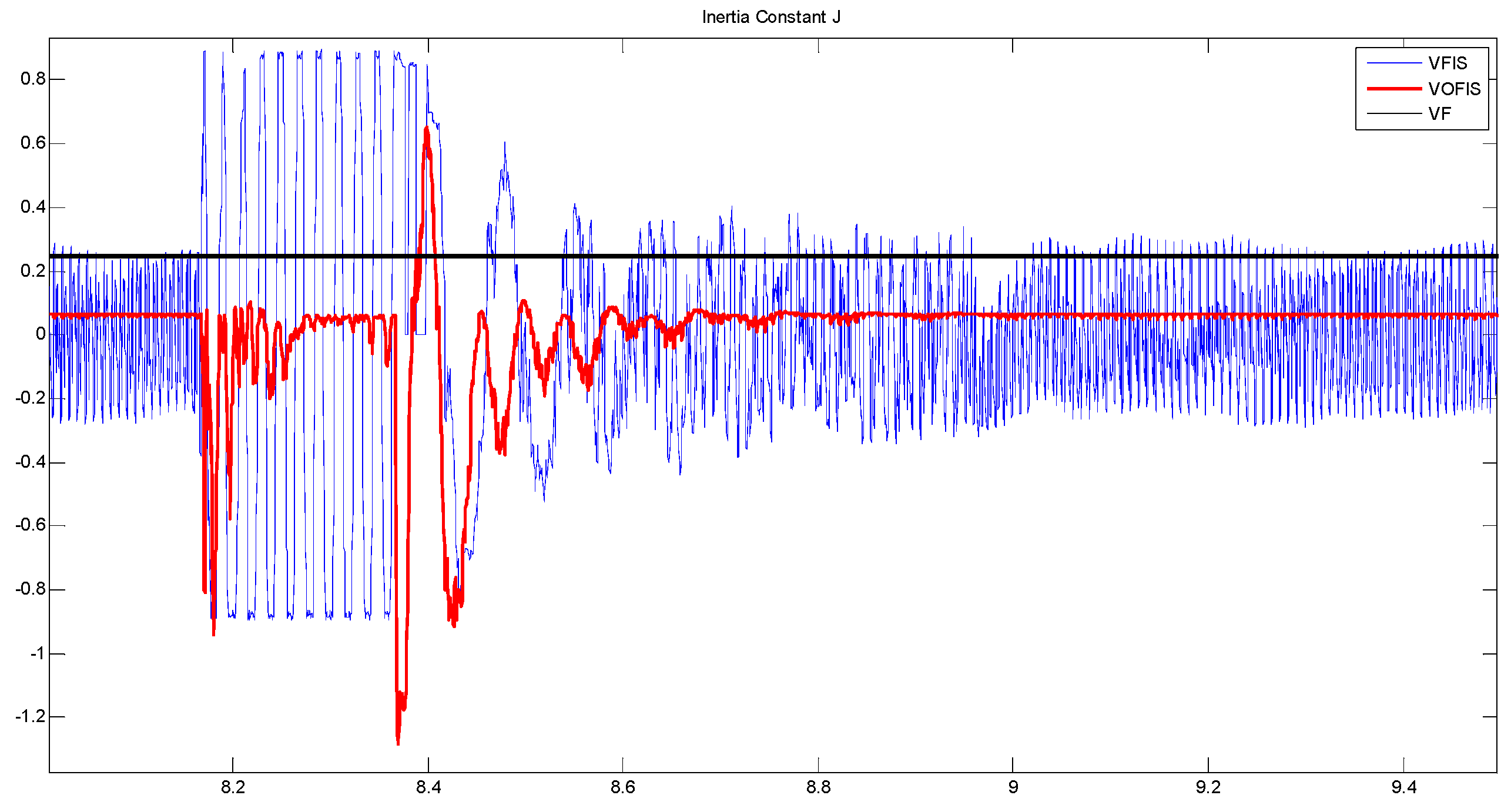
. Figure 11 and Figure 12 show the comparison of the J and D value used for the VSG controller. Figure 11 and Figure 12 compare the difference between VFIS and VOFIS fuzzy controller output. As was anticipated, VOFIS has produced a more accurate value for J and D according to the changes in the frequency. VFIS produced an inaccurate value because its MF range was not optimized for the frequency changes.

4.2. Scenario 2: Solar Variation (Irradiance Change)

In this scenario, the transient response of the system was analyzed by varying the solar irradiance after steady state was attained. At a steady state, solar irradiance was maintained at 900 W/m² generating 1.32 MW from PV farm. Solar irradiance changes from 900 W/m² to 100 W/m² at 8.16 s for 0.2 s while retaining the temperature of the solar panel, which was set at 40 °C. This scenario simulates the intermittent nature of a solar farm. As a result, power generated from PV farm dropped from 1.32 MW to 0.2 MW, subsequently causing an under-frequency event due to power deficit. At t = 8.36 s, the solar irradiance changes from 100 W/m² back to 900 W/m². At this point, an over-frequency event occurs due to the sudden injection of solar power.

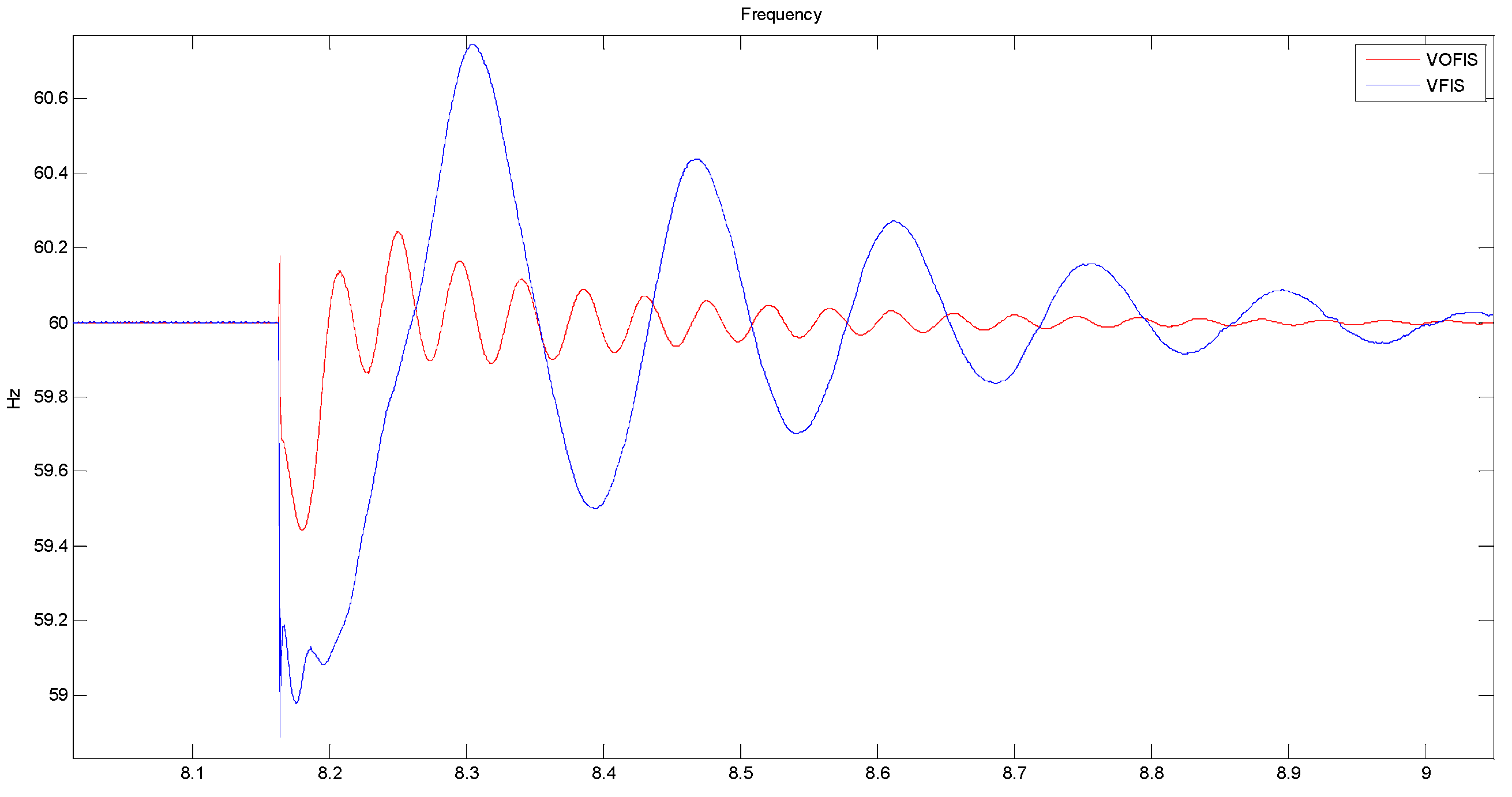
Both Figure 13 and Figure 14 shows the frequency response of scenario 2, where Figure 14 is the zoom-out version of Figure 13. From figures, FN for VOFIS dropped to 59.56 Hz, while for VFIS, the frequency dropped to 59.03 Hz with a high oscillating pattern. VOFIS recovers the frequency faster at 100 ms compared to VFIS at 2 s. From

Table 6. Frequency nadir, peak, and damping ratio comparison for scenario 2.

Controller Strategies	Frequency Nadir, FN (Hz)	1st Transition Damping Ratio, DR (%)	Frequency Peak, FP (Hz)	2nd Transition Damping Ratio, DR (%)
NV	58.93	<0.01	63.82	5.606
VF	58.64	<0.01	63.27	4.771
VFIS	59.03	0.0849	61.18	1.853
VOFIS	59.56	0.5208	60.87	1.293

, DR for VOFIS and VFIS is 0.5208 and 0.0849. This proved that VFIS produced a high oscillation response compared to VOFIS. Therefore, the transient response for VFIS is longer compared to VOFIS. DR for both VF and NV is lower than 0.01. At t = 8.36 s, VOFIS reduced the over-frequency spikes to only 60.9 Hz compared to VFIS 61.5 Hz. With a VF controller, the frequency spike up to 63 Hz. The ability of the VOFIS controller to absorb excess power and use them to charge the energy storage reduced the frequency spike. Figure 13 shows that frequency recovery using VOFIS is faster and smoother as compared to the other controller. 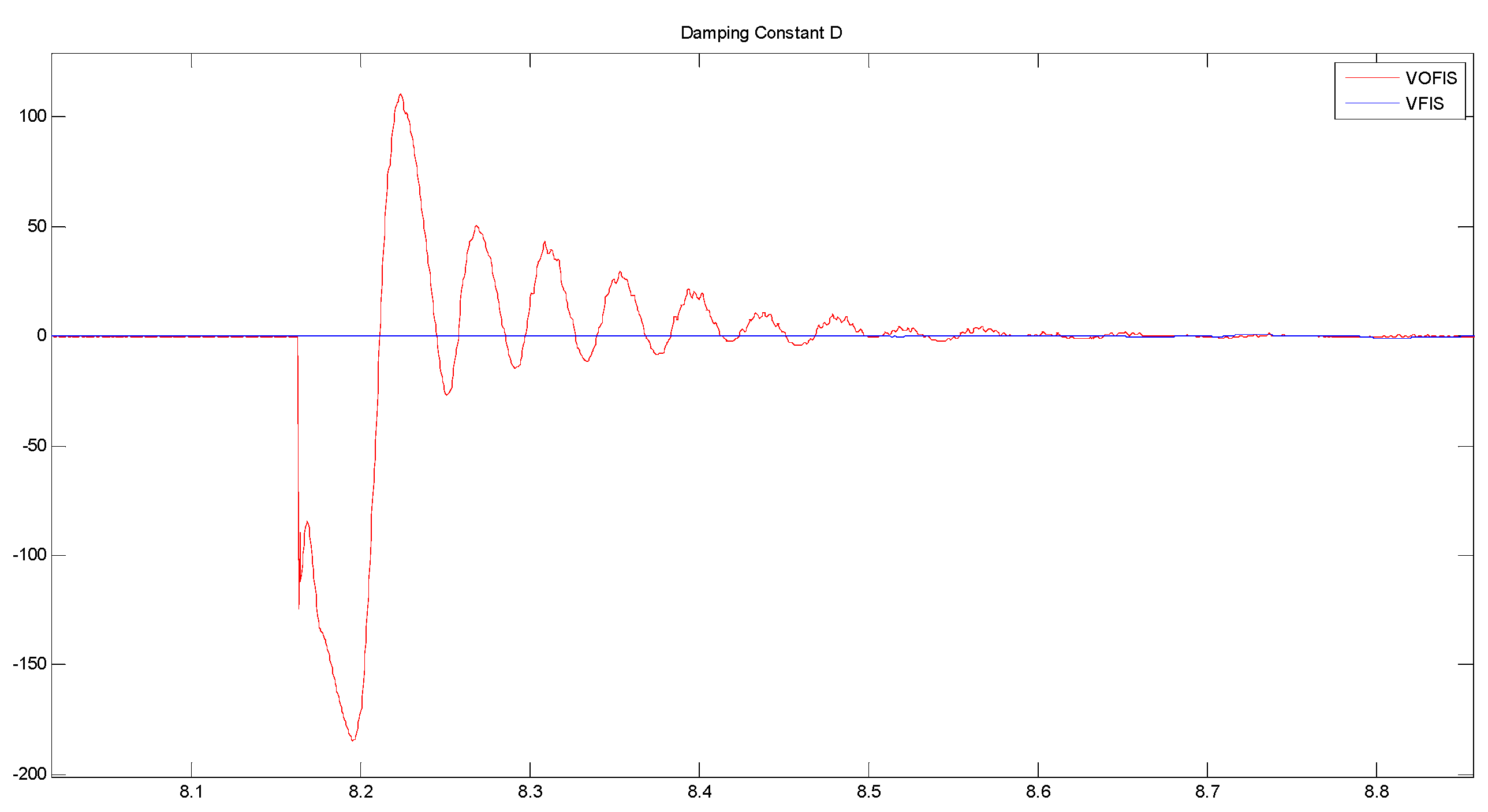Figure 15 shows the comparison between the value and range of J and D between VOFIS and VFIS. The value of J and D for VOFIS is optimized and fine-tuned according to the changes in the frequency. As a result, VOFIS able to inject and absorb sudden changes in the power hence maintaining the system frequency within the safe operation. Figure 15 and Figure 16 compare the fuzzy output value for VFIS and VOFIS.

4.3. Scenario 3: Islanding Event

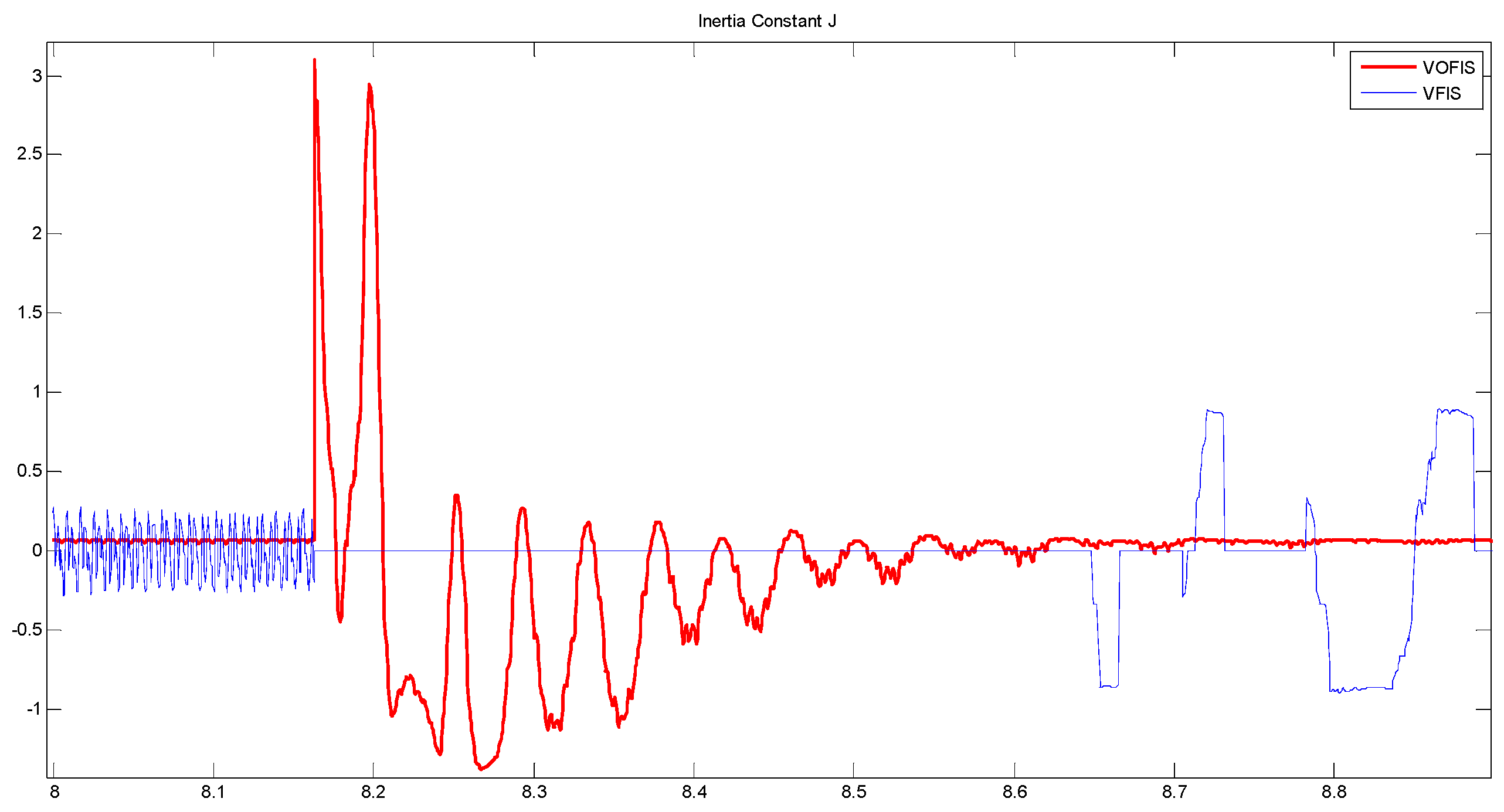
In this scenario, DS was islanded at time t = 8.16 s by opening the main grid circuit breaker. Figure 17 shows that VOFIS can reach stability without overshooting beyond safe frequency operation. VFIS, on the other hand, could not react to the islanding event. This could be seen from the value of J and D in Figure 18 and Figure 19. The controller was unable to produce a new variation of J and D as the frequency detected is out of the input MF range. Both J and D were set to zero during the islanding process. On the other hand, VOFIS reacted and reduced the frequency changes during the inertial phase. The FN for VOFIS dropped to 59.44 Hz while 48.87 Hz for VFIS. As shown in

Table 7. Frequency nadir, peak, and damping ratio comparison for scenario 3.

Controller Strategies	Frequency Nadir, FN (Hz)	1st Transition Damping Ratio, DR (%)
VFIS	48.87	9.163
VOFIS	59.44	0.203

, the DR for VFIS is overdamped at 9.163, while DR for VOFIS is underdamped at 0.203. Even though the DR for VOFIS is underdamped, the response time for the frequency to stable. VOFIS recovers 7 s after islanding while VFIS 9 s after.

5. Conclusions

In this paper, a new active power controller for VSG has been developed based on ANFIS, in which membership functions are optimized using GA. The values of inertia constant, J, and damping constant, D, in a VSG controller are controlled through the proposed controller to ensure the improved operation of the VSG controller. Through the simulations conducted in the PSCAD platform on an 11 kV Malaysian practical distribution system for various cases, it has been proved that the proposed ANFIS-GA-based controller has improved the performance of the VSG compared to the conventional VSG controller.

From the simulation results, it has been observed that the proposed controller managed to maintain the DS frequency within the safe operating limit of 60 ± 1.8 Hz, better transient response, and faster recovery time during all the three cases (100% solar drop, solar irradiation changes, and islanding event). VOFIS able to recover the frequency 22% faster compared to the other controllers.

From the analysis of the above results, it can be concluded that the values of J and D for the proposed VOFIS are optimized and fine-tuned according to the changes in the frequency. As a result, VOFIS able to inject and absorb sudden changes in the power hence maintaining the system frequency within the safe operation. This paper serves as an initial work for coordinating multiple energy storage systems in VSG as an ancillary service to the DS. Furthermore, different types of metaheuristic optimization should be implemented and compared to obtain the best method for VSG application. Optimization of J and D constants in the VSG controller plays a vital role in regulating the VSG power output to maintain stable frequency operation during islanded DS operation. Without the help from VSG as an ancillary service, DS could not maintain the frequency in the safe operating region, which may result in the malfunction of DS. Therefore, it can be said that through the implementation of the proposed optimized GA-ANFIS-based VSG controller, the sustainable and reliable operation of DS has been ensured.