Development of a Sharing Concept for Industrial Compost Turners Using Model-Based Systems Engineering, under Consideration of Technical and Logistical Aspects

Abstract

The trend of sharing concepts is constantly increasing, whether this may be for economic or environmental reasons. Consequently, numerous scientific research works have addressed the subject of sharing concepts. Many of these works have dealt with questions on the topic of sharing concepts itself, however, much less research has been dedicated to the question of how the sharing concept can be developed in the very first place. Thus, the purpose of this work was to systematically use systems engineering methods to develop a sharing concept for heavy-duty agricultural vehicles, while having a strong focus on technical and logistical aspects. Due to the multidisciplinary complexity of the sharing concept, a method from the field of model-based systems engineering, ARCADIA, was chosen. On ARCADIA’s top level, operational analysis was carried out to identify the key stakeholders. The next level, systems analysis, showed that the sharing model can be divided into three main processes: (1) data acquisition and preparation; (2) location planning; (3) and route planning. For these main processes, corresponding methods, algorithms and models were sought and compared against each other in the last level, logical analysis. It can be concluded that the ARCADIA method has provided a framework for evaluating the correlations and interrelationships between methods, algorithms and models at different levels to develop a sharing concept for compost turners from a technical perspective.

1. Introduction

1.1. Megatrend Sharing Economy

The fundamental idea of a sharing concept is by no means new, and was already practised in the early days of humankind [1]. Due to the rapid increase in digitalisation and the associated technologies, new forms of sharing concepts are emerging, resulting in a steady growth of the sharing industry in the last decade [2,3,4]. From an economic perspective, sharing concepts may provide an economic advantage, such as a significant reduction in costs [5,6] or increased convenience for customers [7,8]. In addition to these economic reasons, the ecological aspects of sharing concepts are seen as a way to more efficiently use resources, especially in the context of growing environmental pollution, by better connecting users through digital technologies [9]. The resulting increase in utilisation is an attempt to mitigate growing consumption-related environmental challenges [10].

1.2. Sharing Concepts and Composting

In the agricultural sector, the trend of machinery sharing concepts is particularly evident in Europe and North America. Farms are increasingly sharing agricultural machinery and equipment with each other [11]. Empirical studies for the agricultural sector in Europe have shown that a wide variety of sharing concepts, ranging from the informal exchange of machinery to the joint use of all machinery and equipment, are beneficial for the vast majority of the studied farms [12,13]. In the US, research has shown that cooperative approaches offer an alternative, especially for small and medium-sized agricultural enterprises, to achieve the efficiency of larger farms and thus remain competitive in an increasingly concentrated agricultural industry. Cooperative approaches have led to an increase in farm profitability and efficiency, as well as an increase in the quality of life for farmers, through the sharing of resources [11].

Closely related to agriculture is the organic waste industry. In Europe, this sector is growing rapidly, as is the sharing sector. The driving force behind the increase in the composting rate is the European Union. The European Union has created an ambitious package of measures within the framework of the European Green Deal, ranging from a determined reduction in greenhouse gas emissions to investments in cutting-edge research and innovation and the preservation of Europe’s natural environment. One of the initiatives of the European Green Deal is the 2030 Climate Action Plan, which aims to reduce net greenhouse gas emissions by at least 55% by 2030 compared to 1990 levels [14]. Another initiative within the Green Deal is the Circular Economy Action Plan. The aim was to implement a high-quality circular economy that provides functional and safe products which are efficient, affordable, last longer and are designed for reuse, repair and high-quality recycling [15]. In addition to achieving a circular economy for electrical devices, packaging and clothing, the initiative also plans reforms in the sector of waste and recycling management. As part of an increase in the recycling rate for municipal waste, which must be at least 65% by 2030, the separation of biological waste is also regulated. Although this is already the case in some EU states, such as Austria, it is to be legally obligatory for all EU states by 2024. Biological waste must then either be collected separately or composted at home to prevent it from being landfilled [16].

The industrial processing of biological waste takes place in an anaerobic biological treatment plant (composting plant). Composting is defined as a controlled aerobic process for the production of compost. The resulting product is called compost and it is the rotting product from the treatment of organic materials or biogenic waste from separate collection after largely completed aerobic rotting, which meets defined quality requirements for use or placing on the market. The produced compost is returned to the economic cycle in legally defined qualities for different applications. Among others, applications are fertilisation and soil improvement in agriculture and hobby gardens [17,18]. The most common industrial method of compost production is the compost windrow process. In this process, the organic waste is placed in long lanes, which, depending on the composting plant, range from 1.2–1.5 m in height and 2.5–3 m in width. This type of compost production is also referred to as “open composting”, as seen in Figure 1 [19].

In central Europe, such as in Austria, open windrow composting has become widely established, resulting in a very communal situation. With 405 composting plants, Austria has a comparatively large number of smaller plants, which tend to be regionally oriented. In order to maintain the biological process of composting, it is essential that the compost windrows are turned at regular intervals. The exact interval depends on several factors, but a maximum frequency of three times per week can be assumed [17]. The process of turning the windrows is carried out by compost turners. In addition to traditional technologies, research is currently being conducted on a fully autonomous, electric compost turner as part of international research projects at the Graz University of Technology [20,21,22,23]. A prototype is shown in Figure 1.

Although a fully autonomous compost turner has a potential utilisation time of 24/7 (including loading), the low turnover frequency of three times per week results in a minimal utilisation of this machine.

1.3. Methodical Approach to the Development of Sharing Concepts

Concerning related research, one notes that methodological approaches for the development of sharing concepts have already been used in many fields, such as car sharing or bike sharing. Various approaches for their development have been described in the literature. According to [24], one possible approach would be to consider sharing concepts, such as bike sharing, as a special form of product-service systems. Although many approaches to system modelling frameworks, which are dedicated to the development of product-service systems, have been developed over the last three decades, research shows that the approach of model-based systems engineering is becoming more and more prevalent in this area. This development seems to be a logical consequence of the fact that model-based systems engineering has already found widespread acceptance in other sectors such as the automotive industry. The advantages are a reduced development risk, improved communication between corresponding development departments and disciplines, as well as the reusability of system models [25,26]. If the focus is on the technical realisation of sharing concepts, for example, in the sense of a specific case study, a strongly problem-oriented approach is usually chosen in the literature. The corresponding approaches and methodologies are adapted to the specific use case, but are usually based on solving an optimisation problem with the respective constraints [27,28,29,30].

It can therefore be stated that, regarding the use of sharing concepts, there are approaches in the literature that deal very intensively with the topic of machinery sharing. However, the focus of these studies is primarily on specific use cases, whereby a systematic development of the underlying sharing concept in the sense of MBSE is not considered in detail. Thus, the study in [31] studies the subject of machinery sharing from a technical perspective, using Nash equilibrium game theoretical model and applied two-farm simulation model to investigate the impact of machinery sharing on engaged firms. Other approaches develop support systems for sharing concepts in the agricultural sector based on deep learning algorithms to assist farmers in achieving their economic growth [32,33]. As discussed, there is also research that intensively focuses on surveys and case studies of sharing concepts in the agricultural sector [11,12,13,34]. Even if the MBSE approach in the field of sharing concepts has not yet found strong acceptance, there is ongoing research dealing with the topic of MBSE in the technical/logistical domain. The use of MBSE in logistics extends from warehouse design [35] over supply chain analysis [36,37] to digital twin design [38,39]. Of particular interest is [40], which investigates a model-driven approach to integrating simulation and optimisation methods by exchanging system designs. Furthermore, it is worth mentioning that [41] uses MBSE to achieve a greater enduring understanding of transport systems. Although the focus of the aforementioned research works varies, they all use an MBSE approach in the logistics field to investigate complex systems.

1.4. The Resulting Research Gap

In summary, one may note that the research presented deals very intensively with the application of sharing concepts in the agricultural sector. However, comparatively little focus is placed on the systematic development of these concepts. Furthermore, it should be noted that the aforementioned studies on machinery sharing mainly use the empirical results obtained from already established plants, i.e., a posteriori. Model-based data, which are generated before the sharing concept is actually implemented, were not used in the presented studies.

1.5. Research Question

In addition to the ecological and economical aspects described in Section 1.1, it is mainly the aspects of a total cost of ownership (TCO) assessment, such as high acquisition costs, low utilisation, operating and maintenance costs, which provide the motivation for a sharing concept. Therefore, this publication is a contribution to demonstrate an efficient procedure of how a sharing model for compost turners under logistic-technical aspects can be developed, using model-based engineering. Thus, the following research questions can be derived:

(1)

How can a sharing concept be developed for compost turners (from a technical perspective)?

(2)

Which boundary conditions must be considered? (Transportation routes, Transportation time, maximum processing time per composting plant, …)?

In this publication, the research question only aims to address the technical feasibility of a sharing concept for compost turners. From an economic standpoint, other perspectives of the sharing economy, such as ownership, value added for different stakeholders, supply network compensation and responsibilities are also of high significance. However, a detailed discussion of these aspects would go beyond the scope of this work; therefore, the economic aspects of the proposed sharing concept will be dealt with in the following publications.

2. Methods, Approach and Tools

Due to the multidisciplinary nature of the sharing concept, which covers a wide range beginning from statistical data processing up to optimisation algorithms for route planning, it was essential to find a method that could cover this complexity. While document-based engineering has historically been of great importance, it is becoming increasingly clear that model-based approaches are on the rise. Therefore, the method chosen is an approach from systems engineering, namely model-based systems engineering (MBSE). The International Council on Systems Engineering defines MBSE as

The formalised application of modelling to support system requirements, design, analysis, verification and validation activities beginning in the conceptual design phase and continuing throughout development and later life cycle phases [42].

The aim is therefore to make use of models in order to support the process (idea, requirement up to architecture). In the concept phase of a project, it is essential to establish a platform for the problem synthesis, analysis and for communication with stakeholders. For that purpose, a combination of methods and corresponding models is used in this systems architecture definition phase. The understanding of the customer needs is the starting point in which a model-based approach provides a more comprehensive information status. The digitisation of these models allows a continuous re-use and a better traceability of changes. Based on the customer needs, functional models on the system level can be directly linked and used for comparison of different problem solutions. The tailoring of system structures in terms of the required deliverables is supported by behavioural simulation. This requires logical and physical architectural models which are derived from the customer needs and required functions. The system model plays in this area a central role, as it connects the different artefacts such as customer need analysis, functional, logical and physical models. It therefore allows a multiple view across disciplines, whereas specific models focus on detailed views. A main element in the model-based approach is the connection of the different models based on specific methods. Depending on the specific view, different system models are used within the development to support the interdisciplinary information exchange. As different modelling languages are used to describe system models, it is essential to clarify the corresponding method for model creation in order to provide a consistent modelling structure. This is even more important for an application of the methodology, as subsequently shown. It can be shown that the MBSE-approach can be applied beneficially for the development of a new sharing concept for compost turners.

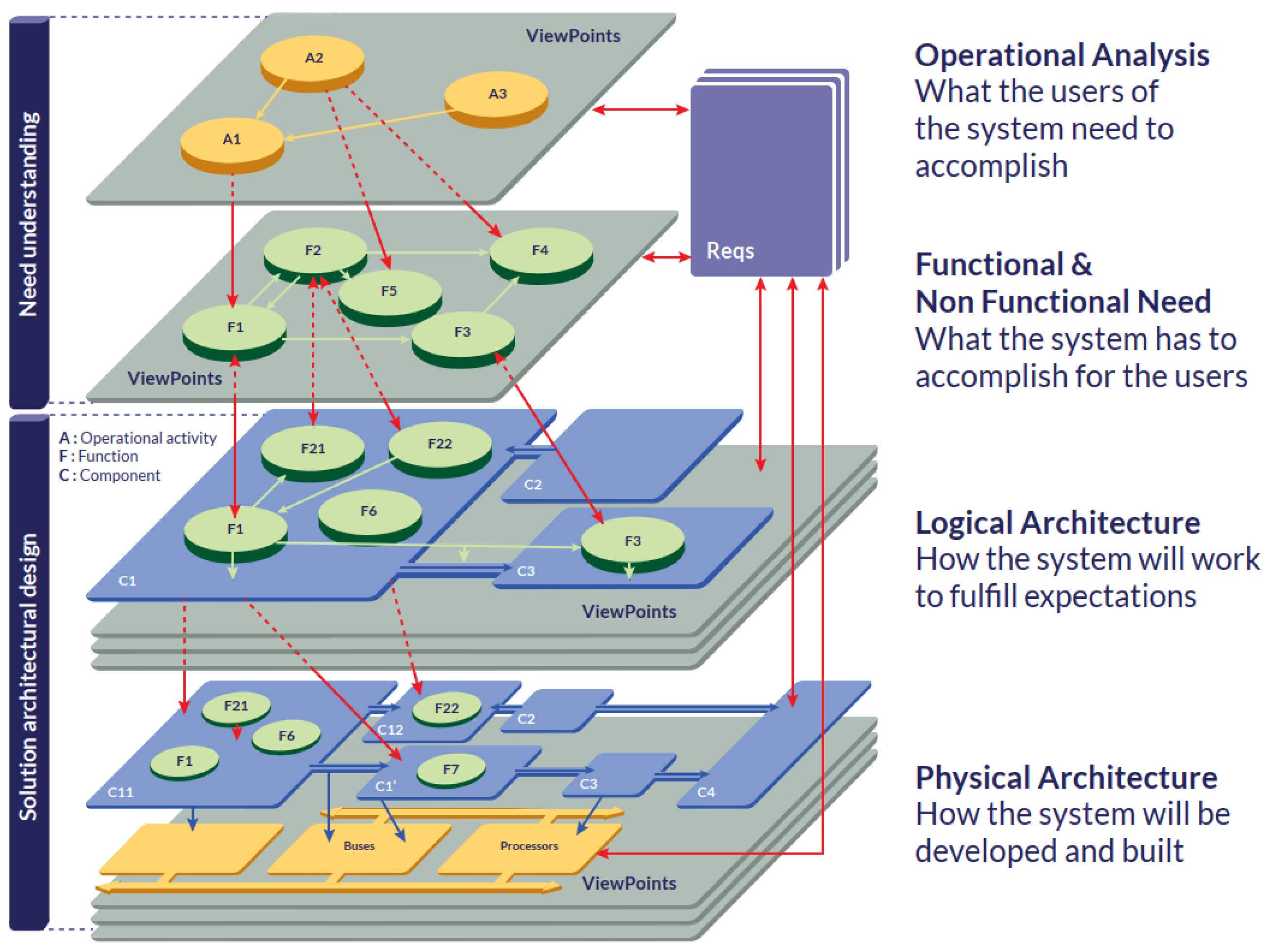
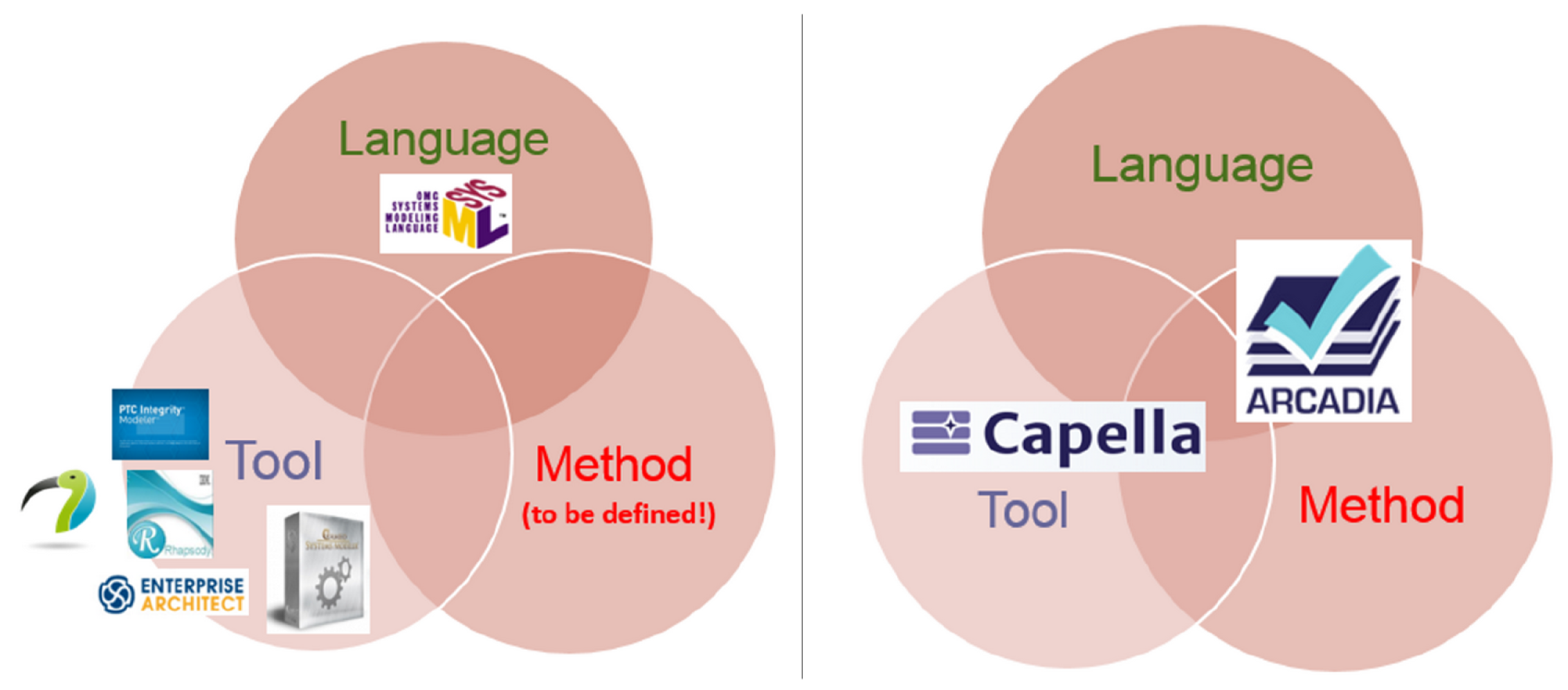
2.1. The ARCADIA Method

There are several concepts and methodologies in the field of MBSE that pursue this aim. The most common are: the object-oriented systems engineering methodology (OOSEM) by Walden et al. [43], the model-based systems engineering methodology by Long and Scott [44], the systems modelling process (SYSMOD) by Weilkiens [45], the harmony SE by IBM [46], object-process methodology (OPM) by Dori [47] and the ARCADIA methodology by Thales [48]. A more comprehensive list can be found in [49]. Since every MBSE methodology has advantages and drawbacks, it is vital to select the one that is most suited to the given task. Our particular case was looking for a method that allows a very structured approach (integrated methodological guide) and that offers a possibility to handle high system complexity (ability to hide complexity, filters, calculated links, accelerators, etc.) [48]. Since the ARCADIA method fulfils these requirements, the authors decided to use this method. It is defined as follows:

ARCADIA is thus a structured engineering method for defining and verifying the architecture of complex systems. It promotes collaborative work among all key players, often in large numbers, from the engineering (or definition) phase of the system and subsystems, until their Independent Verification and Validation (IVV) [50].

Summarising, ARCADIA is a systems engineering method based on the use of models. It focuses on the collaborative definition, evaluation and use of the model architecture. As a result, the method enables collaboration between all stakeholders involved.

The Design of ARCADIA Using Four Layers/Working Levels

The ARCADIA method consists of four working levels, which are shown in Figure 2. These levels become increasingly technically specific with increasing depth. The top level (“Customer Operational Need Analysis”) can be considered the most abstract level. The aim was to show what a user of the system wishes to achieve. The focus is on the stakeholders of the system.

The level below is called “System/Software/Hardware Need Analysis”. Now, the problem definition of the top level is inverted. The aim is to show what the system has to achieve for the user. The focus of this level is on the system itself, whereby the system is considered to be a black box only. While the first two levels address the needs of the stakeholders and the system, levels three and four are dedicated to possible solutions. The third level is the “logical architecture design”. The system is now seen as a white box. The aim is to show how the system works in order to fulfil the requirements from the “operational analysis” and the “system need analysis”. The focus is on examining the interrelationships between different subsystems. The fourth level, “physical architecture design”, takes this one step further and represents the specific technical implementation of the “logical analysis”. This level describes how the system should actually be built [48].

2.2. The Capella Tool

The ARCADIA method was implemented using the associated open source software Eclipse Capella. Classical MBSE approaches distinguish between method, tool and MBSE language. While many commercial tools are available (such as Enterprise Architect from Sparx Systems, MagicDraw from NoMagix or Rational Rhapsody from IBM) and a well-known MBSE language is present in the form of SysML, a methodological approach is lacking, especially in the engineering field, which is not represented by SysML. This is the great advantage of the ARCADIA/Capella combination, as shown in Figure 3. Through this combination, both method and language (ARCADIA) as well as the tool (Capella) are embedded in a coherent, intuitive environment [48].

2.3. Representation of a System versus Representation of the Development of a System

From the perspective of model-based system engineering, there is an essential difference between modelling the final system and modelling the development of the system. In the first case, the focus of the MBSE model is on the system (which usually does not yet exist at the beginning) that is to be described. In the second case, the focus is on the development of the system. MBSE should therefore be used to describe the process to the finished system and not the finished system itself. While ARCADIA/Capella was historically designed for the first case, i.e., modelling a (final) system, the modelling of the development of a system is certainly feasible. In combination with the highly engineering-oriented modelling environment, this point in particular was decisive for the choice of MBSE method ARCADIA/Capella in the present publication.

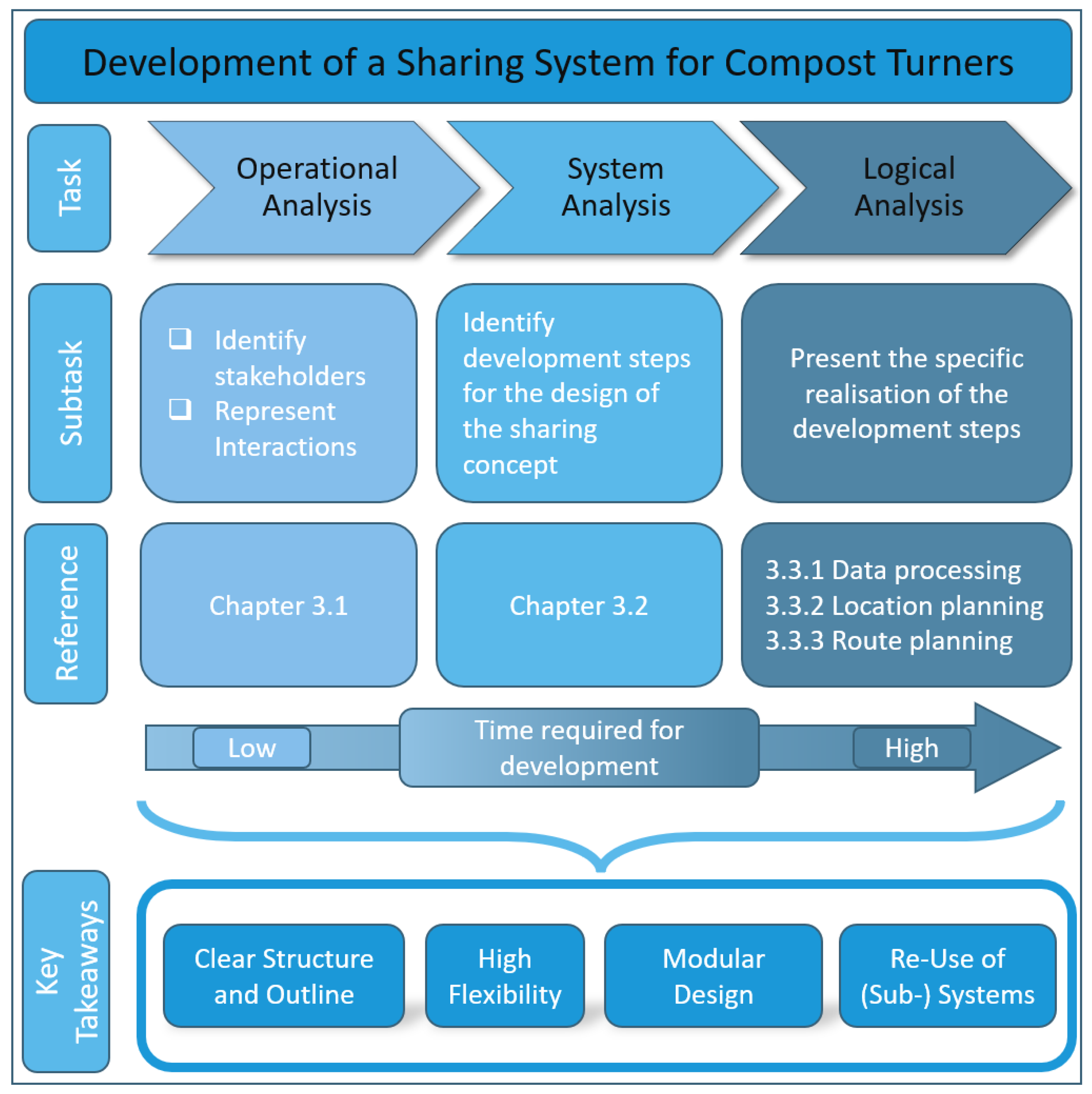
3. Development, Applications and Results

As mentioned in Section 2, a key challenge of this work is to deal with the complexity of different disciplines. Although there is a wide range of methodologies for dealing with complex systems in the literature [51,52], the interdisciplinary nature of the research project makes the ARCADIA method particularly suitable.

Since the main focus of this publication is on the technical feasibility of a sharing concept, the focus of the MBSE model is placed on the logical architecture. A detailed consideration of the underlying layer, the “physical layer”, would not serve any purpose for this publication, as this layer is mainly dedicated to the implementation of a system. Positioned between the abstract system architecture and the technically specific physical architecture, the logical architecture offers the ideal starting point for modelling the development of a sharing concept. To maintain consistency, the levels are presented—as in ARCADIA—in a top–down approach.

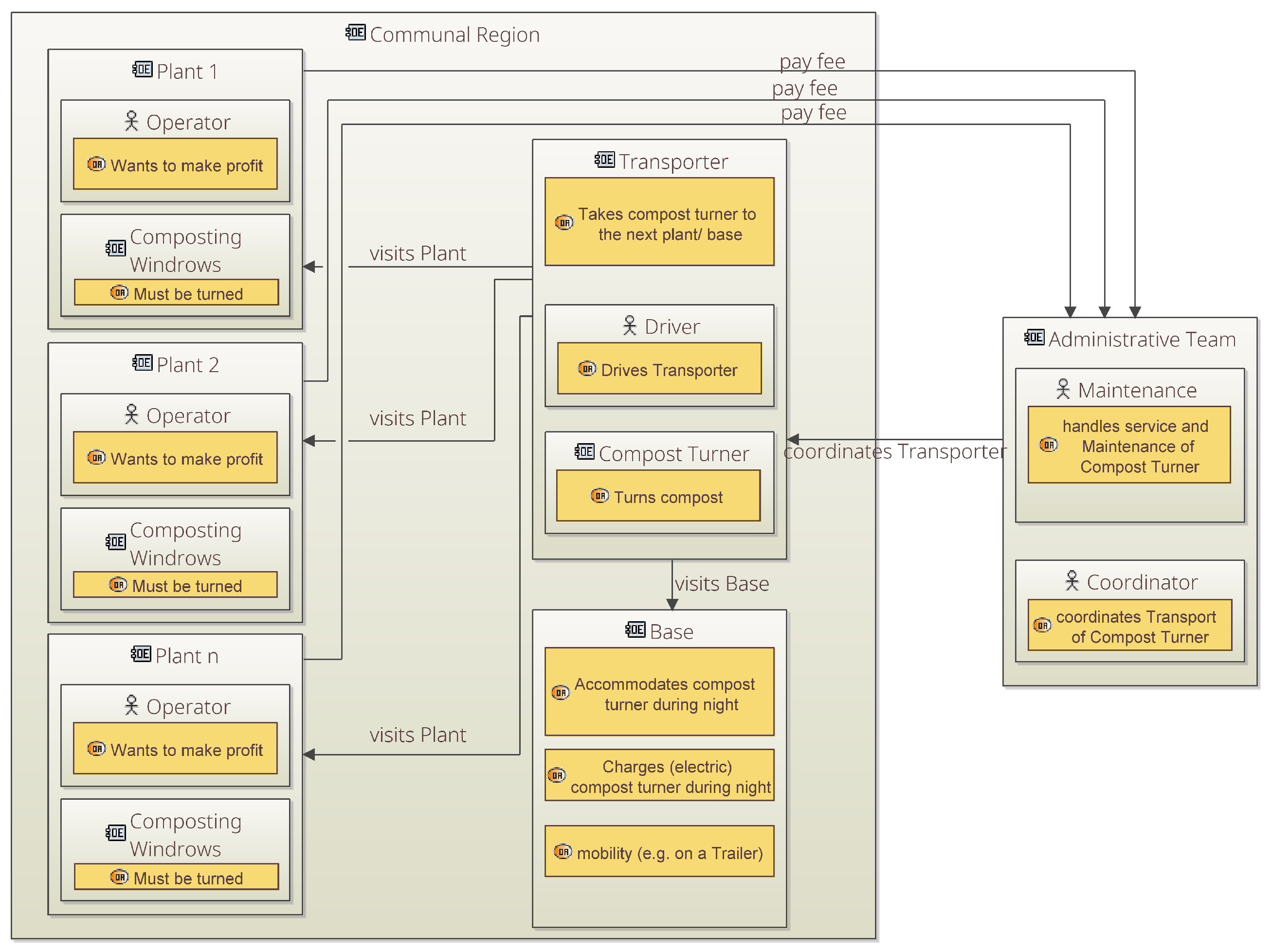
3.1. Operational Analysis—Identifying Stakeholders

The operational analysis is the most abstract level. In the first step, the interactions of all stakeholders of the sharing concept are identified. Figure 4 shows the architectural diagram of the operational analysis. Before presenting the details of this analysis, a brief overview as well as a description of the system boundaries will be given. A communal region is considered, as it is often found in the central European area. The main stakeholders are composting plants one to n. The compost turner is transported from the base—which is not yet further specified at this level—to the individual plants by a transporter. The planning of the routes is performed by an administrative team. The system is assumed to be static for further consideration. Modelled functions and behaviour do not change unless otherwise stated. Thus, higher levels, such as material flow planning (transport of material to and from the composting plants) or general growth planning are outside the system boundaries and are not dealt with.

The individual elements in Figure 4 each consist of sub-elements in ARCADIA called “operational entity” or “operational actor”. For the operational entity “composting plant one to n”, the sub-element “operator” and “compost windrow” are of importance at this level. The aim of the operator is to gain a financial advantage through the sharing concept, represented by the operational activity “wants to make profit”. For the operational unit “compost windrow”, only the property “must be turned” is relevant at this level. It is worth pointing out that “wants to make profit” is only one of many operational activities and was chosen based on expert interviews. Nevertheless, this cost-driven approach does not contradict the idea of optimising sustainability, as this represents the fundamental idea of a sharing concept (see Section 1.1). The base of the compost turner has the properties “accommodates compost turner overnight”, “charging of compost turner” and “mobility”. The sub-elements of the unit “transporter/truck” are the “driver” who is driving the transporter and the “compost turner” which is able to drive autonomously through the compost windrows. In the administrative team, a “maintenance” and “coordinator” unit is necessary. These units are responsible for the technical maintenance and coordination of the compost turner, respectively.

At this abstract level, the specific implementation of the concept is not yet dealt with. Thus, it is possible that, at a later stage, the base of the compost turner—which will be among other things responsible for charging—will not necessarily be located on a separate hub, but directly on a composting plant. It is one of the basic concepts of ARCADIA/Capella that such different scenarios can be compared precisely at a later stage of development.

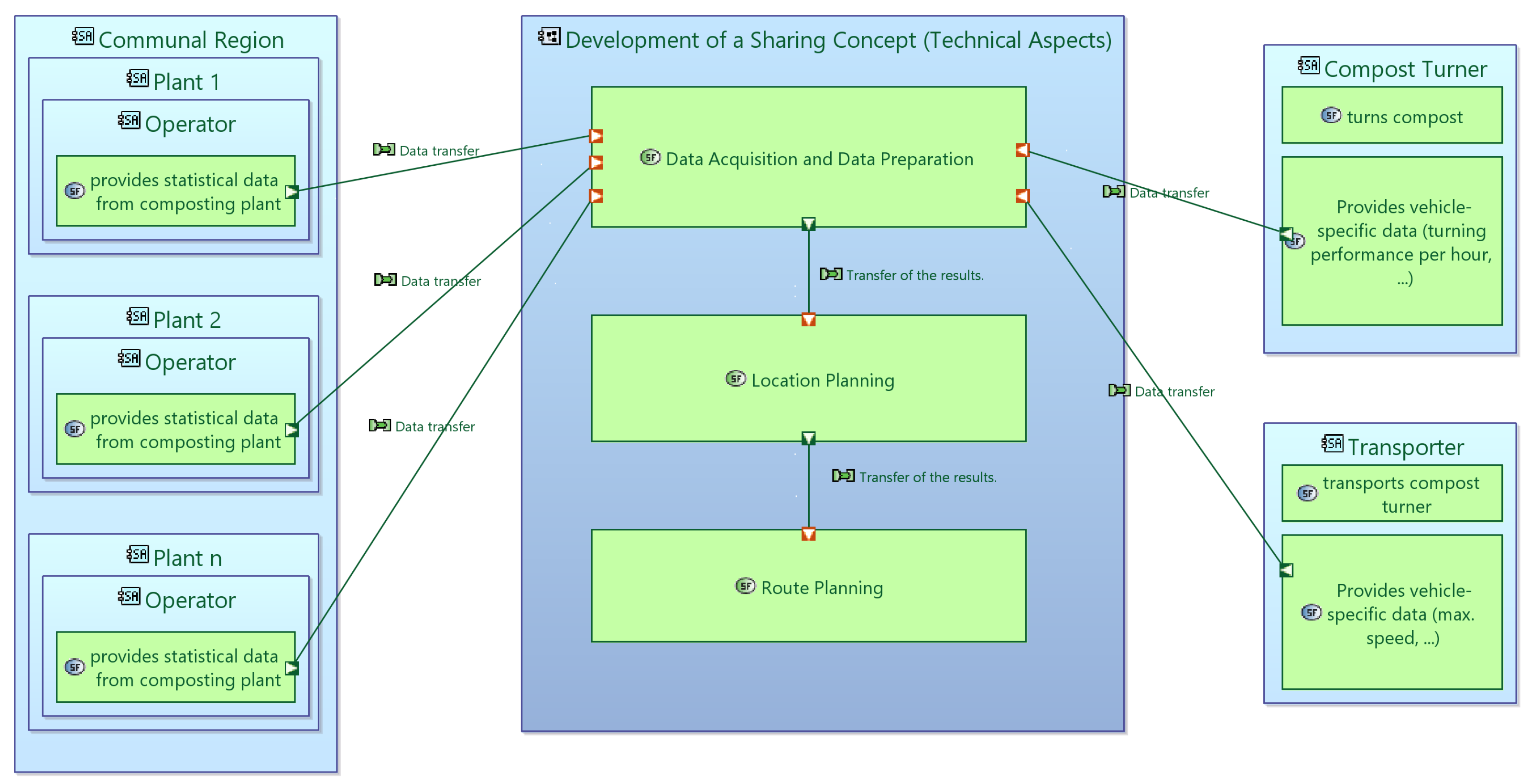
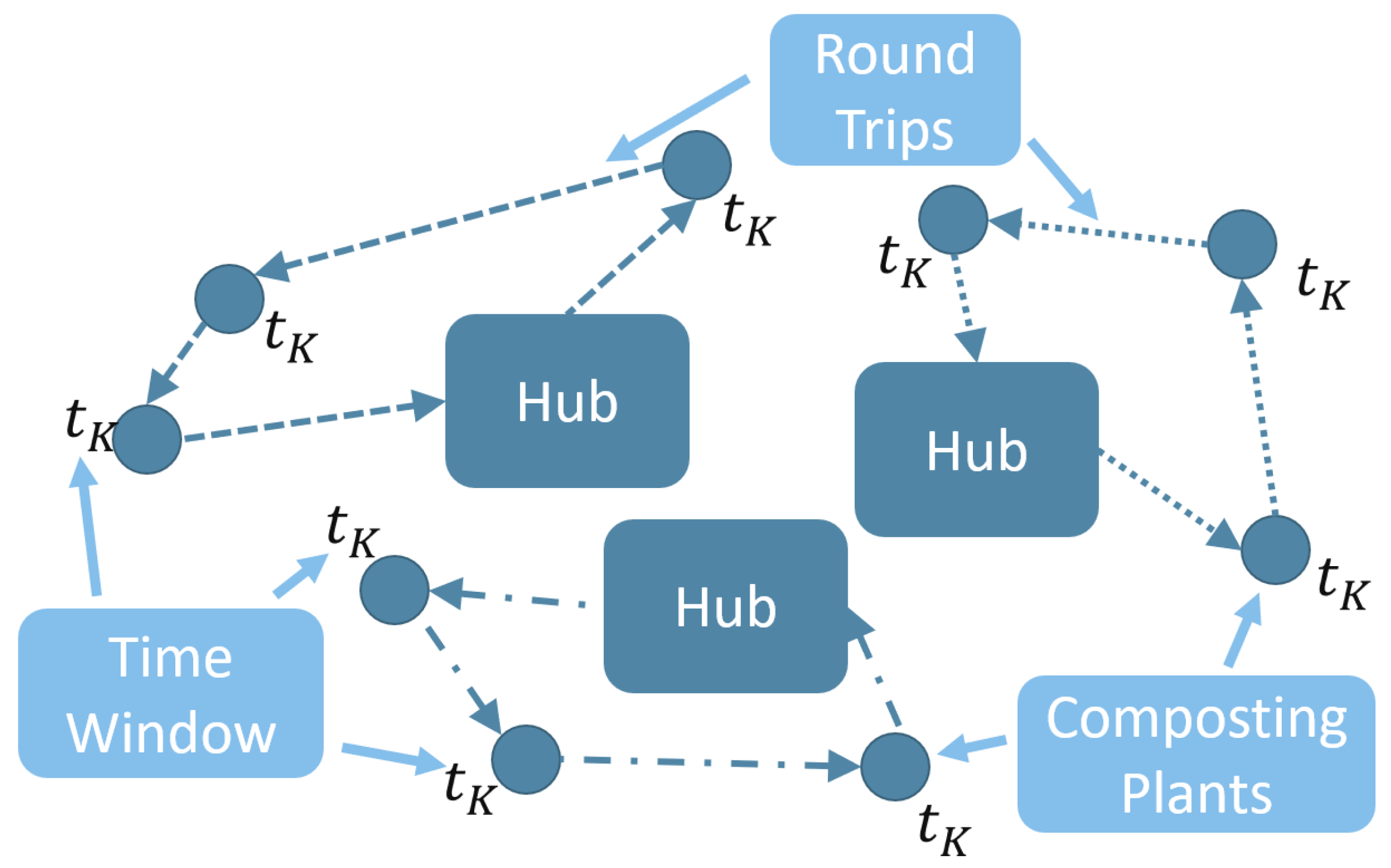
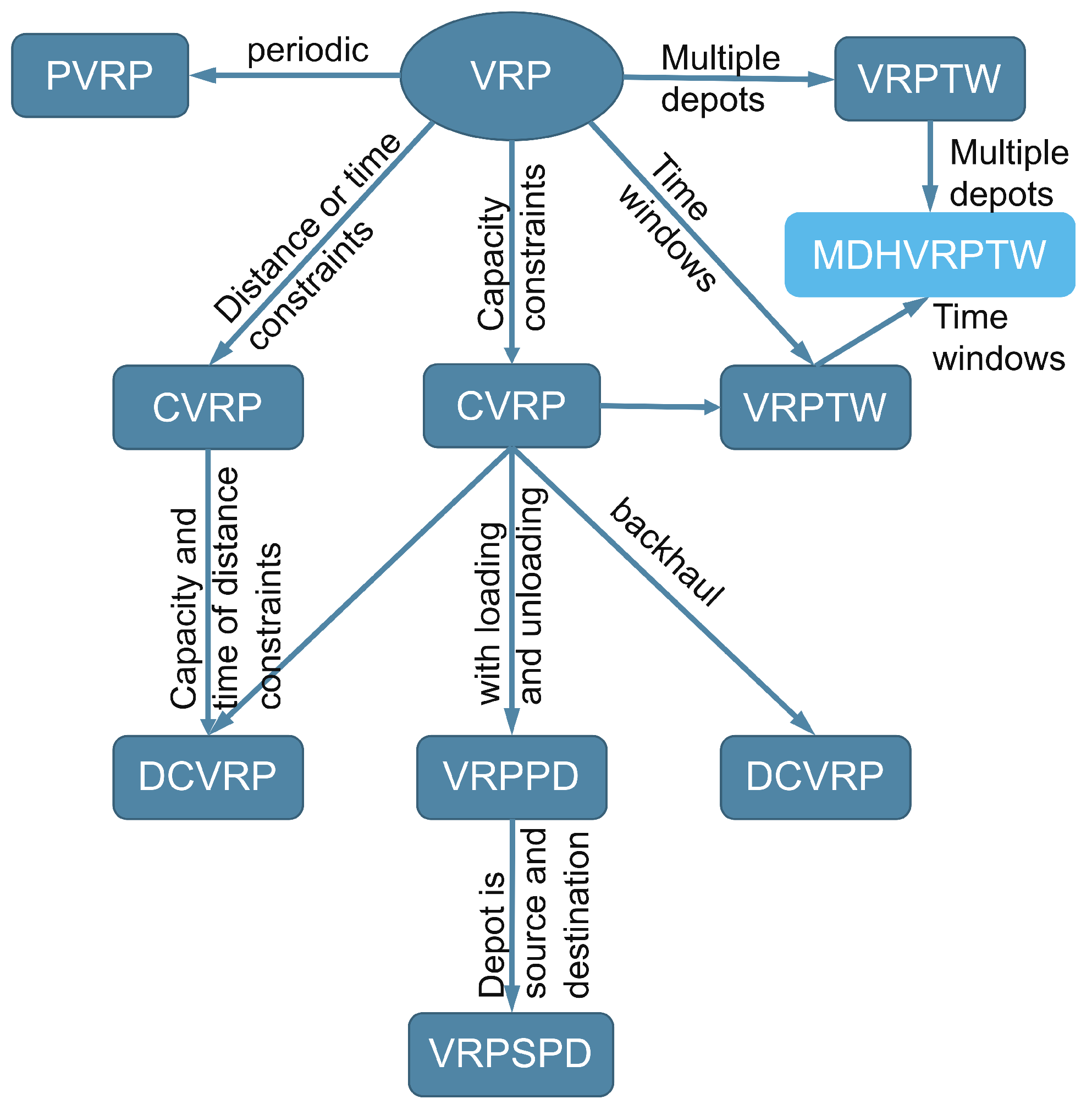
3.2. System Analysis—From Plant Locations to Route Planning

Figure 5 shows the “System Architectural Diagram”, whereby it should be noted that, from this level onwards, the focus is already on the development of the sharing concept and no longer—as in the previous level—on the sharing concept itself. The aim of the system needs analysis is on an abstract level to show what the system needs to accomplish, i.e., what is required for the development of a sharing concept. The system is seen as a black box, the focus is on the question “which steps have to be carried out for the development of the sharing concept?”, regardless of how these steps will be realised (this is the task of the logical analysis). Figure 5 shows the results of the system analysis. Similar to SysML, diagrams are used to represent both structures and behaviour. One can easily observe that the technical development of a sharing concept should be based on three main functions:

• Data acquisition and data preparation
• Location planning;
• Route planning.

The first function, data acquisition and data preparation, is responsible for processing the statistically collected data from composting plants, transporters and compost turners. The location planning function is used to determine optimal hub positions, which will serve as the base, i.e., the starting point, for the sharing concept. The transporter will travel from a base to the individual composting plants and return to the base when the work is completed. The third function, route planning, is responsible for calculating optimal routes for the compost turner’s transporter.

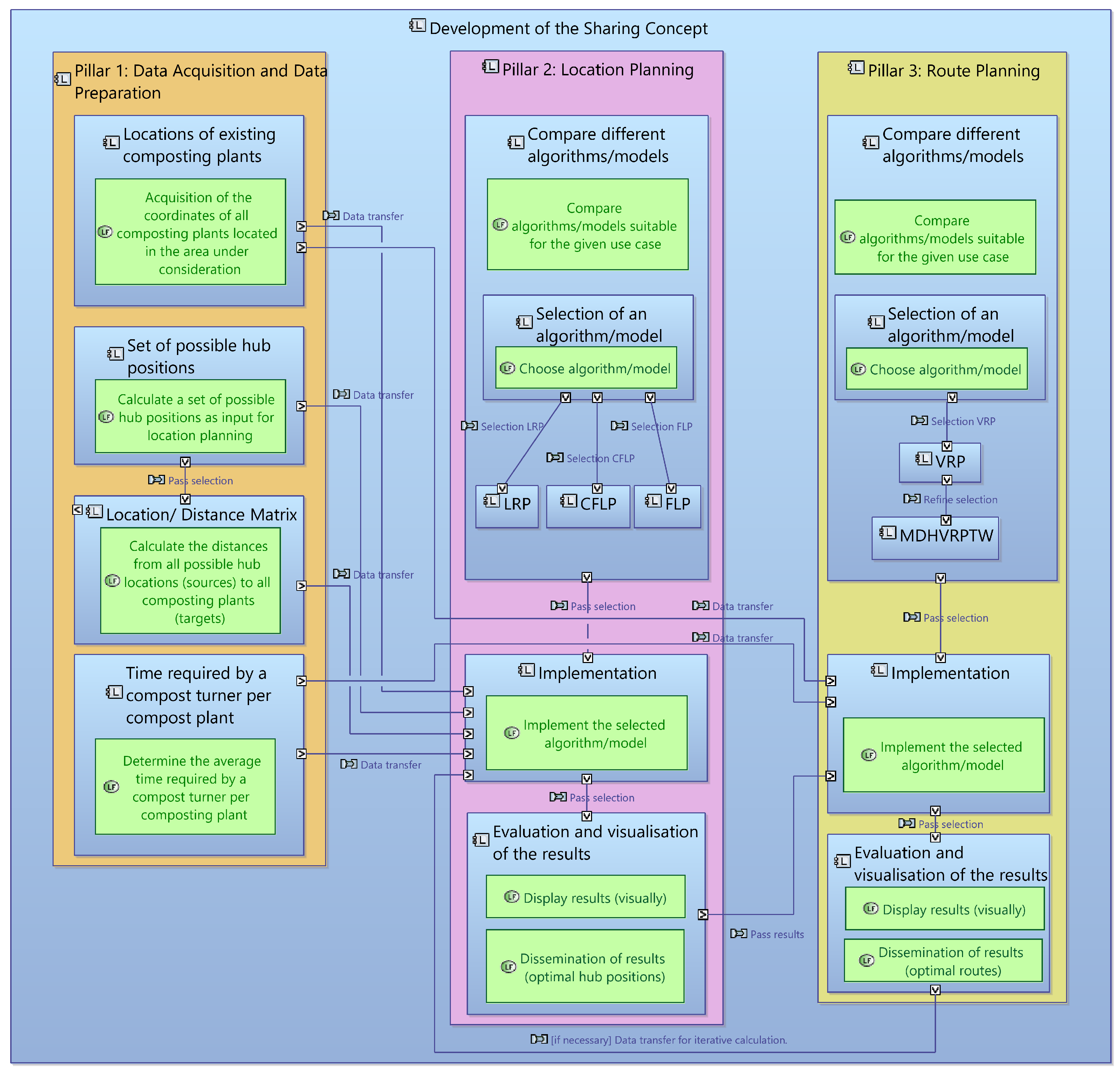
3.3. Logical Analysis—Developing the Sharing Concept as a System of Systems

The system was considered a black box at the system level. In the logical level, the box is opened and the internal relationships of the system are analysed. The logical architecture diagram is shown in Figure 6. The development of the sharing concept is structured in three main pillars, which were derived from the system needs analysis: data acquisition and data preparation, location planning and route planning. These three pillars, including their respective subsystems, are presented below.

3.3.1. Pillar 1: Data Acquisition and Data Preparation

The data preparation pillar serves to collect and prepare real world data, which will subsequently represent the input parameters for the algorithms of the Location and Route Planning pillars. It is divided into four subsystems:

• “Locations of existing composting plants”;
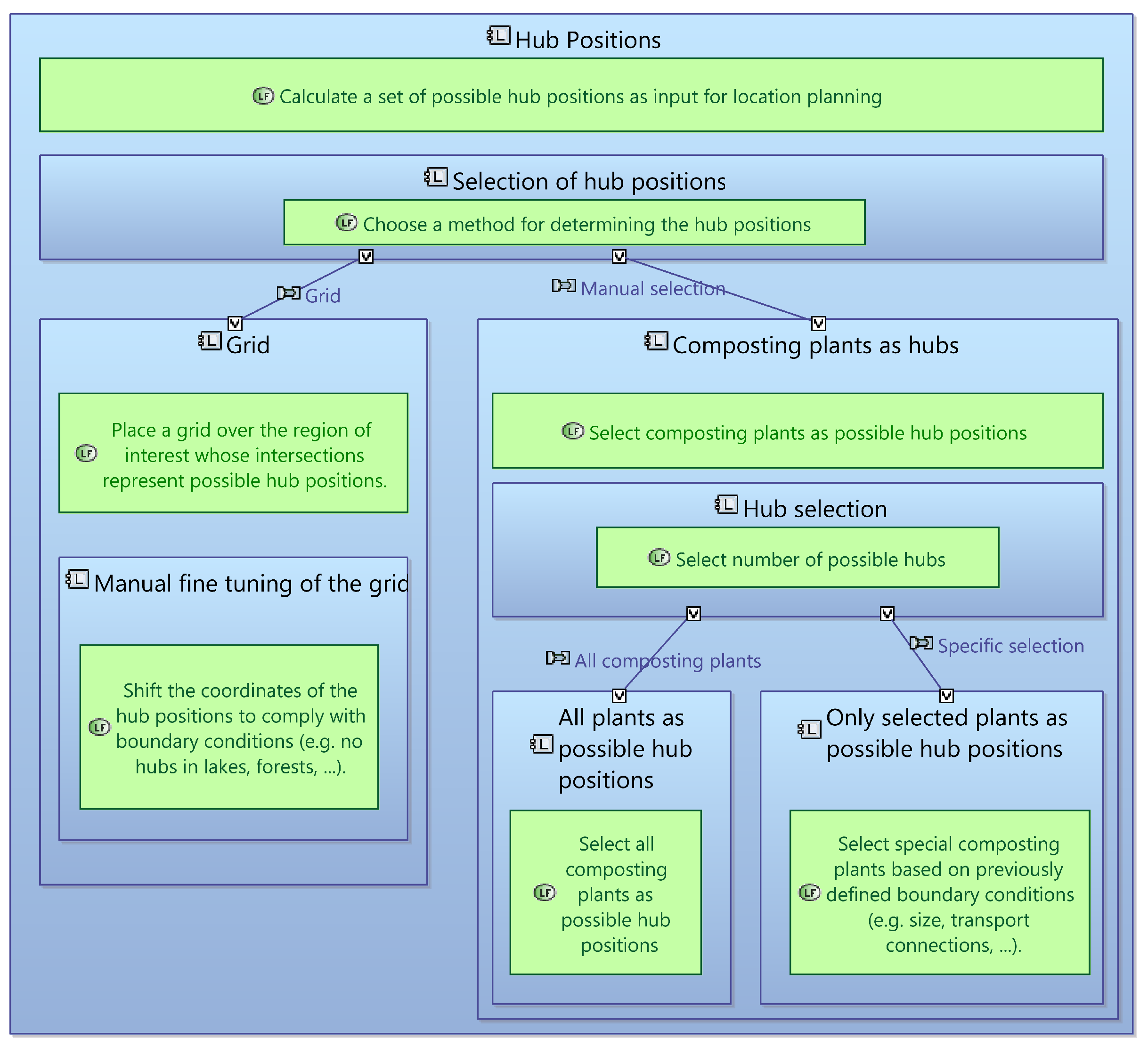
• “Set of possible hub positions”;
• “Location/distance matrix”;
• “Time requirement of a compost turner per compost site”.

These subsystems will be presented in the following chapters. In the first sub-element, Locations of existing composting plants, real-world position coordinates of composting plants in an area of interest are determined. This could be, for example, a municipal region in central Europe. The collection of these data was carried out through usual procedures such as Internet research, writing surveys and conducting expert interviews.

The second sub-element, Set of possible hub positions, covers the search for a set of possible hub positions for the base of the compost turner. These will be essential for the location planning algorithm pillar. A detailed representation of this subsystem is shown in Figure 7. There are several options how to select such a set of possible hub positions. One option would be to place a grid over the region of interest, whose intersections represent a possible hub position. This proves to be useful to fine-tune this grid afterwards, as some intersection points will have rather unfavourable coordinates. These hub positions might be located in a lake, forest, mountain or any other unsuitable positions. The manual fine-tuning of these positions is carried out under self-chosen boundary conditions, e.g., the relocation of the hub position to the nearest traffic connection, within a circular area, whose centre is the original intersection point. From a mathematical perspective, such fine-tuning would not be necessary, as the optimisation algorithm would evaluate the unfavourable positions accordingly and would therefore not select them as the optimum. From a technical-practical point of view, it is desired that each position of the entire set of possible hub positions, which is passed to the algorithm, should not be immediately excluded due to insufficient practical suitability (e.g., position is located in a lake). In addition to the generation of possible hub positions using a grid, the positioning of hubs at already existing composting facilities is also suitable for the development of the sharing concept, as shown in the subsystem “Composting plants used as hubs” in Figure 6. In this case, a distinction can be made as to whether all composting plants in the area under consideration should serve as possible hubs, or whether only specific plants should be selected through manual refinement.

Another essential input parameter for the location planning of the second pillar is the Location/Distance Matrix, which is represented by the third sub-element, as shown in Figure 6. The aim is to determine all possible combinations of distances from source (possible hub positions) to target (compost plant locations). The distance can be either the actual path length in meters from the source to target or the time a vehicle (e.g., a truck) needs for this path. The latter is more suitable for the given sharing concept.

The fourth sub-element in Figure 6, Time required by a compost turner per compost plant, deals with the question of how long a compost turner needs on a composting plant on statistical average. This parameter is needed for the algorithms in both Pillar 2 “Site Planning” and Pillar 3 “Route Planning”.

A process analysis commonly used in the literature, namely an REFA model, was carried out to determine this parameter. Figure 8 provides an overview of the mentioned process analysis by visualising the process type structure related to the operating resources, whereby the processing times are marked ([53], p. 104).

The effective time required by a compost turner per compost plant $t_K$ is the sum of the processing times depicted in Figure 8 and can thus be calculated as:

$$t_K=t_{BH}+t_{BN}+t_{BZ}+t_{BA}+t_{BS}+t_{BE}+t_{BP}+t_{BL}+t_{BR}$$

(1)

The detailed results of this analysis for the application case composting plant, that is all determined processing times, are listed in detail in

Table A1. List of all identified processing times.

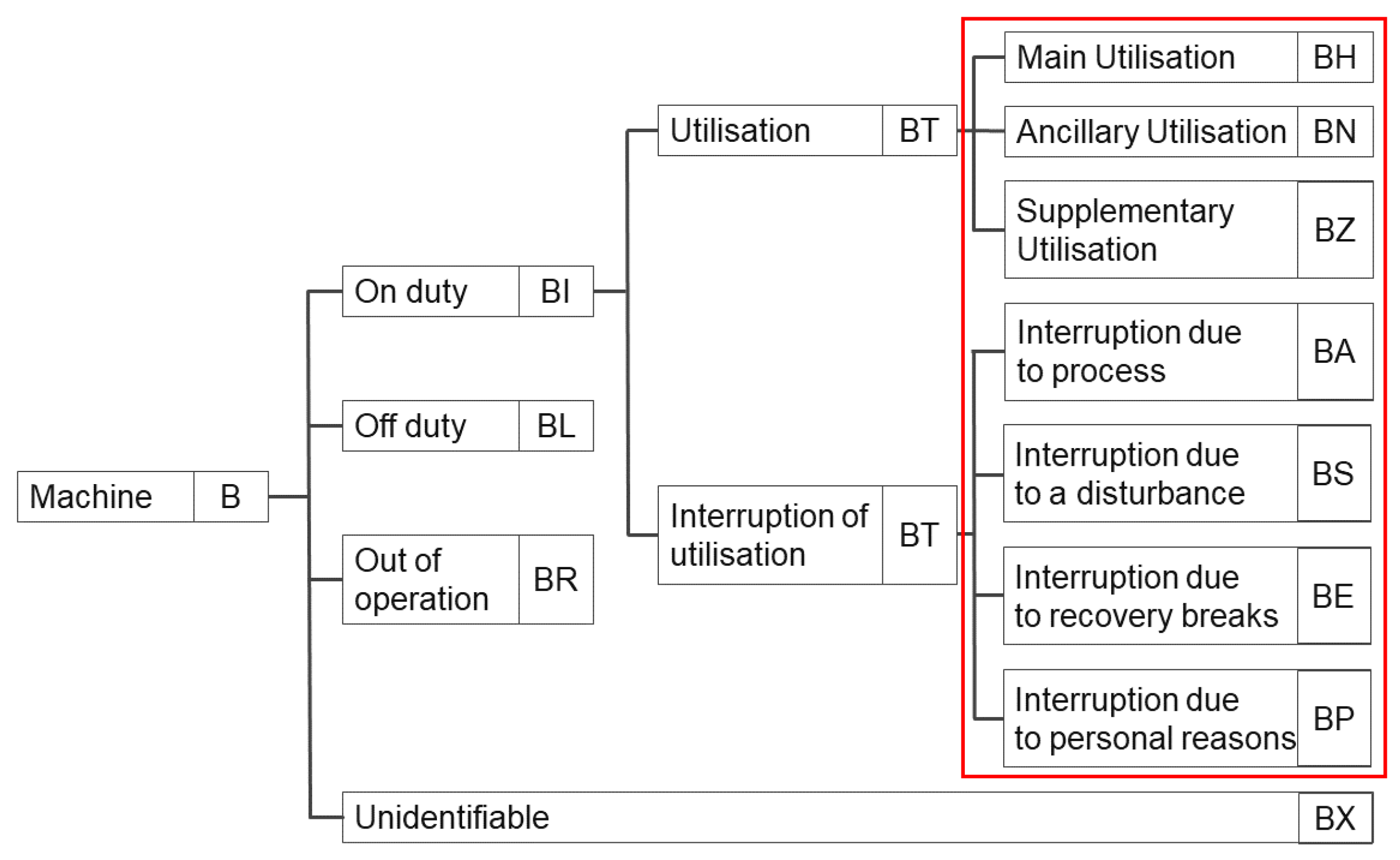
No.	Processing Times	Abbreviation	Dependent on Parameters
BH	Main utilisation
1.	Turning	$t_{B{H}_w}$	$l_m$, $v_w$;
BN	Ancillary utilisation
2.	Transfer between windrows	$t_{B{N}_m}$	$l_e$, $v_f$;
3.	Transfer between windrow and truck	$t_{B{N}_l}$	$l_l$, $v_f$;
4.	Transport between composting plants	$t_{B{N}_k}$	$l_k$, $v_{lkw}$;
5.	Charging the battery of the compost turner	$t_{B{N}_a}$	$e_v$ ($l_m$, $l_e$), $p_v$;
6.	Loading/unloading the compost turner on the truck	$t_{B{N}_b}$
7.	Preparing for turning process	$t_{B{N}_{before}}$
8.	Preparation after turning process	$t_{B{N}_{after}}$
9.	Planned waiting times	$t_{B{N}_w}$
BZ	Supplementary utilisation
10.	Delays in transport	$t_{B{Z}_v}$
11.	Unpredictable conditions/events at the composting plant	$t_{B{Z}_u}$
BA	Interruption due to process
12.	Waiting time for workers after turning process	$t_{B{A}_{wa}}$
13.	Modifications to the compost turner	$t_{B{A}_a}$
14.	Waiting time for truck	$t_{B{A}_{wl}}$
BS	Interruption due to disturbance
15.	Maintenance work	$t_{B{S}_r}$
16.	Refuelling truck	$t_{B{S}_t}$
17.	Organisational tasks	$t_{B{S}_a}$
BE	Interruption due to recovery breaks
BP	Interruption due to personal reasons
18.	Unscheduled breaktimes of the operator	$t_{B{P}_u}$
BL	Off duty
19.	Major repair work	$t_{B{L}_r}$
20.	Service	$t_{B{L}_s}$
21.	Modifications and updates	$t_{B{L}_u}$
BR	Out of operation
22.	unused	$t_{B{R}_o}$

in the Appendix A. These individual process times are in turn made up of sub-components. To give an example, the ancillary utilisation time $t_{BN}$ shall be mentioned at this point, which can be calculated as:

$$t_{BN}=\sum t_{B{H}_m}+\sum t_{B{H}_l}+\sum t_{B{N}_k}+\sum t_{B{N}_a}$$

(2)

A distinction must be made between processing times which can be calculated based on known parameters and those which can only be estimated statistically.

Table 1. Processing times.

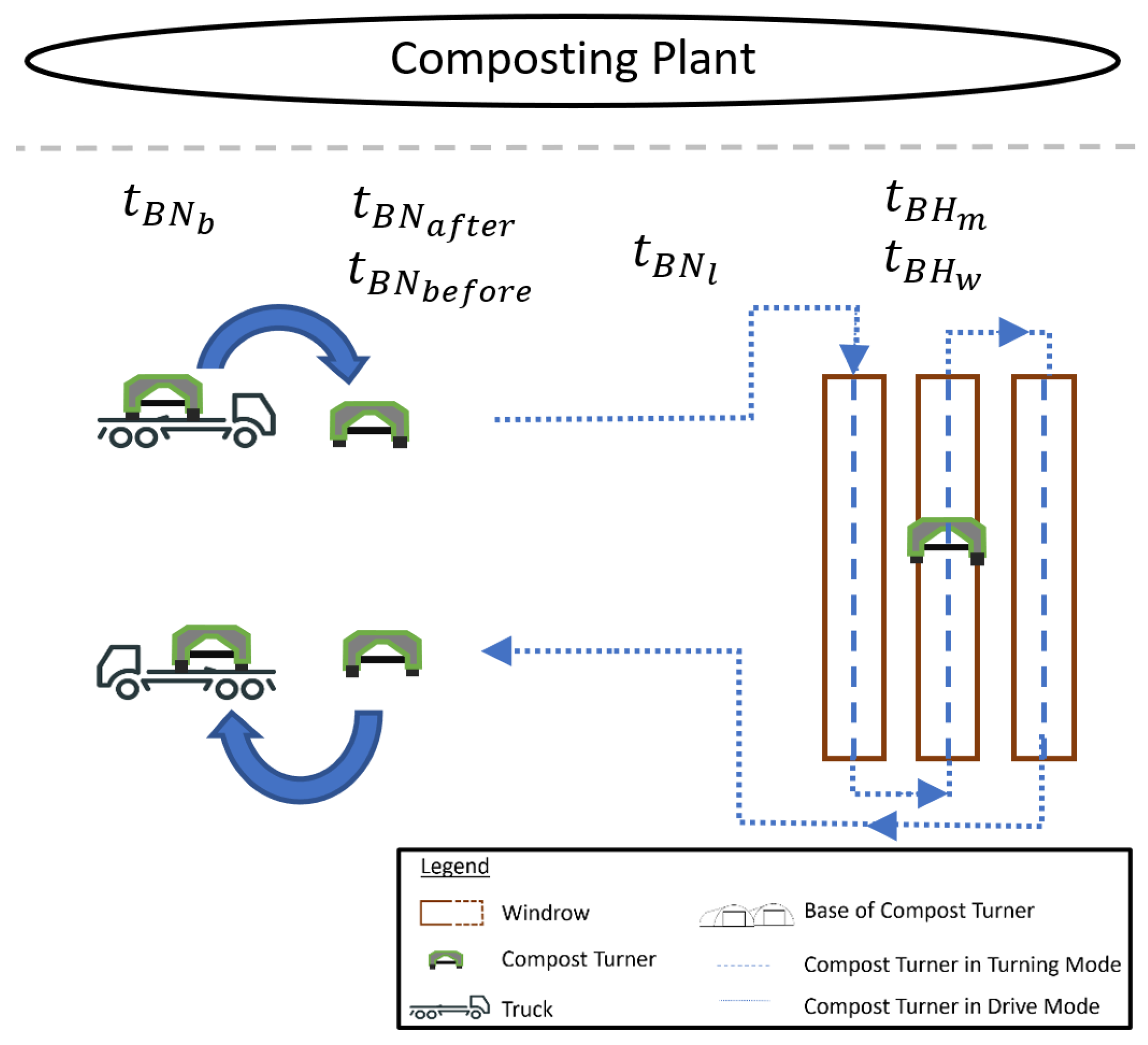
Measurable or Numerically Calculable Processing Times			Estimable Processing Times
Operating Time	Abbreviation	Formulaic Relationship	Scheduled Maintenance	${\mathit{t}}_{\mathit{B}{\mathit{N}}_{\mathit{w}}}$
Turning	$t_{B{H}_w}$	$t_{B{H}_w}$ = $l_m$/$v_w$	Unpredictable conditions/events at the composting plant	$t_{B{Z}_u}$
Transfer between windrows	$t_{B{N}_m}$	$t_{B{N}_m}$ = $l_e$/$v_f$	Waiting time for operators after turning	$t_{B{A}_{wa}}$
Transfer between windrow and truck	$t_{B{N}_l}$	$t_{B{N}_l}$ = 2 * $l_l$/$v_f$	Modifications to the compost turner	$t_{B{A}_a}$
Charging the battery of the compost turner.	$t_{B{N}_a}$	$t_{B{N}_a}$ = ($t_{B{H}_w}$ * $p_w$ + ($t_{B{N}_w}$ + $t_{B{N}_l}$) * $p_f$)/$p_v$	Waiting time for truck	$t_{B{A}_{wl}}$
Loading/unloading the compost turner on the truck.	$t_{B{N}_b}$		Organisational tasks	$t_{B{S}_a}$
Preparing for turning process	$t_{B{N}_{before}}$		Unscheduled breaktimes of the operator	$t_{B{P}_u}$
Preparation after turning process	$t_{B{N}_{after}}$

summarises the processing times that can be measured or calculated by known parameters, as well as the processing times that can only be estimated.

The parameters shown in

Table 2. Parameters for calculation of processing times.

Parameter	Unit	Description
$l_m$	(m)	Total windrow length
$l_{m_{mean}}$	(m)	Mean windrow length
$v_w$	(m/s)	Turning speed
$n_m$	()	Number of windrows
$l_e$	(m)	Distance between windrows
$l_{e_{mean}}$	(m)	Mean distance between windrows
$v_f$	(m/s)	Speed of the compost turner while not turning
$l_l$	(m)	Distance between windrows and trucks
$l_k$	(m)	Distance between composting plants
$v_{lkw}$	(m/s)	speed truck
$e_v$	(kWh)	Electrical power consumption of the compost turner
$p_v$	(kW)	Charging power
$p_w$	(kW)	Electrical power during turning of the compost turner
$p_f$	(kW)	Electrical power while the compost turner is in drive mode

can be numerically determined based on statistical surveys.

Figure 9 shows a graphical representation of the processing times from the above Table 2. Decisive for the effective time that the compost turner needs per composting plant is the time for loading/unloading the compost turner onto the truck $t_{B{N}_b}$, the preparation and post-processing for turning $t_{B{N}_{before}}$ and $t_{B{N}_{after}}$, the transfer between truck and windrow $t_{BNl}$, the transfer between the windrows $t_{B{H}_m}$ and the time needed for turning the windrow $t_{B{H}_w}$. These effectively measurable or calculable times are summarised in the “composting site production and set-up time” $t_{CPR}$.

$$t_{CPR}=t_{B{N}_b}+t_{B{N}_{before}}+t_{B{N}_{after}}+t_{B{N}_l}+t_{B{H}_m}+t_{B{H}_w}$$

(3)

The exclusively estimable processing times can, of course, not exactly be determined, but it has proven useful in industry and research to estimate them as a percentage of the total time required $t_{KPR}$. For agricultural machines, this time-share is in the order of 5%. The sum of the exclusively estimable processing times $t_R$ results in:

$$t_R=\frac{t_{CPR}}{100}·5\%$$

(4)

This results in the average time that a compost turner needs per compost plant

$$t_K=t_{CPR}+t_R$$

(5)

It should be noted that the calculated time components are assumed to be constants at this stage. Research is already being carried out on dynamic system models, which will be presented in subsequent publications.

3.3.2. Pillar 2: Location Planning

The second pillar of the logical analysis, Figure 6, deals with location planning. This domain has been intensively studied in the field of logistics research. Hence, the algorithms/models discussed in the following are examined only to the level of detail necessary for this publication. For a more in-depth consideration, one may refer to the respective literature. Based on a set of possible hub positions, which was determined by the corresponding subsystem from Pillar 1: “data acquisition and data preparation”, a set of optimal hub positions is now to be generated. These will be used as input data for the following algorithms. As a first step, three different algorithms/models are compared with each other in order to select the one that is best suited for the development of a sharing concept for compost turners. The three algorithms/models are the warehouse location problem (WLP), the location routing problem (LRP) and the capacitated facility location problem (CFLP), which are presented in the following chapters. The selection of the most suitable algorithm/model will be explained in more detail.

In the warehouse location problem, also known as the uncapacitated facility location problem, the task is to decide, given a number of customers and a number of warehouse locations, where warehouses should optimally be built in order to be able to supply the customers as efficiently as possible. The mathematical model of the warehouse location problem is based on a set of customers (targets) $i=1,\cdots ,n$, and a set of possible locations (sources) $j=1,\cdots ,m$ where new warehouses could be opened. If a location is opened, this is associated with the fixed costs $f_i$. The (transport) cost matrix $c_{ij}$ represents the costs of supplying a target i from source j. The model can thus be formulated as a minimisation problem with constraints. The weighting factor $x_{ij}$ indicates the extent to which a target i is supplied by the source j. The binary variable $y_j$ indicates whether the source j is still needed at all. This leads to the mathematical formulation, which one may study in detail in [54] (p. 52).

$$\begin{array}{cccccc}& \mathrm{minimize}:\hfill & & \sum _{j=1}^m{f}_j{y}_j+\sum _{i=1}^n\sum _{j=1}^m{c}_{ij}{x}_{ij}\hfill & & \end{array}$$

(6)

$$\begin{array}{cccccc}& \mathrm{subject}\mathrm{to}:\hfill & & \sum _{j=1}^m{x}_{ij}=1\hfill & & \mathrm{for}i=1,\cdots ,n\hfill \end{array}$$

(7)

$$\begin{array}{cccccc}& & & x_{ij}\le y_j\hfill & & \mathrm{for}i=1,\cdots ,n;\mathrm{for}j=1,\cdots ,m\hfill \end{array}$$

(8)

$$\begin{array}{cccccc}& & & x_{i,j}\in \left\{0,1\right\}\hfill & & \mathrm{for}i=1,\cdots ,n;\mathrm{for}j=1,\cdots ,m\hfill \end{array}$$

(9)

$$\begin{array}{cccccc}& & & y_j\in \left\{0,1\right\}\hfill & & \mathrm{for}j=1,\cdots ,m\hfill \end{array}$$

(10)

The capacitated facility location problem builds on the warehouse location problem. Again, a set of targets $i=1,\cdots ,n$ and a set of sources $j=1,\cdots ,m$ is defined. The weighting factor $x_{ij}\ge 0$ again indicates the proportion of a target i that is supplied by the source j. The binary variable $y_j=1$ if the facility is built at location j. If this is not the case, $y_j=0$ applies. In addition, the maximum capacity of a warehouse $M_j$ is now added as a boundary condition. This specifies the amount of storage capacity in a warehouse (source), regardless of whether the capacity of the transporter is sufficient to pick up this amount or not.

The demand $d_j$ of the customers (targets) is introduced as a further condition. This specifies the amount to be delivered to a target, regardless of whether this capacity is available in the warehouses or not. The capacitated facility location problem can thus be mathematically formulated as: [54] (p. 53)

$$\begin{array}{cccccc}& \mathrm{minimize}:\hfill & & \sum _{j=1}^m{f}_j{y}_j+\sum _{i=1}^n\sum _{j=1}^m{c}_{ij}{x}_{ij}\hfill & & \end{array}$$

(11)

$$\begin{array}{cccccc}& \mathrm{subject}\mathrm{to}:\hfill & & \sum _{j=1}^m{x}_{ij}=d_i\hfill & & \mathrm{for}i=1,\cdots ,n\hfill \end{array}$$

(12)

$$\begin{array}{cccccc}& & & \sum _{i=1}^n{x}_{ij}\le M_j{y}_j\hfill & & \mathrm{for}j=1,\cdots ,m\hfill \end{array}$$

(13)

$$\begin{array}{cccccc}& & & x_{ij}\le d_i{y}_j\hfill & & \mathrm{for}i=1,\cdots ,n;\mathrm{for}j=1,\cdots ,m\hfill \end{array}$$

(14)

$$\begin{array}{cccccc}& & & x_{ij}\ge 0\hfill & & \mathrm{for}i=1,\cdots ,n;\mathrm{for}j=1,\cdots ,m\hfill \end{array}$$

(15)

$$\begin{array}{cccccc}& & & y_j\in \left\{0,1\right\}\hfill & & \mathrm{for}j=1,\cdots ,m\hfill \end{array}$$

(16)

The location routing problem is a combined problem, consisting of location planning and route planning. The former deals with the question of which hubs (sources) should be opened and where they should be opened. The latter deals with the question of which route is the optimal one to visit all targets under given constraints, starting from the hub/source. As already mentioned in the CFLP, one of the constraints is the capacity, that is the maximum number of targets that a truck can visit within one working day.

The location routing problem is thus an iterative optimisation process of location and route planning. Since both are optimisation tasks themselves, their iterative combination leads to considerable challenges due to the resulting high computational power required. This research area has been extensively studied in the literature, however, all solutions have in common that the computational cost remains very high, even under optimal conditions [55,56].

The Selected model/algorithm for the proposed sharing concept will be discussed within the following lines. While some authors argue that location and route planning can only be solved by an iterative approach, that is, a location routing problem (see [57,58]), others argue that solving the two optimisation algorithms separately is sufficient, since a high number of iterations considerably increases the computational effort, but only slightly improves the solution [59] (p. 862).

Due to the aforementioned arguments, it therefore seems appropriate for the development of the proposed sharing concept to carry out the location and route planning separately or by means of a small number of iteration steps, respectively. As a result, the “warehouse location problem” and the “capacitated facility location problem” remain as possible candidates, and will now be further evaluated based on the required boundary conditions. The logical analysis in Figure 6 illustrates the aforementioned iterative process through the data flow “[if necessary] Data transfer for iterative calculation” from Pillar 3 to Pillar 2.

In Section 1.5, the research question was raised as to which boundary conditions are necessary for the present sharing concept. If we look at location planning in the form of a warehouse location problem, we see that the sharing concept would lack one essential requirement: namely, the boundary condition that the time $t_K$, which a compost turner needs per composting plant, is not considered in this model. This time component $t_K$, whose calculation was explained in detail in Section 3.3.1, can be considered as a constraint in the form of the maximum capacity of a warehouse M in the capacitated facility location problem. Applied to the sharing concept, the capacity M is the number of composting facilities that the transporter can approach within the given time period $t_{max}$. As a starting value for the first iteration step, the maximum capacity M can be defined as:

$$M=\frac{t_{max}·(1-p)}{t_K}$$

(17)

where $t_{max}$ is the maximum time that the compost turner can be in use per day for the sharing concept. This time includes the transport time to the respective composting plant. For example, $t_{max}=8h$ can be applied for a working day. The variable $p\in [0,1]$ estimates for the first iteration the percentage of the maximum time $t_{max}$ which the compost turner’s transport takes up (e.g., $p=20\%$). This estimation is necessary because the exact transport time is the result of route planning and is therefore not yet known at this stage. For the sharing concept, the boundary condition of the demand $d_j$ of a target specifies how often the compost turner should visit a composting plant in the given time frame $t_{max}$. Due to the biological process of composting and the legal regulations based on it, a boundary condition of:

$$d_j=1$$

(18)

could be considered useful for the proposed sharing concept. The compost turner therefore visits a composting plant exactly once per time period $t_{max}$.

In conclusion, the choice of an algorithm/model falls due to the required boundary conditions and the resulting considerations on the “capacitated facility location problem”. It should be noted, that a more in-depth consideration of the algorithms/model might seem possible at this point. However, since the focus of this publication is on linking methods rather than their in-depth analysis, the latter seems outside the scope.

3.3.3. Pillar 3: Route Planning

The results of the second pillar in the MBSE diagram (cf. Figure 6) were that, for the development of a sharing concept for compost turners, the location planning in the form of a capacitated facility location problem (CFLP) proves to be useful. The aim of this chapter is now to find the optimal routes so that the transporters loaded with the compost turners can reach all composting facilities in the shortest time possible. Figure 10 schematically depicts the communal situation mentioned in “Section 1: Introduction” with many, smaller composting plants. The exact positions of the composting plants as well as the optimal positions of the hubs have already been determined (cf. Section 3.3.1), in the following, we will now determine which algorithm/model is best suited for route planning of the proposed sharing concept.

For the sharing concept, it is assumed that the transporter carries the compost turner in the form of a round trip starting from the hub (source) to all composting plants (targets) back to the hub, as shown in Figure 10. This corresponds to the classical vehicle routing problem (VRP), which can be mathematically formulated as:

$$\begin{array}{cccccc}& \mathrm{minimize}:\hfill & & \sum _{i\in V}\sum _{j\in V}{c}_{ij}{x}_{ij}\hfill & & \end{array}$$

(19)

$$\begin{array}{cccccc}& \mathrm{subject}\mathrm{to}:\hfill & & \sum _{i\in V}{x}_{ij}=1\hfill & & \forall j\in V\backslash \left\{0\right\}\hfill \end{array}$$

(20)

$$\begin{array}{cccccc}& & & \sum _{j\in V}{x}_{ij}=1\hfill & & \forall i\in V\backslash \left\{0\right\}\hfill \end{array}$$

(21)

$$\begin{array}{cccccc}& & & \sum _{i\in V}{x}_{i0}=K\hfill & & \end{array}$$

(22)

$$\begin{array}{cccccc}& & & \sum _{j\in V}{x}_{0j}=K\hfill & & \end{array}$$

(23)

$$\begin{array}{cccccc}& & & \sum _{i\notin S}\sum _{j\in S}{x}_{ij}\ge r\left(S\right),\hfill & & \forall S\subseteq V\backslash \left\{0\right\},S\ne \varnothing \hfill \end{array}$$

(24)

$$\begin{array}{cccccc}& & & x_{ij}\in \left\{0,1\right\}\hfill & & \forall i,j\in V\hfill \end{array}$$

(25)

where $c_{ij}$ represents the cost of the trip from source i to target j. The binary variable $x_{ij}$ has the value of 1 if the trip from source i to target j is considered part of the round trip and hence part of the solution. Otherwise, it has the value 0. The set K is the number of available vehicles and $r\left(S\right)$ corresponds to the minimum number of vehicles required to serve the set S. Let the depot node be 0 [60].

The classical vehicle routing problem is to be extended by the constraint that this round trip takes place within the time $t_{max}$, which is approximately one working day, and that the transporter should wait at each composting plant for the time $t_K$ until the compost turner has performed its activity. The vehicle routing problem (VRP) thus becomes a vehicle routing problem with time windows (VRPTW), as can be seen in Figure 11.

Another constraint arises as soon as a larger region, such as a municipal region is considered: if it is no longer possible to serve all targets from one hub within the time span $t_{max}$, additional hubs must be set up, from each of which a transporter loaded with a compost turner starts. Figure 10 shows the situation with three hubs, where one transporter starts from each hub. The calculation model needed for this is the multiple-depot vehicle routing problem (MDVRP), see Figure 11.

Taking into account the aforementioned boundary conditions, a calculation model is sought which takes into account both the time component (time windows) and the fact that several hubs (multi-depot) are required. Therefore, the multi-depot heterogeneous vehicle routing problem with time windows (MDHVRPTW) is proposed for route planning in the development of a sharing concept for compost turners [60,61]. For a more in-depth consideration, please refer to the respective literature [62].

4. Discussion

In this work, a procedure for the development of a sharing concept for a compost turner was presented. By applying model-based systems engineering, specifically the ARCADIA method, this procedure could be systematically demonstrated. Since historically document-based procedures were predominantly used for the development of new concepts, the focus was also previously limited to the development within individual disciplines. While this established a “silo thinking” that promoted communication within the respective discipline, collaboration between disciplines was very difficult to achieve. Therefore, the presented development of a sharing concept should be an incentive to move away from “silo thinking” and towards multidisciplinary cooperation. Since the presented systems and subsystems—which are necessary for this development—are based on different disciplines, it is essential to have a close communication between these disciplines. The introduced MBSE models, which range from the abstract operational analysis to the more technically specific logical analysis, are meant to realise this essential aspect.

In addition, one major strength of the presented development for a sharing concept is its clear structure and outline, which stems from the MBSE/ARCADIA method. Regarding the aforementioned need for good communication between individual disciplines, the advantage of a clear structure provides a significantly increased flexibility for the development process. Compared to traditional development approaches, the MBSE structure allows a clear traceability of all changes in respective systems and subsystems, as well as their impact on other components. Even major changes that affect the overall system, such as modified or new boundary conditions, algorithms or mathematical approaches for location/route planning, can thus be represented.

Figure 12 shows a process model of the most important development steps and the reference to the corresponding chapter. Furthermore, an assessment is given of the time required for the development of the proposed process steps as well as the corresponding key takeaways. In summary, it can be concluded that the operational analysis deals with the identification of stakeholders on an abstract level, as discussed in detail in Section 3.1. The time required to create this MBSE model is estimated to be comparatively low. The system analysis identifies which development steps are necessary to create a sharing concept for compost turners. In the corresponding Section 3.2, three aspects were identified, namely the data preparation and processing, location planning and route planning. The time required to create this level is estimated to be higher than for the operational analysis. The logical analysis is the main part of this work. The aspects identified in the system analysis were addressed in detail in the form of three pillars. Specific development steps were proposed, some of which left open scenario-based decision options (see Section 3.3.1 “Set of possible hub positions” and Figure 6). In the pillars of location planning and route planning, various algorithms were compared with each other in order to be able to make a clear recommendation as to which algorithm/model is best suited for the proposed sharing concept. At this stage, the development effort is considered to be comparatively high. On the one hand, there are numerous process steps in the first pillar that require the collection of statistical data. Since these data most likely have to be collected beforehand, this will require substantial amounts of time. The location and route planning pillars, on the other hand, are characterised by a high level of complexity, which is reflected in the development effort in the form of higher time expenditure for their implementation.

The presented development for a sharing concept is based on systems, subsystems, and their interactions, due to ARCADIA. In addition to the benefits already discussed, this modular design of the MBSE model also offers organisational advantages. Firstly, it makes clear which tasks, framework conditions and system boundaries the respective (sub-) systems have. As a result, distinct tasks can be derived for each operating unit. Errors due to unclear communication interfaces can thus be significantly reduced. Furthermore, this design also allows the easy reuse of systems. Thus, similar processes can be reused in a modified form. The logical architecture from Figure 6 should serve as an example. It can be seen that the subsystems “Evaluation and visualisation of the results” occur both in location planning from Pillar 1 and in route planning from Pillar 2. Therefore, it can already be seen from the MBSE model that close cooperation between the operating units implementing these systems will be necessary. Developing a sharing concept for compost turners using MBSE thus also has the significant advantage of shortening the implementation and commissioning process.

Upon closer assessment, one realises that the MBSE model created in this work does not, of course, claim to represent the only way to develop a sharing concept for compost turners. The ARCADIA method allows for a clearly defined, structured approach during development, but still leaves room for creativity. This creativity leads to the situation that the presented MBSE model for the development of a sharing concept should not be considered as a static object, but rather a model that evolves. Thus, following the ARCADIA method, new, alternative models can be developed, which outperform the old model. One should only keep in mind that the alternative models must always fulfil the boundary conditions and requirements that have been initially defined.

At this point, a critical remark should be made, especially with regard to the logical architecture. From a logistical-technical point of view, it is immediately clear that the models and algorithms presented are by no means novel. This is only right because this work does not claim to present new, optimal mathematical concepts for the logistics field. Nor was it the aim, from a systems engineering point of view, to devise new kinds of workflows in terms of operational research. The present work has instead shown how, using elements from different disciplines, a sharing concept can be developed that both follows the highly structured approach from model-based systems engineering as well as presenting the mathematical models from a logistical-technical perspective. From the authors’ point of view, this interdisciplinary approach represents the novelty of the presented work.

5. Industrial Application and Further Research

There is a clear interest from the industry, especially the operators of composting plants, in increasing the utilisation of compost turners, as would be possible through the sharing concept presented. This also applies to the question of the extent to which fully autonomous compost turners, which are currently in the prototype phase, could be used in the course of the sharing concept. Such a prototype of a fully autonomous compost turner was developed within several research projects in the framework of national and international cooperation between industry and research, with significant involvement from the Graz University of Technology.

While this publication has presented the feasibility of developing a sharing model from a technical perspective, the economic component still needs to be considered. One especially critical issue is the interaction between technical and economic aspects, since a separate consideration would not be sufficient to depict all the relations and dependencies. Similarly to the procedure presented for the technical aspects, such considerations could be investigated using the MBSE method. There are already initial approaches in this regard, which the authors will publish in the near future.