Cold Chain Logistics Distribution Path Planning of Fresh Products in Beijing Subcenter
Abstract
:1. Introduction
2. Literature Review
2.1. Fresh Product Logistics and Distribution
2.2. Logistics Distribution Path Planning
3. Distribution Path Optimization Model
3.1. State of Development of Beijing Subcenter
3.2. Assumptions for Distribution Path Optimization Model
- The geographic locations of the distribution center and locations for delivery in the subcenter are determined. There is no refusal to deliver, no delivery personnel are unable to complete the delivery or deliver the goods during delivery, and every delivery is completed.
- One type of distribution vehicle is considered with the same basic configuration, maximum load capacity, and maximum operating distance. In addition, no differences regarding service time and minor faults are considered. The demand for goods at each distribution location is below the maximum load capacity of the vehicle.
- Items from different distribution locations can be mixed and transported without affecting the movement of vehicles or the loading and handling of goods.
- All types of items at each distribution location can be mixed and transported simultaneously, and the required transport and storage conditions can be ensured by any vehicle.
- Regardless of driving and road conditions, all the transport vehicles travel at the same speed.
- All the roads are clear, without uncertain conditions, such as blockages and road closures, and the wait time for traffic lights is expressed as a distance, which is the same per kilometer of travel.
- The distribution center has enough goods for delivery, without shortage. In addition, a logistics distribution vehicle can travel to different distribution locations to deliver the remaining goods after completing a delivery in one place and then return. However, each distribution location can only have one delivery vehicle, thus preventing multiple vehicles from carrying goods for the same delivery.
- A proportion of goods may be damaged during transportation, and the damage is related to the time for distribution. Thus, damage to goods only occurs during transportation. As conditions such as road status and speed are assumed constant during transportation, the distance is directly proportional to the damage rate of goods.
- The distribution vehicle returns to the distribution center after completing the assigned delivery.
3.3. Distribution Path Optimization Modeling
3.3.1. Symbol Description
- k = : Number of refrigerated trucks owned by the distribution center;
- : Average speed of a refrigerator vehicle, unit ;
- : Cost per unit fresh product, unit ;
- : Unit gas pollutant emission cost, unit ;
- : Unit fixed-use cost of refrigerated vehicle, unit ;
- : Unit fuel consumption cost, unit ;
- : Unit cooling cost during transportation, unit ;
- : Unit cooling cost during unloading, unit ;
- : Represents the corruption rate in the process of transporting fresh products;
- : Represents the corruption rate in the handling process of fresh products;
- : Represents the distance between delivery locations and , unit ;
- Q: Maximum load of refrigerated truck, unit ;
- : Represents the demand amount of the distribution point , unit ;
- : Represents the remaining cargo weight of the refrigerated truck when it leaves the distribution location , unit ;
3.3.2. Determine the Objective Function
- (1)
- Fixed cost
- (2)
- Fuel consumption cost
- (3)
- Cost of goods damage
- (4)
- Refrigeration cost
- (5)
- Carbon emission cost
- : carbon emissions;
- : fuel consumption, ;
- : fuel emission factor.
3.3.3. Define the Constraints
- (1)
- Transport vehicles uniformly start from the processing and distribution center and return to the processing and distribution center after serving all the designated distribution locations.
- (2)
- Each distribution location shall have only one refrigerated truck for distribution and the required distribution quantity of the store shall be met.
- (3)
- The sum of demand at each distribution location on each path should not exceed the maximum carrying weight of the refrigerated trucks, and the total number of distribution paths should not exceed the number of vehicles.
- (4)
- The refrigerated vehicle runs on the path at a constant speed, and the driving distance of each refrigerated vehicle cannot exceed the prescribed maximum driving distance.
3.3.4. Construct the Path Optimization Model
4. Algorithm Design and Result Analysis
4.1. Ant Colony Optimization
4.1.1. Overview
- (1)
- In the absence of pheromones, ants choose the direction to move in according to their own habits. When a pheromone is detected, the ants move according to the probability of pheromone concentration.
- (2)
- Ants leave behind pheromone traces associated with their home/food when searching for food/their home. As the distance travelled increases, less pheromones are deposited.
- (3)
- The pheromones evaporate over time.
4.1.2. Algorithm Formulation
- (1)
- Path construction:where is the probability that k ants in the t-th generation choose to move from location i to j, α is the pheromone importance, β is the relative importance of heuristic factor , and represents the available locations for selection by ant k (each location can be visited only once). In this study, we set = .
- (2)
- Pheromone update:where denotes the pheromone left along the path from location i to j by the ant in the t-th generation. The amount of information along path (i, j) at generation t + can be adjusted according to Equation (25), where:which denotes the pheromones left by ants along path (i, j) andwhich denotes the pheromones left by ant k along path (i, j). In the equations above, is the total number of pheromones possessed by an ant over its lifetime, is the circumference length of ant k, n is the number of ants, and is the rate of pheromone evaporation.
4.2. Improved Ant Colony Optimization
4.2.1. Improvements to Ant Colony Optimization
- (1)
- Ants have different rules for state transition;
- (2)
- Different pheromone update rules are defined;
- (3)
- A constraint is added to the ant path considering the model of this study, such that the path constraint not only reflects state transition but also existing knowledge when the ant selects the next node to visit.
- (1)
- Improved state transition rules for ant colony optimization. In the original ant colony optimization, ants move according to the probabilistic transition rule in Equation (24), which can easily lead to long search times owing to the lack of learning from previous search results. To improve the search performance, we explore new paths and establish equilibrium using existing knowledge through a novel path selection mechanism.WhenWhenwhere is a random number in [0, 1] and is a pseudo-random factor. When , the probability search is carried out. Using the ant state transition rule of improved ant colony optimization, ant k considers the amount of pheromone along each path for selecting the next node, j, to visit, and a random factor combined with a random proportion is used to balance existing knowledge with the exploration of new paths. When ant k selects its next location, existing knowledge is first considered to determine the probability of moving from location i to j. Individual ants tend to use existing knowledge for selecting the next location, ensuring that all the possibilities that satisfy the model requirements are traversed and likely reaching a realistic global optimum.
- (2)
- Pheromone update rules. In the original ant colony optimization, the pheromone update mechanism is relatively simple. For the next move, the shortest path information obtained in the previous loop is mostly neglected, undermining the algorithm’s performance. We introduce the following improvements into the pheromone update rule:where is the amount of pheromones generated by an ant after completing the current round of visits, is the length of the currently available optimal path, and T is the combination of nodes at each distribution location along the current optimal path.
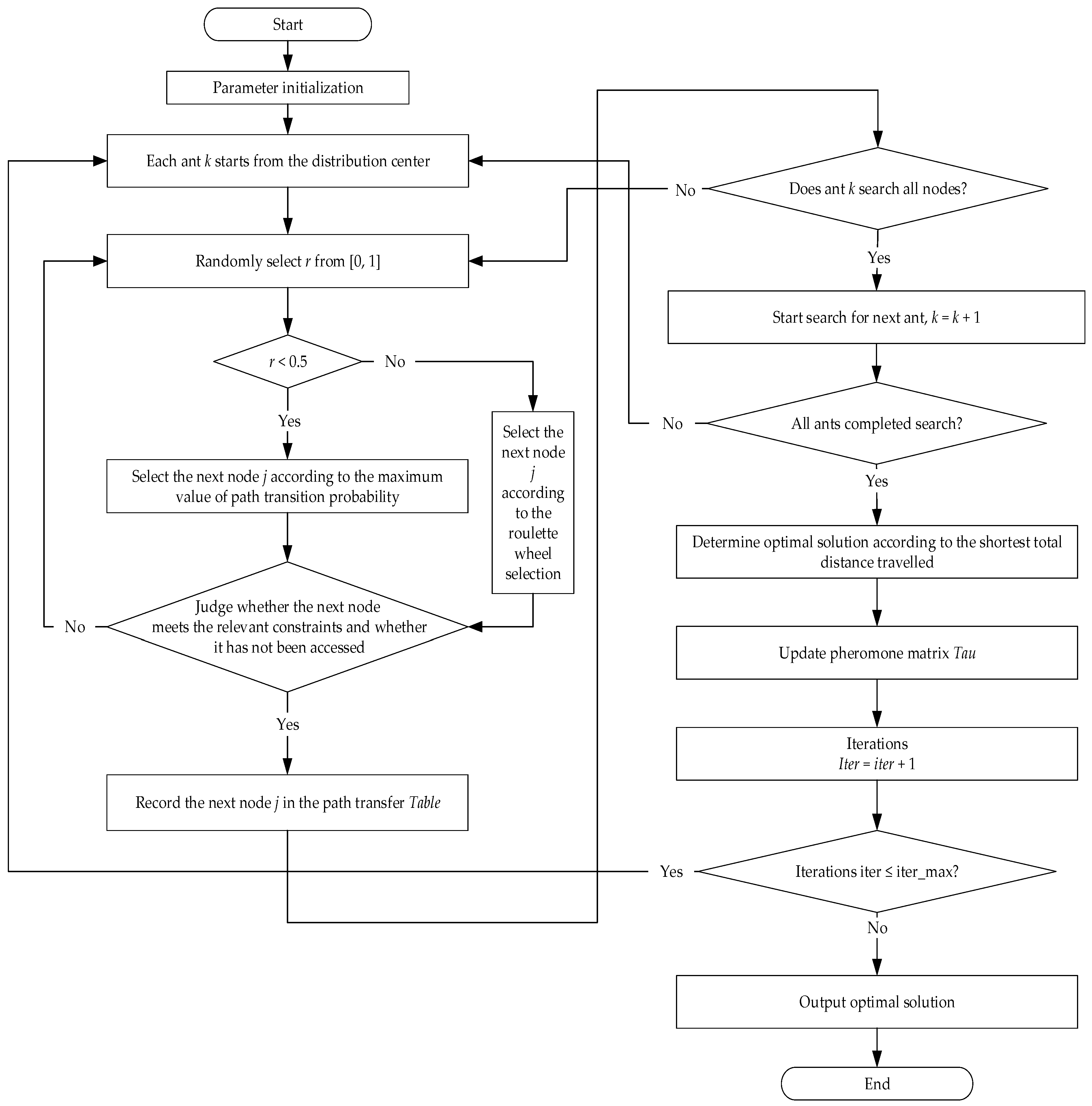
4.2.2. Solving Procedure
- (1)
- Parameter initialization is applied to define and assign the distance matrix, demand matrix, and other model parameters. In this study, we set the number of ants to 80 and constructed pheromone matrix Tau and path record Table.
- (2)
- When the number of iterations is below the maximum, i.e., iter < iter_max, ant colony optimization proceeds as follows.
- (3)
- First, construct the paths of all ants. Each ant starts from the distribution center, and for each ant, r is randomly assigned a value in [0, 1]. If r < 0.5, the path transition probability is calculated for each remaining distribution location that has not been visited, and the next location, j, to be visited is selected based on the maximum path transition probability. If r > 0.5, the path transition probability is recorded, and the node is selected according to the roulette-wheel method for the next location, j, to be visited. The selected node is placed in the Table, which contains the recorded paths.
- (4)
- After moving to the first visited distribution location, the next possible location to be visited is selected based on the relevant constraints among the available unvisited locations. The next location that can be visited must satisfy the following conditions: (i) the node has not been searched, and (ii) the total distance currently travelled is less than the maximum distance that can be travelled by a vehicle. If a location satisfies the above conditions, according to the transition rule in step 3, the next distribution location to be visited is determined from the available locations, and the location is added to the Table. If no location satisfies the conditions, ant k must return to the distribution center and visit a new location starting from there.
- (5)
- If ant k has searched all the locations, go to step 6. Otherwise, return to step 3.
- (6)
- The next ant starts visiting the locations according to steps 3–5. After constructing the paths of all ants when the search finishes, closed routes starting and ending at the distribution center are obtained, thus filling the Table.
- (7)
- The total distance travelled by each ant along its path is calculated, and the optimal path is selected according to the shortest distance. This optimal path is stored, and the corresponding optimal value is obtained.
- (8)
- The optimal path is used to update pheromone matrix Tau and obtain the corresponding optimal path and solution.
- (9)
- The number of iterations is increased by one. Steps 1–7 are repeated, and the optimal solution of the current iteration is compared with that of the previous iteration. The solution with the shortest paths is stored along with the corresponding optimal path. This optimal solution is used to update pheromone matrix Tau, and the corresponding optimal path and solution are obtained.
- (10)
- Repeat step 9 until reaching the maximum number of iterations, iter_max. Then, the algorithm terminates by providing the optimal solution and paths across iterations. We draw the optimal paths and determine the optimal solution for distribution.
4.3. Main Fresh Food Distribution Center and Distribution Locations in Beijing Subcenter
4.3.1. Selection of Distribution Centers and Locations and Geographic Area
4.3.2. Distance Analysis of Distribution Locations
- (1)
- These methods facilitate large-scale path planning, save costs, and a correlation exists between the straight-line and actual distances, thus providing a valid reference.
- (2)
- Many actual routes are difficult to determine, and considering straight lines avoids the time-consuming determination of actual distances between distribution locations.
- (3)
- A route involves various elements, and the application of path planning should have data support and guidance, but this is not as simple and convenient as considering the straight-line distance.
- (1)
- The recommended route with the shortest path is preferred.
- (2)
- The route with fewer traffic lights is preferred if the candidate route lengths are similar.
- (3)
- For a moderate difference in route length and a large divergence in the number of traffic lights, the route with fewer traffic lights is preferred. The distances between the distribution center and locations identified in Table 1 are listed in Table 2 and Table 3. The numbers 1 to 29 in Table 2 and Table 3 correspond to the numbers of the names of each distribution place in Table 1, respectively.
4.3.3. Distribution Vehicles
4.3.4. Demand at Distribution Locations
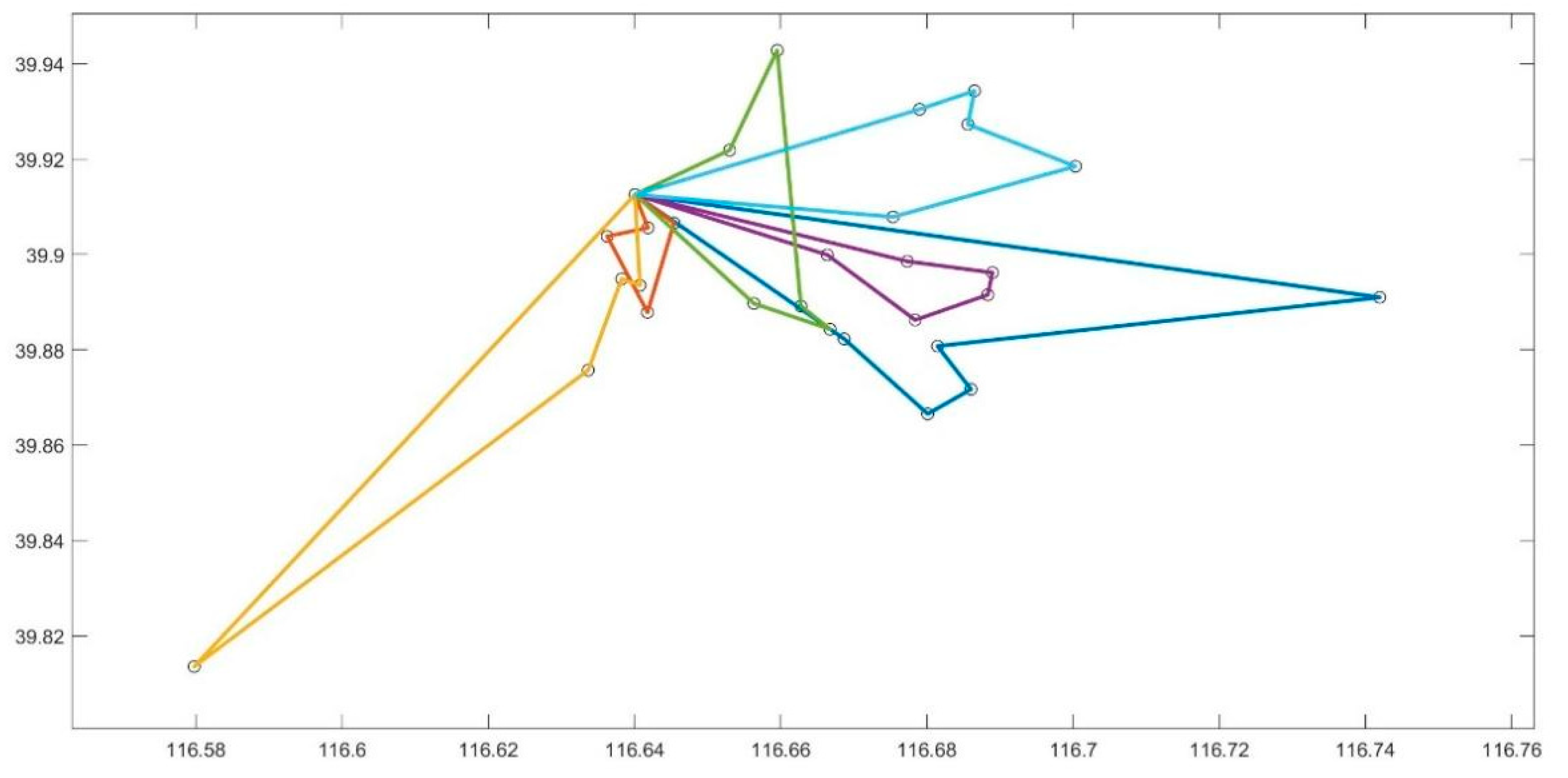
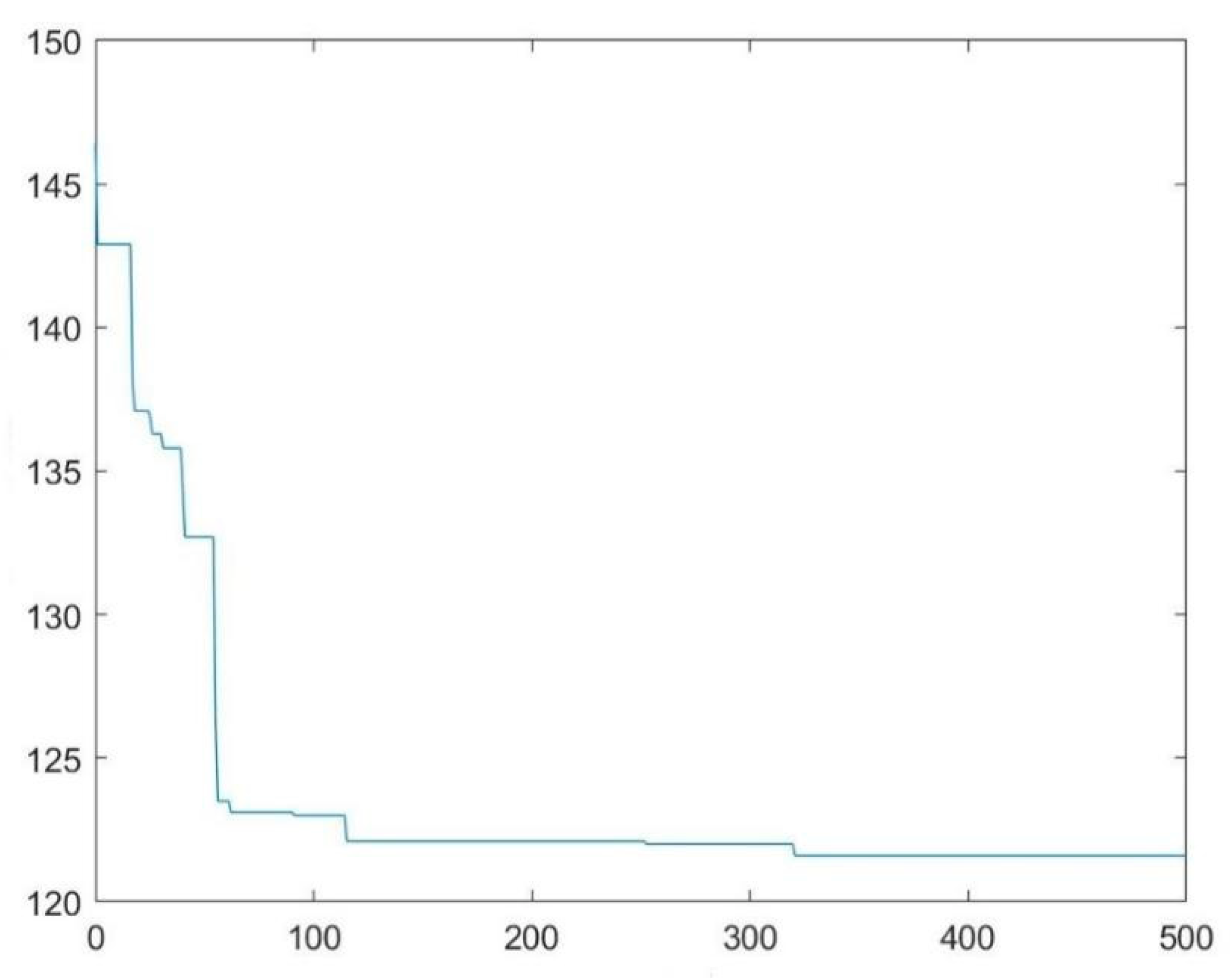
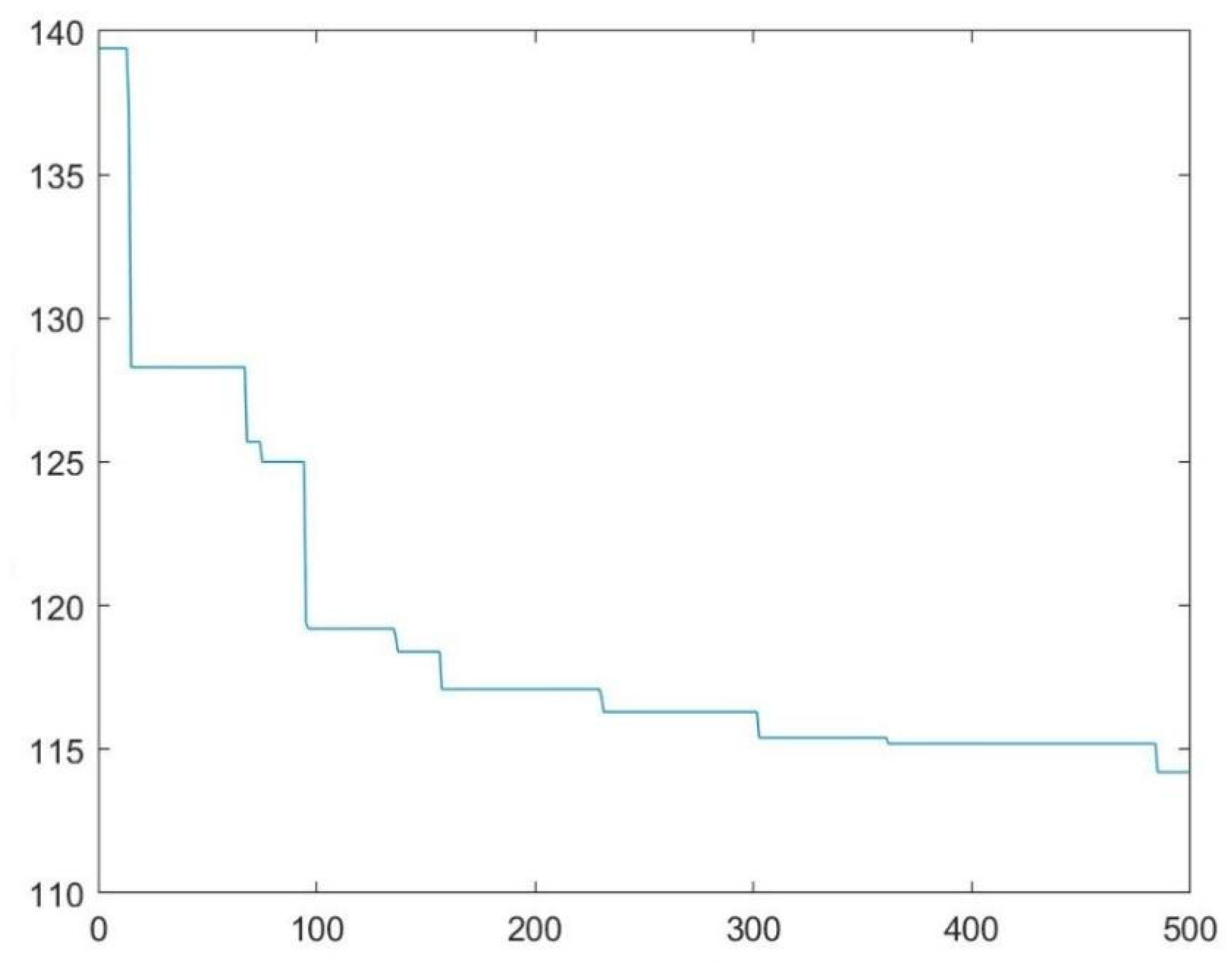
4.4. Results and Analysis
- (1)
- Results with load tolerance
- (2)
- Results without tolerance
- (3)
- Analysis of results
5. Conclusions
- (1)
- We neglected road conditions during actual transportation, leading to errors in the estimated distribution time. In addition, different fresh products may require a combination of different models of refrigerated vehicles for distribution. Thus, future work can consider complex road conditions and multiple optimization models.
- (2)
- The demand of distribution locations in a model should be accurate. As real demand data of the distribution locations were unavailable, we estimated them based on the average of the total demand. However, the demand likely varies across regions, and the average may be erroneous. Thus, future work can explore methods for accurately estimating the demand of specific locations.
- (3)
- We considered a single distribution center, but some locations have multiple concurrent suppliers. Future work can consider optimization for multiple distribution centers.
- (4)
- We did not consider location prioritization, which may be required in some cases with varying constraints. Prioritization can be included in future work.
- (5)
- We disregarded simultaneous delivery and pickup. In addition, when a location needs to return goods, the vehicle load changes. Moreover, one vehicle can supply various locations along its route. These aspects can also be considered in future work.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ran, W.; Shi, X.; Huasen, F.U.; Yang, G. Application research on ant colony algorithm in logistic distribution route-optimization of fresh agricultural products. Int. J. Digit. Content Technol. Its Applic. 2013, 7, 391–399. [Google Scholar] [CrossRef]
- Chen, J.; Xu, S.; Chen, H.; Zhao, C.; Xue, K. Research on optimization of food cold chain logistics distribution route based on internet of things. J. Phys. Conf. Series. 2020, 1544, 012086. [Google Scholar] [CrossRef]
- Wang, C.; Wang, Y.; Zeng, Z.; Lin, C.; Yu, Q. Research on logistics distribution vehicle scheduling based on heuristic genetic algorithm. Complexity 2021, 2021, 8275714. [Google Scholar] [CrossRef]
- Zhao, B.; Gui, H.; Li, H.; Xue, J. Cold chain logistics path optimization via improved multi-objective ant colony algorithm. IEEE Access. 2020, 8, 142977–142995. [Google Scholar] [CrossRef]
- Pershin, Y.V.; Ventra, M.D. Memcomputing Implementation of Ant Colony Optimization. Neural Process. Lett. 2016, 44, 265–277. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stützle, T. Ant Colony Optimization: Artificial Ants as a Computational Intelligence Technique. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Wen, H.; Xu, J. Research on vehicle routing problem based on improved ant colony algorithm. J. Highw. Transp. Res. Dev. 2009, 26, 125–129. [Google Scholar] [CrossRef]
- Li, J.; Fu, P.; Li, X.L.; Zhang, J.H.; Zhu, D.L. Research on vehicle path problem and forbidden search algorithm in low carbon environment. China Manag. Sci. 2015, 23, 98–106. [Google Scholar] [CrossRef]
- Yao, Y.; He, S. Research on cold chain logistics distribution path optimization of agricultural products based on traffic big data. Manag. Rev. 2019, 31, 240–253. [Google Scholar] [CrossRef]
- Kuo, J.C.; Chen, M.C. Developing an advanced Multi-Temperature Joint Distribution System for the food cold chain. Food Control. 2010, 21, 559–566. [Google Scholar] [CrossRef]
- Morganti, E.; Gonzalez-Feliu, J. The Last Food Mile Concept as a City Logistics Solution for Perishable Products; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2014. [Google Scholar] [CrossRef]
- Bortolini, M.; Faccio, M.; Ferrari, E.; Gamberi, M.; Pilati, F. Fresh food sustainable distribution: Cost, delivery time and carbon footprint three-objective optimization. J. Food Eng. 2016, 174, 56–67. [Google Scholar] [CrossRef]
- Pan, S.; Giannikas, V.; Han, Y.; Grover-Silva, E.; Qiao, B. Using Customer-related Data to Enhance E-grocery Home Delivery. Ind. Manag. Data Syst. 2017, 117, 1917–1933. [Google Scholar] [CrossRef]
- Ganji, M.; Kazemipoor, H.; Molana, S.M.H.; Sajadi, S.M. A green multi-objective integrated scheduling of production and distribution with heterogeneous fleet vehicle routing and time windows. J. Clean. Prod. 2020, 259, 120824. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, X.; Zhou, X. Distribution route optimization for electric vehicles in urban cold chain logistics for fresh products under time-varying traffic conditions. Mathem. Prob. Eng. 2020, 2020. [Google Scholar] [CrossRef]
- Wang, X.; Cao, W. Research on optimization of distribution route for cold chain logistics cooperative distribution of fresh e-commerce based on price discount. J. Phys. Conf. Ser. 2021, 1732, 012041. [Google Scholar] [CrossRef]
- Feng, Y.; Hu, Y.; He, L. Research on coordination of fresh agricultural product supply chain considering fresh-keeping effort level under retailer risk avoidance. Discrete Dynam. Nature Soc. 2021, 2021, 5527215. [Google Scholar] [CrossRef]
- Dantzig, G.B.; Ramser, J.H. The Truck Dispatching Problem. Manag. Sci. 1959, 6, 80–91. [Google Scholar] [CrossRef]
- Kuo, R.J.; Zulvia, F.E. Hybrid genetic ant colony optimization algorithm for capacitated vehicle routing problem with fuzzy demand—A case study on garbage collection system. In Proceedings of the 2017 4th International Conference on Industrial Engineering and Applications (ICIEA), Nagoya, Japan, 21–23 April 2017; pp. 244–248. [Google Scholar]
- Hosseinabadi, A.A.R.; Vahidi, J.; Balas, V.E.; Mirkamali, S.S. OVRP_GELS: Solving open vehicle routing problem using the gravitational emulation local search algorithm. Neural Comput. Appl. 2018, 29, 955–968. [Google Scholar] [CrossRef]
- Poonthalir, G.; Nadarajan, R. Green vehicle routing problem with queues. Expert Syst. Appl. 2019, 138, 112823. [Google Scholar] [CrossRef]
- Heler, K. Exact Algorithms for the Multi-Compartment Vehicle Routing Problem with Flexible Compartment Sizes. Eur. J. Oper. Res. 2021, 294, 188–205. [Google Scholar] [CrossRef]
- Sadykov, R.; Uchoa, E.; Pessoa, A. A Bucket Graph-Based Labeling Algorithm with Application to Vehicle Routing. Transp. Sci. 2021, 55, 4–28. [Google Scholar] [CrossRef]
- Goel, R.K.; Maini, R. Evolutionary ant colony algorithm using firefly-based transition for solving vehicle routing problems. Int. J. Comput. Sci. Eng. 2020, 21, 281. [Google Scholar] [CrossRef]
- Gunawan, A.; Widjaja, A.T.; Vansteenwegen, P.; Vincent, F.Y. A matheuristic algorithm for the Vehicle Routing Problem with Cross-Docking. Appl. Soft Comput. 2021, 103, 107163. [Google Scholar] [CrossRef]
- Zhao, J.; Xiang, H.; Li, J.; Liu, J.; Guo, L. Research on logistics distribution route based on multi-objective sorting genetic algorithm. Int. J. Artif. Intell. Tools. 2020. [Google Scholar] [CrossRef]
- Zhu, D.D.; Sun, J.Q. The path optimization algorithm of car navigation system considering node attributes under time-invariant network. Mob. Inf. Systems. 2021, 2021, 2963092. [Google Scholar] [CrossRef]
- Hu, C.; Xia, Y.; Zhang, J. Adaptive operator quantum-behaved pigeon-inspired optimization algorithm with application to uav path planning. Algorithms 2018, 12, 3. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, L.; Wang, T. Research on hybrid time window e-commerce logistics path optimization based on improved intelligent water drop algorithm. Sci. Technol. Manag. Res. 2018, 38, 8. [Google Scholar]
- Zhang, Y.; Jin, Z.; Chen, Y. Hybridizing grey wolf optimization with neural network algorithm for global numerical optimization problems. Neural Comput. Appl. 2020, 32, 14. [Google Scholar] [CrossRef]
- Zou, Y.; Si, W. Research on logistics distribution in e-commerce environment based on particle swarm optimization algorithm. J. Phys. Conf. Ser. 2021, 1881, 042059. [Google Scholar] [CrossRef]
- Yang, S. Optimization of urban logistics distribution path under dynamic traffic network. Int. Core J. Eng. 2020, 6, 243–248. [Google Scholar] [CrossRef]
- Jiang, J.; Yu, N.; Ye, J.; Bai, W. Vehicle logistics path optimization based on ant colony and particle hybrid algorithm. J. Phys. Conf. Ser. 2021, 1865, 042086. [Google Scholar] [CrossRef]
- Li, L.; Gao, T.; Jiang, Y. Night parking demand forecasting based on survival analysis. J. Southeast Univ. Nat. Sci. Ed. 2020, 50, 192–199. [Google Scholar] [CrossRef]
- Miao, J.; Liu, A.; Wang, R.; Lu, H. The influence of information asymmetry on the strategic inventory of deteriorating commodity. Omega 2022, 107, 102558. [Google Scholar] [CrossRef]
- Xiao-Nian, H.E. Capacitated logistic distribution vehicle routing optimization. Comput. Eng. Appl. 2009, 45, 236–238. [Google Scholar] [CrossRef]
- Peidong, W. Improved Ant Colony Algorithm and Its Application in Path Planning Problem. Ph.D. Thesis, Ocean University of China, Qingdao, China, 2012. [Google Scholar]
- Ali, H.; Kar, A.K. Discriminant analysis using ant colony optimization—An intra-algorithm exploration. Procedia Comput. Sci. 2018, 132, 880–889. [Google Scholar] [CrossRef]
- Liu, A.; Liu, T.; Ji, X.; Lu, H.; Li, F. The Evaluation Method of Low-Carbon Scenic Spots by Combining IBWM with B-DST and VIKOR in Fuzzy Environment. Multidiscip. Digit. Publ. Inst. 2019, 17, 89. [Google Scholar] [CrossRef]
- Meiqiong, W. Application of Genetic Algorithm in Logistics Distribution Path Planning Problem. Ph.D. Thesis, Nanjing University of Science and Technology, Nanjing, China, 2006. [Google Scholar]
- Xiao, Y.; Zhao, Q.; Kaku, I.; Xu, Y. Development of a fuel consumption optimization model for the capacitated vehicle routing problem. Comput. Oper. Res. 2012, 39, 1419–1431. [Google Scholar] [CrossRef]
- Lakshmisha, I.P.; Ravishankar, C.N.; Ninan, G.; Mohan, C.O.; Gopal, T.K.S. Effect of Freezing Time on the Quality of Indian Mackerel (Rastrelliger kanagurta) during Frozen Storage. J. Food Sci. 2008, 73, S345–S353. [Google Scholar] [CrossRef]
- Scott, C.; Urquhart, N.; Hart, E. Influence of topology and payload on CO2 optimized vehicle routing. In Lecture Notes in Computer Science, Proceedings of the International Conference on Applications of Evolutionary Computation, Istanbul, Turkey, 7–9 April 2010; Springer: Berlin/Heidelberg, Germany, 2010; Volume II, Chapter 15; pp. 141–150. [Google Scholar] [CrossRef]
- Cheng, Z.; Ji, W.; Lu, X. Optimization model and algorithm of logistics distribution path based on urban road network time-varying. IOP Conf. Ser. Mater. Sci. Eng. 2019, 688, 044045. [Google Scholar] [CrossRef]
- Liao, Z.; Quan, Y.; Jian, K.; Guo, Y. Research on the optimization model of cold chain logistics distribution path under the constraint of carbon emission. J. Phys. Conf. Ser. 2019, 1423, 012034. [Google Scholar] [CrossRef]
- Zhan, Y.; Wan, G. Vehicle routing and appointment scheduling with team assignment for home services. Comput. Operat. Res. 2018, 100, 1–11. [Google Scholar] [CrossRef]

| Number | Name | Address |
|---|---|---|
| 1 | Beijing Baliqiao Agricultural Products Center Wholesale Market | No. A27, Tonghui North Road, Tongzhou District, Beijing |
| 2 | Yonghui Supermarket | B1F, Wanda Plaza, Tongzhou District, Beijing |
| 3 | Carrefour (Beijing Tongzhou Store) | 2F, Sunshine New Life Plaza, No. 48 JiuKeShu West Road, TongZhou District, Beijing |
| 4 | Woomei Supermarket (Ximen Store) | No. 256 Xinhua Street, Tongzhou District, Beijing |
| 5 | Grocery Store | No. 103, Tong Chao Street, Tongzhou District, Beijing |
| 6 | Beijing Hualian | B1, Building 14, Tianshi Mingyuan, Yangzhuang Beili, Tongzhou District, Beijing |
| 7 | China Resources Vanguard (Vanguardlife) | The ground floor of Building No. 18, Barker Residence, Yile North Street, Tongzhou District, Beijing |
| 8 | Material Mart (Tongzhou Longhu Store) | No. 25, Hanbidian Street, Tongzhou District, Beijing |
| 9 | Jingkelong (Beiguan Store) | Houyao Shang Village, Yongshun Town, Tongzhou District, Beijing |
| 10 | Yonghui Supermarket (Hanbi Store) | Halfbidian Commercial Street, Yiluzhong Street, Tongzhou District, Beijing |
| 11 | Jingkelong (Yudaihe Store) | No. 350, Yudaihe East Street, Tongzhou District, Beijing |
| 12 | Woomei Supermarket (Liyuan Store) | B1F, Guiyou Building, No. 1 Yunjing East Road, Liyuan Town, Tongzhou District, Beijing |
| 13 | Jingkelong (Jukeshu Store) | No. 29, JiuKeShu East Road, TongZhou District, Beijing |
| 14 | Jingkelong (Dongguan Store) | No. 32 Xinhua East Street, Tongzhou District, Beijing (near Dongguan Bridge) |
| 15 | Material Mart (Luyuan Store) | No. 59, Luyuan South Street, Tongzhou District, Beijing |
| 16 | Material Mart (Tuqiao) | Near the entrance of Tuqiao Station of the Batong Line, Liyuan Town, Tongzhou District, Beijing |
| 17 | Material Mart (Tongzhou Sanmaifang Store) | 1F, Jiafolin Building, No. 186 Liyuan North Street, Tongzhou District, Beijing |
| 18 | Yue Man Street Life Supermarket | 119_116, North Gate of Yueshanshui District, Tongzhou District, Beijing |
| 19 | Miojin Supermarket (Huaye Oriental Rose Store) | B1F, Building 33, Linheli Road, Tongzhou District, Beijing |
| 20 | Supermarket Fat (Tongrui Jiayuan Store) | B1F, Building 20, Tongrui Jiayuan, Luyuan East Road, Yongshun Town, Tongzhou District, Beijing |
| 21 | Material Mart (Yuqiao Middle Road Store) | 2/F, No. 6 Yuqiao Middle Road, Tongzhou District, Beijing |
| 22 | Lotus (Tongzhou Store) | No. 132, Yunhe West Street, Tongzhou District, Beijing |
| 23 | Jingkelong Supermarket (Longwangzhuang Store) | Longwangzhuang Village, Yongshun Town, Tongzhou District, Beijing (near Jinshitan Dalian Seafood Farmers’ Cuisine) |
| 24 | BHG Life Supermarket (Tongzhou Wuyi Hualian Store) | B1, BHG Mall Beijing Hualian Wuyi Shopping Center, No. A3, Tonghu Street, Tongzhou District, Beijing |
| 25 | Jingkelong (Qiaozhuang Store) | Building 34, Yunqiao Home, Tongzhou District, Beijing |
| 26 | Zhengda Youxiang (Liyuan Store) | The ground floor of No. 10 building, Yuanjing East Road, Liyuan Town, Tongzhou District, Beijing |
| 27 | Yonghui Supermarket (Taihu Taihe Store) | 1F, G/F, Taihe No. 1 Courtyard, South 3rd Street, Zhanqian Street, Tongzhou District, Beijing |
| 28 | Material Mart (California Town Store) | No. 153, Qunfang Zhong San Street, Tongzhou District, Beijing |
| 29 | Material Mart (Longqing Yuan Store) | B-4-01, Building 38, No. 2, Longqing Garden, Tongzhou District, Beijing |
| dij | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | - | 1.4 | 4.6 | 1.2 | 1.5 | 2.2 | 4.3 | 6.5 | 2.3 | 5.3 | 4.1 | 6 | 5.4 | 4.3 | 5.6 |
| 2 | 1.4 | - | 2.9 | 1.3 | 2.5 | 1.1 | 2.9 | 5.1 | 3.5 | 3.9 | 2.4 | 4.6 | 3.3 | 4 | 8 |
| 3 | 4.6 | 2.9 | - | 3.8 | 2.1 | 3.8 | 1.6 | 3 | 5.1 | 2.5 | 2.7 | 1.4 | 2.1 | 4.5 | 8.3 |
| 4 | 1.2 | 1.3 | 3.8 | - | 3.3 | 1.4 | 3.7 | 5.8 | 3 | 4.7 | 2.6 | 4.5 | 3.4 | 2.8 | 5.2 |
| 5 | 1.5 | 2.5 | 2.1 | 3.3 | - | 2.9 | 2.3 | 3.1 | 5.7 | 2.3 | 4.5 | 4.3 | 3.9 | 6.2 | 10 |
| 6 | 2.2 | 1.1 | 3.8 | 1.4 | 2.9 | - | 2.1 | 4.3 | 3.7 | 3.1 | 2.6 | 3.8 | 2.9 | 4.2 | 10.2 |
| 7 | 4.3 | 2.9 | 1.6 | 3.7 | 2.3 | 2.1 | - | 2.2 | 5.3 | 1.4 | 3.3 | 2.9 | 2.2 | 5 | 8.9 |
| 8 | 6.5 | 5.1 | 3 | 5.8 | 3.1 | 4.3 | 2.2 | - | 7 | 1.1 | 4.7 | 4 | 3.6 | 6.4 | 9.4 |
| 9 | 2.3 | 3.5 | 5.1 | 3 | 5.7 | 3.7 | 5.3 | 7 | - | 6 | 3.3 | 5.2 | 4.6 | 2.9 | 3.2 |
| 10 | 5.3 | 3.9 | 2.5 | 4.7 | 2.3 | 3.1 | 1.4 | 1.1 | 6 | - | 4.3 | 3.7 | 3.2 | 6.1 | 9.9 |
| 11 | 4.1 | 2.4 | 2.7 | 2.6 | 4.5 | 2.6 | 3.3 | 4.7 | 3.3 | 4.3 | - | 2.6 | 2.9 | 1.9 | 5.5 |
| 12 | 6 | 4.6 | 1.4 | 4.5 | 4.3 | 3.8 | 2.9 | 4 | 5.2 | 3.7 | 2.6 | - | 1.9 | 5 | 8.6 |
| 13 | 5.4 | 3.3 | 2.1 | 3.4 | 3.9 | 2.9 | 2.2 | 3.6 | 4.6 | 3.2 | 2.9 | 1.9 | - | 3.6 | 7.6 |
| 14 | 4.3 | 4 | 4.5 | 2.8 | 6.2 | 4.2 | 5 | 6.4 | 2.9 | 6.1 | 1.9 | 5 | 3.6 | - | 4.5 |
| 15 | 5.6 | 8 | 8.3 | 5.2 | 10 | 10.2 | 8.9 | 9.4 | 3.2 | 9.9 | 5.5 | 8.6 | 7.6 | 4.5 | - |
| 16 | 8.7 | 7.4 | 4.2 | 7.2 | 7.1 | 6.6 | 6.1 | 6 | 7.9 | 5.7 | 4.9 | 4.1 | 3.8 | 5 | 9 |
| 17 | 6.4 | 4.8 | 3.2 | 5 | 5 | 4.5 | 3.8 | 5.1 | 5.5 | 4.6 | 2.1 | 2.4 | 2.1 | 2.7 | 6.7 |
| 18 | 5 | 4.6 | 6.9 | 5.1 | 8.4 | 6.4 | 7.4 | 8.8 | 2.7 | 8.4 | 6.1 | 8.5 | 6.6 | 4.9 | 3.8 |
| 19 | 7.8 | 6.1 | 3.3 | 6.3 | 6.1 | 5.6 | 5.2 | 5.1 | 7 | 4.8 | 4 | 3.2 | 2.8 | 4.1 | 8.1 |
| 20 | 6.5 | 7.8 | 8.3 | 6.5 | 10 | 8.2 | 8.8 | 10 | 4.2 | 9.9 | 5.5 | 8.6 | 8.1 | 4.1 | 1 |
| 21 | 6.2 | 4.4 | 3.6 | 4.6 | 5.4 | 4.7 | 4.2 | 5.6 | 4.9 | 5.2 | 2 | 3.8 | 2.5 | 2 | 5.8 |
| 22 | 6.4 | 5 | 3.8 | 5.2 | 5.6 | 5.1 | 4.3 | 5.7 | 5.5 | 5.3 | 2.8 | 3.8 | 3 | 2.7 | 6.7 |
| 23 | 5.7 | 7 | 7.6 | 5.8 | 9.3 | 9.4 | 8.1 | 9.5 | 3.5 | 9.1 | 4.7 | 7.8 | 7.3 | 3.3 | 0.8 |
| 24 | 6.7 | 6.5 | 6.9 | 5.2 | 10.5 | 6.7 | 11.2 | 8.9 | 5 | 8.5 | 4.4 | 7.5 | 6 | 2.9 | 3.4 |
| 25 | 6.5 | 4.8 | 4.1 | 4.9 | 5.9 | 5.4 | 4.6 | 6 | 5.2 | 5.7 | 2.4 | 4.2 | 2.8 | 2.3 | 6 |
| 26 | 6.7 | 5.1 | 2.3 | 5.2 | 5.1 | 4.6 | 3.4 | 3.6 | 6 | 3.4 | 3.4 | 1 | 1.8 | 4.5 | 8.6 |
| 27 | 14.7 | 13.3 | 11.2 | 14 | 11.7 | 12.5 | 10.7 | 8.7 | 14.7 | 10.6 | 13.5 | 12.2 | 11.6 | 14.7 | 27.4 |
| 28 | 8.1 | 6.5 | 3.6 | 6.6 | 6.5 | 6 | 4.9 | 4.7 | 7.4 | 5 | 4.7 | 3.5 | 3.2 | 5.5 | 9.5 |
| 29 | 11.3 | 10.1 | 9.2 | 9.8 | 12.2 | 10.3 | 9.7 | 11.1 | 11.9 | 10.7 | 7.7 | 9.2 | 8 | 7.5 | 10.3 |
| dij | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 8.7 | 6.4 | 5 | 7.8 | 6.5 | 6.2 | 6.4 | 5.7 | 6.7 | 6.5 | 6.7 | 14.7 | 8.1 | 11.3 |
| 2 | 7.4 | 4.8 | 4.6 | 6.1 | 7.8 | 4.4 | 5 | 7 | 6.5 | 4.8 | 5.1 | 13.3 | 6.5 | 10.1 |
| 3 | 4.2 | 3.2 | 6.9 | 3.3 | 8.3 | 3.6 | 3.8 | 7.6 | 6.9 | 4.1 | 2.3 | 11.2 | 3.6 | 9.2 |
| 4 | 7.2 | 5 | 5.1 | 6.3 | 6.5 | 4.6 | 5.2 | 5.8 | 5.2 | 4.9 | 5.2 | 14 | 6.6 | 9.8 |
| 5 | 7.1 | 5 | 8.4 | 6.1 | 10 | 5.4 | 5.6 | 9.3 | 10.5 | 5.9 | 5.1 | 11.7 | 6.5 | 12.2 |
| 6 | 6.6 | 4.5 | 6.4 | 5.6 | 8.2 | 4.7 | 5.1 | 9.4 | 6.7 | 5.4 | 4.6 | 12.5 | 6 | 10.3 |
| 7 | 6.1 | 3.8 | 7.4 | 5.2 | 8.8 | 4.2 | 4.3 | 8.1 | 11.2 | 4.6 | 3.4 | 10.7 | 4.9 | 9.7 |
| 8 | 6 | 5.1 | 8.8 | 5.1 | 10 | 5.6 | 5.7 | 9.5 | 8.9 | 6 | 3.6 | 8.7 | 4.7 | 11.1 |
| 9 | 7.9 | 5.5 | 2.7 | 7 | 4.2 | 4.9 | 5.5 | 3.5 | 5 | 5.2 | 6 | 14.7 | 7.4 | 11.9 |
| 10 | 5.7 | 4.6 | 8.4 | 4.8 | 9.9 | 5.2 | 5.3 | 9.1 | 8.5 | 5.7 | 3.4 | 10.6 | 5 | 10.7 |
| 11 | 4.9 | 2.1 | 6.1 | 4 | 5.5 | 2 | 2.8 | 4.7 | 4.4 | 2.4 | 3.4 | 13.5 | 4.7 | 7.7 |
| 12 | 4.1 | 2.4 | 8.5 | 3.2 | 8.6 | 3.8 | 3.8 | 7.8 | 7.5 | 4.2 | 1 | 12.2 | 3.5 | 9.2 |
| 13 | 3.8 | 2.1 | 6.6 | 2.8 | 8.1 | 2.5 | 3 | 7.3 | 6 | 2.8 | 1.8 | 11.6 | 3.2 | 8 |
| 14 | 5 | 2.7 | 4.9 | 4.1 | 4.1 | 2 | 2.7 | 3.3 | 2.9 | 2.3 | 4.5 | 14.7 | 5.5 | 7.5 |
| 15 | 9 | 6.7 | 3.8 | 8.1 | 1 | 5.8 | 6.7 | 0.8 | 3.4 | 6 | 8.6 | 27.4 | 9.5 | 10.3 |
| 16 | - | 3.1 | 9.2 | 1.3 | 8.5 | 3.8 | 3.7 | 7.8 | 8.3 | 3.8 | 3.1 | 13 | 1.2 | 8.6 |
| 17 | 3.1 | - | 7.3 | 2.1 | 6.4 | 1.8 | 1.8 | 5.7 | 5.3 | 2.1 | 2.1 | 13.2 | 3.5 | 6.8 |
| 18 | 9.2 | 7.3 | - | 9.6 | 5.8 | 7.5 | 8.2 | 5.9 | 8.1 | 7.9 | 9.1 | 26.5 | 10.5 | 12.6 |
| 19 | 1.3 | 2.1 | 9.6 | - | 7.4 | 2.7 | 2.4 | 6.7 | 7.2 | 2.8 | 2.2 | 12.9 | 2.1 | 7.5 |
| 20 | 8.5 | 6.4 | 5.8 | 7.4 | - | 5.8 | 7.1 | 0.8 | 3.4 | 5.9 | 8.4 | 17.7 | 9.2 | 9.7 |
| 21 | 3.8 | 1.8 | 7.5 | 2.7 | 5.8 | - | 2 | 4.1 | 3.7 | 1.7 | 4 | 14.1 | 4.8 | 7 |
| 22 | 3.7 | 1.8 | 8.2 | 2.4 | 7.1 | 2 | - | 5.6 | 5.2 | 0.5 | 3.6 | 13.9 | 4.1 | 5.5 |
| 23 | 7.8 | 5.7 | 5.9 | 6.7 | 0.8 | 4.1 | 5.6 | - | 2.6 | 5.1 | 7.5 | 17.6 | 13.9 | 8.9 |
| 24 | 8.3 | 5.3 | 8.1 | 7.2 | 3.4 | 3.7 | 5.2 | 2.6 | - | 4.5 | 7 | 24.1 | 7.8 | 7.3 |
| 25 | 3.8 | 2.1 | 7.9 | 2.8 | 5.9 | 1.7 | 0.5 | 5.1 | 4.5 | - | 3.9 | 14.3 | 4.5 | 5.9 |
| 26 | 3.1 | 2.1 | 9.1 | 2.2 | 8.4 | 4 | 3.6 | 7.5 | 7 | 3.9 | - | 12.5 | 2.7 | 8.2 |
| 27 | 13 | 13.2 | 26.5 | 12.9 | 17.7 | 14.1 | 13.9 | 17.6 | 24.1 | 14.3 | 12.5 | - | 12.1 | 25 |
| 28 | 1.2 | 3.5 | 10.5 | 2.1 | 9.2 | 4.8 | 4.1 | 13.9 | 7.8 | 4.5 | 2.7 | 12.1 | - | 9.4 |
| 29 | 8.6 | 6.8 | 12.6 | 7.5 | 9.7 | 7 | 5.5 | 8.9 | 7.3 | 5.9 | 8.2 | 25 | 9.4 | - |
| Parameter | Value |
|---|---|
| Displacement | 6.2 L |
| Fuel consumption per 100 km | 25 L |
| Type of machinery | Insulated car |
| Chassis model | DFH1180E7 |
| Power rating | 180 kW |
| Rated load capacity | 9990 kg |
| Tire specification | 10 |
| Number of tires | 6 |
| Emission standards | National 6 |
| Drive method | Rear drive |
| Fuel type | Diesel |
| Model | DFH5180XLCEX7 |
| Overall mass | 7880 kg |
| Wheelbase | 5000 mm |
| Number of axes | 2 |
| Total mass | 18,000 kg |
| Maximum speed | 105 km/h |
| Item number | 13,647,299,677 |
| Number | Distribution Location | Estimated Demand (Tons) |
|---|---|---|
| 2 | Yonghui Supermarket | 1.992 |
| 3 | Carrefour (Beijing Tongzhou Store) | 1.992 |
| 4 | Woomei Supermarket (Ximen Store) | 1.992 |
| 5 | Grocery Store | 1.992 |
| 6 | Beijing Hualian | 1.992 |
| 7 | China Resources Vanguard (Vanguardlife) | 1.992 |
| 8 | Material Mart (Tongzhou Longhu Store) | 1.992 |
| 9 | Jingkelong (Beiguan Store) | 1.992 |
| 10 | Yonghui Supermarket (Hanbi Store) | 1.992 |
| 11 | Jingkelong (Yudaihe Store) | 1.992 |
| 12 | Woomei Supermarket (Liyuan Store) | 1.992 |
| 13 | Jingkelong (Jukeshu Store) | 1.992 |
| 14 | Jingkelong (Dongguan Store) | 1.992 |
| 15 | Material Mart (Luyuan Store) | 1.992 |
| 16 | Material Mart (Tuqiao) | 1.992 |
| 17 | Material Mart (Tongzhou Sanmaifang Store) | 1.992 |
| 18 | Yue Man Street Life Supermarket | 0.996 |
| 19 | Miojin Supermarket (Huaye Oriental Rose Store) | 1.992 |
| 20 | Supermarket Fat (Tongrui Jiayuan Store) | 1.992 |
| 21 | Material Mart (Yuqiao Middle Road Store) | 1.992 |
| 22 | Lotus (Tongzhou Store) | 0.996 |
| 23 | Jingkelong Supermarket (Longwangzhuang Store) | 1.992 |
| 24 | BHG Life Supermarket (Tongzhou Wuyi Hualian Store) | 0.996 |
| 25 | Jingkelong (Qiaozhuang Store) | 1.992 |
| 26 | Zhengda Youxiang (Liyuan Store) | 0.996 |
| 27 | Yonghui Supermarket (Taihu Taihe Store) | 1.992 |
| 28 | Material Mart (California Town Store) | 0.996 |
| 29 | Material Mart (Longqing Yuan Store) | 1.992 |
| Vehicle | Distribution Route | Full Load Rate |
|---|---|---|
| 1 | 1–26–28–16–19–29–1 | 84.00% |
| 2 | 1–4–7–6–2–1 | 84.00% |
| 3 | 1–5–10–8–27–1 | 84.00% |
| 4 | 1–21–25–22–17–11–1 | 94.50% |
| 5 | 1–3–12–13–18–9–1 | 94.50% |
| 6 | 1–15–20–23–24–14–1 | 94.50% |
| Vehicle | Distribution Route | Full Load Rate |
|---|---|---|
| 1 | 1–5–10–8–27–7–1 | 99.70% |
| 2 | 1–2–11–14–22–25–1 | 89.70% |
| 3 | 1–3–12–26–19–16–28–1 | 99.70% |
| 4 | 1–29–24–23–20–15–18–1 | 99.70% |
| 5 | 1–9–21–17–13–6–1 | 99.70% |
| 6 | 1–4–1 | 19.90% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Ai, W.; Ju, T. Cold Chain Logistics Distribution Path Planning of Fresh Products in Beijing Subcenter. Sustainability 2022, 14, 10622. https://doi.org/10.3390/su141710622
Li F, Ai W, Ju T. Cold Chain Logistics Distribution Path Planning of Fresh Products in Beijing Subcenter. Sustainability. 2022; 14(17):10622. https://doi.org/10.3390/su141710622
Chicago/Turabian StyleLi, Feng, Wenjing Ai, and Tianli Ju. 2022. "Cold Chain Logistics Distribution Path Planning of Fresh Products in Beijing Subcenter" Sustainability 14, no. 17: 10622. https://doi.org/10.3390/su141710622
APA StyleLi, F., Ai, W., & Ju, T. (2022). Cold Chain Logistics Distribution Path Planning of Fresh Products in Beijing Subcenter. Sustainability, 14(17), 10622. https://doi.org/10.3390/su141710622






