A Heuristic for the Two-Echelon Multi-Period Multi-Product Location–Inventory Problem with Partial Facility Closing and Reopening
Abstract
:1. Introduction
2. Literature Review
3. Proposed Mathematical Formulation
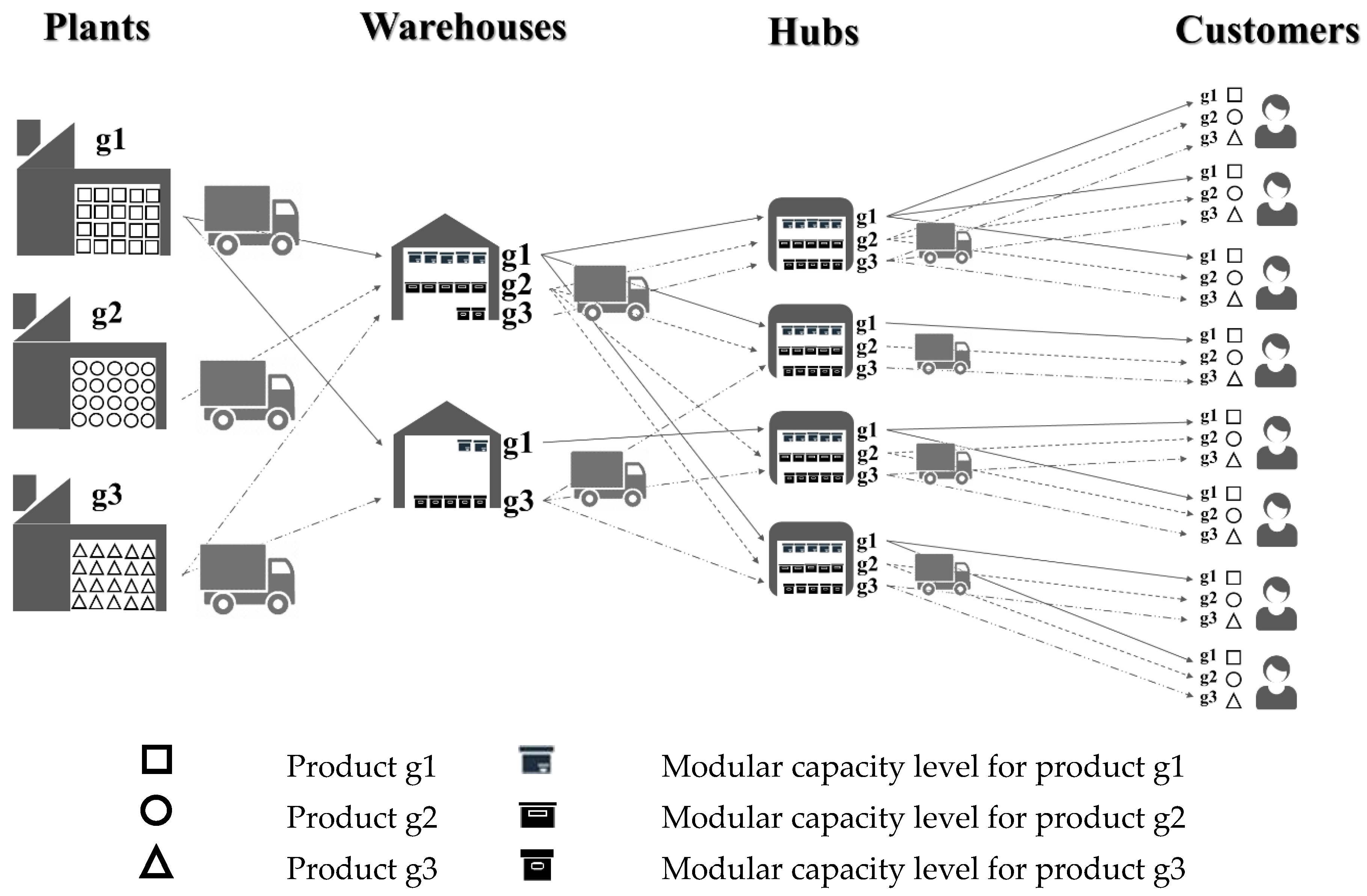
3.1. Problem Description
3.2. Notations
3.2.1. Deterministic Parameters
- F1 = Set of candidate warehouses.
- F2 = Set of candidate hubs.
- F = Set of candidate facilities F1∪ F2.
- CL = Set of modular capacity levels = {0, 1, …, NCL}.
- G = Set of products.
- C = Set of customers.
- T = Set of time periods.
- Nt = Number of days in period t.
- W = Weight of total number of different located facilities over the planning horizon.
- α = Probability of unfulfilled demand during the lead time at warehouses.
- β = Maximum probability of inventory capacity violation at warehouses.
- γ = Maximum probability of violation of daily throughput capacity at hubs.
- z1−α= The lower 100(1 − α) percentage points of standard normal distribution.
- dij = Roadway distance between nodes i and j.
- rUL = A fraction of inventory capacity as a practical upper limit of reorder point at warehouses.
- rLL = A fraction of maximum order quantity as a lower limit of the implied maximum order quantity.
- AllCapi,t = Overall open capacity for combined products at facility i ∈ F in period t.
- lig and nig = Initial open capacity level and initial existing capacity level at facility i.
- RCwg = Unit transportation cost between plant and warehouse w (USD/product unit/day).
- TCig = Unit transportation cost for vehicles based at facility i ∈ F (USD/distance unit/product unit).
- OCwg = Fixed ordering cost at warehouse w (USD/order).
- HCwg = Unit holding cost at warehouse w (USD/product unit/day).
- LTwg = Lead time that the plant takes to fulfill an order from warehouse w (day).
- μcgt and σ2cgt = Mean and variance of stochastic daily demand of customer c (independent and normally distributed across products, customers, and periods) (product unit/day and (product unit/day)2).
- Capilg = Facility capacity (inventory capacity for warehouse and daily throughput capacity for hub) for l open capacity levels (product unit).
- Qwlgmax = Maximum order quantity which can be set as the vehicle capacity from the plant to warehouse w with l open capacity levels (product unit).
- CONilg = Cost for constructing l capacity levels (USD).
- OFilg = Operating fixed cost with l open capacity levels during a period (USD).
- NFilg = Non-operating fixed cost to maintain l temporarily closed capacity levels during a period (USD).
- Reopenilg = Cost to reopen l capacity levels (USD).
- Closeilg = Cost to temporarily close l capacity levels (USD).
- flp,l,np,nigt = Capacity adjustment cost (USD) to change from open and existing capacity levels (lp, np) in period t − 1 to (l, n) in period t, calculated from Equation (1) [13]:
- ncon = n − np Capacity levels to be constructed in period t.
- nof = l Open capacity levels to be operated in period t.
- nnf = n − l Temporarily closed capacity levels to be maintained in period t.
- nreo = max{0, (l − lp)-(n − np)} Capacity levels to be reopened in period t.
- nclo = max{0, (lp − l) + n − np} Capacity levels to be closed temporarily in period t.
3.2.2. Decision Variables
- yyi = 1 If facility i ∈ F is established over the planning horizon; and 0 otherwise.
- = 1 If facility I ∈ F changes its capacity levels (lp, np) in period t − 1 to (l, n) in period t for product g; and 0 otherwise ∀lp ≤ np, l ≤ n, np ≤ n.
- = 1 If product-g period-t demand of customer c is served by hub h with capacity levels (), which is served by warehouse w with capacity levels (l, n); and 0 otherwise.
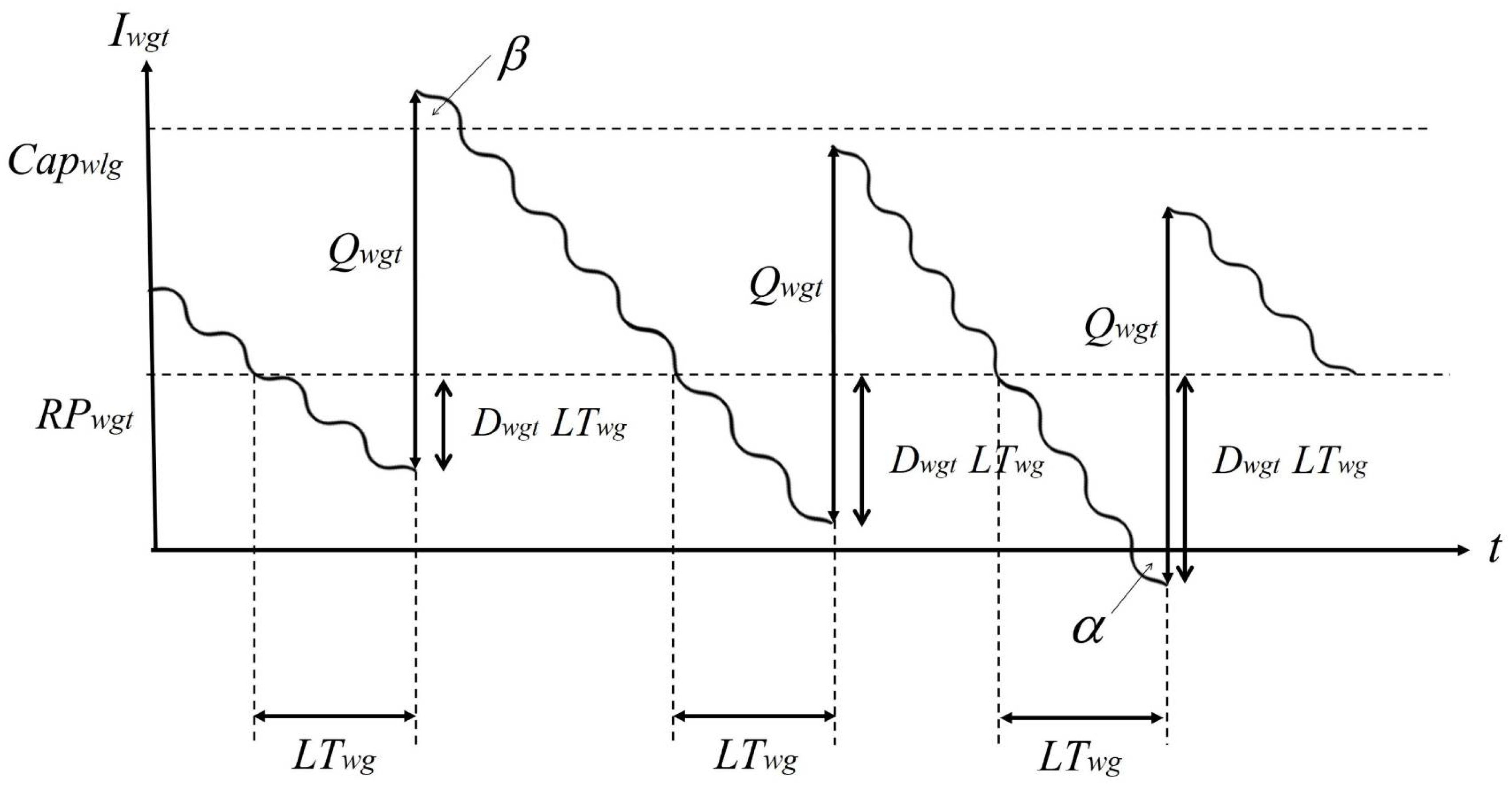
- RPwgt; SSwgt; Qwgt = Reorder point; safety stock; order quantity for product g at warehouse w in period t (product unit).
- EDigt and VDigt = Mean and variance of Digt, daily product-g demand served by facility i ∈ F in period t (product unit/day and (product unit/day)2).
- AllCapi,t = Overall open capacity of combined products at facility i ∈ F in period t (product unit).
3.3. Mathematical Model
4. Proposed Multi-Start Construction and Tabu Search Improvement Heuristic
| Algorithm 1: MS-CTSIH(strategy s) |
 |
| Algorithm 2: Modified MS-CTSIH |
 |
- Additional Variables for the Current Solution
- LFg,tv = The set of located facilities for echelon v, product g, and period t (facilities are warehouses if v = 1 and hubs if v = 2); UFg,tv = Fv\LFg,tv.
- Nigtallocated = The set of demand nodes serviced by facility i ∈ F for product g and period t, i.e., customers serviced by hub h in the second-echelon problem, and hubs serviced by warehouse w in the first-echelon problem.
- L_Fgv = The set of located facilities for echelon v and product g; U_Fgv = Fv\L_Fgv.
- L__Fv = The set of located facilities for echelon v; U__Fv = Fv\L__Fv.
- ocligt and ecligt = Open and existing modular capacity levels for facility i ∈ F, product g, and period t.
- EnterPig = The earliest period that facility i ∈F is constructed to serve product g, e.g., hub h1 is located from periods 3 to 10 to serve product g1; then EnterPh1,g1 = 3.
- Enter_Pi = The earliest period that facility i ∈ F is constructed to serve any product.
- z = The objective value of the current solution.
- z*= The objective value of the best solution found so far.
- z′* = The objective value corresponding to the best move.
- Algorithmic Variables
- tabui = The last iteration number that a move of node i (demand or facility location) is prohibited.
- tenure = Number of iterations that a move is prohibited.
- freqig = The frequency that facility i ∈ F enters L_Fgv (i.e., unlocated facility i becomes a located facility serving product g) in the current solution.
- freqi = The frequency that facility i enters L__Fv in the current solution.
- Algorithmic Parameters
- max_it2 = Maximum number of non-improvement iterations.
- div_it2 = Number of non-improvement iterations to activate the diversification procedure in the facility replacement phase (note that div_it2 < max_it2).
- MS_iterations = Number of multi-start iterations.
4.1. Stage I: Construction
| Algorithm 3: Construct_Solution(v) |
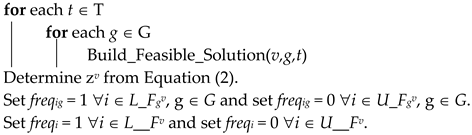 |
4.1.1. Procedure Build_Feasible_Solution(v,g,t)
| Algorithm 4: Build_Feasible_Solution(v,g,t) |
 |
4.1.2. Procedure Allocate_Demand_Nodes(v,g,t)
| Algorithm 5: Allocate_Demand_Node(v,g,t) |
 |
4.1.3. Procedure Determine_Inventory_Policies(g,t)
| Algorithm 6: Determine_Inventory_Policies(g,t) |
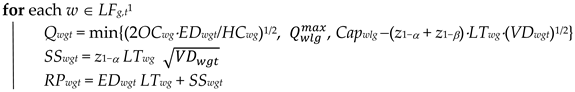 |
4.2. Stage II: Improvement
| Algorithm 7: Improve_Solution(v,s) |
 |
4.2.1. Procedures Insert_Demand_Node(v,g,t,s) and Swap_Demand_Node(v,g,t,s)
| Algorithm 8: Insert_Demand_Node(v,g,t,s)/Procedure Swap_Demand_Node(v,g,t,s) |
 |
Sub-Procedure find_best_demand_node_insertion_move(v,g,t)
| Algorithm 9: Sub-procedure find_best_demand_node_insertion_move(v,g,t) |
 |
Sub-Procedure find_best_demand_node_swap_move(v,g,t)
| Algorithm 10: Sub-procedure find_best_demand_node_swap_move(v,g,t) |
 |
4.2.2. Procedures Replace_Facility(v,g,s) and Add_Facility(v,g,s)
| Algorithm 11: Replace_Facility(v,g,s)/Procedure Add_Facility(v,g,s) |
 |
Sub-Procedure find_best_facility_replacement_move(v,g)
| Algorithm 12: Sub-procedure find_best_facility_replacement_move(v,g) |
 |
Sub-Procedure find_best_facility_addition_move(v,g)
| Algorithm 13: Sub-procedure find_best_facility_addition_move(v,g) |
 |
4.2.3. Procedures Replace_Facility(v,s) and Add_Facility(v,s)
| Algorithm 14: Replace_Facility(v,s)/Procedure Add_Facility(v,s) |
 |
Sub-Procedure find_best_facility_replacement_move(v)
| Algorithm 15: Sub-procedure find_best_facility_replacement_move(v) |
 |
Sub-Procedure find_best_facility_addition_move(v)
| Algorithm 16: Sub-procedure find_best_facility_addition_move(v) |
 |
5. Computational Experiences
5.1. Data
5.1.1. Large Problem Instance
5.1.2. Small Problem Instance
5.2. Experimental Results
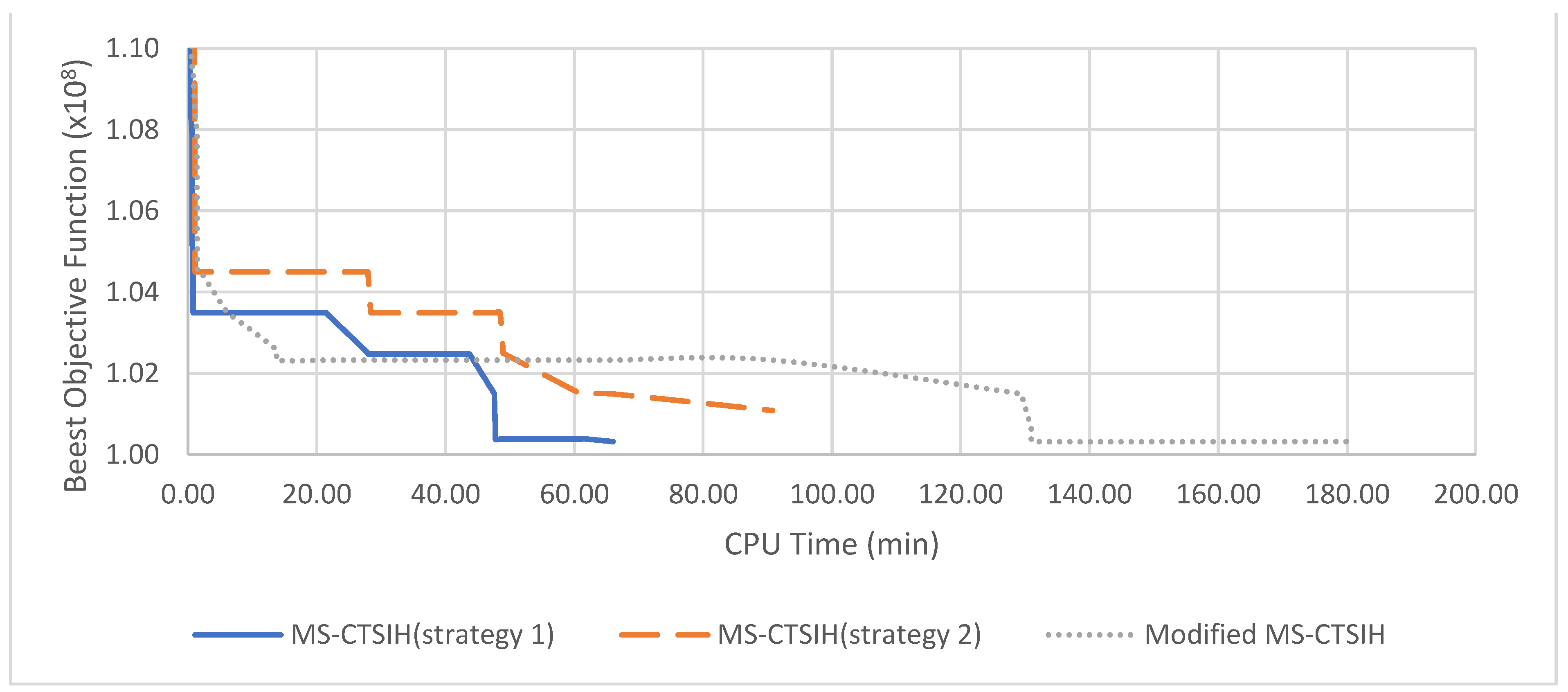
5.2.1. Comparison of Improvement Strategies
5.2.2. Comparison of Proposed Heuristic and Analytical Solution Method
5.2.3. Examination of Heuristic Solution on the Small Problem Instance
5.2.4. Sensitivity Analysis
5.2.5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Silva, A.; Aloise, D.; Coelho, L.C.; Rocha, C. Heuristics for the dynamic facility location problem with modular capacities. Eur. J. Oper. Res. 2021, 290, 435–452. [Google Scholar] [CrossRef]
- Crainic, T.G.; Sforza, A.; Sterle, C. Tabu search heuristic for a two-echelon location-routing problem, Research Report, interuniversity research centre on enterprise networks, logistics and transportation. In CIRRELT-2011-07; CIRRELT: Montréal, QC, Canada, 2011. [Google Scholar]
- Crainic, T.G.; Ricciardi, N.; Storchi, G. Advanced freight transportation systems for congested urban areas. Transp. Res. Part C Emerg. Technol. 2004, 12, 119–137. [Google Scholar] [CrossRef]
- Crainic, T.G.; Ricciardi, N.; Storchi, G. Models for evaluating and planning city logistic transportation systems. Transp. Sci. 2009, 43, 432–454. [Google Scholar] [CrossRef]
- Boccia, M.; Crainic, T.G.; Sforza, A.; Sterle, C. Location-Routing Models for Designing a Two-Echelon Freight Distribution System. In CIRRELT-2011-06 January Report; CIRRELT: Montréal, QC, Canada, 2011. [Google Scholar]
- Correia, I.; Captivo, M.E. A Lagrangean heuristic for a modular capacitated location problem. Ann. Oper. Res. 2003, 122, 141–161. [Google Scholar] [CrossRef]
- Shulman, A. An algorithm for solving dynamic capacitated plant location problems with discrete expansion sizes. Oper. Res. 1991, 39, 423–436. [Google Scholar] [CrossRef]
- Melo, M.T.; Nickel, S.; Saldanha da Gama, F. Facility location and supply chain management-a review. Eur. J. Oper. Res. 2009, 196, 401–412. [Google Scholar] [CrossRef]
- Wesolowsky, G.O. Dynamic facility location. Manag. Sci. 1973, 19, 1241–1248. [Google Scholar] [CrossRef]
- Dias, J.; Captivo, M.E.; Climaco, J. Efficient primal-dual heuristic for a dynamic location problem. Comput. Oper. Res. 2007, 34, 1800–1823. [Google Scholar] [CrossRef]
- Jena, S.D.; Cordeau, J.-F.; Gendron, B. Dynamic facility location with generalized modular capacities. Transp. Sci. 2015, 49, 484–499. [Google Scholar] [CrossRef]
- Jena, S.D.; Cordeau, J.-F.; Gendron, B. Modeling and solving a logging camp location problem. Ann. Oper. Res. 2015, 232, 151–177. [Google Scholar] [CrossRef]
- Jena, S.D.; Cordeau, J.-F.; Gendron, B. Solving a dynamic facility location problem with partial closing and reopening. Comput. Oper. Res. 2016, 67, 143–154. [Google Scholar] [CrossRef]
- Jena, S.D.; Cordeau, J.-F.; Gendron, B. Lagrangian heuristics for large-scale dynamic facility location with generalized modular capacities. INFORMS J. Comput. 2017, 29, 388–404. [Google Scholar] [CrossRef]
- Miranda, P.A.; Garrido, R.A. A Simultaneous Inventory Control and Facility Location Model with Stochastic Capacity Constraints. Netw. Spat. Econ. 2006, 6, 39–53. [Google Scholar] [CrossRef]
- Punyim, P.; Karoonsoontawong, A.; Unnikrishnan, A.; Xie, C. Tabu search heuristic for joint location-inventory problem with stochastic inventory capacity and practicality constraints. Netw. Spat. Econ. 2018, 18, 51–84. [Google Scholar] [CrossRef]
- Zhang, Z.-H.; Unnikrishnan, A. A coordinated location-inventory problem in closed-loop supply chain. Transp. Res. Part B Methodol. 2016, 89, 127–148. [Google Scholar] [CrossRef]
- Keskin, B.B.; Uster, H. Production/distribution system design with inventory considerations. Nav. Res. Logist. 2012, 59, 172–195. [Google Scholar] [CrossRef]
- Teo, C.; Shu, J. Warehouse-retailer network design problem. Oper. Res. 2004, 52, 396–408. [Google Scholar] [CrossRef]
- Daskin, M.S.; Coullard, C.R.; Shen, Z.-J.M. An inventory-location model: Formulation, solution algorithm and computational results. Ann. Oper. Res. 2002, 110, 83–106. [Google Scholar] [CrossRef]
- Shen, Z.-J.M.; Coullard, C.; Daskin, M.S. A joint location-inventory model. Transp. Sci. 2003, 37, 40–55. [Google Scholar] [CrossRef]
- Miranda, P.A.; Garrido, R.A. Incorporating inventory control decisions into a strategic distribution network design model with stochastic demand. Transp. Res. Part E 2004, 40, 183–207. [Google Scholar] [CrossRef]
- Ozsen, L.; Coullard, C.R.; Daskin, M.S. Capacitated warehouse location model with risk pooling. Nav. Res. Logist. 2008, 55, 295–312. [Google Scholar] [CrossRef]
- Vidyarthi, N.; Çelebi, E.; Elhedhli, S.; Jewkes, E. Integrated production-inventory-distribution system design with risk pooling: Model formulation and heuristic solution. Transp. Sci. 2007, 41, 392–408. [Google Scholar] [CrossRef]
- Park, S.; Lee, T.-E.; Sung, C.S. A three-level supply chain network design model with risk pooling and lead times. Transp. Res. Part E 2010, 46, 563–581. [Google Scholar] [CrossRef]
- Shahabi, M.; Unnikrishnan, A.; Jafari-Shirazi, E.; Boyles, S.D. A three level location-inventory problem with correlated demand. Transp. Res. Part B 2014, 69, 1–18. [Google Scholar] [CrossRef]
- Battiti, R.; Tecchiolli, G. The Reactive Tabu Search. ORSA J. Comput. 1994, 6, 126–140. [Google Scholar] [CrossRef]
- Glover, F. Tabu Search—Part I. ORSA J. Comput. 1989, 1, 190–206. [Google Scholar] [CrossRef]
- Glover, F. Tabu Search—Part II. ORSA J. Comput. 1990, 2, 4–32. [Google Scholar] [CrossRef]
- Hoefer, M. Experimental comparison of heuristic and approximation algorithms for uncapacitated facility location. In Lecture Notes in Computer Science, Proceedings of the Second International Workshop on Experimental and Efficient Algorithms (WEA 2003), Ascona, Switzerland, 26–28 May 2003; Jansen, K., Margraf, M., Mastrolilli, M., Rolim, J.D.P., Eds.; Springer: New York, NY, USA, 2003; Volume 2647, p. 2647. [Google Scholar]
- Al-Sultan, K.S.; Al-Fawzan, M.A. A tabu search approach to the uncapacitated facility location problem. Ann. Oper. Res. 1999, 86, 91–103. [Google Scholar] [CrossRef]
- Sun, M. A Tabu Search Heuristic Procedure for the Capacitated Facility Location Problem. J. Heuristics 2012, 18, 91–118. [Google Scholar] [CrossRef]
- Nagy, G.; Salhi, S. Nested heuristic methods for the location-routing problem. J. Oper. Res. Soc. 1996, 47, 1166–1174. [Google Scholar] [CrossRef]
- Tuzun, D.; Burke, L.I. A two-phase tabu search approach to the location routing problem. Eur. J. Oper. Res. 1999, 116, 87–99. [Google Scholar] [CrossRef]
- Karoonsoontawong, A.; Unnikrishnan, A. Inventory Routing Problem with Route Duration Limits and Stochastic Inventory Capacity Constraints: Tabu Search Heuristics. Transp. Res. Rec. J. Transp. Res. Board 2013, 2378, 43–53. [Google Scholar] [CrossRef]
- Solomon, M.M. Algorithm for the vehicle routing and scheduling problem with time window constraints. Oper. Res. 1987, 35, 254–265. [Google Scholar] [CrossRef]
- Terouhid, S.A.; Ries, R.; Fard, M.M. Towards Sustainable Facility Location—A Literature Review. J. Sustain. Dev. 2012, 5, 18–34. [Google Scholar] [CrossRef]
- Marsh, M.T.; Schilling, D.A. Equity measurement in facility location analysis: A review and framework. Eur. J. Oper. Res. 1994, 74, 1–17. [Google Scholar] [CrossRef]
- Briassoulis, H. Environmental criteria in industrial facility siting decisions: An analysis. Environ. Manag. 1995, 19, 297–311. [Google Scholar] [CrossRef]

| Research Work | Problem Features | Formulation | Solution Methods | |||||
|---|---|---|---|---|---|---|---|---|
| Echelon | Period | Product | Capacity Level | Relocate Capacity | Temporary Partial Capacity Closing and Reopening | |||
| Joint Location–Inventory Problem | ||||||||
| Daskin et al. (2002) [20] | Single | Single | Single | Single | N/A | N/A | INLP | Lagrangian relaxation (LR) |
| Shen et al. (2003) [21] | ” | ” | ” | ” | ” | ” | INLP, IP | Column generation |
| Miranda and Garrido (2004, 2006) [15,22] | ” | ” | ” | ” | ” | ” | MINLP | Heuristic based on LR and sub-gradient method |
| Teo and Shu (2004) [19] | ” | ” | ” | ” | ” | ” | IP | Column generation |
| Ozsen et al. (2008) [23] | ” | ” | ” | ” | ” | ” | INLP | LR |
| Correia and Captivo (2003) [6] | Single | Single | Single | Multi | N/A | N/A | MIP | LR |
| Zhang and Unnikrishnan (2016) [17] | ” | ” | ” | ” | ” | ” | MICQ | Outer approximation |
| Punyim et al. (2018) [16] | ” | ” | ” | ” | ” | ” | MINLP | Tabu search |
| Vidyarthi et al. (2007) [24] | Two | Single | Multi | Single | N/A | N/A | MINLP | LR |
| Park et al. (2010) [25] | Two | Single | Single | Single | N/A | N/A | INLP | LR |
| Keskin and Üster (2012) [18] | ” | ” | ” | ” | ” | ” | MINLP | Heuristic |
| Shahabi et al. (2014) [26] | ” | ” | ” | ” | ” | ” | MICQ | Outer approximation |
| Dynamic Facility Location Problem | ||||||||
| Dias et al. (2007) [10] | Single | Multi | Single | Single | No | No | MIP | Primal-dual heuristic |
| Shulman (1991) [7] | Single | Multi | Single | Multi | No | No | MIP | LR |
| Jena et al. (2015) [11] | Single | Multi | Single | Multi | Yes | Yes | MIP | CPLEX solver |
| Silva et al. (2021) [1] | ” | ” | ” | ” | ” | ” | MIP | Heuristics |
| Jena et al. (2015) [12] | Single | Multi | Multi | Multi | Yes | Yes | MIP | CPLEX solver |
| Jena et al. (2016; 2017) [13,14] | ” | ” | ” | ” | ” | ” | MIP | LR-based heuristic |
| Joint Dynamic Location–Inventory Problem | ||||||||
| Our work | Two | Multi | Multi | Multi | No | Yes | MINLP | Heuristic |
| Period t − 1 | Period t | ncon | nof | nnf | nreo | nclo |
|---|---|---|---|---|---|---|
| Open and Existing Modular Capacity Levels (lp, np) | Open and Existing Modular Capacity Levels (l, n) | =n − np | =l | =n − l | = max{0, (l − lp) − (n − np)} | max{0, (lp − l) + n − np} |
| (0, 2) | (1, 2) | 0 | 1 | 1 | 1 | 0 |
| (0, 2) | (1, 3) | 1 | 1 | 2 | 0 | 0 |
| (0, 2) | (1, 4) | 2 | 1 | 3 | 0 | 1 |
| Tabu Search Procedure | Improvement Strategy | |
|---|---|---|
| 1 | 2 | |
| Swap_Demand_Node(v,g,t,s) | None | Insert_Demand_Node(v,g,t,s) |
| Replace_Facility(v,g,s) | None | Insert_Demand_Node(v,g,t,s) for t = t_enter, …, |T|Swap_Demand_Node(v,g,t,s) for t = t_enter, …, |T| |
| Replace_Facility(v,s) | None | Insert_Demand_Node(v,g,t,s) for g∈G, t = t_enter, …, |T|Swap_Demand_Node(v,g,t,s) for g∈G, t = t_enter, …, |T| |
| Add_Facility(v,g,s) | None | Insert_Demand_Node(v,g,t,s) for t = t_enter, …, |T|Swap_Demand_Node(v,g,t,s) for t = t_enter, …, |T|Replace_Facility(v,g) |
| Add_Facility(v,s) | None | Insert_Demand_Node(v,g,t,s) for g∈G, t = t_enter, …, |T|Swap_Demand_Node(v,g,t,s) for g∈G, t = t_enter, …, |T|Replace_Facility(v,s) for g∈G |
| Period | g1 | g2 | g3 |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 2 | 1.1 | 1.2 | 0.9 |
| 3 | 1.21 | 1.44 | 0.81 |
| 4 | 1.331 | 1.296 | 0.972 |
| 5 | 1.4641 | 1.1664 | 1.1664 |
| Warehouse | x | y | Capw,l1,g | OFw,l1,g | Hub | x | y | Caph,l1,g | OFh,l1,g |
|---|---|---|---|---|---|---|---|---|---|
| w1 | −11 | 63 | 250 | 400 | h1 | 1 | 7 | 90 | 200 |
| w2 | 30 | −4 | 200 | 200 | h2 | 3 | 68 | 70 | 100 |
| w3 | 13 | 93 | 250 | 400 | h3 | 91 | 27 | 90 | 200 |
| w4 | 49 | 90 | 250 | 400 | h4 | 66 | 36 | 90 | 200 |
| w5 | 102 | 23 | 200 | 200 | h5 | 42 | 82 | 70 | 100 |
| w6 | 47 | −4 | 300 | 600 | h6 | 12 | 58 | 110 | 300 |
| w7 | 31 | 92 | 250 | 400 | h7 | 74 | 51 | 90 | 200 |
| w8 | −6 | 10 | 200 | 200 | h8 | 31 | 18 | 70 | 100 |
| w9 | 100 | 65 | 250 | 400 | h9 | 33 | 83 | 90 | 200 |
| w10 | 66 | −12 | 200 | 200 | h10 | 19 | 63 | 70 | 100 |
| w11 | −3 | 26 | 300 | 600 | h11 | 18 | 31 | 110 | 300 |
| w12 | −2 | 77 | 250 | 400 | h12 | 35 | 21 | 90 | 200 |
| w13 | 99 | 71 | 200 | 200 | h13 | 29 | 63 | 70 | 100 |
| w14 | 7 | −10 | 250 | 400 | h14 | 58 | 71 | 90 | 200 |
| w15 | 87 | 88 | 250 | 400 | h15 | 89 | 47 | 90 | 200 |
| w16 | 99 | 47 | 250 | 400 | h16 | 1 | 48 | 90 | 200 |
| w17 | 70 | 97 | 200 | 200 | h17 | 59 | 56 | 70 | 100 |
| w18 | −8 | 38 | 200 | 200 | h18 | 19 | 69 | 70 | 100 |
| w19 | 90 | −6 | 200 | 200 | h19 | 65 | 16 | 70 | 100 |
| w20 | 105 | 11 | 250 | 400 | h20 | 30 | 30 | 90 | 200 |
| Period | g1 | g2 |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 0.75 | 1.5 |
| 3 | 1 | 2 |
| (a) Large Problem Instance | ||||||||||||
| W | MS-CTSIH (Strategy 1) | MS-CTSIH (Strategy 2) | Modified MS-CTSIH | |||||||||
| Best Obj. (×108) | Iter. | No. of Fac. | Total CPU (h) | Best Obj. (×108) | Iter. | No. of Fac. | Total CPU (h) | Best Obj. (×108) | Iter. | No. of Fac. | Total CPU (h) | |
| 107 | 2.91525 | 0 | 18 | 1.12 | 2.95075 | 0 | 18 | 1.64 | 2.91418 | 0 | 18 | 2.94 |
| 106 | 1.25349 | 31 | 24 | 0.99 | 1.25802 | 31 | 24 | 0.87 | 1.24970 | 31 | 23 | 2.15 |
| 105 | 1.03294 | 77 | 27 | 1.06 | 1.03815 | 82 | 28 | 1.47 | 1.03294 | 77 | 27 | 2.06 |
| 0 | 1.00320 | 77 | 28 | 1.10 | 1.01086 | 77 | 29 | 1.51 | 1.00320 | 77 | 28 | 3.02 |
| (b) Small Problem Instance | ||||||||||||
| W | MS-CTSIH (Strategy 1) | MS-CTSIH (Strategy 2) | Modified MS-CTSIH | |||||||||
| Best Obj. (×106) | Iter. | No. of Fac. | Total CPU (min) | Best Obj. (×106) | Iter. | No. of Fac. | Total CPU (min) | Best Obj. (×106) | Iter. | No. of Fac. | Total CPU (min) | |
| 107 | 38.4486 | 15 | 3 | 0.121 | 38.4284 | 15 | 3 | 0.324 | 38.4284 | 15 | 3 | 0.527 |
| 106 | 11.0912 | 0 | 4 | 0.139 | 11.0876 | 0 | 4 | 0.255 | 11.0876 | 0 | 4 | 0.463 |
| 105 | 7.49123 | 0 | 4 | 0.113 | 7.48756 | 0 | 4 | 0.250 | 7.48756 | 0 | 4 | 0.449 |
| 0 | 7.09123 | 0 | 4 | 0.113 | 7.08756 | 0 | 4 | 0.253 | 7.08756 | 0 | 4 | 0.440 |
| (a) First-Echelon Solution | ||||||||||||||||
| Period | t1 | t2 | t3 | |||||||||||||
| Product | g1 | g2 | g1 | g2 | g1 | g2 | ||||||||||
| located warehouse | w2 | w2 | w2 | w2 | w2 | w2 | ||||||||||
| open inventory capacity, Capwlg | 400 | 200 | 400 | 400 | 400 | 400 | ||||||||||
| existing inventory capacity | 400 | 200 | 400 | 400 | 400 | 400 | ||||||||||
| served mean demand, EDwgt | 190 | 108 | 142.5 | 162 | 190 | 216 | ||||||||||
| served demand variance, VDwgt | 1175 | 431.5 | 660.94 | 970.88 | 1175 | 1726 | ||||||||||
| assigned hubs | h1, h3 | h1 | h1, h3 | h1, h3 | h1, h3 | h1, h3 | ||||||||||
| construction cost | 400,000 | 200,000 | 0 | 200,000 | 0 | 0 | ||||||||||
| operating fixed cost | 40,000 | 20,000 | 40,000 | 40,000 | 40,000 | 40,000 | ||||||||||
| non-operated fixed cost | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||||
| reopen cost | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||||
| temporary close cost | 0 | 0 | 0 | 0 | 0 | 0 | ||||||||||
| transport cost (plants–warehouses), rcwgt | 69,350 | 39,420 | 52,012.5 | 59,130 | 69,350 | 78,840 | ||||||||||
| transport cost (warehouses–hubs) | 310,677 | 122,266 | 181,804 | 236,650 | 310,677 | 381,074 | ||||||||||
| holding cost, hcwgt | 42,772.7 | 23,985.7 | 36,642 | 40,541.1 | 42,772.7 | 47,971.4 | ||||||||||
| ordering cost, ocwgt | 34,675 | 39,420 | 26,006.2 | 29,565 | 34,675 | 39,420 | ||||||||||
| Continuous-Review Inventory Control Policy | ||||||||||||||||
| order quantity, Qwgt | 100 | 50 | 100 | 100 | 100 | 100 | ||||||||||
| reorder point, RPwgt | 257.19 | 148.71 | 192.89 | 223.07 | 257.19 | 297.43 | ||||||||||
| safety stock, SSwgt | 67.19 | 40.71 | 50.39 | 61.07 | 67.19 | 81.43 | ||||||||||
| (b) Second-Echelon Solution | ||||||||||||||||
| Period | t1 | t2 | t3 | |||||||||||||
| Product | g1 | g2 | g1 | g2 | g1 | g2 | ||||||||||
| located hub | h1 | h3 | h1 | h1 | h3 | h1 | h3 | h1 | h3 | h1 | h3 | |||||
| open max served daily demand, Caphlg | 180 | 180 | 180 | 180 | 90 | 180 | 90 | 180 | 180 | 180 | 180 | |||||
| existing max served daily demand | 180 | 180 | 180 | 180 | 180 | 180 | 90 | 180 | 180 | 180 | 180 | |||||
| served mean demand, EDhgt | 120 | 70 | 108 | 127.5 | 15 | 123 | 39 | 120 | 70 | 116 | 100 | |||||
| served demand variance, VDhgt | 850 | 325 | 431.5 | 604.69 | 56.25 | 814.5 | 156.38 | 850 | 325 | 1062 | 664 | |||||
| assigned customers | 4, 2, 8, 9, 7 | 6, 3, 1, 5 | 1–9 | 2–9 | 1 | 5, 4, 9, 7, 8, 2 | 1, 3, 6 | 4, 2, 8, 9, 7 | 6, 3, 1, 5 | 5, 8, 9, 2 | 3, 1, 4, 6, 7 | |||||
| construction cost USD 1K | 200 | 200 | 200 | 0 | 0 | 0 | 100 | 0 | 0 | 0 | 100 | |||||
| operating fixed USD 1K | 20 | 20 | 20 | 20 | 10 | 20 | 10 | 20 | 20 | 20 | 20 | |||||
| non-operated fixed cost USD 1K | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | |||||
| reopen cost (USD 1K) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5 | 0 | 0 | |||||
| temporary close cost (USD 1K) | 0 | 0 | 0 | 0 | 2.5 | 0 | 0 | 0 | 0 | 0 | 0 | |||||
| transport cost (hubs– customers) (USD 1K) | 431.0 | 341.6 | 415.1 | 479.9 | 72.2 | 452.1 | 189.9 | 431.0 | 341.6 | 407.9 | 486.8 | |||||
| Period | Total Mean Demand (Product Units/Day) | Total Demand Variance (Product Units/Day)2 | First-Echelon Facility | Second-Echelon Facility | |||||
|---|---|---|---|---|---|---|---|---|---|
| w2 | h1 | h3 | |||||||
| g1 | g2 | all g | g1 | g2 | all g | all g | all g | all g | |
| t1 | 190 | 108 | 298.0 | 1175 | 431.5 | 1606.5 | 600 | 360 | 180 |
| t2 | 142.5 | 162 | 304.5 | 660.9 | 970.9 | 1631.8 | 800 | 360 | 180 |
| t3 | 190 | 216 | 406.0 | 1175 | 1726 | 2901.00 | 800 | 360 | 360 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Punyim, P.; Karoonsoontawong, A.; Unnikrishnan, A.; Ratanavaraha, V. A Heuristic for the Two-Echelon Multi-Period Multi-Product Location–Inventory Problem with Partial Facility Closing and Reopening. Sustainability 2022, 14, 10569. https://doi.org/10.3390/su141710569
Punyim P, Karoonsoontawong A, Unnikrishnan A, Ratanavaraha V. A Heuristic for the Two-Echelon Multi-Period Multi-Product Location–Inventory Problem with Partial Facility Closing and Reopening. Sustainability. 2022; 14(17):10569. https://doi.org/10.3390/su141710569
Chicago/Turabian StylePunyim, Puntipa, Ampol Karoonsoontawong, Avinash Unnikrishnan, and Vatanavongs Ratanavaraha. 2022. "A Heuristic for the Two-Echelon Multi-Period Multi-Product Location–Inventory Problem with Partial Facility Closing and Reopening" Sustainability 14, no. 17: 10569. https://doi.org/10.3390/su141710569
APA StylePunyim, P., Karoonsoontawong, A., Unnikrishnan, A., & Ratanavaraha, V. (2022). A Heuristic for the Two-Echelon Multi-Period Multi-Product Location–Inventory Problem with Partial Facility Closing and Reopening. Sustainability, 14(17), 10569. https://doi.org/10.3390/su141710569








