Experimental Study on Damage Evolution Characteristics of Concrete under Impact Load Based on EMI Method
Abstract
:1. Introduction
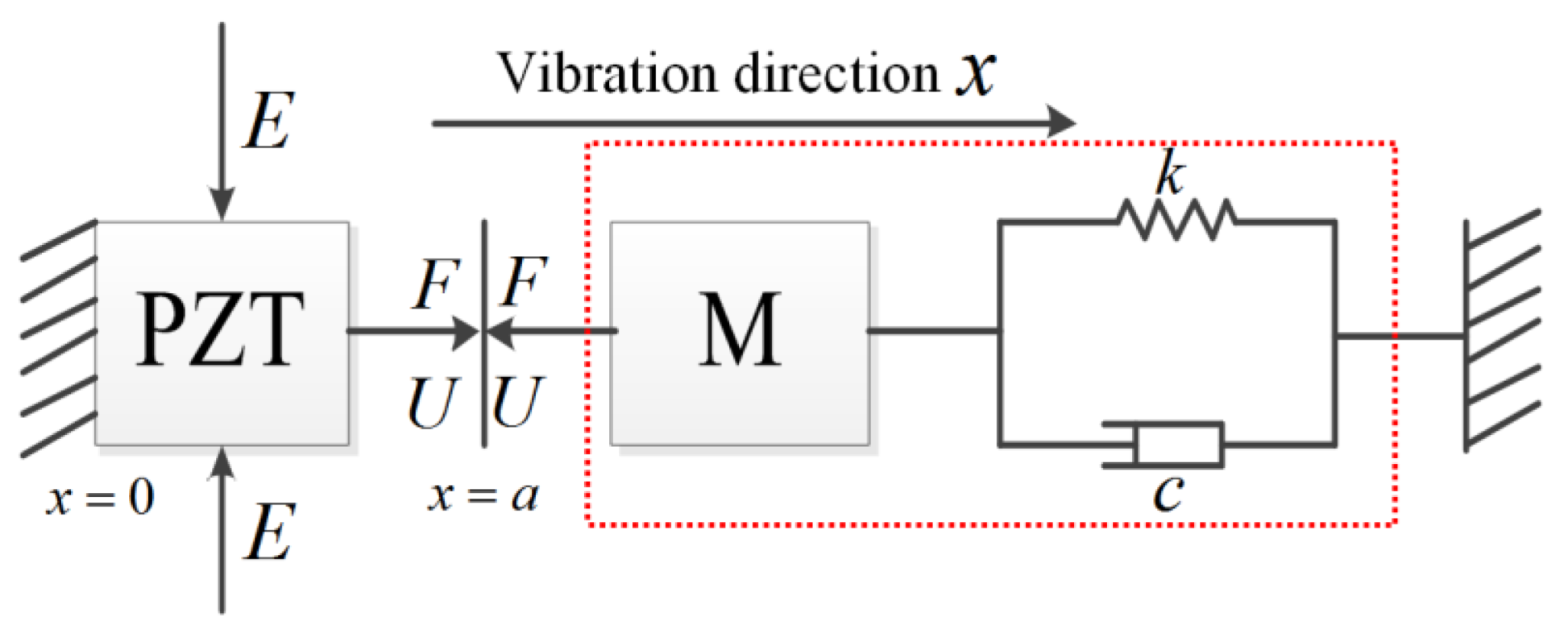
2. The Principle of Parallel Tests
3. Design of the Test
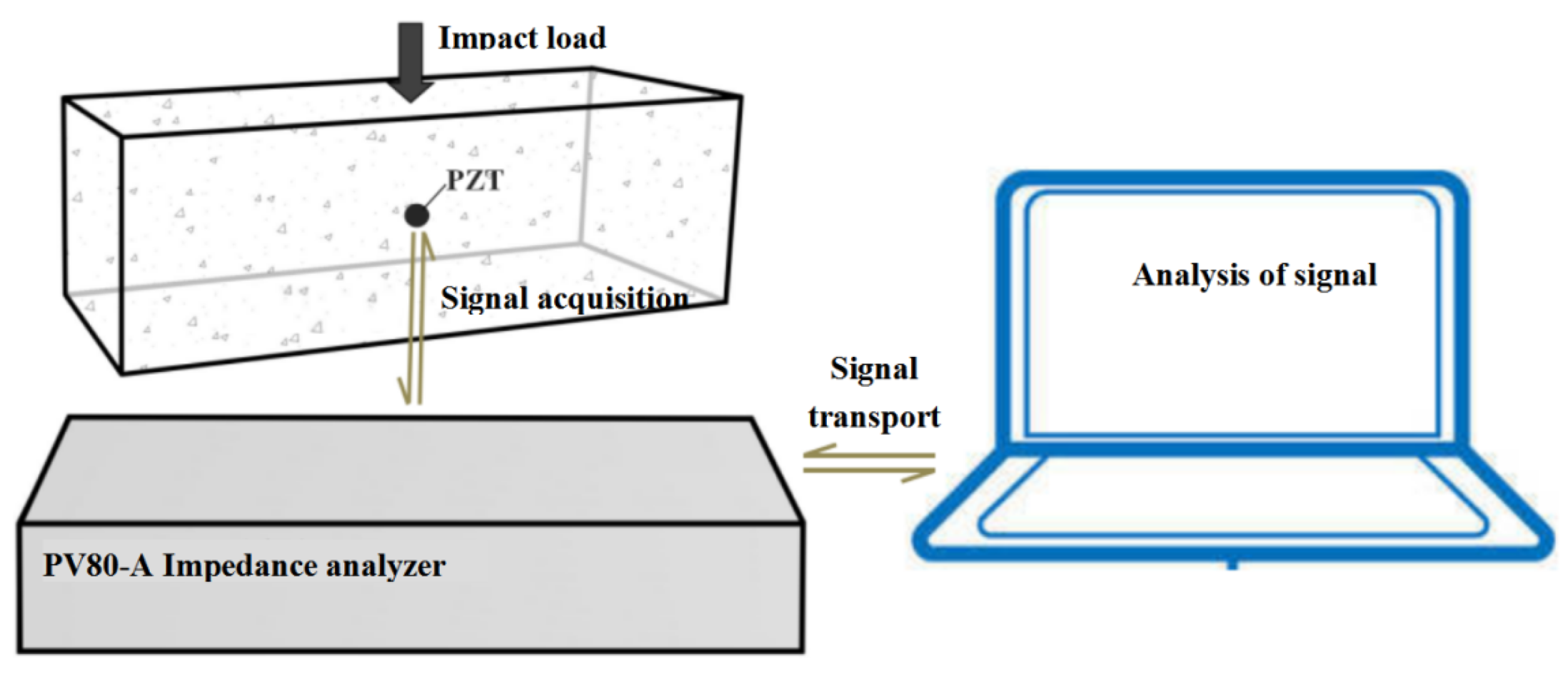
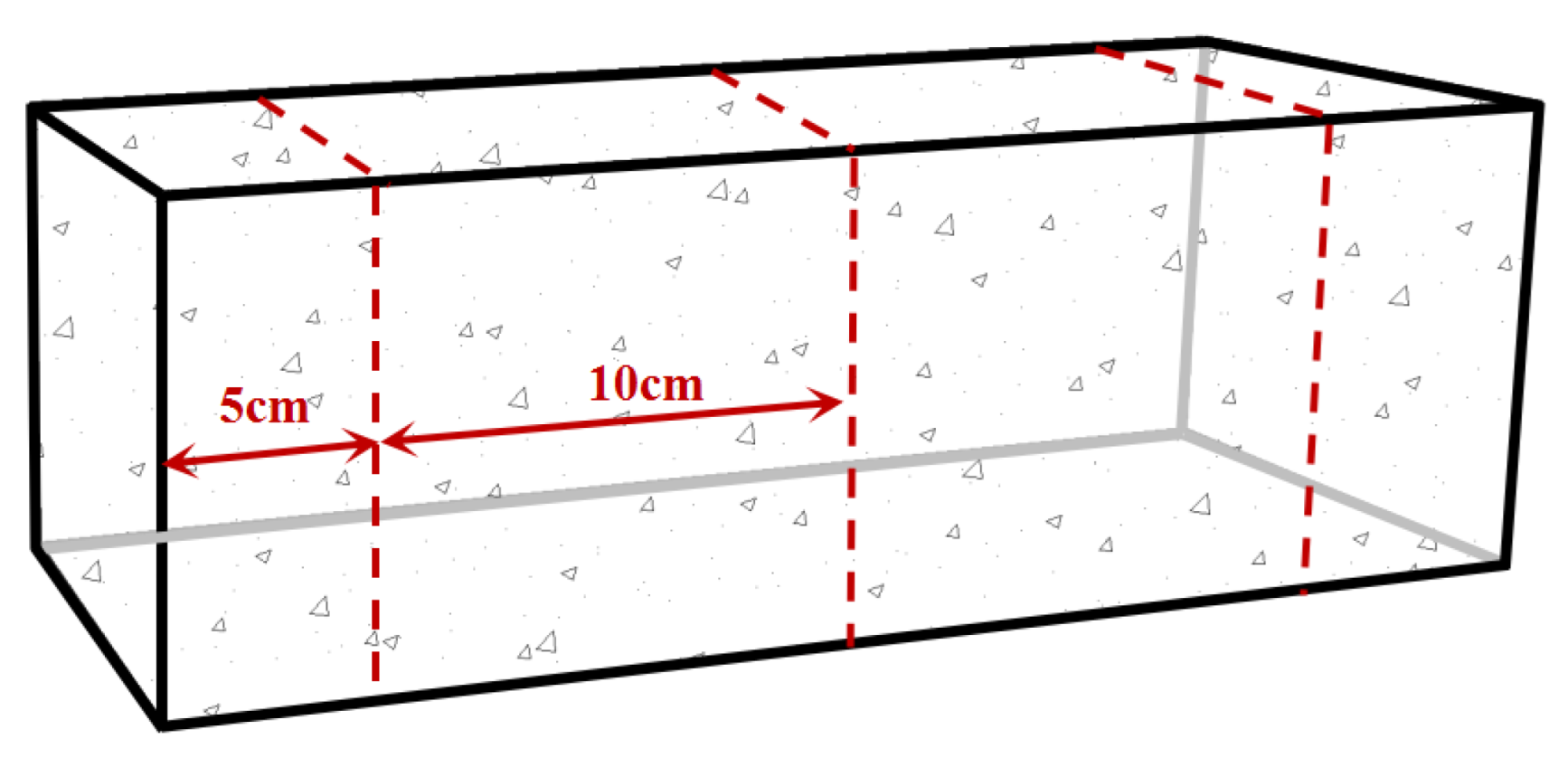
3.1. The Specimen and the Test Equipment
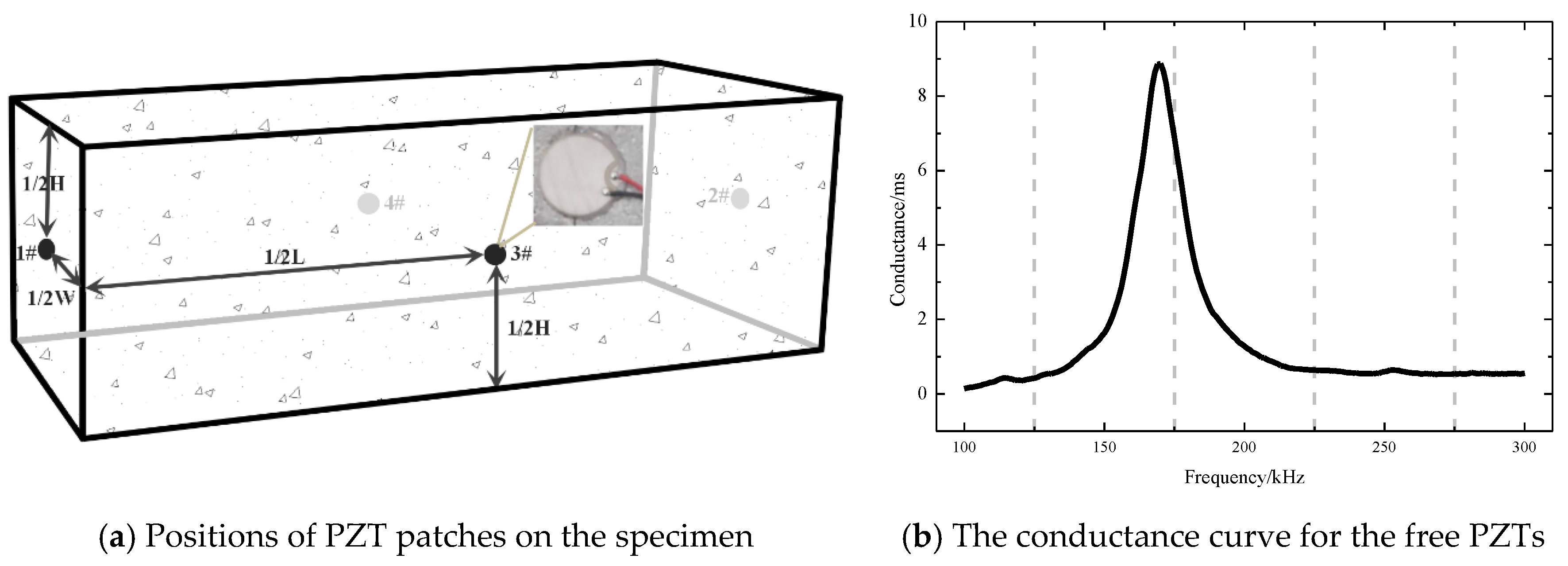
3.2. Experimental Scheme
3.3. The Test Equipment
4. Analysis of Test Results
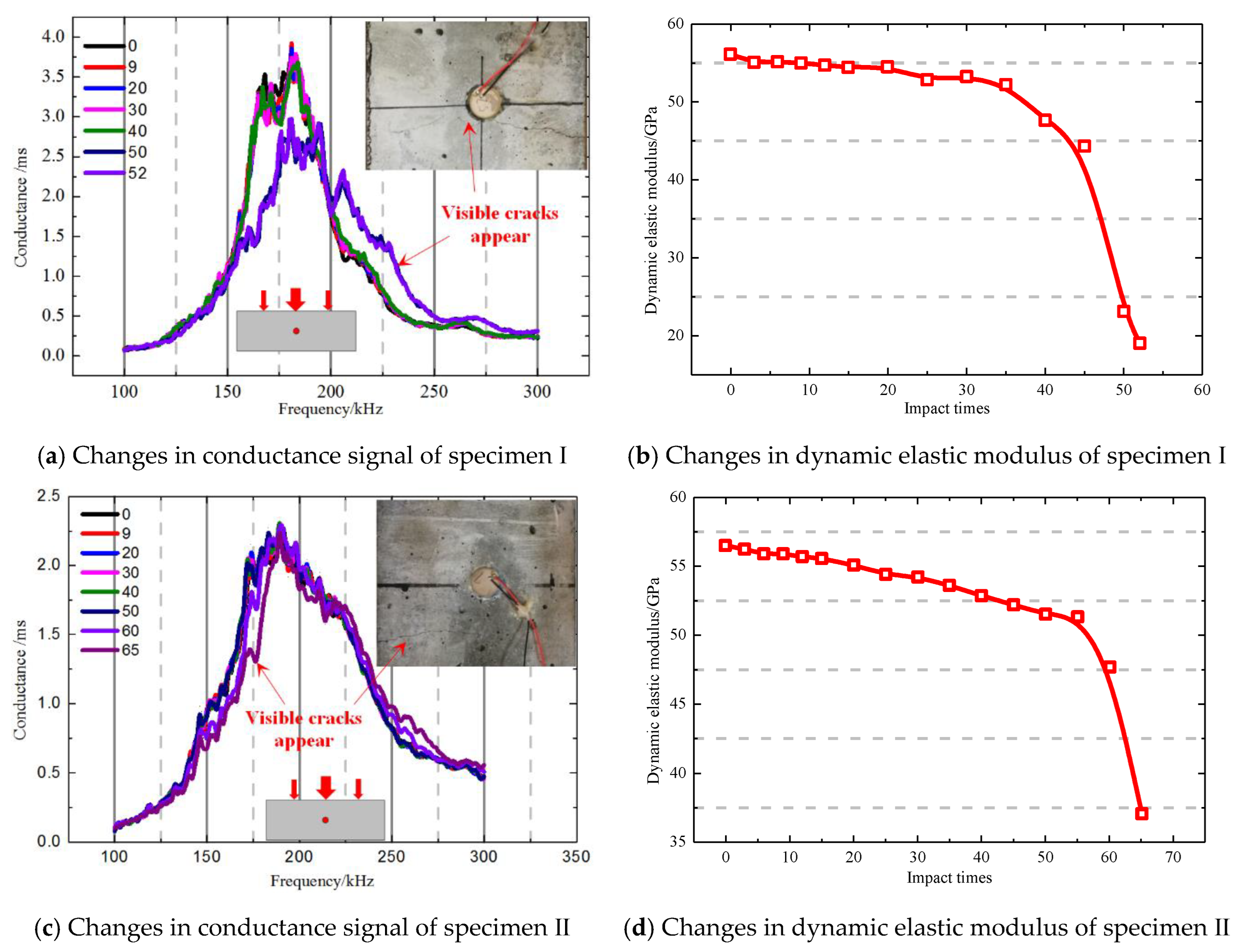
4.1. Analysis of Piezoelectric Signals
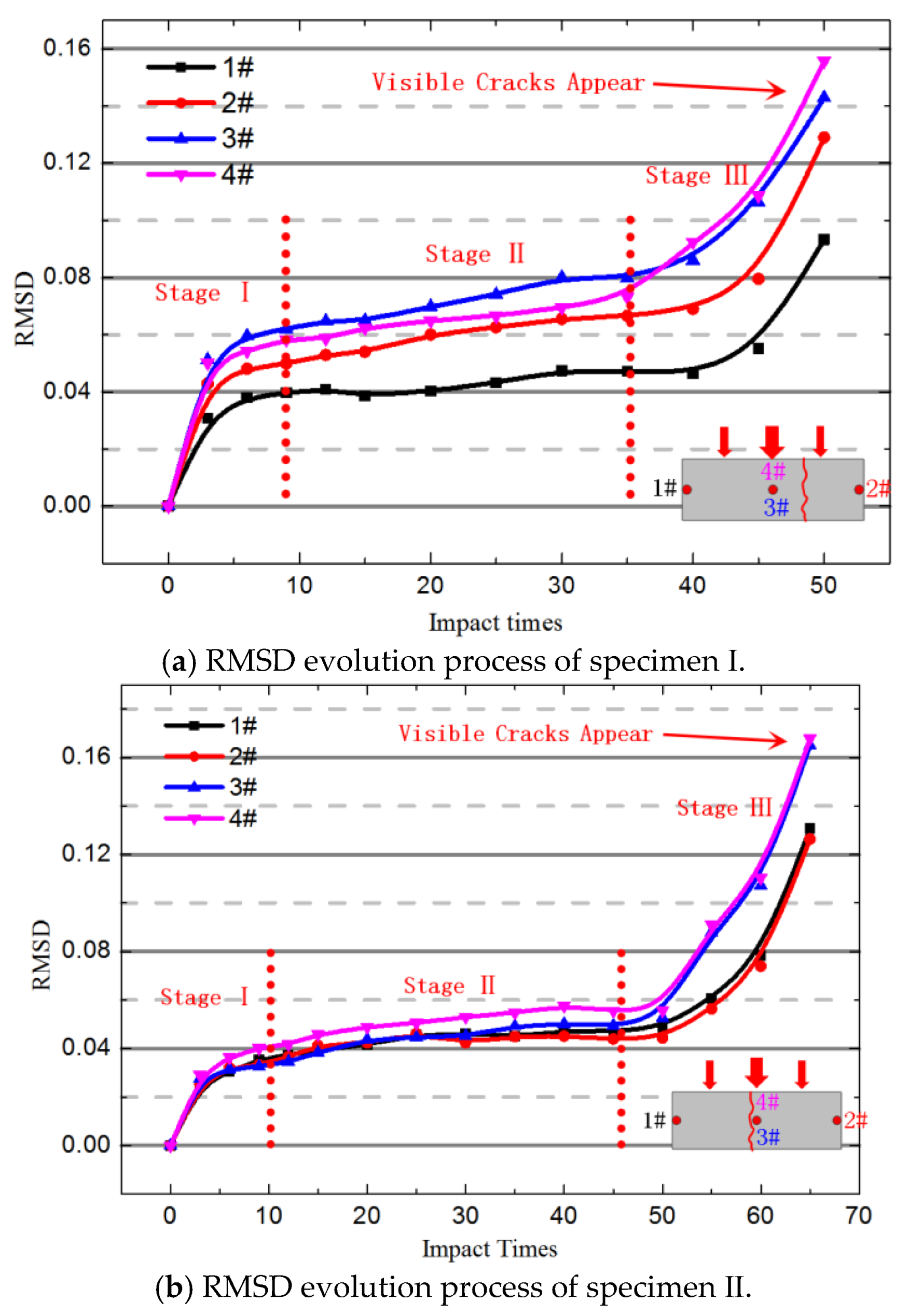
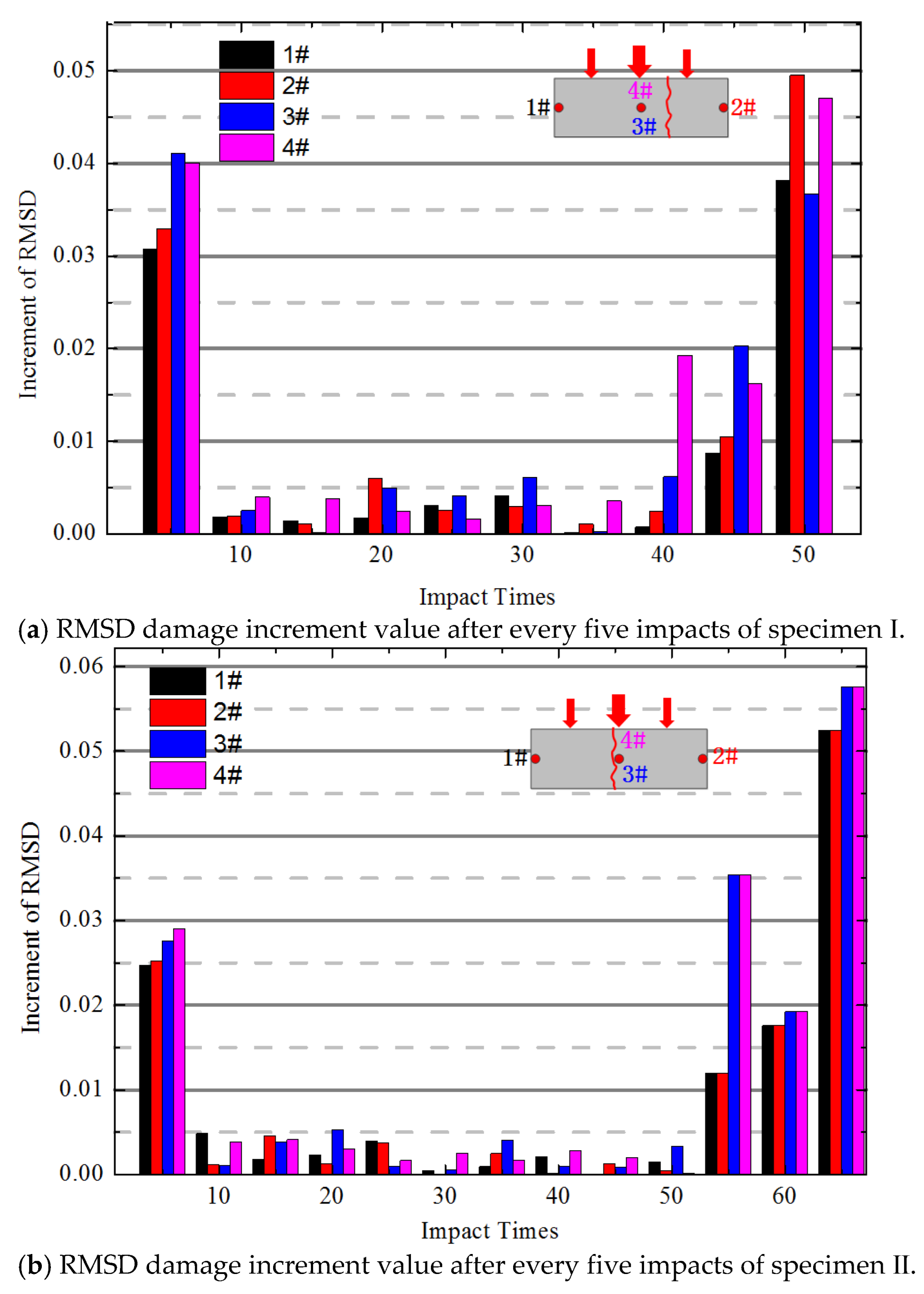
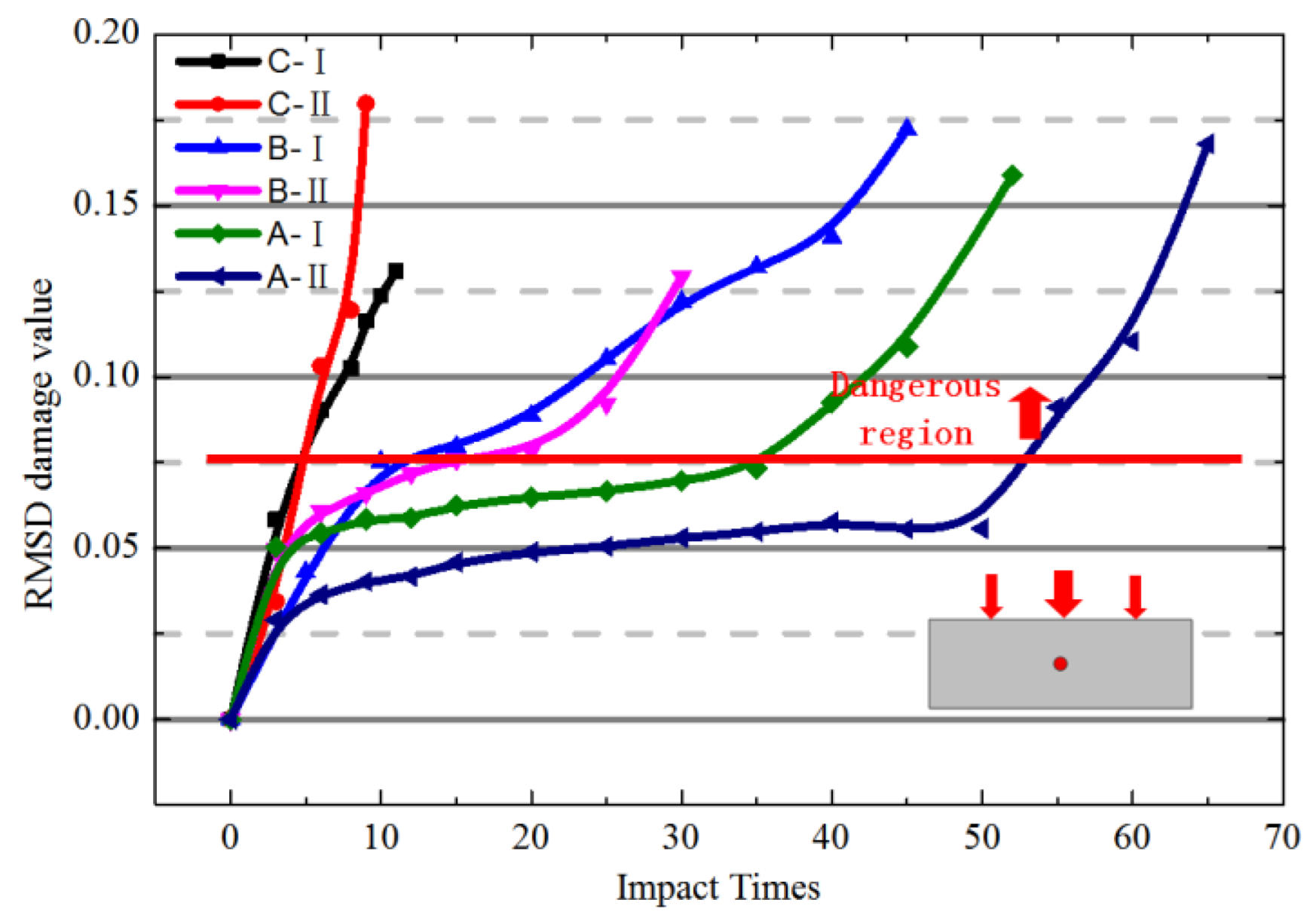
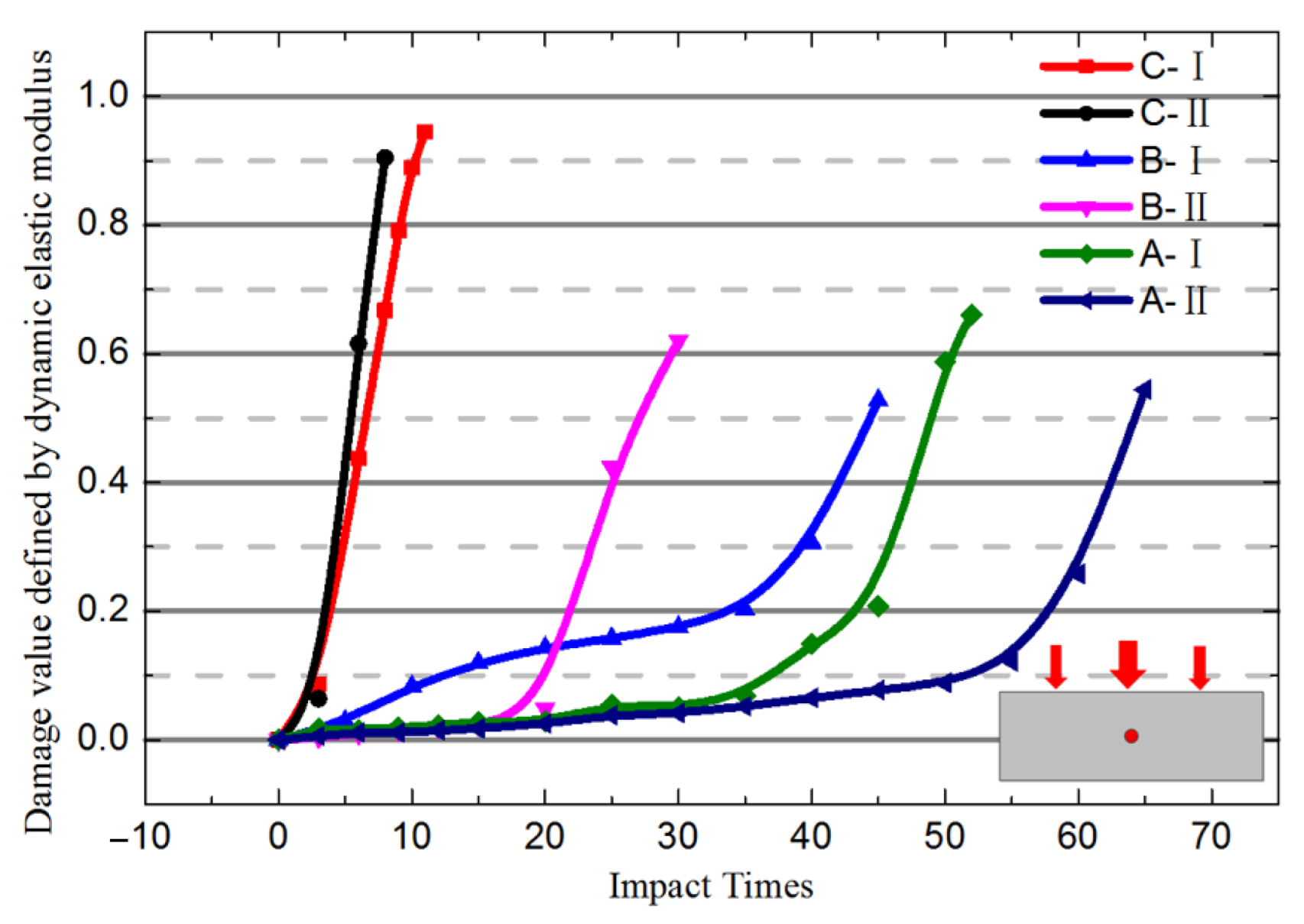
4.2. Analysis of Parallel Verification Test Results
4.3. Analysis of the Results of Splitting Tensile Strength
5. Summary
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sun, F.P.; Chaudhry, Z.A.; Liang, C.; Rogers, C.A. Truss structure intergrity identification using PZT sensor-actuator. J. Intell. Mater. Syst. Struct. 1995, 6, 134–139. [Google Scholar] [CrossRef]
- Ayres, J.W.; Rogers, C.A.; Chaudhry, Z.A. Qualitative health monitoring of a steel bridge structure joint via piezoelectric actuator/sensor patches. Proc. SPIE. Int. Soc. Opt. Eng. 1996, 2719, 123–131. [Google Scholar] [CrossRef]
- Ayres, J.W.; Lalande, F.; Chaudhry, Z.; Rogers, C.A. Qualitative impedance-based health monitoring of civil infrastructures. Smart Mater. Struct. 1998, 7, 599–605. [Google Scholar] [CrossRef]
- Giurgiutiu, V.; Reynolds, A.; Rogers, C.A. Experimental investigation of E/M impedance health monitoring for spot-welded structural joints. J. Intell. Mater. Syst. Struct. 2000, 10, 802–812. [Google Scholar] [CrossRef]
- Soh, C.K.; Tseng, K.K.; Bhalla, S.; Gupta, A.K. Performance of smart piezoceramic patches in health monitoring of a RC bridge. Smart Mater. Struct. 2000, 9, 533–542. [Google Scholar] [CrossRef]
- Bhalla, S.; Soh, C.K.; Tseng, K.K.H.; Naidu, A.S. Diagnosis of incipient damage in steel structures by means of piezoceramic patches. In Proceedings of the 8th East Asia-Pacific Conference on Structural Engineering and Construction, Singapore, 5–7 December 2001; pp. 238–248. Available online: https://www.researchgate.net/publication/264038295 (accessed on 7 June 2022).
- Tseng, K.K.H.; Naidu, A.S.K. Health monitoring of concrete structures subjected to environmental attacks. Proc. SPIE. Int. Soc. Opt. Eng. 2002, 4696, 168–175. [Google Scholar] [CrossRef]
- Tseng, K.K.H.; Wang, L. Smart piezoelectric transducers for in situ heath monitoring of concrete. Smart. Mater. Struct. 2004, 13, 1017–1024. [Google Scholar] [CrossRef]
- Ai, D.; Zhu, H.; Luo, H. Sensitivity of embedded active PZT sensor for concrete structural impact damage detection. Constr. Build. Mater. 2016, 111, 348–357. [Google Scholar] [CrossRef]
- Zhu, H.; Luo, H.; Ai, D.; Wang, C. Mechanical impedance-based technique for steel structural corrosion damage detection. Measurement 2016, 88, 353–359. [Google Scholar] [CrossRef]
- Liu, N.; Peng, L.; Shi, C.; Lei, M. Experimental and model study on dynamic behaviour and fatigue damage of tunnel invert. Constr. Build. Mater. 2016, 126, 777–784. [Google Scholar] [CrossRef]
- Huang, L.; Huang, S.; Lai, Z. On the energy-based criteria for defining slope failure considering spatially variable soil properties. Eng. Geol. 2020, 264, 105323. [Google Scholar] [CrossRef]
- Huang, L.; Ma, J.; Lei, M.; Liu, L.; Lin, Y.; Zhang, Z. Soil-water inrush induced shield tunnel lining damage and its stabilization: A case study. Tunn. Undergr. Space Tech. 2020, 97, 103290. [Google Scholar] [CrossRef]
- Huang, L.; Huang, S.; Lai, Z. On optimizing site investigation program using centroidal Voronoi tessellation and random field theory. Comput. Geotech. 2020, 118, 103331. [Google Scholar] [CrossRef]
- Yin, P.; Zhao, C.; Ma, J.; Yan, C.; Huang, L. Experimental study of non-linear fluid flow though rough fracture based on fractal theory and 3D printing technique. Int. J. Rock Mech. Min. Sci. 2020, 129, 104293. [Google Scholar] [CrossRef]
- Gesualdo, A.; Fortunato, A.; Penta, F.; Monaco, M. Structural identification of tall buildings: A reinforced concrete structure as a case study. Case Stud. Constr. Mater. 2021, 15, e00701. [Google Scholar] [CrossRef]
- Modano, M.; Fabbrocino, F.; Gesualdo, A.; Matrone, G.; Farina, I.; Fraternali, F. On the forced vibration test by vibrodyne. COMPDYN-ECCOMAS Themat. In Proceedings of the 5th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering Methods in Structural Dynamics and Earthquake Engineering, Crete Island, Greece, 25–27 May 2015; pp. 209–217. [Google Scholar] [CrossRef]
- Negi, P.; Chhabra, R.; Kaur, N.; Bhalla, S. Health monitoring of reinforced concrete structures under impact using multiple piezo-based configurations. Constr. Build. Mater. 2019, 222, 371–389. [Google Scholar] [CrossRef]
- Dixit, A.; Bhalla, S. Prognosis of fatigue and impact induced damage in concrete usinembedded piezo-transducers. Sens. Actuators A Phys. 2018, 274, 116–131. [Google Scholar] [CrossRef]
- Lin, Y.X.; Yin, Z.; Wang, X.; Huang, L. A systematic 3D simulation method for geomaterials with block inclusions from image recognition to fracturing modelling. Theo. Appl. Fract. Mech. 2021, 117, 103194. [Google Scholar] [CrossRef]
- Lin, Y.X.; Wang, X.; Ma, J.; Huang, L. A systematic framework for the 3D finite-discrete modelling of binary mixtures considering irregular block shapes and cohesive block-matrix interfaces. Powder Technol. 2021, 398, 117070. [Google Scholar] [CrossRef]
- Lin, Y.X.; Wang, X.; Ma, J.; Huang, L. A finite-discrete element based appoach for modelling the hydraulic fracturing of rocks with irregular inclusions. Eng. Fract. Mech. 2022, 261, 108209. [Google Scholar] [CrossRef]
- Kucíková, L.; Šejnoha, M.; Janda, T.; Sýkora, J.; Padevetand, P.; Marseglia, G. Mechanical properties of spruce wood extracted from GLT beams loaded by fire. Sustainability 2021, 13, 5494. [Google Scholar] [CrossRef]
- Liang, C.; Sun, F.P.; Rogers, C.A. Electro-mechanical impedance modeling of active material systems. J. Intell. Mater. Syst. Struct. 1994, 21, 232–252. [Google Scholar] [CrossRef]
- Su, Y.-F.; Han, G.; Amran, A.; Nantung, T.; Lu, N. Instantaneous monitoring the early age properties of cementitious materials using PZT-based electromechanical impedance (EMI) technique. Constr. Build. Mater. 2019, 225, 340–347. [Google Scholar] [CrossRef]
- Park, G.; Sohn, H.; Farrar, C.R.; Inman, D.J. Overview of piezoelectric impedance-based health monitoring and path forward. Shock Vib. Dig. 2003, 35, 451–463. [Google Scholar] [CrossRef]
- Zhao, S.; Fan, S.; Chen, J. Quantitative assessment of the concrete gravity dam damage under earthquake excitation using electro-mechanical impedance measurements. Eng. Struct. 2019, 191, 162–178. [Google Scholar] [CrossRef]
- Bhalla, S.; Kaur, N. Prognosis of low-strain fatigue induced damage in reinforced concrete structures using embedded piezo-transducesrs. Int. J. Fatigue. 2018, 113, 98–112. [Google Scholar] [CrossRef]



| Components | Mass (kg/m3) |
|---|---|
| Cement (42.5 MPa) | 380 |
| Fly ash (classI) | 100 |
| Fine aggregate (Medium sand) | 692 |
| Coarse aggregate (5–25 mm continuous grading) | 1128 |
| Water | 150 |
| Water reducing agent (solid polycarboxylate acid) | 0.5 |
| Specimens’ size | 100*100*300 mm |
| Compression specimens’ size | 100*100*100 mm |
| Rest Curing Time (h) | Heating Rate (°C/h) | Constant Temperature Time (h) | Constant Temperature (°C) | Cooling Rate (°C/h) |
|---|---|---|---|---|
| 3 | 15 | 3 | 50 | 15 |
| Dynamic Elastic Modulus (MPa) | Shear Modulus (MPa) | Compressive Strength (MPa) | Poisson’s Ratio |
|---|---|---|---|
| 56.3 | 23.6 | 52.4 | 0.23 |
| Group | Number of Specimens | Impact Height/cm | The Mass of the Punching Ball |
|---|---|---|---|
| A | 4 | 20 | 4 kg |
| B | 4 | 25 | |
| C | 4 | 30 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, B. Experimental Study on Damage Evolution Characteristics of Concrete under Impact Load Based on EMI Method. Sustainability 2022, 14, 10557. https://doi.org/10.3390/su141710557
Tan B. Experimental Study on Damage Evolution Characteristics of Concrete under Impact Load Based on EMI Method. Sustainability. 2022; 14(17):10557. https://doi.org/10.3390/su141710557
Chicago/Turabian StyleTan, Bin. 2022. "Experimental Study on Damage Evolution Characteristics of Concrete under Impact Load Based on EMI Method" Sustainability 14, no. 17: 10557. https://doi.org/10.3390/su141710557
APA StyleTan, B. (2022). Experimental Study on Damage Evolution Characteristics of Concrete under Impact Load Based on EMI Method. Sustainability, 14(17), 10557. https://doi.org/10.3390/su141710557





