Abstract
The study of an urban center’s hierarchical structure is an important subject if one wishes to understand the city. Previous studies on urban hierarchical structure focused mostly on qualitative or quantitative research based on factors such as format, transportation, and economy, and lacked quantitative measurement from the perspective of street networks. This study examined the urban central area of Lujiazui, Shanghai, from the perspective of the percolation of the street network in the urban central area. Then, combined with the actual urban space function, the connotation and fractal nature of the hierarchical structure of the central area of the mega-city were obtained. The resulting nested hierarchies represent a reorganization of these highly agglomerated urban centers that contribute to sustainability. The fractal results were verified by the box counting method. Finally, this study fulfills its main purpose, which is to propose a new method for the study of the hierarchical structure of urban central areas.
1. Introduction
Goal 11 of the United Nations Sustainable Development 2030 Agenda proposes to “Make cities and human settlements inclusive, safe, resilient and sustainable” [1]. As the core zone for information, the economy, transportation, and other urban elements, the central area of the city is the starting point for many urban activities, and this can be the foundation for the “basic path focus” [2]. With explosive population growth, the problem of “overloading” appears in the urban central area. Therefore, the construction of efficient, intensive, and sustainable urban centers has gradually become an urgent problem. The optimization of the spatial structure is an important step in promoting the sustainable development of the urban central area. At present, the research on the spatial structure of urban central areas can be roughly divided into the following categories: phenomenological research focusing on retail formats, urban functions, and urban attractiveness [3]; examinations of the scope and structure of urban central areas from the perspective of multivariate data [4]; evolutionary research conducted from the perspective of block evolution and business development in urban central areas [5]; and research on the urban structure obtained by using mathematical modeling from an economic perspective [6,7]. Traditional research on the structure of the urban central area mostly uses multivariate data, starting from the space, function, and form of the urban central area, and focuses on identification [8], evolution [9], and phenomena [10]. However, there are few studies on the hierarchical structure of the urban central area. Therefore, in view of this gap in the research, this study starts from a hierarchical perspective to re-explore the structure of the urban central area.
Hierarchical Structure and Percolation Analysis
The earliest hierarchical model of urban economic geography was the central place theory, which was proposed by Christaller and Lösch in the 1930s and 1940s [11]. Many studies subsequently and rapidly developed using the same logic, verifying the economic and geographical spatial location theory from different perspectives [12]. The hierarchical models are categorized into four types: nested, containment, subsumptive containment, and compositional containment hierarchies. The nested hierarchy is a sorting structure with recursive properties, while the other three hierarchical structures are more specific extensions of the nested structure with different emphases, focusing on the relationship between object attributes in the computer field. Therefore, in this study, the nested hierarchical structure is used to express the implicit, relatively primary inclusive relationship between urban block spaces so as to discover the interactive relationship between space and functional attributes.
At present, the research on hierarchical structure in the field of urban planning mostly judges the entire city from the perspective of economic theory [13,14]. Xiaoyan [15] used the gravity model to study the hierarchical structure of urban hierarchy structure. Beckmann [16] used a mathematical modeling approach to study the urban scale hierarchy. Carol [17] qualitatively divided the hierarchical structure of the urban center through field research on commodity prices and services. There is currently a lack of quantitative hierarchical structure research at the level of urban central areas.
Percolation analysis at street intersections provides a new approach to the study of sustainable urban center hierarchies. Piovani explored the linkages between the agglomeration characteristics of British urban retail formats and the penetration of street network intersections, illustrating the implicit connection between economic factors and urban transportation networks [18]. Dong applied percolation theory to explore the spatial co-location results of roads and infrastructure networks and verified the relationship between road networks and urban internal structural systems [19]. These studies confirmed that the distribution characteristics of street intersections at a regional level can express the hidden hierarchical structure characteristics for different distance ranges. Therefore, this study aims to provide a new perspective on the study of urban spatial structure through research based on the percolation theory.
In fact, the percolation analysis algorithm for the urban realm was originally developed in 2015, and Arcaute applied it to street intersections across the UK, finally creating a continuous hierarchy in the UK and realizing the zoning of the entire UK [20,21]. Maddison applied percolation theory to the detection and exploration of ancient sites and grouped them in a reasonable manner [22]. Arcaute and Maddison were pioneers in applying percolation analysis algorithms to regional-level urban spatial problems, and we have applied this technique to our study of the hierarchy of urban centers.
This study thus followed the above-mentioned research method based on the percolation theory of street networks, applied it to the urban center at the block level, and uses the results to discuss the hierarchical structure, fractal properties, and evolutionary context of the urban center at different scales. The resulting nested hierarchical structure reorganizes its spatial system from the highly agglomerated urban center, making it conducive to building a sustainable urban center in the future, from the perspective of blocks.
The main research question of this study is: Can percolation analysis at street intersections be used as a new method to study the spatial structure of urban central areas? To answer this question, we formulated the following sub-questions:
1. What is the practical significance of the hierarchical structure of the city center obtained by this method?
2. What practical significance does the transition and change of the city center obtained by this method have?
3. Can the method be verified?
The remainder of this study is structured as follows: Section 2 briefly introduces the principle and application method of the percolation theory based on the street network and explains the process of obtaining the intersection data. Section 3 discusses the hierarchical structure and fractal properties of the city center under different distance parameters. Section 4 provides a summary of the study, discusses its limitations, and uses the box counting method for validation. Section 5 provides an overview of the findings from a sustainability perspective.
2. Method and Dataset
The theory of percolation originated from an idea put forward by chemist Paul Flory in the 1940s when he was studying the gelation of polymers [23]. It can be considered as a kind of porous probabilistic study focusing on the formation process of infinite star clusters that appear as the probability increases. Li used a large porous stone as a case in an article entitled “Percolation on complex networks: Theory and application” [24] in an endeavor to understand the percolation process. That study postulates that, when a porous stone is immersed in water, water slowly soaks into the center of the stone. The connection between adjacent pores indicates a probability, that is, the probability of occupation. Different pore parameters can form multiple groups of different clusters, so we can perform multi-scale agglomeration analyses on the research object by adjusting the pore size. Currently, percolation theory has been generalized and deduced from basic physics to many research fields in human life such as predicting the spread of epidemics in medicine [25], predicting species distribution in forestry [26], and the penetration of coastlines in natural landscapes [27].
In the field of physics, percolation theory is mainly concerned with the clusters that appear when a surrounding lattice is occupied by an event as the p increases. This agglomeration feature is usually expressed by the size of the star cluster. The formula is:
where N represents the size of the entire system (site number) and is the number of sites in the largest cluster. As probability increases, different giant star clusters are formed.
Percolation has three characteristics: threshold phenomenon, fractal phenomenon, and connectivity [28]. In fact, these three properties have a complementary relationship. The threshold phenomenon represents the morphological transition and critical phenomenon in the agglomeration process of street intersections; the fractal phenomenon expresses the morphological similarity and change process between different groups in the results of percolation analysis; and connectivity expresses the implicit relationship between street intersections. In summary, we apply percolation theory to street intersections in the city center to further understand the hierarchical structure of the city center at different scales. The main research methods and workflow of this study are depicted in Figure 1.
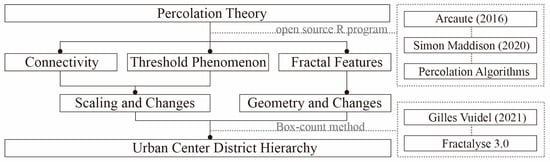
Figure 1.
A demonstration of the main methods and workflow used in this study [21,22]. (Fractalyse 3.0: downloaded from http://fractalyse.org, accessed on 11 July 2021).
Specifically, the research methodology of this study is divided into the following three parts: in the first part, the percolation analysis algorithm is used to perform hierarchical clustering analysis on street intersections in the central area of Lujiazui and to ascertain the hierarchical structure of that area. In the second part, the hierarchical structure obtained in the previous part is analyzed, the hierarchical nested structure is obtained, and its fractal properties are interpreted. The third part summarizes the results and uses the box counting method to conduct fractal verification of street intersections in the city center.
In the next section, we will briefly introduce the data acquisition of Lujiazui city center in Shanghai and its road intersections.
2.1. Case Selection and Data Acquisition of Street Intersections
This study chose the central area of Lujiazui, Shanghai, as a research object. Lujiazui is one of the major financial centers in Shanghai, China, and has the scale and structural characteristics of an emerging city. Shanghai Lujiazui is different from the central area of the old city. It is an urban space dominated by cars, public transportation, and traveling residents. The spatial structure of its urban central area was gradually formed through overall urban planning, regulatory detailed planning, and gradual urban development. At the spatial level, it has the scale characteristics and advantages of the new era. Therefore, this study hypothesizes that the development of Shanghai’s Lujiazui urban center is a demonstration area with comprehensively developed cultural, economic, political, and other elements, and can be used as a typical case for the study of the spatial hierarchy of high-density urban centers based on street networks.
First, the preliminary acquisition of OpenStreetMap (OSM) data and the definition of the central area of Lujiazui, Shanghai are as follows. This study obtained data from OSM (https://www.Openstreetmap.org/#map=6/46.449/2.210, accessed on 11 July 2021) to collect the street network data of the central area of Lujiazui, Shanghai, and imported it to GIS. We referred to Yang and Hu’s method of defining the boundary of the urban central area [4], learning that the urban central area of Lujiazui is about (Figure 2). On this basis, the redundant road types in the obtained OSM data were screened and eliminated, and finally four levels of roads in the central area of the city (primary, secondary, tertiary, and residential roads) were retained (Figure 3).
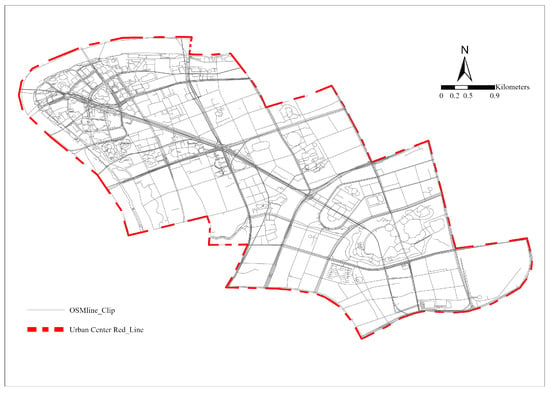
Figure 2.
The definition of the central area of Lujiazui in Shanghai, and the acquisition of OSM data.
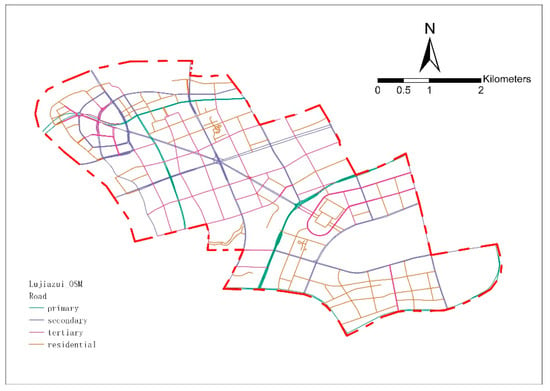
Figure 3.
Four types of retained roads: primary, secondary, tertiary, and residential.
Second, OSM road centerlines were extracted. A 25-m buffer analysis was performed on the OSM road network by preliminary sorting, and the TIFF image in a monochrome threshold format with color mode 1 was exported (Figure 4). ArcScan was used to vectorize the exported TIFF image of the central area of Lujiazui, and the road centerline of the central area of Lujiazui was finally extracted (Figure 5).
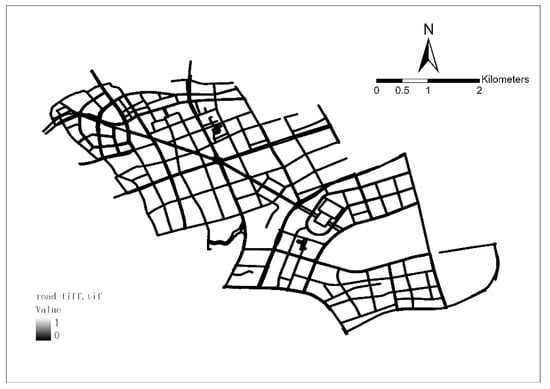
Figure 4.
A 25 m buffer analysis of the road network was performed to export a TIFF image in monochrome threshold format with color mode 1.
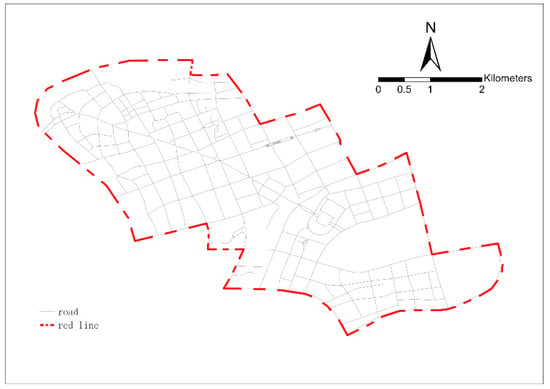
Figure 5.
Vectorized TIFF image using ArcScan.
Again, based on Figure 5, the street road network data were corrected and proofread with Tianditu (China Online Map) and Amap (https://www.amap.com, accessed on 11 July 2021). We finally acquired a street network dataset in the central area of Lujiazui containing 352 nodes and 576 links. Figure 6 illustrates the results of the filtered city center street intersections and links. (Data S1: data; shp).
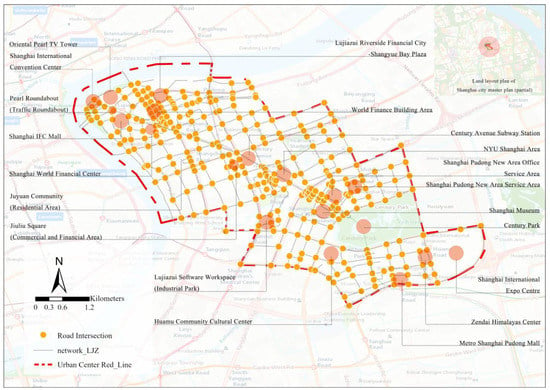
Figure 6.
Shanghai Lujiazui city center road data and main function node.
It is worth noting that there is a certain distance error between the road center line established by OSM and the actual road network data, but the impact of such an error is usually negligible and can be ignored.
2.2. The Percolation Algorithm
Next, we briefly introduce the principle of percolation analysis. Figure 7 shows that, in the finite system, the percolation analysis algorithm divides the characteristic points into two clusters.
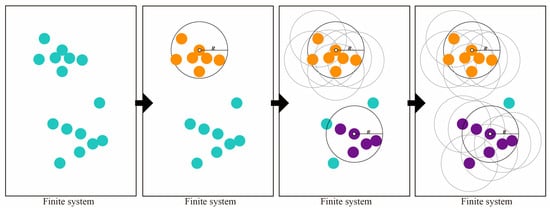
Figure 7.
Principles of percolation analysis in a finite range. Different colors represent different clusters.
The clustering features obtained by the percolation analysis are defined by a given distance threshold (). The technique selects an arbitrary point as a starting point, defines the distance threshold () as the radius of cluster selection, and performs cluster analysis by identifying “points” that fall within the range. Subsequent distance thresholds () will follow this definition. Specifically, the percolation analysis algorithm based on street intersections pays attention to the Euclidean distance between two-dimensional points. If the Euclidean distance is less than the given distance threshold (), then the feature point is assigned to this cluster; if a cluster has less than two feature points, then it is determined that the cluster does not exist. Eventually, all points at different locations will be detected and classified. It is worth noting that the City Clustering Algorithm (CCA), which is based on the identification of population density to determine the urban boundary, was developed based on the percolation theory.
The development and evolution of the street network is closely related to the development of the structure of the city center. In 2015, Murcio applied street intersections to the fractal research of urban street networks for the first time. He found that, in statistical analyses, the degree distribution of the city street network was close to the Poisson distribution, so street intersections and segments can be considered equivalent [29]. Therefore, this study maintains that the analysis results based on street intersections can be used to characterize the study of street network structure.
This study selected the road intersection as the feature point, taking the street intersection in the central area of Shanghai Lujiazui as the center of the circle and using the given radius as the distance threshold () for clustering calculation. Under each set of distance thresholds (), different percolation analysis results were obtained at street intersections in the city center, revealing different cluster characteristics. Finally, we obtained the results of stratified percolation based on street intersections in the city center. Simultaneously, with the expansion of the distance threshold (), the different types of cluster features obtained also showed the spatial nesting structure and percolation evolution process of high-density urban central areas. This provides a new perspective and method for the preliminary research, scale control, and functional connectivity of the future urban central area.
2.3. Box Counting Method
The term “fractal” was coined by mathematician Benoît Mandelbrot. In nature, similar shapes with different volumes can always be found; fractal theory jumps out of the four-dimensional space and adopts the method of fractal dimensions to describe similarities of complex systems. In theory, the fractal dimension is used to describe the filling degree of a fractal on the space. The fractal dimension definition methods include the box counting dimension, Hausdorff dimension, topological dimension, and so on.
The box counting dimension, also known as the Minkowski dimension, is a method of measuring the fractal dimension of the distance space in fractal geometry. Imagine placing the research object on a uniformly divided grid, using the minimum number of grids to cover the fractal. The box dimension is calculated by setting grids of different scales to see the change in the number of fractals that cover it. The box count estimator is obtained by a scaling law that defines the dimension of the box.
The number of points that fall into the grid are counted as the evaluation process of the box counting method. The sequence of points (, ) is formed into an empirical curve. If the empirical curve follows the fractal law, the corresponding estimated curve form is a power-law distribution (such as a parabola). The formula is:
where is the box threshold (the pore diameter distance); is , the number of count elements; is the error estimate; and is the score dimension.
We found the logarithm on both sides of the experience curve to result in a linear regression graph. The formula is:
3. Results
3.1. Hierarchical Structure of Lujiazui City Center
Through multiple selections of percolation experiments defined by different distance scales, we selected three groups of parameters for systematic calculation and analysis. The first set of parameters had a threshold range of 50–800 m. With 25 m as the radius step, 50 m as the minimum distance threshold (), and 800 m as the maximum distance threshold (), the most significant features can be observed in percolation analysis and calculation (Figure 8).
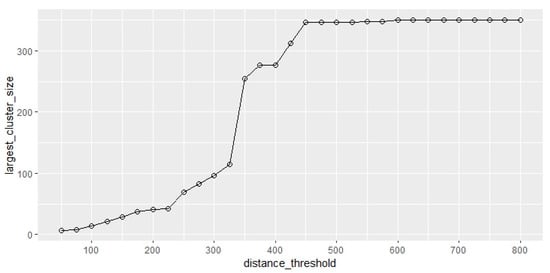
Figure 8.
Clustering features calculated by percolation analysis with 25 m as the radius step, 50 m as the minimum radius distance threshold, and 800 m as the maximum radius distance threshold.
The second set of selected parameters had a threshold range of 300–500 m. As the slope of percolate changes between 300 m and 500 m appeared to be larger compared with the analysis results of the first group, we decided to perform a detailed percolation analysis on this range to identify any subtle changes. We took 50 m as the radius step, 300 m as the minimum distance threshold (), and 500 m as the maximum distance threshold () (Figure 9).
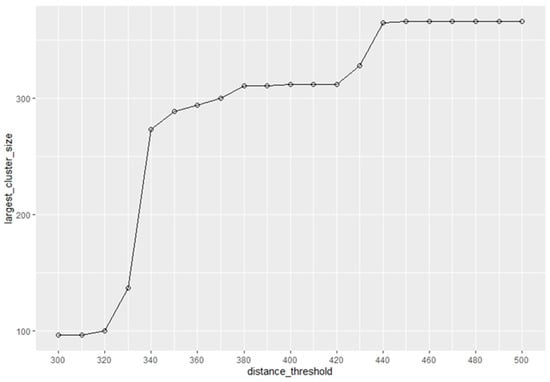
Figure 9.
Clustering features calculated by percolation analysis with 50 m as the radius step, 300 m as the minimum radius distance threshold, and 500 m as the maximum radius distance threshold.
The third set of parameters’ threshold range was 100–8000 m. To include the entire central area of Lujiazui in our range, we set 8000 m as the maximum distance threshold to analyze its variation characteristics, that is, a radius of 100 m as the step size, 100 m as the minimum distance threshold (), and 8000 m as the maximum distance threshold (). The percolation clustering characteristics did not change after the distance threshold () was set to 500 m (Figure 10).
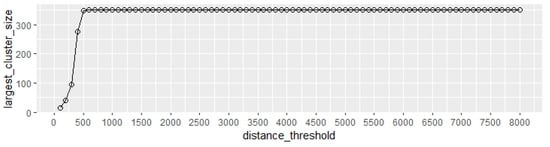
Figure 10.
Clustering features calculated by percolation analysis with 100 m as the radius step, 100 m as the minimum radius distance threshold, and 8000 m as the maximum radius distance threshold.
We further scrutinized the percolation results obtained with different distance thresholds (). The clusters were divided into 15 cluster levels according to the percolation process: the red cluster represents the highest level, and the blue cluster is the second highest level. The clustering feature of sites below level 15, indicated in gray, was not obvious. We extracted the distance thresholds () with salient features for analysis as depicted in Figure 11, Figure 12 and Figure 13, the hierarchical clustering being a step length of 25 m and a maximum radius distance threshold of 500 m.
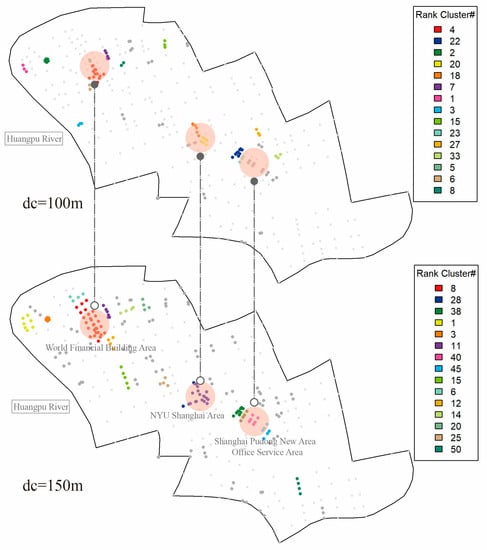
Figure 11.
Percolation analysis results from to .
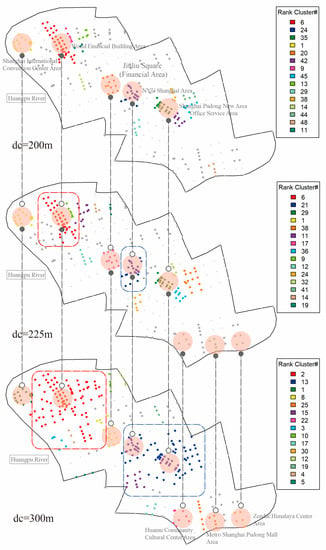
Figure 12.
Percolation analysis results from to .
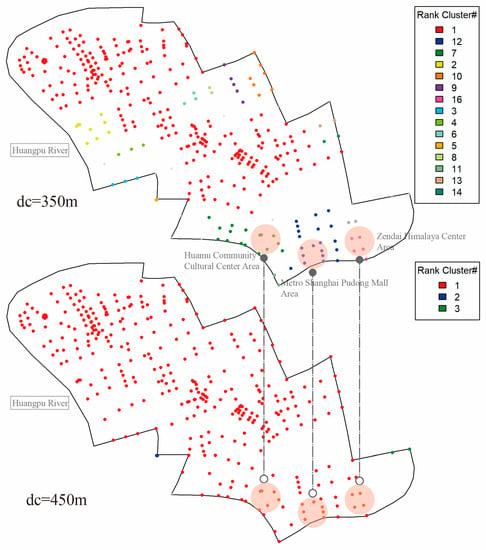
Figure 13.
Percolation analysis results from to .
With as the initial state, significant agglomeration characteristics were not reflected. With the expansion of the radius distance threshold (), the agglomeration effect caused by percolation slowly increased, and a slight but obvious enhancement occurred when . Compared to the initial value, this transition displayed a clear representativeness of the urban core area. It would form three main cores, that is, the World Financial Building Area, NYU Shanghai Area, and Shanghai Pudong New Area Office Service Area, and multiple secondary cores along Century Avenue. Simultaneously, several main cores tended to expand to the surrounding areas. When , the structural transformation of Lujiazui city center reflected the economic center of Shanghai Lujiazui and the political and cultural nature of the region (Figure 11).
We further observed that there were multiple cores between and , forming a process of expanding to the center, with Century Avenue as the axis. When , a relatively stable multi-core structure feature was formed, and the fractal feature obtained at this time was the most obvious. It is worth noting that, when , with the business district of Century Avenue Metro Station as the divider, the degree of agglomeration was strengthened, and there was an obvious two-level differentiation on both sides. We noticed that, while the two major cores are “competing” for development, with Century Park as the boundary, new clusters of clusters gradually emerged in the opposite area. This shows to a certain extent that the existence of natural elements, such as parks, had a restrictive effect on the agglomeration and development of cities. On the whole, this transition process also gradually presented a process of evolution to the Century Avenue Subway Station Area which somewhat reflected the importance of the development and construction of the Century Avenue Subway Station Area in the future urban central area (Figure 12).
The next transition was when . The two cores of the central area of Lujiazui were integrated and separated from the opposite side by Century Park, forming a new gathering area headed by Huamu Community Cultural Center area, Metro Shanghai Pudong Mall area, and Zendai Himalaya Center area. Eventually, with the expansion of the distance threshold (), the whole Lujiazui core area of full penetration was formed when (Figure 13).
Although the method of exploring the economic division of the spatial structure along the road had certain limitations, (for example, the actual connectivity and timeliness of the road intersections needed to be verified), the central area of the megacity was still divided into multiple cores within a certain tolerance range. Concomitantly, the central area of Lujiazui was divided into different dominant functional areas on the block scale level, which helped to explain the connectivity between urban block functions in the evolution of different areas.
3.2. Fractal Properties of Lujiazui Urban Center
The percolation effect of street intersections was accompanied by fractal features. The urban central area could transition to form multiple sets of core areas with different agglomeration patterns through recursive infiltration at different scales. When a certain distance scale is reached, a large agglomeration core can be formed. Simultaneously, it can be observed that, with the expansion of the distance threshold (), the transformation of the morphological structure of the urban center could be summarized as a fractal nested structure with the block scale as the scale.
Specifically, when the distance threshold of , the culturally led area with the Shanghai International Conference Center area as its main attraction formed a relatively obvious fractal with the Lujiazui financial area, and this area held its leading cultural position to a certain extent. When , star clusters of different grades gathered along the main road, Century Avenue, to achieve a relatively stable structure. When , the star clusters on the north side of Lujiazui were integrated with Century Park as the boundary. With the expansion of distance, the evolution process of this complex tree-like structure essentially expressed the hierarchical relationship of “financial-dominated, political-secondary, and cultural-third” on the north side of the central area of Lujiazui. This included policy factors in the division of the spatial structure and disclosed the driving force leading the development of the entire Lujiazui city center to a certain extent. After , the southern area of Century Park gradually showed agglomeration that could be divided into three major areas led by the Huamu Community area, Metro Shopping Mall area, and International Expo Center area. This reflected the hierarchical relationship of “internationalization–livable–leisure” on the south side of Century Park. When , the maximum percolation result was achieved, and the central area of the city merged into a huge cluster of a single core. Figure 14 shows the spatial hierarchy nesting characteristics of the central area of Lujiazui.
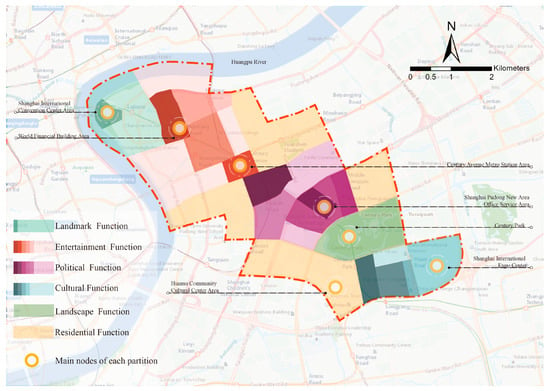
Figure 14.
The spatial nesting structure of seven different functional groups.
From the clustering evolution process obtained at different spatial scales, the percolation analysis method revealed the relationship between different clusters, forming a nested model of the spatial structure from the perspective of the block scale. Figure 14 clearly shows the bottom-up agglomeration process and scale dependence in the city center. Overall, the urban core of Lujiazui could be divided into the Shanghai International Convention Center Area, Financial Center Area, Shanghai Pudong New Area Office Service Area, International Expo Center Area, Century Park, and Huamu Community Area, which could be transposed into the six functional elements of “landmark–business–politics–culture–landscape–livable”. Then, we could also divide the six functional areas into multiple groups according to the percolation results, which showed the hierarchical nesting relationship of urban spatial structure at different scales. In fact, we could also initially explore the connectivity between functional groups, expressing the hierarchical nesting model presented by the spatial structure of the urban center and providing a new method for the quantitative implementation of urban renewal strategies at the block scale in the urban center.
Overall, the geographical space (rather than time) showed a trend of evolution toward the Century Avenue Subway Station Area, which means that the Century Avenue Subway Station might become an important node for the further development and construction of the Lujiazui city center.
4. Discussion
This study demonstrates a method for quantitatively analyzing the hierarchical structure of urban centers. Based on the existing aggregated results of street intersections in the urban center, we selected the hierarchical nesting results obtained when the distance thresholds () are 450 m, 350 m, 325 m, and 250 m for analysis (Figure 15).
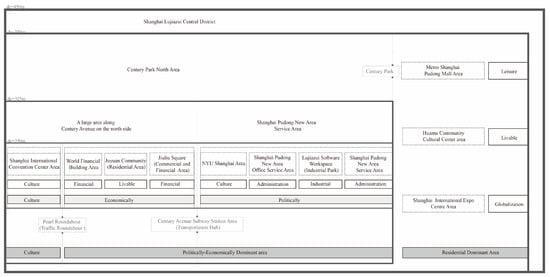
Figure 15.
The hierarchical structure of the city when .
It is evident that the central area of Lujiazui, Shanghai, is bounded by Century Park and is divided into an “economically and politically dominated area” on the northern side and a “residentially dominated area” on the southern side. The northern area of Lujiazui, which is bounded by the Century Avenue Metro area, is divided into an “economically dominant area” and a “politically dominant area”. It is worth noting that the Shanghai International Conference Center area at the “fish mouth” of Lujiazui serves as a cultural node space for “guidance” and “sign” in the northern area of Lujiazui and plays an important role in the central area of the city (Figure 15). It is worth noting that Phearson [30] argues that sustainable cities have redundant and resilient modular subsystems. The hierarchically nested structure obtained in this study also expresses a similar elastic system to a certain extent, which may further deepen the understanding of the structure of urban central areas.
Judging from the results of the spatial structure division of the urban central area, according to the actual function of the urban central area, and when the distance threshold ) is 250 m, a relatively obvious grouping of the spatial structure of the urban central area from the block perspective is indicated. Furthermore, this study believes that 25–50 m can be set as a buffer zone, and the current situation analysis and guidance can be carried out in the subsequent spatial arrangement of urban central areas. What needs to be explained here is that the functions of different urban central areas differ, and the spatial structures reflected under the guidance of non-spatial attributes, such as policies, culture, and economy, also differ. Therefore, the hierarchical percolation results obtained in the urban central area of Lujiazui in Shanghai are not generalizable to other cities. In the future, we can further summarize the scale-dependent characteristics of different types of urban spatial hierarchies.
This study has certain limitations. From the perspective of the research object, it only conducts percolation analysis at street intersections, but in fact the complex and diverse composition of urban central areas still requires more diverse perspectives to interpret it. For example, Behnisch [31] applied percolation theory to quantify building connectivity in order to detect different urban boundaries. Arcaute [20] used commuting and population density to define the boundaries of urban systems and explored the relationship between urban indicators and scale. Cao [32] performed percolation analysis on population, roads, and nighttime lights to quantify urban extent. Montero [33] found that the MorphoLim method and percolation method obtained different morphological boundaries for urban agglomerations. From the perspective of research methods, this study only analyzes urban space, but lacks the consideration of location economy. At present, the research on the urban hierarchy is mostly based on the central place theory, from the perspective of microeconomics. For example, Hsu [7] used the equilibrium model to obtain the urban spatial hierarchy from the perspective of microeconomics, which verified the central place theory. Tabuchi [34] used the equilibrium method to provide a new economic research basis for the central place theory. Space and economy are both components of the spatial structure of urban central areas, and how to combine the two may be an important direction for future research. From the research results, this study obtains the static urban spatial structure at different scales through the percolation method, but lacks a dynamic urban spatial evaluation. For example, Li [35] conducted traffic congestion assessment from the nodes of dynamic traffic percolation transition. He [36] constructed a temporal hierarchical network through human movement data to control the spread of infectious diseases at multiple scales. In terms of the generality of the conclusions, the results of the division of the block-scale spatial structure in the central area of Lujiazui based on the percolation theory are not universal, and the block-scale and hierarchical structure of different types of urban central areas may need to be further discussed in the future.
In general, this study illustrates the validity of the percolation theory in the study of spatial hierarchies in urban centers. Although it has some limitations from the perspective of urban space, it undoubtedly complements existing market economy-led urban hierarchy research.
Fractal Verification
In the field of urban research, the theoretical model of percolation is used as a model to describe the agglomeration characteristics of random media in urban elements, and it is often accompanied by the fractal characteristics of urban elements under different distance thresholds (). Presently, many studies in the field of urban research have demonstrated the fractal characteristics of urban elements. They suggest that the degree of filling urban space follows scaling laws, which means that the urban form of different elements is similar in scale [37]. The box counting method in the fractal statistical method can be used to describe the fractal shape or structure of an element to fill the space [38]. This section therefore presents statistical analyses based on the spatial location and quantity of street intersections in the city center. Fractal statistical characteristics to preliminarily verify the accuracy of the urban spatial structure were arrived at by the percolation analysis of street intersections in the city center (Figure 16).
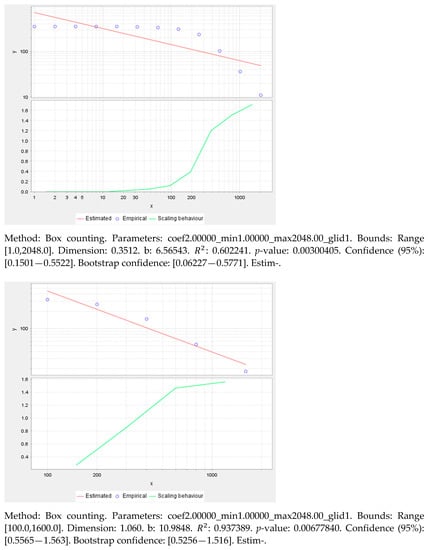
Figure 16.
Box counting method for the statistics of estimated values of street intersections.
Finally, we can record that the fractal characteristics of Shanghai Lujiazui city center obtained by the box counting method were not obvious when the box size was about 300 m (Figure 17). The avenues were distributed on the axis, and the percolation analysis reached the most significant fractal characteristics at this time (Figure 18). The clustering features with Century Avenue as the axis centered on the Shanghai International Conference Center area, Century Avenue Subway Station, Metro Shopping Mall area, and so on, had a certain similarity with the percolation clustering features at the intersection of street. When the size of the box was about 900 m, with the Shanghai Pudong New Area People’s Government area and the Shanghai International Convention Center area as the two cores, the overall box count presents a relatively uniform distribution dimension (Figure 19).
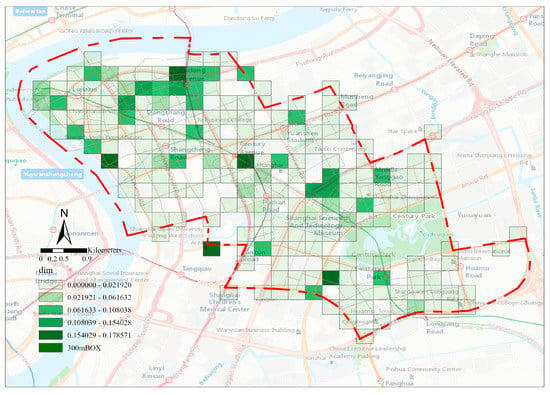
Figure 17.
The size of the box is 300 m, and the fractal properties are not yet obvious.
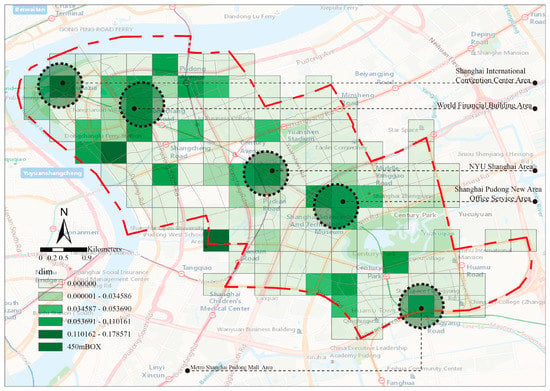
Figure 18.
When the box size is about 450 m, the boxes with higher fractal dimension are roughly distributed around Century Avenue.
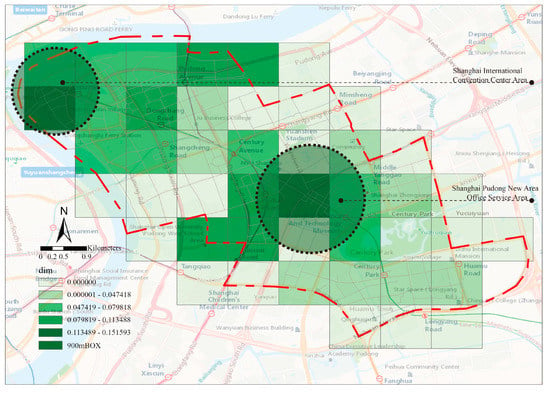
Figure 19.
When the size of the box is about 900 m, take the Shanghai Pudong New Area People’s Government Area and the Shanghai International Convention Center Area as the two largest box dimensions.
The results indicated a certain linkage relationship with the percolation results. Although the appearances of the two results are different, their implied meanings are similar. Probability distribution and statistics can, to a certain extent, verify the accuracy of the urban central area hierarchy of street intersections obtained by percolation analysis. Figure 17, Figure 18 and Figure 19 represent the box dimensions of street intersections in the city center when the percolation thresholds were 150 m, 250 m, and 450 m, reflecting the fractal characteristics of street intersections in the city center according to the box counting method.
5. Conclusions
The urban central area hierarchy is the focus of this study. Ultimately, the hierarchical structural features and evolutionary features we obtained deepen our understanding of the spatial structure of urban central districts.
The hierarchical nested structure provides theoretical support for a sustainable urban system and realizes the reorganization of functional areas in the urban center. The hierarchical nested structure obtained by the percolation analysis of road intersections in this study expresses the redundant (mostly manifested as residential function) and elastic modular system in the sustainable urban system. From the perspective of epistemology, the results supplement the concept of sustainable management of highly intensive urban central areas.
The starting “node” of percolation will become the focus of block-scale management in the urban central area. Along with the percolation process, the initial “central node” will gradually form multiple agglomeration areas (clusters), and eventually all nodes will merge into a single giant core. This may represent the important role implied by each “central node” in its neighborhood in a complex urban system. Therefore, these initial “central nodes” may become the “core nodes” for the management of urban central areas in the future.
Percolation transition “nodes” can provide theoretical support for the implied connectivity of urban central areas. The percolation analysis scales with the largest transition in this study are and . These two scales are not the average scales of Lujiazui neighborhoods but were obtained after considering the correlation between intersections. Therefore, by analyzing the percolation transition “nodes”, it is possible to detect the connected nature and characteristics of the urban center structure, providing theoretical support for urban planning and management to a certain extent.
Future studies may need to focus on the driving mechanism of the hierarchical structure of the urban center to enable researchers to further analyze the evolution results of the urban spatial structure of different functions from a more comprehensive perspective.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/su14169981/s1, Data S1: data; shp.
Author Contributions
Conceptualization, Methodology, Project Administration, Writing—review and editing, Supervision, X.H.; Methodology, Investigation, Writing—original draft, Resources, Writing—review & editing, Y.W.; Methodology, Supervision, H.W.; Writing—review and editing, Methodology, Supervision, Y.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Foundation [the Priority Academic Program Development of Jiangsu Higher Education Insitutions], China, [grant number 164120595].
Data Availability Statement
The data presented in this study are available in [Data S1].
Acknowledgments
Thanks for the support of Research Center for Digital Innovation Design Nanjing Forestry University (NFU-RCDID). The main R-package used in the research is ‘percopackage’ developed by Maddison, MS and Schmidt, SC., 2020. The fractal verification software used in the Discussion section was Fractalyse 3.0 developed by Gilles Vuidel in the frame of research activities of Pierre Frankhauser and Cécile Tannier at ThéMA laboratory (Besançon, France).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Desa, U.N. Transforming Our World: The 2030 Agenda for Sustainable Development. 2016. Available online: https://stg-wedocs.unep.org/bitstream/handle/20.500.11822/11125/unepswiosm1inf7sdg.pdf?sequence=1 (accessed on 31 May 2022).
- Mitković, P.; Dinic, M. City center organization and its influence on the city structure. Facta Univ.-Ser. Archit. Civ. Eng. 2004, 3, 41–56. [Google Scholar] [CrossRef]
- Karlsson, S.; Nilsson, M. What Makes a City Centre Attractive from a Consumer Perspective? A Comparison between Residents and Visitors of Kristianstad City Centre. 2017. Available online: https://www.diva-portal.org/smash/get/diva2:1114796/FULLTEXT01.pdf (accessed on 31 May 2022).
- Hu, X.; Yang, J. Quantitative Analysis of the Urban Factors Limiting Central District Plane Form Expansion: Twenty-one Case Studies of Asian Megacities’ Central Districts. J. Asian Archit. Build. Eng. 2018, 17, 345–351. [Google Scholar] [CrossRef]
- Jiang, J. Space Evolvement of Shenzhen Urban Central District. Urban Archit. 2005, 5, 22–25. (In Chinese) [Google Scholar] [CrossRef]
- Hsu, W. Central Place Theory and City Size Distribution. Econ. J. 2012, 122, 903–932. [Google Scholar] [CrossRef]
- Hsu, W.; Holmes, T.; Morgan, F. Optimal city hierarchy: A dynamic programming approach to central place theory. J. Econ. Theory 2014, 154, 245–273. [Google Scholar] [CrossRef]
- Sun, Y.; Fan, H.; Li, M.; Zipf, A. Identifying the city center using human travel flows generated from location-based social networking data. Environ. Plan. B Plan. Des. 2016, 43, 480–498. [Google Scholar] [CrossRef]
- Hu, X.; Wang, Q.; Li, C. Analysis of the evolution characteristics of land under construction in the central area of megacities—Taking the central area of Xinjiekou in Nanjing as an example. Huazhong Archit. 2019, 7, 93–97. (In Chinese) [Google Scholar] [CrossRef]
- Kohijoki, A.; Koistinen, K. The Attractiveness of a City-Centre Shopping Environment: Older Consumers’ Perspective. Urban Plan. 2019, 4, 5–17. [Google Scholar] [CrossRef]
- Christaller, W. Die Zentralen Orte in Suddeutschland; Gustav Fischer: Jena, Germany, 1933. [Google Scholar]
- Camagni, R. From City Hierarchy to City Network: Reflections about an Emerging Paradigm. In Structure and Change in the Space Economy; Springer: Berlin/Heidelberg, Germany, 1993; pp. 66–87. [Google Scholar]
- Hoyt, H. The Structure and Growth of Residential Neighborhoods in American Cities; US Government Printing Office: Washington, DC, USA, 1939.
- Han, X.; Hao, Q.; Wang, B.; Zhou, T. Origin of the scaling law in human mobility: Hierarchy of traffic systems. Phys. Rev. E 2011, 83, 036117. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Zuo, Z.; Wang, D. Analysis of the spatial hierarchy of the urban belt around the Bohai Sea and its guidance to traffic. Inn. Mong. Sci. Technol. Econ. 2010, 21, 6–7. (In Chinese) [Google Scholar]
- Beckmann, M.J.; McPherson, J.C. City size distribution in a central place hierarchy: An alternative approach. J. Reg. Sci. 1970, 10, 25–33. [Google Scholar] [CrossRef]
- Carol, H. The hierarchy of central functions within the city. Ann. Assoc. Am. Geogr. 1960, 50, 419–438. [Google Scholar] [CrossRef]
- Piovani, D.; Molinero, C.; Wilson, A. Urban retail location: Insights from percolation theory and spatial interaction modeling. PLoS ONE 2017, 12, e0185787. [Google Scholar]
- Dong, S.; Wang, H.; Mostafizi, A.; Song, X. A network-of-networks percolation analysis of cascading failures in spatially co-located road-sewer infrastructure networks. Phys. A Stat. Mech. Its Appl. 2020, 538, 122971. [Google Scholar] [CrossRef]
- Arcaute, E.; Hatna, E.; Ferguson, P.; Youn, H.; Johansson, A.; Batty, M. Constructing cities, deconstructing scaling laws. J. R. Soc. Interface 2015, 12, 20140745. [Google Scholar] [CrossRef]
- Arcaute, E.; Molinero, C.; Hatna, E.; Murcio, R.; Vargas-Ruiz, C.; Masucci, P.; Batty, M. Cities and regions in britain through hierarchical percolation. Open Sci. 2016, 3, 150691. [Google Scholar] [CrossRef] [PubMed]
- Maddison, M.S.; Schmidt, S.C. Percolation Analysis—Archaeological Applications at Widely Different Spatial Scales. J. Comput. Appl. Archaeol. 2020, 3, 269–287. [Google Scholar]
- Flory, P.J. Molecular size distribution in three dimensional polymers. I. Gelation. J. Am. Chem. Soc. 1941, 63, 3083–3090. [Google Scholar] [CrossRef]
- Li, M.; Liu, R.; Lü, L.; Hu, M.; Xu, S.; Zhang, Y. Percolation on complex networks: Theory and application. Phys. Rep. 2021, 907, 1–68. [Google Scholar] [CrossRef]
- Newman, M.E.; Jensen, I.; Ziff, R.M. Percolation and epidemics in a two-dimensional small world. Phys. Rev. E 2002, 65, 021904. [Google Scholar] [CrossRef] [PubMed]
- He, F.; Hubbell, S. Percolation Theory for the Distribution and Abundance of Species. Phys. Rev. Lett. 2003, 91, 198103. [Google Scholar] [CrossRef] [PubMed]
- Berx, J.; Bervoets, E.; Giuraniuc, C.V.; Indekeu, J.O. Coastlines and percolation in a model for hierarchical random deposition. Phys. A Stat. Mech. Its Appl. 2021, 574, 125998. [Google Scholar] [CrossRef]
- Saberi, A.A. Recent advances in percolation theory and its applications. Phys. Rep. 2015, 578, 1–32. [Google Scholar] [CrossRef]
- Murcio, R.; Masucci, A.; Arcaute, E.; Batty, M. Multifractal to monofractal evolution of the London street network. Phys. Rev. E 2015, 92, 062130. [Google Scholar] [CrossRef] [PubMed]
- McPhearson, T.; Pickett, S.T.A.; Grimm, N.B.; Niemelä, J.; Alberti, M.; Elmqvist, T.; Weber, C.; Haase, D.; Breuste, J.; Qureshi, S. Advancing urban ecology toward a science of cities. BioScience 2016, 66, 198–212. [Google Scholar] [CrossRef]
- Behnisch, M.; Schorcht, M.; Kriewald, S.; Rybski, D. Settlement percolation: A study of building connectivity and poles of inaccessibility. Landsc. Urban Plan. 2019, 191, 103631. [Google Scholar] [CrossRef]
- Cao, W.; Dong, L.; Wu, L.; Liu, Y. Quantifying urban areas with multi-source data based on percolation theory. Remote Sens. Environ. 2020, 241, 111730. [Google Scholar] [CrossRef]
- Montero, G.; Tannier, C.; Thomas, I. Delineation of cities based on scaling properties of urban patterns: A comparison of three methods. Int. J. Geogr. Inf. Sci. 2021, 35, 919–947. [Google Scholar] [CrossRef]
- Tabuchi, T.; Thisse, J.F. A new economic geography model of central places. J. Urban Econ. 2011, 69, 240–252. [Google Scholar] [CrossRef]
- Li, D.; Fu, B.; Wang, Y.; Lu, G.; Berezin, Y.; Stanley, H.E.; Havlin, S. Percolation transition in dynamical traffic network with evolving critical bottlenecks. Proc. Natl. Acad. Sci. USA 2015, 112, 669–672. [Google Scholar] [CrossRef]
- He, H.; Deng, H.; Wang, Q.; Gao, J. Percolation of temporal hierarchical mobility networks during COVID-19. Philos. Trans. R. Soc. A 2022, 380, 20210116. [Google Scholar] [CrossRef]
- Batty, M.; Xie, Y. Preliminary Evidence for a Theory of the Fractal City. Environ. Plan. A Econ. Space 1996, 28, 1745–1762. [Google Scholar] [CrossRef]
- Gneiting, T.; Ševčíková, H.; Percival, D.B. Estimators of fractal dimension: Assessing the roughness of time series and spatial data. Stat. Sci. 2012, 27, 247–277. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).