Identifying the Real Income Disparity in Prefecture-Level Cities in China: Measurement of Subnational Purchasing Power Parity Based on the Stochastic Approach
Abstract
:1. Introduction
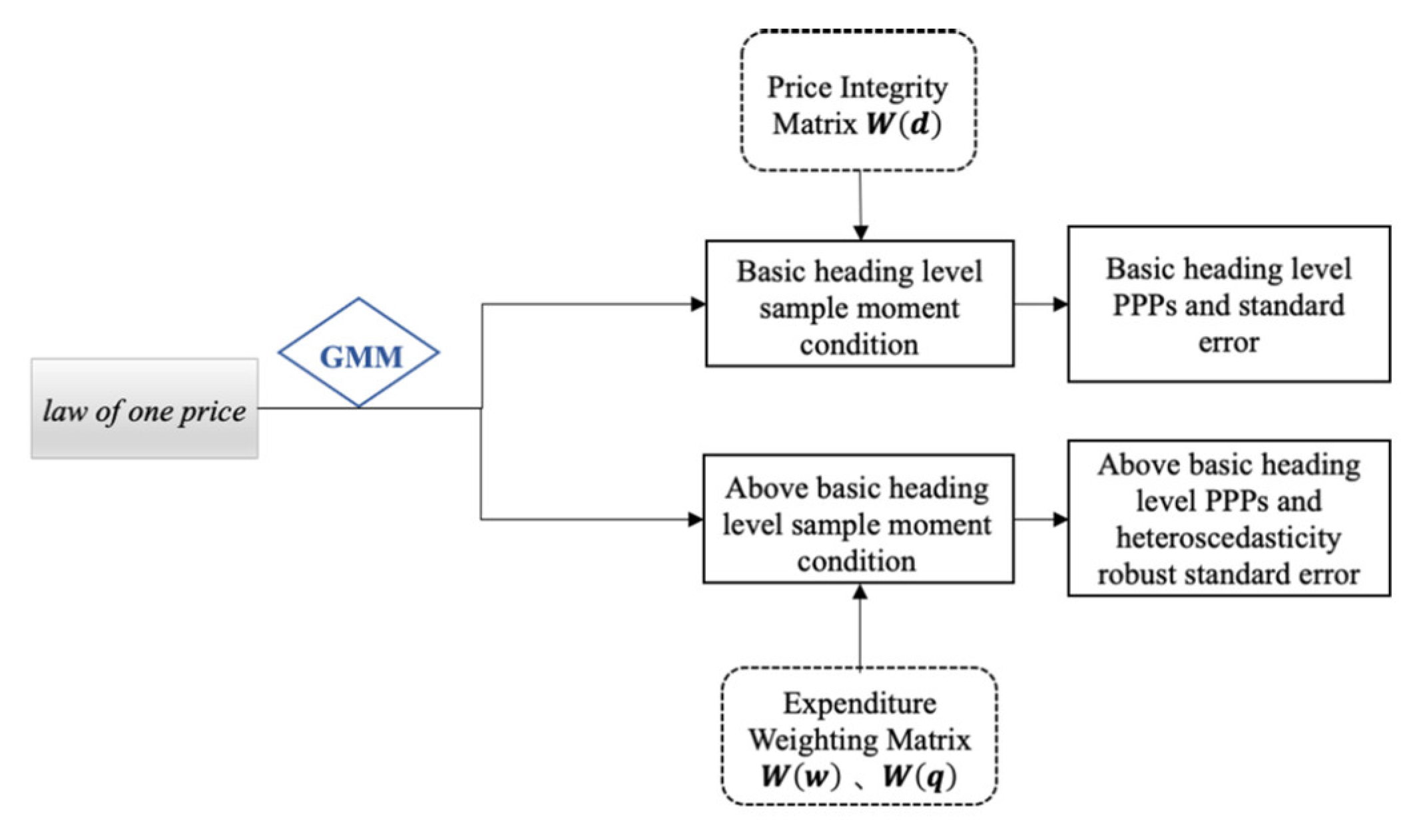
2. Methodology
2.1. The Generalized Framework under the Stochastic Approach
2.2. The GK System under the Stochastic Approach
2.2.1. The Basic Heading Level
2.2.2. Above the Basic Heading Level
2.3. The Rao System under the Stochastic Approach
2.3.1. The Basic Heading Level
2.3.2. Above the Basic Heading Level
3. The Dataset
3.1. Data Acquisition and Collation
3.1.1. The Prices
3.1.2. The Weights
3.2. Data Quality Validation
3.2.1. Validation of Homogeneous and Comparable Price Data
3.2.2. Comparative Analysis of Price Levels in Cities with Similar Levels of Economic Development
4. Empirical Study
4.1. Reliability Analysis of the Multilateral Index System under the Stochastic Approach
4.1.1. Reliability Analysis of Subnational PPPs at the Basic Heading Level
4.1.2. Reliability Analysis of Subnational PPPs above the Basic Heading Level
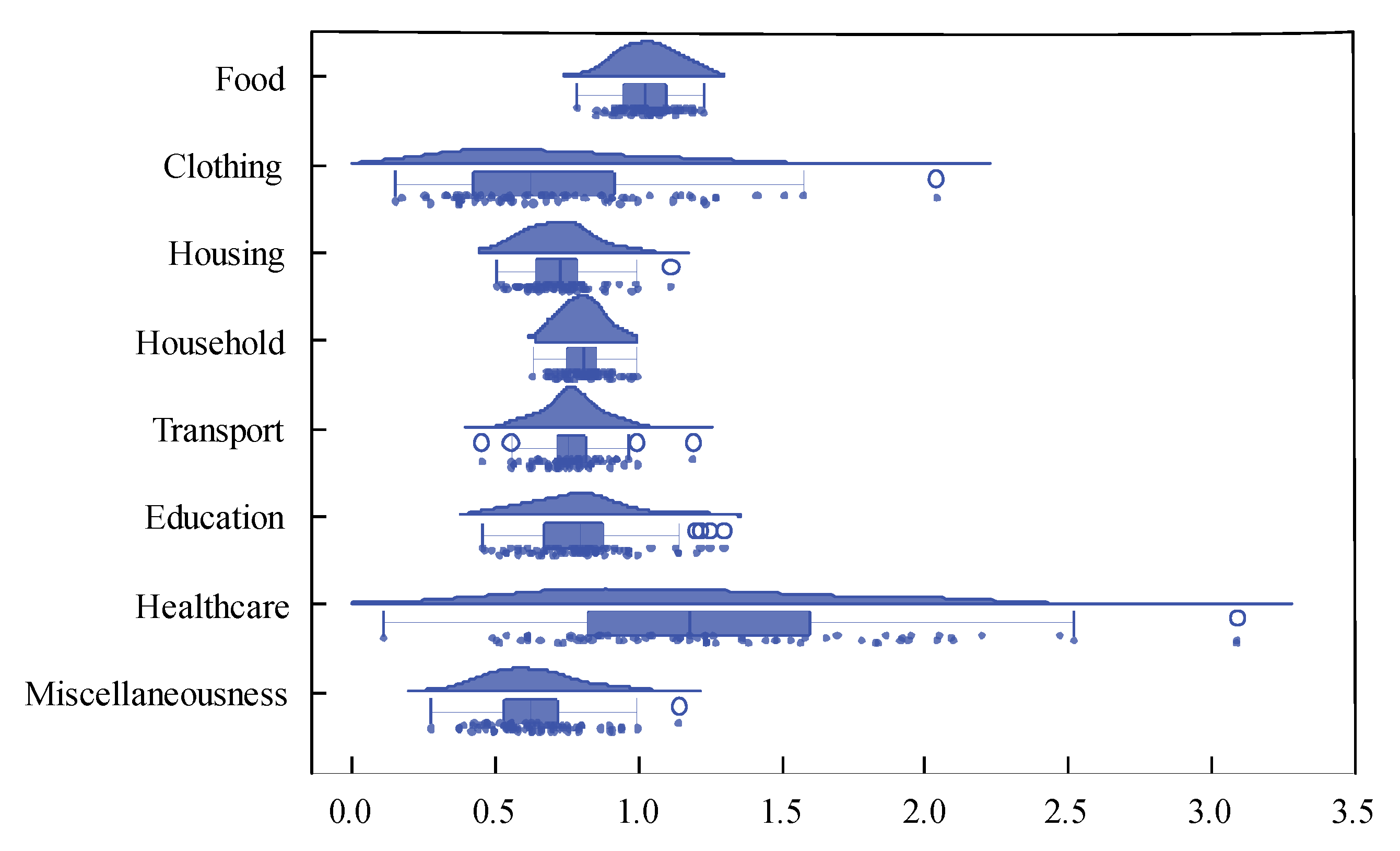
4.2. Analysis of Price Level Differences between Cities in China
4.2.1. Subnational PPPs of the Eight Main Categories
4.2.2. Subnational PPPs in China
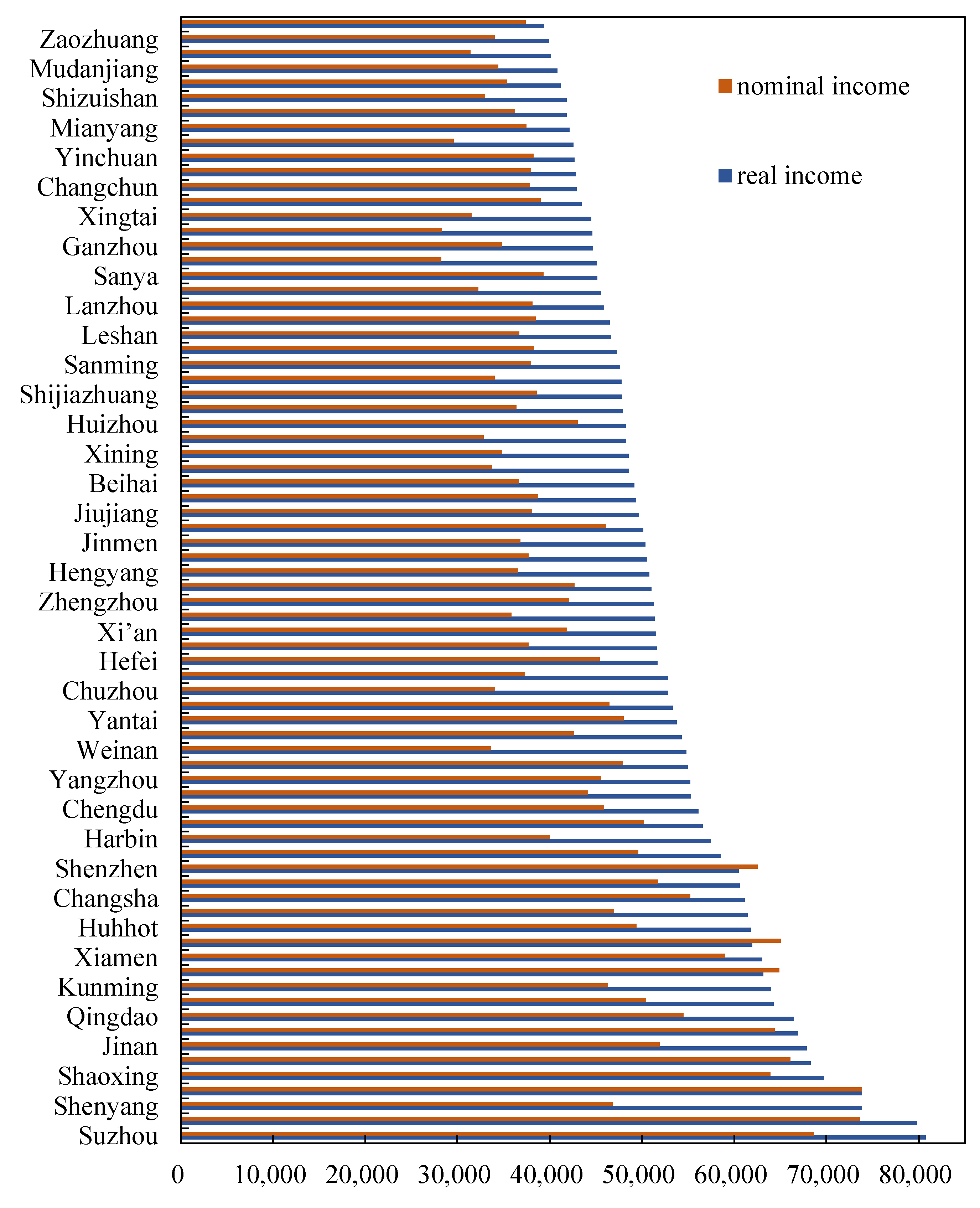
4.3. Analysis of the Real Income Disparity in Prefecture-Level Cities in China
4.3.1. Disparity between Nominal and Real Incomes
4.3.2. Geographical Distribution Characteristics of Real Income
5. Conclusions, Limitations, and Future Research
5.1. Conclusion and Discussion
5.2. Limitations
5.3. Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
| Consumption of urban residents | Main category | Representative specification commodities |
| Food, tobacco, and liquor | Japonica rice, standard flour, special flour, late indica rice, corn flour, potato, tofu, rapeseed oil, soybean oil, peanut oil, soybean blend oil, lean meat, rib meat, skin-on ham, rib, tendon, brisket, fresh boneless lamb, fresh bone-in lamb, chicken, egg, hairtail, grass carp, carp, silver carp, yellow croaker, sea shrimp, bighead carp, crucian carp, celery, Chinese cabbage, rapeseed, cucumber, radish, eggplant, tomato, carrot, green pepper, bell pepper, cabbage, beans, garlic moss, leek, ginger, garlic, edible salt, soy sauce, vinegar, monosodium glutamate, white sugar, brown sugar, medium and low-grade domestic cigarettes, imported cigarettes, high-end domestic cigarettes, mineral water, carbonated beverages, medium and low-grade liquor, high-grade wine, high-grade liquor, medium and low-grade wine, bottled beer, canned beer, pear, apple, banana, watermelon, orange, biscuit, bag milk, boxed milk, domestic milk powder, imported milk powder, instant noodles. | |
| Clothing and footwear | Men’s underwear, women’s underwear, men’s shirts, men’s sweaters, women’s sweaters. | |
| Housing | The rental price of the residential market in the first-class area, the rental price of the residential market in the second-class area, and the rental price of the residential market in the third-class area, pipeline natural gas, residential water, residential electricity, property service fees, liquefied petroleum gas, property administrators, community property cleaners, community property order maintenance workers, maintenance workers, hotel room attendant, strong worker. | |
| Household equipment, furnishings, and services | Front-loading washing machines, air conditioners, laundry powder, detergent, soap, float flat glass, tempered flat glass, household hourly workers (yuan/hour), housekeepers, elderly care, elderly can take care of themselves or partially, housekeepers to take care of children, non-baby. | |
| Transport and communications | Gasoline, diesel, taxi rental prices, road shuttle passenger fares for intra-provincial routes, road shuttle passenger fares for inter-provincial routes, local network business area calling fee, local network business area calling fee, fixed telephone monthly rental fee, mobile phone tariff, China Unicom, mobile phone tariff, mobile China card, mobile phone tariff, mobile global pass, Internet access fee, wired (digital) TV bill, mobile phone. | |
| Education, culture, and recreation | Color TV, computer, digital camera, comprehensive college tuition fees for colleges, art colleges for college tuition fees, normal college tuition fees for colleges, municipal demonstration schools for high school tuition fees, ordinary high school tuition fees, general vocational high school tuition fees, public childcare education fees, private childcare education fees, student housing accommodation fees, attraction tickets. | |
| Healthcare and medical services | Ward bed fee, registration fee, chemotherapy fee, examination fee—Cranial CT scan, examination fee—Liver function test-blood test, examination fee—urine routine examination, operation fee for appendectomy, operation fee for cesarean section, municipal hospital outpatient service consultation fee, injection fee. | |
| Miscellaneous goods and services | Express processing center sorter, courier, hotel accommodation. |
| Region | PPPs of Food, Tobacco, and Liquor | PPPs of Clothing and Footwear | PPPs of Housing | PPPs of Household Equipment, Furnishings, and Services | PPPs of Transport and Communications | PPPs of Education, Culture, and Recreation | PPPs of Healthcare and Medical Services | PPPs of Miscellaneous Goods and Services |
| Beijing | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Tianjin | 1.027 | 0.982 | 0.814 | 0.839 | 0.913 | 1.047 | 1.265 | 0.650 |
| Shijiazhuang | 0.933 | 0.783 | 0.654 | 0.807 | 0.799 | 0.748 | 2.202 | 0.559 |
| Tangshan | 0.915 | 0.754 | 0.763 | 0.773 | 0.795 | 0.834 | 0.811 | 0.521 |
| Xingtai | 0.883 | 0.554 | 0.615 | 0.788 | 0.723 | 0.827 | 0.619 | 0.534 |
| Taiyuan | 1.006 | 1.230 | 0.625 | 0.793 | 0.768 | 0.717 | 0.618 | 0.560 |
| Datong | 0.946 | 0.431 | 0.618 | 0.732 | 0.773 | 0.735 | 0.933 | 0.379 |
| Huhhot | 1.013 | 0.523 | 0.616 | 0.791 | 0.728 | 0.874 | 1.697 | 0.630 |
| Baotou | 1.018 | 0.874 | 0.589 | 0.909 | 0.763 | 0.618 | 0.829 | 0.945 |
| Shenyang | 1.001 | 0.263 | 0.687 | 0.727 | 0.776 | 0.700 | 0.114 | 0.872 |
| Dalian | 1.131 | 0.559 | 0.805 | 0.972 | 0.654 | 0.968 | 1.183 | 0.793 |
| Changchun | 0.954 | 0.909 | 0.752 | 0.787 | 0.692 | 0.953 | 1.658 | 0.785 |
| Tonghua | 0.915 | 0.375 | 0.682 | 0.634 | 0.456 | 0.601 | 1.831 | 0.394 |
| Harbin | 0.917 | 0.468 | 0.685 | 0.753 | 0.737 | 0.557 | 0.872 | 0.583 |
| Mudanjiang | 0.961 | 0.744 | 0.625 | 0.863 | 0.586 | 0.971 | 2.054 | 0.445 |
| Shanghai | 1.130 | 0.453 | 0.883 | 0.805 | 0.872 | 0.885 | 1.449 | 0.761 |
| Nanjing | 1.190 | 0.816 | 0.982 | 0.987 | 0.726 | 0.918 | 1.273 | 0.758 |
| Xuzhou | 1.028 | 0.607 | 0.789 | 0.855 | 0.780 | 0.828 | 1.925 | 0.545 |
| Suzhou | 1.081 | 1.190 | 0.728 | 0.786 | 0.790 | 0.822 | 0.792 | 0.706 |
| Nantong | 1.068 | 0.940 | 0.787 | 0.864 | 0.727 | 0.796 | 1.920 | 0.548 |
| Yangzhou | 0.950 | 0.723 | 0.714 | 0.860 | 0.755 | 0.857 | 1.585 | 0.561 |
| Hangzhou | 1.220 | 1.123 | 0.996 | 0.985 | 0.863 | 0.923 | 0.767 | 0.806 |
| Ningbo | 1.194 | 1.136 | 0.808 | 0.812 | 0.955 | 1.253 | 1.839 | 0.913 |
| Shaoxing | 1.049 | 1.043 | 0.812 | 0.779 | 0.851 | 0.676 | 2.475 | 0.654 |
| Quzhou | 1.100 | 0.682 | 0.621 | 0.790 | 0.718 | 0.803 | 0.767 | 0.422 |
| Hefei | 1.013 | 2.044 | 0.740 | 0.713 | 0.798 | 0.682 | 1.784 | 0.684 |
| Huainan | 0.887 | 0.431 | 0.666 | 0.748 | 0.660 | 0.582 | 1.138 | 0.663 |
| Anqing | 0.988 | 0.949 | 0.693 | 0.688 | 0.727 | 0.518 | 0.506 | 0.379 |
| Chuzhou | 0.917 | 0.361 | 0.540 | 0.712 | 0.562 | 0.682 | 0.619 | 0.469 |
| Fuzhou | 1.054 | 1.272 | 0.814 | 0.940 | 0.719 | 0.632 | 1.534 | 0.756 |
| Xiamen | 1.145 | 1.183 | 0.888 | 0.882 | 0.688 | 0.855 | 1.569 | 0.664 |
| Sanming | 1.078 | 0.383 | 0.656 | 0.686 | 0.926 | 0.854 | 1.149 | 0.571 |
| Quanzhou | 1.029 | 0.399 | 0.892 | 0.839 | 0.826 | 0.671 | 1.386 | 0.722 |
| Nanchang | 0.921 | 0.636 | 0.804 | 0.835 | 0.790 | 0.645 | 1.124 | 0.699 |
| Jiujiang | 1.015 | 0.560 | 0.709 | 0.848 | 0.751 | 0.666 | 0.863 | 0.477 |
| Ganzhou | 1.056 | 0.382 | 0.706 | 0.691 | 0.735 | 0.776 | 1.237 | 0.564 |
| Jinan | 0.987 | 0.408 | 0.732 | 0.766 | 0.787 | 0.583 | 1.237 | 0.564 |
| Qingdao | 1.069 | 0.336 | 0.937 | 0.697 | 0.820 | 0.837 | 0.841 | 0.730 |
| Zaozhuang | 0.858 | 0.900 | 0.579 | 0.909 | 0.720 | 1.303 | 3.093 | 0.652 |
| Yantai | 0.937 | 0.664 | 0.770 | 0.839 | 0.838 | 1.134 | 3.093 | 0.427 |
| Taian | 1.019 | 0.876 | 0.645 | 0.819 | 0.625 | 0.726 | 0.619 | 0.900 |
| Heze | 0.857 | 0.381 | 0.546 | 0.856 | 0.569 | 0.543 | 0.866 | 0.906 |
| Zhengzhou | 1.038 | 1.513 | 0.733 | 0.791 | 0.718 | 0.818 | 0.594 | 0.666 |
| Zhoukou | 0.790 | 0.442 | 0.625 | 0.713 | 0.629 | 0.461 | 0.800 | 0.498 |
| Wuhan | 1.099 | 0.542 | 0.808 | 0.834 | 0.857 | 0.968 | 0.742 | 0.794 |
| Huangshi | 0.978 | 0.565 | 0.732 | 0.755 | 0.795 | 0.624 | 1.237 | 0.943 |
| Yichang | 1.047 | 0.372 | 0.828 | 0.950 | 0.774 | 0.735 | 1.209 | 0.555 |
| Xiangyang | 0.985 | 0.258 | 0.575 | 0.750 | 0.905 | 0.780 | 0.866 | 0.611 |
| Jinmen | 0.941 | 0.546 | 0.652 | 0.852 | 0.715 | 0.826 | 0.720 | 0.611 |
| Changsha | 1.088 | 1.275 | 0.683 | 0.819 | 0.837 | 0.883 | 1.485 | 0.711 |
| Hengyang | 0.944 | 0.381 | 0.746 | 0.798 | 0.878 | 0.491 | 1.237 | 0.474 |
| Guangzhou | 1.233 | 1.152 | 0.888 | 0.978 | 0.901 | 1.205 | 1.946 | 0.738 |
| Shenzhen | 1.191 | 0.609 | 1.116 | 0.845 | 0.838 | 1.220 | 0.990 | 1.145 |
| Shantou | 1.107 | 0.156 | 0.738 | 0.882 | 1.194 | 0.467 | 1.481 | 0.635 |
| Huizhou | 1.169 | 0.889 | 0.783 | 0.851 | 0.731 | 0.892 | 1.146 | 0.741 |
| Nanning | 1.045 | 0.619 | 0.712 | 0.902 | 0.689 | 0.543 | 0.660 | 0.567 |
| Liuzhou | 1.166 | 1.581 | 0.684 | 0.746 | 0.816 | 0.936 | 1.868 | 0.453 |
| Beihai | 0.996 | 0.367 | 0.731 | 0.802 | 0.751 | 0.654 | 0.898 | 0.280 |
| Haikou | 1.198 | 1.417 | 0.774 | 0.893 | 0.810 | 0.780 | 0.953 | 0.624 |
| Sanya | 1.100 | 0.381 | 0.816 | 0.824 | 0.968 | 0.860 | 1.235 | 0.491 |
| Chongqing | 1.056 | 0.958 | 0.736 | 0.893 | 0.771 | 1.142 | 1.052 | 0.633 |
| Chengdu | 1.109 | 0.332 | 0.756 | 0.811 | 0.833 | 0.803 | 1.367 | 0.690 |
| Mianyang | 1.132 | 0.699 | 0.646 | 0.743 | 0.926 | 0.795 | 2.044 | 0.698 |
| Leshan | 1.147 | 0.379 | 0.651 | 0.859 | 0.624 | 0.782 | 1.366 | 0.542 |
| Guiyang | 1.136 | 0.176 | 0.785 | 0.904 | 0.751 | 0.856 | 2.103 | 0.499 |
| Zunyi | 0.959 | 0.492 | 0.770 | 0.754 | 0.755 | 0.965 | 2.094 | 0.710 |
| Kunming | 1.029 | 0.489 | 0.528 | 0.815 | 0.629 | 0.715 | 1.237 | 0.554 |
| Xi’an | 1.076 | 1.237 | 0.819 | 0.684 | 0.725 | 0.799 | 0.520 | 0.536 |
| Weinan | 0.923 | 0.276 | 0.579 | 0.744 | 0.570 | 0.850 | 0.495 | 0.430 |
| Hanzhong | 0.983 | 0.520 | 0.588 | 0.743 | 0.559 | 0.820 | 0.544 | 0.474 |
| Lanzhou | 1.150 | 0.911 | 0.633 | 0.914 | 0.795 | 0.586 | 1.046 | 0.616 |
| Xining | 1.089 | 0.534 | 0.617 | 0.757 | 0.674 | 0.703 | 0.619 | 0.629 |
| Yinchuan | 0.946 | 0.705 | 0.668 | 0.785 | 0.767 | 1.144 | 2.524 | 0.580 |
| Shizuishan | 0.950 | 0.744 | 0.536 | 0.719 | 0.650 | 0.825 | 1.955 | 0.471 |
| Wuzhong | 0.917 | 0.668 | 0.509 | 0.857 | 0.652 | 0.530 | 1.029 | 0.706 |
| Wulumuqi | 1.039 | 0.681 | 0.774 | 0.820 | 0.746 | 0.776 | 1.182 | 0.805 |
| Region | Standard Error of Food, Tobacco, and Liquor | Standard Error of Clothing and Footwear | Standard Error of Housing | Standard Error of Household Equipment, Furnishings, and Services | Standard Error of Transport and Communications | Standard Error of Education, Culture, and Recreation | Standard Error of Healthcare and Medical Services | Standard Error of Miscellaneous Goods and Services |
| Beijing | - | - | - | - | - | - | - | - |
| Tianjin | 0.042 | 0.189 | 0.079 | 0.074 | 0.079 | 0.183 | 0.425 | 0.089 |
| Shijiazhuang | 0.038 | 0.150 | 0.061 | 0.071 | 0.072 | 0.165 | 1.675 | 0.077 |
| Tangshan | 0.038 | 0.145 | 0.076 | 0.076 | 0.077 | 0.133 | 0.273 | 0.102 |
| Xingtai | 0.038 | 0.106 | 0.064 | 0.071 | 0.070 | 0.204 | 0.471 | 0.073 |
| Taiyuan | 0.042 | 0.236 | 0.058 | 0.070 | 0.065 | 0.115 | 0.214 | 0.086 |
| Datong | 0.039 | 0.088 | 0.063 | 0.064 | 0.065 | 0.118 | 0.324 | 0.074 |
| Huhhot | 0.043 | 0.100 | 0.056 | 0.070 | 0.062 | 0.148 | 0.570 | 0.087 |
| Baotou | 0.042 | 0.168 | 0.057 | 0.090 | 0.064 | 0.104 | 0.272 | 0.185 |
| Shenyang | 0.041 | 0.050 | 0.063 | 0.064 | 0.070 | 0.155 | 0.087 | 0.170 |
| Dalian | 0.047 | 0.107 | 0.074 | 0.085 | 0.056 | 0.155 | 0.388 | 0.109 |
| Changchun | 0.039 | 0.174 | 0.069 | 0.069 | 0.064 | 0.210 | 1.261 | 0.108 |
| Tonghua | 0.038 | 0.072 | 0.079 | 0.056 | 0.053 | 0.133 | 1.393 | 0.054 |
| Harbin | 0.038 | 0.090 | 0.062 | 0.068 | 0.064 | 0.091 | 0.286 | 0.090 |
| Mudanjiang | 0.040 | 0.143 | 0.061 | 0.085 | 0.068 | 0.214 | 1.562 | 0.087 |
| Shanghai | 0.048 | 0.101 | 0.081 | 0.071 | 0.078 | 0.145 | 0.487 | 0.117 |
| Nanjing | 0.049 | 0.157 | 0.089 | 0.087 | 0.062 | 0.147 | 0.428 | 0.104 |
| Xuzhou | 0.043 | 0.117 | 0.088 | 0.084 | 0.066 | 0.140 | 0.647 | 0.107 |
| Suzhou | 0.046 | 0.228 | 0.078 | 0.077 | 0.092 | 0.181 | 0.602 | 0.138 |
| Nantong | 0.044 | 0.181 | 0.088 | 0.085 | 0.071 | 0.135 | 0.645 | 0.107 |
| Yangzhou | 0.039 | 0.139 | 0.086 | 0.085 | 0.073 | 0.150 | 0.598 | 0.110 |
| Hangzhou | 0.050 | 0.216 | 0.090 | 0.087 | 0.079 | 0.204 | 0.584 | 0.111 |
| Ningbo | 0.049 | 0.218 | 0.073 | 0.071 | 0.081 | 0.200 | 0.603 | 0.126 |
| Shaoxing | 0.044 | 0.200 | 0.081 | 0.077 | 0.099 | 0.149 | 1.882 | 0.128 |
| Quzhou | 0.046 | 0.131 | 0.085 | 0.078 | 0.084 | 0.177 | 0.584 | 0.082 |
| Hefei | 0.042 | 0.392 | 0.067 | 0.063 | 0.068 | 0.109 | 0.601 | 0.094 |
| Huainan | 0.037 | 0.088 | 0.091 | 0.074 | 0.077 | 0.129 | 0.866 | 0.091 |
| Anqing | 0.041 | 0.182 | 0.080 | 0.068 | 0.070 | 0.088 | 0.166 | 0.074 |
| Chuzhou | 0.038 | 0.080 | 0.060 | 0.065 | 0.065 | 0.151 | 0.471 | 0.092 |
| Fuzhou | 0.044 | 0.282 | 0.074 | 0.083 | 0.067 | 0.140 | 1.167 | 0.104 |
| Xiamen | 0.047 | 0.263 | 0.081 | 0.078 | 0.060 | 0.137 | 0.544 | 0.091 |
| Sanming | 0.046 | 0.085 | 0.084 | 0.068 | 0.090 | 0.144 | 0.399 | 0.079 |
| Quanzhou | 0.043 | 0.089 | 0.093 | 0.083 | 0.077 | 0.148 | 1.054 | 0.111 |
| Nanchang | 0.038 | 0.122 | 0.077 | 0.073 | 0.068 | 0.103 | 0.369 | 0.096 |
| Jiujiang | 0.042 | 0.108 | 0.069 | 0.080 | 0.073 | 0.107 | 0.283 | 0.073 |
| Ganzhou | 0.043 | 0.073 | 0.079 | 0.068 | 0.069 | 0.171 | 0.941 | 0.110 |
| Jinan | 0.041 | 0.078 | 0.066 | 0.067 | 0.072 | 0.129 | 0.941 | 0.077 |
| Qingdao | 0.044 | 0.064 | 0.085 | 0.061 | 0.075 | 0.185 | 0.640 | 0.100 |
| Zaozhuang | 0.035 | 0.173 | 0.079 | 0.090 | 0.084 | 0.288 | 2.353 | 0.127 |
| Yantai | 0.039 | 0.127 | 0.076 | 0.083 | 0.078 | 0.250 | 2.353 | 0.083 |
| Taian | 0.042 | 0.168 | 0.089 | 0.081 | 0.073 | 0.160 | 0.471 | 0.176 |
| Heze | 0.036 | 0.073 | 0.063 | 0.084 | 0.070 | 0.120 | 0.659 | 0.177 |
| Zhengzhou | 0.043 | 0.290 | 0.067 | 0.070 | 0.065 | 0.181 | 0.452 | 0.092 |
| Zhoukou | 0.034 | 0.085 | 0.072 | 0.104 | 0.054 | 0.074 | 0.270 | 0.097 |
| Wuhan | 0.045 | 0.104 | 0.073 | 0.073 | 0.080 | 0.214 | 0.565 | 0.109 |
| Huangshi | 0.040 | 0.108 | 0.081 | 0.074 | 0.093 | 0.138 | 0.941 | 0.184 |
| Yichang | 0.043 | 0.071 | 0.080 | 0.094 | 0.075 | 0.118 | 0.397 | 0.076 |
| Xiangyang | 0.041 | 0.049 | 0.079 | 0.066 | 0.106 | 0.172 | 0.659 | 0.120 |
| Jinmen | 0.039 | 0.105 | 0.066 | 0.084 | 0.066 | 0.182 | 0.548 | 0.120 |
| Changsha | 0.044 | 0.245 | 0.064 | 0.072 | 0.081 | 0.195 | 1.129 | 0.139 |
| Hengyang | 0.039 | 0.073 | 0.076 | 0.079 | 0.083 | 0.108 | 0.941 | 0.093 |
| Guangzhou | 0.051 | 0.221 | 0.081 | 0.086 | 0.077 | 0.204 | 0.675 | 0.144 |
| Shenzhen | 0.049 | 0.117 | 0.103 | 0.083 | 0.081 | 0.269 | 0.753 | 0.157 |
| Shantou | 0.046 | 0.030 | 0.101 | 0.087 | 0.139 | 0.103 | 1.126 | 0.124 |
| Huizhou | 1.169 | 0.889 | 0.783 | 0.851 | 0.731 | 0.892 | 1.146 | 0.741 |
| Nanning | 1.045 | 0.619 | 0.712 | 0.902 | 0.689 | 0.543 | 0.660 | 0.567 |
| Liuzhou | 1.166 | 1.581 | 0.684 | 0.746 | 0.816 | 0.936 | 1.868 | 0.453 |
| Beihai | 0.996 | 0.367 | 0.731 | 0.802 | 0.751 | 0.654 | 0.898 | 0.280 |
| Haikou | 1.198 | 1.417 | 0.774 | 0.893 | 0.810 | 0.780 | 0.953 | 0.624 |
| Sanya | 1.100 | 0.381 | 0.816 | 0.824 | 0.968 | 0.860 | 1.235 | 0.491 |
| Chongqing | 1.056 | 0.958 | 0.736 | 0.893 | 0.771 | 1.142 | 1.052 | 0.633 |
| Chengdu | 1.109 | 0.332 | 0.756 | 0.811 | 0.833 | 0.803 | 1.367 | 0.690 |
| Mianyang | 1.132 | 0.699 | 0.646 | 0.743 | 0.926 | 0.795 | 2.044 | 0.698 |
| Leshan | 1.147 | 0.379 | 0.651 | 0.859 | 0.624 | 0.782 | 1.366 | 0.542 |
| Guiyang | 1.136 | 0.176 | 0.785 | 0.904 | 0.751 | 0.856 | 2.103 | 0.499 |
| Zunyi | 0.959 | 0.492 | 0.770 | 0.754 | 0.755 | 0.965 | 2.094 | 0.710 |
| Kunming | 1.029 | 0.489 | 0.528 | 0.815 | 0.629 | 0.715 | 1.237 | 0.554 |
| Xi’an | 1.076 | 1.237 | 0.819 | 0.684 | 0.725 | 0.799 | 0.520 | 0.536 |
| Weinan | 0.923 | 0.276 | 0.579 | 0.744 | 0.570 | 0.850 | 0.495 | 0.430 |
| Hanzhong | 0.983 | 0.520 | 0.588 | 0.743 | 0.559 | 0.820 | 0.544 | 0.474 |
| Lanzhou | 1.150 | 0.911 | 0.633 | 0.914 | 0.795 | 0.586 | 1.046 | 0.616 |
| Xining | 1.089 | 0.534 | 0.617 | 0.757 | 0.674 | 0.703 | 0.619 | 0.629 |
| Yinchuan | 0.946 | 0.705 | 0.668 | 0.785 | 0.767 | 1.144 | 2.524 | 0.580 |
| Shizuishan | 0.950 | 0.744 | 0.536 | 0.719 | 0.650 | 0.825 | 1.955 | 0.471 |
| Wuzhong | 0.917 | 0.668 | 0.509 | 0.857 | 0.652 | 0.530 | 1.029 | 0.706 |
| Wulumuqi | 1.039 | 0.681 | 0.774 | 0.820 | 0.746 | 0.776 | 1.182 | 0.805 |
References
- Peilin, L.; Tao, Q.; Xianhai, H.; Xuebing, D. The connotation, realization path and measurement method of common prosperity for all. J. Manag. World 2021, 37, 117–129. [Google Scholar]
- Thomas, C.P.; Marquez, J.; Fahle, S. Measures of international relative prices for china and the USA. Pac. Econ. Rev 2009, 14, 376–397. [Google Scholar] [CrossRef]
- Ravallion, M. Price levels and economic growth: Making sense of revisions to data on real incomes. Rev. Income Wealth 2013, 59, 593–613. [Google Scholar] [CrossRef]
- Ray, R.; Singh, P. Regionally disaggregated estimates of global income inequality with evidence on sensitivity to purchasing power parity. J. Asia. Pac. Econ. 2021, 26, 252–270. [Google Scholar] [CrossRef]
- Osberg, L.; Xu, K. How should we measure poverty in a changing world? Methodological issues and Chinese case study. Rev. Dev. Econ. 2008, 12, 419–441. [Google Scholar] [CrossRef]
- Deaton, A. Letter from America—It’s a big country, and how to measure it. R. Econ. Soc. 2014, 167, 3–4. [Google Scholar]
- WorldBank. Purchasing Power Parities and the Size of World Economies: Results from the 2017 International Comparison Program; World Bank: Washington, DC, USA, 2020. [Google Scholar]
- Asian Development Bank. 2017 International Comparison Program for Asia and the Pacific: Purchasing Power Parities and Real Expenditures—A Summary Report; Asian Development Bank: Mandaluyong, Philippines, 2020. [Google Scholar]
- Biggeri, L.; Laureti, T.; Polidoro, F. Computing sub-national PPPs with CPI data: An empirical analysis on Italian data using country product dummy models. Soc. Indic. Res. 2017, 131, 93–121. [Google Scholar] [CrossRef]
- Chamon, M.; de Carvalho, I. Consumption based estimates of urban Chinese growth. China Econ. Rev. 2014, 29, 126–137. [Google Scholar] [CrossRef]
- Larsen, E.R. Does the CPI mirror the cost of living? Engel’s law suggests not in Norway. Scand. J. Econ. 2007, 109, 177–195. [Google Scholar] [CrossRef]
- Costa, D.L. Estimating real income in the united states from 1888 to 1994: Correcting CPI bias using Engel curves. J. Polit. Econ. 2001, 109, 1288–1310. [Google Scholar] [CrossRef] [Green Version]
- Gluzmann, P.; Sturzenegger, F. An estimation of CPI biases in Argentina 1985–2005 and its implications on real income growth and income distribution. Latin. Am. Econ. Rev. 2018, 27, 1–50. [Google Scholar] [CrossRef] [Green Version]
- Emery, J.C.H.; Guo, X.L. Using an Engel curve approach to infer cost of living experienced by Canadian households. Can. Public Policy Anal. Polit. 2020, 46, 397–413. [Google Scholar] [CrossRef]
- Chen, M.; Wang, Y.; Rao, D.S.P. Measuring the spatial price differences in china with regional price parity methods. World Econ. 2020, 43, 1103–1146. [Google Scholar] [CrossRef]
- Aten, B.H. Interarea price levels: An experimental methodology. Mon. Labor Rev. 2006, 129, 47–61. [Google Scholar]
- Kokoski, M.F. New research on interarea consumer price differences. Mon. Labor Rev. 1991, 114, 31–34. [Google Scholar]
- Montero, J.M.; Laureti, T.; Minguez, R.; Fernandez-Aviles, G. A stochastic model with penalized coefficients for spatial price comparisons: An application to regional price indexes in Italy. Rev. Income Wealth 2020, 66, 512–533. [Google Scholar] [CrossRef]
- Majumder, A.; Ray, R.; Sinha, K. Estimating purchasing power parities from household expenditure data using complete demand systems with application to living standards comparison: India and Vietnam. Rev. Income Wealth 2015, 61, 302–328. [Google Scholar] [CrossRef]
- Aten, B.H. Regional price parities and real regional income for the united states. Soc. Indic. Res. 2017, 131, 123–143. [Google Scholar] [CrossRef]
- Hearne, D. Regional prices and real incomes in the UK. Reg. Stud. 2021, 55, 951–961. [Google Scholar] [CrossRef]
- Benedetti, I.; Biggeri, L.; Laureti, T. Sub-national spatial price indexes for housing: Methodological issues and computation for Italy. J. Off. Stat. 2022, 38, 57–82. [Google Scholar] [CrossRef]
- Jiang, X.J.; Li, H. Smaller real regional income gap than nominal income gap: A price-adjusted study. China World Econ. 2006, 14, 38–53. [Google Scholar] [CrossRef]
- Biggeri, L.; Ferrari, G.; Zhao, Y. Estimating cross province and municipal city price level differences in china: Some experiments and results. Soc. Indic. Res. 2017, 131, 169–187. [Google Scholar] [CrossRef]
- Chen, M.G. Sub-national ppps based on house and real income disparity across china: A distinctive spatial deflator. J. Real Estate Financ. Econ. 2021, 62, 187–219. [Google Scholar] [CrossRef]
- Summers, R. International price comparisons based upon incomplete data*. Rev. Income Wealth 1973, 19, 1–16. [Google Scholar] [CrossRef]
- Selvanathan, E.; Rao, D.S. Index Numbers: A Stochastic Approach; The University of Michigan Press: Ann Arbor, MI, USA, 1994. [Google Scholar]
- Diewert, E. New methodological developments for the international comparison program. Rev. Income Wealth 2010, 56, S11–S31. [Google Scholar] [CrossRef]
- Rao, D.S.P.; Hajargasht, G. Stochastic approach to computation of purchasing power parities in the international comparison program (ICP). J. Econom. 2016, 191, 414–425. [Google Scholar] [CrossRef] [Green Version]
- Hajargasht, G.; Rao, D.S.P. Stochastic approach to index numbers for multilateral price comparisons and their standard errors. Rev. Income Wealth 2010, 56, S32–S58. [Google Scholar] [CrossRef] [Green Version]
- Geary, R.C. A note on the comparison of exchange-rates and purchasing power between countries. J. R. Stat. Soc. Ser. a-Gen. 1958, 121, 97–99. [Google Scholar] [CrossRef]
- Fenoaltea, S. Of economics and statistics: The “gerschenkron effect”. PSL Q. Rev. 2019, 72, 195–205. [Google Scholar]
- Rao, D.S.P. Chapter 6—A system of log-change index numbers for multilateral comparisons. In Contributions to Economic Analysis; Rao, D.S.P., Ed.; Elsevier: Amsterdam, The Netherlands, 1990; Volume 194, pp. 127–139. [Google Scholar]
- Research Group on “The Index Method and Application for Regional of Price Difference”. Research on the differentials of regional price level in China. Stat. Res. 2014, 31, 22–30. [Google Scholar]
- Samuelson, P.A. Facets of balassa-samuelson thirty years later. Rev. Int. Econ. 1994, 2, 201–226. [Google Scholar] [CrossRef]
- Hassan, F. The price of development: The penn-balassa-samuelson effect revisited. J. Int. Econ. 2016, 102, 291–309. [Google Scholar] [CrossRef]
- Ishaq, M.; Ghouse, G.; Bhatti, M.I. Another prospective on real exchange rate and the traded goods prices: Revisiting Balassa–Samuelson hypothesis. Sustainability 2022, 14, 7529. [Google Scholar] [CrossRef]


| Region | PPPs of GK System under Stochastic Approach | Heteroskedastic Robust Standard Errors of GK System under Stochastic Approach | PPPs of Rao System under Stochastic Approach | Heteroskedastic Robust Standard Errors of Rao System under Stochastic Approach |
|---|---|---|---|---|
| Beijing | 1.000 | - | 1.000 | - |
| Tianjin | 1.065 | 0.974 | 0.920 | 0.087 |
| Shijiazhuang | 0.832 | 0.791 | 0.807 | 0.113 |
| Tangshan | 0.856 | 0.774 | 0.785 | 0.086 |
| Xingtai | 0.707 | 0.643 | 0.709 | 0.082 |
| Taiyuan | 0.834 | 0.753 | 0.760 | 0.111 |
| Datong | 0.746 | 0.680 | 0.709 | 0.085 |
| Huhhot | 0.907 | 0.824 | 0.800 | 0.091 |
| Baotou | 0.901 | 0.818 | 0.784 | 0.098 |
| Shenyang | 0.514 | 0.475 | 0.634 | 0.208 |
| Dalian | 0.991 | 0.911 | 0.872 | 0.080 |
| Changchun | 0.947 | 0.848 | 0.882 | 0.103 |
| Tonghua | 0.613 | 0.559 | 0.694 | 0.126 |
| Harbin | 0.722 | 0.663 | 0.697 | 0.081 |
| Mudanjiang | 0.762 | 0.690 | 0.843 | 0.113 |
| Shanghai | 0.945 | 0.877 | 0.922 | 0.085 |
| Nanjing | 1.040 | 0.950 | 0.961 | 0.082 |
| Xuzhou | 0.954 | 0.877 | 0.866 | 0.083 |
| Suzhou | 0.892 | 0.820 | 0.850 | 0.082 |
| Nantong | 0.894 | 0.821 | 0.888 | 0.086 |
| Yangzhou | 0.907 | 0.838 | 0.825 | 0.084 |
| Hangzhou | 1.023 | 0.934 | 0.967 | 0.098 |
| Ningbo | 1.105 | 1.018 | 1.028 | 0.102 |
| Shaoxing | 0.935 | 0.863 | 0.916 | 0.103 |
| Quzhou | 0.629 | 0.580 | 0.764 | 0.089 |
| Hefei | 1.015 | 0.941 | 0.879 | 0.128 |
| Huainan | 0.735 | 0.682 | 0.698 | 0.078 |
| Anqing | 0.792 | 0.739 | 0.713 | 0.116 |
| Chuzhou | 0.568 | 0.521 | 0.646 | 0.102 |
| Fuzhou | 0.904 | 0.857 | 0.872 | 0.098 |
| Xiamen | 0.967 | 0.910 | 0.936 | 0.086 |
| Sanming | 0.740 | 0.696 | 0.797 | 0.091 |
| Quanzhou | 0.846 | 0.794 | 0.848 | 0.097 |
| Nanchang | 0.879 | 0.822 | 0.798 | 0.087 |
| Jiujiang | 0.870 | 0.814 | 0.767 | 0.081 |
| Ganzhou | 0.785 | 0.732 | 0.780 | 0.086 |
| Jinan | 0.873 | 0.809 | 0.765 | 0.088 |
| Qingdao | 0.848 | 0.788 | 0.820 | 0.124 |
| Zaozhuang | 0.885 | 0.810 | 0.853 | 0.173 |
| Yantai | 0.885 | 0.814 | 0.892 | 0.121 |
| Taian | 0.723 | 0.654 | 0.746 | 0.100 |
| Heze | 0.592 | 0.546 | 0.635 | 0.084 |
| Zhengzhou | 0.865 | 0.789 | 0.822 | 0.109 |
| Zhoukou | 0.803 | 0.738 | 0.626 | 0.081 |
| Wuhan | 0.870 | 0.797 | 0.853 | 0.087 |
| Huangshi | 0.690 | 0.641 | 0.785 | 0.083 |
| Yichang | 0.733 | 0.674 | 0.828 | 0.091 |
| Xiangyang | 0.665 | 0.621 | 0.707 | 0.113 |
| Jinmen | 0.739 | 0.679 | 0.731 | 0.084 |
| Changsha | 0.915 | 0.833 | 0.903 | 0.096 |
| Hengyang | 0.738 | 0.672 | 0.720 | 0.109 |
| Guangzhou | 1.075 | 1.004 | 1.050 | 0.091 |
| Shenzhen | 0.928 | 0.870 | 1.034 | 0.107 |
| Shantou | 0.692 | 0.666 | 0.783 | 0.145 |
| Huizhou | 0.880 | 0.830 | 0.891 | 0.076 |
| Nanning | 0.791 | 0.731 | 0.730 | 0.100 |
| Liuzhou | 1.045 | 0.988 | 0.950 | 0.099 |
| Beihai | 0.793 | 0.762 | 0.744 | 0.118 |
| Haikou | 0.880 | 0.826 | 0.897 | 0.081 |
| Sanya | 0.845 | 0.802 | 0.871 | 0.091 |
| Chongqing | 0.952 | 0.872 | 0.887 | 0.089 |
| Chengdu | 0.863 | 0.807 | 0.818 | 0.096 |
| Mianyang | 0.856 | 0.793 | 0.889 | 0.090 |
| Leshan | 0.781 | 0.733 | 0.787 | 0.105 |
| Guiyang | 0.683 | 0.637 | 0.809 | 0.140 |
| Zunyi | 0.765 | 0.691 | 0.859 | 0.099 |
| Kunming | 0.885 | 0.805 | 0.723 | 0.090 |
| Xi’an | 0.869 | 0.792 | 0.812 | 0.119 |
| Weinan | 0.624 | 0.582 | 0.615 | 0.132 |
| Hanzhong | 0.756 | 0.695 | 0.680 | 0.108 |
| Lanzhou | 0.874 | 0.815 | 0.831 | 0.091 |
| Xining | 0.780 | 0.715 | 0.718 | 0.104 |
| Yinchuan | 0.931 | 0.843 | 0.896 | 0.122 |
| Shizuishan | 0.892 | 0.821 | 0.790 | 0.104 |
| Wuzhong | 0.764 | 0.694 | 0.696 | 0.091 |
| Wulumuqi | 0.864 | 0.783 | 0.837 | 0.073 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Yu, X.; Zhao, J. Identifying the Real Income Disparity in Prefecture-Level Cities in China: Measurement of Subnational Purchasing Power Parity Based on the Stochastic Approach. Sustainability 2022, 14, 9895. https://doi.org/10.3390/su14169895
Wang C, Yu X, Zhao J. Identifying the Real Income Disparity in Prefecture-Level Cities in China: Measurement of Subnational Purchasing Power Parity Based on the Stochastic Approach. Sustainability. 2022; 14(16):9895. https://doi.org/10.3390/su14169895
Chicago/Turabian StyleWang, Chunyun, Xiaoxi Yu, and Jiang Zhao. 2022. "Identifying the Real Income Disparity in Prefecture-Level Cities in China: Measurement of Subnational Purchasing Power Parity Based on the Stochastic Approach" Sustainability 14, no. 16: 9895. https://doi.org/10.3390/su14169895
APA StyleWang, C., Yu, X., & Zhao, J. (2022). Identifying the Real Income Disparity in Prefecture-Level Cities in China: Measurement of Subnational Purchasing Power Parity Based on the Stochastic Approach. Sustainability, 14(16), 9895. https://doi.org/10.3390/su14169895






