Optimized Self-Adaptive Power Distribution for Microgrids in a Typical Tourism Water Village of Northern China under COVID-19 Background
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Object
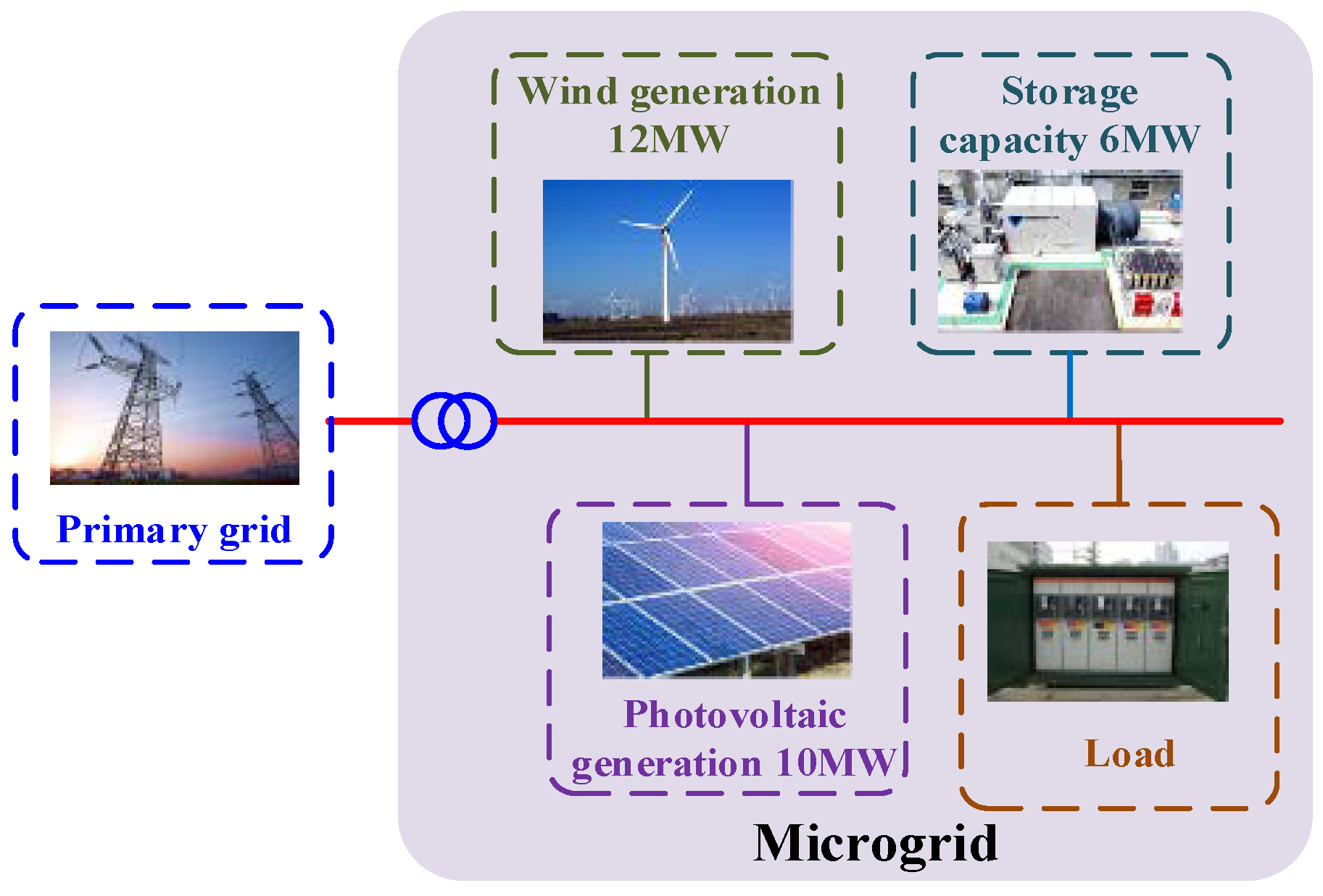
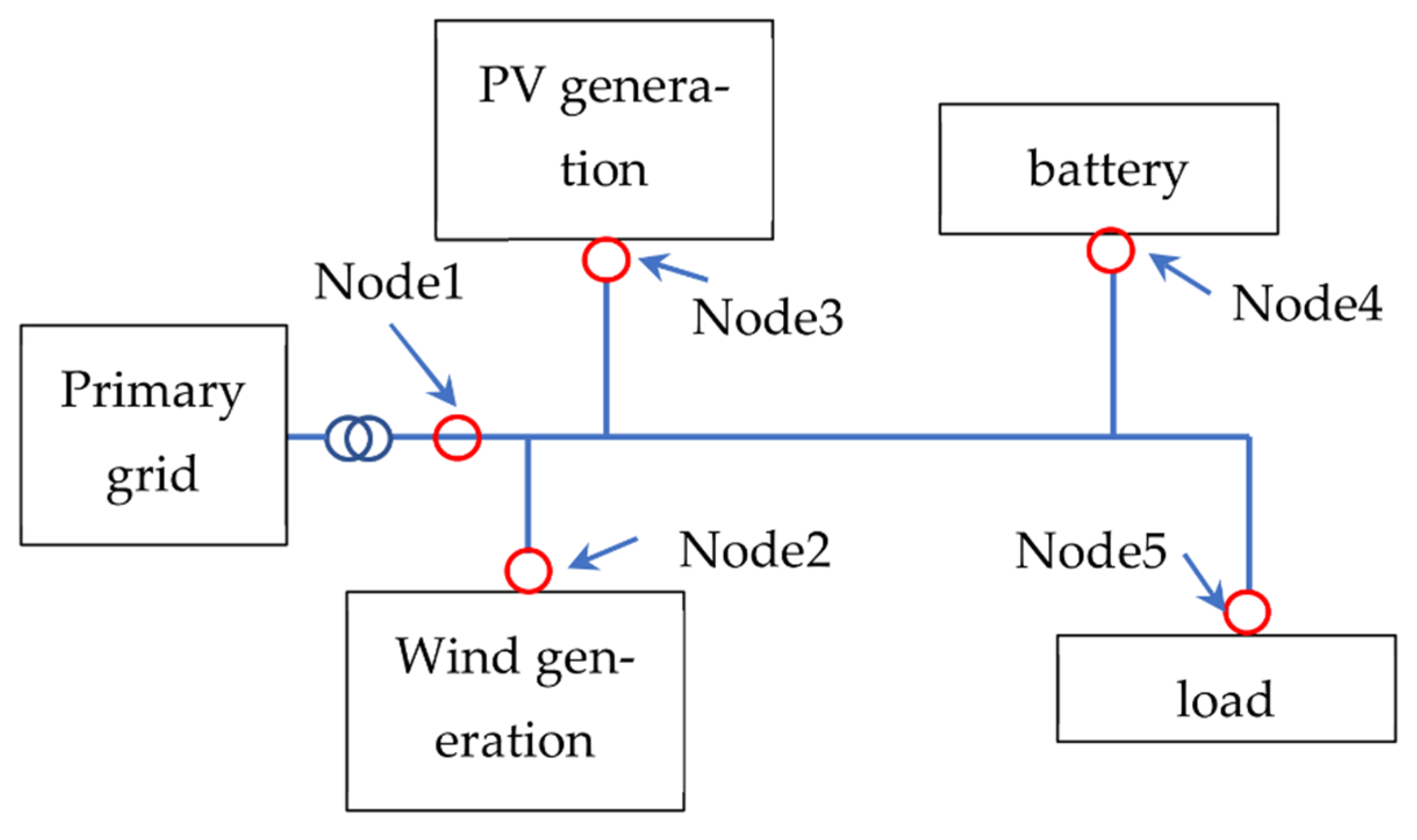
2.1.1. Microgrid Topology
2.1.2. Specific Conditions under COVID-19 Background
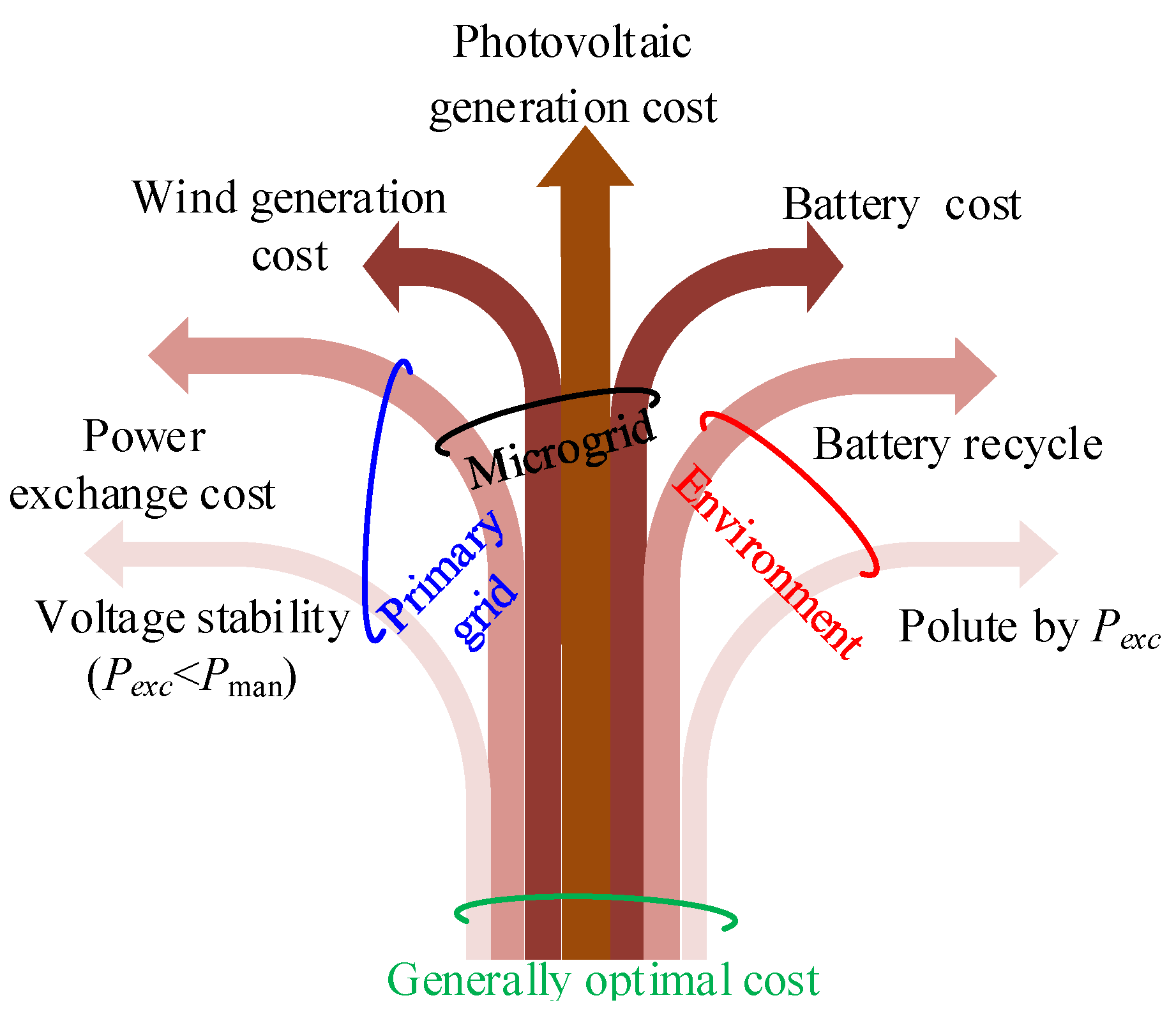
2.2. Optimized Self-Adaptive Power Distribution Scheme
2.2.1. Microgrid Model
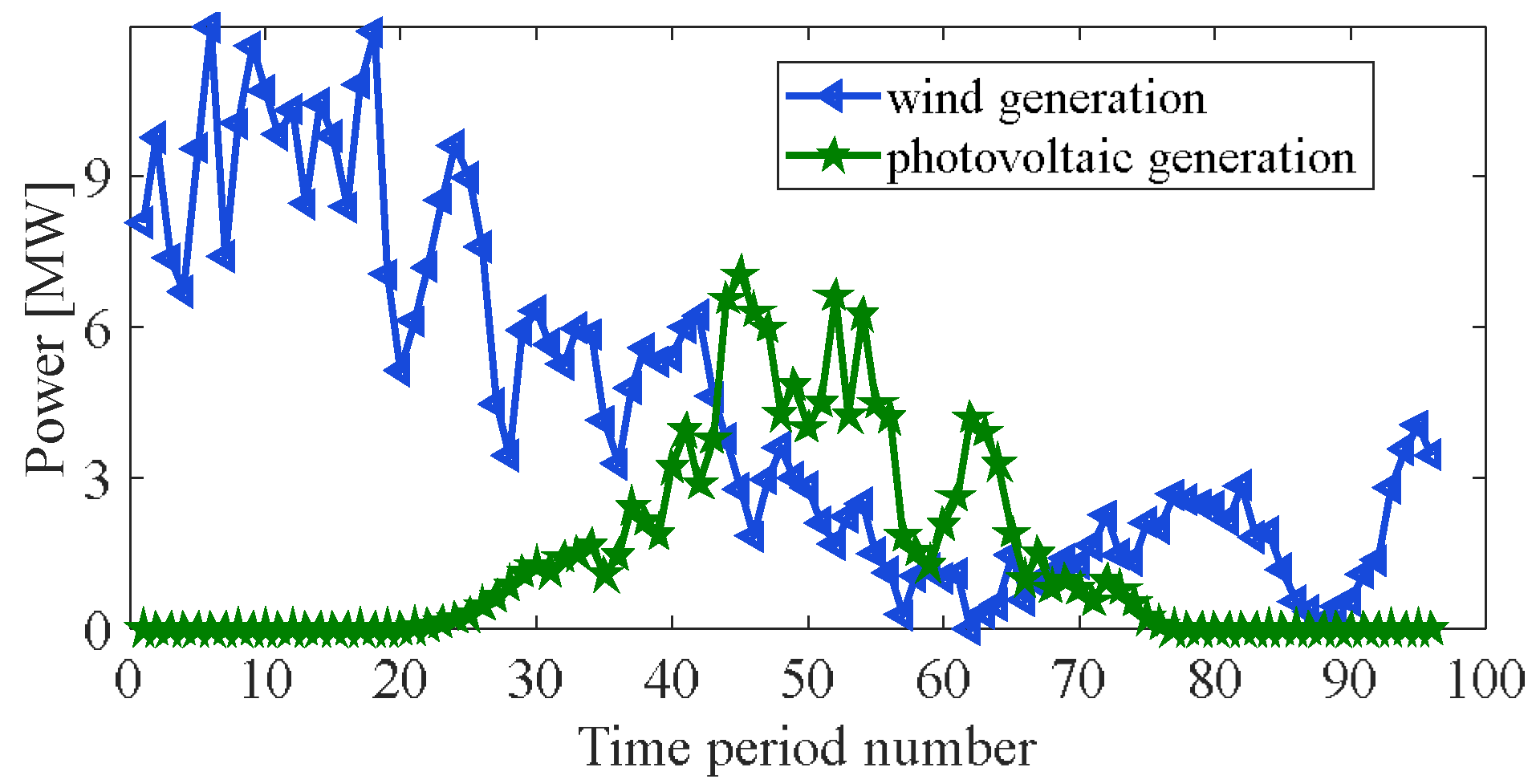
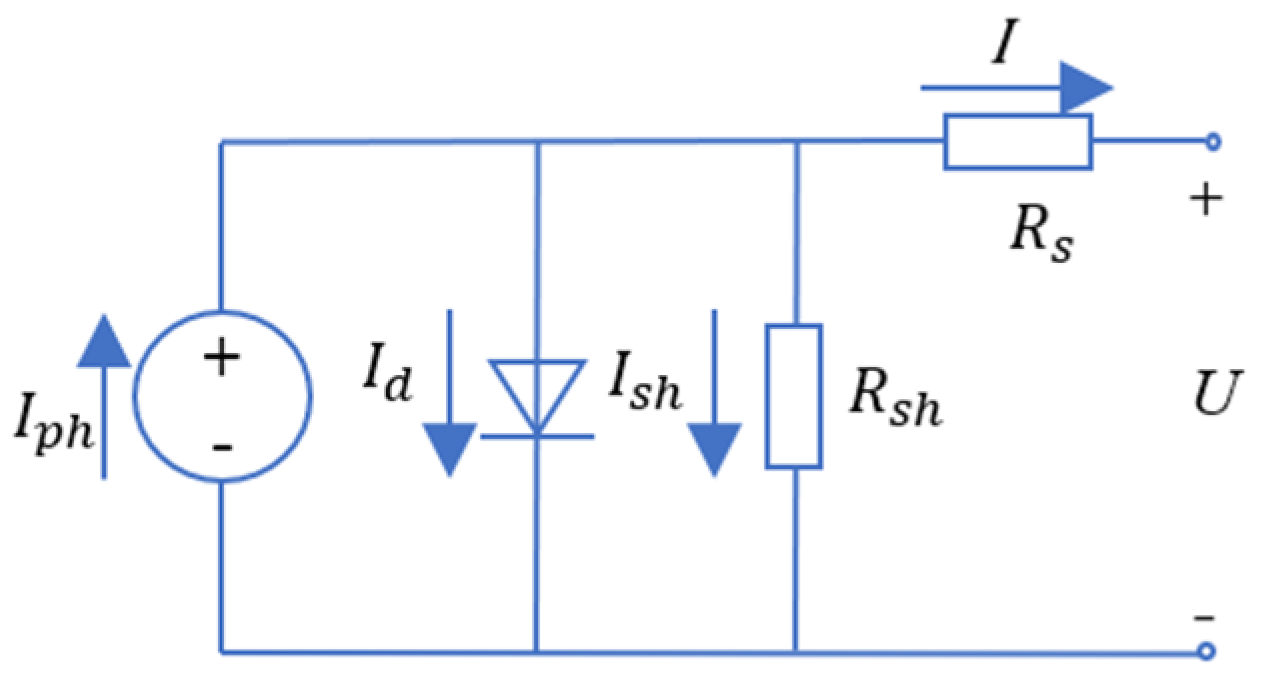
- Model of wind generator;
- Photovoltaic;
- Battery.
2.2.2. Boundary Condition and Limitation
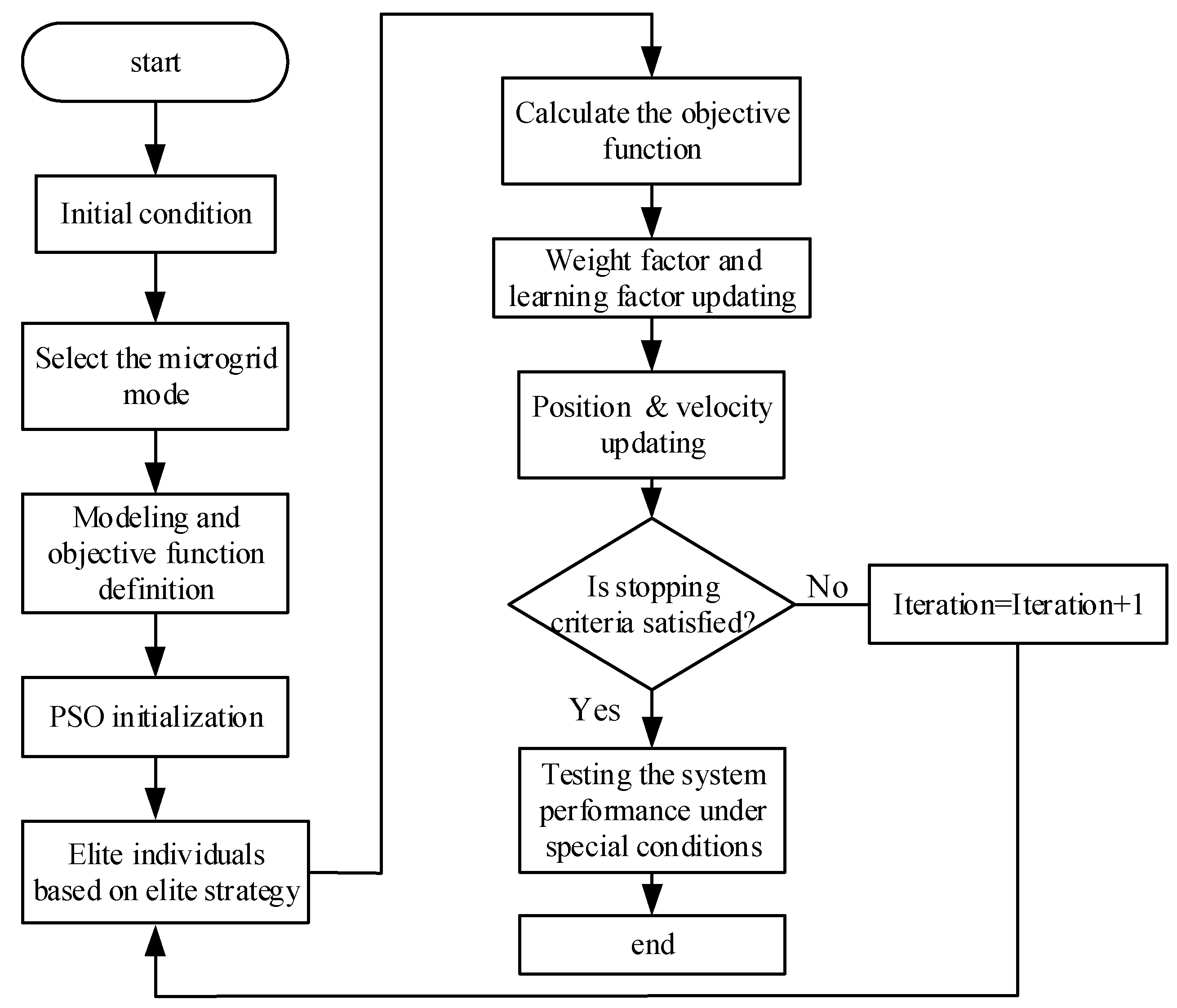
2.2.3. Improved PSO Algorithm for Typical Condition under COVID-19 Background
- Improved PSO algorithm application;
- elite strategy;
- The elite strategy is used to generate elite reverse individuals. The fitness value of each particle is calculated. Meanwhile, the fitness value of the particle is stored in pBest. Further, the next generation population is generated based on the best value of the objective function. Moreover, the fitness value of the best individual is stored in gBest.
- Weight factor and acceleration updating.
- Objective functions and optimization scheme.
2.3. Power Dispatching Optimization Case Study
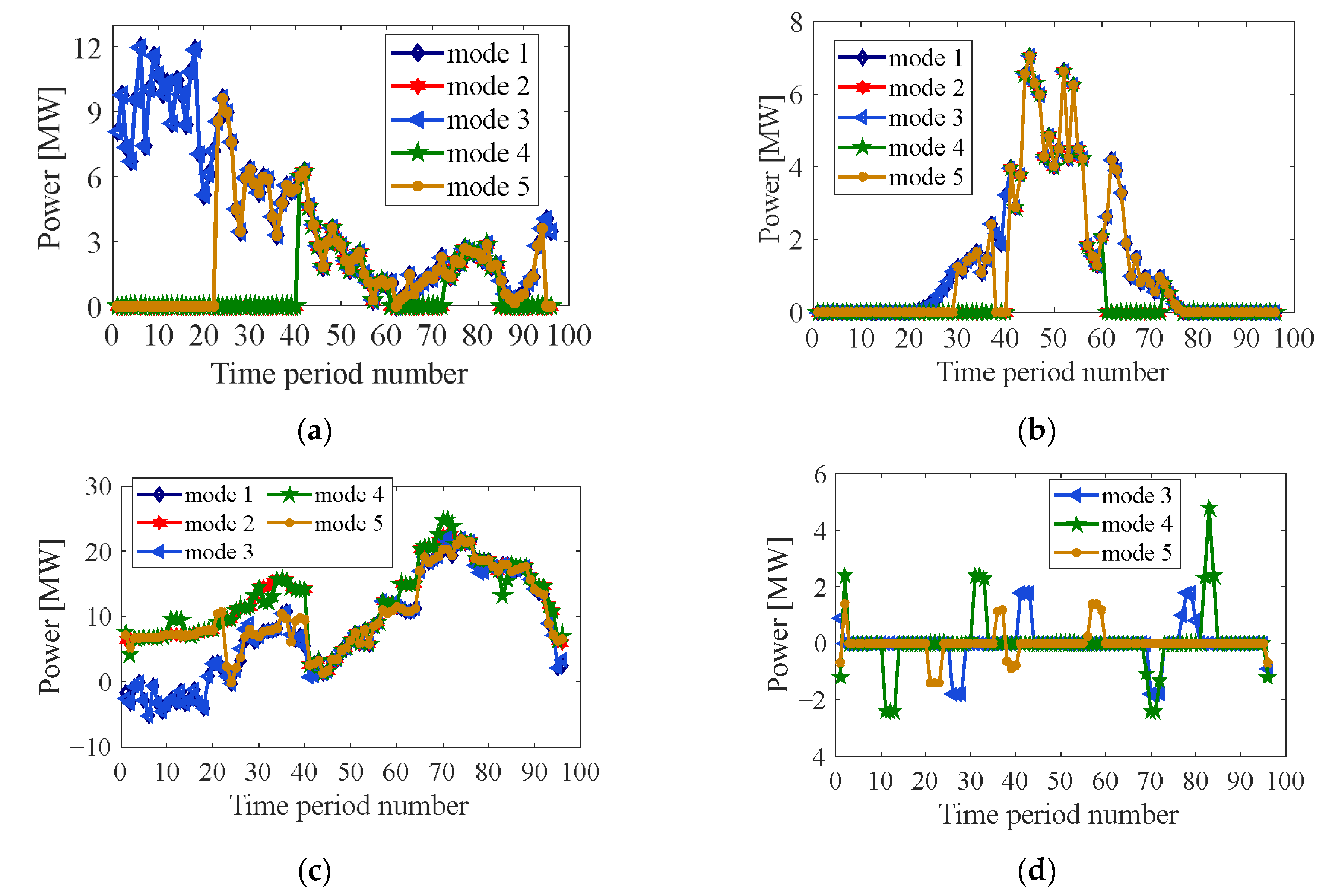
2.3.1. Five Modes
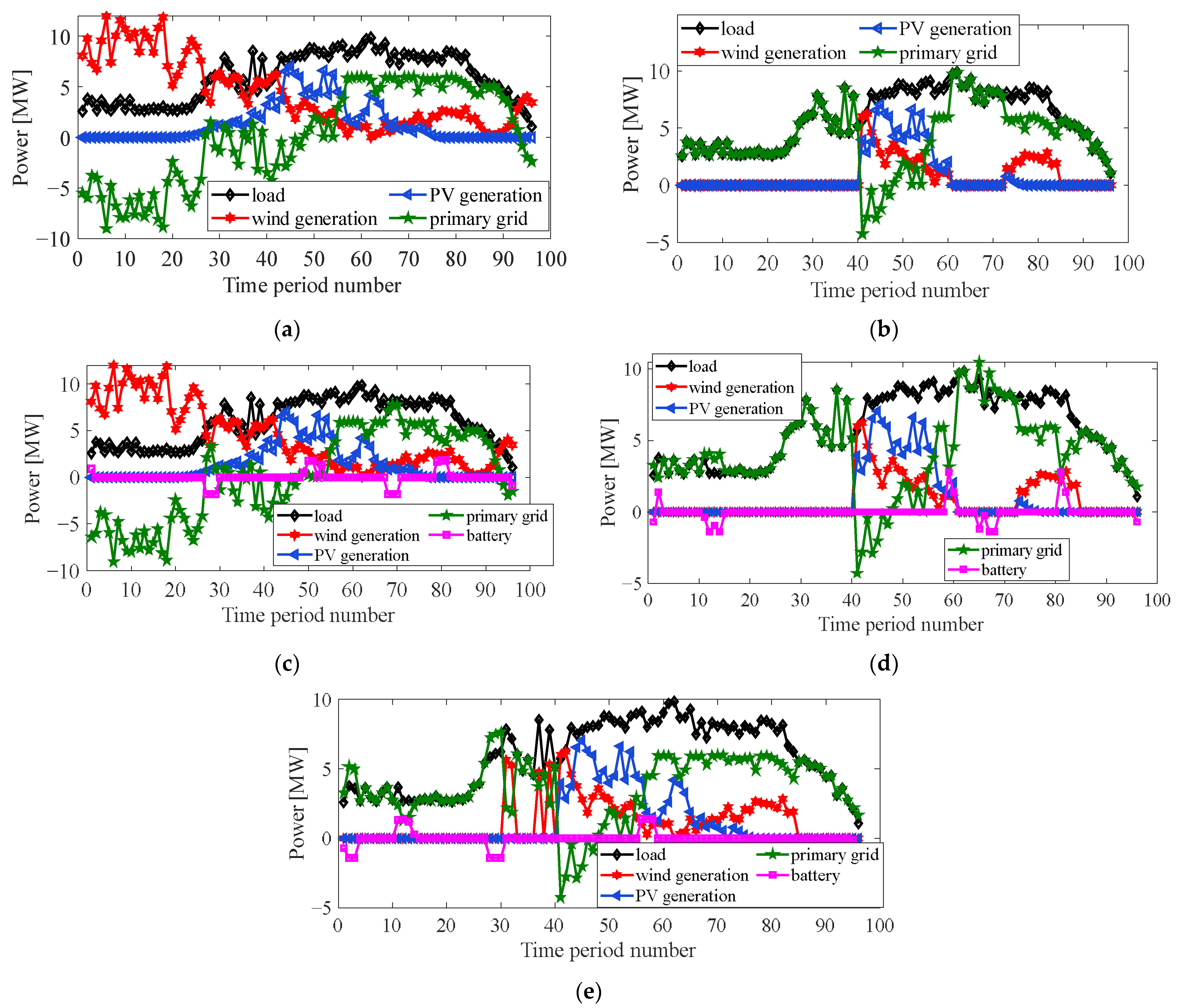
2.3.2. Power Dispatching Optimization without Epidemic
2.3.3. Power Dispatching Optimization with Epidemic
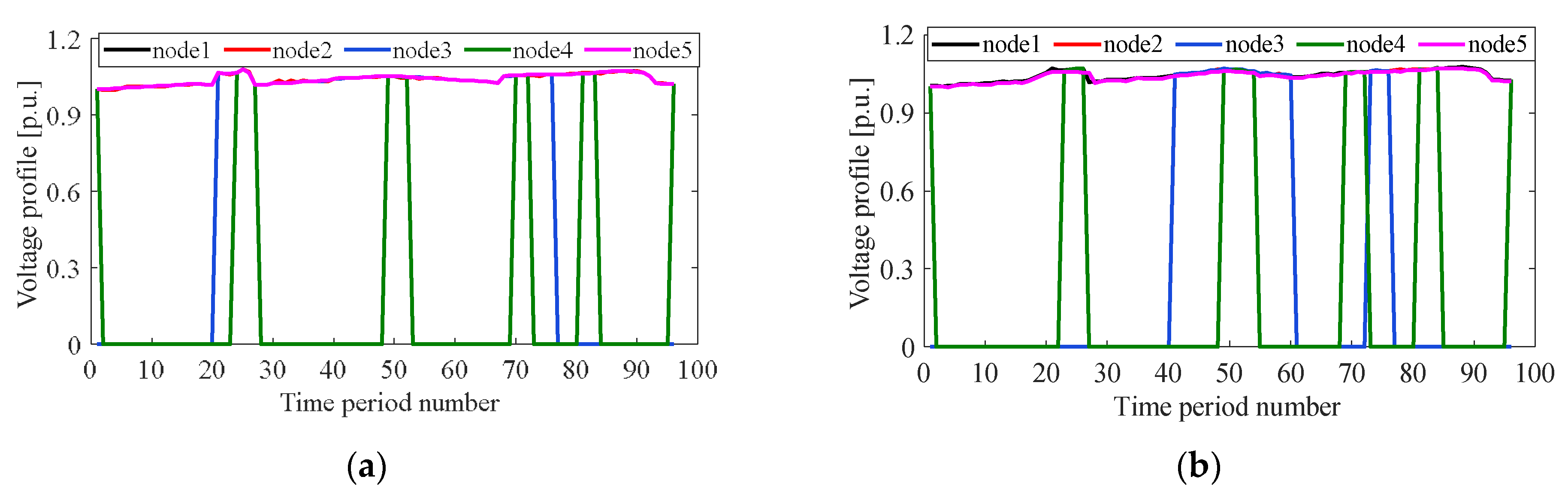
3. Results and Discussion
3.1. Comparison among Five Modes
3.2. Impact on Microgrid Economic Due to Epidemic
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ding, S.; Liu, L. Review of microgrid research. Pop. Stand. 2021, 22, 225–227. [Google Scholar]
- Xin, B.; Shan, B.; Li, Q.; Yan, H.; Wang, C. Rethinking of the “Three Elements of Energy” Toward Carbon Peak and Carbon Neutrality. Proc. CSEE 2022, 42, 311. [Google Scholar]
- Yuan, W.; Wang, Y.; Chen, Z. New Perspectives on Power Control of AC Microgrid Considering Operation Cost and Efficiency. IEEE Trans. Power Syst. 2021, 36, 4844–4847. [Google Scholar] [CrossRef]
- Elrayyah, A.; Sozer, Y.; Elbuluk, M.E. A Novel Load-Flow Analysis for Stable and Optimized Microgrid Operation. IEEE Trans. Power Deliv. 2014, 29, 1709–1717. [Google Scholar] [CrossRef]
- Rohouma, W.; Metry, M.; Balog, R.S.; Peerzada, A.A.; Begovic, M.M.; Zhou, D. Analysis of the Capacitor-Less D-STATCOM for Voltage Profile Improvement in Distribution Network with High PV Penetration. IEEE Open J. Power Electron. 2022, 3, 255–270. [Google Scholar] [CrossRef]
- Moghbel, M.; Masoum, M.A.; Fereidouni, A.; Deilami, S. Optimal Sizing, Siting and Operation of Custom Power Devices with STATCOM and APLC Functions for Real-Time Reactive Power and Network Voltage Quality Control of Smart Grid. IEEE Trans. Smart Grid 2018, 9, 5564–5575. [Google Scholar] [CrossRef]
- Ismail, B.; Wahab, N.I.A.; Othman, M.L.; Radzi, M.A.M.; Vijyakumar, K.N.; Naain, M.N.M. A Comprehensive Review on Optimal Location and Sizing of Reactive Power Compensation Using Hybrid-Based Approaches for Power Loss Reduction, Voltage Stability Improvement, Voltage Profile Enhancement and Loadability Enhancement. IEEE Access 2020, 8, 222733–222765. [Google Scholar] [CrossRef]
- Cho, J.; Kim, H.; Cho, Y.; Kim, H.; Kim, J. Demonstration of a DC Microgrid with Central Operation Strategies on an Island. In Proceedings of the 2019 IEEE Third International Conference on DC Microgrids (ICDCM), Matsue, Japan, 20–23 May 2019; pp. 1–5. [Google Scholar]
- Babayomi, O.; Li, Z.; Zhang, Z. Distributed secondary frequency and voltage control of parallel-connected vscs in microgrids: A predictive VSG-based solution. CPSS Trans. Power Electron. Appl. 2020, 5, 342–351. [Google Scholar] [CrossRef]
- Simpson-Porco, J.W.; Shafiee, Q.; Dörfler, F.; Vasquez, J.C.; Guerrero, J.M.; Bullo, F. Secondary Frequency and Voltage Control of Islanded Microgrids via Distributed Averaging. IEEE Trans. Ind. Electron. 2015, 62, 7025–7038. [Google Scholar] [CrossRef]
- Guo, F.; Wen, C.; Mao, J.; Song, Y.D. Distributed Secondary Voltage and Frequency Restoration Control of Droop-Controlled Inverter-Based Microgrids. IEEE Trans. Ind. Electron. 2015, 62, 4355–4364. [Google Scholar] [CrossRef]
- Basu, A.K.; Chowdhury, S.; Chowdhury, S.P. Chowdhury, Impact of Strategic Deployment of CHP-Based DERs on Microgrid Reliability. IEEE Trans. Power Deliv. 2010, 25, 1697–1705. [Google Scholar] [CrossRef]
- Bani-Ahmed, A.; Rashidi, M.; Nasiri, A.; Hosseini, H. Hosseini, Reliability Analysis of a Decentralized Microgrid Control Architecture. IEEE Trans. Smart Grid 2019, 10, 3910–3918. [Google Scholar] [CrossRef]
- Wu, X.; Zhao, W.; Wang, X.; Li, H. An MILP-Based Planning Model of a Photovoltaic/Diesel/Battery Stand-Alone Microgrid Considering the Reliability. IEEE Trans. Smart Grid 2021, 12, 3809–3818. [Google Scholar] [CrossRef]
- Tan, L.; Han, J.; Zhang, H. Ultra-Short-Term Wind Power Prediction by Salp Swarm Algorithm-Based Optimizing Extreme Learning Machine. IEEE Access 2020, 8, 44470–44484. [Google Scholar] [CrossRef]
- Wu, F.; Liao, X. Short-term Wind Power Forecast for Wind Farm Base on Artificial Neural Network. In Proceedings of the 2017 International Conference on Computer Technology, Electronics and Communication (ICCTEC), Dalian, China, 19–21 December 2017. [Google Scholar]
- Kim, G.G.; Choi, J.H.; Park, S.Y.; Bhang, B.G.; Nam, W.J.; Cha, H.L.; Ahn, H.K. Prediction Model for PV Performance with Correlation Analysis of Environmental Variables. IEEE J. Photovolt. 2019, 9, 832–841. [Google Scholar] [CrossRef]
- Han, X.H.; Wang, F.; Chen, M. Economic Evaluation of Micro-Grid System in Commercial Parks Based on Echelon Utilization Batteries. IEEE Access 2019, 7, 65624–65634. [Google Scholar] [CrossRef]
- Gonzalo, G.; Aguila, A.; González, D.; Ortiz, L. Optimum location and sizing of capacitor banks using VOLT VAR compensation in micro-grids. IEEE Lat. Am. Trans. 2020, 18, 465–472. [Google Scholar] [CrossRef]
- Herath, P.U.; Fusco, V.; Cáceres, M.N.; Venayagamoorthy, G.K.; Squartini, S.; Piazza, F.; Corchado, J.M. Computational Intelligence-Based Demand Response Management in a Microgrid. IEEE Trans. Ind. 2018, 55, 732–740. [Google Scholar] [CrossRef]
- Helmi, A.M.; Carli, R.; Dotoli, M.; Ramadan, H.S. Efficient and Sustainable Reconfiguration of Distribution Networks via Metaheuristic Optimization. IEEE Trans. Autom. Sci. Eng. 2021, 19, 82–98. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Z.; Cao, R.; Zhang, H. Research on Two-Level Energy Optimized Dispatching Strategy of Microgrid Cluster Based on IPSO Algorithm. IEEE Access 2021, 9, 120492–120501. [Google Scholar] [CrossRef]
- Harasis, S.; Sozer, Y.; Elbuluk, M. Reliable Islanded Microgrid Operation Using Dynamic Optimal Power Management. IEEE Trans. Ind. Appl. 2020, 57, 1755–1766. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Z.; Yang, R. Intelligent Multiagent Control System for Energy and Comfort Management in Smart and Sustainable Buildings. IEEE Trans. Smart Grid 2012, 3, 605–617. [Google Scholar] [CrossRef]
- Nikmehr, N.; Ravadanegh, S.N. Optimal Power Dispatch of Multi-Microgrids at Future Smart Distribution Grids. IEEE Trans. Smart Grid 2015, 6, 1648–1657. [Google Scholar] [CrossRef]
- Mao, M.; Jin, P.; Chang, L.; Xu, H. Economic Analysis and Optimal Design on Microgrids With SS-PVs for Industries. IEEE Trans. Sustain. Energy 2014, 5, 1328–1336. [Google Scholar] [CrossRef]
- Soon, J.J.; Low, K.S. Photovoltaic Model Identification Using Particle Swarm Optimization with Inverse Barrier Constraint. IEEE Trans. Power Electron. 2012, 27, 3975–3983. [Google Scholar] [CrossRef]
- Semero, Y.K.; Zhang, J.; Zheng, D. PV power forecasting using an integrated GA-PSO-ANFIS approach and Gaussian process regression based feature selection strategy. CSEE J. Power Energy Syst. 2018, 4, 210–218. [Google Scholar] [CrossRef]
- Huang, Y.C.; Huang, C.M.; Chen, S.J.; Yang, S.P. Optimization of Module Parameters for PV Power Estimation Using a Hybrid Algorithm. IEEE Trans. Sustain. Energy 2019, 11, 2210–2219. [Google Scholar] [CrossRef]
- Ma, K.; Hu, S.; Hu, G.; Bai, Y.; Yang, J.; Dou, C.; Guerrero, J.M. Energy Management Considering Unknown Dynamics Based on Extremum Seeking Control and Particle Swarm Optimization. IEEE Trans. Control Syst. Technol. 2019, 28, 1560–1568. [Google Scholar] [CrossRef]
- Li, S.B.; Kang, Z.T. Capacity Optimization of Clean Renewable Energy in Power Grid Considering Low Temperature Environment Constraint. IEEE Access 2021, 10, 2740–2752. [Google Scholar] [CrossRef]
- Chen, G.; Wang, J.M.; Yuan, X.D.; Chen, L.; Zhao, L.J.; He, Y.L. Chinese National Condition Based Power Dispatching Optimization in Microgrids. J. Control Sci. Eng. 2018, 2018, 8695391. [Google Scholar] [CrossRef]
- Qudsi, O.A.; Windarko, N.A.; Priyadi, A.; Purnomo, M.H. Optimized GDPWM based on Spontaneous Evolutionary GA for reducing switching losses on inverter. In Proceedings of the 2013 International Conference on Information Technology and Electrical Engineering, Yogyakarta, Indonesia, 7–8 October 2013; pp. 391–396. [Google Scholar]
- Gohil, G.; Bede, L.; Teodorescu, R.; Kerekes, T.; Blaabjerg, F. Comparative evaluation of modulation schemes for grid-connected parallel interleaved inverters. In Proceedings of the 2016 IEEE 7th International Symposium on Power Electronics for Distributed Generation Systems, Vancouver, BC, Canada, 27–30 June 2016; pp. 1–8. [Google Scholar]
- Liu, L. Research on Power Coordination Control and Economic Operation Strategy of Low Voltage Microgrid; Xihua University: Chengdu, China, 2019. [Google Scholar]
- Ropp, M.E.; Gonzalez, S. Development of a MATLAB/Simulink model of a single-phase grid-connected photovoltaic system. IEEE Trans. Energy Conv. 2009, 24, 195–202. [Google Scholar] [CrossRef]
- Chao, K.H.; Li, C.J.; Ho, S.H. Modeling and fault simulation of photovoltaic generation systems using circuit-based model. In Proceedings of the 2008 IEEE International Conference on Sustainable Energy Technologies, Singapore, 24–27 November 2008; pp. 290–294. [Google Scholar]
- Tharwat, A.; Elhoseny, M.; Hassanien, A.E.; Gabel, T.; Kumar, A. Intelligent Bézier curve-based path planning model using Chaotic Particle Swarm Optimization algorithm. Clust. Comput. 2019, 22, 4745–4766. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, K. Research on civil aviation universal service standard based on tessellation model and particle swarm optimization. Int. J. Adv. Manuf. Technol. 2020, 106, 3381–3388. [Google Scholar] [CrossRef]
- Wang, X. The way of estimation and evaluation methods for loss of power transmission and transformation in the energy assessment process. Energy Energy Conserv. 2013, 2013, 79–80. [Google Scholar]
- Guo, Z. Research on Optimal Scheduling of Microgrid Considering Efficiency of Energy Conservation and Emission Reduction. Ph.D. Thesis, Shandong University of Technology, Zibo, China, 2017. [Google Scholar]




| The Serial Number | Time Serial Number | Corresponding Period of Time |
|---|---|---|
| 1 | 0–24 | 0:00~6:00 |
| 2 | 25–40 | 6:00~10:00 |
| 3 | 41–60 | 10:00~15:00 |
| 4 | 61–72 | 15:00~18:00 |
| 5 | 73–84 | 18:00~21:00 |
| 6 | 85–96 | 21:00~24:00 |
| Mode | Description | ||
|---|---|---|---|
| Use of Battery | Use of New Energy Generation | Exchange between Microgrid and Primary Grid | |
| mode 1 | no | mandatory | no |
| mode 2 | no | free | no |
| mode 3 | yes | mandatory | no |
| mode 4 | yes | free | no |
| mode 5 | yes | free | yes |
| Mode | Without Pandemic | With Pandemic | ||||||
|---|---|---|---|---|---|---|---|---|
| Total Cost (105 RMB) | Change Ratio | Average Price (RMB/kWh) | Change Ratio | Total Cost (105 RMB) | Change Ratio | Average Price (RMB/kWh) | Change Ratio | |
| mode 1 | 8.58 | / | 0.78 | / | 4.81 | / | 0.82 | 0.00% |
| mode 2 | 8.01 | 6.64% | 0.69 | 11.54% | 3.94 | 18.01% | 0.72 | 12.20% |
| mode 3 | 8.39 | 2.21% | 0.72 | 7.69% | 4.15 | 13.72% | 0.75 | 8.54% |
| mode 4 | 7.68 | 10.49% | 0.60 | 23.08% | 3.61 | 24.95% | 0.63 | 23.17% |
| mode 5 | 7.81 | 8.97% | 0.65 | 16.67% | 3.79 | 21.21% | 0.65 | 20.73% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.-L.; Zeng, S.-M.; Xu, W.-T.; Du, X.-D.; He, Y.-L. Optimized Self-Adaptive Power Distribution for Microgrids in a Typical Tourism Water Village of Northern China under COVID-19 Background. Sustainability 2022, 14, 9839. https://doi.org/10.3390/su14169839
Zhao J-L, Zeng S-M, Xu W-T, Du X-D, He Y-L. Optimized Self-Adaptive Power Distribution for Microgrids in a Typical Tourism Water Village of Northern China under COVID-19 Background. Sustainability. 2022; 14(16):9839. https://doi.org/10.3390/su14169839
Chicago/Turabian StyleZhao, Jian-Li, Si-Ming Zeng, Wen-Tao Xu, Xiao-Dong Du, and Yu-Ling He. 2022. "Optimized Self-Adaptive Power Distribution for Microgrids in a Typical Tourism Water Village of Northern China under COVID-19 Background" Sustainability 14, no. 16: 9839. https://doi.org/10.3390/su14169839
APA StyleZhao, J.-L., Zeng, S.-M., Xu, W.-T., Du, X.-D., & He, Y.-L. (2022). Optimized Self-Adaptive Power Distribution for Microgrids in a Typical Tourism Water Village of Northern China under COVID-19 Background. Sustainability, 14(16), 9839. https://doi.org/10.3390/su14169839







