Approach to an Equivalent Freight-Based Sustainable Joint-Quotation Strategy for Shipping Blockchain Alliance
Abstract
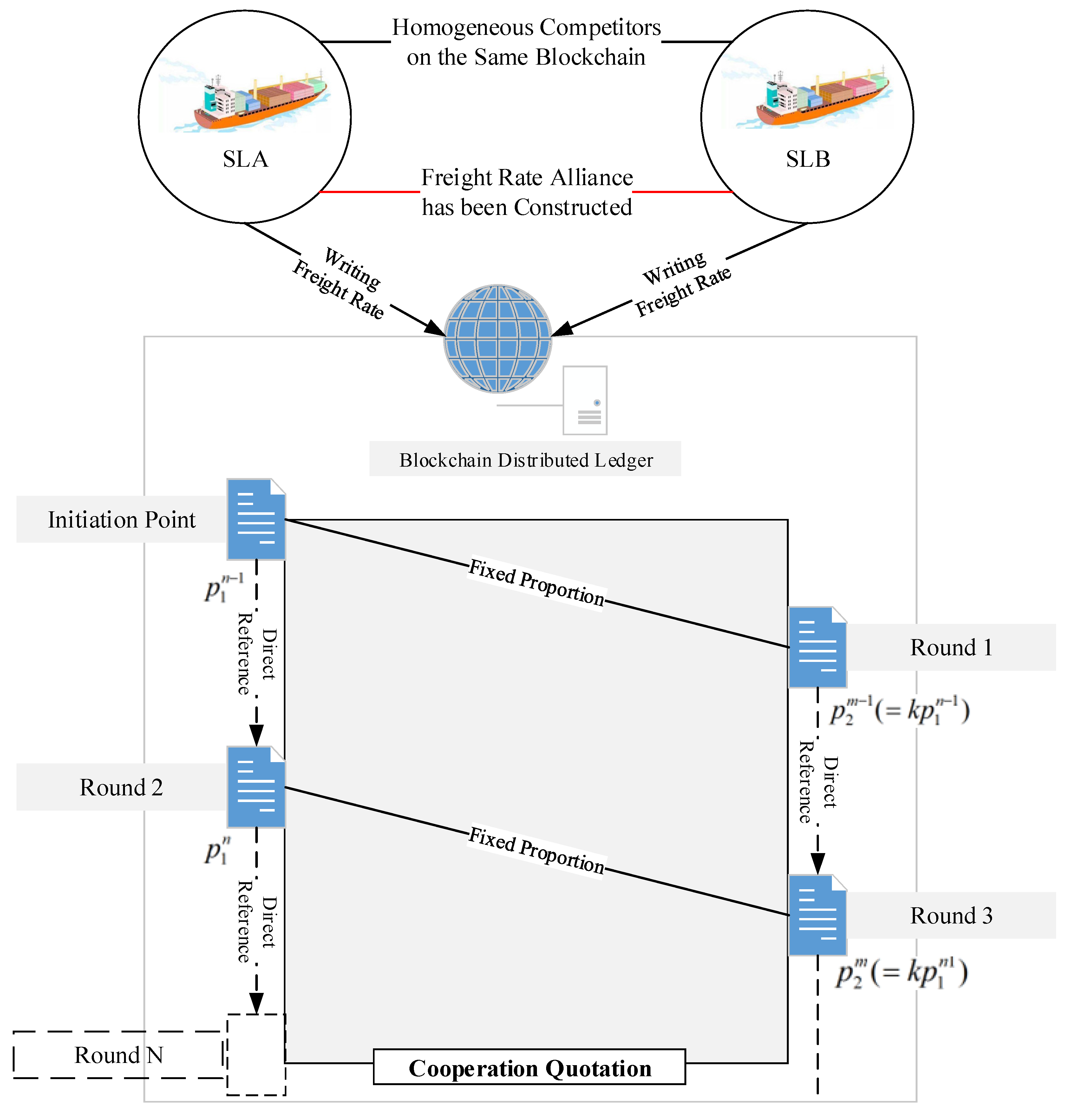
1. Introduction
2. Literature Review
3. Model Development
3.1. Basic Assumptions
- (1)
- The SLA and SLB are all in the same container shipping blockchain as the members. That means, quoting of freight is necessary for both SLs as members in accordance with the consensus on blockchain.
- (2)
- Both SLs involved in this paper are all rational decision-makers. They have the same goals of improving their operation profit by healthy competition and cooperation on blockchain and avoiding the risk of a vicious price war. Additionally, the freight change is a pure rational behavior of SLs regardless of its impact on goodwill and the SLs’ operation.
- (3)
- It is assumed that both SLs can provide container shipping services from the same origin to the same destination on the same route. The impact of container shipping service diversity on the decision-making of SLs are not considered in this paper according to Zheng et al. [43].
- (4)
- During the research period, the unit cost of each SL remains unchanged, because, based on the assumption of homogeneous service, unit cost reflects the scale effects of both SLs. Under the context of the transportation overcapacity and the market risk, the SLs with heavy asset characteristics will not easily adjust the asset allocation in the short term to prevent breaking the scale effect.
- (5)
- (6)
- (1)
- Because SLA is larger than SLB. , and .
- (2)
- The freight sensitivity of the larger one is lower because of the scale effect and the long-term characteristics of the demand. That means, .
- (3)
- The substitution effect from SLA will be stronger than that from SLB. So, .
- (4)
- Because of the characteristics of the oligarchy and the long-term demand, the impact of substitution effect of shipping services on demand will be significantly lower than the freight. So, .
3.2. Fundamental Model
3.3. Model Analysis
4. Numerical Experiment
4.1. Numerical Experiment Result
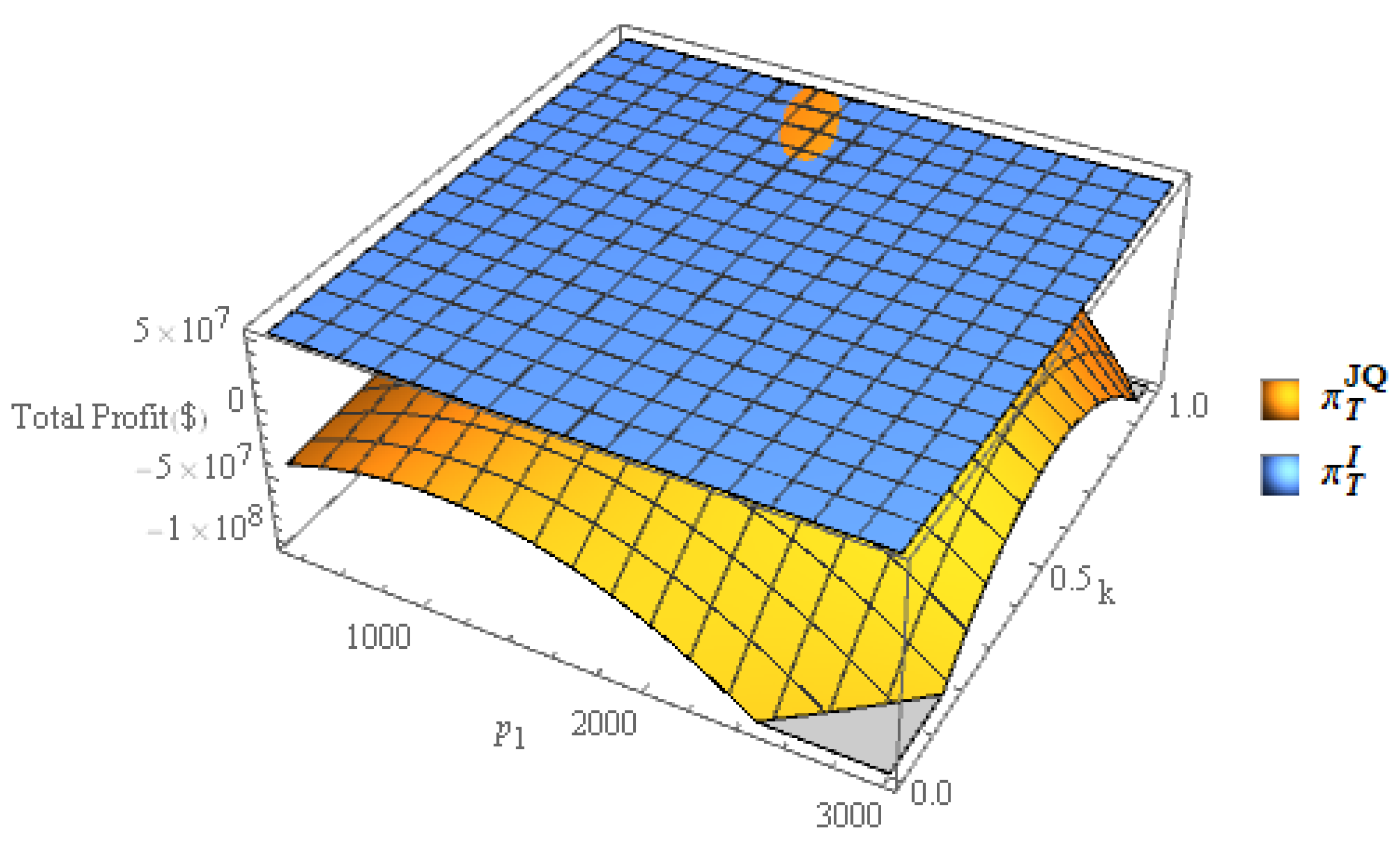
4.2. Sensitivity Analysis
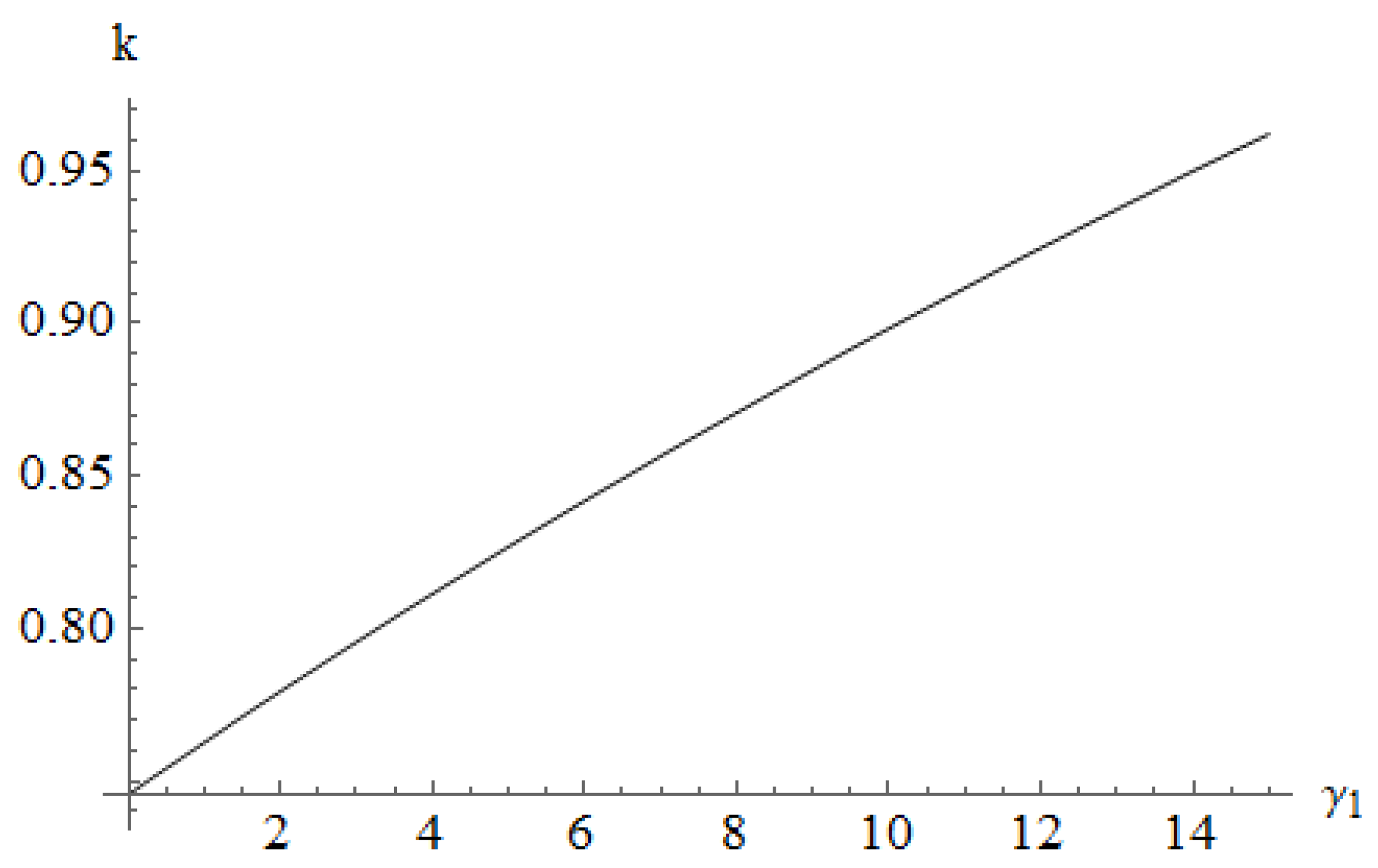
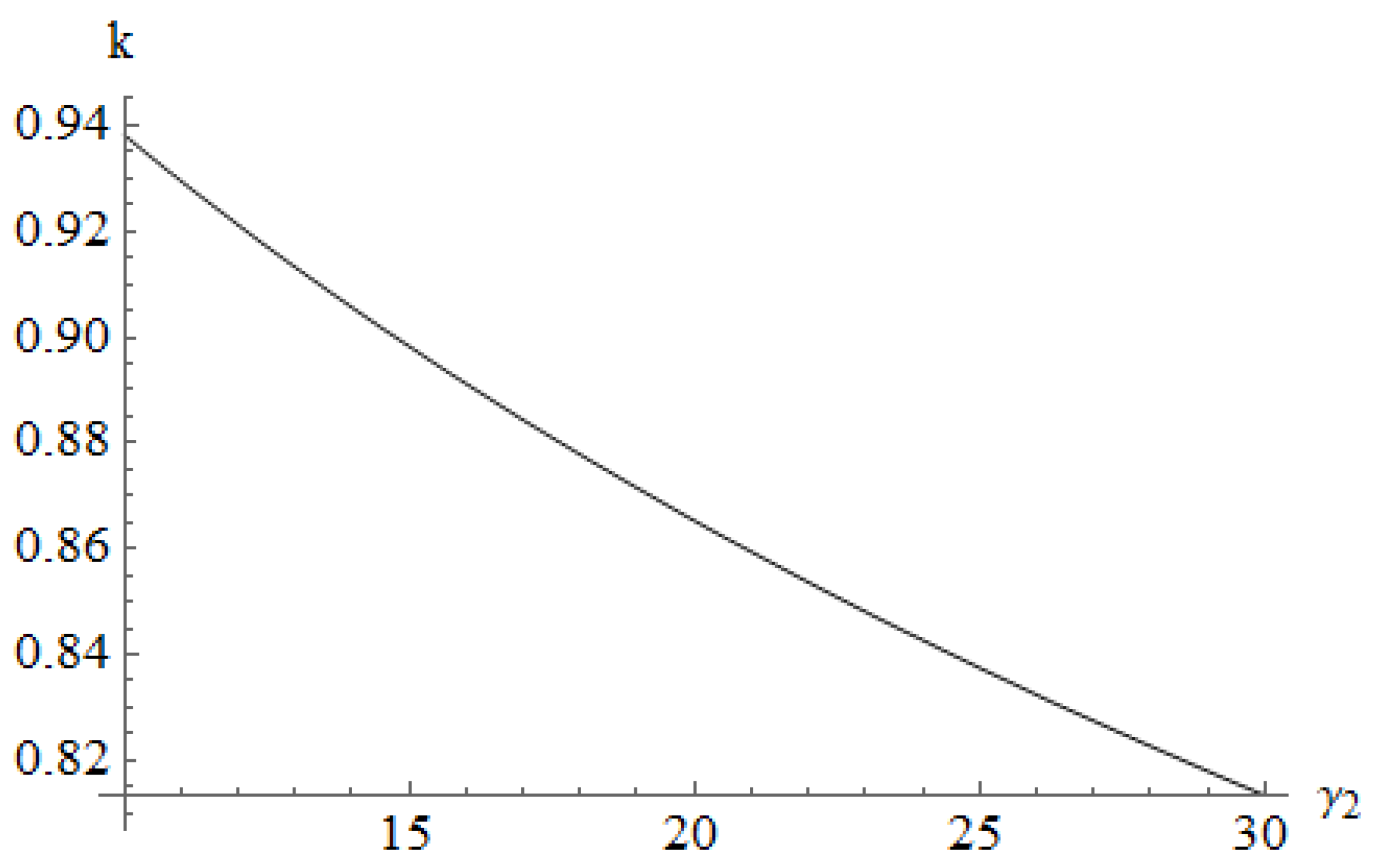
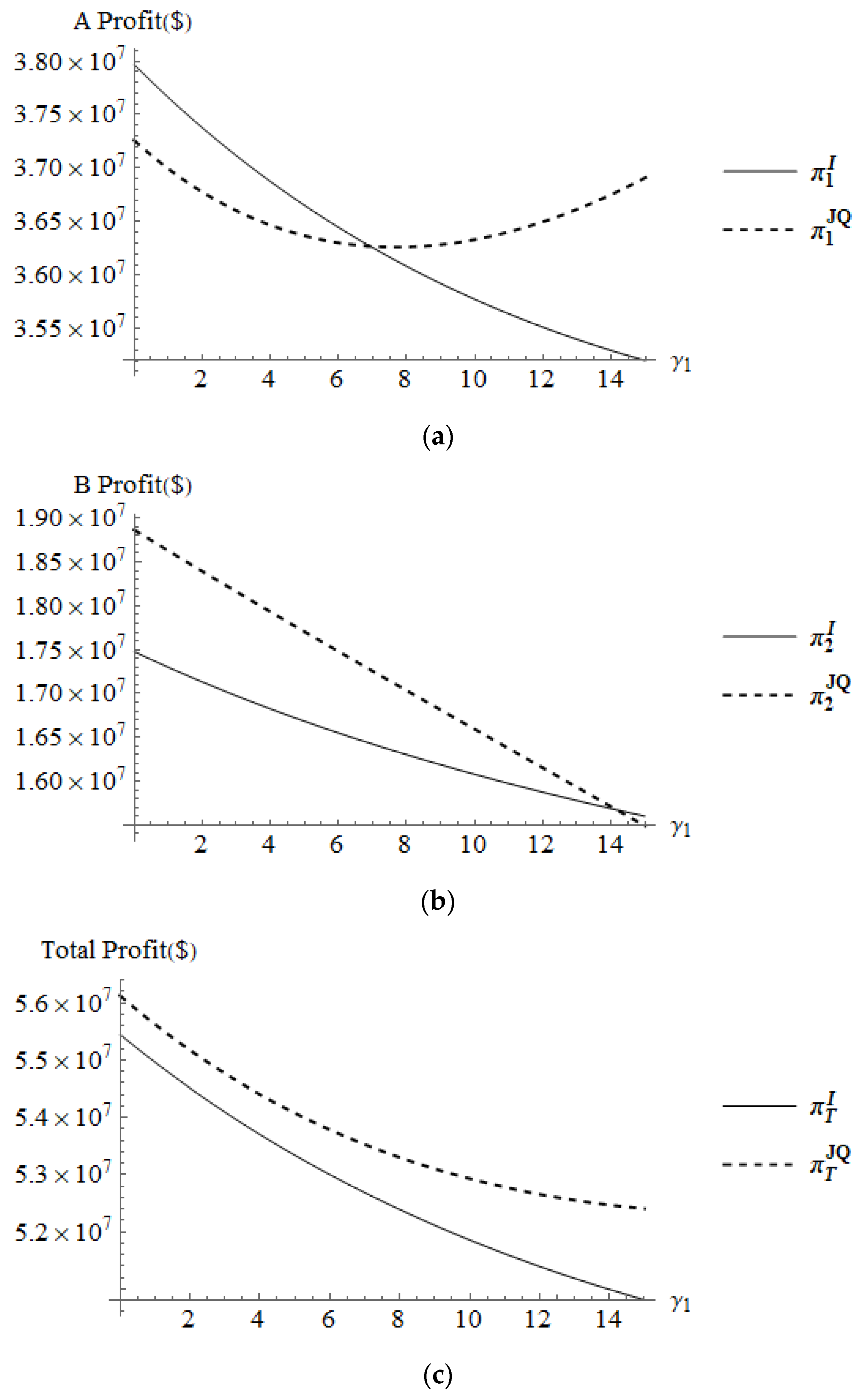
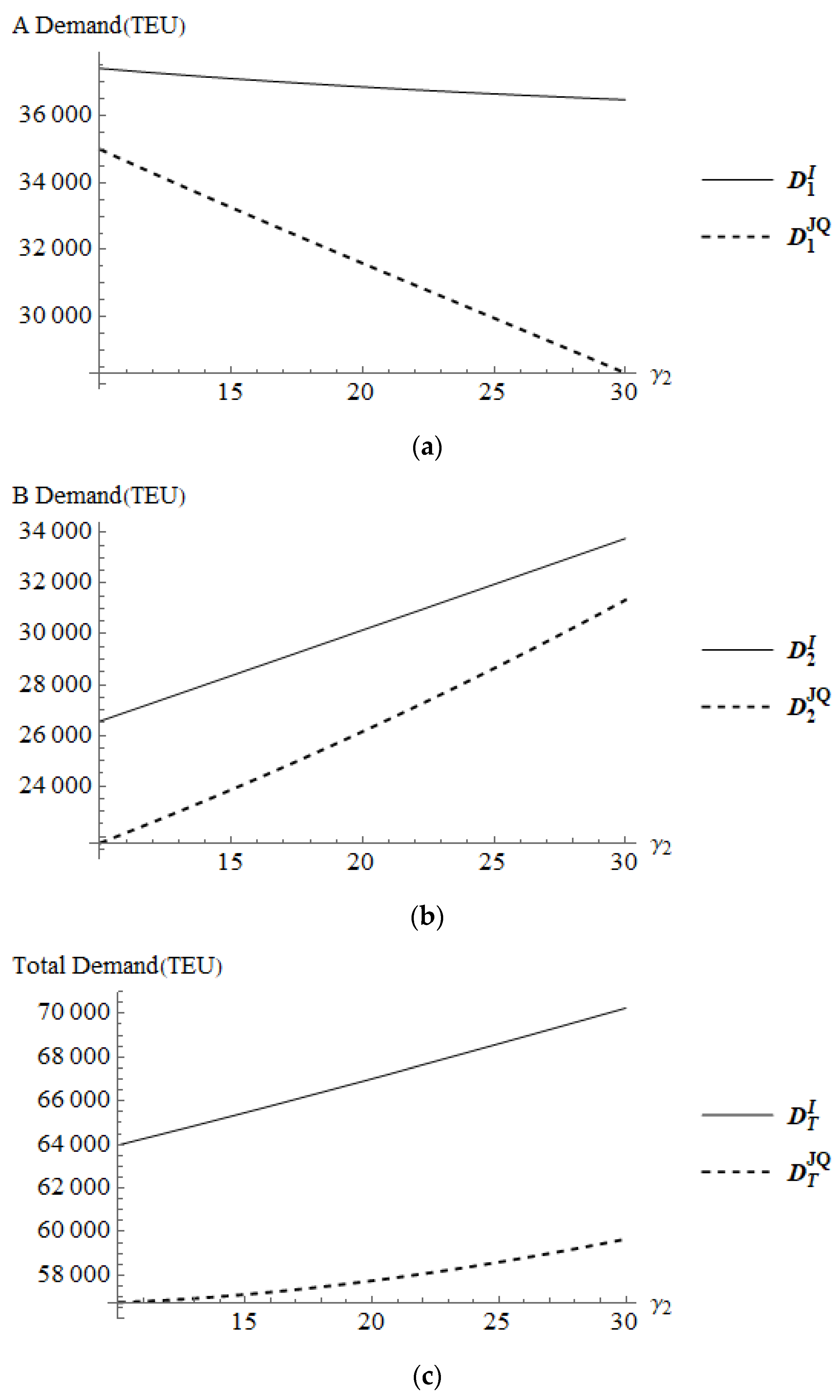
4.2.1. The Relative Freight Sensitivities on the Competition Intensity Coefficients
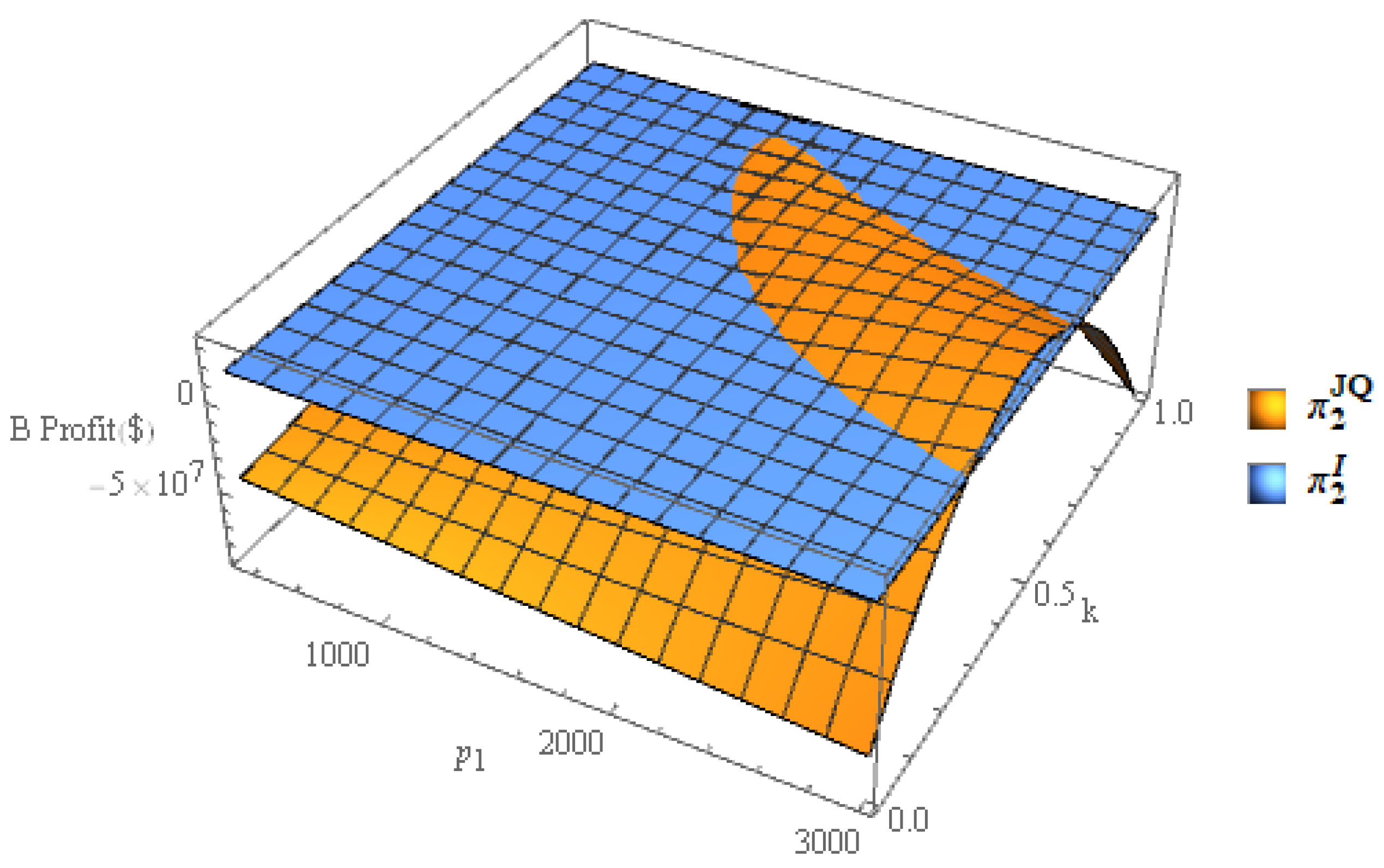
4.2.2. The Profit Sensitivities on the Competition Intensity Coefficients
4.2.3. The Demand Sensitivities on the Competition Intensity Coefficients
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Munim, Z.H.; Schramm, H.J. Forecasting container shipping freight rates for the Far East—Northern Europe trade lane. Marit. Econ. Logist. 2017, 19, 106–125. [Google Scholar] [CrossRef]
- Gu, Y.M.; Dong, X.X.; Chen, Z.X. The relation between the international and China shipping markets. Res. Transp. Bus. Manag. 2020, 34, 100427. [Google Scholar] [CrossRef]
- Park, B.I.; Min, H. A game-theoretic approach to evaluating the competitiveness of container carriers in the Northeast Asian shipping market. Asia Pac. J. Mark. Logist. 2017, 29, 854–869. [Google Scholar] [CrossRef]
- Fan, L.X.; Zhang, S.J.; Yin, J.B. Structural Analysis of Shipping Fleet Capacity. J. Adv. Transp. 2018, 2018, 3854090. [Google Scholar] [CrossRef]
- Mankowski, C.; Charlampowicz, J. Managing Maritime Container Ports’ Sustainability: A Reference Model. Sustainability 2021, 13, 10030. [Google Scholar] [CrossRef]
- Jerebic, V.; Pavlin, S. Global Economy Crisis and Its Impact on Operational Container Carrier’s Strategy. Promet-Traffic Transp. 2018, 30, 187–194. [Google Scholar] [CrossRef]
- Cao, X.; Yang, Z.Y.; Hong, W.C.; Xu, R.Z.; Wang, Y.T. Optimizing Berth-quay Crane Allocation considering Economic Factors Using Chaotic Quantum SSA. Appl. Artif. Intell. 2022, 36, 2073719. [Google Scholar] [CrossRef]
- Charlampowicz, J. Market Concentration of Strategic Alliances Members in the Maritime Container Shipping Market on Trade Lanes Passing across the Atlantic and the Pacific—Selected Issues. In Proceedings of the International Conference on Traffic and Transport Engineering (Ictte 2018), Belgrade, Serbia, 2–28 September 2018; pp. 373–377. [Google Scholar]
- Zheng, S.Y.; Luo, M.F. Competition or cooperation? Ports’ strategies and welfare analysis facing shipping alliances. Transp. Res. Part E Logist. Transp. Rev. 2021, 153, 102429. [Google Scholar] [CrossRef]
- Choi, T.M.; Chung, S.H.; Zhuo, X.P. Pricing with risk sensitive competing container shipping lines: Will risk seeking do more good than harm? Transp. Res. B Methodol. 2020, 133, 210–229. [Google Scholar] [CrossRef]
- Alkhoori, O.; Hassan, A.; Almansoori, O.; Debe, M.; Salah, K.; Jayaraman, R.; Arshad, J.; Rehman, M.H.U. Design and Implementation of CryptoCargo: A Blockchain-Powered Smart Shipping Container for Vaccine Distribution. IEEE Access 2021, 9, 53786–53803. [Google Scholar] [CrossRef]
- Allen, D.W.E.; Berg, C.; Davidson, S.; Novak, M.; Potts, J. International policy coordination for blockchain supply chains. Asia Pac. Policy Stud. 2019, 6, 367–380. [Google Scholar] [CrossRef]
- Bae, H.S. The Interaction Effect of Information Systems of Shipping and Logistics Firms and Managers’ Support for Blockchain Technology on Cooperation with Shippers for Sustainable Value Creation. Sustainability 2021, 13, 4493. [Google Scholar] [CrossRef]
- Chiao, Y.C.; Lin, C.C.; Huang, C.J. Competing and cooperating globally: How firms’ multimarket contact relates to joint price elevation in coopetition networks. J. Bus. Ind. Mark. 2020, 36, 1678–1691. [Google Scholar] [CrossRef]
- Chen, J.H.; Ye, J.; Zhuang, C.L.; Qin, Q.D.; Shu, Y.Q. Liner shipping alliance management: Overview and future research directions. Ocean Coast. Manag. 2022, 219, 106039. [Google Scholar] [CrossRef]
- Do, T.M.H.; Park, G.K.; Choi, K.H.; Yang, X.F. The application of uncertain three-player two-stage game to the competition among shipping alliances. J. Shipp. Transp. Logist. 2021, 13, 600–623. [Google Scholar] [CrossRef]
- Chiu, R.H.; Wang, D.H. Collaboration Enhances Utilization of Production Factors in Container Shipping Industry. J. Mar. Sci. Technol. 2019, 27, 81–90. [Google Scholar]
- Tan, Z.J.; Meng, Q.; Wang, F.; Kuang, H.B. Strategic integration of the inland port and shipping service for the ocean carrier. Transp. Res. Part E Logist. Transp. Rev. 2018, 110, 90–109. [Google Scholar] [CrossRef]
- Charlampowicz, J. Supply Chain Efficiency on the Maritime Container Shipping Markets—Selected Issues. In Proceedings of the 18th International Scientific Conference Business Logistics in Modern Management, Osijek, Croatia, 11–12 October 2018; pp. 357–368. [Google Scholar]
- Charlampowicz, J. Measurement of Supply Chain Efficiency—Selected Issues for Research and Applications. In Proceedings of the 17th International Scientific Conference Business Logistics in Modern Management, Osijek, Croatia, 12–13 October 2017; pp. 471–484. [Google Scholar]
- Gonzalez-Laxe, F.; Novo-Corti, I.; Pociovalisteanu, D.M. New Maritime Alliances and Competition in a New Economic Environment. Promet-Traffic Transp. 2016, 28, 311–320. [Google Scholar] [CrossRef]
- Wang, C.X.; Wang, L.L. Green investment and vertical alliances in the maritime supply chain. Environ. Dev. Sustain. 2022. [Google Scholar] [CrossRef]
- Tran, N.K. Market structure and horizontal growth strategies—A case study of the container shipping industry. Ger. Econ. Rev. 2022, 23, 3. [Google Scholar] [CrossRef]
- Ma, H.L.; Wong, C.W.H.; Leung, L.C.; Chung, S.H. Facility sharing in business-to-business model: A real case study for container terminal operators in Hong Kong port. Int. J. Prod. Econ. 2020, 221, 107483. [Google Scholar] [CrossRef]
- Tijan, E.; Jovic, M.; Aksentijevic, S.; Pucihar, A. Digital transformation in the maritime transport sector. Technol. Forecast. Soc. Chang. 2021, 170, 120879. [Google Scholar] [CrossRef]
- Jiang, Y.; Xu, X.L.; Gao, H.H.; Rajab, A.D.; Xiao, F.; Wang, X.H. LBlockchainE: A Lightweight Blockchain for Edge IoT-Enabled Maritime Transportation Systems. IEEE Trans. Intell. Transp. Syst. 2022, 1–15. [Google Scholar] [CrossRef]
- Sangeerth, P.S.; Lakshmy, K.V. Blockchain based Smart Contracts in Automation of Shipping Ports. In Proceedings of the 6th International Conference on Inventive Computation Technologies (Icict 2021), Coimbatore, India, 20–22 January 2021; pp. 1248–1253. [Google Scholar]
- Pu, S.Y.; Lam, J.S.L. Blockchain adoptions in the maritime industry: A conceptual framework. Marit. Policy Manag. 2021, 48, 777–794. [Google Scholar] [CrossRef]
- Li, L.; Zhou, H.G. A survey of blockchain with applications in maritime and shipping industry. Inf. Syst. E-Bus. Manag. 2021, 19, 789–807. [Google Scholar] [CrossRef]
- Wong, S.; Yeung, J.K.W.; Lau, Y.Y.; So, J. Technical Sustainability of Cloud-Based Blockchain Integrated with Machine Learning for Supply Chain Management. Sustainability 2021, 13, 8270. [Google Scholar] [CrossRef]
- Ahn, Y.G.; Kim, T.; Kim, B.R.; Lee, M.K. A Study on the Development Priority of Smart Shipping Items-Focusing on the Expert Survey. Sustainability 2022, 14, 6892. [Google Scholar] [CrossRef]
- Hvolby, H.H.; Steger-Jensen, K.; Bech, A.; Vestergaard, S.; Svensson, C.; Neagoe, M. Information Exchange and Block Chains in Short Sea Maritime Supply Chains. Procedia Comput. Sci. 2021, 181, 722–729. [Google Scholar] [CrossRef]
- Pu, S.Y.; Lam, J.S.L. A game theoretic approach of optimal adoption time of blockchain: A case of ship operators. Comput. Ind. Eng. 2022, 169, 108219. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, P.; Wu, B.; Wan, C.P.; Yang, Z.L. A trustable architecture over blockchain to facilitate maritime administration for MASS systems. Reliab. Eng. Syst. Saf. 2022, 219, 108246. [Google Scholar] [CrossRef]
- Baygin, M.; Yaman, O.; Baygin, N.; Karakose, M. A blockchain-based approach to smart cargo transportation using UHF RFID. Expert Syst. Appl. 2022, 188, 116030. [Google Scholar] [CrossRef]
- Hu, Z.H.; Dong, Y.J. Evolutionary Game Models of Cooperative Strategies in Blockchain-Enabled Container Transport Chains. Asia-Pac. J. Oper. Res. 2022, 39, 2140029. [Google Scholar] [CrossRef]
- Sousa, C.M.P.; Bradley, F. Antecedents of international pricing adaptation and export performance. J. World Bus. 2008, 43, 307–320. [Google Scholar] [CrossRef]
- Sabri, O.; Djedidi, A.; Hani, M. When does coopetition affect price unfairness perception? The roles of market structure and innovation. J. Bus. Ind. Mark. 2021, 36, 209–229. [Google Scholar] [CrossRef]
- Hani, M.; Dagnino, G.B. Global network coopetition, firm innovation and value creation. J. Bus. Ind. Mark. 2020, 36, 1962–1974. [Google Scholar] [CrossRef]
- Sun, Y.Q.; Wu, Z.P.; Zhu, W.S. When do firms benefit from joint price and lead-time competition? Eur. J. Oper. Res. 2022, 302, 497–517. [Google Scholar] [CrossRef]
- Lu, L.; Liu, Z.X.; Qi, X.T. Coordinated price quotation and production scheduling for uncertain order inquiries. IIE Trans. 2013, 45, 1293–1308. [Google Scholar] [CrossRef]
- Oner-Kozen, M.; Minner, S. Dynamic pricing, leadtime quotation and due date based priority dispatching. Int. J. Prod. Res. 2018, 56, 5118–5130. [Google Scholar] [CrossRef]
- Zheng, W.; Li, B.; Song, D.P. Effects of risk-aversion on competing shipping lines’ pricing strategies with uncertain demands. Transp. Res. B Methodol. 2017, 104, 337–356. [Google Scholar] [CrossRef]
- Liu, M.M.; Ma, Y.H.; Song, L.; Liu, C.Y. Understanding the game behavior with sentiment and unequal status in cooperation network. Knowl.-Based Syst. 2021, 212, 106588. [Google Scholar] [CrossRef]
- Yang, J.Q.; Zhang, X.M.; Zhang, H.Y.; Liu, C. Cooperative Inventory Strategy in a Dual-Channel Supply Chain with Transshipment Consideration. Int. J. Simul. Model. 2016, 15, 365–376. [Google Scholar] [CrossRef]
- Quan, T. Research on the Cooperative Game of Manufacturing Industry Ecological Environment Governance on Wuhan City Circle of China. In Proceedings of the 11th International Conference on Innovation and Management, Vaasa, Finland, 17–19 November 2014; pp. 147–151. [Google Scholar]
- Song, D.P.; Dong, J.X. Cargo routing and empty container repositioning in multiple shipping service routes. Transp. Res. B Methodol. 2012, 46, 1556–1575. [Google Scholar] [CrossRef]
- Du, Y.Q.; Chen, Q.S.; Quan, X.W.; Long, L.; Fung, R.Y.K. Berth allocation considering fuel consumption and vessel emissions. Transp. Res. E Logist. 2011, 47, 1021–1037. [Google Scholar] [CrossRef]
- Lee, C.-Y.; Tang, C.S.; Yin, R.; An, J. Fractional Price Matching Policies Arising from the Ocean Freight Service Industry. Prod Oper Manag 2015, 24, 1118–1134. [Google Scholar] [CrossRef]
- Chen, R.; Dong, J.-X.; Lee, C.-Y. Pricing and competition in a shipping market with waste shipments and empty container repositioning. Transp. Res. B Methodol. 2016, 85, 32–55. [Google Scholar] [CrossRef]





| Parameters | Actual Meanings | Units |
|---|---|---|
| ξ | The total demand forecast of container shipping blockchain market | TEU |
| The expected market demand share of SLA | TEU | |
| The expected market demand share of SLB | TEU | |
| The freight sensitivity coefficient for SLA | TEU/USD (TEU per dollar) | |
| The freight sensitivity coefficient for SLB | TEU/USD (TEU per dollar) | |
| The freight of SLA | USD | |
| The freight of SLB | USD | |
| The benchmark freight of container shipping blockchain market | USD | |
| The competition intensity of SLA from SLB | TEU/USD (TEU per dollar) | |
| The competition intensity of SLB from SLA | TEU/USD (TEU per dollar) | |
| The unit cost of SLA | USD | |
| The unit cost of SLB | USD | |
| The container shipping demand of SLA | TEU | |
| The container shipping demand of SLB | TEU | |
| The profit of SLA | USD | |
| The profit of SLB | USD | |
| The utility of SLA | USD | |
| The utility of SLB | USD |
| Parameters | Meaning and Description | SLA (The Larger Shipping Line) (i = 1) | SLB (The Smaller Shipping Line) (i = 2) | Parameter and Variable Units |
|---|---|---|---|---|
| The expected market demand share of the shipping lines. ( refers to the expected market demand share of SLA. refers to the expected market demand share of SLB.) | 0.6 | 0.4 | % | |
| The nominal freight sensitivity coefficient for the shipping line. ( refers to the nominal freight sensitivity coefficient for SLA. refers to the nominal freight sensitivity coefficient for SLB.) | 30 | 35 | TEU/USD (TEU per dollar) | |
| The competition intensity of the shipping line. ( refers to the competition intensity of SLA from SLB. refers to the competition intensity of SLB from SLA.) | 10 | 15 | TEU/USD (TEU per dollar) | |
| The unit cost of the shipping line ( refers to the unit cost of SLA. refers to the unit cost of SLB.) | 350 | 600 | USD (dollar) | |
| The benchmark freight of container shipping blockchain market. | 1000 | USD (dollar) | ||
| ξ | The total demand forecast of container shipping blockchain market. | 80,000 | TEU | |
| According to the parameter substitution relationship, for SLA , and for SLB . The actual freight sensitivity coefficient for the shipping line. ( refers to the actual freight sensitivity coefficient for SLA. refers to the actual freight sensitivity coefficient for SLB.) | 40 | 50 | TEU/USD (TEU per dollar) | |
| According to the parameter substitution relationship, for SLA , and for SLB The actual market share for the shipping line. ( refers to the actual market share for SLA. refers to the actual market share for SLB.) | 78,000 | 67,000 | TEU/USD (TEU per dollar) | |
| Initial Theoretical Equilibrium Strategy | Joint Quotation Strategy | |||
|---|---|---|---|---|
| Decision Maker | SLA | SLB | SLA | SLB |
| Freight (USD) | 1314 | 1167 | 1442 | 1296 |
| Demand (1000 TEU) | 37.1 | 28.4 | 33.3 | 23.9 |
| Total Demand (1000 TEU) | 65.5 | 57.1 | ||
| Profit (1000 USD) | 35,775 | 16,080 | 36,333 | 16,594 |
| Total Profit (1000 USD) | 51,855 | 52,928 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Gu, Y. Approach to an Equivalent Freight-Based Sustainable Joint-Quotation Strategy for Shipping Blockchain Alliance. Sustainability 2022, 14, 10441. https://doi.org/10.3390/su141610441
Zhang F, Gu Y. Approach to an Equivalent Freight-Based Sustainable Joint-Quotation Strategy for Shipping Blockchain Alliance. Sustainability. 2022; 14(16):10441. https://doi.org/10.3390/su141610441
Chicago/Turabian StyleZhang, Fa, and Yimiao Gu. 2022. "Approach to an Equivalent Freight-Based Sustainable Joint-Quotation Strategy for Shipping Blockchain Alliance" Sustainability 14, no. 16: 10441. https://doi.org/10.3390/su141610441
APA StyleZhang, F., & Gu, Y. (2022). Approach to an Equivalent Freight-Based Sustainable Joint-Quotation Strategy for Shipping Blockchain Alliance. Sustainability, 14(16), 10441. https://doi.org/10.3390/su141610441





