Assessment of Efficiency of Heat Transportation in Indirect Propane Refrigeration System Equipped with Carbon Dioxide Circulation Loop
Abstract
1. Introduction
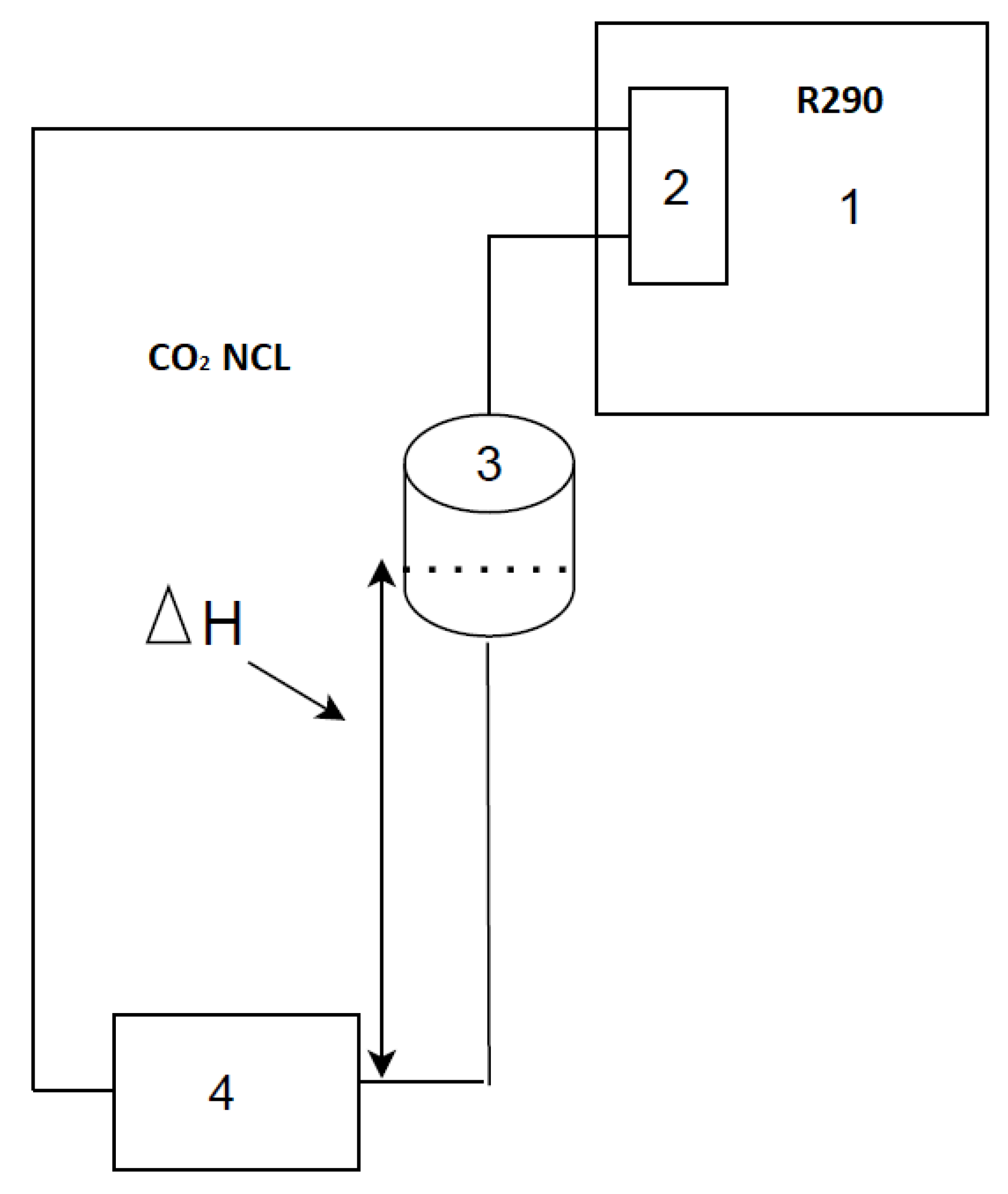
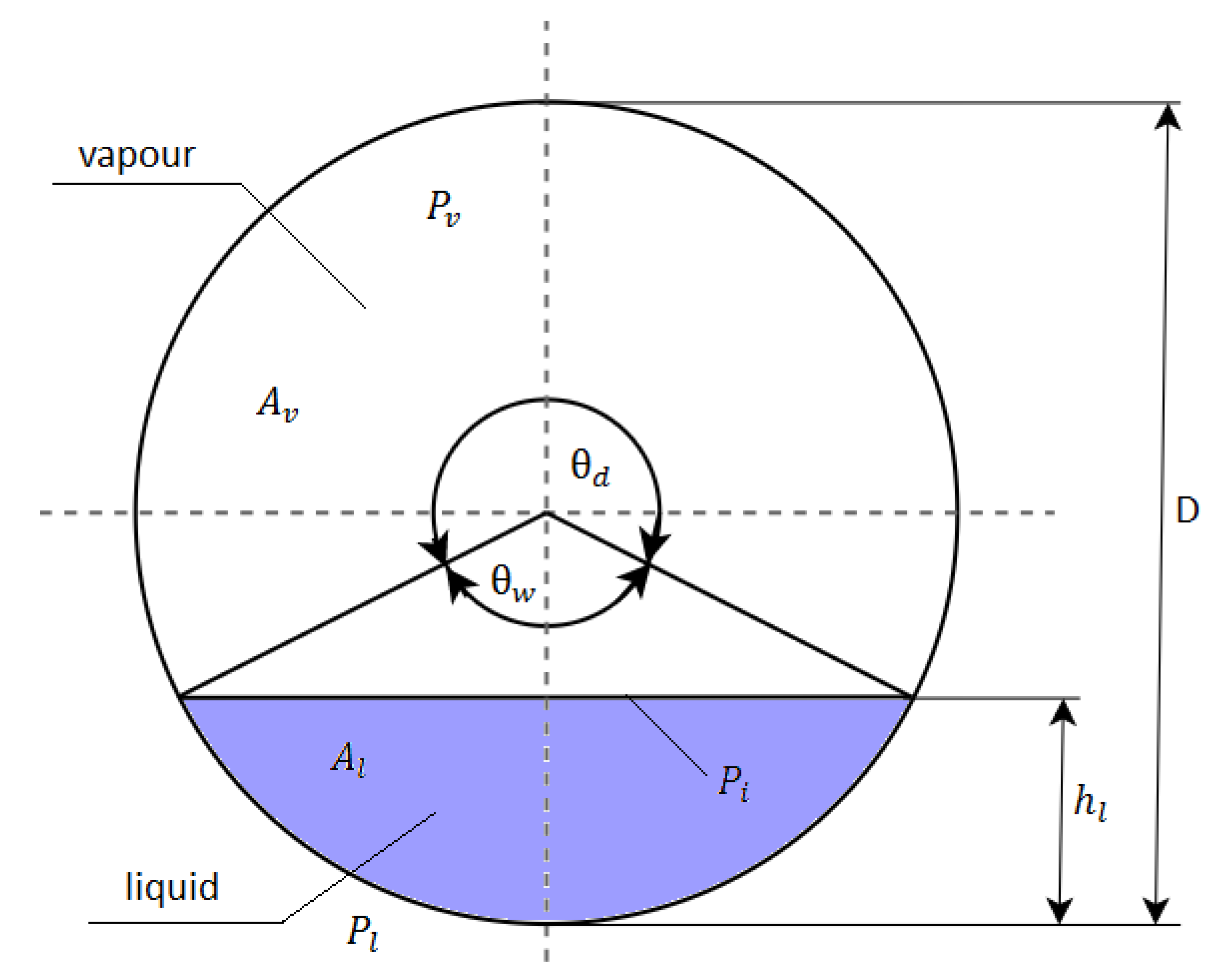
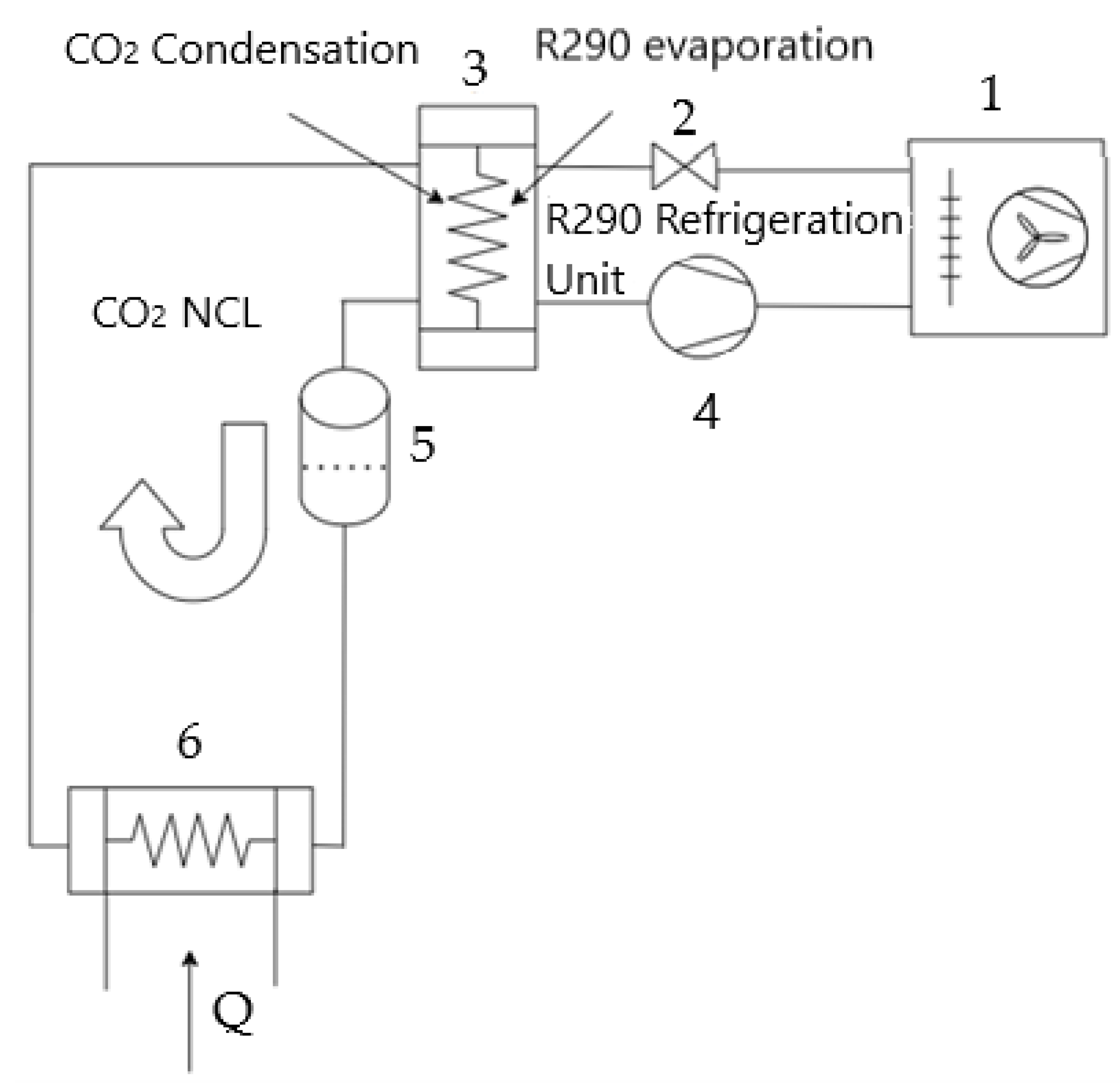
2. Calculation Model
3. Model Validation
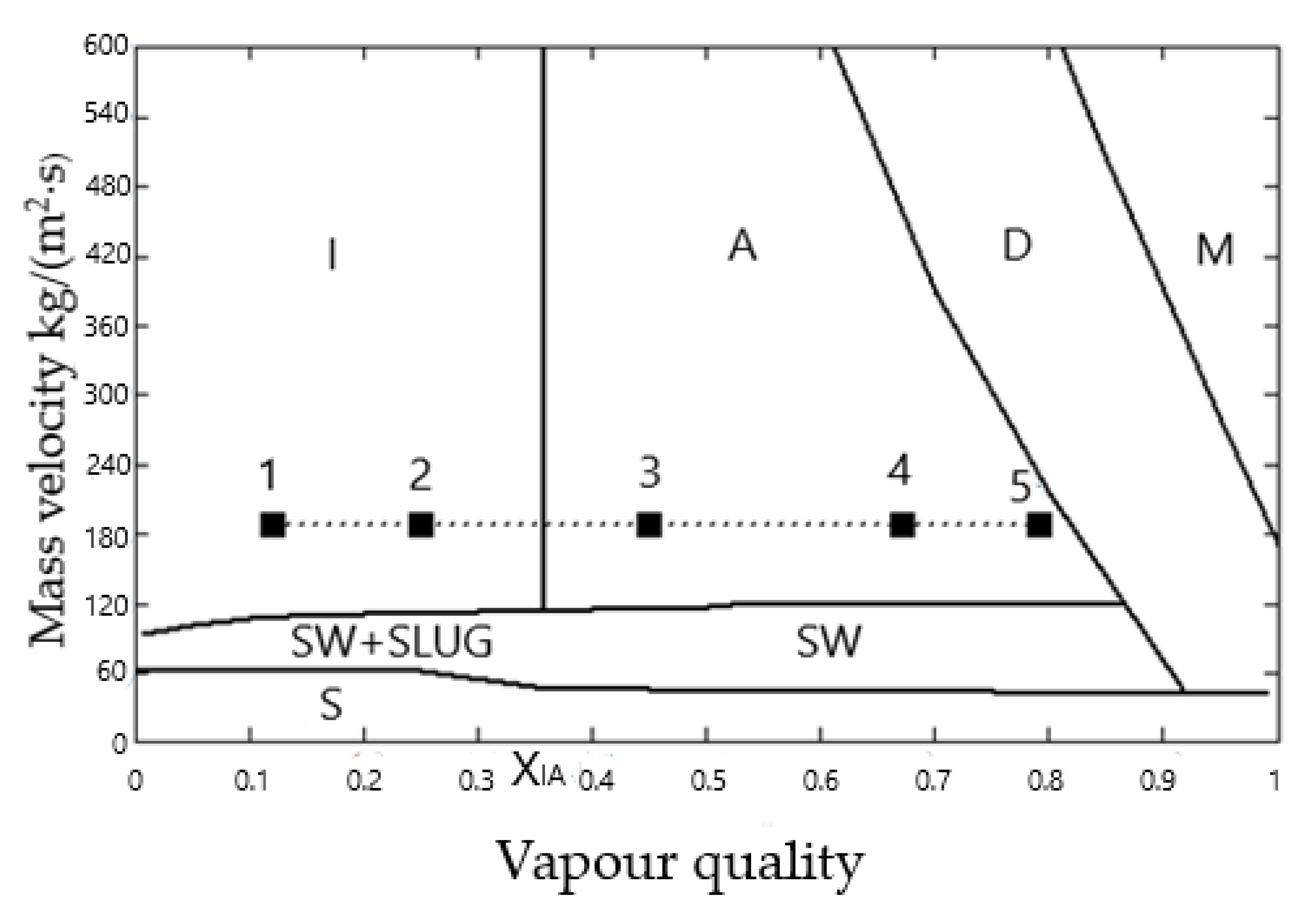
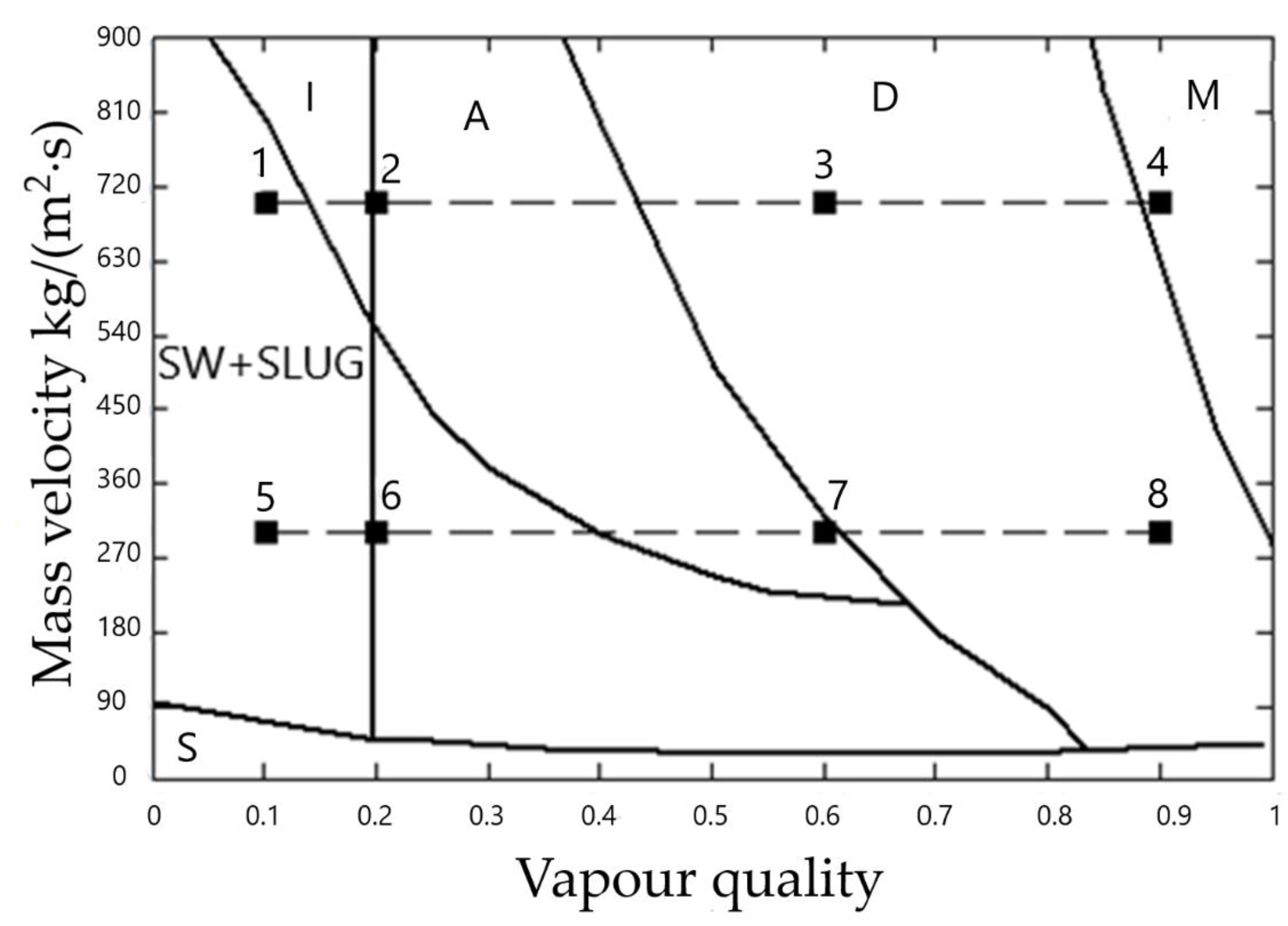
3.1. Validation of Two-Phase Flow Pattern Prediction
3.2. Validation for Thermal Performance Prediction
4. Results and Discussion
5. Conclusions
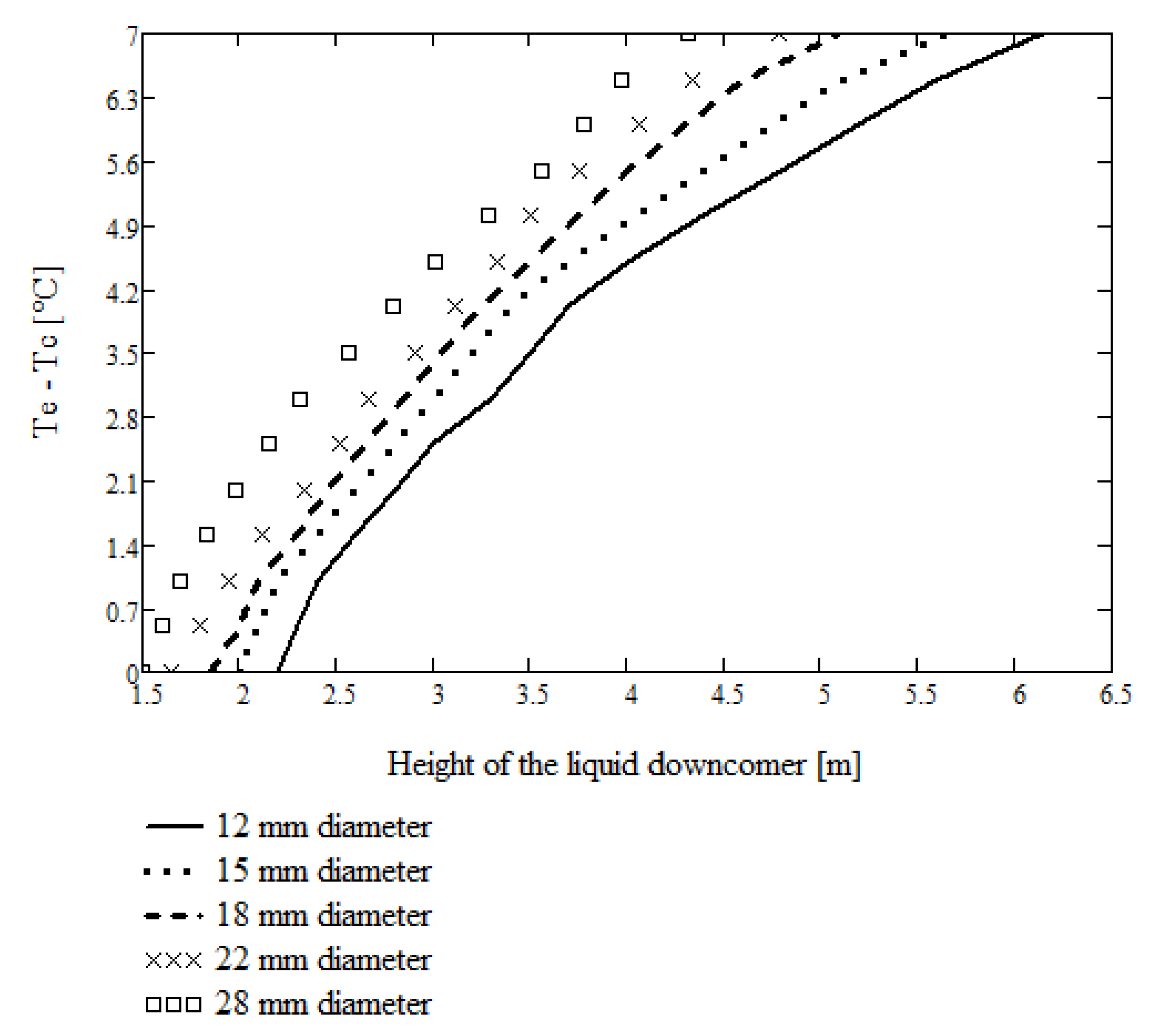
- An analytical model is presented for the design of refrigeration systems with a circulation loop. The model considers the local pressure drop that is particular to the geometry of the loop. The optimum height of the liquid downcomer can be determined, depending on the flow resistance of the entire loop and the diameter of the pipeline.
- The validation of experimental studies shows that the presented model shows reasonable agreement and can be applied to the design of various circulating loop systems. In the validation of two-phase flow pattern prediction, the points on the flow pattern maps overlap by 70% compared with the literature results.
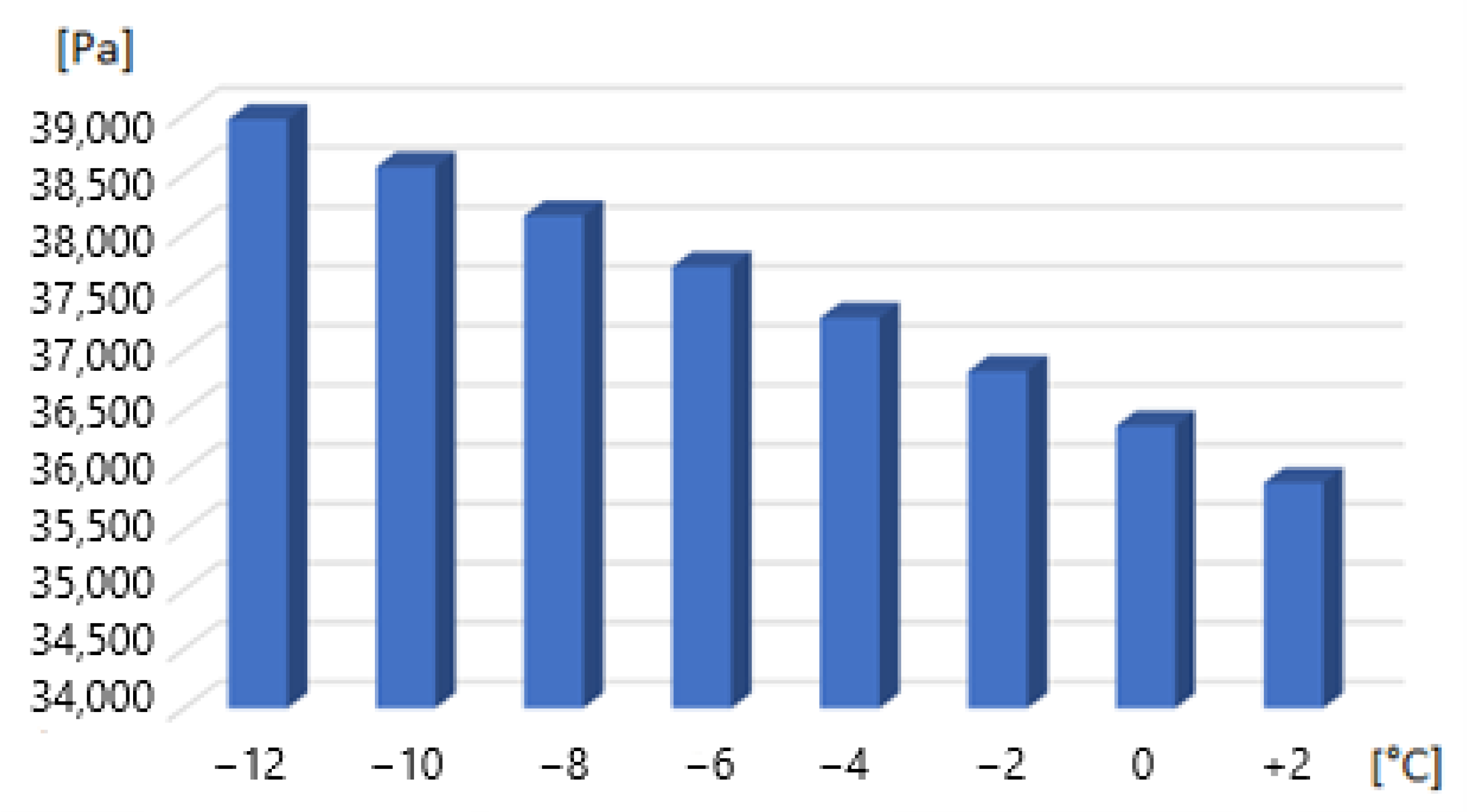
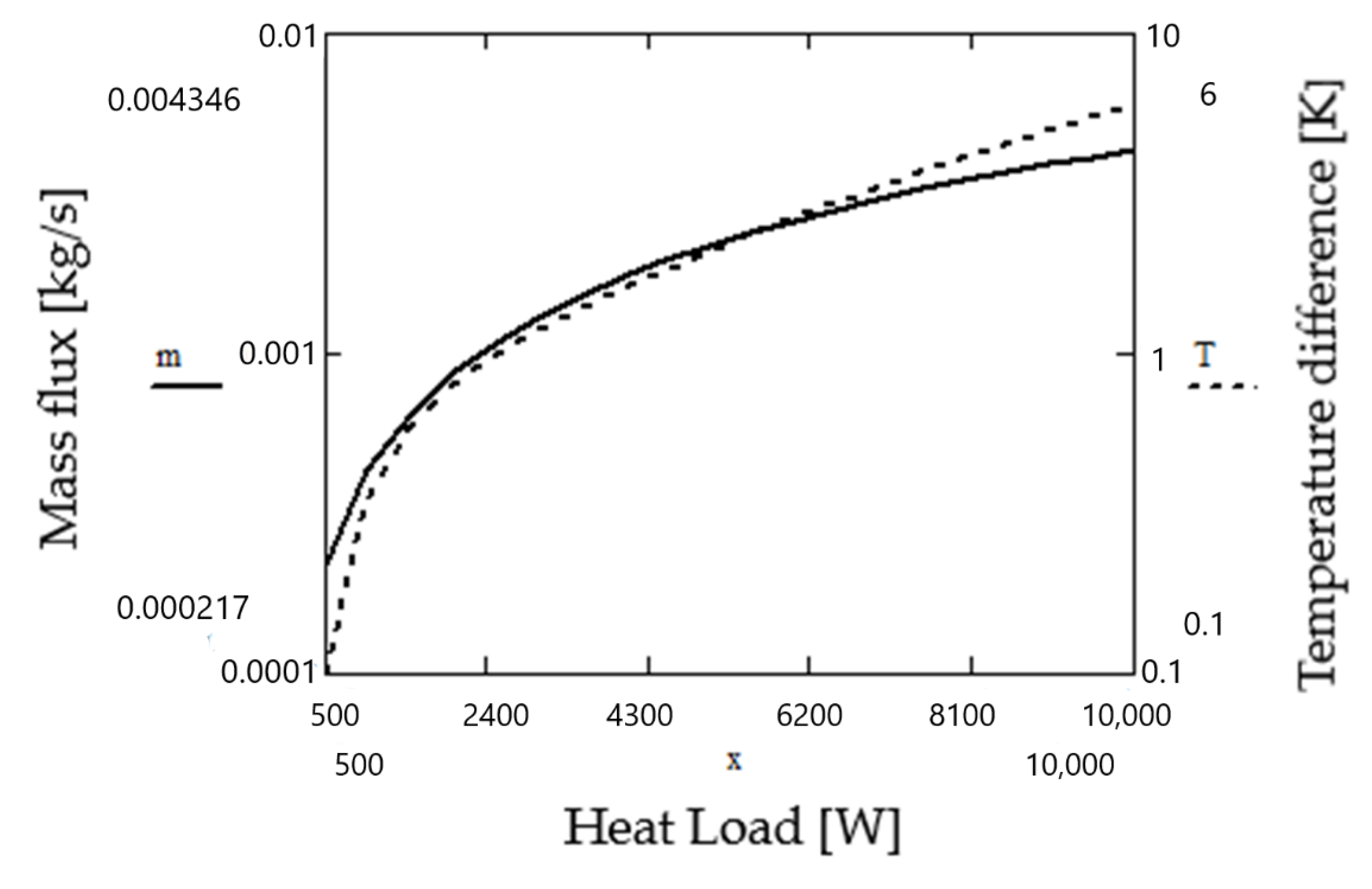
- It has been shown that as the mass flux of CO2 as a working fluid increases, the temperature difference between evaporation and condensation increases, and it becomes necessary to increase the height of the liquid downcomer or increase the diameter of the pipeline.
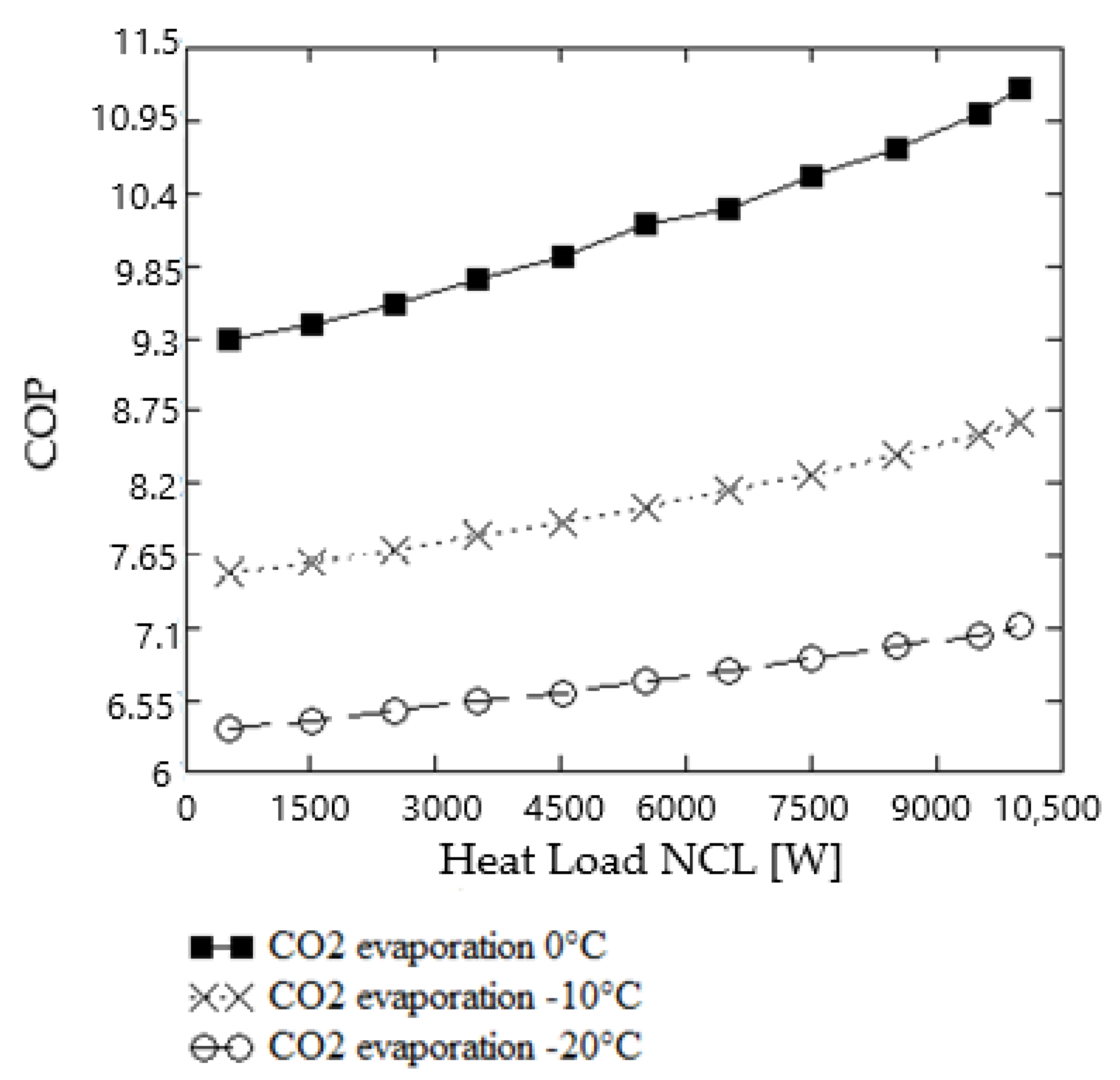
- The effect of a change in the refrigeration capacity of the circulating loop on the COP level of the coupled propane compressor refrigeration system was analysed for the first time. The highest COP was obtained for a CO2 evaporation temperature of 0 °C; then, the COP value was 9.3 for a thermal capacity of 0.5 kW and 11.2 for a thermal capacity of 10 kW. An up to 23% increase in system efficiency was found as the refrigeration capacity of the system increases. Therefore, operation of the indirect refrigeration system with a CO2 circulation loop should be avoided with a reduced refrigeration capacity.
- Raising the evaporation CO2 temperature in the circulation loop from −20 °C to 0 °C improves the COP of the entire indirect refrigeration system by about 50%. This is of significant importance in terms of the applicability of such systems.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | heat transfer surface area, |
| D | inlet diameter, m |
| hydraulic diameter, m | |
| Fr | Froude number |
| constant dependent on the angle of the channel extrusions | |
| g | gravitational acceleration, |
| G | mass flux density (mass velocity), kg/(m2⋅s) |
| single plate width, m | |
| h | specific enthalpy, J/kg |
| H | height of the exchanger plate, m |
| k | heat transfer coefficient, W/ |
| L | length of pipeline, m |
| mass flux, kg/s | |
| number of plates of heat exchanger | |
| number of parallel fluid streams | |
| Nu | Nusselt number |
| Pr | Prandtl number |
| R | thermal resistance in the condenser, K/W |
| Re | Reynolds number |
| distance between plates, m | |
| heat exchanger heat transfer surface area, | |
| t | saturation temperature, °C |
| Q | thermal capacity, W |
| w | velocity, m/s |
| We | Weber number |
| x | two-phase flow quality |
| Lockhart–Martinelli parameter | |
| Greek Symbols | |
| turbulence damping factor | |
| forced turbulence coefficient | |
| coefficient of resistance to flow in a smooth channel | |
| ∆H | liquid downcomer, m |
| ∆p | pressure drop, Pa |
| frictional pressure losses in single-phase fluid flow, Pa | |
| ∆T | temperature difference, K |
| pressure loss ratio | |
| ɛ | void fraction |
| dynamic viscosity, Pa⋅s | |
| ⍴ | density, |
| ratio of liquid and gas density | |
| two-phase flow multiplier | |
| local loss coefficient | |
| Subscripts | |
| av | average |
| c | condenser |
| e | evaporator |
| in | inlet |
| ll | flow inside the straight sections of the loop |
| lt | the local flow resistances |
| out | outlet |
| Abbreviations | |
| COP | coefficient of performance |
| FCL | forced circulation loop |
| GWP | global warming potential |
| HFC | hydrofluorocarbons |
| NCL | natural circulation loop |
| ODP | ozone depletion potential |
References
- United Nation. Kigali Amendment to the Montreal Protocol on Substances that Deplete the Ozone Layer; Miscellaneous Series No. 2; United Nation: New York, NY, USA, 2016.
- Polonara, F.; Kuijpers, L.; Peixoto, R. Potential impacts of the Montreal Protocol in Kigali Amendment to the choice of refrigerant alternatives. Int. J. Heat Technol. 2017, 35, S1–S8. [Google Scholar] [CrossRef]
- Purohit, P.; Borgford-Parnell, N.; Klimont, Z.; Höglund-Isaksson, L. Achieving Paris climate goals calls for increasing ambition of the Kigali Amendment. Nat. Clim. Change 2022, 12, 339–342. [Google Scholar] [CrossRef]
- Al-Joboory, H.N.S. Experimental investigation of gravity-assisted wickless heat pipes (thermosyphons) at low heat inputs for solar application. Arch. Thermodyn. 2020, 41, 257–276. [Google Scholar]
- Allouhi, A.; Benzakour Amine, M.; Buker, M.S.; Kousksou, T.; Jamil, A. Forced-circulation solar water heating system using heat pipe-flat plate collectors: Energy and exergy analysis. Energy 2019, 180, 429–443. [Google Scholar] [CrossRef]
- Karampour, M.; Sawalha, S. State-of-the-Art Integrated CO2 Refrigeration System for Supermarkets: A Comparative Analysis. Int. J. Refrig. 2018, 86, 239–257. [Google Scholar] [CrossRef]
- Nisrene, M.A.; Puzhen, G.; Solomon, B. Natural circulation systems in nuclear reactors: Advantages and challenges. IOP Conf. Ser. Earth Environ. Sci. 2020, 467, 012077. [Google Scholar]
- Wang, S.; Lin, U.C.; Wang, G.; Ishii, M. Experimental investigation on flashing-induced flow instability in a natural circulation scaled-down test facility. Ann. Nucl. Energy 2022, 171, 109023. [Google Scholar] [CrossRef]
- Bieliński, H.; Mikielewicz, J. Application of a two-phase thermosyphon loop with minichannels and a minipump in computer cooling. Arch. Thermodyn. 2016, 37, 3–16. [Google Scholar] [CrossRef][Green Version]
- Tong, Z.; Zang, G. Effect of the diameter of riser and downcomer on an CO2 thermosyphon loop used in data centre. Appl. Therm. Eng. 2021, 182, 116101. [Google Scholar] [CrossRef]
- Usman, H.; Ali, H.M.; Arshad, A.; Ashraf, M.J.; Khushnood, S.; Janjua, M.M.; Kazi, S.N. An experimental study of pcm based finned and un-finned heat sinks for passive cooling of electronics. Heat Mass Transf. 2018, 54, 3587. [Google Scholar] [CrossRef]
- Zhang, X.W.; Niu, X.D.; Yamaguchi, H.; Iwamoto, Y. Study on a supercritical CO2 solar water heater system induced by the natural circulation. Adv. Mech. Eng. 2018, 10, 1–15. [Google Scholar] [CrossRef]
- Amaya, A.; Scherer, J.; Muir, J.; Patel, M.; Higgins, B. GreenFire Energy Closed-Loop Geothermal Demonstration using Supercritical Carbon Dioxide as Working Fluid. In Proceedings of the 45th Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 10–12 February 2020. [Google Scholar]
- Baek, S.; Jung, Y.; Cho, K. Cryogenic two-phase natural circulation loop. Cryogenics 2020, 111, 103188. [Google Scholar] [CrossRef]
- Cobanoglu, N.; Dogacan Koca, H.; Mete Genc, A.; Haktan Karadeniz, Z.; Ekren, O. Investigation of Performance Improvement of a Household Freezer by Using Natural Circulation Loop. Sci. Technol. Built Environ. 2021, 27, 85–97. [Google Scholar] [CrossRef]
- Kumar, A.; Khalid, S. CO2 Based Natural Circulation Loops for Domestic Refrigerators. Saudi J. Eng. Technol. 2019, 4, 192–200. [Google Scholar]
- Andrzejczyk, R.; Muszyński, T. The performance of H2O, R134a, SES36, ethanol, and HFE7100 two-phase closed thermosyphons for varying operating parameters and geometry. Arch. Thermodyn. 2017, 38, 3–21. [Google Scholar] [CrossRef]
- Bai, Y.; Wang, L.; Zhang, S.; Lin, X.; Peng, L.; Chen, H. Characteristic map of working mediums in closed loop two-phase thermosyphon: Thermal resistance and pressure. Appl. Therm. Eng. 2020, 174, 115308. [Google Scholar] [CrossRef]
- Thippeswamy, L.R.; Kumar, Y.A. Heat transfer enhancement using CO2 in a natural circulation loop. Sci. Rep. 2020, 10, 1507. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Liu, S.; Huang, Y. Analysis of Heat Transfer Deterioration and Natural Circulation Flow Characteristics of Supercritical Carbon Dioxide in A Simple Circulation Loop. 2022. Available online: https://ssrn.com/abstract=4171532 (accessed on 10 July 2022).
- Deng, B.; Chen, L.; Zhang, X.; Jin, L. The flow transition characteristics of supercritical CO2 based closed natural circulation loop (NCL) system. Ann. Nucl. Energy 2019, 132, 134–148. [Google Scholar] [CrossRef]
- Wahidi, T.; Arunachala Chandavar, R.; Kumar Yadav, A. Supercritical CO2 flow instability in natural circulation loop: CFD analysis. Ann. Nucl. Energy 2021, 160, 108374. [Google Scholar] [CrossRef]
- Thimmaimah, S.; Wahidi, T.; Yadav, A.; Arun, M. Comparative computational appraisal of supercritical CO2-based natural circulation loop: Effect of heat-exchanger and isothermal wall. J. Therm. Anal. Calorim. 2020, 141, 2219–2229. [Google Scholar] [CrossRef]
- Thimmaimah, S.; Wahidi, T.; Yadav, A.; Arun, M. Numerical Instability Assessment of Natural Circulation Loop Subjected to Different Heating Conditions. In Recent Trends in Fluid Dynamics Research; Springer: Berlin/Heidelberg, Germany, 2022; pp. 249–262. [Google Scholar]
- Bai, Y.; Wang, L.; Zhang, S.; Lin, X.; Peng, L.; Chen, H. Numerical analysis of a closed loop two-phase thermosyphon under states of single-phase, two-phase, and supercritical. Int. J. Heat Mass Flow Transf. 2019, 135, 354–367. [Google Scholar] [CrossRef]
- Zhang, P.; Shi, W.; Li, X.; Wang, B.; Zhang, G. A performance evaluation index for two-phase thermosyphon loop used in HVAC systems. Appl. Therm. Eng. 2017, 17, 11577. [Google Scholar] [CrossRef]
- Zhang, P.; Yang, X.; Rong, X.; Zhang, D. Simulation on the thermal performance of two-phase thermosyphon loop with large height difference. Appl. Therm. Eng. 2019, 163, 114327. [Google Scholar] [CrossRef]
- Tong, Z.; Liu, X.H.; Jiang, Y. Three typical operating states of an R744 two-phase thermosyphon loop. Appl. Energy 2017, 206, 181–192. [Google Scholar] [CrossRef]
- Saikiran, A.P.; Banoth, P.; Maddali, R. Dynamic model of supercritical CO2 based natural circulation loops with fixed charge. Appl. Therm. Eng. 2020, 169, 114906. [Google Scholar]
- Tong, Z.; Liu, X.H.; Jiang, Y. Experimental study of the self-regulating performance of an R744 two-phase thermosyphon loop. Appl. Energy 2017, 186, 1–12. [Google Scholar] [CrossRef]
- Würfel, R.; Ostrowski, N. Experimental investigations of heat transfer and pressure drop during the condensation process within plate heat exchangers of the herringbone-type. Int. J. Therm. Sci. 2004, 24, 59–68. [Google Scholar] [CrossRef]
- McDonough, J.M. Lectures in Elementary Fluid Dynamics: Physics, Mathematics and Applications; University of Kentucky: Lexington, KY, USA, 2004. [Google Scholar]
- Thome, J.R.; El Hajal, J. Two-phase flow pattern map for evaporation in horizontal tubes: Latest version. In Proceedings of the First International Conference on Heat Transfer, Fluid Mechanics and Thermodynamics, Kruger Park, South Africa, 8–10 April 2002; pp. 182–188. [Google Scholar]
- Cheng, L.; Ribatski, G.; Quiben, J.M.; Thome, J.R. New prediction methods for CO2 evaporation inside tubes: Part I—A two-phase flow pattern map and a flow pattern based phenomenological model for two-phase flow frictional pressure drops. Int. J. Heat Mass Transf. 2008, 51, 111–124. [Google Scholar] [CrossRef]
- Kattan, N.; Thome, J.R.; Favrat, D. Flow boiling in horizontal tubes. Part 1: Development of a diabatic two-phase flow pattern map. J. Heat Transf. 1998, 120, 140–147. [Google Scholar] [CrossRef]
- Wojtan, L.; Ursenbacher, T.; Thome, J.R. Investigation of flow boiling in horizontal tubes: Part I—A new diabatic two-phase flow pattern map. Int. J. Heat Mass Transf. 2005, 48, 2955–2969. [Google Scholar] [CrossRef]
- Schmid, D.; Verlaat, B.; Petagna, P.; Revellin, R.; Schiffmann, J. Flow pattern observations and flow pattern map for adiabatic two-phase flow of carbon dioxide in vertical upward and downward direction. Exp. Therm. Fluid Sci. 2022, 131, 110526. [Google Scholar] [CrossRef]
- Hsieh, Y.Y.; Lin, T.F. Saturated flow boiling heat transfer and pressure drop of refrigerant R-410A flow in a vertical plate heat exchanger. Int. J. Heat Mass Transf. 2002, 45, 1033–1044. [Google Scholar] [CrossRef]
- Quiben, J.M.; Thome, J.R. Flow pattern based two-phase frictional pressure drop model for horizontal tubes. Part I: Diabatic and adiabatic experimental study. Int. J. Heat Fluid Flow 2007, 28, 1060–1072. [Google Scholar] [CrossRef]
- Park, C.Y.; Hrnjak, P.S. CO2 and R410A flow boiling heat transfer, pressure drop, and flow pattern at low temperatures in a horizontal smooth tube. Int. J. Refrig. 2007, 30, 166–178. [Google Scholar] [CrossRef]
- Flack, K.A.; Shultz, M.P. Roughness effects on wall-bounded turbulent flows. Phys. Fluids 2014, 26, 101305. [Google Scholar] [CrossRef]
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer, 6th ed.; Wiley: New York, NY, USA, 2006. [Google Scholar]
- Gasche, J.L. Carbon dioxide evaporation in a single micro-channel. J. Braz. Soc. Mech. Sci. Eng. 2006, 28, 69–83. [Google Scholar] [CrossRef]
- Ozawa, M.; Ami, T.; Ishihara, I.; Umekawa, H.; Matsumo, R.; Tanaka, Y.; Yamamoto, T.; Ueda, Y. Flow pattern and boiling heat transfer of CO2 in horizontal small-bore tubes. Int. J. Multiph. Flow 2009, 35, 699–709. [Google Scholar] [CrossRef]
- Mitrovic, J. Heat Exchangers—Basics Design Application; IntechOpen: London, UK, 2012. [Google Scholar]
- Yang, X.; Zhang, P.; Li, Y.; Zhang, D. A practical design method for two-phase thermosyphon loop based on approaching degree to “ideal cycle”. Appl. Therm. Eng. 2021, 182, 116059. [Google Scholar] [CrossRef]
- Khodabandeh, R. Heat transfer in the evaporator of an advanced two-phase thermosyphon loop. Int. J. Refrig. 2005, 28, 190–202. [Google Scholar] [CrossRef]
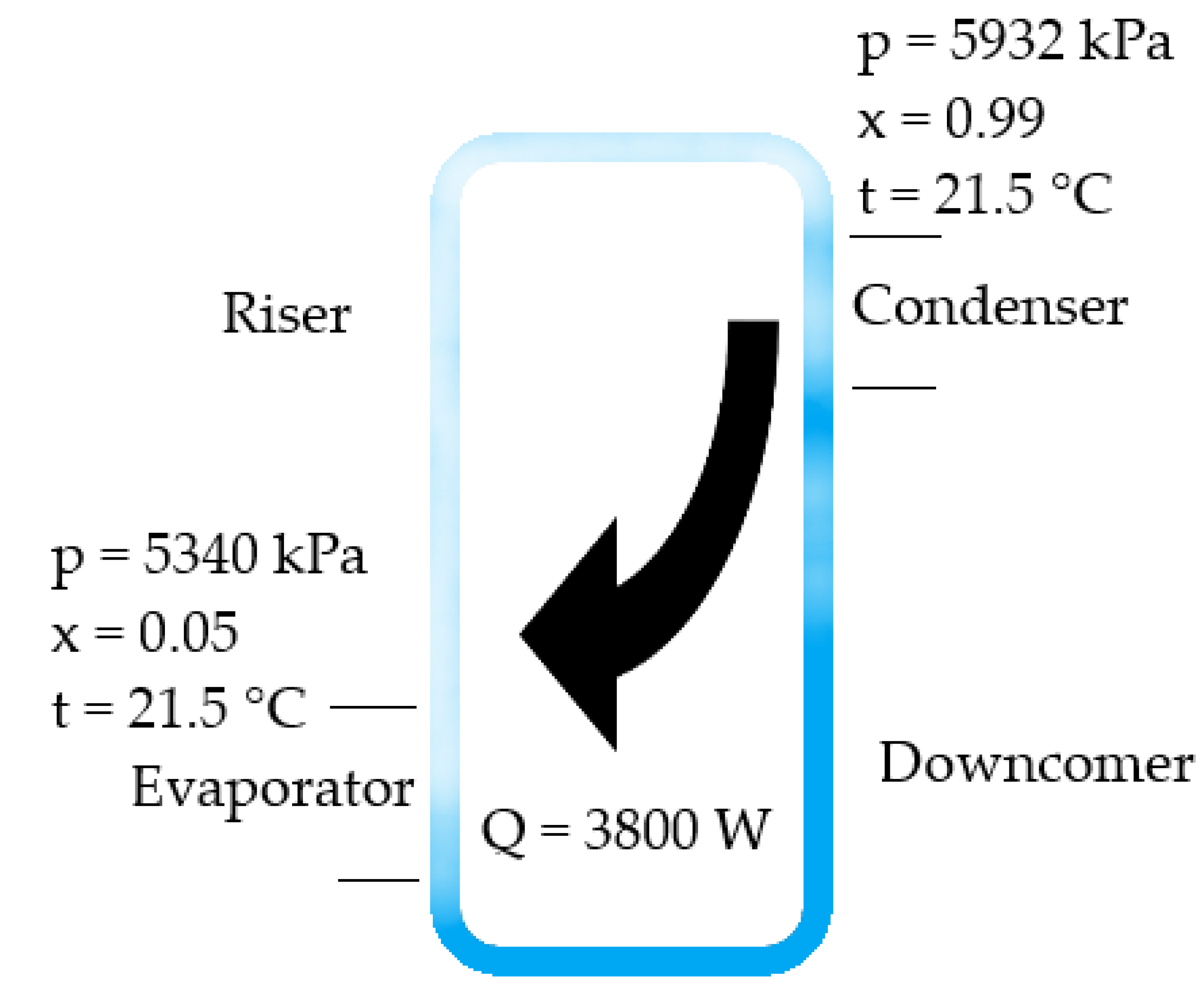
| Regular 90° flanged elbows | 0.30 |
| Regular 90° threaded elbows | 1.50 |
| Long radius 90° flanged elbows | 0.20 |
| Long radius 90° threaded elbows | 0.70 |
| Line flow flanged tees | 0.20 |
| Line flow threaded tees | 0.90 |
| Union threaded | 0.08 |
| CO2 Condenser | CO2 Evaporator | ||
|---|---|---|---|
| Angle of embossing of the channels of adjacent plates ϒ | 60°/30° | Angle of embossing of the channels of adjacent plates ϒ | 30°/30° |
| 0.10 | 0.10 | ||
| p | 0.30 | p | 0.40 |
| 1.0 | 0.86 | ||
| H [m] | 0.50 | H | 0.30 |
| [m] | 0.002 | 0.0018 | |
| Plate width [m] | 0.145 | Plate width | 0.150 |
| Heat transfer area [m2] | 1.015 | Heat transfer area | 1.80 |
| Predicted flow resistance depends on mass flux in terms of 0.005–0.05 kg/s [kPa] | 0.67–1.64 | Predicted flow resistance depends on mass flux in terms of 0.005–0.05 kg/s [kPa] | 3.59–10.26 |
| Q | Diameter of Pipe | Experimental Loop Height and Pressure Losses | Calculated Loop Height and Pressure Losses |
|---|---|---|---|
| 4000 W | 12.7 mm | 0.65 m; 7.83 kPa | 0.89 m; 10.72 kPa |
| 8000 W | 15.9 mm | 0.75 m; 9.04 kPa | 0.94 m; 11.33 kPa |
| 10,000 W | 19.1 mm | 0.40 m;4.82 kPa | 0.65 m; 7.83 kPa |
| Re | Pr | Nu | ΔT°C | |||||
| 14,820 | 2.23 | 0.029 | 2.98 | 3.59 | 170.5 | 5754 | 1543.2 | 1.67 |
| Parameters of the evaporation R290 side | ||||||||
| Re | Pr | Nu | ||||||
| 5710 | 1.75 | 0.036 | 2.99 | 3.59 | 76.13 | 2227 | ||
| side→−10 °C | ||||||||
| Re | Pr | Nu | ΔT °C | |||||
| 16,657 | 2.2 | 0.028 | 2.98 | 3.59 | 183.25 | 5613.9 | 1658.4 | 1.56 |
| Parameters of the evaporation R290 side | ||||||||
| Re | Pr | Nu | ||||||
| 6190 | 2.16 | 0.036 | 2.98 | 3.59 | 90.95 | 2509.2 | ||
| side→0 °C | ||||||||
| Re | Pr | Nu | ΔT °C | |||||
| 18,662 | 2.27 | 0.027 | 2.98 | 3.59 | 201.01 | 5549.38 | 1855.29 | 1.39 |
| Parameters of the evaporation R290 side | ||||||||
| Re | Pr | Nu | ||||||
| 6684 | 2.95 | 0.035 | 2.98 | 3.59 | 113.01 | 2993.92 | ||
| Evaporation Temperature of CO2 → −20 °C | |||||
|---|---|---|---|---|---|
| Heat Load of NCL [kW] | Mass Flux of CO2 [kg/s] | Evaporation Temperature of Propane [°C] | Mass Flux of Propane [kg/s] | Enthalpy Difference ∆h [kJ/kg] | Power of the Compressor P [kW] |
| 500 | 0.00177 | −21.37 | 0.00650 | 64.19 | 0.414 |
| 1500 | 0.00531 | −20.77 | 0.00652 | 62.86 | 0.410 |
| 2500 | 0.00885 | −20.07 | 0.00654 | 62.05 | 0.406 |
| 3500 | 0.01240 | −19.37 | 0.00655 | 61.23 | 0.401 |
| 4500 | 0.01593 | −18.67 | 0.00657 | 60.42 | 0.397 |
| 5500 | 0.01947 | −17.97 | 0.00658 | 59.61 | 0.392 |
| 6500 | 0.02301 | −17.17 | 0.00660 | 58.68 | 0.387 |
| 7500 | 0.02655 | −16.37 | 0.00661 | 57.75 | 0.382 |
| 8500 | 0.03009 | −15.57 | 0.00663 | 56.83 | 0.377 |
| 9500 | 0.03363 | −14.77 | 0.00665 | 55.91 | 0.372 |
| 10,000 | 0.03541 | −14.27 | 0.00666 | 55.33 | 0.369 |
| Evaporation temperature of CO2→ −10 °C | |||||
| Heat load of NCL [kW] | Mass Flux of CO2 [kg/s] | Evaporation temperature of propane [°C] | Mass flux of propane [kg/s] | Enthalpy difference ∆h [kJ/kg] | Power of the compressor P [kW] |
| 500 | 0.00193 | −11.24 | 0.00672 | 51.96 | 0.349 |
| 1500 | 0.00580 | −10.64 | 0.00673 | 51.29 | 0.345 |
| 2500 | 0.00967 | −9.94 | 0.00675 | 50.49 | 0.341 |
| 3500 | 0.01353 | −9.24 | 0.00676 | 49.70 | 0.336 |
| 4500 | 0.01740 | −8.54 | 0.00678 | 48.90 | 0.332 |
| 5500 | 0.02127 | −7.84 | 0.00680 | 48.11 | 0.327 |
| 6500 | 0.02514 | −7.04 | 0.00681 | 47.32 | 0.322 |
| 7500 | 0.02900 | −6.24 | 0.00683 | 46.42 | 0.317 |
| 8500 | 0.03287 | −5.44 | 0.00685 | 45.52 | 0.312 |
| 9500 | 0.03674 | −4.54 | 0.00687 | 44.51 | 0.306 |
| 10,000 | 0.03867 | −4.04 | 0.00689 | 43.95 | 0.303 |
| Evaporation temperature of CO2→0°C | |||||
| Heat load of NCL [kW] | Mass Flux of CO2 [kg/s] | Evaporation temperature of propane [°C] | Mass flux of propane [kg/s] | Enthalpy difference ∆h [kJ/kg] | Power of the compressor P [kW] |
| 500 | 0.02170 | −1.09 | 0.00696 | 40.55 | 0.282 |
| 1500 | 0.00650 | −0.51 | 0.00698 | 39.91 | 0.279 |
| 2500 | 0.01083 | +0.21 | 0.00700 | 39.15 | 0.274 |
| 3500 | 0.01516 | +0.91 | 0.00701 | 38.35 | 0.269 |
| 4500 | 0.01949 | +1.61 | 0.00703 | 37.58 | 0.264 |
| 5500 | 0.02382 | +2.31 | 0.00705 | 36.78 | 0.259 |
| 6500 | 0.02815 | +3.01 | 0.00707 | 36.05 | 0.255 |
| 7500 | 0.03248 | +3.81 | 0.00709 | 35.18 | 0.249 |
| 8500 | 0.03681 | +4.61 | 0.00711 | 34.31 | 0.244 |
| 9500 | 0.04114 | +5.51 | 0.00714 | 33.34 | 0.238 |
| 10,000 | 0.04331 | +6.01 | 0.00713 | 33.88 | 0.234 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pawłowski, M.; Gagan, J.; Butrymowicz, D. Assessment of Efficiency of Heat Transportation in Indirect Propane Refrigeration System Equipped with Carbon Dioxide Circulation Loop. Sustainability 2022, 14, 10422. https://doi.org/10.3390/su141610422
Pawłowski M, Gagan J, Butrymowicz D. Assessment of Efficiency of Heat Transportation in Indirect Propane Refrigeration System Equipped with Carbon Dioxide Circulation Loop. Sustainability. 2022; 14(16):10422. https://doi.org/10.3390/su141610422
Chicago/Turabian StylePawłowski, Mateusz, Jerzy Gagan, and Dariusz Butrymowicz. 2022. "Assessment of Efficiency of Heat Transportation in Indirect Propane Refrigeration System Equipped with Carbon Dioxide Circulation Loop" Sustainability 14, no. 16: 10422. https://doi.org/10.3390/su141610422
APA StylePawłowski, M., Gagan, J., & Butrymowicz, D. (2022). Assessment of Efficiency of Heat Transportation in Indirect Propane Refrigeration System Equipped with Carbon Dioxide Circulation Loop. Sustainability, 14(16), 10422. https://doi.org/10.3390/su141610422







